Visual Abstract
Keywords: calcium, central pattern generator, modeling, neuromodulation, stomatogastric
Abstract
In oscillatory circuits, some actions of neuromodulators depend on the oscillation frequency. However, the mechanisms are poorly understood. We explored this problem by characterizing neuromodulation of the lateral pyloric (LP) neuron of the crab stomatogastric ganglion (STG). Many peptide modulators, including proctolin, activate the same ionic current (IMI) in STG neurons. Because IMI is fast and non-inactivating, its peak level does not depend on the temporal properties of neuronal activity. We found, however, that the amplitude and peak time of the proctolin-activated current in LP is frequency dependent. Because frequency affects the rate of voltage change, we measured these currents with voltage ramps of different slopes and found that proctolin activated two kinetically distinct ionic currents: the known IMI, whose amplitude is independent of ramp slope or direction, and an inactivating current (IMI-T), which was only activated by positive ramps and whose amplitude increased with increasing ramp slope. Using a conductance-based model we found that IMI and IMI-T make distinct contributions to the bursting activity, with IMI increasing the excitability, and IMI-T regulating the burst onset by modifying the postinhibitory rebound in a frequency-dependent manner. The voltage dependence and partial calcium permeability of IMI-T is similar to other characterized neuromodulator-activated currents in this system, suggesting that these are isoforms of the same channel. Our computational model suggests that calcium permeability may allow this current to also activate the large calcium-dependent potassium current in LP, providing an additional mechanism to regulate burst termination. These results demonstrate a mechanism for frequency-dependent actions of neuromodulators.
Significance Statement
Oscillatory neurons respond to synaptic input in complex ways that depend on the polarity, amplitude, and rate of the input, and intrinsic properties of the cell. As a result, neuromodulator inputs that activate voltage-gated ionic currents can have indirect and state-dependent effects. We show that when a target of neuromodulation is a transient ionic current, an additional layer of complexity of the response emerges in which the oscillation frequency and the indirect influence of other ionic currents shape the amplitude and temporal properties of the neuronal response to the modulator.
Introduction
Neuron and network activity is tuned by neuromodulators that influence neuronal excitability and synaptic function, often through G-protein-coupled receptor signaling (Marder, 2012; Nadim and Bucher, 2014; Burke and Bender, 2019). An important aspect of this is the modulation of the gating properties of voltage-gated ion channels. The effect of activation or modulation of a voltage-gated current on the activity and response properties of a neuron depends on the complement, magnitude, and temporal trajectory of other currents, as neuron output is shaped by complex nonlinear interactions of multiple ionic mechanisms and their dependence and effect on the membrane potential (Taylor et al., 2009). As such, the contribution of each voltage-gated ionic current critically depends on the voltage trajectory, i.e., both the range of the membrane potential and its time-dependent changes, which are in turn influenced by synaptic inputs.
This dependence is particularly apparent in rhythmically active neurons. For example, thalamocortical neurons produce bursting oscillations arising from the T-type calcium current (ICaT), but only when the baseline membrane potential is hyperpolarized (Steriade and Contreras, 1995; Amarillo et al., 2014). Additionally, responses of bursting neurons critically depend on strength, frequency, short-term plasticity, and temporal trajectory of their synaptic input (Martinez et al., 2019). In many circuits, neurons burst on rebound from synaptic inhibition (Huguenard and McCormick, 2007; Bucher et al., 2015). The shape and strength of inhibitory input to such a neuron would produce very different effects if the rebound were because of a persistent current such as the persistent sodium current (INaP), a transient current such as ICaT, or a hyperpolarization-activated current such as Ih. While persistent currents show little dependence on the history of activity, the voltage and time dependence of channel inactivation makes the contribution of transient currents dependent on oscillation frequency and prior activation (Baukrowitz and Yellen, 1995; Roeper et al., 1997; Armstrong and Roberts, 2001; Carter and Bean, 2011).
Interactions between ionic currents and the amplifying or inhibitory effects of neuromodulators on individual currents can generate great flexibility in circuit operation. However, because of the complexity of such interactions, neuromodulation of any individual ionic current may produce effects that are not easily predictable. Here, we explored how the actions of neuromodulators may depend on the membrane potential trajectory of the target neuron and on the frequency of inputs it receives in an oscillatory network.
Neuromodulation has been extensively studied in oscillatory circuits such as the central pattern generators (CPGs) of the brain stem respiratory system (Doi and Ramirez, 2008; Ramirez and Baertsch, 2018), and the crustacean stomatogastric nervous system (STNS; Marder and Bucher, 2007; Stein, 2009; Daur et al., 2016), where a multitude of neuromodulators influence circuit activity patterns. The crustacean pyloric circuit is a well-studied CPG that produces oscillations in a broad range of frequencies. Pyloric oscillations are driven by pacemaker neurons that drive all follower neurons with strong inhibitory synapses. The follower neurons rebound from this inhibition to produce a burst of action potentials (Fig. 1A). Excitatory neuropeptides and muscarinic agonists activate a fast, voltage-dependent persistent current (the modulator-activated inward current, IMI), which is crucial for oscillatory activity in pacemaker neurons (Golowasch and Marder, 1992; Goaillard et al., 2010; Zhao et al., 2010; Bose et al., 2014). However, the effect of IMI on follower neurons, which can provide feedback to pacemaker neurons, is less understood. The strength, shape and frequency of inhibition influence the voltage trajectory of the burst response of follower neurons (Harris-Warrick et al., 1995a,b; Hooper, 1998; Kloppenburg et al., 1999; Martinez et al., 2019). Because this voltage trajectory determines the activation of all voltage-gated ionic currents, it also controls the levels of currents regulated by such modulators. Meanwhile, the modulatory current in turn influences the voltage trajectory.
Figure 1.
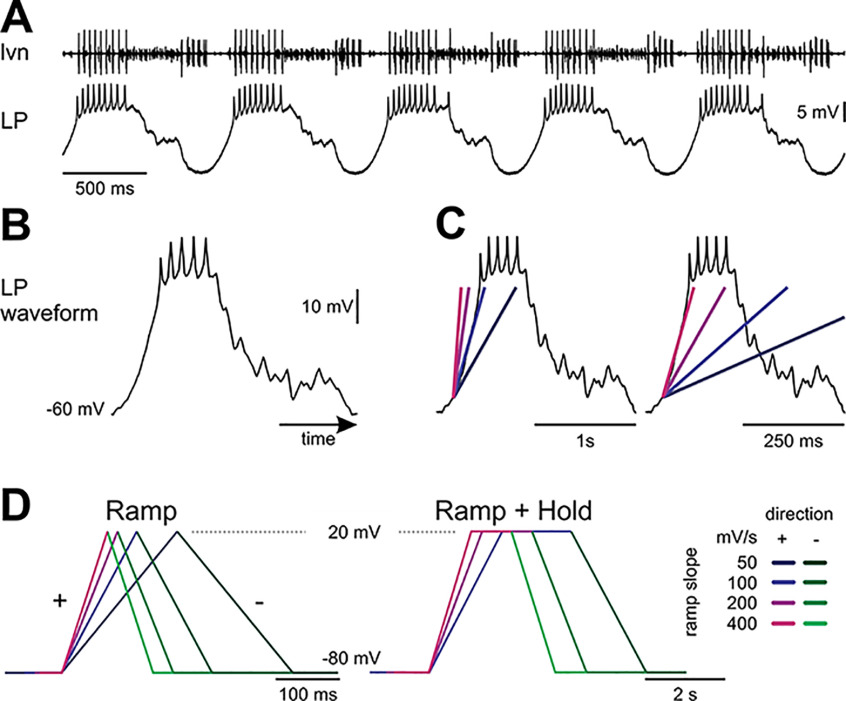
Voltage-clamp paradigms. A, Extracellular lateral ventricular nerve (lvn) and intracellular LP neuron recording. The lvn carries the axons of several neurons participating in the triphasic pyloric rhythm. The largest action potentials in the lvn recording are from the LP neuron. Different units can be recognized by different amplitudes. The follower neuron LP oscillates in time with the pyloric rhythm because of strong periodic inhibitory input and fires bursts of action potentials on rebound from inhibition. B, Canonical waveform of LP. This prerecorded waveform was used to drive LP’s membrane potential in voltage clamp to mimic a realistic LP neuron activity. In the voltage-clamp experiments, the slow-wave oscillation was scaled so that it ranged from a trough potential of −60 mV to −20 mV. C, LP’s depolarization rate can be approximated with different slopes (colored lines) for different pyloric cycle periods. D, These slopes were used to construct symmetrical ramp or ramp-and-hold stimuli to sample I-V relationships for proctolin-activated currents at different polarization rates, which roughly correspond to different cycle periods (Extended Data Fig. 1-1). The same color-code for slopes is used for all figures with purple colors for positive (+) ramps and green colors for negative (–) ramps.
Depolarization rates for different cycle periods of the unitary realistic LP voltage waveform. Download Figure 1-1, XLSX file (9.5KB, xlsx) .
Among the best studied neuropeptide modulators of the pyloric circuit is proctolin, which activates IMI in all but one pyloric neuron type (Swensen and Marder, 2001), including the lateral pyloric (LP) neuron. To address whether the actions of proctolin on the follower LP neuron vary dependent on circuit frequency, we used a variety of voltage-clamp paradigms. We measured the current–voltage (I-V) relationship of proctolin-activated currents with voltage ramps of different slopes that correspond to LP depolarization rates at different cycle frequencies and used realistic LP neuron waveforms applied at different cycle frequencies. We found that the proctolin-activated current is more complex than previously determined and contains an inactivating component. Using a computational model, we explored the possible role of this inactivating component and show that its frequency dependence can produce state-dependent effects at the circuit level.
Materials and Methods
Solutions
Cancer borealis saline contained the following: 440 mm NaCl, 26 mm MgCl2, 13 mm CaCl2, 11 mm KCl, 10 mm Tris base, and 5 mm maleic acid, buffered to pH 7.4–7.5. Custom synthesized Proctolin (RS Synthesis, sequence RYLPT) was dissolved in distilled water and stored as 10−3 m aliquots at −20°C. Immediately before usage, proctolin stock was diluted in saline to a final concentration of 10−6 m. To prevent neurons from spiking during voltage-clamp experiments, we added 10−7 m tetrodotoxin (TTX; Alomone Labs), stored as 10−4 m stock solution in distilled water at 4°C, to the saline to block voltage-dependent Na+ currents. In some experiments, we added 2 × 10−4 m Cd2+ to the saline to block Ca2+ channels (Golowasch and Marder, 1992).
Electrophysiology
Male Jonah crabs (C. borealis) were anesthetized by placing them in ice for at least 30 min. Their STNS was dissected as described previously (Gutierrez and Grashow, 2009) and pinned dorsal side up in a Sylgard (Ellsworth Adhesives) lined Petri dish. The sheath around the stomatogastric ganglion (STG) was removed with fine tungsten pins to facilitate electrode penetration and chemical uptake by the neurons. The STG was constantly perfused with 10–13°C saline during the experiments. We recorded the pyloric rhythm for cell identification with stainless steel pin electrodes inside Vaseline wells built around the lateral ventricular nerve (lvn). Extracellular electrodes were connected to a differential AC amplifier (Model 1700, AM Systems). LP was identified by matching its intracellularly recorded activity to the extracellularly recorded pyloric rhythm (Fig. 1A).
We used the two-electrode voltage-clamp technique to measure proctolin-activated currents in the soma of the LP neuron. Electrodes were pulled from borosilicate capillaries with filament and filled with 0.6 m K2SO4 + 20 mm KCl (resistance: 20–25 MΩ). Intracellular signals were amplified (Axoclamp 900A, Molecular Devices), and all recordings digitized at 5 kHz (Digidata 1440A, Molecular Devices) and recorded with Clampex 10.6 (Molecular Devices). Voltage-clamp waveforms were created with MATLAB (R2019a; MathWorks) and delivered via Clampex.
To measure the proctolin-activated currents, we removed all intrinsic neuromodulators by transecting the stomatogastric nerve (nerve that carries the axons of all modulatory projection neurons from central ganglia) and/or by perfusing the STG with 10−7 m TTX saline to block action potentials, which prevents transmitter release from the terminals of modulatory projection neurons.
To apply proctolin, we built a separate Vaseline well around the STG and superfused the drug only on the STG to reduce application and wash times. We waited at least 10 min after cessation of action potentials before starting voltage-clamp measurements in control condition. Proctolin-activated currents (henceforth proctolin currents, IProc) were calculated as the difference between total currents measured in normal saline and in the presence of 10−6 m proctolin (IProc = Imod − Ictrl; Golowasch and Marder, 1992). Proctolin currents were measured after at least 10 min of proctolin bath application.
During an ongoing pyloric rhythm, LP produces bursts of spikes on top of slow-wave oscillations (Fig. 1A,B) with periods typically ranging from 0.5 to 2 Hz across experiments. We approximated LP’s depolarization rate at different cycle frequencies as linear ramps (Fig. 1C) with slopes ranging from 50 mV/s to 400 mV/s (Extended Data Fig. 1-1).
To measure the I-V relationship of proctolin currents, we voltage clamped the LP neuron at −80 mV and ramped its voltage symmetrically from −80 to +20 mV [positive (+) ramp] and back to −80 mV [negative (–) ramp] with different slopes (Swensen and Marder, 2000; Garcia et al., 2015; Fig. 1D, left). We repeated each triangular ramp five times with 5 s intervals in between, during which time the cell was held at −80 mV. In these measurements, we assumed fast activation of the proctolin currents (Golowasch and Marder, 1992), and assumed that the current measured in the negative ramp excluded currents that inactivated during the positive ramp. Since the proctolin current is a difference current, unmodulated currents are removed by the subtraction and do not contribute to either of the thus measured currents on the positive or negative ramps. To measure the proctolin-activated current in the absence of Ca2+ as done previously (Golowasch and Marder, 1992), we blocked Ca2+ with 200 μm Cd2+ (Sigma-Aldrich), added to the saline both in control and in the presence of proctolin.
To ensure complete exclusion of the inactivating proctolin currents during the negative ramp I-V relationship, in some experiments we used the same voltage range and slopes as before but held the voltage at +20 mV between the positive and negative ramps. Additionally, these ramp-and-hold waveforms were repeated until the I-V relationships reached a steady state. Thus, in these experiments the positive and negative ramps each contributed to 25% of one stimulus cycle; after the positive ramp, the voltage was held at +20 mV for 25% of the cycle, and after the negative ramp at −80 mV for 25% of the cycle, and this waveform scaled with ramp slope (Fig. 1D, right). Each ramp-and-hold stimulus was repeated 30 times.
We also measured IProc with realistic LP neuron voltage waveforms. A realistic unitary waveform was obtained by recording a typical LP neuron cycle of activity, averaging 10 cycles, and scaling the voltage so that the slow-wave amplitude ranged from −60 to −20 mV (Fig. 1B). The unitary waveform was applied periodically (for 20 cycles with cycle periods between 250 ms and 2 s, depolarization rates are listed in Extended Data Fig. 1-1) to the voltage-clamped LP neuron in control and proctolin-containing saline. The same realistic unitary waveform was used in all experiments.
Data were discarded if the LP neuron input resistance dropped below 5 MΩ during the experiment, if electrode offset was greater than ±5 mV at the end of the experiment, or if no inward difference current was present at the peak of the realistic waveforms.
Analysis
All data were analyzed with custom written MATLAB scripts. Raw traces were first smoothed with a Savitzky–Golay filter (polynomial order: 5; frame length: 51 for V, 101 for I). Then, we subtracted the currents measured in control condition from the currents measured in the presence of proctolin to get the proctolin currents IProc. We averaged the last three stimulation cycles for the ramp stimulations, and the last five cycles for the ramp-and-hold stimulations. We fitted the averaged IProc separately for the positive ramps and negative ramps with a logistic equation:
where V is the membrane potential, g the maximal conductance, Erev the reversal potential, V½ the half-maximal activation voltage, and the activation slope factor. We then used these fits to identify the maximum inward current (Imax) and the corresponding voltage (VImax) at Imax at different slopes (Fig. 2B,Ci).
Figure 2.
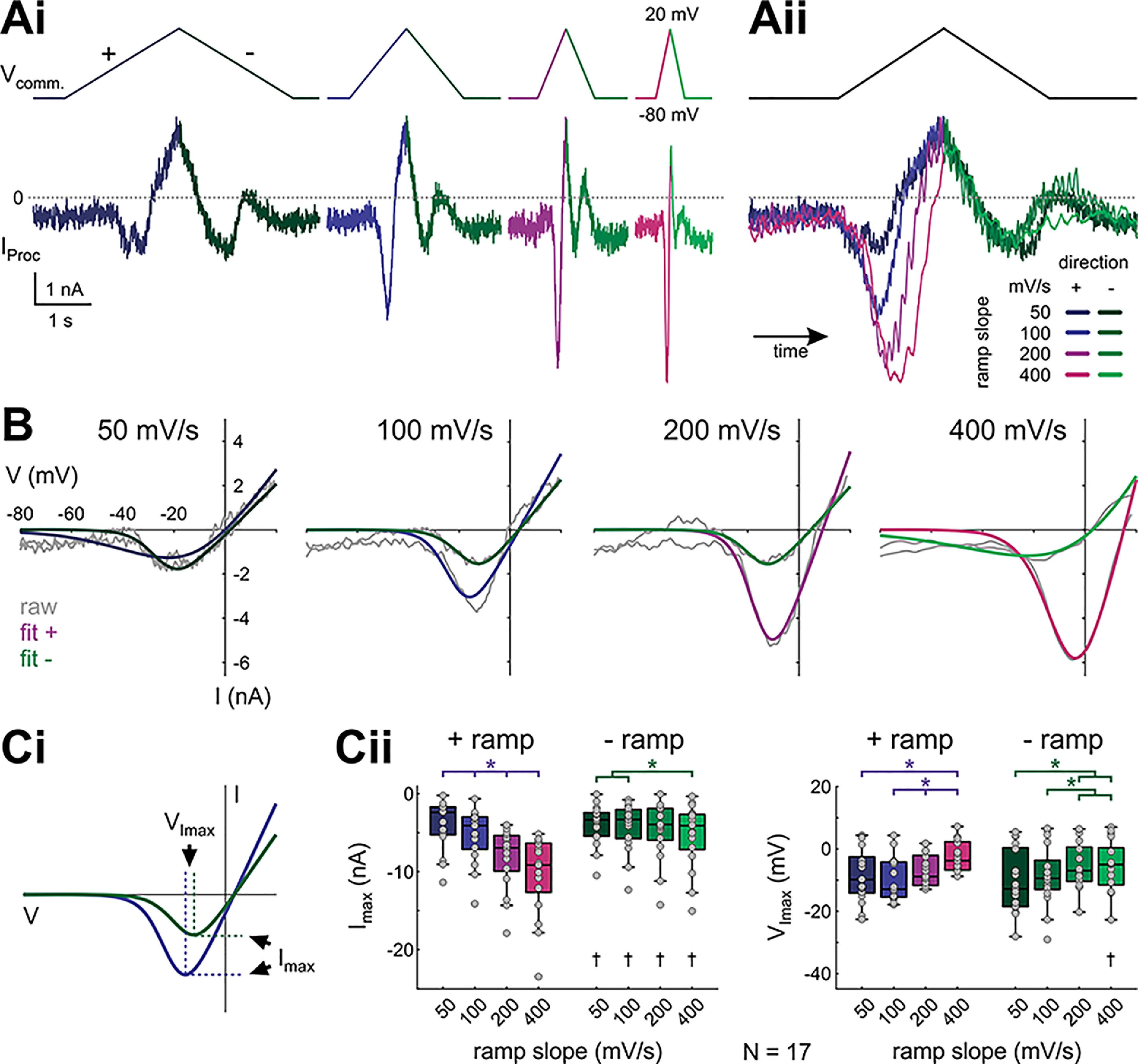
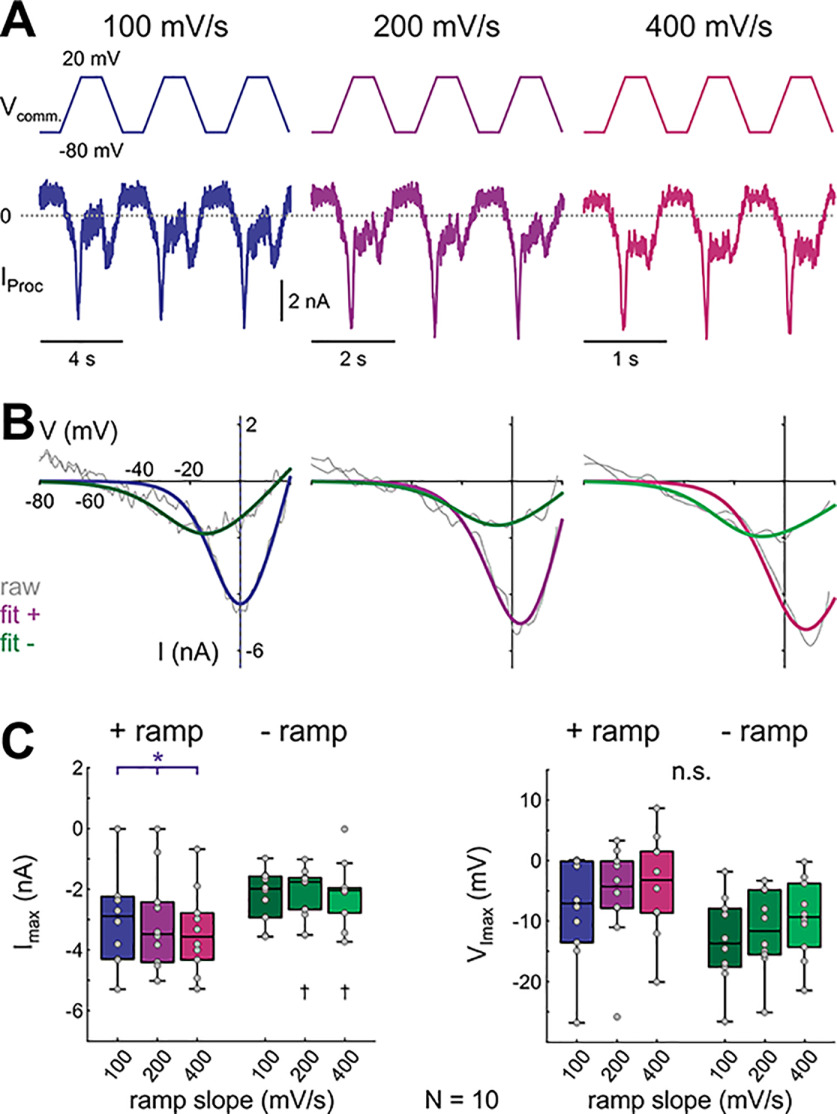
Proctolin-activated currents depend on ramp slope and direction. Ai, Proctolin-activated currents (IProc) evoked by symmetrical ramp stimulations with four different slopes (color-coded for ramp steepness and ramp direction), averaged over the last three (out of five) sweeps from one experiment. Aii, Overlay of the proctolin currents shown in Ai, normalized by time. B, I-V curves for IProc shown in A, separated by ramp slope. Gray curves show raw recordings, colored curves show logistic fits that were used to smoothe the raw data. C, Quantitative analysis of the peak inward current Imax (Cii, left, indicated by dashed horizontal lines in Ci) and voltage at peak inward current VImax (Cii, right, indicated by dashed vertical lines in Ci) for different ramp slopes and ramp directions (N = 17). Dots represent data from individual experiments. Imax and VImax are both sensitive to ramp slope on the + ramp. On the – ramp, Imax and VImax are only significantly different between extreme slope differences (two-way RM ANOVA; Table 1; results in Extended Data Fig. 2-1). Asterisks indicate significant differences between slopes within the same direction, daggers indicate significant differences between directions within the same slope at α = 0.05.
Two-way RM ANOVA for initial state I-V parameters. α = 0.05. Direction: positive or negative. Slope (in mV/s): 50, 100, 200, 400. Data for VImax failed normality and equal variance tests. Download Figure 2-1, XLSX file (9.7KB, xlsx) .
Data for panel Cii. Download Figure 2-2, XLSX file (12.7KB, xlsx) .
To calculate the time constant for the slow inactivation, we fitted the normalized, integrated IProc across the 30 ramp-and-hold sweeps with an exponential decay function:
where t is time and IProc (t0) and IProc (∞) are, respectively, the initial and steady state value of IProc.
To measure IProc acquired with the realistic waveform stimulations, the current was baseline subtracted and filtered (Savitzky–Golay filter, polynomial order: 3, frame length: 901). Baseline current was measured as the average current in the 2 s before the start of stimulation. IProc was averaged for the last five cycles of stimulation, and we obtained Imax as well as the phase of Imax with LP trough potential as reference.
All statistical analyses were performed in SigmaPlot 12.0 (Systat Software). For parameters obtained from ramp and ramp-and-hold stimulations, we used two-way repeated measures ANOVA (RM ANOVA) to test for effects of ramp slope (in mV/s: 50, 100, 200, 400), ramp direction (positive, negative), and interaction between the two factors. For the maximum inward current and phase of the maximum inward current obtained from realistic waveform stimulations, as well as the ratio of slow inactivation across ramps, we used one-way RM ANOVA. We compared time constants of slow inactivation across ramps with one-way ANOVA on ranks. To compare changes in Imax between normal and Cd2+- saline we used two-way ANOVA. We used Tukey’s post hoc test for all pairwise comparisons. Data passed all tests for normality (Shapiro–Wilk) and equal variance (Levene’s test) unless noted otherwise. Significance level is α = 0.05. Results of statistical tests and raw data are provided in Extended Data Figures 2-1, 3-1, 3-2, 4-1, 5-1, 7-1, 8-1, 8-2, 8-3, and 2-2, 3-3, 4-2, 5-2, 7-2, 8-4, 8-5, 8-6, 9-1, respectively. An overview of the statistical tests is provided in Table 1.
Table 1.
Statistical tests
| Source | Data structure | Type of test | Power or [25%, 75%] | |
|---|---|---|---|---|
| Fig. 2 | I max | Normal | Two-way RM ANOVA | Sign: 1 |
| Speed: 1 | ||||
| Interaction: 1 | ||||
| Fig. 2 | V Imax | Non-normal | Two-way RM ANOVA | Sign: 0.05 |
| Speed: 1 | ||||
| Interaction: 0.808 | ||||
| Fig. 3 | Steady/initial state | Normal | RM ANOVA | 0.999 |
| Fig. 3 | τ | Non-normal | ANOVA on ranks | 100 mV/s: [3.3, 16.55] |
| 200 mV/s: [3.7, 11.98] | ||||
| 400 mV/s: [3.15, 3.93] | ||||
| Fig. 4 | I max | Normal | Two-way RM ANOVA | Sign: 0.622 |
| Speed: 0.067 | ||||
| Interaction: 0.449 | ||||
| Fig. 4 | V Imax | Normal | Two-way RM ANOVA | Sign: 0.452 |
| Speed: 0.333 | ||||
| Interaction: 0.05 | ||||
| Fig. 5 | I max | Normal | RM ANOVA | 1 |
| Fig. 5 | φImax | Normal | RM ANOVA | 0.998 |
| Fig. 7 | I max | Normal | Two-way RM ANOVA | Sign: 0.05 |
| Speed: 0.05 | ||||
| Interaction: 0.089 | ||||
| Fig. 7 | V Imax | Normal | Two-way RM ANOVA | Sign: 0.878 |
| Speed: 0.05 | ||||
| Interaction: 0.05 | ||||
| Fig. 8 | I max | Normal | Two-way RM ANOVA | Sign: 0.709 |
| Speed: 0.996 | ||||
| Interaction: 0.672 | ||||
| Fig. 8 | V Imax | Normal | Two-way RM ANOVA | Sign: 0.379 |
| Speed: 0.206 | ||||
| Interaction: 0.543 | ||||
| Fig. 8 | Cd2+ slopes | Non-normal | Two-way ANOVA | Sign: 0.05 |
| Saline: 0.351 | ||||
| Interaction: 0.068 | ||||
| Fig. 8 | I Proc(max) | Normal | Two-way RM ANOVA | State: 0.465 |
| Speed: 0.446 | ||||
| Interaction: 0.232 | ||||
Modeling the voltage-clamp currents
The previously identified persistent current activated by proctolin has been found to be the same current as the persistent inward current activated by other modulators (Golowasch and Marder, 1992; Swensen and Marder, 2000) and thus later named the modulator-activated inward current, IMI. Here, the steady-state IProc was modeled as a sum of two currents, the persistent current IMI and a transient current IMI-T:
where the kinetic variables (mMI, mMI-T and hMI-T—denoted as x) obeyed standard Hodgkin–Huxley style kinetics:
| (1) |
The parameters for the model are provided in Table 2. The slowly decaying current was modeled by modeling IMI-T as a (putative) calcium current using the Goldman–Hodgkin–Katz formalism:
| (2) |
where PCa is the total permeability of the current, mCa and hCa are activation and inactivation variables obeying Equation 1, vol is the volume of the microdomain influencing the current, F is Faraday’s constant, R is the universal gas constant and T is temperature. [Ca] is the calcium concentration outside (out) and inside (in) the cell. The internal calcium concentration obeyed the equation
| (3) |
where ICa denotes the total calcium current flowing into the cell (in this case, ICa = IMI-T) and [Ca]∞ denotes the steady state calcium concentration inside the cell, and P1 is the maximal per cluster permeability of ICa and P is the total permeability over all clusters of interest (Taylor et al., 2009). The parameters of IMI-T(Ca) were PCa = 0.014 cm/s, T = 283.15 K, [Ca]out = 13 mm, P1 = 1.1675 μm3/s, P = 0.0369 cm/s, vol = 6.49 μm3, [Ca]∞ = 0.02 mm, h∞([Ca]) = 1/(1+([Ca]/0.015)4) and τCa = 12 s.
Table 2.
Parameters of the steady-state model of the proctolin-activated current
| Variable/parameter | Value |
|---|---|
| MI, MI-T (nS) | 0.125, 1.00 |
| EMI, EMI-T (mV) | 35, 24 |
| mMI∞(V) | |
| τ mMI (V) | 2 |
| mMI-T∞(V) | |
| τ mMI-T (V) | |
| hMI-T∞(V) | |
| τ hMI-T (V) |
In this table, S(x) denotes the logistic sigmoid function 1/(1+exp(–x)). Time constants are in milliseconds.
The LP model neuron
LP model implementation
An LP inspired model was adapted from Taylor et al. (2009), reduced to two compartments: a soma/neurite and an axon. We built this model explicitly as a two-compartment model rather than using neuron’s in-built compartmentalization process. The two compartments were each built to have a diameter and length of 200 μm and were coupled with a conductance of 0.15 μS. The soma/neurite currents included were Ileak, IA, Ih, ICa, IK(Ca), IMI, and IMI-T. Intracellular calcium accumulation was tracked in the soma/neurite compartment according to Equation 3. The ionic currents included in the axon were Ileak, INa, and IK. Except for ICa, all currents were modeled in the standard Hodgkin–Huxley formalism as:
where X denotes the current name, Ex is the reversal potential and mx and hx respectively denote the current activation and inactivation (obeying Eq. 1) with appropriate powers, a and b. ICa was modeled as in Equation 2. The reversal potentials (in mV) for the ionic currents were set to ENa = 50, EK = EA = −80, Eh = −10, Eleak = −55, EMI = −10, EMI-T = −16. The maximal conductances (in μS/mm2) were set to , , , , , , , , and . The values of and were adjusted as described in the figure legends. The membrane capacitance (in μF/cm2) was set to 0.795 (axon) and 3.183 (soma/neurite). The parameters of ICa were PCa = 0.00187 nm/ms, T = 283.15 K, [Ca]out = 13 mm, P1 = 1.168 μm3/s, P = 0.0467 nm/ms, vol = 6.49 μm3. The equations for the ionic currents are given in Table 3.
Table 3.
LP neuron model equations
| m ∞ | τm | h ∞ | τh | Compartment | ||
|---|---|---|---|---|---|---|
| I A | m 2 h | 15 | 100 | Soma/neurite | ||
| I Ca | m 2 h | 100 | Soma/neurite | |||
| I h | m 2 | 200 | - | - | Soma/neurite | |
| I K(Ca) | mh | 100 | 10 | Soma/neurite | ||
| I MI | m | 2 | - | - | ||
| I MI-T | m 3 h | Soma/neurite | ||||
| I Na | m 3 h | 2 | 5 | Axon | ||
| I K | m 4 | - | - | Axon |
In this table, S(x) denotes the logistic sigmoid function 1/(1+exp(–x)), f+(x) denotes the positive part of f(x) (with the negative portions set to 0), voltage (v) is in mV, intracellular calcium concentration ([Ca]in) is in millimolar, and time constants (τm, τh) are in milliseconds.
Inhibitory synaptic input was modeled as a symmetric triangular conductance waveform with a duty cycle of 0.5, a maximum value of 1 μS/mm2 and a reversal potential of −80 mV. The model was then manually tuned to produce an LP-like voltage waveform.
Frequency effects on the model LP neuron
Modulator receptors are thought to be localized far away from the soma (Golowasch and Marder, 1992). It is reasonable to assume that, in a voltage-clamp experiment, voltages in distal compartments are different from the somatic clamped voltage. To account for this, we shifted the voltage dependencies of equations describing the parameters of IMI-T in our model LP neuron. This shift was estimated by adjusting the model for the steady state ramp-and-hold to respond as if IMI and IMI-T were expressed in a compartment ∼0.3 length constants away from the soma, rather than in the soma (fitting not shown). All simulations of the model LP neuron were done with these shifted values (Table 3).
To examine the frequency-dependent effects of IMI and IMI-T versus IMI or IMI-T alone, we built three different models and matched the spike numbers in all three models at a cycle frequency of 1 Hz. We then modified the cycle frequency of the synaptic input in each model and examined the effect of the cycle frequency in each case. Activity was simulated for 20 cycles to reach a steady state, with only the last four cycles considered for analysis. The bursting attributes we measured were phase (relative to the peak of the synaptic conductance input) and instantaneous spike frequency (defined as the reciprocal of the inter-spike interval). Simulations were done in the Python NEURON (version 7.7.2) environment (Carnevale and Hines, 2006), and analyses were performed using custom Python scripts.
The code described in the paper is freely available online at https://github.com/fnadim/IMI-T and also as the Extended Data 1.
The codes used in the study. Download Extended Data 1, ZIP file (4.9MB, zip) .
Results
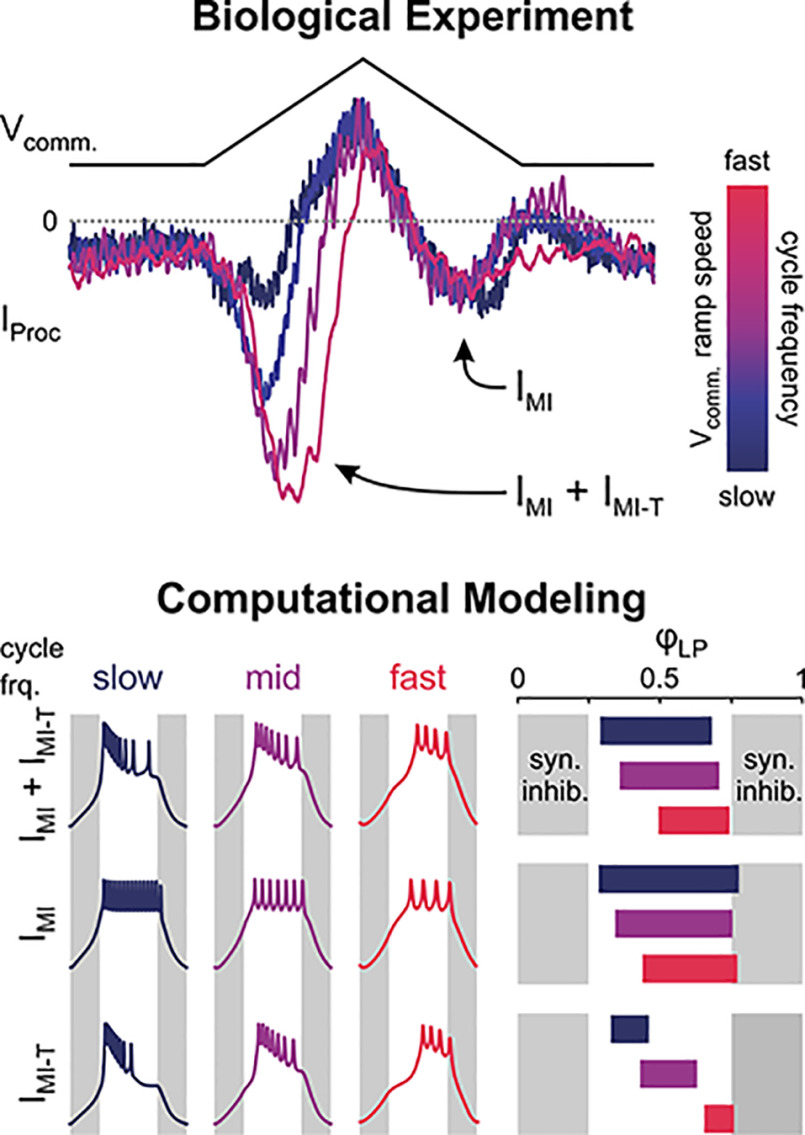
Previous measurements of peptide neuromodulation of pyloric neurons demonstrated that multiple peptides activate a fast voltage-dependent persistent inward current, IMI (Swensen and Marder, 2000), which was first characterized as a proctolin-activated current in the LP neuron (Golowasch and Marder, 1992). Here, we explored the possibility that modulatory neuropeptides may activate additional currents in pyloric neurons that would allow their modulatory effect to be sensitive to the frequency of oscillations and thus increase the dynamic range of neuromodulatory responses of these cells.
The amplitude of IProc is sensitive to the slope and direction of voltage ramps
During an ongoing pyloric rhythm, the LP neuron membrane potential expresses slow-wave oscillations in time with the pyloric rhythm (Fig. 1A). We approximated the LP neuron waveform (Fig. 1B) slow-wave depolarization slope at different cycle periods (Fig. 1C) and measured the proctolin-activated current IProc with ramp voltage protocols with corresponding slopes (Fig. 1D; Extended Data Fig. 1-1; see Materials and Methods).
With both positive and negative voltage ramps, proctolin elicited a voltage-gated inward current (IProc), which had a similar appearance for all ramp slopes (Fig. 2A). However, the maximum magnitude (Imax) of IProc was larger on the positive ramp than on the negative ramp. Furthermore, the magnitude of the current was sensitive to the slope of the positive ramp, with larger slopes eliciting larger currents (Fig. 2, raw difference currents of one example experiment in A, corresponding I-V curves with fits in B, quantification in C). For the negative ramp, Imax was mostly independent of slope value, except for the largest slope of 400 mV/s. Additionally, the voltage (VImax) at which Imax was attained was more depolarized for larger slopes on the positive ramp, and less so on the negative ramp (Fig. 2C; two-way RM ANOVA results in Extended Data Fig. 2-1). Together, these data suggested that IProc includes both a persistent and a transient (inactivating) component. Both components activated with the positive ramp, but the negative ramp elicited mostly the persistent component because, by this time, the other component had inactivated. The presence of these two components would explain (1) the difference between the current amplitudes on the positive and negative ramps; (2) the slope dependence of the current amplitude on the positive ramps; (3) the fact that the largest negative ramp slope also revealed a larger current compared with other negative ramps, likely because of incomplete inactivation of the transient component; and (4) the shift of VImax to more depolarized values for larger slopes because with these more depolarized voltages are reached in a shorter amount of time, before complete inactivation of the transient component.
The component of IProc measured with negative ramps was (mostly) independent of ramp slope and qualitatively matched the previously described IMI (Golowasch and Marder, 1992; Swensen and Marder, 2000; Goaillard et al., 2009; Gray and Golowasch, 2016). Therefore, we will refer to this persistent component as IMI, and to the inactivating (transient) component as IMI-T. Thus, the negative ramp current consists primarily of IMI, whereas the positive ramp current consists of IMI + IMI-T.
IProc has an additional, slow inactivating component
In the ramp measurements (Fig. 2), we allowed a 5 s time interval between ramps, so that the currents measured could recover from any inactivation. Hence, there was little difference between currents in subsequent identical ramp measurements. However, in normal biological conditions, the pyloric rhythm is active continuously and, therefore, IProc would be at some steady-state level of inactivation. To measure the steady-state levels of IMI and IMI-T, we applied symmetric ramp-and-hold stimuli repetitively for 30 cycles in a separate set of experiments (Fig. 3A). We switched to a ramp-and-hold protocol, expecting that the addition of a depolarized hold interval between the positive and negative ramp would allow for full inactivation of any inactivating component and, therefore, a better separation of IMI and IMI-T.
Figure 3.
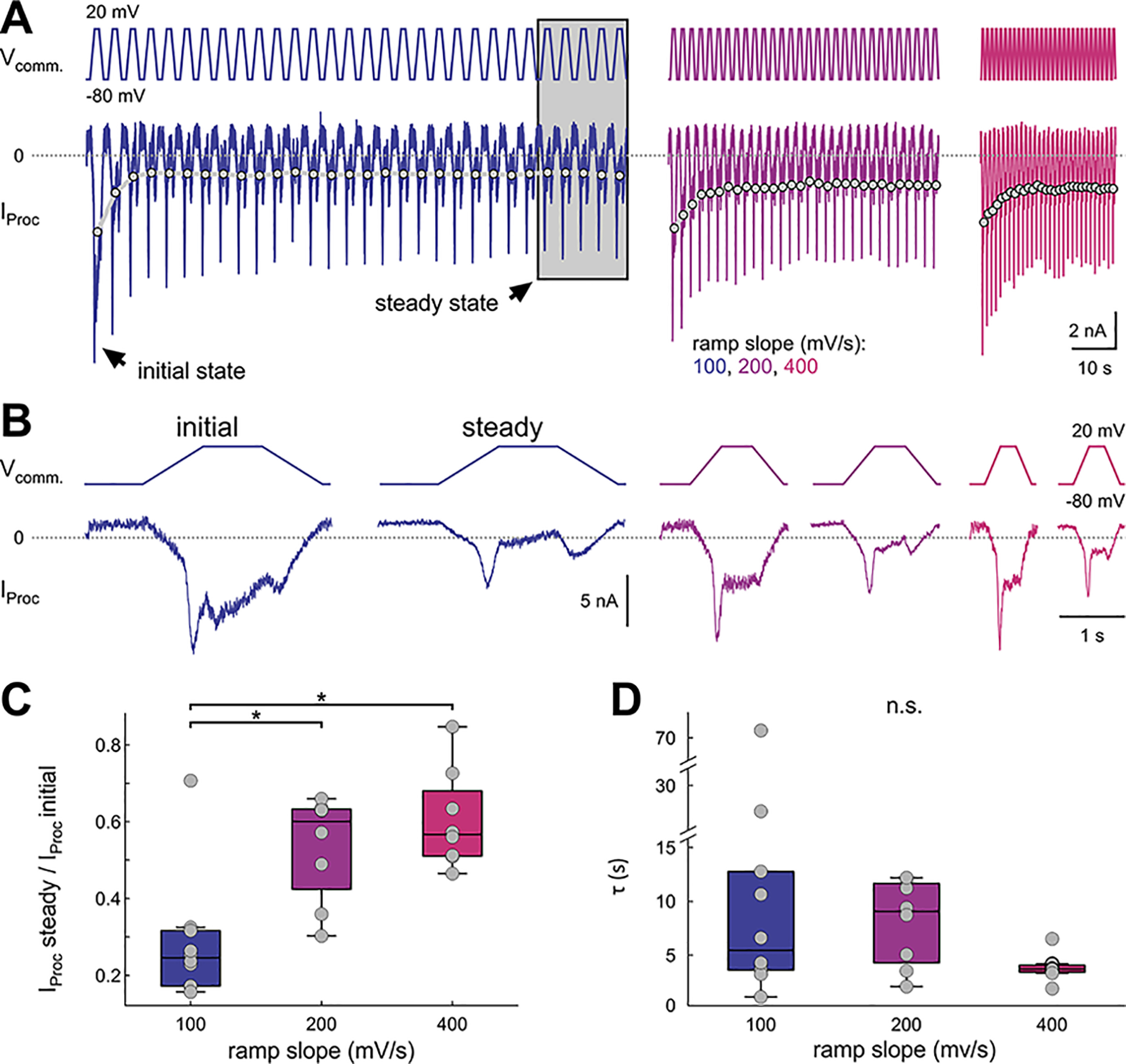
Proctolin-activated currents show slow inactivation. A, Proctolin-activated currents (IProc) in response to 30 sweeps of ramp-and-hold stimuli with different slopes (color-coded). The gray dots connected by lines depict the average IProc for each sweep in this experiment. We refer to IProc during the first sweep as initial state, and to the average of the last five sweeps as steady state (gray box). B, First (initial state) and averaged last five (steady state) sweeps from the experiment in A. C, Ratio of IProc between steady state and initial state. The slow inactivation of IProc is greater at 100 mV/s ramps compared with 200 and 400 mV/s ramps (RM ANOVA; Table 1; results in Extended Data Fig. 3-1). Each dot represents an individual experiment. D, Time constants for slow inactivation. Each dot represents an individual experiment. Time constants were not significantly different between slopes (ANOVA on ranks; Table 1; results in Extended Data Fig. 3-2). Asterisks indicate significance at α = 0.05. n.s. indicates no significant changes.
One-way RM ANOVA for the steady/initial state ratios of IProc. α = 0.05. Slopes (in mV/s): 100, 200, 400. Missing N: 200 mV/s: 2; 400 mV/s: 2. Download Figure 3-1, XLSX file (9.4KB, xlsx) .
One-way ANOVA on ranks for the time constant of the slow inactivation. α = 0.05. Slope (in mV/s): 100, 200, 400. Missing N: 200 mV/s: 2; 400 mV/s: 2. Download Figure 3-2, XLSX file (9.4KB, xlsx) .
Data for panels C, D. Download Figure 3-3, XLSX file (11.1KB, xlsx) .
The repeated depolarization in this longer protocol revealed a clear slow reduction in the amplitude of the total current (Fig. 3; raw difference currents across all sweeps of one experiment in A, initial and steady state sweeps of the same experiment in B, quantification of the levels of slow inactivation in C and of the time course in D). We refer to the response to the first depolarizing ramp-and-hold stimulus in each run as the initial state, and to the average of the last five responses as steady state (Fig. 3A,B). The distinction between the positive and negative ramp currents was present both in the initial state and at steady state (Fig. 3A,B). The first stimulus produced a current that was comparable to the currents we measured with triangular ramps and analyzed in Figure 2, and therefore we do not repeat that analysis here. To quantify the slow change, we measured the average inward current amplitude during each stimulus (Fig. 3A, gray dots connected by lines). A comparison of the initial response amplitude with that at steady state showed a slope-dependent reduction in amplitude for all ramp slopes (Fig. 3C; statistical comparisons in Extended Data Fig. 3-1). Note that this reduction in amplitude was very slow, in the range of several seconds (Fig. 3D) and therefore distinct from the fast inactivation effect that distinguished the positive and negative ramp currents. The time constant of the reduction of the current amplitude at this slow timescale did not depend on the steepness of the ramp slope (ANOVA on ranks; results in Extended Data Fig. 3-2).
We explored the effect of ramp slopes at steady state (Fig. 4, raw difference currents of three steady state cycles of one experiment in A, corresponding I-V curves with fits in B, quantification in C) as in the triangular ramp experiments without a depolarized hold interval. Generally, the steady-state I-V curves showed the same slope and directional dependencies as in the simple ramp currents described in Figure 2 (Fig. 4B,C; two-way RM ANOVA results in Extended Data Fig. 4-1), with one exception: Imax and VImax values at steady state on the negative ramp no longer showed slope dependence, probably because this difference was due to incomplete inactivation of the transient component with the triangular ramps.
Figure 4.
Steady-state levels of the proctolin-activated currents elicited by a periodic ramp-and-hold stimulus depend on ramp slope and direction. A, Proctolin-activated currents (IProc) in response to the last three of 30 sweeps of ramp-and-hold stimuli with different slopes (color-coded). Data are from the same experiments as Figure 3A. B, Steady-state I-V curves for different ramp slopes (color-coded) from one experiment (same experiment as in A). Gray lines show raw current recordings, colored lines show logistic fits that were used to smoothe the raw data. C, Quantitative analysis of Imax (left) and VImax (right) for different ramp slopes and ramp directions (N = 10). Dots represent data from individual experiments. Imax is sensitive to ramp slope on the + ramp but not to the – ramp (two-way RM ANOVA; Table 1; results in Extended Data Fig. 4-1). Asterisks indicate significant differences between slopes within the same direction, daggers indicate significant differences between directions within the same slope at α = 0.05. n.s. indicates no significant changes.
Two-way RM ANOVA for steady state I-V parameters (ramp-and-hold). α = 0.05. Direction: positive or negative. Slope (in mV/s): 100, 200, 400. Download Figure 4-1, XLSX file (9.6KB, xlsx) .
Data for panel C. Download Figure 4-2, XLSX file (10.5KB, xlsx) .
Together, these findings led to two conclusions. First, IProc has a slowly inactivating component, with a time constant of several seconds, that diminishes the total current activated and measured across frequently repeated stimuli until it reaches stable levels at steady state. Second, even at steady state, IProc has a persistent component (IMI) and a component that inactivates rapidly during depolarizing ramps (IMI-T).
The amplitude of IProc is sensitive to the cycle period of the pyloric rhythm
The I-V curves revealed that IProc was most sensitive to the depolarizing slope. Because the pyloric rhythm operates over a large range of cycle periods (Bucher et al., 2005), and the shape of the voltage waveform (e.g., rising and falling slopes) is influenced by this period, the size of the inward current activated by proctolin would also be expected to be influenced by the period. We, therefore, measured how the cycle period of the LP waveform influenced the total current activated by proctolin. To do so, we repeatedly played back a prerecorded LP voltage waveform scaled to, and applied at, different cycle periods in the voltage-clamped LP neuron, in control and in the presence of proctolin, and measured IProc as the difference current (Fig. 5A). We used periods of 250–2000 ms (4–0.5 Hz), which corresponds to rates of membrane potential rise of ∼100–950 mV/s (see Fig. 1C; Extended Data Fig. 1-1).
Figure 5.
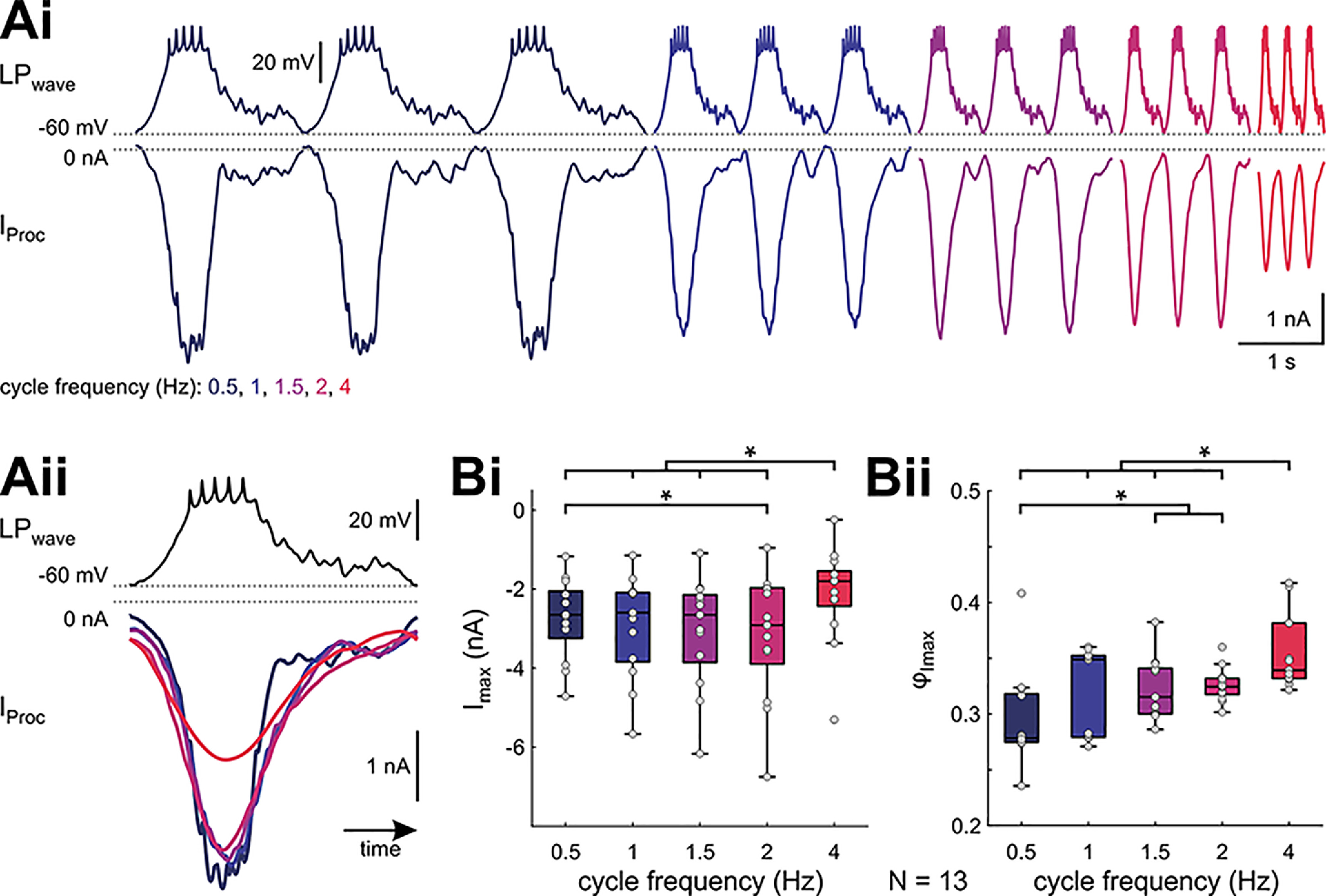
Slope-sensitivity of proctolin-activated currents is different during ongoing LP activity. Ai, The last three (of 20) sweeps of the proctolin-activated currents IProc in response to voltage clamping with a realistic LP waveform. Shown is one experiment at different cycle frequencies (color-coded). Aii, Overlay of the averages of the last five cycles (same experiment as Ai), normalized to time. B, Imax and phase of Imax (ϕImax) are sensitive to cycle frequency (RM ANOVA; Table 1; results in Extended Data Fig. 5-1). Dots represent data from individual experiments. Asterisks indicate significant differences between frequencies at α = 0.05.
RM ANOVA for parameters obtained with realistic waveform stimulation. Download Figure 5-1, XLSX file (9.5KB, xlsx) .
Data for panel B. Download Figure 5-2, XLSX file (10.2KB, xlsx) .
Based on our ramp and ramp-and-hold measurements we expected that IProc would increase with increasing waveform cycle frequency (or shorter cycle period), which corresponds to an increase in its depolarization slope. There was a small increase in the average IProc amplitude as cycle frequency was increased up to 2 Hz (Fig. 5Bi), but this increase was not observed in every experiment (Fig. 5Aii). Surprisingly, and contrary to our expectation from the ramp measurements, the peak IProc value (Imax) was significantly smaller for the highest frequency tested (4 Hz; Fig. 5Bi; RM ANOVA results in Extended Data Fig. 5-1). Finally, the phase (peak time relative to the trough potential divided by period) at which Imax was measured at each period got slightly but significantly delayed at the higher cycle frequencies (Fig. 5Bii).
IMI-T explains the observed frequency dependence of proctolin effects
Our findings so far led to three observations on IProc in the LP neuron. (1) Ramps activate a current whose amplitude depends on the steepness and sign of the slope. (2) Realistic waveforms produce a current whose amplitude somewhat increases with increasing cycle frequencies (and thus larger positive slopes) up to 2 Hz but decreases at the highest frequency tested (4 Hz) in contrast to what is predicted from the ramp experiments. (3) The size of the current decreases gradually to a steady state over a timescale of several seconds when stimuli are repeated at frequencies consistent with pyloric cycle frequencies.
To see how these observations could be explained by proctolin activating voltage-dependent currents, we resorted to computational modeling. We first examined the steady-state effects of the ramp-and-hold protocols. We found that the steady-state slope-dependent effects of the data could be explained assuming that proctolin activated two voltage-gated currents (Fig. 6A). This match required that at least one of the two currents (which we have referred to as IMI-T) be an inactivating current but could not be explained with a single persistent inward current that has been previously described (Golowasch and Marder, 1992; Swensen et al., 2000).
Figure 6.
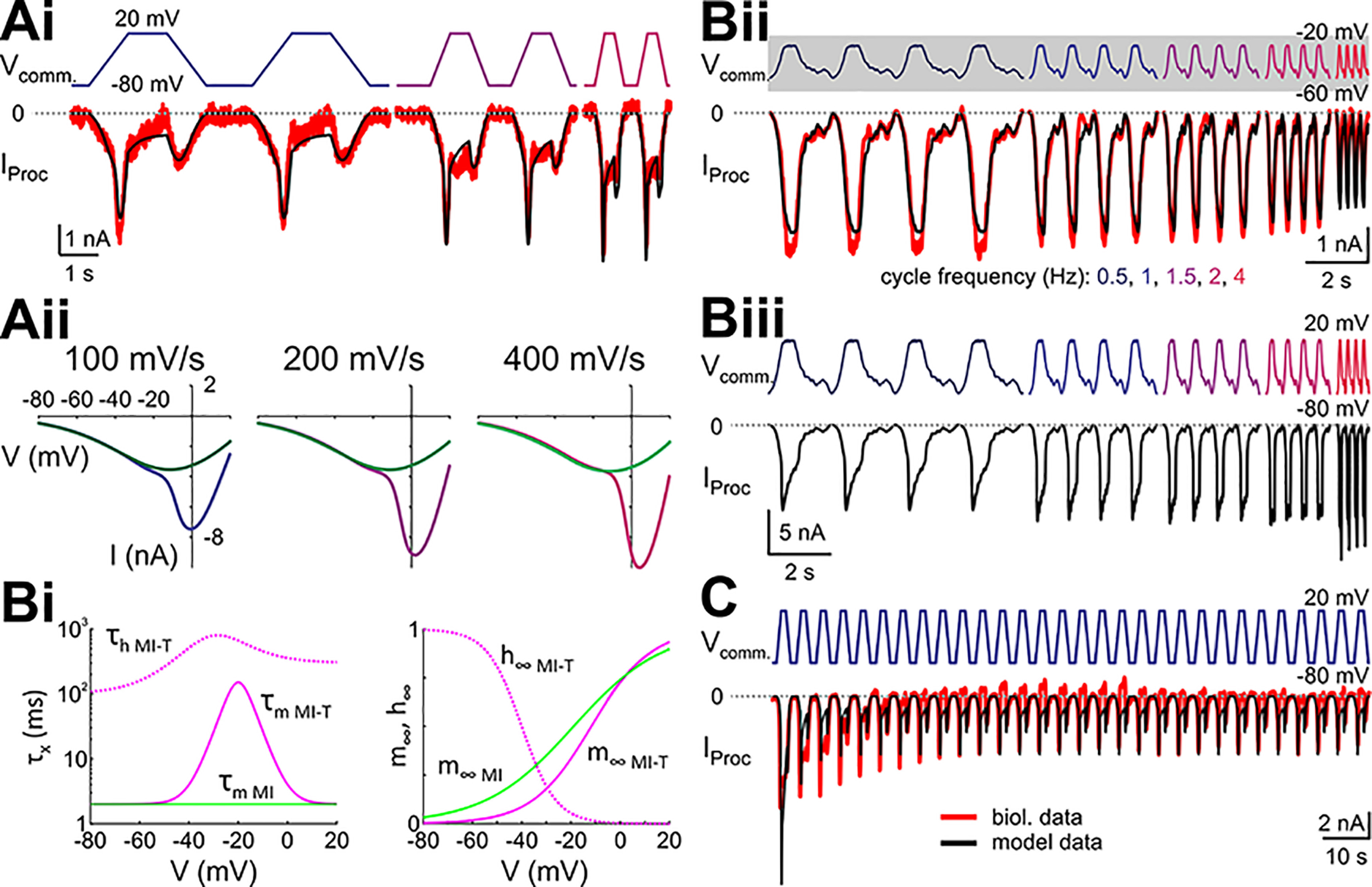
A model with only IMI and IMI-T adequately captures the fast and slow inactivations. A, Model parameters for IMI and IMI-T were tuned to capture the steady-state IProc trajectories, i.e., a larger inward current on the positive ramps, and larger inward currents with larger slopes. Ai, Overlay of the biological (red) and model (black) IProc trajectories in response to steady-state ramp-and-hold stimuli. Aii, I-V curves separated by positive (purple) and negative (green) ramps similar to those shown in Ai. I-V curves for the positive ramps were obtained after holding the voltage at –80 mV to remove inactivation, and the negative ramps after holding the voltage at +20 mV to maximize inactivation of the transient current. Bi, Time constants for the activation (solid lines) and inactivation (dashed lines) gates of the model IMI (green) and IMI-T (pink). Bii, Model response to realistic LP waveform stimulations with different cycle frequencies (based on the biological data from the same preparation as in Ai). The gray shading around Vcomm. indicates the voltage range of the ramp and ramp-and-hold stimuli used in Ai. Biii, Model response to the same waveforms as in Bii but with an upscaled amplitude that is similar to the amplitude of the ramp and ramp-and-hold stimuli. C, The slow inactivation of the proctolin-activated current can be mimicked in a computational model by modeling IMI-T as Ca2+ current following the Goldman–Hodgkin–Katz formalism.
However, a simple division of IProc into a persistent and an inactivating component did not explain the second observation. As described above, the measurement of IProc using realistic LP neuron voltage waveform protocols (slow-wave oscillation range −60 to −20 mV) showed that the amplitude of the current did not consistently follow the same slope dependence as the current using the ramp protocols. Rather, the value of IProc decreased at the largest applied cycle frequency of 4 Hz (largest depolarization slope), which was the opposite of what we expected from the ramp experiments. As expected, when we simulated the simplest model that fit the ramp data with the LP voltage waveforms it produced the expected result that the current became consistently larger, not smaller, with increased cycle frequencies, and thus did not replicate the realistic waveform data (not shown). However, we noted that in our experiments the ramps spanned a voltage range (−80 to +20 mV) that was much larger than that of the realistic waveforms (−60 to −20 mV). It was therefore possible that the currents involved have different kinetics in the more restricted voltage range. Because the persistent current IMI has very fast activation kinetics (Golowasch and Marder, 1992), we focused on the kinetics of the inactivating current IMI-T. We found that an adjustment of the kinetics of IMI-T to have slower activation over the voltage range of the realistic waveform but remain fast outside of this range (Fig. 6Bi, pink trace), was sufficient to reproduce the effect of the realistic waveform in that increasing cycle frequency would lead to a smaller IProc (Fig. 6Bii). A prediction of this modified model would be that applying the realistic waveform in the larger range of −80 to +20 mV should produce an increase of IProc when cycle frequency is increased. Indeed, this was precisely what we observed in the model (Fig. 6Biii).
So far, we focused on describing how the model currents matched the slope-dependent effects of IProc at steady state, both for ramps and for realistic waveforms. However, these currents could not reproduce the third observation, that the total current decayed slowly when the ramp-and-hold protocol was applied repeatedly (Fig. 3). This was because both IMI and IMI-T had fast activation, and the inactivation time constant of the model IMI-T was <800 ms throughout the voltage range, which did not allow the current to keep a memory over repeated voltage waveforms. It is possible that the slow decay of IProc over several seconds involves yet another slower inactivation component or another slow-inactivating proctolin-activated ionic current altogether. However, there is an alternative and perhaps simpler possibility. Previous studies have suggested that the peptide-activated ion channels (such as those underlying IProc) in the STG may have calcium permeability or even be calcium currents (Zhao et al., 2011; Oh et al., 2012; Rodriguez et al., 2013; Gray et al., 2017). If IMI-T were a calcium current, calcium entry due to this current could change local internal calcium concentrations so that the driving force of the current would be reduced over repetitive depolarizations. To examine this possibility, we modeled IMI-T as a calcium current using the Goldman–Hodgkin–Katz formalism (see Materials and Methods). Although we did not attempt to optimize the parameters of this model (many of which remain unmeasured), we found that this formalism could sufficiently explain how the current amplitude reduced with repetitive depolarization (Fig. 6C).
Examining the model predictions
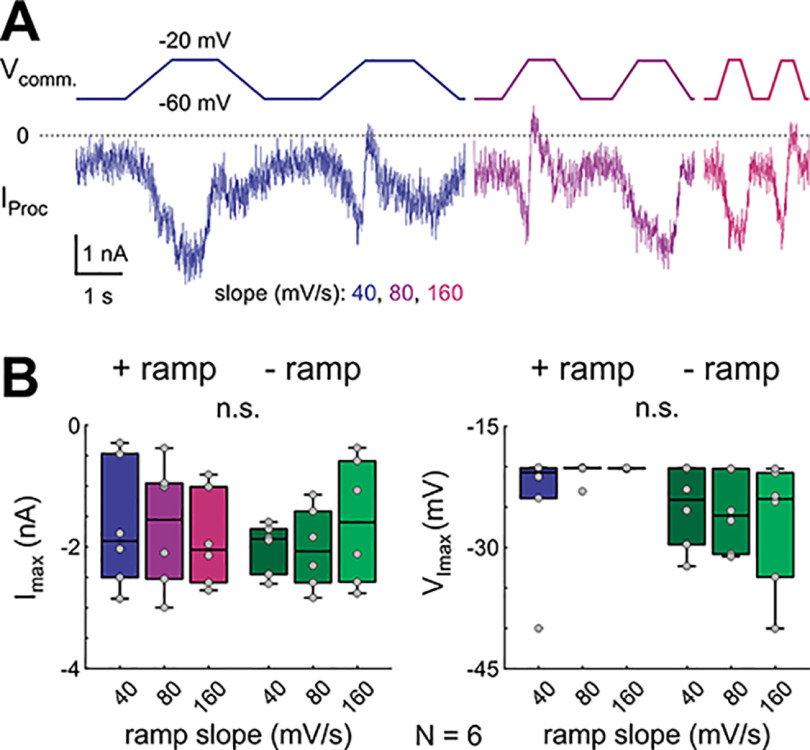
To examine the prediction of the model that low-amplitude stimuli produce a different slope-dependent or frequency-dependent effect than high-amplitude stimuli (Fig. 6B), we repeated the ramp-and-hold experiments but reduced the amplitude to match the original realistic waveform voltage range of −60 to −20 mV and scaled the cycle frequencies to match the pyloric frequencies commonly observed in experiments at 12°C (∼0.5−1 Hz; Tang et al., 2012; Haddad and Marder, 2018; Rosenbaum and Marder, 2018; Kushinsky et al., 2019; Fig. 7A). In this voltage range, IProc largely lost its slope dependence, both for Imax and VImax (Fig. 7B; two-way RM ANOVA results in Extended Data Fig. 7-1), as predicted by the model.
Figure 7.
Decreasing the amplitude of ramps to that of the realistic waveforms removes the slope dependence of IMI-T. A, IProc measured in LP in response to downscaled ramp-and-hold stimuli with an amplitude similar to the realistic LP wave stimulus. B, Quantification of steady state Imax and VImax for the downscaled ramp-and-hold stimuli (N = 6). Dots represent data from individual experiments. There is no significant slope dependence (n.s.; two-way RM ANOVA; Table 1; results in Extended Data Fig. 7-1).
Two-way RM ANOVA for steady state I-V parameters at small stimulus amplitude (ramp-and-hold). α = 0.05. Directions: positive or negative. Slope (in mV/s): 40, 80, 160. Download Figure 7-1, XLSX file (9.6KB, xlsx) .
Data for panel B. Download Figure 7-2, XLSX file (9.7KB, xlsx) .
We also tested the possibility that IMI-T is a calcium current by repeating our ramp protocols with LP in saline containing 200 μm Cd2+, which blocks Ca2+ channels in the LP neuron (Golowasch and Marder, 1992). In Cd2+ saline, the slope dependence was greatly reduced (Fig. 8A–C, raw difference currents of one example in A, example I-V curve with fits of the same experiment in B, quantification in C). Only the largest positive slope of 400 mV/s resulted in a significantly larger Imax compared to the smallest slope of 50 mV/s (Fig. 8C). Additionally, except for the largest slope, Imax and VImax of IMI and IMI-T were not different in Cd2+ saline (Fig. 8C; two-way RM ANOVA results in Extended Data Fig. 8-1). In normal saline, the increase in IProc across positive ramp slopes was approximately linear. Therefore, we compared the slopes of linear fits across all positive and negative ramps between normal saline and Cd2+ saline. For the positive ramps, this slope was significantly smaller in Cd2+, and unchanged for the negative ramps (Fig. 8D; two-way ANOVA results in Extended Data Fig. 8-2), indicating that IProc did not depend on depolarization slope in this voltage range in Cd2+. We were unable to calculate time constants for the slow inactivation because IProc at steady-state was not different from IProc at the initial state in Cd2+ saline (Fig. 8E; two-way RM ANOVA; results in Extended Data Fig. 8-3). From these experiments we conclude that Ca2+ is at least partially involved in IMI-T, possibly as the charge carrier, and it also appears to be necessary for the slow decay of the current.
Figure 8.
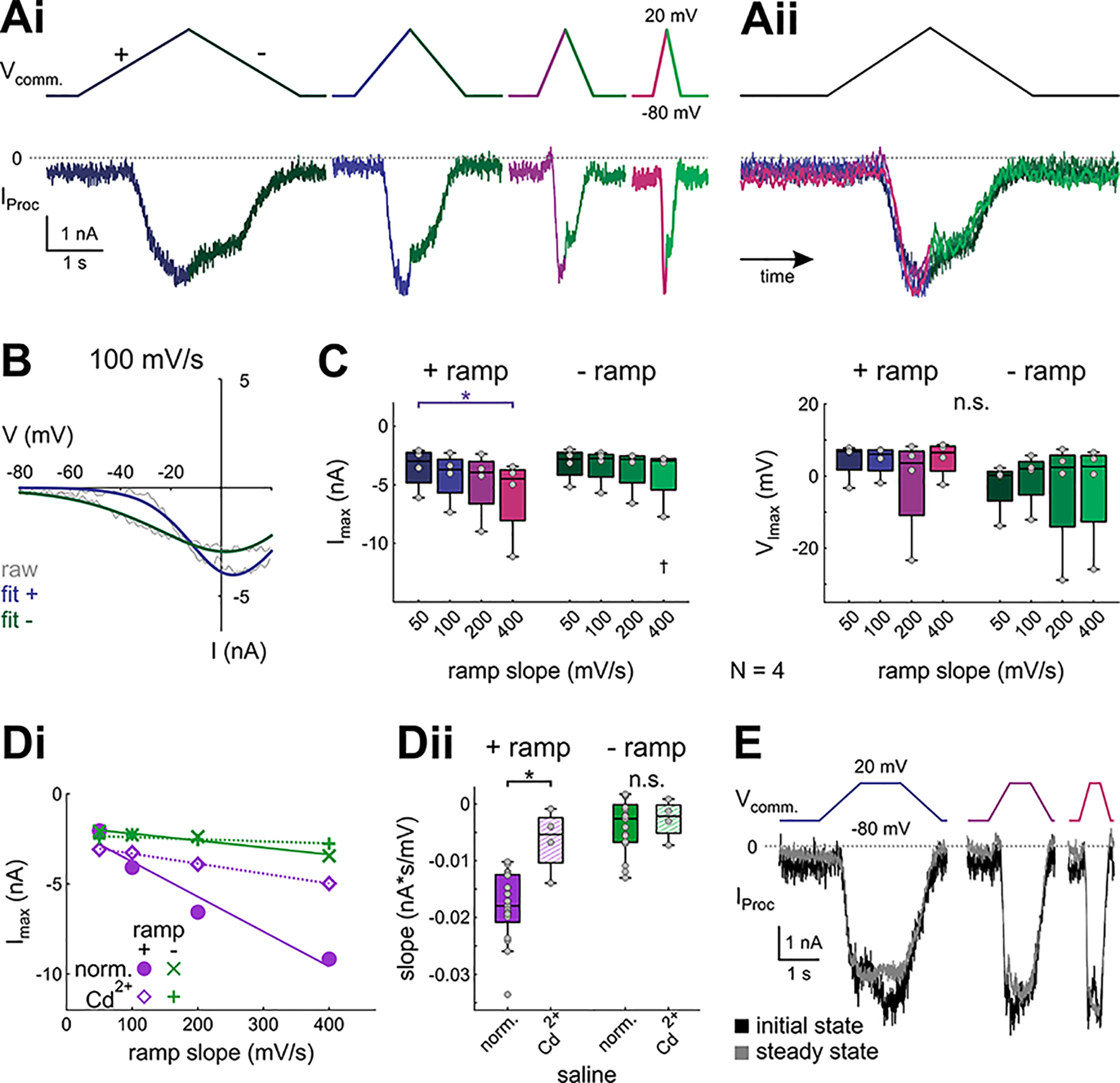
Proctolin-activated currents are partially blocked by cadmium. Ai, Proctolin-activated currents in Cd2+ saline evoked by symmetrical ramp stimulations with four different slopes (color-coded), averaged over the last three of five sweeps of one experiment. Aii, Overlay of the proctolin currents shown in Ai, normalized by time. B, Example I-V curves for Iproc shown in A, 100 mV/s. Gray solid lines show original current recordings, colored solid lines show logistic fits. C, Quantitative analysis of Imax (left) and VImax (right) for different ramp slopes and ramp directions (N = 4). Dots represent data from individual experiments. Ramp slope and direction show statistically significant interactions for Imax (two-way RM ANOVA; Table 1; results in Extended Data Fig. 8-1). Asterisks indicate significant differences between slopes within a direction, daggers indicate significant differences between directions within a slope at α = 0.05. n.s. indicates no significant changes. D, Linear fits for Imax. Di, Example showing the fits from a linear regression model to the Imax for different ramp slopes and directions in normal saline and Cd2+ saline. Dii, Slopes of linear fits for Imax in normal saline (filled boxes) and Cd2+ saline (hatched boxes). Cd2+ significantly reduced the slope of Imax for the + ramps (purple), but not the – ramps (green), indicating a reduction of IMI-T in the presence of Cd2+ (two-way ANOVA; Table 1; results in Extended Data Fig. 8-2). E, Example (same preparation as in A) showing the initial (black) and steady-state (gray, average of the last five sweeps) responses to ramp-and-hold stimuli in Cd2+ saline. In all four experiments, IProc was not significantly different between initial and steady state (two-way RM ANOVA; Table 1; results in Extended Data Fig. 8-3).
Two-way RM ANOVA for initial state I-V parameters (ramps) in Cd2+ saline. α = 0.05. Direction: positive or negative. Slope (in mV/s): 50, 100, 200, 400. Download Figure 8-1, XLSX file (9.7KB, xlsx) .
Two-way ANOVA for the slopes of the linear fits across ramps with the same direction. α = 0.05. Direction: positive or negative. Saline: normal or Cd2+. Failed normality and equal variance tests. Download Figure 8-2, XLSX file (9.6KB, xlsx) .
Two-way RM ANOVA for IProc in initial and steady state in normal saline and Cd2+ saline. α = 0.05. State: initial or steady. Slope (in mV/s): 100, 200, 400. Download Figure 8-3, XLSX file (9.5KB, xlsx) .
Data for panel C. Download Figure 8-4, XLSX file (9.6KB, xlsx) .
Data for panel Dii. Download Figure 8-5, XLSX file (9.5KB, xlsx) .
Data for Extended Data Figure 8-3E. Download Figure 8-6, XLSX file (8.9KB, xlsx) .
The roles of IMI and IMI-T in the activity patterns of the LP neuron at different cycle periods
The bursting activity of follower pyloric neurons and, in particular, the LP neuron is exquisitely sensitive to the action of neuromodulation (Marder and Bucher, 2007; Stein, 2009; Harris-Warrick and Johnson, 2010), including proctolin (Nusbaum and Beenhakker, 2002; Daur et al., 2016). It is therefore natural to ask how the two currents IMI and IMI-T may differentially influence the LP bursting activity. Because we currently do not have an experimental method of separating the two components of IProc during the ongoing activity (no pharmacological blockers of these currents exist), we addressed this question in a computational model of the LP neuron (see Materials and Methods) based on the model developed by Taylor et al. (2009). Because the LP neuron bursts in response to periodic inhibition it receives from the pyloric pacemaker neurons, we drove the model with a periodic inhibitory synaptic input. We then examined the effect of the proctolin modulation on the bursting activity of the model neuron. IMI and IMI-T were adjusted to account for the spatial distance to the putative receptor location distal from the soma (see Materials and Methods). Note that the lack of slope dependence with small amplitude stimulations (Fig. 7) could be because of incomplete space clamp. All data shown from these modeling results are at steady state once the transient response of the model neuron has finished.
To see how Ca2+ permeability would influence the activity of the model neuron, we drove the LP neuron with synaptic input at a cycle frequency of 1 Hz, a typical average pyloric cycle frequency, and compared the effect of IProc = IMI + IMI-T at steady state, when the current was assumed to be permeable to Ca2+ (IMI-T(Ca)) and when it was not (Fig. 9Ai, black traces: not Ca2+ permeable, purple traces: Ca2+ permeable). We found that permeability to Ca2+ did not change the burst onset of the model neuron but shortened the burst duration so that the burst terminated before the arrival of the periodic inhibition. Consistent with the shorter burst, the number of spikes and the intra-burst spike frequency were both reduced, but there was no change in the burst structure in that the instantaneous spike frequency (finst = 1/interspike interval) decayed during each burst in both cases (Fig. 9Ai). To understand these effects, we compared the ionic currents of the models and found that the changes in the burst duration and spike number were because of the additional activation of the outward Ca2+-dependent K+ current, IK(Ca), when the model IProc was assumed to be permeable to Ca2+ (Fig. 9Aii, IMI-T(Ca), purple and pink traces), whereas the other ionic currents (which were not influenced by Ca2+ entry) were not affected (data not shown).
Figure 9.
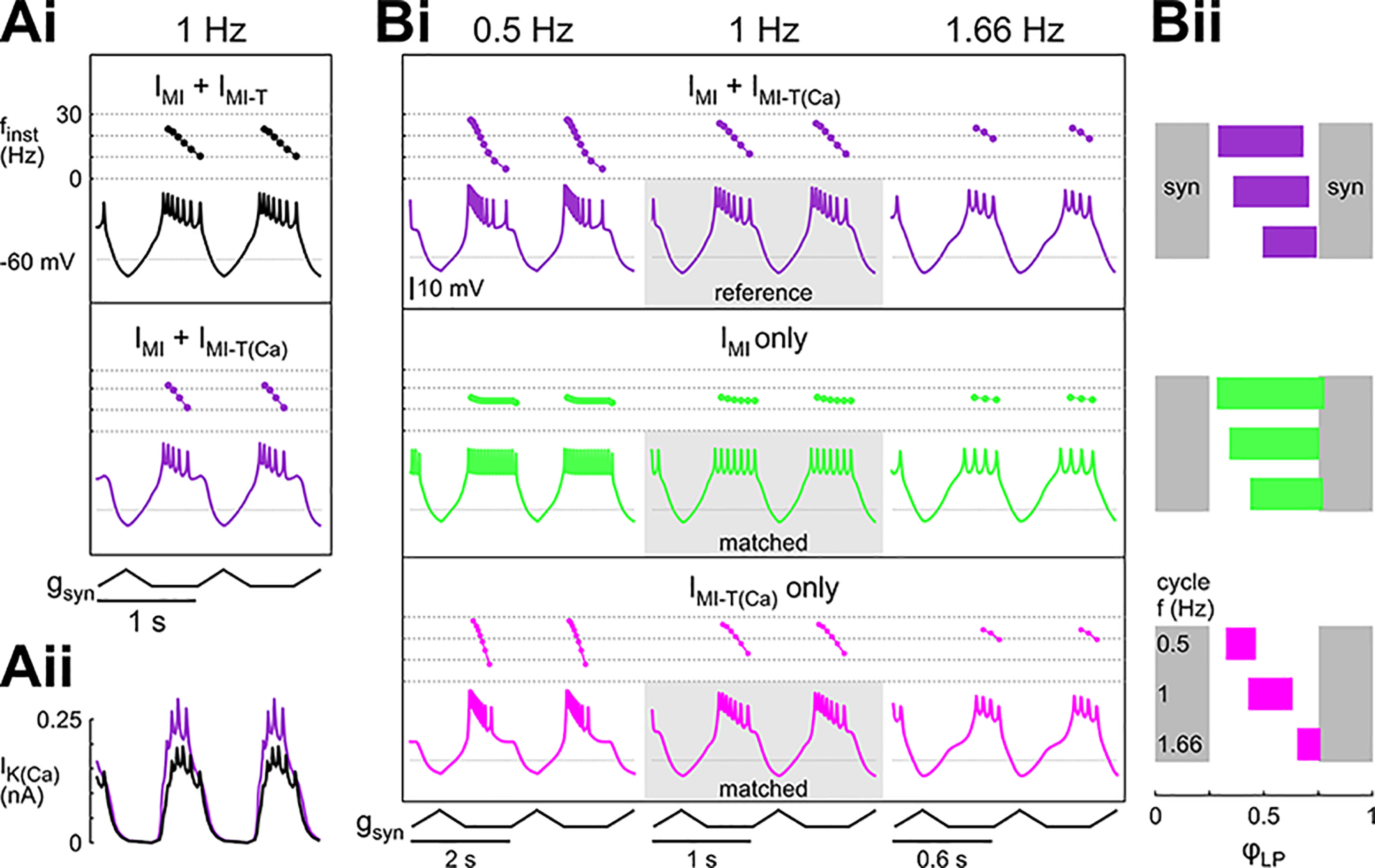
The frequency dependence of IMI-T shifts the burst phases in a model of the LP neuron. LP model with IK and INa in the axon compartment, leak current in both axon and soma/neurite compartment, and IA, Ih, ICa, IK(Ca), IMI, and IMI-T in the soma/neurite compartment. Calcium permeability is indicated by the subscripted addition of (Ca) to IMI-T. Ai, Model voltage waveforms and the corresponding instantaneous spike frequencies (finst) within a burst with IMI and IMI-T where IMI-T is either contributing to the intracellular Ca2+ concentration (purple; IMI-T(Ca)) or not (black). The model received periodic inhibition (gsyn) at 1 Hz. Aii, Levels of IK(Ca) when IMI-T is either contributing to the intracellular Ca2+ concentration (purple) or not (black). The larger IK(Ca) contributes to the earlier burst termination. The model equations and parameters are as described in Materials and Methods. B, Contribution of the different components to the activity phases of the model neuron at different cycle frequencies. Currents were matched so that the model produced the same number of spikes per burst at 1 Hz (gray rectangles in Bi). Bi, Voltage trajectories and instantaneous frequencies within a burst at 0.5, 1, and 1.66 Hz when the model contained IMI and IMI-T(Ca) (purple), when the model contained only IMI but not IMI-T(Ca) (green), and when the model contained only IMI-T(Ca) but not IMI (pink). Bii, Phase plots of the activity at different cycle frequencies. IMI-T(Ca) had a substantially greater effect on phase than IMI (Extended Data Fig. 9-1). Gray bars indicate the duration of the inhibitory synaptic current. In this panel, the model parameters for IMI and IMI-T were adjusted as follows: IMI + IMI-T(Ca): , ; IMI only: , ; IMI-T(Ca) only: , .
To examine the frequency-dependent effects of the two proctolin-activated currents, IMI and IMI-T, we started with the model in Figure 9A (with Ca2+ permeability) at the cycle frequency of 1 Hz and tuned the levels of the modulatory currents to have seven spikes per burst. We refer to this as the reference model. We then changed the frequency of the periodic inhibitory synaptic input without changing the duty cycle, shape, or amplitude of this synapse. For simplicity, we only show the activity of the model neuron at two other frequencies, one lower (0.5 Hz) and one higher (1.66 Hz). Decreasing the cycle frequency slightly advanced the onset and end phases of the burst, and increased the number of spikes per burst, but did not affect the burst structure, in that finst followed the same decreasing trend within each burst (Fig. 9Bi, purple traces). Consistent with this, increasing the cycle frequency did the opposite. We then examined how proctolin modulation would influence LP activity if proctolin were to activate only IMI or only IMI-T. However, simply removing IMI-T from our reference model resulted in a complete absence of spiking at all three frequencies. Therefore, to do this comparison in the IMI only case, we first increased the maximal conductance of IMI so that, for the 1 Hz case, the number of spikes per burst matched the number of spikes of the reference model. Similarly, in the IMI-T only case, we increased the maximal conductance of IMI-T to achieve the same. These cases are denoted as “matched.” We then changed the frequency of the periodic input in each case and compared the effects with the reference case.
In the IMI only case, changing the cycle frequency simply increased or decreased the number of spikes in the burst but the spike structure (finst) of the model neuron remained relatively constant for the duration of the burst. In contrast, in the IMI-T only case, both increasing and decreasing the cycle frequency shortened the duty cycle, but at 1.66 Hz, the burst was delayed in its onset, whereas at 0.5 Hz, it was advanced. In this case, the burst structure was also influenced by the change in cycle frequency. When cycle frequency was decreased, finst dropped dramatically within each burst (pink trace at 0.5 Hz), whereas it became somewhat more constant as cycle frequency was increased (pink trace at 1.66 Hz). The changes in the burst onset and end were reflected in the phase diagram of the model neuron (Fig. 9Bii). In the reference model (purple), there was a shift in the burst onset and a smaller shift in the burst end with increased cycle frequency. These shifts were reduced in the IMI only case (green) and the phases were more similar across cycle frequencies. In contrast, the shifts became more pronounced in the IMI-T only case (pink) and both the beginning and the end of the burst greatly shifted with increasing cycle frequency. Together, these modeling results indicate the ability of the two modulatory-activated currents to provide different influences on the burst structure, with IMI producing a consistent burst duration and strength across all cycle frequencies and IMI-T producing a dynamic change in burst structure across different cycle frequencies.
Discussion
Oscillatory neuronal network activity can be stereotyped when conditions are stable (Bucher et al., 2005; Vajda et al., 2008) and can be highly dynamic when conditions are more variable, such as during development (Ben-Ari et al., 1989; Meister et al., 1991; Sharples and Whelan, 2017) or in injury states (Luther et al., 2003; Hamood and Marder, 2015). The activity transitions often depend on changes in neuromodulatory input that the networks receive. Such neuromodulatory inputs can generate activity patterns that depend on the original activity or excitation state of the network (Nusbaum and Marder, 1989; Doi and Ramirez, 2010; Sharples and Whelan, 2017), which in turn may depend on a neuron’s ionic conductances and synaptic inputs, as well as the specific ionic conductance(s) the neuromodulator regulates (Marder et al., 2014). At the individual neuron level, in neurons expressing oscillatory activity, neuromodulators may have variable effects because they may act differently depending on the neuron’s oscillation frequency.
Frequency-dependent interactions in the nervous system are typically thought of as changes in neural activity that depend on the input frequency, as is the case with short-term synaptic plasticity. Neuromodulators can modify the frequency dependence of the effects of such inputs (Ito and Schuman, 2008). However, the oscillatory membrane potential trajectory of a neuron can also affect how neuromodulators influence its activity in a frequency-dependent manner. When a neuron’s voltage is oscillatory, independent of whether the oscillation is imposed or intrinsic, the oscillation pattern affects how ionic currents activate, how they interact with each other, and consequently how they shape the voltage output of that cell and ultimately the activity of a network. For example, slow inactivation of an ionic current interacts with the rates of voltage change. Consequently, the mean level of an inactivating current could depend on the oscillation frequency because of incomplete recovery from inactivation. Neuromodulator-mediated changes of the gating properties of such transient currents will therefore have frequency-dependent effects. Currents activated by neuromodulators influence the voltage trajectory of the neuron, which alters the activation of other ionic currents as well as synaptic release. Thus, frequency dependence of neuromodulator effects on circuit activity may depend on activation of currents that are not directly targeted by the modulator.
Crustacean pyloric neurons are modulated by a host of endogenous peptides (Marder and Bucher, 2007). Most of these peptides increase the excitability of their target neurons, an effect that has been attributed to the fact that the peptides (as well as muscarinic agonists) convergently activate the fast persistent voltage-gated inward current IMI (Golowasch and Marder, 1992; Swensen and Marder, 2000). Here, we show that one of these peptides, proctolin, additionally activates a transient current, IMI-T, in the follower LP neuron. IMI and IMI-T have similar voltage dependencies of activation but have different kinetics. Together, these two currents reproduce the LP neuron’s steady-state proctolin-mediated response to stimulation with different voltage waveforms, including voltage ramps and realistic waveforms at different cycle frequencies, in a computational model (Fig. 6). However, IMI and IMI-T make different contributions to the activity of the LP neuron. These distinct contributions arise from the effects of the voltage dynamics of the neuron on the activation and inactivation of the transient current, and interactions of both currents with other currents expressed by the LP neuron. One important interaction that we propose is with a Ca2+-activated K+ current (IK(Ca)). Large levels of IK(Ca), among other potassium currents, have been shown to prevent neurons from oscillating, even when pacemaker currents were enhanced (Golowasch et al., 2017), and play a key role in regulating neuronal excitability (Haedo and Golowasch, 2006). Although our results do not provide proof of Ca2+ permeability of IMI-T, they provide strong evidence that this current is at least partly carried by Ca2+ ions (see below). Such Ca2+ permeability of IMI-T would lead to the activation of IK(Ca) (see Fig. 9Aii), with the important consequence that IMI-T, through its activation of IK(Ca), will terminate the burst of spikes earlier than when only the persistent IMI is active (Fig. 9Ai,Bi, green trace). Thus, it seems that the IMI-T effect on the follower LP neuron’s bursting activity is 2-fold: it boosts early excitability by inducing postinhibitory rebound (see below), and it provides a brake on prolonged excitability because of its transient nature and the recruitment of an outward current.
Persistent versus transient modulator activated currents
Persistent currents are thought to amplify excitatory synaptic inputs and cause membrane bistability (Jahnsen and Llinás, 1984; Lee and Heckman, 1998; Manuel et al., 2014). Like other persistent inward currents (Cantrell and Catterall, 2001; Tryba et al., 2006; Dunmyre et al., 2011), IMI is known to act as a pacemaker current in the pacemaker neurons of the pyloric network (Bose et al., 2014). This pacemaker activity depends on a balance between IMI and IK(Ca) (Golowasch et al., 2017). However, follower neurons of this network, such as the LP neuron, express outward currents at such large amplitudes that they preclude IMI from driving oscillatory activity (Golowasch et al., 2017). Although in the LP neuron the transient inward current IMI-T has an even higher maximal conductance value than IMI, it does not elicit oscillatory activity in this neuron. This is probably because, in the absence of inhibitory input, the resting membrane potential of the LP neuron is fairly depolarized (Martinez et al., 2019), leading to the inactivation of IMI-T.
Consistent with the transient nature of IMI-T, the total proctolin-elicited current (IMI + IMI-T) is more strongly activated by faster and positive-slope voltage ramps (Figs. 2-4). To get a better idea of how these currents are activated during natural ongoing oscillations, we measured them by voltage-clamping the LP neuron with a prerecorded realistic voltage waveform. To our surprise, the current measured with realistic waveforms had a negligible change in amplitude with faster voltage waveforms and became only slightly larger at 2 Hz compared with 0.5 Hz (Fig. 5Bi). Furthermore, the same voltage waveform applied at a higher frequency of 4 Hz elicited a much smaller current. This discrepancy could be because of the different activation and inactivation rates of IMI-T in the voltage range used for ramps (−80 to +20 mV) compared with those of the realistic waveforms (−60 to −20 mV; Fig. 6). At the peak voltage of the realistic waveforms, the activation time constant for IMI-T is relatively long. Thus, at fast cycle frequencies, IMI-T cannot reach the same levels as at slower cycle frequencies and therefore the total proctolin current was smallest at the fastest cycle frequency we tested. Generally, slower time constants within a certain voltage range have been observed since the first description of the voltage-dependent transition rate constants by Hodgkin and Huxley (Hodgkin and Huxley, 1952; Ermentrout and Terman, 2010).
Is it possible that such a transient current, weakly activated in the normal voltage range of these cells, can significantly impact neuronal activity? To address the potential role of the modulator-activated currents on the activity of the LP neuron we resorted to computational modeling. During its normal biological activity, the LP neuron receives strong inhibitory input from the pyloric pacemaker neurons and rebounds from this inhibition to produce a burst of action potentials. Because it is fast and non-inactivating, IMI influences the spiking frequency of the LP neuron independent of the frequency of the synaptic inhibition. In contrast, the effect of IMI-T is different depending on the frequency of the synaptic input. At low frequencies (e.g., 0.5 Hz) the current is strongly activated and generates a postinhibitory rebound but inactivates within the duration of a burst. Consequently, the burst terminates before the onset of the next cycle of inhibition (Fig. 9 Bi, pink and purple traces). At high frequencies (>1 Hz), however, the rapid cycling of the voltage prevents full recovery from inactivation and the total available IMI-T is lower. This leads to a delayed onset of action potential firing at high frequencies. Together, these two neuromodulator-activated currents lead to shorter bursts with smaller duty cycles and higher transient spiking frequencies at all synaptic input frequencies compared with the case if only the persistent current were activated. As for how the two currents influence the activity phases of the LP neuron, the persistent IMI supports consistent spiking when LP is not inhibited, whereas the transient IMI-T allows for a modulation of the phases of burst onset and termination at different input frequencies (Fig. 9B). The activity phase of the LP neuron is known to regulate the pyloric cycle period through its synaptic inhibition of the pyloric pacemaker group (Johnson et al., 2011). Additionally, the same study showed that monoamines differentially modulate the LP activity phase, which influences the impact of the synaptic feedback from the follower LP neuron on the cycle period. However, the mechanism by which amines regulate the activity phase most likely does not involve IMI-T since those amines do not activate IMI. On the other hand, we predict that other neuromodulators, which activate IMI in LP and other neurons, activate IMI-T as well.
Most of the previous studies on peptide-activated currents in the STG measured the response as a difference current at steady state using voltage-step protocols or slow ramps (Li et al., 2018). Because the peptide-activated currents are relatively small compared with the large outward currents in STG neurons (often in hundreds of nA), it is extremely difficult to measure transient difference currents even if outward currents are pharmacologically blocked (which is never perfect), as even small variations in the measurement done at different times (control vs modulator saline) can lead to significant errors. We found that ramp protocols partially remedy this problem (by partially inactivating the large outward currents) and provide consistent modulator-elicited difference currents measurements over many repetitions. Since we used relatively fast ramps, we were able to measure transient currents before complete inactivation. Because of the time-dependent inactivation of IMI-T during the positive ramp, the total current activated by proctolin was larger at faster depolarization rates and the peak of this current shifted to more depolarized membrane potentials: depolarized voltages were reached in a shorter time. It is noteworthy, however, that transient currents are often not easily identifiable with ramp protocols (but see Park et al., 2013). Nevertheless, one advantage of using ramp (over step) protocols is that a range of voltages can be sampled continuously. Additionally, changing the slope of a voltage ramp mimics the voltage changes that an oscillating neuron experiences during each cycle of realistic oscillatory activity, which can help gain insight into the physiological relevance of the current. On the other hand, an important drawback of using ramps is that an incomplete inactivation during a positive voltage ramp can influence the current measured on the negative voltage ramp (Fig. 2). A clear indication of this drawback was that parameter differences during negative ramps were no longer present in the steady state measurements during ramp-and-hold protocols (Fig. 4).
Rodriguez et al. (2013) identified two voltage-dependent transient currents activated by a neuropeptide in an STG gastric mill circuit neuron. These currents were not evident with ramp protocols because of inactivation and could only be observed with voltage step protocols. Rodriguez et al. (2013) indicated the presence of the faster of the two currents but did not further characterize it. The slower current, ITrans-LTS, shares some similarities with IMI-T in that both are transient, modulator-activated, voltage-gated currents that are probably carried by a combination of Na+ and Ca2+ ions. Furthermore, both inactivate completely during slow voltage ramps. However, ITrans-LTS is evident in voltage-step-elicited raw current recordings because it activates slowly (500 ms), whereas IMI-T is much faster to activate and also inactivates rapidly. It is therefore unlikely that IMI-T is the same current as ITrans-LTS, but it is possible that IMI-T is the same as the fast transient current observed, but not further characterized, by Rodriguez et al. (2013).
ITrans-LTS, enables postinhibitory rebound bursting. Such rebound bursting has been shown to be important in the activity of a number of neurons (Llinas, 1988; Getting, 1989), including the rebound properties sometimes required to generate network oscillatory activity (e.g., half-center oscillators; Rodriguez et al., 2013), bistability (Hounsgaard et al., 1988), and even as a form of intrinsic short-term memory mechanism (Goaillard et al., 2010). As mentioned above, our modeling results show that IMI contributes to continuous spiking in the LP neuron when it is not inhibited, whereas IMI-T can produce a postinhibitory rebound significantly larger than the baseline activity, which would contribute to this neuron’s role in the pyloric CPG, as well as to activating its target muscles. These two modes of bursting (periodic inhibitory pauses of baseline activity vs significant rebound from inhibition) can have vastly different effects on postsynaptic neurons. For example, a recent report shows that dopaminergic neurons in the substantia nigra generate robust postinhibitory rebound bursts following inhibition by striatal neurons, whose transmissions target both GABA-A and GABA-B receptors. In contrast, inhibition of the same neurons by globus pallidus neurons, which activate only GABA-A receptors, does not generate rebound activity, but just pauses ongoing spiking (Evans et al., 2020). Importantly, only the former postinhibitory rebound bursts produce phasic release of dopamine in the striatum by the nigral neurons, which is a key factor in striatal synaptic plasticity and reinforcement learning (Yagishita et al., 2014; Shindou et al., 2019).
Voltage dependence and the role of calcium
Previous studies that examined peptide modulation of STG neurons were mostly done in the presence of Ca2+ blockers (Golowasch and Marder, 1992; but see Rodriguez et al., 2013), which may explain why they did not find evidence of IMI-T. Although the slow inactivation of IMI-T over multiple cycles (Fig. 3) could in principle be accounted for by an additional slow inactivation gate, such a slow gating property would predict distinct time constants of IMI-T reduction at different depolarization frequencies. However, Figure 3A,C shows that no such difference can be detected. A simple Goldman–Hodgkin–Katz model of IMI-T as a Ca2+ current indicated that intracellular accumulation of Ca2+ is sufficient to explain the slow inactivation of the current over many seconds (Fig. 6C). This is consistent with the previously reported Ca2+ dependence of IMI. IMI appears to be sensitive to both extracellular and intracellular Ca2+, and the intracellular Ca2+ is likely modified by Ca2+ flux through the IMI channels themselves (Gray and Golowasch, 2016; Gray et al., 2017). Our findings suggest that IMI-T may be similarly permeable to Ca2+ and perhaps even depend on it for its activation and inactivation. Altogether, several neuromodulator-activated and voltage dependent currents appear to be present in several STG neurons. They all bear resemblance to the better characterized non-inactivating IMI (Golowasch and Marder, 1992; Swensen and Marder, 2000, 2001; Gray and Golowasch, 2016; Gray et al., 2017), but some express inactivation (IMI-T, ITrans-LTS), and all seem to vary in activation and inactivation kinetics. It is not known, but remains possible, that all convergently respond to multiple neuromodulators like IMI does (Swensen and Marder, 2000, 2001). This would suggest that the ion channels that produce IMI-T and IMI, and perhaps also ITrans-LTS, could all be isoforms of the same channel. It is well known that ion channel isoforms can be generated by various mechanisms, including alternative splicing (Soldatov, 1994) and gene duplication (Piontkivska and Hughes, 2003), and that isoforms may be unevenly distributed within tissues (Tellez et al., 2006). The isoform composition of an ion channel gives it distinct isoform-dependent characteristics, e.g., electrophysiological properties and blocker sensitivity (for review, see Hameed, 2019), or pH sensitivity (Khan et al., 2006). Similarly, channel isoforms have already been identified in the transcriptomes of C. borealis and the lobster Homarus americanus for multiple ion channel types (Northcutt et al., 2016). This is all consistent with the possibility that the various voltage-gated ionic current modulated by neuropeptides in this system are isoforms within an ion channel family, whose identity and precise distribution has yet to be determined.
Overall, the transient nature and resulting frequency dependence, and Ca2+ permeability of IMI-T give this current the potential to widely influence the activity of a neuron. Since LP is the only follower neuron that synapses onto the pacemaker group, frequency dependent changes in LP activity could in turn feed back to the pacemakers and stabilize the pyloric rhythm at a preferred frequency. It remains to be shown if IMI-T can be activated by other neuropeptides, similar to IMI, and if and to what extent IMI-T is present in other neurons.
Data for panel Bii. Download Figure 9-1, XLSX file (8.7KB, xlsx) .
Acknowledgments
Acknowledgements: We thank Elizabeth Cronin for providing representative recordings in different neuromodulatory conditions and Horacio G. Rotstein and Rodrigo F. O. Pena for helpful discussions to tune the LP model.
Synthesis
Reviewing Editor: Alexey Semyanov, Shemyakin-Ovchinnikov Institute of Bioorganic Chemistry
Decisions are customarily a result of the Reviewing Editor and the peer reviewers coming together and discussing their recommendations until a consensus is reached. When revisions are invited, a fact-based synthesis statement explaining their decision and outlining what is needed to prepare a revision will be listed below. The following reviewer(s) agreed to reveal their identity: Bruce Johnson.
Two reviewers have seen the manuscript, and they both liked it. Nevertheless, they made several comments which you may be able to address.
Reviewer #1
This is a very well-written manuscript that thoroughly describes the contributions of two modulator-activated currents to regulating activity of an oscillatory neuron. Importantly, the authors provide a mechanism for state-dependent modulatory actions on oscillatory neurons, namely the frequency-dependence of an inactivating current.
Major comments.
Line 388-394/figure 7 results. I’m having difficulty reconciling the lack of slope dependence across ramps from -60 to -20 mV (realistic voltage range) with the results presented in figure 9. In figure 9, the actions of IMI-T vary across frequency, which I thought indicates a slope dependence of the current amplitude. Are the small (n.s.) differences in Imax across slopes (figure 7) sufficient to explain the frequency dependence in figure 9? I think this needs to be explicitly addressed. How do the data in figure 7 and 9 fit together?
Minor Comments.
Line 2 (also 18). Can the authors be more explicit that the “frequency-dependent effects” or “frequency-dependent actions” of neuromodulators refers to their dependence on the oscillatory frequency of the neurons? Line 6 sort of addresses this as “temporal properties of neuronal activity” but I think all of this is too implicit. I think frequency-dependent effects of neuromodulators is likely to make many readers think that the authors are referring to potential frequency-dependence of release of neuromodulators, or synaptic frequency-dependence. This is such a big point of the study, I think it is worth being more explicit. Maybe referring to it as bursting or oscillation frequency throughout the abstract would help? Something similar to line 56-57 would be very helpful in the abstract.
Line 9 change know to known.
Line 11. Insert “increasing” before ramp slope.
Line 405 (and 900). Are the traces in Fig. 8E in Cd++? Would be helpful to explicitly indicate why there was no inactivation here.
Line 426 and 433. It would be useful to indicate the color code for Ca++ permeable or not in the text.
Line 479. insert “a” between “on neuron’s"
Line 539. Please provide context for the different activation/inactivation rates used for -60 to -20 mV. Are there examples in the literature of slower rates across a voltage range with faster rates above and below that range?
Line 613. Delete “do"
Line 626. The discussion feels like it ends abruptly. Maybe a brief summary/conclusion?
Line 788. Change “on lvn” to “in the lvn recording"
Line 792. Comma after 40 mV
Line 793. Change “ranging from -60 mV to -20 mV” to “from a trough potential of -60 mV to a peak potential of -20 mV”. As currently written it sounds to me like the potential varies across experiments.
Line 805. Change “of” to “from"
Line 878. The end of the title for this figure legend is missing.
Line 914. A more informative title for this figure would be useful. It is not simply a model of the LP neuron, it is presenting an important result about the contributions of the two currents (in a model of the LP neuron).
Figures
I recommend increasing the size of all subscripts in figures.
Fig. 6C. The same thickness of the red and black lines makes it difficult to see the results. It might be easier to see if the line in the background was thicker than the line in the foreground. This is less of a problem for 6Ai and Bii as the traces are not as compressed as in 6C, but it would be easier to see both traces in all three sets if a thick black trace was behind a thin red trace for example.
Fig. 9. It would be helpful to the reader to have labels or legends for calcium permeable/not included in the figure.
Reviewer #2
General Comments:
This is a very interesting paper that carefully dissects a previously noted modulatory current
activated by proctolin in an identified neuron in the crab stomatogastric system. It addresses the ionic current mechanisms by which neuromodulators can determine the intrinsic properties of neurons active in neural networks such as central pattern generators. The paper thoughtfully combines newly gathered experimental data to build a computational model of the modulatory action at the ion channel level, and then tests predictions of the model with further experimental data. The paper is a good example of the best interactive use of experimental and computational approaches to answer mechanisms of neuromodulatory shaping of neural network activity. This is a dense paper with the modelling and electrophysiological data, but it is well written and mostly guides the reader though the details well. I only have moderate and minor comments on the manuscript.
Moderate comments:
Methods -Line 129: It may be a safe assumption that “ current measured in the negative ramp excluded currents that inactivated during the positive ramp", but could other currents not related to the proctolin effect like Ih be deactivating slowly enough to still be a factor during the negative ramp? Line Results 259: - Sometimes the text descriptions of the figure parts go by too quickly to understand all the figure parts shown. I suggest making sure that all figure parts are briefly described or at least referred to in the Results text so the reader can rely less on the figure legends to understand detailed figures. For example, mention Fig 2A, B specifically in line 263 instead of just Fig 2.
Discussion: Line 513- The Ca activation of IKCa as break on excitability needs more context from the literature showing that this happens in oscillating networks. Maybe move up the reference to Golowasch et al 2017 here for the context.
Line 554- Amines can also shape the LP activity phases though action on ionic currents to have an impact on network activity. Consider mentioning your results relate to other neuromodulators too. See Johnson et al 2011 J Neurophysiol 105:293.
Line 624: The isoform idea is interesting but only brought up in a sentence at the end of the paper. It’s important enough to put in the abstract and deserves a little more discussion here. Are there other examples in the literature to provide support for this idea?
Minor comments;
Line 9- should be “known"
Line 613 delete “do”.
References
- Amarillo Y, Zagha E, Mato G, Rudy B, Nadal MS (2014) The interplay of seven subthreshold conductances controls the resting membrane potential and the oscillatory behavior of thalamocortical neurons. J Neurophysiol 112:393–410. 10.1152/jn.00647.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong CE, Roberts WM (2001) Rapidly inactivating and non-inactivating calcium-activated potassium currents in frog saccular hair cells. J Physiol 536:49–65. 10.1111/j.1469-7793.2001.00049.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baukrowitz T, Yellen G (1995) Modulation of K+ current by frequency and external [K+]: a tale of two inactivation mechanisms. Neuron 15:951–960. 10.1016/0896-6273(95)90185-X [DOI] [PubMed] [Google Scholar]
- Ben-Ari Y, Cherubini E, Corradetti R, Gaiarsa JL (1989) Giant synaptic potentials in immature rat CA3 hippocampal neurones. J Physiol 416:303–325. 10.1113/jphysiol.1989.sp017762 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bose A, Golowasch J, Guan Y, Nadim F (2014) The role of linear and voltage-dependent ionic currents in the generation of slow wave oscillations. J Comput Neurosci 37:229–242. 10.1007/s10827-014-0498-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bucher D, Prinz AA, Marder E (2005) Animal-to-animal variability in motor pattern production in adults and during growth. J Neurosci 25:1611–1619. 10.1523/JNEUROSCI.3679-04.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bucher D, Haspel G, Golowasch J, Nadim F (2015) Central Pattern Generators. In: eLS, pp 1–12. Hoboken: John Wiley & Sons. [Google Scholar]
- Burke KJJ, Bender KJ (2019) Modulation of ion channels in the axon: mechanisms and function. Front Cell Neurosci 13:221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantrell AR, Catterall WA (2001) Neuromodulation of Na+ channels: an unexpected form of cellular plasticity. Nat Rev Neurosci 2:397–407. 10.1038/35077553 [DOI] [PubMed] [Google Scholar]
- Carnevale NT, Hines ML (2006) The NEURON book. Cambridge: Cambridge University Press. [Google Scholar]
- Carter BC, Bean BP (2011) Incomplete inactivation and rapid recovery of voltage-dependent sodium channels during high-frequency firing in cerebellar Purkinje neurons. J Neurophysiol 105:860–871. 10.1152/jn.01056.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daur N, Nadim F, Bucher D (2016) The complexity of small circuits: the stomatogastric nervous system. Curr Opin Neurobiol 41:1–7. 10.1016/j.conb.2016.07.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doi A, Ramirez JM (2008) Neuromodulation and the orchestration of the respiratory rhythm. Respir Physiol Neurobiol 164:96–104. 10.1016/j.resp.2008.06.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doi A, Ramirez JM (2010) State-dependent interactions between excitatory neuromodulators in the neuronal control of breathing. J Neurosci 30:8251–8262. 10.1523/JNEUROSCI.5361-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunmyre JR, Del Negro CA, Rubin JE (2011) Interactions of persistent sodium and calcium-activated nonspecific cationic currents yield dynamically distinct bursting regimes in a model of respiratory neurons. J Comput Neurosci 31:305–328. 10.1007/s10827-010-0311-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout GB, Terman DH (2010) Mathematical foundations of neuroscience. New York: Springer. [Google Scholar]
- Evans RC, Twedell EL, Zhu M, Ascencio J, Zhang R, Khaliq ZM (2020) Functional dissection of basal ganglia inhibitory inputs onto substantia nigra dopaminergic neurons. Cell Rep 32:108156. 10.1016/j.celrep.2020.108156 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia VJ, Daur N, Temporal S, Schulz DJ, Bucher D (2015) Neuropeptide receptor transcript expression levels and magnitude of ionic current responses show cell type-specific differences in a small motor circuit. J Neurosci 35:6786–6800. 10.1523/JNEUROSCI.0171-15.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Getting PA (1989) Emerging principles governing the operation of neural networks. Annu Rev Neurosci 12:185–204. 10.1146/annurev.ne.12.030189.001153 [DOI] [PubMed] [Google Scholar]
- Goaillard JM, Taylor AL, Schulz DJ, Marder E (2009) Functional consequences of animal-to-animal variation in circuit parameters. Nat Neurosci 12:1424–1430. 10.1038/nn.2404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goaillard JM, Taylor AL, Pulver SR, Marder E (2010) Slow and persistent postinhibitory rebound acts as an intrinsic short-term memory mechanism. J Neurosci 30:4687–4692. 10.1523/JNEUROSCI.2998-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Marder E (1992) Proctolin activates an inward current whose voltage dependence is modified by extracellular Ca2+. J Neurosci 12:810–817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Bose A, Guan Y, Salloum D, Roeser A, Nadim F (2017) A balance of outward and linear inward ionic currents is required for generation of slow-wave oscillations. J Neurophysiol 118:1092–1104. 10.1152/jn.00240.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray M, Golowasch J (2016) Voltage dependence of a neuromodulator-activated ionic current. eNeuro 3:ENEURO.0038-16.2016. 10.1523/ENEURO.0038-16.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray M, Daudelin DH, Golowasch J (2017) Activation mechanism of a neuromodulator-gated pacemaker ionic current. J Neurophysiol 118:595–609. 10.1152/jn.00743.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutierrez GJ, Grashow RG (2009) Cancer borealis stomatogastric nervous system dissection. J Vis Exp (25):1207. 10.3791/1207 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haddad SA, Marder E (2018) Circuit robustness to temperature perturbation is altered by neuromodulators. Neuron 100:609–623.e3. 10.1016/j.neuron.2018.08.035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haedo RJ, Golowasch J (2006) Ionic mechanism underlying recovery of rhythmic activity in adult isolated neurons. J Neurophysiol 96:1860–1876. 10.1152/jn.00385.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hameed S (2019) Nav1.7 and Nav1.8: role in the pathophysiology of pain. Mol Pain 15:1744806919858801. 10.1177/1744806919858801 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamood AW, Marder E (2015) Consequences of acute and long-term removal of neuromodulatory input on the episodic gastric rhythm of the crab Cancer borealis. J Neurophysiol 114:1677–1692. 10.1152/jn.00536.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris-Warrick RM, Johnson BR (2010) Checks and balances in neuromodulation. Front Behav Neurosci 4:47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris-Warrick RM, Coniglio LM, Barazangi N, Guckenheimer J, Gueron S (1995a) Dopamine modulation of transient potassium current evokes phase shifts in a central pattern generator network. J Neurosci 15:342–358. 10.1523/JNEUROSCI.15-01-00342.1995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris-Warrick RM, Coniglio LM, Levini RM, Gueron S, Guckenheimer J (1995b) Dopamine modulation of two subthreshold currents produces phase shifts in activity of an identified motoneuron. J Neurophysiol 74:1404–1420. 10.1152/jn.1995.74.4.1404 [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF (1952) A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117:500–544. 10.1113/jphysiol.1952.sp004764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hooper SL (1998) Transduction of temporal patterns by single neurons. Nat Neurosci 1:720–726. 10.1038/3721 [DOI] [PubMed] [Google Scholar]
- Hounsgaard J, Hultborn H, Jespersen B, Kiehn O (1988) Bistability of alpha-motoneurones in the decerebrate cat and in the acute spinal cat after intravenous 5-hydroxytryptophan. J Physiol 405:345–367. 10.1113/jphysiol.1988.sp017336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huguenard JR, McCormick DA (2007) Thalamic synchrony and dynamic regulation of global forebrain oscillations. Trends Neurosci 30:350–356. 10.1016/j.tins.2007.05.007 [DOI] [PubMed] [Google Scholar]
- Ito HT, Schuman EM (2008) Frequency-dependent signal transmission and modulation by neuromodulators. Front Neurosci 2:138–144. 10.3389/neuro.01.027.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahnsen H, Llinás R (1984) Ionic basis for the electro-responsiveness and oscillatory properties of guinea-pig thalamic neurones in vitro. J Physiol 349:227–247. 10.1113/jphysiol.1984.sp015154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson BR, Brown JM, Kvarta MD, Lu JY, Schneider LR, Nadim F, Harris-Warrick RM (2011) Differential modulation of synaptic strength and timing regulate synaptic efficacy in a motor network. J Neurophysiol 105:293–304. 10.1152/jn.00809.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan A, Kyle JW, Hanck DA, Lipkind GM, Fozzard HA (2006) Isoform-dependent interaction of voltage-gated sodium channels with protons. J Physiol 576:493–501. 10.1113/jphysiol.2006.115659 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kloppenburg P, Levini RM, Harris-Warrick RM (1999) Dopamine modulates two potassium currents and inhibits the intrinsic firing properties of an identified motor neuron in a central pattern generator network. J Neurophysiol 81:29–38. 10.1152/jn.1999.81.1.29 [DOI] [PubMed] [Google Scholar]
- Kushinsky D, Morozova EO, Marder E (2019) In vivo effects of temperature on the heart and pyloric rhythms in the crab Cancer borealis. J Exp Biol 222:jeb199190. 10.1242/jeb.199190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee RH, Heckman CJ (1998) Bistability in spinal motoneurons in vivo: systematic variations in persistent inward currents. J Neurophysiol 80:583–593. 10.1152/jn.1998.80.2.583 [DOI] [PubMed] [Google Scholar]
- Li X, Bucher D, Nadim F (2018) Distinct co-modulation rules of synapses and voltage-gated currents coordinate interactions of multiple neuromodulators. J Neurosci 38:8549–8562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinas RR (1988) The intrinsic electrophysiological properties of mammalian neurons: insights into central nervous system function. Science 242:1654–1664. 10.1126/science.3059497 [DOI] [PubMed] [Google Scholar]
- Luther JA, Robie AA, Yarotsky J, Reina C, Marder E, Golowasch J (2003) Episodic bouts of activity accompany recovery of rhythmic output by a neuromodulator- and activity-deprived adult neural network. J Neurophysiol 90:2720–2730. 10.1152/jn.00370.2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manuel M, Zytnicki D, Meunier C (2014) The dendritic location of the L-type current and its deactivation by the somatic AHP current both contribute to firing bistability in motoneurons. Front Comput Neurosci 8:4. 10.3389/fncom.2014.00004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E (2012) Neuromodulation of neuronal circuits: back to the future. Neuron 76:1–11. 10.1016/j.neuron.2012.09.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, Bucher D (2007) Understanding circuit dynamics using the stomatogastric nervous system of lobsters and crabs. Annu Rev Physiol 69:291–316. 10.1146/annurev.physiol.69.031905.161516 [DOI] [PubMed] [Google Scholar]
- Marder E, O’Leary T, Shruti S (2014) Neuromodulation of circuits with variable parameters: single neurons and small circuits reveal principles of state-dependent and robust neuromodulation. Annu Rev Neurosci 37:329–346. 10.1146/annurev-neuro-071013-013958 [DOI] [PubMed] [Google Scholar]
- Martinez D, Anwar H, Bose A, Bucher DM, Nadim F (2019) Short-term synaptic dynamics control the activity phase of neurons in an oscillatory network. Elife 8:e46911. 10.7554/eLife.46911 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meister M, Wong RO, Baylor DA, Shatz CJ (1991) Synchronous bursts of action potentials in ganglion cells of the developing mammalian retina. Science 252:939–943. 10.1126/science.2035024 [DOI] [PubMed] [Google Scholar]
- Nadim F, Bucher D (2014) Neuromodulation of neurons and synapses. Curr Opin Neurobiol 29:48–56. 10.1016/j.conb.2014.05.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Northcutt AJ, Lett KM, Garcia VB, Diester CM, Lane BJ, Marder E, Schulz DJ (2016) Deep sequencing of transcriptomes from the nervous systems of two decapod crustaceans to characterize genes important for neural circuit function and modulation. BMC Genomics 17:868. 10.1186/s12864-016-3215-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusbaum MP, Marder E (1989) A modulatory proctolin-containing neuron (MPN). II. State-dependent modulation of rhythmic motor activity. J Neurosci 9:1600–1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusbaum MP, Beenhakker MP (2002) A small-systems approach to motor pattern generation. Nature 417:343–350. 10.1038/417343a [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh M, Zhao S, Matveev V, Nadim F (2012) Neuromodulatory changes in short-term synaptic dynamics may be mediated by two distinct mechanisms of presynaptic calcium entry. J Comput Neurosci 33:573–585. 10.1007/s10827-012-0402-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park YY, Johnston D, Gray R (2013) Slowly inactivating component of Na+ current in peri-somatic region of hippocampal CA1 pyramidal neurons. J Neurophysiol 109:1378–1390. 10.1152/jn.00435.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piontkivska H, Hughes AL (2003) Evolution of vertebrate voltage-gated ion channel α chains by sequential gene duplication. J Mol Evol 56:277–285. 10.1007/s00239-002-2399-9 [DOI] [PubMed] [Google Scholar]
- Ramirez JM, Baertsch NA (2018) The dynamic basis of respiratory rhythm generation: one breath at a time. Annu Rev Neurosci 41:475–499. 10.1146/annurev-neuro-080317-061756 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez JC, Blitz DM, Nusbaum MP (2013) Convergent rhythm generation from divergent cellular mechanisms. J Neurosci 33:18047–18064. 10.1523/JNEUROSCI.3217-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roeper J, Lorra C, Pongs O (1997) Frequency-dependent inactivation of mammalian A-type K+ channel KV1.4 regulated by Ca2+/calmodulin-dependent protein kinase. J Neurosci 17:3379–3391. 10.1523/JNEUROSCI.17-10-03379.1997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum P, Marder E (2018) Graded transmission without action potentials sustains rhythmic activity in some but not all modulators that activate the same current. J Neurosci 38:8976–8988. 10.1523/JNEUROSCI.2632-17.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharples SA, Whelan PJ (2017) Modulation of rhythmic activity in mammalian spinal networks is dependent on excitability state. eNeuro 4:ENEURO.0368-16.2017. 10.1523/ENEURO.0368-16.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shindou T, Shindou M, Watanabe S, Wickens J (2019) A silent eligibility trace enables dopamine-dependent synaptic plasticity for reinforcement learning in the mouse striatum. Eur J Neurosci 49:726–736. 10.1111/ejn.13921 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soldatov NM (1994) Genomic structure of human L-type Ca2+ channel. Genomics 22:77–87. 10.1006/geno.1994.1347 [DOI] [PubMed] [Google Scholar]
- Stein W (2009) Modulation of stomatogastric rhythms. J Comp Physiol A Neuroethol Sens Neural Behav Physiol 195:989–1009. 10.1007/s00359-009-0483-y [DOI] [PubMed] [Google Scholar]
- Steriade M, Contreras D (1995) Relations between cortical and thalamic cellular events during transition from sleep patterns to paroxysmal activity. J Neurosci 15:623–642. 10.1523/JNEUROSCI.15-01-00623.1995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swensen AM, Marder E (2000) Multiple peptides converge to activate the same voltage-dependent current in a central pattern-generating circuit. J Neurosci 20:6752–6759. 10.1523/JNEUROSCI.20-18-06752.2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swensen AM, Marder E (2001) Modulators with convergent cellular actions elicit distinct circuit outputs. J Neurosci 21:4050–4058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swensen AM, Golowasch J, Christie AE, Coleman MJ, Nusbaum MP, Marder E (2000) GABA and responses to GABA in the stomatogastric ganglion of the crab Cancer borealis. J Exp Biol 203:2075–2092. 10.1242/jeb.203.14.2075 [DOI] [PubMed] [Google Scholar]
- Tang LS, Taylor AL, Rinberg A, Marder E (2012) Robustness of a rhythmic circuit to short- and long-term temperature changes. J Neurosci 32:10075–10085. 10.1523/JNEUROSCI.1443-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor AL, Goaillard JM, Marder E (2009) How multiple conductances determine electrophysiological properties in a multicompartment model. J Neurosci 29:5573–5586. 10.1523/JNEUROSCI.4438-08.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tellez JO, Dobrzynski H, Greener ID, Graham GM, Laing E, Honjo H, Hubbard SJ, Boyett MR, Billeter R (2006) Differential expression of ion channel transcripts in atrial muscle and sinoatrial node in rabbit. Circ Res 99:1384–1393. 10.1161/01.RES.0000251717.98379.69 [DOI] [PubMed] [Google Scholar]
- Tryba AK, Peña F, Ramirez J-M (2006) Gasping activity in vitro: a rhythm dependent on 5-HT2A receptors. J Neurosci 26:2623–2634. 10.1523/JNEUROSCI.4186-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vajda I, van Pelt J, Wolters P, Chiappalone M, Martinoia S, van Someren E, van Ooyen A (2008) Low-frequency stimulation induces stable transitions in stereotypical activity in cortical networks. Biophys J 94:5028–5039. 10.1529/biophysj.107.112730 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yagishita S, Hayashi-Takagi A, Ellis-Davies GCR, Urakubo H, Ishii S, Kasai H (2014) A critical time window for dopamine actions on the structural plasticity of dendritic spines. Science 345:1616–1620. 10.1126/science.1255514 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao S, Golowasch J, Nadim F (2010) Pacemaker neuron and network oscillations depend on a neuromodulator-regulated linear current. Front Behav Neurosci 4:21. 10.3389/fnbeh.2010.00021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao S, Sheibanie AF, Oh M, Rabbah P, Nadim F (2011) Peptide neuromodulation of synaptic dynamics in an oscillatory network. J Neurosci 31:13991–14004. 10.1523/JNEUROSCI.3624-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Depolarization rates for different cycle periods of the unitary realistic LP voltage waveform. Download Figure 1-1, XLSX file (9.5KB, xlsx) .
Two-way RM ANOVA for initial state I-V parameters. α = 0.05. Direction: positive or negative. Slope (in mV/s): 50, 100, 200, 400. Data for VImax failed normality and equal variance tests. Download Figure 2-1, XLSX file (9.7KB, xlsx) .
Data for panel Cii. Download Figure 2-2, XLSX file (12.7KB, xlsx) .
The codes used in the study. Download Extended Data 1, ZIP file (4.9MB, zip) .
One-way RM ANOVA for the steady/initial state ratios of IProc. α = 0.05. Slopes (in mV/s): 100, 200, 400. Missing N: 200 mV/s: 2; 400 mV/s: 2. Download Figure 3-1, XLSX file (9.4KB, xlsx) .
One-way ANOVA on ranks for the time constant of the slow inactivation. α = 0.05. Slope (in mV/s): 100, 200, 400. Missing N: 200 mV/s: 2; 400 mV/s: 2. Download Figure 3-2, XLSX file (9.4KB, xlsx) .
Data for panels C, D. Download Figure 3-3, XLSX file (11.1KB, xlsx) .
Two-way RM ANOVA for steady state I-V parameters (ramp-and-hold). α = 0.05. Direction: positive or negative. Slope (in mV/s): 100, 200, 400. Download Figure 4-1, XLSX file (9.6KB, xlsx) .
Data for panel C. Download Figure 4-2, XLSX file (10.5KB, xlsx) .
RM ANOVA for parameters obtained with realistic waveform stimulation. Download Figure 5-1, XLSX file (9.5KB, xlsx) .
Data for panel B. Download Figure 5-2, XLSX file (10.2KB, xlsx) .
Two-way RM ANOVA for steady state I-V parameters at small stimulus amplitude (ramp-and-hold). α = 0.05. Directions: positive or negative. Slope (in mV/s): 40, 80, 160. Download Figure 7-1, XLSX file (9.6KB, xlsx) .
Data for panel B. Download Figure 7-2, XLSX file (9.7KB, xlsx) .
Two-way RM ANOVA for initial state I-V parameters (ramps) in Cd2+ saline. α = 0.05. Direction: positive or negative. Slope (in mV/s): 50, 100, 200, 400. Download Figure 8-1, XLSX file (9.7KB, xlsx) .
Two-way ANOVA for the slopes of the linear fits across ramps with the same direction. α = 0.05. Direction: positive or negative. Saline: normal or Cd2+. Failed normality and equal variance tests. Download Figure 8-2, XLSX file (9.6KB, xlsx) .
Two-way RM ANOVA for IProc in initial and steady state in normal saline and Cd2+ saline. α = 0.05. State: initial or steady. Slope (in mV/s): 100, 200, 400. Download Figure 8-3, XLSX file (9.5KB, xlsx) .
Data for panel C. Download Figure 8-4, XLSX file (9.6KB, xlsx) .
Data for panel Dii. Download Figure 8-5, XLSX file (9.5KB, xlsx) .
Data for Extended Data Figure 8-3E. Download Figure 8-6, XLSX file (8.9KB, xlsx) .
Data for panel Bii. Download Figure 9-1, XLSX file (8.7KB, xlsx) .