Abstract
Purpose:
To demonstrate methods for Receiver-Operating Characteristic (ROC) analysis of correlated eye data.
Methods:
We applied the Obuchowski’s nonparametric approach and cluster bootstrap for estimating and comparing the area under ROC curve (AUC) between different sets of predictors to three datasets with varying inter-eye correlation.
Results:
In an optic neuritis (ON) study of 152 eyes (80 patients), the AUC of optical coherence tomography retinal nerve fiber layer thickness for diagnosing ON (inter-eye kappa=0.13) was 0.71 (95% confidence interval (95%CI): 0.622, 0.792) from the naïve approach without accounting for inter-eye correlation was narrower than from nonparametric (95%CI: 0.613, 0.801) or cluster bootstrap (95%CI: 0.614, 0.797) approaches.
In an analysis of 198 eyes (135 patients), the baseline AREDS scale predicted 5-year incidence of advanced AMD (inter-eye kappa=0.23) with AUC of 0.72. The 95%CI from the naïve approach was slightly narrower (0.645, 0.794) than from the nonparametric (0.641, 0.797) or cluster bootstrap (0.641, 0.793) approaches.
In an analysis of 1542 eyes (771 infants), birth-weight and gestational-age predicted treatment-requiring retinopathy of prematurity (inter-eye kappa=0.98) with AUC of 0.80. Furthermore, the 95%CI from the naïve approach was narrower (0.769, 0.835) than from the nonparametric (0.755, 0.848) or cluster bootstrap (0.755, 0.845) approaches. 95%CIs for AUC differences between different models were narrower in the naïve approach than the nonparametric or cluster bootstrap approaches.
Conclusion:
In ROC analysis of correlated eye data, ignoring inter-eye correlation leads to narrower 95%CI with under-estimation dependent on magnitude of inter-eye correlation. Nonparametric and cluster bootstrap approaches properly account for inter-eye correlation.
Keywords: Ocular test, area under ROC curve, ROC analysis, cluster bootstrap, correlated eye data
INTRODUCTION
In ophthalmology and vision science, diagnostic or screening tests/tools including summary risk scores incorporating multiple predictors play an important role for the diagnosis and management of eye diseases.1–5 As many eye diseases can be bilateral,6 ocular tests or summary risk scores are often available in both eyes of a subject, yielding correlated eye data. Examples include ophthalmic imaging (e.g., optical coherence tomography (OCT)) in both eyes for the diagnosis of retinal diseases and tests of tear break-up time in both eyes for the diagnosis of dry eye. Before a new ocular test is adopted, its performance for the diagnosis or prediction of disease must be evaluated in a sample of the targeted population. Ocular tests that provide a binary determination of disease status (present or absent) are usually evaluated by sensitivity and specificity.7 However, for ocular tests that provide ordinal or continuous measures (e.g., OCT retinal thickness for retinal diseases), or a summary risk score for predicting development of advanced age-related macular degeneration,8 the sensitivity and specificity at various cutpoints of continuous or ordinal measures are calculated to yield the receiver operating characteristic (ROC) curve, and the area under the curve (AUC) is often used to evaluate the overall performance of the test for discriminating or predicting the disease.9 When data from both eyes are used to calculate the AUC or to compare two AUCs from two diagnostic tests or two prediction models, the inter-eye correlation needs to be accounted for, particularly with respect to the estimation of variance of the estimated AUC or AUC difference that affects the confidence interval and p-value. However, the methods for ROC analysis with correlated eye data are not well known by most ophthalmic and vision researchers. This tutorial paper describes two statistical approaches for calculating AUC, its 95% confidence interval (95% CI) and the comparison of two AUCs for correlated eye data. We demonstrate the application of these approaches to analyze three correlated eye datasets from real clinical ophthalmic studies.
METHODS
We start the description of ROC analysis by calculating the AUC, its 95% CI, and comparing AUCs from two tests under the assumption of independent samples, for example if only one eye from each subject is evaluated, or the evaluation occurs at the subject level. We then describe the statistical methods to account for inter-eye correlation in calculating the 95% CIs of AUC and in the comparison of two AUCs when ocular measures are taken from both eyes.
ROC Analysis for Independent Samples
For the independent sample case, AUC and its 95% CI can be obtained through logistic regression models by using the continuous or ordinal diagnostic test result as the predictor and the true disease status (yes/no) as the outcome variable. The c-index from the logistic regression model is equivalent to the AUC. The AUC is equal to the probability that a random eye with the disease has a higher value of the test result than a random eye without the disease (assuming a higher value of the test indicates a higher likelihood of abnormality). The AUC usually ranges from 0.5 to 1, with 0.5 indicating no discrimination and 1 indicating perfect discrimination.9 An AUC greater than 0.9 is considered excellent, 0.8 to 0.9 very good, 0.7 to 0.8 good, 0.6 to 0.7 average, and less than 0.6 poor.10
The comparison of two AUCs needs to consider whether two AUCs are from the same subjects or not. If two AUCs are from the same subjects (i.e., paired data), the ROCCONTRAST statement in SAS for fitting a logistic regression model can be used to compare AUCs using the method of Delong.11 However, the Delong method was found not appropriate when: (1) the AUCs are from two nested models (e.g. a base model with one or more predictors and a more comprehensive model that includes all predictors in the base model plus additional predictors); and (2) the additional predictors in the more comprehensive model are not associated with the disease.12 If two AUCs for comparison are from two different samples (e.g., unpaired data), a logistic regression model can be fitted for each sample to get their AUCs and their standard errors. The chi-square test can then be applied to compare two independent AUCs using the followingformula.13
where AUC1 and AUC2 are areas under two independent ROC curves, and s1 and s2 are their respective standard errors from two logistic regression models for two independent samples.14 The p-value corresponding to the above χ2 statistic with one degree of freedom can then be calculated.
ROC Curve Analysis for Correlated Eye Data
When data from both eyes of at least some subjects are available, it is often desirable to perform the ROC analysis at the eye-level (i.e., using the eye as the unit of analysis) to maximize the use of data, while accounting for the inter-eye correlation. When an ocular test is performed in two eyes of a subject, it is appropriate to calculate the point estimate for AUC using the same approach as for independent data. However, the calculation of variance for estimated AUC and 95% CI for AUC, or comparison of two AUCs needs to account for the inter-eye correlation. Here we describe two approaches for ROC analysis of correlated eye data including the Obuchowski nonparametric ROC analysis for clustered data,15 and the cluster bootstrap.16
Nonparametric ROC Analysis for Clustered Data
Obuchowski described a method for estimating the variance and standard error of the AUC from clustered data based on the concepts of design effect and effective sample size.15 This method allows estimation of the standard error of the AUC for a single test or of the difference of two AUCs, for example arising from two different risk scores applied to the same clustered data. Obuchowski used the structural components approach to ROC curve estimation of DeLong et al, 11 but extended it to clustered ROC data using ideas from Rao and Scott 17 that are based on the concepts of design effect and effective sample size used in the analysis of data from sample surveys. The Obuchowski method is nonparametric, thus it does not require specification of the intra-cluster correlation structure. The method can be used to account for inter-eye correlation in the dichotomous disease status and inter-eye correlation in test results that are either continuous or ordinal. Her Monte Carlo simulation study suggests that the method is robust to a variety of intra-cluster correlation patterns, as well as to non-normally distributed test results. The technical details and the formulas for calculations of the variance, standard error of AUC and AUC differences, and their 95% CIs for correlated eye data can be found in Supplemental Note 1. R functions for performing Obuchowski’s nonparametric ROC analysis of clustered data are available at https://www.lerner.ccf.org/qhs/software/roc_analysis.php.
Cluster Bootstrap for ROC Analysis of Clustered Data
Bootstrapping18 is a resampling technique involving computing a statistic of interest (e.g., AUC) repeatedly based on a large number of random samples (with replacement) drawn from the original sample, so that the variability of the statistic of interest can be determined. Thus, the bootstrap provides a way of making probability-based, assumption-free inference for the AUC.
For the bootstrap of correlated eye data, the same number of subjects as that in a given sample are randomly selected with replacement. For each subject selected, all eligible eyes are included in the bootstrapped sample. The AUC is computed using the bootstrapped sample and the process is repeated B times. The nonparametric 95% CI for AUC can be derived based on the 2.5th percentile and 97.5th percentile of the ordered distribution of AUC from the B samples. The 95% CI for the AUC can also be calculated as asymptotic normal intervals using mean where the mean and SD of AUC are calculated from the AUCs of B bootstrap samples. Simulation studies have shown that percentile intervals have better coverage than asymptotic normal intervals.19 However, the percentile-based 95% confidence interval has two potential limitations. First, it does not use the AUC estimate from the original data; the estimate is based only on bootstrap resamples. Second, it does not adjust for the skewed distribution of the bootstrapped AUC estimates. The bias-corrected/accelerated (BCa) bootstrap confidence interval was developed to improve the percentile-based confidence interval,20 as the BCa method can correct for bias and skewness in the distribution of the bootstrapped AUC estimates. The R codes for calculating both the percentile-based confidence interval and BCa confidence interval using clustered bootstrap are in Supplemental Note 2. Although guidelines have been suggested as to the optimal number of bootstrap replications, 1,000 replications is generally considered acceptable for standard error estimates.16
When bootstrapping the AUC from a multivariable logistic regression model (i.e., with more than one predictor in the logistic regression model), the risk score from the multivariable logistic regression model in the original sample should be first calculated as , where α is the intercept, and βk is the regression coefficient for the kth predictor Xk in the multivariable logistic model. These risk scores are used in the calculation of the point estimate of the AUC. To calculate the 95% CI for the AUC, we re-sample the dataset of the risk scores and calculate the AUC for each re-sampled dataset using a univariable logistic regression model with risk score as the only predictor. It is important to use risk scores calculated from the original sample for calculating the AUC for each bootstrap sample. In this way, a subject will have the same risk score for AUC calculation across all bootstrap samples. Otherwise, if a multivariable logistic regression model were fitted for each bootstrap sample, the risk score for a subject would be different across bootstrap samples, which could result in a biased estimate of the AUC and its 95% CI.
The cluster bootstrap approach can also be used to compare two AUCs from two different risk scores or two different tests, by calculating their AUC difference (ΔAUC) and its 95% CI, following the similar bootstrap procedure as described above. For the cluster bootstrap of ΔAUC, the two AUCs correspond to two different tests or risk scores and their AUC difference (ΔAUC) were calculated from each bootstrap sample, and this cluster bootstrap process is repeated B times to generate the distribution of ΔAUC. The nonparametric 95% CI for ΔAUC can be derived based on the 2.5th percentile and 97.5th percentile of the ordered distribution of ΔAUC from the B bootstrap samples. If the predictor(s) of interest are significantly associated with the outcome, the p-value for testing whether the ΔAUC from these additional predictor(s) is significantly different from 0 (e.g. two AUCs differ significantly or not) can be calculated based on the test statistic ΔAUC/SD, which asymptotically follows a N(0, 1) distribution.
The SAS macro for performing these cluster bootstrap AUC analyses is in Supplemental Note 3.
We applied the Obuchowski’s nonparametric approach and cluster bootstrap for estimating and comparing AUC to the data from three clinical studies as described below.
Example 1: ROC Analysis of Retinal Nerve Fiber Layer Thickness for Diagnosis of Optic Neuritis in Patients with Multiple Sclerosis
Eyes of patients with multiple sclerosis (MS) have a reduced number of retinal ganglion cell axons.21 Ocular imaging techniques, including optical coherence tomography (OCT) and scanning laser polarimetry with variable corneal compensation (GDx) have demonstrated retinal nerve fiber layer (RNFL) thinning from optic neuritis (ON) in patients with MS. A study22 was conducted to examine the capacity of RNFL thickness measurements from OCT and GDx to distinguish between MS eyes with and without a history of ON. The study included a total of 152 eyes from 80 MS patients, 66 eyes from 50 patients had a history of ON and 86 eyes from 60 patients did not have a history of ON. Of note, 30 patients had one eye with ON but the fellow eye without ON (Online Table 1). The study excluded 8 eyes with ongoing ON or having an ON episode within 3 months of testing. Each patient underwent measurement of the RNFL thickness for eligible eyes using OCT and GDx. The AUC was calculated to determine the capacity of RNFL thickness to distinguish eyes with a history of ON from eyes without a history of ON by using OCT alone and GDx alone. The AUCs for OCT and GDx were compared to determine whether their discrimination ability for ON eyes was the same or different. Since most patients contributed both eyes for analysis (although their ON status may have differed) and RNFL thickness from two eyes are correlated, we applied Obuchowski’s nonparametric ROC analysis and the cluster bootstrap. For comparison, the ROC analysis for independent samples (e.g., naïve analysis that ignored the inter-eye correlation) was also performed. The SAS codes for the naïve analysis and cluster bootstrap and R codes for Obuchowski’s nonparametric ROC analysis are in Supplemental Note 4.
Example 2: ROC Analysis for Predicting Incidence of Advanced Age-related macular Degeneration
The Age-related Eye disease Study (AREDS) is a multi-center study of the clinical course, prognosis, and risk factors for age-related macular degeneration (AMD) and cataract.23 The study included a randomized, placebo-controlled clinical trial of treatment with high-dose antioxidant vitamins and/or zinc on the incidence of advanced AMD and vision loss. During the study, the AREDS study group developed a 9-step AREDS severity scale for AMD to predict its progression to advanced AMD.24 This eye-specific 9-step severity scale was determined based on the drusen area and pigmentary abnormalities of the retina. Higher scores on the severity scale were found to be strongly associated with increased risk of progression to advanced AMD in the AREDS Study.24
We performed ROC analyses of the AREDS severity scale for predicting the 5-year incidence of advanced AMD among high risk eyes (defined as baseline AREDS severity scale of 5 or above) that were followed at least for 5 years. Among 1355 patients eligible for this analysis, a random sample of 135 patients (198 eyes) were selected, consisting of 63 patients (126 eyes) with both eyes eligible, 34 patients with one eye eligible because the fellow eye had a severity scale below 5, and 38 patients with one eye eligible because the fellow eye already had advanced AMD at baseline. We further evaluated whether including baseline demographics (age, gender, smoking status), the randomized treatment group and the fellow eye status (e.g., severity scale below 5, severity scale 5 to 8, or advanced AMD) improves the prediction for 5-year incidence of advanced AMD by comparing the AUC from a prediction model using only the baseline AREDS severity scale to a prediction model using the baseline AREDS severity scale plus these baseline covariates.
Since both the AREDS severity scale and outcome measure (e.g. incidence of advanced AMD) are eye-specific, it is desirable to perform the ROC analysis at the eye-level. For comparison purposes, we performed ROC analysis using several approaches: (1) naïve approach using the eye as the unit of analysis without accounting for inter-eye correlation; (2) Obuchowski’s nonparametric ROC analysis of clustered data; (3) cluster bootstrap; (4) ROC analysis for right eye and left eye separately; (5) person-level ROC analysis using the severity scale from the worse eye for predicting advanced AMD in either eligible eye. The SAS and R codes for these ROC analyses are in Supplemental Note 5.
Example 3: ROC Analysis for Predicting the Treatment-Requiring Retinopathy of Prematurity
Using data from the Telemedicine Approaches to Evaluating Acute-Phase Retinopathy of Prematurity Study,25 we previously developed a model for predicting development of treatment-requiring ROP (TR-ROP).5 The prediction model was based on data from 771 infants with birth weight <1251 grams who completed one retinal imaging session by 34 weeks of postmenstrual age and one subsequent retinopathy of prematurity (ROP) examination by study-certified ophthalmologists to determine the TR-ROP. The factors in the model were: birth weight (BW), gestational age (GA), findings from the first image session (number of quadrants with preplus disease, presence of blot hemorrhage, ROP stage and zone), respiratory status and weight gain rate by the first image session. We calculated the AUC from a prediction model using all of the above factors, and compared it to the AUC using BW and GA only. The analysis codes are in Supplemental Note 6.
RESULTS:
ROC Analysis of Retinal Nerve Fiber Layer Thickness for Diagnosis of Optic Neuritis in Patients with Multiple Sclerosis.
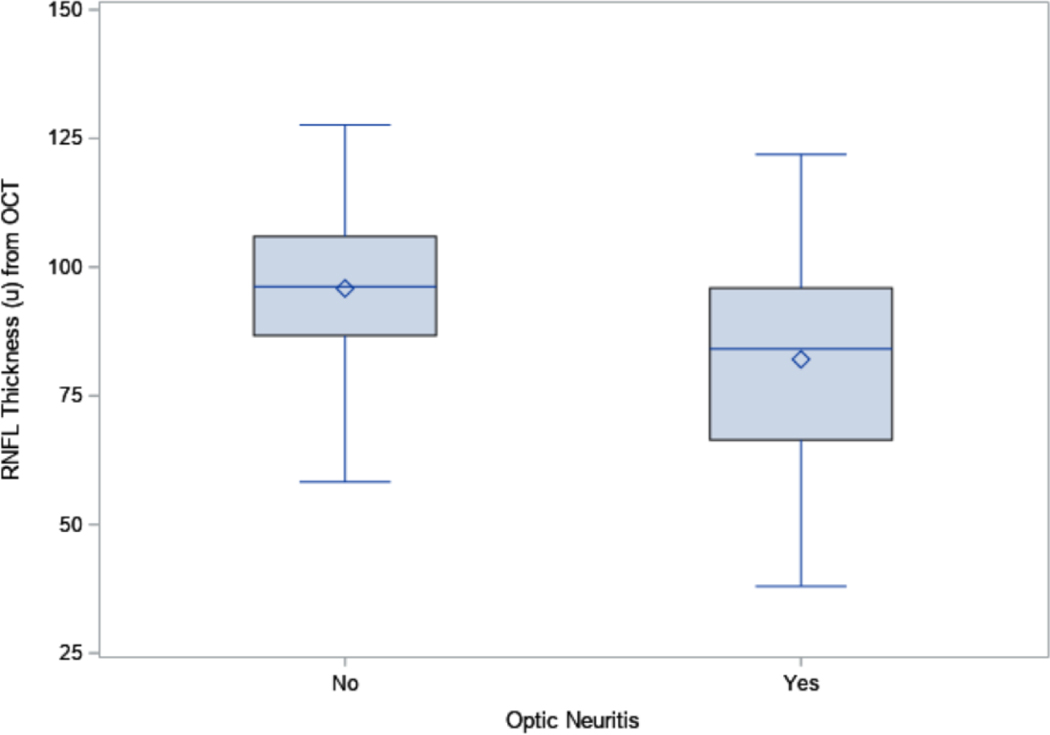
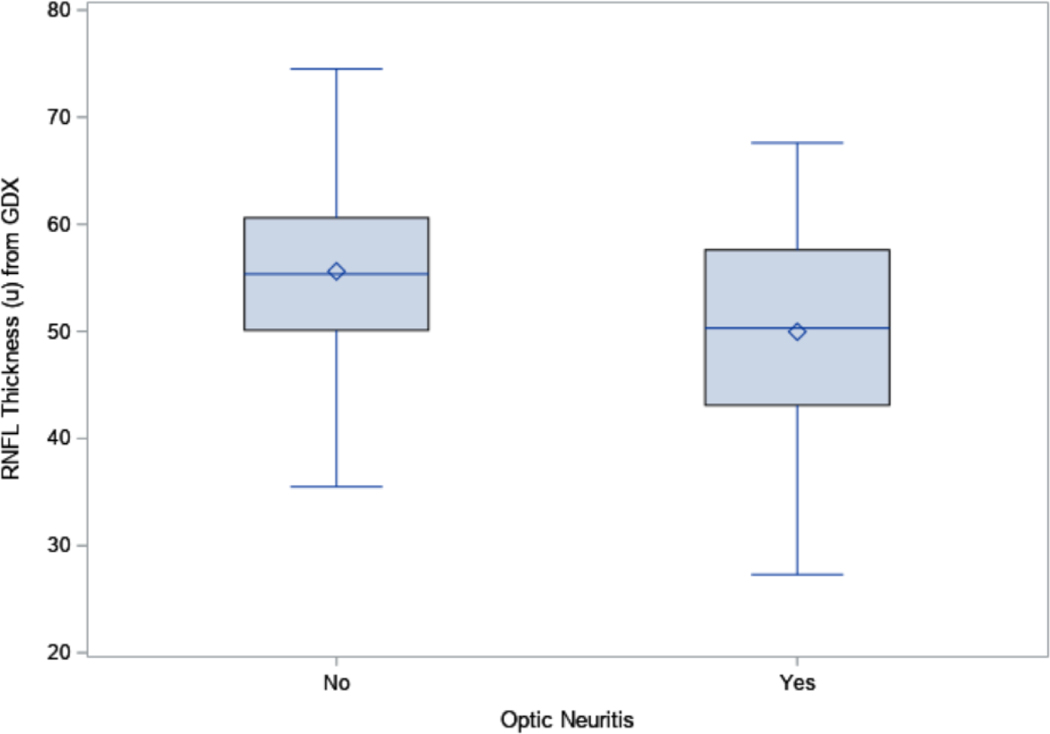
The RNFL was significantly thinner in the 66 eyes with ON than in the 86 eyes without ON for both OCT (82.1 μm vs. 95.8 μm, p<0.0001, Figure 1A) and GDx (50.0 μm vs. 55.6 μm, p<0.0001, Figure 1B). The inter-eye correlation for RNFL thickness was moderate for both OCT (Spearman correlation coefficient=0.55) and GDx (Spearman correlation coefficient=0.61). The RNFL thickness from OCT and GDx were also moderately correlated (Spearman correlation coefficient=0.61). The inter-eye agreement on ON status was low (percent agreement=52.5%, kappa=0.13, Online Table 1).
Figure 1A:
Boxplots for the retinal nerve fiber layer (RNFL) thickness from optical coherence tomography (OCT) in eyes with and without optic neuritis
Figure 1B:
The Boxplots for the retinal nerve fiber layer (RNFL) thickness from GDx in eyes with and without optic neuritis
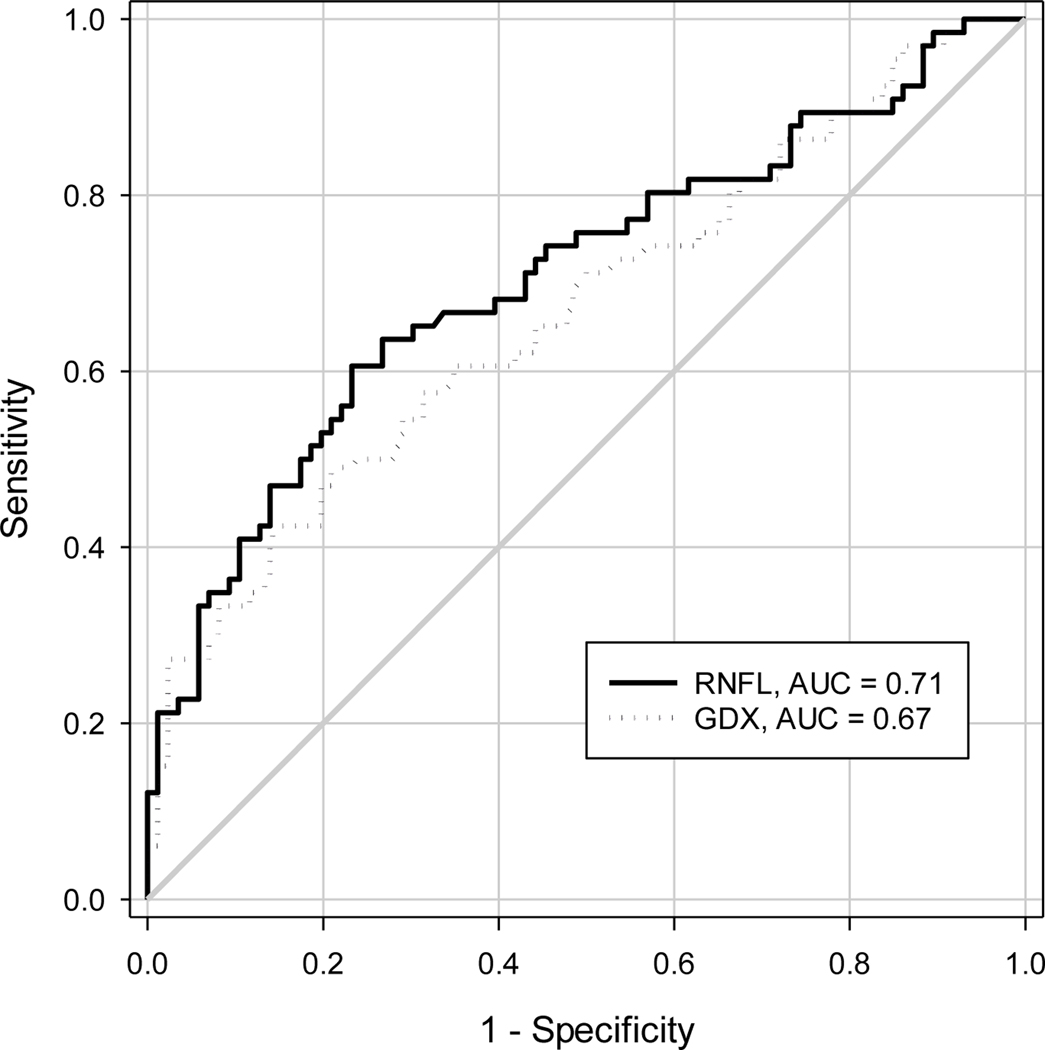
The AUC and 95% CI from various ROC analyses are shown in Table 1. The point estimate of AUC for RNFL thickness from various analysis approaches were similar (0.71 for OCT, 0.67 for GDx, Figure 2), but their 95% CIs were different. The naïve approach provided a narrower 95% CI than the approaches that accounted for inter-eye correlation, with the width of the 95% CI for AUC from the naïve approach, nonparametric approach, and bootstrap approach in SAS 0.170, 0.188, 0.183, respectively for OCT, 0.176, 0.199 and 0.191 respectively for GDx. When the AUCs for OCT and GDx were compared, all three analysis approaches did not yield a statistically significant difference (all p≥0.35); the width of the 95% CI for the AUC difference between OCT and GDx was 0.167, 0.180, and 0.176 respectively for the naïve approach, nonparametric approach, and cluster bootstrap. The percentile-based 95% confidence interval and the BCa confidence interval from the cluster bootstrap were similar for both AUC and AUC difference (Table 1).
Table 1:
Area under ROC curve from various analysis approaches using RNFL thickness from OCT and GDX for distinguish eyes with vs. without optic neuritis
| Analysis Approach | OCT RNFL thickness | GDx RNFL thickness | Difference OCT vs. GDX | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| All eyes analysis | AUC | 95% CI | Width | AUC | 95% CI | Width | AUC | 95% CI | Width | P-value |
| Naïve approach | 0.707 | 0.622, 0.792 | 0.170 | 0.667 | 0.579, 0.755 | 0.176 | 0.040 | −0.043, 0.124 | 0.167 | 0.35 |
| Nonparametric ROC analysis | 0.707 | 0.613, 0.801 | 0.188 | 0.667 | 0.568, 0.766 | 0.199 | 0.040 | −0.050, 0.130 | 0.180 | 0.38 |
| Cluster bootstrap: percentile-based in SAS | 0.710 | 0.614, 0.797 | 0.183 | 0.670 | 0.572, 0.763 | 0.191 | 0.039 | −0.047, 0.129 | 0.176 | 0.38 |
| Cluster bootstrap: BCa in R | 0.709 | 0.614, 0.798 | 0.184 | 0.670 | 0.561, 0.763 | 0.202 | 0.038 | −0.045, 0.138 | 0.183 | NA |
| One Eye Analysis | ||||||||||
| Using a random eye (36 eyes with ON, 44 eyes without non-ON) | 0.717 | 0.598, 0.835 | 0.237 | 0.665 | 0.541, 0.790 | 0.249 | 0.051 | −0.069, 0.171 | 0.240 | 0.40 |
ON=optic neuritis; OCT=optical coherence tomography; GDx=scanning laser polarimetry with variable corneal compensation; RNFL=retinal nerve fiber layer; AUC=area under ROC curve; BCa=Bias-corrected/accelerated; NA=not available.
Figure 2:
Receiver-Operating Characteristic (ROC) curves from optical coherence tomography (OCT) and GDx RNFL thickness of all eyes
To demonstrate the loss of precision from choosing one eye per patient for analysis which avoids the need to account for inter-eye correlation, we also randomly chose one eye for analysis. This analysis included 36 eyes with ON and 44 eyes without ON. The AUC (95% CI) from this analysis was 0.717 (95% CI: 0.598, 0.835) for OCT, 0.665 (95% CI: 0.541, 0.790) for GDx, and 0.051 (95% CI: −0.069, 0.171) for their difference. These 95% CIs were wider than in the analyses using all eyes with accounting for the inter-eye correlation (Table 1).
ROC Analysis for Predicting Incidence of Advanced Age-related Macular Degeneration
The frequency distribution of baseline AREDS severity scale scores and the 5-year risk of advanced AMD in the bilateral and unilateral eyes are shown in Table 2. The 5-year advanced AMD risk was highest (47%) in the unilateral eyes whose fellow eye had advanced AMD at baseline, while lowest (8.8%) in the unilateral eyes whose fellow eye had baseline severity scale less than 5, while the bilateral eligible eyes had a 5-year advanced AMD rate of 21%. For all included eyes, the 5-year risk of advanced AMD increases with higher baseline AREDS severity scale (Table 2).
Table 2:
Risk of progression to advanced AMD in 5 years by baseline AREDS severity scale in each group of patients (N=135 patients, 198 eyes)
| Bilateral patients (N=63 patients, 126 eyes) | Unilateral patients where the fellow eye had severity scale <5 (N=34 patients, 34 eyes) | Unilateral patients where the fellow eye had advanced AMD (N=38 patients, 38 eyes) | ||||
|---|---|---|---|---|---|---|
| Baseline AREDS Severity Scale | # of eyes | # of eyes progressing to advanced AMD in 5-year (%) | # of eyes | # of eyes progressed to advanced AMD in 5-year (%) | # of eyes | # of eyes progressing to advanced AMD in 5-year (%) |
| 5 | 20 | 2 (10.0%) | 19 | 0 (0.0%) | 3 | 0 (0.0%) |
| 6 | 39 | 6 (15.4%) | 7 | 0 (0.0%) | 9 | 3 (33.3%) |
| 7 | 58 | 14 (24.1%) | 6 | 2 (33.3%) | 19 | 9 (47.4%) |
| 8 | 9 | 4 (44.4%) | 2 | 1 (50.0%) | 7 | 6 (85.7%) |
| Total | 126 | 26 (20.6%) | 34 | 3 (8.8%) | 38 | 18 (47.4%) |
The inter-eye agreement of the baseline AREDS severity scale among the 63 bilateral eligible subjects is shown in Online Table 2. Their inter-eye agreement is low, with percent of agreement 44.4% and weighted kappa (weight calculated using Cicchetti and Allison method26) of 0.33 (95% CI: 0.16, 0.49). The risk score calculated from regression coefficients of the multivariable logistic regression model (Online Table 3) had inter-eye correlation of 0.60.
Among 63 bilateral eligible subjects, 21 (33.3%) subjects (26 eyes, 20.6%) developed advanced AMD by 5-years, with 5 (7.9%) subjects having bilateral advanced AMD and 16 (25.3%) subjects having unilateral advanced AMD. The inter-eye agreement for incidence of advanced AMD was low, with a percent of agreement of 75% and kappa of 0.23 (95% CI: −0.05, 0.50) (Online Table 4).
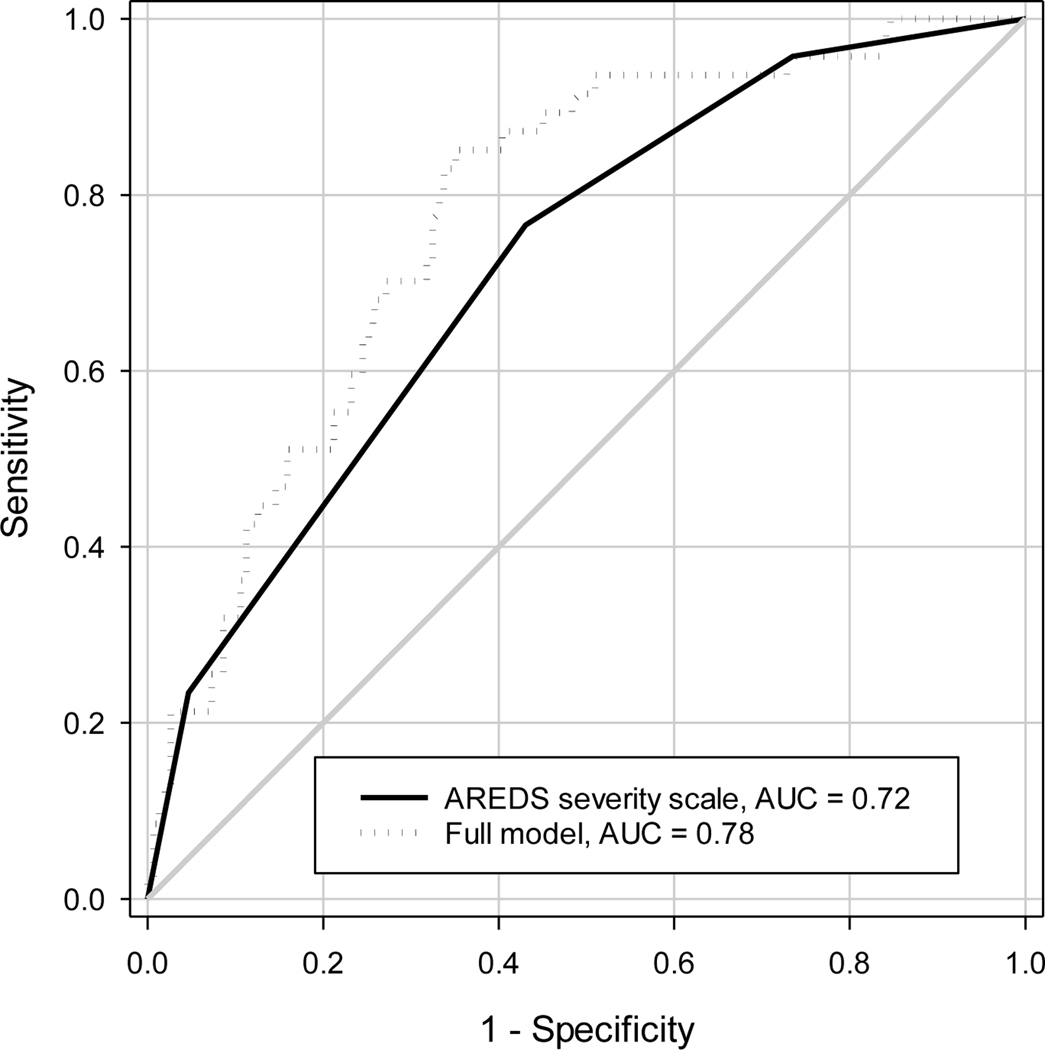
The prediction model for advanced AMD in an eye within 5 years using only the baseline AREDS severity scale had the area under the ROC curve of 0.719 (Figure 3). The 95% CIs of the AUC calculated from various approaches are shown in Table 3. The naïve approach that ignored the inter-eye correlation had the narrowest 95% CI (width of 95% CI: 0.149), while the 95% CIs from the nonparametric clustered ROC analysis and cluster bootstrap in SAS were slightly wider than the naïve approach (0.156, 0.152, respectively). When the ROC analyses were performed for left eyes and right eyes separately, the AUC from right eyes was higher than that from left eyes (0.745 vs. 0.691), and the 95% CIs were all wider (width 0.205 and 0.218 respectively) than that from the analysis using both eyes, reflecting the loss of information from a single eye analysis. Similarly, when the AREDS severity scale scores from the worse eye were used to predict 5-year incidence of advanced AMD in either eye, the AUC was 0.727 (width of 95% CI: 0.161).
Figure 3:
Receiver-Operating Characteristic (ROC) curves for predicting 5-year incidence of advanced AMD using baseline severity scale only and using the combination of baseline severity scale along with demographics and treatment. AUC=Area under ROC curve.
Table 3:
The AUC from prediction of 5-year incidence of advanced AMD using baseline AREDS severity scale without or with inclusion of demographics and treatment among patients with baseline AREDS severity scale 5 or above (N=135 patients, 198 eyes)
| Analysis Approach | AREDS severity scale only* | AREDS severity scale + demographics + treatment + fellow eye group* | Difference in AUC (95% CI) | P-value | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Two Eyes Analysis | AUC | 95% CI | Width | AUC | 95% CI | Width | AUC | 95% CI | Width | |
| Naïve approach | 0.719 | 0.645, 0.794 | 0.149 | 0.783 | 0.709, 0.857 | 0.148 | 0.064 | 0.009, 0.119 | 0.110 | 0.02 |
| Nonparametric clustered ROC analysis | 0.719 | 0.641, 0.797 | 0.156 | 0.783 | 0.708, 0.859 | 0.151 | 0.064 | 0.008, 0.120 | 0.112 | 0.03 |
| Cluster Bootstrap: percentile-based in SAS | 0.722 | 0.641, 0.793 | 0.152 | 0.785 | 0.706, 0.855 | 0.149 | 0.063 | 0.009, 0.120 | 0.111 | 0.03 |
| Cluster bootstrap: BCa in R | 0.720 | 0.640, 0.798 | 0.158 | 0.785 | 0.702, 0.856 | 0.154 | 0.065 | 0.004, 0.121 | 0.117 | NA |
| Left Eye Analysis (N=102) | ||||||||||
| Standard logistic regression | 0.691 | 0.583, 0.801 | 0.218 | 0.786 | 0.692, 0.890 | 0.198 | 0.094 | −0.004, 0.192 | 0.196 | 0.06 |
| Right Eye Analysis (N=96) | ||||||||||
| Standard logistic regression | 0.745 | 0.643, 0.848 | 0.205 | 0.823 | 0.722, 0.924 | 0.202 | 0.077 | 0.006, 0.149 | 0.143 | 0.03 |
| Worse eye analysis (N=135) | ||||||||||
| Standard logistic regression | 0.727 | 0.647, 0.808 | 0.161 | 0.772 | 0.692, 0.853 | 0.161 | 0.045 | −0.013, 0.103 | 0.116 | 0.13 |
Include age, gender, current smoking status, fellow eye status, and randomized treatment group. AREDS severity scale was modelled as categorical measure; BCa=Bias-corrected/accelerated; NA=not available.
Inclusion of baseline demographics, AREDS assigned treatment, and status of the contralateral eye in the prediction model improved the AUC by 0.064 (Figure 3). This improvement was statistically significant (p<0.05) in each analytic approach except for the left eye (p=0.06) and worse eye (p = 0.13) analysis (Table 3). The 95% CI for the AUC improvement was slightly narrower with the naïve approach (width: 0.110) than for the nonparametric clustered ROC analysis (width: 0.112) and cluster bootstrap (width: 0.111). The percentile-based 95% confidence interval and the BCa confidence interval from the cluster bootstrap were similar for both AUC and AUC difference (Table 3).
ROC Analysis for the Treatment-Requiring Retinopathy of Prematurity
Among 771 infants, 85 (11.0%) developed TR-ROP, including 82 (10.6%) infants requiring treatment in both eyes, and 3 (0.4%) infants requiring treatment in the right eye only. There was high inter-eye agreement in TR-ROP, with a percent agreement of 99.6% and kappa of 0.98 (95% CI: 0.96–1.00) (Online Table 5).
The inter-eye correlation for findings from the first image session were mild to moderate for presence of blot hemorrhage (kappa=0.26, Online Table 6), for number of quadrants with preplus disease (weighted kappa=0.41, Online Table 7), ROP stage and zone (weighted kappa=0.49, Online Table 8). The inter-eye correlation for the risk scores from the multivariable logistic regression that included BW, GA and these image evaluation findings was 0.95.
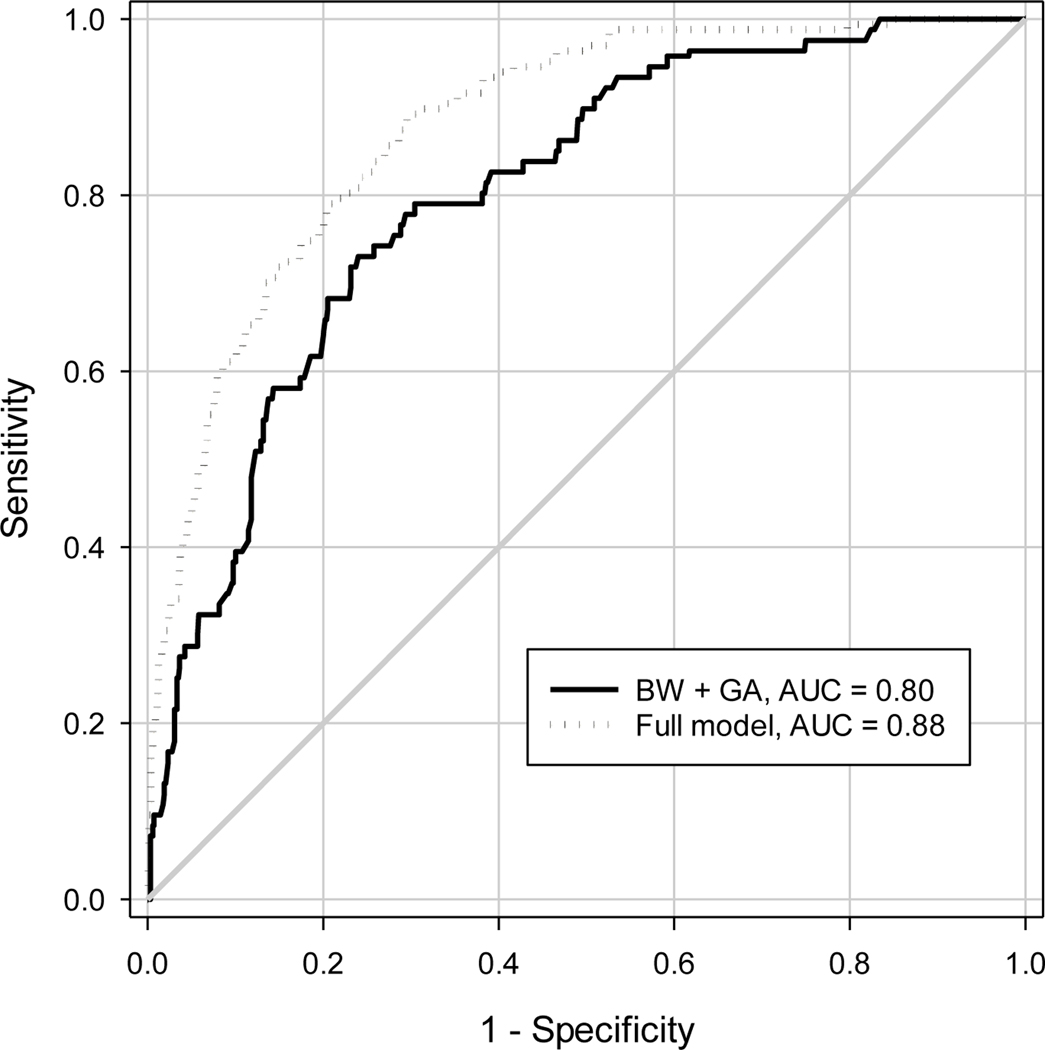
A comparison of the AUCs from the models predicting TR-ROP using BW and GA only, and using BW, GA and the first image session findings are shown in Figure 4 and Table 4. The point estimates of the AUC from the model with BW and GA were approximately 0.802 from the naïve approach, nonparametric cluster ROC analysis and cluster bootstrap, but the 95% CIs differed substantially. The naïve approach had a narrower width for the 95% CI (0.066) than the nonparametric ROC analysis approach (0.093) and the cluster bootstrap in SAS (0.090). The AUCs from the prediction model using BW, GA and the first image session findings were 0.878 from each of these three approaches, but the 95% CIs were different, with a narrower 95% CI from the naïve approach (0.050) than from the nonparametric cluster ROC analysis (0.066) and cluster bootstrap in SAS (0.068). The inclusion of first image session findings significantly improved the AUC by 0.076, with narrower 95% CI of AUC improvement from the naive analysis (0.053) than from the nonparametric cluster ROC analysis (0.070) and cluster bootstrap approach in SAS (0.070). The percentile-based 95% confidence interval and the BCa confidence interval from the cluster bootstrap were similar for both AUC and AUC difference (Table 4).
Figure 4:
Receiver-Operating Characteristic (ROC) curves for predicting treatment-requiring retinopathy of prematurity (ROP) using birth weight (BW) and gestational age (GA) only and using the combination of birth weight, gestational age and findings of the first image session. AUC=Area under ROC curve.
Table 4:
The AUC from prediction of treatment-requiring ROP birth weight and gestational age without or with inclusion of first image session findings
| Analysis Approach | BW + GA* | BW + GA + First image session findings * | Difference in AUC (95% CI) | P-value | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Two Eyes Analysis | AUC | 95% CI | Width | AUC | 95% CI | Width | AUC | 95% CI | Width | |
| Naïve approach | 0.802 | 0.769, 0.835 | 0.066 | 0.878 | 0.853, 0.903 | 0.050 | 0.076 | 0.049, 0.102 | 0.053 | <0.0001 |
| Nonparametric clustered ROC analysis | 0.802 | 0.755, 0.848 | 0.093 | 0.878 | 0.844, 0.912 | 0.068 | 0.076 | 0.041, 0.111 | 0.070 | <0.0001 |
| Cluster bootstrap-percentile: based in SAS | 0.801 | 0.755, 0.845 | 0.090 | 0.878 | 0.842, 0.908 | 0.066 | 0.075 | 0.042, 0.112 | 0.070 | <0.0001 |
| Cluster bootstrap: BCa in R | 0.802 | 0.753, 0.844 | 0.091 | 0.878 | 0.842, 0.908 | 0.066 | 0.076 | 0.043, 0.112 | 0.069 | NA |
| Left Eye Analysis (N=771) | ||||||||||
| Standard logistic regression | 0.800 | 0.753, 0.846 | 0.093 | 0.876 | 0.839, 0.912 | 0.073 | 0.076 | 0.038, 0.114 | 0.076 | <0.0001 |
| Right Eye Analysis (N=771) | ||||||||||
| Standard logistic regression | 0.804 | 0.757, 0.850 | 0.093 | 0.881 | 0.847, 0.916 | 0.069 | 0.078 | 0.041, 0.114 | 0.073 | <0.0001 |
| Worse Eye Analysis (N=771) | ||||||||||
| Standard logistic regression | 0.800 | 0.753, 0.846 | 0.093 | 0.871 | 0.835, 0.908 | 0.073 | 0.072 | 0.032, 0.112 | 0.080 | 0.0005 |
BW=birth weight; GA=gestational age; AUC=area under the ROC curve; BCa=Bias-corrected/accelerated; NA=not available.
Including the number of quadrants with preplus disease, ROP stage and zone, weight gain, and respiratory support.
The analyses using one eye only (left eye, or right eye, or worse eye) provided almost the same results as the analyses using two eyes for the prediction model based on BW and GA. However, for the prediction model using BW, GA and first image findings, the analyses of one eye provided wider 95% CIs of the AUCs and the difference between two AUCs (Table 4).
DISCUSSION
In this tutorial paper, we illustrated two approaches (i.e., Obuchowski’s nonparametric approach and the cluster bootstrap) to account for inter-eye correlation in ROC analysis and demonstrated their use in analyzing correlated eye data from three clinical studies with substantially different degrees of inter-eye correlation. We demonstrated that ignoring inter-eye correlation can lead to under-estimation of the variability of AUC, making its 95% CI too narrow, while analyzing data from left eyes and right eyes separately is inefficient (as evidenced by the wider 95% CIs than for the AUCs from the ROC analysis of two eyes).
The impact of ignoring the inter-eye correlation on the AUC is dependent on the magnitude of inter-eye correlation in both the test results and the ocular disease status. As shown in the analysis of AREDS data, when the inter-eye correlation for the predictors and inter-eye correlation in outcome are all relatively small, ignoring the inter-eye correlation using the naïve approach provides slightly narrower 95% CI of AUC, compared to the nonparametric ROC analysis and cluster bootstrap that properly account for the inter-eye correlation. However, when the inter-eye correlation is high, as in the TR-ROP data, the naïve approach that ignores the inter-eye correlation substantially under-estimates the 95% CIs for the AUCs and the AUC difference, compared to the two approaches that properly adjust for the inter-eye correlation. The cost of inappropriately narrow confidence intervals can lead to incorrect inferences, such as incorrectly concluding that a more complicated model meaningfully enhances discrimination.
The cluster bootstrap approach provides a powerful tool to account for inter-eye correlation in calculating the 95% CI for AUC and AUC difference. The bootstrap approach requires no distributional assumptions. For correlated eye data resulting from ocular tests on two eyes of a subject, the cluster bootstrap is performed at the cluster level (e.g., subject level) instead of at the eye level, and the statistic calculated from many bootstrap samples (e.g., 2000) yields an empirical distribution of the AUC, which provides the basis for calculating a percentile-based 95% CI or bias-corrected/accelerated 95% CI for single AUC and for AUC comparisons. The cluster bootstrap approach can be easily implemented in most statistical packages as demonstrated in SAS and R (Supplemental Notes 2–6). Obuchowski’s approach is a nonparametric analytic approach. Although calculating the variances for the AUC and AUC differences involves several formulas, an R function is available to perform these calculations. Results from these two different approaches to adjust for inter-eye correlation in ROC analyses were very similar, but not exactly the same. Previous Monte Carlo simulation studies found that Obuchowski’s nonparametric approach can handle a variety of intra-cluster correlation structures between disease status and test results,15 and that the cluster bootstrap had performance similar to Obuchowski’s nonparametric ROC analysis.19
Many variations of the bootstrap have been developed to improve the statistical inference when data are clustered.27 In our ROC analysis of three example datasets, we calculated both percentile-based confidence intervals and bias-corrected/accelerated confidence intervals from the cluster bootstrap. We did not find any substantial differences in their confidence intervals. Their similarity may be due to the fact that each study had a moderate or large sample size and the distribution of AUC and the AUC difference from the bootstrap samples were not skewed. Simulation studies are needed to evaluate the performance of various bootstrap approaches for deriving 95% confidence intervals under different settings for number of clusters, cluster size (1 or 2), and magnitude of inter-eye correlation.
In the past, a common practice for dealing with correlated eye data from ocular tests was to analyze data from one eye only, or to analyze data from left and right eyes separately. In our examples, we demonstrated that such analyses are inefficient in that their 95% CIs were usually wider compared to the appropriate analyses that account for inter-eye correlation. Furthermore, analyzing left eye and right eye separately can yield somewhat different results, making the interpretation of results complicated.
In conclusion, using ROC analysis to evaluate ocular test data from both eyes needs to account for the inter-eye correlation. There are valid methods (Obuchowski’s nonparametric approach and cluster bootstrap) available to account for the inter-eye correlation that are executable in statistical packages (SAS or R). Ignoring the inter-eye correlation can lead to over-statement of the precision of AUC and invalid conclusions about differences in AUCs. While analyzing data from each eye separately avoids the need to account for the inter-eye correlation, such analyses are inefficient.
Supplementary Material
Acknowledgments
Supported by grants R01EY022445 and P30 EY01583-26 from the National Eye Institute, National Institutes of Health, Department of Health and Human Services.
Footnotes
All authors have no conflict of interest disclosure to disclose.
References:
- 1.Ferris FL, Davis MD, Clemons TE, et al. A simplified severity scale for age-related macular degeneration: AREDS Report No. 18. Arch Ophthalmol. 2005;123(11):1570–1574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hardy RJ, Palmer EA, Dobson V, et al. Risk analysis of prethreshold retinopathy of prematurity. Arch Ophthalmol. 2003;121(12):1697–1701. [DOI] [PubMed] [Google Scholar]
- 3.Ocular Hypertension Treatment Study Group, European Glaucoma Prevention Study Group. Validated prediction model for the development of primary open-angle glaucoma in individuals with ocular hypertension. Ophthalmology. 2007;114(1):10–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ying GS, Maguire MG, Complications of Age-related Macular Degeneration Prevention Trial Research G. Development of a risk score for geographic atrophy in complications of the age-related macular degeneration prevention trial. Ophthalmology. 2011;118(2):332–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ying GS, VanderVeen D, Daniel E, Quinn GE, Baumritter A, Telemedicine Approaches to Evaluating Acute-Phase Retinopathy of Prematurity Cooperative G. Risk Score for Predicting Treatment-Requiring Retinopathy of Prematurity (ROP) in the Telemedicine Approaches to Evaluating Acute-Phase ROP Study. Ophthalmology. 2016;123(10):2176–2182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Maguire MG. Assessing Intereye Symmetry and Its Implications for Study Design. Invest Ophthalmol Vis Sci. 2020;61(6):27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ying GS, Maguire MG, Glynn RJ, Rosner B. Calculating Sensitivity, Specificity, and Predictive Values for Correlated Eye Data. Invest Ophthalmol Vis Sci. 2020;61(11):29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Seddon JM, Reynolds R, Yu Y, Rosner B. Validation of a prediction algorithm for progression to advanced macular degeneration subtypes. JAMA Ophthalmol. 2013;131(4):448–455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143(1):29–36. [DOI] [PubMed] [Google Scholar]
- 10.Choi BC. Slopes of a receiver operating characteristic curve and likelihood ratios for a diagnostic test. Am J Epidemiol. 1998;148(11):1127–1132. [DOI] [PubMed] [Google Scholar]
- 11.DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44(3):837–845. [PubMed] [Google Scholar]
- 12.Demler OV, Pencina MJ, D’Agostino RB, Sr. Misuse of DeLong test to compare AUCs for nested models. Stat Med. 2012;31(23):2577–2587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Margolis DJ, Bilker W, Boston R, Localio R, Berlin JA. Statistical characteristics of area under the receiver operating characteristic curve for a simple prognostic model using traditional and bootstrapped approaches. J Clin Epidemiol. 2002;55(5):518–524. [DOI] [PubMed] [Google Scholar]
- 14.Gonen M. Analyzing Receiver Operating Characteristic Curves with SAS. Cary, NC: SAS Institute Inc.; 2007. [Google Scholar]
- 15.Obuchowski NA. Nonparametric analysis of clustered ROC curve data. Biometrics. 1997;53(2):567–578. [PubMed] [Google Scholar]
- 16.Huang FL. Using Cluster Bootstrapping to Analyze Nested Data With a Few Clusters. Educ Psychol Meas. 2018;78(2):297–318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rao JN, Scott AJ. A simple method for the analysis of clustered binary data. Biometrics. 1992;48(2):577–585. [PubMed] [Google Scholar]
- 18.Efron B, Gong G. A leisurely look at the bootstrap, the jackknife, and cross-validation. Am Statistician. 1983;37:36–48. [Google Scholar]
- 19.Rutter CM. Bootstrap estimation of diagnostic accuracy with patient-clustered data. Acad Radiol. 2000;7(6):413–419. [DOI] [PubMed] [Google Scholar]
- 20.Efron B. Better Bootstrap Confidence Intervals (with Discussion). Jornal of the American Statistical Association. 1987;82:171–200. [Google Scholar]
- 21.Evangelou N, Konz D, Esiri MM, Smith S, Palace J, Matthews PM. Size-selective neuronal changes in the anterior optic pathways suggest a differential susceptibility to injury in multiple sclerosis. Brain. 2001;124(Pt 9):1813–1820. [DOI] [PubMed] [Google Scholar]
- 22.Zaveri MS, Conger A, Salter A, et al. Retinal imaging by laser polarimetry and optical coherence tomography evidence of axonal degeneration in multiple sclerosis. Arch Neurol. 2008;65(7):924–928. [DOI] [PubMed] [Google Scholar]
- 23.The Age-related Eye Disease Study Research Group. The Age-Related Eye Disease Study (AREDS): design implications. AREDS report no. 1. Control Clin Trials. 1999;20(6):573–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Davis MD, Gangnon RE, Lee LY, et al. The Age-Related Eye Disease Study severity scale for age-related macular degeneration: AREDS Report No. 17. Arch Ophthalmol. 2005;123(11):1484–1498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Quinn GE, Ying GS, Daniel E, et al. Validity of a telemedicine system for the evaluation of acute-phase retinopathy of prematurity. JAMA Ophthalmol. 2014;132(10):1178–1184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cicchetti DV, Alison T. A New Procedure for Assessing Reliability of Scoring EEG Sleep Recordings. American Journal of EEG Technology. 1971;11:101–109. [Google Scholar]
- 27.Cameron AG JB; Miller DL. Bootstrap-basead Improvements for Inference with Clustered Errors. The Review of Economics and Statistics. 2008;90(3):414–427. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.