Global impacts from high-latitude storms on Titan

Abstract

One of the first large cloud systems ever observed on Titan was a stationary event at the southern pole that lasted almost two full Titan days. Its stationary nature and large extent are puzzling given that low-level winds should transport clouds eastward, pointing to a mechanism such as atmospheric waves propagating against the mean flow. We use a composite of 47 large convective events across 15 Titan years of simulations from the Titan Atmospheric Model to show that Rossby waves trigger polar convection—which halts the waves and produces stationary precipitation—and then communicate its impact globally. In the aftermath of the convection, forced waves undergo a complicated evolution, including cross-equatorial propagation and tropical-extratropical interaction. The resulting global impact from convection implies its detectability anywhere on Titan, both via surface measurements of pressure and temperature and through remote observation of the outgoing longwave radiation, which increases by ~0.5% globally.

Plain Language Summary

Saturn’s moon Titan hosts a methane hydrologic cycle with occasional large cloud events that are sometimes stationary and last for up to 30 days at a time. These events have previously been speculated to be caused by convective thunderstorms, but for the first time, we show that their formation is reliant on the interaction between a particular type of high-latitude atmospheric wave, a Rossby wave, and instability caused by increased surface heating during the summer. Convectively forced growth of the Rossby wave accounts for the lack of movement as waves in the summer hemisphere interact with waves that have been forced in the winter hemisphere. The resulting global impact from the forced convection may be detected both from Earth as changes in outgoing longwave radiation and on the surface, which may have relevance for the Dragonfly mission.

1. Introduction

Methane storms form an important component of Titan’s hydrological cycle (Mitchell & Lora, 2016), shape surface features (Poggiali et al., 2016; Faulk et al., 2017), and participate in the latitudinal transport of latent heat (Lora & Mitchell, 2015). However, we are only just beginning to connect their variability to atmospheric forcing features. Some progress has been made in understanding storm development via numerical simulations (e.g. Mitchell et al., 2011; Rafkin & Barth, 2015; Lora & Mitchell, 2015), but many facets of their characteristics and temporal evolution remained unexplained.

Clouds on Titan take multiple morphologies and generally follow the seasons, with clusters of convective clouds (Brown et al., 2002; Roe et al., 2002; Griffith et al., 2005; Roe et al., 2005; Schaller, Brown, Roe, & Bouchez, 2006) and several hundred kilometer long cloud streaks occurring during southern summer (Griffith et al., 2009; Schaller et al., 2009; Turtle, Del Genio, et al., 2011), a large arrow-shaped cloud occurring after southern autumnal equinox (Turtle, Perry, et al., 2011), and northern hemisphere streaks appearing around northern summer solstice (Turtle et al., 2018). Many of these cloud features have been noted to be relatively stationary (Roe et al., 2005; Schaller, Brown, Roe, & Bouchez, 2006; Rodriguez et al., 2009; Ádámkovics et al., 2010). In particular, one of the first observed large, convective events occurred near the south pole just after southern summer solstice and was near-stationary (Schaller, Brown, Roe, & Bouchez, 2006). The entire event lasted approximately 30 days or about two Titan days (Tsols). Within this period, multiple individual cloud features developed and faded and were interpreted as convective cells exhausting the local supply of methane.

Separately, two types of waves have been hypothesized to help explain observed cloud features. Kelvin waves, which are symmetric about the equator, have been diagnosed in global circulation model (GCM) simulations at the low latitudes (Mitchell et al., 2011; Yamamoto, 2019). These waves move quickly to the east with a phase speed of approximately 12 m s⁻¹ and are not coupled to convection (Mitchell et al., 2011) so cannot be the cause of the stationary clouds. Mitchell et al. (2011) also described a slow, westward-traveling equatorial wave that was coupled to convection in their simulations that initiated near the equator and progressed towards the mid-latitudes. While they noted that the associated precipitation features had structures that resembled Rossby waves, they did not determine exactly what kind of wave mode was responsible for generating convection. Schaller et al. (2009) suggested a stationary Rossby wave train may have been responsible for the appearance of clouds near the equator and at the south pole successively, but Rossby waves and their interactions with prevalent summertime, high-latitude convection have not been investigated using a GCM.

Finally, Lora et al. (2019) noted that parameterized convection was the likely cause of bursts of strong, near-surface winds at low latitudes in a Titan GCM. All of these considerations —the stationarity of clouds, previous wave hypotheses, and the potential tails of the equatorial wind distributions—motivate the present study, in which we investigate the connection between high-latitude waves and polar stationary cloud features during summertime. Importantly, we identify global impacts and provide predictions for future observations.

2. Model and Methods

We investigate the response to local convective forcing within the Titan Atmospheric Model (TAM) (Lora et al., 2015) (model details are provided in the Supplemental Information). To do this, we select the 47 largest convective events in the northern hemisphere across 15 Titan years (~440 Earth years) of simulations (Battalio et al., 2021) and average across their evolution to study the behavior of forced waves. Events are selected if their daily cumulative precipitation exceeds the 90th percentile of all precipitation Tsols. Thirty Tsols on either side of the timestep of the maximum precipitation are used to create a composite event. For each identified convective event, the location of the eddy (deviation from the zonal mean) surface pressure maximum at the timestep of maximum precipitation is identified (Govekar et al., 2011; Naud et al., 2012), and all convective events are shifted to 0° relative longitude and averaged. The initiation latitude is similar across all convective events, so we do not shift it. Results are robust if other percentile thresholds or event durations are selected. Events preferentially occur between 200° and 0°E in the northern hemisphere and between 0° and 50°E in the southern hemisphere due to heterogeneity in the topography used by the hydrology scheme in the model (Faulk et al., 2020). Events occur similarly in both hemispheres, but only the northern hemisphere is shown.

3. Results

Large, convective events at the high latitudes of both hemispheres occur during summer and are triggered by phasing of multiple modes of baroclinic Rossby waves; they are stationary features that alter the global dynamics, with observable impacts across Titan’s atmosphere. Even averaged over 47 separate events over 15 Titan years, the composite follows a remarkably coherent and robust evolution, indicating common mechanisms between the events, regardless of their exact locations. The uniformity in the development, progression, and decay of these events implies common observables across events that can be searched for systematically.

3.1. Evolution of the convective event

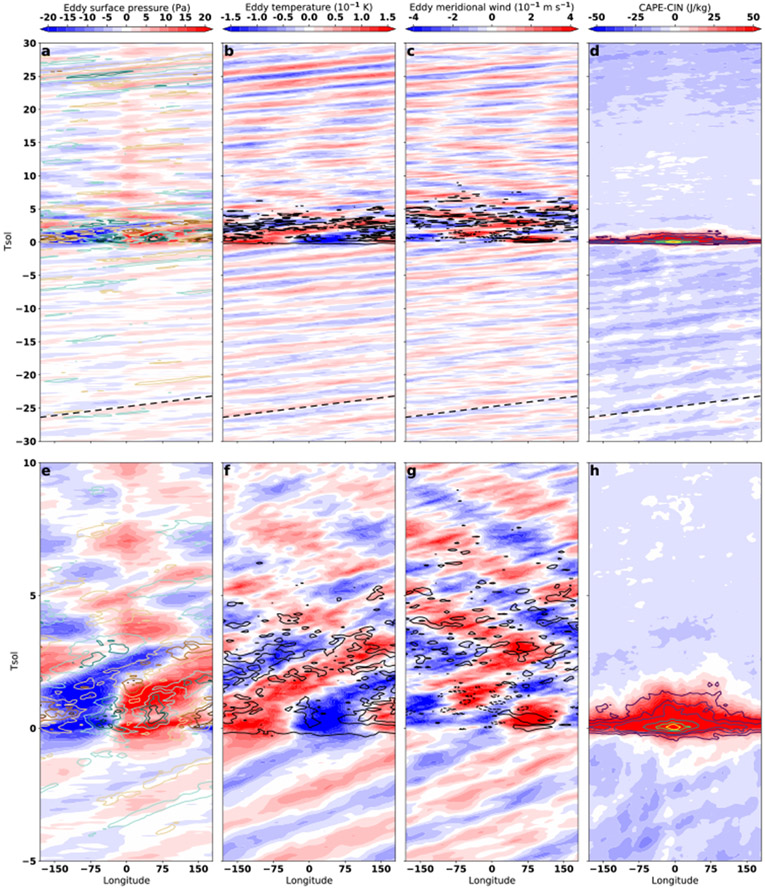
Before the convective event is triggered, high-latitude Rossby waves are prevalent. (A full period of a single Rossby wave is indicated by the dashed line in Fig. 1a-d.) The waves are highly regular in time, traveling around a latitude circle repeatedly, even up to 30 Tsols before the event occurs. This indicates that the triggering of large convective events depends on the coincidence of favorable Rossby wave phase and sufficient thermodynamic instability. The waves are baroclinic (Lora & Mitchell, 2015) and propagate west but travel east due to advection by the mean flow. These waves are easily observable in the near-surface eddy temperature (Fig. 1b&f, shading), but their signature occurs in the eddy surface pressure (Fig. 1a&e, shading), eddy meridional wind (Fig. 1c&g, shading) and in measures of thermodynamic instability, specifically the convective available potential energy minus the convective inhibition (CAPE–CIN), which, when positive, means that convection is occurring in TAM (Fig. 1d&h, shading).

Figure 1.

Hovmöller diagram of composite precipitation events averaged over 41°–85°N. The bottom row repeats the top row over a narrower length of time. Eddy surface pressure (shading) and eddy specific humidity at 1410 hPa (every 10⁻⁴ g g⁻¹ starting at −3, contours) (a, e). Eddy temperature (shading) and eddy meridional heat flux (0.2 K m s⁻¹, contour) at 1410 hPa (b, f). Eddy meridional wind (shading) and eddy momentum flux (0.8 m² s⁻², contours) at 1280 hPa (c, g). CAPE – CIN (shading) and precipitation (contoured at 5, 10, 15, 30, 45, 60 mm d⁻¹) (d, h). The dashed lines in panels a–d indicate one period of a single Rossby wave.

Combined with sufficient levels of CAPE, the timing of convective events may be modulated by additional wave modes, some of which may be Kelvin-like modes (Mitchell et al., 2011) or higher-wavenumber Rossby waves. During the convective event, the traveling Rossby waves halt in place approximately 1 Tsol prior to the peak precipitation. Precipitation begins in earnest approximately 0.5 Tsols before the event maximum (Fig. 1h).

The phasing of the incipient, extratropical Rossby waves is such that eddy high temperatures are colocated with poleward wind located just downstream of the eddy low pressure (compare Figs. 1 e, f, g at Tsol=−5), as would be expected in a baroclinically unstable extratropical wave. Unlike a terrestrial cyclone, CAPE reaches a peak within both the warm and cold sectors of the cyclone. This is due to Titan’s near-surface moisture increasing towards the northern pole, partly because Titan’s seas are concentrated at the northern high latitudes. Thus, within high-latitude traveling waves, northerly winds draw in regions of anomalous low temperatures and high moisture, whereas southerly winds transport anomalous high temperatures associated with low moisture (Fig. 2). Because CAPE–CIN increases both with higher surface moisture and higher temperature, these competing changes generally balance out such that the overlapping wavenumber 1 signals of temperature and moisture combine to form a wavenumber 2 structure in the CAPE–CIN (Fig. 1d). The convective event occurs in the phase of the wave aligning with high eddy moisture instead of high eddy temperatures because the meridional gradient of moisture is larger than that of temperature (not shown); therefore, the increase of CAPE–CIN corresponding to high eddy moisture is larger than the increase from high eddy temperature.

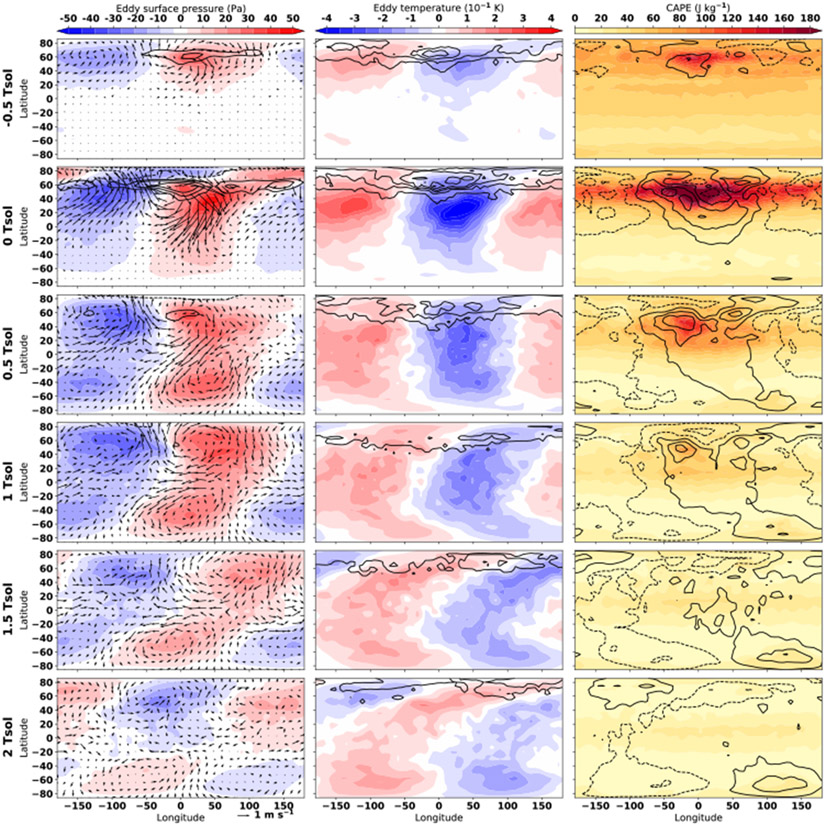
Figure 2.

Composite evolution of the forced wave in the eddy surface pressure (shading), vertical velocities (every 10 Pa s⁻¹, contours), and eddy winds (vectors) at 1410 hPa (left column); eddy temperatures (shading) and precipitation at 1410 hPa (contoured at 1, 10, 20, 30, 45, 60 mm d⁻¹) (middle column); and CAPE (shading) and eddy moisture at 1410 hPa (contoured at −5, −3, −1, 1, 3, 5×10⁻⁴ g g⁻¹ contours) (right column).

At the time of maximum precipitation (Tsol=0), the stationary Rossby wave rapidly amplifies to a magnitude approximately three times that of the antecedent traveling Rossby waves measured from the eddy surface pressure amplitudes. The longitude of the precipitation maximum coincides with a low-level, cold high pressure, surrounded by eddy low-level moisture (Fig. 1a, contours), that is offset to the east from the precipitation maximum (Fig. 2, shading, right column). At this time, the influence of the stationary Rossby wave begins to extend into the southern hemisphere (Fig. 2, second row). Large values of eddy meridional wind are directed from the northern into the southern hemisphere as a result of low-level vertical subsidence between 1300 and 1400 hPa, as indicated by the large positive values (downward motion) of vertical velocities (Fig. 2, left column, contours). Coincident with the precipitation event, eddy heat fluxes (Fig. 1b, contours), eddy momentum fluxes (Fig. 1c, contours), and the low-level mid-latitude jet (not shown) increase across all longitudes as the stationary wave amplifies in response to the convective forcing, as reflected in the large, positive values of CAPE – CIN.

For the following 2 Tsols, the forced wave remains stationary but becomes global in scale, but at later times, the wave takes on a chevron shape (Fig. 2, row 4), with an eastward tilt in the poleward direction. Once convection and precipitation cease after approximately Tsol=2, the wave in the northern hemisphere no longer remains stationary and begins traveling eastward for approximately 1 Tsol. During this time, the wave decays back to the pre-event amplitudes, along with eddy heat and momentum fluxes. The CAPE – CIN becomes negative again but with no discernible wave structure in the field, indicating that the entire northern hemisphere has been thermodynamically stabilized (Fig. 1d, shading). The induced wave in the southern hemisphere has no initial eastward motion and begins traveling west even before the convection in the northern hemisphere completely ends, by about Tsol=1 (Fig. 2, bottom row and Supplemental Fig. 1).

After Tsol=4, the eastward traveling northern hemisphere wave and westward traveling southern wave phase lock to form a global wave, with characteristics of an equatorial Rossby wave, with mirrored high and low pressure on either side of the equator (Kiladis & Wheeler, 1995; Yang et al., 2007a; Kiladis et al., 2009). Due to the slow rotation of Titan, the radius of deformation for this wave, $R_e=(\sqrt{g{h}_e}∕\beta {)}^{1∕2}>10,000$ km, encompasses the entire globe (g = 1.35 m s⁻¹ is the acceleration due to gravity, h_e = 8 km is the effective depth of the wave—assuming a height of 400 hPa≈25 km and a vertical wavenumber 1, and $\beta =\mathcal{O}({10}^{-12})$ is the meridional change of the Coriolis parameter). The global wave moves west until Tsol=10 (Fig. 1 and Supplemental Fig. 1).

After Tsol=10, the southern portion of the wave decays, and northern modes retreat back to the high-latitudes and become eastward traveling. After the convective event, there is a stationary wave signal that lingers in the eddy surface pressure around 0° relative longitude from Tsol=0–30 (Fig. 1a, shading) due to increased surface moisture from the precipitation, indicating surface-atmosphere coupling.

3.2. Convective forcing of the stationary wave

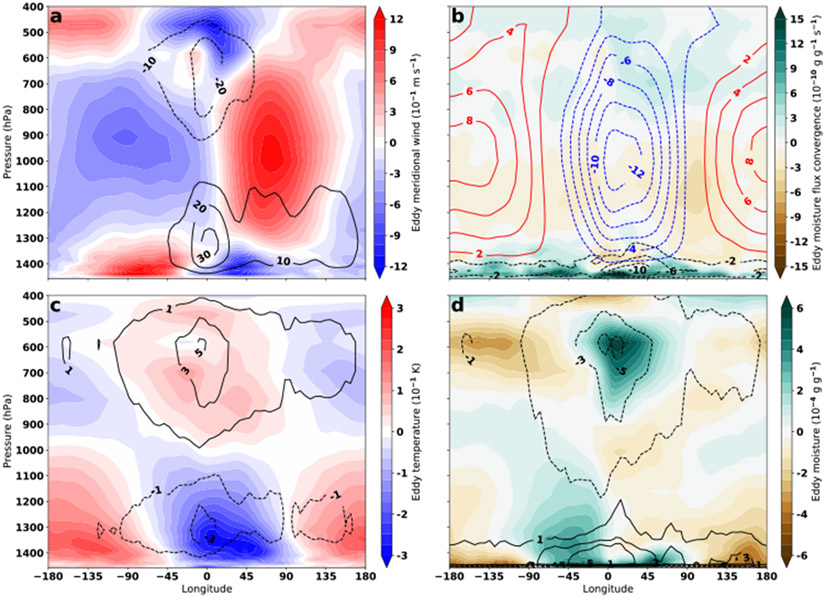
The vertical structure of the event allows us to understand how convection generates and sustains the stationary wave. The stationary wave initially resembles a baroclinic Rossby wave (Moore & Montgomery, 2005; Lora & Mitchell, 2015) as it has a westward tilt with height in the eddy temperatures (Fig. 3c, shading). However, the vertical winds reverse with height, with rising motions in the mid-levels and descending air below 1200 hPa (Fig. 3a, contours), which does not follow idealized baroclinic structure (Moore & Montgomery, 2005). The descent near the surface aligns with diabatic cooling and the core of precipitation, as a result of the tilt of the wave and convective instability (and the resulting parameterized convection). Deep convection forces the stationary wave by directly adjusting the temperature profile by warming between 600–800 hPa (Fig. 3c, contours), to force positive eddy temperatures (Fig. 3c, shading) and cooling the low-levels from above the surface to 1200 hPa (Fig. 3c, contours), to generate negative eddy temperatures centered above the surface high pressure (Fig. 3 c, shading) (Battalio et al., 2021). This forcing alters the large-scale dynamics (Yang et al., 2007b) such that high pressure is generated at the surface (Fig. 2 left column, shading), and anomalous low geopotential heights are generated above the surface hight at 950 hPa (Fig 3b, red and blue contours). The result is cyclonic motion and horizontal convergence centered between the eddy high temperature and eddy low temperature centers around 900–1000 hPa, accompanied by a surface eddy high pressure and anticyclonic winds (Fig. 3a, shading).

Figure 3.

Vertical structure of the composited wave averaged over 0–0.5 Tsol and meridionally averaged over 41°–75°N. Eddy meridional wind (shading) and vertical wind (Pa s⁻¹, contours) (a). Eddy moisture flux convergence (shading), eddy heat flux convergence (10⁻⁷ K s⁻¹, black contours), and eddy geopotential heights (m, blue and red contours) (b). Eddy temperatures (shading) and temperature tendency caused by convection (10⁻⁶ K s⁻¹, contours) (c). Eddy moisture (shading) and moisture tendency caused by convection (10⁻⁹ g g⁻¹ s⁻¹, contours) (d).

The diabatic heating caused by the convection forms a thermal boundary upon which the stationary wave grows (Held et al., 2002; Chang, 2009). The low-level cooling and mid-level warming caused by convection (Fig. 3c, contours), along with the divergence of eddy heat flux in the low-levels at all longitudes (Fig. 3b, black contours) acts to stabilize the vertical temperature profile. In combination with drying of the very lowest levels by convection (Fig. 3d, contours), this decreases the CAPE–CIN. However, the near-surface moistening caused by the convergence of eddy moisture flux (Fig. 3b, shading) opposes that, increasing the CAPE so that the storm becomes self-sustaining. The largest precipitation and convection occur within a narrow longitudinal range for up to a full Tsol. The high pressure system at the surface, with anti-cyclonic circulation, transports moisture around its center upstream of the main precipitation, remoistening the convecting region (Fig. 2, right column, contours). Thus, the disturbance can be thought of as a diabatically forced stationary wave coupled to convection (Moore & Montgomery, 2004). Once the forcing feature is exhausted—that is, once the environment is depleted of CAPE—the stationary heating forcing the wave disappears, and the wave becomes a free mode again, propagating at a speed equal to the sum of its intrinsic phase speed and the background mean flow.

Finally, convection forces the vertical moisture distribution as well; however, the eddy moisture anomalies do not align with the moisture tendencies from convection. Drying in the mid-levels (Fig. 3d, contours) is colocated with the mid-level warming and positive anomalous eddy moisture. Instead, the convergence of eddy moisture fluxes (Fig. 3b, shading) contributes to eddy anomalies both aloft around 600 hPa and near the surface. While moistening at the surface approximately coincides with cooling, eddy moisture anomalies are longitudinally offset from the positive eddy moisture due to the combination of eddy fluxes and convective tendencies. This is a similar structure to convectively forced equatorial Rossby waves on Earth (Fuchs-Stone et al., 2019).

3.3. Causes of wave motion

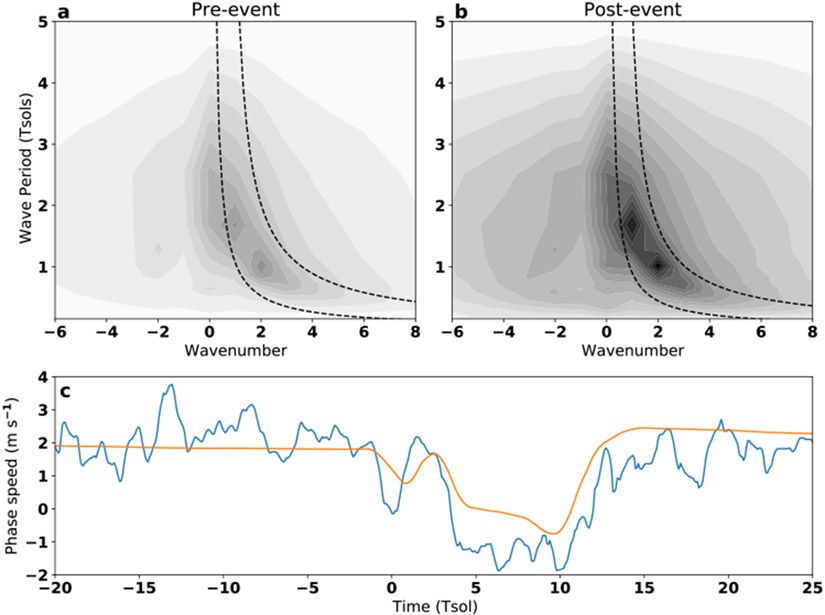
The eastward traveling waves that occur before and after the forced stationary event are baroclinic Rossby waves, which we confirm by comparing the frequency-zonal wavenumber power spectrum of the eddy heat fluxes to the wave dispersion relation (Fig. 4) for baroclinic Rossby waves in a stratified fluid:

$$\omega =Uk-\frac{\beta k}{k^2+l^2+{\gamma }^2+m^2{f}_0^2∕N^2},$$ (1)

where ω is the frequency of the wave, U is the mean zonal wind, and k, l, and m are the zonal, meridional, and vertical wavenumbers; γ is related to the Rossby deformation radius (L_d) by $\gamma =f_0^2∕(4N^2{H}^2)=1∕(2L_d{)}^2$, where f₀ is the Coriolis parameter, N² is the Brunt-Väisälä frequency—a measure of the vertical stratification—, and H is the depth of the fluid. Calculating each of the terms for latitudes of 70°−85°N (see Supplemental Information) provides a dispersion relation that closely matches that of the simulated waves (Fig. 4a&b, dashed lines). The wavenumber 1 wave with a 1.5 Tsol period and wavenumber 2 with a 1 Tsol period dominate, but additional power is found at wavenumber 3 with a ~0.5 Tsol period. The wave power spectra are slightly different before and after the event due to the change in zonal-mean zonal wind as a result of eddy momentum fluxes (Fig. 1c&g, contours). The slight change is reflected in the idealized dispersion relations calculated from Eq. 1 as well, providing further evidence that these are Rossby waves.

Figure 4.

Spectra in frequency-wavenumber space of the meridional heat transport at 1410 hPa (top). The dashed lines enclose the idealized Rossby wave dispersion relation for waves calculated from Eq. 1 at latitudes of 70°–85°using the mass-weighted zonal-mean zonal wind over 70°–85°N and below 400 hPa. Shown are the spectra before the convective event (Tsols=−30– −2) (a) and after the event (Tsols=2–30) (b). At bottom, the simulated phase speed of the highest amplitude wavenumber 1 in the northern hemisphere in TAM from the eddy surface temperature (blue) and the idealized phase speed for a Rossby wave (orange) (c).

Rossby waves also explain much of the behavior of wave activity immediately after the convection ends. The phase speed of the dominant zonal wavenumber 1 (Fig. 4c, blue) matches well with that of the idealized phase speed for a Rossby wave calculated using Eq. 1 (Fig. 4c, orange) at about 2 m s⁻¹ (see Supplemental Information). When the convective event occurs, the wave becomes stationary—a phase speed of 0 m s⁻¹—at Tsol=0. Immediately after the convection ceases and the wave becomes a freely propagating mode again, the wave briefly travels eastward again for 1 Tsol but then reverses back to the west for 8 Tsols. This complex behavior emerges as a result of phasing between the northern and southern waves. After convection ceases, the southern component of the global Rossby wave immediately travels west, but the northern component heads east. The difference in motion between hemispheres is due to differences in the zonal winds in each hemisphere. The convergence and divergence of eddy momentum fluxes accelerate the low-level wind in the summer hemisphere but slow the wind in the winter hemisphere, respectively (not shown). Phase locking of the wave occurs when the zonal-mean winds in each hemisphere become similar in direction and magnitude. Phase locking and the subsequent decrease in wavenumber result in westward motion globally, because smaller wavenumbers result in larger westward phase speed by the Rossby wave dispersion relation. Westward motion continues until the southern wave decays, whereupon the northern wave returns to eastward propagation due to the Doppler shifting of the zonal-mean winds as its wavenumber increases and intrinsic phase speed decreases.

4. Discussion and Conclusions

We have generated a composite of intense convective events in the high latitudes of a simulated Titan atmosphere using TAM. Traveling, extratropical Rossby waves locally increase the CAPE – CIN so that large convective events occur. Once convection initiates, the adjustment of the vertical temperature and moisture profiles via latent heating imposes stationary thermal forcing that halts the progression of the incipient waves. The forced stationary wave sets up a self-sustaining feedback mechanism by converging moisture by eddy fluxes to feed convection until the entire hemisphere is scoured of CAPE after about 2 Titan days. The convectively forced stationary wave expands from the summer hemisphere into the winter hemisphere, transporting heat as it expands to homogenize temperatures (Supplemental Fig. 2) and exciting an equatorial Rossby wave, which happens because the equatorial waveguide extends well into the high latitudes due to Titan’s slow rotation rate. As the convective event ends, the global stationary wave again becomes freely propagating and splits into separate traveling wave modes in the northern and southern hemispheres that each travel according to the background flow and their intrinsic phase speeds.

While we rely on a simplified Betts-Miller convective parameterization (Frierson, 2007; Battalio et al., 2021) to simulate convection during the stationary event, once the convection ends, the waves evolve according to the model’s resolved dynamics and therefore are robust features. Convection forces the upper-level structure of the waves as happens on Earth (Yang et al., 2007c) and Titan (Fig. 3a), but the pre-existing lower-level waves trigger the initial convection. The latitudinal extent of the global Rossby waves after the convective event are unique to Titan (Fig. 2), though cross-equatorial growth in weak westerly wind regimes is consistent across both Titan and Earth (Simmons, 1982).

The initial and convective stages of the stationary wave event exhibit similarities to forced Rossby waves and mixed Rossby-gravity waves in Earth’s atmosphere (Held et al., 2002; Chang, 2009). Many of these convective developments are organized by existing extratropical Rossby waves (Boettcher & Wernli, 2013) that provide a positive feedback mechanism on the wave (Zappa et al., 2011) and in turn force equatorial Rossby and mixed Rossby-gravity wave features (Yang et al., 2007b), as they seem to do in Titan’s atmosphere (Fig. 2). Equatorial Rossby waves are symmetric about the equator, with wind patterns that do not cross the equator, but mixed Rossby-gravity waves are antisymmetric and exhibit equator-crossing winds (Kiladis et al., 2009). The strong cross equatorial winds at Tsol=0 and 0.5 point towards mixed Rossby-gravity waves initially (Fig. 2). The waves at this time have antisymmetric cyclonic and anticyclonic centers across the equator (Kiladis et al., 2009, 2016). They transition to purely equatorial Rossby waves after Tsol=1 when they exhibit four centers of circulation: mirrored anticyclonic and cyclonic circulations in the eastern and western relative hemispheres, respectively (Kiladis & Wheeler, 1995). Further evidence of brief mixed Rossby-gravity waves transitioning to pure equatorial Rossby waves is provided by the wave motion, which is eastward immediately after the convective forcing ceases. Equatorial Rossby waves have only a westward phase speed, though they can have an eastward group speed, while mixed Rossby-gravity waves can have an eastward phase speed (Kiladis et al., 2016).

The expansion of the wave in the meridional direction towards and across the equator has two distinct speeds. The first speed (~2 m s⁻¹) follows the meridional propagation of CAPE and eddy surface pressure (Supplemental Fig. 2a) and is close to the meridional phase speed of Rossby waves (Supplemental Fig. 2a) (Schaller, Brown, Roe, & Bouchez, 2006). The second speed is tied to the initial changes in outgoing longwave radiation (OLR) and eddy temperatures (Supplemental Fig. 2b) and is close to the phase speed of pure gravity waves of ~30 m s⁻¹ (Supplemental Fig. 2b); however, the Rossby wave speed is apparent at later times in the OLR as well. Because Rossby waves meridionally transport energy away from their source latitudes, this indicates that both gravity and Rossby waves serve to transport energy across the globe, but the contribution from each wave type and the coupling between them requires further investigation.

The global impact and remarkable repeatability of the convective events suggest their observability both from landed craft and remote sensing. Vertical temperatures are altered by these large precipitation events (Fig. 3c), with impacts in both hemispheres (Fig. 2). The temperature drops at the surface but is warmed in the mid- and upper-levels. These temperature changes stabilize the atmosphere to further precipitation activity, as was inferred by the reduction in frequency of clouds (Schaller, Brown, Roe, Bouchez, & Trujillo, 2006) after the October 2004 stationary cloud outburst (Schaller, Brown, Roe, & Bouchez, 2006). As a result of these forced temperature changes, the globally averaged OLR increases by 0.5% after these events occur. Because this is a composited result, the global change occurs regardless of the location of the event. Thus, an observational campaign from Earth may be able to detect these changes even if the cloud and precipitation event is not directly observed.

Further, though cloud cover is not directly simulated here, clouds must occur during precipitation; thus, the timing of waves on Titan indicates several relevant timescales when interpreting cloud cover observations. Most importantly, the simulated convective event matches a large, stationary, convective outburst at the southern high latitudes that lasted for a similar duration as the composited event (about 30 days or two Tsols) (Schaller, Brown, Roe, & Bouchez, 2006). Other cloud observations from the lower and middle latitudes also remain stationary for multiple days (Roe et al., 2005; Rodriguez et al., 2009; Ádámkovics et al., 2010). The stationary nature of these forced waves should perhaps be interpreted as propagation westward compared to the zonal-mean flow. Beyond the convective event, the regular waves before and after convection might further suggest a specific period for non-precipitating, high-latitude clouds of 1 to 2 Tsol, since the waves modify the relative humidity (Fig. 1). Importantly, the motion of such features need not follow the wind speed alone but would instead track the phase speeds of the waves. Indeed, even during the convective event, the precipitation is stationary despite the fact that the zonal wind does not slow substantially.

For landed craft, the global impact from large convective events may be detectable at low latitudes. While the direction and wavenumber will be difficult to directly measure (Barnes, 1980), measurement of wave period and amplitude should serve to discriminate between wave types due to the differences in wave period for the fast Kelvin (Mitchell et al., 2011) and slower Rossby modes. For the equatorial latitudes, the maximum composite surface pressure response (see Supplemental Information) appears initially as a single 4 Tsol period wave, then slowing to ~2.5 Tsol (Supplemental Fig. 3a) as it decays. The maximum eddy temperature and moisture (Supplemental Fig. 3b, c) are approximately 30° of longitude out of phase but align in time. Individual events are six to eight times the composite amplitude (not shown), and the Dragonfly mission could perhaps measure these wave modes. The large near-surface winds generated in the convective event (Supplemental Fig. 3d) increase rapidly just above the surface, explain large, near-surface wind anomalies at the equator (Lora et al., 2019), and may be a hinderance to powered flight.

We have shown that high-latitude convective events on Titan are instigated by high-latitude Rossby waves in the summer hemisphere. These large events impact the entire atmosphere regardless of their longitude of initiation. This indicates that convective events may be detected both remotely from Earth and on the surface by Dragonfly. Finally, our results demonstrate that the interaction of tropical and extratropical waves on Titan may be as important as the connection of the tropics and high-latitudes is on Earth.

Key Points:

• Development of convection on Titan involves the coordinated interaction of Rossby waves with convective instability.

• Convection temporarily halts the movement of waves, which may explain stationary cloud features in the middle and high latitudes.

• Global impacts imply that observables like surface pressure and outgoing longwave radiation may reveal instances of convection.