Abstract
This work aims to experimentally report the radiation attenuation factors for four different clays (red, ball, kaolin and bentonite clays) at four selected energies (emitted from Am-241, Cs-137, and Co-60). The highest relative difference in the mass attenuation coefficient (MAC) is equal to −3.02%, but most of the other results are much smaller than this value, proving that the experimental and theoretical data greatly agree with each other. From the MAC results, the shielding abilities of the clay samples at 0.060 MeV follow the order of: bentonite > red > ball > kaolin. Thus, at low energies, the bentonite clay sample provides the most effective attenuation capability out of the tested clays. The half value layer (HVL) increases as energy increases, which suggests that, only a thin clay sample is needed to sufficiently absorb the radiation at low energies, while at higher energies a thicker sample is needed to shield the same amount of high energy radiated. Furthermore, bentonite clay has the lowest HVL, while the kaolin clay has the greatest HVL at all energies. The radiation protection efficiency (RPE) values at 0.060 MeV are equal to 97.982%, 97.137%, 94.242%, and 93.583% for bentonite clay, red clay, ball clay, and kaolin clay, respectively. This reveals that at this energy, the four clay samples can absorb almost all of the incoming photons, but the bentonite clay has the greatest attenuation capability at this energy, while kaolin clay has the lowest.
Keywords: clay, radiation attenuation, WinXCom program, mass attenuation coefficient
1. Introduction
Radiation and nuclear technologies are widely applied in fields such as optimizing industrial processes, continuous form goods and products, nuclear power plants, radiology and nuclear medicine departments, and nuclear research and accelerator centers [1,2,3,4,5]. The harm caused by this technology is exposure to a high level of radiation to individuals, the public and the environment. Radiation protection aims to protect people and the environment from the harmful effects of ionizing radiation exposure, and shielding is the most effective factor of the radiation protection process, as it can decrease the intensity of the incident radiation. Hence, it is very important to determine radiation shielding parameters of different kinds of building material to assess their capability of attenuating ionizing radiation when they are used as building materials in places that contain radiation sources [6,7,8,9,10,11,12].
The MAC is a fundamental radiation shielding parameter defining the interaction of gamma rays within the material. This parameter is used to assess the capability of the material to attenuate gamma rays. Due to its high density, lead is commonly utilized as shielding material against gamma radiation; however, it has environmental toxicity and is expensive when used in large dimensions application. Concrete and other building materials are also used as radiation shielding materials [13,14,15]. Many studies have aimed at calculating the mass attenuation coefficients of different construction materials in order to evaluate their gamma ray attenuation abilities [16,17,18].
In the present study, some types of Egyptian clays which are considered as natural building material were investigated as radiation shielding material. The interest in studying those types of building material arises from their high chemical durability, weathering resistance, low hydraulic conductivity and relatively high hardness beside their natural availability. Clays have less resistance to chemical and environmental factors compared to other shielding materials, and are more available in Egypt [19,20].
The present clays are clean and environmentally friendly construction materials, can be used in radiation protection application as a radiation shield, and can be added to concrete mixes as an alternative to sand in certain proportions which lead to increase their density enhancing gamma ray attenuation. The high melting point of these clays indicates their thermal stability in case of long exposure to high energy radiation and their compressive strength is suitable for producing high-quality shielding materials. Thus, the determination of radiation shielding parameters of different types of clays is very useful.
The present work discusses the attenuation parameters for different clays, which is different from the previous work [21], which talks about improving bentonite clay with cement and not bentonite raw materials, and the results show a clear difference between the two studies. Additionally, in the research that studies the attenuation coefficient of both ball and kaolin clays [22], these clays were extracted from Nigeria, while our clays were extracted from Egypt, in addition to studying two other types of clay (bentonite and red clays), which gives an important overview to the reader as it is a combined materials study.
2. Materials and Methods
Red, ball, kaolin, and bentonite are four types of clay that were obtained from quarries in Egypt’s Aswan, Abuznima, and Fayoum governments. They were stoned, ground to powder size, and sun-dried. The samples were sieved to 100 μm size, then they were thoroughly mixed with water, sectioned into sectors, and dried in the sun rays. Afterwards temperatures of 500 °C were used to bake the samples. Figure 1 illustrates bentonite, red, ball and kaolin clay samples labeled as A,B,C and D respectively. The porosity, P of the sample known as the ratio between the void volume and the total volume and can be calculated using the following equation [23,24].
| (1) |
where W (g), is the saturated mass of clay sample (the sample immersed in boiling water for 2 h), D (g), is the dried mass of clay sample (the sample dried in the oven at 110 °C for 48 h) and V(cm3) is the exterior (total) volume of the sample (V = W × S), where S (g), is the suspended weight of sample in water.
Figure 1.
The different prepared clay samples.
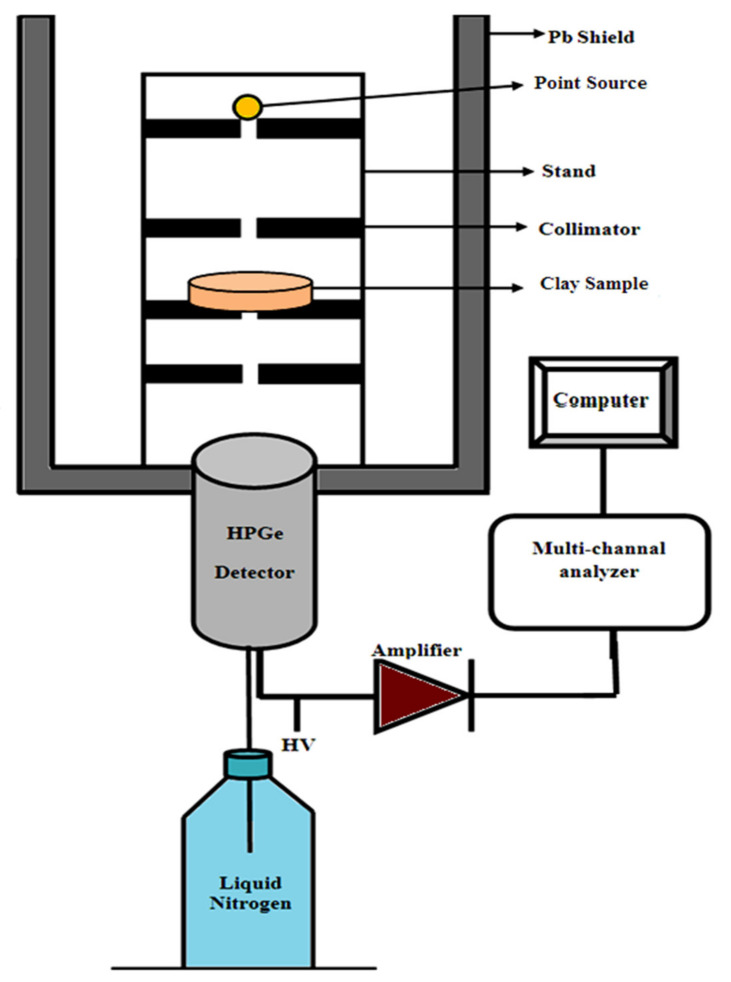
A scanning electron microscope (SEM, was used to show the distribution of particle inside each clay type as shown in Figure 2. To determine the elemental compositions of these clays, energy dispersive X-ray (EDX) analysis was used. The compositions are tabulated in Table 1. By knowing these compositions, the MAC can be calculated theoretically using the WinXCom program [25,26,27]. On the other hand, to calculate the MAC experimentally, the HPGe detector and three point sources of different energies were used. The sample was placed between the source and the detector as shown in Figure 3 and the measurement was done for a sufficient time so that the statistical uncertainty of the area under the peak was less than 1% and the counting rate was calculated in the presence and absence of the sample. The MAC is calculated according to the following equation [28,29,30]:
| (2) |
where, A and A o represent the areas under the peak or the count rates obtained from the spectrum in presence and absence of the absorbing sample respectively, x (cm), the thickness of the measured clay sample and ρ (g/cm3) the density. The linear attenuation coefficient or LAC defined as the probability of photons with matter per unit path length and was calculated to determine other important shielding parameters (such as HVL and TVL) where the LAC equal MAC*ρ. The HVL and TVL represent the thickness needed to attenuate 50% and 90% of initial photon intensity, respectively, and can be evaluated by the following equations [31,32]:
| (3) |
Figure 2.
SEM images for four the different clays discussed in the present work (a) bentonite clay, (b) red clay, (c) ball clay (d) kaolin clay.
Table 1.
The chemical compositions of four different clays and their density.
| Sample | Red Clay 2.02 g/cm3 |
Ball Clay 1.99 g/cm3 |
Bentonite 2.1 g/cm3 |
Kaolin 1.99 g/cm3 |
|---|---|---|---|---|
| Na2O | 0 | 0 | 1.3 ± 0.11 | 0 |
| MgO | 0.89 ± 0.32 | 0 | 1.18 ± 0.21 | 2.99 ± 0.16 |
| Al2O3 | 27.34 ± 0.24 | 35.08 ± 0.21 | 20.35 ± 0.14 | 35.53 ± 0.24 |
| SiO2 | 55.95 ± 0.11 | 58.26 ± 0.21 | 49.65 ± 0.22 | 55.26 ± 0.11 |
| SO3 | 0 | 0 | 1.96 ± 0.46 | 0 |
| K2O | 0.98 ± 0.25 | 0 | 1.28 ± 0.13 | 0 |
| CaO | 0 | 0 | 10.92 ± 0.25 | 1.24 ± 0.42 |
| TiO2 | 2.43 ± 0.41 | 2.5 ± 0.21 | 2.74 ± 0.14 | 2.76 ± 0.25 |
| FeO | 12.41 ± 0.02 | 4.16 ± 0.21 | 10.62 ± 0.19 | 2.22 ± 0.17 |
Figure 3.
The schematic diagram of the setup used in the present work.
The radiation protection efficiency (RPE) was determined for the studied clays to show the most efficient clay from the following equation [33].
| (4) |
3. Results and Discussion
Table 2 lists the experimental and theoretical mass attenuation coefficients (MAC) at four selected energies (energies emitted from Am-241, Cs-137, and Co-60) for the four investigated clays. The percent difference between the theoretical and experimental values was also determined. For example, the theoretical MAC value of ball clay at 0.060 MeV calculated from the XCOM software is equal to 0.287 cm2/g while the experimental value is equal to 0.282 ± 0.0062 cm2/g. These values have a relative difference of 1.54%. Meanwhile, kaolin clay has a theoretical MAC of 0.276 at 0.060 MeV and an experimental MAC of 0.270 ± 0.0055, or a R.D% of 2.05%. The highest overall MAC R.D (%) is equal to −3.02%, but most of the other results are much smaller than this value, proving that the experimental and theoretical data greatly agree with each other. This step is important to determine that the experimental data is correct and that the experimental setup used is suitable to determine the MAC of the tested clay samples.
Table 2.
The experimental and theoretical MAC by XCOM program as well as the relative deviation between the two results.
| Clay Type | Nuclide | Energy (MeV) | MAC (cm2.g−1) | R.D (∆%) | |
|---|---|---|---|---|---|
| XCOM | Experimental | ||||
| red clay | Am (241) | 0.060 | 0.352 | 0.346 ± 0.006 | 1.55 |
| Cs (137) | 0.662 | 0.076 | 0.077 ± 0.007 | −2.01 | |
| Co (60) | 1.172 | 0.058 | 0.056 ± 0.001 | 1.95 | |
| 1.333 | 0.054 | 0.053 ± 0.005 | 0.98 | ||
| ball clay | Am (241) | 0.060 | 0.287 | 0.282 ± 0.006 | 1.54 |
| Cs (137) | 0.662 | 0.077 | 0.076 ± 0.001 | 1.22 | |
| Co (60) | 1.172 | 0.058 | 0.058 ± 0.005 | −0.88 | |
| 1.333 | 0.055 | 0.054 ± 0.004 | 1.11 | ||
| kaolin clay | Am (241) | 0.060 | 0.276 | 0.270 ± 0.005 | 2.05 |
| Cs (137) | 0.662 | 0.077 | 0.075 ± 0.005 | 1.95 | |
| Co (60) | 1.172 | 0.058 | 0.059 ± 0.007 | −2.85 | |
| 1.333 | 0.055 | 0.054 ± 0.001 | 1.66 | ||
| bentonite clay | Am (241) | 0.060 | 0.372 | 0.383 ± 0.006 | −3.02 |
| Cs (137) | 0.662 | 0.077 | 0.078 ± 0.002 | −1.55 | |
| Co (60) | 1.172 | 0.058 | 0.057 ± 0.005 | 0.88 | |
| 1.333 | 0.055 | 0.054 ± 0.006 | 0.78 | ||
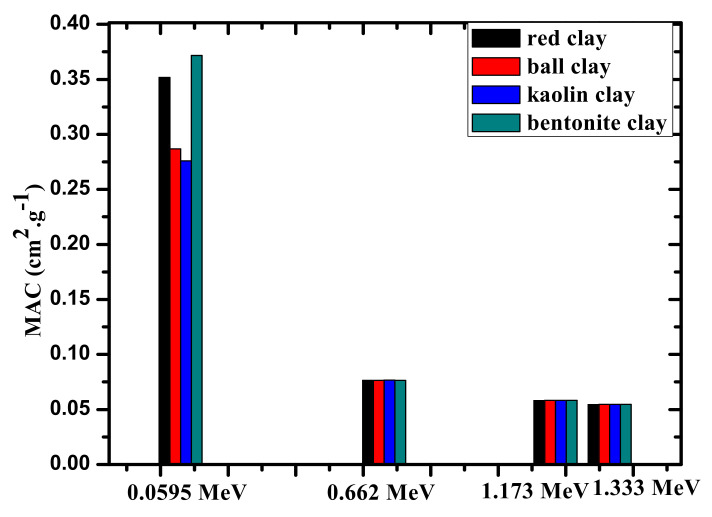
Figure 4 demonstrates the experimental MAC values for the four investigated clay samples at four selected energies. At the lowest tested energy, the difference between the MAC values is very clearly noticeable, while at higher energies the MACs are almost equal to each other. More specifically, at 0.060 MeV, the MAC values are equal to 0.346, 0.282, 0.270, and 0.383 cm2/g for red-clay, ball clay, kaolin clay, and bentonite-clay, respectively. This result shows that the shielding abilities of the clay samples at 0.060 MeV follow the order of: bentonite > red > ball > kaolin. At higher energies, this trend remains; however, the difference between the values is much smaller, meaning that the shielding capability at higher energies is practically identical. Thus, at low energies, the bentonite clay sample provides the most effective attenuation capability of the tested clays.
Figure 4.
The experimental MAC values for the four investigated clay samples at four selected energies.
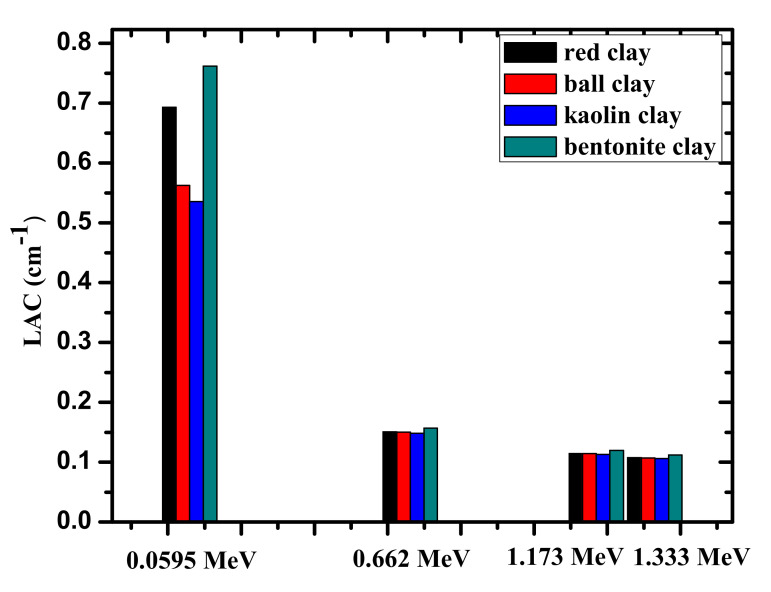
The linear attenuation coefficients (LACs) of the four investigated clay samples are plotted in Figure 5 at the four selected energies. Like the MAC, the difference between the LAC values is noticeable at low energies, but as energy increases, the values approach each other, resulting for all the samples in almost identical LACs. Bentonite clay has the greatest LAC at all four energies due to its high density due to its high FeO and CaO content. Meanwhile, kaolin and ball clays have the same density, but ball clay has a higher LAC than kaolin clay because it contains a larger amount of FeO and SiO2.
Figure 5.
The experimental LAC values for the four investigated clay samples at four selected energies.
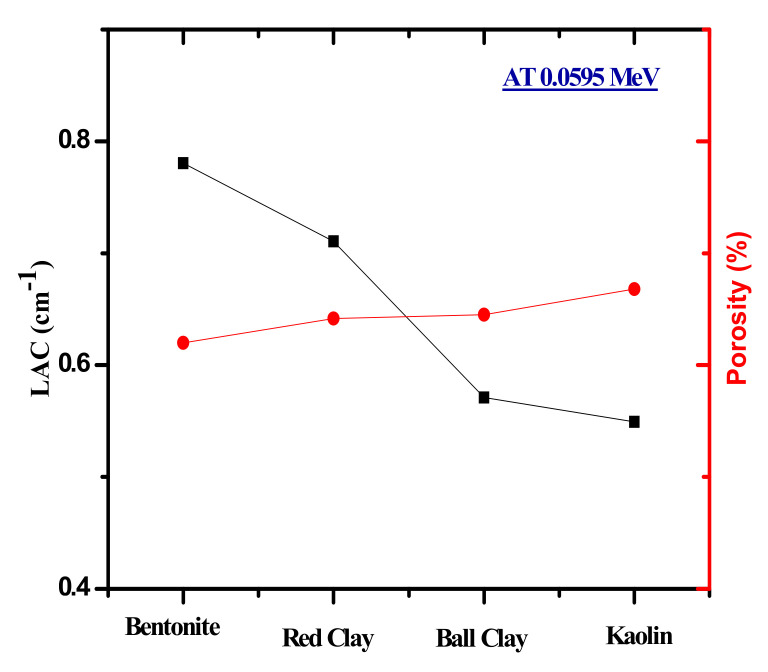
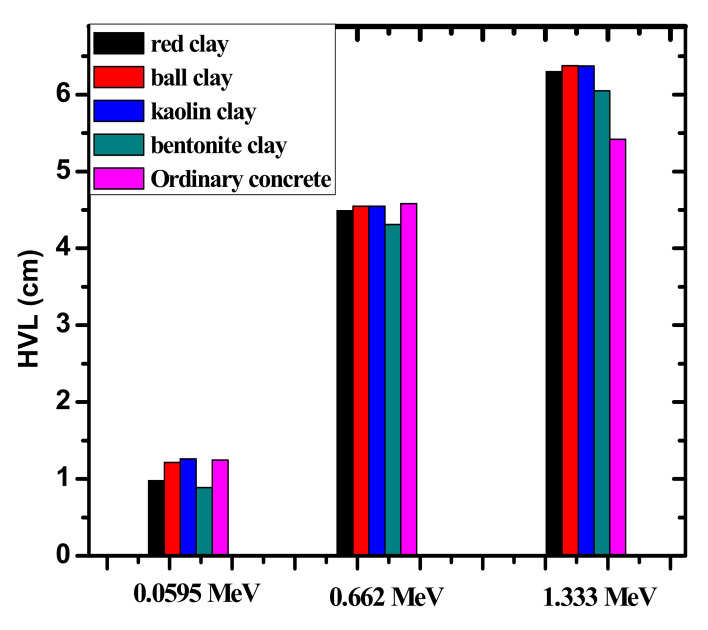
The porosity of the four clays was calculated and the results indicate that bentonite clay has the lowest level of porosity, while kaolin clay has the highest. This is reflected in the LAC, as it turns out that the one with the lowest porosity has the highest attenuation coefficient as shown in Figure 6. Figure 7 presents the half value layer (HVL) of the clay shields at low, medium, and high energies, alongside the HVL of ordinary concrete for comparison. The figure shows that the HVL increases as the energy increases. For example, the HVL of red clay increases from 0.9754 to 4.4896 cm and to 6.2973 cm at 0.060, 0.662, and 1.333 MeV, respectively, while kaolin clay has HVL values of 1.2620, 4.5466, and 6.3724 cm for the same respective energies. This result suggests than only a thin clay sample is needed to sufficiently absorb the radiation at low energies, while at higher energies a thicker sample is needed to shield the same amount of high energy radiation. More specifically, at 0.060 MeV, bentonite clay has an HVL equal to 0.8880 cm and the kaolin clay has an HVL of 1.2620 cm. This result shows that the bentonite clay is the most suitable for radiation shielding applications at low energies (below 100 keV).
Figure 6.
The porosity as a function of clay samples as well as the LAC values for the four investigated clay at 0.060 MeV.
Figure 7.
The experimental HVL values for the four investigated clay compared with ordinary concrete samples at three selected energies.
When comparing the ordinary concrete reported in [34] with the clay samples as shown in Table 3, it can be seen that at 0.060 MeV, the HVL for ordinary concrete is almost the same as the HVL for Kaolin clay (1.2469 vs 1.2620 cm) and is higher than bentonite clay (0.8880 cm) and red clay (0.9754 cm). As energy increases to 0.662 MeV, however, the HVL for ordinary concrete is almost the same as kaolin and red clay (4.5813, 4.5466, and 4.4896 cm, respectively). Lastly, at 1.333 MeV, the ordinary concrete outperforms all four of the tested clays. Thus, the figure proves that the investigated samples have a comparable shielding ability to other common radiation shields, demonstrating their potential in shielding applications. In Table 3, the present data were compared with the previous works reported in [21] and [22]. The results showed superiority in the current work for the attenuation coefficients at low and high energies.
Table 3.
The shielding parameters of four clays compared with previously published data.
| Attenuation Parameters | Energy (MeV) | This Work | [21] | [22] | [34] | ||||
|---|---|---|---|---|---|---|---|---|---|
| Bentonite Clay | Red Clay | Ball Clay | Kaolin Clay | Bentonite/Cement | Ball Clay | Kaolin Clay | Ordinary Concrete | ||
| LAC | 0.060 | 0.7806 | 0.7106 | 0.5709 | 0.5492 | 0.5911 | 0.5631 | 0.5421 | 0.5559 |
| 0.662 | 0.1608 | 0.1544 | 0.1524 | 0.1525 | 0.1511 | 0.1513 | 0.1504 | 0.1513 | |
| 1.170 | 0.1224 | 0.1175 | 0.1161 | 0.1161 | 0.1241 | 0.1196 | 0.1196 | 0.1366 | |
| 1.330 | 0.1146 | 0.1101 | 0.1087 | 0.1088 | 0.1161 | 0.1124 | 0.1124 | 0.1279 | |
| HVL | 0.060 | 0.8880 | 0.9754 | 1.2141 | 1.2620 | 1.1726 | 1.231 | 1.279 | 1.2469 |
| 0.662 | 4.3101 | 4.4896 | 4.5484 | 4.5466 | 4.5873 | 4.581 | 4.609 | 4.5813 | |
| 1.170 | 5.6645 | 5.8990 | 5.9725 | 5.9694 | 5.5854 | 5.796 | 5.796 | 5.0743 | |
| 1.330 | 6.0475 | 6.2973 | 6.3759 | 6.3724 | 5.9703 | 6.167 | 6.167 | 5.4194 | |
| MFP | 0.060 | 1.2811 | 1.4072 | 1.7515 | 1.8207 | 1.6918 | 1.776 | 1.845 | 1.7989 |
| 0.662 | 6.2182 | 6.4772 | 6.5619 | 6.5594 | 6.6181 | 6.609 | 6.649 | 6.6094 | |
| 1.170 | 8.1721 | 8.5104 | 8.6165 | 8.6120 | 8.0580 | 8.361 | 8.361 | 7.3206 | |
| 1.330 | 8.7246 | 9.0851 | 9.1985 | 9.1934 | 8.6133 | 8.897 | 8.897 | 7.8186 | |
| TVL | 0.060 | 2.9499 | 3.2402 | 4.0330 | 4.1923 | 3.8954 | 4.089 | 4.248 | 4.1421 |
| 0.662 | 14.3180 | 14.9142 | 15.1094 | 15.1035 | 15.2388 | 15.219 | 15.310 | 15.2187 | |
| 1.170 | 18.8170 | 19.5959 | 19.8402 | 19.8300 | 18.5543 | 19.252 | 19.252 | 16.8564 | |
| 1.330 | 20.0892 | 20.9193 | 21.1803 | 21.1686 | 19.8328 | 20.486 | 20.486 | 18.0030 | |
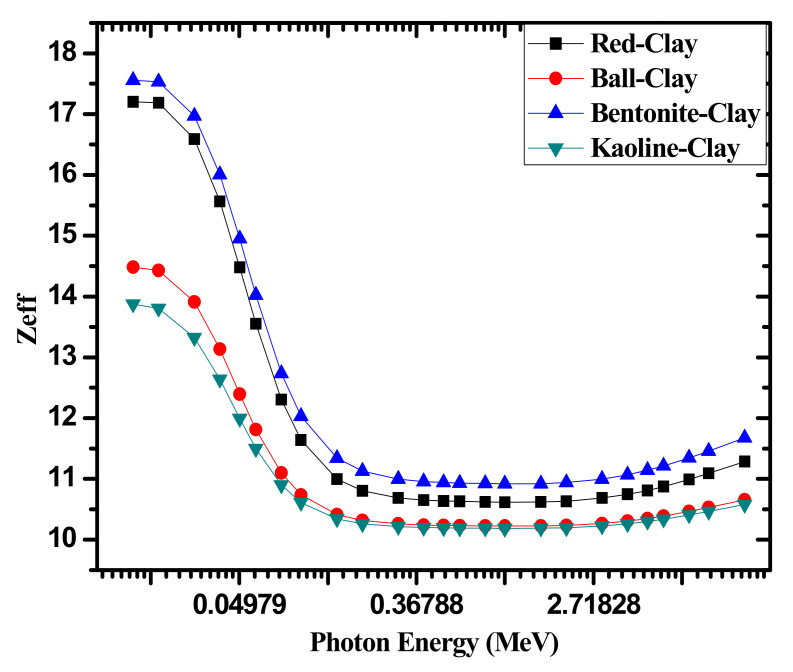
The effective atomic number, or Zeff, (equation given in [35]) of the four investigated clay samples are graphed against increasing photon energy in Figure 8. At very low energies, Zeff can be observed to sharply drop as energy increases, which can be attributed to the large inverse correlation between the photoelectric effect and energy. In the middle energy range, Zeff’s descent greatly slows down as the Compton scattering process takes over, and lastly as energy increases past 1 MeV, the pair production process causes Zeff to increase with increasing photon energy. The figure also reveals that at all tested energies, bentonite clay has the greatest Zeff, followed by red clay, then ball clay, and lastly kaolin clay. Bentonite clay has the highest Zeff which can be attributed to its greater concentration of Ca and S oxides, as opposed to Si, which have slightly greater atomic numbers than the metal oxides of the other samples. By that same logic, the kaolin clay has high amounts of Mg, Al, and Si compared to the other clays, which have relatively low atomic numbers, which lower its overall Zeff. Therefore, based on the figure, it can be concluded that bentonite clay has the greatest potential for radiation shielding applications.
Figure 8.
The effective atomic number Zeff values for the four investigated clay samples at different energies.
Figure 9 represents the radiation protection efficient, or RPE (%), of 5 cm thick samples of the tested clays against increasing energy. The figure reveals that in the three illustrated energies the RPE values follow the order of: bentonite clay > red clay > ball clay > kaolin clay. For example, at 0.060 MeV, the RPE values are equal to 97.982%, 97.137%, 94.242%, and 93.583% for bentonite clay, red clay, ball clay, and kaolin clay, respectively. This trend reveals that at this energy, the four clay samples can absorb almost all of the incoming photons, but the bentonite clay has the greatest attenuation capability of this energy, while kaolin clay has the least. In addition, as energy increases, RPE greatly begins to decrease. For instance, ball clay’s RPE decreases to 53.325% at 0.662 MeV and to 41.933% at 1.330 MeV. The decrease in value indicates that clays are much more effective at absorbing incoming photons at lower energies, while at higher energies the thickness of the samples must be increased to provide the same levels of attenuation.
Figure 9.
The experimental RPE values for the four investigated clay samples at three selected energies.
4. Conclusions
We aimed in this experimental work to report the radiation attenuation factors for four different clays (red, ball, kaolin and bentonite clays) at certain defined energies (emitted from Am-241, Cs-137, and Co-60). The relative difference of the experimental and XCOM results in the MAC are small and confirmed the experimental setup. At 0.060 MeV, the MAC data demonstrated that the shielding abilities of the chosen clay samples follow the order of: bentonite > red > ball > kaolin. This proved that at low energies, bentonite clay sample provides the most effective attenuation capability out of the tested clays. The HVL results indicated that only a thin clay sample is needed to sufficiently absorb the radiation at low energies, while at higher energies a thicker sample is needed to shield the same quantity of high energy radiated. The Zeff results also reveal that, e bentonite clay has the greatest Zeff, followed by red clay, then ball clay, and lastly kaolin clay. Therefore, based on the Zeff parameter, it can be concluded that the bentonite clay has the greatest potential for radiation shielding applications. The RPE values at 0.060 MeV are equal to 97.982%, 97.137%, 94.242%, and 93.583% for bentonite clay, red clay, ball clay, and kaolin clay, respectively.
Acknowledgments
Not Applicable.
Author Contributions
Conceptualization, M.E., Y.K.; Data curation, M.E., M.I.S. and Y.K.; Formal analysis, M.E., M.I.S. and Y.K.; Funding acquisition, M.A.; F.I.A.; Investigation, M.E., M.I.S. and Y.K.; Methodology, M.E., M.I.S. and Y.K.; Project administration, M.A.; F.I.A. and I.H.S.; Resources, M.E., M.I.S. and I.H.S.; Software, M.I.S. and Y.K.; Supervision, I.H.S. and M.E.; Validation, M.E., M.I.S. and I.H.S.; Visualization, M.A.; F.I.A.; Writing—original draft M.E. and Y.K.; Writing—review and editing, M.I.S. and M.E. All authors have read and agreed to the published version of the manuscript.
Funding
Not Applicable.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
All data are available in the manuscript.mdpi.com/ethics. You might choose to exclude this statement if the study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Esra Kavaz E.H., Ghanim A.S. Abouhaswa, Optical, structural and nuclear radiation security properties of newly fabricated V2O5-SrO-PbO glass system. J. Non-Cryst. Solids. 2020;538:120045. doi: 10.1016/j.jnoncrysol.2020.120045. [DOI] [Google Scholar]
- 2.Sayyed M.I., Mahmoud K.A., Tashlykov O.L. Mayeen Uddin Khandaker, M.R.I. Faruque, 2021. Enhancement of the Shielding Capability of Soda–Lime Glasses with Sb2O3 Dopant: A Potential Material for Radiation Safety in Nuclear Installations. Appl. Sci. 2021;11:326. doi: 10.3390/app11010326. [DOI] [Google Scholar]
- 3.Obaid S.S., Gaikwad D.K., Pawar P.P. Determination of gamma ray shielding parameters of rocks and concrete. Radiat. Phys. Chem. 2018;144:356–360. [Google Scholar]
- 4.Gökçe H.S., Yalçınkaya Ç., Tuyan M. Optimization of reactive powder concrete by means of barite aggregate for neutrons and gamma rays. Constr. Build. Mater. 2018;189:470–477. doi: 10.1016/j.conbuildmat.2018.09.022. [DOI] [Google Scholar]
- 5.Yasmin S., Barua B.S., Khandaker M.U., Rashid M.A., Bradley D.A., Olatunji M.A., Kamal M. Studies of ionizing radiation shielding effectiveness of silica-based commercial glasses used in Bangladeshi dwellings. Results Phys. 2018;9:541–549. doi: 10.1016/j.rinp.2018.02.075. [DOI] [Google Scholar]
- 6.Sayyed M.I., Jecong J.F.M., Hila F.C., Balderas C.V., Alhuthali A.M., Guillermo N.R.D., Al-Hadeethi Y. Radiation shielding characteristics of selected ceramics using the EPICS2017 library. Ceram. Int. 2021;47:13181–13186. doi: 10.1016/j.ceramint.2021.01.183. [DOI] [Google Scholar]
- 7.Yasmin S., Rozaila Z.S., Khandaker M.U., Barua B.S., Chowdhury F.U.Z., Rashid M.A., Bradley D.A. The radiation shielding offered by the commercial glass installed in Bangladeshi dwellings. Radiat. Eff. Defects Solids. 2018;173:657–672. doi: 10.1080/10420150.2018.1493481. [DOI] [Google Scholar]
- 8.Almuqrin A.H., Sayyed M.I. Radiation shielding characterizations and investigation of TeO2–WO3–Bi2O3 and TeO2–WO3–PbO glasses. Appl. Phys. A. 2021;127:190. [Google Scholar]
- 9.Abouhaswa A.S., Kavaz E. A novel B2O3-Na2O-BaO-HgO glass system: Synthesis, physical, optical and nuclear shielding features. Ceram. Int. 2020;46:16166–16177. [Google Scholar]
- 10.Mhareb M.H.A. Physical, optical and shielding features of Li2O–B2O3–MgO–Er2O3 glasses co-doped of Sm2O3. Appl. Phys. A. 2020;126:71. doi: 10.1007/s00339-019-3262-9. [DOI] [Google Scholar]
- 11.Sayyed M.I., Mahmoud K.A., Lacomme E., AlShammari M.M., Dwaikat N., Alajerami Y.S.M., Alqahtani M., El-bashir B.O., Mhareb M.H.A. Development of a novel MoO3-doped borate glass network for gamma-ray shielding applications. Eur. Phys. J. Plus. 2021;136:108. doi: 10.1140/epjp/s13360-020-01011-5. [DOI] [Google Scholar]
- 12.Dong M., Xue X., Yang H., Li Z. Highly cost-effective shielding composite made from vanadium slag and boron-rich slag and its properties. Radiat. Phys. Chem. 2017;141:239–244. doi: 10.1016/j.radphyschem.2017.07.023. [DOI] [Google Scholar]
- 13.Aygün B. High alloyed new stainless steel shielding material for gamma and fast neutron radiation. Nucl. Eng. Technol. 2020;52:647–653. [Google Scholar]
- 14.Gökç H.S., Canbaz-Öztürk B., Çam N.F., Andiç-Çakır Ö. Gamma-ray attenuation coefficients and transmission thickness of high consistency heavyweight concrete containing mineral admixture. Cem. Concr. Compos. 2018;92:56–69. [Google Scholar]
- 15.Sayyed M.I., Al-Hadeethi Y., AlShammari M.M., Ahmed M., Al-Heniti S.H., Rammah Y.S. Physical, optical and gamma radiation shielding competence of newly borotellurite based glasses: TeO2–B2O3–ZnO–Li2O3–Bi2O3. Ceram. Int. 2021;47:611–618. doi: 10.1016/j.ceramint.2020.08.168. [DOI] [Google Scholar]
- 16.Sayyed M.I., Mhareb M.H.A., Alajerami Y.S.M., Mahmoud K.A., Imheidat M.A., Alshahri F., Alqahtani M., Al-Abdullah T. Optical and radiation shielding features for a new series of borate glass samples. Optik. 2021;239:166790. doi: 10.1016/j.ijleo.2021.166790. [DOI] [Google Scholar]
- 17.Dong M., Xue X., Yang H., Liu D., Wang C., Li Z. A novel comprehensive utilization of vanadium slag: As gamma ray shielding material. J. Hazard. Mater. 2016;318:751–757. doi: 10.1016/j.jhazmat.2016.06.012. [DOI] [PubMed] [Google Scholar]
- 18.Sirin M. The effect of titanium (Ti) additive on radiation shielding efficiency of Al25Zn alloy. Prog. Nucl. Energy. 2020;128:103470. [Google Scholar]
- 19.Sousa L., Barabasch J., Stein K.J., Siegesmund S. Characterization and quality assessment of granitic building stone deposits: A case study of two different Portuguese granites. Eng. Geol. 2017;221:29–40. [Google Scholar]
- 20.Huang B., Lu W. Experimental investigation of the uniaxial compressive behavior of thin building granite. Constr. Build. Mater. 2021;267:120967. [Google Scholar]
- 21.El-Khatib A.M., Elsafi M., Almutiri M.N., Mahmoud R.M.M., Alzahrani J.S., Sayyed M.I., Abbas M.I. Enhancement of Bentonite Materials with Cement for Gamma-Ray Shielding Capability. Materials. 2021;14:4697. doi: 10.3390/ma14164697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Olukotun S., Gbenu S., Ibitoye F., Oladejo O., Shittu H., Fasasi M., Balogun F. Investigation of gamma radiation shielding capability of two clay materials. Nucl. Eng. Technol. 2018;50:957–962. doi: 10.1016/j.net.2018.05.003. [DOI] [Google Scholar]
- 23.ASTM Standards . Standard Test Methods for Apparent Porosity, Water Absorption, Apparent Specific Gravity, and Bulk Density of Burned Refractory Brick and Shapes by Boiling Water. ASTM International; West Conshohocken, PA, USA: 2015. ASTM C20-00. [Google Scholar]
- 24.Saleh H.M., Bondouk I.I., Salama E., Esawii H.A. Consistency and shielding efficiency of cement-bitumen composite for use as gamma-radiation shielding material. Prog. Nucl. Energy. 2021;137:103764. doi: 10.1016/j.pnucene.2021.103764. [DOI] [Google Scholar]
- 25.Mavi B. Experimental investigation of c-ray attenuation coefficients for granite. Ann. Nucl. Energy. 2012;44:22–25. doi: 10.1016/j.anucene.2012.01.009. [DOI] [Google Scholar]
- 26.Ozyurt O., Altinsoy N., Karaaslan Ş.İ., Bora A., Buyuk B., Erk İ. Calculation of gamma ray attenuation coefficients of some granite samples using a Monte Carlo simulation code. Radiat. Phys. Chem. 2018;144:271–275. [Google Scholar]
- 27.Elsafi M., Alrashedi M.F., Sayyed M.I., Al-Hamarneh I.F., El-Nahal M.A., El-Khatib M., Khandaker M.U., Osman H., Askary A.E. The Potentials of Egyptian and Indian Granites for Protection of Ionizing Radiation. Materials. 2021;14:3928. doi: 10.3390/ma14143928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Elsafi M., El-Nahal M.A., Alrashedi M.F., Olarinoye O.I., Sayyed M.I., Khandaker M.U., Osman H., Alamri S., Abbas M.I. Shielding Properties of Some Marble Types: A Comprehensive Study of Experimental and XCOM Results. Materials. 2021;14:4194. doi: 10.3390/ma14154194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sayyed M.I., Albarzan B., Almuqrin A.H., El-Khatib A.M., Kumar A., Tishkevich D.I., Trukhanov A.V., Elsafi M. Experimental and Theoretical Study of Radiation Shielding Features of CaO-K2O-Na2O-P2O5 Glass Systems. Materials. 2021;14:3772. doi: 10.3390/ma14143772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Al-Harbi N., Sayyed M.I., Al-Hadeethi Y., Kumar A., Elsafi M., Mahmoud K.A., Khandaker M.U., Bradley D.A. A novel CaO-K2O-Na2O-P2O5 Glass Systems for Radiation Shielding Applications. Radiat. Phys. Chem. 2021;188:109645. doi: 10.1016/j.radphyschem.2021.109645. [DOI] [Google Scholar]
- 31.Knoll G.F. Radiation Detection and Measurement. 3rd ed. John Wiley and Sons; New York, NY, USA: 2000. [Google Scholar]
- 32.Kumar A. Gamma ray shielding properties of PbO-Li2O-B2O3 glasses. Radiat. Phys. Chem. 2017;136:50–53. doi: 10.1016/j.radphyschem.2017.03.023. [DOI] [Google Scholar]
- 33.Mann H.S., Brar G.S., Mudahar G.S. Gamma ray shielding effectiveness of novel light weight clay flyash bricks. Radiat. Phys. Chem. 2016;127:97–101. [Google Scholar]
- 34.Bashter I. Calculation of radiation attenuation coefficients for shielding concretes. Ann. Nucl. Energy. 1997;24:1389–1401. doi: 10.1016/S0306-4549(97)00003-0. [DOI] [Google Scholar]
- 35.Kaçal M.R., Akman F., Sayyed M.I. Evaluation of gamma-ray and neutron attenuation properties of some polymers. Nucl. Eng. Technol. 2019;51:818–824. doi: 10.1016/j.net.2018.11.011. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data are available in the manuscript.mdpi.com/ethics. You might choose to exclude this statement if the study did not report any data.