Mathematical assessment of constant and time-dependent control measures on the dynamics of the novel coronavirus: An application of optimal control theory

Abstract

The coronavirus infectious disease (COVID-19) is a novel respiratory disease reported in 2019 in China. The COVID-19 is one of the deadliest pandemics in history due to its high mortality rate in a short period. Many approaches have been adopted for disease minimization and eradication. In this paper, we studied the impact of various constant and time-dependent variable control measures coupled with vaccination on the dynamics of COVID-19. The optimal control theory is used to optimize the model and set an effective control intervention for the infection. Initially, we formulate the mathematical epidemic model for the COVID-19 without variable controls. The model basic mathematical assessment is presented. The nonlinear least-square procedure is utilized to parameterize the model from actual cases reported in Pakistan. A well-known technique based on statistical tools known as the Latin-hypercube sampling approach (LHS) coupled with the partial rank correlation coefficient (PRCC) is applied to present the model global sensitivity analysis. Based on global sensitivity analysis, the COVID-19 vaccine model is reformulated to obtain a control problem by introducing three time dependent control variables for isolation, vaccine efficacy and treatment enhancement represented by $u_1\left(t\right)$, $u_2\left(t\right)$ and $u_3\left(t\right)$, respectively. The necessary optimality conditions of the control problem are derived via the optimal control theory. Finally, the simulation results are depicted with and without variable controls using the well-known Runge–Kutta numerical scheme. The simulation results revealed that time-dependent control measures play a vital role in disease eradication.

Introduction

The COVID-19 is caused by a new virus from the coronavirus family known as severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). The first case confirmed with this novel infection was reported in Wuhan, China, in December 2019. World Health Organization (WHO), declared COVID-19 as a global pandemic on 11th of March, 2020. According to the WHO recent reports published on 27th September 2021, the confirmed infected people crossed 231 million figures and it has caused 4.74 million deaths globally [1]. Although, the world is facing fourth wave of the ongoing pandemic, its symptoms are still variable, ranging from mild to severe illness and in some cases, it leads to the life-threatening situation. The incubation period of the novel infection is from 2 to 14 days based on the clinical observation [1], [2]. It is noticed that in some cases, a COVID-19 patient tests as positive and capable of transmitting the infection but experiences no symptoms. Such cases are categorized as asymptomatic infected people. On the other hand, a COVID-19 patient may exhibit disease symptoms or signs and is categorized as symptomatic infected people. In COVID-19 patients, some cases have different disease signs, although with the same infection and their symptoms may vary over the passage of time. The common symptoms identified in a COVID-19 patient include muscle and joint pain, headache, fever, fatigue, vomiting, diarrhea, loss of taste combined with loss of smell and in some severe cases it may lead to shortness of breath. The COVID-19 infection is transmitted to others when they are physically close to the infectious people. There is still no specific and effective treatment for the COVID-19. Thus, to overcome the infection and reduce the disease burden, many prevention strategies have been utilized. Main prevention strategies include: getting vaccinated as soon as possible, staying at home, use of face masks in public areas, avoiding crowded places, and use of other non-pharmaceutical measures [2], [3].

The assessment of infectious diseases can be carried out using mathematical models. These models are helpful to explore the disease insights and are useful to set effective prevention measures [4], [5], [6], [7], [8]. The epidemic models of disease dynamics result in the system of nonlinear differential equations. Recently, a number of compartmental models based on COVID-19 dynamics have been studied with different approaches [9], [10]. These epidemic models are mainly constituted via the classical integer or in some cases with fractional order and stochastic differential systems. The dynamics of COVID-19 in selected countries with high disease burdens are studied in detail in [11], where the authors used the classical integer order differential systems in model formulation. A fractional study describing the deeper insights of the COVID-19 dynamics has been conducted in [12], where the authors parameterized the model with actual infected cases reported in Saudi Arabia. The epidemic modeling based on stochastic and deterministic approaches has been presented in order to explore the dynamical behavior of ongoing pandemics in Africa and Europe [13]. Moreover, in [13], the authors presented a detailed mathematical analysis and state-level infection forecasting. Recently, a numerical based approach has been adopted to explore the dynamical aspect of a SITR type COVID-19 compartmental model [14]. A stochastic epidemic modeling approach has been recently used to explore the dynamics of novel infection under various controlling measures, including quarantine, community-wide lockdown, and testing [15]. The analysis and forecast of the third wave of the COVID-19 have been studied in [16] using the classical integer order epidemic model. The study conducted in [16] provides a better prediction of the pandemic in the selected region. Additionally, the authors presented the graphical results showing the importance of various model control parameters on the disease incidence and control. The novel application of piecewise differential coupled with the integral operators to predict the third wave of the ongoing pandemic in three countries has been studied in [13]. The authors in [13], provided the existence and uniqueness of the problem and then presented a detailed simulation to support the theoretical results.

Optimal control theory is one of the useful mathematical tools to formulate control problems in order to investigate a better intervention for disease eradication. This analysis optimized the control problem and utilized the well-known Pontryagin maximum principle to set the necessary optimality conditions [17]. The optimal control theory has been used to develop the appropriate control strategies for different disease outbreaks in various regions in the world; for instance see [18], [19], [20], [21], [22], [23] (and the reference cited therein). Recently, mathematical modeling approach with different controlling measures have been analyzed to mitigate the ongoing COVID-19 pandemic globally and with case studies. A mathematical model based on classical integer order system has been studied to explore the transmission dynamics of the infection and to set an effective intervention for disease minimization in Nigeria [24]. The authors in [24] first formulate the control model by introducing control variables and optimize the model to provide an appropriate intervention for disease in a selected region. Mathematical modeling approach addressing the impact of contact and time-dependent variable interventions on the infection incidence has been depicted in [25]. The authors in [25] initially studied the model simulation with constant controls and then incorporated the variable control measures in the model. It was found that the variable control measures play a vital role in disease eradication. In [26], the authors applied the well-known control theory in order to explore the impact of various intervention strategies on disease dynamics. The impact of time-dependent interventions along with the cost-effective analysis for COVID-19 is carried out in [27]. The authors in [27] performed detailed global stability analysis and provided a realistic approach by considering the actual cases reported in Ghana. Recently, an application of optimal control theory to optimize a simple SIER compartmental model for the dynamics of COVID-19 has been done in [28].

In continuation of the previous work, the current study presents the impact of constant and time-dependent control measures on the disease dynamics, including vaccination intervention. Initially, the model is formulated with constant controls (without variable control measures) using an integer order nonlinear differential system consisting of six equations. The sensitivity analysis has been carried out to point out the most sensitive parameters. The model is fitted to the actual cases reported in Pakistan to estimate the parameters. The model is further extended to formulate an optimal control problem by introducing three time dependent control variables for isolation, vaccination efficacy and treatment enhancement. The model is simulated with and without variable control measures and the detailed graphical results are depicted. The details of paper organization are as follows: The mathematical formulation with constant controls is presented in the next section. Moreover, the estimation of parameters is also carried out in this section. The basic theoretical analysis is illustrated in Section ‘Basic mathematical analysis of model’. Section ‘Global sensitivity analysis’ accomplishes the sensitivity analysis of the model parameters versus the basic reproduction number. Section ‘Optimal control analysis of the COVID-19 vaccine model’ presents the formulation along with simulation results and discussion. In Section ‘Conclusion’, the work is concluded with the main findings of the present study.

Formulation COVID-19 vaccine model without optimal control

This section presents briefly the formulation of a mathematical model to assess the dynamics of COVID-19. The formulation of the model is performed using ordinary nonlinear differential equations. For this purpose, the available population is categorized into six different groups with details: susceptible individuals $S\left(t\right)$, exposed (infected but not capable of transmitting the infection yet) $E\left(t\right)$, asymptomatically infected with no/mild disease symptoms $I_A\left(t\right)$, symptomatic infected who fully exhibit the disease symptoms $I_S\left(t\right)$ and the removed or recovered individuals are shown by $R\left(t\right)$. $N\left(t\right)$ shows the total population such that $N\left(t\right)=S\left(t\right)+E\left(t\right)+I_S\left(t\right)+I_A\left(t\right)+V\left(t\right)+R\left(t\right)$. For construction of the model, we assume that the population in all compartments is homogeneous and can freely mixing with each other. The symptomatic and asymptomatic individuals can transmit the virus to susceptible people. The resulting compartmental model for addressing the dynamical aspects of novel COVID-19 with impact of vaccination is organized as follows:

$$\left\{\begin{array}{c}\frac{dS}{dt}=\Delta +{\psi }_{V}V-\frac{\beta (I_S+{\beta }_1{I}_A)S}{N}-(d+{\omega }_V)S,\hfill \\ \frac{dE}{dt}=\frac{\beta (I_S+{\beta }_1{I}_A)S}{N}-(\kappa +d)E,\hfill \\ \frac{d{I}_S}{dt}=(1-\eta )\kappa E-(d+d_1+{\gamma }_1)I_S,\hfill \\ \frac{d{I}_A}{dt}=\eta \kappa E-(d+{\gamma }_2)I_A,\hfill \\ \frac{dV}{dt}={\omega }_{v}S-({\psi }_V+d)V,\hfill \\ \frac{dR}{dt}={\gamma }_1{I}_S+{\gamma }_2{I}_A-dR,\hfill \end{array}\right)$$ (1)

along with the initial conditions

$$S\left(0\right)=S_0\ge 0,E\left(0\right)=E_0\ge 0,I\left(0\right)=I_0\ge 0,I_A\left(0\right)={I_A}_0\ge 0,V\left(0\right)=V_0,R\left(0\right)=R_0\ge 0.$$

In the above system (1), the natural death rate is represented by $d$, and that death caused from COVID-19 is represented by $d_1$. The recovery rates at the symptomatic and asymptomatic compartments are denoted by ${\gamma }_1$ and ${\gamma }_2$ respectively. The incubation period is shown by $\kappa$, where we assumed that a fraction $\eta$ of the exposed individuals move to $I_A\left(t\right)$ at time t, while the remaining people denoted by $(1-\eta )$, move to the symptomatically infected class $I_S\left(t\right)$. The effective contact rates causing the disease transmission to susceptible human(s) is denoted as $\beta$ and ${\beta }_1$. The parameter ${\beta }_1$ shows the transmission probability of infection from individuals in the $I_A$ compartment. The susceptible individuals are vaccinated at a rate ${\omega }_V$. The vaccinated individuals become susceptible again at rate ${\psi }_V$. The parameter $\lambda$ shows the force of infection at which the susceptible joins the exposed class. The visual flow among different compartments is described in Fig. 1.

Fig. 1.

Chart showing flow among different population compartments.

Data fitting procedure of model to the reported cases

Estimating the model parameters from the reported statistical data is an essential aspect of the present study. This procedure makes the study valuable and provides comparatively more realistic predictions about the disease dynamics in a selected region. For this purpose, the well-known nonlinear least square method is employed to provide a better fit using model simulated cases to the real cases reported in Pakistan for a selected period of the pandemic i.e., from first March till mid of August, 2020. The demographic parameters i.e., $\Delta$ (the recruitment rate) and $d$ (the natural mortality rate) are calculated from the literature as given in the below Table 1. Further, by using the least square technique, the remaining parameters are estimated from the reported infected statistics. The detail parameter estimations procedure can be described as:

Table 1.

The estimated values with physical meaning of the model parameters.

Parameter	Physical meaning	Value taken in days	Reference
$\Delta$	birth rate	$N\left(0\right)\times d$	Estimated
$d$	natural mortality rate	$1/(67.7\ast 365)$	[29]
$d_1$	death rate caused due to infection	0.022	[2]
${\gamma }_1$	recovery/removal rate in $I_S$ compartment	0.4958	Fitted
${\gamma }_2$	recovery/removal rate in $I_A$ compartment	0.1110	Fitted
$\beta$	disease transmission rate	0.6022	Fitted
${\beta }_1$	infection transmission probability relative $I_A$ class	0.7459	Fitted
$\kappa$	incubation period	0.5171	Fitted
$\eta$	proportion of exposed people join $I_A$ class	0.8833	Fitted
${\omega }_V$	vaccine rate	0.0313	Fitted
${\psi }_V$	vaccine waning/loss of immunity	0.0233	Fitted

Since Pakistani people have 67.7 average lifespans [29], the estimated value of the natural death rate is $d=1/(67.7\ast 365)$ per day. The birth rate $\Delta$ is computed from the total population of Pakistan, therefore $\Delta =8939$ per day. The other parameters values are estimated from the COVID-19 incidence data via the least square technique. The applied objective function in the estimation procedure is described as follows:

$$\hat{\Phi }=\sum _{\tau =1}^k{({\chi }_{t_{\tau }}-{\tilde{\chi }}_{t_{\tau }})}^2,$$ (2)

where ${\tilde{\chi }}_{t_{\tau }}$ are the confirmed cases, ${\chi }_{t_{\tau }}$ are the solution of model (1) at time $t_{\tau }$, and $k$ denotes the available actual data points. The predicted simulated curve of infected individuals by proposed model (1) is shown by a black solid-dotted curve, while the actual reported cases are shown by blue stars, as illustrated in Fig. 2. It shows a good fit to the actual curve. The resulting estimated as well as fitted values of the model parameters are presented in Table 1. The initial conditions taken into account here are $S\left(0\right)=220870336,E\left(0\right)=2000,I_S\left(0\right)=4,I_A\left(t\right)=200,V\left(0\right)=R\left(0\right)=0$.

Fig. 2.

Observed COVID-19 cases in Pakistan (shown by blue stars) and the model predicted cumulative infected cases (shown by black solid-dotted line).

Basic mathematical analysis of model

To proceed with the control analysis, we firstly present some basic theoretical properties of the proposed model (1), including positivity, boundedness, disease free and endemic equilibria. Additionally, an analytical expression for the basic reproductive number having biological importance is provided. We begin with the following lemma deals with the epidemic model (1) solution positivity and boundedness.

Positivity and boundedness

Lemma 1

From the initial conditions, it indicates that all parameters are non-negative. With such initial data for simplicity, say $\delta \left(0\right)$ whereas $\delta \left(t\right)=(S,E,I_S,I_A,V,R)$ shows the state variables, then all solution curves of (1) will be non-negative for all positive values of $t$ . Additionally,

$$\underset{t\to \infty }{lim}supN\left(t\right)\le \Delta /d.$$

Proof

Let $t_1=sup\{t>0:\delta \left(t\right)>0\}$ and taking the first equation of epidemic model with constant control (1), we have

$$\frac{dS}{dt}=\Delta -(\lambda \left(t\right)+{\omega }_V+d)S+{\psi }_{V}V\ge \Delta -(\lambda \left(t\right)+{\omega }_V+d)S,$$

where, $\lambda \left(t\right)$ is the force of infection. Further simplification leads to

$$\frac{d}{dt}\left(S\left(t\right)exp\left((d+{\omega }_V)t+{\int }_0^t\lambda \left(\xi \right)d\xi \right)\right)\ge \left(\Delta \right)\left(exp\left((d+{\omega }_V)t+{\int }_0^t\lambda \left(\xi \right)d\xi \right)\right),$$

by integrating we have,

$$S\left(t_1\right)\ge S\left(0\right)\left\{-exp\left((d+{\omega }_V)t_1+{\int }_0^{t_1}\lambda \left(\xi \right)d\xi \right)\right\}+\left\{-exp\left((d+{\omega }_V)t_1+{\int }_0^{t_1}\lambda \left(\xi \right)d\xi \right)\right\}\times {\int }_0^{t_1}\Delta exp\left((d+{\omega }_V)p+{\int }_0^p\lambda \left(\xi \right)d\xi \right)dp>0.$$

Similarly, we can proceed with the rest of the equations of the model (1). Thus, we are confident to state that the solution of the problem will be non-negative $\forall$ $t>0$.

For the prove of remaining part of the lemma, we have $0<\delta \left(0\right)\le N\left(t\right)$, and further adding all equations the epidemic model (1) we lead to the following inequity

$$\frac{dN\left(t\right)}{dt}=\Delta -dN\left(t\right)-d_1{I}_s\left(t\right)\le \Delta -dN\left(t\right).$$

Hence,

$$\underset{t\to \infty }{lim}sup\left\{N\left(t\right)\right\}\le \Delta /d.\square$$

Invariant region

In view of the above results, the constant control model (1) will be analyzed in a feasible region given as

$$\Sigma \subset {\mathbb{R}}_{+}^6,$$

where

$$\Sigma =\left\{(S,E,I_S,I_A,V,R)\in {\mathbb{R}}_{+}^6:N\left(t\right)\le \Delta /d\right\}.$$

To make the model biologically feasible, it is important to confirm that the region described in the above set $\Sigma$ is positively invariant, with respect to the model (1).

Lemma 2

The region shown by $\Sigma \subset {\mathbb{R}}_{+}^6$ is positively invariant for the system (1) with non-negative initial conditions in ${\mathbb{R}}_{+}^6$ .

Proof

As we know from Lemma 1,

$$\frac{dN\left(t\right)}{dt}\le \Delta -dN\left(t\right).$$ (3)

It is clear that

$$\frac{dN\left(t\right)}{dt}\le 0,ifN\left(0\right)\ge \frac{\Delta }{d}.$$

After some manipulation we lead to the following solution of (3)

$$N\left(t\right)\le N\left(0\right)e^{-dt}+\frac{\Delta }{d}(1-e^{-dt}).$$

Particularly, $N\left(t\right)\le \Delta /d$, and thus, the region $\Sigma$ is positively invariant. Moreover, all solutions trajectories will be attracted in ${\mathbb{R}}_{+}^6$. □

Model equilibria and basic reproduction number

Model (1) has at the most two equilibrium points. The disease-free equilibrium (DFE) given by

$${\mathcal{K}}_0=\left(S^0,0,0,0,V_0,0\right)=\left(\frac{\Delta }{d},0,0,0,\frac{\Delta {\omega }_V}{{\psi }_V{\omega }_V-(d+{\omega }_V)({\psi }_V+d)},0\right).$$

To present the basic reproduction number, the well-known next generation method presented in [30] is taken in the consideration. The resulting expression of ${\mathcal{R}}_0$ is obtained as:

$${\mathcal{R}}_0=\frac{\beta \kappa ({\psi }_V+d)(\eta {\beta }_1(d+d_1+{\gamma }_1)+k_3(1-\eta ))}{(d+d_1+{\gamma }_1)(\kappa +d)(d+{\gamma }_2)({\psi }_V+d+{\omega }_V)}.$$ (4)

Endemic equilibrium (EE) of the model

The endemic equilibrium (EE) of the COVID-19 vaccine model (1) denoted by ${\mathcal{K}}_1(S^{\ast \ast },E^{\ast \ast },I_S^{\ast \ast },I_A^{\ast \ast },V^{\ast \ast },R^{\ast \ast })$ with

$$\left\{\begin{array}{c}{S}^{\ast \ast }=\frac{\Delta k_4}{{\lambda }^{\ast \ast }{k}_4+k_0{k}_4-{\psi }_V{\omega }_V},\hfill \\ E_{=}^{\ast \ast }\frac{\Delta {\lambda }^{\ast \ast }{k}_4}{k_1\left({\lambda }^{\ast \ast }{k}_4+k_0{k}_4-{\psi }_V{\omega }_V\right)},\hfill \\ I^{\ast \ast }=\frac{\Delta \kappa {\lambda }^{\ast \ast }{k}_4(1-\eta )}{k_2{k}_1\left({\lambda }^{\ast \ast }{k}_4+k_0{k}_4-{\psi }_V{\omega }_V\right)},\hfill \\ I_A^{\ast \ast }=\frac{\Delta \kappa {\lambda }^{\ast \ast }{k}_4\eta }{k_1{k}_3\left({\lambda }^{\ast \ast }{k}_4+k_0{k}_4-{\psi }_V{\omega }_V\right)},\hfill \\ V^{\ast \ast }=\frac{\Delta {\omega }_V}{{\lambda }^{\ast \ast }{k}_4+k_0{k}_4-{\psi }_V{\omega }_V},\hfill \\ R^{\ast \ast }=\frac{\Delta \kappa {\lambda }^{\ast \ast }{k}_4\left(k_3(1-\eta ){\gamma }_1+k_2\eta {\gamma }_2\right)}{k_1{k}_2{k}_{3}d\left({\lambda }^{\ast \ast }{k}_4+k_0{k}_4-{\psi }_V{\omega }_V\right)},\hfill \end{array}\right)$$ (5)

where,

$$k_0=(d+{\omega }_V),k_1=(\kappa +d),k_2=(d+d_1+{\gamma }_1),k_3=(d+{\gamma }_2),k_4=({\psi }_V+d).$$

Substituting the values from (5) into the force of infection given in the following equation:

$${\lambda }^{\star \star }=\frac{\beta ({I_S}^{\star \star }+{\beta }_1{I}_A^{\star \star })}{N^{\star \star }}.$$ (6)

After some manipulations, the non-zero equilibria of the model satisfies the following equation

$$C_0{\lambda }^{\star \star }+C_1=0,$$ (7)

with the coefficients

$$C_0=k_4\left\{\kappa k_3(1-\eta )({\gamma }_1+d)+k_2\left(k_{3}d+\kappa \eta (d+{\gamma }_2)\right)\right\},$$

$$C_1=\mu k_1{k}_2{k}_3(k_4+{\omega }_V)\left(1-{\mathcal{R}}_0\right).$$

Lemma 3

The COVID-19 model without variable controls (1) possess a unique endemic equilibrium, shown by ${\mathcal{K}}_1$ , whenever ${\mathcal{R}}_0>1$ .

Global sensitivity analysis

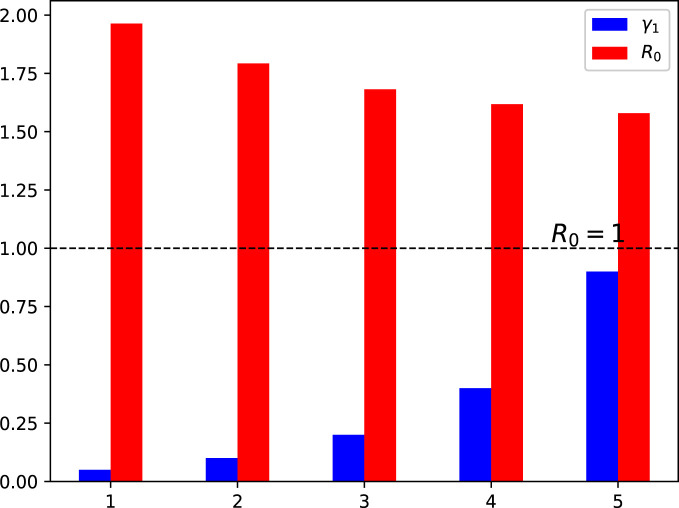
Global sensitivity analysis plays a significant role in various fields of science including epidemiology. This analysis is utilized to assess the uncertainty in outputs relative to the uncertainty in each input parameter on their entire range of consideration. On the other hand, in the local sensitivity analysis, the influence of one input parameter on the model output is carried out with other parameters being constant. Unlike the local case, the global sensitivity analysis quantifies the influence when all input parameters or factors are simultaneously vary. In most complex and nonlinear processes, including infectious diseases, the global sensitivity analysis rather than the local are appropriate in order to justify the importance of system input and their impact with respect to model output. Several approaches have been adopted for this purpose. In this study, the well-known method based on the LHS and PRCC is utilized [31] for quantifying the uncertainty level in the problem under consideration. The parameter with a relatively smaller $p$-value and higher PRCC indicates that it significantly impacts the prevalence of infection. The corresponding PRCC and $p$-values of the model parameters are presented in Table 2. Further, the PRCC values of the considered parameters in terms of the bar graph are also depicted as in Fig. 10. This graphical interpretation shows that to minimize the disease incidence, we need to reduce the effective contacts among the infectious and susceptible population, enhance the vaccine efficacy and improve the treatment strategy.

Table 2.

Table showing the PRCC and corresponding $p$-values regarding ${\mathcal{R}}_0$ for model parameters.

Parameter	PRCC values	$p$ values
${\beta }_1$	0.7209	0.000
$\beta$	0.9061	0.000
${\psi }_V$	0.2782	0.000
${\omega }_V$	−0.4226	0.000
$\omega$	−0.5291	0.000
$\kappa$	0.2369	0.427
$\eta$	−0.3135	0.000
$\mu$	−0.2821	0.000
${\gamma }_1$	−0.4001	0.000
${\gamma }_2$	−0.6408	0.000
${\mu }_1$	−0.3253	0.000

Fig. 10.

PRCC of model parameters versus the reproduction number ${\mathcal{R}}_0$.

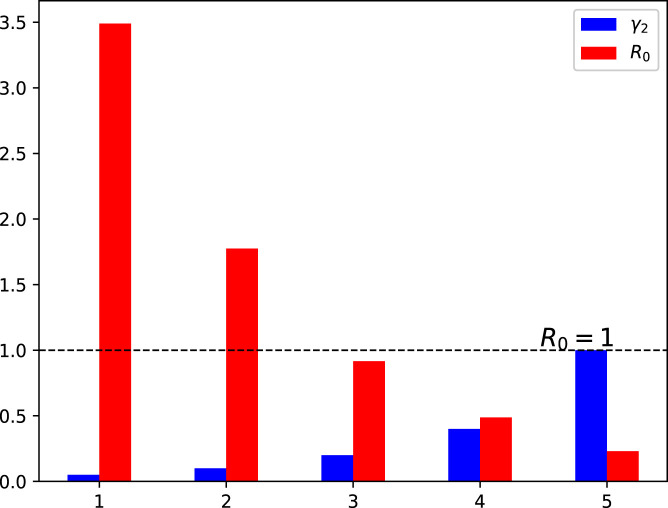
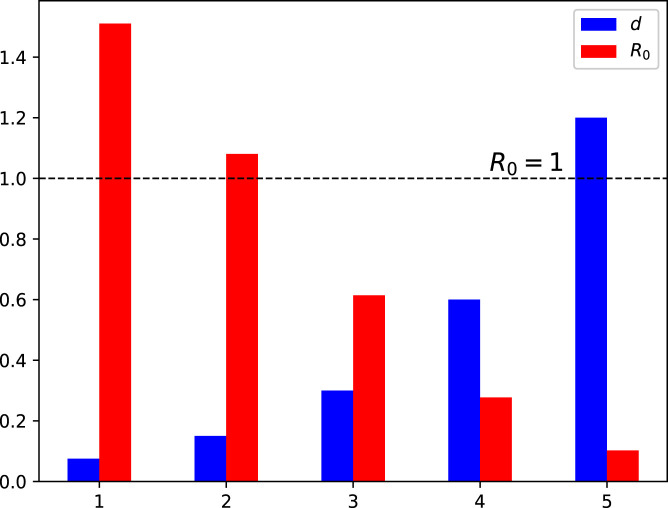
Moreover, this section presents the nature of ${\mathcal{R}}_0$ versus various model parameters. This interpretation is shown using the bar graphs 3–9. The analysis conducted in this section helps to investigate the most sensitive parameter(s) that need to be utilized in formulation of the control problem for the better eradication of COVID-19 pandemic. The impact of effective contact rates $\beta$ and ${\beta }_1$ is depicted in Fig. 3, Fig. 4, respectively. The reduction in these parameters results in the value of ${\mathcal{R}}_0$ decreasing to less than 1. Fig. 5, Fig. 6 demonstrate the impact of recovery rates ${\gamma }_1$ and ${\gamma }_2$ upon ${\mathcal{R}}_0$. The impact of ${\gamma }_1$ is not significant, whereas the increase in ${\gamma }_2$ decreases ${\mathcal{R}}_0$ to a value less than 1. The impact of natural death rate $d$ is depicted in 7. Fig. 8, Fig. 9 respectively show the impact of vaccine waning rate ${\psi }_V$ and vaccination rate ${\omega }_V$. It is observed that ${\mathcal{R}}_0$ can be reduced significantly by enhancing the vaccination rate and reducing the vaccine waning rate. Based on the global sensitivity study, in the next section, we will introduce three time-dependent control variables denoted by $u_1\left(t\right),u_2\left(t\right)$ and $u_3\left(t\right)$ in the COVID-19 epidemic model (1) to construct the control problem.

Fig. 3.

Impact of variation in the contact rate $\beta$ on the reproduction number ${\mathcal{R}}_0$.

Fig. 9.

Influence of variation in the vaccination rate ${\omega }_V$ on the reproduction number ${\mathcal{R}}_0$.

Fig. 4.

Impact of variation in the contact rate ${\beta }_1$ on the reproduction number ${\mathcal{R}}_0$.

Fig. 5.

Influence of variation in the recovery rate ${\gamma }_1$ on the reproduction number ${\mathcal{R}}_0$.

Fig. 6.

Influence of variation in the recovery rate ${\gamma }_2$ on the reproduction number ${\mathcal{R}}_0$.

Fig. 7.

Influence of variation in the natural mortality rate $d$ on the reproduction number ${\mathcal{R}}_0$.

Fig. 8.

Influence of variation in the vaccination waning rate ${\psi }_V$ on the reproduction number ${\mathcal{R}}_0$.

Optimal control analysis of the COVID-19 vaccine model

The previous section presented the sensitivity analysis of the key parameters of the model. This analysis provides a clue for suggesting a better controlling strategy. Based on the PRCC indices, we extend the COVID-19 vaccine epidemic model (1) to a control problem by introducing three time dependent control variables instead of constant control parameters. We optimize the problem using optimal control theory in order to explore an effective intervention strategy to eradicate or minimize the COVID-19 infection. The considered control variables are as follows:

• •Isolation control $u_1\left(t\right)$: This control variable reduces the effective contacts among susceptible and infectious (symptomatic or asymptomatic) individuals causing disease transmission in the population.
• •Vaccine efficacy control $u_2\left(t\right)$: The second time dependent control variable is used for the enhancement in vaccine efficacy (rate) of the susceptible individuals.
• •Treatment control $u_3\left(t\right)$: The third control variable is for the treatment purpose to enhance the recovery of infected individuals.

Firstly, we depict the impact of vaccination rate with the constant rate on the dynamics of COVID-19. This section aims to formulate an optimal control problem with the help of the aforementioned controls to describe how the variable control measures play a role in disease eradication. The developed control problem is given in the system (8). Based on the global sensitivity results, the desired controls are chosen. Thus, by incorporating the above mentioned control variables, the resulting control model is formulated as

$$\left\{\begin{array}{c}\frac{dS}{dt}=\Delta +{\psi }_{v}V-\frac{\beta (I_S+{\beta }_1{I}_A)S}{N}(1-u_1\left(t\right))-(d+u_2\left(t\right))S,\hfill \\ \frac{dE}{dt}=\frac{\beta (I_S+{\beta }_1{I}_A)S}{N}(1-u_1\left(t\right))-(\kappa +d)E,\hfill \\ \frac{d{I}_S}{dt}=(1-\eta )\kappa E-(d+d_1+u_3\left(t\right))I_S,\hfill \\ \frac{d{I}_A}{dt}=\eta \kappa E-(d+u_3\left(t\right))I_A,\hfill \\ \frac{dV}{dt}=u_2\left(t\right)S-({\psi }_v+d)V,\hfill \\ \frac{dR}{dt}=u_3\left(t\right)I_A+u_3\left(t\right)I_S-dR,\hfill \end{array}\right)$$ (8)

subject to the non-negative initial conditions $S\left(0\right),E\left(0\right),I_S\left(0\right),I_A\left(0\right),V\left(0\right),R\left(0\right)$. The respective cost functional is described as:

$$J(u_1,u_2,u_3)={\int }_0^{T_f}\left\{C_{1}E+C_{2}V+C_3{I}_S+\frac{1}{2}(C_4{u}_1^2+C_5{u}_2^2+C_6{u}_3^2)\right\}.$$ (9)

To reduce the COVID-19 transmission incidence, we need to minimized (9), where the constants $C_i$ for $i=1,2,\dots ,6$, denote the balancing cost factors. The expression $T_f$ shows is the final time step. The objective functional considered in the study is quadratic due to the existence of nonlinear intervention among the population for more evaluation, see references therein [20], [25], [32].

The main objective of our investigation is to seek optimal controls $u_1^{\ast }$, $u_2^{\ast }$ and $u_3^{\ast }$ for isolation, vaccine efficacy and enhancement of treatment, respectively, so that

$$J(u_1^{\ast },u_2^{\ast },u_2^{\ast })=\underset{\Omega }{min}\left\{J(u_1,u_2,u_3)\right\}.$$

The corresponding control set is given by

$$\Omega =\{(u_1,u_2,u_3):[0,T_f]\to [0,1],(u_1,u_2,u_3)isaLebesguemeasurable\}.$$

For the developed control system (8), the Lagrangian and Hamiltonian denoted respectively by $\mathcal{L}$ and $\mathcal{H}$ which are defined by

$$\mathcal{L}=C_{1}E+C_{2}V+C_3{I}_S+\frac{1}{2}(C_4{u}_1^2+C_5{u}_2^2+C_6{u}_3^2),$$ (10)

and

$$\mathcal{H}=C_{1}E+C_{2}V+C_3{I}_S+\frac{1}{2}(C_4{u}_1^2+C_5{u}_2^2+C_6{u}_3^2)+{\lambda }_1\left[\Delta +{\psi }_{V}V-\frac{\beta (I_S+{\beta }_1{I}_A)S}{N}(1-u_1\left(t\right))-(d+u_2\left(t\right))S\right]+{\lambda }_2\left[\frac{\beta (I_S+{\beta }_1{I}_A)S}{N}(1-u_1\left(t\right))-(\kappa +d)E\right]+{\lambda }_3[(1-\eta )\kappa E-(d+d_1+u_3\left(t\right))I_S]+{\lambda }_4[\eta \kappa E-(d+u_3\left(t\right))I_A]+{\lambda }_5[u_2\left(t\right)S-({\psi }_V+d)V]+{\lambda }_6[u_3\left(t\right)I_S+u_3\left(t\right)I_A-dR],$$ (11)

where the symbols ${\lambda }_{\iota }$, for $\iota =1,\dots ,6$, represent the adjoint variables.

Solution of the optimal control problem

This part is devoted to investigating the solution of the optimal control problem considered in (8) for COVID-19 dynamics. For this purpose, the well-known Pontryagin’s maximum principle [17] is utilized. The desired optimal solution is shown by $u_1^{\ast }$, $u_2^{\ast }$ and $u_3^{\ast }$. Furthermore, the corresponding necessary optimality conditions used in the solution procedure are stated as follows:

$$\left\{\begin{array}{c}\frac{dz}{dt}=-\frac{\partial }{\partial {\lambda }_j}\mathcal{H}(t,{\mathrm{u}}_{\mathrm{j}}^{\ast },{\lambda }_j),\hfill \\ \frac{\partial }{\partial \mathrm{u}}\mathcal{H}(t,{\mathrm{u}}_{\mathrm{j}}^{\ast },{\lambda }_j)=0,\hfill \\ \frac{d{\lambda }_j\left(t\right)}{dt}=-\frac{\partial }{\partial z}\mathcal{H}(t,{\mathrm{u}}_{\mathrm{j}}^{\ast },{\lambda }_j).\hfill \end{array}\right)$$ (12)

The criterions mentioned in (12) and the subsequent theorem have been taken in account to obtain the solution of optimality system.

Theorem 1

The controls $u_1^{\ast }$ , $u_2^{\ast },u_3^{\ast }$ and the solutions $S^{\ast }$ , $E^{\ast }$ , $I_S^{\ast }$ , $I_A^{\ast }$ , $V^{\ast }$ and $R^{\ast }$ of the corresponding control system (8) that minimize the objective functional $J(u_1,u_2,u_3)$ over $\Omega$ . Then we can find the respective adjoint variables ${\lambda }_{\iota }$ , where $\iota =1,\dots ,6$ ,. Further, the transversality conditions is ${\lambda }_i\left(T_f\right)=0$ such that

$$\frac{d{\lambda }_1}{dt}=\beta (I_S^{\ast }+{\beta }_1{I}_A^{\ast })\frac{N^{\ast }-S^{\ast }}{N^{\ast 2}}(1-u_1\left(t\right))({\lambda }_1-{\lambda }_2)+u_2\left(t\right)({\lambda }_1-{\lambda }_5)+{\lambda }_{1}d,$$

$$\frac{d{\lambda }_2}{dt}=-C_1+\frac{\beta (I_S^{\ast }+{\beta }_1{I}_A^{\ast })S^{\ast }}{N^{\ast 2}}(1-u_1\left(t\right))({\lambda }_2-{\lambda }_1)+\kappa {\lambda }_2-(1-\eta )\kappa {\lambda }_3-\eta \kappa {\lambda }_4+{\lambda }_{2}d,$$

$$\frac{d{\lambda }_3}{dt}=-C_3+\frac{\beta (N^{\ast }-(I_S^{\ast }+{\beta }_1{I}_A^{\ast }))S^{\ast }}{N^{\ast 2}}(1-u_1\left(t\right))({\lambda }_1-{\lambda }_2)+u_3\left(t\right)({\lambda }_3-{\lambda }_6)+(d+d_1){\lambda }_3,$$

$$\frac{d{\lambda }_4}{dt}=\frac{\beta ({\beta }_1{N}^{\ast }-(I_S^{\ast }+{\beta }_1{I}_A^{\ast }))S^{\ast }}{N^{\ast 2}}(1-u_1\left(t\right))({\lambda }_1-{\lambda }_2)+u_3\left(t\right)({\lambda }_4-{\lambda }_6)+{\lambda }_{4}d,$$

$$\frac{d{\lambda }_5}{dt}=-C_2+\frac{\beta (I_S^{\ast }+{\beta }_1{I}_A^{\ast })S^{\ast }}{N^{\ast 2}}(1-u_1\left(t\right))({\lambda }_2-{\lambda }_1)+{\psi }_V({\lambda }_5-{\lambda }_1)+{\lambda }_{5}d,$$

$$\frac{d{\lambda }_6}{dt}=\frac{\beta (I_S^{\ast }+{\beta }_1{I}_A^{\ast })S^{\ast }}{N^{\ast 2}}(1-u_1\left(t\right))({\lambda }_2-{\lambda }_1)+{\lambda }_{6}d.$$ (13)

Furthermore, the associated optimal controls $u_1^{\ast }$ , $u_2^{\ast }$ and $u_3^{\ast }$ are given by

$$\begin{array}{c}{u}_1^{\ast }=min\left\{1,max\left(\frac{\beta S^{\ast }(I_S^{\ast }+{\beta }_1{I}_A^{\ast })({\lambda }_2-{\lambda }_1)}{C_4{N}^{\ast }},0\right)\right\},\hfill \\ u_2^{\ast }=min\left\{1,max\left(0,\frac{S^{\ast }({\lambda }_1-{\lambda }_4)}{C_5}\right)\right\},\hfill \\ u_3^{\ast }=min\left\{1,max\left(0,\frac{I_S^{\ast }({\lambda }_3-{\lambda }_6)+A_S^{\ast }({\lambda }_4-{\lambda }_6)}{C_6}\right)\right\}.\hfill \end{array}$$ (14)

Proof

By utilizing the condition mentioned in (12), the transversality conditions and results given in (13) are obtained for the Hamiltonian function given in (11), settings $S=S^{\ast }$, $E=E^{\ast }$, $I_S=I_S^{\ast }$, $I_A=I_A^{\ast }$, $V=V^{\ast }$ and $R=R^{\ast }$. Moreover, using the condition $\frac{\partial \mathcal{H}(t,{\mathrm{u}}_{\mathrm{j}}^{\ast },{\lambda }_j)}{\partial {\mathrm{u}}_{\mathrm{j}}}=0$ given in (12), the optimal controls $u_1^{\ast }$, $u_2^{\ast }$ and $u_3^{\ast }$ in (13) are obtained. □

Simulation of the control problem

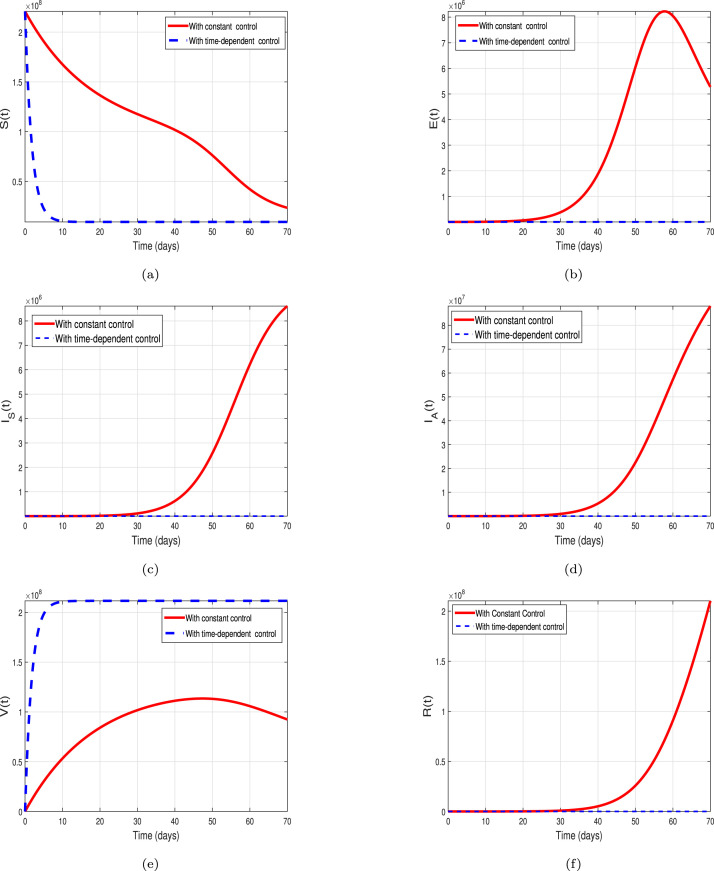
This section presents the simulation results of the COVID-19 model, with variable controls (8) and without control (with constant controls) (1). The purpose of this section is to analyze the important role of the suggested control strategies on the disease incidence and possible mitigation. The simulation process is conducted via an efficient iterative scheme known as RK4. The parameters used in simulation are estimated from the reported cases and tabulated in Table 1, whereas the weights as well as balancing constants are chosen as $C_1=0.01,C_2=0.01,C_3=10,C_4=100,C_5=5,C_6=10$. It is worth mentioning that the numerical values of the weighted and balancing constant are assumed for simulation purposes. The dynamical behavior of different populations with variable control measures shown by the blue dashed curves, and without variable controls, (or constant control parameters) shown by red solid curves are demonstrated in Fig. 11 with sub-figures (a-f). The corresponding control profile of the respective control variables $u_1$, $u_2$ and $u_3$ is depicted in Fig. 12. We simulate the control model by activating the isolation, vaccination and treatment control measures at the same time in order to analyze their combined dynamical impact on the COVID-19 incidence. For this purpose the control set chosen as $u_1\ne 0,u_2\ne 0$ and $u_3\ne 0$. The resulting graphical results for various population classes are depicted in Fig. 11(a-f). The dynamics of susceptible individuals are shown in 11(a). It can be seen that the susceptible population reduces well in the presence of optimal controls application. The dynamics of exposed, symptomatic and asymptomatic COVID-19 infective population is analyzed in sub- Figs. 11(b), 11(c) and 11(d) respectively. One can clearly observe that the population in each infected class dramatically decreases (or almost vanishes) in the presence of time-dependent control interventions. Thus the application of time dependent control measures plays a significant role in the disease mitigation as compare without (or constant) control strategy. The impact of variable controls on the dynamics of the vaccinated population is explored in Fig. 11(e), showing a significant increase in the presence of variable interventions. Finally, the dynamics of the recovered population in the presence of variable controls are shown in Fig. 11(f). Moreover, Fig. 12, describes the corresponding control profile. Initially, all the control measures are implemented at their maximum level. Overall, we concluded that implementing the proposed control measures simultaneously is more appropriate and significant to mitigate the infection in a community.

Fig. 11.

Graphical results of the model (8) with time-dependent effective contact, vaccine efficacy and treatment controls i.e., $u_1\ne 0$, $u_2\ne 0$ and $u_3\ne 0$. The resulting results are shown by dashed blue curves. These simulation also describe the simulation of the COVID-19 model without optimal control (constant controls) shown by solid red curves.

Fig. 12.

The corresponding control profile.

Conclusion

Although, the current situation of the recent coronavirus pandemic is not severe as it was in its first outbreak, still it has a serious impact on the whole world. Scientists worldwide are trying to implement different mitigation strategies to reduce the burden on healthcare. It is revealed that only non-pharmaceutical intervention can reduce disease incidence but are not enough for disease eradication. Currently, vaccination coupled with some other interventions has been used an effective tool to minimize the pandemic burden. The current study presented the impact of constant and variable control measures on the dynamical behavior and incidence of COVID-19 with the help of a mathematical modeling approach. The model sensitivity analysis for crucial parameters is presented graphically. Moreover, with the use of optimal control theory, the model is optimized to set the suitable control intervention for infection minimization. The model is initially simulated to describe the impact of constant vaccination rate and then it is simulated with time-dependent control interventions. The main findings extract from this analysis are listed as:

• i.The model is fitted to the actual data of the confirmed coronavirus infected population in Pakistan. As a result, the embedded epidemiological parameters in model (1) are estimated via the least square technique.
• ii.The basic reproductive number ${\mathcal{R}}_0$ is evaluated both numerically and theoretically.
• iii.The equilibria of model (1) are obtained.
• iv.The impact of various model parameters on the basic reproductive number ${\mathcal{R}}_0$ is shown via bar graphs.
• v.The global sensitivity analysis of the model is carried out using the PRCC approach to indicate the most sensitive parameter(s) to disease incidence.
• vi.Based on sensitivity analysis, we formulate the control model by introducing three time dependent controls $u_1\left(t\right)$ (isolation to reduce effective interactions), $u_2\left(t\right)$ (to enhance vaccine efficacy) and $u_3\left(t\right)$(to enhance treatment) in the proposed COVID-19 model. To obtain the necessary optimal conditions of the proposed control model, Pontryagin’s maximum principle is used.
• vii.From the simulation results of the control model, it is concluded that in comparison with constant controls, the time-depended control measures play an essential role to minimize the infection.

CRediT authorship contribution statement

Lei Zhang: Conceptualization, Methodology, Supervision, Formal analysis, Validation. Saif Ullah: Conceptualization, Investigation, Methodology, Validation, Software, Control analysis, Writing – original draft. Basem Al Alwan: Conceptualization, Supervision, Simulation, Reviewing, Control analysis. Ahmed Alshehri: Formal analysis, Methodology, Supervision, Simulation, Reviewing. Wojciech Sumelka: Formal analysis, Methodology, Data analysis, Funding acquisition, Supervision, Reviewing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.