Abstract
Coupled Wells-Riley (WR) and Computational Fluid Dynamics (CFD) modelling (WR-CFD) facilitates a detailed analysis of COVID-19 infection probability (IP). This approach overcomes issues associated with the WR ‘well-mixed’ assumption. The WR-CFD model, which makes uses of a scalar approach to simulate quanta dispersal, is applied to Chinese long-distance trains (G-train). Predicted IPs, at multiple locations, are validated using statistically derived (SD) IPs from reported infections on G-trains. This is the first known attempt to validate a coupled WR-CFD approach using reported COVID-19 infections derived from the rail environment. There is reasonable agreement between trends in predicted and SD IPs, with the maximum SD IP being 10.3% while maximum predicted IP was 14.8%. Additionally, predicted locations of highest and lowest IP, agree with those identified in the statistical analysis. Furthermore, the study demonstrates that the distribution of infectious aerosols is non-uniform and dependent on the nature of the ventilation. This suggests that modelling techniques neglecting these differences are inappropriate for assessing mitigation measures such as physical distancing. A range of mitigation strategies were analysed; the most effective being the majority (90%) of passengers correctly wearing high efficiency masks (e.g. N95). Compared to the base case (40% of passengers wearing low efficiency masks) there was a 95% reduction in average IP. Surprisingly, HEPA filtration was only effective for passengers distant from an index patient, having almost no effect for those in close proximity. Finally, as the approach is based on CFD it can be applied to a range of other indoor environments.
Keywords: CFD, Wells-Riley equation, COVID-19, Infection probability, Passenger train
Nomenclature
- c
Quanta concentration (quanta/m3)
- I
Number of index patients
- p
Infection probability
- p1
Infection probability without wearing face covering
- p2
Infection probability with index patient wearing face covering
- p3
Infection probability with susceptible wearing face covering
- p4
Infection probability with all passengers wearing face covering
- pv
Infection probability for vaccinated population
- pnv
Infection probability for unvaccinated population
- q
Quanta generation rate (quanta/h)
- Q
Carriage ventilation rate (m3/h)
- SY
Source term of scalar Y (kg/m3s)
- t
Exposure time (h)
- v
Pulmonary ventilation rate of each susceptible (m3/h)
- y
Rate of quanta extracted from the carriage by the ventilation system (quanta/h)
- Y
Scalar variable
- x
Proportion of the population who wear face coverings
- α
Proportion of the extracted carriage air being recycled
- η
Filtration efficiency of the ventilation system
- ρ
Density (kg/m3)
1. Introduction
The COVID-19 pandemic, caused by the transmission of the SARS-CoV-2 virus, has claimed more than 3.88 million lives with more than 178.8 million people known to be infected worldwide (World Health Organization (WHO) and Coronavirus, 2021) (at the time of writing in June 2021). As part of the international effort to combat COVID-19, researchers have employed computational modelling techniques to assess the potential efficacy of non-pharmaceutical mitigation strategies for a range of indoor environments (Ronchi and Lovreglio, 2020, Vuorinen et al., 2020, Malki-Epshtein et al., 2020, Marcus et al., 2020, Buonanno et al., 2020, Rencken et al., 2021, Zhang et al., 2021, Li et al., 2021, Mirzaie et al., 2021). An issue of societal concern is the possibility of contracting COVID-19 while confined to the small volume of the passenger compartment of a train carriage (saloon), where passengers are seated in close proximity. Of particular concern are long distance trains, where passenger journey times can vary from 1 to 8 h. Long distance trains are a popular and essential mode of public transport in many countries (Gravert et al., 2020, Hu et al., 2021) and so it is important to quantify the infection probability (IP) and the factors that may impact the risk. Thus, the main motivations of this work are to develop a modelling technique that can be used to quantify COVID-19 IP for susceptible occupants in a variety of indoor ventilated spaces, verify the model for rail applications and use the verified model to explore the efficacy of various mitigation strategies employed in long-distance train travel.
Hu et al. (Hu et al., 2021) collected a large amount of data concerning the risk of COVID-19 transmission on long distance trains in China – the so-called G-trains. They quantified the IP of COVID-19 (also termed ‘attack rate’ by Hu et al. (Hu et al., 2021) to passengers using data from 2334 index patients and 72,093 close contacts who had co-travel times of between 0 and 8 h from 19 December 2019 through 6 March 2020. They examined the spatial and temporal distribution of COVID-19 transmission amongst the passengers to determine the associations between infection, spatial distance, and co-travel time. Of the 72,093 close contacts, whose seat was located within three rows from an index patient, 234 were subsequently confirmed as secondary COVID-19 cases. Whilst the data collected and derived IPs are useful, the generality of this empirical data to other scenarios is uncertain as the dispersion of virion laden respiratory particles will be strongly dependent on the local airflows, geometric layout and ventilation characteristics of the environment. Furthermore, the IPs associated with the dispersed aerosols will be dependent on the transmissibility of the current dominant virus variant.
The SARS-CoV-2 virus can be transmitted between infected and susceptible people through the air via droplet- or aerosol- transmission (Prather et al., 2020, Morawska and Milton, 2019, Wang et al., 2021, Wells, 1955) and via the less likely route of fomites (surface contamination) (Meyerowitz et al., 2021, Kampf et al., 2020). In droplet transmission, an infected person generates large respiratory droplets (around 100 µm in diameter (Prather et al., 2020), containing SARS-CoV-2 virions, when speaking or through sneezing and coughing. The large droplets travel through the air in short (around 2 m) ballistic trajectories and deposit either on surfaces (including exposed skin, clothing or objects, thus generating potential for fomite infection) or contaminate a nearby person either through inhalation or deposition on the eyes. Aerosol transmission involves much smaller respiratory droplets (less than 100 µm (Prather et al., 2020), generated by breathing and speaking as well as through coughing and sneezing, which can remain airborne for long periods of time (minutes to hours). The suspended aerosols can then be carried aloft by the prevailing air currents over long distances.
As with many other confined spaces, the air exchange rate for train saloons is a primary determining factor for transmission of COVID-19. There are a wide range of ventilation systems on trains, depending on the countries, ages, and types of rolling stock. Most modern saloons are air-conditioned, with sealed windows, while old-style saloons rely on open windows for ventilation. The air-conditioned ventilation rates vary widely, ranging from about 8–10 ACH (air changes per hour) (Flynn, 2020, A rapid review of the engineering approaches to mitigate the risk of COVID-19 transmission on public transport, National Engineering Policy Centre, a-rapid-review-of-the-engineering-approaches-to-mi (raeng.org.uk). Accessed on 24th June, 2021) to about 44 ACH (Wang et al., 2014). Within air-conditioned saloons, typically between 60 and 70% of the air within the carriage is recycled to maintain thermal comfort levels (Flynn, 2020). Prior to passing the recycled air back into the saloon, the air is typically passed through a filtration system to remove contaminants. The effectiveness of the filtration system varies significantly from country to country and design of train carriage. The filtration systems typically found on UK long distance trains are EN779 Class grade 4 and can remove 35–85% of particles greater than 3 µm (Anozie, 2020).
Computational Fluid Dynamics (CFD) is a well-established modelling approach for simulating fluid flows within complex environments (Patankar, 1980). Established applications of CFD include vehicle aerodynamics (Gu et al., 2018, Thabet and Thabit, 2018), fire simulation (Galea, 1989), ventilation studies (Wang et al., 2014), refrigeration (Foroozesh et al., 2020) and turbine design (Hoseinzade et al., 2021, Yazdani and Lakzian, 2020). CFD has also been used to model the transmission of airborne infectious disease through the simulation of the transport of respiratory aerosols within ventilated spaces (Peng et al., 2020). There are broadly two methodologies to simulate the dispersion of aerosols in CFD: the Eulerian approach, where the aerosol cloud is approximated by a scalar gas tracer (Foroozesh et al., 2020, Hoseinzade et al., 2021); and the Lagrangian approach, where the aerosols are treated as a distribution of suspended particles with specific masses, volumes and physical properties (Wang et al., 2014, Yazdani and Lakzian, 2020, Crowe et al., 1977). Heathway et al. (Hathway et al., 2011) demonstrated, through comparison with experimental data that both Eulerian and Lagrangian approaches are appropriate for modelling small bioaerosols.
Several previous applications of CFD to infectious disease transmission have adopted the Eulerian approach (Malki-Epshtein et al., 2020, Rencken et al., 2021, Zhang et al., 2021, Li et al., 2021, Peng et al., 2020, Hathway et al., 2011, Lim et al., 2010, You et al., 2019, Zhu et al., 2012). The Eulerian approach has the advantage of not requiring the aerosol size and mass distribution, composition or thermodynamic properties be specified and is also very computationally efficient, enabling large complex cases to be more readily simulated. However, as aerosol particles are not explicitly modelled, the method does not easily represent the evaporation of respiratory droplets. Nevertheless, during the COVID-19 pandemic researchers have used the Eulerian approach to explore the dispersion of respiratory aerosols within complex ventilated environments (Malki-Epshtein et al., 2020, Rencken et al., 2021, Zhang et al., 2021, Li et al., 2021). For example, early in the pandemic, Malki-Epshtein et al. (Malki-Epshtein et al., 2020) used the Eulerian approach to simulate the dispersion of respiratory aerosols from an index patient on a London bus. Their study explored the impact of mitigations, such as enhancements to the driver security screen, to reduce their exposure to passenger respired aerosols. As droplets were not explicitly modelled, the driver exposure was calculated using time-weighted average exposure to the fraction of exhaled breath from the index patient.
The Lagrangian approach has also been applied to applications concerning infectious disease transmission (Vuorinen et al., 2020, Mirzaie et al., 2021, Wang et al., 2014, Peng et al., 2020, Yan et al., 2017, Zhang and Li, 2012, Yang et al., 2018). As the Lagrangian approach treats the discrete respiratory aerosol particles as a collection of droplets that are individually tracked through space, it is necessary to specify the initial droplet size distribution, composition and thermodynamic properties – which are not necessarily known. Furthermore, given that the discrete phase is directly modelled, with each particle or groups of particles represented, the Lagrangian approach is potentially more computationally demanding than the Eulerian approach. Previous CFD studies of infectious disease transmission utilising the Lagrangian approach have primarily focused on predicting the distribution of respiratory droplets produced by an index patient (Mirzaie et al., 2021, Wang et al., 2014, Peng et al., 2020, Zhang and Li, 2012, Yang et al., 2018). In addition, some studies have also attempted to determine infection risk based on the predicted droplet distributions (Vuorinen et al., 2020, Peng et al., 2020, Yan et al., 2017).
In the early stages of the COVID-19 pandemic, Vuorinen et al. (Vuorinen et al., 2020) used CFD to simulate the dispersion of aerosols within supermarkets using the Lagrangian approach. By determining the exposure time to a critical number of aerosol particles they estimated IP. However, there are a number of uncertainties associated with this approach including the nature of the aerosol distribution produced by respiration and the dose required to cause infection. Furthermore, the use of exposure time to determine infection can be misinterpreted by some readers who infer the situation is considered safe, provided the exposure time is below the critical exposure time (Wang et al., 20212021).
As an alternative to detailed CFD simulation, a probabilistic model to determine risk associated with COVID-19 infection for long distance train travel has been developed by the European Union Agency for Railways (European Union Agency for Railways). This model is based on empirical data from a number of different sources, including the work of Hu et al. (Hu et al., 2021). Inherent in this model is the questionable implicit assumption that the empirical data upon which the model relies is appropriate for use in applications involving layouts and ventilation conditions different from those in which the data was collected.
The Wells-Riley model (Riley et al., 1978) (WRM) is used by engineers and epidemiologists to estimate IP in confined spaces using ventilation and quanta generation rates. Quanta, a term defined by Wells (Wells, 1955); is a representation of infectious dose, where inhalation of one quanta leads to an IP of 63%. The quanta concept provides a means of circumventing the knowledge gap associated with a new disease such as COVID-19; it avoids the need to specify unknown viral infectivity parameters such as, virion emission rates, the size distribution of respiratory particles, the number of virions carried by respiratory particles, aerosol deposition location within the respiratory tract and the virion dose required to cause infection. Appropriate quanta generation rates are typically determined by back calculations of known infection events (Buonanno et al., 2020, Azimi et al., 2020, Buonanno et al., 2020, Hota et al., 2020, Miller et al., 2020) and are disease- and scenario- specific. The original WRM has also been extended to include phenomena such as transient accumulation, droplet deposition, virion half-life and HVAC filtration (To and Chao, 2010, Gammaitoni and Nucci, 1997, Stephens, 2012).
The WRM assumes that the volume of space is well mixed with a uniform quanta distribution throughout the volume of the enclosure. Thus, the estimated IP represents an average value for the considered volume and duration (Dai and Zhao, 2020, Furuya, 2007, Zemouri et al., 2020). As a result, the WRM is insensitive to geometric layout, distance between index(es) and susceptibles, and local airflows. In many practical applications, complexities in geometric layout, asymmetries within the volume and the nature of the ventilation system mean that the air within the space is unlikely to be well-mixed. In order to reflect the non-uniform quanta distributions in confined spaces, the WRM has been coupled with stochastic zone models (Marcus et al., 2020, Noakes and Sleigh, 2009) and CFD models (Eulerian (Zhu et al., 2012) and Lagrangian (Yan et al., 2017) approaches) to calculate the local quanta concentrations. A limitation of all these coupled approaches is that they have not been validated using real infection data, in particular for COVID-19.
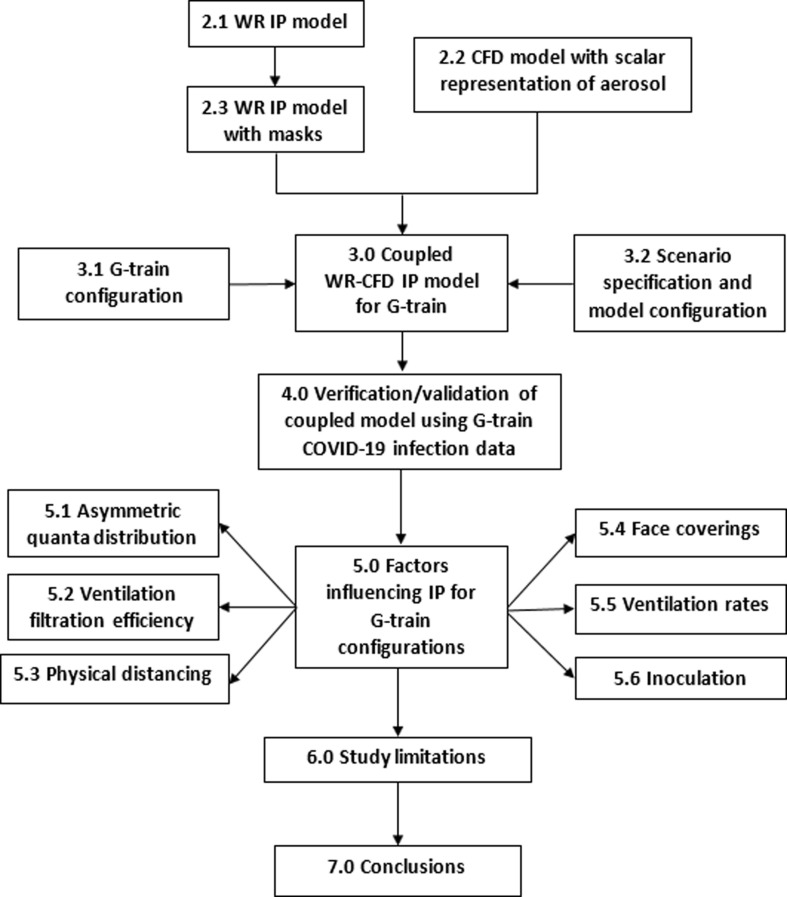
This study numerically investigates the prediction of COVID-19 IPs for passengers travelling on long distance trains in China, reported by Hu et al. (Hu et al., 2021) by localising the WRM calculation (see Section 2.3) and coupling it with CFD simulation (see Section 2.2) (WR-CFD). While passive scalar- and particle tracking- approaches are both appropriate for modelling small particle bioaerosols (Hathway et al., 2011); the CFD methodology adopted in this analysis represents aerosol concentration as an Eulerian scalar. In order to derive an estimation of absolute risk (rather than relative risk), the predicted scalar concentrations from the CFD analysis are first converted to quanta concentrations and IPs are then derived by applying the WRM (Zhu et al., 2012). This methodology removes the limitations of using empirically derived probabilistic models and the WRM assumption of a well-mixed environment. Furthermore, using the quanta approach means that it is not necessary to define respiratory aerosol particle size distributions, viral concentrations in droplets or viral dose required to cause infection. The CFD modelling setup for the G-train environment is described in Section 3. The WR-CFD approach is validated by comparing the predicted IPs with the data of Hu et al (Hu et al., 2021) (Section 4). Using the validated model, various mitigation strategies and the effects of key parameters that impact the spread of aerosols, are investigated in Section 5. Limitations of the analysis are described in Section 6. Finally, conclusions concerning the performance of the WR-CFD approach and the investigated mitigation strategies for G-train environments are provided. The layout of the main work is illustrated in Fig. 1 .
Fig. 1.
Logical structure of the work presented in this paper.
2. The models and simulations
2.1. Wells-Riley model
The WRM (Riley et al., 1978) (see Equation (1)) determines the IP under a given ventilation condition in a confined space,
| (1) |
where p is the IP (risk); I is the number of index patients; v is the pulmonary ventilation rate of each susceptible (m3/h); Q is the ventilation rate (m3/h); q is the quanta generation rate produced by one index patient (quanta/h); and t is the exposure time (h). The term Iqvt/Q represents the dose of quanta inhaled by the susceptible. This type of exponential dose–response model was also found to be a suitable for modelling IP due to SARS-CoV-1 (Watanabe et al., 2010).
2.2. CFD model
A research version of SMARTFIRE V5.1 is used to perform the airflow simulations in this study (Ewer et al., 2020, Wang et al., 2017, Grandison et al., 2006, Wang et al., 2001). The CFD engine in SMARTFIRE has many physics features that are required for airflow modelling, such as mass, momentum, energy, turbulence, and species conservation. Turbulence is modelled using the two-equation K-Epsilon closure with buoyancy modification (Galea, 1989). Along with the usual CFD transport equations required to accurately model the bulk- and local- ventilation air flows (Patankar, 1980, Ewer et al., 2020), the CFD model uses a simplified transportation model to represent the quanta dispersal. The model utilises a scalar tracer gas to represent the spread of respired aerosols from an index patient, as follows:
| (2) |
where Y stands for the scalar and SY is its source term. Y is a dimensionless variable representing the mass fraction of exhaled aerosol within the mixture of ambient air and exhaled aerosol. As the exhaled aerosol particles are typically very small (Buonanno et al., 2020) (of the order of 5 µm), drag forces will dominate gravitational forces, and so the aerosols are carried by the prevailing flow i.e., the aerosols do not require their own velocity description. This is particularly appropriate for the scenarios investigated in this paper which are characterised by high ventilation rates (see Section 3.2) which leads to air flow velocities orders of magnitude higher than the settling velocity of the aerosols.
Thus, in the CFD analysis presented in this paper, it is assumed that the respired aerosol cloud of droplets can be modelled using a simple scalar gas concentration release (Hathway et al., 2011). This approach to representing aerosols utilises the well-known Eulerian-Eulerian method (Hoseinzade et al., 2021). Furthermore, the current modelling assumes that there is no loss of virus infected droplets (as a concentration reduction) due to deposition on surfaces or loss of virus infectivity due to decay. The implications of these assumptions are discussed in the Study Limitations, Section 6.
2.3. Infection probability calculation
In the original WRM (Equation (1)), Iq/Q can be interpreted as the uniform concentration of quanta within the confined space (quanta/m3) in a well-mixed steady state. With a given quanta generation rate q and pulmonary ventilation rate v, the quanta concentration in the flow generated from the breath of an index patient is q/v quanta/m3. In the analysis, the scalar value in the breathing stream of the index patient is 1. If the average scalar value in a target volume is Y, the quanta concentration in this volume is then obtained with equation:
| (3) |
Therefore, by replacing Iq/Q in Equation (1) with c, the local IP based on the CFD simulation is calculated using Equation (4) given by,
| (4) |
If the index patient wears a face mask with efficiency a in preventing aerosols being released (i.e. captures a fraction a of the droplets), then Equation (4) becomes,
| (5) |
If the susceptibles wear face masks with efficiency b (prevents a fraction b of the aerosols from being inhaled) then Equation (4) becomes,
| (6) |
If both the index patient and the susceptibles wear face coverings, Equation (4) becomes,
| (7) |
If x is the proportion of the population (including susceptibles and index patients) who are likely to wear face coverings (i.e. the probability of a passenger wearing face covering is x), then the probabilities of the possible combinations are: both the index patient and an individual susceptible are not wearing face coverings (1-x)2; the index patient is wearing a face covering but the susceptible is not x(1-x); the index patient is not wearing a face covering but the susceptible is (1-x)x; and both index and susceptible are wearing face coverings x 2. Then the IP with a proportion x of the population wearing face coverings is given by,
| (8) |
3. G-train simulation set up and infection probability calculation
3.1. COVID-19 transmissions on G-trains
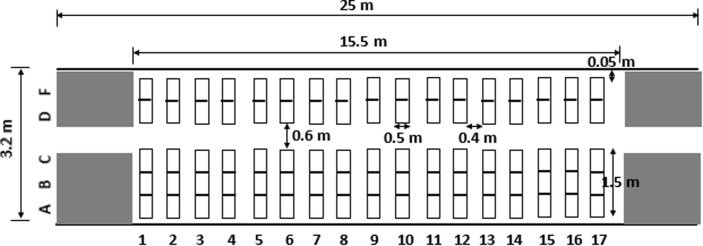
Hu et al. (Hu et al., 2021) assumed that the COVID-19 IP within the G-train saloon depends on distance from the index patient (measured in seat rows) and duration of exposure (measured in co-travel time). A typical G-train saloon layout and seating configuration is presented in Fig. 2 . There are a total of 85 passenger seats in 17 rows with five seats abreast. There is a small and non-constant gap, running the full height of the seat back, between adjacent seats in a row that is considered negligible and was not represented within the modelling performed in this paper.
Fig. 2.
Schematic of the seating configuration of the G-train (plan view, not to scale).
3.2. CFD simulation
It is not known if all the data collected by Hu et al. (Hu et al., 2021) was from saloons with identical layouts. There are several different types of G-train saloon. Fig. 2 represents a second-class G-train saloon configured with 5 abreast seating. It is believed that five out of eight carriages on a G-train have this configuration. In this analysis it is assumed that the data is collected from saloons that are identical to that shown in Fig. 2, or at least, very similar.
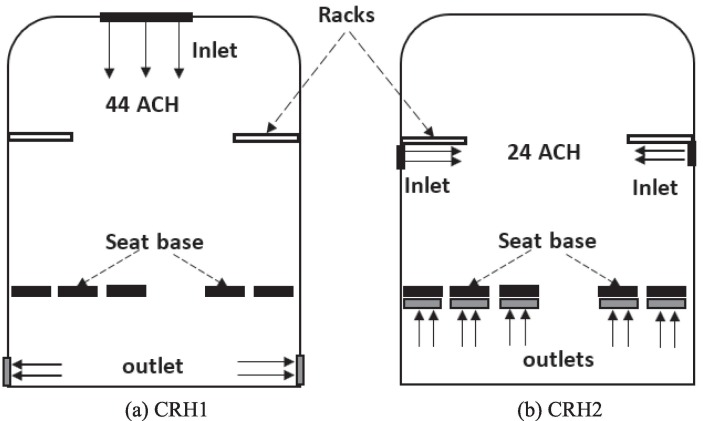
As ventilation is one of the most critical factors that affect the transmission of respiratory diseases within confined spaces, the CFD scenarios are configured to the ventilation characteristics of G-trains. It is important to note that there may have been several different ventilation configurations on the G-trains during the data collection period. These could have involved different air change rates and ventilation configurations and so the data is likely to have been generated under different airflow conditions, which may in turn impact the dispersion of respiratory aerosols. There are thought to be four G-train models currently running in China. Depicted in Fig. 3 are two typical G-train ventilation configurations (Wang et al., 2014, http://www.360doc.com/content/16/0903/12/, 2020) for Chinese Rail High-Speed (CRH) trains. Among the four G-train models, CRH1 (with top inlet as shown in Fig. 3(a)) has an air change rate of 44 ACH (6200 m3/h including maximum 2120 m3/h fresh air) while CRH2 (with side wall inlet as shown in Fig. 3(b)) has an air exchange rate of 24 ACH (4400 m3/h including maximum 900–1800 m3/h fresh air). Model CRH5 also has an air exchange rate of 44 ACH but different inlet/outlet locations (Wang et al., 2014). Another model, CRH3 has an unknown ventilation configuration.
Fig. 3.
Ventilation configurations for two typical G-trains (a) train CRH1: top inlet and side wall outlet and (b) train CRH2: side wall inlet (under the racks) and seat bottom outlet (cross section view, not to scale).
As only two of the four G-train models have known ventilation configurations, these are the only two represented in this study, CRH1 (Scenario 1, see Fig. 3(a)) and CRH2 (Scenario 2, see Fig. 3(b)). Summarised in Table 1 are the parameters required by the CFD simulations for the aerosol dispersion within the G-train saloon.
Table 1.
Key parameters defining the two ventilation scenarios.
| Scenario 1 | Scenario 2 | Notes | |
|---|---|---|---|
| Computational domain | Dimensions as shown in Fig. 2 but only includes the seating area with approximate length of 15.5 m and carriage height of 2.3 m. | Different carriages have heights between 2.2 m and 2.4 m (Wang et al., 2014). | |
| Inlet air flow rate (m3/h) for the simulated passenger seat area | 5500 | 4000 | Ventilation rates of 6200 m3/h and 4400 m3/h are for the entire CHR1 and CHR2 saloons respectively. Specified rates are for passenger seating area. |
| Inlet | 1.2 m wide running along the ceiling above the centre of the saloon, with a temperature of 18 °C and velocity of 0.08333 m/s. | 0.05 m high on each side wall just under the luggage racks with a temperature of 18 °C and velocity of 0.7276 m/s. | In CHR2 saloons there are also inlet vents (gaspers) located above the windows, which are adjustable by passengers (http://www.360doc.com/content/16/0903/12/, 2020). However, these are not modelled. |
| Outlet | 0.15 m high vents at the bottom of each side wall running along the length of the saloon with a pressure of 101325 Pa. | At the bottom of each seat base with dimensions equal to that of the seat base with a pressure of 101325 Pa. | In CHR2 saloons the seat bottom vent opening has dimensions 0.48 × 0.49 m2 (Wang et al., 2014). |
| Mass ratio of recirculated air to dumped air | 0.66 | 0.59 | Derived from the known ventilation and fresh air rates. |
| Filtration efficiency | 20% | G-trains assumed to have EU grade 3 and better filters. | |
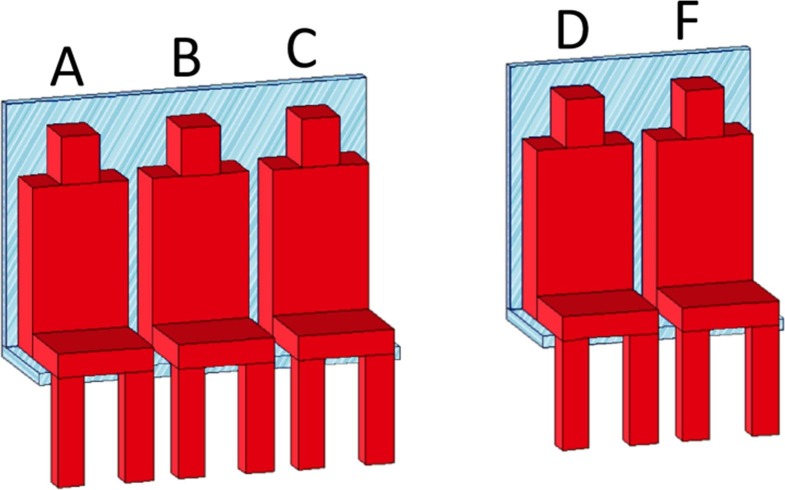
| Seats | Represented as obstacles. The seat base is square with side length of 0.5 m with top face 0.45 m above the floor. Top of seat back is 1.45 m above floor. | See Fig. 5. | |
| Passengers | Represented as a simple set of solid obstacles with dimensions (depth × height × width); Head: 0.2 m × 0.2 m × 0.16 m, Body trunk: 0.2 m × 0.7 m × 0.4 m, Lap: 0.35 m × 0.1 m × 0.4 m, and Each leg: 0.1 m × 0.45 m × 0.12 m. A heat release rate of 50 W/m2 is applied to the full exposed surface of all passengers. | See Fig. 5. | |
| Index locations | Seat A, B, C, D and F in Row 6. | ||
| Quanta source | (1) A 0.04 m wide and 0.05 m high inlet with 0.35 m3/h flow rate (0.049 m/s, 30 °C) representing pulmonary ventilation rate located at the mouth of index patient (2) The scalar value at the inlet is set to 1.0 (3) Quanta generation rate is 14 quanta/h per index patient. |
Quanta generation rate assumed for a source at rest (Buonanno et al., 2020, Wang et al., 2021, Dai and Zhao, 2020). Also see Supplementary Material Section S2. | |
| Mesh (cells) | (1) Scenario 1: 2,245,320 (378 × 60 × 99). (2) Scenario 2: 2,170,476 (378 × 58 × 99). |
||
| Timestep size (s) | 0.5 | ||
| Target volume for quanta concentration calculation | For individual passengers, the simulated quanta concentration is the average value in a volume 0.16 m wide, 0.20 m deep and 0.2 m high, adjacent to the passenger nose. | ||
| Face covering | (1) 40% of population wear face masks (2) Face mask efficiency a (50%) for index patient and b (30%) for susceptible. |
(1) Assumed value according to video footage (Youtube video clip, 2020), see also Supplementary Material Section S7.1. (2) See (Davies et al., 2013). For reference surgical mask efficiency is reported to be between 35% and 75% (Rossettie et al., 2020). |
|
The computational domain for the two ventilation scenarios covers the entire saloon volume containing the seated passengers. While the length of this section is not known precisely, it is estimated to be approximately 15.5 m (see Fig. 2). The height of the saloon is approximately 2.3 m (Wang et al., 2014). Two solid luggage racks, located along the side walls, have an assumed width of 0.5 m and are located at a height of 1.8 m above the floor. It is believed that approximately 90% of the air is delivered to the passenger saloon seating area, as opposed to the saloon end vestibules. Therefore, ventilation rates of 5500 m3/h and 4000 m3/h are used in Scenario 1 and Scenario 2 respectively. The inlet location for Scenario 1 runs along the ceiling above the centre of the saloon with an assumed width of 1.2 m (Fig. 3(a)). The outlets are 0.15 m high vent openings at the bottom of each side wall running along the entire length of the carriage. For Scenario 2, two 0.05 m inlets are located on each side wall just under the parcel racks. The outlets are located at the bottom of each seat base with the same dimensions as the seat base (Fig. 3(b)).
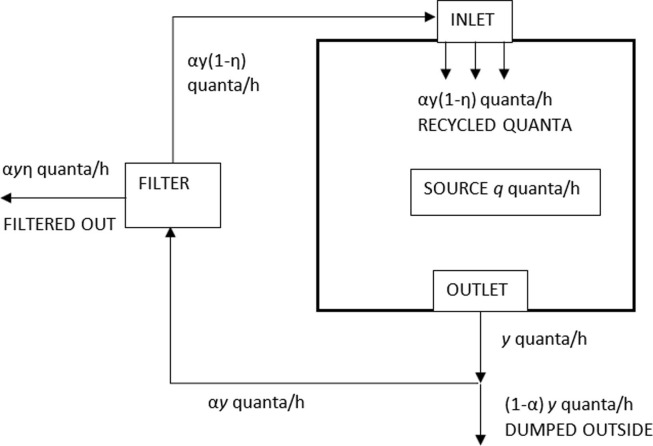
Air recycling is an important mechanism that can spread respiratory aerosols within the saloon. Presented in Fig. 4 is the assumed quanta transport paths within the saloon CFD model. It is assumed that quanta are generated at a rate of q quanta/h per index patient. Some of these quanta (y quanta/h) are extracted from the carriage by the ventilation system. A proportion (α) of the extracted carriage air is recycled and so a proportion of the extracted aerosols (αy) pass through to the ventilation filtration system. The filtration system extracts a proportion (η) of the aerosols from the recycled air resulting in a reduced proportion (αy(1-η)) of the aerosols being re-introduced into the saloon via the ventilation inlets. The proportion of the recycled air can be calculated from the ventilation rate and the fresh air rate. For CHR1 saloon, the ventilation rate is 6200 m3/h with a fresh air rate of 2120 m3/h. For CHR2 saloon, the ventilation rate is 4400 m3/h with a fresh air rate of 1800 m3/h. Therefore, the proportion α is 0.66 and 0.59 for Scenario 1 and Scenario 2 respectively. The ventilation filters in the G-trains are believed to be equivalent to EN7779 grade 3 and above. For a grade 3 filter, the efficiency in capturing particles with size greater than 3 µm is no more than 20% (Anozie, 2020). Considering that much of the aerosols from respiration are less than 3 µm, an overall filtration efficiency (FE) of 20% is applied for the G-trains in this study.
Fig. 4.
Quanta transport paths in rail carriage.
For a system with continuous inlets and outlets extending over the entire length of the enclosure, if the quanta concentration at the inlet is fixed, the quanta concentration within the system will be uniform with the same level as at the inlet after some time. Therefore, at steady state, quanta injected into the carriage by the ventilation system from the recirculated air is uniformly distributed over the entire carriage volume. This contribution to the quanta distribution within the saloon is defined here as the background quanta concentration. From the quanta transport paths shown in Fig. 4, at steady state, the inlet quanta concentration (background quanta concentration) is given by Equation (9) (see Supplementary Material Section S3 for details),
| (9) |
Thus, the quanta concentration at any location inside the carriage is the sum of the concentration calculated from a simulation without recycled quanta (assuming a 100% FE) and the background quanta concentration for the corresponding FE.
The seats (blue/striped) and passengers (solid red) are simply modelled as sets of cuboid obstacles as shown in Fig. 5 and defined in Table 1. It is assumed the seat base is 0.4 m above the floor and the top of the seat back is 1.45 m above the floor. The heat generated by a human body will affect the airflow pattern and the transport of quanta inside the saloon (Craven and Settles, 2006). An average heat release rate of 50 W/m2 for resting people (Thermal energy created by human body, 2020) is applied for all the passengers with an effective body area of 1.2 m2.
Fig. 5.
Seat and passenger representation used within the CFD simulations.
As part of the CFD analysis it is essential to identify the seat location of the index patient. Of particular importance is the transverse location, i.e. seat A to seat F. The index patient distribution within the cases investigated by Hu et al. (Hu et al., 2021), are not specified. However, information provided enables the seat location of the index patients to be determined (see Supplementary Material Section S1.1 for details) and from this analysis it is concluded that the number of index patients seated in seats A, B, C, D and F, over the study period, are 480, 280, 500, 517 and 548 respectively. Five representative index locations in row 6, (representing A, B, C, D, and F seat columns), have been simulated. The analysis in Section 4 primarily focuses on the index location weighted average IP to compare with the specific statistical data (see Supplementary Material Section S1.2 for details), where the index weights are given in Table S1 in the Supplementary Material. The analysis in Section 5 utilises the simple average IP for general train infection patterns.
The quanta source from an index patient’s mouth is modelled as a CFD inlet (an area that releases respired air as a continuous out breath) with dimensions of 0.04 m wide and 0.05 m high at the location of the mouth of each index patient. The flow rate and the scalar value at this inlet are 0.35 m3/h and 1.0 respectively. The quanta generation rate is an unknown quantity. It is thought to be dependent on the degree of infection of the index patient and the nature of the activity they are involved in, e.g. breathing while resting, breathing while involved in light/heavy activity, vocalisation volume, etc. As a result, a wide variety of quanta generation rates are suggested or derived from data for various COVID-19 transmission events reported in the literature (Marcus et al., 2020, Buonanno et al., 2020, Buonanno et al., 2020, Hota et al., 2020, Miller et al., 2020, Dai and Zhao, 2020). Passengers seated on a train are assumed to be at a low activity level, generally in the ‘rest state’.
Clearly, the quanta generation rate in each of the infection events investigated by Hu et al. (Hu et al., 2021), is unknown and is likely to have been different in each event. In this study a single quanta generation rate of 14 quanta/h is applied in each scenario, which is assumed to be representative of infectious individuals in China at the time of their study. Evidence justifying the quanta generation rate used in this analysis is presented in the Supplementary Material (Section S2) and is briefly summarised here. The quanta generation rate represents the minimum value from a Chinese study of infection events in public spaces (Dai and Zhao, 2020). Further evidence supporting this quanta generation rate is derived from Buonanno et al. (2020). From this study, there are a wide range of quanta generation rates produced by a variety of respiratory activities (breathing, talking and talking loudly), while at rest, which vary from 0.024 quanta/h to 532 quanta/h. The 14 quanta/h quanta generation rate is representative of the upper percentile range for breathing and speaking sources and the mid percentile range for speaking loudly. Furthermore, a study of inflight infection risk by Wang et. al. (Wang et al., 2021) suggests that quanta generation rates from 5 to 20 quanta/h are consistent with inflight transmission cases involving 9265 airline close contacts on 291 flights analysed by Hu et al. (Hu et al., 2020). It is also noted that the quanta generation rate will be dependent on the transmissibility of the appropriate variant of the SARS-CoV-2 virus. Thus, the quanta generation rates adopted in this study are specific to early variants of SARS-CoV-2 at the time of the original study. It is noted that Burridge et al. have suggested that scaling the quanta generation rate by the transmission increase factor is one approach of dealing with more transmissible variants (Burridge et al., 2009). Finally, while uncertainty in the quanta generation rate will impact the absolute calculated IP, it does not affect the trends in the IP distribution within the saloon.
All the CFD predictions presented in this paper were performed using a computational mesh consisting of 2,245,320 (378 × 60 × 99) cells for Scenario 1 and 2,170,476 (378 × 58 × 99) cells for Scenario 2. A mesh sensitivity study was performed on scenario 1 using three meshes, a coarser mesh of 1,095,444 (378 × 46 × 63) cells, and a finer mesh of 5,091,240 (399 × 88 × 145) cells, in addition to the selected mesh (see Supplementary Material Section S4 for details). While all three computational meshes produced results with similar flow patterns, quanta concentration distributions and calculated IPs, the absolute values for the predicted IP produced by the medium mesh were more consistent with that produced by the finer mesh. Thus, while all three meshes would lead to the same conclusions, particularly in terms of relative effectiveness of the mitigation strategies explored, the medium mesh was considered appropriate for the purposes of this study.
In addition to the mesh sensitivity study, a time step size sensitivity study was also undertaken. The investigation focused on Scenario 1 (with the 2,245,320 cell budget) using three time step sizes: 0.25 s, 0.5 s and 1.0 s. The results suggest that all three time step sizes produced virtually identical results. However, given the high flow speeds generated by the ventilation, the 0.5 s time step was adopted for the analysis presented in this paper to improve computational stability (see Section S4 of the Supplementary Material for details). The analysis used a parallel implementation of SMARTFIRE (Wang et al., 2017, Ewer et al., 2020). The computer used in this study has a 3.6 GHz eight-core processor with 64 GB of memory. Each simulation scenario, covering 990 s of simulated time (to reach steady state), required approximately 60 h of computation.
In order to estimate the IP, a target volume adjacent to each individual passenger with dimensions of 0.16 m wide, 0.20 m deep and 0.2 m high is defined.
While no mention of the use of face coverings was made by Hu et al. (Hu et al., 2021), it is likely that some people would have been wearing face coverings during the data collection period. Video footage of people queuing to board trains in Wuhan Rail station during the data collection period, show many (if not most) wearing face coverings (Youtube video clip, 2020). Thus, in this study it is assumed that 40% of the population on the G-train were wearing face coverings (see Table 1 and Supplementary Material Section S7.1 for details).
4. Comparing predicted and reported infection probabilities
In this section the WR-CFD predicted IPs are compared with the reported IPs of Hu et al. (Hu et al., 2021). Note that while only limited results of the CFD simulations are presented in this paper, a description of the temperatures and airflows predicted by the CFD simulations may be found in Supplementary Material Section S5.
The CFD simulations reach a quasi steady state for quanta concentrations at approximately 840 s for ventilation Scenario 1 and 990 s for ventilation Scenario 2 respectively. While the simulation was run only for approximately 990 s, it is assumed that the scalar concentration distribution, and hence the quanta distribution, remained constant after this time as the flow has established a quasi steady state. Considering the long exposure time in this analysis (1–8 h), the IP calculation is based on the quanta concentrations from this quasi steady state. For each scenario, a single index source has been considered located within seat row 6. As there are five possible seat locations within a row, five simulations were performed for each scenario assuming the single index patient was located in seat 6A, 6B, 6C, 6D, or 6F (See Fig. 2). The presented probabilities are weighted averages (see Supplementary Material Table S1) based on the derived ratios of index cases. Furthermore, it is assumed that the results are independent of seat row (see limitations section and Supplementary Material Section S1.3).
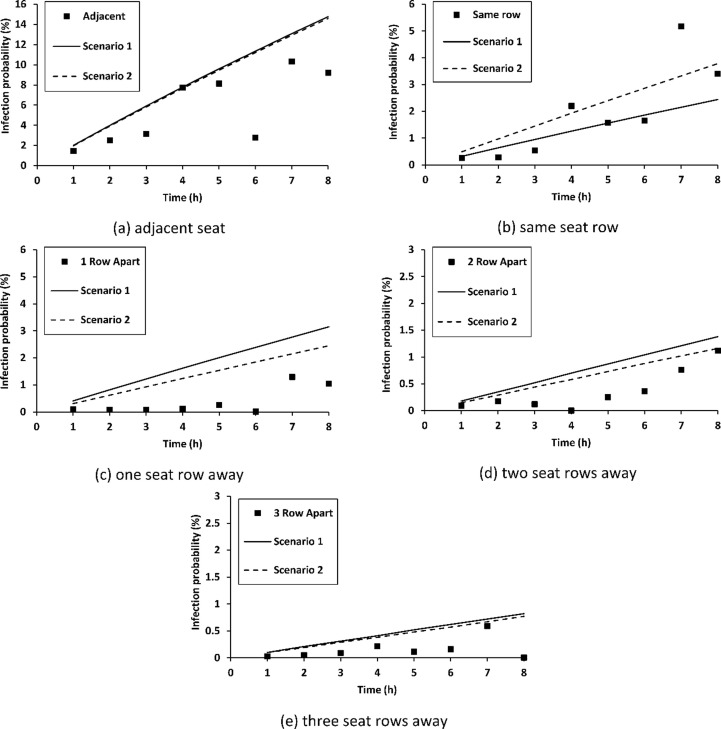
Hu et al. (Hu et al., 2021) presented the IP as a function of time and five spatial separations from the index patient: i.e. adjacent seat; same seat row; one-; two-; and three- seat rows away. The predicted IPs are compared with the reported IPs for these spatial distributions in Fig. 6 .
Fig. 6.
Reported (Hu et al., 2021) and WR-CFD predicted IP for susceptible seated (a) in seat adjacent to index patient; (b) in same seat row as index patient but excluding adjacent seats; (c) one row away from the index patient; (d) two rows away from the index patient and (e) three rows away from the index patient.
In Fig. 6a, the data from Hu et al. (Hu et al., 2021) for locations adjacent to the index patients, suggests that the statistical IP increases from 1.4% for a one-hour exposure to a maximum of 10.3% for a seven-hour exposure. The WR-CFD predictions for both ventilation scenarios produce this observed trend while the predictions match the upper bound of the measured cluster values. Compared with the maximum observed IP of 10.3%, the predicted maximum IPs are 14.8% for Scenario 1 and 14.6% for Scenario 2. For the susceptible seated in the same row as the index patient, the predicted IPs from both ventilation scenarios are within the upper and the lower boundaries of the statistical cluster data (Fig. 6b). Therefore, the WR-CFD predictions are in good agreement with the reported data for the susceptible seated in this area.
For the susceptible seated one seat row away from the index patient, the predicted IPs for both ventilation scenarios are much higher than the reported data (Fig. 6c). The maximum reported SD IP is just 1.3% while the predictions are 3.2% and 2.5% in Scenario 1 and Scenario 2, respectively.
For the susceptible seated two- and three- rows away from the index patient, the WR-CFD predictions for both ventilation scenarios produce the observed trends with the predictions matching the upper bound of the reported cluster values (Fig. 6d and Fig. 6e). When index and susceptibles are separated by two rows, the reported maximum IP is 1.1 %, while those for scenarios 1 and 2 are 1.4% and 1.2% respectively. When the index and susceptibles are separated by three rows, the reported maximum IP is 0.59 % while those for scenarios 1 and 2 are 0.82% and 0.77% respectively.
As can be seen from Fig. 6, the WR-CFD analysis produces reasonable agreement with the broad trends observed in the statistical analysis of the actual infection data presented by Hu et al. (Hu et al., 2021). In particular, the trends in terms of IP increasing with exposure duration and decreasing with distance from the source. Not only are the trends reproduced but the magnitudes of the predicted IPs are comparable to those derived from the statistical analysis.
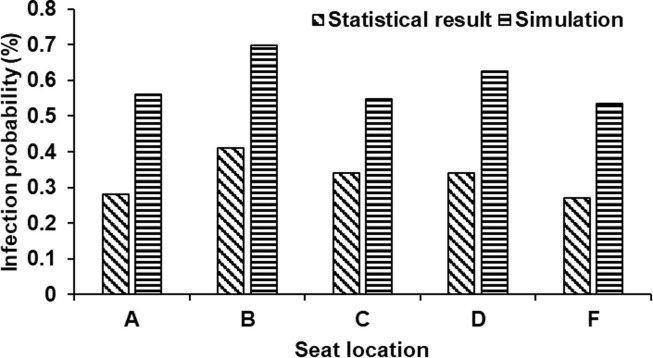
The statistical analysis by Hu et al. (Hu et al., 2021) suggests that passengers located in the window seats (A and F) have the lowest IP while those located in the middle seat (B) have the highest IP. The reported average IPs for an average travel time of 2.1 h are 0.28%, 0.41%, 0.34%. 0.34% and 0.27% for passengers at seat A, B, C, D and F respectively (see Fig. 7 ). The predicted average IPs (determined from all index cases across both ventilation scenarios) for seat rows 3 to 9 (i.e. within three seat rows of the index patient consistent with the statistical analysis (Hu et al., 2021) for an exposure time of 2.1 h are 0.56%, 0.70%, 0.55%, 0.63% and 0.53% for passengers at seats A, B, C, D and F, respectively. The model predictions reproduce the observed highest-IP seat location (seat B) and the lowest-IP seat location (seat F) (see Fig. 7). It should be noted that the reported exposure times could be as short as 8 min (Hu et al., 2021). However, the predicted IP is based on the quanta concentrations at a developed quasi steady state. Therefore, the overall predicted IP at each seat location is expected to be higher than suggested by the reported statistical data.
Fig. 7.
Statistical and simulated average infection probability (determined from all index cases across both ventilation scenarios) at various seat locations.
The broad agreement between the model predictions and the reported data demonstrates that the CFD analysis (and by implication the computational mesh used (see Supplementary Material Section S4)) reasonably represented the aerosol dispersion environment of the saloon. However, the WR-CFD analysis also provides an opportunity to explore the identified relationships in greater detail and to consider the impact of ventilation and mask wearing on IP.
5. Further analysis of factors impacting aerosol dispersion within the saloon
In this section, a detailed analysis is provided of the predicted aerosol dispersion within the saloon and the impact of the saloon ventilation system, passenger mask wearing, and passenger inoculation on IP.
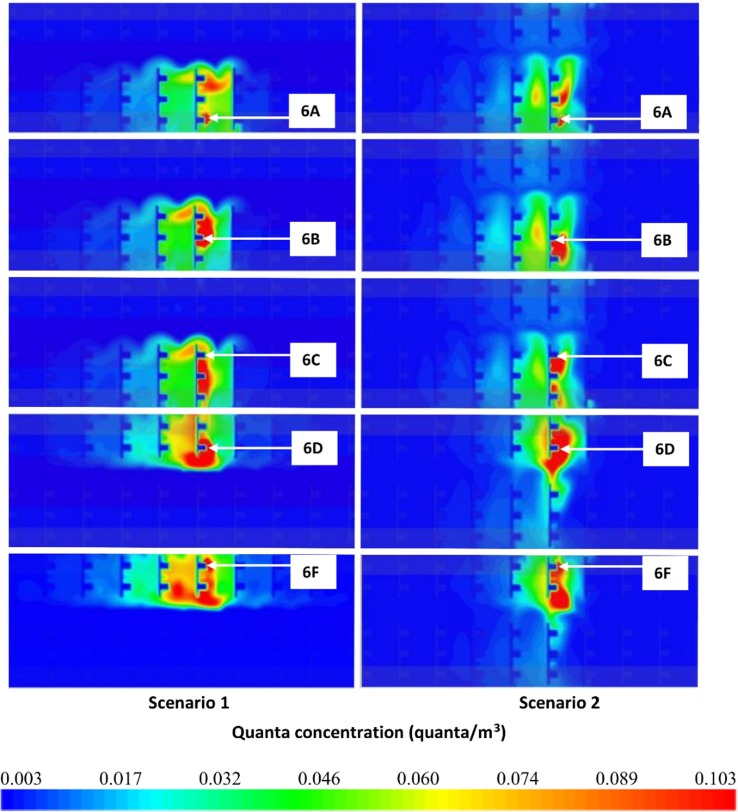
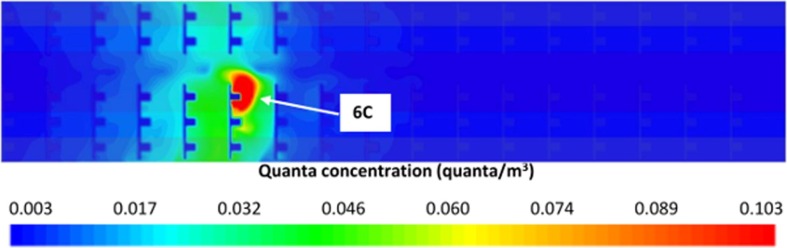
Presented in Fig. 8 are the quanta concentration distributions in a horizontal cutting plane located at nose height (passing through the centre of the target volume defined in Table 1) after quasi-steady-state conditions have been reached. Only the first nine seat rows are presented in Fig. 8 as beyond these the quanta concentration is no higher than the minimum (background) value. The differences observed in the quanta distributions on the left and right side of the aisle, and between scenario 1 and 2, can be explained by the nature of the flows created by the ventilation systems (see Supplementary Material Section S5). Note that the scale of the quanta distributions presented in Fig. 8 is truncated at 0.103 quanta/m3.
Fig. 8.
Quanta concentrations (quanta/m3) in a horizontal cut plane at nose height generated by the CFD simulations with index patient(s) located in various seats in row 6 (note, only rows 1–9 are depicted).
The background quanta concentration in the saloon, due to the recycled air, is 0.0028 quanta/m3 for Scenario 1 and 0.0031 quanta/m3 for Scenario 2 (see Equation (9)). It is thus noted that the uniform background quanta concentration, at steady state, is too low to significantly impact the distribution of quanta due to the mixing effect of the ventilation system (see Fig. 8). In the high impact zone, containing the seats in the section with the index patient (i.e. the three or two seat blocks) and the corresponding section immediately behind the index patient, the background quanta concentration is less than one tenth that resulting from the mixing caused by the ventilation.
5.1. Asymmetry in quanta distribution
The first important observation concerns the non-uniform quanta concentrations within the saloon resulting from the dispersion produced by the ventilation system. While this is dependent on the seating location of the source and the nature of the ventilation system, there appear to be general trends in the quanta distribution. As seen in Fig. 8, very high quanta concentrations occur in the seat row containing the index patient up to two seat rows behind the index patient, with lower but still relatively high concentrations up to one seat row ahead of the index patient. The quanta distribution drops off significantly outside these regions. The higher quanta concentrations behind, rather than ahead of, the index patient are due to the complex interaction between the ventilation system, seating arrangement and thermal field generated by the seated passengers. Similar dispersal trends have been observed in other numerical simulations of contaminant dispersal in G-train configurations (Yang et al., 2018) and in experimental studies of aerosol dispersion in passenger aircraft cabins (Silcott et al., 2020).
For complex environments, such as a train saloon with asymmetries in configuration and complex ventilation systems, a well-mixed uniform state, which is a core assumption of the WRM, is invalid (See Supplementary Material Section S6). Wells-Riley applications that predict low IPs for complex spaces such as classrooms, aircraft cabins, etc. (Dai and Zhao, 2020), need to be carefully reconsidered as they are likely to fail to identify high IPs in the vicinity of the index patients. Furthermore, the IP based on an average quanta concentration, as assumed by the WRM, is not necessarily the same as the actual average IP based on averaging the probabilities from a non-uniform quanta distribution.
The second observation concerns the impact of the asymmetric quanta distribution on IPs. The observed asymmetry is significant and is observed in the longitudinal direction along the length of the saloon either side of the index patient and in the transverse direction either side of the aisle. As seen in Fig. 8, the seat block that includes the index patient, has significantly higher quanta concentration than the opposite seat block. Thus, the quanta distribution is concentrated on the side containing the index patient. For Scenario 1, with ceiling inlet and a high ventilation rate, the effect is extreme with virtually no aerosols spreading to the other side of the aisle. The ventilation system effectively segments the space creating two zones separated by the aisle, trapping the aerosol on the side with the source. Due to the asymmetry of the seating arrangement, the volumes of the two zones are also significantly different which in turn will impact IPs within each zone. For Scenario 2, with air inlets located on the side walls, some aerosols are transported to the seat block on the other side of the aisle, opposite to the index patient. However, the quanta concentration on the side of the aisle with the index patient is higher than that on the opposite side. Furthermore, in both Scenario 1 and 2, quanta concentrations are higher up to four seat rows behind the index patient compared to the same number of rows ahead. This difference can be significant up to two seat rows away.
This is clearly seen in Table 2 where the IPs for an eight-hour exposure are displayed for Scenarios 1 and 2 for each index seating location. Note that these IPs include the contribution from the uniform background quanta distribution, which results in an IP of 0.5% at locations remote from the index patient. As can be seen the IP is not symmetrically distributed. The IP for a given number of seat rows ahead of the index patient is not the same as that for the same number of seat rows behind the index patient. Furthermore, the IP across the aisle from an index patient is considerably smaller than that on the same side of the aisle.
Table 2.
Predicted IPs for Scenario 1 and Scenario 2 with various index patient locations for an 8 h exposure period.
|
Scenario 1 |
Scenario 2 |
||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | Seat | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11–17 | Index | Seat | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11–17 |
| (a) 6A | F | 0.5 | 0.5 | 0.5 | 0.6 | 0.7 | 0.7 | 0.6 | 0.5 | 0.5 | 0.5 | 0.5 | (f) 6A | F | 0.6 | 0.7 | 0.9 | 1.3 | 2.3 | 2.5 | 1.0 | 0.6 | 0.5 | 0.5 | 0.5 |
| D | 0.5 | 0.5 | 0.6 | 0.6 | 0.7 | 0.7 | 0.6 | 0.5 | 0.5 | 0.5 | 0.5 | D | 0.6 | 0.7 | 0.9 | 1.3 | 2.1 | 2.2 | 1.0 | 0.6 | 0.5 | 0.5 | 0.5 | ||
| C | 0.7 | 0.8 | 1.5 | 2.8 | 8.5 | 14.7 | 1.5 | 0.7 | 0.5 | 0.5 | 0.5 | C | 0.6 | 0.7 | 1.1 | 1.5 | 3.7 | 8.3 | 0.9 | 0.6 | 0.5 | 0.5 | 0.5 | ||
| B | 0.6 | 0.9 | 1.5 | 3.0 | 7.2 | 11.0 | 1.2 | 0.6 | 0.5 | 0.5 | 0.5 | B | 0.6 | 0.8 | 1.4 | 2.3 | 6.4 | 18.4 | 0.6 | 0.6 | 0.5 | 0.5 | 0.5 | ||
| A | 0.6 | 0.8 | 1.3 | 2.6 | 6.3 | 1.3 | 0.6 | 0.5 | 0.5 | 0.5 | A | 0.6 | 0.8 | 1.3 | 2.8 | 7.3 | 0.7 | 0.6 | 0.5 | 0.5 | 0.5 | ||||
| (b) 6B | F | 0.5 | 0.5 | 0.5 | 0.6 | 0.7 | 0.6 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | (g) 6B | F | 0.6 | 0.7 | 1.0 | 1.8 | 2.7 | 2.1 | 0.8 | 0.6 | 0.6 | 0.5 | 0.5 |
| D | 0.5 | 0.5 | 0.6 | 0.7 | 0.7 | 0.7 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | D | 0.6 | 0.8 | 1.0 | 1.7 | 2.5 | 1.9 | 0.9 | 0.6 | 0.6 | 0.5 | 0.5 | ||
| C | 0.7 | 0.8 | 1.6 | 3.2 | 10.3 | 15.8 | 0.9 | 0.6 | 0.5 | 0.5 | 0.5 | C | 0.6 | 0.8 | 1.4 | 2.5 | 4.8 | 6.0 | 0.8 | 0.6 | 0.6 | 0.5 | 0.5 | ||
| B | 0.6 | 0.9 | 1.5 | 3.2 | 8.7 | 0.9 | 0.5 | 0.5 | 0.5 | 0.5 | B | 0.6 | 0.9 | 1.6 | 3.7 | 8.3 | 0.6 | 0.6 | 0.5 | 0.5 | 0.5 | ||||
| A | 0.6 | 0.8 | 1.3 | 2.8 | 7.6 | 6.7 | 0.8 | 0.5 | 0.5 | 0.5 | 0.5 | A | 0.6 | 0.9 | 1.7 | 3.6 | 9.3 | 15.7 | 0.6 | 0.6 | 0.5 | 0.5 | 0.5 | ||
| (c) 6C | F | 0.5 | 0.5 | 0.5 | 0.6 | 0.7 | 0.6 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | (h) 6C | F | 0.6 | 0.7 | 0.9 | 1.4 | 2.2 | 2.5 | 0.9 | 0.6 | 0.5 | 0.5 | 0.5 |
| D | 0.5 | 0.5 | 0.6 | 0.7 | 0.7 | 0.7 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | D | 0.6 | 0.7 | 0.9 | 1.3 | 2.0 | 2.4 | 1.0 | 0.6 | 0.5 | 0.5 | 0.5 | ||
| C | 0.7 | 0.8 | 1.6 | 3.0 | 10.4 | 1.1 | 0.6 | 0.5 | 0.5 | 0.5 | C | 0.6 | 0.7 | 1.1 | 1.7 | 4.0 | 0.9 | 0.6 | 0.5 | 0.5 | 0.5 | ||||
| B | 0.6 | 0.9 | 1.5 | 3.1 | 8.7 | 25.3 | 1.0 | 0.6 | 0.5 | 0.5 | 0.5 | B | 0.6 | 0.8 | 1.3 | 2.8 | 7.0 | 12.1 | 0.8 | 0.5 | 0.5 | 0.5 | 0.5 | ||
| A | 0.6 | 0.8 | 1.3 | 2.8 | 7.6 | 12.1 | 0.9 | 0.6 | 0.5 | 0.5 | 0.5 | A | 0.6 | 0.8 | 1.2 | 2.7 | 6.7 | 13.2 | 0.7 | 0.5 | 0.5 | 0.5 | 0.5 | ||
| (d) 6D | F | 0.7 | 1.0 | 1.8 | 4.1 | 11.6 | 10.6 | 1.5 | 0.9 | 0.7 | 0.6 | 0.5 | (i) 6D | F | 0.6 | 0.6 | 0.8 | 1.5 | 5.2 | 12.9 | 0.8 | 0.5 | 0.5 | 0.5 | 0.5 |
| D | 0.7 | 1.1 | 2.1 | 4.9 | 11.0 | 1.3 | 0.9 | 0.6 | 0.5 | 0.5 | D | 0.6 | 0.6 | 0.8 | 1.5 | 6.0 | 0.9 | 0.5 | 0.5 | 0.5 | 0.5 | ||||
| C | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | C | 0.6 | 0.6 | 0.8 | 1.2 | 2.0 | 6.0 | 0.7 | 0.5 | 0.5 | 0.5 | 0.5 | ||
| B | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | B | 0.6 | 0.7 | 0.9 | 1.7 | 2.8 | 1.5 | 0.7 | 0.5 | 0.5 | 0.5 | 0.5 | ||
| A | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | A | 0.6 | 0.7 | 0.9 | 1.7 | 2.9 | 1.7 | 0.6 | 0.5 | 0.5 | 0.5 | 0.5 | ||
| (e) 6F | F | 0.7 | 1.2 | 2.2 | 5.1 | 13.1 | 2.0 | 1.2 | 0.8 | 0.6 | 0.5 | (j) 6F | F | 0.6 | 0.6 | 0.8 | 1.5 | 4.9 | 0.8 | 0.5 | 0.5 | 0.5 | 0.5 | ||
| D | 0.8 | 1.2 | 2.5 | 6.1 | 16.3 | 16.0 | 1.9 | 1.1 | 0.7 | 0.6 | 0.5 | D | 0.6 | 0.6 | 0.8 | 1.5 | 5.4 | 19.0 | 0.8 | 0.5 | 0.5 | 0.5 | 0.5 | ||
| C | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | C | 0.6 | 0.6 | 0.7 | 0.9 | 1.7 | 3.8 | 0.7 | 0.6 | 0.5 | 0.5 | 0.5 | ||
| B | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | B | 0.6 | 0.6 | 0.8 | 1.2 | 2.1 | 1.7 | 0.6 | 0.5 | 0.5 | 0.5 | 0.5 | ||
| A | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | A | 0.6 | 0.6 | 0.8 | 1.2 | 2.3 | 1.9 | 0.6 | 0.5 | 0.5 | 0.5 | 0.5 | ||
For example, the average IP in row 7 in Scenario 1/Scenario 2 with index patient located in seat 6A is 1.0%/0.8%, while in seat row 5 it is 4.7%/4.4%, which is nearly 5 times greater (see Table 2). Furthermore, in these asymmetrical seating arrangements, the IPs are dependent on the side of the saloon that the susceptible is seated. For example, when the index patient is located on the three-seat side of the aisle, in seat 6A, the average IP in seat row 5 on the opposite side of the aisle in Scenario 1/Scenario 2 is 0.7%/2.2%, while on the same side as the index patient it is 7.4%/5.8%, some 13/2.6 times greater (see Table 2).
These asymmetries are significant and are not factored into the analysis undertaken by Hu et al. (Hu et al., 2021), where it was assumed that IP ahead or behind the index patient row are identical and that IP either side of the aisle was the same. As demonstrated in this study, the observed asymmetries will have a profound impact on the relationship between IP and seat location.
5.2. The impact of filtration efficiency (FE)
To explore the impact of FE on IP, the FE was increased from 20% to 100%. With a 100% FE, all returned air is free of infected aerosol. IPs for Scenario 1, for an 8-hour exposure with 20% FE and index located in seat 6C are presented in Table 2c, while corresponding IPs for 100% FE are presented in Table 3 a.
Table 3.
Predicted IPs resulting from (a) filtration efficiency, (b) mask wearing and (c) ventilation rate changes to scenario parameters for Scenario 1 with index patient located in seat 6C.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13–17 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) Scenario 1 with ventilation filtration efficiency of 100 %1 | F | 0.0 | 0.0 | 0.1 | 0.2 | 0.2 | 0.2 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| D | 0.0 | 0.0 | 0.1 | 0.2 | 0.3 | 0.2 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| C | 0.2 | 0.3 | 1.1 | 2.6 | 10.0 | 0.6 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| B | 0.2 | 0.4 | 1.0 | 2.7 | 8.2 | 25.0 | 0.5 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| A | 0.1 | 0.3 | 0.8 | 2.3 | 7.2 | 11.7 | 0.4 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| (b) Scenario 1 with 90% of passengers wearing face coverings | F | 0.3 | 0.3 | 0.3 | 0.4 | 0.4 | 0.4 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| D | 0.3 | 0.3 | 0.3 | 0.4 | 0.4 | 0.4 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | |
| C | 0.4 | 0.5 | 0.9 | 1.7 | 6.1 | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | ||
| B | 0.4 | 0.5 | 0.9 | 1.8 | 5.1 | 15.5 | 0.6 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | |
| A | 0.3 | 0.5 | 0.7 | 1.6 | 4.4 | 7.1 | 0.5 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | |
| (c) Scenario 1 with air change rate of 14 ACH | F | 1.8 | 2.1 | 2.8 | 4.1 | 5.9 | 5.8 | 2.9 | 2.0 | 1.8 | 1.7 | 1.6 | 1.5 | 1.5 |
| D | 1.7 | 2.1 | 3.0 | 4.3 | 5.7 | 5.0 | 2.6 | 2.0 | 1.8 | 1.7 | 1.6 | 1.6 | 1.5 | |
| C | 1.7 | 2.1 | 3.0 | 4.8 | 8.4 | 2.8 | 2.1 | 1.8 | 1.7 | 1.6 | 1.6 | 1.5 | ||
| B | 1.7 | 2.2 | 2.9 | 4.6 | 8.0 | 10.9 | 2.6 | 2.1 | 1.8 | 1.7 | 1.6 | 1.5 | 1.5 | |
| A | 1.7 | 2.1 | 3.0 | 4.7 | 7.7 | 7.1 | 2.9 | 2.0 | 1.8 | 1.7 | 1.6 | 1.5 | 1.5 |
1IPs less than 0.05% are presented as 0.0.
The average IP on the index’s side of the aisle (right side) in the three rows with highest IPs (i.e. 4, 5, 6) is 9.13% and 8.70% with 20% and 100% FE respectively, a relative reduction of 4.7%. Further from the index, in rows 9–17, the average IP is 0.5% with 20% FE and 0.0028% with 100% FE, a relative reduction of 99%. Scenario 1 results (with index in seat 6C) suggest only a modest decrease in IP for passengers near the index (high IP zone) when FE increases from 20% to 100%. However, for passengers seated further away, there is a significant reduction in IP, although it is noted that these passengers’ already have low IPs.
To better clarify the impact of FE on IPs, for the whole saloon, consider both ventilation Scenarios (1 and 2) and all five index seat locations within row 6 (see Table 4 ). The average IP over all seats within the saloon with 20% FE in Scenario 1/2 is 1.22%/1.19%, while for 100% FE it is 0.75%/0.67%. For Scenario 1/2 these IPs result in 1.03/1.00 expected secondary infections for 20% FE and 0.63/0.56 for 100% FE, a reduction of 39%/44% (See Table 4). Increasing FE to 100% for Scenarios 1 and 2, assuming four saloons per train, one index per saloon, and 25 journeys, the expected number of secondary infections fall from 103 to 63 in Scenario 1 and 100 to 56 in Scenario 2.
Table 4.
Estimated maximum and average IP in the saloon and the expected secondary infections for an 8-hour exposure (for all five index patient cases) resulting from various changes to the scenario specification.
|
Maximum IP (%) |
Average IP (%) |
Expected # of secondary infections |
||||
|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 1 | Scenario 2 | Scenario 1 | Scenario 2 | |
| Base case scenarios (using parameters fromTable 1) | 16.7 | 15.8 | 1.22 | 1.19 | 1.03 | 1.00 |
| 100% air conditioning filtration efficiency | 16.3 | 15.4 | 0.75 | 0.67 | 0.63 | 0.56 |
| 90% population wearing face coverings | 10.0 | 9.4 | 0.71 | 0.69 | 0.60 | 0.58 |
| 90% population wearing face coverings with 90% efficiency | 0.92 | 0.86 | 0.06 | 0.06 | 0.05 | 0.05 |
| 2 m physical distancing | 2.8 | 2.7 | 0.66 | 0.76 | 0.086 | 0.10 |
These results suggest that whilst there is a reduction in IP with increased FE far from the index patient, in the vicinity of the index patient there is virtually no improvement. Thus, while it may be argued that on a societal level improving the ventilation FE can result in marked reductions in expected secondary infections, on a personal level, for those in the vicinity of the index patient there is little benefit from improved ventilation FE.
5.3. Impact of index patient seating location and ventilation configuration on infection probability
The impact of index patient seating location on IP is explored by examining the differences in IP by varying the location of the index patient in row 6 for Scenario 1 and 2. The IP data for each case, on a seat by seat basis, is presented in Table 2 with the maximum and average values summarised in Table 5 .
Table 5.
Comparison of IPs for index patient seating location and saloon ventilation scenario.
|
Scenario 1 |
Scenario 2 |
Scenario 1 with 14 ACH |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
Index patient seating location |
|||||||||||
| 6A | 6B | 6C | 6D | 6F | 6A | 6B | 6C | 6D | 6F | 6C | |
| Max IP (%) | 14.7 | 15.8 | 25.3 | 11.6 | 16.3 | 18.4 | 15.7 | 13.2 | 12.9 | 19.0 | 10.9 |
| Average IP over 3 rows (%) | 7.0 | 7.3 | 9.1 | 8.4 | 11.3 | 4.0 | 4.3 | 3.9 | 2.9 | 3.0 | 6.2 |
| Average # secondary infections per index case | 1.02 | 1,02 | 1.17 | 0.88 | 1.05 | 1.06 | 1.11 | 1.05 | 0.89 | 0.89 | 2.16 |
| Average # secondary infections per scenario | 1.03 | 1.00 | 2.16 | ||||||||
Consider ventilation Scenario 1 (see Table 5) with the index patient located in the block of three seats, at seat 6A or 6B or 6C. If the index patient is located in 6A the maximum IP is 14.7% while if they are located in 6C, it is as high as 25.3%. And if the index patient is located in 6B, the maximum IP is 15.8%. In addition, the average IP for the block of seats with the highest average IP (the two rows behind the index patient and on the same side of the aisle (i.e. six seats) and the row containing the index patient (two seats)) is 7.0% when the index is located in 6A, 7.3% when located in 6B and 9.1% when located in 6C. This suggests that if located in the block of three seats, from the point of view of the surrounding passengers, it is preferable for the index patient to occupy the A or B seat rather than the C seat. Similarly, if the index patient is located in the block of two seats it is preferable for the index patient to occupy the D seat rather than the F seat (see Table 5). Furthermore, considering the five seating locations, locating the index patient in seat A is marginally better than seat D for those in the immediate vicinity of the index patient (i.e. based on the average IP over the three seat rows with the highest IPs). However, when considered from a societal point of view, i.e. considering everyone in the saloon, it is preferable for the index patient to be located in the D seat as this results in the minimum overall number of expected secondary infections (see Table 5).
This has potential implications for mitigation strategies involving blocking seats using physical distancing measures. Presented in Table 6 is a summary of the expected number of secondary infections that may occur for 84 susceptible passengers, the equivalent of a single full saloon, due to a single index patient employing four different seating strategies for ventilation Scenario 1. The seat blocking mitigation strategies involve seating passengers in the following configurations: the A, C and F seats; the odd seat rows; the A, C and F seats in odd seat rows; and a 2 m physical distancing strategy. The physical distancing strategy is based on seating passengers only in odd rows with the A and F seats used in the first odd row followed by C seat in the next odd row; this pattern is then repeated throughout the saloon. These strategies are compared with the case in which all seats are occupied. These seat blocking measures reduce the seating capacity of a saloon, from 85 to 51, 45, 27 and 14 passengers respectively. As the strategies involve reducing the usable capacity of the saloon, it is necessary to add additional carriages to accommodate the same number of passengers (see Table 6). Taking the extreme 2 m physical distancing measure, reducing occupancy of each saloon to 14 passengers, will reduce the number of expected secondary infections (for 84 passengers) from 1.03 to 0.086 for Scenario 1. This represents a 92% reduction in the number of secondary infections with an approximate sixfold increase in the required number of saloons.
Table 6.
Impact of seat blocking mitigation measures on secondary infections in Scenario 1.
| Seating Scenario | # paxs per saloon (excluding index) | Number of carriages required (to carry 85 pax) |
Average IP in saloon with index patient (%) |
Expected # secondary infections for 84 passengers |
||
|---|---|---|---|---|---|---|
| WR-CFD | WRM | WR-CFD | WRM | |||
| Full | 84 | 1 | 1.22 | 0.9 | 1.03 | 0.76 |
| A, C, F seats | 50 | 1.67 | 1.14 | 0.9 | 0.57 | 0.45 |
| Odd rows | 44 | 1.89 | 1.22 | 0.9 | 0.54 | 0.40 |
| A,C,F seats in odd rows | 26 | 3.15 | 1.05 | 0.9 | 0.27 | 0.23 |
| 2 m physical distancing | 13 | 6.07 | 0.66 | 0.9 | 0.086 | 0.12 |
As seen in Table 6, both the WR-CFD model and the WRM predict that the number of secondary infections per 84 passengers decrease if appropriate seat blocking measures are implemented. However, for the WRM, the average IP for the entire saloon remains constant regardless of the seating strategy employed whereas for the WR-CFD model, the average IP decreases as the seat blocking strategy becomes more severe. As a result, the 84% reduction in secondary infections among the 84 passengers predicted by the WRM for the extreme seat mitigation measure is simply the result of the reduction in passenger number within the saloon containing the index passenger (see Table 6). With the WR-CFD model, the corresponding 92% reduction in secondary infections reflects not only the impact of the reduced number of passengers, but also the localised nature of the aerosol dispersion. Thus, only when using the WR-CFD model can the impact of seat mitigation measures on expected secondary infections be truly assessed.
Furthermore, the ventilation condition found in Scenario 2, even though it has a lower ACH, appears marginally preferable on a personal level (lower maximum and three seat row average IPs) and similarly on a societal level (resulting in a slightly smaller number of expected secondary infections) (see Table 5). Thus Scenario 2, with the side wall air delivery configuration, appears to be marginally preferable to the ceiling mounted air delivery configuration, even though it has a smaller ventilation rate.
This suggests that the IP distribution is sensitive to the seating location of the index patient and the ventilation configuration.
5.4. Impact of face coverings
The impact of face covering on IP is explored by examining the differences in IP by varying the proportion of passengers wearing face coverings and by changing the efficiency of the face coverings for Scenario 1 and 2.
It is noted that the IPs presented in Table 2 assume that 40% of the passengers are wearing face coverings. These probabilities are derived using Equation (8) and represent a weighted outcome of the four possible states of mask wearing for index and susceptible assuming a 40% chance that either are wearing a face covering (see Equations (4), (5), (6), (7)). For example, the average IP for an 8-hour exposure for a susceptible in seat 6B in Scenario 1 with the index patient seated in 6C is 25.3% (See Table 2c). However, if in this scenario the index patient and the susceptible were not wearing face coverings, the IP of the susceptible would be 34.5%, while if they were both wearing face coverings, it would be 13.7% (see Supplementary Material Section S7.2). This demonstrates that wearing a face covering can have a significant impact on reducing both personal and overall IPs on long train journeys.
If the proportion of passengers wearing face coverings was increased from 40% to 90%, the predicted IPs in Scenario 1, with index patient located in seat 6C, are substantially decreased as seen in Table 3b. Furthermore, the expected number of secondary infections, in both Scenarios 1 and 2, are reduced by approximately 42% and the average and maximum IPs are reduced by approximately 42% and 40% respectively (see Table 4). Thus, a significant reduction (42%) in average IP for all passengers can be achieved if 90% of the passengers wear face coverings.
Finally, if higher efficiency face coverings were used, such as N95 masks (worn correctly), filtration efficiencies for both index and susceptible could approach 0.9. In this case (with a = b = 0.9 in Equation (8)) and if 90% of passengers wear face coverings (see Supplementary Material Section S7.3 for details), the maximum IP, the average IP and the number of expected secondary infections, in both Scenarios 1 and 2 are all reduced by approximately 95% (See Table 4). This case is even superior to the seat blocking case with 2 m physical distancing (assuming 84 passengers in 6 saloons), producing approximately 42% fewer secondary infections than that found in the seat blocking case (see Table 4).
Thus, a significant reduction (95%) in average IP, for all passengers, can be achieved if 90% of passengers correctly wear high efficiency face coverings for long distance travel on trains.
5.5. Impact of ventilation rate
The impact of ventilation rate on IP is explored by examining the differences in IP by reducing the ventilation rate in Scenario 1 with index patient located in seat 6C from 44 ACH to 14 ACH.
In Scenario 1, the ventilation rate is 5500 m3/h, which is approximately equivalent to an air change rate of 44 ACH for the CHR1 train. In this analysis, Scenario 1 is repeated with a ventilation rate of 1800 m3/h, equivalent to an air change rate of approximately 14 ACH. As seen in Fig. 9 and Table 3c, the low ventilation rate allows a large proportion of the released quanta to cross the aisle to the side of the saloon opposite to the index patient compared with Fig. 8.
Fig. 9.
Quanta concentrations (quanta/m3) in a horizontal plane at nose height for Scenario 1 with index patients 6C with an air change rate of 14 ACH.
With the lower ventilation rate and index patient located in seat 6C, the maximum IP is decreased from 25.3% to 10.9%, a relative reduction of 57% (see Table 5). Furthermore, the average IP for the two rows behind the index patient and the row containing the index patient with the lower ventilation rate (14 seats) is 6.2%, compared to 9.1% with the higher ventilation rate (8 seats), a relative reduction of 32%. Thus, both the maximum and average IP, in the high IP region, has decreased with the lower ventilation rate. However, the average number of expected secondary infections in the whole saloon is 2.16 (see Table 5), approximately twice that of the case with higher ACH (i.e. 1.17, see Table 5). Thus, while reducing the ventilation rate reduces the maximum IP and the IPs of those seated close to the index patient, it significantly increases the average IP and hence the expected number of secondary infections.
5.6. Impact of inoculation
Finally, the impact of inoculation on IP is explored by estimating the expected reduction in IP assuming part of the population is partially or fully vaccinated with the required doses. As part of this analysis, it is assumed that the index patient is unvaccinated as this could affect transmission.
As the pandemic progresses the effect of population vaccination programmes will also affect the transmission of the virus. For the purpose of demonstration, the current inoculation data for the UK (circa June 2021) is used. For the B.1.617.2 (Delta) variant, PHE data (Bernal et al., 2021, Covid-19 vaccine surveillance report: Week 19, 2021) suggests that one vaccination dose is 33.5% effective and two doses are 80.9% effective against infection. Assuming 51% of the (adult) population have been partially vaccinated and 30% have been fully vaccinated, then the average IP for the vaccinated population () is related to the previously calculated IP of the non-vaccinated population () by Equation (10) and leads to a relative decrease of 41.4%.
| (10) |
To determine the IPs for the G-train scenario assuming a (partially) vaccinated population, it would be necessary to first determine appropriate for the same strain of the virus i.e. the delta strain. This would require repeating the analysis presented in this paper with an appropriate quanta generation rate for the delta strain of the virus.
Another factor that could be included in the analysis is the natural immunity conferred by prior infection. While this has not been included in equation (10), it could be easily incorporated in a manner similar to the effect of vaccination; this would require an estimation of the proportion of the population that have been previously infected and the degree of protection this provides. For example, a Danish study (Hansen et al., 2021) has suggested that those under 65 years of age have an effective protection of 80% whilst those over 65 had an effective protection of 47%.
6. Study limitations
As in any numerical investigation of a complex process, some assumptions are required to simplify the analysis and to accommodate the various uncertainties in the data. In this section, the main limitations of the work presented in this study are discussed. The simulation results are compared with the statistical data reported by Hu et al. (Hu et al., 2021); which are based on analysis of passenger infections on G-trains from 19 December 2019 through 6 March 2020 in China. Although representative model parameter values are selected to reflect general COVID-19 transmission characteristics and the configuration of G-trains, and passengers’ behaviours during the time period considered, there are a number of limitations of the work:
-
•
A quanta generation rate of 14 quanta/h is used in this study, which is representative of resting state values and predicted values for a number of inflight transmission events in China during the same period as the train transmission events in reality. For the known 2334 index patients present on the G-trains, it is likely that some of the index patients may have had larger values, while some may have had smaller values. A larger/smaller quanta generation rate will increase/decrease the absolute values of estimated IP. However, the spatially and temporally dependent infection trends described in this study will not change.
-
•Although a reasonable compromise to the wide variety of index patients’ physiology and behaviour is considered, there are some differences between the simulation configuration and conditions during the infection events:
-
○The quanta source from an index patient, is modelled as a mouth inlet with dimensions of 0.04 m wide and 0.05 m high. This approach considers that the index patient occasionally engages in speech during the journey. Furthermore, wearing a face covering would complicate the air exhalation flow from the index patient.
-
○All the simulated passengers are seated in an upright position with the tops of their heads slightly below the top of seat back. In reality, some passengers might have their head above the top of seat back. Furthermore, some passengers are likely to recline their seat back increasing the gap between neighbouring seats, thus impacting local air recirculation. In addition, turbulent wakes produced by passengers walking along the aisles, as well as issues of spread due to a moving index, were not considered.
-
○As this is a quasi steady state simulation the effect of transient breathing, e.g. exhalation and inhalation breathing cycle are not modelled.
-
○
-
•
It is assumed that the filtration efficiency of the ventilation system is uniform, and that the ventilation system has uniform and continuous inlet airflows and extraction along the entire length of the train saloon. However, ventilation inlet/outlet sizes/locations may not be the same in different generations of G-trains. Furthermore, changes due to temperature control (heating/cooling) and sensor-controlled fan adjustment were not considered.
-
•
It is assumed that the filtration efficiency of the ventilation system is uniform, and that the ventilation system has uniform and continuous inlet airflows and extraction along the entire length of the train saloon. However, ventilation inlet/outlet sizes/locations may not be the same in different generations of G-trains. Furthermore, changes due to temperature control (heating/cooling) and sensor-controlled fan adjustment were not considered.
-
•
It is assumed that the filtration efficiency of face coverings is constant throughout the wearing period, all passengers have the same face covering and that the face covering filtration efficiency is the same for all susceptibles. This is known not to be the case; indeed it has been shown experimentally that the same face covering can result in different filtration efficiencies (Wang et al., 2021). While it is possible to provide each face covering represented within the simulation with its own filtration efficiency, the simulations presented in this paper has simply assumed an average filtration efficiency is applied to each face covering (see Supplementary Material Section S7.1),
-
•
The reduction of virions due to the deposition of respiratory droplets on solid surfaces and the decay of active airborne virions over time (Lin and Marr, 2020) are not considered. Excluding these phenomena from the analysis will result in an overestimation of IP, in particular for longer journey times. However, at present there is considerable uncertainty concerning the parameters required to specify these phenomena. Furthermore, while approximations to these phenomena can be represented in the approach adopted in this study, it is suggested that a coupled Euler-Lagrange approach, where the aerosol is represented by a droplet distribution rather than a scalar, would be the preferred approach.
-
•
Index patients located in the end rows of the saloon have not been explicitly modelled. The ends of the saloon are likely to produce regions of stagnant air potentially increasing the likely IP for those seated there, especially if the index patient is also located in the end region. However, susceptibles located in the end rows will have reduced likelihood of proximity to an index patient (since if seated in the first rows, there are fewer rows behind and if seated in the last rows, fewer rows ahead) decreasing the likely IP. It is expected that the impact of “end effects” for the specific (geometry and ventilation) configuration investigated are likely to contribute little to the overall IPs.
-
•
It is assumed that the index patient seating locations modelled (i.e. 6A, 6B, 6C, 6D and 6F) are representative of an index patient sat in any location on average, with the possible exception of the extreme ends of the saloon. Thus, the conclusions derived from the simulation involving an index patient located in 6A are similar to those that would be derived if they were located in any ‘A’ seat. Spot analysis comparing IPs resulting from index patients located in seats 6D and 13D and in seats 6F and 13F suggest that this is a reasonable assumption (see Supplementary Material Section S1.3).
-
•
In the seat blocking strategy analysis, as passengers are removed from the simulations, their absence will impact the thermal environment within the saloon, which may in turn impact the aerosol dispersion. Furthermore, the physical absence of the removed passengers will also impact the nature of the flow environment within the saloon. Neither of these issues were considered in the seat blocking analysis and so the results presented here should be considered preliminary subject to further investigation.
-
•
The IP analysis presented in this paper is based on the quanta concentrations at a quasi steady state developed after 840 s in Scenario 1 or 990 s in Scenario 2. However, in situations involving shorter duration exposure times or where temporal changes in the scenario are likely, a transient WR-CFD approach is suggested.
-
•
It is assumed that the motion of the train does not create any additional forces that could affect the flow field, i.e. the train is moving with a constant velocity. Furthermore, the external weather conditions and tunnel traversal are assumed to have no impact on the ventilation conditions and airflows within the carriages. It is known that these issues will have some impact on the airflows in the train.
7. Conclusions
The coupled Wells-Riley CFD model (WR-CFD) described in this paper was validated using actual infection data reported for passengers travelling on long-distance trains (G-train) in China for the period from 19 December 2019 to 6 March 2020. The reported infection data resulted from exposures ranging from 1 to 8 h with secondary infections reported up to three seat rows from the index patient. The WR-CFD model was able to reproduce, with reasonable agreement, trends in COVID-19 infection probabilities (IPs). The model successfully predicts:
-
•
the maximum IP (10.3% reported while predicted values were between 14.8% and 14.6% for the two ventilation scenarios simulated) and,
-
•
the seat locations with the highest and lowest IP (seat B and F respectively).
-
•
the IPs, as a function of exposure time and distance from the index patient, with good agreement with the reported data at four of the five reported seating locations.
The differences between model predictions and observed values for IP are considered reasonable given the uncertainties in specifying actual conditions within the environment during the observation period.
The importance of this work is not only that it validates, for the first time, the WR-CFD modelling approach for predicting COVID-19 IPs within a forced ventilated rail carriage with recirculated air environment, but that it provides invaluable insight into the nature of the aerosol dispersion within these complex and ventilated environments. This enables the impact of proposed infection mitigation strategies for specific environments to be quantified, allowing regulatory authorities to identify the effectiveness and associated costs of competing strategies.
The validated WR-CFD model was also used to explore the nature of respiratory aerosol dispersion within G-train saloons resulting from a single seated index patient and the efficacy of non-pharmaceutical interventions such as physical distancing, face coverings and ventilation on reducing COVID-19 IP. The main observations of this analysis include:
-
•The dispersion of respiratory aerosol (quanta) within the ventilated passenger compartment is extremely non-uniform.
-
○The nature of the dispersion is unintuitive, with high aerosol concentration (and hence IP) within the seat row and side of the carriage containing the index patient and up to two seat rows behind the index patient. In contrast, the seat rows ahead of the index patient have relatively low aerosol concentration.
-
○Beyond the specific G-train application, this observation has implications for simpler analysis methods such as the Wells-Riley method (WR) which assume that the space is well mixed, resulting in a uniform quanta distribution. This is clearly inappropriate for complex geometries such as train carriages or situations where there are complex bulk/local airflows. In these situations, the simplified approach may not only grossly underestimate IP, it may as a result fail to correctly assess the impact of mitigation strategies such as physical distancing.
-
○
-
•For long distance rail travel, the average IP is inversely related to the ventilation air change rate.
-
○For an 8-hour exposure, there is an 85% increase in the expected average number of secondary infections if the air exchange rate is decreased from 44 ACH to 14 ACH. Counter intuitively, higher air change rates also significantly increases the maximum and localised IPs of those seated close to the source.
-
○There is also a link between carriage ventilation filtration efficiency of the recirculated air and average IP. If the ventilation filtration efficiency is increased from 20% to 100%, there is an up to 44% reduction in the average number of secondary infections. However, counter intuitively, for those seated in the vicinity of the infected passenger, there is only a small reduction in IP.
-
○
-
•The 2-m physical distancing strategy (reducing capacity from 85 to 14) results in a predicted reduction in average IP of 46% according to the WR-CFD model while the WR model suggests that there would be no reduction in IP.
-
○Furthermore, the WR-CFD model suggests that there would be a 92% reduction in secondary infections while the WR model suggests that there would be an 84% reduction (due only to the reduced occupancy).
-
○Introducing inaccuracies of this type and magnitude can make a difference between accepting or rejecting a potential mitigation strategy.
-
○
-
•Assuming 90% of the passengers correctly wear high efficiency face coverings (with a filtration efficiency of 90%) there is a 95% reduction in the average number of secondary infections compared to the case where 40% of the passengers wear low efficiency face coverings (with a filtration efficiency of 50% for index and 30% for susceptible).
-
○This case is even superior to the seat blocking case with 2-m physical distancing (assuming 84 passengers in 6 saloons), producing approximately 42% fewer secondary infections than the seat blocking case
-
○It is acknowledged that achieving such a high rate of correctly donned high efficiency face coverings is not without its challenges, especially for durations of up to 8 h. Nevertheless, encouraging passengers to correctly wear face coverings at all times while travelling on long distance trains appears to be very effective in reducing secondary infections.
-
○
In addition, the WR-CFD approach is also capable of exploring the impact of vaccination and changing population immunity through appropriate modifications of the IPs. As demonstrated, such applications rely on additional information such as current vaccination rates and vaccine population efficacies.
It is acknowledged that many of the specific findings are generally limited to the Chinese G-trains with their specific geometric arrangements and ventilation characteristics. In particular, with up to 44 ACH, the G-trains have exceptionally high air change rates, more typical of passenger aircraft than passenger trains found in Europe and the UK. For comparison, air change rates in some UK trains are typically about 8 ACH. However, the WR-CFD model can readily be applied to other scenarios, e.g. UK passenger trains, passenger aircraft, cruise and ferry ships and buildings, to allow detailed analysis of mitigation strategies, provided the environmental setup is sufficiently well described.
CRediT authorship contribution statement
Zhaozhi Wang: Conceptualization, Methodology, Software, Formal analysis, Investigation, Visualization, Writing – original draft, Writing – review & editing. Edwin R. Galea: Conceptualization, Funding acquisition, Supervision, Methodology, Writing – review & editing. Angus Grandison: Conceptualization, Methodology, Visualization, Formal analysis, Writing – review & editing. John Ewer: Conceptualization, Funding acquisition, Methodology, Visualization, Writing – review & editing. Fuchen Jia: Conceptualization, Methodology, Formal analysis, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was partially supported by the University of Greenwich’s proof of concept award [Fund Code 14621].
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.ssci.2021.105572.
Appendix A. Supplementary material
The following are the Supplementary data to this article:
References
- A rapid review of the engineering approaches to mitigate the risk of COVID-19 transmission on public transport, National Engineering Policy Centre, https://www.raeng.org.uk/publications/reports/a-rapid-review-of-the-engineering-approaches-to-mi (Accessed on 24th June 2021).
- Anozie, P., 2020. RDG Guidance: Maintenance of On-Train HVAC Modules & Filters during the COVID-19 Pandemic, V1.1, Rail Delivery Group, UK, 26th May, 2020.
- Azimi P., Keshavarz Z., Cedeno Laurent J.G., et al. Estimating the nationwide transmission risk of measles in US schools and impacts of vaccination and supplemental infection control strategies. BMC Infect. Dis. 2020;20 doi: 10.1186/s12879-020-05200-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernal, B.J., Andrews, N., Gower, C., et al., 2021. Effectiveness of COVID-19 vaccines against the B.1.617.2 variant. medRxiv Preprint. Doi: 10.1101/2021.05.22.21257658. [DOI] [PubMed]
- Buonanno G., Stabile L., Morawska L. Estimation of airborne viral emission: quanta emission rate of SARS-CoV-2 for infection risk assessment. Environ. Int. 2020;141:105794. doi: 10.1016/j.envint.2020.105794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buonanno G., Morawska L., Stabile L. Quantitative assessment of the risk of airborne transmission of SARS-CoV-2 infection: prospective and retrospective applications Environment International. Environ. Int. 2020;145:106112. doi: 10.1016/j.envint.2020.106112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burridge, H.C., Fan, S., Jones, R.L., et al., 2021. Predictive and retrospective modelling of airborne infection risk using monitored carbon dioxide. eprint arXiv:2009.02999.
- Covid-19 vaccine surveillance report: Week 19, GOV-8305, May 2021, Public Health England (PHE), UK, 2021.
- Craven B.A., Settles G.S. A computational and experimental investigation of the human thermal plume. J. Fluids Eng. 2006;128(6):1251–1258. doi: 10.1115/1.2353274. [DOI] [Google Scholar]
- Crowe C.T., Sharma M.P., Stock D.E. The particle-source-in cell (PSI-CELL) model for gas-droplet flows. ASME. J. Fluids Eng. 1977;99(2):325–332. doi: 10.1115/1.3448756. [DOI] [Google Scholar]
- Dai H., Zhao B. Association of the infection probability of COVID-19 with ventilation rates in confined spaces. Build. Simul. 2020;13(6):1321–1327. doi: 10.1007/s12273-020-0703-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies A., Thompson K., Giri K., et al. Testing and efficacy of homemade masks: would they protect in an influenza pandemic? Disaster Med Public Health Prep. 2013;7(4):413–418. doi: 10.1017/dmp.2013.43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- European Union Agency for Railways, 2021. Travel safety during COVID-19 for passengers travelling long distance by train and other modes, version 1.4, 2 June 2021. www.era.europa.eu/sites/default/files/events-news/docs/travel_safety_during_covid-19_final_en.pdf. Accessed on 15th June 2021.
- Ewer, J., Jia, F., Grandison, A., et al., 2020. SMARTFIRE V5.1 User Guide and Technical Manual, Fire Safety Engineering Group, University of Greenwich, UK.
- Flynn, I., 2020. Transmission of Covid-19 via Airflow on Trains – Simplified Risk Models v0.4, TECHNICAL LEADERSHIP GROUP C-19 WORKING GROUP, Rail Delivery Group (RDG) UK, meeting on 16th June 2020.
- Foroozesh F., Khoshnevis A.B., Lakzian E. Improvement of the wet steam ejector performance in a refrigeration cycle via changing the ejector geometry by a novel EEC (Entropy generation, Entrainment ratio, and Coefficient of performance) method. Int. J. Refrig. 2020;110:248–261. doi: 10.1016/j.ijrefrig.2019.11.006. [DOI] [Google Scholar]
- Furuya H. Risk of transmission of airborne infection during train commute based on mathematical model. Environ. Health Prev. Med. 2007;12(2):78–83. doi: 10.1007/BF02898153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galea E.R. On the field modelling approach to the simulation of enclosure fires. J. Fire. Prot. Eng. 1989;1(1):11–22. [Google Scholar]
- Gammaitoni L., Nucci M.C. Using a mathematical model to evaluate the efficacy of TB control measures. Emerg. Infect. Dis. 1997;3(3):335–342. doi: 10.3201/eid0303.970310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grandison A.J., Galea E.R., Patel M.K., et al. A suggested procedure for benchmarking fire field models. Int. J. Eng. Perf.-Based Fire Codes. 2006;8(4):132–144. [Google Scholar]
- Gravert, C., Nagl, P., Lang, H.P., et al., 2020. Preliminary Implications of COVID-19 on Long-Distance Traffic of Deutsche Bahn, working paper, https://www.researchgate.net/publication/342353367_Preliminary_Implications_of_COVID-19_on_Long-_Distance_Traffic_of_Deutsche_Bahn.
- Gu X., Ciampa P.D., Nagel B. An automated CFD analysis workflow in overall aircraft design applications. CEAS Aeronaut. J. 2018;9(1):3–13. doi: 10.1007/s13272-017-0264-1. [DOI] [Google Scholar]
- Hansen C.H., Michlmayr D., Gubbels S.M., et al. Assessment of protection against reinfection with SARS-CoV-2 among 4 million PCR-tested individuals in Denmark in 2020: a population-level observational study. Lancet. 2021;397(10280):1204–1212. doi: 10.1016/S0140-6736(21)00575-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hathway E.A., Noakes C.J., Sleigh P.A., Fletcher L.A. CFD simulation of airborne pathogen transport due to human activities. Build. Environ. 2011;46(12):2500–2511. doi: 10.1016/j.buildenv.2011.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoseinzade D., Lakzian E., Hashemian A. A blackbox optimization of volumetric heating rate for reducing the wetness of the steam flow through turbine blades. Energy. 2021;220:119751. doi: 10.1016/j.energy.2020.119751. [DOI] [Google Scholar]
- Hota B., Stein B., Lin M., et al. Estimate of airborne transmission of SARS-CoV-2 using real time tracking of health care workers. medRxiv. 2020 doi: 10.1101/2020.07.15.20154567. [DOI] [Google Scholar]
- http://www.360doc.com/content/16/0903/12/140754_588085660.shtml. Accessed 6th October 2020.
- Hu, M., Wang, J.F., Lin, H., et al., 2020. Transmission risk of SARS-CoV-2 on airplanes and high-speed trains. medRxiv 2020.12.21.20248383, 10.1101/2020.12.21.20248383. [DOI]
- Hu M., Lin H., Wang J., et al. The risk of COVID-19 transmission in train passengers: an epidemiological and modelling study. Clin. Infect. Des. 2021;72(4):604–610. doi: 10.1093/cid/ciaa1057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kampf G., Brüggemann Y., Kaba H.E.J., Steinmann J., Pfaender S., Scheithauer S., Steinmann E. Potential sources, modes of transmission and effectiveness of prevention measures against SARS-CoV-2. J. Hosp. Infect. 2020;106(4):678–697. doi: 10.1016/j.jhin.2020.09.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y., Qian H., Hang J., Chen X., Cheng P., Ling H., Wang S., Liang P., Li J., Xiao S., Wei J., Liu L.i., Cowling B.J., Kang M. Probable airborne transmission of SARS-CoV-2 in a poorly ventilated restaurant. Build. Environ. 2021;196:107788. doi: 10.1016/j.buildenv.2021.107788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim T., Cho J., Kim B.S. The predictions of infection risk of indoor airborne transmission of diseases in high-rise hospitals: tracer gas simulation. Energy Build. 2010;42(8):1172–1181. doi: 10.1016/j.enbuild.2010.02.008. [DOI] [Google Scholar]
- Lin K., Marr L.C. Humidity-dependent decay of viruses, but not bacteria, in aerosols and droplets follows disinfection kinetics. Environ. Sci. Technol. 2020;54(2):1024–1032. doi: 10.1021/acs.est.9b04959. [DOI] [PubMed] [Google Scholar]
- Malki-Epshtein, L., Stoesser, T., Ciric, L., et al., 2020. Report on Scientific advice to TfL on bus driver assault screen modifications due to the Covid-19 pandemic, UCL Department of Civil, Environmental and Geomatic Engineering, London, UK. https://discovery.ucl.ac.uk/id/eprint/10116423.
- Marcus, L.J., et al., 2020. Assessment of Risks of SARS-CoV-2 Transmission During Air Travel and Non-Pharmaceutical Interventions to Reduce Risk, Phase One Report: Gate-to-Gate Travel Onboard Aircraft. Faculty and Scientists at the Harvard T.H. Chan School of Public Health. National Preparedness Leadership Initiative, Cambridge, MA 02238, USA. https://cdn1.sph.harvard.edu/wp-content/uploads/sites/2443/2020/10/HSPH-APHI-Phase-One-Report.pdf.
- Meyerowitz E.A., Richterman A., Gandhi R.T., Sax P.E. Transmission of SARS-CoV-2: a review of viral, host, and environmental factors. Ann. Intern. Med. 2021;174(1):69–79. doi: 10.7326/M20-5008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller S.L., Nazaroff W.W., Jimenez J.L., et al. Transmission of SARS-CoV-2 by inhalation of respiratory. Indoor Air. 2020;31(2):314–323. doi: 10.1111/ina.12751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirzaie M., Lakzian E., Khan A., et al. COVID-19 spread in a classroom equipped with partition – A CFD approach. J. Hazard. Mater. 2021;420 doi: 10.1016/j.jhazmat.2021.126587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morawska L., Milton D.K. It is time to address airborne transmission of coronavirus disease 2019 (COVID-19) Clin. Infect. Dis. 2019;71(9):2311–2313. doi: 10.1093/cid/ciaa939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noakes C.J., Sleigh P.A. Mathematical models for assessing the role of airflow on the risk of airborne infection in hospital wards. J. R. Soc. Interface. 2009;6:S791–S800. doi: 10.1098/rsif.2009.0305.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patankar S. Intertext Books; McGraw Hill, New York: 1980. Numerical Heat Transfer and Fluid Flow. [Google Scholar]
- Peng S., Chen Q., Liu E. The role of computational fluid dynamics tools on investigation of pathogen transmission: prevention and control. Sci. Total Environ. 2020;746:142090. doi: 10.1016/j.scitotenv.2020.142090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prather K.A., Marr L.C., Schooley R.T., et al. Airborne transmission of SARS-CoV-2. Science. 2020;368(6498):1422–1424. doi: 10.1126/science.abc6197. [DOI] [PubMed] [Google Scholar]
- Rencken, G.K., Rutherford, E.K., Ghanta, N., et al., 2021. Patterns of SARS-CoV-2 aerosol spread in typical classrooms. medRxiv 2021.04.26.21256116. Doi: 10.1101/2021.04.26.21256116. [DOI] [PMC free article] [PubMed]
- Riley E.C., Murphy G., Riley R.L. Airborne spread of measles in a suburban elementary school. Am. J. Epidemiol. 1978;107(5):421–432. doi: 10.1093/oxfordjournals.aje.a112560. [DOI] [PubMed] [Google Scholar]
- Ronchi E., Lovreglio R. EXPOSED: an occupant exposure model for confined spaces to retrofit crowd models during a pandemic. Saf. Sci. 2020;130:104834. doi: 10.1016/j.ssci.2020.104834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossettie S., Perry C., Pourghaed M., Zumwalt M. Effectiveness of manufactured surgical masks, respirators, and home-made masks in prevention of respiratory infection due to airborne microorganisms. Southwest Respir. Crit. Care Chronicles. 2020;8(34):11–26. doi: 10.12746/swrccc.v8i34.675. [DOI] [Google Scholar]
- Silcott, D., Kinahan, S., Santarpia, J., et al., 2020. TRANSCOM/AMC Commercial Aircraft Cabin Aerosol Dispersion Tests, Submitted to: United States Transportation Command (USTRANSCOM) & Air Mobility Command (AMC), Scott Air Force Base, Illinois, US, https://www.usTRANSCOM.mil/cmd/docs/TRANSCOM%20Report%20Final.pdf Accessed 18 June 2021.
- Stephens, B., 2012. HVAC filtration and the Wells-Riley approach to assessing risks of infectious airborne diseases, NAFA Foundation Report, The National Air Filtration Association (NAFA) Foundation, Virginia Beach, VA 23462.
- Thabet S., Thabit T.H. CFD Simulation of the air flow around a car model (ahmed body) Int. J. Sci. Res. Publ. 2018;8:517–525. doi: 10.29322/IJSRP.8.7.2018.p7979. [DOI] [Google Scholar]
- Thermal energy created by human body, Engeersedge, https://www.engineersedge.com/heat_transfer/thermal_energy_created_13777.htm. Accessed 31st December 2020.
- To G.N.S., Chao C.Y.H. Review and comparison between the Wells–Riley and dose-response approaches to risk assessment of infectious respiratory diseases. Indoor Air. 2010;20(1):2–16. doi: 10.1111/j.1600-0668.2009.00621.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vuorinen V., Aarnio M., Alava M., Alopaeus V., Atanasova N., Auvinen M., Balasubramanian N., Bordbar H., Erästö P., Grande R., Hayward N., Hellsten A., Hostikka S., Hokkanen J., Kaario O., Karvinen A., Kivistö I., Korhonen M., Kosonen R., Kuusela J., Lestinen S., Laurila E., Nieminen H.J., Peltonen P., Pokki J., Puisto A., Råback P., Salmenjoki H., Sironen T., Österberg M. Modelling aerosol transport and virus exposure with numerical simulations in relation to SARS-CoV-2 transmission by inhalation indoors. Saf. Sci. 2020;130:104866. doi: 10.1016/j.ssci.2020.104866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z., Jia F., Galea E.R., Patel M.K., Ewer J. Simulating one of the CIB W14 round robin test cases using the SMARTFIRE fire field model. Fire Saf. J. 2001;36(7):661–677. doi: 10.1016/S0379-7112(01)00018-2. [DOI] [Google Scholar]
- Wang Z., Jia F., Galea E.R., Choi J.-H. A forensic analysis of a fatal fire in an indoor shooting range using coupled fire and evacuation modelling tools. Fire Saf. J. 2017;91:892–900. doi: 10.1016/j.firesaf.2017.03.029. [DOI] [Google Scholar]
- Wang Z., Galea E.R., Grandison A., et al. Inflight transmission of COVID-19 based on experimental aerosol dispersion data. J. Travel Med. 2021;28(4) doi: 10.1093/jtm/taab023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H., Lin M., Chen Y. Performance evaluation of air distribution systems in three different China railway high-speed train cabins using numerical simulation. Build. Simul. 2014;7(6):629–638. [Google Scholar]
- Watanabe T., Bartrand T.A., Weir M.H., et al. Development of a dose-response model for SARS coronavirus. Risk Anal. 2010;30(7):1129–1138. doi: 10.1111/j.1539-6924.2010.01427.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells W.F. Cambridge University Press; Cambridge MA: 1955. Airborne Contagion and Air Hygiene; pp. 117–122. [Google Scholar]
- World Health Organization (WHO), WHO Coronavirus (COVID-19) Dashboard | WHO Coronavirus (COVID-19) Dashboard With Vaccination Data. Accessed on 24 June 2021.
- Yan Y., Li X., Shang Y., Tu J. Evaluation of airborne disease infection risks in an airliner cabin using the Lagrangian-based Wells-Riley approach. Build. Environ. 2017;121:79–92. doi: 10.1016/j.buildenv.2017.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang L., Li M., Li X., et al. The effects of diffuser type on thermal flow and contaminant transport in high-speed train (HST) cabins – a numerical study. Int. J. Vent. 2018;17(1):48–62. doi: 10.1080/14733315.2017.1351736. [DOI] [Google Scholar]
- Yazdani S., Lakzian E. Numerical simulation and passive control of condensing flow through turbine blade by NVD Method Using Eulerian-Lagrangian Model. Comput. Math. Appl. 2020;80(1):140–160. doi: 10.1016/j.camwa.2020.03.007. [DOI] [Google Scholar]
- You R., Lin C.-H., Wei D., Chen Q. Evaluating the commercial airliner cabin environment with different air distribution systems. Indoor Air. 2019;29(5):840–853. doi: 10.1111/ina.v29.510.1111/ina.12578. [DOI] [PubMed] [Google Scholar]
- Youtube video clip. https://www.youtube.com/watch?v=625Yh_LO0YY. Accessed 31st December 2020.
- Zemouri C., Awad S.F., Volgenant C.M.C., Crielaard W., Laheij A.M.G.A., de Soet J.J. Modeling of the transmission of coronaviruses, measles virus, influenza virus, mycobacterium tuberculosis, and legionella pneumophila in dental clinics. J. Dent. Res. 2020;99(10):1192–1198. doi: 10.1177/0022034520940288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z., Han T., Yoo K.H., Capecelatro J., Boehman A.L., Maki K. Disease transmission through expiratory aerosols on an urban bus. Phys. Fluids. 2021;33(1):015116. doi: 10.1063/5.0037452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L., Li Y. Dispersion of coughed droplets in a fully-occupied high-speed rail cabin. Build. Environ. 2012;47:58–66. doi: 10.1016/j.buildenv.2011.03.015. [DOI] [Google Scholar]
- Zhu S., Srebric J., Spengler J.D., et al. An advanced numerical model for the assessment of airborne transmission of influenza in bus microenvironments. Build. Environ. 2012;47:67–75. doi: 10.1016/j.buildenv.2011.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.