Covid-19 recognition from cough sounds using lightweight separable-quadratic convolutional network

Abstract

Automatic classification of cough data can play a vital role in early detection of Covid-19. Lots of Covid-19 symptoms are somehow related to the human respiratory system, which affect sound production organs. As a result, anomalies in cough sound is expected to be discovered in Covid-19 patients as a sign of infection. This drives the research towards detection of potential Covid-19 cases with inspecting cough sound. While there are several well-performing deep networks, which are capable of classifying sound with a high accuracy, they are not suitable for using in early detection of Covid-19 as they are huge and power/memory hungry. Actually, cough recognition algorithms need to be implemented in hand-held or wearable devices in order to generate early Covid-19 warning without the need to refer individuals to health centers. Therefore, accurate and at the same time lightweight classifiers are needed, in practice. So, there is a need to either compress the complicated models or design light-weight models from the beginning which are suitable for implementation on embedded devices. In this paper, we follow the second approach. We investigate a new lightweight deep learning model to distinguish Covid and Non-Covid cough data. This model not only achieves the state of the art on the well-known and publicly available Virufy dataset, but also is shown to be a good candidate for implementation in low-power devices suitable for hand-held applications.

1. Introduction

[1] Millions of Covid-19 cases caused by the corona virus have been confirmed since beginning of this pandemic. Infected people are identified in more than 200 countries around the world, at the time of writing this article. The Covid-19 epidemic has a wide range of effects on the population, from asymptomatic disease to sever life-threatening medical conditions.

According to the World Health Organization (WHO), dry cough, feeling of pressure at chest, fever, fatigue, confusion, loss of appetite, and breath shortness are the main symptoms of Covid-19. Heavy droplets that contain Covid-19 virus are spread in the environment, when an infected person sneezes or coughs. Even breathing and talking to someone close to an corona-positive person, can cause infection.

Having an easy-to-use tool for accurate and fast screening and detecting the virus and making early warnings is critical to slow down the epidemic spread. An automated approach to detecting and monitoring the presence of Covid-19 or its symptoms can be developed using deep learning models.

Deep learning models have shown significant success in different recognition tasks, especially in image and speech processing domains. Moreover, they have been recently successfully in use in different medical applications. For example, deep learning methods have been successfully utilized for post-stroke pneumonia prediction [2]. Deep CNNs have also been used for segmentation and classification of mammograms [3] and measurement of blood pressure [4].

Thus there is a great potential for using deep models in cough recognition for Covid-19 detection. Authors in [5] were among the first ones to leverage learning methods in Covid-19 related applications. CNN based analysis of X-ray or CT images of lungs for have been the main deep learning tool for prediction of Covid-19 [6], [7], [8], [9]. Also, it is shown in [10] that learning approaches based on speech and other audio modalities have many possible applications in medical applications.

Sound has been in use as a health indicator for many years. Physicians have used stethoscopes to detect and recognize abnormalities in body by listening to sounds from different parts of an individual, such as heart or lung. Deep learning, has also achieved notable success in automatic audio recognition and interpretation with application to various diseases such as asthma [11], and wheezing [12] levering sound data wearable devices or smart phones. There are many open source datasets like AudioSet [13] and Freesound [14] which have been gathered to speed up research in this domain.

Cough sound is amongst the most important health related sounds and can be used as an indicator of many respiratory diseases. Triaging patients based on their cough sounds can be interesting for hospitals and health-care systems as it is pretty simple and significantly reduces burden on the health centers.

Disease detection based on analyzing cough sounds has been in use for several years. For example, authors in [15], [16] detected tuberculosis (TB) from cough sounds, accurately, and Larson et al. [17] could track the recovery process of TB patients solely using cough detection. Similar efforts but for detection of Covid-19 have recently attracted a significant attention which are reviewed in Section 2.

The first step before cough classification is cough detection, in which cough sound is distinguished from other audio signals like breathing or speech. Although cough detection is not the subject of this work, we review some important cough detection algorithms. In [18], Mel Frequency Cepstral Coefficients (MFCCs) are used as features to detect coughs. Non-negative Matrix Factorization (NMF) is used by the authors of [19] for cough detection, to improve the results obtained with MFCC. Short Time Fourier Transform (STFT) and MFCC are used in [20] as the input features to convolutional Neural Networks (CNNs), and Long-Short Term Memory (LSTM) networks to further improve cough detection performance. As a similar effort, spectrogram feature and CNN architecture are combined to detect cough by the authors of [21]. Cough detection using MFCC features and random forest classifier is also explored in [22].

Covid-19 alters the cough sound in a unique way, which resembles the application of cough sound recognition in Covid-19 detection. The work by He et al. confirms that Covid-19 makes an undeniable effect on the respiratory system [23], [24]. Actually, the respiratory system is the main organ to produce cough sounds, as the air flows from lungs to the mouth and nasal cavities to make cough sounds. As a result, respiratory diseases will affect the cough sound. As a familiar example, The reader may have observed the of flu on changing the sound of coughing. Following this intuition, the primary focus of this paper is on Covid-19 classification based on cough sounds.

Cough recognition from cough sounds is not as straightforward as it seems. Unfortunately, a lot of bacterial or viral respiratory infections or even some non-respiratory illnesses may result in coughs and it is hard to distinguish Covid-19 solely from cough [25], [26], [27].

Actually, an untrained human may not distinguish coughs caused by COVID-19 from coughs caused by other diseases. However, an experienced physician can discriminate these two types of cough. This is possible because the nature and location of infection caused by Covid-19 and the way Covid-19 affects the respiratory system are different from other diseases, leading to completely distinct cough sounds [24]. Actually, CT scan images show that Covid-19 infection in lungs has a higher amount of peripheral distribution, ground-glass opacity, and vascular thickening [28].

Imran et al. [24] perform an initial study on Covid-19 recognition based on cough data. They train a combination of deep and shallow models on the cough data under examination. Authors of [29] investigate the same problem, where a binary prediction model is trained on unconstrained worldwide coughs and breathing sounds.

In [30] speech recordings from Covid-19 patients are processed to automatically categorize the patients. Another dataset comprised of breath sound, cough sound, and voice has been released to integrate voice into recognition of Covid-19 [31].

ResNet-18 [32] pre-trained on ImageNet is used as the backbone network for Covid-19 recognition, in [33], The authors also add two fully connected layers to perform transfer learning and use the network for cough recognition.

The main contribution of this paper is employing a unique combination of quadratic kernels with the idea of separable kernels in deep neural networks to simultaneously boost the recognition accuracy and keep the computational costs at a low level. We construct a new convolution layer with this idea a use it in a lightweight structure to reveal its efficiency.

The rest of the paper is organized in the following way. Cough features, quadratic-form kernels, and kernel separation are described in Section 2. The proposed work is discussed in Section 3 and experimental results are presented in Section 4. The paper is concluded with Section 5.

2. Materials and methods

2.1. Cough Features

Although the raw cough sound could be fed to a deep neural network to be classified, as being either Covid or Non-Covid, employing hand-designed feature extraction may help the overall recognition rate. There are different types of information which could be extracted from raw cough sounds.

In the literature, the features of log energy, zero-crossing rate, kurtosis, spectral centroid and spectral roll-off are frequently extracted from cough sounds. The advantage of using these features is to extract meaningful information from complicated cough sound which usually results in a better classification of them.

Moreover, using features like these instead of raw cough signals enables the designers to achieve reasonable recognition results with relatively simpler ML models. Especially, in case of CNNs first few layers automatically and implicitly extract low level features. So, sophisticated hand-crafted features can eliminate the need to these layers (low level feature extractors), hence reducing the total number of layers. Although, using the above features might not be well compatible with the spirit of deep learning (end-to-end classification), they are widely used for the above mentioned advantages.

However, in this study only MFCCs were preferred. As MFCCs are comprehensive features converting 1D cough signal into 2D temporal-frequency signal and have shown a great success in audio and speech processing tasks, we choose them as the input features to our lightweight deep model. Naturally, combination of several of these features as early fusion could improve the recognition results in expense of more computational burden. As we aim to use the recognition model on embedded hand-held devices, and want to explore the potential of quadratic kernels in cough detection as a proof of concept, we only use MFCC.

2.2. Quadratic-form kernels

The core idea behind the network layer based on the quadratic form expansion [34] is that it generalizes the linear convolution by taking into account the cross correlation between the input elements within the receptive field of the layer kernel. In other words, in addition to ordinary convolution between the input and the weight, a second-order convolution between the input and an expanded weight tensor is computed which improves the final performance in terms of classification accuracy. The layer based on quadratic form expansion is therefore expressed as:

$${\mathbf{Y}}_{\mathrm{Q}}={\mathbf{X}}^H⊛{\mathbf{W}}_{Q_2}⊛\mathbf{X}+\mathbf{X}⊛{\mathbf{W}}_{{\mathbf{Q}}_{\mathbf{1}}}+{\mathbf{b}}_{\mathbf{Q}}$$ (1)

in which $\mathbf{X}\in {\mathbb{R}}^{H\times W\times C}$ is the input to the layer, ${\mathbf{W}}_{Q_1}\in {\mathbb{R}}^{N\times d\times d\times C}$ and ${\mathbf{W}}_{Q_2}\in {\mathbb{R}}^{N\times d^2\times d^2\times C}$ are the ordinary and quadratic weight tensors, in which N is the number of filters in the convolutional layer, d is the filter height (width), C is the input depth, and H and W are the height and width of the input to the layer, respectively. ${\mathbf{b}}_Q\in {\mathbb{R}}^N$ is the bias vector, and ${()}^H$ is the Hermitian operator.

Eq. (1) is the same as regular convolution, except for the added quadratic term ${\mathbf{X}}^H⊛{\mathbf{W}}_{Q_2}⊛\mathbf{X}$. This quadratic term improves the recognition accuracy, as will be shown in the Section 4, mainly due to modeling second-order dependencies of the input features.

For the regular part of the convolution, i. e, the linear convolution part in Eq. (1), we compute several products like {$x_{\mathit{ij}}*w_{{Q_1}_{\mathit{ij}}},\forall i,j\in 1,2,\dots ,d$}. In other words, we only compute the first order products, in regular convolution. This is while in quadratic kernel convolution part in Eq. (1), we also compute terms like {$x_{\mathit{ij}}*w_{{Q_2}_{\mathit{ij}}}*w_{{Q_2}_{\mathit{km}}}*x_{\mathit{kl}},\forall i,j,k,l\in 1,2,\dots ,d^2$}, i. e. quadratic terms. This increases the computational cost from proportional to $d^2$ to something proportional to $d^4$.

As it will be shown in the next part, applying kernel separation on quadratic kernel reduces its computational complexity from $O(d^4)$ to $O(d^2)$. This is because kernel separation can reduce the time complexity of a convolution with power $1/2$ in terms of kernel size.

2.3. Kernel separation

Employing quadratic kernels to add more nonlinearity to the CNN and account for cross correlation between different input pixels at different network layers comes with more computational cost. As stated in previous part, the computational cost of convolutional layers with quadratic kernel would be proportional to $d^4$, where d is the height (width) of convolution kernel. This is while in regular convolution, the computational cost is proportional to $d^2$. To mitigate this shortcoming, we use kernel separation to reduce computational cost and make it proportional to $d^2$.

The complexity of convolving a 3D input volume with size $H\times W\times C$ (where C is the depth of the volume) with N 3D filters of size $d\times d\times C$ is $O({\mathit{CNd}}^2\mathit{HW})$ [35]. Approximation of such convolution filters with separable filters is proposed in [36]. We can think of a 4D convolutional filter $\mathrm{\Omega }\in {\mathbb{R}}^{N\times d\times d\times C}$ for a convolutional layer as a combination of N 3D filters as {${\mathrm{\Omega }}_n,n=1,2,\dots N$} which can be decomposed as:

$${\widehat{\mathrm{\Omega }}}_n^c={\displaystyle \sum _{k=1}^K}{\mathbb{H}}_n^k{({\mathbb{V}}_k^c)}^T$$ (2)

where K controls the rank of horizontal filter $\mathbb{H}\in {\mathbb{R}}^{N\times 1\times d\times K}$ and vertical filter $\mathbb{V}\in {\mathbb{R}}^{K\times d\times 1\times C}$ and ${()}^T$ denotes transposition.

The computational gain for this approximation is that overall complexity of a convolutional layer decreases from those mentioned earlier for regular convolution, i. e. from $O({\mathit{CNd}}^2\mathit{HW})$, to $O(\mathit{dK}(N+C)\mathit{HW})$ [35]. This makes the time complexity proportional to d rather than $d^2$. A direct result is that if the original complexity was $O(d^4)$ (as the case for the quadratic convolution), the complexity after kernel separation would be $O(d^2)$. More exactly, if the original complexity was $O({\mathit{CNd}}^4\mathit{HW})$, the complexity after kernel separation would be $O(d^{2}K(N+C)\mathit{HW})$, which is obtained by replacing d with $d^2$ in the above mentioned terms for computational complexity.

3. Proposed lightweight model for cough recognition

3.1. Proposed separable quadratic layer

The concept of quadratic convolution has not yet been applied to cough detection or recognition problem. We are the first who use the method in computationally constraint environments in order to boost the recognition accuracy of cough recognition. Considering cross correlation between pixels of each 2D feature map input to the convolutional layer, we account for covariance of the input map values to boost the recognition performance. Additionally, we use kernel separation to reduce computational costs, making the cough recognition system suitable for embedded applications.

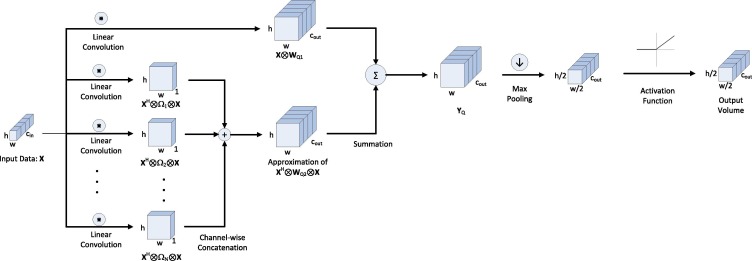
The flow diagram of the proposed layer is shown in Fig. 1 . The 3D data volume as the input to each network layer is fed to both regular and quadratic-form convolution. Regular max pooling with $2\times 2$ filters and stride = 2, and ReLU activation are then applied to the output. Note that the placement of pooling and activation are changed in the proposed pipeline to further reduce computations. Actually, it is evident that the result of first applying max pooling with $2\times 2$ filters and stride = 2 and then applying ReLU is equivalent to first applying ReLU and then applying the aforementioned max pooling. However, the former needs less computational resources, as we need 75 percent less element-wise ReLU computations compared to the latter case.

Fig. 1.

Flow diagram of the proposed cough detection quadratic layer: MFCCs are fed as the input to the first layer of this kind. The approximate separate kernels are applied to the input, and the resulting feature maps are concatenated. Afterwards, linear and quadratic convolutions are summed together. Max pooling is used before and activation function to further reduce computations.

3.2. Network structure

Since this research aims at developing a lightweight model for cough recognition, we use a simple deep structure like to LeNet-1 [37]. Indeed, more complex models dominate the employed model in terms of final classification performance. However, this is quite enough for a proof of concept, and the proposed layer could be promptly used in more complex networks with no headache. The network has two convolutional layers followed by a single fully connected layer, with each convolutional layers being a combination of regular and quadratic convolution filters and the quadratic convolution being implemented as separable kernels.

For the CNN model, we used a simple structure for cough recognition from the beginning. The choice of this structure instead of a more complex one not only makes the design proper for computationally constrained applications, but also lowers the chance of overfitting. To battle overfitting in the training loop, we used dropout with 50% rate to make the network more robust to overfitting the training data. Moreover, we used ${\ell }_1$ regularization in loss function with penalty parameter $\lambda$=0.02 to avoid the weights memorize the noise in training cough samples. Dropout rate, regularization penalty value, and other hyper-parameters are all selected by 5-fold cross validation.

Additionally, early stopping was employed to monitor the classification error on validation set and stop training when the error does not decrease over validation set for five consecutive epochs.

Also, to deal with such a small-sized dataset we employed data augmentation on training set. To this end, we used audiomentations Python library available on Github1 . Original cough sounds were augmented with adding Gaussian noise with two different signal to noise ratio (SNR) values, shifting the waveforms temporally to the left and to the right by at most 0.5 s, and changing the pitch randomly by at most 20% of the maximum frequency of the raw cough signal. We also added an augmentation in frequency-temporal domain by adding time and frequency masks to the spectrogram, i. e., zeroing out a small vertical and a small horizontal bar of the spectrogram with random position.

The proposed layer and the resulting network are implemented in PyTorch v1.4.0. The code for this paper will also be made freely available, upon publication of the paper. Dropout is also used to prevent over-fitting. As mentioned earlier, max-pooling is placed before applying activation function to reduce computations.

Fig. 2 shows the resulting feature maps in different network layers. The network is comprised of two proposed separable quadratic convolutional layers, and a fully-connected layer with two neurons. The height and width of activations after the pooling operation in each proposed layer is halved. The dimensions of different activations are mentioned shown beside the corresponding dimensions.

Fig. 2.

Feature maps of the full network comprised of two separable quadratic layers. MFCCs are fed as the input to the first layer and the classification results appear at the feature map of the fully-connected layer.

4. Experiments

4.1. Dataset

The proposed model is evaluated on Virufy dataset [38]. Virufy is a small-sized dataset and is among the benchmarks for Covid-19 cough detection and recognition.

There are 121 single cough sounds in Virufy, 73 of which have a negative PCR test and 48 are reported to have positive PCR test result. Each sample is approximately 1 s long. 70%, 15%, and 15% split for training, validation, and test sets, respectively, corresponds to 51,11,11, negative cough samples and 34, 7, 7, positive cough samples for training, validation, and test sets, respectively.

Since the dataset is small, a single test set may cause a huge bias in performance prediction of the proposed model. Actually the small randomly selected test set may contain very hard or very easy cough samples (a hard sample means a sample which is very hard to classify because it is not very similar to other samples of the same class.

Similarly, an easy sample means a sample which is very easy to classify because it is very similar to other samples of the same class). So, to obtain a fair assessment of the proposed method, we use the method of repeated random split and randomly split the whole dataset 4 times. Each time we did a standard 5-fold cross validation and tuned the hyper-parameters and computed true positive, true negative, false positive and false negative over the test set. Averaging the above values for 4 rounds gave us the mean true positive, mean true negative, mean false positive, and mean false negative.

Then we constructed the confusion matrix by these mean values and normalized them column-wise to show the normalized confusion matrix.

To ensure the balance between Covid and Non-Covid cough samples in training, test and validation sets, we used stratified sampling by employing StratifiedShuffleSplit function from Python sklearn library.

For our evaluations, the accuracy of the proposed method against the baseline algorithms is evaluated based on five popular metrics: accuracy, recall, precision, specificity, and F1-score.

4.2. Data pre-processing

The 1D input cough samples are converted to a 2D MFCCs before being fed to the lightweight network. Each input cough waveform is segmented into 30 ms windows which have an overlap of 10 ms.

The selected values for window width and window overlap are widely used in the literature for cough, sound, and speech recognition applications. The choice is mainly based on the work of Paliwal et al. [39], who showed that a window size of 15–35 ms is optimum in speech recognition tasks. The overlap is usually taken something between 30% to 60% of the window size. The same parameters are also used in cough sound recognition applications, like in [40], in breath and snore sound recognition like in [41], and sound source separation like in [42].

However, to better assess the effect of window size we added four pairs of [window size, window overlap] = [[20,6], [25], [8], [30], [10], [35], [12]] milliseconds to the cross-validation loop for selection of best hyper-parameters based on validation accuracy. The accuracy of using pairs [30], [10] was the same as that of [35], [12] but was about 2.5% and 4.5% better than the pairs [25], [8], [20], [6], respectively.

Then, Mel-frequency cepstral coefficients (MFCCs) are extracted from samples of each window. Since the configuration is aimed to be used in computationally constrained environments, only 20 cepstral coefficients are kept at each window. This is while more audio processing methods leveraging MFCC use 40 or even more coefficients to boost the performance, e. g., [43], [44]. However, it is believed that 15 cepstral coefficients is enough for preserving the essential information in the raw waveform and increasing the number beyond this will improve the performance marginally. This is also confirmed in our experiments.

The resulting single channel 2D MFCC $\in {\mathbb{R}}^{N_{\mathrm{MFCC}}\times N_{\mathrm{windows}}}$ is finally normalized using Z-score, where $N_{\mathrm{MFCC}}$ is the number of MFCC coefficients and $N_{\mathrm{windows}}$ is the number of hamming windows over the raw cough waveform.

4.3. Hyper-parameters

We use 100 epochs in our simulations, and employ early-stopping on validation data to avoid over-fitting. The mini-batch size is set to 10, and the kernel size for the ordinary convolution is set to $3\times 3$. This implies a $9\times 9$ kernel for the quadratic convolution, before applying idea of separable kernels.

Padding size, stride, and dilation are equal to unity. The number of filters in convolutional layers are 20, and the fully connected layers has only 2 neurons corresponding to the number of classes. Drop-out with 50% rate is also used to further prevent over-fitting. Adam optimizer with learning rate equal to 0.01 is used for network training.

The hyper-parameters of the network are chosen from a dictionary of possible values by means of 5-fold cross validation. For each hyper-parameter we take some potential values. Then, we split the training set randomly into 5 subsets, and take one as validation and the others as the new training set. We train models with those potential hyper-parameters over the new training set and compute the accuracy over the validation set.

Each combination of hyper-parameters (each model) results in a validation accuracy. Then we select another fold as validation and the other folds as the new training set and repeat the above procedure to compute validation accuracy for each combination of hyper-parameters.

After 5 times, each fold has been used as the validation set once. Assuming N possible combinations of model hyper-parameters, we reach to $5\times N$ accuracy values. Taking the average of the values over folds we reach to N mean accuracy values. We select the combinations of hyper-parameters which result in the highest mean accuracy.

Actually, an exhaustive grid search selects the best hyper-parameters and at the same time the performance of the model on unseen samples is predicted.

A nested cross validation has been also used for accuracy prediction. Nested cross validation has the added benefit of reducing the bias in prediction of performance, since it uses separate validation set (validation set which is not used in the inner standard cross validation) for computing accuracy. However, as the results were not different with those of the standard cross validation, it was not used in our experiments.

The resulting hyper-parameters of the above mentioned procedure for the proposed and compared conventional classifiers are given in Sections 3.2, 4.5.3, respectively.

4.4. Evaluation metrics

In this section, the evaluation metrics which are used to quantify the efficiency of the proposed approach are introduced. Confusion matrix as well as accuracy, precision (class-wise and macro average), recall, specification, and F1-Score are employed. The four last metrics are computed class-wise using macro averaging.

In the following true positive (TP) refers to samples for which both actual label and model prediction are positive (Covid-19 case). True negative (TN) refers to samples for which both actual label and model prediction are negative (Non-Covid-19 case). False positive (FP) outcomes are those which are erroneously predicted by the model to be positive (the actual label is negative). Finally, False negative (FN) outcomes are those that are erroneously predicted by the model to be negative (the actual label is positive).

• •Confusion matrix: It represents all TP, TN, FP, and FN values as a single $2\times 2$ matrix. To be more illustrative, it can show the normalized values of TP, TN, FP, and FN.
• •
  Accuracy: It is the ratio of correct predictions to the total number of predictions

  $$\mathrm{Accuracy}=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}$$ (3)
• •
  Recall (Sensitivity): It is the fraction of Covid-19 samples which are successfully retrieved by the model

  $$\mathrm{Recall}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}$$ (4)
• •
  Specificity: It is the fraction of Non-Covid-19 samples which are successfully retrieved by the model

  $$\mathrm{Specificity}=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}}$$ (5)
• •
  Precision: It is the fraction of correctly predicted Covid-19 samples to the total number of samples which are predicted as being Covid-19 by the model

  $$\mathrm{Precision}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}$$ (6)
• •
  F1-Score: It shows the harmonic mean of precision and recall values

  $$\mathrm{F}1-\mathrm{Score}=2\times \frac{\mathrm{Recall}\times \mathrm{Precision}}{\mathrm{Recall}+\mathrm{Precision}}$$ (7)

4.5. Experimental results

4.5.1. Covid/non-covid classification

Fig. 3 shows the accuracy versus training epochs on training and validation sets for the network composed of the proposed separable quadratic convolutional layers. As could be inferred from Fig. 3 the proposed method convergence to a high accuracy on both training and validation subsets.

Fig. 3.

Accuracy curves on training and validation sets, over Virufy dataset.

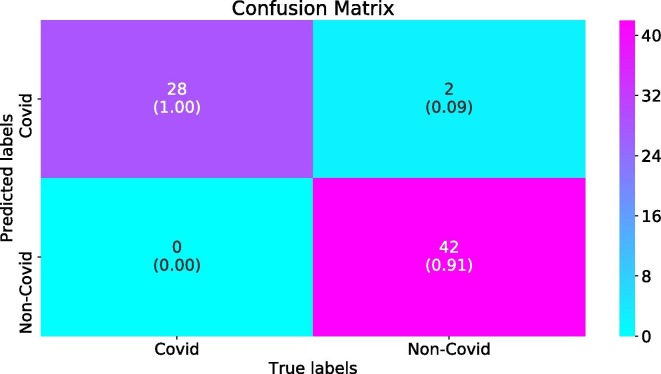
Fig. 4, Fig. 5 show the confusion matrices for the regular model (having regular convolutional layers) and the proposed model over the test set, respectively. As shown, the values of the diagonal elements in the confusion matrix for the proposed method are higher and the off-diagonal entries are less. This roughly implies the superiority of the proposed method.

Fig. 4.

Confusion matrix for the LeNet-1 with regular convolutional layers, over test set of Virufy dataset.

Fig. 5.

Confusion matrix for the LeNet-1 with proposed separable quadratic convolutional layers, over test set of Virufy dataset.

Since the dataset is small, we used repeated train/test split to achieve the fairest assessment of the current work and comparison to results of the state-of-the-art. This repeated splitting is common in applications with few data samples.

Actually, we repeated train/test four times and averaged over the TP, TN, FP, and FN results. There are 11 Non-Covid and 7 Covid (totally 18) test samples. However after this repeated splitting four times, we actually have 11$\times$4 = 44 Non-Covid and 7$\times$4 = 28 Covid (totally 72) test samples. The obtained numbers for TP, TN, FP, and FN are given in confusion matrices Fig. 4, Fig. 5 (the normalized values are given inside parenthesis).

Table 1 shows the precision, recall, and F-score of the proposed model on Virufy dataset for both regular and quadratic separable convolution. As depicted, the network comprised of the proposed layer outperforms the network with regular convolutions in terms of all shown evaluation metrics.

Table 1.

Performance comparison of the proposed with ordinary convolutional layer over test set of Virufy dataset.

Method	Accuracy	Recall(Sensitivity)	Specificity	Precision	F1-score
Ordinary	95.0	90.0	100.0	100.0	94.7
Separable quadratic	97.5	95.2	100.0	100.0	97.6

4.5.2. Subject dependency of the model

Generally, K-fold cross validation could be employed to assess the robustness of a ML algorithm. 5-fold cross validation is used through the whole experiments to determine model hyper-parameters, and according to our experiments, the variance between accuracy values obtained from different folds was relatively low.

The special case of K-fold cross validation for which the number of folds is equal to the number of training samples (Leave-one out cross validation) or LOOCV also gives an illustration of model robustness. Generally LOOCV is the most computation intensive type of cross validation, but in the case of a small dataset, like that in our application, the computational burden of LOOCV is not annoying.

Each fold in LOOCV corresponds to a subject, hence showing subject dependency of the model. After performing LOOCV on Virufy dataset, mean and standard deviation of accuracy over single samples of validation set are 95.5% and 0.2%, respectively. So, according to the experiments of LOOCV the variance of the proposed method is relatively low, suggesting a good robustness to different subjects.

Additionally, to overcome the bias in prediction of performance of the model on test set a nested cross validation could be employed in which firstly the training set is divided into training and validation sets, and cross validation is applied on the new training set only and validated on validation set. So, there is a nested loop in which the outer loop divides the training set into a smaller training set and a validation set, in each iteration, and the inner loop does a normal cross validation on the smaller training set (which is again divided into new training and validation sets). As the results of the nested cross validation and the normal cross validation were not different, we used standard cross validation in decision for early stopping of the training.

4.5.3. Comparison with conventional classifiers

To compare the performance of the proposed approach with those of conventional classifiers, the MFCC features are vectorized and fed to SVM (with linear and RBF kernel), random forest, kNN, MLP, and logistic regression classifiers and the results are given in Table 2 .

Table 2.

Performance comparison of the proposed with conventional classifiers with MFCC features, over Virufy dataset.

Classifier	Accuracy
KNN	78.4
Linear SVM	89.8
RBF SVM	93.2
Random Forest	76.1
MLP	84.1
Logistic Regression	80.7
Separable quadratic	97.5

As Table 2 shows the conventional classifiers show different levels of performance. Although SVM with RBF kernel has the best accuracy among the compared conventional classifiers, it does not outperform the proposed separable quadratic network. The hyper-parameters of these classifiers are also determined with 5-fold cross validation. A dictionary of hyper-parameters for these classifiers are used and 5-fold cross validation is used to select the ones with the best resulting average accuracy over validation set on different folds.

For kNN the values of k = 1, k = 3, k = 5, and k = 7 were used as possible number of neighbors. After cross validation k = 3 resulted in best accuracy.

For linear kernel SVM, the possible values of penalty (C) are considered to be 0.01, 0.1, 1, 10, and 100, for which C = 10 resulted in the best accuracy.

For SVM with RBF kernel, the possible values of penalty (C) are selected from of C = 0.01, 0.1, 1, 10, 100 and the parameter of the exponential kernel ($\gamma$) is set to its default value in Python sklearn library, which is $\gamma =\frac{1}{\mathit{numberoffeatures}\times \mathit{var}}$ where the $\mathit{numberoffeatures}$ is equivalent to the product of $N_{\mathit{MFCC}}$ by $N_{\mathit{windows}}$ and var denotes the variance of the training samples. Again, C = 10 resulted in the best accuracy for RBF kernel SVM.

For random forest, the number of trees in the forest is selected from the set 10, 50, 100, 200, and 100 resulted in the best accuracy.

For ANN, we applied a two layer MLP to the dataset with $N_{\mathit{windows}}\times N_{\mathit{MFCC}}$ input layer and a hidden layer of the same size with tangent hyperbolic activation along with an output softmax layer. The regularization parameter ($\alpha$) was selected from the set 0.001,0.01,0.1,1 for which 0.01 performed the best.

Finally, for the logistic regression the penalty parameter for the default ${\ell }_2$ norm regularization is chosen from the values 0.01, 0.1, 1, 10, for which 0.1 performed the best.

These conventional classifiers with tuned hyper-parameters are then trained over the whole training set and tested over the test set with repeated splitting.

The reason why a CNN is used for classification, even the dataset is small, is that the input features to the network are in the form of images (spectrograms). So, an ANN would need to extremely higher number of parameters than a CNN which uses weight sharing. For example at the input layer it needs $N_{\mathit{windows}}\times N_{\mathit{MFCC}}$. This also holds for other conventional classifiers. Conversion of spectrograms to 1D vectors suitable to be fed to SVM or other conventional classifiers will result in some sort of curse of dimensionality (i. e. few number of training samples with huge number of features), which degrades the generalization capability of the classifier.

Moreover, highly non-linear behavior of Covid/Non-Covid classification problem could be better dealt with the nonlinear quadratic kernel and the non-linear ReLU activation. We think this is also the reason why SVM with RBF kernel outperforms other conventional classifiers in this application.

4.5.4. Computational complexity

As discussed in Section 2, the computational complexity for regular convolution is $O({\mathit{CNd}}^2\mathit{HW})$, while that is $O(d^{2}K(N+C)\mathit{HW})$ for quadratic convolution combined with kernel separation. For our experiments $d=3,N=20$, and C is either 1 or 20 (the depth of input MFCC is 1, while the depth of input to the second convolutional layer is 20). H and W are 20 and 10, respectively. K is the number of separable kernels. Substituting the values in the above mentioned complexity equation, the complexity of the regular convolution would be $O(1\times 20\times 3^3\times 20\times 10)$ or $O(36,000)$ for the first convolutional layer and $O(20\times 20\times 3^3\times 20\times 10)$ or $O(720,000)$ for the second convolutional layer. The numbers for the separable quadratic kernel in first and second convolutional layers would be $O(3^2\times K\times (20+1)\times 20\times 10)$ or $O(37,800\times K)$, and $O(3^2\times K\times (20+20)\times 20\times 10)$ or $O(72,000\times K)$. This shows that for deeper layers (layers except the first one), choosing the number of separable kernels to be below 10 not only improves the recognition results, but also adds an additional computational cost which is less than the original cost. The preceding statement is evident by comparing $O(720,000)$ for the regular convolution cost with $O(72,000\times K)$ for separable quadratic term.

The above complexity terms show both time and space complexity (power/memory consumption). To better illustrate the complexity of the proposed approach, we show the complexity in terms of deployment time of a test sample for the employed CNN with conventional and proposed layers on a server with Nvidia GeForce GTX 1080 graphics card.

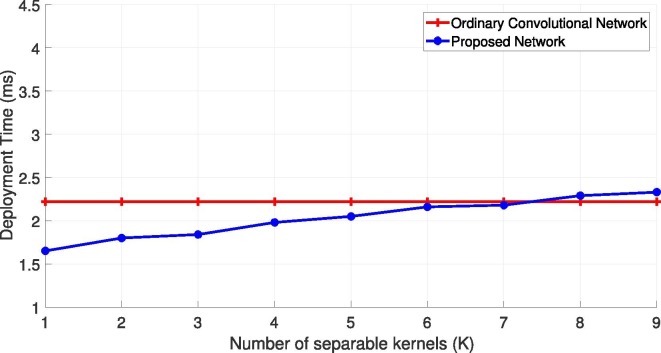
Fig. 6 illustrates the complexity of the proposed network based on the deployment time. So, the deployment time for a single cough sample is computed by averaging the deployment time over the whole test set versus the number of separable kernels (K).

Fig. 6.

Comparison of the convolutional, and proposed networks in terms of deployment time over Virufy dataset.

As can be seen, the deployment times of the proposed model lower than that of an ordinary convolutional network for K$<$8. This is while we took K = 5 in our experiments, since increasing K beyond 5 didn’t improve the overall accuracy of the model. This also shows proficiency of the proposed layer which not only improves the accuracy but also reduces the computations.

4.5.5. Comparison to the state-of-the-art

Since the research in field of Covid-19 detection by cough sound recognition has just recently been launched actively, the related datasets are pretty new.

Table 3 shows the comparison of the proposed work with those of the state of the art. The first three compared methods have used Virufy as one of the datasets in their experiments. Since these methods have not used only Virufy for reporting the results, we re-implemented their pipeline to compute the accuracy over the Virufy and achieve a fair comparison to our work.

Table 3.

Performance comparison of the proposed method with those of the state-of-the-art, in terms of accuracy, over test set of Virufy dataset.

Method	Accuracy
MFCC  + RF [31]	76.1
VGGsih/MFCC  + LR [29]	81.8
MFCC  + CNN [24]	94.3
VGGish  + SVM [29]	90.9
VGGish  + GRU [46]	89.8
Ordinary Convolution	95.0
Separable quadratic Convolution	97.5

The authors of [24] use a combination of MFCC features with a CNN with four convolutional and two fully connected layers. In [29] a combination of VGGish features and MFCC is fed to a logistic regression (LR) classifier to distinguish Covid/Non-Covid samples. In [31] MFCCs, spectral roll-off, spectral centroid, mean square energy,and some other simple features are concatenated to represent each 500 ms of cough signals resulting in a 28-D feature vector. A random forest (RF) classifier with 30 trees then was trained on the training set.

Also, since there are not too many published results on Virufy dataset, we implemented two more state-of-the-art approaches on Covid-19 cough recognition and applied them on Virufy, by ourselves. These last two methods in Table 3 were not tested on Virufy dataset in the original work.

These last two methods are based on applying a CNN pre-trained on Audioset [13] called VGGish [45], which is available on GitHub2 . It takes spectrogram as the input and acts as a feature extractor providing a 128D vector at the output of last fully connected layer. It is far more complicated than that of our proposed network having more convolutional and fully connected layers, but is widely used in audio recognition applications. The output 128D vector of VGGish is then fed to SVM with RBF kernel as described in [29]. The output 128D vector was also fed to a gated recurrent unit (GRU) as described in [46], followed by a softmax layer. For both methods cross validation for hyper-parameter tuning was applied. The results of these two last methods are shown at the last two rows of Table 3.

As inferred from Table 3, the proposed method is quite competitive with the state of the art ones. This is worth mentioning that the proposed method uses a very lightweight network (a structure similar to basic LeNet-1), while compared methods uses much more complex networks for cough classification, e. g. the cough recognition network in [24] is comprised of four convolutional and two fully connected layers.

The main reason why the proposed method outperforms the state-of-the-art ones is the presence of quadratic kernel which takes into account the cross correlation of the spectrogram. The separability helps to reduce the computational costs. Also, the fine tuning of hyper-parameters using cross validation and preparations to avoid overfitting are other factors for better behavior of the proposed method.

5. Conclusion

Employing a quadratic extension of the ordinary convolutional layer combined with the idea of kernel separation led to an efficient and accurate layer which is highly attractive for computationally constrained environments, where the resource limitations will not allow to use complex highly deep networks. High recall, precision, and F-score, along with pretty low order of computational complexity reveals that the proposed method could be promising for implementation in hand-held devices like cell-phones to recognize cough sounds and generate early Covid-19 warnings. Future work will involve using the proposed layer jointly with network compression techniques, and also employing it in few shot learning cough recognition problems, where training cough sound examples are scarce.

CRediT authorship contribution statement

Mohammad Soltanian: Conceptualization, Methodology, Writing - review & editing, Data curation. Keivan Borna: Supervision, Software, Validation, Conceptualization, Methodology.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.