Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2022 Oct 29.
Published in final edited form as: Biomed Phys Eng Express. 2021 Oct 29;7(6):10.1088/2057-1976/ac3055. doi: 10.1088/2057-1976/ac3055

Deep Learning-based Thoracic CBCT Correction with Histogram Matching

Richard LJ Qiu 1,#, Yang Lei 1,#, Joseph Shelton 1, Kristin Higgins 1, Jeffrey D Bradley 1, Walter J Curran 1, Tian Liu 1, Aparna H Kesarwala 1, Xiaofeng Yang 1
PMCID: PMC8591620  NIHMSID: NIHMS1753850  PMID: 34654011

Abstract

Kilovoltage Cone-beam Computed Tomography (CBCT)-based image-guided radiation therapy (IGRT) is used for daily delivery of radiation therapy, especially for stereotactic body radiation therapy (SBRT), which imposes particularly high demands for setup accuracy. The clinical applications of CBCTs are constrained, however, by poor soft tissue contrast, image artifacts, and instability of Hounsfield unit (HU) values. Here, we propose a new deep learning-based method to generate synthetic CTs (sCT) from thoracic CBCTs. A deep-learning model which integrates histogram matching (HM) into a cycle-consistent adversarial network (Cycle-GAN) framework, called HM-Cycle-GAN, was trained to learn mapping between thoracic CBCTs and paired planning CTs. Perceptual supervision was adopted to minimize blurring of tissue interfaces. An informative maximizing loss was calculated by feeding CBCT into the HM-Cycle-GAN, to evaluate the image histogram matching between the planning CTs and the sCTs. The proposed algorithm was evaluated using data from 20 SBRT patients who each received 5 fractions and therefore 5 thoracic CBCTs. To reduce the effect of anatomy mismatch, original CBCT images were pre-processed via deformable image registrations with the planning CT before being used in model training and result assessment. We used planning CTs as ground truth for the derived sCTs from the correspondent co-registered CBCTs. The mean absolute error (MAE), peak signal-to-noise ratio (PSNR), and normalized cross-correlation (NCC) indices were adapted as evaluation metrics of the proposed algorithm. Assessments were done using Cycle-GAN as the benchmark. The average MAE, PSNR, and NCC of the sCTs generated by our method were 66.2 HU, 30.3 dB, and 0.95, respectively, over all CBCT fractions. Superior image quality and reduced noise and artifact severity were seen using the proposed method compared to the results from the standard Cycle-GAN method. Our method could therefore improve the accuracy of IGRT and corrected CBCTs could help improve online adaptive RT by offering better contouring accuracy and dose calculation.

Keywords: CBCT correction, deep learning, histogram matching, lung SBRT

1. Introduction

Lung cancer is the most common cause of cancer death in the United States, with a five-year survival rate of approximately twenty percent (Cronin et al., 2018). Radiation therapy plays an important role in the management of lung cancer, and the quality of radiation therapy continues to improve significantly secondary to technological advancements such as image-guided radiation therapy (IGRT) (Eberhardt et al., 2015). More recently, wide adoption of SBRT has resulted in good outcomes for early-stage non-small cell lung cancer (NSCLC) patients (Postmus et al., 2017). In contrast to conventionally fractionated radiation, SBRT delivers a high dose per fraction (10 Gy to 34 Gy) over 1 to 5 fractions. It is therefore critical to have precise tumor alignment both to ensure adequate PTV coverage and avoid unnecessary treatment toxicities to organs at risk (OARs). The quality assurance of SBRT could be improved with more accurate fractional dose distributions.

IGRT is currently the most used technique for fractional treatment setup while treating lung cancer patients with SBRT. The current standard IGRT technique of linac-mounted kV CBCT, however, is prone to image artifacts. One major issue is streaking and cupping artifacts caused by scattering photons (Grimmer and Kachelriess, 2011), which is exacerbated in both frequency and severity for lung cancer patients because of respiratory motion (Zhang et al., 2010). Image artifacts can lead to errors in CT numbers, making it more it difficult to reliably obtain the accurate electron density information needed for dose calculations from CBCT Hounsfield unit (HU) values (Thing et al., 2016). It is therefore highly desirable to improve the quality of CBCT images to the quality level of planning CT images.

The many correction methods for CBCT artifacts which exist in the literature are mainly divided into two categories. The first includes pre-processing methods based on hardware, such as air-gap (Siewerdsen and Jaffray, 2000), bowtie filter (Mail et al., 2009), and anti-scatter grid methods (Siewerdsen et al., 2004). The underlying principle of these methods is to remove some of the scattered photons which reach the detector. The second is post-processing techniques that reduce image artifacts by estimating the effects of scattering photons in the projection or image domains. Examples of these include analytical modeling (Boone and Seibert, 1988), Monte Carlo simulation (Colijn and Beekman, 2004), measurement-based methods (Ning et al., 2004), and modulation methods (Zhu et al., 2006). For instance, high quality planning CT images can be used as prior knowledge to enhance CBCT images of the same patient in either the image (Brunner et al., 2011) or projection domains (Niu et al., 2010). Other methods mitigate shading artifacts by estimating the low-frequency shading field from the CT or CBCT images, which is achieved by sophisticated image segmentation methods (Wu et al., 2015) or ring-correction methods (Fan et al., 2015). Implementing these methods to improve scatter correction performance, requires concurrent consideration of computational complexity, imaging dose, scan time, practicality, and efficacy.

Recently, deep learning-based methods have been used to correct CBCT images across many body sites, such as brain, head and neck (Chen et al., 2020), and pelvis (Lei et al., 2019; Hansen et al., 2018). Studies showed that deep learning-based methods result in better image quality in corrected CBCTs than conventional correction methods using the same datasets (Xie et al., 2018). Adrian et al. showed that their U-Net method outperformed two conventional methods, deformable image registration and analytical image-based correction, with the lowest mean absolute error (MAE) of the resulting synthetic CT (sCT), the lowest spatial non-uniformity, and the most accurate bone geometry (Thummerer et al., 2020). Harms et al. observed lower noise in sCTs and a more similar appearance to planning CT when compared with a conventional image-based correction method (Harms et al., 2019). Conventional correction methods are designed to enhance a specific aspect of image quality, while deep learning-based methods force the overall image quality of sCT to be close to planning CT. Compared with brain and pelvis, generating sCTs from abdomen CBCT is more challenging due to the anatomical variations in the abdomen introduced by respiratory motion and peristalsis. Recently, good results have been obtained in abdominal sites with respiratory motion (Liu et al., 2020). Liu et al. recently developed a cycle-consistent generative adversarial network (Cycle-GAN) method to generate sCTs from CBCT for pancreatic adaptive radiation therapy (Liu et al., 2020). To our knowledge, there are no studies in the literature specifically tailored to thoracic CBCT correction using deep learning-based methods. Given the even greater effects of respiratory motion in the chest compared to the abdomen, thoracic CBCT correction provides a challenge to the effectiveness of deep learning-based methods.

In this study, we proposed a new deep learning-based method for thoracic CBCT correction, which integrates histogram matching into a Cycle-GAN framework, called HM-Cycle-GAN, to learn mapping between thoracic CBCT images and paired planning CT images. Perceptual supervision was adopted to suppress interface blurring, which is needed to get accurate lung contours and volume for normal tissue toxicity evaluations. Global histogram matching was performed via an informative maximizing (MaxInfo) loss calculated between planning CT and sCT derived by feeding CBCTs into the HM-Cycle-GAN. Histogram matching is important in the thorax, which has high tissue heterogeneity. The accurate HU around the boundary is important to dose calculation, particularly to SBRT and proton therapy. Our method produced high quality thoracic sCT images that can be used for dose calculation and organ segmentations.

2. Methods and materials

2.A. Data and Data Annotation

A set of planning CT images with registered fractional CBCTs of twenty lung SBRT patients were collected and anonymized. Each patient had 5 fractional CBCTs. In order to reduce the complexity of our data set, we purposely selected breathhold patients to minimize motion-induced artifacts. All planning CT images were acquired on a Siemens SOMATOM Definition AS CT scanner with a resolution of 0.977×0.977×2mm3. All fractional CBCT images were acquired using the on-board CBCT imager on the Varian Truebeam medical linear accelerator (Varian Medical System). Patients were coached to hold their breath during both simulation and radiation delivery.

To reduce the impact of anatomy mismatch, original CBCT images were pre-processed via a two-step deformable image registration process with the planning CT in VelocityAI 3.2.1 (Varian Medical Systems, Palo Alto, CA). First, rigid registration was performed to align both images. Second, the deformable image registration (DIR) algorithm in VelocityAI was used to register the CBCT to the planning CT. The resulting deformation vector field morphed the CBCT into a deformed CBCT, adopting the DICOM coordinates of the planning CT. The deformed CBCT and planning CT were then used as input for training our algorithm. The 5 fractional CBCTs along the course of the treatment have appreciable anatomical differences, which enhance the diversity of our data. In addition, data augmentation, such as rotation, flipping, re-scaling, and rigid deformation is used to enlarge the data variation. Furthermore, this patch-based strategy will also enlarge the training sample size.

2.B. Workflow

Figure 1 outlines the schematic flow chart of proposed HM-Cycle-GAN, which consists of two stages in the proposed CBCT correction algorithm: a training stage and a correction stage. As stated before, the CBCT fractions were first registered to the planning CT using deformable image registration algorithms in VelocityAI 3.2.1. The planning CT was used as the deep learning-based target of each CBCT image. Due to the artifacts in the CBCT images, there remained small residual mismatches between CBCT and planning CT images after deformable image registration. Those mismatches can be propagated and amplified to larger error during the CBCT-to-CT transformation as the trained model was highly under-constrained. In existing literature, a Cycle-GAN has been introduced to address this issue by simultaneously supervising an inverse CBCT-to-CT transformation model (Zhu et al., 2017). Unlike the original Cycle-GAN implementation, we used paired data in this work instead of unpaired training data. This removes intra-patient variation, which could further improve the network performance. Given the high similarity between the source image (CBCT) and the target image (planning CT), the residual image, i.e. the difference between the source and target images, was used to train the network. This structure of training the network is called a residual network, which has been shown to enhance convergence (He et al., 2016a).

Figure 1.

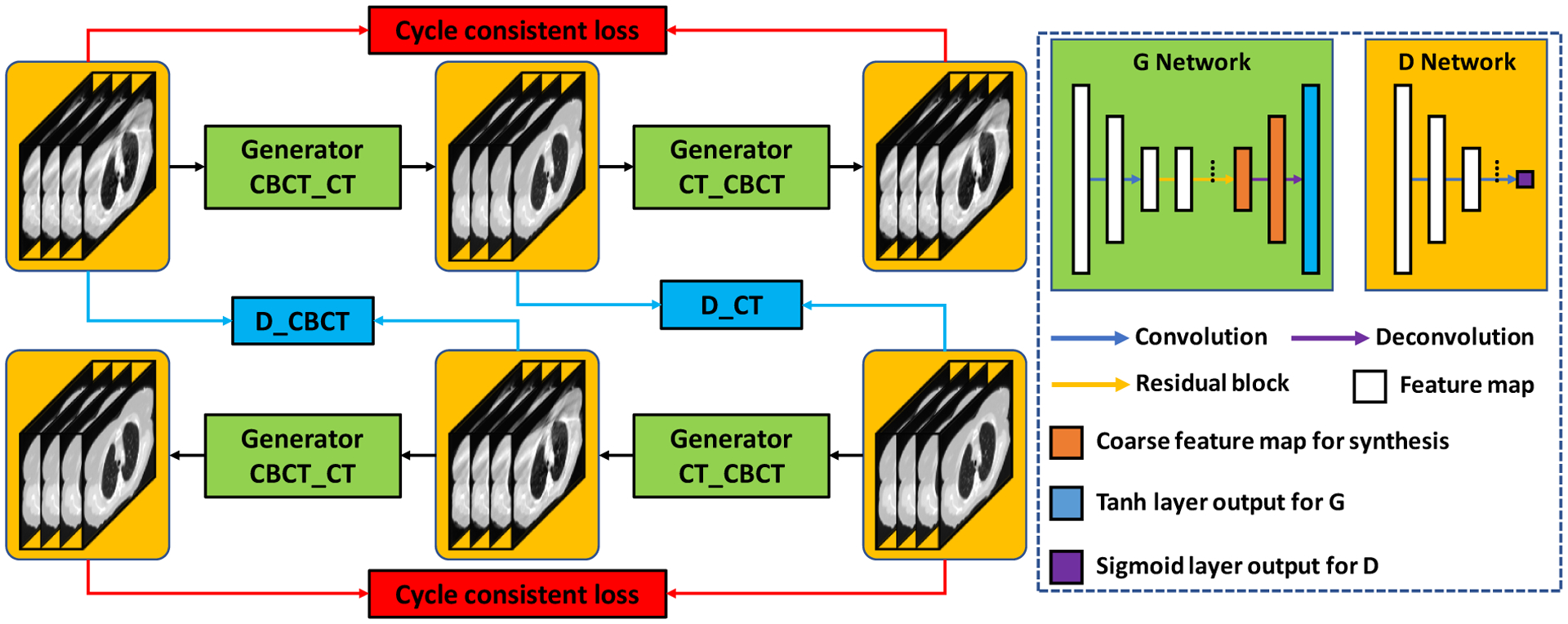
Figure 1.

Open in a new tab

Flow chart of the proposed HM-Cycle-GAN. The left panel shows the framework and the right panel the generator and discriminator used in the framework.

2.C. Cycle-GAN

GANs rely on two sub-networks, a generator, and a discriminator, which work with opposite goals. The goal of the generator is to fool the discriminator while the goal of the discriminator is to identify false data provided by the generator. The competition between the generator and the discriminator leads to improved performance of the network. In our scenario, one set of training data is a planning CT and the paired CBCT. First, the network was trained to map a CBCT image towards a CT-like image (termed corrected CBCT (CCBCT) throughout this paper). The generator tries to improve the CCBCT image so the following discriminator cannot distinguish it from a planning CT. Conversely, the discriminator’s training objective is to increase the accuracy of its judgment in separating CCBCTs from planning CTs. The competition results in the generation of more accurate CCBCTs (Goodfellow et al., 2014). The two networks are then optimized under the zero-sum framework. To further double constrain the model, a Cycle-GAN adds the inverse transformation, i.e., translating the planning CT image back to a CBCT-like image.

2.D. Convolutional residual block

Promising results have been accomplished using residual block in tasks where the target and source image modalities share good similarity, such as CBCT and planning CT images (He et al., 2016b). A convolutional residual block is constructed with a residual connection as well as several convolutional hidden layers. An input feature map or image bypasses the hidden convolutional layers of a residual block via the residual connection, therefore assigning the hidden convolutional layers to learn the image differences between CBCT and planning CT. Figure 1 illustrates the generator architecture: it starts with two convolution layers with stride size of 2 which are installed to downscale the feature map. The feature map passes by multiple residual blocks and two deconvolution layers to accomplish the end-to-end mapping.

2.E. Loss functions

The challenge of mapping a thoracic CBCT to a planning CT is the residual anatomical mismatch between the deformed CBCT and planning CT. In this scenario, Cycle-GAN cannot produce sharp boundaries if only image distance loss (e.g., MAE and GDE) is used as it mixes the two sources of mismatches. Due to its ability to force the semantic similarity between estimated image and ground truth image, (Johnson et al., 2016), perceptual loss was integrated into the loss function to prioritize generating accurate tissue boundaries in the transformed 3D images. The perceptual loss is defined as the difference between estimated image and ground truth image in feature space. The features are extracted via a trained classification or segmentation network’s hidden layers. In this work, in order to let the features well-represent the lung boundary, a feature pyramid network (FPN), a segmentation network trained on paired thoracic CTs with lung contours (Yang et al., 2018), is used as the feature extracting network for perceptual loss.

Letting Fs denotes this FPN for feature extraction, we can extract multiple pyramid level (number of N) feature maps via Fs. Namely, the feature maps extracted from planning CT (ICT) and sCT (IsCT) is represented by fCT=∪i=1NFSi(ICT) and fsCT=∪i=1NFSi(IsCT), respectively. The perceptual loss is then described as follows:

Lp(ICT,IsCT)=∑i=1NωiCi⋅Hi⋅Wi⋅Di‖Fsi(ICT)−Fsi(IsCT)‖22, (1)

where Ci denotes the number of feature map channels at ith pyramid level. Hi, Wi and Di denote the height, width, and depth of that feature map.

The competition between a generator network and a discriminator network boosts the final performance of the GAN network. Individually, each network’s performance is dictated by the design of the loss function. The original Cycle-GAN study used a two-part loss function which included an adversarial loss and a cycle-consistency loss (Zhu et al., 2017). The adversarial loss function was employed in both the CBCT-to-CT generator (GCBCT−CT) and the CT-to-CBCT generator (GCT−CBCT). The adversarial loss was calculated on the output of discriminators. The global generator loss function can be written as:

(GCT−CBCT,GCBCT−CT)=argminGCT−CBCT,GCBCT−CT{λadv[Ladv(DCT)+Ladv(DCBCT)]+Lcyc(GCBCT−CT,GCT−CBCT)} (2)

where λadv is a regularization parameter that control the weights of the adversarial loss.

Since both the forward and inverse transformations between the source image and target image are within the Cycle-GAN framework, it has the capability to differentiate synthetic images from real images, namely the planning CT. Therefore, a model trained under this framework can better process images with noise and artifacts. Given that CBCTs and planning CTs have similar underlying structures, in this work the Cycle-GAN is designed to predict the sCT to reach a similar level of both intensity accuracy and histogram distribution as the planning CT. Thus, the Lcyc(GCBCT−CT,GCT−CBCT) term consists of several losses, namely, MAE loss used to force the sCT’s voxel-wise intensity accuracy, GDE used to force the sCT’s structure to be similar to planning CT and thus reduce the scatter artifact, and MaxInfo loss, introduced in Eberhardt et al. (Eberhardt et al., 2015), to force the sCT to reach a similar histogram distribution level to that of the planning CT.

MaxInfo loss is used to quantify the mutual dependency between two probability distributions.

MaxInfo(X,Y)=∑i,j,kp(Xi,j,k,Yi,j,k)logp(Xi,j,k,Yi,j,k)p(Xi,j,k)⋅p(Yi,j,k) (3)

where p(x, y) is a joint probability function of x and y. p(x) and p(y) are marginal probability functions of x and y.

2.F. Evaluation and Validation

Five-fold cross-validation was used for evaluation. Specifically, we first randomly and equally separated the twenty patients’ data into five subgroups. Four subgroups served as training datasets and the remaining subgroup was used for our model testing. We repeated the experiment five times to allow each subgroup to be used exactly once as testing data.

Planning CT was used as the ground truth for the purpose of assessing sCTs derived from CBCTs. Four metrics were used in our study for quantitative comparison: MAE, peak signal-to-noise ratio (PSNR), normalized cross correlation (NCC) and structural similarity index (SSIM). MAE is a magnitude of the absolute difference between the planning CT and sCT. PSNR is used to compare the noise level between the sCT and planning CT. NCC, which is commonly used in pattern matching and image analysis, is a measure of the similarity of image structures. SSIM is a measurement of the similarity between two images. The calculations of these metrics were conducted over the valid image volume of the CBCT and within the body outlines. To demonstrate the superior performance of the proposed method comparing to the benchmark method, paired t-tests were conducted and p-values were calculated.

3. Results

To improve the performance of our network, we integrated two steps of supervision into the tradition Cycle-GAN. To demonstrate the significance of these two steps, we performed an ablation test for each step, i.e., comparing Cycle-GAN with perceptual supervision (Cycle-GAN+Perceptual) and Cycle-GAN with perceptual and Maxinfo supervision (Cycle-GAN+Perceptual+MaxInfo) against the benchmark used in this study, the traditional Cycle-GAN.

Fig. 2 displays the axial views of the deformed CBCT, planning CT, and the CTs generated by the three deep-learning-based methods listed above for a selected case. For this case, substantial streaking artifacts were seen on the CBCT, which could be a result of inconsistent breathholds during CBCT acquisition. As the result, unlike the planning CT, the thoracic outline, and internal structures on the CBCT were blurred, as shown in the yellow boxes. False inhomogeneity in HU values were observed within the breast tissue, with examples shown in in the red boxes. Compared to sCTs from the benchmark Cycle-GAN method, the sharpness of the interfaces was greatly improved in the sCTs from both methods with perceptual supervision. The body outline, diaphragm, bony structures, esophagus, trachea, heart, and other organs were easier to identify. Additionally, the correspondent sCTs had fewer errors across around tissue interfaces compared to CBCTs. The final proposed method, which added MaxInfo loss, further suppressed the false HU inhomogeneity within the breast tissue and other organs. Overall image noise level was also reduced. In the CBCT-CT difference images (Fig. 2 (a3) and (a4)), major differences were seen in both breasts, mediastinum, and lung. The proposed method with both perceptual supervision and MaxInfo loss had the fewest residual differences. It demonstrated the benefits of each individual modification, both perceptual supervision and MaxInfo loss, in terms of improving the Cycle-GAN methods. Finally, the line profile shown in Fig. 2 (f) also demonstrated that the HUs of the sCT from our proposed method were closest to that of the planning CT.

Figure 2.

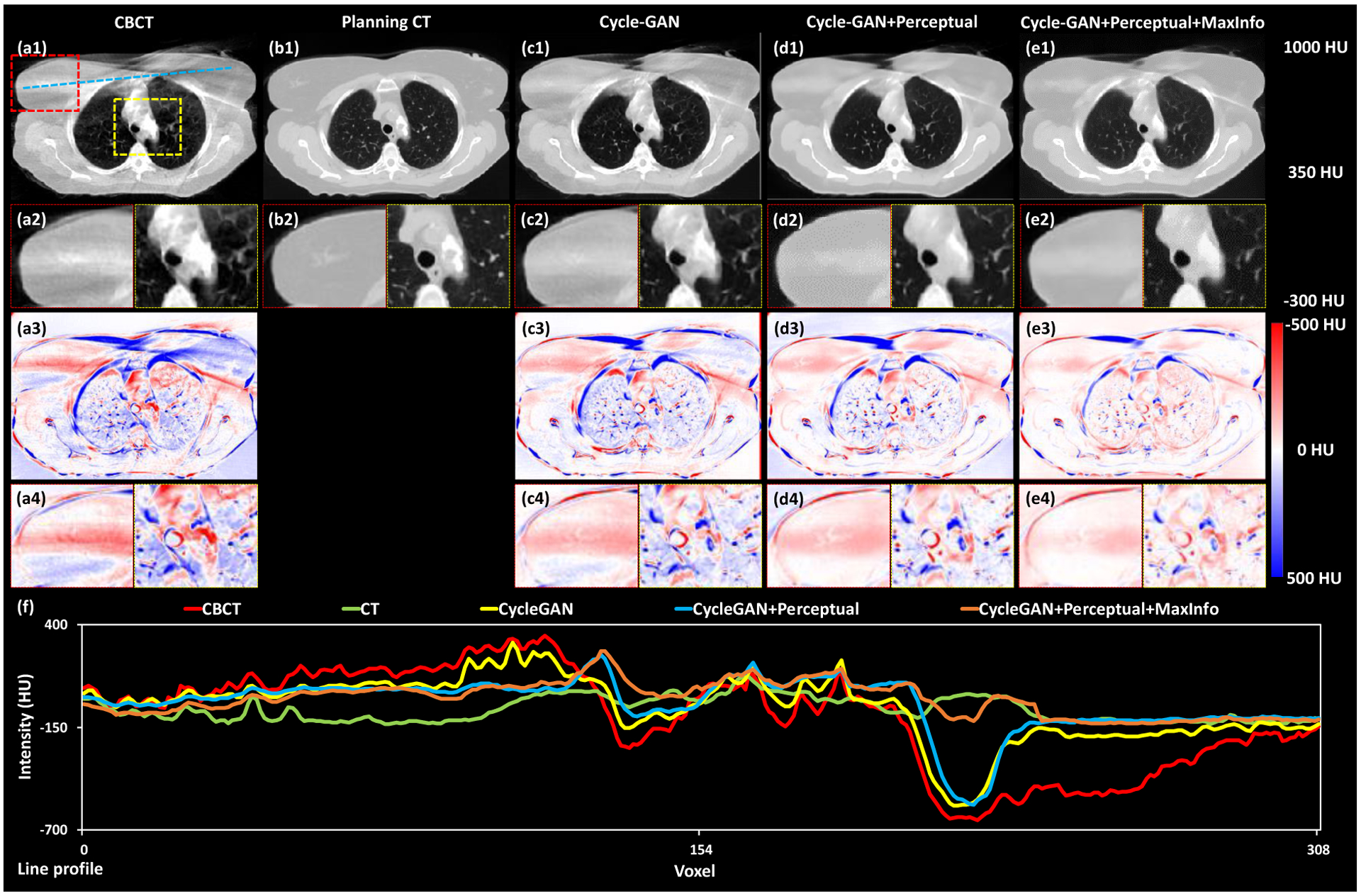
Figure 2.

Open in a new tab

Axial views of the deformed CBCT, planning CT and these CTs generated by the three deep-learning-based methods. The first row (a1, b1, c1, d1 and e1) shows the axial views of CBCT, planning CT, sCT obtained via Cycle-GAN, Cycle-GAN+Perceptual and proposed method, respectively. The second row (a2, b2, c2, d2 and e2) shows two zoomed-in subregions highlighted in the red and yellow dash line rectangles in (a1). The third row (a3, c3, d3 and e3) shows the difference images between planning CT and CBCT, sCT obtained via Cycle-GAN, Cycle-GAN+Perceptual and proposed method, respectively. The fourth row (a4, c4, d4 and e4) shows two zoomed-in subregions highlighted in red and yellow dash line rectangles in (a1). The line profiles of CBCT, planning CT, sCT obtained via Cycle-GAN, Cycle-GAN+Perceptual and proposed method are plotted in (f).

Fig. 3 shows the coronal views of the deformed CBCT, planning CT, and the CTs generated by the three deep-learning-based methods. Here the improvements in resolution of the diaphragm, heart, and surrounding tissues were easier to observe. Particularly, the blurring of the diaphragm was decreased in sCTs generated from the methods with perceptual supervision, which could be seen in both the sCT and the difference images. Again, the proposed method with both perceptual supervision and MaxInfo loss had the fewest residual difference when compared to the planning CT. The line profile in Figure 3f again showed that the HUs of the sCT from our method were closest to that of the planning CT.

Figure 3.

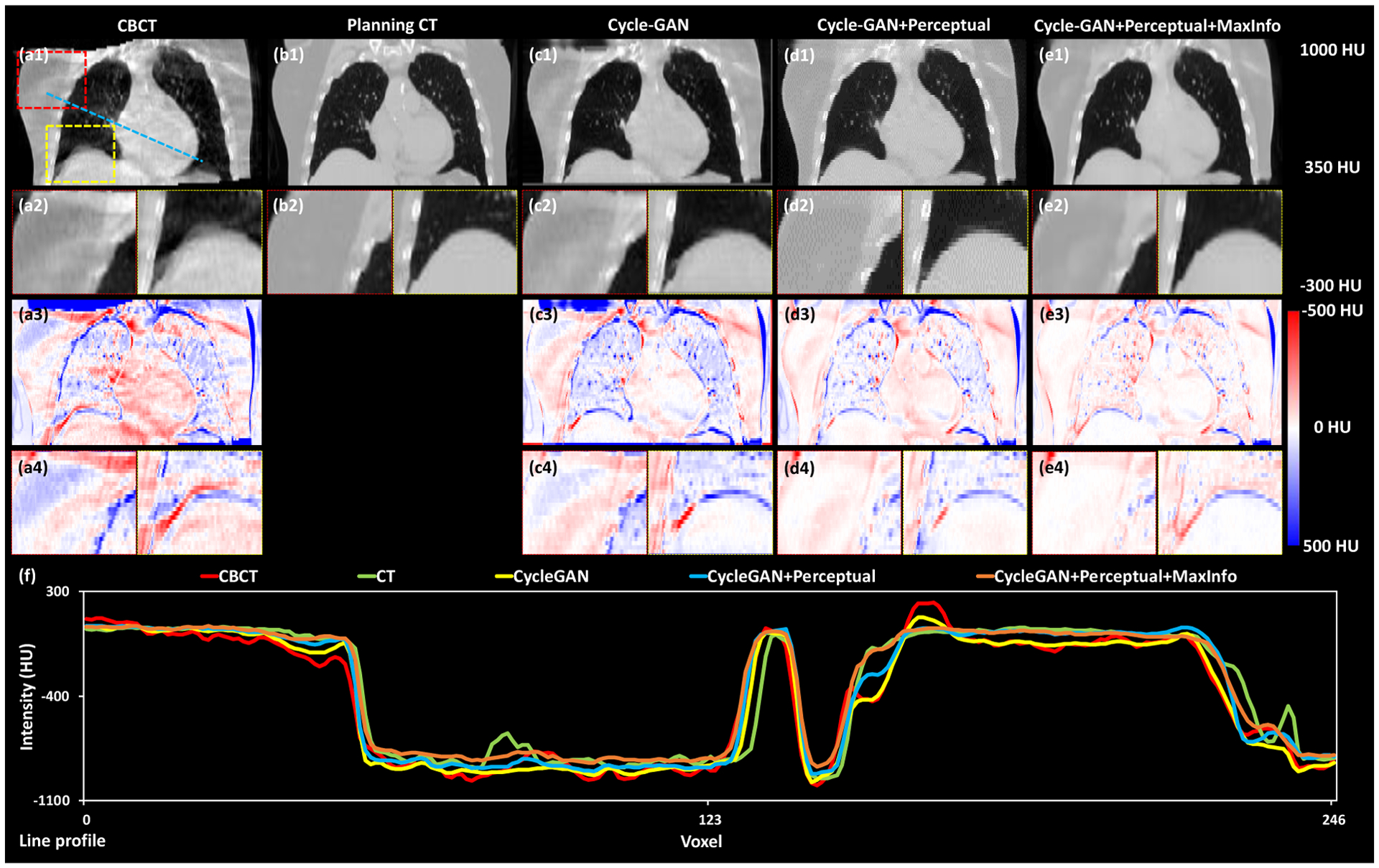
Figure 3.

Open in a new tab

Coronal views of the deformed CBCT, planning CT and these CTs generated by the three deep-learning-based methods. The first row (a1, b1, c1, d1 and e1) shows the coronal views of CBCT, planning CT, sCT obtained via Cycle-GAN, Cycle-GAN+Perceptual and proposed method, respectively. The second row (a2, b2, c2, d2 and e2) shows two zoomed-in subregions highlighted in the red and yellow dash line rectangles in (a1). The third row shows (a3, c3, d3 and e3) the difference images between planning CT and CBCT, sCT obtained via Cycle-GAN, Cycle-GAN+Perceptual and proposed method, respectively. The fourth row (a4, c4, d4 and e4) shows two zoomed-in subregions highlighted in shown by red and yellow dash line rectangles in first row(a1). The line profiles of CBCT, planning CT, sCT obtained via Cycle-GAN, Cycle-GAN+Perceptual and proposed method are plotted in (f).

The histogram profile in Figure 4 again shows that the sCT from our HM-Cycle-GAN closely resembles the planning CT. It is known that the HU profile of the CBCT is drastically different from the planning CT, and therefore cannot be used to determine accurate dose delivery. With the inclusion of the perceptual supervision and Maxinfo loss, the HU histogram of the sCT (brown line in Figure 4) was more similar to that of the planning CT (green line). Particularly, the peak around −100 HU was enhanced, indicating that the soft tissue contrast was greatly improved; both perceptual supervision and Maxinfo loss contributed to this improvement.

Figure 4.

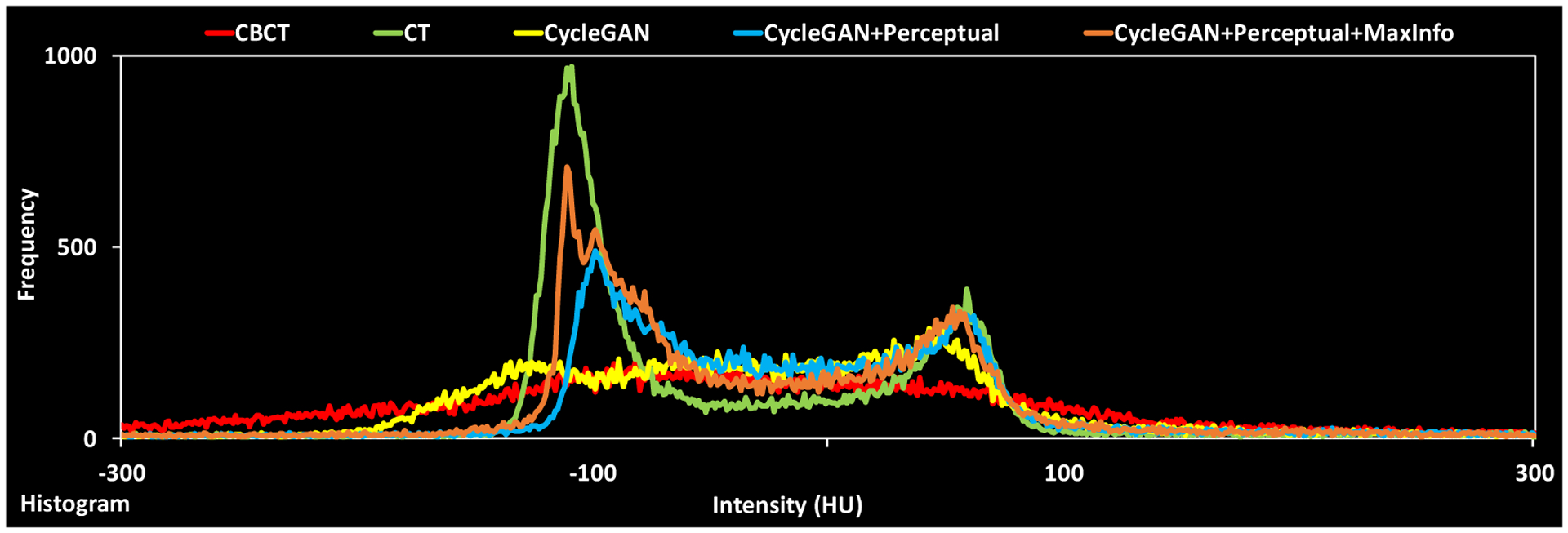
Figure 4.

Open in a new tab

Histograms of CBCT, planning CT, sCT obtained via Cycle-GAN, Cycle-GAN+Perceptual and proposed method, respectively.

Table 1 presents the averages and standard deviations of the MAE, PSNR. NCC and SSIM values within the body contour of the CBCT and the sCT generated by the benchmark Cycle-GAN method, Cycle-GAN+Perceptual method and our final proposed method, Cycle-GAN+Perceptual+MaxInfo, across the entire dataset, using the planning CT as ground truth. Incorporating perceptual supervision and MaxInfo loss into Cycle-GAN methods boosted the image quality of the generated sCT. Our proposed method had the best results, with MAE, PSNR, NCC and SSIM values of 66.2±8.2 HU, 30.3±6.1dB, 0.95±0.04, and 0.91±0.05, respectively. The standard deviations were the smallest, indicating that our method not only performed the best, but also generated the most consistent results. Table 2 shows the p-values of the paired t-tests comparing our proposed methods vs. the other two methods. All the p values are below 0.001, demonstrating the statical significance of the improvements. The performances of all the methods within the bony region are shown in Table 3. Our proposed method yielded superior outcome across all metrics. Paired t-tests were conducted and the p values are listed in Table 4. As can be seen from these two tables, our proposed method outperformed the other two methods within the bony region (all p values < 0.001).

Table 1.

Model performance results on all patients’ data. Data are reported as mean ± STD.

MAE (HU) PSNR (dB) NCC SSIM
CBCT 110.0±24.9 23.0±4.0 0.87±0.06 0.85±0.05
Cycle-GAN 82.0±17.3 28.3±6.9 0.93±0.06 0.89±0.06
Cycle-GAN+Preceptual 72.8±11.5 29.1±6.8 0.94±0.04 0.90±0.05
Proposed 66.2±8.2 30.3±6.1 0.95±0.04 0.91±0.05
Open in a new tab

Table 2.

P-values from the paired t-test comparing the proposed method and benchmark method.

MAE (HU) PSNR (dB) NCC SSIM
Cycle-GAN <0.001 <0.001 <0.001 <0.001
Cycle-GAN+Preceptual <0.001 <0.001 <0.001 <0.001
Open in a new tab

Table 3.

Model performance within the bony region on all patients’ data. Data are reported as mean ± STD.

MAE (HU) PSNR (dB) NCC SSIM
Cycle-GAN 165.4±42.3 20.1±7.3 0.58±0.16 0.54±0.20
Cycle-GAN+Preceptual 127.0±35.2 20.6 ±7.4 0.62±0.16 0.57±0.20
Proposed 95.5±41.7 21.5±7.3 0.78±0.17 0.69±0.20
Open in a new tab

Table 4.

P-values from the paired t-test comparing the proposed method and benchmark method within the bony region.

MAE (HU) PSNR (dB) NCC SSIM
Cycle-GAN <0.001 <0.001 <0.001 <0.001
Cycle-GAN+Preceptual <0.001 <0.001 <0.001 <0.001
Open in a new tab

4. Discussion

Our proposed algorithm-generated sCT closely resembles the planning CT. It has a similar HU histogram profile to the planning CT, which will allow for more accurate dose calculation. Our results were better than a recent study that used Cycle-GAN for head and neck, lung, and breast (Maspero et al., 2020). Our results proved that high-fidelity sCTs can be generated while also taking thoracic motion into account by modifying the general Cycle-GAN network, in this case by adopting perceptual supervision and Maxinfo loss. Another reason for our high fidelity is the use of paired training data instead of unpaired data, as anatomical mismatches in paired data are less profound compared to unpaired data. Although Cycle-GAN can be trained via un-paired data, the larger mismatch between learning target (CT) and source image (CBCT), may lead to decreased intensity accuracy of the synthetic CT. Paired training data frees the algorithm from tackling those anatomical mismatches, thereby allowing it to focus on reducing image artifacts and enhancing soft tissue contrast. Additionally, it made the training process faster as the initial relative differences in dataset are smaller.

Although the planning CT was treated as the ground truth for performance evaluation in this study, the planning CT is by no means the real ground truth. The planning CT was acquired at simulation, prior to the course of SBRT, while CBCT images were acquired on different days during the treatment course. One would therefore not expect the sCT to match fully the planning CT, since residual anatomical differences were persistent even after deformable image registration. However, the improvement in image quality, such as diminishing of scatter artifact, improving lung boundary contrast, and improving the histogram distribution of CBCT to be close to that of planning CT is substantial. Deformable image registration (DIR) does have inherent limitations. There is not a fully clinical usable DIR algorithm to this date; all of the current options have to be manually assessed when running individual DIRs. Often, the DIR results are not acceptable. We chose Varian Velocity Al since it is a widely known algorithm and does relatively acceptable DIR. DIR for Lung SBRT patients is especially challenging due because of the respiratory motion. The example shown in the manuscript is one of the challenging cases with large motion-induced artifacts. In this study, we manually examined all CT-CBCT registration results to ensure all training data had acceptable registration accuracy.

One of the reasons that the proposed algorithm did well in CBCT image correction is that the CBCT and planning CT images are inherently similar, meaning the initial differences are small. However, the algorithm does not consider any physical information, compared to the conventional scatter-based methods. Therefore, the quality of the sCT images is fundamentally limited by the image quality of the initial planning CT images. If there are artifacts in the planning CT, they will be present in the sCT. For example, a sCT would inherit artifacts from implants such as shoulder prostheses, cardiac devices, or lung fiducial markers, if the artifacts are not corrected in the planning CT. Another limitation comes from the image quality of the incoming CBCT images, especially the motion-induced artifacts for chest CBCT. Although motion management techniques such as deep inspiration breath hold can reduce such artifacts, the image quality of thoracic CBCT remains suboptimal due to residual respiratory motion. Those artifacts may get propagated to the final sCT.

In the context of adaptive radiation therapy (ART), one needs a reliable HU-electron density conversion on fractional IGRT images for dose calculation purposes. Such a requirement is difficult to meet for CBCT due to streaking and shading artifacts, especially at tissue boundaries. If those issues can be solved, accurate dose calculation on CBCT images could be achieved. Unlike conventional scatter or artifact corrections that typically cannot correct HU values, our sCT images have similar HU distributions to planning CTs, making it possible to obtain accurate dose calculations. Although not demonstrated in this work, recent work by our group studied the dosimetric impact of the random forest-based method, which is a tradition machine learning-based method (Wang et al., 2019). Since the current method is more accurate than the random forest method due to the using of deep features as compared to knowledge-based features, we would expect improved accuracy of dose calculation on sCT from this method. Finally, like other deep-learning-based methods, the generation of the sCT only took several seconds, which would meet the demand for online ART.

A further application of the proposed algorithm could lie in target delineation and treatment planning. The model could be used to predict deformed dose distributions or organ contours by adopting the same CBCT image corrections (Nguyen et al., 2019). It could save dose calculation time and further shorten patient waiting time on the treatment couch for online ART. Dosimetric studies are currently in progress to further assess the model from the proposed method.

Conclusion

In this work, a deep-learning-based algorithm that corrects image artifacts in thoracic CBCT images is presented. The proposed algorithm was trained with paired planning CT-CBCT data. The proposed algorithm reduced the MAE from planning CT images to CBCT images from an average of 110.0 HU to an average of 66.2 HU and effectively reduced the streaking and shading artifacts. More accurate HU distributions of sCT images could also offer more opportunities in quantitative imaging using CBCT.

Acknowledgments

This research is supported in part by the National Cancer Institute of the National Institutes of Health under Award Number R01CA215718, and a pilot grant provided by the Winship Cancer Institute of Emory University.

Footnotes

DISCLOSURES

The authors declare no conflicts of interest.

Reference

  1. Boone JM and Seibert JA 1988. An analytical model of the scattered radiation distribution in diagnostic radiology Med Phys 15 721–5 [DOI] [PubMed] [Google Scholar]
  2. Brunner S, Nett BE, Tolakanahalli R and Chen GH 2011. Prior image constrained scatter correction in cone-beam computed tomography image-guided radiation therapy Phys Med Biol 56 1015–30 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Chen L, Liang X, Shen C, Jiang S and Wang J 2020. Synthetic CT generation from CBCT images via deep learning Med Phys 47 1115–25 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Colijn AP and Beekman FJ 2004. Accelerated simulation of cone beam X-ray scatter projections IEEE Transactions on Medical Imaging 23 584–90 [DOI] [PubMed] [Google Scholar]
  5. Cronin KA, Lake AJ, Scott S, Sherman RL, Noone AM, Howlader N, Henley SJ, Anderson RN, Firth AU, Ma J, Kohler BA and Jemal A 2018. Annual Report to the Nation on the Status of Cancer, part I: National cancer statistics Cancer 124 2785–800 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Eberhardt WE, De Ruysscher D, Weder W, Le Péchoux C, De Leyn P, Hoffmann H, Westeel V, Stahel R, Felip E and Peters S 2015. 2nd ESMO Consensus Conference in Lung Cancer: locally advanced stage III non-small-cell lung cancer Ann Oncol 26 1573–88 [DOI] [PubMed] [Google Scholar]
  7. Fan Q, Lu B, Park JC, Niu T, Li JG, Liu C and Zhu L 2015. Image-domain shading correction for cone-beam CT without prior patient information J Appl Clin Med Phys 16 65–75 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A and Bengio Y Adv. Neural Info. Proc. Sys,2014), vol. Series) pp 2672–80 [Google Scholar]
  9. Grimmer R and Kachelriess M 2011. Empirical binary tomography calibration (EBTC) for the precorrection of beam hardening and scatter for flat panel CT Med Phys 38 2233–40 [DOI] [PubMed] [Google Scholar]
  10. Hansen DC, Landry G, Kamp F, Li M, Belka C, Parodi K and Kurz C 2018. ScatterNet: A convolutional neural network for cone-beam CT intensity correction Med Phys 45 4916–26 [DOI] [PubMed] [Google Scholar]
  11. Harms J, Lei Y, Wang T, Zhang R, Zhou J, Tang X, Curran WJ, Liu T and Yang X 2019. Paired cycle-GAN-based image correction for quantitative cone-beam computed tomography Med Phys 46 3998–4009 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. He K, Zhang X, Ren S and Sun J Proceedings of the IEEE conference on computer vision and pattern recognition,2016a), vol. Series) pp 770–8 [Google Scholar]
  13. He K, Zhang X, Ren S and Sun J Eur. Conf. Comput. Vis., (Cham, 2016b) (Computer Vision – ECCV 2016, vol. Series): Springer International Publishing; ) pp 630–45 [Google Scholar]
  14. Johnson J, Alahi A and Fei-Fei L 2016. Perceptual Losses for Real-Time Style Transfer and Super-Resolution European Conference on Computer Vision (ECCV) arXiv:1603.08155 [Google Scholar]
  15. Lei Y, Tang X, Higgins K, Lin J, Jeong J, Liu T, Dhabaan A, Wang T, Dong X, Press R, Curran WJ and Yang X 2019. Learning-based CBCT correction using alternating random forest based on auto-context model Med Phys 46 601–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Liu Y, Lei Y, Wang T, Fu Y, Tang X, Curran WJ, Liu T, Patel P and Yang X 2020. CBCT-based synthetic CT generation using deep-attention cycleGAN for pancreatic adaptive radiotherapy Med Phys 47 2472–83 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Mail N, Moseley DJ, Siewerdsen JH and Jaffray DA 2009. The influence of bowtie filtration on cone-beam CT image quality Med Phys 36 22–32 [DOI] [PubMed] [Google Scholar]
  18. Maspero M, Houweling AC, Savenije MHF, van Heijst TCF, Verhoeff JJC, Kotte ANTJ and van den Berg CAT 2020. A single neural network for cone-beam computed tomography-based radiotherapy of head-and-neck, lung and breast cancer Physics and Imaging in Radiation Oncology 14 24–31 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Nguyen D, Jia X, Sher D, Lin M-H, Iqbal Z, Liu H and Jiang S 2019. 3D radiotherapy dose prediction on head and neck cancer patients with a hierarchically densely connected U-net deep learning architecture Physics in Medicine & Biology 64 065020. [DOI] [PubMed] [Google Scholar]
  20. Ning R, Tang X and Conover D 2004. X-ray scatter correction algorithm for cone beam CT imaging Med Phys 31 1195–202 [DOI] [PubMed] [Google Scholar]
  21. Niu T, Sun M, Star-Lack J, Gao H, Fan Q and Zhu L 2010. Shading correction for on-board cone-beam CT in radiation therapy using planning MDCT images Med Phys 37 5395–406 [DOI] [PubMed] [Google Scholar]
  22. Postmus PE, Kerr KM, Oudkerk M, Senan S, Waller DA, Vansteenkiste J, Escriu C and Peters S 2017. Early and locally advanced non-small-cell lung cancer (NSCLC): ESMO Clinical Practice Guidelines for diagnosis, treatment and follow-up Ann Oncol 28 iv1–iv21 [DOI] [PubMed] [Google Scholar]
  23. Siewerdsen JH and Jaffray DA 2000. Optimization of x-ray imaging geometry (with specific application to flat-panel cone-beam computed tomography) Med Phys 27 1903–14 [DOI] [PubMed] [Google Scholar]
  24. Siewerdsen JH, Moseley DJ, Bakhtiar B, Richard S and Jaffray DA 2004. The influence of antiscatter grids on soft-tissue detectability in cone-beam computed tomography with flat-panel detectors Med Phys 31 3506–20 [DOI] [PubMed] [Google Scholar]
  25. Thing RS, Bernchou U, Mainegra-Hing E, Hansen O and Brink C 2016. Hounsfield unit recovery in clinical cone beam CT images of the thorax acquired for image guided radiation therapy Phys Med Biol 61 5781–802 [DOI] [PubMed] [Google Scholar]
  26. Thummerer A, Zaffino P, Meijers A, Marmitt GG, Seco J, Steenbakkers R, Langendijk JA, Both S, Spadea MF and Knopf AC 2020. Comparison of CBCT based synthetic CT methods suitable for proton dose calculations in adaptive proton therapy Phys Med Biol 65 095002. [DOI] [PubMed] [Google Scholar]
  27. Wang T, Lei Y, Manohar N, Tian S, Jani AB, Shu H-K, Higgins K, Dhabaan A, Patel P, Tang X, Liu T, Curran WJ and Yang X 2019. Dosimetric study on learning-based cone-beam CT correction in adaptive radiation therapy Med. Dosimetry In Press [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Wu P, Sun X, Hu H, Mao T, Zhao W, Sheng K, Cheung AA and Niu T 2015. Iterative CT shading correction with no prior information Phys Med Biol 60 8437–55 [DOI] [PubMed] [Google Scholar]
  29. Xie S, Yang C, Zhang Z and Li H 2018. Scatter Artifacts Removal Using Learning-Based Method for CBCT in IGRT System IEEE Access 6 78031–7 [Google Scholar]
  30. Zhang Q, Hu YC, Liu F, Goodman K, Rosenzweig KE and Mageras GS 2010. Correction of motion artifacts in cone-beam CT using a patient-specific respiratory motion model Med Phys 37 2901–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Zhu J-Y, Park T, Isola P and Efros AA Int. Conf. Comput. Vis,2017), vol. Series) [Google Scholar]
  32. Zhu L, Bennett NR and Fahrig R 2006. Scatter Correction Method for X-Ray CT Using Primary Modulation: Theory and Preliminary Results IEEE Transactions on Medical Imaging 25 1573–87 [DOI] [PubMed] [Google Scholar]

RESOURCES