Generalized Zero-shot Chest X-ray Diagnosis through Trait-Guided Multi-view Semantic Embedding with Self-training

Abstract

Zero-shot learning (ZSL) is one of the most promising avenues of annotation-efficient machine learning. In the era of deep learning, ZSL techniques have achieved unprecedented success. However, the developments of ZSL methods have taken place mostly for natural images. ZSL for medical images has remained largely unexplored. We design a novel strategy for generalized zero-shot diagnosis of chest radiographs. In doing so, we leverage the potential of multi-view semantic embedding, a useful yet less-explored direction for ZSL. Our design also incorporates a self-training phase to tackle the problem of noisy labels alongside improving the performance for classes not seen during training. Through rigorous experiments, we show that our model trained on one dataset can produce consistent performance across test datasets from different sources including those with very different quality. Comparisons with a number of state-of-the-art techniques show the superiority of the proposed method for generalized zero-shot chest x-ray diagnosis.

1. Introduction

Zero-shot learning (ZSL) is the art that empowers machine learning strategies to identify objects from previously unseen classes with the help of their semantic descriptions. Typically, a ZSL method is trained with data points from several classes called seen classes. The trained model is expected to identify test data points from classes not seen during training (unseen classes). This is achieved through the use of auxiliary information about seen and unseen classes in the form of semantic descriptions. Therefore, auxiliary information are of pivotal importance in a ZSL method [1]. A generalized ZSL (GZSL) method is the one where the test data may belong to either seen or unseen classes.

There have been several remarkable developments in the design of ZSL methods involving natural images for applications including classification [2], [3], object detection [4]–[6], and segmentation [7], [8]. Because of its ability to identify new classes, ZSL may be potentially useful in radiology diagnosis, especially for the diagnosis of rare diseases from radiology images. However, due to a number of compelling factors, there has been practically no development in designing ZSL methods for radiology diagnosis. One such challenge is the presence of noisy (incorrect) labels in large scale radiology image datasets. Most such datasets employ automated rule-based approaches for the extraction of labels from radiology reports. Even with small ambiguities in sentences, such models may end up producing wrong labels. The noise in labels presents a major difficulty in training ZSL systems.

Typical ZSL methods operate by mapping some form of feature vectors corresponding to input data (such as visual feature vectors if image is input) to a semantic space constructed from auxiliary information. The semantic space contains points bearing the characteristics of each target class. These points are called semantic signatures of the corresponding target classes. Classification of the input data is performed based on the semantic signature closest to the projection of input data in the semantic space. However, semantic spaces constructed from text-based auxiliary information are often devoid of cues about visual traits that define a class. This gives rise to semantic gaps in embeddings [9] and adversely affects the performance of a ZSL method. Furthermore, since semantic spaces are important in the design of ZSL methods, meaningful use of multiple semantic spaces is likely to facilitate a ZSL method [10]. However, constructing multiple independent semantic spaces and meaningfully combining them is a challenging problem, especially in the field of radiology diagnosis due to the relative scarcity of auxiliary information.

We propose a novel GZSL method for chest x-ray diagnosis by addressing the above challenges. Our goal is to train a model with the chest x-ray images corresponding to a set of abnormalities in such a way that the model can be used for the diagnosis of a different set of abnormalities from chest x-rays alongside the abnormalities used for training the model. To that end, we introduce a first-of-its-kind trait-guided multi-view semantic embedding strategy. Our model consists of three semantic spaces. While two of the semantic spaces are constructed from x-ray and CT radiology reports, respectively, visual traits are used for designing the third. Most diseases and conditions diagnosable from chest x-rays can also be diagnosed from chest CTs having richer information. Hence, the CT semantic space, alongside the x-ray semantic space is also expected to provide useful information for chest x-ray diagnosis. We design a two-branch autoencoder to perform semantic embeddings into the above two semantic spaces. The third semantic space is constructed from visual traits used by the radiologists for the diagnosis of the target diseases. In each of the two branches of our model, we introduce a novel guiding network that exploits the trait-based semantic space to alleviate the problem of semantic gaps for embeddings into the x-ray and CT semantic spaces. Finally, we introduce a self-training which involves fine tuning the initial model by data points, most confidently identified by the initial model. Self-training helps to address the problem of noisy labels in training data and improve performance for unseen classes. In this work, our contributions are as follows:

• We design a method for generalized zero-shot diagnosis of chest x-rays.

• Information from three semantic spaces created using x-ray reports, CT reports and visual traits, respectively, are meaningfully combined using a two-branch autoencoder.

• We utilize visual traits through a novel guiding network to alleviate the problem of semantic gaps in embeddings.

• The problem of noisy labels is addressed using a self-training method that also helps to improve the performance for unseen classes.

• Our model, trained on one dataset, can be used for test data from a diverse set of sources.

The rest of the paper is organized as follows. After presenting the related works in Section II, we describe the proposed method in Section III. The experiments are presented in Section IV followed by conclusions in Section V.

II. Related Work

A. Zero-shot Learning

Most existing ZSL techniques project input data points to a semantic space where the target classes are represented by a point, termed as semantic signatures. Based on the availability of training data points, ZSL methods are divided into two categories, inductive ZSL and transductive ZSL. Inductive methods use data points only from the seen classes during training. Among the inductive methods, Romera-Paredes et al. have proposed a linear mapping from input features to class-specific attributes [11]. An autoencoder based method has been designed in [12]. For a generative model that operates by learning visual-semantic and semantic-visual mappings, see [3]. Bucher et al. have introduced a zero-shot semantic segmentation method with self-training [7]. In [13], the authors propose to re-train a pre-trained neural feature extractor to learn the mapping from extracted features to semantic signatures. ZSL by synthesizing examples through a variational autoencoder has been presented in [14].

Transductive ZSL methods assume the availability of unlabelled training data from unseen classes alongside labelled training data from seen classes. Among transductive ZSL methods, ZSL via shared model space learning has been proposed in [15]. Ye et al. [16] have designed an ensemble of networks for ZSL. See [2] for ZSL through the use of gradient matching generative networks [2]. In [17], the authors use priors from visual structures to learn semantic embedding. The use of structural constraints in this method helps to alleviate the domain shift problem.

B. Multi-view Learning

Learning through the use of multiple independent (generated independently from each other) semantic spaces (views) is called multi-view learning. Independent and useful information from multiple semantic spaces is likely to facilitate ZSL [10]. However, there are very few ZSL methods that have explored multi-view learning due to challenges in designing complementary semantic spaces. Among those, Zhang et al. have designed a multi-modality fusion method for ZSL [10]. A strategy of multi-view ZSL through score level fusion can be found in [1]. In [18], the authors propose a transductive ZSL method to address the domain shift problem through the use of multiple semantic views. This model employs canonical correlation analysis for learning the embedding space.

C. Deep Learning for Chest X-ray Diagnosis

The advent of deep learning has revolutionized the field of automated diagnosis of radiology images including chest x-rays. Lakhani et al. have designed a CNN model to detect pulmonary tuberculosis from chest x-rays [19]. Attention-guided CNN for thorax disease diagnosis from chest x-rays has been proposed in [20]. See [21], for a deep learning based model to detect pulmonary nodules. In [22], an ensemble of deep neural networks has been introduced for localization of pneumonia in chest x-rays. Recent works based on deeper and denser networks [23]–[25] seem to provide a promising direction for automated diagnosis of chest radiographs.

However, all of the above methods are data-hungry. Data-efficient deep learning models are relatively rare for medical images. Out of those methods, see [26] for few-shot and [27] for one-shot MRI segmentation. A few-shot chest x-ray diagnosis model has been proposed in [28]. Data-efficient models have also been used for brain imaging modality recognition [29], medical image registration [30], volumetric medical image segmentation [31], and differential diagnosis at brain MRI [32]. Nevertheless, zero-shot diagnosis of chest radiographs is mostly unexplored. To the best of our knowledge, apart from our recently published method [33], there exists no other method for the zero-shot diagnosis of chest radiographs. In [33], we find that an ensemble learning strategy with autoencoders may be useful for zero-shot diagnosis of chest x-rays. In the present work, we design a transductive GZSL method through multi-view semantic embedding with self-training for chest x-ray diagnosis. Although we use the proposed model for chest x-ray diagnosis, our design principle may be potentially extended to other modalities of radiology images as well.

III. Methods

In designing a GZSL method for the diagnosis of chest x-rays, we first divide the chest diseases and conditions of interest into seen and unseen classes. Next we consider the fact that the use of disease-specific auxiliary information from different independent sources may lead to improvement in performance [10]. Hence, we design a multi-view semantic embedding (MVSE) network using two semantic spaces constructed from x-ray reports and CT reports, respectively. Thus, x-ray reports and CT reports act as the sources of auxiliary information in our design. The motivation of using CT reports for the diagnosis of x-ray images stems from the following fact. All the diseases and conditions diagnosable from chest x-rays can also be diagnosed from chest CTs [34]. Therefore, chest CT reports may provide useful cues about such diseases.

However, the semantic spaces constructed from the above radiology reports do not explicitly incorporate the visual traits that a radiologist may use for the diagnosis of x-ray images. This causes the problem of semantic gaps [9] when we try to perform semantic embedding for x-ray images. To address this problem, we construct a third semantic space using visual traits that guides the semantic embeddings to the semantic spaces constructed from the x-ray and CT reports through guiding networks integrated inside the MVSE network. Thus, the visual traits are the third source of auxiliary information alongside x-ray reports and CT reports in our method.

Most radiology image datasets, including the ones we use, contain noisy labels that adversely affect training. To deal with this, we introduce a self-training step in our method. Self-training also helps to improve the performance of the model for unseen classes. From a functional perspective, the proposed method is divided into three steps, namely, pre-training, multi-view semantic embedding and self-training. The steps are described next. A schematic diagram of the proposed model is presented in Fig. 1.

Fig. 1.

A schematic diagram of the proposed method with the feature extractor and the multi-view semantic embedding (MVSE) network. In this diagram, Ψ_X (·), Ψ_CT (·) and Ψ_T (·) are the x-ray, CT and trait signatures corresponding to different diseases and conditions. The MVSE network has a common input layer (CIL) and two parallel branches (x-ray branch and CT branch) with guiding networks.

A. Pre-training

Pre-training involves two operational sub-steps. Those are: construction of semantic spaces and feature extraction.

1). Construction of Semantic Spaces:

Three semantic spaces are used in our model. These are as follows:

X-ray Semantic Space:

This semantic space is constructed from x-ray reports using the word2vec [35] model of [36]. The model, trained with x-ray reports outputs a vector of real numbers for each seen and unseen class. These vectors are referred to as x-ray signatures.

CT Semantic Space:

The CT semantic space, consisting of CT signatures is constructed using Intelligent Word Embedding [37], [38], a word2vec model. Note that the x-ray and CT signatures are generated offline from x-ray and CT reports, respectively, without paired images. Apart from signature generation, we do not use x-ray or CT reports in any stage of our method. Both the x-ray and CT semantic spaces only capture the semantic context of the corresponding radiology reports. They lack visual cues causing semantic gaps in embedding. To overcome this problem, we construct trait semantic space with the help of visual traits.

Trait Semantic Space:

In constructing trait semantic space, we utilize visual traits which radiologists use to recognize the diseases (classes) of interest. These traits (and their possible values) are: location (lung/pleura, or mediastinum), position (upper half of image, or lower half of image), opacity (high, medium, or low), distribution (focal, local, bilateral, or diffuse), border sharpness (clear-cut edge, or indistinctive edge), size (less than 25% of lungs, 25 to 50% of lungs, or more than 50% of lungs), and aspect ratio (low [round], or high [elongated]). A detailed description of visual traits for different diseases and conditions of interest are presented in the Appendix titled On the Visual Traits.

Since there are 18 possible values across 7 traits, we create 18-dimensional trait signatures for each disease of interest. Each dimension usually assume one of three values: 0, 0.5 or 1. These values are crude estimates of their frequency of occurrence for the given class of finding: 0 indicates relatively low (tending to zero) frequency, 1 indicates relatively high frequency, and 0.5 indicates uncertain or medium frequency. Thus the trait signatures provide a crude-form information obtained from the visual observation of a lesion by a radiologist.

2). Feature Extraction:

Prior to semantic embedding for GZSL, we extract visual features from x-ray images. A CNN based feature extractor [39] with DenseNet [23] backbone is used for this purpose. We choose this feature extractor because of its success in few-shot chest x-ray diagnosis [28]. DenseNet can utilize information from the seen classes for useful feature extraction through strengthening feature propagation and encouraging feature re-use during training. The output from the penultimate layer of the feature extractor network is used as the feature vector for an input chest x-ray image. Note that the feature extractor is trained with x-ray images of only the seen classes.

B. Multi-view Semantic Embedding

For generalized zero-shot diagnosis of a chest x-ray, we need to map the visual feature vector, extracted from the x-ray image, to the semantic signatures of a disease or condition from the set of diseases and conditions of interest. Recall that for each disease and condition of interest, we have three semantic signatures obtained from x-ray reports, CT reports and visual traits, respectively. We utilize these signatures in a way such that semantic embeddings are performed by minimizing semantic gaps between visual features and semantic signatures.

To this end, we design a multi-view semantic embedding (MVSE) network. This network aims to map the visual feature vector extracted from an x-ray image to the x-ray signature and CT signature corresponding to a disease or condition present in that x-ray image. We propose a novel approach to guide these mappings with the help of trait signatures.

Since our feature extractor is trained with images of only the seen classes, the feature vectors corresponding to the images of unseen classes are likely to be noisy. Additionally, as discussed earlier, there may be noisy labels associated with the training images (of seen classes) as well. Training the feature extractor with such noisy labels may encourage noise in feature vectors corresponding to the images of seen classes too. Autoencoders [40] are useful in dealing with noise in the input feature vectors. Therefore, we design the MVSE network using autoencoder architectures.

The MVSE network is a two-branch autoencoder with a common input layer (see Fig. 1). The visual feature vectors obtained from the feature extractor are applied to this layer. Each of the two branches of the MVSE network has an encoder-decoder architecture [40]. While one branch maps the visual feature vectors to the x-ray semantic space (x-ray branch), the other branch maps those feature vectors to the CT semantic space (CT branch). Let the dimension of each x-ray signature and CT signature be d. Then the x-ray branch and the CT branch have hidden layers of dimension d.

1). X-ray Branch & CT Branch:

Consider input feature vectors F applied to the common input layer of the MVSE network. The x-ray branch creates a hidden space representation H_X of F before reconstructing it as F_X at the output. Therefore H_X is a point in the x-ray semantic space. The CT branch performs similar operation by creating a hidden space representation H_CT for F and reconstructs it at the output as F_CT.

The hidden spaces of the x-ray branch and the CT branch are meant to be the x-ray and CT semantic spaces, respectively. Therefore, the hidden space representations of an input feature vector should ideally lie close to its corresponding semantic signatures in x-ray and CT semantic spaces. To ensure this, we use an embedding loss alongside the standard reconstruction loss of autoencoders at each branch.

Reconstruction Loss:

Both the x-ray and the CT branch of the MVSE network have a reconstruction loss component. For the x-ray branch with input feature vectors F and reconstructed output F_X, the reconstruction loss is

$$L_X^{re}=\Vert {\text{F}}_X-\text{F}\Vert .$$ (1)

The CT branch has a similar reconstruction loss. Considering the reconstructed output F_CT from the CT branch for input feature vectors F, the reconstruction loss for the CT branch is

$$L_{CT}^{re}=\Vert {\text{F}}_{CT}-\text{F}\Vert .$$ (2)

Embedding Loss:

The embedding loss components are meant to capture the proximity of projections in the hidden layer for the input feature vectors from their corresponding semantic signatures. Consider a data point n from class c. Let its projection in the hidden layers of x-ray branch and CT branch be H_X (n) and H_CT (n), respectively. In the x-ray semantic space, let D_X (n) be the distance between hidden layer projection H_X (n) and the x-ray signature of class c. Then for the set of training data N_tr, the embedding loss for the x-ray branch is

$$L_X^{em}=\sum _{n\in N_{\text{tr}}}{D}_X\left(n\right).$$ (3)

Similar embedding loss can be defined in CT branch. Let D_CT (n) be the distance between projection H_CT (n) and the CT signature of class c in the CT semantic space. The embedding loss for the CT branch is defined as

$$L_{CT}^{em}=\sum _{n\in N_{\text{tr}}}{D}_{CT}\left(n\right).$$ (4)

As mentioned earlier, semantic embeddings by minimization of the above loss functions are likely to give rise to semantic gaps [9] due to not having visual cues in the above semantic spaces. The problem of the gaps can be alleviated if embeddings can be guided by visual traits. Considering this fact, we utilize explicit visual cues through trait signatures. We introduce guiding networks to guide the semantic embeddings to the x-ray and CT semantic spaces.

2). Guiding Networks:

The guiding networks have an encoder-decoder architecture. There are two guiding networks (see Fig. 1), one integrated to the x-ray branch (abbreviated as GN-X) and the other to the CT branch (abbreviated as GN-CT). The goal of the guiding networks are to make the hidden space representations of the x-ray and CT branches richer in terms of visual cues.

Towards that end, GN-X takes H_X (the hidden space representations in x-ray branch) as input and projects it to a guiding hidden space which is meant to be the trait semantic space. Let the guiding hidden space representation of H_X by GN-X be H_X−G. In order to incorporate visual information in H_X from the trait semantic space, we want H_X−G to lie close to the corresponding trait signatures. This is achieved by the minimization of embedding loss in GN-X. Since guiding networks follow an autoencoder architecture, we also minimize standard reconstruction loss. Thus a guiding network is an autoencoder inside an autoencoder.

The guiding network of CT branch (GN-CT) also operates identically. H_CT, the hidden space representation of F in the CT branch as applied as input to the GN-CT. Let the guiding hidden space projection of H_CT in GN-CT be H_CT−G. The two guiding networks GN-X and GN-CT are trained by minimizing the following loss functions.

Reconstruction Losses of the Guiding Networks:

For GN-X, let the input be H_X, and the reconstructed output be $\widehat{{\text{H}}_X}$. Similarly, for GN-CT, let the output for input H_CT be $\widehat{{\text{H}}_{CT}}$. Then the reconstruction losses for GN-X and GN-CT, respectively, are

$$\begin{gathered} L_{X-G}^{re}=\Vert {\text{H}}_X-\widehat{{\text{H}}_X}\Vert , \\ {L}_{CT-G}^{re}=\Vert {\text{H}}_{CT}-\widehat{H_{CT}}\Vert . \end{gathered}$$ (5)

Embedding Losses of the Guiding Networks:

The embedding losses for the guiding networks measure the proximity of projections from trait signatures in the trait semantic space. For training data n, belonging to class c, let the hidden space representation by GN-X and GN-CT be H_X−G(n) and H_CT−G(n), respectively. Assume the distance of the corresponding trait signature (i.e. trait signature of class c) from H_X−G(n) in the trait semantic space of GN-X to be D_X−G(n) and that distance from H_CT−G(n) in the trait semantic space of GN-CT to be D_CT−G(n). Then the embedding losses for GN-X and GN-CT, respectively, are

$$\begin{gathered} L_{X-G}^{em}=\sum _{n\in N_{\text{tr}}}{D}_{X-G}\left(n\right), \\ {L}_{CT-G}^{em}=\sum _{n\in N_{\text{tr}}}{D}_{CT-G}\left(n\right). \end{gathered}$$ (6)

Minimization of the above loss components in the guiding network during the training of the multi-view semantic embedding network (MVSE) requires H_X (hidden space representation in x-ray branch) and H_CT (hidden space representation in CT branch) to contain meaningful visual information. Thus, through the use of the guiding networks, the representations of the input feature vectors in the x-ray and the CT semantic (hidden) spaces (i.e. H_X and H_CT) are made to have meaningful visual cues. This alleviates the problem of semantic gaps.

3). Training:

The training of the MVSE network involves training of the x-ray and CT branches and the corresponding guiding networks GN-X and CN-CT. In order to train the MVSE network, we first define the total loss of x-ray branch and the total loss of CT branch. The total loss of x-ray branch consists of reconstruction loss of x-ray branch (i.e. $L_X^{re}$) from (1), embedding loss of x-ray branch (i.e. $L_X^{em}$) from (3), reconstruction loss of GN-X (i.e. $L_{X-G}^{re}$) from (5), and embedding loss of GN-X ((i.e. $L_{X-G}^{em}$) from (6). The total loss of the x-ray branch is

$$L_X=L_X^{re}+\alpha L_X^{em}+\lambda \left(L_{X-G}^{re}+\alpha L_{X-G}^{em}\right),$$ (7)

where α is a pre-defined constant indicating the relative importance of reconstruction loss and embedding loss. The constant λ indicates the relative importance of the loss component of guiding network w.r.t. that of the x-ray branch. In a similar fashion, the total loss of the CT branch is

$$L_{CT}=L_{CT}^{re}+\alpha L_{CT}^{em}+\lambda \left(L_{CT-G}^{re}+\alpha L_{CT-G}^{em}\right),$$ (8)

Then, using the total losses of x-ray and CT branch, we define the total loss of the network

$$L=L_X+\gamma L_{CT},$$ (9)

with γ being a pre-defined constant indicating the relative important of x-ray and CT branches. The MVSE network is trained by minimizing the total loss L. Notice that the minimization of L enforces minimization of the loss of the guiding networks resulting in reduction of semantic gaps as discussed before.

C. Self-training of MVSE Network

Once the MVSE network is trained, we perform a self-training of the network. The novel self-training strategy helps to deal with the problem of noisy labels and improves the diagnosis of the unseen classes. For self-training, we form a self-training set with unlabeled x-ray images from both the seen and unseen classes.

Self-training involves two steps, initial inference and model fine-tuning. During initial inference, we predict class probabilities of images from the self-training set. Then for each seen and unseen class, we choose the M images identified by the trained MVSE network with the highest confidence. Finally, we fine-tune the model with these M images per class. Since the images used for self-training are the images predicted with the highest confidence by the MVSE network, it is less likely that their predicted labels would be incorrect. Therefore, self-training the MVSE network with these images (and the corresponding predicted labels) alleviate the problem of noisy labels that might be present in the initial training data. Also, since we use unlabeled images from unseen classes as well during self-training, the self-trained MVSE network is likely to have richer information about the unseen classes leading to improvement in performance. The steps of self-training are described next.

1). Initial Inference:

In this step, we use unlabeled images from the self-training set to find the top M images per seen and unseen classes, identified with the highest confidence by the trained MVSE network. Consider an input x-ray image I(n). Let R_X (n, k) be the distance between its projection in the x-ray semantic space and the x-ray signature of the k^th class. Also assume the distance between the projection of I(n) in the CT semantic space and the CT signature of the k^th to be R_CT (n, k). If R_X (n, k) is small, the x-ray branch should assign class label k to the self-training data n with more confidence. The same is true for the CT branch with R_CT (n, k). Therefore, we define the confidence of the x-ray branch in assigning class label k to self-training data n to be β_X (n, k) = 1/R_X (n, k); and that for the CT branch to be β_CT (n, k) = 1/R_CT (n, k). Consequently, the overall confidence of the trained MVSE network for assigning class label k to the self-training data n is

$$\beta \left(n,k\right)=\frac{1}{2}\left({\beta }_X\left(n,k\right)+{\beta }_{CT}\left(n,k\right)\right).$$ (10)

The top M self-training data per class (seen and unseen) based on the above confidence score are used for fine-tuning the model.

2). Model Fine-tuning:

The initial trained model of the MVSE network is next fine-tuned with the above top M data per class by minimizing the loss of (9). The self-trained model is used for generalized zero-shot diagnosis of chest x-rays.

D. Generalized Zero-shot Diagnosis of Chest X-rays

Since we design a GZSL method, the test chest x-ray image may belong to either seen or unseen classes. Consider a test image I(te). Let the extracted feature vector be F(te) with its projections H_X (te) and H_CT (te) in the x-ray and CT semantic spaces, respectively. Assume R_X (te, k) to be the distance of H_X (te) from the x-ray signature of class k. Similarly, consider R_CT (te, k) to be the distance of H_CT (te) from the CT signature of class k. The smaller the values of R_X (·, ·) and R_CT (·, ·), the higher the corresponding class probabilities. Hence considering a total of C classes, the class probability assigned to the test image by the x-ray branch and CT branch, respectively, are :

$$\begin{gathered} p_X\left(te,k\right)=\frac{{\left(R_X\left(te,k\right)\right)}^{-1}}{\sum _{k=1}^C{\left(R_X\left(te,k\right)\right)}^{-1}} \\ {p}_{CT}\left(te,k\right)=\frac{{\left(R_{CT}\left(te,k\right)\right)}^{-1}}{\sum _{k=1}^C{\left(R_{CT}\left(te,k\right)\right)}^{-1}}. \end{gathered}$$ (11)

To find out the final class probability assigned to the test x-ray image by the self-trained MVSE network, we assign a dynamic importance to the x-ray and CT branches. Since each branch has an autoencoder architecture, the importance is assigned based on the quality of reconstruction of the test feature vector F(te) by each of the branches. Following (1) and (2), we calculate the reconstruction error for F(te) in the x-ray and CT branches. Let these errors be E_X (te) and E_CT (te), respectively. We want the branch with the lower error to have a more significant role in the diagnosis of the particular test x-ray image. Therefore, the final class probability from the self-trained MVSE network for the test image is

$$p\left(te,k\right)=\frac{{\left(E_X\left(te\right)\right)}^{-1}{p}_X\left(te,k\right)+{\left(E_{CT}\left(te\right)\right)}^{-1}{p}_{CT}\left(te,k\right)}{{\left(E_X\left(te\right)\right)}^{-1}+{\left(E_{CT}\left(te\right)\right)}^{-1}}$$ (12)

Consequently, the class label assigned by the self-trained MVSE network is given by

$$c\left(te\right)=\underset{k}{\text{argmax}}\hspace{0.5em}p\left(te,k\right).$$ (13)

Thus the final diagnosis of an input x-ray is performed using the self-trained MVSE network.

E. Implementation Details

1). Signature Generators & Feature Extractor:

The signature generators for creating x-ray and CT signatures are implemented using word2vec [36] models. In particular, to design the CT signature generator, we use the Intelligent Word Embedding method [37], pre-trained on 117,816 CT reports (obtained from Stanford medical center and University of Pittsburgh medical center [37]). The x-ray signature is implemented by training the word2vec model of [36] using 112,120 Chest X-ray reports corresponding to the images of NIH chest x-ray dataset [41]. For both the signature generators, we use standard pre-processing of texts [37]. The above signature generators produce 160-dimensional signature vectors for each disease of interest.

We use DenseNet-121 following the weight initialization protocol of [39] to design the feature extractor. The model is trained by minimizing the summation of weighted binary cross-entropy losses [41] for multi-label chest x-ray disease classification on the seen classes with a mini-batch size of 16. We employ the Adam optimizer with the standard parameters (β₁ = 0.9 and β₂ = 0.999) [42] and an initial learning rate of 0.001 (with a decay factor of 10 whenever the validation loss reaches a plateau after an epoch) for training. The model with the lowest validation loss is used as the feature extractor. The feature extractor is frozen before training the MVSE network. We flatten the 1024 feature maps of dimensions 7×7 from the penultimate layer of DenseNet-121 to get a 50176-dimensional feature vector corresponding to each input x-ray image.

2). MVSE Network:

A two-branch autoencoder with a common input layer (CIL) is used for designing the MVSE network. CIL is a fully connected layer that maps the 50176-dimensional feature vectors from the feature extractor to 10000 dimensions. CIL is followed by a batch-normalization, an activation and a dropout layer with dropout probability 0.5. Subsequently, we have an x-ray branch and a CT branch, both with encoder-decoder architectures. The encoder layers of both the branches map 10000-dimensional output from CIL to 2048, 512 and 160 dimensions (hidden space), respectively. The decoder layers of both the branches perform the inverse operation by mapping 160-dimensional hidden space representations to 512, 2048, 10000 and 50176 dimensions, respectively. The encoder and decoder layers of both the branches (except the last encoder layer of x-ray branch) are followed by a batch-normalization, and an activation function. We use leaky ReLU (with a negative slope of 0.01) as the activation functions.

The guiding networks in the x-ray and CT branches also have encoder-decoder architectures. The encoder layers of the guiding networks of x-ray and CT branch map the 160-dimensional hidden space representations of the corresponding branches to 40 and 18 dimensions, respectively. The decoder layers map the 18-dimensional guiding hidden space representations to 40 and 160 dimensions, respectively. Each encoder and decoder layer of guiding networks is followed by batch-normalization. While the last encoder layers of the guiding networks use a ReLU activation, a leaky ReLU (with a negative slope of 0.01) activation is used after every other layer of the guiding networks.

During initial training of the MVSE network, we take a mini-batch size of 128. Self-training is performed with a mini-batch size of 32. The Adam optimizer with the standard parameters (β₁ = 0.9 and β₂ = 0.999) [42] is employed for both initial training and self-training. We use different combinations of seen and unseen classes for our experiments. Following are the values for α, λ, and γ for combinations 1, 2, and 3 (abbreviated C1, C2 and C3, respectively) for the initial training and self-training. The values of α for the initial training involving C1, C2 and C3 are 1, 0.0001, and 0.0001, respectively. The values for of α for self-training involving C1, C2 and C3 are 0.03, 0.0001, and 0.1, respectively. The values of λ for the initial training involving C1, C2 and C3 are 0.01, 0.01, and 1, respectively. The values of λ for self-training involving C1, C2 and C3 are 0.001, 0.01, and 1, respectively. The values of γ for the initial training involving C1, C2 and C3 are 1000, 1, and 0.1, respectively. The values of γ for self-training involving C1, C2 and C3 are 1000, 10, and 1000, respectively. The MVSE network is trained with one label corresponding to each training feature vector. If there are multiple labels associated with a training feature vector, we randomly choose one of those labels for training.

IV. Experiments & Results

A. Dataset & Experimental Settings

We use three different chest x-ray datasets for our experiments. These are the NIH chest x-ray dataset [41] (abbreviated as NIH), Open-i dataset [43] (abbreviated as Open-i), and a dataset created using the chest x-ray images mined from PubMed Central [44] (abbreviated as PMC). Frontal images from these datasets are used for our experiments. As explained earlier, the image labels of the above datasets are likely to be noisy due to the use of rule-based label extraction. Hence, we use a hand-labeled subset of 900 images from NIH dataset (abbreviated as NIH-900) [45] to evaluate the performance of our method on a dataset with less noisy labels. The NIH, NIH-900, Open-i and PMC datasets contain 11014, 508, 531, and 103 test images, respectively. We also perform experiments on a subset from the CheXpert dataset [46] containing 4236 images. Through these experiments, we look into the utility of the proposed method in the diagnosis of fracture and support devices as unseen classes from the CheXpert dataset alongside the aforementioned seen classes of different combinations from the NIH-900 dataset. IRB approvals have been obtained for the use of the images of the NIH [41] and NIH-900 [45] datasets and the corresponding reports. The research on the anonymized Open-i [43], PMC [44], and CheXpert [46] images did not require IRB approval.

While our model is trained using the training images of NIH dataset, it is tested on NIH-900, Open-i, PMC and the test images of NIH dataset. Therefore, the performance of our model on Open-i and PMC indicates the robustness of the proposed training across datasets from different sources. Images of the PMC dataset are obtained from the published research papers. As a result, these images may be of lower resolution compared to the images of the NIH dataset. Hence, the performance on PMC would indicate the applicability of our method on images of different qualities as well.

For our experiments, we consider nine classes of chest diseases and conditions, namely, cardiomegaly, consolidation, edema, effusion, emphysema, infiltration, nodule, pneumonia, and pneumothorax. The x-ray, CT and trait signatures for this nine classes are visualized in the corresponding semantic spaces through t-SNE plots in Fig. 2. We form three different combinations of seen and unseen classes from these. For each combination, three out of these nine classes are randomly selected (without replacement) as unseen classes while the rest are treated as seen classes. Note that the unseen classes of each combination are disjoint. We perform one set of experiments for each of the three combinations. The names of the unseen classes for each combination are presented in Table I (the rest of the nine classes are seen classes for the corresponding combination). While the trait signatures for most of these classes are obtained following the procedure mentioned in Section III-A, the trait signature for pneumonia is obtained by adding a small constant value to every dimension of the trait signature of consolidation due to their similarities of appearance. The initial learning rate for initial training (ILR-IN), initial learning rate for self-training (ILR-SE), and M (the number of data points per class used for self-training) for each combination are also presented in the table. We run the initial training for 15, 20, and 30 epochs, respectively, for combinations 1, 2, and 3. Self-training is performed through 32, 30, and 20 epochs, respectively, for combinations 1, 2, and 3. The datasets in our experiments are multi-label datasets. Hence, for an input images, if the class label predicted by our model matches with one of the ground-truth class labels, we consider it as a true positive diagnosis.

Fig. 2.

A visualization of the semantic spaces through t-SNE plots. The signatures corresponding to the different diseases and conditions of interest in the x-ray, CT and trait semantic spaces are presented using different colors.

TABLE I.

The name of the unseen classes, initial learning rate for initial training (ILR-IN), initial learning rate for self-training (ILR-ST), and number of data points per class used for self-training (M) for the different combinations (C) of the unseen and seen classes.

C	Unseen Classes	ILR-IN	ILR-ST	M
1	Cardiomegaly, Edema, Emphysema	10−6	10−6	25
2	Consolidation, Effusion, Pneumothorax	10−6	10−7	25
3	Infiltration, Nodule, Pneumonia	10−7	10−6	45

B. Comparisons and Analysis of Performance

Following the usual protocol, we evaluate the performance of the proposed GZSL method in terms of its performance for the seen and unseen classes [9], [12]. In particular, we evaluate recall on seen classes $\left({\mathrm{Re}}_{\mathcal{S}}\right)$, recall on unseen classes $\left({\mathrm{Re}}_{\mathcal{U}}\right)$, and the harmonic mean of the recall values for the seen and unseen classes $\left({\mathrm{Re}}_{\mathcal{H}}\right)$. The seen recall is the ratio of the sum of true positive detections for individual seen classes to the total number of examples in seen classes. The unseen recall is the sum of true positive detections for individual unseen classes to the total number of examples in unseen classes.

We consider several state-of-the-art methods for comparison. These methods are ESZSL [11], DeViSe [13], SAE [12], GMN [2], and GDAN [3]. However, each of the above competing methods can utilize only one semantic space in contrast to two semantic spaces (and a guiding semantic space) in the proposed method. Therefore, we train each competing method with x-ray and CT signatures separately and evaluate the corresponding performance. Hence, for each competing method, we have two sets of results; one corresponding to x-ray signatures (indicated by (X) following the name of the method) and the other corresponding to CT signatures (indicated by (CT) following the name of the method).

The performances of different methods for combination 1 of seen and unseen classes are presented in Table II. Notice that the proposed method outperforms all the competing methods for all the datasets in terms of ${\mathrm{Re}}_{\mathcal{H}}$ by a significant margin. For a GZSL method, the test data may come from either seen or unseen classes. Hence ${\mathrm{Re}}_{\mathcal{H}}$ (that takes into account both the seen recall and unseen recall) is the most important performance metric for GZSL. Thus we find that for combination 1 of seen and unseen classes, the proposed method is superior.

TABLE II.

Comparative performances of different methods in terms of seen recall $\left({\text{RE}}_{\mathcal{S}}\right)$, unseen recall $\left({\text{RE}}_{\mathcal{U}}\right)$ and harmonic mean of seen and unseen recall $\left({\text{RE}}_{\mathcal{H}}\right)$ for combination 1 of seen and unseen classes from TABLE I. Bold fonts indicate the best values in each column.

Methods	NIH				NIH-900				Open-i				PMC
	$\mathbf{\text{R}}{\mathbf{\text{e}}}_{\mathcal{S}}$	$\mathbf{\text{R}}{\mathbf{\text{e}}}_{\mathcal{U}}$	$\mathbf{\text{R}}{\mathbf{\text{e}}}_{\mathcal{H}}$		$\mathbf{\text{R}}{\mathbf{\text{e}}}_{\mathcal{S}}$	$\mathbf{\text{R}}{\mathbf{\text{e}}}_{\mathcal{U}}$	$\mathbf{\text{R}}{\mathbf{\text{e}}}_{\mathcal{H}}$		$\mathbf{\text{R}}{\mathbf{\text{e}}}_{\mathcal{S}}$	$\mathbf{\text{R}}{\mathbf{\text{e}}}_{\mathcal{U}}$	$\mathbf{\text{R}}{\mathbf{\text{e}}}_{\mathcal{H}}$		$\mathbf{\text{R}}{\mathbf{\text{e}}}_{\mathcal{S}}$	$\mathbf{\text{R}}{\mathbf{\text{e}}}_{\mathcal{U}}$	$\mathbf{\text{R}}{\mathbf{\text{e}}}_{\mathcal{H}}$
ESZSL(X)	38.14	0.00	0.00		38.63	0.00	0.00		29.34	0.00	0.00		25.71	0.00	0.00
ESZSL(CT)	24.23	1.42	2.68		32.67	0.00	0.00		45.10	0.00	0.00		30.00	0.00	0.00
DeVise(X)	0.00	34.79	0.00		0.00	14.90	0.00		0.00	22.07	0.00		0.00	21.21	0.00
DeVise(CT)	5.49	0.15	0.29		14.33	0.00	0.00		21.23	0.00	0.00		17.14	0.00	0.00
SAE(X)	29.57	8.00	12.59		30.67	9.13	14.08		34.25	10.39	15.94		11.43	9.09	10.13
SAE(CT)	29.17	8.63	13.32		29.67	9.62	14.52		29.45	11.43	16.47		11.43	12.12	11.76
GMN(X)	32.88	6.07	10.24		33.08	3.51	6.34		37.33	5.48	9.56		17.07	11.76	13.93
GMN(CT)	35.07	5.33	9.25		26.26	1.56	2.94		30.48	1.60	3.04		12.20	2.94	4.74
GDAN(X)	34.94	7.27	12.04		27.78	8.97	13.56		35.27	5.94	10.16		26.93	2.94	5.30
GDAN(CT)	32.14	8.95	14.00		29.80	6.24	10.32		31.51	4.57	7.98		31.71	5.88	9.92
Proposed	30.12	19.67	23.80		40.72	45.40	42.93		37.74	41.13	39.36		25.71	30.30	27.82

Similar trends may be observed from Fig. 3 (a) and Fig. 3 (b) where we have presented the results of different methods for combination 2 and combination 3, respectively. From these figures, it is evident that with rare exceptions, our method is better than other methods in terms of the harmonic mean of seen and unseen recall $\left({\mathrm{Re}}_{\mathcal{H}}\right)$. Notice that although some of the competing methods outperform the proposed method in terms of seen recall, those methods fall well behind our method in terms of the performance on the unseen classes. Therefore in terms of a balanced performance for both the seen and unseen classes, our method is found to be superior. The performance of the proposed method in terms of seen precision, unseen precision, and the harmonic mean of seen and unseen precision is presented in Table III. The seen precision is the ratio of the sum of true positive detections for individual seen classes to the sum of the total detections for individual seen classes. The unseen recall is the sum of true positive detections for individual unseen classes to the sum of the total detections for individual unseen classes.

Fig. 3.

Comparative performances of different methods in terms of seen recall, unseen recall and harmonic mean of seen and unseen recall (Harmonic Mean) for (a) combination 2, and (b) combination 3 of seen and unseen classes from Table I

TABLE III.

Performance of the proposed method in terms of seen precision $\left({\text{PR}}_{\mathcal{S}}\right)$, unseen precision $\left({\text{PR}}_{\mathcal{U}}\right)$, and harmonic mean of seen and unseen precision $\left({\text{PR}}_{\mathcal{H}}\right)$ for different combinations of seen and unseen classes from TABLE I.

	Test Dataset	${\mathbf{\text{Pr}}}_{\mathcal{S}}$	${\mathbf{\text{Pr}}}_{\mathcal{U}}$	${\mathbf{\text{Pr}}}_{\mathcal{H}}$
Combination 1	NIH	37.23	11.27	17.31
	NIH-900	49.64	33.76	40.19
	Open-i	28.17	48.11	35.53
	PMC	34.62	19.61	25.03
Combination 2	NIH	8.52	32.28	13.48
	NIH-900	28.16	36.8	31.9
	Open-i	36.75	20.54	26.35
	PMC	12.99	38.46	19.42
Combination 3	NIH	8.71	9.25	8.97
	NIH-900	22.08	15.16	17.98
	Open-i	40.76	13.99	20.83
	PMC	16.28	11.67	13.59

In reviewing Table I and Fig. 3, we find our method to be more consistent in performance across datasets from different sources compared to the competing counterparts. This is an important observation since we use the proposed model trained only on the NIH training dataset to evaluate performance on test datasets from different sources. This consistency indicates the robustness of our model across datasets, an important requirement in developing clinically applicable systems. Detection results on some example x-ray images from different datasets are presented in Fig. 4. The performance of our method for the PMC dataset demands special attention in this context. From Fig. 4, notice that the PMC images may contain external markings (such as an arrow in the PMC image of the second last column) as well. Given the difference in the quality of the PMC images (including the possible presence of such external markings) compared to the high-resolution training images, the performance of the proposed method is encouraging. We further statistically compare the performance of the proposed method with two of its closest competitors SAE(X) and SAE(CT). The comparison is performed through Wilcoxon Signed-Rank Test [47]. The results indicate that the performance of the proposed method in terms of harmonic mean is statistically significantly higher (p < 0.01) than that of SAE(X). Also, the performance of the proposed method in terms of harmonic mean is statistically significantly higher (p < 0.01) than that of SAE(CT).

Fig. 4.

The performance of the proposed method on chest x-ray images from different datasets for combination 3 of seen (S) and unseen classes (U). If the detected label matches with one of the ground truth labels, it is considered as a correct (green) detection; otherwise, it is considered as an incorrect (red) detection. The PMC image of the second last column is an example showing the presence of external marking (an arrow).

From the description of the visual traits in the Appendix titled On the Visual Traits, we find that different diseases and conditions of interest have different visual presentations in x-ray images. Therefore, when the feature extractor is trained with the images of seen classes from a particular combination of seen and unseen classes, the feature extractor learns to differentiate those seen classes based on their distinctive visual characteristics. These visual characteristics may also help to differentiate each unseen class of that combination from all other seen and unseen classes. In such a situation, our MVSE network is expected to achieve superior performance using the feature vectors from the feature extractor. However, if such visual characteristics are not helpful in discriminating different unseen classes from other seen and unseen classes, the performance of the MVSE network may not be good.

Consider combination 1. The seen classes are consolidation, effusion, pneumothorax, infiltration, nodule, and pneumonia. As evident from the description of the visual traits, the feature extractor is likely to differentiate the seen classes based on visual features related to six out of the seven visual traits, namely position, opacity, distribution, border sharpness, size, and aspect ratio. The feature extractor may not utilize the visual features related to the trait location since this trait does not help to differentiate among the seen classes. From the Appendix titled On the Visual Traits, we find that the visual features related to the aforementioned six visual traits are also useful for differentiating the unseen classes of combination 1 (i.e. cardiomegaly, emphysema, and edema). Therefore, for combination 1, the performance of the MVSE network is superior.

For the other two combinations, the seen classes include cardiomegaly which can be differentiated from all other classes merely based on visual features related to the trait location. Cardiomegaly is a dominant finding in our training dataset. As a result, for combinations 2 and 3, the feature extractor may rely predominantly on visual features related to the trait location. However, as evident from the descriptions of the visual traits, visual features based on location may not be useful for differentiating the other classes. This is likely to cause the inferior performance of our model for combinations 2 and 3.

We present several examples of incorrect diagnosis from the NIH-900 dataset in Fig. 5. There are several possible reasons why our method fails for these examples. First, small size of a lesion often makes it hard to detect. Consider the left most image in Fig. 5. Edema is a reasonable detected label for this image since the lungs have a diffusely reticular pattern. However, the ground truth label pneumothorax is tiny and hard to detect. Similarly, in the third image from left, our system misses the ground truth label nodule which is very tiny. Second, insufficient or incorrect ground truth labels may also cause failure of the method. Consider the second image from the left. The ground truth labels for this image should have included both edema and pneumonia. In that situation, the predicted label by the model (pneumonia) would have been a correct label and this would have been a true positive detection. However, because of the insufficient ground truth labels (ground truth label is edema), this example is considered as an incorrect detection. Finally, multiple factors together may be responsible for incorrect diagnosis. Consider the right most image in Fig. 5. It should have been a normal image since the blood vessels are very clear and numerous in both lungs. Therefore, the ground truth label cardiomegaly is incorrect. However, since our system assigns one of the nine target diseases and conditions to a query image, the detected label (edema in this case) is wrong. While we could not detect a normal image due to a design constraint (that our model has to assign one disease or condition to a query image), an incorrect ground truth label is also noted for this example. A normal versus abnormal chest x-ray classifier such as [48] might be useful in this context as a pre-processing step to filter normal chest x-ray images prior to applying chest x-rays in our model.

Fig. 5.

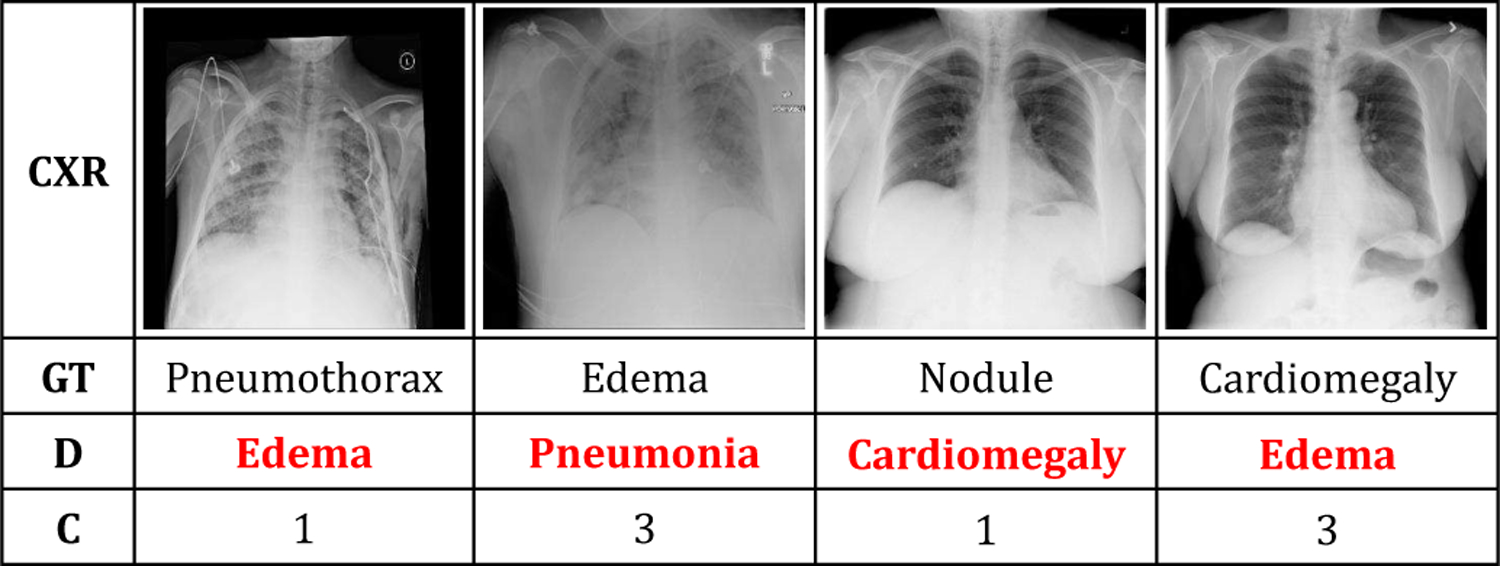
Examples of incorrect diagnosis in the NIH-900 dataset using the proposed method (CXR, GT, D, and C indicate chest x-ray images, ground truth labels, detected labels, and the combination of seen and unseen classes, respectively).

Next, we look into the role of self-training in our formulation. For this, we evaluate the different recall values using our method after the initial multi-view semantic embedding and after self-training. These values are presented in Table IV. Notice that in most of the cases, the harmonic mean values of seen and unseen recall have improved after self-training. In the majority of cases, this is due to improvement in unseen recall after self-training. This shows the utility of self-training in performance improvement, especially for the unseen classes.

TABLE IV.

The effect of self-training with different recall values (seen recall, unseen recall and harmonic mean of seen and unseen recall (Harmonic Mean) after the initial multi-view semantic embedding (Init) and after self-training (ST).

	Test Dataset	Seen Recall		Unseen Recall		Harmonic Mean
		Init	ST	Init	ST	Init	ST
Combination 1	NIH	33.22	30.12	15.3	19.67	20.95	23.8
	NIH-900	46.29	40.72	34.5	45.4	39.54	42.93
	Open-i	52.12	37.74	24.32	41.13	33.16	39.36
	PMC	31.43	25.71	12.12	30.3	17.5	27.82
Combination 2	NIH	7.66	8.68	33.22	31.9	12.45	13.65
	NIH-900	33.17	38.24	29.74	27.96	31.36	32.3
	Open-i	27.94	34.15	31.25	28.75	29.5	31.22
	PMC	20.34	16.95	25	22.73	22.43	19.42
Combination 3	NIH	20	9.28	3.22	8.83	5.54	9.05
	NIH-900	27.33	17.23	6.73	19.81	10.8	18.43
	Open-i	32.74	24.87	6.43	29.08	10.75	26.81
	PMC	15.28	9.72	9.68	22.58	11.85	13.59

Finally, we perform experiments involving classes outside the combinations presented in Table I. For this, we take the CheXpert [46] dataset. We choose fracture and support devices as unseen classes alongside the seen classes of combinations 1, 2, and 3 as mentioned in Table I. Following the existing experimental protocols, we do not use any labeled images of unseen classes for initial training or self-training. However, unlabeled images of different classes are used for self-training. Thus, for these experiments, the unseen classes in each combination are replaced by fracture and support devices. We also generate x-ray, CT and trait signatures for fracture and support devices offline prior to these experiments. The performance is evaluated on a mixed dataset that contains images of seen classes from the NIH-900 dataset, and images of unseen classes from a subset of the CheXpert dataset. The results of these experiments are reported in Table V. Notice that even with the new unseen classes from CheXpert dataset, the performance in two out of the three combinations (combinations 1, and 2) are comparable to the performances for the original combinations using the proposed method (see Table II, and Fig. 3 ). This shows the utility of the proposed method for the diagnosis of new unseen classes from a different dataset.

TABLE V.

Results on the mixed dataset containing images of seen classes from the NIH-900 dataset and images of unseen classes from the CheXpert dataset through seen recall $\left({\text{RE}}_{\mathcal{S}}\right)$, unseen recall $\left({\text{RE}}_{\mathcal{U}}\right)$ and harmonic mean of seen and unseen recall $\left({\text{RE}}_{\mathcal{H}}\right)$ for different combinations of seen classes.

Seen Combination	${\mathbf{Re}}_{\mathcal{S}}$	${\mathbf{Re}}_{\mathcal{U}}$	${\mathbf{Re}}_{\mathcal{H}}$
1	15.19	68.03	24.83
2	41.67	29.4	34.47
3	29.75	7.01	11.35

C. Ablation Studies

1). On Decision Making using the Two Branches:

In the proposed MVSE network, the final decision on the class label of an input is made using decisions from both the x-ray and CT branches. We look into the contribution of each branch in this decision making process. For this, we perform two sets of experiments, one using only the x-ray branch for decision making (abbreviated as MVSE (X)) and the other using only the CT branch (abbreviated as MVSE (CT)). The harmonic mean of recall values using the above experiments, alongside those using the proposed method are presented in Table. VI. While MVSE (X) show poor performance for most of the cases, the performance of MVSE (CT) is usually better. However, very rarely the performance of single branch (either x-ray or CT) is better than that of the proposed method. This justifies our decision making using the decisions from two branches instead of decision making using one of the branches. Thus, we conclude that both the branches are important in our design. The x-ray branch and the CT branch use x-ray and CT signatures, respectively, for decision making. Therefore, we also conclude that both the x-ray and CT signatures (generated from x-ray and CT reports, respectively) play important roles in the performance of our model.

TABLE VI.

Harmonic mean values of seen and unseen recall using only the x-ray branch of the MVSE network (MVSE (X)), only the CT branch of the MVSE network (MVSE (CT)), only the trait signatures (MVSE(T)), and the proposed method for different datasets and combinations.

	Dataset	MVSE (X)	MVSE (CT)	MVSE (T)	Proposed
Combination 1	NIH	0.00	23.61	7.28	23.8
	NIH-900	0.00	38.62	15.74	42.93
	Open-i	0.00	35.64	15.93	39.36
	PMC	0.00	24.35	0.00	27.82
Combination 2	NIH	10.99	1.26	7.39	13.65
	NIH-900	25.24	3.92	8.70	32.3
	Open-i	21.93	2.66	2.08	31.22
	PMC	10.76	0.00	3.36	19.42
Combination 3	NIH	5.90	11.67	8.56	9.05
	NIH-900	14.52	19.08	10.22	18.43
	Open-i	11.41	28.62	11.85	26.81
	PMC	9.70	10.99	12.95	13.59

2). Role of the Guiding Networks:

Next we look into the role of the guiding networks. For this, we calculate the harmonic mean of recall values using the proposed method without the guiding networks in x-ray and CT branches. The improvement in results obtained using the guiding networks in the proposed method compared to that obtained without the guiding networks in the proposed method are presented in Fig. 6. Notice that in eleven out of the twelve cases, there have been improvements due to the use of the guiding networks. These results clearly indicate the usefulness of visual traits employed through the guiding networks in the proposed design.

Fig. 6.

Percentage of improvements in harmonic mean values for different datasets and combinations from Table I using the proposed method with the guiding network compared to the proposed method without the guiding network.

3). On the Usefulness of Text-based Semantic Spaces:

We use two text-based semantic spaces constructed from radiology reports in our design. These are the x-ray and CT semantic spaces. Next we look into the importance of these two text-based semantic spaces in our design. To that end, we exclude the x-ray signatures and CT signatures from our design and use only the trait signatures for training and testing. Therefore, for this study, the network is trained without using the embedding loss of x-ray branch (see (3)) and the embedding loss of CT branch (see (4)) (since these are the loss components that use x-ray and CT signatures). Self-training is also performed in a similar fashion excluding the embedding losses of x-ray and CT branches. After self-training, the final diagnosis of an input x-ray image is performed using its projections in the hidden spaces of the guiding networks of x-ray branch and CT branch. Let these projections corresponding to an input query image I(te) be H_X−G(te) and H_CT−G(te), respectively. We evaluate the class probabilities following (11) using H_X−G(te) in place of H_X (te), H_CT−G(te) in place of H_CT (te), and trait signatures in place of x-ray and CT signatures. Using these class probabilities, we find the class label assigned to the query x-ray image following (12) and (13). Thus, we perform the diagnosis of input x-ray images through the use of only trait signatures in our network. The results of this ablation study are presented in Table VI alongside the performance of the proposed method. Notice that the performances using only the trait signatures are significantly inferior to that using the proposed method for all the datasets and combinations. This shows the utility of the text-based semantic space (x-ray and CT semantic spaces) in our design.

4). Effect of the Number of Data Points for Self-training:

During the self-training phase of our method, we use the top M data per class to self-train the model. A small value of M implies the use of a small number of data, identified with high confidence for self-training. On the other hand, when M is large, the number of data points for self-training is large. But those data includes the one identified with less confidence as well. Hence, it is non-trivial to find an optimal value of M. Towards this end, we calculate the harmonic mean values of seen and unseen recall by self-training our model with number of data points corresponding to different values of M. An example plot of harmonic mean values as a function of M has been presented in Fig. 7. Notice that for most of the datasets, the best value of harmonic mean is achieved for M = 45 in combination 3 of seen and unseen classes. Hence we choose M = 45 for combination 3. In the case of combinations 1 and 2, the best values are obtained for M = 25. Thus the number of data points for self-training affects the performance of our model. We find the optimal value of M through this study.

Fig. 7.

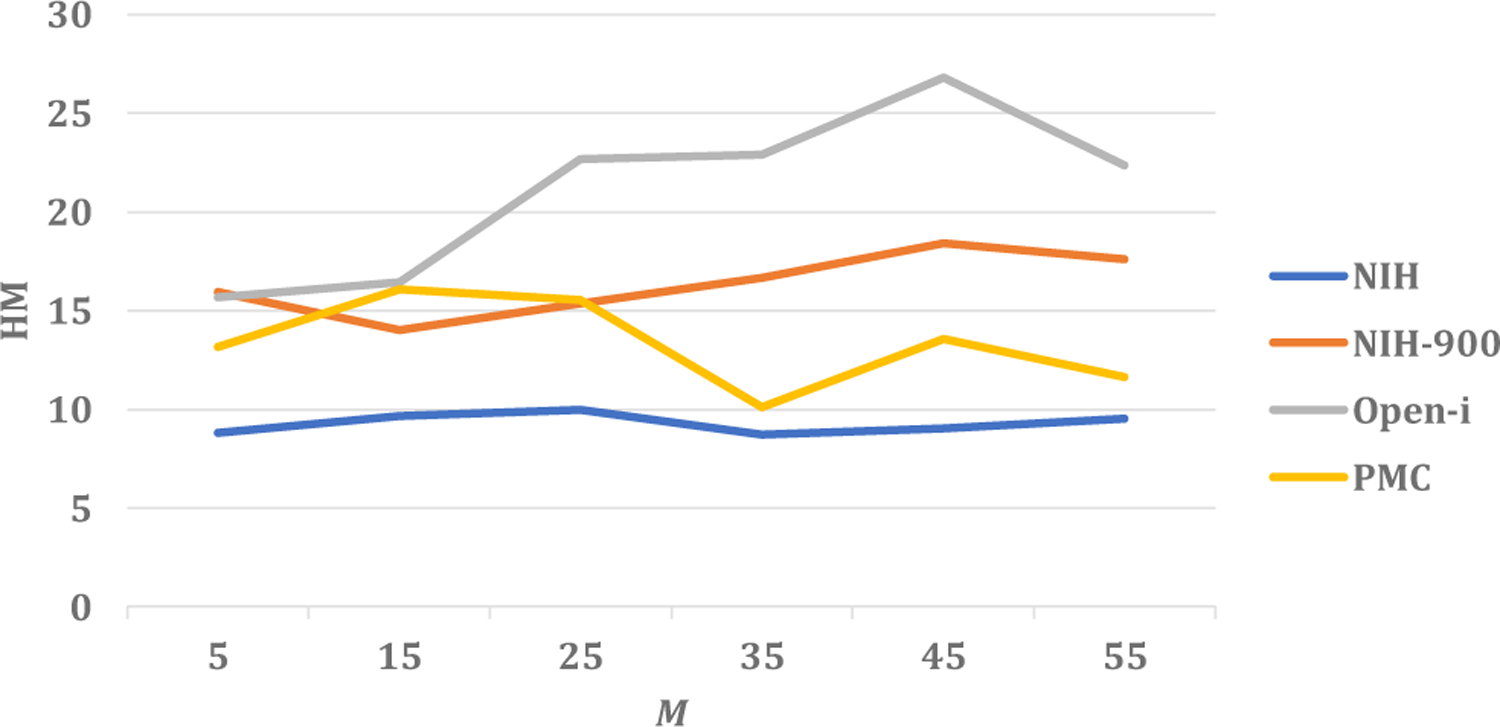
The harmonic mean values of seen and unseen recall (HM) for different values of the number of data per class for self-training (M) in case of combination 3 of seen and unseen classes.

5). On the Feature Extractor:

We use DenseNet-121 as our feature extractor. In order to look into the importance of DenseNet backbone for the feature extractor, we re-run all the experiments for every combination of seen and unseen classes and for all the datasets by using a feature extractor with a different backbone network. In particular, we take ResNet-18 [49] as the backbone network, and train the ResNet-based feature extractor with the images of seen classes for every combination. Thus, for training the ResNet-based feature extractor, we follow a training protocol similar to that of our DenseNet-based feature extractor. The 512 feature maps of dimensions 7 × 7 from the penultimate layer of ResNet-18 are flattened to obtain a 25088-dimensional feature vector corresponding to an input x-ray image. The initial training, and self-training of the proposed MVSE network and inference by the MVSE network after self-training are performed using these 25088-dimensional feature vectors following the protocols similar to the proposed method. The results obtained using these feature vectors from the ResNet-based feature extractor for the different combinations of seen and unseen classes and different test datasets are presented in Table VII. This table also shows the performance of the proposed method with the feature extractor having DenseNet-121 as the backbone network. Notice that the ResNet-based feature extractor performs better compared to our DenseNet-based feature extractor for the unseen. However, when it comes to the recall values for the unseen classes (and harmonic mean of seen and unseen recall values), the performance of ResNet-18 is significantly inferior compared to DenseNet-121. Thus, we conclude that the DenseNet-based feature extractor used in our method generalizes better for the unseen classes compared to its ResNet-based counterpart.

TABLE VII.

Performance of the MVSE network using feature extractor with ResNet-18 as backbone ( ResNet-18), and DenseNet-121 as backbone (Proposed) in terms of seen recall $\left({\text{RE}}_{\mathcal{S}}\right)$, unseen recall $\left({\text{RE}}_{\mathcal{U}}\right)$ and harmonic mean of seen and unseen recall $\left({\text{RE}}_{\mathcal{H}}\right)$ for different combinations (C) of seen and unseen classes.

C	Test Dataset	ResNet-18			Proposed
		${\mathbf{Re}}_{\mathcal{S}}$	${\mathbf{Re}}_{\mathcal{U}}$	${\mathbf{Re}}_{\mathcal{H}}$	${\mathbf{Re}}_{\mathcal{S}}$	${\mathbf{Re}}_{\mathcal{U}}$	${\mathbf{Re}}_{\mathcal{H}}$
1	NIH	36.18	8.74	14.08	30.12	19.67	23.80
	NIH-900	49.85	6.06	10.81	40.72	45.40	42.93
	Open-i	65.45	3.01	5.75	37.74	41.13	39.36
	PMC	31.43	6.06	10.16	25.71	30.30	27.82
2	NIH	20.01	2.33	4.17	8.68	31.90	13.65
	NIH-900	33.64	2.38	4.45	38.24	27.96	32.30
	Open-i	24.33	3.61	6.29	34.15	28.75	31.22
	PMC	16.95	0.00	0.00	16.95	22.73	19.42
3	NIH	27.77	7.94	12.35	9.28	8.83	9.05
	NIH-900	25.25	2.96	5.29	17.23	19.81	18.43
	Open-i	25.83	0.00	0.00	24.87	29.08	26.81
	PMC	23.61	3.23	5.68	9.72	22.58	13.59

V. Conclusions

We introduce a multi-view semantic embedding network, guided by visual traits for generalized zero-shot diagnosis of chest radiographs. The performance of the model is enhanced through a self-training that helps to deal with noise in labels alongside boosting the performance for unseen classes. The robustness of our method for datasets from different sources is established through rigorous experiments with different combinations of seen and unseen classes. The robustness achieved through our model may be potentially helpful in the development of a clinically applicable system from our proof-of-concept design. Through our experiments, we show that integrating auxiliary information from different complementary sources is beneficial for GZSL methods. It is also found that inclusion of visual traits for auxiliary information may help to alleviate the problem of semantic gaps in embedding leading to improvement in performance. Finally, self-training is found to have significant impact on the performance of a GZSL method, especially for the unseen classes. In the future, we would like to use the visual traits for finding trait-based salient image features to be utilized in a zero-shot diagnosis model. We would also look into alleviating the potential impact of class imbalance in our training data.

APPENDIX. On the Visual Traits

For our experiments, we consider nine classes of chest diseases and conditions, namely, cardiomegaly, consolidation, edema, effusion, emphysema, infiltration, nodule, pneumonia, and pneumothorax. These nine classes can be visually described using the following seven traits manually defined by a radiologist.

• Location: Anatomical location-wise, cardiomegaly is not within the lung area, while the other eight classes always occur within the lung area.

• Position: In terms of pixel position, edema and emphysema may appear in both the upper and lower portion of the images. Effusion and cardiomegaly often appear in the mid to lower part of the image, while the other four classes may appear in single or multiple random locations.

• Opacity: Among the diseases and conditions of our interest, pneumothorax and emphysema always have low opacities (air density), while the other seven classes may have medium (soft tissue density) to high (bone density) opacities. Bone density includes calcification in fracture, fibrosis, mass, and nodule.

• Distribution: Among the nine classes, edema and emphysema may appear on both left and right sides of the image. While nodules usually appear unilaterally, cardiomegaly always appears in the center. The other five classes appear randomly.

• Border Sharpness: The sharpness of the border of lesions corresponding to different diseases are different. Pneumothorax, effusion, and cardiomegaly always have clear-cut margins. However, the other six classes have indistinct margins.

• Size: The typical sizes of different lesions are different. Nodules are mostly less than 25% of the lung volume, whereas edema, infiltration, and emphysema may exceed 50% or more of the lungs. The other five classes are diverse in size.

• Aspect Ratio: Some lesions can be visually distinguished in terms of their shapes. Pneumothorax and effusion have linear shapes (high aspect ratios), while the other seven classes of lesions have round or varied shapes (low aspect ratios).

Thus, while some diseases may share certain imaging features in terms of the visual traits (for example, pneumothorax and effusion both have high aspect ratios), each disease possesses a unique set of visual traits.