Modeling the effects of preventive measures and vaccination on the COVID-19 spread in Benin Republic with optimal control

Abstract

Coronavirus disease (COVID-19) onset in December 2019 is a contagious disease caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). Since, the spread of the virus and mortality due to COVID-19 have continued to increase daily leading to a pandemic. In absence of approved medicine and vaccines, many countries imposed policies such as social distancing, mask wearing, hand washing, airport screening, quarantine and others. But rapidly, they were confronted with the high economic and social cost resulting from those policies. Many vaccines have been proposed but their efficiency is still controversial. Now, governments and scholars search for how manage with preventives measures policies and vaccination campaigns to stop the COVID-19 spread. This work studied the effects of these different strategies as time-dependent interventions using mathematical modeling and optimal control approach to ascertain their contribution in the dynamic transmission of COVID-19. The model was proven to have an invariant region and was well-posed. The basic reproduction number was computed with and without respect of preventives measures. The optimal control analysis was carried out using the Pontryagin’s maximum principle to figure out the optimal strategy necessary to curtail the disease. The findings revealed that the optimal implementation of preventive measures reduce highly the number of infected individuals but zero infection was not achieved in the population. That was obtained with the optimal implementation of vaccination campaigns which reduce the number of infected individuals. But the optimal and combined implementation of the two interventions performed better with less costs than the two singular implementations.

Introduction

Coronaviruses (CoVs) are a large family of zoonotic viruses, that means they are transmitted from animals to humans, and cause symptoms ranging from the common cold to more serious diseases such as Middle East Respiratory Syndrome (MERS), which is transmitted from dromedaries to humans, or Severe Acute Respiratory Syndrome (SARS), which is transmitted from civets to humans. Several known coronaviruses that have not yet infected humans and are circulating among some animals. Coronavirus disease onset in December 2019, called commonly “COVID-19”, is a contagious disease caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). The coronavirus SARS-CoV-2 is a new strain of coronavirus that had not yet been identified in humans, where respiratory symptoms, fever, cough are common signs of infection of the new coronavirus pandemic. In more severe cases, this disease can cause pneumonia, severe acute respiratory syndrome, kidney failure, and even death. For transmission, small droplets and aerosols containing the virus can be spread from the nose and mouth of an infected person while breathing, coughing, sneezing, singing or talking. Other people become infected if the virus enters their mouths, noses or eyes [1], [2], [3], [4].

Many countries imposed policies like closing social and professional interactions, lockdowns, curfew and other strict measures to guarantee social distancing. But rapidly, they have been confrontated to the high economic and human cost resulting from those policies.

Today several vaccines have been developed and several countries have launched mass vaccination campaigns, but it is still unclear to what extent vaccines protect not only against disease, but also against infection and transmission. Also, vaccines are not yet accepted in entire world population, leading each country to manage preventives measures policies to better in order to stop the crisis on its territory [5], [6]. According to the accessed data on 20/07/2021 from the Center for Systems Science and Engineering (CSSE) of Johns Hopkins University (JHU) (https://github.com/CSSEGISandData/COVID-19), the COVID-19 pandemic is growing day by day in Benin. There are more than 13,000 cases of COVID-19 infection and more than 120 deaths already reported. However, we notice a slackening of the population in the respect of the preventive measures and many persons do not understand the necessity of a COVID-19 vaccination campaign. And one of most important question is how vaccination campaigns will reduce or stop the pandemic of COVID-19. Given the severity of this pandemic, all resources are being mobilized for the “fight”. Mathematical modeling is a powerful tool and widely used in epidemiology for the prediction of new cases and the control of the transmission of epidemics.

Thus, many mathematical models have been proposed to study, understand the behavior of epidemics, forecast, and to control their spread within the population [7], [8], [9], [10], [11], [12], [13]. Indeed, mathematical models have provided information and give to the authorities a vision to take the right decisions on the effectiveness of the strategies implemented [14], [15], [16], [17]. When it comes to contagious diseases, it is common to use compartmental models, such as SIR or SEIR models or their variants to model the disease dynamics [18], [19].

Using compartmental models, researchers predict the spread of COVID-19 in many countries. Yang et al. [20] used compartmental models to predict the course of the pandemic in China under public health interventions. Tiwari et al. [21] analyzed and predicted the evolution of the COVID-19 pandemic during a period of containment in India. Their aim is to provide a more precise prediction of epidemic peak and to evaluate the impact of lockdown on epidemic peak shift in India. Zamir et al. [22] formulated a mathematical model to analyze the transmission of the infection through different human compartments. Madubueze et al. [23] studied the effect of different control strategies as time-dependent interventions using mathematical modeling and optimal control approach to ascertain their contribution in the dynamic transmission of COVID-19. Zakary et al. [24] tried to estimate and predict the situation of the new coronavirus pandemic (COVID-19) in countries under quarantine measures. To do that, they propose discrete-time mathematical model describing the evolution of the COVID-19 in a population under quarantine and investigate the impact of people who underestimate the quarantine by considering an optimal control strategy to reduce this category. Etxeberria-Etxaniz et al. [25] investigated a susceptible–exposed–infectious–recovered (SEIR) epidemic model with demography under two vaccination effort strategies. Firstly, the model is investigated under vaccination of newborns, secondly it is investigated under a periodic impulsive vaccination on the susceptible in the sense that the vaccination impulses are concentrated in practice in very short time intervals around a set of impulsive time instants subject to constant inter-vaccination periods. Silva et al. [26] proposed a forecasting mathematical model to test various scenarios of pandemic management, ensuring the responsiveness of the health system in Portugal. By analyzing social media, they identificate the population readiness to follow social restrictions, and incorporate this effect in a version of the model. Also, they applied optimal control theory to maximize the number of people returning to “normal life” and minimizing the number of active infected individuals with minimal economical costs while warranting a low level of hospitalizations. MacIntyre et al. [27] used a compartmental model to analyze the impact of vaccination of newborns, of periodic vaccination on the evolution of the COVID-19 pandemic.

Moreover, in most of previously listed works, authors did not consider the fact that the immunity of recovered people is not permanent, but it is proven that after a period recovered people can be infected again [28], [29]. Also, there is no body of knowledge about the simultaneous effect of vaccination campaigns and preventive measures policies on the evolution of COVID-19 in Benin. This paper presents a model to analyze the evolution of COVID-19 in countries with a health situation like Benin. We performed an optimal control on the policies implemented with respect to preventive measures, and to vaccination campaign to see the impact they could have on the spread of COVID-19 within the population.

Model formulation

In this section, the formulation of a deterministic model for COVID-19 is presented. The model is extended from SEIRD model by incorporating the compartment $J$ of infected persons not knowing their infection. This compartment is added to take into account the infected people who are asymptomatics or who confuse their infection by COVID-19 with other diseases (such as malaria which presents sometimes same symptoms as COVID-19). Those people are a lot in countries where there is no health monitoring system and many people do not go to hospital. They must be taken into account because they might participate the most in the spread of COVID-19. The total population $N$(t) at time $t$ is divided into six (06) subpopulations. That is susceptible humans $S$(t), exposed humans $E$(t), humans infected with COVID-19 disease who are tested positive $I$(t), humans infected with COVID-19 disease but not knowing their infected status $J$(t), recovered humans $R$(t) and humans who died from COVID-19 $D$(t). Therefore,

$$N\left(t\right)=S\left(t\right)+E\left(t\right)+I\left(t\right)+J\left(t\right)+R\left(t\right)$$ (1)

In the Susceptible compartment, S(t), people are recruited into the population at a constant rate, $\Lambda$, through immigration/birth of no risk population and through a proportion, $p$, of exposed individuals that return to susceptible compartment after incubation period without COVID-19 infection. People exit the susceptible compartment through infection induced by the disease with the force of infection, $\Psi$ such as:

$$\Psi =\beta (J+a_{1}E+a_{2}I)/N$$ (2)

where $a_1$, $a_2$, are the modification factors for the exposed and known infected individuals.

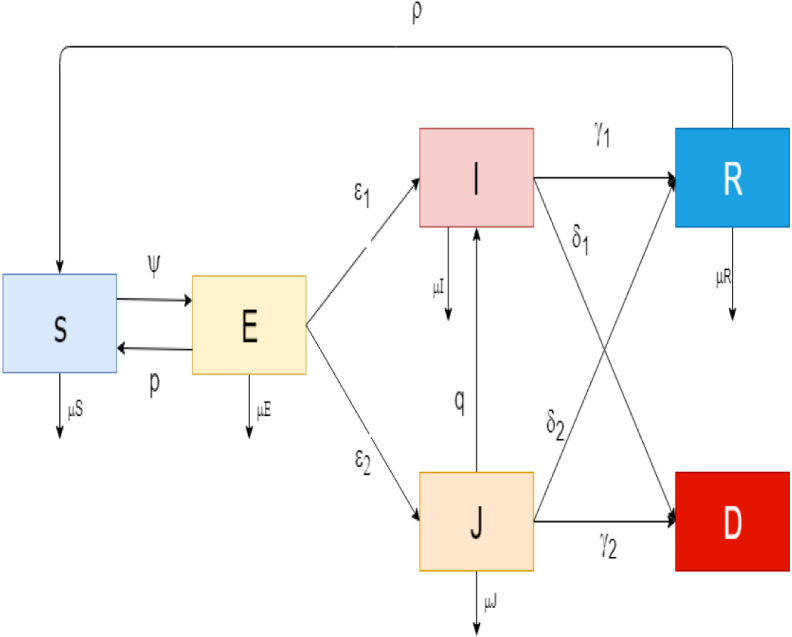
The description of the parameters in the COVID-19 model is presented in Table 1. The system diagram for the transmission of COVID-19 is shown in Fig. 1. From the schematic diagram in Fig. 1, the model equations are derived as follows:

$$\left\{\begin{array}{c}\frac{dS}{dt}=-(\Psi +\mu )S+pE+\rho R+\Lambda \hfill \\ \frac{dE}{dt}=\Psi S-(p+{\varepsilon }_1+{\varepsilon }_2+\mu )E\hfill \\ \frac{dI}{dt}={\varepsilon }_{1}E+qJ-({\gamma }_1+{\delta }_1+\mu )I\hfill \\ \frac{dJ}{dt}={\varepsilon }_{2}E-(q+{\gamma }_2+{\delta }_2+\mu )J\hfill \\ \frac{dR}{dt}={\gamma }_{1}I+{\gamma }_{2}J-(\rho +\mu )R\hfill \\ \frac{dD}{dt}={\delta }_{1}I+{\delta }_{2}J\hfill \end{array}\right)$$ (S)

Table 1.

Description of the model parameters.

Parameters	Description
$\Lambda$	Recruitment rate of individuals
$\beta$	Transmission rate
$a_1$	Contribution factor of exposed to the force of infection
$a_2$	Contribution factor of infected who are tested positive to the force of infection
$\rho$	Rate at which recovered individuals loss their immunity
$p$	Rate of exposed individuals returning in susceptible compartment
${\varepsilon }_1$	Progression rate from exposed to infected tested positive compartment
${\varepsilon }_2$	Progression rate from exposed to undiscovered infected compartment
$q$	Progression rate from undiscovered infected to infected tested positive compartment
${\gamma }_1$	Recovery rate of infectious individuals tested positive
${\gamma }_2$	Recovery rate of undiscovered infectious individuals
${\delta }_1$	The death-induced rate for infectious individuals tested positive
${\delta }_2$	The death-induced rate for undiscovered infectious individuals
$\mu$	Natural death rate

Fig. 1.

The diagram of the COVID-19 model.

Model analysis

In this section, we will carry out the quantitative study of COVID-19 which involves the positivity and boundedness of the solutions, invariant region of the COVID-19 model and existence of equilibrium points for COVID-19 model.

Using $S=\frac{S}{N}$, $E=\frac{E}{N}$, $I=\frac{I}{N}$, $Q=\frac{Q}{N}$ and $R=\frac{R}{N}$ to normalize the system (3), we obtain:

$$\left\{\begin{array}{c}\frac{dS}{dt}=-(\beta (J+a_{1}E+a_{2}I)+\mu )S+pE+\rho R+\Lambda \hfill \\ \frac{dE}{dt}=\beta (J+a_{1}E+a_{2}I)S-(p+{\varepsilon }_1+{\varepsilon }_2+\mu )E\hfill \\ \frac{dI}{dt}={\varepsilon }_{1}E+qJ-({\gamma }_1+{\delta }_1+\mu )I\hfill \\ \frac{dJ}{dt}={\varepsilon }_{2}E-(q+{\gamma }_2+{\delta }_2+\mu )J\hfill \\ \frac{dR}{dt}={\gamma }_{1}I+{\gamma }_{2}J-(\rho +\mu )R\hfill \\ \frac{dD}{dt}={\delta }_{1}I+{\delta }_{2}J\hfill \end{array}\right)$$ (SR)

Invariant region, positivity and boundedness of solution

Positivity of solution

Theorem 1

Let the initial solution satisfy $S\left(0\right)\ge 0$ , $E\left(0\right)\ge 0$ , $I\left(0\right)\ge 0$ , $J\left(0\right)\ge 0$ , $R\left(0\right)\ge 0$ . So, the model has nonnegative solutions $\forall t>0$ .

Proof

From the system (SR):

$$\frac{dS}{dt}=-\left[(\beta (J+a_{1}E+a_{2}I)+\mu )\right]S+pE+\rho R+\Lambda \ge \Lambda -(\beta (J+a_{1}E+a_{2}I)+\mu )S$$ (3)

Using Grönwall’s lemma, Eq. (3) can be expressed as:

$$S\left(t\right)\ge S\left(0\right)e^{B\left(t\right)}+{\int }_0^t\Lambda \left(e^{B\left(t\right)-B\left(u\right)}\right)du>0$$ (4)

where

$$B\left(t\right)={\int }_0^t-[\beta (J+a_{1}E+a_{2}I)+\mu ]du$$

In the same way, we can prove that $E\left(t\right)\ge 0$, $I\left(t\right)\ge 0$, $J\left(t\right)\ge 0$, $R\left(t\right)\ge 0$.

Invariant region

The solutions of the model are uniformly bounded in a positive invariant region $\Omega$.

$$\Omega =\{(S\left(t\right),E\left(t\right),I\left(t\right),J\left(t\right),R\left(t\right))\in {\mathbb{R}}_5^{+}:N\left(t\right)\le \frac{\Lambda }{\mu }\}$$ (5)

The variation of total population at any time $t$ is:

$$\frac{dN}{dt}=\Lambda -\mu N-{\delta }_{1}I-{\delta }_{2}J\le \Lambda -\mu N$$ (6)

By solving Eq. (6) using Groonwall’s lemma, we obtain:

$$N\left(t\right)\le N\left(0\right)e^{-\mu t}+\frac{\Lambda }{\mu }(1-e^{-\mu t})$$ (7)

When, $t⟼\infty ,N\left(0\right)\le max(N\left(0\right),\left(\frac{\Lambda }{\mu }\right))$. Hence, the nonnegative solution set of the model equations (SR) enters the feasible region, $\Omega$, which is a positively invariant set.

Boundedness of the solution

Theorem 2

The initial solutions $S\left(0\right)$ , $E\left(0\right)$ , $I\left(0\right)$ , $J\left(0\right)$ , $R\left(0\right)$ are bounded. That is,

$$\underset{t\to \infty }{lim\; sup}N\left(t\right)\le \frac{\Lambda }{\mu }$$ (8)

Proof

From Eq. (6),

$$\frac{dN}{dt}=\Lambda -\mu N-{\delta }_{1}I-{\delta }_{2}J$$ (9)

Also, $0<I\left(t\right)\le N\left(t\right)$ and $0<J\left(t\right)\le N\left(t\right)$ Hence,

$$\Lambda -(\mu +{\delta }_1+{\delta }_2)N\left(t\right)\le \frac{dN\left(t\right)}{dt}\le \Lambda -\mu N\left(t\right)$$ (10)

This can be written as,

$$\frac{\Lambda }{(\mu +{\delta }_1+{\delta }_2)}\le \underset{t\to \infty }{lim\; inf}N\left(t\right)\le \underset{t\to \infty }{lim\; sup}N\left(t\right)\le \frac{\Lambda }{\mu }$$ (11)

Existence of disease-free equilibrium (DFE) state

The “Disease Free Equilibrium State”, $E_0$, is obtained when there are no infected people in the population and no new infected immigrants into the population. $E_0$ is obtained by solving the system:

$$\left\{\begin{array}{c}\frac{dS}{dt}=0\hfill \\ \frac{dE}{dt}=0\hfill \\ \frac{dI}{dt}=0\hfill \\ \frac{dJ}{dt}=0\hfill \\ \frac{dR}{dt}=0\hfill \\ \frac{dD}{dt}=0\hfill \end{array}\right)$$ (12)

with $I=0$ and $J=0$.

And we find:

$$E_0=\{\frac{\Lambda }{\mu },0,0,0,0,0\}.$$

Existence of endemic equilibrium point

Endemic equilibrium point ($E_1$) exists when $I$ is non-zero and by setting the derivatives on the right-hand side equations of COVID-19 model (SR) to be zero.

By solving these simultaneously, we obtain the endemic equilibrium point, $E_1=(S^{\ast },E^{\ast },I^{\ast },J^{\ast },R^{\ast })$, where:

$$S^{\ast }={\beta }^{-1}\frac{fgh}{{\varepsilon }_{2}h+{\varepsilon }_{1}g{a}_2+{\varepsilon }_{2}q{a}_2+gh{a}_1}$$$$J^{\ast }=\frac{{\epsilon }_{2}h(\rho +\mu )(\Lambda -\mu S^{\ast })}{\rho {\gamma }_1({\epsilon }_{1}g+{\epsilon }_{2}q)+\rho {\gamma }_2{\epsilon }_{2}h-(\rho +\mu )({\epsilon }_1+{\epsilon }_2+\mu )gh}$$$$E^{\ast }=\frac{g}{{\epsilon }_2}{J}^{\ast }$$$$I^{\ast }=\frac{{\epsilon }_{1}g+{\epsilon }_{2}q}{{\epsilon }_{2}h}{J}^{\ast }$$$$R^{\ast }=\frac{{\gamma }_1{\epsilon }_{1}g+{\gamma }_1{\epsilon }_{2}q+{\gamma }_2{\epsilon }_{2}h}{{\epsilon }_2(\rho +\mu )h}{J}^{\ast }$$ (13)

with

$$f=p+{\varepsilon }_1+{\varepsilon }_2+\mu$$$$g={\gamma }_2+{\delta }_2+q+\mu$$$$h={\gamma }_1+{\delta }_1+\mu$$ (14)

Basic reproduction number

The $R_0$ is the average number of people that an infected person can infect. This rate is applied to calculate from a population that is entirely susceptible to infection, $i.e.$, that has not yet been vaccinated or immunized against the infectious agent. It is also used to determine the minimum proportion of a population $\left(P\right)$ that must be immunized by natural infection or by vaccination (if available) to prevent the onset or persistence of an epidemic: $P=1-\frac{1}{R_0}$.

There are several techniques to calculate the basic reproduction number $R_0$, and in this work we used the “Next Generation Methods” of Driessche and Watmough, where $R_0$ is the spectral radius of the “Next Generation” matrix. So, to construct this matrix, first, we define the transmission and transition function matrix respectively $F$ and $V$ defined from the system (SR).

The rates of new infections and the transfer from in and out the infected compartments are given respectively by:

$$F=\left[\begin{array}{c}\hfill \psi S\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right]\text{and}V=\left[\begin{array}{c}\hfill fS\hfill \\ \hfill -{\varepsilon }_{1}E-qJ+hI\hfill \\ \hfill -{\varepsilon }_{2}E+gJ\hfill \end{array}\right]$$ (15)

The partial derivatives of $F$ and $V$ at the “Disease Free Equilibrium State”, $E_0$, yield:

$$U=\frac{\beta \Lambda }{\mu }\left[\begin{array}{ccc}\hfill a_1\hfill & \hfill a_2\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\text{and}V=\left[\begin{array}{ccc}\hfill f\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\varepsilon }_1\hfill & \hfill h\hfill & \hfill -q\hfill \\ \hfill -{\varepsilon }_2\hfill & \hfill 0\hfill & \hfill g\hfill \end{array}\right]$$ (16)

$R_0$ is the spectral radius of the matrix, $U{V}^{-1}$ is given as:

$$R_0=\beta \Lambda \frac{{\varepsilon }_{2}h+{\varepsilon }_{1}g{a}_2+{\varepsilon }_{2}q{a}_2+gh{a}_1}{\mu fgh}$$ (17)

Table 2.

Value of parameters of the model (3).

Parameters	Value	Source
$\beta$	0.25	[23]
$a_1$	0.30	[23]
$a_2$	0.10	[23]
$\rho$	0.0056	[28]
$p$	0.0962	Estimated
${\varepsilon }_1$	0.0385	Estimated
${\varepsilon }_2$	0.0577	Estimated
$q$	0.0107	Estimated
${\gamma }_1$	0.0389	Fitted
${\gamma }_2$	0.0246	[23]
${\delta }_1$	0.0008307	Fitted
${\delta }_2$	0.0003571	Estimated
$\mu$	0.003324588	[30]

Optimal control model

Optimal control is one of the important tools used in mathematical biology to eradicate or minimize the rate of infection in exposed and infected humans in the population. In order to minimize COVID-19 transmission, we propose a model which is an extension of the model (3) by incorporating two control measures into the model. These are $\alpha$, the public health education effort being made by government, resulting from educating the population, through social media, television, radio and local communities in the community, to observe social distancing and hand washing, to avoid groupings; the establishment of sanitary cords; containments, curfews. And $\eta$ the vaccination effort, representing the rate of people vaccinated at each time t. We assume here, that the immunity is not permanent, $i.e.$ a vaccinated person can still be infected after a while just like people who have been cured.

By introducing those parameters in the model (3), the control model is given by:

$$\left\{\begin{array}{c}\frac{dS}{dt}=-((1-\alpha )\Psi +\eta +\mu )S+pE+\rho R+\Lambda \hfill \\ \frac{dE}{dt}=(1-\alpha )\Psi S-(p+{\varepsilon }_1+{\varepsilon }_2+\mu )E\hfill \\ \frac{dI}{dt}={\varepsilon }_{1}E+qJ-({\gamma }_1+{\delta }_1+\mu )I\hfill \\ \frac{dJ}{dt}={\varepsilon }_{2}E-(q+{\gamma }_2+{\delta }_2+\mu )J\hfill \\ \frac{dR}{dt}={\gamma }_{1}I+{\gamma }_{2}J+\eta S-(\rho +\mu )R\hfill \end{array}\right)$$ (S’)

with the initial conditions, $S\left(0\right)\ge 0$, $E\left(0\right)\ge 0$, $I\left(0\right)\ge 0$, $J\left(0\right)\ge 0$, $R\left(0\right)\ge 0$.

Description of optimal control

In this section, we minimize the total number of infected people in the population using the control variables in the model. We define the cost function as:

$$C(\alpha \left(t\right),\eta \left(t\right))={\int }_0^{t_f}(I\left(t\right)+\frac{1}{2}{c}_1\alpha {\left(t\right)}^2+\frac{1}{2}{c}_2\eta {\left(t\right)}^2)dt$$ (18)

where $\alpha \left(t\right)$ et $\eta \left(t\right)$ are assumed to be bounded and Lebesgue measurable time-dependent functions on the interval $[0,t_f]$. The control effort set is defined as:

$$\Phi =\{(\alpha \left(t\right),\eta \left(t\right)),0<\alpha \left(t\right)<1,0<\eta \left(t\right)<1\}$$

The terms $\frac{1}{2}{c}_1\alpha {\left(t\right)}^2$ et $\frac{1}{2}{c}_2\eta {\left(t\right)}^2$ represent respectively the costs associated with preventive measures policies and vaccination. The parameters $c_1$ et $c_2$ being the balancing factors associated to these costs. Based on the literature for the optimal control of epidemics, the cost of the controls is assumed to be nonlinear and quadratic. [23].

Existence of the optimal control

The necessary conditions that an optimal solution must satisfy are obtained by applying the Pontryagin’s Maximum Principle to the equations of control model. This principle converts system (S’) and the cost function (Eq. (18)) into a problem of minimizing pointwise Hamiltonian, $H$, given as:

$$H\left(t\right)=(I\left(t\right)+\frac{1}{2}{c}_1\alpha {\left(t\right)}^2+\frac{1}{2}{c}_2\eta {\left(t\right)}^2)+{\lambda }_1\left(\frac{dS}{dt}\right)+{\lambda }_2\left(\frac{dE}{dt}\right)+{\lambda }_3\left(\frac{dI}{dt}\right)+{\lambda }_4\left(\frac{dJ}{dt}\right)+{\lambda }_5\left(\frac{dR}{dt}\right)$$ (19)

where ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4$, ${\lambda }_5$ denote the associated co-states variables for the state variables $S,E,I,J,R$. The existence of optimal control of the model (S’) would be considered by applying the following theorem.

Theorem 3

There exists an optimal control$(\alpha {\left(t\right)}^{\ast },\eta {\left(t\right)}^{\ast })$such as the control model(S’)with initial conditions at $t=0$ and

$$C(\alpha {\left(t\right)}^{\ast },\eta {\left(t\right)}^{\ast })=\underset{(\alpha \left(t\right),\eta \left(t\right)\in \Phi )}{min}C(\alpha \left(t\right),\eta \left(t\right))$$ (20)

Proof

The states variables and control variables of the model are positive values and the control set $\Phi$ is close and convex. The objective function $C$ (Eq. (18)) is a convex function of $(\alpha {\left(t\right)}^{\ast },\eta {\left(t\right)}^{\ast })$ on the control set $\Phi$. Since the state solutions are bounded, then Lipschitz property of the state system with respect to the state variables is satisfied. It can also be seen that:

$$\exists u_1,u_2\ge 0,\epsilon \ge 1/C(\alpha \left(t\right),\eta \left(t\right))\ge u_1{({\left|\alpha \right|}^2+{\left|\eta \right|}^2)}^{\epsilon /2}-u_2$$ (21)

Therefore, the state variables are bounded and the existence of optimal control of the model is concluded.

Uniqueness of the optimal control

Theorem 4

Given$(S^{\ast },E^{\ast },I^{\ast },Q^{\ast },R^{\ast })$an optimal state solutions associated with optimal control$(\alpha {\left(t\right)}^{\ast },\eta {\left(t\right)}^{\ast })$for the optimal control problem in model(S’)and Eq. (20) , the co-states $({\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4,{\lambda }_5)$ verify the system (A) with the transversality conditions in Eq. (24) , and the control variables $(\alpha {\left(t\right)}^{\ast },\eta {\left(t\right)}^{\ast })$ verify Eq. (25) .

Proof

Differentiating the Hamiltonian function $H$ with respect to $S$, $E$, $I$, $J$ and $R$, the differential equations governing the co-states variables are obtained as follows:

$$\left\{\begin{array}{c}\frac{d{\lambda }_1}{dt}=-\frac{\partial H}{\partial S},{\lambda }_1\left(t_f\right)=0\hfill \\ \frac{d{\lambda }_2}{dt}=-\frac{\partial H}{\partial E},{\lambda }_2\left(t_f\right)=0\hfill \\ \frac{d{\lambda }_3}{dt}=-\frac{\partial H}{\partial I},{\lambda }_3\left(t_f\right)=0\hfill \\ \frac{d{\lambda }_4}{dt}=-\frac{\partial H}{\partial J},{\lambda }_4\left(t_f\right)=0\hfill \\ \frac{d{\lambda }_5}{dt}=-\frac{\partial H}{\partial R},{\lambda }_5\left(t_f\right)=0\hfill \end{array}\right)$$ (22)

with $t\in [0,t_f]$.

Let:

$${\Psi }_1=\frac{J+a_{1}E+a_{2}I}{N}$$ (23)

From Eq. (22), we obtain the following systems of equations:

$$\left\{\begin{array}{c}\begin{array}{cc}\hfill \frac{d{\lambda }_1}{dt}=& ({\lambda }_1-{\lambda }_2)(1-\alpha \left(t\right))\beta {\Psi }_1(1-\frac{S}{N})\hfill \\ \hfill & +({\lambda }_1-{\lambda }_5)\eta \left(t\right)+\mu {\lambda }_1\hfill \\ \hfill \frac{d{\lambda }_2}{dt}=& ({\lambda }_2-{\lambda }_3){\varepsilon }_1+({\lambda }_2-{\lambda }_4){\varepsilon }_2\hfill \\ \hfill & +({\lambda }_1-{\lambda }_2)(1-\alpha \left(t\right))\frac{\beta }{N}(a_1-{\Psi }_1)S\hfill \\ \hfill & -({\lambda }_1-{\lambda }_2)p+\mu {\lambda }_2\hfill \\ \hfill \frac{d{\lambda }_3}{dt}=& -1+({\lambda }_3-{\lambda }_5){\gamma }_1+({\delta }_1+\mu ){\lambda }_3\hfill \\ \hfill & +({\lambda }_1-{\lambda }_2)(1-\alpha \left(t\right))\frac{\beta }{N}(a_2-{\Psi }_1)S\hfill \\ \hfill \frac{d{\lambda }_4}{dt}=& ({\lambda }_4-{\lambda }_3)q+{\gamma }_2({\lambda }_4-{\lambda }_5)+({\delta }_2+\mu ){\lambda }_4\hfill \\ \hfill & +({\lambda }_1-{\lambda }_2)(1-\alpha \left(t\right))\frac{\beta }{N}(1-{\Psi }_1)S\hfill \\ \hfill \frac{d{\lambda }_5}{dt}=& -({\lambda }_1-{\lambda }_2)(1-\alpha \left(t\right))\frac{\beta }{N}{\Psi }_{1}S\hfill \\ \hfill & +\rho ({\lambda }_5-{\lambda }_1)\hfill \end{array}\hfill \end{array}\right)$$ (A)

with the transversality conditions

$${\lambda }_1\left(t_f\right)={\lambda }_2\left(t_f\right)={\lambda }_3\left(t_f\right)={\lambda }_4\left(t_f\right)={\lambda }_5\left(t_f\right)=0$$ (24)

To evaluate the optimal control of the control variable, we differentiate the Hamiltonian function, $H$, with respect to $\alpha$ and $\eta$ on the optimal state solutions $(S^{\ast },E^{\ast },I^{\ast },Q^{\ast },R^{\ast })$. We obtain:

$$\left\{\begin{array}{c}\frac{\partial H}{\partial \alpha }=c_1\alpha \left(t\right)+({\lambda }_1-{\lambda }_2)\Psi S^{\ast }=0\hfill \\ \frac{\partial H}{\partial \eta }=c_2\eta \left(t\right)+({\lambda }_5-{\lambda }_1)S^{\ast }=0\hfill \end{array}\right)$$ (25)

By solving Eq. (25) on $\Phi$, we obtain the following equations:

$$\left\{\begin{array}{c}\alpha {\left(t\right)}^{\ast }=max(0,min(1,\frac{{\lambda }_2-{\lambda }_1}{c_1}\Psi S^{\ast }))\hfill \\ \eta {\left(t\right)}^{\ast }=max(0,min(1,\frac{{\lambda }_1-{\lambda }_5}{c_2}{S}^{\ast }))\hfill \end{array}\right)$$ (26)

This shows that, the uniqueness of the optimal control of the model has been achieved for small $t_f$ based on prior boundedness of the state variables as well as adjoint variables. This is made possible through the use of Lipschitz property of the ordinary differential equations.

Results

In this part, we carried out numerical simulations to investigate the impact of preventive measures and the vaccination. The optimality system consists of state system (S’), optimal control set in Eq. (26), adjoint system (A), boundaries conditions and initial conditions. The initial conditions for the state variables are as follows: $S\left(0\right)=13$ millions, $E\left(0\right)=I0\ast 4$, $J\left(0\right)=I0\ast 1.5$ (estimated), $I\left(0\right)=4384$, $R\left(0\right)=8854$ and $D\left(0\right)=128$ (according to [31]) while $\Lambda =500$ and the balance costs in the objective function are $c_1=50\ast 10^3$ et $c_2=10\ast 10^3$.

The others parameters values are given in Table 2. The systems of differential equation are solved with the method of Runge–Kutta 4. The optimality of the system is solved using the forward–backward sweep scheme. The details of the scheme are presented by Lenhart and Workman. All simulations have been done with Matlab 2020.

Discussion

The model is for human–human transmission that involves imported cases and community spread. The model is proven to have an invariant region, this region is where the model is well-posed and makes biological sense to be carried out for the human population. When there is no control on the effort related to the respect of preventive measures (respect of barrier actions, establishment of curfews, sanitary cordons...), the basic reproduction number is $R_0=2.43$ but decreases until it reaches $0$ when an optimal control is done on this effort. This implies that an infected individual can infect any person in an environment where preventive measures policies are very well respected, as opposed to more than two (02) persons in an environment where they are not observed.

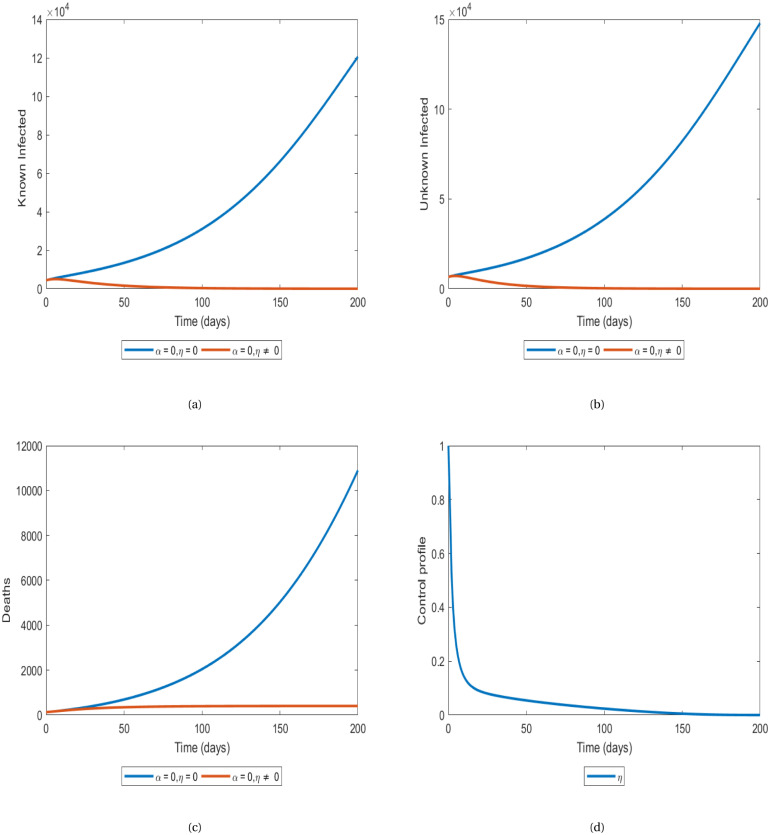
Fig. 2 shows the impact of the best implementation of preventive measures policies (control $\alpha$) in eradicating COVID-19 in Benin. The Fig. 2(a) shows that when no control is applied, the number of infected identified by the COVID-19 tests keeps on increasing from $4384$ at time $t=0$ until it reaches 120.000 in just $200$ days but when an optimal control is implemented on the preventive measures policies, it decreases rapidly from $4384$ at time $t=0$ to $114$ at time $t=200$ days. The Fig. 2(b) shows a similar scenario where the number of infected unidentified keeps on increasing from $6576$ at time $t=0$ and reaches $140000$ at $t=200$ days but decreases to $138$ with an optimal control on the preventive measures policies. At the same time, the number of deaths (Fig. 2(c)) increases from $120$ to $1200$ in $200$ days but when the optimal control on preventive measures is implemented, it does not exceed $415$ at time $t=200$. The control profile (Fig. 2(d))) shows that the respect of preventive measures is at its maximum value from the starting point until time $t=120$ days before decreasing to the minimum value.

Fig. 2.

Evolution of numbers of individuals in the compartments I (Fig. 2(a)), J (Fig. 2(b)) and D (Fig. 2(c)) with optimal control on preventive measures.

The Fig. 3 presents the impact of the optimal implementation of vaccination (control $\alpha$) in eradicating COVID-19 in Benin. In absence of vaccination, the number of infected people identified by the COVID-19 tests (Fig. 3(a)) keeps on increasing from $4384$ at time $t=0$ until it reaches 120.000 in just $200$ days but when a control is implemented on the vaccination, the number of infected identified by the COVID-19 tests, decreases from $4384$ at time $t=0$ to $13$ at time $t=200$ days. The number of infected unidentified (Fig. 3(b)) keeps on increasing from $6576$ at time $t=0$ and reaches $140000$ at $t=200$ days in absence of vaccination. On the other hand with optimal vaccination control, it decreases from $6576$ at time $t=0$ to $10$ at time $t=200$ days. The number of deaths (Fig. 3(c)) increases from $120$ to $1200$ in $200$ days when no controls are implemented. With vaccination implementation, it increases not as fast as without control and reaches $403$ at time $t=200$. Concerning the control profile (Fig. 3(d)), the vaccination campaign starts at first days from its maximum value and decreases rapidly to reach less than 10% of its maximum at time $t=20$, then it decreases slowly to the minimum value.

Fig. 3.

Evolution of numbers of individuals in the compartments I (Fig. 3(a)), J (Fig. 3(b)) and D (Fig. 3(c)) with optimal control on vaccination.

The Fig. 4 presents the impact of the preventive measures policies (control $\alpha$) and on the vaccination (control $\eta$) to stop the COVID-19 spread when either on the effort related to the preventive instructions and on the vaccination are implemented. In absence of control $\alpha$ and $\eta$, the number of infected identified by the COVID-19 tests keeps on increasing from $4384$ at time $t=0$ until it reaches 120.000 in just $200$ days, when both controls $\alpha$ and $\eta$ were implemented (Fig. 4(a)), it rapidly decreases from $4384$ at time $t=0$ to reach $10$ at time $t=200$ days. The number of infected unidentified keeps on increasing from $6576$ at time $t=0$ and reaches $140000$ at $t=200$ days in absence of controls. With controls $\alpha$ and $\eta$ (Fig. 4(b)), it decreases from $6576$ at time $t=0$ to $8$ at time $t=200$ days. The number of deaths increases from $120$ to $1200$ in $200$ days when no control is implemented. When both controls $\alpha$ and $\eta$ were implemented(Fig. 4(c)), it increases less and reaches $384$ at time $t=200$. Concerning the control profile (Fig. 4(d)), the vaccination campaign is between 50% and 60% at the starting and decreases rapidly the first days and slowly after to the minimum value. On the other side, the respect of preventive measures policies start from its maximum value and decreases rapidly the first days and slowly after to the minimum value.

Fig. 4.

Evolution of the numbers of individuals in the compartments I (Fig. 4(a)), J (Fig. 4(b)), D (Fig. 4(c)), with optimal control on the effort vaccination and preventive measures.

The implementation of preventive measures policies reduces the force of infections, so the number of exposed in the population. It results to the reduction of the number of infected and the number of deaths due to COVID-19 in the population. The implementation of vaccination increases the number of immune people in the population and this reduces the number of infected people in the population. To achieve zero infection with just control on the preventive measures, the control must be at its maximum value during a long period (more than 200 days), and this will be very difficult to implement due to its high economic and social cost. On the other hand, to achieve zero infection with just control on vaccination, practically all the population must be vaccinated. By combining control on simultaneously vaccination and preventive measures, we can achieve zero infection in the population with less effort than if we try one without the other.

Conclusion

In this paper, a new deterministic mathematical model of COVID-19 was formulated by subdivising the population into six (06) compartments: Susceptible, Exposed, Known Infected, Unknown Infected, Recovered, Deaths. The model was also used as a prototype to extensively investigate the individual and combined contributions of preventive measures and vaccination campaigns in curbing the transmission and spread of COVID-19. The model analysis includes the establishment of the invariant region and positivity of the model, the existence of disease-free equilibrium, or endemic equilibrium point and computation of the basic reproduction number $R_0$. It was found that the basic reproduction number, $R_0$, is 2.43 when no one in the community respects the preventive measures but can decrease even to $0$ when the respect of preventive measures is optimal.

It is shown that the optimal implementation of preventive measures policies or the vaccination campaigns will highly reduce the number of infected individuals. But the simultaneous implementation of the two interventions reduces and with less costs the number of infected than the individual implementation of two interventions in the infected population. This means that COVID-19 may be eradicated with the optimal implementation of the preventive measures policies and vaccination campaigns. However, others interventions can be analyzed to reinforce the model and help to stop the spread of COVID-19 more quickly.

CRediT authorship contribution statement

Onésime Agossou: Data curation, Software, Writing – original draft. Mintodê Nicodème Atchadé: Conceptualization, Resources, Visualization, Writing – review & editing, Validation. Aliou Moussa Djibril: Formal analysis, Supervision.