Abstract
A series of six coumarin based dye derivatives were investigated and their geometry and optoelectronic properties elucidated for suitability in dye-sensitized solar cells (DSSCs) using TD-DFT/B3LYP with 6-31G basis set. D-π-A schemes were developed by attaching various donors and acceptors to coumarin dye (CM) to calculate changes in their photovoltaic properties. D2-CM-A2 and D4-CM-A4 showed less dihedral angle because of the low steric effect between donor and connector. The D1-CM-A1 and D2-CM-A2 results of intramolecular charge transfer were higher because of low bond length and a strong group of electron donors. The results revealed that LUMO energies of D1-CM-A1, D2-CM-A2, D3-CM-A3 and D4-CM-A4 were higher than the conduction band edge of TiO2 electrode (−4.0 eV) suggesting that these dyes will inject the electrons into the conduction band of the semiconductor. In addition, the light harvest efficiency (LHE), open-circuit voltage (VOC) and band energy gap (Eg) values are calculated in the gas phase, as well as in the solvent phase. This study shows that D1-CM-D1 and D2-CM-A2 derivatives have better properties for application in the DSSCs.
Keywords: Coumarin dye, Donor, Acceptor, DFT method and photovoltaic properties, DSSCs
Keywords: Coumarin dye, donor, acceptor, DFT method and photovoltaic properties; DSSCs.
1. Introduction
The population growth and related development activities have led to an enormous increase in global demand for energy [1]. Energy consumption has increased rapidly since the beginning of the last century. Today's energy demand is 13 TW, and it is anticipated rise up to 23 TW by 2050 [2]. Fossil fuels, which are predicted to diminish in oil and natural gas by 2042, are the dominant current power source [3]. The overuse of fossil fuels is associated with the global rise in the concentration of greenhouse gases, which contributes to climate change impact [4]. Therefore, innovative renewable energy technologies are urgently needed so that to meet the global problems of energy stability, climate change and sustainable development.
Since O'Regan and Grätzel's first report on high-efficient dye sensitized solar cells in 1991 [5], DSSCs have received considerable attention [4] as the production of DSSCs in comparison with conventional silicon-based solar cells is relatively cheap. The conversion of the sun to electricity by DSSCs is thus an affordable source of renewable energy [6]. In the last decades, numerous DSSC-based research reports with more than 1,000 published papers have been documented, and this trend still increases [7]. Theoretical and experimental researches are underway to develop high-efficiency organic-dye-based solar cells [8, 9, 10]. The majority of researches focus on developing new dye sensitizing agents, which are a key component in the functional theory of DSSC. The metal-free dye based on the architecture D-π-A can deliver high-efficient photovoltaic output [11] with the current highest record of 11 per cent [12]. The existence of a π-conjugated linker in an organic sensitizer expands the visible region absorption band by enlarging the π-combination mechanism. The structural changes to the α-conjugated connector will boost the efficiency of DSSC significantly [12]. Numerous electron-donor (D) and acceptor (A) groups including Triarylamine [13], coumarin [14], carbazole [15], fluorine [16], phenothiazine [17, 18],cyanoacrylic acid [19], carboxylic acid [20], and rhodanine-3-acetic acid [21] have been studied experimentally and theoretically.
The electronic and optical properties of coumarin-based dyes, which have been systematically studied by Hara and Arakawa [22, 23], make them one of the most promising groups of organic sensitizers. They are called type I dyes in which electrons are injected through an indirect mechanism. Many experimental procedures have been used to obtain new, more effective, organic coumarin dyes. Though experimental molecular change is a powerful and easy way to get new dyes, the synthesis process is costly and takes time. Therefore, the primary way to improve the performance of the DSSC has been by making promising molecular changes to existing dyes. Since the costs of these experimental methods are generally very high, the technique is restricted to a relatively small number of candidates' dyes. A greater understanding of the link between molecular structure and photovoltaic efficiency would help to speed up and make new dyes more available [24]. Although experimental methods have been employed in most of this effort, there has been an increasing tendency to use computational methods, especially QSPR [25] models.
2. Material and methodology
2.1. Design of coumarin dye and its derivatives
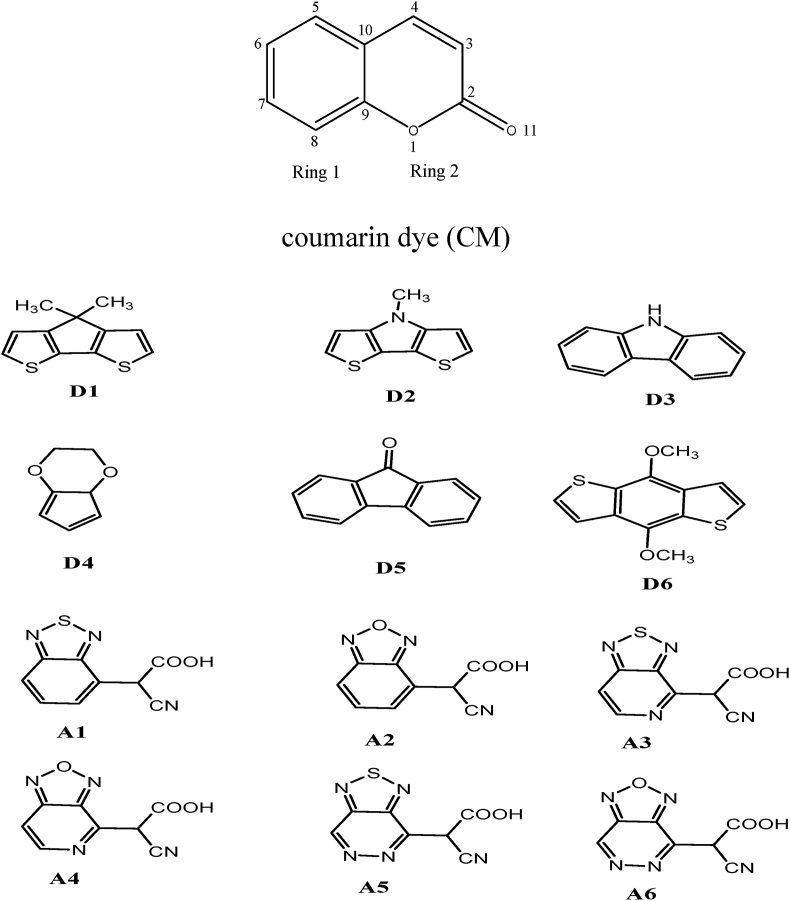
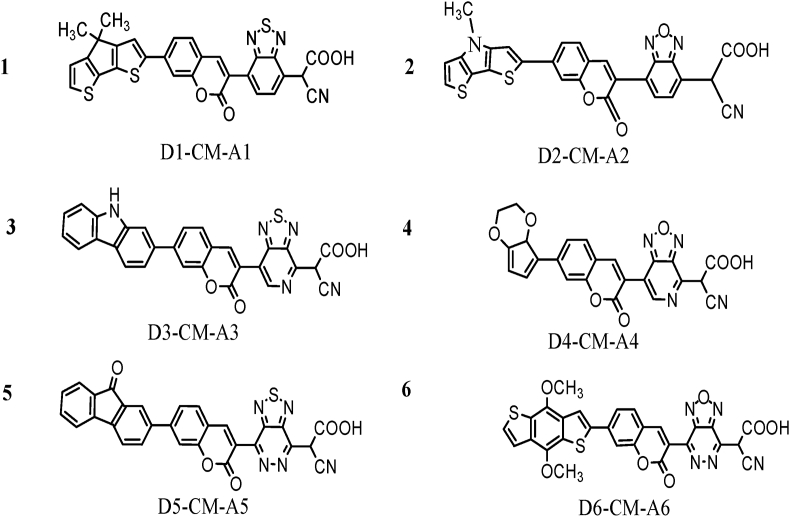
The structures of coumarin (CM) dye, donor (D) and acceptor (A) molecules were sketched by using Chem Draw software (Figure 1). In this work; we designed six coumarins based D-π-A dyes: D1-CM-A1, D2-CM-A2, D3-CM-A3, D4-CM-A4, D5-CM-A5 and D6-CM-A6 by attaching the donors (D1, D2, D3, D4, D5 and D6) at 7th position and acceptors (A1, A2, A3, A4, A5 and A6) at 3rd position of coumarin dye (CM) as shown in Figure 2. These donors were selected because of their excellent stability, non-polar molecular configuration, easy anchoring groups modification, electron mobility, high electron capability, multiple locations, and aggregation resistance.
Figure 1.
Structural form of coumarin (CM) dye, donor and acceptor molecules.
Figure 2.
Designed structures of D-π-A dye. Donor is seven (7) positions, and acceptor is third (3) positions in coumarin dye.
2.2. Computational methodology
All the optimization calculations of the ground state structures were carried using the density functional theory (DFT) in gas and chlorobenzene solvent. The optimization geometry of all D-π-Adyes in the ground state in the gas phase and solvent, without symmetry constraints, has been done by the DFT approach combined with B3LYP exchange-correlation function [28, 29] and 6-31 basis set. Frequency analyses were performed to obtain the lowest energy geometries. No imaginary frequency was observed from the results proving that all the geometries are at a global minimum. The energy levels of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) were calculated along with their electron density. The UV-Vis spectra of the geometries were evaluated using TD-DFT with same level using gas phase B3LYP method with 6-31G basis set. The calculations in a solvent were conducted using a polarizable continuum model (PCM) in solvent (chlorobenzene) [30, 31]. All calculations are carried out in gas state and chloroform solvent using the Gaussian 09W software [32]. GaussView 5.0 [33] was used to organize the input files and output files results were interpreted and plots of the optical absorption spectra are simulated using Gabedit software [34].
3. Results and discussion
3.1. Geometric parameters
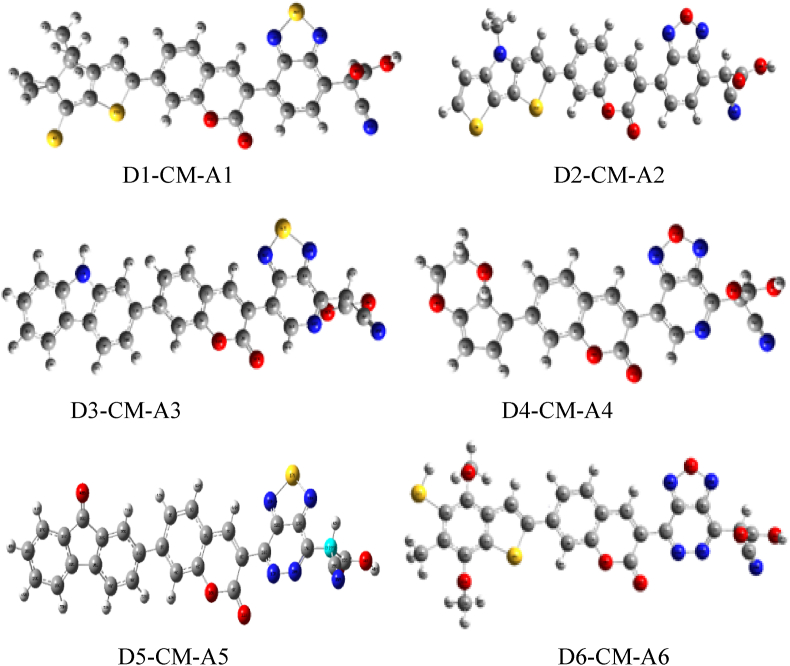
The geometrical parameters such as the bond length, bond angle and dihedral angles are calculated from geometry optimization of ground state studied D-π-A structures and are listed in Tables 1 and 2 in the gas and solvent. The optimized geometry structures in the solvent phase of coumarin based D-π-A dyes are shown in Figure 3. In general, the shorter the length of the connection, the stronger the bond and the more stable the molecule is [35]. The connection between electron donor and π conjugated bridge is in the range of 1.451Å to 1.482Å and 1.450Å to 1.482Å for gas and solvent phases, respectively. At the same time, the connection between electron acceptor and the spacer is in the range of 1.465Å to1.481Å and 1.464Å to 1.479Å for gas and solvent phases, respectively.
Table 1.
The selected bond lengths of the D-π-A dyes obtained by B3LYP/6-3IG level in the gas and solvent phases.
| Dye D-π-A |
Gas |
Solvent |
||
|---|---|---|---|---|
| Donor-coumarin (D-π) | Coumarin-acceptor (π- A) | Donor-coumarin (D-π) | Coumarin-acceptor (π- A) | |
| D1-CM-A1 | 1.45828 | 1.48176 | 1.45846 | 1.47925 |
| D2-CM-A2 | 1.45165 | 1.47547 | 1.45018 | 1.47548 |
| D3-CM-A3 | 1.48249 | 1.47883 | 1.48255 | 1.47852 |
| D4-CM-A4 | 1.45385 | 1.47194 | 1.45061 | 1.47111 |
| D5-CM-A5 | 1.48278 | 1.47072 | 1.48272 | 1.46485 |
| D6-CM-A6 | 1.45798 | 1.46551 | 1.45739 | 1.47049 |
Table 2.
The selected dihedral angles of the D-π-A dyes obtained by DFT/B3LYP/6-3IG level in the gas and solvent phases.
| Dye D-π-A |
Gas |
Solvent |
||
|---|---|---|---|---|
| Dihedral angle | Å | Dihedral angle | Å | |
| D1-CM-A1 | 22C-21C-27C-25 (CM-A) | −175.84 | 22C-21C-27C-25C (CM-A) | −156.36 |
| 11S-10C-16C-15 (CM-D) | −162.19 | 15C-16C-10C-11S (CM-D) | −162.19 | |
| D2-CM-A2 | 19C-18C-24C-22C (CM-A) | −178.92 | 19C-18C-24C-22C (CM-A) | −179.98 |
| 10C-9C-13C-12C (CM-D) | −172.87 | 12C-13C-9C-10S (CM-D) | 177.77 | |
| D3-CM-A3 | 9C-8C-14C-12C (CM-A) | −178.98 | 9C-8C-14C-12C (CM-A) | −179.02 |
| 38C-37C-3C-12C (CM-D) | −145.37 | 2C-3C-37C-38C (CM-D) | 146.84 | |
| D4-CM-A4 | 2C-3C-34C-35C (CM-A) | −176.46 | 9C-8C-14C-12C (CM-A) | −179.94 |
| 12C-14C-8C-9C (CM-D) | −179.58 | 2C-3C-34C-35C (CM-D) | 178.59 | |
| D5-CM-A5 | 4C-3C-37C 36C (CM-A) | 147.14 | 7C-8C-14C-15N (CM-A) | 144.29 |
| 9C-8C-14C-12C (CM-D) | 146.24 | 4C-3C-37C-36C (CM-D) | 147.35 | |
| D6-CM-A6 | 7C-8C-14C-15N (CM-A) | 154.89 | 7C-8C-14C-15N (CM-A) | 152.51 |
| 35C-37C-3C-4C (CM-D) | 165.12 | 4C-3C-37C-35C (CM-D) | 171.87 | |
Figure 3.
The geometry optimized structures of D- π –A of coumarin based dyes in solvent phase, calculated by DFT/B3LYP with 6-3G basis set.
The calculated bond lengths of the model compounds showed same decreasing order in both gas and solvent phases when acceptor group is attached at the position 3 with the trend of D5-CM-A5 > D3-CM-A3 > D1-CM-AI > D6-CM-A6 > D4-CM-A4 > D2-CM-A2 for the donor and the π conjugated bridge and D1-CM-A1> D3-CM-A3 > D2-CM-A2 > D4-CM-A4 > D5-CM-A5 > D6-CM-A6 for the π conjugated bridge and the acceptor. In the transfer of charge from the donor to the acceptor group in solar cells, the size of the bond between the donor and the conjugated linker is very critical, with ICT more preferred with shorter bond distances [36]. The results show that D2-CM-A2 coumarin derivatives have favourable bond lengths for easy intramolecular charge transfer. On the other hand, the bond length of the connection between donor and acceptor decreases [37]. The results show that in solvent phases some of the bond length increases and some of them decreases, this is due to the nature of bond formed. If the bond is non-polar bond after addition of polar solvent the bond length wills decreases and if the bond is polar bond after addition of polar solvent the bond length will increase.
Another parameter determining the stability of the molecule is the dihedral angle. The greater the dihedral angle, the steric impediment between donor and spacer is apparent [38]. The greater dihedral angle value will result in more distortion; hence, the molecule becomes unstable, resulting in decreased dye aggregation. The molecule with a lower dihedral angle value is less uneven and therefore stable [35]. When the dihedral angle is small, the acceptor (cyanoacrylic unit) is coplanar with π-spacer. The electron transfer from donor to acceptor through π- conjugated linker if the dye molecule is coplanar [35]. D-CM-A systems dihedral angles range between 145.37 and 179.58° and 144.29 and 179.94° in gas and solvent, respectively. According to the results, D4-CM-A4 has a lower value of the dihedral angle. This indicates the smaller conjugation effect compared to other compounds where coplanarity is observed—these molecules allowing exhibiting the formation of π- stacked aggregation efficiently [38]. Therefore, the coplanar molecular structure enhances the electron transfer employing the conjugated connection between the donor and the electron acceptor.
3.2. Intramolecular charge transfer (ICT)
Intramolecular Charge Transfer is the summation of all Milliken charges circulation of electron donor and electron acceptor [39]. The ICT is the critical indicator for transferring the electron from a donor to an anchoring group within dye-sensitized solar cells. As intra-molecular charge transfer increases, the HOMO and LUMO energy levels are stabilized, and the energy difference between the HOMO and LUMO is reduced. Conversely, when the intramolecular charge transfer value is low, resulting in charge separation, the electrons are directly transferred from the donor to an anchoring group.
The ICT significantly increases the electron's delocalization and thus decreases model compound bond length [39]. The bond length between donor and π-spacer is crucial in the transferred electron between donor and acceptor in solar cells because it is favoured when shorter [39]. The larger ICT is usually due to nitrogen atoms in the dye ring, which can locate electrons with high electronegativity. Table 3 shows the order of ICT values of both in the gas and solvent phases are: In D-π-A, D6-CM-A6 > D2-CM-A2 > D1-CM-A1 >D3-CM-A3 > D4-CM-A4 > D5-CM-A5 and D5-CM-A5 > D6-CM-A5 > D2-CM-A2 > D2-CM-A1 > D3-CM-A3 > D4-CM-A4 for the gas and solvent phases. Results show that D1-CM-A1 and D2-CM-A2 have higher values of ICTs because of small bonds and heavy electron donors. The electrons are then transferred from the donor directly to an anchoring group. When the ICT value is zero, electrons between the donor and acceptor group are not moving. The candidates for the DSSC should be, therefore, D1-CM-A1 and D2-CM-A2.
Table 3.
Intramolecular charge transfer (ICT) of the optimized compounds at DFT/B3LYP/6-3IG level in gas and solvent phase.
| Dyes D-π-A |
Gas | Solvent |
|---|---|---|
| D1-CM-A1 | 2.5 × 10−8 | 2.6 × 10−8 |
| D2-CM-A2 | 5.2 × 10−8 | 5.3 × 10−8 |
| D3-CM-A3 | 2.5 × 10−8 | 2.8 × 10−18 |
| D4-CM-A4 | 4.0 × 10−8 | 2.9 × 10−8 |
| D5-CM-A5 | 5.0 × 10−8 | 1.0 × 10−7 |
| D6-CM-A6 | 7.3 × 10−8 | 7.3 × 10−8 |
3.3. Dipole moment and quadruple moment
The molecule with a significant dipole moment and stronger asymmetry in electronic charge distribution may have greater responsiveness and sensitivity to change its electronic properties and structure through external electric fields. Table 4 shows the dipole moment values in gas and solvent phases. The order of the decrease in dipole moment is: D4-π-A4 > D2-CM-A2 > D5-CM-A5 > D6-CM-A6 and D1-CM-A1 > D2-CM-A4 > D3-D3-CM-A3 > D2-CM-A2 > D5-CM-A5> D6-CM-A6 for gas and solvent phases respectively. Due to the addition of solvent (chlorobenzene) to the dye molecules that contain the most electronegative element (chlorine) has greater dipole moments in solvent greater than in gas phases. These findings show that the most responsive and reactive dye derivatives in DSSCs are, thus, D1-CM-A1, D4-CM-A4 and D5-CM-A5.
Table 4.
Quadruple moments (in Debye) of the model calculated by DFT/B3LYP/6-31G level in the gas and solvent phases.
| D-π-A (position 3) gas | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Dye | XX | YY | ZZ | XY | YZ | XZ | Qii | Q | μ |
| D1-CM-A1 | −221.64 | −251.72 | −241.48 | −66.89 | −11.12 | −45.94 | −238.28 | 30.08 | 10.93 |
| D2-CM-A2 | −170.25 | −237.77 | −231.97 | −42.58 | −4.22 | −18.21 | −213.33 | 67.52 | 10.66 |
| D3-CM-A3 | −213.69 | −231.84 | −230.69 | −27.27 | −15.14 | −24.54 | −225.40 | 18.15 | 11.04 |
| D4-CM-A4 | −181.42 | −211.62 | −200.26 | −31.44 | −2.39 | −21.29 | −197.76 | 30.2 | 11.14 |
| D5-CM-A5 | −204.21 | −243.36 | −235.73 | 30.29 | −5.16 | −26.93 | −227.76 | 39.15 | 9.24 |
| D6-CM-A6 |
−265.41 |
−267.50 |
−247.50 |
3.30 |
−5.68 |
−34.17 |
−260.13 |
2.09 |
8.66 |
|
D-π-A (position 3) solvent | |||||||||
| D1-CM-A1 | −249.27 | −264.69 | −243.09 | 19.72 | −3.41 | 6.54 | −252.35 | 15.42 | 14.37 |
| D2-CM-A2 | −173.46 | −240.39 | −235.45 | 20.35 | −3.70 | −15.82 | −216.43 | 66.93 | 12.82 |
| D3-CM-A3 | −215.99 | −232.00 | −230.44 | −32.62 | −16.95 | −28.54 | −226.14 | 16.01 | 13.40 |
| D4-CM-A4 | −160.05 | −213.44 | −198.76 | −13.45 | 3.63 | 18.99 | −190.75 | 53.39 | 13.58 |
| D5-CM-A5 | −182.78 | −244.66 | −245.75 | 75.34 | 9.70 | −10.18 | −224.39 | 61.88 | 11.77 |
| D6-CM-A6 | −247.29 | 253.07 | −259.15 | −14.74 | −14.74 | 54.27 | −84.45 | 50.4 | 11.26 |
The quadruple moment is a distribution of the charge with more electrical symmetry than a dipole moment. It is not a vector but a tensor. Two equal dipoles are arranged anti-parallel. It occurs in a complex system with different complexity orders. Qii expresses the mean (average) of a diagonal quadrupole moment tensor element calculate by using Eq. (1); Q represents the single quadrupole moment which is calculate using Eq. (2). Where is the meaning of Qii
| (1) |
| (2) |
The quadruple moment tensor of all diagonal dye derivatives is expressed as negative to ensure that the negative charge distribution was strongly separated from the centre of nucleus charges. The molecules which have the large dipole and quadrupole moment represent a strong electron donor indeed; therefore, these molecules will be suitable for the application of DSSCs [36]. The quadruple improve charging interaction and lead to complex molecules being built and stabilized. The smallest exponential orbital and basis sets of polarized function should be used to achieve good results of QZZ. As the small electronegativity in a molecule occurs, the less electrical density reduction (inductive effect) results in more negative QZZ.
However, QZZ is higher if the replacement number increases; this is because the electron density has a resonance effect pulled back into the ring. Table 4 shows that the values of the non-diagonal QXZ and QYZ components are lower and can be attributed to the presence of a symmetrical plane almost perpendicular to the Z-axis. The quadruples were ordered as D-π-A, D6-CM-A6 > D 5-CM-A5 > DI-CM-A1 > D3-CM-A3 > D2-CM-A3 > D4-CM-A4 and D1-CM-A1 > D3-CM-A3 in both gas-induced and solvent phases respectively. The findings show that D1-CM-A1 has the highest quadruple moment values than other dye derivatives in solvent phase because of the strong electron donor in D-π-A molecules. We may also assume these molecules are more reactive and sensitive than other molecules. Therefore, D1-CM-A1 proposed to be a promising DSSCs candidate.
3.4. Electronic parameters
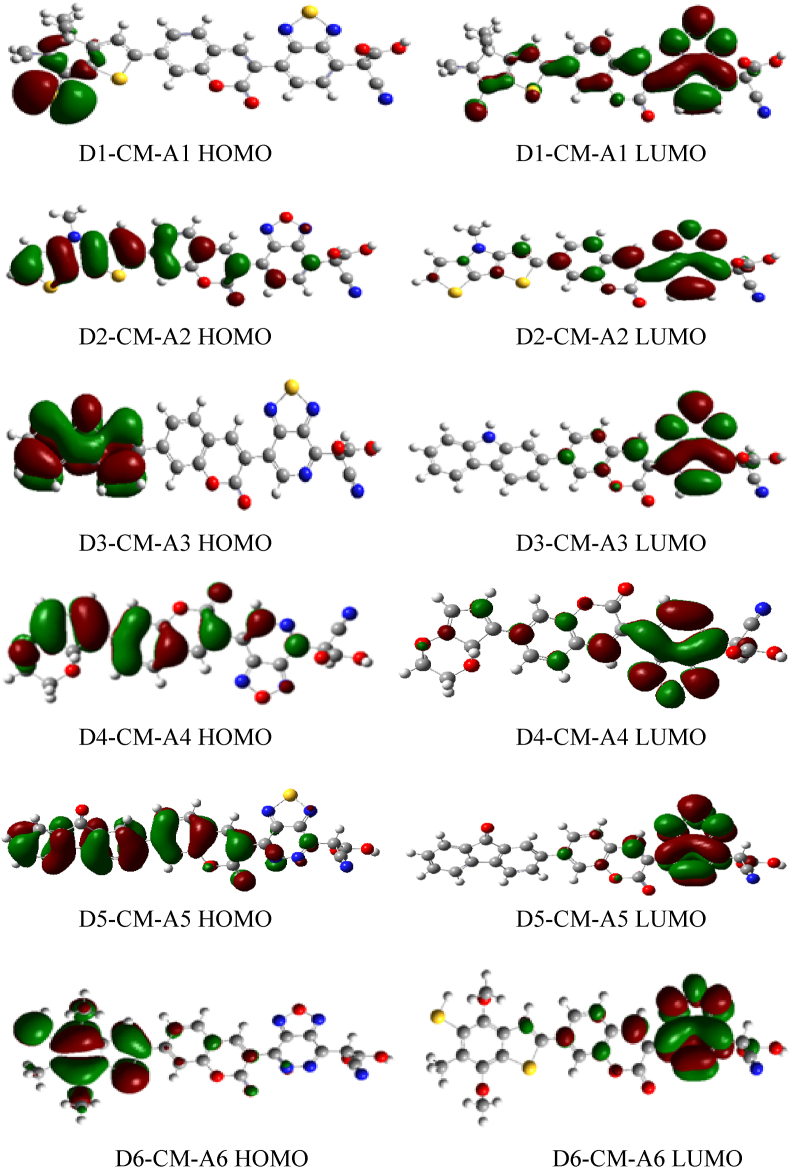
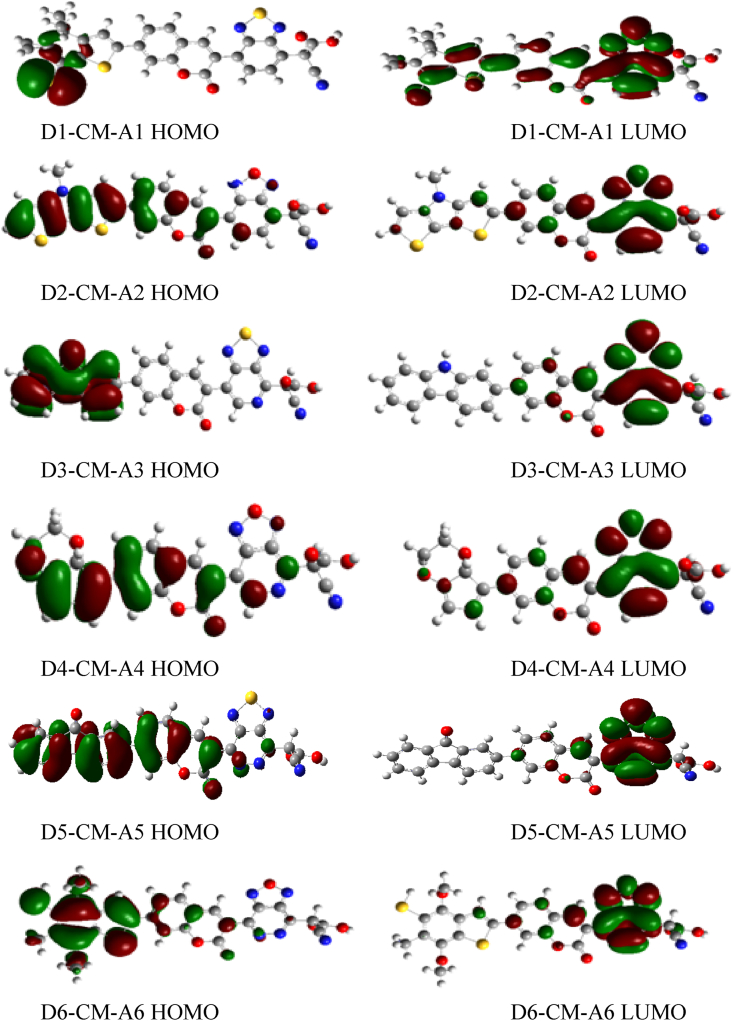
Electronic parameters of a dye are recognized to play an important role to determine the efficiency of DSSCs. These parameters include the highest occupied molecular orbital (HOMO), the lowest unoccupied molecular orbital (LUMO) energy level and the bandgap energy. Frontier molecular orbitals (FMOs) described as HOMO and LUMO contribution is very important in determining the charge-separated states of the dye sensitizers. It is known that the distribution of FMOs of the sensitizers has a significant influence on the electronic charge transfer characteristics of dyes. Normally, charge transfers from the donor to electron acceptor groups determine the quality of sensitizers [40]. For example, it can be seen in Figures 4 and 5 gas and solvent, all HOMO orbitals are localized on the donor part, while the LUMO orbitals are mainly found on the acceptor group (cyanoacrylic acid group).
Figure 4.
The contour plots of HOMO and LUMO orbital calculated by DFT/B3LYP/6-31G level for D-π-A dyes in the gas phase.
Figure 5.
The contour plots of HOMO and LUMO orbital calculated by DFT/B3LYP/6-31G of coumarin dyes of D-π-A in the solvent phase.
On the other hand, HOMO possesses bonding characters, while the LUMO orbital of all molecules presents antibonding characters. They do so to create efficient charge separation states [41]. One of the most important features of metal-free organic dye in DSSCs is ICT from donor to acceptor. The propensity for electron transfer of the dyes is determined by the contribution of electron density of each atom added to the donor and acceptor group [42].
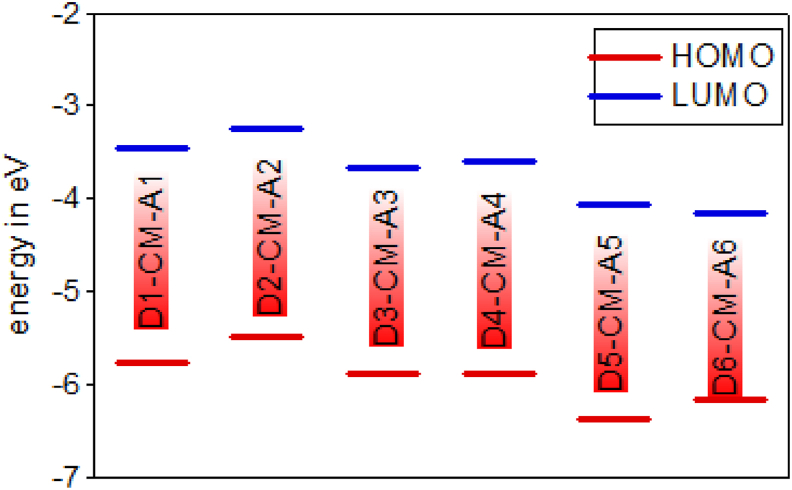
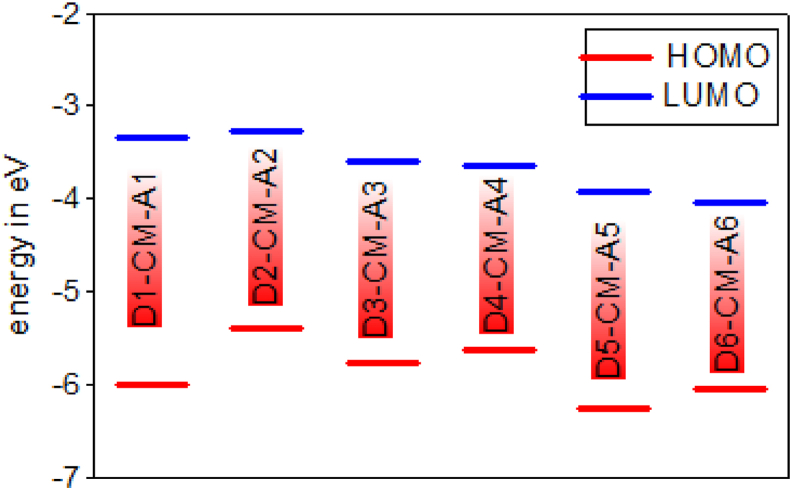
In analysing organic solar cells, HOMO and LUMO energies are essential parameters that determine if the charge transfer will happen between donor and acceptor. The electron-donating ability of the electron donor in D– A molecule tends to influence the electrochemical properties. D–π– A dyes with a stronger electron-donating group should give a high HOMO compared to a weaker electron donor. The energy level for HOMOs of D1-CM-A1 to D6-CM-A6 are −5.766, −5.478, −5.891, −5.891, −6.363, −6.151 and −6.002, −5.380, −5.753, −5.624, −6.243, −6.049 eV for gas and solvent phases respectively and the absolute energies of LUMOs of D1-CM-A1 to D6-CM-A6 are −3.459, −3.246, −3.658, −3.604, −4.006, −4.147 and −3.331, −3.265, −3.595, −3.635, −3.919, −4.04 for gas and solvent phases respectively.
The dye levels of HOMO and LI∖UMO used in DSSC must correspond to the TiO2 conductive edge energy level and the electrolyte redox potential for effective charge separation and dye recovery process. Therefore, the HOMO level has to be sufficiently more positive than the redox potential (−4.0 eV) and the LUMO of the dye has to be sufficiently more negative than the ECB of TiO2 (−5.0 V) is necessary for effective electron injection from excited dye to conduction band [27]. The results show that LUMO energies of DI-CM-AI, D2-CM-A2, D3-CM-A3 and D4-CM-A4 are higher than the conduction band edge of TiO2 electrode (−4.0 eV). Therefore, these dyes will inject the electrons into the semiconductor's conduction band, but D5-CM-A5 and D6-CM-A6 have a lower value of LUMO than TiO2, cannot hence inject electrons into the conduction band of the semiconductor, as shown in Figures 6 and 7.
Figure 6.
HOMO and LUMO energy level of the D-π-A dyes by DFT/B3LYP/6-31G level in the gas phase.
Figure 7.
HOMO and LUMO energy level of the D-π-A dyes by DFT/B3LYP/6-31G level in solvent.
The energy gap is the difference between the highest occupied molecules orbital and the lowest unoccupied molecule orbital of the given dye molecule [40]. The bandgap is the main factor determining the photocurrent of the dye. Generally, the smaller the band gap influences the transferring of electrons from HOMO to LUMO by absorbing light energy with relevant wavelength. The calculated energy gaps of the studied model compounds decrease in the following order in gas and solvent phase respectively; D1-CM-A1 > D5-CM-A5 > D4-CM-A4 > D3-CM-A3 > D2-CM-A2 > D6-CM-A6 and D1-CM-A1> D5-CM-A5 > D3-CM–A3 > D2-CM-A2 > D6-CM-A6 > D4-CM-A4. The findings demonstrate lower energy difference for D4-CM-A4 and D6-CM-A6 than in comparison to other dye derivatives. The electron from HOMO to LUMO can therefore take place easily. Thus, it is proposed that D4-CM-A4 should be a successful DSSC candidate, whereas D1-CM-A1 will be more stable because it has a higher energy gap (Figures 6 and 7).
3.5. Absorption properties
Absorption properties determine the extent of the light absorbed by the molecule; such properties are oscillator strengths (f), which are related to the maximum absorption wavelength λmax and the vertical transition energy of the dye from the ground state to an excited state. Tables 5 and 6 depict the absorption wavelength λmax nm, excitation energies and oscillator strengths (f) of the dye molecules for gas and chlorobenzene solvent. Depending on the donator group linked to the coumarin dye, the vertical excitation energies of the dye molecules were changed. The decreasing trends of energy level are as follow; D4-CM-A4 > D2-CM-A2> D1-CM-A1 > D3-CM-A3 > D5-CM-A5> D6-CM-A6 and D4-CM-A4 > D2-CM-A2> D1-CM-A1 > D2-CM-A2 > D6-CM-A6> D5-CM-A5 for gas and solvent phases respectively. Increasing vertical excited energy of dye depends on the donating group; the more the conjugation of the donor group, the higher the vertical excited energy [43].
Table 5.
The absorption properties of studied D-π-A dyes derivatives obtained by DFT/B3LY/6-31G level in the gas phase.
| Gas | |||||
|---|---|---|---|---|---|
| Dye | SN | λmax (nm) |
eV | (f) | MO Contribution |
| D1-CM-A1 | S1 | 685 | 1.8092 | 0.0 | H →L (54.07%) |
| H →L +1 (40.18%) | |||||
| H →L + 2 (5.22%) | |||||
| S2 | 552.19 | 2.2453 | 0.0 | H →L (45.85%) | |
| H →L + 1 (49.33%) | |||||
| H →L + 2 (4.33%) | |||||
| S3 | 533.17 | 2.3254 | 0.5075 | H – 1→ L (95.52%) | |
| S4 | 430.26 | 2.8816 | 0.4739 | H -2→ L (71.35%) | |
| H -1 → L (27.38%) | |||||
| S5 | 420.9 | 2.9457 | 0.4991 | H -2 → L (22.54%) | |
| H -2 → L+1 (5.15%) | |||||
| H -1 → L (4.01%) | |||||
| H -1 → L (64.20%) | |||||
| H -1 →L (2.788%) | |||||
| S6 | 393.22 | 3.153 | 0.0006 | H →L+1 (10.33%) | |
| H →L +2 (86.62%) | |||||
| D2-CM-A2 | S1 | 614.86 | 2.0164 | 0.521 | H→L (98.90%) |
| S2 | 472.03 | 2.6266 | 0.0021 | H -1 L (98.79%) | |
| S3 | 438.89 | 2.825 | 1.032 | H -2→L (8.44%) | |
| H→L +1 (90.28%) | |||||
| S4 | 420.2 | 2.9506 | 0.0154 | H -2 →L (86.82%) | |
| H→L +1 (7.48%) | |||||
| S5 | 367.31 | 3.3755 | 0.0156 | H→L (97.98%) | |
| S6 | 361.13 | 3.4332 | 0.0212 | H -1 →L+1 (94.54%) | |
| D3-CM-A3 | S1 | 622.05 | 1.9932 | 0.0418 | H -1 –L (6.62%) |
| HL (92.85%) | |||||
| S2 | 616.57 | 2.0109 | 0.2079 | H -1→L (91.37%) | |
| H→L (6.88%) | |||||
| S3 | 476.81 | 2.6003 | 0.0572 | H -2→L (96.56) | |
| S4 | 435.31 | 2.8482 | 0.0003 | H -7L (7.32%) | |
| H -5→L (91.58%) | |||||
| S5 | 405.95 | 3.0541 | 0.0023 | H -3 L (96.40%) | |
| S6 | 399 | 3.1074 | 0.0125 | H -L +1 (97.93%) | |
| D4-CM-A4 | S1 | 633.44 | 1.9573 | 0.3501 | H -L (98.87%) |
| S2 | 435.62 | 2.8462 | 0.185 | H -2→L (2.43%) | |
| H -1→L (89.62%) | |||||
| H →L +1 (6.59%) | |||||
| S3 | 415.3 | 2.9854 | 0.6973 | H -1 →L (5.64%) | |
| H →L+1 (91.46%) | |||||
| S4 | 409.37 | 3.0287 | 0.0004 | H -→5→L (10.91%) | |
| H -4 →L (2.18%) | |||||
| H -3→L (85.56%) | |||||
| S5 | 393.78 | 3.1485 | 0.0234 | H -2 →L (94.67%) | |
| H -1 →L (2.54%) | |||||
| S6 | 343.76 | 3.6067 | 0.0002 | H -5 →L (81.26%) | |
| H -4→L (3.95) | |||||
| H -3 →L (12.91%) | |||||
| D5-CM-A5 | S1 | 643.86 | 1.9256 | 0.1515 | H -2→L (9.13%) |
| H -1→L (18.72%) | |||||
| H →L (6.59%) | |||||
| S2 | 589.46 | 2.1034 | 0.0663 | H -2→L (46.20%) | |
| H -1→L (25.45%) | |||||
| H →L (25.93%) | |||||
| S3 | 492.34 | 2.5183 | 0.0186 | H -2→L (41.06) | |
| H -1→L (54.44%) | |||||
| H →L (2.04%) | |||||
| S4 | 430.2 | 2.882 | 0.01 | H -4→L (11.12%) | |
| H -3→L (83.57%) | |||||
| H -3→L (2.29%) | |||||
| S5 | 422.95 | 2.9314 | 0.0501 | H -4→L (83.37%) | |
| H -3→L (10.63%) | |||||
| S6 | 420.95 | 2.9468 | 0.1183 | H -1→L (23.36%) | |
| H →L +1 (79.02%) | |||||
| H →L +2 (12.14%) | |||||
| D6-CM-A6 | S1 | 695.17 | 1.7835 | 0.0841 | H →L (98.83%) |
| S2 | 653.87 | 1.8962 | 0.2448 | H -4→L (3.21%) | |
| H -1→L (94.49%) | |||||
| S3 | 584.44 | 2.1214 | 0.0111 | H -3→L (54.88%) | |
| H -2→L (38.42%) | |||||
| H -1→L (4.41%) | |||||
| S4 | 481.28 | 2.5761 | 0.0751 | H -4→L (3.60) | |
| H -3→L (39.35%) | |||||
| H -2→L (55.14%) | |||||
| S5 | 424.14 | 2.9232 | 0.0243 | H -4→L (10.36%) | |
| H -1→L+1 (3.99%) | |||||
| H→L +1 (83.58%) | |||||
| S6 | 421.47 | 2.9417 | 0.0829 | H -4→L (82.19%) | |
| H →L +1 (9.81%) | |||||
Table 6.
The absorption properties of studied D-π-A dyes derivatives obtained by DFT/B3LYP/6-31G level in solvent phase.
| Solvent | |||||
|---|---|---|---|---|---|
| Dye | SN | λmax (nm) |
eV | (f) | MO Contribution |
| D1-CM-A1 | S1 | 608.12 | 2.0388 | 0 | H →L (50.27%) |
| H →L +1 (43.60%) | |||||
| H →L+2 (5.43%) | |||||
| S2 | 518.58 | 2.3902 | 0.8443 | H -1→L (96.05%) | |
| S3 | 478.34 | 2.592 | 0 | H →L (49.39%) | |
| H →L +1 (47.66%) | |||||
| H →L+2 (2.62%) | |||||
| S4 | 440.42 | 2.8151 | 0.753 | H -2→L+1 (2.10%) | |
| H -1→L +1 (94.67%) | |||||
| S5 | 412.33 | 3.007 | 0.0142 | H -2 →L (92.59%) | |
| H -1→L (2.42%) | |||||
| S6 | 365.93 | 3.3882 | 0.0358 | H -2→L+1 (84.02%) | |
| H -1→L +2 (8.57%) | |||||
| D2-CM-A2 | S1 | 668.43 | 1.8548 | 0.6506 | H →L (99.41%) |
| S2 | 496.04 | 2.4995 | 0.0023 | H -1 → (98.81%) | |
| S3 | 466.82 | 2.6559 | 1.0644 | H -2→L (3.15%) | |
| H→L+1 (96.14%) | |||||
| S4 | 432.86 | 2.8643 | 0.0548 | H -2 →L (93.62%) | |
| H→L +1 (2.86%) | |||||
| S5 | 381.17 | 3.2527 | 0.0204 | H -1→L +1 (98.11%) | |
| S6 | 366.9 | 3.3792 | 0.0145 | H -4→L (2.70%) | |
| H -3→L (94.29%) | |||||
| D3-CM-A3 | S1 | 647.08 | 1.9161 | 0.0179 | H→L (98.78%) |
| S2 | 630.12 | 1.9676 | 0.3253 | H -1 →L (97.15%) | |
| S3 | 474.15 | 2.6149 | 0.0943 | H -2→L (96.84%) | |
| S4 | 413.16 | 3.0009 | 0.0295 | H -1→L +1 (98.58%) | |
| S5 | 407.19 | 3.0449 | 0.0004 | H -7→L (6.93%) | |
| H -6→L (54.18%) | |||||
| H -5→L (37.02%) | |||||
| S6 | 405.18 | 3.0599 | 0.0683 | H -4→L (10.80%) | |
| H -3→L (73.59%) | |||||
| H -1-→L +1 (13.47%) | |||||
| D4-CM-A4 | S1 | 717.65 | 1.7276 | 0.4486 | H→L (99.56) |
| S2 | 454.76 | 2.7263 | 0.6223 | H -1→L (56.30%) | |
| H→L +1 (42.56%) | |||||
| S3 | 440.9 | 2.8121 | 0.2681 | H -1 –→L (40.85%) | |
| H→L+1 (56.50%) | |||||
| S4 | 407.62 | 3.0417 | 0.0177 | H -2→L (96.73%) | |
| S5 | 393.27 | 3.1526 | 0.0006 | H -6-→L (11.83%) | |
| H -4→L (86.74%) | |||||
| S6 | 361.91 | 3.4258 | 0.001 | H -3→L (97.56%) | |
| D5-CM-A5 | S1 | 624.88 | 1.9841 | 0.2706 | H -1→L (4.54%) |
| H→L (94.24%) | |||||
| S2 | 529.83 | 2.3401 | 0.0035 | H -4→L (4.31%) | |
| H -3→L (17.82%) | |||||
| H -2→L (47.53%) | |||||
| H -1→L (24.96%) | |||||
| H→L (3.53%) | |||||
| S3 | 472.9 | 2.6218 | 0.0468 | H -3→L (10.28%) | |
| H -2→L (17.68%) | |||||
| H -1→L (68.93%) | |||||
| S4 | 436.15 | 2.8427 | 0.1345 | H→L +1 (68.93%) | |
| H→L+2 (11.39%) | |||||
| S5 | 421.51 | 2.9415 | 0.0503 | H -5→L (2.47%) | |
| H -4→L (76.33%) | |||||
| H -3→L (76.33%) | |||||
| S6 | 404.17 | 3.0676 | 0.0014 | H -4→L (11.95%) | |
| H -3→L (40.42%) | |||||
| H -3-L+1 (9.73%) | |||||
| H -3→L +2 (2.68%) | |||||
| H -2→L (25.57%) | |||||
| H - 2-L+1 (5.86%) | |||||
| D6-CM-A6 | S1 | 713.08 | 1.7387 | 0.2077 | H -1→L (2.88%) |
| H→L (96.50%) | |||||
| S2 | 666.63 | 1.8599 | 0.2303 | H -1→L (95.52%) | |
| H→L (3.08%) | |||||
| S3 | 534.6 | 2.3192 | 0 | H -4→L (62.24%) | |
| H -3→L (6.91%) | |||||
| H -2→L (27.83%) | |||||
| S4 | 474.21 | 2.6145 | 0.0978 | H -4→L (30.80%) | |
| H -2→L (66.30%) | |||||
| S5 | 430.07 | 2.8829 | 0.1873 | H -1-L +1 (2.29%) | |
| H→L +1 (95.73%) | |||||
| S6 | 428.47 | 2.8937 | 0.113 | H -4→L (4.32%) | |
| H -3→L (88.63%) | |||||
| H -2→L (2.67%) | |||||
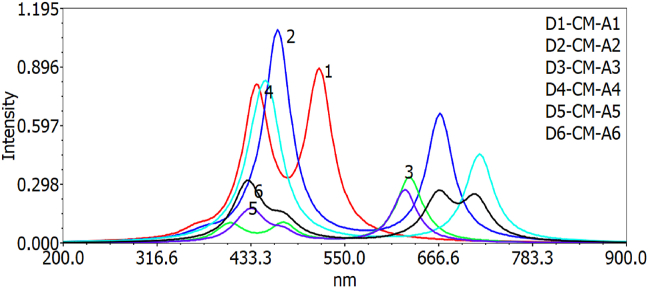
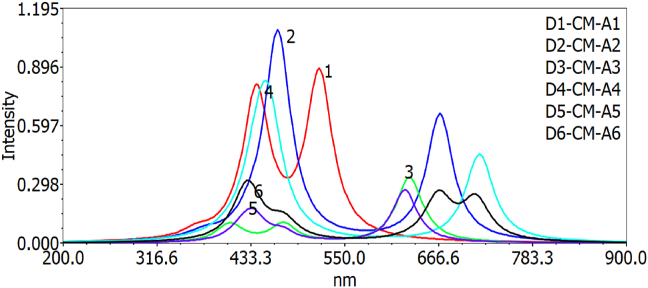
The oscillator strength values decrease in the following order for gas and chlorobenzene solvent respectively: D2-CM-A2 > D1-CM-A1> D6-CM-A6> D3-CM-A3> D4-CM-A4 > D5-CM-A5 and D2-CM-A2 > D1-CM-A1> D4-CM-A4> D3-CM-A3> D5-CM-A5 > D6-CM-A6. The results show that the values of oscillator strengths in gas change after addition of chlorobenzene solution to the dye molecules. Hence D1-CM-A1 and D2-CM-A2 has higher oscillator strength than other molecules. The optical absorption spectra of D–CM–A1 to D6-CM-A6 are 533.17, 438.89, 616.57, 435.62, 643.86, 653.87 and 518.58, 466.82, 630.12, 454.76, 624.88 and 666.63 for both gas and solvent phases respectively. The molecules with longer wavelengths can exhibit redshift and influence the photo to the current conversion efficiency of the DSSC. The results show that D6-CM-A6 and D5-CM-A5 have longer wavelengths than other molecules. Still, these dye derivatives could not inject the electrons to the semiconductor's conduction band due to having a lower value of LUMO energy levels; instead, D1-CM-A1 and D2-CM-A2 have higher absorption wavelength as indicated in Figures 8 and 9.
Figure 8.
Simulated UV-Visible optical absorption spectra of the studied D-π-A dye calculated by TD-DFT/B3LYP/6-31G level in the gas phase.
Figure 9.
Simulated UV-Visible optical absorption spectra of the studied D-π-A dye calculated by TD-DFT/B3LYP/6-31G level in the solvent phase.
3.6. Photovoltaic properties
The dye-sensitive solar cell system's efficiency can be estimated by considering photovoltaic properties. These include light-harvesting efficiency (LHE), negative free energy of injection (ΔGinject), oxidation energy of dye in the ground state (Edye), oxidation energy of dye in an excited state (Edye) and open-circuit voltage (VOC), electron regeneration energy (ΔGregen), electron injection efficiency (φinject), and charge collection efficiency (ղcollect) and their results are presented in Table 7.
Table 7.
Photovoltaic properties of studied molecules at DFT/B3LYP/6-3IG level in the gas and solvent phases.
| D-π-A (position 3) gas | |||||||
|---|---|---|---|---|---|---|---|
| Dye | LHE | (eV) | (eV) | (eV) | Voc | |VRP| | ԏ (ns) |
| D1-CM-A1 | 0.689 | −7.576 | −11.576 | 0.91668 | 0.54005 | −3.76668 | 8.42 |
| D2-CM-A2 | 0.907 | −7.495 | −11.495 | 0.62823 | 0.75393 | −3.47823 | 2.81 |
| D3-CM-A3 | 0.380 | −7.848 | −11.884 | 1.04104 | 0.34194 | −3.89104 | 27.48 |
| D4-CM-A4 | 0.346 | −7.848 | −11.848 | 1.04104 | 0.39582 | −3.89104 | 15.42 |
| D5-CM-A5 | 0.294 | −8.289 | −12.228 | 1.51398 | −0.06623 | −4.36398 | 39.56 |
| D6-CM-A6 |
0.430 |
−7.935 |
−11.935 |
1.30145 |
−0.14705 |
−4.15145 |
26.25 |
|
D-π-A (position 3) solvent | |||||||
| D1-CM-A1 | 0.856 | −8.041 | −12.041 | 1.15206 | 0.6685 | −4.00206 | 4.79 |
| D2-CM-A2 | 0.913 | −7.235 | −11.235 | 0.53001 | 0.7343 | −3.38001 | 3.08 |
| D3-CM-A3 | 0.527 | −7.669 | −11.669 | 0.90308 | 0.4045 | −3.75308 | 18.35 |
| D4-CM-A4 | 0.761 | −7.352 | −11.352 | 0.77464 | 0.3648 | −3.62464 | 4.99 |
| D5-CM-A5 | 0.463 | −8.228 | −12.228 | 1.39397 | 0.0802 | −4.24397 | 21.69 |
| D6-CM-A6 | 0.411 | −7.788 | −11.788 | 1.19968 | −0.0455 | −4.04968 | 29.00 |
3.6.1. Light harvesting efficiency (LHE)
Light harvesting efficiency (LHE) is the fraction of light intensity absorbed by the dye molecules. The light harvesting efficiency is one of the most crucial factors in organic dyes, which play the main role in DSSCs. The LHE must be high to promote the photocurrent reaction. The higher the oscillator strength, the more LHE, the higher electron injection efficiency and more JSC, as described in Eq. (3) [36].
| LHE = 1–10−f | (3) |
Here, f represents the oscillator strength of absorbed dye molecule.
From Table 7, the values of LHE increase in the following order; D2-CM-A2 > D1-CM-A1 > D6-CM-A6 > D3-CM-A3 > D4-CM-A4 > D5-CM-A5 and D2-CM-A2 > D1-CM-A1 > D4-CM-A4 > D3-CM-A3 > D5-CM-A5 > D6-CM-A6 for gas and solvent phases respectively. The results show that D2-CM-A2 and D1-CM-A1 have the highest values of LHE since they have the strong electron donating capability with -conjugate double bond with lone pairs. Therefore they are suggested to be a good candidate in the DSSCs application.
3.6.2. Electron injection efficiency (ΔGinject)
The capability of dye molecules to inject the electron from lower unoccupied molecular orbital (LUMO) to the conduction band of the semiconductor is called electron injection efficiency. It is calculated by using Eq. (4) and their results are shown in Table 7.
| ΔGinject = Edye∗ + ECB | (4) |
Where Edye∗ represents the oxidation potential energy in excited state and ECB is reduction potential of the semiconductor whose value is −4.0 eV. The oxidation potential energy of the dye in an excited state as Eq. (5);
| Edye∗ = Edye – E00 | (5) |
Edye is the dye's oxidation potential energy in the ground state and E00 is the vertical electronic transition energy corresponding to the wavelength maximum (λmax). The ΔGinject can be evaluated through two schemes which are the relaxed and un-relaxed paths. In a relaxed path, an electron injects the molecule from the ground state directly to the semiconductor's conduction band [44]. Whereas the un-relaxed path is determined when the electron injects from the excited state of the dye to the semiconductor conduction band, the un-relaxed path is truly worthy. It was observed that ΔGinject decreased in the following order: D2-CM-A2 >D1-CM-A1 >D4-CM-A4 >D3-CM-A3 >D6-CM-A6 >D5-CM-A5 and D2-CM-A2 > D4-CM-A4 >D3-CM-A3 > D6-CM-A6 > D1-CM-A1 > D5-CM-A5 for gas and solvent phases, respectively. The results show that D2-CM-A2 has a higher value of ΔGinject. Therefore, it is suggested to be good in the application of DSSCs. LHE and ΔGinject are two important factors that influence Jsc factor and the highest short circuit current density can be obtained if and only if the LHE is large [38, 40].
3.6.3. Electron regeneration energy ΔGregen
The capability of dye to regain electron from the electrolyte after photoexcitation is called Electron Regeneration efficiency (ΔGregen).
The dye regeneration energy is one of the essential factors that affect photoelectric conversion efficiency [45]. It is calculated by using the following Eq. (6) and their results are presented in Table 7;
| (6) |
Is the redox potential of tri iodide-iodide which is given as (−4.85 eV) [46]
Is the oxidation potential energy of the dye in the ground state.
Results depicted that D5-CM-A5 dyes derivatives at positions 3 and 4 in gas and solvent phases have the highest values of electron regeneration efficiency than other dye molecules.
The following decreasing trend of the electron regeneration efficiency was observed: D5-CM-A5 >D6-CM-A6 >D3-CM-A3 = D4-CM-A4 >D1-CM-A1 >D2-CM-A2 and D5-CM-A5 > D6-CM-A6 > D1-CM-A1 > D3-CM-A3 > D4-CM-A4 > D2-CM-A2 in gas and solvent phases respectively. Therefore the large (ΔGregen) observed in D5-CM-A5 can promote dye regeneration and consequently the JSC will increase.
3.6.4. Open circuit voltage (VOC)
The open-circuit voltage is used to estimate the power conversion efficiency (ղ) in DSSCs. Usually, the electron transfer occurs from LUMO of the dye molecules to the semiconductor conduction band; hence if ELUMO is high, the VOC will be as well, and the bigger the driving force regeneration can improve ɳreg. The VOC values were depicted in Table 7 as follow; D2-CM-A2 > D1-CM-A1 > D4-CM-A4 > D3-CM-A3 > D5-CM-A5 > D6-CM-A6 for gas phase and D2-CM-A2>D1-CM-A1> D3-CM-A3> D4-CM-A4>D5-CM-A5> D6-CM-A6 for solvent phase. The results show that D2-CM-A2 and D1-CM-A1 have higher value of VOC. Therefore, they are suggested to be a good candidate in the DSSCs application.
3.6.5. Excited-state lifetime (τ)
The efficiency of charge transferring can be affected by the existence of lifetime of the first excited states. The lengthier of the life span of the molecule will donate so much in charge transferring and will be longer remain in cationic form, to be more conductive on charge transfer. The incensement of excited state lifetime enhances to the retardation of charges recombination process and increase the efficiency of photovoltaic cells. Furthermore, the long radioactive lifetime enhances the movement of an electron from the LUMO of electron donor to the LUMO of electron acceptor. As a consequence, the highest light Emitting efficiency is obtained. The following Eq. (7) gives the exciting lifetime (ԏ):
| (7) |
Where c is called the velocity of light, E is the excitation energy, and f is known as oscillator strength [47, 48]. The corresponding values are shown in Table 7. The results shows that, D5-CM-A5 (39.56 ns)> D3-CM-A3 (27.48 ns)> D6-CM-A6 (26.25 ns) > D4-CM-A4 (15.42 ns) > D1-CM-A1 (8.42 ns) > D2-CM-A2 (2.81 ns) and D6-CM-A6 (29.00 ns) > D5-CM-A5 (21.69 ns) > D3-CM-A3 (18.35 ns) > D4-CM-A4 (4.99 ns) > D1-CM-A1 (4.79 ns)> D2-CM-A2 (3.08 ns) in both gas and solvent phases respectively. D2-CM-A2 has lowest value because it has the highest value of oscillator strength. Therefore D2-CM-A2 is predicted to have the higher light harvesting efficiency and ΔGinject without disturbance on the JSC. The greater the solvent polarity, the greater the exciting life span.
3.6.6. Electronic coupling constant
Electronic coupling constant is the theory that explains the movement of an electron from the dye molecule to the conduction band of the semiconductor through the process of electron injection by implies a certain pair of states (initial state and final state). For example, the classical Marcus theory explained the electron injection through coupling constant as follows Eq. (8); [49, 50].
| (8) |
Where Kinjects, is the rate constant (in S−1) when the electron injects from dye molecule to the semiconductor.
KB, is the free energy of injection and is called coupling constant between the reaction and product potential curves. According to this equation, the higher value of the coupling constant implies the higher the rate constant, which finally leads to the best dye (sensitizer) and this lead to the strongest electron coupling between two states and the electron movement will take place very fast.
The Generalized Milliken – Hush (GMH) assumed the coupling constant calculation from Eqs. (9) and (10) as follows.
| (9) |
| (10) |
Here; ECB is the conduction band of semiconductor which is obtained through the experimentation ECBTi02 = −4.0 eV [49]. Table 7, show the corresponding values. The results are in order of D5-CM-A5 > D6-CM-A6 > D4-CM-A4 ≈ D3-CM-A3 > D1-CM-A1 > D2-CM-A2 and D5-CM-A5 > D6-CM-A > D1-CM-A1 > D3-CM-A3 > D4-CM-A4> D2-CM-A2 in gas and solvent phases, respectively. D5-CM-A5 shows the greater tendency of coupling, so the electron will move very fast from the dye molecule to the conduction band of a semiconductor which implies that it is the best sensitizer than all other dye derivatives.
4. Conclusion
A computational study was conducted to investigate optoelectronic properties of coumarin based dyes derivative for application in dye sensitizing solar cells (DSSC). All calculations for geometric optimization, electronics and optoelectronic properties of dyes were done using DTF and TD-DFT/B3LYP/6-31G. In donor-π- acceptor, the chemical structures were modified to improve the given dye molecules' electronic properties and optical characteristics. The energy gap was 2.66 to 1.98 eV and 2.67 to 1.98 eV for gas and solvent phases. The lowest energy gap was observed for D6-CM-A6, which was associated with the effect of intermolecular charge transfer (ICT).
The presence of stronger ICT causes the molecule to have the different maximum absorption wavelength, and when the bandgap decrease, the wavelength absorption increases. The total energies HOMOs of DI-CM-A1 to D6-CM-A6 were; −5.76, −5.47, −5.89, −5.89, −6.36, −6.15 eV and −6.00, −5.38, −5.75, −5.62, −6.24, −6.04 eV for gas and solvent phases respectively. Whereas, the total energies of LUMOs were; −3.45, −3.3, −24, −3.65, −3.90, −4.0, −4.14 eV in gas phase. The electrotransfer from the excited dye of the TiO2 conduction band is possible for all dye derivatives except D5-CM-A5 and D6-CM-A6 because they exceed the TiO2 conduction band energy value (−4.0 eV). The time-dependent density functional calculation through TD-B3LYP/6-31 Glevel was used in optical transition to predict the excited state and emission state. In both phases, D1-CM-A1 and D2-CM-A2 have the highest LHE and ΔGinject compared to other dye molecules. Therefore, these dyes would be more favoured for DSSC applications. To ascertain their application, an experimental study is recommended to confirm their efficiencies.
Declarations
Author contribution statement
Said A. H. Vuai: Conceived and designed the experiments; Wrote the paper.
Mwanahadia Salum Khalfan: Performed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Numbury Surendra Babu: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data availability statement
Data will be made available on request.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Orebiyi J., Barnes B., Das K.S. 2018. Dye-Sensitized Solar Cells. [Google Scholar]
- 2.Kalyanasundaram K., de Lausanne E.C.P.F. Press; Lausanne, Switzerland: 2010. Dye-Sensitized Solar Cells, 2010. [Google Scholar]
- 3.Shafiee S., Topal E. Appl. Energy. 2010;87(3):988–1000. [Google Scholar]
- 4.Xu J., Zhang H., Liang G., Wang L., Weilin X., Cui W., Zengchang L. J. Serb. Chem. Soc. 2010;75(2):259–269. [Google Scholar]
- 5.O Regan B., Graätzel M. Nature. 1991 353/6346, 737–740–740. [Google Scholar]
- 6.Grätzel M. J. Photochem. Photobiol. C Photochem. Rev. 2003;4(2):145–153. [Google Scholar]
- 7.Peter L.M. J. Phys. Chem. Lett. 2011;2(15):1861–1867. [Google Scholar]
- 8.Srinivas K., Yesudas K., Bhanuprakash K., Rao V.J., Giribabu L. J. Phys. Chem. C. 2009;113(46):20117–20126. [Google Scholar]
- 9.Teng C., Yang X., Yang C., Li S., Cheng M., Hagfeldt A., Sun L. J. Phys. Chem. C. 2010;114(19):9101–9110. [Google Scholar]
- 10.Xu J., Wang L., Liang G., Bai Z., Wang L., Xu W., Shen X. Acta A Mol. Biomol. Spectrosc. 2011;78(1):287–293. doi: 10.1016/j.saa.2010.10.008. [DOI] [PubMed] [Google Scholar]
- 11.Chen Z., Li F., Huang C. Curr. Org. Chem. 2007;11(14):1241–1258. [Google Scholar]
- 12.Grätzel M. Inorg. Chem. 2005;44(20):6841–6851. doi: 10.1021/ic0508371. [DOI] [PubMed] [Google Scholar]
- 13.Zhang H., Fan J., Iqbal Z., Kuang D.-B., Wang L., Cao D., Meier H. Dyes Pigments. 2013;99(1):74–81. [Google Scholar]
- 14.Zhang J., Li H.-B., Geng Y., Wen S.-Z., Zhong R.-L., Wu Y., Fu Q., Su Z.-M. Dyes Pigments. 2013;99(1):127–135. [Google Scholar]
- 15.Tan L.L., Xie L.J., Shen Y., Liu J.M., Xiao L.M., Kuang D.B., Su C.Y. Dyes Pigments. 2014;100:269–277. [Google Scholar]
- 16.Yella A., Humphry-Baker R., Curchod B.F.E., Ashari Astani N., Teuscher J., Polander L.E., Mathew S., Moser J.-E., Tavernelli I., Rothlisberger U., Grätzel M., Nazeeruddin M.K., Frey J. Chem. Mater. 2013;25(13):2733–2739. [Google Scholar]
- 17.Tian H., Yang X., Chen R., Pan Y., Li L., Hagfeldt A., Sun L. Chem. Commun. 2007;3743:3741. doi: 10.1039/b707485a. [DOI] [PubMed] [Google Scholar]
- 18.Yang S., Sun I.C., Hwang H.S., Shim M.K., Yoon H.Y., Kim K. J. Mater. Chem. B. 2021;9(19):3983–4001. doi: 10.1039/d1tb00397f. [DOI] [PubMed] [Google Scholar]
- 19.Ducasse L., Castet F., Méreau R., Nénon S., Idé J., Toupance T., Olivier C. Chem. Phys. Lett. 2013;556:151–157. [Google Scholar]
- 20.Hart A.S., Chandra B.K., Gobeze H.B., Sequeira L.R., D′Souza F. Porphyrin-sensitized solar cells: effect of carboxyl anchor group orientation on the cell performance. ACS Appl. Mater. Interfaces. 2013;5(11):5314–5323. doi: 10.1021/am401201q. [DOI] [PubMed] [Google Scholar]
- 21.Ham H.W., Kim Y.S. Thin Solid Films. 2010;518(22):6558–6563. [Google Scholar]
- 22.Hara K., Dan-Oh Y., Kasada C., Ohga Y., Shinpo A., Suga S., Sayama K., Arakawa H. Langmuir. 2004;20(10):4205–4210. doi: 10.1021/la0357615. [DOI] [PubMed] [Google Scholar]
- 23.Wang Z.S., Hara K.Y., Dan-oOh, Kasada C., Shinpo A., Suga S., Arakawa H., Sugihara H. J. Phys. Chem. B. 2005;109(9):3907–3914. doi: 10.1021/jp044851v. [DOI] [PubMed] [Google Scholar]
- 24.Mishra A., Fischer M.K., Bäuerle P. Angew. Chem. Int. Ed. Engl. 2009;48(14):2474–2499. doi: 10.1002/anie.200804709. [DOI] [PubMed] [Google Scholar]
- 25.Le T., Epa V.C., Burden F.R., Winkler D.A. Chem. Rev. 2012;112(5):2889–2919. doi: 10.1021/cr200066h. [DOI] [PubMed] [Google Scholar]
- 27.Becke A.D. J. Chem. Phys. 1993;98(2):1372–1377. [Google Scholar]
- 28.Lee C., Yang W., Parr R.G. Phys. Rev. B Condens. Matter. 1988;37(2):785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 29.Cossi M., Barone V., Cammi R., Tomasi J. Chem. Phys. Lett. 1996;4(6):327–335. [Google Scholar]
- 30.Tomasi J., Mennucci B., Cammi R. Chem. Rev. 2005;105(8):2999–3093. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
- 31.Frisch M.J., Trucks G.W., Schlegel H.B., et al. Vol. 9. Gaussian Incorp.; Wallingford, U.K.: 2009. (Gaussian). [Google Scholar]
- 32.Dennington R., Keith T., Millam Gauss J. Semichem Inc.; Shawnee Mission: 2009. View. version 5. [Google Scholar]
- 33.Allouche A.R. Gabedit. 2017 [Google Scholar]
- 34.Wang H., Liu Q., Liu D., Su R., Liu J., Li Y. Int. J. Photoenergy. 2018:1–17. [Google Scholar]
- 35.Bourass, M.; Benjelloun, A. T.; Benzakour, M.; Mcharfi, M.; M Hamidi, 2015, 6 (6), 1542–1553.
- 36.El Assyry A., Hallaoui A., Zarrouk A., El Hezzat M., Assouag M., Boukhris S., El Assyry A. Materials. 2015;7(10):128–138. [Google Scholar]
- 37.Bourass M., Benjelloun A.T., Benzakour M., Mcharfi M., Hamidi M., Bouzzine S.M., Bouachrine M. Chem. Cent. J. 2016;10:67. doi: 10.1186/s13065-016-0216-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.El Malki Z., Bouachrine M., Hamidi M., Bejjit L., Haddad M. Theor. Stud. Struct. Electron. Opt. Prop. 2012 [Google Scholar]
- 39.Prakasam, A.; Sakthi, D.; P. M. Anbarasan, 2013, 12 (1), 8–22.
- 40.Tseng C., Taufany F., Nachimuthu S., Jiang J., Liaw D. eElectronics. 2014;15(6):1205–1214. [Google Scholar]
- 41.Oprea C.I., Panait P., Fanica C., Ferbinteanu M. Materials (Basel) 2013;6(6):2372–2392. doi: 10.3390/ma6062372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Park K., Serrano L.A., Ahn S., Hoon M., Wiles A.A., Cooke G., Hong J. Tetrahedron. 2017;73(8):1098–1104. [Google Scholar]
- 43.El Azzouzi M., Aouniti A., Tighadouin S., Elmsellem H., Radi S., Hammouti B., Zarrouk A. J. Mol. Liq. 2016;221:633–641. [Google Scholar]
- 44.Daeneke T., Mozer A.J., Uemura Y., et al. J. Soc. 2012;134(41):16925–16928. doi: 10.1021/ja3054578. [DOI] [PubMed] [Google Scholar]
- 45.Boschloo G., Hagfeldt A. Acc. Chem. Res. 2009;42(11):1819–1826. doi: 10.1021/ar900138m. [DOI] [PubMed] [Google Scholar]
- 46.Yang Z., Liu Y., Liu C., Lin C., Shao C. Spectrochim. Acta Part Mol. Biomol. Spectrosc. 2016;167:127–133. doi: 10.1016/j.saa.2016.05.041. [DOI] [PubMed] [Google Scholar]
- 47.Li M., Kou L., Diao L., Zhang Q., Li Z., Wu Q., Lu W., Pan D., Wei Z. J. Phys. Chem. C. 2015;119(18):9782–9790. doi: 10.1021/acs.jpca.5b00798. [DOI] [PubMed] [Google Scholar]
- 48.Pourtois G., Beljonne D., Cornil J., Ratner M.A., Brédas J.L. J. Am. Chem. Soc. 2002;124(16):4436–4447. doi: 10.1021/ja017150+. [DOI] [PubMed] [Google Scholar]
- 49.Hsu C.P. Acc. Chem. Res. 2009;42(4):509–518. doi: 10.1021/ar800153f. [DOI] [PubMed] [Google Scholar]
- 50.Marcus R.A. Rev. Mod. Phys. 1993;65(3):599–610. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.