Neural tracking in infants – An analytical tool for multisensory social processing in development

Abstract

Humans are born into a social environment and from early on possess a range of abilities to detect and respond to social cues. In the past decade, there has been a rapidly increasing interest in investigating the neural responses underlying such early social processes under naturalistic conditions. However, the investigation of neural responses to continuous dynamic input poses the challenge of how to link neural responses back to continuous sensory input. In the present tutorial, we provide a step-by-step introduction to one approach to tackle this issue, namely the use of linear models to investigate neural tracking responses in electroencephalographic (EEG) data. While neural tracking has gained increasing popularity in adult cognitive neuroscience over the past decade, its application to infant EEG is still rare and comes with its own challenges. After introducing the concept of neural tracking, we discuss and compare the use of forward vs. backward models and individual vs. generic models using an example data set of infant EEG data. Each section comprises a theoretical introduction as well as a concrete example using MATLAB code. We argue that neural tracking provides a promising way to investigate early (social) processing in an ecologically valid setting.

1. Introduction

Humans live in a dynamic, ever-changing environment. They constantly receive input from numerous sensory channels, and in most cases effortlessly manage to combine these different input streams into one coherent percept of their surroundings. How the human brain manages to accomplish this feat has long been the subject of investigation, in both adult and developmental neuroscience. To investigate the mechanisms underlying the processing of naturalistic multisensory input, it is essential to move beyond traditional cognitive neuroscience experiments, in which participants are seated in front of a screen and are presented with well-controlled, often static and repetitive stimuli (Hamilton and Huth, 2020).

While this is true for both, adult and developmental research, using a complex and dynamic environment is important in developmental research for another reason. Children, especially younger children, and children from special populations, often cannot follow experimental instructions as well as adults can. Hence, it becomes of paramount importance to design experiments that are engaging enough to capture the participant’s attention for a sufficient amount of time and provide motivation for the participant to engage with the experimental set-up.

From an experimental point of view, however, using dynamic, non-repetitive experimental designs poses the challenge of how to align such highly variable input to the recorded brain data. One approach to do so is the use of linear models to investigate the neural tracking of continuous sensory input using electro- or magnetoencephalographic (EEG or MEG) data. For the present purpose, we will only focus on EEG data, since this method is most prominent in developmental cognitive neuroscience, but in principle, the same approach can be applied to MEG data or hemodynamic (e.g., NIRS; near-infrared spectroscopy) signals.

The key idea here is essentially the one familiar to social scientists from regression, or more parsimoniously, the general linear model: A relatively simple mathematical model is used to relate continuous EEG traces to continuous environmental input. This relation can go in two directions: in encoding (or forward) models, stimulus features are used to “predict” the neural signal; in decoding (or backward) models, the neural signal is used to “reconstruct” the input signal (Abbott and Dayan, 2001; Naselaris et al., 2011).

The use of encoding/decoding models has become increasingly popular over the past decade in adult cognitive neuroscience, especially in the field of auditory neuroscience (Crosse et al., 2016). These models provide in principle two separable but analytically related measures of “neural tracking”: First, in analogy to the beta estimate in a simple regression, we might be interested in the change in predicted EEG voltage that a one-unit change in the predictor (e.g., change in luminance, or change in sound pressure level at a given time point, e.g. 100 ms before) yields. In forward encoding models, however, we do this not only for one specific, arbitrary lag of stimulus and brain response at a time, but for a whole set of time-lagged or stacked “copies” of the stimulus. This yields a whole set of time-lagged beta estimates, jointly making up the so-called “temporal response function” or TRF. As we will see below, the TRF is often interpreted in close reference to established interpretations of the evoked brain response in classical, event-related designs (see also Simon et al. (2007)). Second, in some analogy to measures of goodness-of-fit in regression like R², this temporal response function can be used, by simple convolution with the entire stimulus time series itself, to yield an entire predicted EEG time series. The correlation of measured and model-predicted time series is then referred to as “predictive accuracy” (in a forward model, where the brain signal is being “predicted”) or “reconstructive accuracy” (in a backward model, where the stimulus is being “reconstructed”).

Both, features of the temporal response function and the correlation-based accuracy are being interpreted as “neural tracking” or “strength of neural representation”, with prominent application in the field of attention research (for review, see e.g. Obleser and Kayser (2019)), psycholinguistics (e.g., Brodbeck et al. (2018), Broderick et al. (2018)) or ageing (e.g., Presacco et al. (2016), Tune et al. (2021)).

While the application of these approaches to developmental neuroscience seems highly promising, it comes with certain challenges. Data quality in young children is often worse compared to data acquired under optimal recording conditions in adults due to more motion artifacts and less time for optimal electrode preparation. Relatedly, data of sufficient quality may not be available for all electrodes, reducing the number of channels to be included in the analysis (see however Montoya-Martinez et al. (2021) who demonstrate that reliable results can be obtained even with a reduced number of electrodes). In addition, less data is typically available, as young children often do not tolerate long recording sessions. These constraints raise the question, whether approaches that can successfully be used in adult research, are also applicable to recordings in infant populations.

Over the past years, though, the feasibility of neural tracking for the analysis of developmental EEG data has been demonstrated in several cognitive domains. In 2018, Kalashnikova et al. (2018) successfully used neural tracking to analyze 7-months-olds neural responses to infant- vs. adult-directed speech and found stronger neural tracking for infant-directed speech. Furthermore, encoding models have been used to analyze brain responses of 7-months-olds watching an audiovisual cartoon movie (Jessen et al., 2019). While both of these studies used encoding models, there is also evidence for the feasibility of applying decoding models. In particular, Attaheri et al. (2021) used a decoding model to analyze the contribution of neural responses at different frequencies in the neural tracking of nursery rhymes presented to infants between 4 and 11 months of age.

Finally, neural tracking can not only be exploited to analyze infant EEG data but also for the analysis of neural data in older children. For instance, linear models have been used to analyze MEG (Destoky et al., 2020) as well as EEG data (Di Liberto et al., 2018) in elementary school children with and without dyslexia to investigate development of literacy.

Neural tracking therefore offers a promising opportunity for state-of-the-art, naturalistic developmental cognitive neuroscience. Yet, the successful application of this analysis technique hinges on a number of methodological considerations that may be unfamiliar to developmental neuroscientists more experienced in the classical event-based analysis of neurophysiological data. In the following, we will provide a step-by-step tutorial, outlining how neural tracking can successfully be used to analyze developmental EEG data. Using an example data set, for each step, we will first provide a theoretical description and motivation before demonstrating the practical application including relevant MATLAB code. We will focus specifically on issues relevant for developmental researchers; for a more general tutorial on the use of neural tracking and the specific application in clinical populations, see Crosse et al. (2021).

2. Methods

2.1. Example data set

The data used as an example here are seven minutes of EEG data collected from a 7-month-old infant listening to a recording of his mother reading a children’s story. When comparing generic and individual model computation (see below), data from nine additional 7-month-olds from the same experimental set-up will be used. All recordings were conducted according to the Declaration of Helsinki, approved by the ethics committee at the University of Lübeck, and parents provided written informed consent. For recording, we used an elastic cap (BrainCap, Easycap GmbH), in which 27 AgAgCl-electrodes were mounted according to the modified international 10–20-system. Data were recorded at a sampling rate of 500 Hz using a BrainAmp amplifier and the BrainVision Recorder software (both Brain Products). The example data set and associated analysis code can be found here: https://osf.io/7h58x/.

2.2. Software

All analyses are conducted in MATLAB 2020a (The MathWorks, Inc., Natick, MA). We used the MATLAB toolbox Fieldtrip (Oostenveld et al., 2011), the multivariate temporal response function (MTRF) toolbox version 2.3 (Crosse et al., 2016), as well as two custom-made scripts which demonstrate the encoding and decoding model approach, respectively.

2.3. Preparation of neural and stimulus data

2.3.1. Data preprocessing

The aim of the preprocessing steps described here is to obtain a data set that contains as little artifacts as possible; hence, the optimal choice of preprocessing steps may vary between experimental designs. In the present case, data were referenced to the mean of all electrodes (average reference) and filtered using a 40 Hz lowpass and a 1 Hz highpass filter as preparation for data cleaning via independent component analysis (ICA). After that, data were segmented into 1-sec-epochs. To detect data segments contaminated by artifacts, the standard deviation was computed in a sliding window of 200 ms length. If the standard deviation exceeded 100 μV in any epoch or at any electrode, the entire epoch was discarded from further analysis. After this step, 412 out of 550 epochs remained in the dataset. On the remaining data, an independent component analysis (ICA) was computed, and components classified as artifactual based on visual inspection were removed. Note, however, that identifying ICA components as artifactual in infants is often challenging (Noreika et al., 2020) and therefore does not necessarily result in greatly improved data quality. Hence, depending on the data set, this step may also be omitted.

Subsequently, a 1-Hz-highpass and 10-Hz-lowpass filter were applied in preparation for linear modelling. Highpass filtering of the EEG helps to attenuate low-frequency artifacts such as slow signal drifts due to sweating. We here chose a 10-Hz-lowpass cut-off since previous studies have shown that neural activity phase-locked to the speech envelope typically occurs below 10 Hz (see e.g. (Ding and Simon, 2013; Golumbic et al., 2013)) and that the inclusion of stimulus-irrelevant signals at higher frequencies negatively impacts prediction accuracy (Fiedler et al., 2019). Note that the cutoff frequencies of the high- and lowpass filters may also be set to focus on specific frequency bands of interest.

An additional 52 1-sec-epochs were removed because in addition to the sound signal of interest, a second sound signal was presented simultaneously which is not of interest for the present approach. In sum, a total of 360 1-sec-epochs were used for modelling.

2.3.2. Stimulus signal preparation

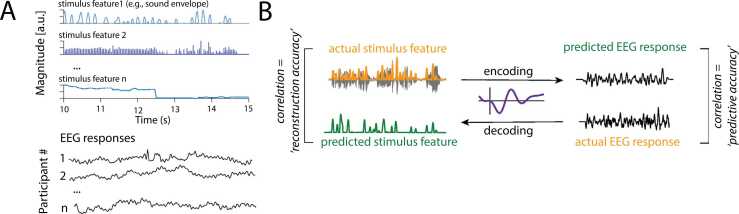
The preparation of the continuous stimulus signal to be used as a predictor in forward, and as predicted output in backward models depends on the characteristics of the stimulus material and the features of interest (Fig. 1A). Such features could include any continuous measure, for example basic physical stimulus properties, such as luminance, amount of visual motion, or sound envelope, but also more complex measures such as physical distance between parent and infant or movement of the child. One property that is helpful in successfully modelling the neural response to a stimulus parameter is a certain variance in the stimulus signal, as too little variance typically leads to poor modelling performance.

Fig. 1.

A) Schematic representation of sensory and neural input. Any number of different continuous stimulus features can be used as input. B) Schematic overview of the encoding vs. decoding approach. As explained in more detail in the text, for an encoding approach the stimulus features are used to generate a predicted EEG response which is then compared to the actual EEG response. For a decoding approach, EEG responses are used to generate a prediction of the stimulus input, which is then compared to the actual input.

It is also possible to include more abstract stimulus features that are detached from the physical properties of a stimulus, such as higher-order linguistic representation (e.g., phonemic or semantic information) of speech inputs. Furthermore, one can also model non-continuous, binary stimulus properties, such as word onset in an auditory signal or the appearance of a face in a visual signal. To do so, time-periods in which the relevant feature occurred (i.e, word onset, face appearance) are marked by ones in a the stimulus input vector, while the remainder of the vector consists of zeros (for further details on this approach, see e.g. (Sassenhagen, 2019)). Finally, several of these measures can be used in combination to investigate, for example, their relative importance in predicting the ensuing neural response.

For the present example, we focus on a single stimulus feature, the onset envelope of the recorded maternal speech that was extracted using the NSL toolbox (Ru, 2001).

2.3.3. Alignment of neural and stimulus signal

As the last preparatory step, we temporally aligned neural and stimulus data in one matrix. Note that it is important that all data need to be transformed (i.e., downsampled or interpolated) to the same frequency. We removed periods for which no neural data was available (as epochs were removed during preprocessing due to artifacts) from the stimulus representation as well. To avoid problems due to data discontinuity when concatenating all remaining epochs of temporally aligned neural and stimulus data, we inserted 1-sec worth of zeros in both the neural and stimulus representation whenever two discontinuous epochs were joined. Note that this approach represents only one possible solution to handling artifact-contaminated periods in the EEG signal. An advantage of this approach is the robustness of TRF estimation in encoding models to even relatively high proportions of zero-replaced epochs (i.e. around 30–40% of modelled data). At the same time, it is important to realize that noisier data, that is, those that require more zero-padding, can lead to a small but counterintuitive increase in predictive performance in the final model evaluation. This is of particular concern when fitting models at the level of the individual participant as differences in data quality could then unduly obscure second-level comparisons. Generic models that combine data across participants, or the estimation of individuals models based on a higher number of shorter continuous periods may offer alternative solutions. However, it is generally advisable to pay close attention to the amount and quality of data that enters linear modelling across participants and/or experimental conditions.

The resultant data structure serves as input data to each of the two custom MATLAB scripts provided with this article. We rely on functions implemented in the mTRF toolbox for model fitting and evaluation (Crosse et al., 2016). While the toolbox offers additional functions to conveniently implement, for example, data segmentation, cross-validation or visualization, for didactic reasons, we supply step-by-step custom code for these purposes. We hope this approach will increase transparency and allow the reader to flexibly adapt the code to their own needs. In the description of our example analysis, we start at its very heart – the fitting of different linear models – to then work ourselves through the outer layers of the analysis that involve concepts such as regularization, cross-validation, and model evaluation.

2.4. Encoding vs. decoding models

As depicted in Fig. 1B, there are two complementary modelling approaches that estimate the mapping between a continuous stimulus and its ensuing continuous neural response. The two approaches differ in the direction in which the stimulus-response mapping function is modelled. Encoding (or forward) models, also termed temporal response functions (TRFs; Ding and Simon, 2012), describe how specific features of a presented stimulus map onto the following neural response. Put differently, this kind of model probes how well the neural responses can be predicted based on stimulus information. Temporal response functions are estimated independently per EEG channel and their beta weights allow for an intuitive, neurophysiological interpretation: they quantify how a neural response changes with each one-unit change in a given stimulus feature. In essence, a forward model describes how sensory information is encoded in neural activity.

Encoding models are particularly useful if one is interested in comparing how strongly or with which temporal delay different stimulus features are encoded across brain regions. An example for such a research question is the study conducted by Kalashnikova et al. (2018), who used encoding models to compare the processing of infant- vs. adult-directed speech, assessing how different features of speech impact cortical tracking. More generally, encoding models can be highly useful in the investigation of preverbal speech processing, as the varying contributions of different speech parameters to neural tracking can be investigated across development and brain areas. These approaches can be further extended into the clinical realm; do for instance children with delayed speech development show reduced neural tracking of specific speech components? A different application of encoding models could be the investigation of how different visual parameters contribute to early social learning; how is for instance biological motion tracked, either from video material but also during live interactions?

The temporal unfolding of the estimated temporal response function is reminiscent of that of event-related potentials and relates to different processing stages (Lalor et al., 2006, Simon et al., 2007). By restricting the included time lags (expressing the delay in the stimulus-response relationship), it is thus possible to specifically focus on particular sensory or cognitive processes. Additionally, given the univariate nature of the forward modelling approach, it is recommended to restrict the analysis to a selection of channels that broadly represent a brain region assumed to be engaged in the process of interest.

Decoding (or backward) models represent an alternative approach to mapping between stimulus and neural response (see Fig. 1B). As the term backward model suggests, it maps between the two domains in the opposite direction. In going from the neural response back to the past stimulus, we ask how well a presented stimulus can be reconstructed or decoded based on the recorded ensuing neural response (Dayan and Abbott, 2001).

A key difference to encoding models is that decoding models are multivariate. This means that the modelling procedure combines information in the neural responses at different channels to jointly reconstruct properties of the presented stimulus. This feature comes with both advantages and disadvantages. On the one hand, the inclusion of all channels makes a priori channel selection redundant and improves sensitivity and specificity by weighting channels based on their informativeness, thus effectively cancelling out noisy signals (Parra et al., 2003, Parra et al., 2005). On the other hand, it complicates the interpretation of model weights (Haufe et al., 2014). When inspecting decoding model weights per channel it can be tempting to interpret them the same way as forward model weights. Unfortunately, such a neurophysiological interpretation is not warranted as the magnitude of model weights does not directly speak to the degree of engagement in a particular process. However, Haufe et al. (2014) proposed a procedure that forward-transforms the decoder weights to facilitate their interpretation.

In developmental neuroscience, decoding models may be particularly useful for the comparison of neural tracking of input signals for which an infant may have differential preferences or may be differentially attentive to. Can we for instance predict an infant’s choice in a preferential looking paradigm based on their prior neural activation? Or is an infant’s habituation to a certain type of input linked to the neural tracking of that input?

Using our example dataset from one participant, in Box 1, we detail how both encoding and decoding models can be estimated using the mTRFtrain function from the mTRF toolbox. In the encoding model, we model how a single stimulus feature of interest, the onset envelope, maps onto the multi-channel EEG response. To facilitate interpretation of model weights, we z-score the EEG signal prior to linear modelling, keeping relative differences between individual channels intact. A similar normalization procedure should be applied to the stimulus representation as well if more than one feature is modelled and in particular if the scales for different features vary strongly. We are using a relatively broad range of time lags of −200–800 ms to inspect the temporal dynamics of the TRF. Note that depending on the specific research question, a more restricted range of positive time lags can boost predictive accuracy by focusing on the signal and processing stages of interest. This may be particularly relevant when probing differences in the neural encoding at a particular processing stage between participant groups or experimental conditions.

Box 1. Model training and transformation.

As described in the main text, there are two different kinds of models to map between stimulus features and neural responses. Luckily, using the mTRF toolbox (Crosse et al., 2016) both encoding (forward) models and decoding (backward) models can be conveniently estimated using regularized (ridge) regression by appropriately adapting the parameters of the following function:

model = mTRFtrain(stim, resp, fs, Dir, tmin, tmax, lambda)

As input to the function, the matrices containing stimulus features and neural responses should be organized in the same way with rows corresponding to observations and columns to variables. The number of observations needs to agree between stimulus and neural responses. In our example, this corresponds to a stimulus matrix of N samples x 1 as we include only one auditory feature, and a matrix of N samples x 27 channels for the neural response. Note that as part of cross-validation, we estimate a model based on multiple data segments (also called folds, see Box 2) by organizing them in cell arrays.

To switch between the estimation of encoding and decoding models, we set the direction parameter ‘Dir’ to either 1 (forward) or –1 (backward). Based on the sampling rate (‘fs’, in Hertz) and range of time lags (‘tmin’ and ‘tmax’, in milliseconds), the function creates the design matrix with time-lagged replications of regressors. Note that for backward models the time lags given by tmin and tmax are automatically reversed. Lastly, the strength of regularization is controlled via the ‘lambda’ parameter.

The function outputs a structure that includes the model weights (model.w), time lags at the provided sampling frequency (model.t).

To allow for a neurophysiological interpretation of model coefficients, for decoding models, we further apply a forward transformation (Haufe et al., 2014) with the following function:

fwd_model = mTRFtransform(bmodel, resp)

The function takes as input the estimated decoding (backward) model as well as the neural response matrix and outputs forward-transformed model weights and time lags.

Estimating a multivariate decoding model is computationally more expensive than fitting the mass-univariate encoding model. For this purpose, we additionally down-sample both neural response and stimulus representation from 500 to 64 Hz to speed up the computation. For the decoding model, we focus on a more restricted range of time lags from 0 to 800 ms to optimize reconstructive performance. Additionally, we demonstrate how backward model weights can be conveniently transformed into forward model weights using the function mTRFtransform.

Independently of whether the stimulus-response function is estimated in the forward or backward direction, to derive a measure of “neural tracking”– reflecting the degree to which neural responses are driven by the presented stimulus – model performance needs to be formally assessed. To this end, model training is complemented with model testing on held-out data to evaluate how well the model generalizes to data not involved in training. In the following section, we will illustrate two different training and testing routines, and discuss how such approaches along with regularized regression help improve generalizability.

2.5. Training and testing

The purpose of model training is to optimize its ability to successfully generalize to new, unseen data rather than capturing the peculiarities of the training data, a phenomenon called overfitting. It is therefore advisable to use so-called cross-validation procedures that efficiently split the data into separate data sets reserved for training and testing, respectively (see Varoquaux et al. (2017) for review). In testing, the trained encoding models are convolved with a new stimulus segment to yield a predicted EEG response per channel, whereas the trained decoding model is convolved with a new segment of EEG data to reconstruct the presented stimulus. Model performance can then be quantified by different metrics. The two most commonly used metrics are the Pearson’s correlation of model predictions with the measured EEG signal (for encoding models) or the presented stimulus (for decoding models), as well as complementary error measures such as the mean squared error (MSE) or mean absolute error (MAE). As described above, the correlation-based accuracy with which an EEG signal can be predicted or a stimulus reconstructed represents a quantification of neural tracking strength. In essence, this measure reflects the degree to which neural responses are driven by a presented stimulus.

2.5.1. Regularization

Up to this point, we have only very generally referred to the fitting of linear models that map between presented stimulus and measured neural response. Yet, it is important to realize that our use case presents a particular challenge for regular regression techniques: due to the inclusion of different time lags, we are a modelling a comparably large number of regressors. Moreover, these regressors are potentially highly correlated as neighboring EEG channels pick up similar signals, and many stimulus regressors such as acoustic envelope exhibit significant autocorrelation. We therefore use a technique referred to as regularized regression to reliably estimate model coefficients and avoid problems such as overfitting (Crosse et al., 2016, Holdgraf et al., 2017).

There are a number of different variants of regularized regression that could be used in such a case (Wong et al., 2018). Here, we apply ridge regression as a form of regularized regression particularly suited for models that involve large numbers of potentially correlated regressors (Hoerl and Kennard, 1970). In essence, ridge regression constrains the magnitude of coefficients by applying a penalty term that effectively smooths the resulting response function (Hastie et al., 2009). The size of the applied penalty terms and thus the strength of regularization is controlled by the hyperparameter λ that can vary between 0 and ∞. For λ = 0 the resultant coefficients would equal those of ordinary least squares (OLS) regression, whereas regularization strength increases with λ > 0.

In practice, the optimal amount of regularization is empirically determined by iterative model training and testing for a given set of lambda values. In our example analyses, we compared model performance across a logarithmically spaced grid of λ values ranging from 10⁻⁷ to 10⁷. Alternatively, one may choose to customize the range of tested λ values based on the autocovariance structure of the regressors (see e.g., Biesmans et al. (2017), Fiedler et al. (2019)).

2.5.2. Individual vs. generic model

As part of our exemplary analysis, we demonstrate how model optimization can be performed either at the level of the individual participant, or alternatively across a larger sample of participants using a “generic” (or subject-independent) model. In each case, the data will be divided into training and test sets and model evaluation will be assessed using a procedure called cross-validation (see Fig. 2A and B).

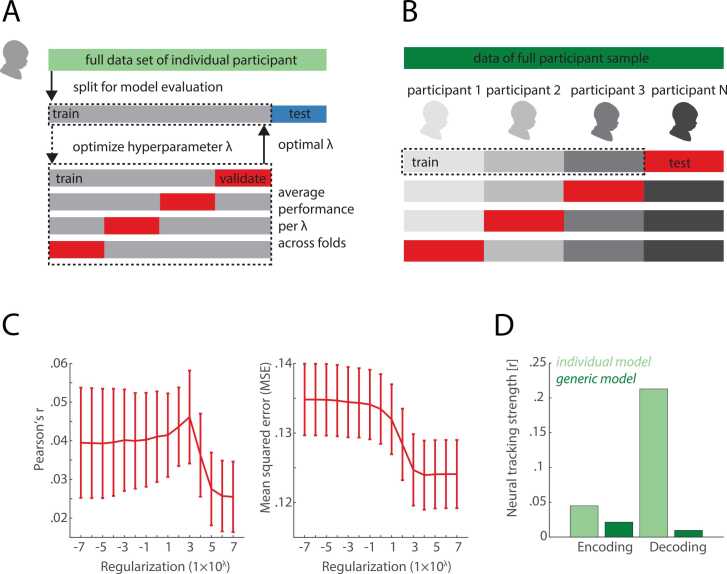
Fig. 2.

Comparison of individual vs. generic model. A) and B) present a schematic overview of the concept of individual (A) and generic (B) model generation. In brief, for an individual model, the data set of a given participant is subdivided into a training and a testing set (in our case 80% vs. 20%). The training data is again split into different parts (in our case 4) to perform the λ optimization. In contrast, for a generic model, data from n-1 participants is used for training while the nth dataset is used for testing. C) Optimization of λ parameter for the individual decoding model in our example analysis. Shown are two measures to assess the impact of choosing different λ parameters, ranging from 10⁻⁷ to 10⁷, namely the Pearson’s r and MSE. D) Model performance for individual (light green) and generic model (dark green) for encoding vs. decoding in our sample date set. As can be seen, for both, encoding and decoding, the individual model generated the better results. However, while for encoding, the difference between individual and generic model was small, the performance of the individual model was by a magnitude better compared to the generic model for the decoding model. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

To illustrate how training and testing at the level of the individual participant can be applied to our example data set, we first need to consider how our data are organized after preprocessing. At this stage, the normalized multi-channel neural responses and temporally aligned stimulus information are stored as continuous recordings rather than individual trials. As a first step, we thus split the continuous data into two data segments, with 80% of the data reserved for training, and the remaining 20% set aside for final model testing.

However, as described above, encoding and decoding models are fit using ridge regression which additionally requires the optimization of the hyperparameter λ. As is considered best practice, the optimization of this hyperparameter should be carried out using yet another set of independent training and validation data (Poldrack et al., 2020). To efficiently use the available data, we apply a technique called k-fold cross-validation. To this end, we further split the training data into 4 equal sized segments, referred to as folds. Within the cross-validation routine, training and validation sets are rotated until each fold has served as validation set while the remaining three folds are jointly used for training (see Fig. 2A).

The overall idea is to optimize the hyperparameter by repeating the training and validation procedure for a number of pre-defined λ values. In the next step, we average model performance (i.e., Pearson’s r and MSE) per tested λ value across folds to identify the λ value that yields the best model performance. Finally, we apply this optimal λ parameter for model estimation using all training data and test it on the initially left-out test data segment. In our example analysis, model evaluation is carried out using the function mTRFevaluate or alternatively mTRFpredict that both return by default Pearson’s r and MSE as evaluation metrics (see Box 2). Lambda tuning curves, showing model performance as a function of regularization strength, are an important diagnostic visual tool (see Fig. 2C).

Box 2. Model evaluation.

For training and testing of the individual model, we employ a nested cross-validation routine (see Fig. 2) in which data of an individual participants are repeatedly split into training and testing data sets. Here, we illustrate how model estimation followed by prediction and evaluation based on left-out data. We use the decoding model as an example and assume that the data have already been split between the inner and outer loop of cross-validation. Within the inner loop, we repeat the following process per fold f and lambda parameter l:

% strain and rtrain are cell arrays containing all but one data segment for training

MODEL(f,l) = mTRFtrain(strain,rtrain,fs,direction,tmin,tmax,lambda);

% apply the model by convolving it with the neural responses of left-out validation sets sval and rval to reconstruct the stimulus

RECON{f,l} = mTRFpredict(sval,rval,MODEL(f,l));

% compare reconstruction to original stimulus

[CV.r(f,l),CV.err(f,l)] = mTRFevaluate(sval, RECON{f,l});

In the code above, the function mTRFpredict convolves the estimated model with the recorded neural responses of a new data segment to reconstruct the presented stimulus. To evaluate how closely the reconstructed stimulus resembles the original stimulus, we make function mTRFevaluate. By default, this function calculates both Pearson’s r and the mean squared error (MSE) but can also be set to calculate Spearman’s correlation and mean absolute error (MAE). Note that the function mTRFpredict can also be used to carry out both prediction and evaluation with a single function call.

Having iterated this procedure across all folds and lambda values, we next average the correlation coefficients across folds to determine the lambda value which yields the best model performance. Note that evaluating model performance based on Pearson’s r or the MSE often converge to the same optimal lambda parameter.

[max_r, idx_max] = max(mean(CV.r));

lambda_opt = lambdas(idx_max);

Finally, we can use this empirically determined optimal lambda value to analogously train and test the decoding model in the outer loop of cross-validation for final, independent model evaluation.

While such a nested procedure in which the optimization of regularization and final testing are carried out on independent data segments may be considered the gold standard for predictive analyses, it requires a relatively large amount of data due to repeated data splitting. In our example, training in the inner loop is based on roughly 4.5 min of data, whereas only about 90 s worth of data remain for validation and final model testing. Within the field of developmental neuroscience, this scenario is rather the norm than an exception as prolonged data recording in infants and children can be especially challenging. Nevertheless, it is advisable to a priori define an inclusion criterion for the minimum of clean data needed per participant and to avoid any extreme imbalances in amount and quality of data between experimental conditions and participants. This is particularly important when fitting models at the level of the individual participant. Previous studies have, for example, used a criterion of at least 100 s of artifact-free EEG data per participant (Kalashnikova et al., 2018, Jessen et al., 2019). Alternatively, when only relatively small amounts of clean neurophysiological data are available, assessing model performance across participants using a subject-independent generic model may be a helpful solution (for a comparison of both approaches see e.g. Jessen et al. (2019)).

To implement training and testing with a generic model approach, we use the data from an additional nine infant participants of the same study. In contrast to the individual model approach, we do not split the data into training and testing at the level of the individual participant but across participants. In practice, we start out by training subject-specific models per λ value using all of the available data for a given participant. We then test model performance using a simpler leave-one-out cross-validation routine in which the same data splits are used for optimization and final testing (see Fig. 2B).

To this end, we create a generic model by averaging across the trained subject-specific models of all by one participant. The generic model is then convolved with the data of the left-out participant to generate and evaluate model predictions. Again, the next step is to identify the λ value that yields optimal model performance. Here, we can take one of two approaches: We can either choose the optimal λ value per individual participant, or as the mean of optimal λ values across participants. The former approach is advisable if the λ parameters yielding best performance differ strongly across participants. Then choosing the same hyperparameter for final model training and testing would most likely lead to suboptimal model fits for individual participants. In our analysis example, we chose to apply the same (average) λ value for final model training and testing of encoding models as the subject-specific optimal λ values strongly converged across participants. For the generic decoding model approach, on the other hand, we chose to pick the optimal lambda value per individual participant as the shape of the λ tuning curve varied strongly across participants.

For most parts, we have effectively used the same training and testing routines for both the encoding and decoding model. However, when it comes to model evaluation, there is one key difference. For encoding models, it is up to the researcher to decide which channels should be included in assessing how well the trained model generalizes to new, unseen data. Because our example analysis focuses on the neural tracking of speech, we defined a 5-channel fronto-central region of interest (ROI) to broadly cover brain regions known to be involved in auditory processing (cf. Jessen et al., 2019). Alternatively, in the absence of strong hypotheses about the spatial extent of involved brain regions, one may also choose to evaluate model performance more globally by averaging across channels the correlation coefficients derived from channel-specific model fitting and evaluation.

In summary, the supplied example analysis code illustrates four different ways of estimating how strongly (the features of) a presented stimulus are tracked by fluctuations in cortical activity. How do these four methods fair in the analysis of our exemplary data set? As shown in Fig. 2D, we observed that the individual model approach, despite working with less data, leads to overall better model performance than the respective generic model approach. Among the two individual model approaches the decoding model (r = 0.21) outperforms the encoding model (r = 0.045).

Lastly, questions pertaining to the many modelling choices and the variety of output metrics might remain for the data analyst. For example, how can the time lags in the model be picked in a principled way? How do I interpret the encoding model’s predictive (or, in case of decoding models, reconstructive) accuracy? A general guideline for both questions is that there are no useful general guidelines, as too much here depends on the scientific problem at hand. Neither the choice of time lags in the regressor matrix, nor the magnitude of resulting betas (in the temporal response function), nor the resulting Pearson’s r (or corresponding R²) values should ever be chosen or interpreted in and by themselves. To elaborate, the time lags we chose (in the present example, –200–800 ms) reflect the sensory process under study and in fact derive from the rich, classic event–related-potentials literature: positive lags, that is, a cascade of stereotypical brain responses that follow or ensue physical changes in the stimulus with a delay of several hundred milliseconds (up to 800 ms, in our model) are certainly most interesting, given what is known about adults’ and infants’ cerebral auditory processing. The choice to also include negative lags (i.e., –200–0 ms) can be understood as a “sanity check”, providing us essentially with a TRF baseline measure: It is not sensible to expect the auditory brain to consistently, but a-causally precede changes in the stimulus with a stereotypical brain “response”, so the TRF segments resulting from these negative lags should be expected to be not statistically different from noise, hovering around zero in the present scenario (see e.g. Fig. 3 in Jessen et al., 2019 or Fig. 4b in Tune et al., 2021).

As for the interpretation of the model’s main output metric, the predictive (or reconstruction) accuracy, we suggest to refrain from interpreting the accuracy value (r) in absolute terms, for two reasons. The first reason is that many technical and ultimately not meaningful influences can affect the absolute or average level of predictive accuracy a data set will yield. The amounts of artifact-free data might vary across subjects, or the number of regressors and/or the range of time lags might vary between models and thus, in both instances, render resulting r values not directly comparable anymore. Second, the nature of an EEG encoding model is such that a biologically and technically noisy signal, determined by a multitude of known and unknown causes – the electroencephalogram – in its entirety is being modelled as a function of a comparably small set of extraneous events (here, the envelope of a presented acoustic signal). It would thus be implausible to here for example expect r values in the .70 range (i.e., explained variance in the 50% range), something that engineers in purely technical contexts or even social scientists would find desirable or even barely satisfying. Encoding/decoding models in EEG yielding r values in the > 0.10 range are thus not per se bad models, and we recommend to strive for fair model comparisons (e.g., by additionally employing information criteria like Akaike’s, AIC, or Bayes-Schwartz, BIC, information criteria that all aim to balance accounted variance by number of parameters and number of observations, when comparing models).

3. Discussion

In this tutorial, we have provided a practical guideline for developmental researchers who want to apply linear modelling approaches to the analysis of EEG data from infant and young children in complex naturalistic designs. Using an example experiment from speech perception, we demonstrate the use of encoding and decoding models and compare different analysis choices, in particular the use of individual vs. generic response functions, and the influence of hyperparameters Box 3.

Box 3. Further Literature.

Readers interested in specific details or further information about different aspects of the analysis pipeline described can find more information in the following articles.

Crosse et al., (2021): Step-by-step practical introduction to linear models for the analysis of EEG data based on the mTRF toolbox, with a special focus on clinical populations.

Haufe et al. (2014): Discusses the interpretation of weights in decoding models with respect to underlying neural processes.

Holdgraf et al. (2017): Provides a more detailed comparison and review of en- vs. decoding models.

Wong et al. (2018): Provides a systematic comparison of different regularization methods for encoding and decoding models.

Varoquaux et al. (2017): Discusses theoretical and practical considerations for cross-validation routines within and across participants.

The biggest limitation in applying neural tracking to developmental data is posed – as for most developmental neurocognitive approaches – by limited amount of data and often-compromised data quality. For the example data from 7-month-old infants used in this tutorial, we were able to achieve a correlation of r = 0.21 for the individual model (Fig. 2D), for which the data set of each individual infant was subdivided and used for both, training and testing. Note, however, that correlation values were lower for the generic models, in which data from n–1 infants was used to compute a model for the nth infant. This pattern suggests that, even with limited data availability as is the case for infants, data from the same individual allows for better predictions compared to averaged data across other individuals (Varoquaux et al., 2017). Consequently, neural tracking not only allows for the investigation of neural responses across groups but can also be used to address interindividual differences (e.g., Tune et al., 2021).

Furthermore, the optimal lambda parameter differed between individual infants, which may be due to a larger variability in data. While this effect was not drastic for encoding models and we therefore opted for a common lambda parameter across participants, the influence was more pronounced for decoding models, for which we hence chose to rely on individual lambda parameters. Therefore, depending on the directionality of the model and the given data set, choosing individual lambda parameters to compensate for larger variance between individuals may be advisable.

As we used a data set of only ten infants as an example for the present tutorial, we cannot rule out the possibility that the difficulties mentioned above (i.e., the necessity to use individual lambda parameters, and the decrease in correlation when using generic models) may be specific to this particular data set. It may for instance be the case that ten individuals are not enough to compute a reliable generic model but that with a larger sample, better predictions may be possible. Hence, future studies using larger sample sizes should keep an open eye regarding these issues in their analysis choices.

In general, while neural tracking as an analysis approach is affected by lower data quality and availability, at the same time, neural tracking may also allow for the design of more engaging experiments due to the possibility of using continuous stimulation rather than a highly repetitive design as is common for classical ERP studies. This in turn may lead to a higher compliance in participants, and thereby the possibility to record data for a longer duration and with a higher signal-to-noise ratio.

As outlined in the introduction, the en- and decoding approaches discussed here have the potential to provide a new avenue for the investigation of neural responses in developmental populations to naturalistic complex stimuli. While most prior studies using this approach have come from the auditory domain, investigating the neural tracking of ongoing speech signals, future studies should expand these approaches to a more wide-ranging representation of environmental input, including in particular visual but also other sensory input.

Furthermore, a highly exciting application of en- and decoding models could be the analysis of neural response during live interactions between two participants (e.g., mother and infant). While a number of recent studies have focused on the interplay between adult and infant brain in interaction (for a recent review, see Wass et al. (2020)), neural tracking could provide a different approach by focusing primarily on the infant brain but using recordings of speech (and potentially other sensory parameters of interest) during the interaction as input vectors and linking the sensory signal to ongoing brain activity.

In sum, neural tracking provides a promising approach to the analysis of continuous developmental EEG data, thereby enabling the development of more engaging experimental designs as well as the analysis of neural responses under more naturalistic and dynamic conditions.

Competing Interest Statement

There are no competing interests.