Impact of Patient-Specific Material Properties on Aneurysm Wall Stress: Finite Element Study.

Abstract

Background:

Finite element analysis (FEA) can be used to determine ascending thoracic aortic aneurysm (aTAA) wall stress as a potential biomechanical predictor of dissection. FEA is dependent upon zero-pressure three-dimensional geometry, patient-specific material properties, wall thickness, and hemodynamic loading conditions. Unfortunately, determining material properties on unoperated patients using non-invasive means is challenging; and we have previously demonstrated significant material property differences among aTAA patients. Our study objective was to determine the impact of patient-specific material properties on aTAA wall stress. Using FEA, we investigated if patient-specific wall stress could be reasonably predicted using population-averaged material properties, which would greatly simplify dissection prediction.

Methods:

ATAA patients (n=15) with both computed tomography (CT) imaging and surgical aTAA specimens were recruited. Patient-specific aTAA CT geometries were meshed and pre-stress geometries determined as previously described. Patient-specific material properties were derived from biaxial stretch testing of aTAA tissue and incorporated into a fiber-enforced hyper-elastic model, while group-averaged material properties were estimated using mean values of each parameter. Population-averaged material properties were also calculated from literature and studied. Wall stress distribution and its magnitude were determined using LS-DYNA FEA software. Peak and averaged stresses and stress distributions were compared between patient-specific and both group- and population-averaged material property models.

Results:

Patient-specific material properties had minimal influence on either peak or averaged wall stress compared to use of group- or population-averaged material properties. Stress distribution was also nearly superimposed among models with patient-specific vs. group- or population-averaged material properties and provided similar prediction of sites most prone to rupture.

Conclusions:

FEA using population-averaged material properties likely provides reliable stress prediction to indicate sites most prone to rupture. Population-averaged material properties may be reliably used in computational models to assess wall stress and significantly simplify risk prediction of aTAA dissection.

Introduction

The incidence of thoracic aortic aneurysm (TAA) has been increasing over the last few decades with ~10.4 TAA cases/100,000person-years(1). TAA most commonly involves ascending thoracic aorta and/or root. A major complication of ascending TAA (aTAA) is aortic dissection, a lethal cardiovascular emergency with high mortality rate(2-5). Aortic dissection occurs at a rate of ~2.9/100,000/year(6). Current management of aTAA is primarily based on aneurysm size, unless family history of dissection, connective tissue disorder, or rapid growth rate are present. ATAAs with ≥5.5cm diameter are recommended for elective surgical repair(7-9). However, we and others have shown that a significant proportion of patients with aortic dissection have aneurysm diameters smaller than that recommended by surgical guidelines, suggesting dissection occurs in small aTAAs(5, 10). There is a pressing clinical need for an improved tool for aortic dissection risk stratification, especially for patients with aneurysm size below the current surgical threshold.

The specific event of aortic dissection is a mechanical failure, which occurs when regional wall stress exceeds aortic wall strength. Unfortunately, it is impossible to noninvasively measure wall stress or strength in vivo. Over the years, researchers have used imaging-based finite element analysis (FEA) to evaluate aneurysm wall stress on a patient-specific basis(11-15). Wall stress is uniquely determined by geometry, loading conditions, and wall material property; in other words, if we determine these parameters accurately on a patient-specific basis, then FEA predicted wall stress should accurately represent the true patient-specific wall stress (16, 17). The advent of modern medical imaging techniques has made it possible to obtain in vivo aortic lumen geometry straightforwardly. However, measurement of in vivo wall material property on a patient-specific basis is extremely challenging and costly, partly due to the non-linearity of aortic tissue. We and others have documented that large variations in material property exist from patient to patient(18-23). Because of such large variations, general concerns exist regarding the suitability of FEA for risk stratification of dissection, when population-based averaged material properties are used. In this work we tested the hypothesis that wall stresses calculated from patient-specific material properties differs significantly from those calculated from population-averaged material properties.

Materials and Methods

Finite element mesh generation

Fifteen aTAA surgical patients were recruited for the study and consented for acquisition of surgical tissue specimens for research. The study was approved by Committee on Human Research at UCSF and Institutional Review Board of San Francisco VA Medical Center. Each patient (n = 15, age 63±10 years) underwent clinical computed tomography (CT) scan before surgical repair. Aneurysm excision was performed from the sinotubular junction to just below the aortic cross-clamp as an intact cylinder. Immediately after excision, aneurysm samples were prepared for mechanical testing, and square specimens were obtained from maximal aTAA diameter by visualization, incorporating square specimens from the anterior and posterior wall. CT images were imported into MeVisLab for segmentation of aTAA lumen and then exported to GeoMagic for 3D surface reconstruction. TrueGrid (XYZ Scientific, Inc) was then used to generate 3D brick element mesh. Average element size of the created mesh was ~1.5 mm. Figure 1 shows a representative FE mesh model of an aTAA.

Figure 1.

Representative mesh for FE simulation of an ascending thoracic aortic aneurysm (aTAA).

Zero-pressure geometry

3D aTAA geometry reconstructed from CT images reflects the deformed geometry under in vivo blood pressure and was therefore considered pre-stressed. We and others have demonstrated the importance of accounting for this pre-stress to accurately determine in vivo wall stress(12, 17, 24). Here, we used modified update-Lagrangian method to calculate pre-stress(25). In this framework FE geometry was virtually fixed in space while pre-stress deformation matrix was obtained through an iterative process.

Collagen-Embedded Hyperelastic Material Model

ATAA wall was modeled as an incompressible hyperelastic material, whose total strain energy density function (SEF) is:

$$\Psi \left(\overline{C}\right)={\Psi }_{matrix}\left(\overline{C}\right)+\sum _{i=1,2}{\Psi }_{collageni}\left(\overline{C}\right)+\Psi (J)$$ (1)

where $\overline{C}=J^{-\frac{2}{3}}C$ is isochoric part of the deformation tensor C and J is Jacobian of deformation gradient. Ψ(J) enforces the incompressibility of aortic tissue. The SEF for the matrix is

$${\Psi }_{matrix}\left(\overline{C}\right)=a\left(I_1\left(\overline{C}\right)-3\right)$$ (2)

where and a is a material constant. Two collagen fibers distributed symmetrically along the circumferential direction:

$${\Psi }_{collageni}\left(\mathbf{C}\right)=\frac{k_1}{2k_2}\left[\text{exp}\left(k_2{\overline{E}}_1^2\right)-1\right],i=1,2$$ (3)

where ${\overline{E}}_i$ is the structure tensor invariant of dispersed fiber (26); k₁ and k₂ are material parameters determined by mechanical testing of the material(27).

Patient-specific and averaged material properties

Each patient’s aTAA tissue was excised intact during surgery. Their material properties were determined using biaxial stretch testing as previously described(23). In this work for each FE model, we used three sets of material properties to run the analysis. One set was the patient-specific material properties, which were obtained by fitting biaxially stretched stress-strain curves(23) Eqn. (1). The next set was the group-averaged material properties obtained by averaging patient-specific parameters among the 15 aTAAs. This set of cases will be referred to group-averaged hereafter. The last set was population-averaged material properties, obtained by fitting the average biaxial stress-strain curves obtained from literature(20). Clinical and material parameters of these three sets are presented in Table 1. No patients had Marfan’s syndrome or other connective tissue disorder apart from bicuspid aortic valve disease.

Table 1.

Material Properties: Patient-Specific, Group-Averaged, and Population-Averaged

Patient ID	Aortic Valve type	Max diameter	AR	AS	Root aneurysm	parK1	parK2	Degree
1	Bicuspid	5.3	Moderate	Mild	N	5.7	4.7	49.3
2	Bicuspid	4.5	Trace	Severe	N	6.7	4.7	43.1
3	Bicuspid	4.7	None	Severe	N	1.6	57.4	48.6
4	Bicuspid	5.5	None	None	N	57.3	0.3	41.7
5	Tricuspid	5	Mild	Severe	N	31.5	0.9	43.8
6	Tricuspid	5	Trace	None	N	37.8	2.6	46.0
7	Tricuspid	6	None	None	N	32.6	15.6	38.8
8	Tricuspid	6.8	Severe	Mild	Y	198.9	65.9	52.5
9	Tricuspid	6	Moderate	None	Y	5.7	4.5	45.2
10	Tricuspid	5.3	Severe	Severe	N	52.3	0.2	42.9
11	Tricuspid	6	Severe	Moderate	N	52.3	0.2	42.9
12	Tricuspid	5	Trace	None	N	15.7	2.6	41.7
13	Tricuspid	5.3	Moderate	None	N	615.7	7.5	46.8
14	Tricuspid	6	None	None	N	17.4	8.9	45.9
15	Tricuspid	6.3	Severe	None	Y	41.1	4.6	44.4
Group-averaged material property						78.2	12.0	44.4
Population-Averaged material property						33.6	0.03	44.5

Finite element simulation

FE simulations were performed by applying human physiologic arterial pressure loading conditions to aTAA inner lumen. While translational motion at the proximal annulus and distal descending aorta were fixed in all directions, all remaining elements were unconstrained. The models were first pre-stressed to diastolic pressure (80mmHg) using the modified update Lagrangian method. Internal pressure was then ramped up from diastolic pressure (80mmHg) to systolic pressure (120mmHg) over 100ms duration, followed by decrease from 120 mmHg back to diastolic pressure (80mmHg) over another 100ms period. After loading, two more cardiac cycles of 800ms duration were applied. The cardiac cycle was composed of 300ms ramp upwards to maximum systolic pressure, followed by 500ms ramp downwards to minimum diastolic pressure. FEA was performed using LS-DYNA (LSTC, Inc.) with a in-house developed user defined material law for Eqn.(1). Material properties of patient-specific, group-averaged, and population-averaged were then applied to the aTAA geometry for comparisons.

Statistical analysis

The 99^th percentile wall stress as described by Speelman et al.(28) from all models was used for statistical analysis. The 99^th percentile wall stress has previously been demonstrated to more reproducibly represent greatest wall stress because it avoids the non-physiologic peak wall stresses that can occur from inhomogeneities in the FE mesh. References to peak wall stresses will hereafter be represented by 99^th percentile wall stress for simplicity in discussion. Peak wall stress calculated from patient-specific, group-averaged, and population-averaged material properties were compared using Mann-Whitney U-test and Kruskal-Wallis test(29). A p-value<0.05 was considered statistically significant. Statistical analyses were performed using R (R 3.4.0 www.r-project.org).

Results

Under systolic blood pressure, peak circumferential stresses were 516.2±209.5kPa for patient-specific material models vs 500.6±169.7kPa for group-averaged (p=0.9), and 456.6±148.9kPa (p=0.2) for population-averaged material models. Peak longitudinal stresses were 344.4±195.3kPa for patient-specific vs. 305.2±157.4kPa (p=0.6) for group-averaged, and 311.2±136.3kPa (p=0.8) for population-averaged material models. Mean circumferential and longitudinal stresses were 180.8±24.7kPa and 103.8±13.4kPa for patient-specific models, respectively, and 182.0±24.5kPa (p=0.9) and 103.4±13.3kPa (p=0.9) for group-averaged, respectively; while for population-averaged material models mean circumferential and longitudinal stresses were 183.5±25.9kPa (p=0.9) and 109.3±16.2kPa (p=0.3), respectively.

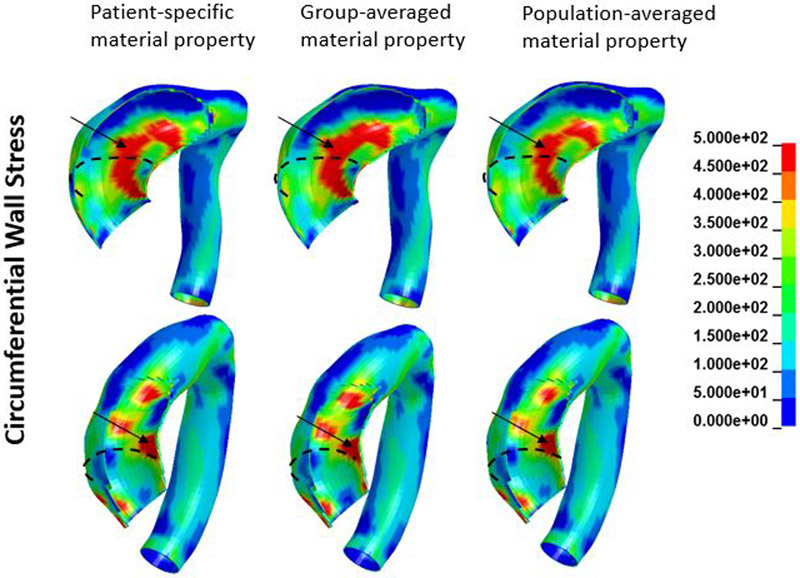
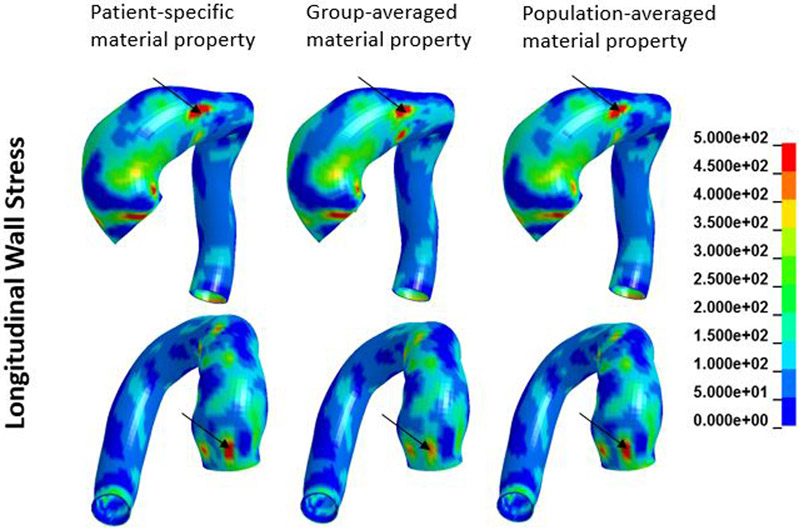
A representative FE model created is shown in Figure 1. Figures 2 and 3 show an example of circumferential and longitudinal wall stress distribution obtained from (a) patient-specific; (b) group-averaged; and (c) population-averaged material properties. As can be seen in figures 2 and 3, overall wall stress distributions from these three sets of material properties were very similar. Patches of elevated circumferential and longitudinal stresses were seen. In this case, higher circumferential stresses mostly appeared in the inner curvature region while higher longitudinal stresses had more random distribution.

Figure 2.

Circumferential wall stress distribution obtained from patient-specific, group-averaged, and population-averaged material properties

Figure 3.

Longitudinal wall stress distribution obtained from patient-specific, group-averaged, and population-averaged material properties

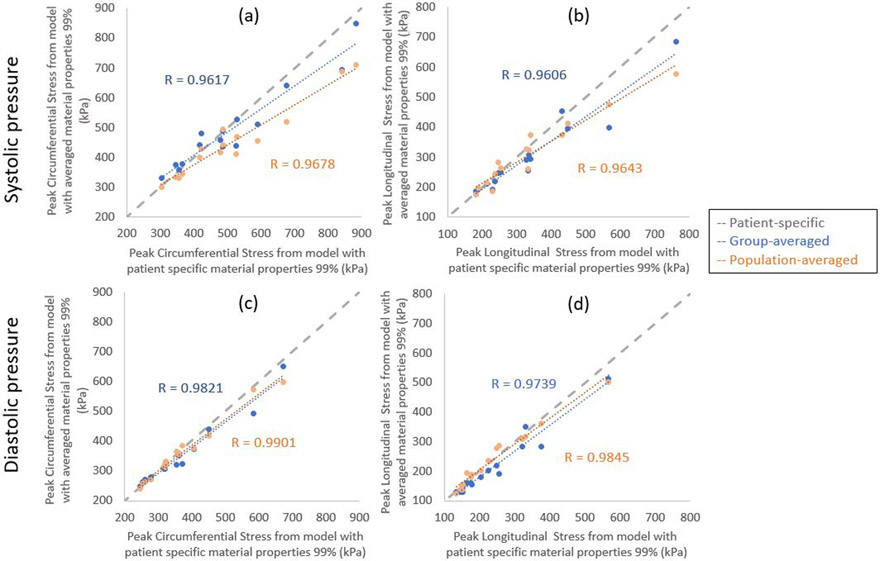
Figures 4 illustrates the correlation of peak diastolic and systolic stresses calculated from patient-specific and group- and population-averaged material models. Correlation of peak wall stresses between patient-specific and group-averaged material models was very strong. Similarly, correlation of peak wall stresses between patient-specific and population-averaged material models were also strong. In systole, correlations between patient-specific and group-averaged models were r=.9617 and r=0.9606, for circumferential and longitudinal wall stresses, respectively; while correlations between patient-specific and population-averaged were r=.9678 and r=0.9643, for circumferential and longitudinal wall stresses, respectively. In diastole, correlations between patient-specific and group-averaged models were r=0.9821 and r=0.9739, for circumferential and longitudinal wall stresses, respectively; while correlations between patient-specific and population-averaged were r=0.9901 and r=0.9845, for circumferential and longitudinal wall stresses, respectively. No statistically significant differences were found between wall stresses predicted from patient-specific and group-averaged or population-averaged material properties.

Figure 4.

Correlation of peak circumferential stresses (a and c) and peak longitudinal stresses (b and d) calculated from patient-specific and group- and population-averaged material models at systolic pressure (a and b) and diastolic pressure (c and d).

Discussion

The most important finding of our study was that wall stresses calculated from FEA were not significantly impacted by the wall material properties used for the simulation. Results from both group-averaged and population-averaged material property models correlated very strongly with results from patient-specific models. Such strong correlation suggests that population-averaged material properties may be sufficient for the purposes of patient-specific risk stratification of aortic dissection, which greatly simplifies clinical application.

Impact of wall material property on calculated wall stress

From a mechanics point-of-view, regional wall stresses can be uniquely determined by the boundary and loading conditions, 3D geometry of the wall, and wall material property. Among these parameters, in vivo wall material properties are the most difficult to measure. Aortic wall material property is non-linear, where the stress-strain relationship is dependent on the loading condition. In order to accurately quantify such non-linear material properties, one needs to use biaxial stretch testing of ex vivo tissue samples. We and others have previously described wall material properties of ascending thoracic aortic aneurysms(18, 23). Both normal ascending aorta and aTAA showed large variations in wall material properties among patients(18, 22, 23). Some have shown regional differences between anterior, posterior, medial, and lateral regions(30). Current biomechanical analyses have used population-averaged material properties due to challenges in acquiring tissue and/or time-consuming costly imaging studies. This difficulty obtaining patient-specific material properties has often been considered to be the Achilles’ heel of modern biomechanical analyses and has caused concern for the reliability of biomechanics-based risk stratification of aneurysm dissection/rupture.

Standard FEA starts from an unloaded geometry and then applies loading conditions to find the deformed geometry and corresponding stresses. Under this scenario it is easy to understand how the material properties would affect the outcome; a softer material, for example, would most likely lead to a larger deformation than that of a stiffer material. Imaging-based in vivo aortic wall stress analysis, however, is very different from the standard FEA. The starting geometry for in vivo wall stress analysis is the deformed geometry while the true unloaded geometry is unknown. Exactly how wall material properties affects calculated wall stresses is much more complicated.

Impact of the choice of material property on FEA calculated wall stresses has been previously investigated for abdominal aortic aneurysms (AAA) and intracranial aneurysms. Several studies suggest the impact of wall material properties on wall stress is quite significant. For example, Rodriguez et al. studied the impact of anisotropy of AAA wall material on wall stress(31). They showed calculated peak wall stresses from anisotropic wall material were much higher than those calculated from isotropic material. Reeps et al. compared AAA wall stresses with linear or nonlinear material models(32). They showed that differences in wall stresses from different wall material models was as large as 210%. Polzer et al. compared AAA wall stresses calculated from patient-specific material properties and averaged material properties(33). They showed calculated wall stresses were strongly affected by the material properties used. However, other studies showed very little impact of wall material properties on calculated wall stresses. Venkatasubramaniam et al. compared wall stresses between ruptured and unruptured AAA(34). They suggested that changing AAA wall material properties would lead to <4% wall stress change. Lu et al. showed that intracranial wall tension was not strongly affected by specific wall material properties used for simulation(35). They reasoned that for thin wall shell like structures without strong bending moment, the primary determinant for wall tension was the regional curvature of the structure and pressure loading. In such cases, wall material properties had limited impact on wall stress distribution.

The current study was designed to address a specifically tailored question: whether using population-averaged wall material properties is good enough for aTAA wall stress calculation. To address this question, we developed FE aTAA models whose specific material properties have been previously determined through biaxial stretching experiments and compared calculated wall stresses using material properties from patient-specific, group-averaged from our specimens, and population-averaged from literature. Our results showed that wall stresses obtained from population-averaged or group-averaged material properties were strongly correlated with those from patient-specific analysis and were not statistically different from patient-specific models.

Role of wall mechanics on aortic dissection

Aortic dissections have separation of the media along the longitudinal direction, with one or more intimal tears. More than 60% of intimal tears are located at the ascending aorta and the majority occur along the transverse direction(36). Whether the intimal tear occurs before separation of media is not known. But, intimal tear is likely the initiating event. In fewer cases, especially with intramural hematoma without an intimal tear(37), separation of the medial layer is the initiating event.

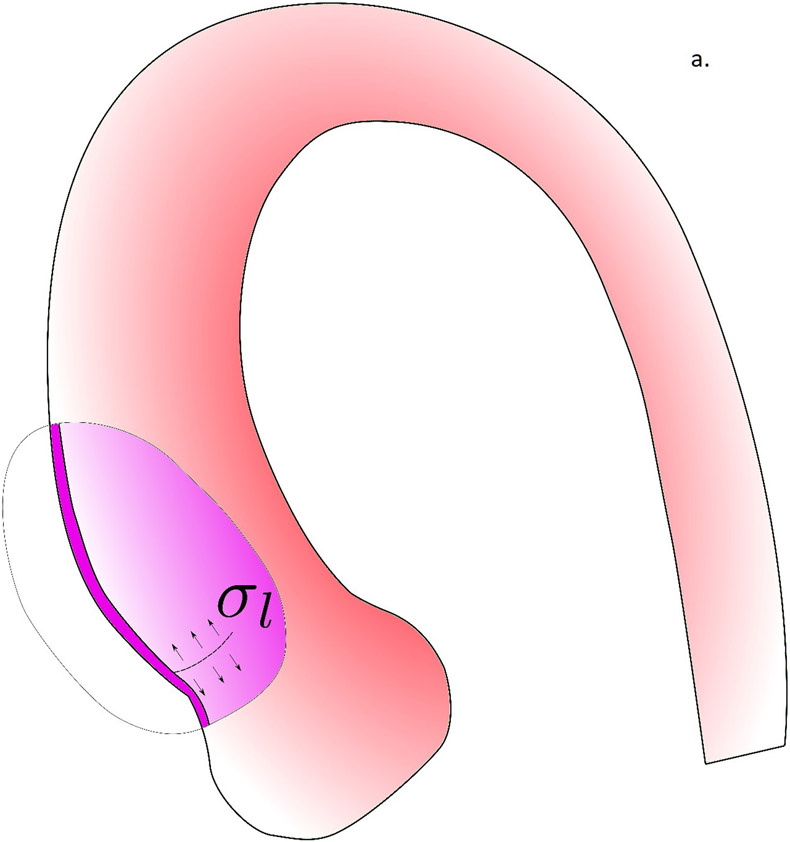
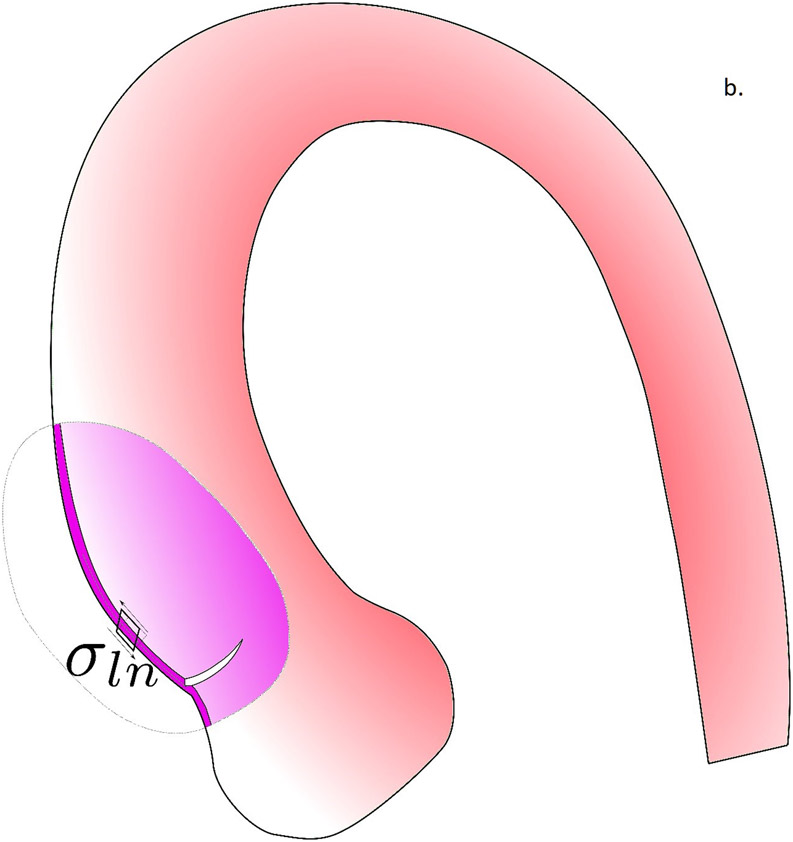
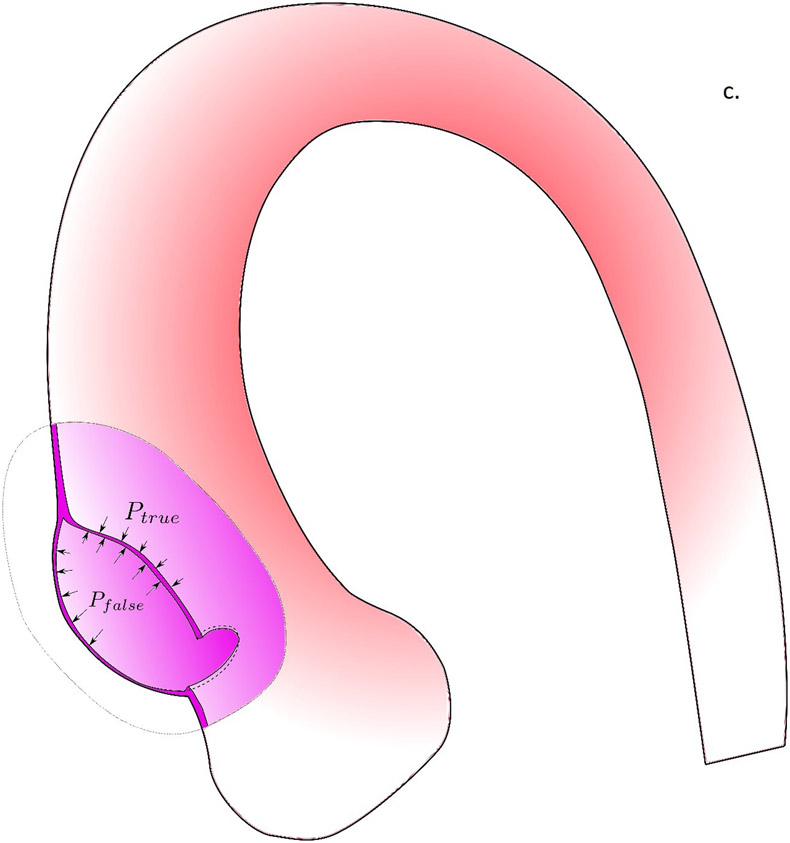
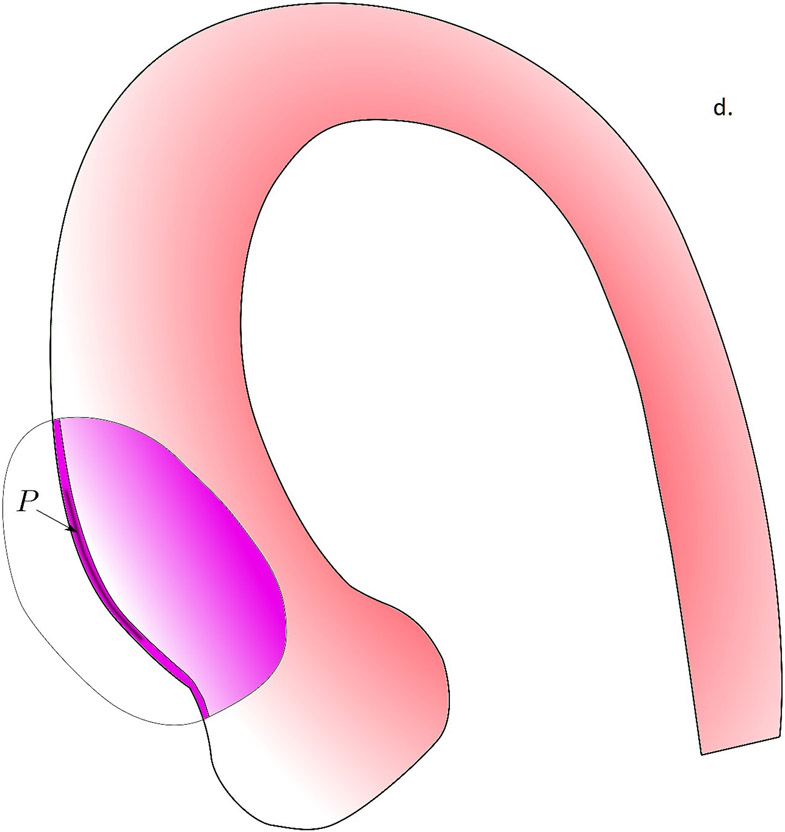
In figure 5, we propose the potential role of biomechanics in the aortic dissection process. In the first scenario, the formation of intimal tear is initiated when the longitudinal wall stresses exceed the longitudinal wall strength of the aortic wall (Fig. 5a). The reason we focus on longitudinal failure is that most intimal tears at the ascending aorta were found to be along the transverse direction(36). Although circumferential wall stresses is often higher than the longitudinal stresses, circumferential wall material strength is known to be much stronger than that in the longitudinal direction(21), likely due to the primarily circumferentially aligned collagen fibers(38). Formation of an intimal tear could subsequently change the loading condition on the wall tissue and creates a significant shearing between the intimal and adventitial layers (Fig. 5b). The shearing stresses could exceed the strength of the medial layer and creates a false lumen with subsequent blood flow into this lumen. As we previously demonstrated, the fluid dynamics in the false and true lumen, without the formation of an exit intimal tear, are drastically different and could create a strong pressure gradient between the false lumen and true lumen. Such pressure gradient would facilitate propagation of dissection. Wall stress analyses conducted in this work could be applicable to identify the risk of intimal tear formation. The second scenario is the intramural hematoma pathway, where the vasa vasorum breaks and leaks blood into the intramural space. The pressure from the leaked blood would push the inner and outer layers of aortic wall to separate to form a hematoma. How vasa vasorum would break and what is the role of biomechanics in this process is unclear and requires further investigation.

Figure 5.

The potential role of biomechanics in the aortic dissection process. a) Formation of the intimal tear is initiated by the longitudinal wall stresses which exceed the longitudinal wall strength of the aortic wall. b) Loading conditions on the wall tissue are changed by the formation of an intimal tear, creating significant shearing between the intimal and adventitial layers. c) When the shearing stresses exceed the strength of the medial layer, a false lumen with subsequent blood flow into this lumen was created. d) In the scenario where no intimal tear exists, the pressure gradient created by drastically different fluid dynamics in the false and true lumen would facilitate the propagation of dissection.

Typical biomechanical analysis of the ascending aorta assumes the aortic wall is intact without formation of intimal tears or medial separation. The results obtained from such analyses could be used to evaluate the risk of intimal tears. Whether and how the formation of an entry tear leads to the separation of media and subsequent propagation is not clear. Other patients, however, have an intimal tear without formation of intramural hematoma(39).

Limitation

Although the specific event of aortic dissection is a biomechanical failure where wall stress exceeds wall strength, to predict the risk of aortic dissection requires one to know both aortic wall stress and strength. The current work focuses on aortic wall stress, exclusively. Currently, it is not possible to evaluate in vivo wall strength on a patient-specific basis, although population-based wall strength data is available from excised tissue. Reconstruction of 3D aTAA lumen geometry from imaging to determine zero-pressure geometry involves uncertainties, while measuring 3D wall thickness in vivo is very challenging. The current work assumes uniform wall thickness, while regional wall thickness could affect calculated wall stresses. The effect of residual stress on wall stress distribution was not accounted for in the current work. Aortic blood flow conditions, such as flow turbulence and helical flow patterns(40), were not considered in this work. However, note that wall shear stress is typically in the order of ~Pa, while wall stresses due to blood pressure is in the order of ~kPa. The impact of blood flow shear stress on calculated wall stress is therefore estimated to be small. The current study has only 15 samples and all samples are from surgical patients. A larger sample size would be ideal to confirm these observations and increase statistical power for clinical translation. However, acquiring fresh aTAA samples for mechanical testing is difficult and time-consuming.Whether the finding in this patient population can be extrapolated to small aneurysm patients should be investigated.

Conclusions

It remains a challenge to manage aTAA patients, especially for those with aneurysm diameters smaller than the current surgical guidelines. The current guideline suggests surgery for aneurysms ≥5.5cm in diameter. Meanwhile, observational studies showed that there are significant portion of dissection patients had diameters below this surgical threshold. Currently these patients with small aneurysms are clinically managed through monitoring. Patient-specific biomechanical analysis could potentially provide better risk stratification tools than current clinically used diameter-based approach. A roadblock for such biomechanical risk stratification revolves around the uncertainties in FEA based on difficulties obtaining in vivo patient-specific material properties. Our current study provides reassurance that FEA calculated wall stresses are reproducible using population-averaged material properties as a surrogate for patient-specific material properties.

Abbreviations and Acronyms

aTAA

ascending thoracic aortic aneurysm

CT

computed tomography

FE

finite element

FEA

finite element analyses

cm

centimeter

kPa

kilopascal