Suture Forces for Closure of Transapical Transcatheter Aortic Valve Replacement: A Mathematical Model

Abstract

Importance:

Transcatheter aortic valve replacement (TAVR) has revolutionized treatment of severe aortic stenosis in high-risk and inoperable patients. TAVR has multiple access routes, transfemoral (TF), transapical (TA), direct aortic (DA), axillary, transcarotid, and transcaval. The most commonly applied algorithm is a TF first approach, where only when patients are unsuitable for TF, are alternatives, such as transapical considered. However, an infrequent, but dreaded risk, is left ventricular (LV) apical bleeding from tearing or rupture with TA approach. With burgeoning transcatheter mitral technology which requires TA, the Holy Grail would be to predict patient-specific risk of apical tearing or rupture based upon myocardial biomechanics.

Objective:

To develop a mathematical model to determine suture forces for transapical closure.

Design:

Preoperative cine-cardiac magnetic resonance imaging (MRI) was used to acquire 3D LV geometry at end-systole and end-diastole. Endo- and epi-cardial boundaries were manually contoured using MeVisLab, a surface reconstruction software. Three-dimensional surfaces of endo- and epi-cardium were reconstructed, and surfaces at end-systole were used to create a 3D LV finite element (FE) mesh. TA access was mimicked by developing a 10mm defect within the LV FE model. LV apex was closed using a virtual suture technique in FE analysis with application of two virtual sutures. After virtual closure, FE analysis was performed of LV model diastolic filling and systolic contraction.

Setting:

This pilot study was performed using the clinical TAVR program from San Francisco VA Medical Center.

Participants:

Severe aortic stenosis patient eligible for TAVR was recruited.

Exposure:

TAVR patient was consented for preoperative research MRI.

Main Outcome Measure:

To determine suture forces for closure of transapical access.

Results:

Proof of concept was achieved to develop an LV transapical access site and perform FE analysis to achieve closure. FE method of virtual suture technique successfully approximated LV apical defect. Peak axial force on virtual sutures at end-diastole and end-systole was 0.445N and 0.736N, respectively.

Conclusions:

We mathematically developed a LV TA access model that evaluated suture tension of the transapical closure process. Further development of this approach may be useful to risk-stratify patients in the future for LV apical tearing.

Introduction

Transcatheter aortic valve replacement (TAVR) has become established therapy for high-risk and inoperable patients with severe symptomatic aortic stenosis (AS). Five-year outcomes of the randomized trial of TAVR vs medical therapy have shown persistent survival improvement with TAVR¹, while TAVR vs surgical aortic valve replacement (SAVR) has shown equivalent mortality at 5 years². TAVR was initially developed using antegrade trans-septal approach but quickly transitioned to the transfemoral (TF) approach. Currently, multiple access routes for TAVR are available, including transfemoral (TF), transapical (TA), direct aortic (DA), axillary, transcarotid, and recently transcaval³. The most widely adopted algorithm is a TF first approach, where patients with suitable iliofemoral access undergo TF-TAVR, while those without suitable access, then consider the alternatives, including TA⁴. However, one dreaded, relatively rare TA complication is left ventricular (LV) apical bleeding from tearing of friable ventricular tissue with possible rupture^5,6. Delayed LV pseudoaneurysm may result as described in several case reports^7–10. Assessing preoperatively myocardial friability, determining patient risk of apical tearing, and optimizing apical access location would be ideal, but currently not possible. The goal of our study was to develop a patient-specific mathematical model of transapical access and closure to determine suture forces for closure.

Materials and Methods

A patient with severe symptomatic AS eligible for TAVR from San Francisco Veterans Administration Medical Center (SFVAMC) was recruited for this pilot study. Informed consent was obtained for subjects to undergo research magnetic resonance imaging (MRI). The study was approved by Committee on Human Research at University of California at San Francisco Medical Center and Institutional Review Board at SFVAMC.

Finite element (FE) model of the baseline LV

Pre-TAVR ECG-gated cardiac magnetic resonance imaging (MRI) was performed to image LV geometry. A series of short-axis images of the heart were obtained using cine gradient echo MRI imaging. MRI data acquisition was triggered by the QRS complex of the electrocardiogram. Acquired images were imported into MeVisLab (Mevislab, Bremen, DE), a surface reconstruction software, to contour endocardial and epicardial boundaries. Contours were then converted to 3D surface masks using algorithm previously described¹¹. Three-dimensional surface meshes were then created using the marching cube algorithm¹². The 3D surface meshes were then imported into GeoMagic Design, (3DSystems, Rock Hill, SC, USA) a CAD (computer aided design) for surface smoothing. Smoothed surfaces were imported into Truegrid (XYZ Scientific, Inc., Livermore, CA, USA) to create 3D finite element (FE) model of LV. Spaces between endocardial and epicardial surfaces were filled with 8-node trilinear brick elements, with a single integration point for computational efficiency, to generate a volumetric mesh that was 4 elements thick transmurally. Myofiber angles were assumed to vary linearly from −60 degrees at the epicardium to 60 degrees at the endocardium (counterclockwise positive when viewed from the epicardium) with respect to the circumferential direction.

LV material properties

Myocardial wall was modeled as a combination of passive and active material. The passive myocardial wall was modeled with a nearly incompressible, transversely isotropic, hyperelastic material constitutive law. Active myocardial contraction was modeled as a time varying elastic term, whose magnitude is controlled by a muscle contractility term and sarcomere length. Passive and active material laws were implemented with a user-defined material subroutine in the commercial explicit FE solver, LS-DYNA (Livermore Software Technology Corporation, Livermore, CA), as previously described¹³. Passive myocardial material property is governed by the following strain energy function:

$$W=\frac{C}{2}\left[e^{Q\left(E\right)}-1\right]$$

with

$$Q\left(E\right)=b_f{E}_{ff}^2+b_t\left(E_{ss}^2+E_{nn}^2+E_{sn}^2+E_{ns}^2\right)+b_{ft}\left(E_{fs}^2+E_{sf}^2+E_{fn}^2+E_{nf}^2\right)$$

where $E_{ij}$ are components of Lagrange-Green strains along the fiber (f), myofiber sheet (s) and normal (n) directions. $C,b_f,b_t,b_{fs}$ are material parameters controlling the stress-strain relationship of the ventricular wall and needed to be determined for the patient. Following Genet¹⁴, $b_t$ was set to be 40% of $b_f$ and $b_{ft}$ to be 70% of $b_f$; therefore, the only passive parameters needed to be determined for the patient-specific model were $C$ and $b_f$. Active contractile tension generated by the myofibers was modeled as

$$T\left(t,E_{ff}\right)=\frac{T_{max}}{2}\frac{C{a}_0^2}{C{a}_0^2+EC{a}_{50}^2\left(E_{ff}\right)}\{1-\cos \left[\omega \left(t,E_{ff}\right)\right]\}$$

where $C{a}_0$ is the peak intracellular calcium concentration, $EC{a}_{50}$ is the length dependent calcium sensitivity, and $\omega$ is a time varying term controlling the output of tension. All these parameters were set to values as previously described¹⁴. $T_{max}$ is a scaling factor controlling the amount of maximum force generation and was determined through an optimization procedure by finding the optimal match between finite element predicted and MRI measured end-systolic volumes¹³.

Hemodynamic loading conditions and constraints.

Patient-specific ventricular pressure data can only be measured through an invasive approach and were not acquired in this study. LV end-diastolic pressure was assumed to be 20mmHg and LV peak systolic pressure was assumed to be 200mmHg, respectively. Pressure was applied uniformly to the endocardial surface. At the time of simulation, endocardial wall was first loaded to end-diastolic pressure with the active tension term set to zero in the myocardial wall model. The active tension term was then activated and end-systolic pressure was loaded to the endocardium.

Virtual Surgery

Endocardial and epicardial surfaces were loaded into Geomagic Design X (3DSystems, Rock Hill, SC, USA), a CAD (computer aided design) software, and a 10mm TA access site was created near the apex. A new finite element mesh was created taking into account the TA access defect. Two virtual sutures were then added to the model. The virtual suture technique has been described previously¹⁵, where essentially the sutures were beam elements with axial tension. The axial tension contracted the beam elements and pulled the two ends of each element toward the center, thus mimicking the suturing process. Virtual tension gauges were added to the end of virtual sutures to measure the tensile force on the sutures¹⁵.

Results

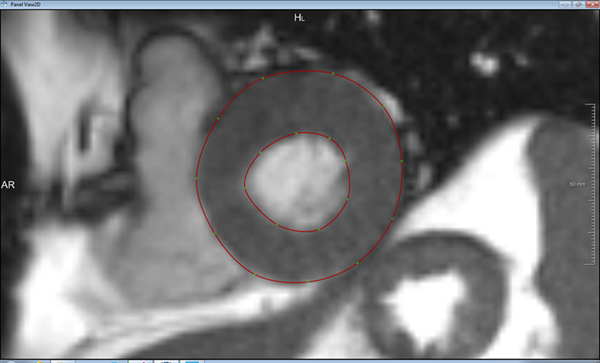
Cine cardiac MRI from which the LV model was derived is shown in video 1. The contouring process of LV endocardium and epicardium from short-axis MRI images is shown in figure 1. The geometric surface model and corresponding FE mesh of the LV is shown in figures 2a and 2b, respectively. The passive and active myocardial material properties after optimization are listed in Table 1. Slow motion animation of LV baseline simulation is presented in video 2. MRI predicted LV end-diastolic and end-systolic volumes were 133.9ml and 34.4ml, respectively. Experimentally measured volumes were 130ml and 35ml, respectively. Transapical access defect was created in the geometric LV surface model as seen in figure 3a–b. The LV FE mesh was recreated with the transapical access defect as demonstrated in figure 4a–b. The virtual sutures were added to the model (figure 5). Animation of the virtual suturing process is portrayed in video 3. At baseline, average end-diastolic and end-systolic myofiber stresses were 13.9kPa and 44.9kPa, respectively (figure 6a). After suture closure of transapical defect, average LV end-diastolic and end-systolic myofiber stresses were 13kPa and 43kPa, respectively (figure 6b). Sutures create high regional stress concentration near the apex (figure 6). Peak tension on the virtual sutures was 0.736N at end-systole and 0.445N at end-diastole.

Figure 1.

Contours (red lines) of endo and epi-cardiums on short axis images of the LV.

Figure 2.

(a) 3D surface model of the LV; (b) finite element mesh for the baseline LV model.

Table 1.

Passive and active material properties after optimization

Parameter	Value
$C$	0.544 kPa
$b_f$	6.6519
$T_{max}$	528 kPa

Figure 3.

(a) Creation of apical access hole; (b) View of apical access hole, en face view.

Figure 4.

(a) Finite element mesh with apical access, side view; (b) finite element mesh with apical access, en face view.

Figure 5.

Virtual sutures.

Figure 6.

Contours of end-systolic myofiber stress at the (a) baseline and (b) after virtual suturing. Sutures create high regional stress concentration near the apex.

Discussion

In this study, we developed a patient-specific LV model, simulated TA access creation and suture closure of the defect. Using FEA, we determined suture forces for TA closure. Balloon-expandable TAVR has demonstrated survival benefit over medical therapy and equivalent survival as surgery at 5 years^1,2. Majority of TAVR programs favor a TF first approach, with only a handful of centers offering an equal TF/TA approach^4,16. Indeed, self-expanding CoreValve (Medtronic, Inc, Minneapolis, MN) does not have a TA approach, so their non-TF approaches are mainly direct aortic or axillary. Advantages of TF over TA approach include 1) TF avoids the mini-thoracotomy which allows for faster patient recovery, 2) TF is less invasive and can often be done completely percutaneously, 3) TF can also be done as a minimalist approach without general anesthesia or transesophageal echocardiography. Some studies suggest that TF has less short-term mortality and fewer early adverse events^17–19. In a propensity-matched comparison of TF vs TA patients from the Placement of Aortic Transcatheter Valves (PARTNER) randomized trials, TA was associated with a higher rate of early death as well as increased risk of bleeding and renal failure¹⁷. However, propensity-matching does not inherently remove all bias and other studies²⁰ showed no differences in survival between TA and TF^20–22. As transcatheter aortic valves (TAV) design has iterated to reduce delivery catheter size to the 14–18Fr range, the pendulum continues to swing toward the TF approach¹⁸, with some centers in Europe approaching 90% TF. Even among alternative therapies, use of TA shows a relative decline compared to other non-TF approaches¹⁸. Nevertheless, TA approach will not become obsolete as burgeoning transcatheter mitral valve replacement (TMVR) technologies require TA access²³. A dreaded complication of TA access is apical bleeding from LV tearing^5,6 or delayed rupture with LV pseudoaneurysm development^7–10. Unfortunately, no preoperative imaging to date has been able to predict soft friable myocardial tissue and tissue quality is not known until visualized by the surgeon in the operating room. This pilot study was undertaken to develop patient-specific LV model and assess suture forces for apical closure as a first step towards patient-specific modeling for risk prediction of apical tearing.

Patient-specific finite element modeling

Tearing of the suture closure points is a mechanical failure, most likely occurring when elevated wall stress created by the sutures exceeds the strength of the myocardial wall. Understanding the mechanical interaction between the sutures and myocardial wall could potentially improve surgical planning for TA-TAVR. Mechanical stress of TA-TAVR access closure is determined by LV geometry, myocardial wall material properties, the pressure loading conditions, as well as surgical suturing process. Not all this information will be available for surgical planning. For example, ventricular pressure data can only be obtained through invasive pressure measuring and is not readily available for preoperative surgical planning, until specifically requested during cardiac catheterization for coronary artery disease. In this study, we used average ventricular pressure values previously reported in the literature²⁴. These pressure data represented average loading conditions in severe AS patients and should be interpreted as such.

Material properties of human myocardial wall have not been fully described, in part due to the scarcity of human tissue. In this work, we used an optimization procedure to find a set of material parameters that led to close matching between finite element modeled and MRI measured ventricular volumes at end-diastole and end-systole. The optimization procedure, however, did not use any regional motion data; therefore, the optimized material parameters did not account for potential regional variation. Future work will incorporate regional motion data to improve the overall accuracy of the model.

Multi-scale simulation

Tearing of the myocardial wall is due to local stress concentration caused by the contact between the sutures and surrounding tissue. Typically 3–0 polypropylene sutures are used and the diameter of these sutures is 0.2 mm. To accurately model the contact between sutures and myocardium, the finite element meshes need to have a resolution smaller than 0.1mm. This is significantly higher than the mesh resolution used in the current work (~2mm). A straightforward mesh refinement would make the computational cost prohibitively expensive. In the future, we will pursue a multi-scale simulation approach where the current large scale model is coupled to a regional model focusing on the apical region only as a more feasible solution. Until such a tool is developed, direct modeling of tearing force on the myocardial wall is not possible. Tension on the virtual sutures, however, provides a surrogate for the tearing force, since the suture tension is mostly balanced by the myocardial wall; higher suture tension would indicate higher stress on the surrounding wall tissues. For this reason, we focused our current work on suture tension.

Access and suture optimization

Ventricular wall stress near the suture is strongly affected by many controlling factors, including access location, size of access defect, number of sutures, and direction of sutures. TA-TAVR closure may be optimized by finding a set of these controlling factors that leads to the least wall stress. Since there are too numerous combinations of these factors, an optimization method that automatically searches among the possible combinations and finds the best design is necessary. Such methods have been previously applied in determining optimal designs of cage for posterior lumbar interbody fusion²⁵, cardiovascular stents²⁶, and hip implants²⁷, among others. Combining our virtual suture model with an optimization method could eventually lead to a powerful tool for pre-surgical planning for TA-TAVR.

Conclusions

A mathematical model that evaluated the suture tension of closure of TA-TAVR access site was developed. Further development of this approach would allow us to pre-surgically evaluate apical tearing risk.

Supplementary Material

video 1

Video 1. Cine cardiac MRI from which the LV model was derived.

video 2

Video 2. Slow motion animation of LV baseline simulation.

video 3

Video 3. Animation of the virtual suturing process.