Rapid cloud removal of dimethyl sulfide oxidation products limits SO₂ and cloud condensation nuclei production in the marine atmosphere

Significance

Ocean emissions of dimethyl sulfide (DMS) are a major precursor for the production and growth of aerosol particles, which can act as seeds for the formation of cloud droplets in the marine atmosphere with the subsequent impacts on Earth’s climate. Global aircraft observations indicate that DMS is efficiently oxidized to hydroperoxymethyl thioformate (HPMTF), a previously unrecognized molecule, which necessitates revisiting DMS oxidation chemistry in the marine atmosphere. We show through ambient observations and global modeling that a dominant loss pathway for HPMTF is uptake into cloud droplets. This loss process short circuits gas-phase oxidation and significantly alters the dynamics of aerosol production and growth in the marine atmosphere.

Abstract

Oceans emit large quantities of dimethyl sulfide (DMS) to the marine atmosphere. The oxidation of DMS leads to the formation and growth of cloud condensation nuclei (CCN) with consequent effects on Earth’s radiation balance and climate. The quantitative assessment of the impact of DMS emissions on CCN concentrations necessitates a detailed description of the oxidation of DMS in the presence of existing aerosol particles and clouds. In the unpolluted marine atmosphere, DMS is efficiently oxidized to hydroperoxymethyl thioformate (HPMTF), a stable intermediate in the chemical trajectory toward sulfur dioxide (SO₂) and ultimately sulfate aerosol. Using direct airborne flux measurements, we demonstrate that the irreversible loss of HPMTF to clouds in the marine boundary layer determines the HPMTF lifetime (τ_HPMTF < 2 h) and terminates DMS oxidation to SO₂. When accounting for HPMTF cloud loss in a global chemical transport model, we show that SO₂ production from DMS is reduced by 35% globally and near-surface (0 to 3 km) SO₂ concentrations over the ocean are lowered by 24%. This large, previously unconsidered loss process for volatile sulfur accelerates the timescale for the conversion of DMS to sulfate while limiting new particle formation in the marine atmosphere and changing the dynamics of aerosol growth. This loss process potentially reduces the spatial scale over which DMS emissions contribute to aerosol production and growth and weakens the link between DMS emission and marine CCN production with subsequent implications for cloud formation, radiative forcing, and climate.

The oceanic emission of dimethyl sulfide (DMS; CH₃SCH₃) is the largest natural source of reduced sulfur to the atmosphere (1, 2). The oxidation of DMS ultimately leads to the production of sulfuric acid (H₂SO₄) and methane sulfonic acid (MSA; CH₃SO₃H), which contribute to new particle formation and growth (3–6). Direct observations of the full suite of DMS oxidation products are limited, making it challenging to interpret the large variability in estimates of global sulfur dioxide (SO₂) yields (31 to 98%), in which SO₂ is an immediate precursor to sulfate aerosol (${\text{SO}}_4^{2-}$) (3, 7). An incomplete representation of DMS oxidation in global models contributes to uncertainty in estimates of the impact of DMS emissions on cloud condensation nuclei (CCN) and climate (7–9), the utility of ice core records of MSA as proxies for historical sea ice extent (10), and the use of MSA and MSA-to-sulfate ratios as a proxy of preindustrial temperature and sulfur emissions (11–14). Uncertainties in the budget of preindustrial aerosols, including those from DMS oxidation, are the largest source of uncertainty in current estimates of radiative forcing caused by the aerosol indirect effect (9).

The recent discovery of hydroperoxymethyl thioformate (HPMTF; HOOCH₂SCHO), a globally ubiquitous DMS oxidation product, necessitates revisiting DMS oxidation mechanisms (15–17). HPMTF is produced by the isomerization of the methylthiomethylperoxy radical (CH₃SCH₂OO•), which is the primary product of DMS hydrogen abstraction by OH. This isomerization process competes with the bimolecular chemistry of CH₃SCH₂OO•, which produces SO₂ at high yield. Veres et al. determined that HPMTF is a dominant oxidation product of DMS, yet the atmospheric fate of HPMTF was unknown. Here, using direct airborne eddy covariance (EC) flux measurements, we constrain the chemical fate of HPMTF in the marine boundary layer (MBL). In the cloudy MBL, we demonstrate that the lifetime of HPMTF from cloud loss (τ_HPMTF,cloud) is less than 2 h and is the dominant HPMTF loss pathway, thus limiting the production of SO₂. In the cloud-free MBL, HPMTF is oxidized by OH-forming SO₂, which can continue along the oxidation trajectory toward H₂SO₄ and, ultimately, CCN production. Low-altitude clouds cover nearly 50% of the global oceans in the annual mean, with stratus and stratocumulus alone covering about 35% of the oceans (18). In some regions, like the eastern subtropical oceans, stratus and stratocumulus coverage reaches 60% (19). Given that low-level clouds are a persistent feature of the marine atmosphere, it is likely that the cloud loss of soluble species within the MBL is a significant component of reactive trace gas budgets. To assess the global significance of HPMTF cloud loss on marine sulfur chemistry, we use a global, atmospheric, and chemical transport model with a method of incorporating cloud chemistry, which accounts for the entrainment of gases into clouds and fractional cloud cover in the chemical rate expression (18).

Results and Discussion

Airborne Flux Observations Reveal Efficient Cloud Loss of HPMTF.

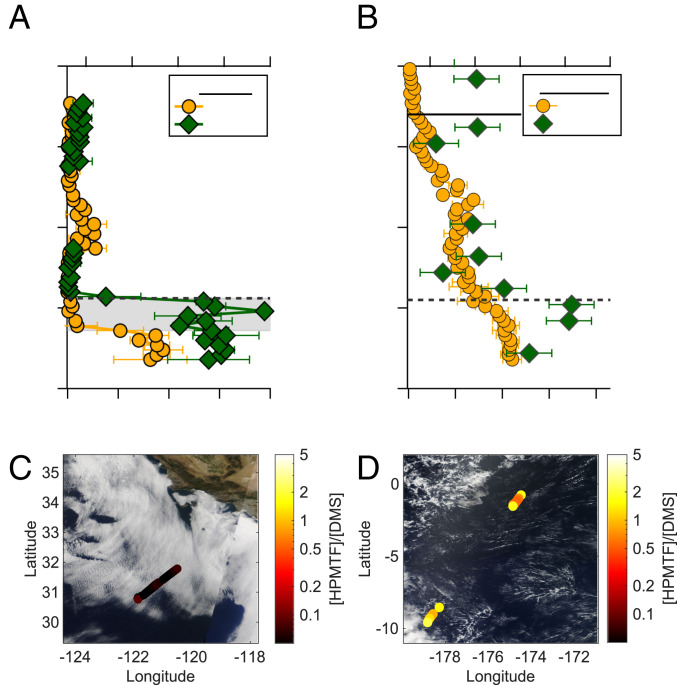
In situ airborne observations of HPMTF mixing ratios and vertical fluxes were acquired during the NASA Atmospheric Tomography (ATom) and Student Airborne Research Program (SARP) 2019 missions on the NASA DC-8 research aircraft. Here, we focus our analysis on two representative flights: 1) a SARP flight, conducted off the coast of Southern California, within a stratocumulus cloud topped MBL on July 17, 2019, and 2) an ATom-4 flight, conducted over the South Pacific Ocean, within a cloud-free MBL on May 1, 2018. Fig. 1 shows vertical profiles of DMS and HPMTF mixing ratios, true color satellite imagery, and flight tracks during the ATom and SARP MBL measurements. Two salient features emerge in the vertical profiles in DMS and HPMTF: 1) For the cloudy SARP flight, complete depletion of HPMTF is observed from cloud base (360 m) to the top of the MBL (560 m), whereas DMS is well mixed throughout the MBL, and 2) the mean [HPMTF]/[DMS] ratio measured below cloud during SARP (0.05 ± 0.03 mol ⋅ mol⁻¹) is significantly smaller than that measured in the cloud-free MBL during ATom (0.8 ± 0.5 mol ⋅ mol⁻¹), for comparable solar zenith angles (25.8 ± 2.5° and 21.2 ± 7.1°, respectively). This suggests either enhanced HPMTF loss (L_HPMTF) or suppressed HPMTF production (P_HPMTF) due to lower OH concentrations in the cloudy MBL. Changes in [OH] below cloud are unlikely to explain this difference, as modeled [OH] is reduced by only 30% below cloud, and a reduction in P_HPMTF would be partially offset by a reduction in L_HPMTF from reactions with OH (see SI Appendix, Table S5 for a full list of reactions contributing to HPMTF production and loss). Nitric oxide (NO) mixing ratios were similar between the regions (8 parts per trillion [ppt] during the clear sky ATom flight and 7 ppt during the cloudy SARP flight), indicating that the bimolecular chemistry which competes with HPMTF formation was comparable. We therefore expect the difference in [HPMTF]/[DMS] to be driven by a large additional L_HPMTF in the cloudy MBL case.

Fig. 1.

Vertical profiles of DMS and HPMTF mixing ratios under cloudy (A) and clear sky conditions (B) observed during the SARP and ATom research flights, respectively. The gray shaded region in A represents the cloudy altitudes in the MBL. The horizontal dashed lines in A and B indicate the boundary layer height. The solid line in B indicates the BuL height. The SARP vertical profile is taken from the ascent at the end of the flux period, and the ATom profile is taken from the descent at the start of the second set of flux legs. C and D show the research flight path colored by the observed [HPMTF]/[DMS] ratio overlaid on true color images from Moderate Resolution Imaging Spectroradiometer Terra for the SARP (C) and ATom (D) flights, respectively. [HPMTF]/[DMS] in C is plotted for below cloud periods only and for altitudes below 1,500-m periods in D.

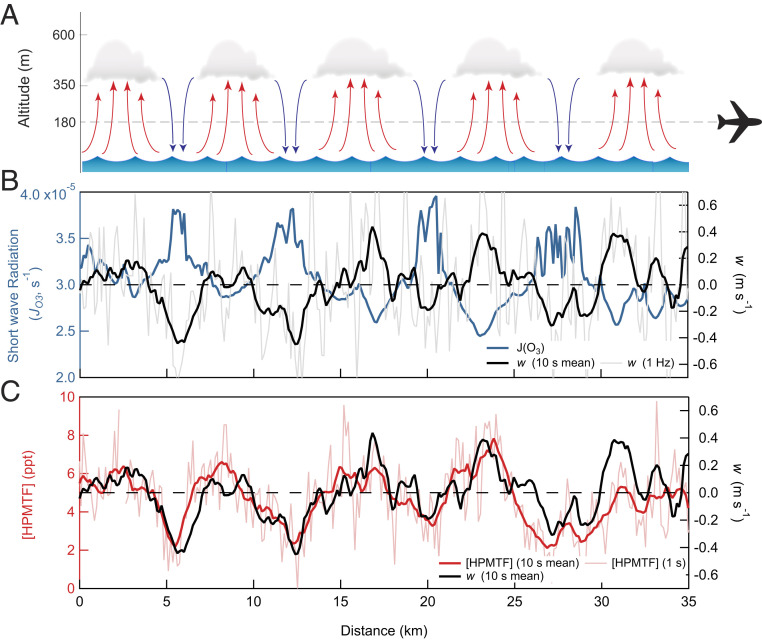
True color satellite imagery (Fig. 1C) and forward-facing camera footage (SI Appendix, Fig. S1) during the SARP flight reveal semiorganized, horizontal, and convective roll structures in the stratocumulus-topped MBL, visible as cloud streets with a period of ca. 7 km. This mesoscale convective structure is a common feature of marine stratocumulus systems and is characterized by counter-rotating horizontal vortices generating updrafts in which the clouds form and downdrafts of cloud-processed air between, shown schematically in Fig. 2A (19, 20). This structure is reflected in the time series (Fig. 2B) of both shortwave radiation (here shown as the photolysis rate of ozone, J_O3) and the vertical wind speed (w), in which J_O3 is enhanced in the cloud-free regions and w is negative (indicating a downdraft). The impact of the convective structure is clearly distinguishable in HPMTF, which is depleted in the downdrafts in which the air has recently passed through a cloud, indicative of irreversible HPMTF loss to cloud droplets (Fig. 2C). Based on the response of [HPMTF] to overhead clouds shown in Fig. 2C, we expect the aircraft measurements of the vertical flux of HPMTF to be positive, despite the absence of an entrainment flux at cloud top because of the negligible difference in concentration between the MBL top and overlying free troposphere and the negative flux at the surface due to dry deposition. The contribution of convective roll structures on new particle formation (21) and surface heat and momentum fluxes have been demonstrated previously (19, 20), but the influence of these boundary layer dynamics on the concentration and vertical transport of reactive chemical species have not previously been considered. Observations from high–time response in situ airborne instruments provide a unique opportunity to quantitatively determine the loss rate of soluble reactive gases to clouds.

Fig. 2.

(A) Schematic of the convective roll structure observed during the SARP research flight in the cloudy MBL with periodic cloudy and clear sky regions associated with updrafts and downdrafts, respectively. (B) Time series of instantaneous vertical wind speed (w, black) and zenith ozone photolysis rates (J_O3, blue), proportional to downward short wave solar radiation, indicates the cloud-free regions. (C) Time series of HPMTF mixing ratios ([HPMTF]) and w showing the depletion of HPMTF in downdraft air parcels which have experienced cloud processing. The 10-s moving average (red) and discreet 1-s time resolution (light red) HPMTF mixing ratios are included in C.

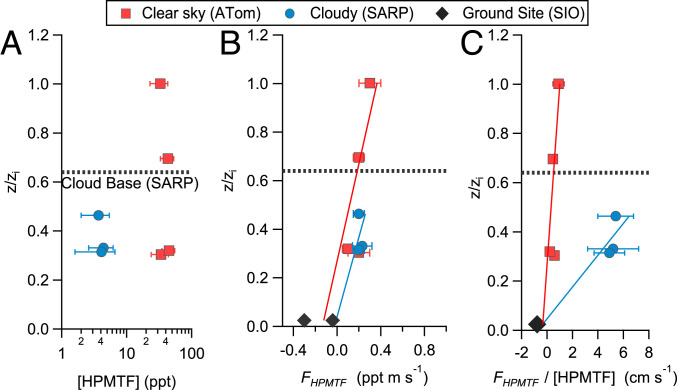
Vertical fluxes of HPMTF during SARP were directly determined in the stratocumulus-topped MBL at three altitudes (170, 180, and 255 m) using the EC technique with the continuous wavelet transform (CWT) method described further in the Materials and Methods and the SI Appendix. Mean (±1σ) HPMTF mixing ratios for these segments were 4.1 ± 1.7, 4.4 ± 1.8, and 3.7 ± 1.7 ppt, respectively. Observed HPMTF vertical fluxes (F_HPMTF) at each altitude were 0.20 ± 0.05, 0.23 ± 0.09, and 0.20 ± 0.05 ppt ⋅ m ⋅ s⁻¹. For comparison, the HPMTF surface flux (−0.04 ppt ⋅ m ⋅ s⁻¹, where a negative flux indicates deposition) was calculated from the mean MBL [HPMTF] and the average wind speed adjusted surface deposition velocity (v_d) measured from Scripps Pier (22), discussed further in SI Appendix, section S4. The large, positive fluxes measured at flight altitude together with the low-HPMTF mixing ratios implies a significant overhead HPMTF loss process. The measured flux cannot be sustained by entrainment from the free troposphere as [HPMTF] is near zero in both the free troposphere and the cloudy fraction at the top of the MBL, leading to a negligible free tropospheric entrainment flux for HPMTF. The vertical profile of the mixing ratio normalized flux (F_HPMTF/[HPMTF]) shown in Fig. 3C highlights the process difference in loss rates aloft between the cloudy and clear sky cases. In the stratocumulus-topped MBL, the extrapolation of the linear flux profile to cloud base (z_cb) permits the calculation of an exchange velocity (v_ex) between the subcloud (sc) and cloud-filled regions of the MBL $\left(F_{\text{HPMTF},z_{cb}}\times {\left({\left[\text{HPMTF}\right]}_{\text{sc}}-{\left[\text{HPMTF}\right]}_{\text{cld}}\right)}^{-1}=v_{ex}=8.6{\text{cm}·\text{s}}^{-1}\right)$, where the HPMTF concentration in the cloud-filled region ([HPMTF]_cld) is near zero. The linear extrapolation of the flux profile is justified as the chemical production and loss terms of HPMTF are constant in the well-mixed boundary layer, meaning only the exchange terms at the ocean surface and cloud base boundaries control the shape of the flux profile. The cloud base flux ($F_{\text{HPMTF},z_{cb}})$ is a measure of the net flux across the cloud base and, therefore, includes any potential HPMTF flux term from the evaporation of cloud droplets turbulently mixed into the subcloud region from the cloud layer.

Fig. 3.

Observed vertical profiles of HPMTF mixing ratios (A), flux (F_HPMTF) (B), and flux normalized by HPMTF mixing ratios (F_HPMTF/[HPMTF]) (C) observed under cloudy (blue) and clear (red) sky conditions during SARP and ATom, respectively. Altitudes were normalized to the boundary layer height (z_i) during each flight. HPMTF exchange velocities measured from a coastal surface site (z = 12 m) from Vermeuel et al. (22) were scaled to horizontal wind speed during each flight to calculate the surface flux (23). Solid lines are ordinary least-square best-fit lines. The dashed horizontal line on all panels indicates the height of the cloud base during the SARP flight.

Our observations indicate that HPMTF is strongly depleted in cloud-processed air. For highly soluble species with irreversible uptake, the loss to cloud droplets occurs at the diffusion limit, resulting in very short in-cloud lifetimes (<5 s) (23) for typical stratocumulus cloud drop diameters and concentrations [d = 15 μm, N_d = 75 cm⁻³ (24)]. If the average residence time of air within stratocumulus clouds is at least comparable to the in-cloud HPMTF loss rate (18) and HPMTF irreversibly reacts within the cloud droplet, we expect cloud uptake to be a significant term in the HPMTF budget. The uptake of select, isoprene-derived hydroxy nitrates to liquid aerosol has recently been shown to account for a significant global NO_x sink, demonstrating the importance of water-mediated multiphase chemistry (25). Despite the critical importance of clouds in regulating reactive trace gases, we are not aware of any direct measurements of the loss rate of soluble molecules to stratocumulus clouds in the MBL to constrain the timescales for the mixing of an airmass into the cloud layer.

Using our airborne flux measurements, we can estimate the mean residence time of MBL air in clouds (T_cld) as $T_{\text{cld}}=d_{\text{cld}}\times {\left(v_{ex}\right)}^{-1}$, where d_cld is the cloud thickness (d_cld = z_i – z_cb = 200 m, where z_i is the boundary layer depth, determined from the vertical gradients of potential temperature, wind speed, and mixing ratios of water vapor, DMS, and HPMTF), and v_ex is the measured v_ex between the subcloud and cloud-filled regions of the MBL. Using this approach, we derive a mean in-cloud residence time of 0.64 ± 0.33 h. These calculations are largely consistent with estimated stratocumulus residence times in the range of 0.25 to 0.66 h (26–29). Results from a large eddy simulation coupled to a trajectory–ensemble model found that individual turbulent air parcels within a nonprecipitating, stratocumulus-topped MBL have a modal cloud residence time of 0.25 h (26–29). Similarly, we can calculate the lifetime of HPMTF in the subcloud region with respect to mixing and subsequent loss in the cloud-filled region as ${\tau }_{\text{mix, cld}}=z_{cb}\times {\left(v_{ex}\right)}^{-1}$. Using the measured v_ex derived above, we determine ${\tau }_{\text{mix, cld}}$to be 1.2 ± 0.6 h.

The vertical flux of HPMTF was also assessed under clear sky conditions during ATom. We use data from the ATom-4 campaign on May 1, 2018, as a case study because of the high-HPMTF mixing ratios and the presence of multiple steady flight legs within the boundary layer, which enables the analysis of the vertical flux profile. The near-surface vertical structure in this region was comprised of a cloud-free, well-mixed, and turbulent MBL with a height of ∼550 m. At the MBL top, there was a weak inversion separating the MBL from a stably stratified buffer layer (BuL) up to a height of 1,700 m containing sparse fair weather cumulus clouds, which is a common structure in tropical trade wind regimes (30–32). Mixing time in the BuL has been estimated to be ∼30 h, compared to less than 1 h in the well-mixed MBL, indicating that the two layers are distinct despite the weak inversion separating them (33). HPMTF EC fluxes were calculated for four sequential flux legs (L1 to L4) at altitudes of 180, 180, 390, and 570 m, respectively, in which the 570 m leg was in the bottom of the BuL. Mean HPMTF mixing ratios for all legs ranged between 30 to 45 ppt. Observed F_HPMTF at each altitude were 0.2 ± 0.1, 0.1 ± 0.05, 0.2 ± 0.05, and 0.3 ± 0.1 ppt ⋅ m ⋅ s⁻¹. A clear sky HPMTF surface flux of −0.33 ppt ⋅ m ⋅ s⁻¹ was calculated from the mean MBL [HPMTF] and the average, scaled surface v_ex. We again observe a positive flux at flight altitude, although the much higher [HPMTF] results in a significantly smaller concentration of normalized flux (F_[HPMTF]/[HPMTF]) shown in Fig. 3C, with a magnitude consistent with entrainment of air by the BuL. The linear extrapolation of the observed flux profile from the surface to the top of the MBL (550 m) yields F_HPMTF = 0.6 ppt ⋅ m ⋅ s⁻¹, which yields an entrainment rate of air to the BuL $w_e=\left(F_{\text{HPMTF},z_{zi}}\times {\left(\left|{\left[\text{HPMTF}\right]}_{\text{MBL}}-{\left[\text{HPMTF}\right]}_{\text{BuL}}\right|\right)}^{-1}=2.9\pm 1.4{\text{cm}·\text{s}}^{-1}\right)$. This entrainment rate is within the range of 1.0 to 3.5 cm ⋅ s⁻¹ observed in similar trade-wind boundary layers with overlying BuL structures, as observed here (31).

Observationally Constrained HPMTF Budget in the Marine Boundary Layer.

To assess the consistency of fast cloud uptake of HPMTF, derived from our flux measurements, with our current understanding of HPMTF production and loss, we use aircraft observations to constrain the HPMTF scalar budget equation (Eq. 1):

$$\frac{\partial \left[\text{HPMTF}\right]}{\partial t}=P-L-A-\hspace{1em}\frac{d\langle w^{\prime }{\left[\text{HPMTF}\right]}^{\prime }\rangle }{dz},$$ [1]

where the time rate of change in the concentration of HPMTF ($\frac{\partial \left[\text{HPMTF}\right]}{\partial t}$) is the sum of the net in situ chemical production and loss rates of HPMTF (P and L), horizontal advection (A), and the vertical flux divergence $\left(\frac{d\langle w^{\prime }{\left[\text{HPMTF}\right]}^{\prime }\rangle }{dz}\right)$. Integrating Eq. 1 from the surface to cloud base (z_cb) and from z_cb to the top of the MBL (z_i) results in a coupled pair of HPMTF budget equations Eq. 2A and Eq. 3A, where the HPMTF flux at cloud base$\left(F_{\text{HPMTF},z_{cb}}={\langle w^{\prime }{\left[\text{HPMTF}\right]}^{\prime }\rangle }_{z_{cb}}=0.38\pm 0.07{\text{ppt}·\text{m}·\text{s}}^{-1}\right)$ is common to both equations as a source to the cloud layer and a loss from the subcloud layer. The HPMTF budget equation for the cloud layer (z_cb < z < z_i) can be written as the following:

$$\frac{\partial {\left[\text{HPMTF}\right]}_{\text{cld}}}{\partial t}=P_{\text{cld}}-A_{\text{cld}}-k_{\text{cld}}{\left[\text{HPMTF}\right]}_{\text{cld}}-\hspace{1em}{k}_{\text{OH}+\text{HPMTF}}{\left[\text{OH}\right]}_{\text{cld}}{\left[\text{HPMTF}\right]}_{\text{cld}}+\frac{{\langle w^{\prime }{\left[\text{HPMTF}\right]}^{\prime }\rangle }_{cb}}{\left(z_i-z_{cb}\right)},$$ [2A]

assuming that 1) [HPMTF] is in steady state in the cloud layer, a valid assumption given that τ_cld < 5s; 2) horizontal advection is negligible; and 3) k_cld >>> k_OH+HPMTF × [OH]_cld, a valid assumption as k_cld > 0.2 s⁻¹, we can rewrite Eq. 2A solving for [HPMTF]_cld as the following:

$${\left[HPMTF\right]}_{cld}={\left(k_{cld}\right)}^{-1}\times \left(P_{cld}+\frac{{\langle w^{\prime }{\left[HPMTF\right]}^{\prime }\rangle }_{cb}}{\left(z_i-z_{cb}\right)}\right).$$ [2B]

For [HPMTF]_cld to be greater than the chemical ionization mass spectrometer (CIMS) detection limit (<1 ppt), P_cld would need to be larger than 700 ppt ⋅ h⁻¹, a value inconsistent with measured [DMS]_cld, modeled [OH], and known DMS oxidation kinetics. This confirms the near-zero HPMTF concentration measured in cloud.

The HPMTF budget equation for the subcloud layer (z < z_cb) can be written as the following:

$$\frac{\partial {\left[\text{HPMTF}\right]}_{\text{sc}}}{\partial t}=P_{\text{sc}}-A_{\text{sc}}-\left(k_{\text{OH}+\text{HPMTF}}{\left[\text{OH}\right]}_{\text{sc}}+k_{\text{het}}+\frac{v_d}{z_{cb}}\right){\left[\text{HPMTF}\right]}_{\text{sc}}-\frac{{\langle w^{\prime }{\left[\text{HPMTF}\right]}^{\prime }\rangle }_{cb}}{z_{cb}},$$ [3A]

where k_het is the rate coefficient for HPMTF loss to aerosol particles. The HPMTF storage term ($\frac{\partial {\left[HPMTF\right]}_{sc}}{\partial t}$) in the subcloud region was calculated to be 0 ± 0.2 ppt ⋅ h⁻¹ based on the time rate of change in [HPMTF] from legs one and three, which passed over the same location. On all three sampling legs during SARP, the along flight track component of horizontal advection in [HPMTF] was small ($\frac{\partial \left[HPMTF\right]}{\partial x}$ < 0.1 ppt ⋅ h⁻¹). Because of limitations in the sampling strategy, we cannot constrain the cross-flight track advection term but expect it to be small because of the homogeneity of the coastal, ocean-sampling region. Taking these two assumptions, we can rearrange Eq. 3A to solve for the HPMTF production rate required to balance the HPMTF budget:

$$P_{sc}=\left(k_{OH+HPMTF}{\left[OH\right]}_{sc}+k_{het}+\frac{v_d}{z_{cb}}\right){\left[HPMTF\right]}_{sc}+\frac{{\langle w^{\prime }{\left[HPMTF\right]}^{\prime }\rangle }_{cb}}{z_{cb}}.$$ [3B]

Concentrations of OH were determined using a 0-D chemical box model constrained by the SARP chemical and meteorological observations, as described in SI Appendix, section S5. The model calculated [OH] (3.3 ± 1 × 10⁶ molecules ⋅ cm⁻³) is consistent with prior model calculations of [OH] in the coastal MBL during summer (34, 35). For [HPMTF]_sc = 4.4 ± 2.1 ppt, the OH-initiated gas-phase loss of HPMTF is estimated at 0.57 ± 0.28 ppt ⋅ h⁻¹, assuming that HPMTF reacts with OH at a rate comparable to the structurally similar molecule methyl thioformate (MTF; CH₃SCHO, k_OH+CH3SCHO = 1.1 × 10⁻¹¹ cm³ ⋅ molecule⁻¹ ⋅ s⁻¹), as there is no literature report of OH+HPMTF. The loss rate of HPMTF to aerosol particles (k_het) was calculated as $\frac{\gamma \omega S_a}{4}$, where γ is the HMPTF reactive uptake coefficient, ω is the HPMTF mean molecular speed, and S_a is the aerosol surface area. At present, γ(HPMTF) for marine aerosol is unknown. If we assume that HPMTF reacts at surfaces at a rate comparable to other soluble reactive gases (γ = 0.01), we predict an HPMTF loss rate to aerosol of 0.14 ± 0.07 ppt ⋅ h⁻¹ for the aerosol surface area concentrations measured below cloud (S_a = 15 μm² ⋅ cm⁻³). There is also no experimentally measured HPMTF photolysis rate; however, the lifetime of the structurally similar molecule MTF to photolysis is 3.7 d at the equator, suggesting that the photolysis of the HPMTF aldehyde group is a minor loss term (<0.1 ppt ⋅ h⁻¹) in the scalar budget analysis (36). HPMTF loss via deposition to the ocean surface is estimated to be 0.4 ± 0.2 ppt ⋅ h⁻¹, based on the wind speed dependent v_d. HPMTF loss to the overhead cloud layer, the final term in Eq. 3B, is determined to be 3.8 ± 0.7 ppt ⋅ h⁻¹ from the extrapolated flux profile, representing the largest loss term in the HPMTF budget. Note that this term represents the net cloud loss flux and therefore includes any potential source of HPMTF from cloud droplet evaporation in the below cloud fraction of the MBL. Collectively, the total HPMTF loss rate and the corresponding HPMTF production rate in the subcloud region is estimated to be 4.9 ± 0.8 ppt ⋅ h⁻¹, where the uncertainty is calculated by propagating the 1σ variance in [HPMTF]_sc and the uncertainty in the interpolated flux profile through Eq. 3B.

For comparison, we can use aircraft observations to estimate HPMTF in situ production from DMS $\left(P_{\text{sc}}=\alpha k_{\text{OH}+\text{DMS}}\left[\text{OH}\right]\left[\text{DMS}\right]\right)$, where α is the fraction of the H abstraction reaction of DMS with OH (k_OH+DMS = 4.7 × 10⁻¹² cm³ ⋅ molecule⁻¹ ⋅ s⁻¹) that yields HPMTF. The α term accounts for the competition between isomerization (that forms HPMTF) and bimolecular chemistry with NO, HO₂, and RO₂ (calculation of α is described in SI Appendix, section S5). We estimate HPMTF production (P_HPMTF) = 4.1 ± 1.0 ppt ⋅ h⁻¹ (α = 0.76, [DMS]_obs = 96 ppt, [OH] = 3.3 × 10⁶ molecules ⋅ cm⁻³). The observationally constrained HPMTF scalar budget and P_HPMTF calculated from DMS, therefore, close to within 1 ppt ⋅ h⁻¹. If the cloud loss term is not included in the scalar budget analysis, the HPMTF budget does not close to within 3 ppt ⋅ h⁻¹.

This analysis indicates the following: 1) rapid cloud loss for HPMTF is required to close the HPMTF budget in the cloud-topped MBL; 2) model estimates for k_OH+HPMTF (1.1 × 10⁻¹¹ cm³ ⋅ molecule⁻¹ ⋅ s⁻¹) are likely accurate to within a factor of 2, otherwise the SARP and ATom budgets would not close; and 3) cloud uptake dominates the fate of HPMTF in the stratocumulus-topped MBL (${\tau }_{\text{mix,\hspace{1em}cld}}$= 1.2 h and ${\tau }_{\text{chem}}$ > 5 h). A diagram of HPMTF chemical budget terms are shown in Fig. 4. Our observations suggest that HPMTF loss to clouds is an irreversible sink for DMS-derived sulfur, in which HPMTF cloud uptake contributes to cloud droplet mass (likely as ${\text{SO}}_4^{2-}$) but quenches the potential for new particle formation, damping the link between DMS emissions and CCN concentrations.

Fig. 4.

The components of the HPMTF scalar budget under cloudy sky conditions, including all chemical production and loss pathways that can be directly constrained from in situ observations.

Impact of HPMTF Cloud Loss on Global Sulfur Chemistry.

To assess the global significance of HPMTF cloud loss on marine sulfur chemistry, we update the DMS and HPMTF chemistry in the Goddard Earth Observing System (GEOS)–Chem chemical transport model (version 12.9.2; ref. 37), which includes a recently developed method of incorporating cloud uptake in the chemical rate expression (18) and recent updates to marine halogen chemistry (38). Globally, we calculate that 46% of emitted DMS forms HPMTF. Prior, the observationally constrained box modeling of HPMTF production showed yields of HPMTF from DMS of 38 and 32% for ATom 3 and 4, respectively (15). In prior global modeling of the chemical fate of HPMTF using the Community Atmosphere Model with Chemistry chemical transport model, the only HPMTF loss process considered was reaction with OH (15). Using the kinetic rates described in SI Appendix, Table S5, we calculate the annual mean fraction of emitted sulfur from DMS, as a function of latitude, that is lost via the primary loss pathways (Fig. 5A). The global mean fraction of DMS-derived sulfur that is lost to clouds as HPMTF is 36%, with zonal means ranging from 10 to 50%. An additional 15% of HPMTF is lost to aerosol particles, meaning that less than half of the sulfur in HPMTF ultimately forms SO₂. During January, when DMS emissions in the Southern Hemisphere are highest, terminal sulfur loss to cloud uptake peaks at 0.58 Gg ⋅ y⁻¹, which accounts for 33% of total DMS loss. A sensitivity test taking k_OH+HPMTF at an upper limit of 5.5 × 10⁻¹¹ cm³ ⋅ molecule⁻¹ ⋅ s⁻¹ (5× base rate) shows that 31% of DMS is lost through the HPMTF cloud uptake channel compared to 36% in the base case, suggesting that uncertainty in the OH+HPMTF rate constant has little impact on this analysis.

Fig. 5.

(A) Pathways for DMS removal, as simulated by GEOS-Chem are the following: 1) OH addition and BrO reaction with DMS leading to MSA and SO₂ (gray); 2) H abstraction of DMS, primarily by OH, resulting in SO₂ production from biomolecular CH₃SCH₂O₂· chemistry (red), the oxidation of DMS by Cl and NO₃ radicals are an additional minor contribution; 3) HPMTF + OH gas-phase chemistry (dark green); 4) HPMTF irreversible uptake to clouds (blue); 5) HPMTF heterogeneous uptake to aerosol particles (orange); and 6) HPMTF wet and dry deposition (purple). Annual mean marine DMS emissions as a function of latitude are also shown on the right y-axis in black. The inclusion of cloud loss and aerosol heterogeneous uptake into the HPMTF budget results in a large reduction in [SO₂] (B) and large increase in [SO₄^2-] (C) for altitudes below 3 km. Results are for the model Test Case 3. The updates to the GEOS-Chem chemical mechanism used in this model implementation are detailed in SI Appendix, Table S4, and conditions for the model test cases are detailed in SI Appendix, Table S5.

The measurements and global model simulations presented here indicate that the cloud uptake of HPMTF is a significant, volatile sulfur loss channel, reducing the SO₂ production from DMS by 35% globally and lowering near-surface (0 to 3 km) SO₂ concentrations over the ocean by 24% (Fig. 5B), with consequent impacts on new particle formation from the nucleation of sulfuric acid (39). The regions with the largest percent change in SO₂ in the western ends of the major ocean gyres are regions where DMS oxidation is both a dominant local source for SO₂ and where HPMTF production and subsequent cloud loss are efficient. In nonprecipitating clouds, the condensed phase products of HPMTF aqueous phase chemistry would contribute to particle mass, following cloud processing, but would not increase particle number density (4, 40). Importantly, the proposed, prompt formation of SO₄²⁻ from aqueous HPMTF cloud chemistry dramatically increases the production rate of ${\text{SO}}_4^{2-}$ in the MBL (by over 500%) and the ${\text{SO}}_4^{2-}$ concentration in the marine lower atmosphere (0 to 3 km) by 22%. While the total, global sulfate burden changes only slightly, the acceleration of DMS conversion to ${\text{SO}}_4^{2-}$ leads to a marked shift in the spatial distribution of sulfate in marine environments (Fig. 5C) and the temporal connections between DMS emissions and SO₄²⁻ formation.

The unified approach of direct ambient measurement of cloud uptake rates and global chemical modeling reveals the substantial role of clouds in regulating the budget of volatile organic molecules in the lower troposphere. We expect that cloud uptake contributes significantly to the budgets of a wide array of reactive trace gases in the atmosphere, with consequent impacts on CCN and chemical budgets in cloudy regions across the globe.

Materials and Methods

HPMTF Airborne Observations.

Full details of the airborne detection of HPMTF are provided by Veres et al., with a brief description given here (15). HPMTF mixing ratios were measured on the NASA ATom and SARP campaigns with an iodide-adduct chemical ionization time-of-flight mass spectrometer (iodide CIMS, Aerodyne Research Inc.). Ambient air was sampled through a temperature, pressure, humidity, and mass flow-controlled inlet. Instrument backgrounds were determined by overflowing the inlet with scrubbed ambient air periodically, and instrument sensitivity to HPMTF was determined in postcampaign laboratory studies. HPMTF is detected as a stable adduct ion with iodide (I-C₂H₄O₃S⁻) at a mass-to-charge ratio (m/z) of 234.8931. This mass is not fully resolvable from the detected product ion of dinitrogen pentoxide (N₂O₅) at the mass resolution of the instrument (m/Δm = 5,000), and data were filtered to remove periods in which N₂O₅ potentially contributed to observed HPMTF. We note that the expected contribution of N₂O₅ to the observed HPMTF signal during the flights discussed here is negligible, as they took place during daytime under low-NO_x conditions in which N₂O₅ concentrations are low (<1 ppt). Subsequent to the publication of Veres et al., further evaluation of the calibration method identified a bias in the experiment, resulting in an overestimation in the originally reported HPMTF mixing ratios. Revised calibration experiments were performed which removed that source of bias, yielding a corrected instrument calibration factor. A corrigendum to Veres et al. has been posted detailing the updated calibration factor and the impact of those changes on the ATom observations reported in that work (15). The HPMTF mixing ratios used here for both the SARP and ATom flights reflect the updated HPMTF calibration factor. The updated ATom dataset is available through the Distributed Active Archive Center for Biogeochemical Dynamics (39, 41). The total uncertainty for HPMTF for the ATom observations was 12% + 0.4 ppt, and 1σ precision was 0.3 ppt for 1 s measurements. For the SARP flight, HPMTF uncertainty was 12% + 0.8 ppt, and 1σ precision was 0.9 ppt. DMS during SARP was measured with a proton transfer time-of-flight mass spectrometer (42). The DMS measurement from ATom used in this analysis was from whole-air samples analyzed with gas chromatography (43). Further details of the DMS measurements and other ancillary airborne measurements during ATom and SARP are listed in SI Appendix, Tables S1 and S2, respectively.

Airborne HPMTF Vertical Flux.

The airborne vertical flux of HPMTF was computed using the EC technique using the CWT method (44–46). CWT methods for computing EC flux have emerged as a powerful technique in airborne flux studies, as it does not require homogeneity or stationarity over the averaging period and because it preserves time information, allowing for the computed flux to resolve changes over heterogeneous surfaces (44, 45, 47). All EC flux determinations for HPMTF were performed at 1-Hz time resolution. Standard flux data processing procedures and uncertainty analysis were implemented as described in SI Appendix, section S2. Flux averaging periods were manually selected for periods of stable aircraft altitude, pitch, and roll and to avoid data gaps in the HPMTF measurement, as described in SI Appendix, section S2. The SARP flight presented here was the only available flight in the MBL below cloud during the SARP or ATom missions. The ATom-4 May 1, 2018, flight was selected as a clear sky comparison case study because of the similar atmospheric conditions (e.g., SZA, O₃, NO, and aerosol surface area) compared to the SARP flight in order to limit differences in HPMTF chemistry between the flights to the presence or absence of clouds.

Global Chemical Transport Model.

The chemistry of DMS and its oxidation products, including HPMTF, were simulated using the GEOS-Chem global chemical transport model (version 12.9.2). The model includes comprehensive, tropospheric oxidant chemistry, with recent updates to halogen chemistry (38) and cloud processing (18). Simulations were performed at 4 × 5° horizonal resolution with 72 vertical levels. Model sensitivity simulations were run at multiple rate constants for HPMTF+OH. The base model case uses a rate constant of 1.11 × 10⁻¹¹ cm³ ⋅ molecules⁻¹ ⋅ s⁻¹. Additional simulations using HPMTF+OH of 5.5 × 10⁻¹¹ cm³ ⋅ molecules⁻¹ ⋅ s⁻¹ are taken to provide an upper limit case of HPMTF gas-phase oxidation by OH, which would reduce the significance of HPMTF cloud uptake. A lower limit HPMTF+OH case was simulated using the calculated rate constant of Wu et al. of 1.40 × 10⁻¹² cm³ ⋅ molecules⁻¹ ⋅ s⁻¹ (16). Heterogeneous uptake to both clouds and aerosols was simulated using a reactive uptake coefficient (γ) of 0.01. Model sensitivity simulations were also performed with and without HPMTF heterogeneous uptake to clouds and aerosols. A full description of the GEOS-Chem model implementation, sensitivity simulations, and model comparison to the ATom observations are provided in SI Appendix, sections S6–S8.

Data Availability

Merged airborne observation data from the ATom campaign is published through the Distributed Active Archive Center for Biogeochemical Dynamics (DAAC) (ref. 41; https://doi.org/10.3334/ORNLDAAC/1925). HPMTF observations during ATom are published through DAAC at https://doi.org/10.3334/ORNLDAAC/1921 (48). All data from the 2019 SARP mission is archived in the Airborne Science Data for Atmospheric Composition database at https://www-air.larc.nasa.gov/cgi-bin/ArcView/sarp.2019. Source code for the GEOS-chem cloud processing model is available in Zenodo at https://zenodo.org/record/3959279#.YUIyKbhKg2w. All other study data are included in the article and/or SI Appendix.