Opportunistic application of phantom-less calibration methods for fracture risk prediction using QCT/FEA

Abstract

Objectives:

Quantitative computed-tomography (QCT)-based finite element analysis (FEA) implements a calibration phantom to estimate bone mineral density (BMD) and assign material properties to the models. The objectives of this study were to 1) propose robust phantom-less calibration methods, using subject-specific tissues, to obtain vertebral fracture properties estimations using QCT/FEA; and 2) correlate QCT/FEA predictions to DXA values of areal BMD.

Methods:

Eighty of a cohort of 111 clinical QCT scans were used to obtain subject-specific parameters using a phantom calibration approach and for the development of the phantom-less calibration equations. Equations were developed based on the HU measured from various soft tissues and regions, and using multiple linear regression analyses. 31 additional QCT scans were used for cross-validation of QCT/FEA estimated fracture loads from the L₃ vertebrae based on the phantom and phantom-less equations. Finally, QCT/FEA-predicted fracture loads were correlated with aBMD obtained from DXA

Results:

Overall, 217 QCT/FEA models from 31 subjects (20 females, 11 men) with mean ages of 69.6 (13.1) and 67.3 (14) were used to cross-validate the phantom-less equations and assess bone strength. The proposed phantom-less equations showed high correlations with phantom-based estimates of BMD (99%). Cross-validation of QCT/FEA-predicted fracture loads from phantom-less equations and phantom-specific outcomes resulted in high correlations for all proposed methods (0.94 – 0.99). QCT/FEA correlation outcomes from the phantom-less equations and DXA-aBMD were moderately high (0.64 – 0.68).

Conclusions:

The proposed QCT/FEA subject-specific phantom-less calibration methods demonstrated the potential to be applied to both prospective and retrospective applications in the clinical setting.

Introduction

Osteoporosis is a public health concern associated with an increase in fracture risk. In this setting, vertebrae are the second most common affected bones with a fracture incidence exceeding 1.4 million annual cases in the U.S. [1–4]. Dual-energy x-ray absorptiometry (DXA) is the most common method for estimation of bone mineral density (BMD) and fracture risk in the clinical setting [5, 6]. However, DXA presents several limitations such as not being able to assess the three-dimensional (3D) details of the vertebrae and potential overestimation of BMD values. This latter limitation is mostly observed in patients presenting with degeneration in the spine and in overweight patients, possibly leading to under-treatment of clinically significant bone loss and an increase in fracture risk [4, 7–9]. Thus, there is a critical need to improve fracture risk detection and treatment.

Measurements of Hounsfield units (HU) from the CT images have been previously used to evaluate longitudinal bone loss [10], osteoporosis diagnosis and prevalent fractures [11, 12], and fracture properties of vertebrae [13]. However, this approach presents inherent limitations. First, while in-vivo HU attenuation of vertebral trabecular bone can be correlated with prevalent vertebral compression fractures observed at other regions of the spine, and with DXA-defined osteoporosis thresholds [11, 12], it is important to acknowledge that the process does not predict fracture properties and the load bearing capacity of the vertebrae at the measured location. Although HU values from a single-slice measurement correlates with experimentally-measured fracture force outcomes [13], this correlation is not strong, possibly due to trabecular bone microarchitecture and density varying from the superior to the inferior regions of the vertebrae. On the other hand, quantitative computed tomography (QCT) combined with finite element analysis (FEA) has become a reliable tool to asses fracture risk. QCT/FEA has been shown to significantly improve the prediction of fracture properties and the risk for fracture as it considers 3D bone geometry, bone distribution, and allows for material properties estimates from the QCT images [4, 6, 9, 14–17].

BMD distribution in the target bone as well as its conversion to Young’s modulus using empirical material equations are critical steps in the development of subject-specific QCT/FEA models. To obtain subject-specific BMD measurements, a calibration phantom – employed for the conversion of HU from the CT images to BMD – is placed underneath the subject during the scanning process. However, these calibration phantoms are expensive, are not always available, and increase the logistic burden during imaging, such as the addition of separate mattresses for the patients to lie on and logistical challenges for research studies involving more than one clinical setting [8, 18]. Pre-calibration of the CT-scanner with a calibration phantom has been introduced as an alternative approach to overcome the use of a phantom in each scan. Although this is a better option than having no calibration in the process, this method is not specific to each subject, does not consider important individual variations such as body size, and cannot be applied retrospectively [2]. An additional approach is the use of a patient-specific phantom-less calibration technique. This process uses the patient’s own tissues, such as fat and muscle, as the calibrating reference materials to convert HU to BMD [2, 7, 9, 16]. With this approach, the reference regions of interest (ROIs) are located close to the vertebral bodies, avoiding any beam hardening and scattering effects, and reducing factors associated to subject body size and the relative positions between patient and calibration phantom [5, 16, 18, 19]. The ROIs are then implemented to obtain a relationship between HU and BMD, yielding high reliability and accuracy of outcomes [2, 5, 6, 8, 18]. Although phantom-less calibration is a promising method for replacing the use of a phantom during QCT scans and performing prospective analyses, to our knowledge, there are no studies describing the relationship between these subject-specific tissues and BMD, and QCT/FEA vertebral fracture prediction outcomes [6, 8, 20]. The phantom-less calibration approach can be used to develop QCT/FEA subject-specific models for fracture risk assessment and surgical planning on routine CT scans acquired for other clinical purposes, without additional radiation exposure and substantial costs.

The aim of this study was to propose robust phantom-less calibration methods, using subject-specific tissues, which could be applied prospectively and retrospectively to databases of CT scans to obtain fracture properties estimations using QCT/FEA. In this study, we developed phantom-less calibration equations using a population cohort and evaluated these equations using QCT/FEA to obtain vertebral fracture loads. Then, the fracture loads obtained with QCT/FEA from the various phantom-less equations were correlated to those obtained using a calibration phantom and to BMD values obtained using DXA.

Methods

Study population and CT scans

The study population comprised the use of pre-existing DXA and QCT scans that had been collected as part of ongoing studies from the Mayo Clinic [21]. All subjects provided written informed consent and the study was approved by the Mayo Clinic Institutional Review Board. DXA imaging of subjects was performed using a single Lunar Prodigy (GE Healthcare) scanner following a standardized clinical scanning and analysis protocol to obtain areal BMD (aBMD) of the spine. Spine QCT scans were performed using a Siemens Sensation-64 CT scanner (Siemens Healthcare). QCT images were obtained using a standardized protocol with the following settings: 120 kVp, 67 mA, 0.8 s rotation time, 0.75 pitch, 20 s scan time, 2.0 mm image thickness, 7.5 mm/rotation table speed, and 10 mm collimation; and reconstructed using a soft kernel (B30). The subjects were scanned together with a calibration phantom (Mindways Inc.) included in the scan field-of-view. The calibration phantom contained five rods of known reference material (K₂HPO₄) used for conversion of HU to K₂HPO₄ equivalent density, as a surrogate for BMD. The QCT scans included a total of 111 subjects (70 females and 41 males). Eighty (50 women and 30 men) of the 111 scans were used to obtain subject-specific parameters using a phantom calibration approach and for the development of phantom-less calibration equations. The remaining 31 scans, including subjects with t-scores in the osteoporotic, osteopenic, and normal ranges, were used for cross-validation of fracture loads using QCT/FEA based on the phantom calibration and phantom-less approach. Subject demographics were also collected as part of the study and are shown in Table 1.

Table 1.

Demographic information

Cohort 1
	Number of subjects	Age (yrs.)	Height (cm)	Weight (kg)
Men	30	67.2 ± 14.0	175.0 ± 7.5	89.7 ± 14.2
Female	50	64.3 ± 11.5	161.9 ± 5.3	73.4 ± 15.0
Total	80	65.4 ± 12.5	166.8 ± 8.9	79.5 ± 16.6
Cohort 2
	Number of subjects	Age (yrs.)	Height (cm)	Weight (kg)
Men	11	67.3 ± 14.0	177.1 ± 5.0	94.1 ± 15.1
Female	20	69.6 ± 13.1	161.3 ± 6.4	73.7 ± 16.0
Total	31	68.8 ± 13.2	166.9 ± 9.7	80.9 ± 18.3

Values are average ± standard deviation

Phantom-specific calibration

Eighty (80) QCT scans were used to obtain subject-specific parameters using a phantom calibration approach. QCT images were imported into Mimics software (Materialise), the L₃ vertebra identified, and a region-of-interest (ROI) placed within the center of the vertebra at a mid-slice to obtain a mean HU value for trabecular bone. Following the phantom manufacturer specifications, HU was then converted into BMD as follows [13]:

$${\rho }_{ash}=K_{2}HP{O}_4=BM{D}_{\left(\mathit{\text{unknow}}\right)}=\frac{{\mu }_{ROI}-{\beta }_{CT}}{{\sigma }_{CT}},$$

where β_CT relates an imaging technique-specific parameter characteristic of the CT number scale, and σ_CT characterizes the response of the CT scanner to changes in pure K₂HPO₄. Outcomes from this process included individual subject-specific β_CT and σ_CT values, and an average of these values representing the population cohort.

Phantom-less calibration

The same 80 subjects used for subject-specific phantom calibration were used to obtain phantom-less calibration equations. A series of phantom-less calibration equations were developed based on the HU measured from various tissues and regions: air (A), fat (F), psoas muscle (M), and subject perimeter (P). In the same middle slice used during the phantom calibration process, ROIs (20–30 mm²) were placed in the (A), (F), (M), and (P) to obtain average HU values, respectively (Fig. 1). These HU values, together with the HU value from the L₃ vertebra of interest, were implemented in a multiple linear regression analyses to obtain phantom-less equations that would estimate the BMD value of the L₃ ROI obtained using subject-specific phantom equations. The HU values obtained for the ROIs [(A), (F), (M), (P), and (L₃)], were used to develop various phantom-less calibration functions:

$$BM{D}_{\mathit{\text{Phantom}}-\mathit{\text{less}}}=C_1+C_2\times \left(P\right)+C_3\times \left(A\right)+C_4\times \left(F\right)+C_5\times \left(M\right)+C_6\times \left(HU\right)$$

where coefficients (C₁ to C₆) were obtained using multiple regression analyses detailed in the statistical section.

Figure 1.

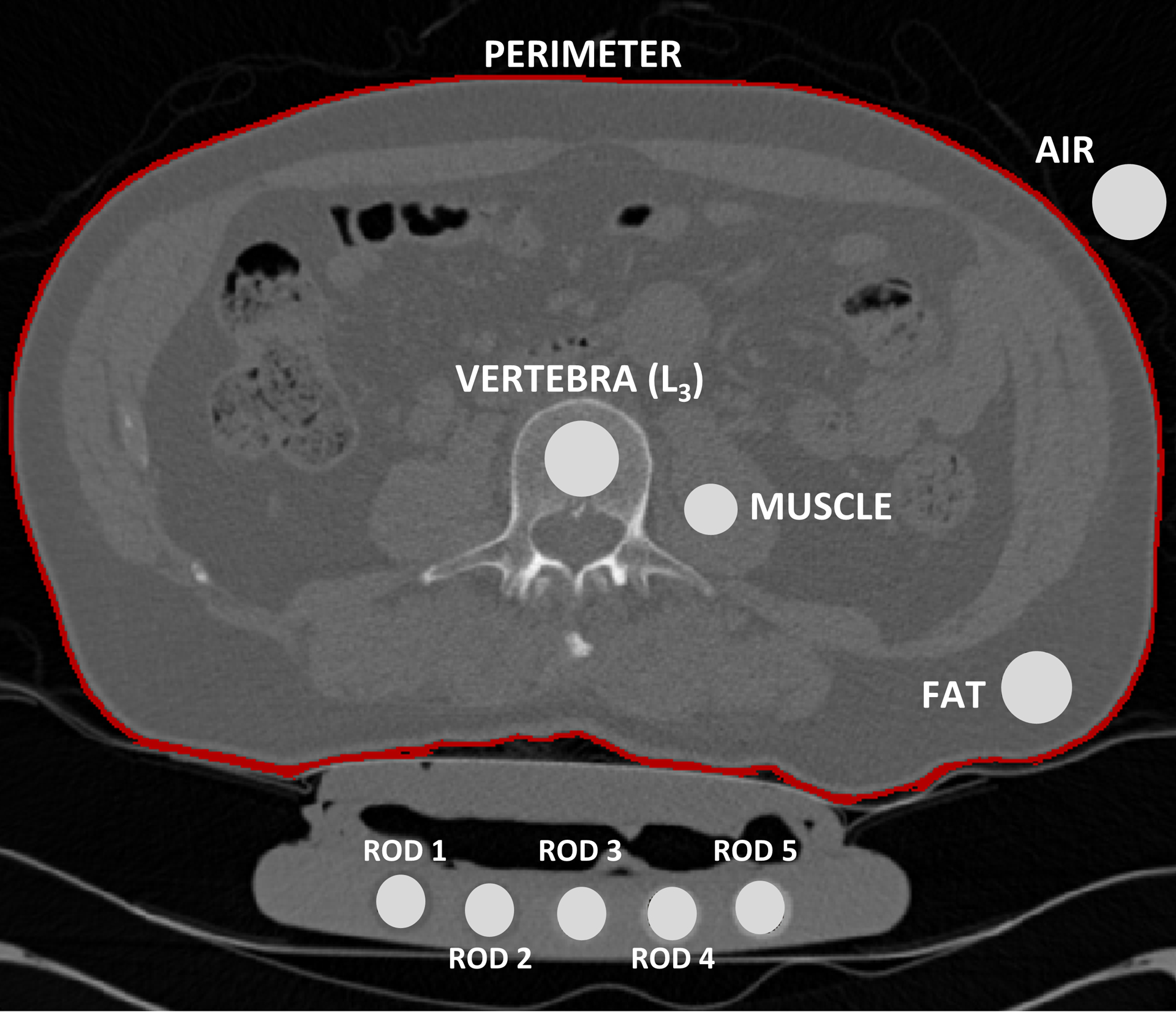
Mean HU values were collected from the various ROIs on the L3 vertebra, psoas muscle, fat, air, and five phantom rods. Calibration phantom specifications were used to convert HU to BMD.

QCT/FEA fracture prediction

Thirty-one (31; 20 females and 11 males) subjects were used to cross-validate the phantom-less equations and the average phantom-specific β_CT and σ_CT, with phantom-specific fracture load outcomes. The QCT/FEA process has been previously validated and described in detail [22]. Briefly, models of the L₃ vertebrae were created from the CT-DICOM images by manual segmentation of the vertebral bodies using Mimics. The cortical and trabecular bones were manually segmented to obtain a 3D geometry and a top and bottom layer were included to allow for uniform boundary conditions and load application. Voxel volume meshes were created maintaining a ratio of 1:1 (FE-voxel:CT-voxel), and each voxel was assigned an HU value corresponding to the CT voxel in the image. To obtain subject-specific properties, the σ_CT and β_CT obtained from the individual phantom calibration process were used to convert the HUs from each voxel to equivalent K₂HPO₄ density. Similarly, for a non-subject-specific approach, the average phantom-specific σ_CT and β_CT values – obtained from the 80-patient cohort – were used to convert HUs to equivalent K₂HPO₄ density. Additionally, five phantom-less equations were implemented to convert HU in the L₃ vertebrae to K₂HPO₄. Thus, QCT/FEA fracture loads were estimated using three different approaches: 1) subject-specific calibration phantom; 2) non-subject-specific phantom calibration parameters; and 3) five different phantom-less calibration equations.

QCT/FEA models of the L₃ vertebra were imported into ANSYS Mechanical APDL (ANSYS) where a Young’s modulus value (E, [MPa]) was assigned to each finite element using a power-law ash density-modulus relation $(E=4730\times {\rho }_{app}^{1.56})$ [23], where a ratio between ash and apparent density $({\rho }_{ash}/{\rho }_{app})$ of 0.6 was used to obtain ash density. Top and bottom layers were assigned an E = 2500 MPa; the bottom layer was fixed in all directions while a displacement was applied to the top layer to induce compression. Fracture load was estimated as a function of vertebral stiffness (K_FE) and height (H) of the vertebra [24] as follows:

$$F_{FE}=0.0068K_{FE}H$$

Our previous studies show the QCT/FEA approach can predict up-to 89% of the experimental fracture loads (supplemental material, [22]). All aspects of the FE modeling were kept the same during the study while only changing the material assignment approach based on the various phantom-based and phantom-less equations.

Statistical analyses

JMP Pro-14 (SAS Institute Inc.) was used for all statistical analyses. Coefficient of determination (R²), calculated with respect to the goodness of fit (Y = mX + b), were obtained using all 111 subjects to evaluate the effect of age on QCT-estimated BMD outcomes obtained using the subject-specific phantom calibration equation. From the cohort of 80-patients, the HU values from the (A), (F), (M), (P), and (L₃), were used to develop phantom-less calibration equations using a multiple linear regression model and the subject-specific L₃-BMD estimated values. Briefly, the ROI from the L₃ was converted from HU to BMD using the calibration phantom. Then, this BMD dependent variable was predicted based on the independent variables (A, F, M, P, and the HU at the L₃). Using the measured HU values, regression equations were obtained by combining PAFM, PFM, AFM, FM, and M. Statistical significance and R² were obtained for each equation with respect to the subject-specific calibration phantom outcomes.

Coefficients of determination (${\widehat{R}}^2$) with respect to Y = X were obtained for the QCT/FEA predicted fracture loads based on the 5 phantom-less equations and the 1 non-subject-specific equation, with respect to the subject-specific phantom calibration equation outcomes. Additionally, QCT/FEA predicted fracture loads from the 31 subjects and from all 7 equations (5 phantom-less equations + 1 non-subject-specific equation + 1 subject-specific equation) were correlated with aBMD obtained from DXA. The level of significance was set at p<0.05.

Results

A cohort of 111 patients was used to develop phantom-less calibration methods to allow for prediction of vertebral fracture properties using QCT/FEA. Figure 2 shows QCT-estimated BMD using the calibration phantom from the 111 subjects vs. age and sex. Correlation coefficients (${\widehat{R}}^2$) for BMD outcomes between the phantom calibration method and the proposed phantom-less methods are shown in Table 2. All phantom-less equations showed high correlations with the phantom-based BMD outcomes. A total of 217 QCT/FEA models were run [31 subjects x (5 phantom-less equations + 1 non-subject-specific equation + 1 subject-specific equation)] to estimate vertebral fracture loads. Fracture loads predicted from the QCT/FEA models developed with the calibration phantom vs. those developed using the phantom-less equations and the non-subject-specific phantom calibration (average σ_CT and β_CT) were assessed in terms of model accuracy (Table 3). Correlation outcomes (${\widehat{R}}^2$) for the non-subject-specific equation and the phantom-less calibration equations were high, ranging between 0.94–0.99. The highest accuracy was obtained for the non-subject-specific equation, and PAFM, PFM and AFM phantom-less equations, with ${\widehat{R}}^2$ values of 0.99 (Table 3).

Figure 2.

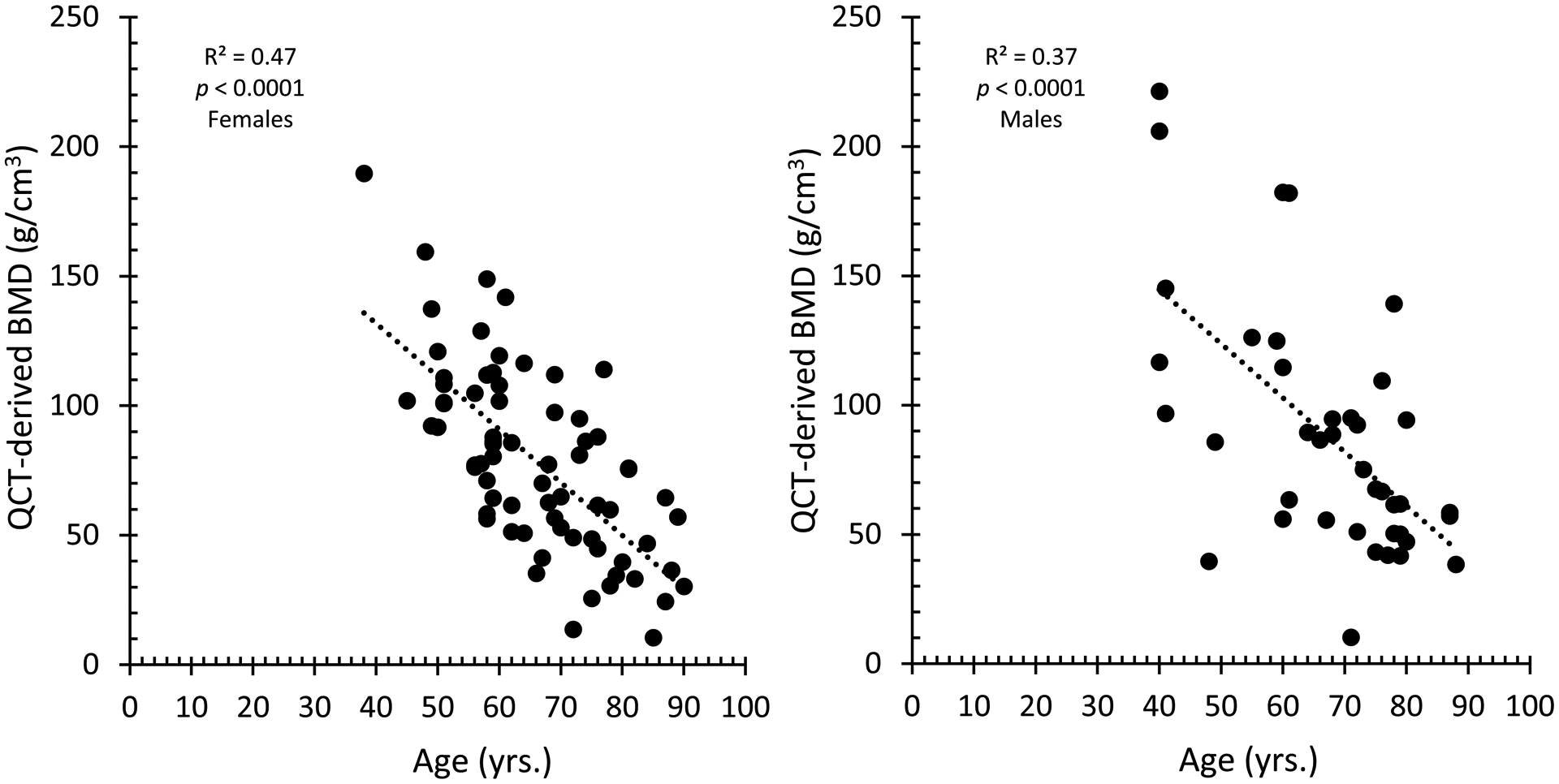
Coefficient of determination (R²) obtained for all 111 subjects to evaluate the effect of age on QCT-estimated BMD outcomes. BMD measurements were negatively correlated with age in both sexes (both p<0.0001).

Table 2.

Phantom-less equations coefficients and BMD correlations obtained using the phantom and phantom-less calibration methods.

Equations		Coefficients							${\widehat{\mathit{R}}}^2$ (Y=X)
		C1	C2	C3	C4	C5	C6
PAFM*		−10.75	−0.097	0.00005	0.003	−0.0020	0.8005		0.994
PFM		−10.99	−0.096	-	0.002	−0.0015	0.8005		0.994
AFM		−25.78	-	−0.00011	−0.057	−0.0181	0.8050		0.993
FM		−25.40	-	-	−0.055	−0.0193	0.8049		0.993
M		−20.28	-	-	-	−0.0020	0.8041		0.992

^*P=Perimeter, A=Air, F=Fat, M=Muscle

Table 3.

Correlation outcomes between QCT/FEA fracture load estimates from the calibration phantom vs. phantom-less equations

	${\widehat{\mathbf{R}}}^2$ (accuracy; y=x)
Average σCT and βCT	0.99
PAFM	0.99
PFM	0.99
AFM	0.99
FM	0.98
M	0.94

Coefficients of determination (R²) between aBMD values obtained from DXA and the predicted fracture loads from QCT/FEA using the 1) calibration phantom, the 2) phantom-less equations, and the 3) non-subject-specific equation are shown in Table 4. Correlation outcomes for all cases were moderately high, ranging from 0.64–0.68. Similar correlation outcomes were obtained for three of the phantom-less equations and the non-subject-specific equation when compared to the calibration phantom process. The FM and M phantom-less equations showed lower correlations, 0.64 and 0.67, respectively.

Table 4.

QCT/FEA predicted fracture loads vs. aBMD from DXA

	Correlation outcomes (R2)
Calibration Phantom	0.68
Average σCT and βCT	0.68
PAFM	0.68
PFM	0.68
AFM	0.68
FM	0.64
M	0.67

Discussion

This study aimed to develop calibration methods, allowing for the conversion of HU to BMD values using a phantom-less calibration approach, to obtain vertebral fracture properties using QCT/FEA. Outcomes demonstrated that the proposed phantom-less methods can successfully be used in QCT/FEA to estimate vertebral failure loads that are highly accurate and correlate with fracture loads obtained using the traditional phantom calibration method.

A strong correlation between the phantom calibration, gold standard for quantitative CT and QCT/FEA, and the proposed phantom-less equations were obtained when comparing BMD values and estimated fracture load outcomes. Equations using solely fat and muscle highly correlated with outcomes using the calibration phantom (${\widehat{\text{R}}}^2$ of 0.98 and 0.94, respectively). On the other hand, these correlations could be significantly improved by incorporating the perimeter of the patient (${\widehat{\text{R}}}^2$=0.99). Additionally, a second calibration method using a non-subject-specific approach resulted in an accuracy (${\widehat{\text{R}}}^2$) of 0.99 when compared to the predicted values using the phantom. In order to validate and evaluate the precision of the predicted fracture load outcomes, aBMD values were correlated to QCT/FEA predictions showing moderate correlations (68%).

While other studies have proposed phantom-less calibration methods, these presents several limitations and significant shortcomings [6, 8, 16, 18, 20]. For example, none of the previous studies have evaluated the differences between the combinations presented in this study; some relate to femur and not vertebrae; a small number of patients/subjects was evaluated; and more importantly, the phantom-less equations may not be described. Lee et al. developed a phantom-less approach using a cohort of 40 subjects and performed QCT/FEA of vertebrae, concluding that their internal calibration process was as good as the phantom calibration [16]. Similarly, Eggermont et al. developed an internal calibration process to convert HU-to-BMD and evaluated femur fracture properties using QCT/FEA in 57 advanced cancer patients [8]. Results showed high correlations (~0.94) between their phantom-less method and the phantom calibration. While these previous studies show the feasibility of the approach, unfortunately, both studies do not present their internal calibration equations, and Eggermont et al. investigates patients with cancer metastasis to the femur, which, while possibly presenting a similar HU values compared to a normal bone, could differ in their intrinsic bone material properties. On the other hand, Han Lee et al. developed a phantom-less calibration method using 39 subjects and performed QCT/FEA of the L2 vertebrae [6]. The group found a high correlation between the estimated BMD using the phantom calibration and the phantom-less approach (0.99). However, the phantom-less approach only included measurements of the subject’s perimeter; the QCT/FEA process did not estimate failure; the predicted outcomes were not correlated to DXA values; and more importantly, the phantom-less equation was not cross-validated against other cohorts.

It is well known that patients’ physical factors such as perimeter can influence the accuracy of the phantom-less calibration method as this can affect the attenuation of radiation and therefore the HU values [6]. By including the waist circumference, a routine abdomen-pelvic, or pelvic CT obtained without a reference phantom has the potential to be used for a phantom-less calibration process using the methodologies proposed in this study. Additionally, the use of internal reference tissues, particularly fat and muscle, offer reliability because of their proximity to the vertebral body reflecting more accurately the local changes in the x-ray spectra and scatter distribution at the target tissue [19]. In clinical practice, phantom-less calibration methods can be critical for identifying patients that are at high risk for fracture. With the proposed phantom-less calibration methods, HU-to-BMD conversion and failure load evaluations of the spine could be extended to retrospective analysis of existing CT images or prospectively avoiding the logistic limitations of the phantom calibration [9, 20]. QCT/FEA analysis without the use of traditional calibration phantoms would allow region-specific evaluation of bone density and quality in the spine, taking advantage of the significant amount of bone information and health within the CT image [7]. In addition, the proposed methods could replace the use of DXA in the future, when CT-scans of subjects are available, avoiding additional radiation exposure as well as a reduction in healthcare costs. Furthermore, the techniques described in this study could be utilized by orthopedic and spinal surgeons to address patients with poor bone quality preemptively with treatment of osteoporosis or with the use of additional instrumentation to improve fixation and prevent catastrophic hardware failure.

A pre-calibration method has been recently introduced to allow for the quantification of BMD without the use of calibration phantom. However, this process does not consider the patients’ physical factors that affect HU values, showing poor repeatability [6]. Placing a phantom underneath the patient also has its inherent limitations. Patient body size, shape and position in the scan field will affect CT numbers and can introduce a shift of these values over the scan field [19]. Having a phantom in a peripheral location underneath the subject magnifies these problems and can lead to inaccurate BMD estimations [5, 19, 25]. Thus, a phantom-less approach would overcome many of the current limitation in this process, such as the use of tissues adjacent to the target bone, accounting for potential beam-hardening and scattering artifacts present in the scan [5, 19].

This study is not without limitations. First, the phantom-less calibration equations were developed using a single scanner with a clinical CT scanning protocol. While using only a single scanner, the process resulted in robust equations that were cross-validated with a large secondary cohort of patients. Second, the proposed methodology is only considered for the spine, and other bone sites such as the femur were not evaluated. Additionally, while the QCT/FEA process has been previously validated using cadaveric studies, the outcomes from the phantom-less QCT/FEA approach, obtained using data from live subjects, cannot be validated for fracture properties. However, predictions were shown to be moderately correlated to aBMD outcomes from DXA. Future studies should consider proposing equations using various scanners and other bone sites.

Conclusion

The use of phantom-less calibration methods for conversion of HU-to-BMD from CT images using the patients’ reference tissues and regions emerges as an accurate method over phantom-based calibration estimations. QCT/FEA predictions of vertebral fracture loads using the phantom-less approach highly correlated to values obtained using the calibration phantom. The QCT/FEA phantom-less approach presented in this study can be used for osteoporosis diagnosis and fracture risk estimations from images previously acquired for other purposes, or prospectively without the use of a calibration phantom, minimizing logistic controls and reproducibility errors associated with external reference phantoms.

Key-Points:

• QCT/FEA overcomes the disadvantages of DXA and improves fracture properties predictions of vertebrae.

• QCT/FEA fracture estimates using the phantom-less approach highly correlated to values obtained using a calibration phantom.

• Phantom-less estimations of BMD is a promising method that can be used prospectively and retrospectively in the clinical setting.

• QCT/FEA predictions using a phantom-less approach is an accurate alternative over phantom-based methods.

Abbreviations:

QCT

Quantitative computed tomography

FEA

Finite element analysis

DXA

Dual x-ray absorptiometry

BMD

Bone mineral density

HU

Hounsfield unit

ROI

region of interest

K₂HPO₄

Potassium phosphate

DICOM

Digital Imaging and Communications in Medicine