Gene-gene interaction analysis incorporating network information via a structured Bayesian approach

Abstract

Increasing evidence has shown that gene-gene interactions have important effects in biological processes of human diseases. Due to the high dimensionality of genetic measurements, interaction analysis usually suffers from a lack of sufficient information and has unsatisfactory results. Biological network information has been massively accumulated, allowing researchers to identify biomarkers while taking a system perspective, conducting network selection (of functionally related biomarkers), and accommodating network structures. In main-effect-only analysis, network information has been incorporated. However, effort has been limited in interaction analysis. Recently, link networks that describe the relationships between genetic interactions have been demonstrated as effective for revealing multi-scale hierarchical organisations in networks and providing interesting findings beyond node networks. In this study, we develop a novel structured Bayesian interaction analysis approach to effectively incorporate network information. This study is among the first to identify gene-gene interactions with the assistance of network selection, while simultaneously accommodating the underlying network structures of both main effects and interactions. It innovatively respects multiple hierarchies among main effects, interactions, and networks. The Bayesian technique is adopted, which may be more informative for estimation and prediction over some other techniques. An efficient variational Bayesian expectation-maximization algorithm is developed to explore the posterior distribution. Extensive simulation studies demonstrate the practical superiority of the proposed approach. The analysis of TCGA data on melanoma and lung cancer leads to biologically sensible findings with satisfactory prediction accuracy and selection stability.

1 |. INTRODUCTION

Gene-gene interactions have high importance for human diseases beyond main genetic effects.¹ Due to higher dimensionality, lower signal-to-noise ratio, and other reasons, there are more challenges in the analysis of interactions compared to main effects. We refer to Alex et al,² Wu and Ma,³ and references therein for more discussions. In recent interaction analysis research, the “main effects-interactions” hierarchy has been generally employed to improve estimation and interpretation.⁴ Specifically, an interaction can be identified only when one of its main effects (weak hierarchy) or both (strong hierarchy) are also identified. Models violating this hierarchy have been demonstrated to be not sensible, as they postulate a special position for the origin and have inferior statistical power.⁵ A number of statistical methods have been developed to identify important interactions and reinforce this hierarchy. Among them, penalization has drawn much attention. Published works include the Lasso for hierarchical interaction,⁵ interaction learning via a hierarchical group-Lasso regularization,⁶ penalized tensor regression,⁷ and quadratic regression under the marginality principle.⁸

Despite the vast literature on penalization and some other techniques, there are very few Bayesian methods for hierarchical interaction analysis. Limited existing studies include Liu et al,⁹ which proposes a Bayesian hierarchical mixture model for interaction analysis and incorporates the natural hierarchical structure using the conditional prior probability technique. In another study, a Bayesian interaction analysis method with a hierarchical prior that fully considers the hierarchy constraint and simultaneously controls the degree of sparsity is developed.¹⁰ There are also a few recent Bayesian methodological developments without reinforcing hierarchy, such as the works of Ren et al¹¹ and Ferrari and Dunson.¹²

With the high dimensions of genetic measurements but limited sample sizes, the existing interaction analysis usually suffers from a lack of information, which leads to unsatisfactory results. To improve identification and prediction performance, in main-effect-only analysis, a promising direction is to incorporate biological network information, and there are roughly two strategies. The first strategy is to take advantage of network selection, where the “main effects-networks” hierarchy is usually reinforced. That is, a main effect can be included in the model only when at least one of its involved networks is also included. As suggested by Stingo et al.,¹³ this constraint needs to be imposed to ensure interpretability and identifiability of the model. Examples include the bi-level selection approach using the group exponential Lasso¹⁴ and the Bayesian sparse group selection with spike and slab priors.¹⁵ Complementary to the first strategy, the second strategy incorporates network structures. A representative technique is the network regularization based on the graph Laplacian matrix. Examples include methods with the Laplacian-based penalty^16,17 and Bayesian methods with the Laplacian Gaussian prior.^18,19 Built on these two strategies, multiple Bayesian methods have been developed to conduct network selection and also effectively account for network structures.^20,21 However, most of the existing methods have been designed for main-effect-only analysis, and methodological developments in the context of interaction analysis are very limited.

As Ahn et al.²² stated, beyond the traditional networks with nodes being the genetic factors, link networks that describe the relationships between genetic interactions can effectively reveal multi-scale hierarchical organisations in networks. Link networks based on, for example, protein-protein interaction and metabolic networks have been shown to have important biological implications.²² They can contribute to predicting more detailed and interpretable roles of oncogenes,²³ revealing cell functional organizations and cellular mechanisms,²⁴ determining whether a drug action area is part of the protein-interaction interface,²⁵ and others. Recent successes of incorporating network information in main-effect-only analysis and importance of link networks call for effective network integration approaches for interaction analysis.

In this study, we propose a new structured Bayesian interaction analysis approach. This study is the first to conduct gene-gene interaction analysis with the assistance of network selection and simultaneously accommodate network structures. The most significant advancement is that both the “main effects-interactions” and “main effects/interactions-networks” hierarchies are respected, which is much more challenging than in the existing interaction analysis or network selection-assisted main-effect-only analysis that reinforces only one hierarchy. Specifically, we extend the “main effects-networks” hierarchy employed in main-effect-only analysis to accommodate interactions. Furthermore, the underlying network structures are explored in the analysis of not only main effects but also interactions, making this study a big step forward from the existing main-effect-only structured analysis. The proposed approach is based on Bayesian techniques, which have multiple advantages over some other techniques. For example, Bayesian techniques are often more informative, as they can automatically estimate variance, and the posterior distribution of parameters can be easily constructed, which is desirable for model selection consistency.²⁶ In addition, they provide a flexible way for estimating other parameters in the model and can provide prediction via predictive distributions.²⁷ Different from most published Bayesian interaction studies based on the Markov Chain Monte Carlo (MCMC) inference technique, we take advantage of the hybrid model integrating conditional and generative components and develop a more efficient variational Bayesian expectation-maximization algorithm. This is especially desirable with the extremely high dimensions in gene-gene interaction analysis. Overall, this study can provide a useful new venue for genetic interaction analysis.

2 |. METHODS

Consider K networks G₁ (V₁, E₁), ⋯, G_K (V_K, E_K), which are constructed using existing biological network information. Here V_k is the node set consisting of p_k genetic factors, and $E_k={\left(e_k(j,l)\right)}_{p_k\times p_k}$ is the set of edges between nodes. Suppose that we have n i.i.d. subjects with X = (X₁, ⋯, X_p) ∈ R^n×p being the matrix of all genetic measurements, and y ∈ R^n×1 being the response vector, where X_j is a n × 1 vector for j = 1, ⋯, p, and $p={\sum }_{k=1}^K{p}_k$. Note that if a genetic factor is involved in multiple networks, the corresponding measurement is duplicated in these networks.

2.1 |. Model

We consider continuous response, and the proposed approach can be extended to other responses. Specifically, consider the linear model:

$$y=\sum _{j=1}^p{\beta }_j^{(\mathbf{1})}{X}_j+\sum _{l_1=1}^p\sum _{l_2>l_1}^p{\beta }_{l_1{l}_2}^{(\mathbf{2})}{X}_{l_1}◦X_{l_2}+ϵ\triangleq \tilde{X}\beta +\mathit{ϵ},$$ (1)

where ◦ denotes the element-wise product, $\tilde{X}\in {\text{R}}^{n\times (p(p+1)/2)}$ is the matrix of all genetic measurements X_j and their interactions $X_{l_1}◦X_{l_2}$, $\beta ={\left({\beta }_1^{(\mathbf{1})},\cdots ,{\beta }_p^{(\mathbf{1})},{\beta }_{12}^{(\mathbf{2})},\cdots ,{\beta }_{(p-1)p}^{(\mathbf{2})}\right)}^{\text{T}}\triangleq {\left({\beta }_j\right)}_{(p(p+1)/2)\times 1}$, and $ϵ~\mathcal{N}\left(0,{\tau }^{-1}I\right)$ with I being an identity matrix and τ being a precision parameter.

To accommodate the network structure for main genetic factors x_j’s (x_j is the jth factor corresponding to X_j), for the kth network G_k(V_k, E_k), an adjacency matrix $A_k^{(1)}$ is constructed, where $A_k^{(\mathbf{1})}(j,l)=1$ if there is an edge e_k (j, l) between the jth and lth factors and $A_k^{(1)}(j,l)=0$ otherwise, and all diagonal elements of $A_k^{(1)}$ are set to be zero. In addition, for the interactions $x_{j_1}{x}_{l_1}$ and $x_{j_2}{x}_{l_2}\left(l_1\ne l_2\right)$ of which the corresponding main genetic factors are involved in the kth network G_k, we construct a line graph with adjacency matrix $A_k^{(2)}$ following Ahn et al.²² Specifically, we set $A_k^{(2)}\left(x_{j_1}{x}_{l_1},x_{j_2}{x}_{l_2}\right)=1$ if j₁ = j₂ (that is, they share a common main genetic factor) and there is an intersection between the neighboring sets of main factors $x_{l_1}$ and $x_{l_2}$, and $A_k^{(2)}\left(x_{j_1}{x}_{l_1},x_{j_2}{x}_{l_2}\right)=0$ otherwise. Here the neighboring set of a main genetic factor is composed of the main genetic factor itself and its neighbors with edges in G_k. Thus, if $A_k^{(2)}\left(x_j{x}_{l_1},x_j{x}_{l_2}\right)=1$, then $x_{l_1}$ and $x_{l_2}$ are either connected in G_k or share some common neighbors. A toy example on the network construction of interactions is provided in Figure 1.

FIGURE 1.

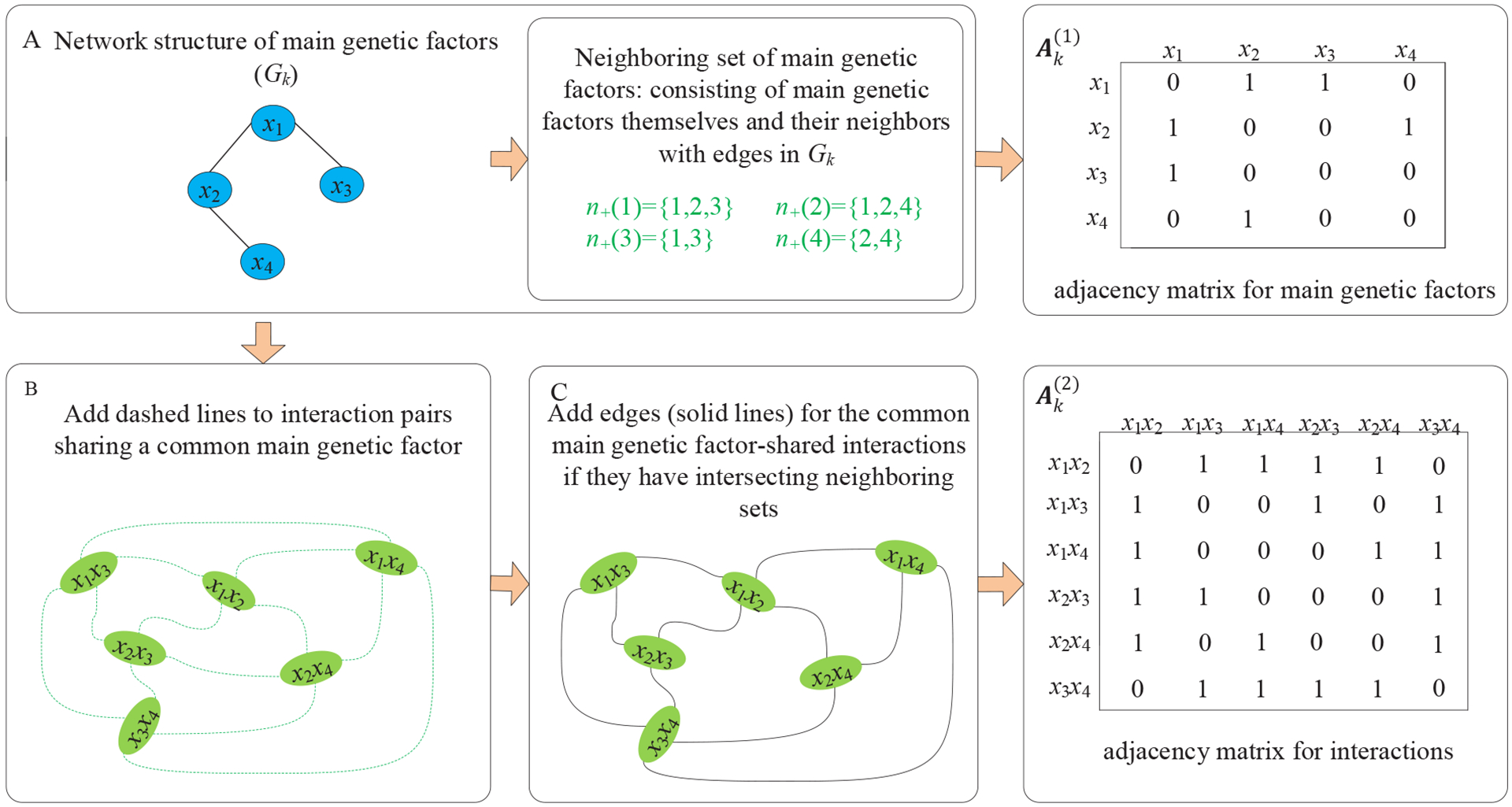
A toy example on the network construction of interactions. A: Network for main genetic factors. Here for the lth main genetic factor x_l, n₊(l) denotes its neighboring set consisting of x_l itself and its neighbors with edges in G_k. B: Establish relationships among interactions. Here the interaction pairs that share a common main genetic factor are connected with a dashed line. C: Construction of the network for interactions, where there is an edge (solid line) between two interactions if they share a common main genetic factor and there is an intersection between the neighboring sets of the other two main factors.

Then, the hierarchical representation of the proposed model is:

$$\begin{gathered} y\left|\beta ~\mathcal{N}\left(\tilde{X}\beta ,{\tau }^{-1}I\right),{\beta }_j\right|{\gamma }_j~\mathcal{N}{\left(0,s_1\right)}^{{\gamma }_j}\mathcal{N}{\left(0,s_2\right)}^{1-{\gamma }_j},{\gamma }_j\mid {\zeta }_j~\text{Bern}\left({\zeta }_j\right),{\zeta }_j~\text{Beta}(a,b), \\ {\overline{\beta }}_{l_1{l}_2}^{(\mathbf{2})}\left|{\gamma }_{l_1}^{(\mathbf{1})}{\gamma }_{l_2}^{(\mathbf{1})}~\mathcal{N}{\left(0,s_1\right)}^{{\gamma }_{l_1}^{(\mathbf{1})}{\gamma }_{l_2}^{(\mathbf{1})}}\mathcal{N}{\left(0,s_2\right)}^{1-{\gamma }_{l_1}^{(1)}{\gamma }_{l_2}^{(\mathbf{1})}},{\overline{\beta }}_{l_1{l}_2}^{(2)}\right|{\beta }_{l_1{l}_2}^{(2)}~1_{\left\{{\overline{\beta }}_{l_1{l}_2}^{(\mathbf{2})}={\beta }_{l_1{l}_2}^{(\mathbf{2})}\right\}}, \\ {\tilde{\beta }}_k\left|{\alpha }_k~\mathcal{N}{\left(0,s_1{\left(L_k+\xi I\right)}^{-1}\right)}^{{\alpha }_k}\mathcal{N}{\left(0,s_{2}I\right)}^{1-{\alpha }_k},{\alpha }_k~\text{Bern}(\theta ),{\tilde{\beta }}_k\right|{\beta }_k~1_{\left\{{\tilde{\beta }}_k={\beta }_k\right\}}. \end{gathered}$$ (2)

Here γ_j is the selection indicator of the jth main effect/interaction, with γ_j = 1 if the jth variable is selected and 0 otherwise. We use ${\gamma }_l^{(\mathbf{1})}$ and ${\gamma }_{l_1{l}_2}^{(2)}$ to denote the main-effect-selection and interaction-selection indicators corresponding to ${\beta }_l^{(1)}$ and ${\beta }_{l_1{l}_2}^{(2)}$ for simplicity. s₁ and s₂ are two parameters with s₁ > s₂ > 0 and s₂ being very small. ${\overline{\beta }}_{l_1{l}_2}^{(2)}$ is the latent variable for ${\beta }_{l_1{l}_2}^{(2)}\cdot 1_{\{\cdot \}}$ is the indicator function. ${\tilde{\beta }}_k$ is the latent vector for ${\beta }_k=\left\{{\beta }_j^{(1)}:j\in V_k\right\}\cup \left\{{\beta }_{l_1{l}_2}^{(2)}:l_1,l_2\in V_k,l_1<l_2\right\}$, which consists of all regression coefficients in the kth network. α_k is the network-selection indicator. $L_k=I-D_k^{-1/2}{A}_k{D}_k^{-1/2}$ with $A_k=\left(\begin{array}{cc}{A}_k^{(\mathbf{1})}& 0\\ 0& A_k^{(\mathbf{2})}\end{array}\right)$ and $D_k=\text{diag}\left({\sum }_{l=1}^{{\widehat{p}}_k}{A}_k(\mathbf{1},l),\cdots ,{\sum }_{l=1}^{{\widehat{p}}_k}{A}_k\left({\widehat{p}}_k,l\right)\right)$, where ${\widehat{p}}_k=p_k\left(p_k+1\right)/2$. ξ is a small constant (ξ = 10⁻⁶ in our numerical studies) to make L_k + ξI strictly positive-definite.

The graphical representation of (2) and detailed posterior computations are given in Section S1 of the Supporting Information. Denote E(γ_j) and E(α_k) as the posterior expectations of the selection indicators. We adopt the thresholding approach following Narisetty et al.,²⁶ where the main effects (interactions) with E(γ_j)’s and networks with E(α_k)’s larger than 0.5 are identified as important.

The proposed model has been motivated by the following considerations. The identification of main effects and interactions is achieved using the spike and slab prior $\mathcal{N}{\left(0,s_1\right)}^{{\gamma }_j}\mathcal{N}{\left(0,s_2\right)}^{1-{\gamma }_j}$. Specifically, γ_j = 0 leads to the spike component related to s₂, and β_j will be truncated to be zero as s₂ has a very small value. Continuous spike and slab priors have been commonly used in practice, because they not only facilitate analysis but also improve the sparse recovery ability of the model²⁷ and have desirable model selection properties.²⁸ ${\overline{\beta }}_{l_1{l}_{\mathbf{2}}}^{(\mathbf{2})}$ with prior based on the main-effect-selection indicators ${\gamma }_{l_1}^{(1)}$ and ${\gamma }_{l_2}^{(1)}$, together with the indicator function $1_{\left\{{\overline{\beta }}_{l_1{l}_2}^{(2)}={\beta }_{l_1{l}_2}^{(2)}\right\}}$, are developed to accommodate the strong “main effects-interactions” hierarchy. Specifically, if an interaction is selected with ${\gamma }_{l_1{l}_2}^{(2)}=1$, then with a high probability ${\beta }_{l_1{l}_2}^{(\mathbf{2})}\ne 0$, and $1_{\left\{{\overline{\beta }}_{l_1{l}_2}^{(2)}={\beta }_{l_1{l}_2}^{(2)}\right\}}$ further promotes ${\overline{\beta }}_{l_1{l}_2}^{(2)}={\beta }_{l_1{l}_2}^{(2)}\ne 0$, leading to ${\gamma }_{l_1}^{(1)}{\gamma }_{l_2}^{(1)}=1$ (i.e., ${\gamma }_{l_1}^{(1)}={\gamma }_{l_2}^{(1)}=1$). ${\tilde{\beta }}_k$ and ${\alpha }_k$ are introduced to assist the selection of interactions (main effects) by network identification and also accommodate the network structures of both main effects and interactions. Here, a mixture prior based on the Laplacian matrix L_k is assumed, motivated by the Bayesian graph-guided regression methods for main-effect-only analysis.^18,19,20 Specifically, when the kth network is selected (α_k = 1), the precision matrix for ${\tilde{\beta }}_k$ is related to the Laplacian matrix L_k, where the jth and lth variables are conditionally dependent if A_k(j, l) = 1. Therefore, the effects of connected factors in the kth network are promoted to be similar. The “main effects/interactions-networks” hierarchy is achieved via $1_{\left\{{\tilde{\beta }}_k={\beta }_k\right\}}$. If α_k = 0, we have ${\beta }_k={\tilde{\beta }}_k\approx 0$, leading to all γ_j’s in the kth network being zero with a high probability. Moreover, if at least one of γ_j’s belonging to the kth network is nonzero, α_k is also nonzero with a high probability. For selection indicators γ_j and α_k, a Bernoulli prior is assumed, which is perhaps the most popular in existing studies. Since results may be sensitive to the choice of hyperparameters ζ_j’s, we introduce a Beta prior on ζ_j to improve stability.

2.2 |. Computation

We rewrite the priors for ${\overline{\beta }}_{l_1{l}_2}^{(2)}$ and ${\tilde{\beta }}_k$ as the generative models with observation vector 0. As such, the proposed approach can be formulated as a hybrid Bayesian model which includes tractable partition functions and can be effectively approximated using the variational Bayesian expectation-maximization (EM) algorithm. Compared to MCMC techniques, variational approximation is computationally more efficient and more feasible with high dimensional parameters. Specifically, we consider minimizing the Kullback-Leibler (KL) divergence between the exact and approximate posterior distributions:

$$\text{KL}(q(\Omega )\Vert p(\Omega \mid y,X;\tau ,\theta ))=\int q(\Omega )\text{log}\left[\frac{q(\Omega )}{p(\Omega \mid y,X;\tau ,\theta )}\right]d\Omega ,$$

where q(Ω) = q(β)q(γ)q(α)q(ζ) is a candidate approximate distribution of the true posterior distribution p(Ω|y, X; τ, θ), and Ω represents all latent variables. Note that with the distributions of ${\overline{\beta }}_{l_1{l}_2}^{(2)}|{\beta }_{l_1{l}_2}^{(2)}$ and ${\tilde{\beta }}_k|{\beta }_k$ being the indicator functions, there is no need to include the separate distributions $q(\tilde{\beta })$ and $q(\overline{\beta })$ in q(Ω). In the E step, we optimize the KL divergence with respect to q(Ω) while holding the model parameters {τ, θ} fixed. After some derivations, we obtain the optimal variational distribution q(Ω) as:

$$\begin{gathered} q(\beta )=\prod _{j=1}^{p(p+1)/2}\mathcal{N}\left(m_j,{\sigma }_j^2\right),q(\gamma )=\prod _{j=1}^{p(p+1)/2}{\eta }_j^{{\gamma }_j}{\left(1-{\eta }_j\right)}^{1-{\gamma }_j}, \\ q(\mathit{\zeta })\propto \prod _{j=1}^{p(p+1)/2}{\left({\zeta }_j\right)}^{{\tilde{a}}_j-1}{\left(1-{\zeta }_j\right)}^{{\tilde{b}}_j-1},q(\alpha )=\prod _{k=1}^K{r}_k^{{\alpha }_k}{\left(1-r_k\right)}^{1-{\alpha }_k}, \end{gathered}$$

where $\left(m_j,{\sigma }_j^2\right)$ and $\left({\tilde{a}}_j,{\tilde{b}}_j\right)$ are the estimated values of the parameters of the Gaussian and Beta distributions, respectively, and η_j and r_k are the expectations of γ_j and α_k under q(Ω). In the M step, we optimize the KL divergence with respect to the model parameters while keeping the variational parameters Ω fixed. The proposed algorithm iteratively updates the estimators between the E and M steps until convergence and adopts the final estimated values of η_j and r_k as the estimators of E(γ_j) and E(α_k). We refer to Section S1 and Algorithm 1 of the Supporting Information for details.

To proceed with this algorithm, following Zhe et al.,²⁰ we consider a uniform Beta prior with a = b = 1. The proposed model involves two tuning parameters s₁ and s₂. For s₁, we first examine eleven values in the range of [0.5, 100] with simulation. The scenarios with ρ = 0.4, K = 100, and $r=1/\sqrt{5}$ are considered (see Section 3 for the detailed data generation, settings, and evaluation measures). Summary results are provided in Table S1 of the Supporting Information. It is observed that the proposed approach is not sensitive to the choice of s₁ when it is in the range of [0.5, 5]. To reduce computational cost, we fix s₁ = 1 in our numerical studies. The value of s₂ is selected using the Bayesian information criterion (BIC). We further examine computer time in Table S2 and Figures S2–S3 of the Supporting Information. Various values of n and p are considered, and analysis is conducted on a computer with 2.00 GHz CPU and 8 GB memory. The proposed analysis is observed to have approximately linear (or slightly quadratic) time complexity and be computationally affordable. Take a simulated dataset with p = 1, 000 and n = 300 as an example. With fixed tuning parameter, the proposed analysis takes about 0.487 minutes. To facilitate data analysis, we have developed R package JNNI implementing the proposed approach, which is publicly available at https://github.com/mengyunwu2020/JNNI and can be installed with devtools.

3 |. SIMULATION

We perform simulation to evaluate performance of the proposed approach under the following settings. (a) n = 300 and p = 1, 000. There are a total of 1, 000 candidate main effects and 499,500 interactions. (b) Consider two settings for the number of networks with K = 100 and 50. (c) We follow the network construction procedure of Zhao and Shojaie.²⁹ Specifically, for the kth network (k = 1, ⋯, K), set the number of genetic factors $p_k=\frac{p}{K}$, generate one transcription factor (TF) x_TF from $\mathcal{N}(0,1)$, and then generate the rest p_k − 1 genetic factors from $\mathcal{N}\left(\rho x_{TF},1-{\rho }^2\right)$ with parameter ρ. Consider ρ = 0.4 and 0.6, representing different dependence between the TF and its target factors in each network. Genetic factors with nonzero correlations are connected in the network. (d) There are three important networks, where 18 main genetic effects and 17 interactions have nonzero coefficients. Both the “main effects/interactions-networks” and “main effects-interactions” hierarchies are satisfied. Nonzero signals of the important TFs are generated from Uniform(0.8,1.2), and the other important main effects and interactions have relatively weaker signals with a ratio r of that of the corresponding important TF. Consider $r=1/\sqrt{5}$ and $1/\sqrt{12}$. Four settings S1-S4 for the important variables are considered. Under setting S1, all signals are positive. Setting S2 is the same as S1, except that the signals in the second network and those between the first and second networks are negative. Under setting S3, within each network, the signals can be positive or negative. Under setting S4, the important interactions only involve the none–TF main effects with weaker signals. We refer to Section S2 of the Supporting Information for more details. (e) We generate y from the Gaussian distribution (1) with variance 1. There are 32 scenarios, comprehensively covering a wide spectrum with different levels of correlations within networks and signals associated with the response, as well as different patterns of networks and associations.

In addition to the proposed approach, seven alternatives are considered. (a) triBayes, a trivial Bayesian approach that adopts the spike and slab Gaussian priors for both main effects and all pairwise interactions directly without accounting for the network information.^26,28 (b) glinternet, which learns a linear interaction model based on the hierarchical group-Lasso regularization and is implemented using R package glinternet.⁶ (c) Lasso, which applies the Lasso penalization to both main effects and all pairwise interactions directly and is realized using R package glmnet. (d) iFORM, which identifies interactions in a greedy forward fashion while maintaining the hierarchical structure.³⁰ (e) HierNet, which is Lasso for hierarchical interactions by adding a set of convex constraints and is realized usingR package HierNet.⁵ (f) Grace, which applies the graph-constrained estimation method developed by Li and Li¹⁶ to both main effects and all pairwise interactions. (g) GEL, which achieves bi-level variable selection for groups and individual predictors (main effects and interactions) in those groups.¹⁴ Among these alternatives, glinternet and iFORM respect the strong “main effects-interactions” hierarchy. We consider HierNet with the weak hierarchy, as the counterpart with strong hierarchy is not computationally feasible in large-scale simulations. TriBayes, Lasso, Grace, and GEL have been developed for main-effect-only analysis, and we extend them to interaction analysis, without reinforcing the “main effects-interactions” hierarchy. Both Grace and GEL incorporate network information, where Grace accommodates network structures, and GEL achieves the joint selection of interactions and networks.

To evaluate identification performance, we compute the numbers of true positives and false positives for main effects (M:TP and M:FP) and interactions (I:TP and I:FP), separately. For the proposed approach and GEL, we also consider the true positives and false positives (N:TP and N:FP) for identifying networks. Estimation performance is assessed using the root sum of squared errors (RSSE) defined as ${\Vert {\widehat{\beta }}_{\mathcal{M}}-{\beta }_{\mathcal{M}}^0\Vert }_2$ and ${\Vert {\widehat{\beta }}_{\mathcal{I}}-{\beta }_{\mathcal{I}}^0\Vert }_2$ for main effects and interactions, respectively, where $\left({\widehat{\beta }}_{\mathcal{M}},{\widehat{\beta }}_{\mathcal{I}}\right)$ and $\left({\beta }_{\mathcal{M}}^0,{\beta }_{\mathcal{I}}^0\right)$ are the estimated and true values of coefficients, respectively. For prediction evaluation, we adopt the prediction median-squared error (PMSE) based on independent testing data with 100 subjects.

Under each scenario, we simulate 100 replications. Summary results for the scenarios with ρ = 0.4 and K = 100 are presented in Table 1 $\left(r=1/\sqrt{5}\right)$ and Table 2 $\left(r=1/\sqrt{12}\right)$, respectively. The rest of the results are provided in Section S2 of the Supporting Information. It is observed that across the whole spectrum of simulation, the proposed approach has superior or similar performance compared to the alternatives with respect to both selection and prediction accuracy. It is able to identify the majority of true positives, while having much fewer false positives. For instance, under the scenario with setting S4 in Table 1, the proposed approach has (M:TP, M:FP, I:TP, I:FP) = (17.94, 2.10, 13.37, 15.10), compared to (15.88, 2.30, 0.10, 0.10) for triBayes, (15.72, 4.06, 7.48, 4.82) for glinternet, (6.68, 0.00, 3.62, 7.88) for Lasso, (12.32, 43.94, 3.80, 38.28) for iFORM, (13.30, 1.10, 6.50, 9.78) for HierNet, (9.50, 0.20, 4.82, 11.42) for Grace, and (17.22, 8.98, 11.78, 98.98) for GEL. Under the scenarios in Table 2 with a lower signal level $\left(r=1/\sqrt{12}\right)$, advantages of the proposed approach become more prominent, especially under setting S4, where the important interactions have main effects with weaker signals. Specifically, the proposed approach has (M:TP, M:FP, I:TP, I:FP) = (16.71, 1.06, 9.15, 8.52), compared to (13.24, 0.42, 0.00, 0.00) for triBayes, (12.90, 1.98, 3.68, 2.84) for glinternet, (5.16, 0.00, 2.38,5.44) for Lasso, (10.12, 46.70, 1.22, 39.96) for iFORM, (9.10, 0.36, 2.78, 5.42) for HierNet, (6.94, 0.12, 2.86, 7.78) for Grace, and (16.56, 7.50, 10.76, 83.72) for GEL. The proposed approach also performs well in estimation. For example, under setting S1 in Table 1, the proposed approach has (M:RSSE, I:RSSE)=(0.35, 0.45), compared to (1.33, 1.35) for triBayes, (0.96, 1.02) for glinternet, (1.48, 1.19) for Lasso, (1.35, 1.32) for iFORM, (1.23, 1.32) for HierNet, (1.46, 1.20) for Grace, and (0.76, 1.93) for GEL. In addition, the proposed approach has higher prediction accuracy. For example, under setting S2 in Table 2, the PMSEs are 0.65 (proposed), 3.22 (triBayes), 1.16 (glinternet), 1.68 (Lasso), 2.52 (iFORM), 1.43 (HierNet), 2.30 (Grace), and 1.67 (GEL), respectively. Furthermore, we note that the proposed approach identifies all of the important networks correctly with N:FP=0 under all scenarios. In contrast, GEL cannot effectively identify important networks (especially under setting S4 with N:TP=2.47 and N:FP=0.06) and often misidentifies networks (details omitted). Glinternet generally has the second best performance. Under some scenarios with a higher within network correlation (ρ = 0.6) and simpler signal patterns (S1 and S2), it behaves competitively in main-effect identification. However, the proposed approach can maintain its superiority in interaction identification, estimation, and prediction. With a larger network size (p_k = 20, K = 50), the proposed approach is again observed to perform favorably.

TABLE 1.

Simulation results under the scenarios with ρ = 0.4, K = 100, and $r=1/\sqrt{5}$. In each cell, mean (SD) based on 100 replicates.

Approach	M:TP	M:FP	M:RSSE	I:TP	I:FP	I:RSSE	PMSE
S1
proposed	17.86(0.35)	2.06(1.06)	0.35(0.10)	16.90(0.30)	9.44(3.64)	0.45(0.09)	0.55(0.10)
triBayes	16.26(1.56)	9.30(1.97)	1.33(0.38)	5.64(3.21)	2.82(1.99)	1.35(0.15)	2.52(1.16)
glinternet	17.34(1.02)	5.60(3.02)	0.96(0.13)	14.42(1.96)	4.84(3.01)	1.02(0.13)	1.51(0.54)
Lasso	8.16(2.62)	0.00(0.00)	1.48(0.10)	11.50(1.96)	14.82(6.52)	1.19(0.12)	2.32(0.71)
iFORM	16.58(1.96)	37.38(4.26)	1.35(0.31)	12.58(3.84)	30.04(3.81)	1.32(0.34)	2.25(1.45)
HierNet	13.72(2.65)	1.00(1.43)	1.23(0.16)	8.76(2.70)	8.28(6.06)	1.32(0.12)	2.31(0.71)
Grace	9.50(2.53)	0.38(0.88)	1.46(0.13)	12.00(1.73)	7.02(7.08)	1.20(0.09)	2.26(0.59)
GEL	17.76(1.17)	9.14(4.90)	0.76(0.16)	12.70(1.47)	104.60(53.00)	1.93(0.51)	1.81(0.74)
S2
proposed	17.30(0.79)	1.77(1.41)	0.43(0.13)	16.57(0.68)	8.17(3.56)	0.52(0.12)	0.69(0.18)
triBayes	15.82(1.30)	4.92(2.81)	1.81(0.25)	0.70(2.08)	0.26(0.85)	1.63(0.08)	4.51(1.28)
glinternet	17.20(1.03)	5.68(3.62)	0.98(0.12)	14.36(1.70)	4.50(2.31)	1.06(0.13)	1.48(0.44)
Lasso	6.48(2.76)	0.20(0.64)	1.49(0.09)	7.86(3.51)	50.80(103.98)	1.44(0.10)	2.91(0.71)
iFORM	15.52(2.76)	38.92(4.81)	1.49(0.43)	11.76(4.52)	30.56(4.12)	1.44(0.42)	2.28(1.17)
HierNet	12.42(3.94)	1.26(1.58)	1.28(0.19)	8.62(2.80)	8.04(5.97)	1.39(0.13)	2.15(0.71)
Grace	5.52(1.61)	0.20(0.49)	1.73(0.05)	4.88(1.38)	7.62(6.81)	1.50(0.05)	3.49(0.95)
GEL	17.78(1.09)	11.30(2.53)	0.78(0.16)	13.08(0.72)	127.00(34.46)	2.06(0.34)	1.86(0.56)
S3
proposed	17.63(0.56)	1.19(1.10)	0.57(0.10)	15.04(1.37)	8.87(4.35)	0.77(0.13)	0.70(0.21)
triBayes	12.60(2.19)	3.96(2.16)	2.01(0.29)	0.00(0.00)	0.00(0.00)	1.57(0.23)	3.68(0.96)
glinternet	13.78(2.12)	3.58(2.82)	1.35(0.15)	7.56(2.29)	2.26(1.79)	1.37(0.10)	1.99(0.54)
Lasso	6.74(2.14)	0.04(0.20)	1.73(0.13)	7.18(2.11)	7.18(4.05)	1.37(0.08)	2.47(0.72)
iFORM	16.04(2.45)	38.16(4.80)	1.44(0.40)	10.84(4.33)	31.98(3.71)	1.45(0.36)	2.35(1.16)
HierNet	10.36(2.05)	0.70(0.86)	1.48(0.12)	5.72(1.87)	5.68(3.68)	1.42(0.08)	2.21(0.66)
Grace	8.98(1.39)	0.20(0.40)	1.55(0.11)	10.08(1.41)	12.30(12.17)	1.28(0.08)	2.08(0.51)
GEL	17.88(0.63)	11.80(2.56)	0.77(0.15)	12.54(0.81)	134.22(25.84)	2.13(0.30)	1.93(0.57)
S4
proposed	17.94(0.24)	2.10(1.12)	0.37(0.07)	13.37(2.17)	15.10(3.98)	0.92(0.20)	0.77(0.20)
triBayes	15.88(1.21)	2.30(1.93)	1.93(0.14)	0.10(0.71)	0.10(0.71)	1.60(0.03)	4.48(1.25)
glinternet	15.72(2.38)	4.06(3.13)	1.06(0.18)	7.48(3.21)	4.82(2.55)	1.44(0.09)	1.83(0.52)
Lasso	6.68(2.17)	0.00(0.00)	1.52(0.08)	3.62(2.28)	7.88(4.98)	1.54(0.07)	2.64(0.84)
iFORM	12.32(3.15)	43.94(5.57)	2.23(0.58)	3.80(4.55)	38.28(3.77)	2.17(0.41)	4.63(2.16)
HierNet	13.30(2.87)	1.10(1.45)	1.22(0.18)	6.50(2.88)	9.78(5.33)	1.62(0.13)	1.92(0.55)
Grace	9.50(2.46)	0.20(0.64)	1.45(0.13)	4.82(2.53)	11.42(8.43)	1.59(0.07)	2.35(0.73)
GEL	17.22(1.89)	8.98(4.75)	0.81(0.19)	11.78(2.39)	98.98(59.10)	1.90(0.51)	1.85(0.66)

TABLE 2.

Simulation results under the scenarios with ρ = 0.4, K = 100, and $r=1/\sqrt{12}$. In each cell, mean (SD) based on 100 replicates.

Approach	M:TP	M:FP	M:RSSE	I:TP	I:FP	I:RSSE	PMSE
S1
proposed	16.92(0.85)	0.68(0.82)	0.42(0.08)	15.70(1.30)	3.44(2.17)	0.40(0.11)	0.60(0.15)
triBayes	13.06(1.72)	2.20(1.96)	1.63(0.17)	0.42(1.69)	0.20(0.81)	1.02(0.05)	2.83(0.78)
glinternet	15.16(2.68)	3.46(2.88)	0.74(0.09)	11.52(2.64)	2.46(2.11)	0.78(0.07)	1.14(0.33)
Lasso	5.84(1.91)	0.00(0.00)	1.02(0.06)	9.14(2.30)	11.12(5.36)	0.84(0.07)	1.46(0.41)
iFORM	11.42(2.12)	44.50(3.45)	1.59(0.19)	5.40(2.17)	34.80(3.36)	1.38(0.12)	2.57(0.79)
HierNet	10.08(2.56)	0.30(0.46)	0.92(0.08)	5.96(2.13)	5.08(3.70)	0.93(0.06)	1.48(0.35)
Grace	7.06(2.05)	0.26(0.66)	1.01(0.08)	10.10(1.96)	5.92(5.60)	0.82(0.06)	1.49(0.44)
GEL	17.32(1.42)	8.22(5.16)	0.69(0.12)	11.88(1.75)	92.68(60.45)	1.56(0.59)	1.45(0.60)
S2
proposed	15.92(1.54)	0.82(0.98)	0.46(0.09)	15.10(1.62)	3.40(2.36)	0.46(0.12)	0.65(0.19)
triBayes	12.16(1.49)	0.38(0.57)	1.62(0.02)	0.00(0.00)	0.00(0.00)	1.07(0.00)	3.22(0.80)
glinternet	14.40(3.28)	3.66(2.85)	0.74(0.12)	10.88(3.56)	2.68(2.14)	0.81(0.10)	1.16(0.36)
Lasso	5.08(1.87)	0.12(0.48)	1.00(0.06)	5.58(2.65)	40.72(95.41)	0.98(0.07)	1.68(0.40)
iFORM	11.02(2.30)	44.94(4.67)	1.62(0.23)	4.74(2.14)	35.94(4.01)	1.43(0.13)	2.52(0.84)
HierNet	8.82(2.81)	0.40(0.76)	0.92(0.07)	5.92(2.27)	4.72(3.30)	0.96(0.07)	1.43(0.39)
Grace	4.06(1.04)	0.14(0.40)	1.34(0.03)	3.78(1.36)	5.48(5.59)	1.00(0.03)	2.30(0.61)
GEL	17.32(1.80)	10.50(3.90)	0.74(0.13)	12.50(1.20)	120.58(45.24)	1.82(0.45)	1.67(0.52)
S3
proposed	16.17(1.44)	0.97(1.27)	0.58(0.08)	12.10(1.97)	4.83(3.70)	0.66(0.09)	0.69(0.18)
triBayes	10.48(1.39)	0.66(0.66)	1.73(0.01)	0.00(0.00)	0.00(0.00)	1.03(0.00)	2.43(0.55)
glinternet	10.64(2.46)	1.88(1.78)	1.00(0.09)	4.86(2.29)	0.88(1.33)	0.94(0.05)	1.30(0.29)
Lasso	5.32(1.56)	0.00(0.00)	1.21(0.10)	5.34(1.76)	5.86(3.84)	0.93(0.04)	1.51(0.40)
iFORM	11.54(2.32)	45.16(3.79)	1.56(0.18)	3.92(2.25)	36.58(3.41)	1.39(0.10)	2.50(0.76)
HierNet	8.38(2.02)	0.44(0.73)	1.06(0.08)	3.98(2.05)	4.22(3.60)	0.96(0.05)	1.38(0.36)
Grace	7.22(1.56)	0.16(0.37)	1.13(0.09)	8.02(1.32)	8.56(9.30)	0.87(0.04)	1.35(0.35)
GEL	17.62(1.58)	11.40(2.67)	0.73(0.12)	11.76(1.49)	131.62(31.37)	1.91(0.30)	1.68(0.47)
S4
proposed	16.71(1.18)	1.06(1.06)	0.46(0.09)	9.15(2.44)	8.52(3.40)	0.83(0.11)	0.77(0.21)
triBayes	13.24(1.46)	0.42(0.54)	1.67(0.02)	0.00(0.00)	0.00(0.00)	1.03(0.00)	3.12(0.81)
glinternet	12.90(2.87)	1.98(2.26)	0.82(0.09)	3.68(2.11)	2.84(2.18)	0.98(0.04)	1.19(0.20)
Lasso	5.16(1.48)	0.00(0.00)	1.02(0.05)	2.38(1.70)	5.44(3.72)	1.01(0.03)	1.47(0.33)
iFORM	10.12(1.89)	46.70(3.32)	1.88(0.19)	1.22(1.45)	39.96(3.36)	1.65(0.12)	3.11(0.82)
HierNet	9.10(2.60)	0.36(0.53)	0.93(0.09)	2.78(1.82)	5.42(3.94)	1.08(0.08)	1.31(0.36)
Grace	6.94(1.91)	0.12(0.48)	1.00(0.06)	2.86(1.93)	7.78(7.08)	1.03(0.04)	1.49(0.35)
GEL	16.56(2.51)	7.50(5.41)	0.71(0.13)	10.76(2.50)	83.72(65.78)	1.51(0.61)	1.39(0.49)

To mimic scenarios under which a genetic factor is involved in multiple networks, we conduct additional simulations with K = 100. Among the 1,000 genetic factors, there are 100 each of which is involved in 2 to 6 networks. Summary results are provided in Tables S9–S12 (Section S2 of the Supporting Information). It is similarly observed that the proposed approach has advantages over the alternatives. In addition, in Tables S13–S16, we examine performance of the proposed approach with various values of n and p. The scenarios with ρ = 0.4, K = 100, and $r=1/\sqrt{5}$ are considered. As expected, all approaches have better performance with a larger sample size and a smaller number of genetic factors. Under these scenarios, the proposed approach again has superior performance compared to the alternatives.

4 |. DATA ANALYSIS

We analyze The Cancer Genome Atlas (TCGA) data on cutaneous melanoma (SKCM) and lung adenocarcinoma (LUAD). As one of the largest cancer genetics programs, TCGA is unique and highly valuable. We consider mRNA gene expression measurements which are downloaded using R package cgdsr. Networks are constructed using information from KEGG.^17,20 Specifically, we follow Gao et al.¹⁷ and obtain network structures from KEGG database using R package KEGGgraph, where each pathway is presented as a network with nodes being molecules (protein, compound, etc.) and edges representing relation types (e.g. activation or phosphorylation).³¹ We set $A_k^{(1)}(j,l)=A_k^{(1)}(l,j)=1$ if the jth and lth genes are connected in the pathway and 0 otherwise.

4.1 |. Cutaneous melanoma (SKCM) data

The response of interest is the (log-transformed) Breslow’s thickness, which is a measure of melanoma growth and has been widely used in the assessment of melanoma. Data are available on 361 subjects and 19,904 gene expression measurements. Although the proposed approach is potentially applicable to a large number of genes, with the consideration that the number of cancer-related genes is not large, as well as to improve stability, a marginal screening is conducted. Specifically, the top 2,000 genes with the smallest p-values computed from marginal linear regression model are selected. Matching with KEGG results in 578 distinct genes and 173 networks, and a network contains on average 8.70 genes.

16 distinct main effects and 34 distinct interactions are identified by the proposed approach (25 main effects and 66 interactions before removing duplicates). The identified genes, their interactions, as well as networks are shown in Figure 2, where two genes are connected if the corresponding interaction is also selected. The detailed estimation results are provided in Table S17 of the Supporting Information. Literature search suggests that the identified genes may be of high significance. For example, it has been found that the higher expression of gene PMM2 is associated with a poorer prognosis in melanoma.³² Gene FBP1, which is involved in three identified networks, has been shown to be significantly down-regulated in human melanoma cells.³³ The expression of gene PCK2 has been found to be down-regulated in melanoma regenerative cells and closely related to the survival of tumor patients.³⁴ Published studies have reported that gene PFKFB4, a known regulator of glycolysis, displays an unconventional role in melanoma cell migration and has increased expression levels in several human tumors including cutaneous melanoma.³⁵ The simultaneous inactivation of genes HK1 and HK2 has been demonstrated to be sufficient to decrease the proliferation and viability of melanoma.³⁶ In addition, gene PMM1 has been identified in published studies as regulated in human melanoma and melanoma-associated pathways.³⁷

FIGURE 2.

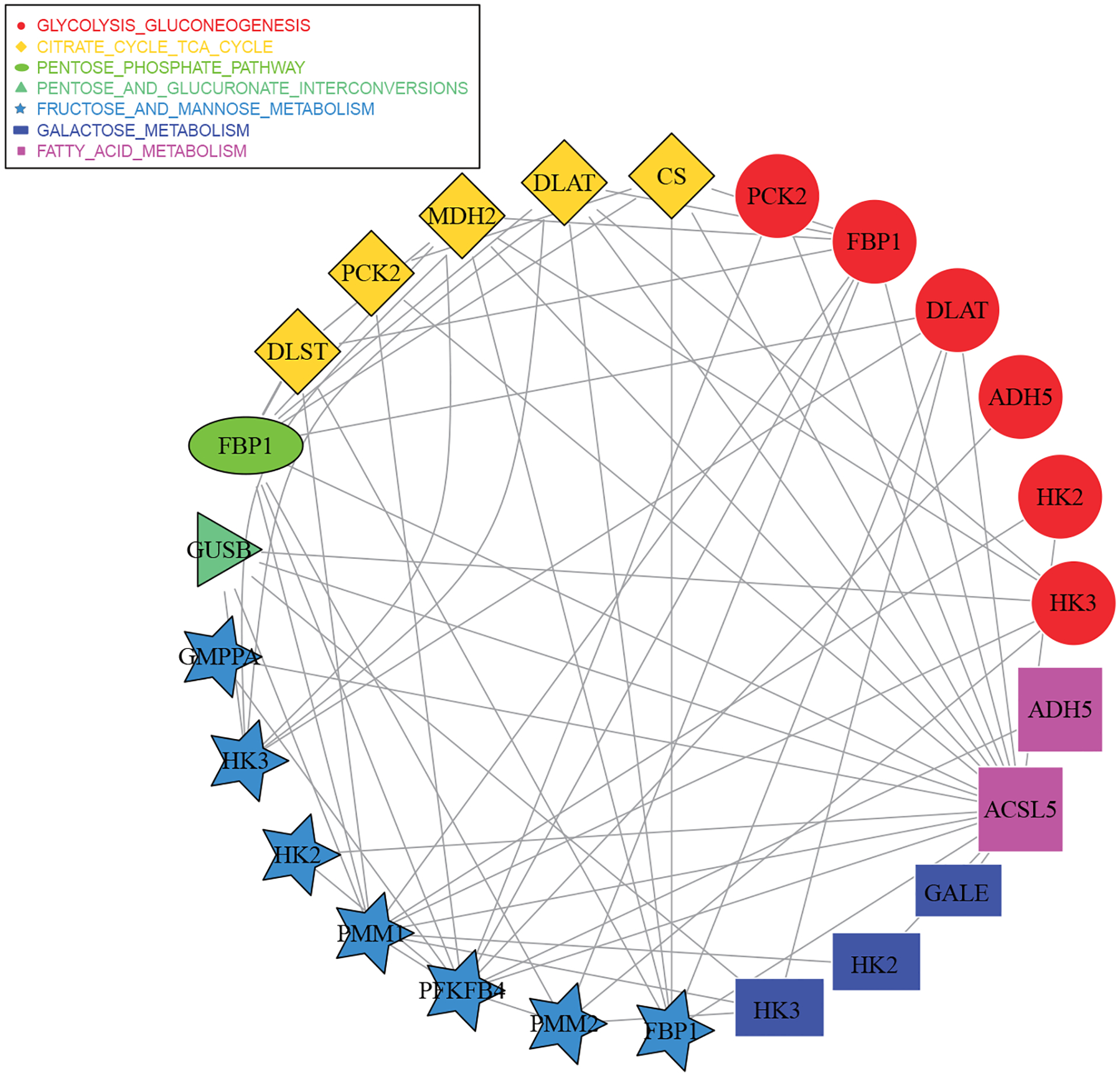
Analysis of the TCGA SKCM data using the proposed approach: identified main genetic effects, interactions, and networks. Genes in different networks are represented by different shapes, and two genes are connected if the corresponding interaction is also selected.

The proposed approach identifies seven networks, all of which are metabolics related and have important biological implications. For example, citrate cycle (TCA cycle) has been suggested to be significantly down-regulated, while galactose metabolism is up-regulated in tumor formation and progression.³⁸ Other interesting networks have been associated with the development, progression, and outcome of melanoma. For instance, fatty acid metabolism has been shown to be essential for cancer cell proliferation.³⁹ Glycolysis has been confirmed to play a significant role in developing metabolic symbiosis in metastatic melanoma progression.⁴⁰ In addition, pentose phosphate has been found to be critical for cancer cell survival and ribonucleotide as well as lipid biosynthesis.⁴¹

We also conduct analysis using the alternatives. Summary comparison results are presented in Table 3, where the numbers of main effects and interactions identified by different approaches, their overlaps, and RV coefficients are provided. Here RV coefficient describes the similarity of two matrices, and a larger value indicates a higher similarity. Different approaches are observed to identify quite different sets of main effects and interactions, and have moderate similarity as suggested by the RV coefficients. In particular, it is observed that triBayes, the most direct competitor of the proposed approach that does not incorporate network information, identifies a moderate number of variables significantly different from the proposed. Lasso, Grace, and GEL, which do not respect the “main effects-interactions” hierarchy, identify a larger number of interactions than main effects. The other four approaches that respect the “main effects-interactions” hierarchy, including the proposed one, select a moderate number of main effects and interactions.

TABLE 3.

Data analysis: numbers of main effects and interactions (diagonal elements) identified by different approaches, and their overlaps and RV coefficients (off-diagonal elements).

SKCM
		proposed	triBayes	glinternet	Lasso	iFORM	HierNet	Grace	GEL
Main	proposed	16	0(0.36)	0(0.27)	0(0.03)	0(0.42)	0(0.40)	0(0.23)	0(0.34)
	triBayes		69	12(0.63)	1(0.15)	19(0.74)	19(0.72)	0(0.18)	2(0.54)
	glinternet			15	1(0.22)	5(0.58)	10(0.62)	0(0.11)	0(0.41)
	Lasso				1	1(0.12)	0(0.03)	0(0.00)	0(0.02)
	iFORM					51	8(0.72)	0(0.19)	1(0.67)
	HierNet						51	1(0.33)	1(0.59)
	Grace							1	0(0.13)
	GEL								28
Interaction	proposed	34	0(0.01)	0(0.02)	0(0.00)	0(0.08)	0(0.00)	0(0.01)	0(0.11)
	triBayes		7	0(0.04)	0(0.11)	0(0.02)	0(0.01)	0(0.00)	0(0.02)
	glinternet			9	6(0.59)	1(0.08)	1(0.40)	0(0.00)	0(0.01)
	Lasso				20	2(0.08)	0(0.08)	0(0.01)	0(0.02)
	iFORM					44	0(0.16)	0(0.01)	1(0.10)
	HierNet						2	0(0.00)	0(0.00)
	Grace							16	1(0.03)
	GEL								363
LUAD
		proposed	triBayes	glinternet	Lasso	iFORM	HierNet	Grace	GEL
Main	proposed	13	0(0.22)	1(0.37)	0(0.24)	0(0.41)	1(0.45)	0(0.00)	1(0.25)
	triBayes		4	3(0.47)	0(0.31)	2(0.43)	3(0.49)	0(0.00)	0(0.21)
	glinternet			16	1(0.49)	8(0.71)	13(0.78)	0(0.00)	0(0.33)
	Lasso				4	2(0.57)	1(0.54)	0(0.00)	0(0.31)
	iFORM					43	20(0.84)	0(0.00)	1(0.45)
	HierNet						67	0(0.00)	0(0.47)
	Grace							0	0(0.00)
	GEL								24
Interaction	proposed	38	0(0.00)	0(0.07)	0(0.13)	0(0.15)	0(0.00)	0(0.02)	0(0.12)
	triBayes		65	1(0.02)	2(0.02)	1(0.03)	0(0.00)	0(0.12)	0(0.01)
	glinternet			12	5(0.34)	0(0.00)	1(0.20)	0(0.00)	0(0.03)
	Lasso				253	4(0.12)	3(0.22)	0(0.01)	2(0.16)
	iFORM					53	1(0.02)	0(0.00)	0(0.06)
	HierNet						13	0(0.00)	0(0.02)
	Grace							17	1(0.03)
	GEL								269

We further use a resampling approach to examine prediction performance and selection stability. The subjects are randomly partitioned into a training and a testing set. The mean PMSEs for the testing subjects over 100 resamplings are 0.57 (proposed), 0.74 (triBayes), 0.60 (glinternet), 0.60 (Lasso), 1.16 (iFORM), 0.57 (HierNet), 0.64 (Grace), and 6.32 (GEL), suggesting satisfactory prediction accuracy of the proposed approach. To evaluate selection stability, for each of the important main effects and interactions, we compute its observed occurrence index (OOI), which is the selection frequency in 100 resamplings. The proposed approach has a mean OOI value of 0.98, compared to 0.21 (triBayes), 0.07 (glinternet), 0.28 (Lasso), 0.15 (iFORM), 0.62 (HierNet), 0.78 (Grace), and 0.50 (GEL). The prediction and stability analysis provides a certain degree of confidence to the proposed analysis.

4.2 |. Lung adenocarcinoma (LUAD) data

The response of interest is the reference value for the pre-bronchodilator forced expiratory volume in one second in percent (FEV1). It is a major indicator of pulmonary function impairment. Data are available on 232 subjects and 18,325 gene expression measurements. We conduct a prescreening, and 499 distinct genes and 181 networks (a network contains on average 7.51 genes) are obtained for downstream analysis..

With the proposed approach, 13 main effects and 38 interactions (all distinct) are identified and presented in Figure 3. The detailed estimation results are provided in Table S18 of the Supporting Information. Strong evidences of their important biological implications have been reported in the literature. For example, the ALDH2 locus has been associated with a higher risk of lung cancer among light smokers.⁴² Activated ACLY has been suggested as a negative prognostic factor in LUAD. Significantly higher ACSS2 expressions have been observed in a substantial number of lung tumor samples.⁴³ Published studies have suggested that late-stage LUAD patients have higher expression levels of HK2 and GBE1 than early-stage ones.⁴⁴ Also, the expressions of PCK1 or PCK2 may be important for the growth of lung cancer due to the high demand for anabolic metabolism and frequently insufficient supply.⁴⁵ In addition, the over-expression of PGAM1 has been observed in multiple human cancer types including lung cancer.⁴⁶

FIGURE 3.

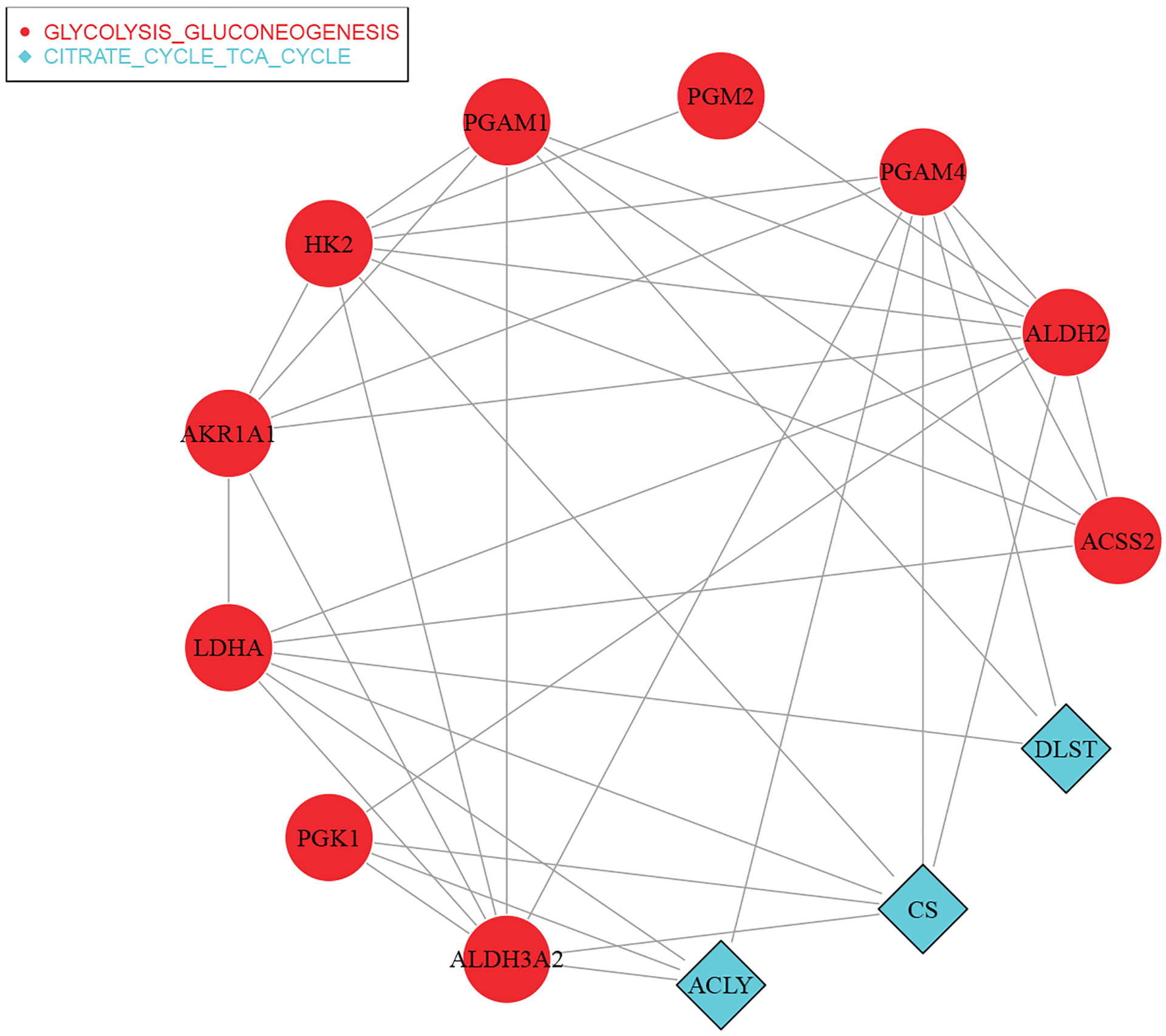
Analysis of the TCGA LUAD data using the proposed approach: identified main genetic effects, interactions, and networks. Genes in different networks are represented by different shapes, and two genes are connected if the corresponding interaction is also selected.

The proposed approach identifies two networks, which have been shown to have associations with lung cancer. As a reverse glycolysis pathway, gluconeogenesis can generate glucose from small carbohydrate precursors, which is crucial for the growth of tumor cells.^47,48 Experiments on genetically engineered lung and pancreatic cancer tumors in mice have shown that the TCA cycle is highly affected by glucose metabolism, resulting in high intra-tumor and inter-tumor variability.^49,50

We also conduct analysis using the alternatives and summarize the comparison results in Table 3. Similar to for the SKCM data, different approaches lead to identification results with low overlapping. Prediction performance and selection stability are examined based on 100 resamplings. The mean (PMSE, OOI) values are (0.05, 0.98) for the proposed approach, (0.04, 0.56) for triBayes, (0.05, 0.68) for glinternet, (0.06, 0.33) for Lasso, (0.22, 0.12) for iFORM, (0.04, 0.08) for HierNet, (0.04, 0.19) for Grace, and (0.73, 0.13) for GEL. The proposed approach again has competitive prediction accuracy and superior selection stability.

5 |. DISCUSSION

In the study of complex diseases, gene-gene interaction analysis has attracted extensive attention. Biological networks have been accumulated, containing information on functionally related genetic groups and within-group structures. Incorporating network information can potentially lead to a deeper biological understanding of phenotypes from a system perspective. In this study, we have developed a new gene-gene interaction analysis, where network information is incorporated. It advances from the existing interaction analyses by taking advantage of network selection, where the “main effects-interactions” hierarchy and “main effects/interactions-networks” hierarchy are respected. In addition, motivated by the importance of link networks for interactions, the graph Laplacian Gaussian prior has been adopted to accommodate the underlying network structures of not only main effects but also interactions. It has been established that under certain regularization conditions, the graph Laplacian Gaussian prior has posterior consistency with a diverging number of nodes and edges.¹⁸ The proposed approach may enjoy broad applicability, and the networks can be sparse or dense. The spike and slab priors for the regression coefficients and conjugate priors for the other parameters have been adopted, which offers the advantage of computational simplification.^26,28 The proposed approach can be formulated as a hybrid Bayesian model, with a solid statistical foundation and the potential to be effectively realized using the variational Bayesian expectation-maximization algorithm. This significantly advances from the published Bayesian interaction analyses that usually adopt MCMC techniques, which have very low computational efficiency. Extensive simulation studies have been conducted, suggesting the practical superiority of the proposed approach in identification, estimation, and prediction. Two TCGA datasets have been used to illustrate application, leading to biologically sensible findings with satisfactory prediction accuracy and selection stability. High stability of the proposed approach can be partly attributable to the consideration of network information.

This study has focused on continuous response and assumed the Gaussian distribution. It can be of interest to extend to handle categorical and censored outcomes. For example, a data augmentation approach based on a probit model for categorical outcome or an accelerated failure time model for censored outcome can be potentially adopted.¹³ However, our preliminary investigation suggests that this extension is nontrivial and warrants a separate work. The strong “main effects-interactions” hierarchy has been explored in this study, which is popular in recent interaction analyses.^6,8 Modification can be made to prior (2) to respect the weak hierarchy. Based on the estimated posterior expectations of the selection indicators, the thresholding approach has been adopted to select important variables. Our numerical investigation has suggested that the estimated values of E(α_k)’s and E(γ_j)’s are close to either 1 or 0. Thus, the value of threshold is not very important. Other approaches, such as the false discovery rate-based, can also be considered for inference. In our study, we have considered the adjacency matrices consisting of either 1 or 0, which has been popular in existing network analysis studies. Other adjacency measures, such as the continuous similarity-based measure, can also be adopted. The duplication strategy has been adopted to accommodate overlappings in networks,^20,51 where we take regression coefficients of main effects (interactions) involved in multiple networks as separate model parameters. As a result, if a main effect (interaction) is selected, our model does not force all the networks this main effect (interaction) is affiliated with to be selected. We note that when networks have high overlapping, the proposed analysis may not be stable. However, in practical data analysis with moderate overlapping, such as the SKCM data where some genes are involved in 30 to 50 networks, the proposed approach has been found to be satisfactory. More prudent strategies are deferred to further investigation. In data analysis, we have utilized KEGG to construct networks. Other information sources, such as Gene Ontology terms and protein-protein interaction networks, can also be adopted. Significantly different identifications across approaches have been observed in data analysis, which is not uncommon in published studies.^52,53 This may due to many reasons, including the complex correlation patterns, low signal-to-noise ratio, small sample size, and others. It is noted that many genes identified by the proposed approach have been independently identified. Others still need critical biological examinations.

DATA AVAILABILITY STATEMENT

The data that support the findings in this paper are openly available in TCGA (The Cancer Genome Atlas) at https://portal.gdc.cancer.gov/.