Abstract
Skin wounds are among the most common and costly medical problems experienced. Despite the myriad of treatment options, such wounds continue to lead to displeasing cosmetic outcomes and also carry a high burden of loss-of-function, scarring, contraction, or nonhealing. As a result, the need exists for new therapeutic options that rapidly and reliably restore skin cosmesis and function. Here we present a new mechanobiological computational model to further the design and evaluation of next-generation regenerative dermal scaffolds fabricated from polymerizable collagen. A Bayesian framework, along with microstructure and mechanical property data from engineered dermal scaffolds and autograft skin, were used to calibrate constitutive models for collagen density, fiber alignment and dispersion, and stiffness. A chemo-biomechanical finite element model including collagen, cells, and representative cytokine signaling was adapted to simulate no-fill, dermal scaffold, and autograft skin outcomes observed in a preclinical animal model of full-thickness skin wounds, with a focus on permanent contraction, collagen realignment, and cellularization. Finite element model simulations demonstrated wound cellularization and contraction behavior that was similar to that observed experimentally. A sensitivity analysis suggested collagen fiber stiffness and density are important scaffold design features for predictably controlling wound contraction. Finally, prospective simulations indicated that scaffolds with increased fiber dispersion (isotropy) exhibited reduced and more uniform wound contraction while supporting cell infiltration. By capturing the link between multi-scale scaffold biomechanics and cell-scaffold mechanochemical interactions, simulated healing outcomes aligned well with preclinical animal model data.
Keywords: type I oligomeric collagen, skin wound healing, engineered dermal scaffolds, finite element analysis, growth and remodeling
Graphical Abstract
1. Introduction
Skin wounds, especially those that are large and impact multiple tissue layers, remain a major burden to those that they affect as well as our healthcare system [1]. Because these tissue defects supersede the bodys natural healing capacity, normal skin anatomy and functional integrity is not restored in an orderly and timely fashion. This, in turn, leads to consequences such as long healing times, pain, infection, scarring, and loss of mobility and function owing to contraction [2]. While numerous options exist for managing such wounds, including bioactive scaffolds, negative pressure wound therapy (wound vacs), or surgical reconstruction with autologous tissue grafts, tissue restoration outcomes in terms of appearance and function are highly variable and difficult to predict. In fact, a primary shortcoming of present-day wound care products is the reliance on the bodys cells to deposit and remodel the necessary tissue collagen scaffolding, a capacity which is obviously limited. Further, conventional implantable materials exhibit inflammatory-mediated foreign body responses and/or degradation, which further compromises healing outcomes [3]. Common challenges associated with surgical reconstruction include limited tissue supply and donor site morbidity. In addition, post-surgical complications, including infection, necrosis, scarring, and contraction, are frequent and contribute to patient debilitation, increased healthcare costs, and overall patient and physician dissatisfaction [4]. Therefore, it is not surprising that one of the grand challenges in medicine has been the development of new tissue regeneration strategies, with the goal of restoring, as closely as possible, original tissue structure, function, and aesthetics.
Fundamentally, cutaneous wound healing is characterized by four overlapping phases: hemostasis, inflammation, proliferation, and remodeling, with the duration of each phase varying based on wound etiology, severity, and presence of co-morbidities. This process is multi-scale in nature, involving molecules, cells, and structural tissue constituents [5] In absence of a tissue graft or implantable biomaterial, the body first forms a blood clot, where platelets are entrapped within an initial fibrin scaffold. While this initial fibrin scaffold is lacking in mechanical integrity, it helps stop bleeding and promotes inflammation. Platelet degranulation signals the influx of inflammatory mediators, which are responsible for eliminating pathogens and tissue debris and attracting key contributors of the proliferative phase, namely fibroblasts and endothelial cells. Primary events of the proliferative phase, where the goal is to fill the tissue void, include vascularization and synthesis and deposition of a fibrillar collagen scaffold. While the newly developed collagen scaffold improves the mechanical integrity of the wound, it is largely disorganized and subject to contraction and scar formation over time [6].
The collagen scaffold of the dermis is a vital determinant of skin structure and function. Additionally, this scaffold is a critical contributor to mechanobiological signaling. For these reasons, our skin restoration strategy has focused on defining how specific collagen microstructure features contribute to the multi-scale healing response. This effort involves the use of type I oligomeric collagen, which represents a fibril-forming (polymerizable) formulation purified from porcine dermis [7, 8]. This biopolymer, together with scalable material manufacturing methods [9], supports multi-scale design of dermal replacement scaffolds, where the total content, spatial gradient, and orientation of component collagen fibers can be controlled [10, 11]. Preclinical evaluation of three Oligomer dermal scaffolds of varied density, namely Oligomer-4, Oligomer-20, and Oligomer-40, using a rat full-thickness skin model revealed that healing outcomes, including extent of wound contraction, vascularization, and cellularization, were dependent upon an interplay of multi-scale mechanobiological design parameters [11]. For example, elastic modulus of the scaffold was critical for minimizing wound contraction, and the aligned, high density architectures reduced rates of cellularization and vascularization. This and other recent tissue restoration studies suggest that maintenance of stromal collagen and its associated mechanobiological continuum yield improved regenerative healing outcomes, including large-volume surgical voids of the breast and full-thickness laryngeal defects [12, 13].
In addition to the development of new biomaterials for improved tissue restoration, there has been increasing interest in continuum models of tissue growth and remodeling, skin biophysics, wound healing, and biomaterial mechanics [14, 15]. To accurately describe the mechanics of collagenous tissues such as skin, computational models that take into consideration the collagen microstructure have been developed [16, 17]. Given the complexity of skin physiology, the interplay of chemical and mechanical signaling of cells during healing, and the broad design space for regenerative healing strategies, integrated use of computational models can assist in i) guiding novel therapeutic approaches through improved mechanistic insight into wound healing mechanobiology, ii) reducing expensive prototyping and animal studies, and iii) informing a wide variety of patient-specific wound healing scenarios through rapid iterations.
While a number of wound healing models include coupled multiphysics components comprised of reaction-diffusion systems and mechanical aspects [18], they lack detailed descriptions of nonlinear skin mechanics, growth, and permanent remodeling. Recent work has advanced the integration of mechanoregulation of cell phenotypes into wound healing models [19]. Wounds and surrounding skin exhibit nonlinear mechanical response, undergo large deformations, and show permanent remodeling of scaffold architecture in response to cellular activity. However, despite wound contracture and collagen architecture being important metrics to assess scar formation, computational models that can describe these features of wound healing are lacking. To bridge this gap, we previously developed a model which incorporates cell-scaffold mechanobiology and a finite growth framework for plastic remodeling [20, 21, 22]. In addition, while some authors have collected experimental mechanics data to calibrate the constitutive laws of skin mechanics [17, 23], the complete integration of architectural and mechanical information with experimental wound healing data is missing. Finally, computational models of wound healing have yet to be applied to inform the design of dermal replacement scaffolds.
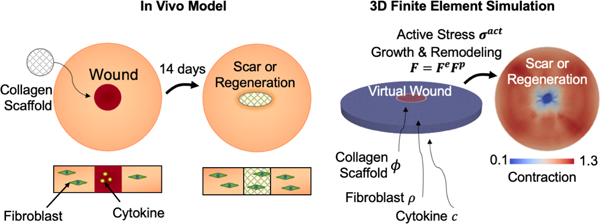
In this study, we extended our prior computational model [21, 22, 24] of wound healing, integrating experimental data relevant to Oligomer dermal scaffold design and preclinical evaluation. This model is able to simulate no-fill control, rat skin autograft, and scaffold-treated wounds (Figure 1). The innovations of this model compared to our previous work and existing models are: improved mechanobiological coupling between cell behavior and collagen microstructure to match our recent longitudinal in vivo experimental results; calibration of structural and mechanical parameters to in vitro dermal scaffold and autograft skin data using a Bayesian model; and custom three-dimensional (3D) finite element implementation. Collectively, this work bridges experimental and computational tools, highlighting the increasing role of mathematical models in tissue engineering design and their potential to improve wound therapies.
Figure 1:
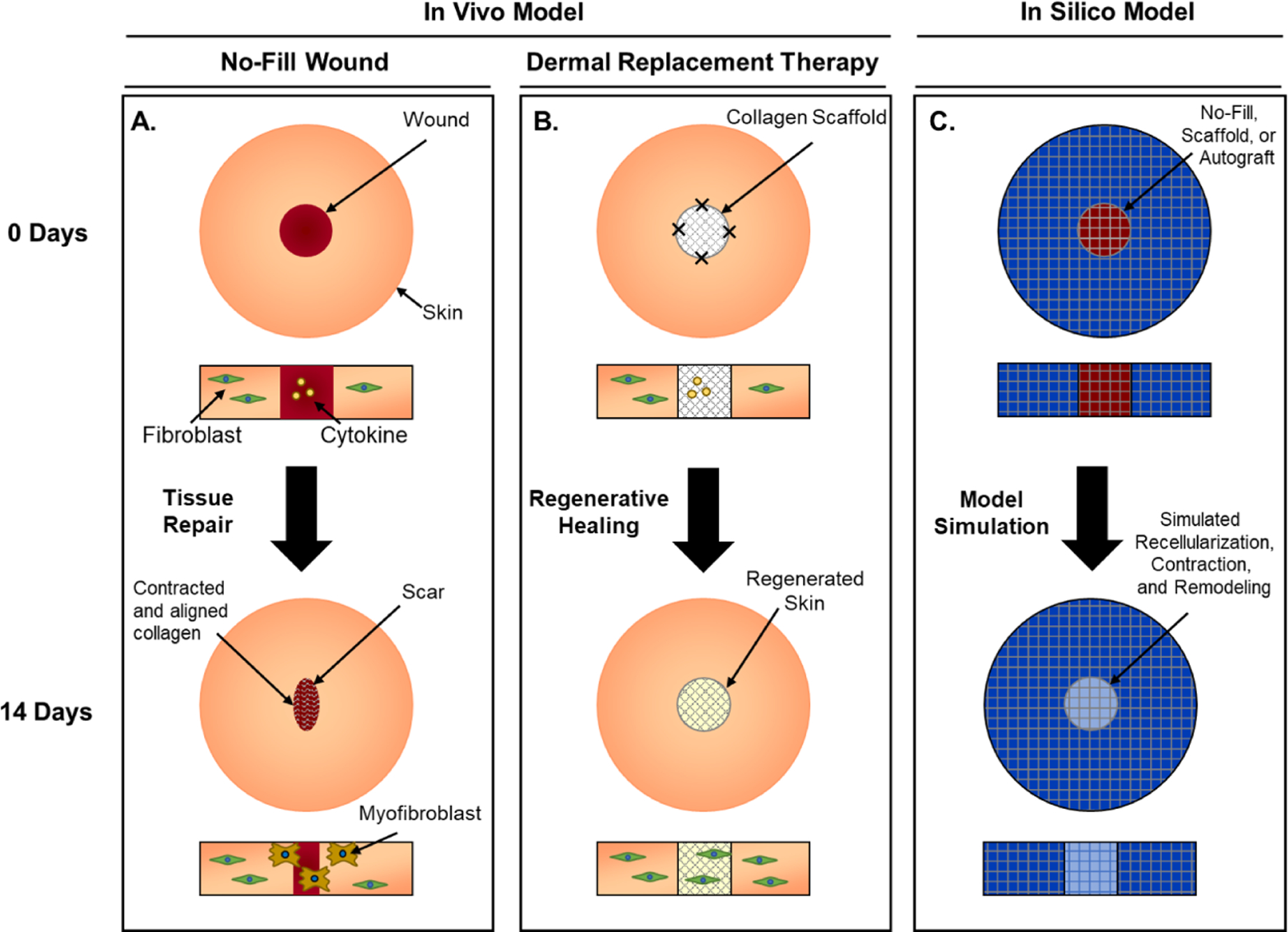
Schematic showing integration of experimental in vivo and in silico models of wound healing, supporting design and development of dermal replacement therapeutic approach. A. No-Fill treated experimental wounds exhibit significant contraction as cells migrate in and interact with the provisional matrix under the influence of chemical and mechanical signals. B. Scaffolds fabricated from polymerizable oligomeric collagen placed within the wounds provides mechanical resistance to contraction and mechanobiological signals which leads to improved regenerative healing. C. Computational model approximates the geometry and conditions of the experimental wounds. Cell, cytokine, and collagen fields are simulated to predict wound healing and contraction outcomes for different treatment conditions.
2. Materials and Methods
2.1. Custom-Fabricated Dermal Scaffolds
Collagen dermal scaffolds representing various total content and spatial gradients of collagen fibers were fabricated from type I oligomeric collagen derived from the dermis of market weight pigs as described previously [9]. In brief, neutralized Oligomer solutions (4.0 mg/mL) were pipetted into 24-well plates at specific volumes (230 μL, 1150 μL, and 2300 μL) and polymerized at 37°C. Following polymerization, wells containing 230 μL Oligomer were not further processed, yielding 4 mg/cm3 scaffolds (Oligomer-4) with a diameter of 15.6 mm and thickness of 1.2 mm to match thickness of rat dermis [25]. Wells containing 1150 μL and 2300 μL Oligomer were subjected to controlled confined compression [9] (0.1/s strain rate) to the same final thickness of 1.2 mm, yielding 20 mg/cm3 (Oligomer-20) and 40 mg/cm3 (Oligomer-40) scaffolds, respectively. All collagen dermal scaffolds were stored in sterile phosphate-buffered saline (PBS) prior to testing or surgical implantation.
2.2. Experimental Full-Thickness Rat Skin Wound Model
Experimental data derived from a previously published rat full-thickness skin wound study [11] was used for computational model calibration and validation. All animal studies were conducted according to protocols approved by the Purdue University Institutional Animal Care and Use Committee. In brief, male Sprague-Dawley rats, weighing 200 to 250 g (7 to 9 weeks of age; Charles River Laboratories, Wilmington, MA), were anesthetized using isoflurane gas. A sterile punch (15 mm diameter) was used to create two full-thickness skin wounds, including the panniculus carnosus muscle, positioned on either side of the sagittal plane of the rat dorsum. Wounds were randomly assigned to experimental treatment and control groups, with treatment groups consisting of Oligomer-4, Oligomer-20 and Oligomer-40 (n = 4–10). For a subset of animals, the excised full-thickness rat skin was applied to the opposite wound, serving as an autograft (positive control). Untreated (no-fill) wounds served as negative controls. Photographs of wound areas were taken with a ruler in the field of view at 0, 7, and 14 days. At 7-and 14-day study endpoints, animals were euthanized and wound areas and associated implants were excised in toto and processed for histopathological analysis.
2.3. Experimental Dataset
Experimental data used to calibrate and validate the computational model consisted of i) collagen density, fibrillar collagen microstructure, mechanical properties of normal rat skin (autograft control) and Oligomer scaffolds and ii) time-dependent wound contraction measured using the rat skin wound model. Further details of the dataset (black nodes in Figure 2) are given next. The microstructure images and mechanical test data of Oligomer scaffolds were collected in a previous study [11]. Wound contraction measurements correspond also to our previously published work [11]. Rat skin mechanical tests are new data with respect to our previous work.
Figure 2:
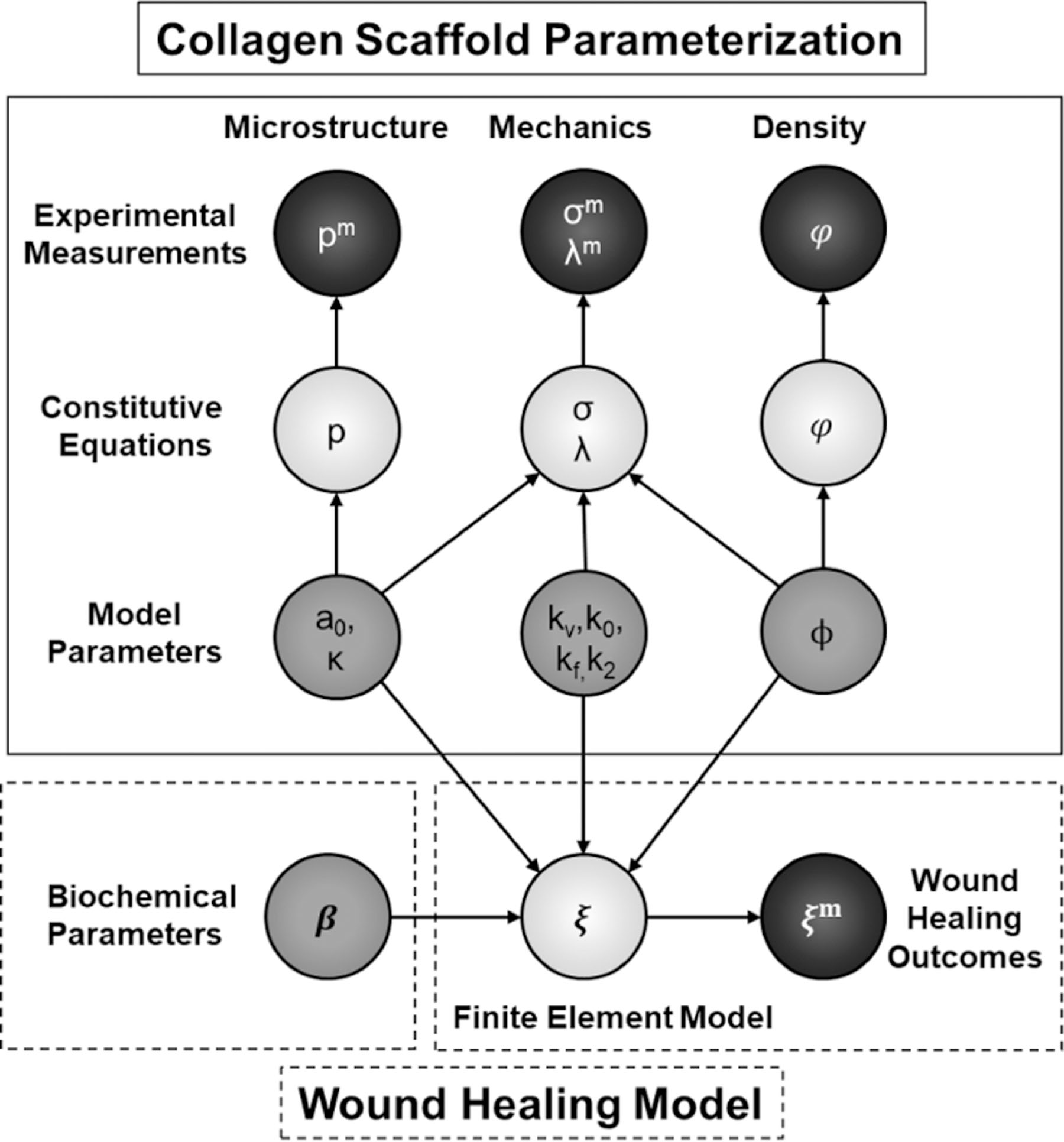
Diagram of the mathematical approach to structural parameter inference for the corresponding constitutive models (top) and implementation of the wound healing finite element model (bottom). Black, light gray, and dark gray circles represent observed experimental measurements, constitutive equations, and model parameters, respectively.
Density data ϕ:
Density of Oligomer scaffolds was calculated based on the total collagen content used for fabrication and final volume of the scaffolds after compression (n = 5 − 10 per group). The collagen density for rat skin was assumed to be on the order of 100mg/cm3 [26].
Microstructure data pm:
Microstructure analysis of Oligomer scaffolds and normal rat skin was performed via cryo-SEM using an FEI NOVA nanoSEM 200 (FEI, Hillsboro, OR) with an Everhart-Thronley detector [9]. Cryo-SEM was selected since this image modality does not require chemical fixation and/or dehydration, allowing visualization of nanoscale features of biological samples with minimal shrinkage and other artifacts [27]. Care was taken to avoid ice layers due to incomplete sublimation and disruption of the fibrillar nanostructure via excessive heat from the focused electron beam. Samples were flash-frozen by submersion into critical point liquid nitrogen, transferred to a CT1000 cold-stage attachment (Oxford Instruments North America, Inc., Concord, MA), and sublimated under vacuum. Samples were subsequently sputter coated with platinum and imaged. Images (3,000× magnification) were analyzed using FIJI/ImageJ and the directionality tool used to create the measured histograms of fiber orientation denoted pm (n = 8−12 per group). The data was smoothed using a moving average filter with a span range of 5° [28].
Mechanics data σm, λm:
Experimental stress (σm) and deformation (λm) data was obtained by performing uniaxial tensile testing in ambient air on dog-bone shaped specimens with a gauge length, width, and thickness of 4 mm, 2 mm, and 1.2 mm, respectively (n = 4 − 12 per group). The duration of mechanical testing from set up to completion was less than 10 seconds and sample dehydration was not observed. Uniaxial tests were performed to failure at a strain rate of 38.4% per second using a servo electric material testing system (TestResources, Shakopee, MN) with a 25 N load cell at a sampling rate of 100 Hz. This mechanical testing procedure has been applied previously to oligomer scaffolds [9] and rat skin [29]. Samples that failed outside the central gauge region and/or showed slippage within the grips were excluded from data analysis. The data used here consists of previous tests on collagen scaffolds [11], and new tests on rat skin.
Wound healing outcomes data ξm:
Various wound healing outcomes ξm included qualitative observations of wound recellularization and changes in collagen architecture, and quantitative measurements of wound contraction. Wound areas were traced and measured on the experimental dataset using a MATLAB (The Mathworks, Natick, MA) script and normalized to the original wound areas.
2.4. Bayesian Parameter Calibration
Given the observed data for collagen fiber density (ϕm), fiber angle probability distribution (pm), and stress/strain (σm,λm), we applied a Bayesian calibration step to determine model parameters (dark grey nodes in Figure 2) that best explain the data. The model parameters were connected to the data through constitutive equations (light grey nodes in Figure 2). Briefly, statistical models of the general form were considered, where is the data, fi(θ) are the constitutive models which depend on parameters θ, and ϵ is the experimental error. The likelihood function is the probability of observing the data given a choice of parameters. The likelihood was assumed Gaussian . In the Bayesian framework, the goal is to obtain posterior probabilities of the parameters θ of the model conditioned on the observed data using Bayes’ rule. However, instead of obtaining the posterior directly, the best strategy is to sample from the posterior without ever achieving an analytical description. To do so, a Markov chain process that samples from this posterior was created [30]. The model was coded in PyStan. Standard normal priors were used for all measured variables, and a weak exponential prior was used for standard deviations. The Hamiltonian Monte Carlo (HMC) No-U Turn (NUTS) sampler was used. Four chains were randomly initialized and run in parallel for 1000 tuned steps and 1000 samples. Specific constitutive equations and parameters are summarized below.
Density parameter ϕ:
The normalized collagen density ϕ is related to the collagen density measurements via ϕ = φ/φRS, i.e. normalized density with respect to rat skin. The parameter ϕ is also included in the constitutive model of the mechanical constitutive behavior below.
Microstructure parameters a0, κ:
The constitutive model used for the microstructure was a circular von Mises distribution for fiber orientation. The circular von Mises distribution can be characterized with two parameters, b, and a0, which represent fiber dispersion and principle direction of the distribution, respectively. Alternatively, the parameter b can be replaced by an equivalent dispersion parameter κ, which is the parameter used in the constitutive model of skin and scaffold mechanics. Additionally, the fiber direction a0 can be described with angle μa such that a0 = [cos(μa), sin(μa), 0]. Note that the fiber orientation and dispersion parameters are needed to describe the anisotropy of the tissue below. The equation for the distribution in two dimensions is
| (1) |
| (2) |
where I(b) is a modified Bessel function.
Mechanics parameters kv, k0, kf, k2:
The constitutive law for the stress as a function of deformation uses a fiber-based generalized structural tensor approach. We assumed that collagen fibers within the scaffold native tissue had similar mechanical properties, as suggested by our previous studies [9]. The fitting procedure follows [17] with a modified strain energy density with parameters kv, k0, kf, k2,
| (3) |
where Je, , are deformation-related quantities which can be derived from the stretch λ imposed in the uniaxial tests. We remark that anisotropy was taken into account through the use of the fiber orientation a0 and dispersion κ parameters, even though only uniaxial and not biaxial data was collected. The model eq. (3) also depends on collagen density ϕ. Parameters were inferred for dermal scaffolds (Oligomer-4, Oligomer-20, and Oligomer-40) and also for rat skin (autograft).
Biochemical parameters β:
The last set of parameters are associated with the finite element model of wound healing. The finite element model incorporates the microstructure, density, and mechanical parameters defined already. It additionally requires a set of biochemical parameters denoted β. One of the many outputs ξ of the finite element model is the area change , which can be compared to the measured wound area . The biochemical parameters are specified next as part of the finite element model description.
2.5. Finite Volume Growth and Remodeling Theory
The continuum finite element model that we had previously developed was modified for use in this work [22]. We applied a finite growth model with a structural tensor approach. Relevant portions of the model are described in brief below. For a full description of the original model see [21, 22].
Kinematics:
The reference geometry of the tissue, B0 is given in material coordinates X ∈ R3. The geometry, meshing, and boundary conditions are shown in Figure 3. The wound was approximated as a full-thickness 15 mm diameter cylinder within a 75 mm diameter cylindrical block of tissue. The mapping from reference to current configuration is . The biological, chemical, and material fields are given by ρ(x, t), c(x, t), and ϕ(x, t), respectively, which may represent a cell (fibroblast) population, activating cytokine, and collagen matrix. The matrix has an associated collagen density (ϕ) and orientation (κ, a0). The deformation gradient describes the local geometric change. The right Cauchy Green deformation tensor is denoted C = F T F. The multiplicative decomposition F = Fe · Fp is used to model the plastic deformation associated with growth. The superscripts e and p refer to elastic and plastic deformation, respectively. Likewise, The elastic part of the Cauchy green deformation tensor is and its invariants are , . The Jacobian can be decomposed as J = JeJp. We assumed plastic deformation (contraction) occurs primarily in the plane of the skin, so we can introduce an orthonormal basis [a0, s0, n0] and construct
| (4) |
where for the current simulations .
Figure 3:
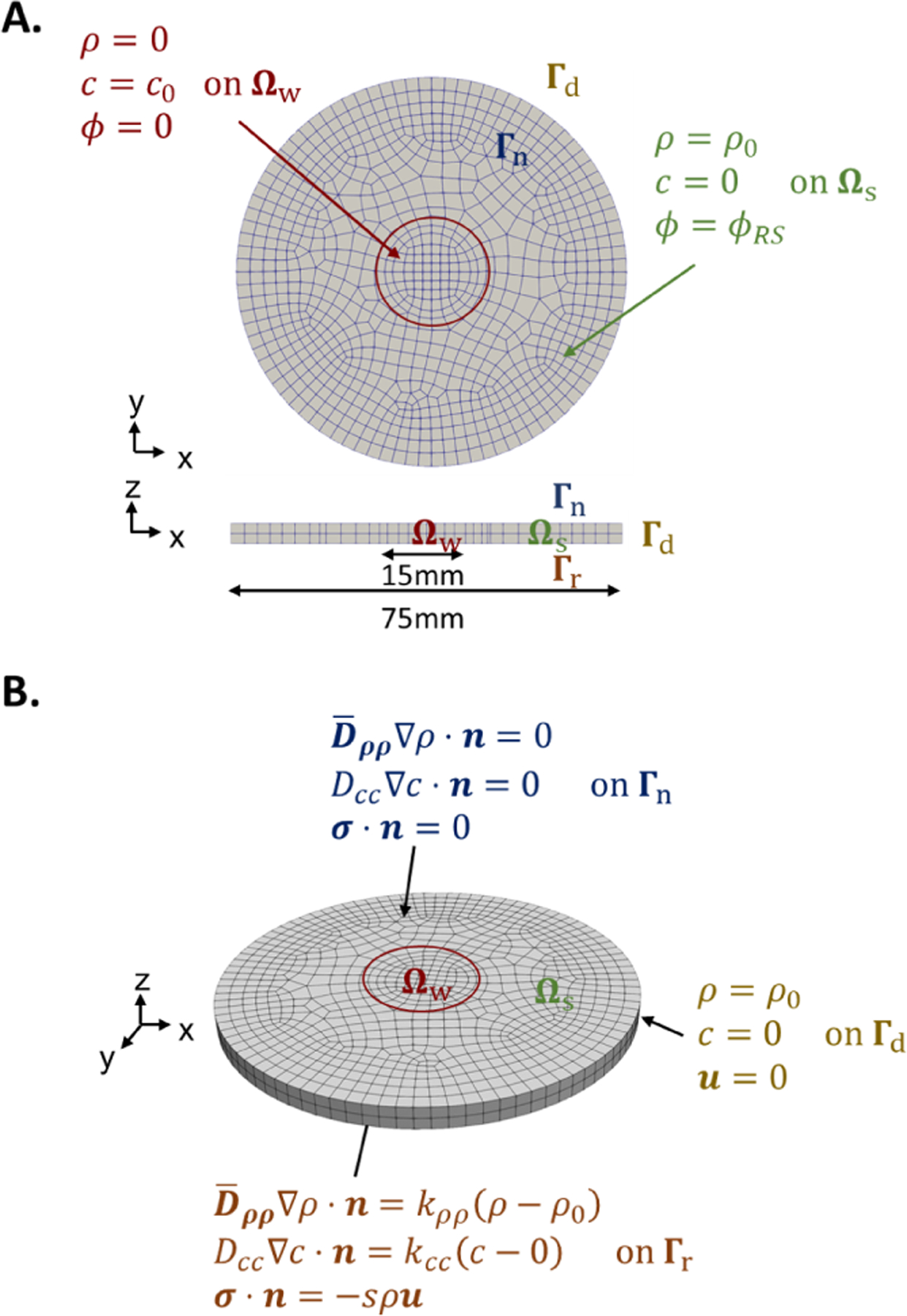
Geometry, meshing, and boundary conditions in projected (A.) and isometric (B.) views. The mesh consists of greater than 10000 linear tetrahedra or 2000 hexahedra. The wound domain at the center, Ωw, is characterized by an initial lack of cells, ρ(Ωw, 0) = 0, and high cytokine concentration, c(Ωw, 0) = c0. The surrounding skin, Ωs, has physiological values. Displacements are constrained on the outer boundary Γd. For the biochemical species, the top boundary, Γn, has no flux conditions and the bottom boundary, Γr, has mixed constraints due to the possibility of interactions with the underlying fascia. For the simulations in this study however, we set k = 0 with the assumption that the majority of cells migrate into the wound through the tissue edge, and set s = 0 so there is no spring force, consistent with the loose skin of rodents [31].
The microstructure of the collagen is described with a generalized structural tensor approach. The principal fiber direction a0 and dispersion parameter κ are used to define the 3D structural tensor A0 = κI +(1 − 3κ)a0 ⊗ a0. Upon deformation, the structural tensor transforms as A = FA0FT = κb + (1 − 3κ)a ⊗ a. After normalization, . Likewise, the updated principal direction is , and . Note that the parameters describing the microstructure of rat skin and wound matrix are the same as those used to model the Oligomer scaffolds.
Balance laws:
The growth and movement of the biological and chemical species was described using transport equations. In this work, a single chemical cytokine and a single fibroblastic cell population were considered. The extracellular matrix mechanics were defined using the balance of mass, linear, and angular momentum. The balance of mass is given by , where ϕ is mass, v is velocity, and g is the mass addition through biological growth. The balance of angular momentum enforces the symmetric stress tensor σ = σT. The balance of linear momentum is ϕa = ∇ · σ + ϕb, but neglecting the inertial term and body force, this reduces to
| (5) |
The equations for cell proliferation and motility as well as cytokine transport are
| (6) |
| (7) |
with Dρρ, Dρc, Dcc diffusion and chemotaxis coefficients.
Constitutive equations:
Starting with the mass balance for the cell field, special attention was given to the modified diffusion coefficient used here, which takes into account the dependence on matrix density and alignment
| (8) |
In the absence of other information we set , but this could be modified to increase the dependence of cell migration on fiber alignment. The source terms for the cells and cytokine are defined as
| (9) |
| (10) |
where is a logistic mechanoactivation function. The nonlinear hyperelastic mechanical behavior of the matrix in both the scaffold and surrounding tissue was introduced already in eq. (3). In addition to the strain energy which described the passive mechanical response of the tissue, an active stress by cell contractility was considered. Following Olsen et al., we include a factor for matrix-mediated inhibition of myofibroblast contractility [26].
| (11) |
This stress, as well as the other constitutive models up to this point, is presented in the current configuration but can be pulled back to the reference configuration [21, 22]. We based the parameters for τf, τm,c, and Kτ off of [26, 32]. However, since rat wounds undergo severe contraction not typically seen in human wounds, we tuned τf and τm,c to increase contraction, while tuning of Kτ was used to control the effect of different collagen densities.
Finally, local extracellular matrix remodeling was described by a system of ordinary differential equations
| (12) |
| (13) |
| (14) |
| (15) |
where is the collagen synthesis rate (first term of equation 16), λi is an eigenvalue and ei the associated eigenvector.
The full list and description of parameters is included in the Supplementary Material in Tables S1 and S2.
Finite element implementation:
The model was implemented in a total Lagrangian nonlinear finite element analysis. The link to the public code repository is available at the end of the manuscript and in the Supplementary Material. A full description of this method can be found in [21, 22]. In brief, the spatial variables were discretized using a Galerkin approach, followed by a time discretization by finite differences. The time derivative was approximated with a backward-Euler scheme and . The resulting system of nonlinear algebraic equations was solved using a Newton-Raphson scheme. The Newton-Raphson scheme was accomplished by a consistent linearization as previously described. For the local problem, we used a forward-Euler method. Note that in this case, as the local solver requires a smaller time step than the global finite element solver, the monolithic procedure requires the chain rule derivatives of the local variables (Θ) with respect to the global variables (Ξ), , which are summed up over all local time steps.
2.6. Uncertainty Propagation through the Finite Element Model
For a local sensitivity analysis of the finite element model to input values, we used a derivative-based perturbation scheme [33]. Approximating the solution locally with a linear truncated Taylor series allowed variance of the contraction output due to uncertainty in the material inputs (θ) to be estimated using a sensitivity vector and covariance matrix Cov[θ] of the constitutive parameters,
| (16) |
and a sensitivity index defined as to measure the sensitivity of the model to each input parameter [33].
3. Results
For a comprehensive description of our experimental animal model results, see [11]. The following sections describe the dermal scaffold microstructural and mechanical data analysis and subsequent simulations of the healing response for the dermal scaffold and control groups evaluated using our animal model.
3.1. Bayesian Calibration of Material Structural and Mechanical Parameters
Differences in the fibrillar microstructure and stress-strain behavior of Oligomer scaffolds and normal rat dermis were readily apparent from both qualitative and quantitative assessments (Figure 4). Constitutive models fit the measured data well, with MCMC diagnostics showing an effective sample size (ESS) greater than 500 for all samples and near 1.0. The 2.5%, 50%, and 97.5% posterior density values for all parameters are listed in Table 1. When considering the width of posterior distributions, the orientation parameters μa and κ parameters were identified with a high degree of certainty. More variation came from the mechanical parameters and density measurements. Additional statistical model results and fittings can be found in Appendix B.
Figure 4:
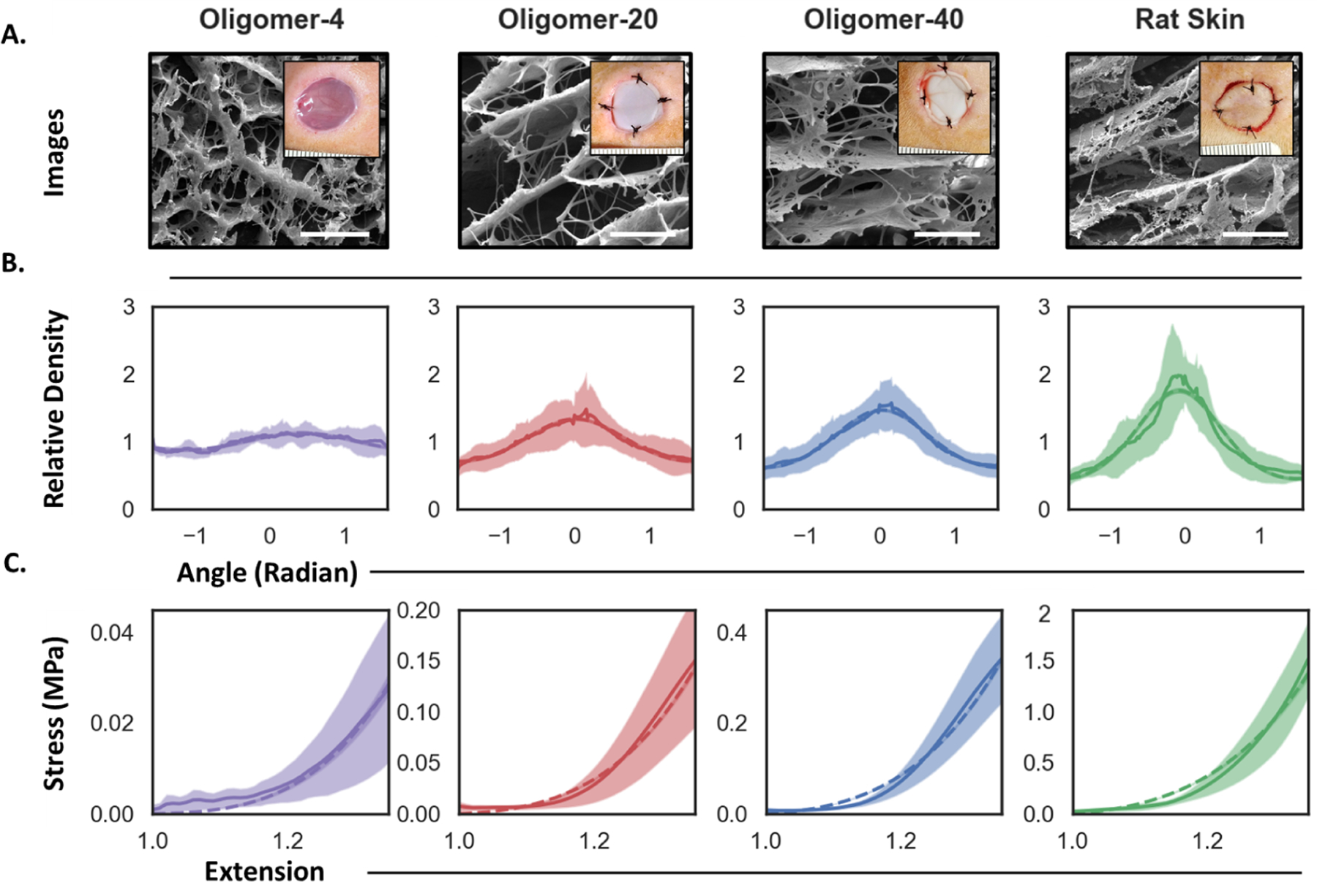
Comparison of collagen microstructure and uniaxial stress-strain plots for Oligomer scaffolds and rat skin. A. Cryo-SEM images of collagen microstructure. Inset shows gross images of scaffolds and rat skin autograft placed within experimental in vivo wounds. Scale bar: 5μm. B.-C. Model calibration results from Bayesian analysis. B. Collagen fiber orientation and dispersion measurements (solid lines indicate mean and shaded region indicate standard deviation) and associated posterior prediction from the calibrated periodic von Mises distribution (dashed lines denote the maximum a posteriori estimate). C. Stress-strain measurements (solid lines and shaded region) and Bayesian posterior prediction using the exponential strain energy based on the structural tensor of fiber orientation (dashed lines).
Table 1:
Posterior mean and confidence intervals for structural and mechanical constitutive parameters for Oligomer scaffolds and rat skin autograft groups inferred with the Bayesian framework.
| Group | Value | Physical Meaning | |||
|---|---|---|---|---|---|
| 2.5% | 50% | 97.5% | |||
| ϕ | Oligomer-4 | 0.08 | 0.09 | 0.11 | Collagen density |
| Oligomer-20 | 0.22 | 0.24 | 0.26 | ||
| Oligomer-40 | 0.39 | 0.42 | 0.46 | ||
| Rat Skin | 1.00 | 1.00 | 1.00 | ||
| κ | Oligomer-4 | 0.310 | 0.312 | 0.314 | Collagen dispersion |
| Oligomer-20 | 0.280 | 0.281 | 0.283 | ||
| Oligomer-40 | 0.262 | 0.263 | 0.265 | ||
| Rat Skin | 0.224 | 0.226 | 0.230 | ||
| μa | Oligomer-4 | 0.37 | 0.42 | 0.46 | Collagen alignment |
| Oligomer-20 | −0.01 | 6e-3 | 0.02 | ||
| Oligomer-40 | 9.9e-3 | 0.02 | 0.03 | ||
| Rat Skin | −0.1 | −0.09 | −0.07 | ||
| kv(MPa) | - | 0.51 | 0.73 | 1.28 | Compressibility |
| k0(MPa) | - | 9.8e-5 | 2.9e-3 | 0.01 | Linear stiffness |
| kf (MPa) | - | 4.16 | 5.41 | 6.47 | Fiber stiffness |
| k 2 | - | 0.3 | 1.92 | 4.0 | Nonlinear stiffening |
Oligomer-4 featured the lowest fiber density ( 13% of rat skin), with an architecture that was roughly isotropic (κ = 0.31). Oligomer-20 and Oligomer-40 scaffolds exhibited increased densities, 32% and 43% of rat skin, respectively, and collagen dispersion and alignment values that progressively approached those found in rat skin (Table 1). Note that a dispersion of κ = 1/3 ≈ 0.33 represents perfect isotropy, i.e. there is no preferred fiber orientation and all the fibers are randomly oriented, while κ = 0 represents perfect anisotropy, i.e. all fibers are aligned in the same orientation characterized by angle μa. Rat skin was anisotropic, with fibers preferentially oriented in-plane. We used the mean orientation of rat skin fibers to define μa ≈ 0 along with a measured dispersion of κ = 0.23.
The tensile stress-strain curves for dermal scaffolds and rat skin (Figure 4C) showed the expected nonlinearity, with different low and high strain regime responses. As expected, Oligomer scaffold stress scaled with increasing density, and both Oligomer scaffold and rat skin properties were consistent with published values [11].
3.2. 3D Simulations of Untreated and Dermal Scaffold Treated Wounds
We first conducted finite element simulations of untreated (no-fill) full-thickness wounds (Figure 5, upper), with gross experimental images of untreated wounds shown for comparison. For these simulations, cells rapidly entered the wound space and proliferated under the influence of the mechanotransductive and chemical signals. By day 14, the wound and surrounding tissue had a high cell density of 1900 cells/mm3, compared to the physiological value of approximately 1000 cells/mm3. Cytokine concentration decayed rapidly due to degradation by cells and diffusion out of the wound. As cells migrated in, they deposited and aligned collagen. Collagen density in the wound increased from ϕ = 0.01 at day 0 to roughly 0.4 at day 14. Collagen fibers in regions surrounding the wound became oriented toward the wound gap, and fibers within the wound slowly reoriented to the direction of maximum tension. Significant permanent contraction Jp was visible in the wound and surrounding tissue, with the surround tissue drawn in tension (Jp > 1) toward the injury. Note that Jp = 1 denotes no change, i.e. the tissue volume stayed the same. At day 0, Jp = 1 for the entire geometry. For the no-fill case, values of Jp in the wound reached 0.2 by day 14, indicative of severe permanent contraction of 80% with respect to the initial area. In the cross-section, we saw dimpling of the skin inward to the centerline, with similar behavior observed histologically in contracted rodent wounds (Figure 5A) [34].
Figure 5:
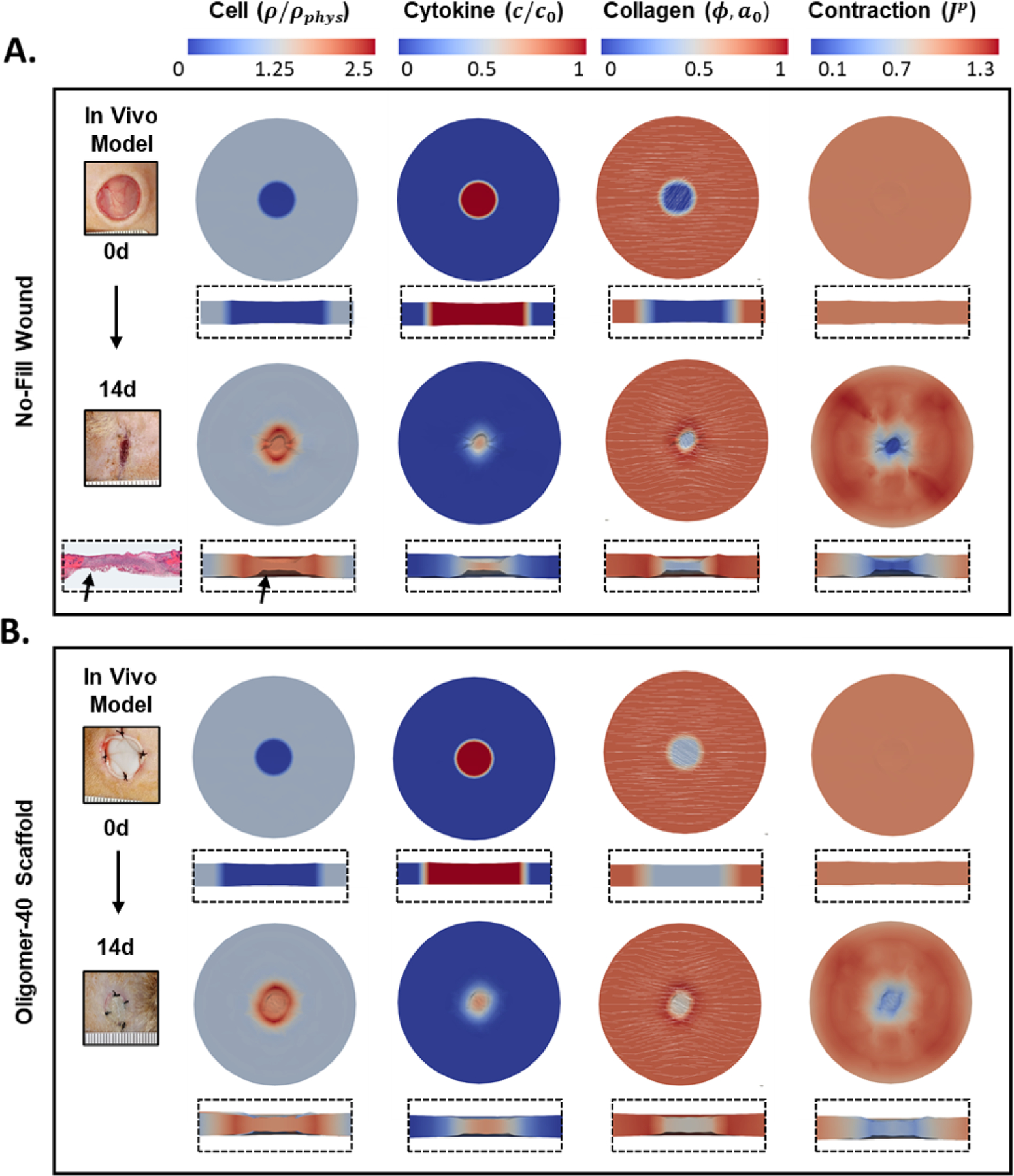
Representative simulation of A. no-fill and B. Oligomer-40 scaffold treated wounds showing cell density, cytokine concentration, collagen density with orientation, and plastic contraction at 0 and 14d time points. Overhead and cross-section perspectives are shown. Representative gross images of experimental in vivo wounds are also shown for comparison, illustrating the similar contraction responses obtained with experimental and computational models. A histological image of no-fill wound is shown for comparison, reproduced from [34] with permission.
The model was then used to predict changes in cellularization and collagen remodeling for scaffold-treated wounds, with Oligomer-40 simulation results provided in Figure 5B. Gross experimental images from in vivo wounds treated with Oligomer-40 are also shown. Model results were in good agreement with experiments that demonstrate collagen density is an important regulator of cellularization, collagen remodeling, and wound contraction. Cells migrated more slowly into scaffold filled wounds, concentrating in an outer ring. Oligomer-40 treatment reduced contraction and fiber alignment compared to untreated wound simulations. Again, these results closely matched those observed in vivo. For Oligomer-40, the permanent volume change reached values of around Jp = 0.35 in the wound periphery but only Jp = 0.55 in the wound center by day 14, in contrast to the severe contraction of Jp = 0.15 in the center of untreated wounds.
Modulation of the healing process by the various treatments was further evident upon evaluation of time dependent changes in the density of cells, cytokine, and collagen as well as collagen dispersion within the wound center (Figure 6). The rate of wound cellularization measured by ρ/ρphys, decreased as collagen density increased (Figure 6A). This was particularly evident for autograft skin, likely due to the high collagen density as well as decreased contraction in this case. For autograft treated wounds, the central region had a normalized cell density still near 0 at day 7, and only reached 0.9 by day 14. For untreated wounds, cell density remained low for 3 days, after which time it increased steadily, reaching two times physiological values by day 14. Such findings are consistent with literature reports for these highly contractile wounds [35, 36]. Similar cellularization trends were observed for scaffold treated wounds, with curves showing a modest rightward shift with increasing collagen content. The cytokine kinetics, c/c0, were similar for all treatment groups, with a slight divergence observed near the end of the simulation (Figure 6B).
Figure 6:
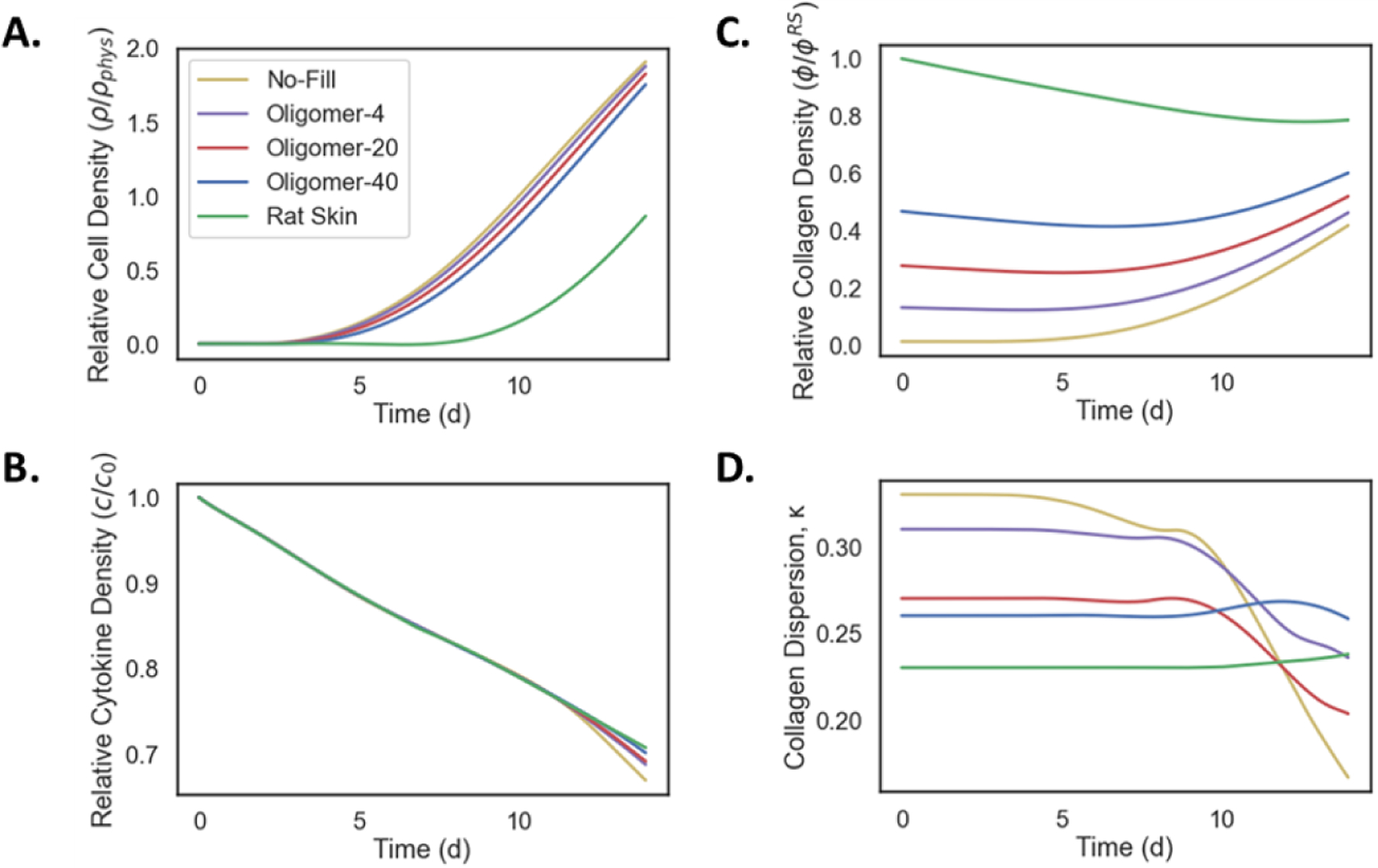
Evolution of model outcomes, including A. cell density, B. cytokine concentration, C. collagen density, and D. collagen dispersion, for collagen scaffold and control groups as measured at the wound center. Cell density shows an increase in all groups which is delayed by increasing collagen density. Cytokine density shows a characteristic decay for all groups. Collagen density also varies between samples, with a slight decrease for the skin graft. Collagen dispersion decreases more rapidly in lower density grafts (decreasing κ corresponds to greater alignment).
When evaluating collagen density over time, ϕ = φ/φRS (Figure 6C), untreated wounds exhibited the most rapid increase, reaching a value of 0.4 by day 14. Scaffold treated wounds maintained their relative collagen densities for the first 4 days of the simulation and then increased for all cases. Collagen density at 14 days ranged from about 0.4 for Oligomer-4 to 0.6 for Oligomer-40. Interestingly, autograft skin underwent a brief period of resorption reaching density values of roughly 0.8 toward the end of the simulation, something that was not apparent in scaffold-treated wounds. While collagen density profiles for no-fill and scaffold-treated wounds displayed progressive increases over time, dispersion (κ) profiles were notably different for these groups (Figure 6D). Scaffolds which begin as dense and aligned (e.g., Oligomer-40) underwent less rapid remodeling during the early stages of wound healing compared to lower density scaffolds or untreated wounds. For Oligomer-40 scaffolds, the initial dispersion was slightly anisotropic (κ ≈ 0.26) and remained relatively constant over the 14 day time period. Autograft skin displayed a similar response. In contrast, the no-fill case, which had a low density and high dispersion (isotropy) at the beginning of the simulation, rapidly surpassed the other groups in becoming aligned due to severe contraction. By 14 days, untreated wounds exhibited a dispersion value of κ = 0.17, indicative of high collagen alignment characteristic of scarring [6, 37, 38].
Both in vivo animal experiments and computational simulations indicated that wound contraction was non-linearly related to initial collagen density within the wound (Figure 7). In experimental studies, autograft treated wounds underwent the least amount of permanent contraction, maintaining 80 − 90% of the initial wound size. The no-fill and Oligomer-4 groups showed similar contraction profiles, yielding wound areas that were roughly 5 − 20% of the initial wound area. Both Oligomer-20 and Oligomer-40 scaffolds decreased contraction, with wound areas that were 20 − 40% of the initial wound area. While Oligomer-20 treated wounds showed a nearly linear decrease in wound area over the 14-day period, Oligomer-40 contraction slowed considerably after 7 days. Computational results aligned with our experimental observations as shown in Figure 7, with modest differences noted in contraction curve shape for each treatment group (Figure 7C).
Figure 7:
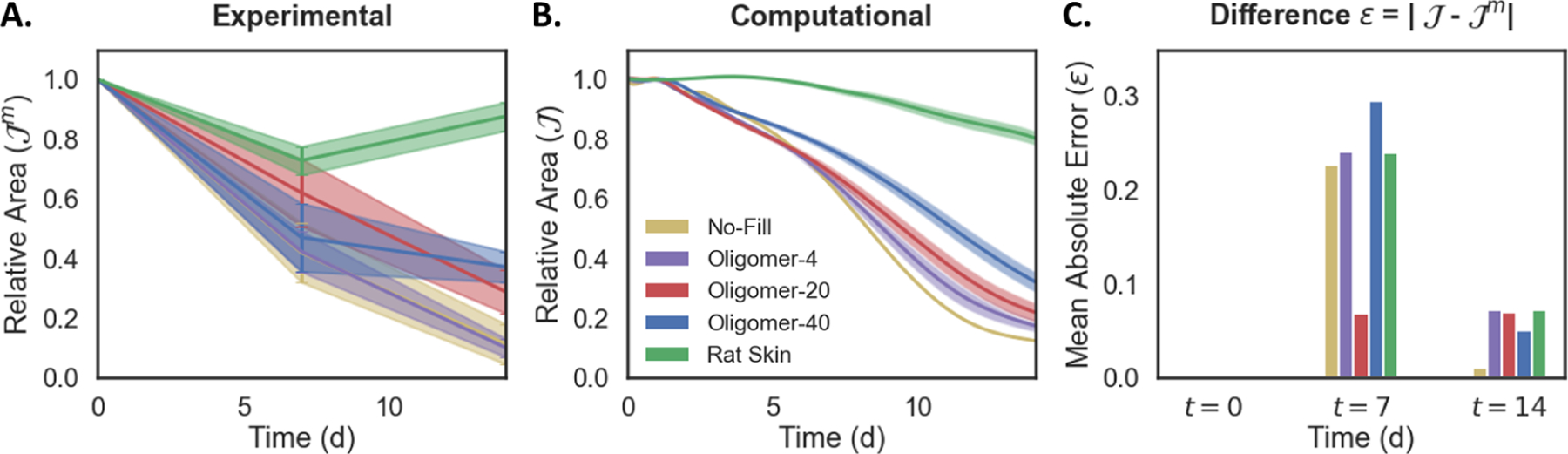
Time-dependent changes in wound area for no-fill, dermal scaffold, and rat skin groups as determined in A. experimental in vivo model and B. computational model, and C. the difference between the two. Note, the no-fill group has no associated uncertainty since mechanical parameters cannot be measured and assigned. Both models indicate that wound contraction is nonlinearly related to initial collagen density within the wound.
3.3. Uncertainty Analysis
We performed uncertainty propagation and sensitivity analyses using a perturbation method to define model features that have the greatest influence on wound healing outcomes, in particular permanent contraction . Sensitivity indices for each model parameter are shown in Figure 8. The model was most sensitive to changes in ϕ and kf, indicating that collagen fiber density and stiffness, respectively, are important scafffold design criteria for controlling wound contraction, J. In contrast, features such as initial fiber dispersion κ or nonlinearity of the stress-strain response had less impact on wound contraction but may contribute to other mechanobiological functions and healing outcomes.
Figure 8:
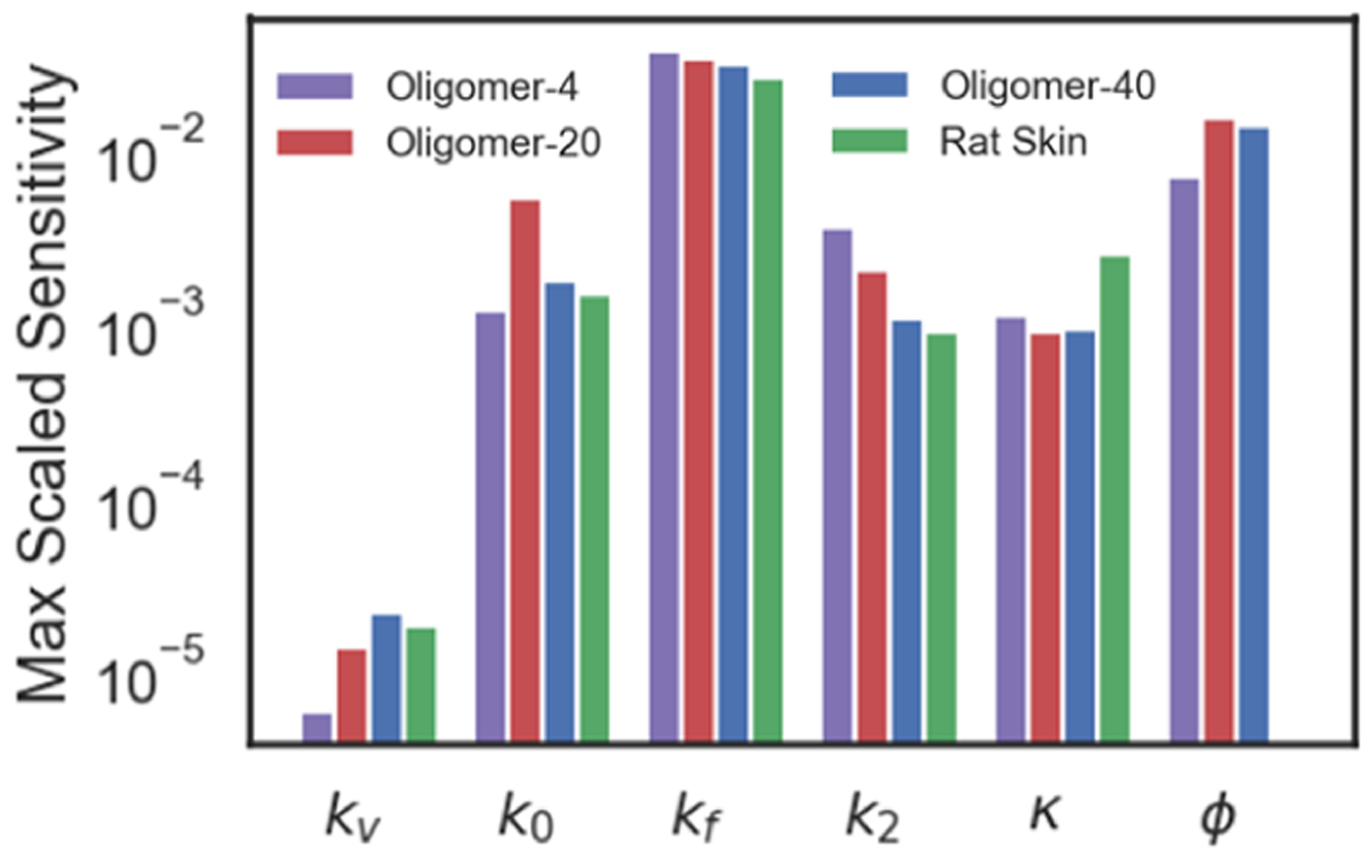
Sensitivity analysis of the computational model to parameter perturbations. The structural parameters with greatest influence, kf and ϕ, describe collagen stiffness and collagen density, respectively.
3.4. Prospective Simulations for Dermal Scaffolds with Varied Collagen Fiber Alignment
To further demonstrate the utility of our model for informing dermal scaffold design iterations for future in vivo evaluation, we investigated a scenario that was not part of the initial experimental dataset. An interesting outcome from initial scaffold simulations was the time-dependent changes in collagen dispersion exhibited by the various groups. While Oligomer-40 showed little change in fiber dispersion, less dense Oligomer-4 scaffold went from fairly isotropic κ = 0.31 to aligned κ = 0.23 over the 14-day period. Because alignment is both a mechanical regulator of cell behavior as well as an indicator of scarring, we quantified the effect of independently controlling collagen dispersion and scaffold fiber orientation relative to that of the surrounding skin. Oligomer-40 scaffolds with either aligned (κ = 0.2) or dispersed (κ = 0.3) fibers and either fibers that were parallel to (μa = 0) or oblique (μa = π/4) to the surrounding tissue were tested, with cellularization and contraction results summarized in Figure 9. While wound contraction was obviously impacted by collagen alignment, no changes in cellularization were observed. Scaffolds with more isotropic fiber microstructures (κ = 0.3) contracted less rapidly and showed more uniform contraction compared to those with low fiber dispersion (κ = 0.2). Interestingly, the fiber orientation angle between the scaffold and surrounding skin impacted the shape of the wound at 14 days. For example, when fibers of the scaffold and surrounding tissue were oriented in the same direction (μa = 0) wounds contracted more in the horizontal direction and wound areas appeared as a vertically aligned ellipse. In addition, the plastic deformation field was relatively symmetric with respect to both the vertical and horizontal axes. However, a mismatch between the angle of fibers in the scaffold and the surrounding skin (μa = π/4) resulted in asymmetric wound contraction. Additional prospective simulations investigating the effect of collagen stiffness, wound size, and wound shape, are available in the Supplementary Material.
Figure 9:
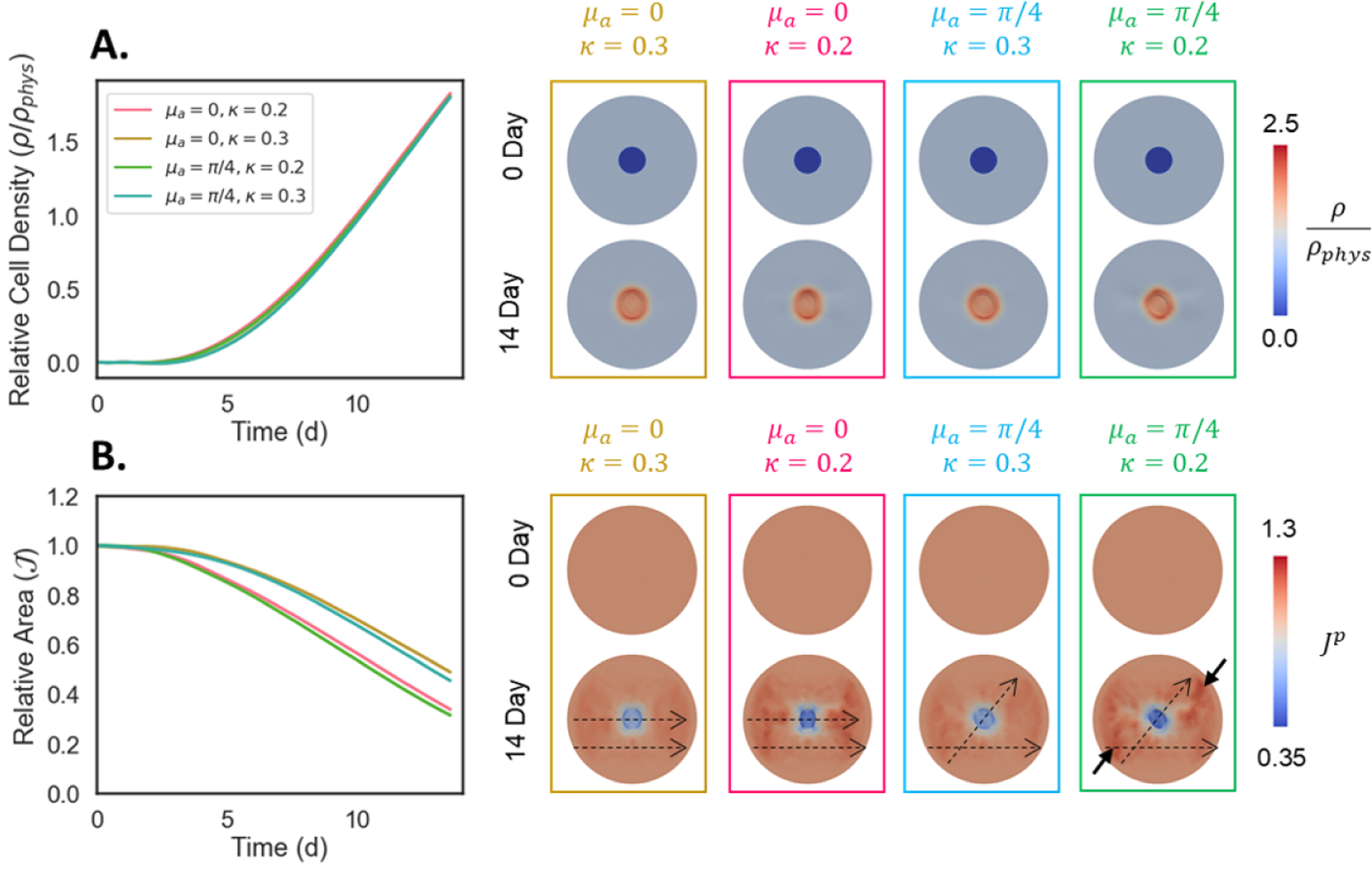
Effect of dermal scaffold (Oligomer-40) fiber orientation relative to normal surrounding skin (μa) and fiber dispersion (κ) on A. cellularization and B. contraction of wounds. Scaffolds with relatively isotropic fiber distributions (κ = 0.3) yield slower and more uniform circular contraction, while aligned scaffolds (κ = 0.2) contract faster. Scaffold fiber orientation dictates the angle of contraction during wound healing. When scaffold fibers are oriented parallel to the surrounding skin (μa = 0) vertically-oriented scars result, while angled scaffolds (μa = π/4) produce asymmetric contraction fields. Dashed arrows show direction of fibers in the graft and surrounding tissue. Solid arrows emphasize the asymmetric deformation field.
4. Discussion
Wound healing is a significant cause of morbidity and mortality world-wide. To address this grand challenge, dermal replacement scaffolds capable of guiding functional skin restoration in lieu of pathological scarring are the subject matter of continued research and development [39, 40]. Unfortunately, fundamental gaps in our understanding of wound mechanobiology and lack of predictive tools pose roadblocks to the efficient engineering design of tissue restorative solutions. Without accurate computational models of wound healing biomechanics and mechanochemical signaling, researchers must rely on conventional trial-and-error approaches, which are tremendously burdensome and inefficient in terms of animal number requirements, resources, and overall time and cost. In this work, we developed a mechanobiological computational model of wound healing that comprehensively describes the large 3D deformation, permanent contraction, and collagen fiber alignment observed in pathological healing. The same modeling framework is also able to capture the outcomes of wounds treated with engineered collagen dermal scaffolds. The core of our computational model is the coupling of a physical description of extracellular matrix/collagen scaffold microstructure and nonlinear mechanics with a cell and cytokine mechanobiological signaling model.
4.1. A Comprehensive Framework for 3D Coupling of Skin Mechanics and Mechanobiology
Accurate modeling of permanent contraction and collagen alignment is essential in the context of wound healing. Rodent skin wounds that are left untreated show significant deformation over time, leading to scar tissue characterized by a closely packed and aligned collagen network [38]. Treatment with Oligomer scaffolds, on the other hand, leads to improved outcomes [11]Permanent changes in tissue volume and properties over time can be described within continuum mechanics. The finite volume growth framework explains permanent changes in tissue volume and mass [41], while use of structural tensors can capture fiber reorientation [42]. These tools have been used previously to successfully describe cardiac muscle adaptation [43], skin growth [20], and brain folding [44], to name a few examples.
The work presented here adopts a similar framework. Here, a multiplicative decomposition of the deformation gradient was used to describe the contraction observed in untreated and dermal scaffold treated rat skin wounds. Tissue microstructure was modeled with a structural tensor that evolved over time based on changes in fiber alignment and dispersion as seen experimentally. In contrast, most existing computational models of wound healing use purely elastic models. For such models, wound contraction remains only as long as the cell population stays constant, which has limited pathophysiologic relevance. To date, permanent contraction and collagen remodeling have only been explored in a select few wound models, such as our own previous work [22], a morphoelastic model for burn healing [45], and a morphoelastic model for dermal wound closure [46], though the latter did not include biochemical coupling. Other wound healing models that address collagen remodeling rely on restrictive simplifying assumptions. For example, the Maxwell fluid model was used to model wounds in the seminal work by Olsen et al. [26], with similar approaches reported by others [47, 48, 49]. Collectively, such models have led to an advanced understanding of cell mechanobiology. In fact, several components of our coupled model are based on insights gained from such efforts. Alternative approaches have focused on collagen geometry while ignoring permanent tissue deformations, as is observed in models prioritizing individual cell behavior [37]. However, by modeling the nonlinear mechanics of soft tissue, including growth and remodeling, we filled an existing need for the design of biomaterial scaffolds that aim to reduce pathological contraction and fiber alignment.
A major outcome of wound healing is tissue contraction and remodeling, the underlying mechanism of which is the mechanobiological response of cells, primarily myofibroblasts, acting on nearby matrix components [50]. This is why many wound healing models have focused on this cellular process [51, 52]. Knowledge from this earlier work on cell mechanobiology was incorporated into our nonlinear mechanics framework, with key innovations in our coupling scheme including: i) active stress by cells, ii) collagen deposition and remodeling linked directly to changes in wound mechanical properties, and iii) feedback from collagen density and structure on cell migration and active stress. In addition to modeling wound healing [19, 26], the use of active stress terms to represent cell contractility has been applied in previous work to describe tissue remodeling following heart valve replacement [53] and fibrin gel remodeling [54]. In our model, the cell population and cytokine densities were coupled to the active stress through eq. (11). Collagen mass fraction change due to cell deposition is a central part of existing wound healing models, e.g. [37]; however, in the present work, the collagen density was also a key determinant of the overall mechanical behavior through eq. (3). Mechanobiology models of cell migration and contractility based on collagen density were proposed in [26, 55], and used here in eqs. (8) and (11). Additionally, strain was coupled to cytokine production, contractility, and collagen deposition in eqs. (10, (11), and (12)). This type of stretch-driven cell behavior is based on previous work on fibroblast mechanobiology modeling [56, 57]. Overall, our computational model integrates a large body of evidence and progress in mechanobiology modeling, coupled with a nonlinear mechanics framework that describes growth and remodeling. As a result, the proposed model represents a unified approach to understand the coupled phenomena characteristic of wound healing.
4.2. Comprehensive Dataset and Bayesian Calibration
In addition to the comprehensive modeling framework, a key contribution of our work is the integration of in vitro and in vivo data from Oligomer scaffold characterization and preclinical animal testing. Due to the inherent complexity of wound healing mechanobiology, computational models of this process entail coupled equations with many parameters, which poses significant challenges for model calibration and validation. We addressed this challenge by generating a dataset of wound healing that reflected the structure and parameters of the modeling framework. The experimental data consisted of uniaxial extension data and microstructure images of engineered Oligomer scaffolds and rat skin, as well as contraction and recellularization measurements in full-thickness rodent wounds. These data informed the corresponding structural and mechanobiological parameters used in the computational model as outlined in Figure 2. The tight integration between simulations and experiments showcased here speaks to the ongoing regulatory push to use computer models as a standard part of medical device design and evaluation [58, 53].
Default calibration of computer models in biomechanics fails to recognize the importance of uncertainty in the mechanical and biological responses of tissues. We addressed this gap by using a Bayesian framework. This approach has been used for calibration of other constitutive equations for fibrous materials [59]. The results of the calibration are summarized in Table 1. The inferred parameters describe the microstructure and mechanical behavior of rat skin and Oligomer collagen scaffolds with applications beyond the wound healing model shown here. The constitutive model, eq. (3), has been used to fit several collagenous soft tissues including skin [60]. In particular, the parameters obtained for rat skin in this paper are similar with those reported in [23] for murine dorsal skin.
Through Bayesian calibration, rat skin and Oligomer scaffold microstructural parameters were identified with high certainty. Slightly more variance was observed with stiffness parameters. This may be due to variability in the samples tested, which is natural for biological samples [23]. This variation may also reflect non-linearity effects [61]. Additionally, the parameters were inferred from uniaxial data in combination with fiber orientation data. However, uniaxial tests in multiple orientations or biaxial tests would likely reduce the uncertainty in the estimation. The tests were performed at a single strain rate, which could also lead to uncertainty in the inferred parameters for skin [62, 63, 64]. Using a perturbation analysis, collagen fiber stiffness and collagen density were then identified as important determinants of wound contraction outcomes. Based on this analysis, additional simulations showing the effect of changing kf over a wide range kf ∈ [2.7, 10.8] MPa are explored in the Supplementary Material. Together, these results highlight the value of Bayesian inference for fitting constitutive models with shared parameters and variables. Additionally, they imply that next iterations of Oligomer scaffold design should focus on controlling tightly and independently the collagen density, stiffness, and microstructure.
4.3. Engineered Dermal Scaffolds Effectively Regulate Collagen Remodeling
Modulation of wound healing outcomes by engineered dermal scaffolds and autograft skin resulted from the complex interplay of biochemical and biomechanical signaling included in our model. We found that increasing scaffold collagen density reduced wound contraction, but also modestly slowed cellularization. These model outputs were consistent with our animal study findings [11]. Previous work on wound healing scaffolds has also identified that stiffness can prevent contraction in vitro and in vivo, but may also prevent recellularization [65, 66]. For the no-fill case, the model captured the rapid influx and proliferation of cells over the first few weeks, similar to other modeling work in the field [32, 52, 67] and experimental observations [36, 68]. As cells migrated and proliferated, the untreated wounds healed through a combination of cell-induced remodeling and extreme permanent contraction of surrounding skin, as expected of rodent wounds [31]. On the other hand, the autograft skin simulation showed the least contraction, not only due to the high stiffness of the autograft, but also because of its inhibition of cell migration and proliferation. Previous work describing cellularization of allograft dermis also supports these results [69]. Special attention has been given to the potential negative effects of the native dense dermal architecture on vascularization, which is necessary to maintain viability of resident graft tissue cells [70]. It is expected that an endothelial cell density field would parallel the cellularization results from our simulations. In fact, our own animal experiments showed reduced vascularization of autograft skin compared to Oligomer scaffold treatment [11] and, in some cases, autograft failure owing to insufficient vascularization. Given that explicit modeling of endothelialization has been explored in other models [47], we plan to incorporate such features in future iterations of our framework. Oligomer treated wounds exhibited a response in between the no-fill and the autograft skin simulations. Increasing the density of the scaffold reduced contraction from approximately 85% to 60% compared to no-fill, while cellular ingrowth was only reduced slightly. Thus, we anticipate that engineered dermal scaffolds can be tailored to regulate this trade-off, minimizing wound contraction while modulating the number and phenotype of infiltrating cell populations. Other leading experts in the field agree with this assessment. For example, Soller et al. [71] suggest the development of porous collagen scaffolds that can promote cell infiltration but prevent contraction.
In addition to the contraction and cellularization of wounds, the remodeling of collagen fiber dispersion was also of interest. No-fill controls began as isotropic, but due to their low collagen density and stiffness, the collagen quickly aligned as the wound contracted, consistent with scar formation in rat wounds [38]. In the other extreme, autograft skin began with a greater degree of alignment and underwent significantly less reorganization owing to its high density and stiffness. Simulated dermal scaffold treatment of wounds also produced insightful results. Here, the degree of alignment by 14 days was found to be nonlinearly related to scaffold parameters. For the Oligomer-4 and Oligomer-20 cases, the scaffolds underwent significant reorganization, while the Oligomer-40 scaffold retained its initial alignment.
The model includes many complex mechanobiological couplings that guide our findings. In fact, the complex interaction between the different mechanisms at play is a key justification for the development of detailed computational models that, when calibrated against experimental observations, identify the relative contribution of individual factors and couplings. The reorganization of fibers is dependent on the collagen turnover rate, initial orientation, as well as tissue elastic deformations as captured in eq. (13). Control of cell phenotype plays a role, which is effectively captured in the matrix-mediated inhibition of myofibroblast contractility in eq. (11). This finding parallels our in vivo experimental observations of decreased α-SMA staining in Oligomer-40 treated wounds [11], which then explains the reduced contraction and alignment of Oligomer-40 treatment wounds versus no-fill controls. This mechanism of regulated contraction through the tuning of collagen scaffold design is in line with other work in the field. Yannas et al. [72] report that a contractile ring at the wound periphery drives contraction, that this contraction is the source of the dense scar tissue formed in the wound, and that scaffolds that prevent contraction but allow cell infiltration promote regeneration. Our model predictions align with this proposed mechanism, see Figure 5.
Equipped with our computational model, a natural next step was to test new designs to develop predictions regarding optimal dermal scaffold design. To better understand the effect of initial collagen dispersion and alignment on the 14-day outcome, we ran additional simulations in which these two parameters were controlled independently. We found that increasing the dispersion of the fibers results in a lesser degree of contraction with minimal impact on cellular infiltration. Isotropic scaffolds may then be more permissive of scaffold integration while reducing permanent contraction. The initial alignment vector of collagen fibers impacted the final orientation of the wound area but not the degree of contraction. These prospective simulations were guided based on our observations of the wound healing process in Figure 4 and the local sensitivity analysis shown in Figure 8. A global sensitivity analysis and future design of experiments is the subject matter of ongoing work, and will be performed by leveraging machine learning tools to create inexpensive metamodels that circumvent the computational cost of the finite element simulations as we have demonstrated before [73]. Additional simulations, not discussed in the main text but motivated by our sensitivity analysis and the uncertainty in mechanical parameters, are shown in Supplementary Material. We explored the effect of changing the stiffness kf, the wound size, and the wound geometry.
4.4. Limitations and Future Work
The primary focus of this study was on permanent contraction and collagen fiber alignment outcomes of wound healing, with experimental data gathered to calibrate and inform the model focused on these mechanobiological outcomes. Although this integration of experimental and computational data provided new perspective and insight, these studies are not without limitations. More specifically, a study limitation includes calibration of the model with only uniaxial experimental data at a single strain rate, which does not fully capture tissue and scaffold anisotropy and viscoelastic behavior. Future model iterations will benefit from more comprehensive characterization of tissue and scaffold mechanical behavior, including biaxial or uniaxial testing in multiple orientations, along with measures of viscoelasticity, including strain-rate dependence. Future efforts will also focus on extending the mechanobiology model, bringing increased definition to other relevant biochemical and cellular parameters, namely vascularization, nutrient supply, and inflammation-related cytokine levels. While the general wound healing process is similar for humans and rodents, we appreciate that important differences exist. Specifically, rodent wounds heal primarily by contraction while those in humans heal primarily via granulation tissue formation [6, 31]. As such, we will explore opportunities to recalibrate the current model to match wound healing outcomes observed within other relevant preclinical wound healing models (e.g., porcine) as well as those seen clinically in humans. The model can also be modified to simulate perturbations of the normal wound healing process, extending our framework to the context of chronic wounds. This model is currently being adapted to address other wound types, including application of in situ scaffold-forming Oligomer formulations for surgical breast tissue voids following breast conserving surgery (lumpectomy) [13].
5. Conclusion
This work presents a 3D computational model of skin wound healing to assist in the design of engineered dermal scaffolds for improved tissue restoration outcomes. Through the integration of experiments and simulations, we found that collagen density and fiber architecture of scaffolds can be used to regulate the permanent contraction and fiber alignment of simulated rodent wounds. This work is a significant improvement over state-of-the-art models by introducing a coupled theory that combines a comprehensive mechanobiological model with a 3D finite element framework of nonlinear mechanics, including growth and remodeling. The model explains contraction and fiber alignment of rodent wounds for no-fill, Oligomer scaffold, and autograft treatment cases. Equipped with this computational tool, we were then able to propose the next iteration of dermal scaffold designs. These scaffolds, in turn, will be further evaluated in follow up preclinical studies. This work represents an important initial step towards the integrated use of in vivo and in silico models to guide novel therapeutic solutions directed at patient-centric wound care.
Supplementary Material
State of Significance.
Skin wounds continue to be a significant burden to patients, physicians, and the healthcare system. Advancing the mechanistic understanding of the wound healing process, including multi-scale mechanobiological interactions amongst cells, the collagen scaffolding, and signaling molecules, will aide in the design of new skin restoration therapies. This work represents the first step towards integrating mechanobiology-based computational tools with in vitro and in vivo preclinical testing data for improving the design and evaluation of custom-fabricated collagen scaffolds for dermal replacement. Such an approach has potential to expedite development of new and more effective skin restoration therapies as well as improve patient-centered wound treatment.
Acknowledgments
This project was supported by the Indiana Clinical Translational Sciences Institute TL1 Fellowship (NIH UL1TR002529), Interdisciplinary Bioengineering Training in Diabetes Research Program (T32 DK101001), Indiana Medical Scientist/Engineering Training Program (MSTP; NIGMS T32 GM077229), and the National Science Foundation (NSF CMMI 1911346). Dr. Voytik-Harbin has significant financial interest in GeniPhys, Inc., a small business that she founded to assist with the commercialization of tissue engineering and regenerative medicine technologies such as those described here. Collagen Oligomer and associated custom fabricated materials are the subject matter of issued and pending patents that are owned by Purdue Research Foundation and licensed to GeniPhys, Inc.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Supplementary Informationl
The finite element model is available at the repositories
https://github.com/davidsohutskay/ACTA_2021_FE
https://github.com/davidsohutskay/ACTA_2021_MCMC
The file S1 file.pdf contains Table S1, Table S2 with all the parameters user in the simulations. It also contains Figures S1-S4 with MCMC fitting information and Figures S5-S8 with additional prospective simulations not shown in the main text.
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Dr. Voytik-Harbin has significant financial interest in GeniPhys, Inc., a small business that she founded to assist with the commercialization of tissue engineering and regenerative medicine technologies such as those described here. Collagen Oligomer and associated custom fabricated materials are the subject matter of issued and pending patents that are owned by Purdue Research Foundation and licensed to GeniPhys, Inc.
References
- [1].Sen CK, Gordillo GM, Roy S, Kirsner R, Lambert L, Hunt TK, Gottrup F, Gurtner GC, Longaker MT, Human skin wounds: a major and snowballing threat to public health and the economy, Wound Repair and Regeneration 17 (6) (2009) 763–771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Eming SA, Martin P, Tomic-Canic M., Wound repair and regeneration: mechanisms, signaling, and translation, Science Translational Medicine 6 (265) (2014) 265sr6–265sr6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Ratner BD, Biomaterials: Been there, done that, and evolving into the future, Annual review of biomedical engineering 21 (2019) 171–191. [DOI] [PubMed] [Google Scholar]
- [4].Aarabi S, Longaker MT, Gurtner GC, Hypertrophic scar formation following burns and trauma: new approaches to treatment, PLoS Med 4 (9) (2007) e234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Keane TJ, Horejs C-M, Stevens MM, Scarring vs. functional healing: matrix-based strategies to regulate tissue repair, Advanced Drug Delivery Reviews 129 (2018) 407–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Reinke J, Sorg H., Wound repair and regeneration, European Surgical Research 49 (1) (2012) 35–43. [DOI] [PubMed] [Google Scholar]
- [7].Kreger S, Bell B, Bailey J, Stites E, Kuske J, Waisner B, Voytik-Harbin S., Polymerization and matrix physical properties as important design considerations for soluble collagen formulations, Biopolymers 93 (8) (2010) 690–707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Bailey J, Critser P, Whittington C, Kuske J, Yoder M, Voytik-Harbin S., Collagen oligomers modulate physical and biological properties of three-dimensional self-assembled matrices, Biopolymers 95 (2) (2011) 77–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Blum KM, Novak T, Watkins L, Neu CP, Wallace JM, Bart ZR, Voytik-Harbin SL, Acellular and cellular high-density, collagen-fibril constructs with suprafibrillar organization, Biomaterials Science 4 (4) (2016) 711–723. [DOI] [PubMed] [Google Scholar]
- [10].Novak T, Seelbinder B, Twitchell CM, van Donkelaar CC, Voytik-Harbin SL, Neu CP, Mechanisms and microenvironment investigation of cellularized high density gradient collagen matrices via densification, Advanced Functional Materials 26 (16) (2016) 2617–2628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Sohutskay DO, Buno KP, Tholpady SS, Nier SJ, Voytik-Harbin SL, Design and biofabrication of dermal regeneration scaffolds: role of oligomeric collagen fibril density and architecture, Regenerative Medicine 15 (2) (2020) 1295–1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Brookes S, Zhang L, Puls TJ, Kincaid J, Voytik-Harbin S, Halum S., Laryngeal reconstruction using tissue-engineered implants in pigs: A pilot study, The Laryngoscope (2020). [DOI] [PMC free article] [PubMed]
- [13].Puls TJ, Fisher CS, Cox A, Plantenga JM, McBride EL, Anderson JL, Goergen CJ, Bible M, Moller T, Voytik-Harbin SL, Regenerative tissue filler for breast conserving surgery and other soft tissue restoration and reconstruction needs, Scientific Reports 11 (1) (2021) 1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Limbert G., Mathematical and computational modelling of skin biophysics: a review, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 473 (2203) (2017) 20170257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Benítez JM, Montans FJ, The mechanical behavior of skin: Structures and models for the finite element analysis, Computers & Structures 190 (2017) 75–107. [Google Scholar]
- [16].Gasser TC, Ogden RW, Holzapfel GA, Hyperelastic modelling of arterial layers with distributed collagen fibre orientations, Journal of the Royal Society Interface 3 (6) (2006) 15–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Annaidh AN, Bruyère K, Destrade M, Gilchrist MD, Maurini C, Ott M énio, G. Saccomandi, Automated estimation of collagen fibre dispersion in the dermis and its contribution to the anisotropic behaviour of skin, Annals of Biomedical Engineering 40 (8) (2012) 1666–1678. [DOI] [PubMed] [Google Scholar]
- [18].Jorgensen SN, Sanders JR, Mathematical models of wound healing and closure: a comprehensive review, Medical & Biological Engineering & Computing 54 (9) (2016) 1297–1316. [DOI] [PubMed] [Google Scholar]
- [19].Javierre E, Moreo P, Doblaré M, García-Aznar J., Numerical modeling of a mechano-chemical theory for wound contraction analysis, International Journal of Solids and Structures 46 (20) (2009) 3597–3606. [Google Scholar]
- [20].Buganza Tepole A, Ploch CJ, Wong J, Gosain AK, Kuhl E., Growing skin: A computational model for skin expansion in reconstructive surgery, Journal of the Mechanics and Physics of Solids 59 (10) (2011) 2177–2190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Buganza Tepole A, Kuhl E., Computational modeling of chemo-biomechanical coupling: a systems-biology approach toward wound healing, Computer Methods in Biomechanics and Biomedical Engineering 19 (1) (2016) 13–30. [DOI] [PubMed] [Google Scholar]
- [22].Buganza Tepole A., Computational systems mechanobiology of wound healing, Computer Methods in Applied Mechanics and Engineering 314 (2017) 46–70. [Google Scholar]
- [23].Meador WD, Sugerman GP, Story HM, Seifert AW, Bersi MR, Buganza Tepole A, Rausch MK, The regional-dependent biaxial behavior of young and aged mouse skin: A detailed histomechanical characterization, residual strain analysis, and constitutive model, Acta Biomaterialia 101 (2020) 403–413. [DOI] [PubMed] [Google Scholar]
- [24].Buganza Tepole A, Constitutive modelling of wound healing, in: Skin Biophysics, Springer, 2019, pp. 101–133. [Google Scholar]
- [25].Takeuchi H, Ishida M, Furuya A, Todo H, Urano H, Sugibayashi K., Influence of skin thickness on the in vitro permeabilities of drugs through sprague-dawley rat or yucatan micropig skin, Biological and Pharmaceutical Bulletin 35 (2) (2012) 192–202. [DOI] [PubMed] [Google Scholar]
- [26].Olsen L, Sherratt JA, Maini PK, A mechanochemical model for adult dermal wound contraction and the permanence of the contracted tissue displacement profile, Journal of Theoretical Biology 177 (2) (1995) 113–128. [DOI] [PubMed] [Google Scholar]
- [27].Voytik-Harbin SL, Brightman AO, Waisner BZ, Robinson JP, Lamar CH, Small intestinal submucosa: A tissue-derived extracellular matrix that promotes tissue-specific growth and differentiation of cells in vitro, Tissue engineering 4 (2) (1998) 157–174. [Google Scholar]
- [28].Schriefl AJ, Reinisch AJ, Sankaran S, Pierce DM, Holzapfel GA, Quantitative assessment of collagen fibre orientations from two-dimensional images of soft biological tissues, Journal of The Royal Society Interface 9 (76) (2012) 3081–3093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Dombi GW, Haut RC, Sullivan WG, Correlation of high-speed tensile strength with collagen content in control and lathyritic rat skin, Journal of Surgical Research 54 (1) (1993) 21–28. [DOI] [PubMed] [Google Scholar]
- [30].Rappel H, Beex LA, Hale JS, Noels L, Bordas S., A tutorial on bayesian inference to identify material parameters in solid mechanics, Archives of Computational Methods in Engineering 27 (2) (2020) 361–385. [Google Scholar]
- [31].Lorenz HP, Longaker MT, Wounds: biology, pathology, and management, in: Surgery, Springer, 2008, pp. 191–208. [Google Scholar]
- [32].Koppenol DC, Vermolen FJ, Niessen FB, van Zuijlen PP, Vuik K., A mathematical model for the simulation of the formation and the subsequent regression of hypertrophic scar tissue after dermal wounding, Biomechanics and Modeling in Mechanobiology 16 (1) (2017) 15–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].McClarren RG, McClarren, Penrose, Uncertainty Quantification and Predictive Computational Science, Springer, 2018. [Google Scholar]
- [34].Evans ND, Oreffo RO, Healy E, Thurner PJ, Man YH, Epithelial mechanobiology, skin wound healing, and the stem cell niche, Journal of the Mechanical Behavior of Biomedical Materials 28 (2013) 397–409. [DOI] [PubMed] [Google Scholar]
- [35].Nagaraja S, Chen L, Zhou J, Zhao Y, Fine D, DiPietro LA, Reifman J, Mitrophanov AY, Predictive analysis of mechanistic triggers and mitigation strategies for pathological scarring in skin wounds, The Journal of Immunology 198 (2) (2017) 832–841. [DOI] [PubMed] [Google Scholar]
- [36].Rognoni E, Pisco AO, Hiratsuka T, Sipil KH, Belmonte JM, Mobasseri SA, Philippeos C, Dilo R, Watt FM, Fibroblast state switching orchestrates dermal maturation and wound healing, Molecular Systems Biology 14 (8) (2018) e8174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].McDougall S, Dallon J, Sherratt J, Maini P., Fibroblast migration and collagen deposition during dermal wound healing: mathematical modelling and clinical implications, Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 364 (1843) (2006) 1385–1405. [DOI] [PubMed] [Google Scholar]
- [38].Quinn KP, Golberg A, Broelsch GF, Khan S, Villiger M, Bouma B, Austen WG Jr, Sheridan RL, Mihm MC Jr, Yarmush ML, et al. , An automated image processing method to quantify collagen fibre organization within cutaneous scar tissue, Experimental Dermatology 24 (1) (2015) 78–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Sohutskay DO, Puls TJ, Voytik-Harbin SL, Collagen self-assembly: biophysics and biosignaling for advanced tissue generation, in: Multi-scale Extracellular Matrix Mechanics and Mechanobiology, Springer, 2020, pp. 203–245. [Google Scholar]
- [40].MacNeil S., Biomaterials for tissue engineering of skin, Materials Today 11 (5) (2008) 26–35. [Google Scholar]
- [41].Eskandari M, Kuhl E., Systems biology and mechanics of growth, Wiley Interdisciplinary Reviews: Systems Biology and Medicine 7 (6) (2015) 401–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Alastrué V, Martinez M, Doblaré M, Menzel A., Anisotropic microsphere-based finite elasticity applied to blood vessel modelling, Journal of the Mechanics and Physics of Solids 57 (1) (2009) 178–203. [Google Scholar]
- [43].Göktepe S, Abilez OJ, Kuhl E., A generic approach towards finite growth with examples of athlete’s heart, cardiac dilation, and cardiac wall thickening, Journal of the Mechanics and Physics of Solids 58 (10) (2010) 1661–1680. [Google Scholar]
- [44].Xu G, Bayly PV, Taber LA, Residual stress in the adult mouse brain, Biomechanics and Modeling in Mechanobiology 8 (4) (2009) 253–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Koppenol DC, Vermolen FJ, Biomedical implications from a morphoelastic continuum model for the simulation of contracture formation in skin grafts that cover excised burns, Biomechanics and Modeling in Mechanobiology 16 (4) (2017) 1187–1206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Bowden L, Byrne H, Maini P, Moulton D., A morphoelastic model for dermal wound closure, Biomechanics and Modeling in Mechanobiology 15 (3) (2016) 663–681. [DOI] [PubMed] [Google Scholar]
- [47].Xue C, Friedman A, Sen CK, A mathematical model of ischemic cutaneous wounds, Proceedings of the National Academy of Sciences 106 (39) (2009) 16782–16787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Flegg JA, Byrne HM, McElwain DS, Mathematical model of hyperbaric oxygen therapy applied to chronic diabetic wounds, Bulletin of Mathematical Biology 72 (7) (2010) 1867–1891. [DOI] [PubMed] [Google Scholar]
- [49].Flegg JA, Menon SN, Maini PK, McElwain D., On the mathematical modeling of wound healing angiogenesis in skin as a reaction-transport process, Frontiers in Physiology 6 (2015) 262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Wong VW, Akaishi S, Longaker MT, Gurtner GC, Pushing back: wound mechanotransduction in repair and regeneration, Journal of Investigative Dermatology 131 (11) (2011) 2186–2196. [DOI] [PubMed] [Google Scholar]
- [51].Sherratt JA, Murray JD, Models of epidermal wound healing, Proceedings of the Royal Society of London. Series B: Biological Sciences 241 (1300) (1990) 29–36. [DOI] [PubMed] [Google Scholar]
- [52].Valero C, Javierre E, García-Aznar JM, Gómez-Benito MJ, A cell-regulatory mechanism involving feedback between contraction and tissue formation guides wound healing progression, PloS One 9 (3) (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Emmert MY, Schmitt BA, Loerakker S, Sanders B, Spriestersbach H, Fioretta ES, Bruder L, Brakmann K, Motta SE, Lintas V., et al. , Computational modeling guides tissue-engineered heart valve design for long-term in vivo performance in a translational sheep model, Science Translational Medicine 10 (440) (2018). [DOI] [PubMed] [Google Scholar]
- [54].De Jesus AM, Aghvami M, Sander EA, A combined in vitro imaging and multi-scale modeling system for studying the role of cell matrix interactions in cutaneous wound healing, PloS One 11 (2) (2016) e0148254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Barocas V, Tranquillo R., An anisotropic biphasic theory of tissue-equivalent mechanics: the interplay among cell traction, fibrillar network deformation, fibril alignment, and cell contact guidance., Journal of Biomechanical Engineering 119 (2) (1997) 137–145. [DOI] [PubMed] [Google Scholar]
- [56].Loerakker S, Obbink-Huizer C, Baaijens FP, A physically motivated constitutive model for cell-mediated compaction and collagen remodeling in soft tissues, Biomechanics and Modeling in Mechanobiology 13 (5) (2014) 985–1001. [DOI] [PubMed] [Google Scholar]
- [57].Moreo P, García-Aznar JM, Doblaré M., Modeling mechanosensing and its effect on the migration and proliferation of adherent cells, Acta Biomaterialia 4 (3) (2008) 613–621. [DOI] [PubMed] [Google Scholar]
- [58].Faris O, Shuren J., An FDA viewpoint on unique considerations for medical-device clinical trials, New England Journal of Medicine 376 (14) (2017) 1350–1357. [DOI] [PubMed] [Google Scholar]
- [59].Brewick PT, Teferra K., Uncertainty quantification for constitutive model calibration of brain tissue, Journal of the Mechanical Behavior of Biomedical Materials 85 (2018) 237–255. [DOI] [PubMed] [Google Scholar]
- [60].Tonge TK, Atlan LS, Voo LM, Nguyen TD, Full-field bulge test for planar anisotropic tissues: Part i–experimental methods applied to human skin tissue, Acta biomaterialia 9 (4) (2013) 5913–5925. [DOI] [PubMed] [Google Scholar]
- [61].Lee T, Turin SY, Gosain AK, Bilionis I, Buganza Tepole A., Propagation of material behavior uncertainty in a nonlinear finite element model of reconstructive surgery, Biomechanics and Modeling in Mechanobiology 17 (6) (2018) 1857–1873. [DOI] [PubMed] [Google Scholar]
- [62].Shergold OA, Fleck NA, Radford D., The uniaxial stress versus strain response of pig skin and silicone rubber at low and high strain rates, International Journal of Impact Engineering 32 (9) (2006) 1384–1402. [Google Scholar]
- [63].Ottenio M, Tran D, Annaidh AN, Gilchrist MD, Bruyère K., Strain rate and anisotropy effects on the tensile failure characteristics of human skin, Journal of the mechanical behavior of biomedical materials 41 (2015) 241–250. [DOI] [PubMed] [Google Scholar]
- [64].Pissarenko A, Yang W, Quan H, Brown KA, Williams A, Proud WG, Meyers MA, Tensile behavior and structural characterization of pig dermis, Acta biomaterialia 86 (2019) 77–95. [DOI] [PubMed] [Google Scholar]
- [65].Abreu EL, Palmer MP, Murray MM, Collagen density significantly affects the functional properties of an engineered provisional scaffold, Journal of Biomedical Materials Research Part A: An Official Journal of The Society for Biomaterials, The Japanese Society for Biomaterials, and The Australian Society for Biomaterials and the Korean Society for Biomaterials 93 (1) (2010) 150–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Chen S, Shi J, Xu X, Ding J, Zhong W, Zhang L, Xing M, Zhang L., Study of stiffness effects of poly (amidoamine)–poly (n-isopropyl acrylamide) hydrogel on wound healing, Colloids and Surfaces B: Biointerfaces 140 (2016) 574–582. [DOI] [PubMed] [Google Scholar]
- [67].Cumming BD, McElwain D, Upton Z., A mathematical model of wound healing and subsequent scarring, Journal of The Royal Society Interface 7 (42) (2010) 19–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Harrison CA, MacNeil S., The mechanism of skin graft contraction: an update on current research and potential future therapies, Burns 34 (2) (2008) 153–163. [DOI] [PubMed] [Google Scholar]
- [69].Wong AK, Schonmeyer BH, Singh P, Carlson DL, Li S, Mehrara BJ, Histologic analysis of angiogenesis and lymphangiogenesis in acellular human dermis, Plastic and Reconstructive Surgery 121 (4) (2008) 1144–1152. [DOI] [PubMed] [Google Scholar]
- [70].Haifei S, Xingang W, Shoucheng W, Zhengwei M, Chuangang Y, Chunmao H., The effect of collagen–chitosan porous scaffold thickness on dermal regeneration in a one-stage grafting procedure, journal of the mechanical behavior of biomedical materials 29 (2014) 114–125. [DOI] [PubMed] [Google Scholar]
- [71].Soller EC, Tzeranis DS, Miu K, So PT, Yannas IV, Common features of optimal collagen scaffolds that disrupt wound contraction and enhance regeneration both in peripheral nerves and in skin, Biomaterials 33 (19) (2012) 4783–4791. [DOI] [PubMed] [Google Scholar]
- [72].Yannas IV, Tzeranis DS, So PT, Regeneration of injured skin and peripheral nerves requires control of wound contraction, not scar formation, Wound Repair and Regeneration 25 (2) (2017) 177–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Lee T, Gosain AK, Bilionis I, Tepole AB, Predicting the effect of aging and defect size on the stress profiles of skin from advancement, rotation and transposition flap surgeries, Journal of the Mechanics and Physics of Solids 125 (2019) 572–590. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


