Step-adjusted Tree-based Reinforcement Learning (SAT-Learning) for Evaluating Nested Dynamic Treatment Regimes using Test-and-Treat Observational Data

Abstract

Dynamic treatment regimes (DTRs) include a sequence of treatment decision rules, in which treatment is adapted over time in response to the changes in an individual’s disease progression and health care history. In medical practice, nested test-and-treat strategies are common to improve cost-effectiveness. For example, for patients at risk of prostate cancer, only patients who have high prostate-specific antigen (PSA) need a biopsy, which is costly and invasive, to confirm the diagnosis and help determine the treatment if needed. A decision about treatment happens after the biopsy, and is thus nested within the decision of whether to do the test. However, current existing statistical methods are not able to accommodate such a naturally embedded property of the treatment decision within the test decision. Therefore, we developed a new statistical learning method, Step-adjusted Tree-based Reinforcement Learning, to evaluate DTRs within such a nested multi-stage dynamic decision framework using observational data. At each step within each stage, we combined the robust semi-parametric estimation via Augmented Inverse Probability Weighting with a tree-based reinforcement learning method to deal with the counterfactual optimization. The simulation studies demonstrated robust performance of the proposed methods under different scenarios. We further applied our method to evaluate the necessity of prostate biopsy and identify the optimal test-and-treat regimes for prostate cancer patients using data from the Johns Hopkins University prostate cancer active surveillance dataset.

1 |. INTRODUCTION

Dynamic treatment regimes (DTRs) have gained increasing interest in the field of precision medicine in the last decade.¹ This research direction generalizes the individualized medical decisions into a time-varying treatment setting, usually at discrete stages, and thus accommodates the updated information for each person at each stage.^2,3 In DTR, actions or decisions based on the individualized features are able to lead to more precise disease prevention and better disease management. However, the current DTR framework is limited when the action of one treatment is nested within the action of another. A more intuitive example that explains the limitation in practice is a test-and-treat scenario: the treatment action only happens after the happening of a diagnostic test action, which means that the treatment action cannot happen when the diagnostic test result is not available. In particular, in medical practice, the procedures to diagnose and treat patients are much more complicated. Most diagnosis procedures or tests, e.g., positron emission tomography, or a biopsy test, occur prior to the selection of treatment to provide more information about disease status, then this information would be used to select treatment. Typically, only patients who have taken the test can be treated, and thus the decision about the treatment assignment is nested within the decision of performing the test.

For example, men with early stage asymptomatic prostate cancer who are in an active surveillance program, would regularly have their prostate-specific antigen (PSA) and prostate tissue measured via a blood test and core needle biopsy test respectively.⁴ Whether to undergo definitive treatment for their prostate cancer would be strongly influenced by the results from their biopsy test. So the possible treatment initiation only happens after having the biopsy test result, and is thus nested within the decision of doing a biopsy or not. Such a nested dynamic clinical decision-making is not limited to prostate cancer. The occult blood test, also known as a stool test, can also be used as a cheap and easy initial screening test for colorectal cancer.⁵ Patients with abnormal finding from the stool test are then referred for a colonoscopy exam, which is costly and invasive, to confirm the diagnosis and decide if more definitive treatment for colorectal cancer is needed. In this scenario the decision of whether to do definitive treatment is nested in the decision of whether to do a colonoscopy which is nested within the decision to do a stool test or not. This kind of nested clinical decision also happens with many other chronic diseases.⁶

In such nested test-and-treat scenarios, the impact of the test should also be considered. For some diseases, the tests used to confirm the diagnosis or decide on the next step are easy to administer and minimally invasive, e.g., blood test and physical examination. But some other tests done for confirmatory purposes are expensive and invasive, including the prostate biopsy and colonoscopy. The potential side effects include pain, soreness, and infections, which should not be overlooked. For prostate cancer, even if the test result suggests progressive disease, it is not always the case that the patient should undergo definitive treatment, which has substantial comorbidity, since prostate cancer is a slow growing disease and a substantial number of men may not develop deadly prostate cancer before dying from some other cause. It is well known that there is overtreatment for prostate cancer, and that a substantial number of men receive unnecessary cancer treatments.⁴ Therefore, careful patient selection for testing is needed to not only reduce the impact on the patient, but also to save medical resources for the patients who truly need them. The current one-fits-all active surveillance protocol is not capable of taking the patient’s personalized medical characteristics into account and then giving an individualized disease management plan.

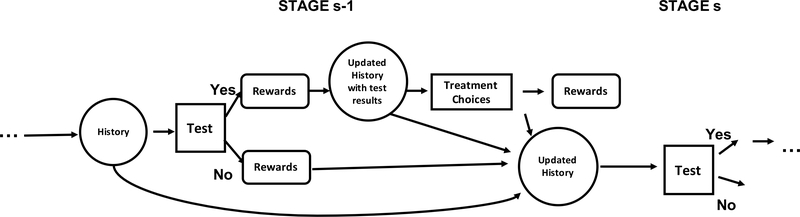
As mentioned above, most existing frameworks using the standard formulation for evaluating DTRs overlook or simplify^7,8,9 such a test-and-treat nested structure during the clinical decision making process. The diagnostic test itself dose not have a direct impact on the disease related outcome, but the potential treatment following the test may improve the disease outcome for the patient substantially. On the other hand, the patient without a diagnostic test at all will not have the health benefit gained from the treatment step. Instead of simply understanding the test and treat as two sequential actions, we distinguish them to emphasize their nested relationship. Overlooking such a test-and-treat nested structure may result in identifying imprecise and non-realistic decision rules especially by applying backward induction. Although the information of previous test and treat history may have been adequately captured, when the general formulation is applied in the treatment step, patients who did not have the test are also included into the decision-making of the treatment steps. The method that applies the standard formulation could inevitably provide an optimal treatment strategy for a patient even without a test. Such a resulting treatment strategy is not compatible with their observed data. Therefore, we propose a new nested dynamic treatment regime (nested-DTR) framework by embedding the treatment step within the test step of each intervention stage as shown in Figure 1. This proposed framework specifically demonstrates how to modify the standard method in the implementation steps to incorporate the nested relationships, implement the restricted optimization, and guarantee the estimation results are compatible with the needs raised from the biomedical problems themselves.

FIGURE 1.

Hypothetical step-adjusted DTR with a treatment step nested within the test step of each intervention stage. The decision of the test step is made based on the health history and the treatment decision is made on the basis of previous health history and the updated history after the test.

In general, DTRs can be estimated from observational data, provided there is enough heterogeneity in the patient features and their actions taken. Similarly the optimal DTR for this new nested-DTR framework can be learned from observational data provided there is enough heterogeneity in data for both the decision to test and the decision to treat.

In addition to extensive work on value of information methods in operations engineering and computer science within the framework of health policy-making^10,11, a great number of statistical methods have been developed to estimate the optimal DTRs using observational data, such as Marginal Structural Model estimated with inverse probability weighting¹², the Marginal Mean Model¹³ and other likelihood-based methods.¹⁴ These methods require a parametric or semi-parametric conditional model for the counterfactual outcome as a component and thus are vulnerable to model mis-specification, especially when the data are high dimensional or time-dependent information is accumulated. More recently, machine learning-based approaches, as a replacement for parametric or semi-parametric models, have become increasingly popular because of their flexibility in model assumptions and their robustness.^8,15 When identifying the optimal DTRs with multiple stages, the problem resembles the reinforcement learning (RL) problem.¹⁶ Therefore, RL methods are currently broadly applied in evaluating the optimal DTRs. Some of this work, which involving reinforcement learning, has focused on developing easily interpretable DTRs for real-world practice.^17,18,19

To the best of our knowledge, however, none of the existing methods can be applied directly to estimate the optimal DTRs when each stage consists of a treatment step nested within a test step. In this paper, we are trying to fill this gap and develop a new non-parametric statistical learning method for identifying the optimal DTR within the nested dynamic decision framework. At each step within each stage, we combine the robust semi-parametric estimator obtained using Augmented Inverse Probability Weighting (AIPW) with a modified tree-based reinforcement learning method to optimize the expected counterfactual outcome. The incorporation of the AIPW estimator facilitates the robustness of the estimated optimal dynamic treatment regime while the tree-based reinforcement learning method is able to provide an interpretable optimal strategy. The remainder of this paper is organized as follows: In Section 2 and 3, we formalize the problem of identifying the optimal DTR within the nested DTR framework in a multiple-stage multiple-step setting from observational data and develop the nested step-adjusted tree-based reinforcement learning method (SAT-Learning). Section 4 presents the detailed implementation of this new method. Numerical simulation studies and an application to the Johns Hopkins University (JHU) prostate cancer active surveillance data are provided in Sections 5 and 6. We conclude with a brief discussion in Section 7.

2 |. MULTIPLE-STAGE NESTED STEP-ADJUSTED DYNAMIC TREATMENT REGIMES

To address the nested decision problem above, we consider a nested multi-stage multi-step decision framework with S decision stages. In clinical practice, every regular clinic visit, which might initiate some form of treatment, can be considered as a stage. Within each stage s, there are J action steps. Let K_sj denote the number of decision options at step j of stage s (K_sj ≥ 2), let D_sj denote the multiple treatment indicators of the action taken at step j of stage s in the observed data, and the value of D_sj is $d_{sj}\in {\mathcal{D}}_{sj}$. Without loss of generality, we consider two steps within each stage, i.e., J = 2, to make the presentation easier. We assume the first step of stage s is the test step (action D_s1) and D_s2 in the treatment step is nested within the decision of D_s1. For example, only the prostate cancer patients who have had the biopsy test are considered for further treatment. We denote the patient’s history prior to action D_sj but after the previous step as X_sj. We will use overbar with subscripts s and j to denote a vector of a variables’s history up to the step j of stage s. For example, ${\overline{X}}_{s2}=\left(X_{11},X_{12},X_{21},\dots ,X_{s1},X_{s2}\right)$. Similarly, the action history up to the treatment step of stage s can be denoted as ${\overline{D}}_{s2}=\left(D_{11},D_{12},D_{21},\dots ,D_{s1}\right)$.

We use Y_sj to denote the intermediate reward outcome at the end of step j of the stage s, and thus the overall rewards vector is (Y₁₁, Y₁₂,…Y_S2). The outcome of interest Y is a function of all rewards, i.e., Y = f(Y₁₁, Y₁₂, Y₂₁,…Y_S2), where f(·) is a pre-specified function (e.g., sum). We also assume that Y is bounded and high values of Y are desirable. The observed data before stage s step j (1 ≤ s ≤ S, 1 ≤ j ≤ 2) are

$${\left\{X_{11},D_{11},Y_{11},X_{12},\dots ,D_{s-1,2},Y_{s-1,2},X_{s1}\right\}}_{i=1}^n\equiv {\left\{{\overline{X}}_{s1},{\overline{D}}_{s-1,2},{\overline{Y}}_{s-1,2}\right\}}_{i=1}^n$$

for step 1, and

$${\left\{X_{11},D_{11},Y_{11},X_{12},\dots ,X_{s1},D_{s1},Y_{s1},X_{s2}\right\}}_{i=1}^n\equiv {\left\{{\overline{X}}_{s2},{\overline{D}}_{s1},{\overline{Y}}_{s1}\right\}}_{i=1}^n$$

for step 2. For brevity, we suppress the subject index i in the following text when no confusion exists. The observed data are assumed to be independent and identically distributed for n subject from the population of interest. The history H_sj is defined as the test results and action history prior to the action assignment D_sj. To be more specific, ${\mathbf{H}}_{s1}=({\overline{D}}_{s-1,2},{\overline{X}}_{s1},{\overline{Y}}_{s-1,2})$ and ${\mathbf{H}}_{s2}=\left({\overline{D}}_{s1},{\overline{X}}_{s2},{\overline{Y}}_{s1}\right)$. To illustrate the method, we also specify two action options in the test step and three options in the treatment step of every stage, i.e., $d_{s1}\in {\mathcal{D}}_{s1}=\{0,1\}$, K_s1 = 2, and $d_{s2}\in {\mathcal{D}}_{s2}=\{0,1,2\}$, K_s2 = 3. When a patient has d_sj = 0, i.e. no treatment or test is given, they will still be kept in the study cohort but not given further treatment until the next stage s + 1. Thus, the reward is Y_sj = 0 when d_sj = 0. A slight modification of this occurs in our illustrative example using the JHU Active Surveillance (AS) dataset. In AS, if a patient receives treatment in some treatment step, i.e., d_s2 = 1 or 2, they no longer needs further tests or treatments, thus would be removed from the study from that time onwards. However, as long as their reward Y is available, their data from already observed steps would still be used in the estimation method by specifying d_s′₁ = 0 and d_s′₂ = 0, where s′ > s.

With a treatment step nested after every test step within a stage, the nested DTR is defined as a personalized test-and-treatment rule sequence. The rule is based on the observed history H_sj about the patient’s health status up to the action in step j of stage s. Let g denote the above nested DTR. Formally, g = (g₁₁, g₁₂,…, g_S2) is defined by a collection of mapping functions, where g_sj is mapped from the domain of history H_sj to the domain of D_sj, i.e.,

$${\mathbf{H}}_{sj}\mapsto g_{sj}\left({\mathbf{H}}_{sj}\right)\in {\mathcal{D}}_{sj},1\le s<S,1\le j\le 2$$

3 |. STEP-ADJUSTED OPTIMIZATION FOR NESTED DTR

Let Y^∗(g) be the counterfactual outcome if all patients follow g to assign treatment or test conditional on previous history. The performance of g is measured by the counterfactual mean outcome E{Y^∗(g)} conditional on the patients’ history. We denote the optimal regime as g^opt. Our goal of identifying the optimal regime is to find the g^opt which satisfies

$$E\left\{Y^{*}\left({\mathbf{g}}^{opt}\right)\right\}\ge E\left\{Y^{*}(\mathbf{g})\right\}$$

for all $\mathbf{g}\in \mathcal{G}$, where $\mathcal{G}$ is the set of all potential regimes.

3.1 |. Optimization of g_S2 and g_S1 for the last stage S

The approach to finding optimal DTR includes backward induction¹³, therefore we illustrate the mathematical formulation from the last stage S. For the last step of the stage, let $Y_{S2}^{*}\left(d_{S2}\right)$ be the counterfactual outcome if a patient makes treatment decision d_S2 conditional on previous history. We denote the optimal regime as $g_{S2}^{opt}$, which satisfies $g_{S2}\in {\mathcal{G}}_{S2}$ for all $E\left\{Y_{S2}^{*}\left(g_{S2}^{opt}\right)\right\}\ge E\left\{Y_{S2}^{*}\left(g_{S2}\right)\right\}$, where ${\mathcal{G}}_{S2}$ is the set of all potential regimes at stage S and step 2.

To connect the counterfactual outcome with observed data $\left\{{\overline{X}}_{S2},{\overline{D}}_{S2},{\overline{Y}}_{S2}\right\}$, we make the following standard casual inference assumptions²:

1. Consistency. The observed outcome coincides with the counterfactual outcome under the treatment a patient is actually given, i.e.,

   $$Y_{S2}=\sum _{d_{S2}\in {\mathcal{D}}_{S2}}{Y}_{S2}^{*}\left(d_{S2}\right)I\left\{g_{S2}\left({\mathbf{H}}_{S2}\right)=d_{S2}\right\}I\left\{d_{S1}=1\right\},$$

   where I(·) is the indicator function that takes the value 1 if · is true and 0 otherwise. The indicator function I(d_S1 = 1) implies only the subjects who decided to take the previous test, i.e., d_S1 = 1, can have their Y_S2 observed.

2. No unmeasured confounding. The observed action D_S2 is independent of potential counterfactual outcomes conditional on the history H_S2, i.e.,

   $$D_{S2}\perp \left\{Y_{S2}^{*}(0),Y_{S2}^{*}(1),Y_{S2}^{*}(2)\right\}\mid {\mathbf{H}}_{S2},$$

   where ⊥ denotes statistical independence. This assumption implies that the potential confounders are fully observed and included in the dataset.

3. Positivity. For the observational data, the propensity score ${\pi }_{d_{S2}}\left({\mathbf{H}}_{S2}\right)$, the probability of receiving a certain treatment conditional on history, is bounded away from 0 and 1, i.e., ${\pi }_{d_{S2}}\left({\mathbf{H}}_{S2}\right)=Pr\left(D_{S2}=d_{S2}\mid {\mathbf{H}}_{S2}\right)\in \left[c_1,c_2\right]$, where 0 < c₁ < c₂ < 1.

For the subjects who do not have the test in the previous step, i.e., d_S1 = 0, their test result that the further treatment decision is based on cannot be observed. Therefore, only the subjects with d_S1 = 1 is able to contribute to the optimization of g_S2. Under the three assumptions, the optimization problem for the treatment of the last stage becomes

$$\begin{gathered} g_{S2}^{opt}\left({\mathbf{H}}_{S2}\right)=\mathit{arg}\underset{g_{S2}\in {\mathcal{G}}_{S2}}{\max }{E}_{{\mathbf{H}}_{S2}}(\sum _{d_{S2}\in {\mathcal{D}}_{S2}}E\left(Y_{S2}\mid D_{S2}=d_{S2},{\mathbf{H}}_{S2}\right) \\ I\left[g_{S2}\left({\mathbf{H}}_{S2}\right)=d_{S2}\right]I\left(d_{S1}=1\right)), \end{gathered}$$ (1)

where $E_{{\mathbf{H}}_{S2}}(.)$ denotes the expectation with respect to the marginal joint distribution of the observed history H_S2. To derive the optimal $g_{S1}^{opt}$ for whether to take the test, i.e., one step before the treatment step within the same stage S, we utilize the backwards induction.² In addition to the counterfactual outcome of stage s step j $Y_{sj}^{*}$ defined in the last section, we also define a nested step-adjusted future optimized counterfactual outcome ${\tilde{Y}}_{S1}^{*}$. More specifically, we have ${\tilde{Y}}_{S1}^{*}=\left\{Y^{*}\left({\overline{D}}_{S-1,2},g_{S1},g_{S2}^{opt}\right)\right\}$, where the treatment for stage S step 2 has been optimized. To determine the optimal $g_{S1}^{opt}$, we propose to maximize the expected nested step-adjusted future optimized counterfactual outcome ${\tilde{Y}}_{S1}^{*}$, i.e., $g_{S1}^{opt}=\arg {\max }_{g_{S1}\in {\mathcal{G}}_{S1}}{E}_{{\mathbf{H}}_{S1}}\left[\left\{Y^{*}\left({\overline{D}}_{S-1,2},g_{S1},g_{S2}^{opt}\right)\right\}\right]$. Similarly, we assume No Unmeasured Confounding, $D_{S1}\perp \left\{{\tilde{Y}}_{S1}^{*}(0),{\tilde{Y}}_{S1}^{*}(1)\right\}\mid {\mathbf{H}}_{s1}$, if d_S1 = 1 and $D_{S1}\perp \left\{Y_{S1}^{*}(0),Y_{S1}^{*}(1)\right\}\mid {\mathbf{H}}_{s1}$, if d_S1 = 0; Positivity ${\pi }_{d_{S1}}\left({\mathbf{H}}_{S1}\right)=Pr\left(D_{S1}=d_{S1}\mid {\mathbf{H}}_{sj}\right)\in \left[c_1,c_2\right]$, where0 < c₁ < c₂ < 1; and then the optimization problem of stage S step 1 can be written as

$$\begin{gathered} g_{S1}^{opt}=\arg \underset{g_{S1}\in {\mathcal{G}}_{S1}}{\max }{E}_{{\mathbf{H}}_{S1}}[\sum _{d_{S1}\in D_{S1}}\{E[{\tilde{Y}}_{S1}^{*}\mid D_{S1}=d_{S1},{\mathbf{H}}_{S1}]I\left(d_{S1}=1\right) \\ +E[Y_{S1}^{*}\mid D_{S1}=d_{S1},{\mathbf{H}}_{S1}]I\left(d_{S1}=0\right)\}I\left\{g_{S1}\left({\mathbf{H}}_{S1}\right)=d_{S1}\right\}]. \end{gathered}$$ (2)

Different from (1), the optimization process (2) of $g_{S1}^{opt}$ is conducted within all eligible subjects, while the optimization of $g_{S2}^{opt}$ is conducted only within the patients who have the test at the previous step. Although the whole cohort contributes to the optimization step in (2), ${\tilde{Y}}_{S1}^{*}$ or $Y_{S1}^{*}$ used in (2) actually depends on the test decision, i.e., d_S1. The subjects who had the test, i.e., d_S1 = 1, essentially have one more chance to optimize their rewards through stage S step 2 compared to those without test, and this chance is nested within the positive exam decision within the same stage.

3.2 |. Optimization of g_s2 and g_s1 for any previous stage before S

For the steps of stage s before the last stage (1 ≤ s < S), the optimal regime $g_{S1}^{opt}$ and $g_{S2}^{opt}$ is expressed via backward induction as well. ${\tilde{Y}}_{sj}^{*}$ is defined as the nested step-adjusted future optimized counterfactual reward, which is given that all future stages’ and steps’ actions are already optimized. More specifically, we have ${\tilde{Y}}_{s1}^{*}\left(g_{s1}\right)=\left\{Y^{*}\left({\overline{D}}_{s-1,2},g_{s1},g_{s2}^{opt},\dots ,g_{S2}^{opt}\right)\right\}$ and ${\tilde{Y}}_{s2}^{*}\left(g_{s2}\right)=\left\{Y^{*}\left({\overline{D}}_{s1},g_{s2},g_{s+1,1}^{opt},\dots ,g_{S2}^{opt}\right)\right\}$. Similar to the assumptions for the last stage, we assume No Unmeasured Confounding and Positivity. Under these assumptions, the optimization problems at stage s step j can be written as

$$g_{s1}^{opt}=\arg \underset{g_{s1}\in {\mathcal{G}}_{s1}}{\max }{E}_{{\mathbf{H}}_{s1}}\left[\sum _{d_{s1}\in {\mathcal{D}}_{s1}}E\left[{\tilde{Y}}_{s1}^{*}\mid D_{s1}=d_{s1},{\mathbf{H}}_{s1}\right]I\left\{g_{s1}\left({\mathbf{H}}_{s1}\right)=d_{s1}\right\}\right]$$ (3)

and

$$g_{s2}^{opt}=\arg \underset{g_s\in {\mathcal{C}}_{s2}}{\max }{E}_{{\mathbf{H}}_{s2}}\left[\sum _{d_s\in {\mathcal{D}}_{s2}}E\left[{\tilde{Y}}_{s2}^{*}\mid D_{s2}=d_{s2},{\mathbf{H}}_{s2}\right]I\left\{g_{s2}\left({\mathbf{H}}_{s2}\right)=d_{s2}\right\}I\left(d_{s1}=1\right)\right].$$ (4)

4 |. STEP-ADJUSTED TREE-BASED REINFORCEMENT LEARNING AND ITS IMPLEMENTATIONS

Given the observational data with test-and-treat nested decision structure, we propose to solve (1), (2), (3), and (4) through the step-adjusted tree-based learning (SAT-Learning) method. In this method, the step-adjusted future optimized pseudo-outcome is iteratively inducted backwards. We further assume, for stages and steps before the last step, i.e., for any s < S, j = 1 or 2, the effect of intermediate outcome reward Y_sj will be cumulatively carried forward to the final outcome²⁰, and denote a nested step-adjusted future optimized pseudo-outcome of stage s step j as PO_sj. Let ${\widehat{\mu }}_{sj,d_{sj}}\left({\mathbf{H}}_{sj}\right)=\widehat{E}\left[P{O}_{sj}\mid D_{sj}=d_{sj},{\mathbf{H}}_{sj}\right]$ be the estimated mean pseudo-outcome of stage s step j. Because of the cumulative property of the reward outcome and the nested connection between the test step and the treatment step, for any s < S, j = 1 or 2, PO_sj can be expressed in a recursive form as $P{O}_{s1}=Y_{s1}+{\sum }_{r=s}^S{\mu }_{r2,g_{r2}^{opt}}\left({\mathbf{H}}_{r2}\right)\times I\left(d_{r1}=1\right)+{\sum }_{r=s+1}^S{\mu }_{r1,g_{r1}^{opt}}\left({\mathbf{H}}_{r1}\right)$ and $P{O}_{s2}=Y_{s1}+{\sum }_{r=s+1}^S[{\mu }_{r2,g_{r2}^{opt}}\left({\mathbf{H}}_{r2}\right)\times I\left(d_{r1}=1\right)+{\mu }_{r1,g_{r1}^{opt}}\left({\mathbf{H}}_{r1}\right)]$. Obviously, when evaluating the pseudo-outcome in last stage, we have PO_S2 = Y_S2 for the second step and $P{O}_{S1}=Y_{s1}+{\mu }_{S1,g_{S1}^{opt}}\left({\mathbf{H}}_{S1}\right)\times I\left(d_{S1}=1\right)$ for the first step.

To reduce the accumulated bias from the conditional mean models, instead of using the model-based values under optimal future treatments ${\widehat{\mu }}_{sj,d_{sj}}\left({\mathbf{H}}_{sj}\right)=\widehat{E}\left[P{O}_{sj}\mid D_{sj}=d_{sj},{\mathbf{H}}_{sj}\right]$ from PO_sj, we use the actual observed intermediate outcomes plus the expected future loss (or gain) due to the sub-optimal treatments as the modified pseudo-outcome $P{O}_{sj}^{\prime }$.²⁰ Specifically, the modified pseudo-outcome of the last stage is $P{O}_{S2}^{\prime }=Y_{S2}$, $P{O}_{S1}^{\prime }=Y_{S1}+{\mu }_{S2,g_{S2}^{opt}}\left({\mathbf{H}}_{S2}\right)-{\mu }_{S2,D_{S2}}\left({\mathbf{H}}_{S2}\right)+Y_{S2}$ and for any s < S, j = 1 or 2,

$$\begin{gathered} P{O}_{sj}^{\prime }=\sum _{r=s+1}^S\left[{\mu }_{r1,g_{r1}^{opt}}\left({\mathbf{H}}_{r1}\right)-{\mu }_{r1,D_{r1}}\left({\mathbf{H}}_{r1}\right)+Y_{r1}+I\left[d_{r1}=1\right][{\mu }_{r2,g_{r2}^{opt}}\left({\mathbf{H}}_{r2}\right)-{\mu }_{r2,D_{r2}}\left({\mathbf{H}}_{r2}\right)+Y_{r2}]\right] \\ +Y_{sj}+I[j=1]I\left[d_{sj}=1\right]\left[{\mu }_{s2,g_{s2}^{opt}}\left({\mathbf{H}}_{s2}\right)-{\mu }_{s2,D_{s2}}\left({\mathbf{H}}_{s2}\right)+Y_{s2}\right] \end{gathered}$$ (5)

In particular, if the subject undergoes the test at stage s, i.e., d_s1 = 1, they might benefit from the potential subsequent treatment within that stage via the optimization of the future treatment step. If the subject does not receive the test at stage s, then their future optimized counterfactual outcome can only be optimized through the optimal actions of the future stages.

We propose to implement SAT-Learning through a modified version of a tree-based reinforcement learning method (T-RL)¹⁷, which employs the classification and regression tree (CART).²¹ In the nested DTR setting, we need to include the step-wise adjustment to account for the nested test-and-treat nature. Thus, we developed a modified tree-based algorithm to implement SAT-Learning for estimating the optimal nested DTR. Traditionally, the decision tree of CART is built to choose a split that would have the purest child nodes. The purest node means having the lowest misclassification rate among all possible nodes. Thus, purity is a crucial measure to grow a decision tree. Different from CART, SAT-Learning at each node selects the split to improve the counterfactual mean reward, which can serve as a measure of purity in nested DTR trees, and then maximizes the population’s counterfactual mean reward of interest. Similarly as in T-RL, to estimate the optimal DTR, we use a purity measure for SAT-Learning based on the augmented inverse probability weighting (AIPW) estimator of the counterfactual mean outcome.

In the process of partitioning of this tree-based reinforcement learning method, for a given partition ω and ω^c of node Ω, let $g_{sj,\omega ,d_1,d_2}$ denote the decision rule that assigns a single test/treatment action d₁ to all subjects in ω and treatment d₂ to subjects in ω^c at stage s step j (1 ≤ s ≤ S, j = 1, 2). Then the purity measure can be defined as

$${\mathcal{P}}_{sj}(\mathrm{\Omega },\omega )=\underset{d_1,d_2\in {\mathcal{D}}_{sj}}{\max }{\mathbb{P}}_n\left[\sum _{d_{sj}=1}^{K_{sj}}{\widehat{\mu }}_{sj,d_{sj}}^{AIPW}\left({\mathbf{H}}_{sj}\right)I\left\{g_{sj,\omega ,d_1,d_2}\left({\mathbf{H}}_{sj}\right)=d_{sj}\right\}I\left({\mathbf{H}}_{sj}\in \mathrm{\Omega }\right)\right],$$ (6)

where ${\mathbb{P}}_n$ is the empirical expectation operator and ${\mathbb{P}}_n\left\{{\widehat{\mu }}_{sj,d_{sj}}^{AIPW}\left({\mathbf{H}}_{\text{sj}}\right)\right\}$ is the AIPW estimator of the counterfactual mean outcome with

$${\widehat{\mu }}_{sj,d_{sj}}^{AIPW}\left({\mathbf{H}}_{sj}\right)=\frac{I\left(D_{sj}=d_{sj}\right)}{{\widehat{\pi }}_{sj,d_{sj}}\left({\mathbf{H}}_{\text{sj}}\right)}{Y}_{sj}+\left\{1-\frac{I\left(D_{sj}=d_{sj}\right)}{{\widehat{\pi }}_{sj,d_{sj}}\left({\mathbf{H}}_{\text{sj}}\right)}\right\}{\widehat{\mu }}_{sj,d_{sj}}\left({\mathbf{H}}_{\text{sj}}\right).$$ (7)

In (7), the propensity score model is denoted as ${\pi }_{sj,d_{sj}}\left({\mathbf{H}}_{\mathbf{s}\mathbf{j}}\right)$ and the conditional mean model is denoted as ${\mu }_{sj,d_{sj}}\left({\mathbf{H}}_{\mathbf{s}\mathbf{j}}\right)$. Under the foregoing three causal inference assumptions, ${\mathbb{P}}_n\left\{{\widehat{\mu }}_{sj,d_{sj}}^{AIPW}\left({\mathbf{H}}_{\text{sj}}\right)\right\}$ is a consistent estimator of the counterfactual mean outcome E{Y^∗(d_sj)} if either the propensity score model ${\pi }_{sj,d_{sj}}\left({\mathbf{H}}_{\mathbf{s}\mathbf{j}}\right)$ or the conditional mean model ${\mu }_{sj,d_{sj}}\left({\mathbf{H}}_{\mathbf{s}\mathbf{j}}\right)$ is correctly specified. Thus this AIPW estimator is doubly robust for estimating the counterfactual mean outcome of the population.¹⁸

In our nested step-adjusted multi-stage setting, for the last step of the last stage, S2, we have Y_S2 in (7) as the observed reward of the last step of the last stage. For other stage s step j before the last one (1 ≤ s < S, j = 1, 2 or s = S, j = 1), Y_sj in (7) is replaced with ${\widehat{PO}}_{sj}^{\prime }$, the corresponding pseudo-outcome defined in (5).

In the process of maximizing ${\mathcal{P}}_{sj}(\mathrm{\Omega },\omega )$, the possible split ω of a given node Ω should be either a subset of a categorical covariate categories or values that are not larger than the threshold. The best criteria ${\widehat{\omega }}^{opt}$ to split a given node is a partition that is able to maximize the improvement in the purity, ${\mathcal{P}}_{sj}(\mathrm{\Omega },\omega )-{\mathcal{P}}_{sj}(\mathrm{\Omega })$, where ${\mathcal{P}}_{sj}(\mathrm{\Omega })$ is for the situation where we assign the same single test/treatment action to all subject in Ω, i.e., no splitting. To control the overfitting and also make practical and meaningful splits, a positive integer n₀ is specified as the minimal node size and a positive constant λ is also provided as a threshold for the meaningful improvement. Besides the two given constant values λ and n₀, we apply similar Stopping Rules as in¹⁷ to grow and split the tree. Our Stopping Rules can be found in the Supplementary materials as Algorithm 1. The depth of a node mentioned in the stopping rules is defined as the number of edges from the node to the tree’s root node, and a root node has a depth of 0. The nested SAT-Learning algorithm given the above purity measures and stopping rules of the partitioning is presented in Algorithm 2 with details. (Also provided in the Supplementary materials). Note the essential difference between steps j=2 and j=1 is that different subjects are included into the calculation of the AIPW estimator. Only the subjects who have taken the test at stage s, i.e., d_s1 = 1, contribute to the optimization of their subsequent treatments.

When implementing SAT-Learning process, the propensity score ${\widehat{\pi }}_{sj,d_{sj}}\left({\mathbf{H}}_{sj}\right)$ in (7) can be estimated by a multinomial logistic regression model. This working model could incorporate linear main effect terms from history H_sj and summary variables or interaction terms based on prior scientific knowledge from individual history H_sj. For continuous outcome, the conditional mean estimates ${\widehat{\mu }}_{sj,d_{sj}}\left({\mathbf{H}}_{sj}\right)$ in (7) could be obtained either from a linear parametric regression model or from other off-the-shelf non-parametric machine learning methods, such as random forests or support vector regression, depending on the history H_sj and the test/treatment action D_sj. For estimating the conditional mean model for binary or other count outcomes, one could use a generalized linear models or other generalized classification tools in machine learning.

5 |. SIMULATION STUDIES

5.1 |. Simulation Studies to Evaluate the General Test-and-treat Nested DTR

We generate simulation study data that mimic the real-world observational test-and-treat study. We assume a two-stage two-step nested dynamic treatment regime, using D_sj with subscript value s = 1, 2 to represent the stage and j = 1, 2 to represent the test and treatment action within each stage. More specifically, we set two options in the test step as d_s1 = 1 or 0 to indicate receiving the test or not, and three treatment options in the treatment step as d_s2 = 0, 1 or 2. We further define the outcome of interest as the sum of intermediate rewards from each stage and step, i.e., Y = Y₁₁ + Y₁₂ + Y₂₁ + Y₂₂. The underlying optimal treatment is supposed to have the largest expected reward. The other two sub-optimal treatments have lower expected rewards. We further consider two cases. One is that the expected reward from the two sub-optimal treatments are equal while in the other case, the expected reward of the two sub-optimal treatments are different. Therefore, in the second case, the sub-optimal reward losses are different because patients may lose more treatment benefit due to choosing one sub-optimal treatment compared to another.

When the test step initiating each intervention step is not expensive or invasive, more patients tend to choose such a test because they might benefit from knowing the test result for the long term disease control purpose. However, when the lab test is unpleasant and costly, such as a prostate biopsy test, the patients would hesitate to take it. Therefore, when generating data we consider three scenarios based on the patients’ willingness to receive the exam by modifying the parameters to set the ratio of having or not having the test as 1:1, 2:1, and 1:2, which correspond to the equal preference, more likely and less likely to take the exam, respectively. This preference ratio, instead of reflecting the willingness of being tested for each individual, is more like a factor that describes the nature of the test, such as the cost, invasiveness and other side effects. For these three scenarios, three covariates, X₁ to X₃, generated as the baseline covariates follow N(0, 1). Two correlated covariates, X₄ and X₅, are generated as time-varying biomarkers which are measured just before the decision time of the test step within each stage. (X₄, X₅)′ ∼ N(μ, Σ), where μ = (0, 0)′ and $\Sigma =\left(\begin{array}{cc}1& 0.1\\ 0.1& 1\end{array}\right)$. After the test step of each stage, the covariates X₁₂ and X₂₂ mimic the test results that contribute to the treatment decision nested within each test decision with other covariates. Typically, the test results, such as biopsy results, are of great importance to the treatment decision making. X₁₂ and X₂₂ follow the distribution of N(0, 1). Details of parameter setting are as follows:

Stage 1: The test decision variables, D₁₁ ∼ Bernoulli(π_11,1) with π_11,1 = exp(0.6X₃−0.2X₂+X₄)/(1+exp(0.6X₃−0.2X₂+X₄)). The reward of step 1 of stage 1 is generated as $Y_{11}=X_4^2+{\left(0.5X_3+3\right)}^2\times I\left[g_{11}^{opt}\left({\mathbf{H}}_{11}\right)=D_{11}\right]-3\left|X_1\right|\times I\left(D_{11}=1\right)+{ϵ}_{11}$ with optimal regimes defined as

$$g_{11}^{opt}\left({\mathbf{H}}_{11}\right)=\{\begin{array}{l}I\left(X_1>-0.5\right)I\left(X_4\le 0.3\right)\text{for}\text{Scenario}1\hfill \\ I\left(X_1>-0.8\right)I\left(X_4\le 1\right)\text{for}\text{Scenario}2\hfill \\ I\left(X_1>0.3\right)I\left(X_4\le 1.3\right)\text{for}\text{Scenario}\text{3,}\hfill \end{array}$$

and ϵ₁₁ ∼ N(0, 1). The Scenarios 1, 2, and 3 corresponds to patients’ equal preference, more likely, and less likely to take the test, respectively. For patients who have taken the test, i.e., D₁₁ = 1, we further generate the treatment assignment D₁₂ for them as D₁₂ ∼ Multinomial(π_12,0, π_12,1, π_12,2) with π_12,0 = 1/(1 + exp(0.5X₁₂ − 0.2X₂) + exp(0.2X₄ + 0.3X₃)), π_12,1 = exp(0.5X₁₂ − 0.2X₂)/(1 + exp(0.5X₁₂ − 0.2X₂) + exp(0.2X₄ + 0.3X₃)) and π_12,2 = exp(0.2X₄ + 0.3X₃)/(1 + exp(0.5X₁₂ − 0.2X₂) + exp(0.2X₄ + 0.3X₃)). Also, $Y_{12}=I\left[D_{12}=g_{12}^{opt}\left({\mathbf{H}}_{12}\right)\right]{\left(2X_{12}+3X_2\right)}^2+\left(X_1+X_3*2+X_4\right)+Y_{11}/3+{ϵ}_{12}$ for equal sub-optimal reward loss; and

$$\begin{gathered} Y_{12}=I\left[D_{12}=g_{12}^{opt}\left({\mathbf{H}}_{12}\right)\right]{\left(2X_{12}+3X_2\right)}^2+\left(X_1+X_3*2+X_4\right)+Y_{11}/3 \\ +0.5I\left(D_{12}=1\right)\left[I\left(g_{12}^{opt}\left({\mathbf{H}}_{12}\right)=1\right)-1\right]+1.2I\left(D_{12}=2\right)\left[I\left(g_{12}^{opt}\left({\mathbf{H}}_{12}\right)=2\right)-1\right]+{ϵ}_{12} \end{gathered}$$

for unequal sub-optimal reward loss with ϵ₁₂ ∼ N(0, 1). The tree-type optimal regime at step 2 is specified as

$$g_{12}^{opt}\left({\mathbf{H}}_{12}\right)=\{\begin{array}{ll}0\hfill & X_{12}>0.2\hfill \\ 1\hfill & X_1>-0.7,X_{12}\le 0.2\hfill \\ 2\hfill & \text{otherwise}.\hfill \end{array}$$

Stage 2: We generate the test decision of stage 2, D₂₁ ∼ Bernoulli (π_21,1) with π_21,1 = exp(0.5X₁−0.6X₂+X₃)/(1+exp(0.5X₁−0.6X₂ +X₃)). The reward of stage 2 step 1 is generated as $Y_{21}=X_5^2+2X_1+{\left(X_3+3.2\right)}^{2}I\left[g_{21}^{opt}\left({\mathbf{H}}_{21}\right)=D_{21}\right]-3I\left(D_{21}=1\right)+{ϵ}_{21}$ with ϵ₂₁ ∼ N(0, 1). The optimal regime $g_{21}^{opt}\left({\mathbf{H}}_{21}\right)$ is specified as

$$g_{21}^{opt}\left({\mathbf{H}}_{21}\right)=\{\begin{array}{l}I\left(X_1\le -0.3\right)+I\left(X_1>-0.3\right)I\left(X_5\ge 1\right)\text{for}\text{Scenario}1\hfill \\ I\left(X_1\le 0.4\right)+I\left(X_1>0.4\right)I\left(X_5\ge 1.2\right)\text{for}\text{Scenario}2\hfill \\ I\left(X_1\le -0.8\right)+I\left(X_1>-0.8\right)I\left(X_5\ge 1\right)\text{for}\text{Scenario}\text{3}.\hfill \end{array}$$

Among the patients who have had the test, i.e., D₂₁ = 1 we generate their treatment assignment D₂₂ for the second step of stage 2. Specifically, we generate treatment D₂₂ ∼ Multinomial(π_22,0, π_22,1, π_22,2) with π_22,0 = 1/(1 + exp(0.35X₂₂ − X₅) + exp(0.3X₂ + 0.2X₃)), π_22,1 = exp(0.35X₂₂ − X₅)/(1 + exp(0.35X₂₂ − X₅) + exp(0.3X₂ + 0.2X₃)), and π_22,2 = exp(0.3X₂ + 0.2X₃)/(1+exp(0.35X₂₂−X₅)+exp(0.3X₂+0.2X₃)). The reward of stage 2 step 2 is generated as $Y_{22}=3I\left[D_{22}=g_{22}^{opt}\left({\mathbf{H}}_{22}\right)\right]+Y_{21}+\left(2+X_4{X}_5+X_3\right)+{ϵ}_{22}$ for equal sub-optimal reward loss; and

$$\begin{gathered} Y_{22}=\left(3+X_{22}\right)I\left[D_{22}=g_{22}^{opt}\left({\mathbf{H}}_{22}\right)\right]+Y_{21}+\left(2+X_4{X}_5+X_3\right) \\ +2I\left(D_{22}=1\right)\left[I\left(g_{22}^{opt}\left({\mathbf{H}}_{22}\right)=1\right)-1\right]+I\left(D_{22}=2\right)\left[I\left(g_{22}^{opt}\left({\mathbf{H}}_{22}\right)=2\right)-1\right]+{ϵ}_{22} \end{gathered}$$

for unequal sub-optimal reward loss, and ϵ₂₂ ∼ N(0, 1). The optimal treatment regime for stage 2 $g_{22}^{opt}\left({\mathbf{H}}_{22}\right)$ is specified as

$$g_{22}^{opt}\left({\mathbf{H}}_{22}\right)=\{\begin{array}{ll}0\hfill & X_{22}>0.5\hfill \\ 1\hfill & X_{22}\le 0.5,X_5<0.3\hfill \\ 2\hfill & \text{otherwise}.\hfill \end{array}$$

Table 1 summarizes the simulation study results across different scenarios as described above. Our SAT-Learning method for estimating the optimal DTR involves a doubly robust semi-parametric estimator, therefore our simulations also try to demonstrate such robustness. In addition to having one estimation scheme with the conditional mean model and the propensity score model both correctly specified, we consider two more schemes with either the propensity score model or the conditional mean model mis-specified by omitting some of the covariates of the true form. We consider a sample size of either 1000 or 2000 for the training dataset, and a sample size of 2000 for the validation, and repeat the simulation 500 times. The training dataset is used to estimate the optimal regime and then predict the optimal test-and-treat decision in the validation dataset, where the underlying true optimal regimes are already known. The percentages of subjects correctly classified to the optimal test-and-treatment decision in both stages combined is denoted as opt%. The average opt% and the empirical standard deviation (SD) among the repetitions evaluate the performance.

TABLE 1.

Simulation results for the general test-and-treat case for the equal and unequal reward loss for sub-optimal treatment options: two intervention stages, three treatment options at each stage nested within the exam at each stage with 500 replications, and n=1000 or 2000. opt% show the empirical mean and standard deviation (SD) of the percentage of subjects correctly classified to their underlying true optimal treatments, estimated by the proposed method when (a) the conditional mean model and the propensity score model are both correctly specified, (b) the conditional mean model is mis-specified and the propensity score model is correctly specified, and (c) the conditional mean model is correctly specified and the propensity score model is mis-specified. Scenarios 1,2 and 3, correspond to the cases when the true ratios of preference for having the exam v.s. not having the exam among all patients are 1:1, 2:1 and 1:2.

	Sub-optiomal		Scenario 1 (1:1)	Scenario 2 (2:1)	Scenario 3 (1:2)
	Reward		opt%	opt%	opt%
N=1000	Equal Loss	(a)	90.1(7.4)	86.1(9.2)	91.9(6.3)
		(b)	84.7(7.5)	81.0(7.9)	86.9(6.4)
		(c)	90.1(7.6)	86.3(9.3)	92.1(6.4)
	Unequal Loss	(a)	96.2(3.8)	96.3(4.0)	97.7(2.0)
		(b)	92.0(6.1)	87.5(12.5)	94.7(4.1)
		(c)	96.0(4.1)	96.2(4.4)	97.6(2.2)
N=2000	Equal Loss	(a)	91.2(7.5)	86.8(9.3)	93.2(6.4)
		(b)	85.8(6.6)	81.9(6.3)	88.2(6.1)
		(c)	91.1(7.5)	86.9(9.3)	93.2(6.4)
	Unequal Loss	(a)	96.9(3.4)	97.7(2.7)	98.2(1.8)
		(b)	96.6(3.6)	93.8(8.8)	97.7(1.7)
		(c)	96.9(3.4)	97.7(2.6)	98.1(1.8)

In Table 1, the results of equal sub-optimal reward case demonstrate the loss due to sub-optimal equally inferior compared to the optimal choice. In scenario 1, where the subjects have an even preference of having test, under the sample size n=1000, 90.1% of the patients are correctly assigned to their optimal DTRs for both stages when both the conditional mean model and the propensity score model are correctly specified. When either the conditional mean model or the propensity score model is mis-specified, but not both, the overall performances are slightly worse, but still reasonably satisfactory. More specifically, when either the propensity score model or the conditional mean model is incorrectly specified, we still get 90.1% and have 84.7% respectively. Similar trends are found in Scenario 2 and Scenario 3, and results improve as sample size goes to N=2000. However, when the reward loss is unequal among sub-optimal treatment options, the optimal regimes stand out among the candidate treatments more obviously according to our data generating process, therefore, it is easier for our proposed method SAT-Learning to distinguish the optimal treatment from sub-optimal ones. Thus, the simulation performance with varying sub-optimal loss is better than when the sub-optimal loss is equal, as expected.

5.2 |. A Special Case when the Treated Patients no Longer Need Further Test or Treatment

We conduct another simulation study for a special case when the treated patients no longer need test and treatment again. This simulation better mimics the monitoring and management in active surveillance for prostate cancer. Because of the significant side-effects of curative intervention and the asymptomatic nature of prostate cancer, according to the American Society of Clinical Oncology, patients with low-risk prostate cancer can consider active surveillance²² Active surveillance involves monitoring prostate cancer by regular exam in its localized stage until further treatment is needed to halt the disease at a curable stage. More specifically, the patients who have taken the biopsy test, only a small proportion of them would switch from the active surveillance to curative intervention. In the active surveillance, the patients who have been treated should be removed from the active surveillance cohort, because physicians consider that they no longer need to be treated and additional treatment is not provided and they are not eligible for the active surveillance. Therefore they should not be considered to evaluate the subsequent test or treatment decision. We generate data under a two-stage nested DTR with two treatment options at each stage. We also modify the parameters in the data generating models to make the rates of taking the curative treatment equal to 5%, 15%, 20% and 25% in both stage. The higher the rate is, the more patients take the treatment and thus more patients will be removed from the surveillance afterwards. The detailed information of data generation can be found in the Supplementary Materials

The simulation results are summarized in Table 2. As the results show, because of the nice doubly robust property, the percentages of subjects correctly classified to their underlying truth both yield satisfying results even when either the propensity score model or the conditional mean model is mis-specified, but not both. Considering sample size N=1000 as an example, when 5% of tested patients have the curative treatment and then are removed from the active surveillance, 92.8% of them are correctly assigned to their optimal DTR for both stages when both the conditional mean model and the propensity score model are correctly specified. We also have 91.8% and 91.6% of the patients correctly classified to their optimal DTR when the propensity score model or the conditional mean model is misspecified respectively. As the treatment rate increases, we are able to estimate better optimal treatment rules from larger heterogeneous samples with more information. Therefore, it is easier for our proposed SAT-Learning to estimate the optimal regime from this more informative sample. Thus, the simulation performance with a higher treatment rate is slightly better than that for the lower rate case.

TABLE 2.

Simulation to mimic the monitoring and management of prostate cancer: two intervention stages, two treatment options at each stage nested within the exam at each stage with 500 replications, and n=1000 or 2000. opt% show the empirical mean and standard deviation (SD) of the percentage of subjects correctly classified to their underlying true optimal treatments, estimated by the proposed method when (a) the conditional mean model and the propensity score model are both correctly specified, (b) the conditional mean model is mis-specified and the propensity score model is correctly specified, and (c) the conditional mean model is correctly specified and the propensity score model is mis-specified. Different treatment rates correspond to different proportions of patients who switch from active surveillance to curative treatment among those who have taken the biopsy test.

Treatment Rate		5%	15%	20%	25%
		opt%	opt%	opt%	opt%
N=1000	(a)	92.8(4.9)	93.8(4.8)	94.9(4.5)	95.3(4.6)
	(b)	91.6(2.1)	93.2(1.9)	93.9(1.5)	94.3(1.4)
	(c)	91.8(5.6)	93.2(5.8)	94.0(5.9)	94.6(5.5)
N=2000	(a)	93.7(4.7)	94.9(4.6)	95.7(4.4)	96.7(3.7)
	(b)	92.6(1.9)	94.0(1.4)	94.5(1.2)	94.7(1.1)
	(c)	92.2(6.5)	93.9(6.6)	94.6(6.5)	95.5(6.1)

6 |. APPLICATION TO PROSTATE CANCER ACTIVE SURVEILLANCE DATA

We illustrate SAT-Learning using the prostate cancer Active Surveillance dataset from Johns Hopkins University.²² In this active surveillance study, enrollment of men with low risk prostate cancer started in 1995 and ended in 2015. Eligible subjects need to have PSA density less than 0.15 μg/L per mL, clinical stage T1c disease or lower, the Gleason score between 2 and 6, at most 2 positive biopsy cores, and at most 50% tumor in any single core, all of which made them low risk. The Johns Hopkins active surveillance protocol includes semiannual PSA and annual prostate biopsy. In the protocol, the primary reason that patients would be recommended to undergo definitive curative radiation therapy or surgery is if the biopsy result showed an adverse change compared to previous biopsies.

There is sufficient evidence that the approach of active surveillance, i.e. delaying curative treatment, for low-risk patients is safe.²³ The issue we will be considering is how it should be implemented. That is, rather than having an annual biopsy, as in the protocol, should it be more individualized, with the decision of whether to undergo a biopsy based on the available data at that time for that patient.

Not all the patients in the study followed the protocol. In the dataset we analyzed, 22% of patients did not have the scheduled biopsy of the first year and 5% of them did not have the biopsy in the first two years. Similarly for curative therapy, quite a number of patients did not follow the protocol.²² Such heterogeneity in the observed data allows us to apply the nested DTR method via our proposed SAT-Learning to decide at each stage whether the patient should have the biopsy, and if so, whether the treatment should be recommended based on the patients’ individualized characteristics. In the analysis presented below we restrict the observational period to be from the diagnosis to year 4 and we make a two-year time unit for each stage, making two stages, stage 1 being from diagnosis to year 2 and stage 2 being from year 2 to year 4. We use D with subscript value s = 1, 2 to denote the decisions of the two stages, and j = 1, 2 to denote the biopsy and treatment actions within the stage. Thus, if the subject had a biopsy at the first stage, we denote D₁₁ = 1, otherwise, D₁₁ = 0. For those with biopsy i.e., D₁₁ = 1, the treatment choice is recorded as D₁₂, 1 for treated and 0 for no treatment, and similarly for D₂₁ and D₂₂. We note that once the patient is treated, no further biopsy or treatment will be observed. After the data preprocessing, 863 patients are kept in the dataset for the analysis, and of these 230 did receive curative treatment. More information regarding data preprocessing can be found in Supplementary Materials.

Although patients, in reality, are subject to different categories of treatments, such as prostatectomy, radiation therapy or hormone therapy, in this analysis, we combine all different kinds of treatments into one category (treated) to preserve a sufficient sample size for the treated subjects. Other patient characteristics, including age, race, baseline biopsy results, and baseline PSA were collected at the enrollment. As the active surveillance proceeded, the corresponding PSA changes and the follow-up biopsy results were also collected. In particular, the quantity of cancer, as measured by biopsy results, is based on both the number of needle cores containing cancer and the characteristic of the cancer tissue found within each single core (Gleason score). How the individualized data was formatted to match the two year time interval for each stage is described in the Supplementary Materials. The reward outcome of interest was chosen to reflect long term disease status, and is defined as the proportion of PSA values which are less than 5 out of all the PSA observations collected from the end of year 4 after diagnosis to the end of study. This reward ranges from 0 to 1, with the lower values implying more undesirable risk of prostate cancer progression. This reward outcome only considers the disease prognosis based on PSA, and ignores the side effects brought by frequent biopsy and unnecessary intervention.²⁴ In particular, the painful biopsy procedure carries nonnegligible short- and long-term risk for patients, while the non-trivial probability of a false negative biopsy also poses challenges to the medical community that advocates for it.²⁵ Thus, after consulting with subject matter experts, we include penalties to discount the patient’s reward and thus to take into account possible side effects. More specifically, if the patient had a biopsy in either one of the two stages, their reward is reduced by a factor of 87% compared to the original reward. For a patient who has ever had treatment, the reward is reduced by a factor of 80% compared to their original reward.

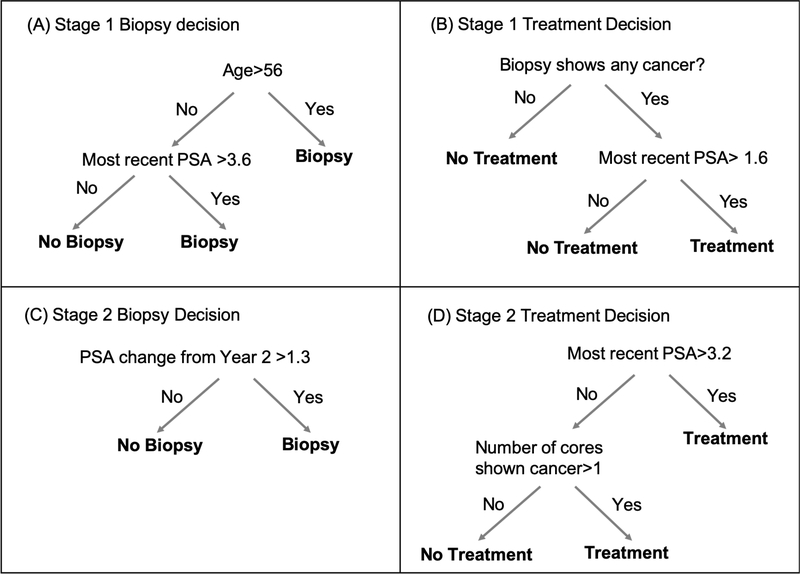
To apply the proposed SAT-Learning algorithm to the active surveillance data described above, we use random forests for the conditional mean model and a logistic regression model for the propensity score model of every step within each stage. The estimated optimal test and treatment DTR of the two stages are shown in Figure 2 According to the estimated optimal DTR, at the first stage, men older than 56 are recommended for a biopsy test. Among those who are younger than 56 years old, the patients with most recent PSA higher than 3.6 are also recommended for a biopsy test. Among those doing the biopsy test, patients with the most recent PSA higher than 3.1 and having biopsy test showing any cancer are recommended for the treatment. At the second stage, the men whose PSA change from beginning of year 2 is larger than 1.3 are recommended for the biopsy test. For those who take the biopsy, if their most recent PSA is higher than 3.2 or the biopsy result has more than one biopsy core needle showing cancer positive, we recommended the physician to offer them the treatment. The standard practice in deciding on curative treatment depends primarily on whether the Gleason grade on the biopsy is greater than or equal to 7. In contrast, the DTR we estimated involves more variables and changes from one stage to the next, so is more individualized. It is also notable that the Gleason thresholds in the above DTR are lower than in standard practice, which is consistent with a suggestion in the literature.²⁶ The reward we use, long run low PSA values, certainly does influence the estimated optimal DTR, which involves lots of decisions based on the current PSA values. The estimated tree-based DTR presented in Figure 2 is also sensitive to the discount factor 87% and 80% which are used to penalize the reward. Other rewards would have given different optimal DTRs. The reward we use of long-run PSA values can be considered as a proxy for clinical meaningful “good” outcome. An ideal reward would involve long term good quality of life and absence of prostate cancer recurrence. But data to construct such a reward is not available for this study. A sensitivity analysis with a modified reward is presented in the Supplementary Materials. It is possible to estimate what the improvement in the reward would have been if the patients from our study cohort had followed the optimal DTR. We calculate that if our study cohort had received the optimal DTR described above, then more than 86% of the study cohort would have seen an increase in their reward. This was especially the case among the patients who had no biopsy experience in the study, by assigning them the optimal regimes, almost everyone will increase the reward according to our estimates. We also calculate that the expected number of patients who would have received curative treatment if they had followed the estimated optimal DTR is 412, which is larger than the actual number of 230, but this number is sensitive to the factor that is used to discount the reward when a patient receives treatment.

FIGURE 2.

The estimated optimal DTR for JHU prostate cancer active surveillance data via SAT-Learning method. The trees show how to provide optimal regime at every step based on the individualized characteristics for (A) stage one biopsy decision, (B) stage one treatment decision if biopsy was taken in stage one, (C) stage two biopsy decision and (D) stage two treatment decision if the biopsy was taken in stage two.

7 |. DISCUSSION

Motivated by the embedded nature of the diagnosis and treatment procedures, we have developed a nested DTR framework, with the treatment decision nested within the test decision in a multi-stage setting, and implemented the estimation of the optimal nested DTR using a step-adjusted tree-based reinforcement learning method (SAT-Learning). This nested DTR framework considers the test decision and the nested treatment decision in the same stage and develops the optimal nested DTRs to maximize the expected long-term rewards, such as disease control. This kind of test-and-treat strategy has been considered previously in the health policy literature.²⁷ These methods discussed the importance of the problem, and the need to accumulate data. They also suggested solutions that focused on the population level, but not in a rigorous mathematical framework. Our proposed method follows the framework of DTR, which enables physicians to repeatedly tailor test and treatment decisions based on each individual’s time-varying health histories, and thus provides an effective tool for the personalized management of disease over time.

SAT-Learning, our proposed method to solve the nested step-adjusted DTR problem, can potentially be implemented via modifying other learning methods that have been considered in DTR literature. However, by using a modified T-RL algorithm¹⁷, SAT-Learning is more straightforward to implement, understand and interpret, and capable of handling various data without distributional assumptions. Additionally, the doubly robust AIPW estimator that we utilize in the purity measure in the tree structure also helps improve the robustness of our method against model mis-specifications.

Several developments and extensions can be explored in future studies. One possible exploration lies on dealing with potentially contradictory multiple outcomes. In SAT-Learning, we consider a nested step-adjusted DTR to reduce the pain and potential infections from frequent biopsy tests, but maintain an effective and in-time treatment to control disease progression. If efficacy is the only purpose, one would expect more frequent tests and more aggressive treatment regardless of possible side effect, but in the meantime, patients might experience more side effects. The desire for efficacy and the desire for less side effects in fact contradict each other. In clinical practice, physicians are often interested in balancing multiple competing clinical outcomes, such as overall survival, patient preference, quality of life and financial burden.²⁸ In order to balance these multiple potentially contradictory objectives, we applied a different discount factor to the patient rewards for different side effects in the application to the JHU Prostate Cancer Active Surveillance data. Other statistical methods have been developed to trade-off between multiple contradictory outcomes.^8,29 One can further incorporate these multiple objective optimization functions into our framework of nested DTR for future research. Another possible exploration may be considering all available actions when the preference of multiple outcomes varies³⁰, which would give more comprehensive information about how the optimality of an action would be changed if the preference is modified. Sensitivity analyses can be done on the optimal regimes and would provide further guidance for the decision maker on developing a more flexible regime among all the available intervention strategy choices.