The Retrosplenial Cortex as a Possible “Sensory Integration” Area: A Neural Network Modeling Approach of the Differential Outcomes Effect in Negative Patterning

Abstract

We explored the hypothesis that learning a Pavlovian negative patterning task would be facilitated when training with differential, as opposed to non-differential, reinforcing outcomes. Two groups of rats received pairings of one visual and one auditory stimulus with food reward when these stimuli were presented on separate training trials, but without reward when both stimuli were presented on simultaneous stimulus compound trials (V+, A+, AV−; similar to an XOR problem). For Group Differential, each stimulus was separately paired with distinctively tasting food rewards, whereas for Group Non-Differential each stimulus was randomly paired with both food reward types across different stimulus element trials. We observed that rats learned the negative patterning task more rapidly and effectively when trained with differential outcomes. These data support a multi-layered connectionist model introduced by Delamater (2012) in which a multi-modal processing structure plays the role of a “sensory integration” area like that hypothesized for the retrosplenial cortex by Dave Bucci and his colleagues (e.g., Todd, Fournier, & Bucci, 2019). We discuss how such a region may develop different “negative occasion setting” and “configural inhibition” mechanisms in solving negative patterning and related tasks.

1. Introduction

The retrosplenial cortex (RSC) was studied extensively by Dave Bucci and his colleagues who showed that it plays important roles in several different basic Pavlovian learning tasks. These tasks include sensory preconditioning (e.g., Fournier, Bucci, & Todd, 2020; Robinson, et al., 2011; Robinson, et al, 2014), the retrieval of remotely acquired cued fear (e.g., Jiang, et al., 2018; Todd et al., 2016), the context-preexposure facilitation effect (Todd et al., 2017), time-based feature discriminations (Todd et al., 2015), feature negative discrimination learning (Keene & Bucci, 2008; Robinson, et al., 2011), and negative patterning learning (Fournier, et al., 2019; but see Nelson, et al., 2018). It is a tribute to Dave’s systematic approach to behavioral neuroscience that he employed a wide variety of behavioral tasks to investigate what he imagined would be a brain structure that was well-positioned to play a variety of important behavioral roles. In their reviews, Bucci and Robinson (2014) and Todd, Fournier, and Bucci (2019) pointed out that the RSC has direct connections with primary auditory and visual sensory cortical areas and indirect connections with other polymodal sensory processing regions (e.g., claustrum, anterior thalamic nucleus, posterior parietal cortex). In addition, Bucci and Robinson (2014) and Todd et al (2019) noted that the RSC has connections with a number of additional brain regions (including limbic system and basal ganglia structures) shown to play important roles in a wide variety of learning and memory paradigms. Prior to Bucci’s contributions to this field, this brain structure had been shown to play some role in spatial learning tasks, but it was really due to Dave’s insights that the RSC should also play key roles in various discrete cue Pavlovian learning tasks.

This is perhaps most easily seen in sensory preconditioning (Brogden, 1939). In one version of this experiment, two neutral stimuli are initially paired together in a “preconditioning” phase on some trials while a control stimulus is presented alone on separate trials (i.e., AB, C). The idea is that an A-B association might be established by AB pairings. However, since the stimuli are neutral any learning of this kind would generally be difficult to detect (although see Honey, Good, & Manser, 1998). Thus, in a second phase of the study, one of the paired stimuli is, itself, paired with a biologically meaningful event such as food reward, for example, on separate B+ trials, in order to establish an observable conditioned response to that cue. In a final test phase, responding to the paired associate of B, cue A, is shown to be superior to the unpaired cue C because of the “preconditioned” A-B association. Bucci and his colleagues used exactly this procedure to demonstrate, convincingly, that RSC disruptions impaired learning and expression of the sensory preconditioning effect (Fournier, Bucci, & Todd, 2020; Robinson, et al., 2011; Robinson, et al., 2014; Todd et al, 2019). The hypothesis was that since RSC accepts inputs from multiple sensory regions it could serve as a key “sensory integration” area that might be involved in other cued learning procedures that should require sensory integration of various kinds.

For the present purposes, two specific learning procedures are of special interest. One of these is called feature negative learning (e.g., Holland, 1985) and the other negative patterning (Woodbury, 1943). In feature negative learning, one cue is reinforced when presented by itself, but not when it is accompanied by a second cue (A+, AB−). In this case, it was recognized as early as Pavlov (1927) that stimulus A should acquire excitatory properties (i.e., as a signal for food reward), but that stimulus B should, in some way, suppress those excitatory tendencies evoked by A (see Rescorla, 1969). Holland (1985) recognized that stimulus B could acquire this capacity in multiple ways. On the one hand, and following Pavlov’s suggestion, B could directly enter into an inhibitory association with food reward (e.g., through a B – No Food association or through an inhibitory B – Food association). That source of inhibition would counteract A’s excitatory association with food reward and suppress the response that would ordinarily be observed when A was presented alone (see also Rescorla & Holland, 1977). However, Holland (1985) suggested that under some training conditions stimulus B might come to suppress responding to A not because of its own direct inhibitory association with reward, but through its ability to suppress retrieval of the A – Food association. Holland (1985; cf. Rescorla, 1985) provided evidence to favor this more “hierarchical” view of B’s inhibitory learning. This behavioral function is referred to as “negative occasion setting” or “modulation” (Fraser & Holland, 2019; Holland, 1985; Rescorla, 1985; Swartzentruber, 1995). Interestingly, Bucci and his colleagues have found that the RSC may be critically involved in this behavioral negative occasion setting function (e.g., Keene & Bucci, 2008; Robinson, et al., 2011).

The negative patterning task is a close cousin of feature negative learning and Bucci and his colleagues appropriately addressed their attention to its study in connection with RSC manipulations. Negative patterning includes A+, B+, and AB− training trials (as opposed to just A+ and AB− trials as in the feature negative task). In this case, the simple solution that Pavlov (1927) identified (where stimulus B becomes a conditioned inhibitor) does not work. Instead, the organism must learn by representing the stimulus compound, in some sense, as different from its constituent elements (in other words, it must learn that the “pattern” of stimulation on compound trials predicts no reward while the individual stimuli predict reward). Initially, Nelson, et al. (2018) showed that pretraining RSC lesions did not negatively impact the development of negative patterning learning in rats, but then Fournier et al. (2019) showed that post-training suppression of the RSC impaired the expression of prior negative patterning learning. This result suggests that the RSC normally participates in negative patterning learning but that other structures can play that role in the absence of the RSC.

All of these results are intriguing because they suggest that in discrete cue Pavlovian learning procedures the RSC may be especially important in tasks that require “sensory integration” or “stimulus selection” or “hierarchical” associative learning type mechanisms. Delamater (2012) introduced a connectionist network framework to understand conceptually how different brain regions might participate in various Pavlovian learning tasks that require stimulus selection and/or hierarchical associative learning mechanisms. Figure 1A shows the general network used in the model. In this approach, it is assumed that conditioned stimuli (e.g., auditory and visual stimuli) consist of collections of features such that a given stimulus will come to activate sensory receptors that are unique to that stimulus and also shared with other stimuli, especially those from the same modality. In Figure 1A, different auditory stimuli, for instance A1 and A2, can both be assumed to activate one sensory feature in common, feature x, but to activate separate features individually, features a and b, respectively. Similarly, different visual stimuli, V1 and V2, are assumed to both activate one feature in common, feature y, but other features selectively, features c and d, respectively. Then, the model assumes that activation of input features gets transmitted in a feedforward manner to a “hidden layer” of processing units that consists of modality specific and multi-modal processing structures and pathways. Specifically, auditory and visual inputs can transmit their activation patterns through distinct auditory and visual pathways that ultimately come to activate output units that are assumed to encode different rewards (unconditioned stimuli, US1 or US2) that might be used in a conditioning experiment. However, importantly, this network also includes at the hidden layer a multi-modal processing area that accepts inputs from both auditory and visual inputs, i.e., inputs from multiple sensory modalities. Delamater (2012) showed how learning in this framework can be seen as involving changes that take place in connection weights between the input and hidden layers and also between hidden and output layers. The model was applied to a wide variety of feature negative and negative patterning tasks (among others), and Delamater (2012) showed that such a network could learn to activate output units appropriately by adjusting these weights according to one popular back-propagation learning algorithm (Rumelhart, Hinton, & Williams, 1986).

Figure 1:

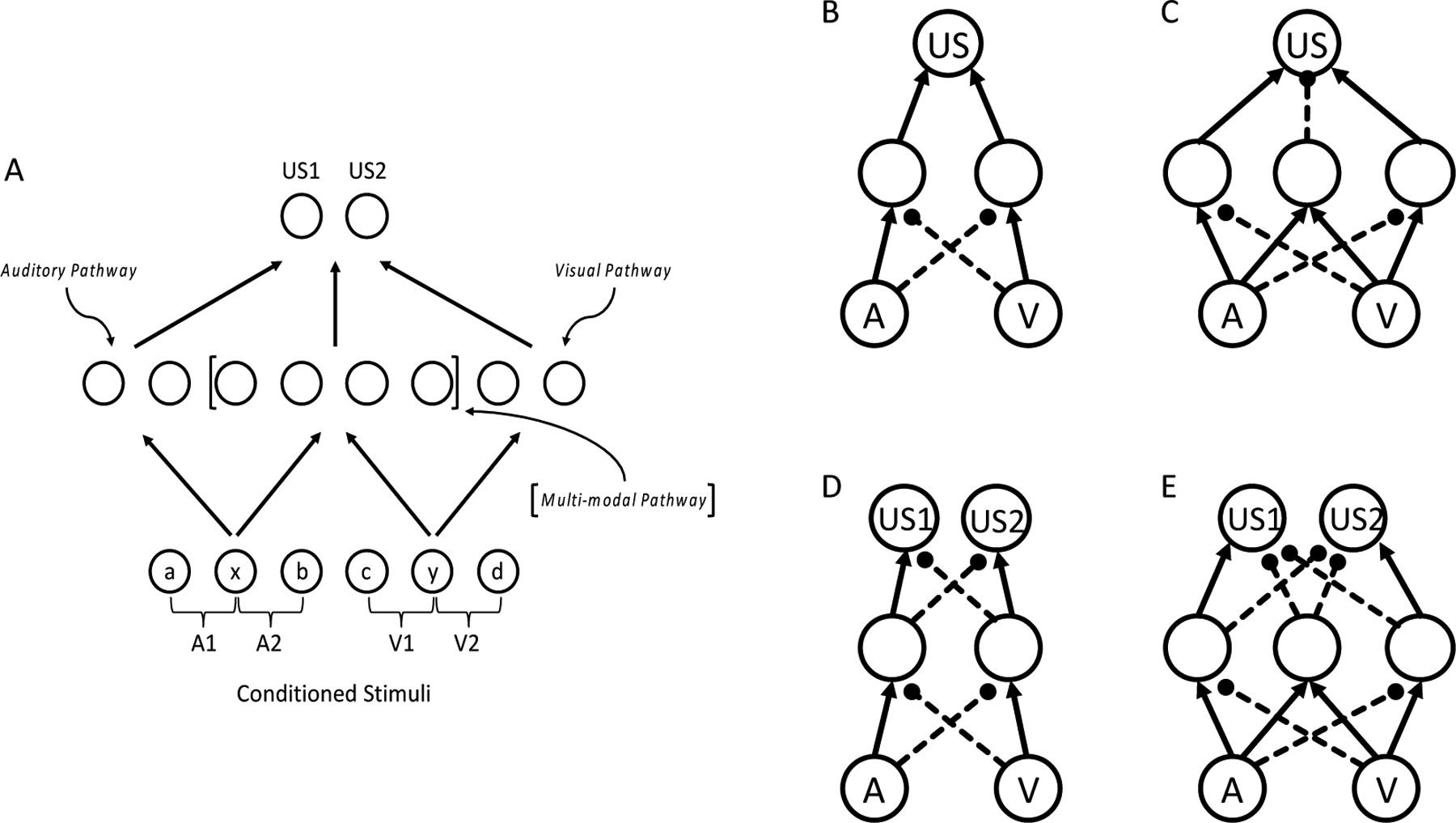
A. A feedforward connectionist model (see Delamater, 2012) with three layers: bottom (input or conditioned stimuli), middle (hidden layer), top (output or unconditioned stimuli). A1 and A2 represent two auditory stimuli which are connected to the auditory and multi-modal pathways in the hidden layer. V1 and V2 represent two visual stimuli and are connected to multi-modal and visual pathways in the hidden layer. Lower case letters refer to individual features activated by input stimuli. Panels B, C, D, and E show simplified networks with only multi-modal units in the hidden layer to illustrate how negative patterning tasks can be solved. B and C show different solutions to a single outcome negative patterning task. D and E, show different solutions to negative patterning tasks that use two outcomes. B and D illustrate competitive “negative occasion setting” solutions, and C and E solutions that include a “configural” mechanism.

While Delamater (2012) did not speculate on which brain structures specifically might play the presumed separate modality-specific and multi-modal processing roles, the RSC is one obvious candidate structure to perform multi-modal hidden layer functions since it also can be considered a sensory integration area. It is instructive to consider how this network can learn new weights to solve the negative patterning task. Figure 1B shows one fairly typical type of solution. To simplify, we show particularly strong excitatory and inhibitory connection weights in a simplified network that only depicts interactions between the input and multi-modal layers. Notice how excitatory connections are established between different input units and distinct hidden units that, in turn, activate the output US unit. This means that when stimulus A is presented alone it will strongly excite hidden unit 1 and this will excite the US unit. Stimulus V will strongly excite hidden unit 2 that will then excite the US unit. However, on AV stimulus compound trials since A also will strongly inhibit hidden unit 2 and V will strongly inhibit hidden unit 1, neither hidden unit will be strongly activated and the US unit, therefore, will also not be strongly activated. In other words, each stimulus comes to inhibit the other stimulus’ pathway to the output unit. This is analogous to the hierarchical “negative occasion setting” mechanism described above by Holland (1985; Fraser & Holland, 2019) where a negative occasion setting stimulus comes to suppress retrieval of an association between a target stimulus and the US. In the case of negative patterning, we show that each stimulus can play the role of a negative occasion setter for the other.

A second type of solution to the negative patterning task can be seen in Figure 1C. In this case, once again each stimulus forms its own pathway to the US unit through different hidden units and inhibits one another’s pathways to the US, but, in addition, each input converges on a new hidden unit that, itself, comes to inhibit the US unit. One can think of this new hidden unit that is most strongly activated by the joint presentation of the two stimuli as a “configural” unit, and it provides a configural solution to the negative patterning problem (see also Grand & Honey, 2008; Pearce, 2002). In our experience, the model most typically develops solutions of the first type, but sometimes does develop solutions that include connections of both types in solving negative patterning problems.

An especially interesting feature of these solutions to the negative patterning problem is that a different pattern of activation of hidden units must occur on the three different trial types of the negative patterning task (A+, V+, AV−). One can characterize the pattern of activation across the hidden units as a kind of “internal representation” of the conditioned stimuli because their input activations get transmitted to the hidden layer in accordance with the newly learned weights. Thus, both network solutions to the problem requires that the input stimuli become especially distinctive on all three trial types, i.e., that they activate different patterns of hidden layer units. If this was not the case, then the network would not easily learn the task. Thus, one prediction that can be derived from this framework is that any procedure that encourages the stimuli to be represented more distinctly across training should facilitate negative patterning learning.

One such procedure is called the acquired distinctive of cues effect (e.g., Delamater, 1998; Honey & Hall, 1989). For instance, consider what would happen if in the negative patterning task stimulus A were reinforced with US1 and stimulus V with US2 (where the two food rewards have different taste qualities, for instance). Prior research has established that when stimuli are associated with the same outcome generalization between them is enhanced, but when the stimuli are associated with different outcomes generalization between them is reduced (e.g., Delamater, 1998; Honey & Hall, 1989; Lawrence, 1949; 1950). Thus, by pairing each stimulus within a negative patterning task with distinctive US types, then this should, in principle, enhance the development of distinctive hidden layer representations that should facilitate the rate at which the network learns the negative patterning task. Delamater (2012) showed through simulations how various acquired equivalence and distinctiveness effects could be readily understood within this connectionist framework.

1.1. Network Simulations

In order to evaluate the prediction that training with a differential outcome procedure should facilitate negative patterning learning, we performed simulations that contrasts the rate at which the network learns the negative patterning task when one US or two US types are used to reinforce the individual stimulus elements. In this simulation, n = 32 simulated subjects were run on either a differential or nondifferential outcome negative patterning task. For each problem there were 150, 10-trial blocks in which each block contained 1 reinforced trial for each (“visual” and “auditory”) element, 2 non-reinforced trials for the (“audiovisual”) stimulus compound, and 6 additional trials in which the experimental context was presented alone non-reinforced in order to simulate the inter-trial interval in such studies. Trials within a block were randomized. For the nondifferential outcome simulation, the network was trained to activate a single US output node on element alone trials and to not activate the output unit on compound trials (as well as context-alone presentations). For the differential outcome simulation, the same network was used but it had two US output nodes. The network was trained to activate US1 only on trials in which the visual input was presented on element trials (i.e., V1-US1 trials) and to activate US2 only when the auditory input was presented on element trials (i.e., A1-US2 trials). On all other simulated trials these output nodes were taught to remain inactive. The networks both included 3 input units, corresponding to 1 visual stimulus, 1 auditory stimulus, and 1 context stimulus (note: the context input unit was active on every type of training trial). At the hidden layer there were 2 units specific to each visual and auditory pathways (but that could also be activated by the context unit), and 4 multi-modal units that could be activated by all inputs. The output layer contained one US unit to simulate the non-differential outcome procedure, or 2 US units to simulate the differential outcome procedure (see Figures S1 to S4). Following Delamater (2012) the networks were trained using a slightly modified back-propagation learning algorithm (see Appendix).

Figure 2A shows the results of the simulations for each simulated experimental group. The mean US activation levels (which varies between 0 and 1) is displayed for reinforced element alone (i.e., for simulated “visual” and “auditory” stimuli), nonreinforced compound, and context alone trials. In addition, in Figure 2B the output activation of the appropriate US node is averaged across both “visual” and “auditory” CS trials in the differential outcome task for the “Element+” score, whereas activation is averaged across both nodes on non-reinforced compound trials and on inter-trial interval context alone trials. These simulations show that the networks learned to appropriately adjust their weights in both tasks, but the network acquired the negative patterning discrimination more rapidly and successfully in the differential outcome training procedure. Output activations on Element+ trials in the differential outcome procedure reached much higher levels over the course of training compared to the non-differential outcome procedure, while output activation levels on compound trials (CpD−) reached somewhat lower levels in the differential outcome procedure as well. Figure 2C shows these simulated data in the form of a discrimination index, in which activation levels on compound trials is subtracted from activation levels on element alone trials. This clearly shows an advantage in acquiring the discrimination with the differential outcome procedure.

Figure 2:

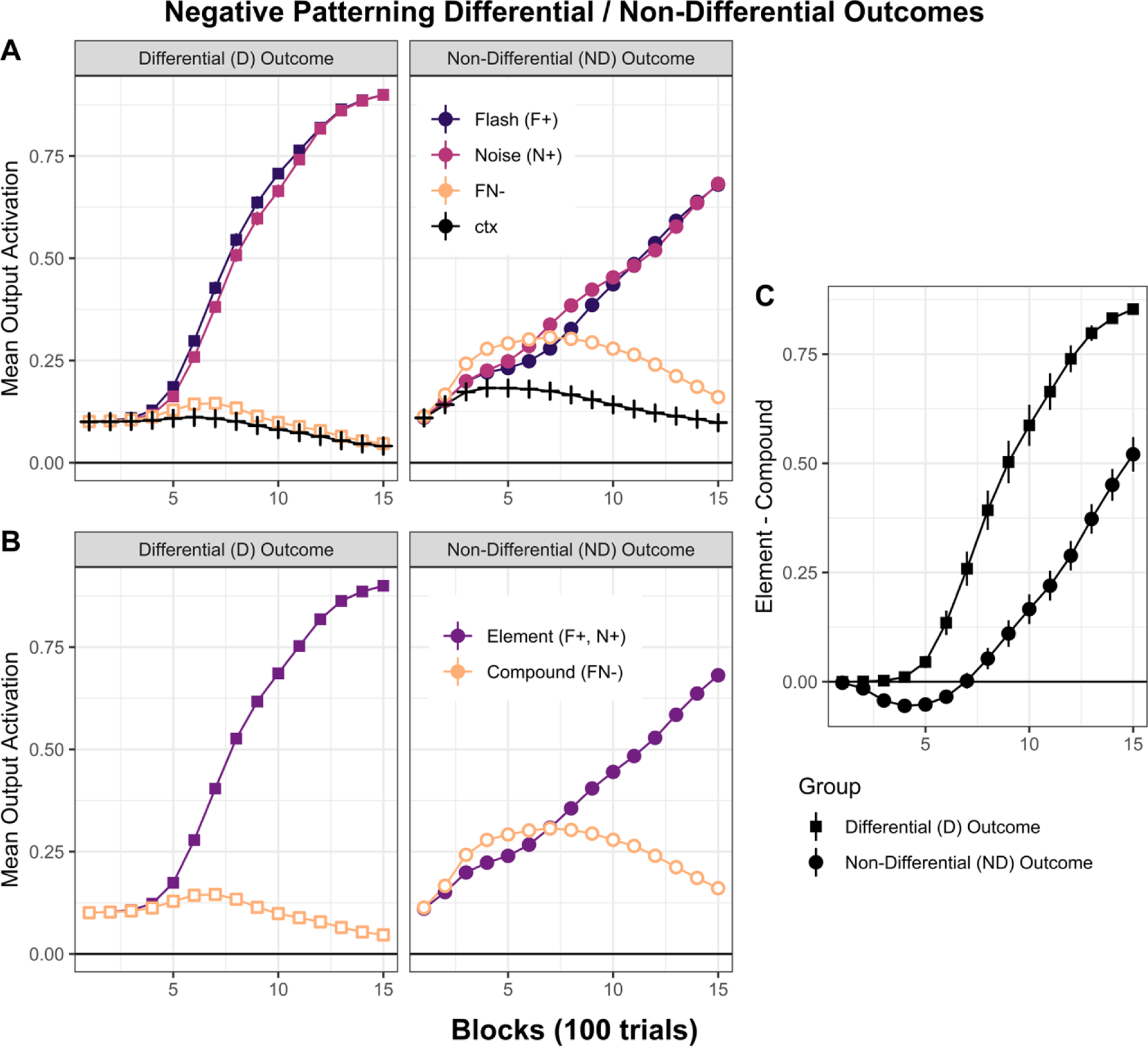
Simulated data (n = 32; per group). Negative patterning learning is more successful when training with differential relative to non-differential outcomes. A. Mean output activation (y-axis) as a function of 10-trials blocks (x-axis) for each of the four trial types (F+, N*, FN−, ctx−, for the Differential outcome groups, and F+, N+, FN−, ctx− for the Non-Differential outcome group). B. Same as in panel A but the average of single element trials (F and N). C. Element minus compound discrimination scores for both groups. All simulation codes are available in https://github.com/santiagocdo/NLM_Bucci_Delamater-Castiello.

We also examined the types of connections formed in these networks across the different simulations. The solutions to the ordinary negative patterning task with one US was very similar to that depicted in Figure 1B (in a simplified version of the network; see also Figure S1). Across the 32 simulated subjects, this was the most common form of solution, although it should be noted that after the amount of training given many of the simulations failed to display strong learning to both reinforced elements. Also, a few networks developed the kind of dual-mechanism solution depicted in Figure 1C where both elements tended to suppress the other’s pathway to the US, but, in addition, the two elements converged on another multi-modal hidden unit that suppressed the US unit (Figure S2). Across the 32 simulated networks in the differential outcome procedure, by far the dominant solution was to learn by developing the kinds of connections shown in a simplified form in Figure 1D. Once again, each element came to inhibit the other element’s pathway to the appropriate US output unit. This could come in the form of mutual inhibition from input to hidden layers, as well as from hidden to output layers (Figure S3). Figure 1E also shows another type of dual-mechanism solution to the differential outcome negative patterning task where both mutual inhibition and configural inhibition mechanisms can be learned. In practice, however, the multi-modal units rarely acquired this configural role when learning negative patterning with differential outcomes.

Another final interesting feature of both differential and non-differential outcome networks is that the pattern of weights developing between the visual and auditory input stimuli to the four multi-modal hidden units were almost invariably negatively correlated (generally r < −0.90), with the exception of the rarely obtained configural solutions found for the non-differential outcomes task where the correlations were positive (Figure S2). This highlights the strong tendencies of the networks to learn by each stimulus coming to act as a kind of “negative occasion setter” for the other by negating their effects on hidden layer units. To the extent that the networks also learned by “configural” type solutions, it tended to happen more frequently in the single outcome nondifferential outcome task.

In order to assess the basic prediction that negative patterning learning would be more efficiently acquired in a differential outcome training procedure, we performed a behavioral experiment with rats that mimicked these simulated procedures. In particular, we were interested in determining if the negative patterning task would be learned more rapidly in a differential outcome relative to a non-differential outcome task, and, if so, whether this would be manifest by higher levels of responding to the reinforced elements, lower responding to the stimulus compound, or both of these tendencies during differential outcome training. As will be shown shortly, the results largely confirmed the model’s prediction.

2. Methods

2.1. Subjects

The subjects were thirty-two experimentally naïve male Long-Evans rats, derived from Charles River laboratories but bred at Brooklyn College. We ran the experiment in two replications (n = 16/replication). The rats were maintained at 85% of their free-feeding weights, which varied from 485 to 683 g in replication 1 and 337 to 433 g in replication 2. They were housed in groups of 2–3 in plastic tub cages with woodchip bedding (43 × 22 × 20 cm, l × w × h) in a colony room with a 14h light/10h dark cycle. The rats were run 7 days per week, were weighed before starting the experiment, and given supplemental feedings after the experimental session that started between 1:30 and 3 PM each day. Before the first day of magazine training the rats were pseudo-randomly assigned to 2 groups: Differential and Non-Differential groups, in an effort to maintain equal mean weights between groups and to ensure equivalent heterogeneity in terms of their parentage.

2.2. Apparatus

All rats were run in the same eight set of identical conditioning chambers (BRS Foringer RC series). Each conditioning chamber was housed in a Med Associates sound- and light-resistant shell. The conditioning chambers measured 30.5 × 24.0 × 25.0 cm. Two end walls were constructed of aluminum, and the sidewalls and ceiling were made from clear Plexiglas. In the center of one aluminum wall, 1.2 cm above the grid floor was a recessed food magazine measuring 3.0 × 3.6 × 2.0 cm (length × width × depth). The floor consisted of 0.60 cm diameter stainless steel rods spaced 2.0 cm apart.

For reinforcers, we used 45 mg pellets supplied by TestDiet (MLab rodent grain pellets) and BioServ (Purified rodent pellets). Pilot studies in our lab revealed that the rats could easily discriminate between these two pellet types. Both of these diets contain similar amounts of calories (3.3 and 3.6 kcal/g, respectively) and similar carbohydrate, protein, and fat profiles, but the BioServ pellets have most of its carbohydrate content coming from sucrose and dextrose, whereas the TestDiet pellet carbohydrate content primarily is derived from starch. Thus, one of these pellet types is sweet and the other is not.

On the inner walls of the recessed magazine were an infrared detector and emitter (Med Associates ENV-303HDA) enabling the automatic recording of head movements inside the magazine. These were located 0.9 cm above the magazine floor and 0.8 cm recessed from the front wall. Located 3.0 cm to the right and left of the magazine and 8.0 cm above the floor were different response levers (4 cm in width), but access to these was prevented by separate sheet-metal covers that were in place at all times. Two 28 volt, 2.8 W light bulbs were mounted on the top of the end wall opposite the wall with the food magazine. These bulbs were covered by a translucent plastic sheet angled between the ceiling and top portion of the rear wall that served to protect the bulbs while diffusely projecting light throughout the chamber. When activated, these light bulbs flashed with equal on-off pulse durations at a frequency of 2/s. A Med Associates white noise module (ENV-225SM) was centrally mounted on the outer side of the ceiling of the conditioning chamber and was used to present a white noise stimulus (6 dB above a background level of 74 dB, C weighting, Radio Shack Sound Level Meter [Cat #33–2050]). The chamber was dark except when the visual stimulus was presented. A fan attached to the outer shell provided cross-ventilation within the shell as well as background noise. All experimental events were controlled and recorded automatically by a Windows PC and Med Associates interfacing equipment located in the same room.

2.3. Behavioral procedures

The rats initially received two days of magazine training, one day with each reward type and with the order of reward types counterbalanced across days. In each 20-min magazine training session, 20 rewards of one type were delivered on a random time 60 s schedule.

Beginning on the day following magazine training, subjects were trained in a negative patterning procedure for 28 daily sessions. Each session consisted of 32 trials with 3 different types of trials: reinforced flashing light (F), reinforced noise (N), and nonreinforced flashing light + noise compound (FN−) trials. There were 4, 8-trial blocks in each training session, in which there were 2 F trials, 2 N trials, and 4 FN− trials. The order of presentation of these three trial types was randomized within each block. Each CS was presented with a 10 s duration and on element alone trials 2 pellets, separated by 0.5 s, were delivered at stimulus offset. On FN− stimulus compound trials, the two stimuli were presented simultaneously for 10 s and the trial ended without reinforcement. The inter-trial intervals, ITI, averaged 2 minutes (with a range from 1 to 3 minutes, according to a uniform distribution). For Differential Outcome group (n=16), F and N element trials were each rewarded with a different pellet type (differing primarily in taste), denoted as N+ and F*, where “+” and “*” represent the two distinctive pellet types. The specific stimulus-pellet type combinations were fully counterbalanced across subjects in this group of rats. In Non-Differential outcome group (n=16), each stimulus element was reinforced equally often with both pellet types across trials, denoted as F+/*, N+/*.

2.4. Statistical analysis

The rate of magazine entry responding was assessed during each of the three training trial types as well as in corresponding 10 s pre-CS periods. Elevation scores were then calculated for each trial type by subtracting pre-CS response rates from that occurring during the training trial. Discrimination scores were calculated for each group during each training session by taking a difference in responding (i.e., elevation scores) to reinforced element trials (averaged across flashing light and noise trials) and nonreinforced stimulus compound trials. The discrimination score data was statistically analyzed using a standard split plot ANOVA that treated session as a within-subject factor and group as a between-subject factor. A significant Group × Session interaction was then followed up with simple main effects tests that compared each group on each training session based on a pooled error term. A preliminary analysis also included replication as another between-subject factor but since there were no main effects or interactions involving this factor the data have been collapsed across this factor. A type 1 error rate criterion was set to 0.05 for all statistical decisions.

3. Results

Figure 3 shows the mean magazine response rate data expressed as elevation scores (CS – Pre CS) for both groups. The data are broken down for each trial type across each session in panel A (i.e., for reinforced flashing light, F, and noise, N, trials and for nonreinforced flash + noise stimulus compound trials, F+N), for reinforced element (averaging across flashing light and noise stimuli) versus nonreinforced compound trials in panel B, and for a discrimination index (element – compound difference scores) for each group in panel C. It is clear from panels A and B that both groups acquired the negative patterning discrimination. By the end of training, they both responded more on reinforced element trials compared to the nonreinforced compound trials. However, the group trained with differential outcomes for each reinforced element achieved, overall, a higher degree of discriminative performance by responding more on reinforced element trials. Between-group differences can clearly be seen in panel C where discriminative responding begins to diverge statistically around session 16.

Figure 3:

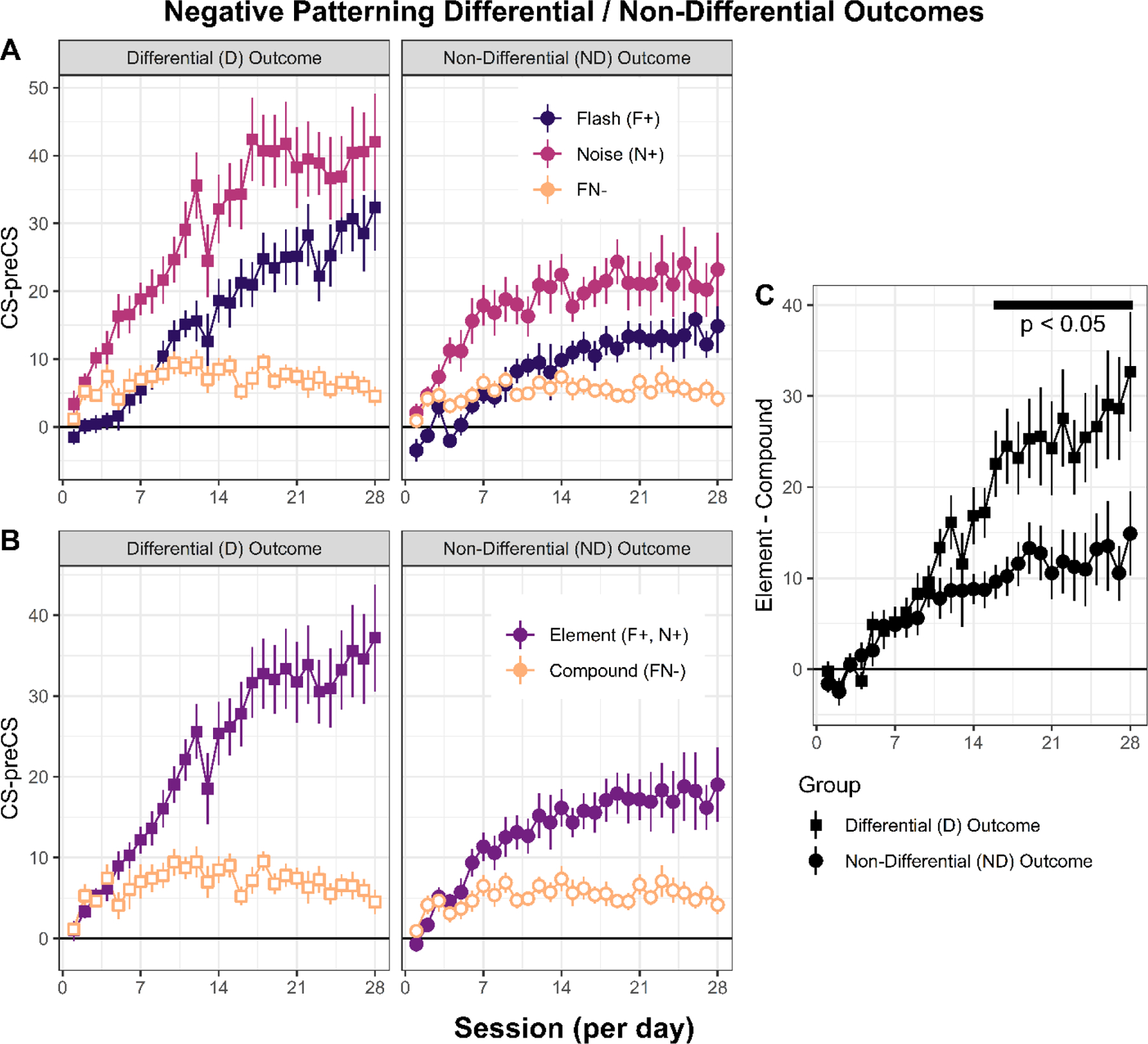
Experimental data (n = 32; 16 per group). Negative patterning learning is more successful when training with differential relative to non-differential outcomes. A. Mean magazine response rates expressed as CS – pre CS elevation scores (y-axis) as a function of 28 daily training sessions (x-axis) for each of the three trial types (F+, N*, FN− for the Differential outcome groups, and F+/*, N+/*, FN− for the Non-Differential outcome group). B. Same as in panel A but the average of single element trials (F and N). C. Element minus compound discrimination scores for Differential and Non-Differential groups; black tick horizontal line represent significance between group differences in each session from sessions 16 to 28, p < 0.05.

The discrimination data in Figure 3C was statistically analyzed with a Group × Session split plot ANOVA that revealed significant main effects of Group, F(1,30) = 6.47, p = 0.016, MSE = 2236.968, Session, F(27,810) = 20.77, p < 0.001, MSE = 89.973, and a significant Group × Session interaction, F(27,810) = 3.73, p < 0.001. To investigate this significant interaction, separate between-group ANOVAs were performed for each conditioning session using a pooled error term, MSE = 166.544, and Satterthwaite’s procedure for correcting the degrees of freedom (Satterthwaite, 1946). This analysis revealed that the groups differed significantly on sessions 16 – 28, smallest F(1,126) = 6.49, ps < 0.012. These data clearly indicate that training with differential outcomes improves discriminative responding in the negative patterning task.

4. Discussion

4.1. Summary of Major Behavioral Findings

The present study examined a unique prediction about the course of negative patterning learning stemming from the connectionist model of Delamater (2012). That model led us to predict that negative patterning learning would be enhanced by manipulations that should help the brain further differentiate between stimuli. We chose an “acquired distinctiveness” manipulation to investigate this (e.g., Delamater, 1998 Honey & Hall, 1989; Lawrence, 1949). One group of rats received pairings of each element of a negative patterning discrimination with different reinforcing outcomes (that differed primarily in terms of their taste qualities). We hypothesized that this would increase the tendency of the brain to segregate (i.e., “pattern separate”) internal representations of those stimuli, and that such segregation was critically important for solution of the negative patterning task. Animals trained in this way learned the negative patterning task more successfully than rats trained with non-differential outcomes occurring on element alone trials. That procedure might be expected to result in “acquired equivalence” between those cues, and the connectionist model predicted that such an effect would tend to interfere with solution of the negative patterning problem. Of course, we cannot determine if our distinctiveness manipulation enhanced or the equivalence manipulation diminished patterning learning, or both. However, the results clearly show that, as predicted, substantial group differences in solving the task emerged over the course of training.

It is worth noting that while we predicted superior learning of the negative patterning task with differential outcome training, the model also anticipated this to be manifested both by an increase in responding to reinforced elements and a decrease in responding to the non-reinforced compound in the differential outcome group compared to the non-differential outcome group (Figure 2). However, whereas the rats receiving differential outcome training responded more to the reinforced elements than the non-differential outcome group, the two groups did not appear to differ in responding to the non-reinforced compound stimulus (Figure 3). We are not sure if a floor effect might have contributed because compound responding was already relatively low in the non-differential group, but also note that the model predicts a larger between-group difference in responding to the reinforced elements than to the non-reinforced compound. Perhaps the reason why we only observed a between group difference in element responding, and not also in compound responding, is related to the fact that the element difference is predicted to be larger, and, therefore, more easily detectable in the rats’ performance.

Another important consideration is that our initial simulation of the non-differential outcome task used only a single US node and our experimental manipulation actually used 2 USs but presented them non-differentially in our control group. In unpublished studies, we have not found any differences in learning rates between a single outcome control versus a two-outcome non-differential control. Other published studies looking at “differential outcome effects” have also readily observed the differential outcome condition to be superior to both single outcome or non-differential outcome conditions (e.g., Blundell, Hall, & Killcross, 2001; Estévez, Fuentes, Marı-Bêffa, González, & Alvarez, 2001; Ramirez & Savage, 2007; Trapold, 1970). Thus, because the two-outcome non-differential control more effectively controls for overall exposure to multiple outcomes, we opted to use that in our experiment.

4.2. “Sensory Integration” in RSC & Neural Net Modelling

The most intriguing aspect of the data we report is that the connectionist model we explored assumes that different collections of internal representational units in the network were called upon to learn the task, and, more specifically, that multi-modal units at the hidden layer appeared largely responsible for problem solution. This “multi-modal” set of hidden layer units in the model largely corresponds to some important roles that Bucci and his collaborators have attributed to the RSC (Bucci & Robinson, 2014; Todd et al., 2019). Both can be thought of as “sensory integration” areas, but the virtue of using a connectionist modeling approach is that it can help us understand more clearly exactly what functional roles such “sensory integration” adopt. We identified at least two separate ways in which the connectionist network depicted in Figure 1 could learn the negative patterning task. One of these involved developing a kind of “negative occasion setting” function that Bucci and his colleagues have already demonstrated is influenced by RSC manipulations (Keen & Bucci, 2008; Robinson et al., 2011; and relatedly, Todd et al., 2015). The unique aspect of our approach is to point out that similar mechanisms might be expected to play a role in both feature negative and negative patterning discrimination learning tasks. Thus, it would not be surprising if RSC were important for both of these types of discrimination learning problems.

Fournier et al. (2019), using a task very similar to the one we use here (but with a single US type), demonstrated that post-training lesion or chemogenetic inhibition of RSC adversely affected the expression of a previously learned negative patterning discrimination. However, neither Fournier et al. (2019) nor Nelson et al. (2018) observed pre-training RSC lesions to impair negative patterning learning. It is worth noting that the overall degree of learning in the Fournier et al. (2019) experiment was extremely modest, and so further training might very well have revealed group differences in acquisition. Compared to the discriminative performance we observe here, their rats were only at the very beginning stages (e.g., day 8) of displaying evidence of learning the task. However, this same conclusion cannot as easily be applied to the Nelson et al. (2018) study, in which more substantial evidence of negative patterning learning was provided without any pretraining lesion effects seen.

4.2.1. Pre versus Post Training Neural Suppression Effects in the Neural Network Model

What are we to make of this difference between pre- versus post-training RSC manipulations in learning and expression of the negative patterning task? We explored this issue with our modeling approach in the following way. First, we note that the model depicted in Figure 1A is highly simplified, and that real brains have considerably more than 4 “multi-modal” units at an intermediate level of processing. Second, how are we to think about modeling lesion and/or neural suppression manipulations? We suppose that these would be analogous to reducing the number of functional processing units within the network. It is worth remembering that the type of model that we described above cannot solve negative patterning tasks, without further assumptions, if they lack hidden layer units. However, so long as some units exist at the hidden layer, these models can learn these types of problems. Indeed, our model initially only assumed 4 multi-modal units. But to explore these ideas further, we performed a variety of simulations in which we “lesioned” the network, or, in other words, “suppressed” neural activity to different degrees. As is true with real brains, no neural manipulation is complete and different percentages of spared neurons remain after the manipulation depending upon the extent of the lesion or the chemogenetic manipulation, etc. Our modeling shows that only a relatively few surviving units would be necessary for the system to learn the task. But to push the idea further, our baseline was to consider a network as “intact” when it contained 64 multi-modal units at the hidden layer and we systematically suppressed different %s of these units in an effort to see how (a) acquisition of the negative patterning task might be affected, and (b) post-training unit suppression, to different degrees, might adversely affect expression of prior learning. The answer to these questions might very well shed some light on the different patterns of results that the Bucci lab has discovered over the years in their experiments.

Figure 4 shows the results of our “pre- versus post-training neural suppression” simulations. We ran the model on a single US negative patterning (task as described above) for a total of 150 training blocks and assessed asymptotic performance levels as a function of the % of the 64 multi-modal units “knocked out” (KO). Figure 4A and 4C show how learning is affected when different percentages of those multi-modal units have been eliminated prior to training on the task. Figures 4B and 4D show how performance of the network is affected when different percentages of multi-modal units have been eliminated after the fully intact network had already learned the problem. In that case, a randomly chosen sub-set of multi-modal units were eliminated after the 64-multi-modal-unit network had first learned the task. Finally, Figure 4E shows, in the form of a discrimination index (output unit activation on element trials – compound trials), how performance is adversely affected when pre-training versus post-training manipulations were used as a function of different degrees of neural suppression. The simulation data in this figure reflect average network performance over 100 simulations conducted with each level (%) of neural suppression.

Figure 4:

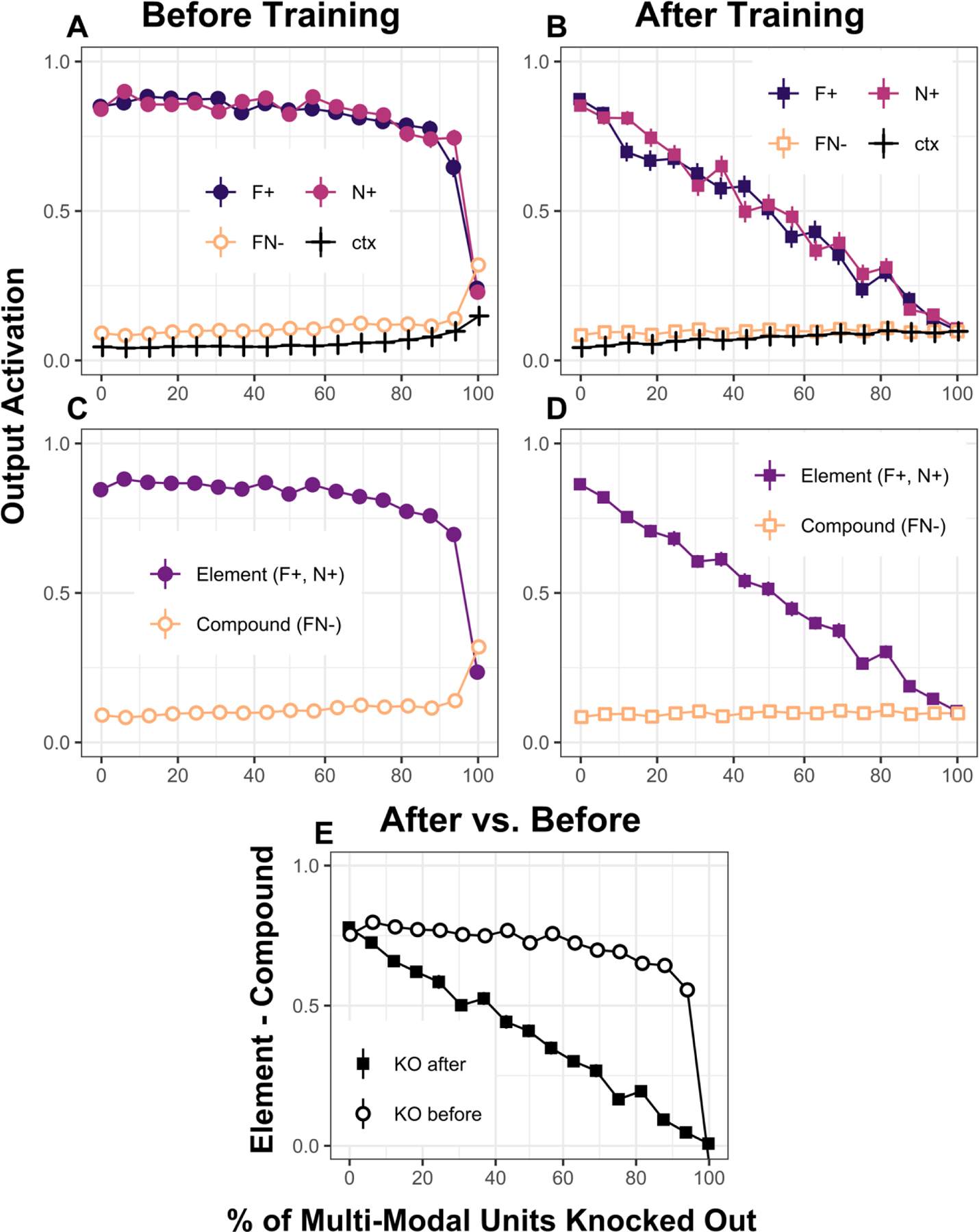
Output unit activation at the end of 150 training blocks as a function of the percentage of multimodal units knocked out. The multi-modal (MM) units were knocked out (KO) either Before (panels A and C) or After (panels B and D) training. For each % of KO MM hidden units, we used 100 networks with an α= 0.3 and β = 0.9 (see Appendix). A and B show activations at the end of training for each of the three trial types. C and D show activations comparing elements against compounds. Panel E shows discrimination indexes (element activation – compound activation) for before versus after training KO. All simulation codes are available in https://github.com/santiagocdo/NLM_Bucci_Delamater-Castiello.

First, note that when 100% of the multi-modal units were eliminated the negative patterning task was not solvable – output activation levels were equivalent across F+, N+, and FN− trials (Figure 4A and 4C). Similarly, if the intact network first learned the task, 100% elimination of the multi-modal units also completely abolished discriminative performance (Figure 4B and 4D). However, the effect of different degrees of multi-modal unit suppression resulted in drastically different effects on network performance before versus after training. There was a much more severe negative impact on expression of prior learning than there was on interference with new learning (Figure 4E). This makes sense because, as described above, relatively few multi-modal hidden units are required for a network to learn a so-called “non-linear” discrimination problem like the negative patterning task, and having more than those relatively few do not drastically affect learning. This means that even if relatively few neurons survive a pre-training lesion, learning can be accomplished and an adverse lesion effect might be difficult to observe even when the structure normally does participate in the learning process. However, the same degree of neural suppression may be expected to have large adverse effects when a normal network is tested after its processing units have been randomly removed because many of those units would have been expected to participate in the learning to begin with. Perhaps this analysis makes sense of why, for instance, Fournier et al. (2019) found post-training neural suppression of the RSC to adversely affect expression but not learning of a negative patterning task.

One caveat here is that Fournier et al (2019) provided evidence that post-training RSC suppression interfered with the expression of negative patterning performance primarily by increasing responding to the nonreinforced compound stimulus. However, our model anticipates a loss of discriminative responding resulting primarily from a reduction in responding to reinforced elements rather than an increase in responding to the nonreinforced compound (see Figure 4B and 4D). It is worth noting that our post-training neural suppression simulations were performed after the network had been trained to near-asymptotic levels of performance whereas rats in the Fournier et al (2019) study displayed only very modest levels of discrimination learning prior to the post-training RSC manipulations. It seems likely that reductions in responding to reinforced cues would be more obvious when such responding is high to begin with, but this remains an empirical question for future research.

Another caveat, is that Keen & Bucci (2008) and Robinson et al. (2011) both found pre-training lesions to negatively affect feature negative learning, while, as noted above, the Bucci lab only found post-training manipulations to negatively impact negative patterning learning. This is an interesting pattern of results, but not necessarily inconsistent with our framework, which suggests only that pre-training manipulations will be more difficult to detect relative to post-training manipulations (at least in negative patterning tasks). It is also interesting, though, that our modeling analysis suggests that negative patterning may be solved partly through negative occasion setting mechanisms (Figure 1B and 1D). In principle, then, both feature negative (especially serial) and negative patterning learning should be affected by RSC manipulations (particularly post-training ones). Relatedly, Todd et al (2017) found that post-training RSC lesions were more effective than pretraining lesions at impairing the context preexposure facilitation effect. It is not clear, however, whether the present model would be relevant to this finding given that this behavioral phenomenon may depend on mechanisms other than those described here (e.g., O’Reilly & Rudy, 2001).

4.2.2. Neural Network Solutions to Negative Patterning – Occasion Setting & Configural Learning Mechanisms

Another important consideration is the form of the “negative occasion setting” mechanisms our network simulations identified. As noted above, the solutions depicted in Figure 1 are consistent with two mechanisms used to describe negative occasion setting, namely, suppression of retrieval of the excitatory target-US association and configural inhibition mechanisms (e.g., Fraser & Holland, 2019; Pearce, 2002). However, another popular approach to understanding negative occasion setting is not that the occasion setter acts to suppress retrieval of the target-US association, but rather that it acts to facilitate retrieval of an inhibitory target-US association (e.g., Bouton, 1991; 1993; 2004; Schmajuk, Lamoureux, & Holland, 1998). It has long been recognized that in a basic feature negative task, the target stimulus can form separate excitatory and inhibitory associations with the US. This is because the target stimulus in this task is both reinforced on some trials and non-reinforced on other trials. Bouton (1991; 1993; 2004) pointed out a formal similarity between negative occasion setting and extinction paradigms, where the experimental context can serve the role of a negative occasion setter. The primary source of evidence for this idea is that extinction learning tends to be highly context-dependent (e.g., Bouton & Bolles, 1979). Thus, if the “extinction memory”, i.e., the inhibitory CS-US association, can only be retrieved when testing occurs in the extinction context, this implies that the extinction context acquires the capacity to retrieve that inhibitory association. Schmajuk, Lamoureux, and Holland (1998) developed a connectionist network model and applied it to a wide variety of occasion setting phenomena and demonstrated that their networks learned feature negative occasion setting discriminations through just this mechanism. Specifically, they showed that the target stimuli acquired both excitatory and inhibitory connections to the US node in their networks, and that the negative occasion setting stimulus acted to strengthen the inhibitory CS-US pathway. In contrast, feature positive occasion setting worked in the opposite way, by disinhibiting the inhibitory CS-US pathway.

In our simulations, each input stimulus primarily came to suppress the other stimulus’ excitatory pathway to the output unit, more consistent with Holland’s original formulation (Holland, 1985; Fraser & Holland, 2019; see Figures 1B and S1). This was especially true of the differential outcome task. In other simulations, most often in the non-differential outcome task, we occasionally observed what we refer to as a “configural” solution (see Figures 1C and S2). However, our nomenclature is based merely on the idea that two stimuli more successfully activate the same hidden unit on stimulus compound than on element alone trials, when that hidden unit itself inhibits output activation. It is convenient to refer to such units as “configural” since they will be more strongly activated by the presence of both input stimuli. However, one can just as easily consider this convergence as resulting in stronger “retrieval” of the inhibitory pathway, as would be more typical of the other negative occasion setting mechanism just described, i.e., by strengthening the inhibitory pathway. But however one wishes to characterize this mechanism, our modeling has made clear that a much more common solution that our network was able to find is of the former (negative occasion setting) than of the latter (configural) type. However, when the network did learn with the configural type of solution, it did so much more frequently in the non-differential outcome procedure and only very rarely in the differential outcome task. The supplemental section illustrates some of these basic network solutions to these two problems in greater detail.

Across 32 simulations on each task, we observed, as noted above, superior learning on the differential outcome task, but, in addition, we observed that network performance was more severely disrupted by post-training elimination of the modality-specific pathways in the differential versus the non-differential outcome procedure. In addition, we found that post-training lesions of all multi-modal units completely abolished discriminative performance by the network in the non-differential outcome task (Figure 4), but while severely disrupting performance in the differential outcome task discriminative performance was still superior to chance. Thus, post-training lesions of a multi-modal area, such as the RSC, might be expected to have stronger effects on a single US non-differential outcome procedure compared to a two US differential outcome task – a prediction that remains to be tested.

Still another connectionist approach to negative patterning discriminations was introduced by Grand and Honey (2008). In their case, it was assumed that different hidden layer units code for “element” or “compound” stimulus presentations. In their case, solution of the basic negative patterning problem is accomplished by each reinforced element coming to activate the same hidden unit that codes for stimulus “elements” on stimulus alone trials, but to activate a different hidden unit on stimulus compound trials that codes for the “compound.” If those distinct hidden units develop excitatory and inhibitory associations, respectively, with the US node then the network learns the negative patterning task. An interesting difference between this approach and the one advocated here is that stimuli paired with the same US on element alone trials should converge on the same “element” hidden unit within the negative patterning task. In Figure 1, our networks primarily learned this task by developing distinctive internal representations on element alone trials at the hidden layer. Most often it was found that the correlations between the weight vectors for input-to-multi-modal hidden units for V and A inputs were negative, and the networks solved the task with a negative occasion setting solution. Only very occasionally was this correlation found to be positive and the network solved the task with a configural solution (see Supplemental Materials). Thus, whereas Grand and Honey (2008) predict acquired equivalence to emerge across the elements of a negative patterning task, a prediction about which they provided some support, the network we studied here (Delamater, 2012) most often predicts reduced acquired equivalence when training occurs in a negative patterning task relative to a non-patterning control problem. This is another prediction that remains to be tested.

4.2.3. Final Thoughts

It remains to be seen with additional research which of these different modelling approaches and their underlying mechanisms best characterize how the animal actually learns in negative patterning and feature negative occasion setting tasks. Answering that question, though, is important because it would give more substance to the issues of just what functions different “sensory integration” areas in the brain actually perform in these tasks.

One final consideration is that given the results from the Bucci lab on the role of the RSC in negative patterning and feature negative learning, further research should be directed to determining if differential outcome manipulations might also be sensitive to RSC manipulations (as noted above). We have argued here that the multi-modal area of information processing within a feedforward connectionist network might function similar to how the RSC functions in processing information in discrete cue Pavlovian learning tasks. Further, we suppose that the advantage conveyed by differential outcome training is processed through a “pattern segregation” type process within that hidden layer structure. It remains to be seen whether RSC manipulations can impact the differential outcome effect that we report for negative patterning learning. Future work can help answer that question, while also shedding more light on the underlying functional roles played by structures like the RSC in solving complex Pavlovian learning tasks.

5. Conclusions

Training with differential outcomes facilitates learning of the negative patterning discrimination in rats and artificial neural networks. The connectionist model used here is compatible with the hypothesis that the retrosplenial cortex is a multi-modal sensory integration area with two emerging mechanisms for non-linear discrimination problems. The first, a negative occasion setting solution, and the second a configural solution; where the former seems to be more frequent in our simulations. These two mechanisms can be differentiated due to completely opposite correlations in their representations at the hidden layer. This hidden representation is negatively correlated for the negative occasion setting, and positively correlated for the configural representation.

Highlights.

• Rats learn a Negative Patterning task more successfully with differential outcomes.

• These results were predicted from a neural net model (Delamater, 2012).

• The retrosplenial cortex (RSC) may function like a “multi-modal” hidden layer.

• “Sensory integration” may occur through occasion-setting and configural processes.

• Our model predicts stronger post- than pre-training neural suppression effects.

Appendix

Connectionist Model: A Brief Summary

The model was implemented with code written in R and is publicly available at the following website: https://github.com/santiagocdo/NLM_Bucci_Delamater-Castiello. The connectionist model consists of a three-layer feedforward neural network, where activations go bottom-up (from CS to US representations) and learning top-down. The layers are: input (L = 0), hidden (L = 1) and output (L = 2). This model can be described with two rules: the activation rule (that calculates unit activations) and the learning rule (that determines changes in weights or connections between units).

The connectivity constraint between the input and the hidden layer given the visual, multimodal, and auditory pathways (Delamater, 2012) is encoded in the C matrix (size: number of input units × number of hidden units), where 1 represents an existent connection and 0 a nonexistent connection; hence, connections between visual input units to auditory hidden layer pathway units will be equal to 0, and similarly for auditory inputs and visual pathways.

The model computes weight matrices W for layers 1 and 2, i.e., between input and hidden (L = 1), and between hidden and output (L = 2), at every trial t. The values of W^L at t = 0 are random variables from a uniform distribution between −0.5 and 0.5. In order to maintain the partial connectivity between input and hidden W¹ is multiplied (via Hadamard product or elementwise multiplication) with C. On the one hand, W¹ maps the connections’ weights between input and hidden units, thereby, the matrix size is the number of inputs × number of hidden units. On the other hand, W² represents the weights between hidden and output units, hence, the matrix size is the number of hidden × number of outputs. At every t, the CS information is encoded in the activation of the input layer, a(n⁰), where this vector contains 0s and 1s, representing presences and absence of CSs). The USs are encoded in a vector λ (size is equal to the number of USs)¹.

Activation Rule.

The first rule of this model specifies how units are activated. The activation of the hidden and output layers is given by a sigmoidal function that receives the net input (n) vector for the current layer L, i.e., n^L:

$$a\left(n^{\text{L}}\right)=1/\left(1+e^{-\left(n^{\text{L}}-2.2\right)}\right).$$ (1)

The activations are a real number between 0 and 1. We subtract 2.2. from n^L to shift the sigmoidal curve to the right and obtain low activation levels when elements n^L is 0. The net input for the hidden layer is:

$$n^{\text{L}}=a{\left(n^{\text{L}-1}\right)}^{\text{T}}\cdot W^{\text{L}},$$ (2)

where ∙ is a matrix multiplication between a transpose (T) column vector (i.e., a row vector), and the matrix.

Learning rule.

The second rule of the model specifies how W^L changes at every t. This rule is an adaptation of backpropagation (Rumelhart, Hinton, & Williams, 1986). In general terms, the weights are the sum of the current weights and the change of those weights at t. Hence:

$$W^{\text{L}}=\{\begin{array}{c}{W}^{\text{L}}+\Delta W^{\text{L}}\odot C,\text{L}=1\\ W^{\text{L}}+\Delta W^{\text{L}},\text{L}=2(\mathit{\text{output layer)}}\end{array},$$ (3)

Where ⊙ is the Hadamard product or elementwise multiplication, and the partial connectivity only applies to input layer (L = 0) to hidden layer (L = 1) connections within the weight matrix W¹. This ensures that weights between units with impermissible connections (e.g., auditory inputs to visual pathway hidden units) are fixed at 0. Changes in weights ΔW^L are determined by:

$$\Delta W^{\text{L}}=\alpha {\delta }^{\text{L}}\cdot a{\left(n^{\text{L}-1}\right)}^{\text{T}}+\beta \Delta W^{\text{L}},$$ (4)

where α and β are free parameters, representing the learning rate (assumed to be 0.3) and the momentum decay (assumed to be 0.9), respectively. Finally, δ^L is a vector of delta values, and encodes the prediction errors that are back-propagated throughout the network, following the next equation:

$${\delta }^{\text{L}}=\{\begin{array}{c}\left(\lambda -a\left(n^{\text{L}}\right)\right)a\left(n^{\text{L}}\right)\left(1-a\left(n^{\text{L}}\right)\right),\text{L}=2\\ \left(W^{\text{L}+1}\cdot {\delta }^{\text{L}+1}\right)a\left(n^{\text{L}}\right)\left(1-a\left(n^{\text{L}}\right)\right),\text{L}=1(\mathit{\text{hidden layer}})\end{array},$$ (5)

where λ is a vector which encodes with 0s (absent) and 1s (present) the USs at every t.