Partially linear single-index generalized mean residual life models

Summary

Mean residual life (MRL) function defines the remaining life expectancy of a subject who has survived to a time point and is an important alternative to the hazard function for characterizing the distribution of a time-to-event variable. Existing MRL models primarily focus on studying the association between risk factors and disease risks using linear model specifications in multiplicative or additive scale. When risk factors have complex correlation structures, nonlinear effects, or interactions, the pre-fixed linearity assumption may be insufficient to capture the relationship. Single-index modeling framework offers flexibility in reducing dimensionality and modeling nonlinear effects. In this paper, we propose a class of partially linear single-index generalized MRL models, the regression component of which consists of both a semiparametric single-index part and a linear regression part. Regression spline technique is employed to approximate the nonparametric single-index function, and parameters are estimated using an iterative algorithm. Double-robust estimators are also proposed to protect against the misspecification of censoring distribution or MRL models. A further contribution of this paper is a nonparametric test proposed to formally evaluate the linearity of the single-index function. Asymptotic properties of the estimators are established, and the finite-sample performance is evaluated through extensive numerical simulations. The proposed models and inference approaches are demonstrated by a New York University Langone Health (NYULH) COVID-19 dataset.

1 |. INTRODUCTION

The mean residual life (MRL) function defines the remaining life expectancy given a subject has survived to a specific time point. For a time-to-event variable T with finite expectation, the MRL at time t is m(t) = E(T − t|T > t), and m(t|X) = E(T − t|T > t, X) as the conditional MRL function given covariates X. In contrast to the hazard function that characterizes the instantaneous risk, the remaining life expectancy has appealing interpretations and lessens communication barriers with patients in practice. Furthermore, the MRL regression model is a desired complement to Cox proportional hazards (PH) model as it directly characterizes the covariate effects on the remaining survival time.

Although the one-to-one correspondence exists among the MRL function and the hazard function, there is no straightforward relationship between the covariate effects on the MRL model and the ones on the hazard model. Under the special case of survival distribution belonging to the Hall-Wellner family, Oakes and Dasu¹ showed the existence of a model that satisfies both the proportional MRL and the PH assumptions. Under general settings or with model specifications beyond two-sample comparison, a constant hazard ratio does not translate to a constant effect on the MRL or any monotonic transformation of the MRL; vice versa, neither a constant effect elongating the MRL additively or proportionally translates to any simple effect on the hazard function. Therefore, the choice between modeling the hazard or the MRL depends on the interest of scientific investigation.

During the coronavirus disease 2019 (COVID-19) pandemic, after a COVID-19 patient is hospitalized, it is of importance to estimate the remaining time to recovery (length of hospital stay) given that the patient has been hospitalized for t days, for which modeling the MRL directly addresses the question. This quantity is of interest not only for individual patients to comprehend their likelihood and speed of recovery but also for hospital management to make arrangements and adjustments to the needs of hospital beds, clinical staff, and many other clinical resources.^2,3 Furthermore, to evaluate COVID-19 disease severity and progression in hospitalized patients, many biomarkers have been studied and found to play important roles in understanding the disease mechanisms and guide treatment strategies.⁴ Petrilli et al⁵ conducted a prospective cohort study in confirmed COVID-19 patients hospitalized in four acute care hospitals of the New York University Langone Health (NYULH) and showed that biomarkers of D-dimer, ferritin, and C-reactive protein (CRP) at admission were positively associated with the risk of developing critical illness that was defined as a composite endpoint of intensive care unit (ICU) admission, mechanical ventilation, and mortality. Although many researches have investigated the association of each biomarker with the COVID-19 progression,⁶ their relative importance and joint effects remain unclear. Motivated by our application to study the time to recovery of COVID-19 hospitalized patients, we are interested in and thus focus on modeling the MRL function in this paper. Specifically, we aim to evaluate the relative importance and overall effects of multiple biomarkers on the time to recovery, allowing potential interactions and nonlinear effects and adjusting for additional covariates.

Sun and Zhang⁷ proposed a class of generalized MRL (GMRL) models,

$$m(t\mid Z)=g\left\{m_0(t)+{\beta }^{T}Z\right\},$$ (1)

which allows a flexible pre-specified link function g(·) and includes multiplicative MRL models^1,8,9 and additive MRL models^10,11 as special cases. When β = 0, g{m₀(t)} denotes the baseline MRL function. Most of the existing MRL models, however, depend on the linearity assumption of the covariate effects on the MRL function. To assess nonlinear covariate effects, Yang and Zhou¹² proposed a class of semiparametric varying-coefficient MRL models that allow coefficients to vary with the level of a given variable. When this specific variable is time, the model returns to the semiparametric time-varying coefficients MRL model as a special case.¹³ However, when the primary interest is to explore the joint effects rather than individual covariate effect, such as the multiple biomarkers in the NYULH COVID-19 study, the linear specification of additive linear effects as in Model (1) may be insufficient. There is a growing need to develop new methodologies that can naturally accommodate flexible forms of nonlinear effects of the covariates and delineate their contributions to the joint effects. Further, flexible MRL models that could handle high-dimensional data are greatly desired.

The single-index technique^14,15,16 provides an effective solution to reduce dimensionality and offers flexibility in capturing the nonlinear joint effects of multiple covariates. The relative scale and direction of the single-index coefficients reflect the contribution of each covariate to the overall effects. In the context of time-to-event data analysis, the single-index modeling technique has been incorporated into the Cox PH model,^17,18 and further extended to the partially linear single-index (PLSI) PH model by allowing both linear and nonlinear components.^19,20 To the best of our knowledge, there has been no research that offers both the flexibility in modeling covariates’ effects from the PLSI construct and straightforward interpretation from the MRL models. Therefore, we propose a class of PLSI generalized MRL (PLSI GMRL) models in this paper and develop estimating equations using the inverse probability of censoring weighting (IPCW) technique to account for censoring. Furthermore, we propose an extension to double-robust estimators to protect against potential model misspecifications. In addition, this paper makes an important contribution by providing a nonparametric testing procedure to evaluate the linearity of the single-index function. Failing to reject this null hypothesis suggests the linear effects of all covariates in the model, and thus we can return to the estimation procedures and inference from the generalized MRL models.⁷

The rest of this article is organized as follows. In Section 2, we present the proposed model and details of interpretation, estimation, inference, as well as double-robust extensions. Our proposed test statistic for the linearity of the single-index function and its nonparametric testing procedure are also presented. Moreover, we provide an extension to the restricted MRL models when it is of interest to restrict the remaining life expectancy within a time range. Section 3 presents extensive numerical simulations. In Section 4, we demonstrate our method via the application to the NYULH COVID-19 de-identified electronic health record (EHR) data. A model diagnosis method is also presented. Discussion and concluding remarks are included in Section 5. Regularity conditions, additional simulation and data application results, and technical proofs are provided in Supporting Information online.

2 |. METHODS

2.1 |. Notation

Let Y and C be the survival time and censoring time, respectively. Then T = min(Y, C) denotes the observed time subject to censoring, and δ = I(Y ≤ C) is the censoring indicator. Assume the support of C is longer than that of the survival time T to ensure an estimable MRL function. Covariates are classified into two groups a priori: X represents the pre-specified covariates to be modeled in linear form and Z represents the covariates to be included in the single-index function. We have i.i.d. copies of {T_i, δ_i, X_i, Z_i, i = 1, …, n} and assume Y and C are conditionally independent given covariates X and Z.

The proposed PLSI GMRL model is specified as

$$m(t\mid X,Z)=g\left\{m_0(t)+{\alpha }^{T}X+\psi \left({\beta }^{T}Z\right)\right\},$$ (2)

where g(·) and m₀(t) are similarly defined as in Model (1), α is a q-dimensional vector of coefficients characterizing the effects of X in the linear component, ψ(·) is an unknown single-index function that represents the joint effects of covariates Z, and β’s are the corresponding p-dimensional single-index coefficients representing the relative importance and direction of Z. When ψ(·) is monotone, the effects of Z can be interpreted qualitatively using the sign of its coefficient β. Specifically, if ψ(·) is monotone increasing, a positive β suggests an increased mean residual time at a larger value of the covariate, and vice versa for a negative sign. The relative importance of each covariate in ψ(·) on the MRL function can be evaluated by examining the magnitude of |β|.

Note that the absolute direction and scale of β are not identifiable since any scale and/or constant shift can be absorbed by ψ(·), so the identifiability constraint is assumed by constraining the Euclidean norm ∥β∥ = 1 with the first component to be positive. In addition, we impose the sum-to-zero constraint²¹ as ${\sum }_{i=1}^n\psi \left({\beta }^T{Z}_i\right)=0$ for the identifiability of ψ(·) because the constant shift can be absorbed by m₀(t). One can also let $\widehat{\psi }(0)=0$ instead. Both constraints on ψ(·) solve the issue of identifiability, but the latter one will have the $\widehat{\psi }(\cdot )$ and its corresponding 95% confidence intervals always pass through the origin (0, 0) with centered single-index covariates, preventing any statistical inference at point 0. To ensure the MRL function is properly defined, g(·) needs to be strictly increasing, twice continuously differentiable, and m(t|X, Z) = g{m₀(t) + α^TX + ψ(β^TZ)} is a proper MRL function for all possible values of X and Z.

Similar to Huang and Liu¹⁸ and Sun et al,¹⁹ we use spline basis functions to approximate the derivative of the unknown single-index function ψ(·),

$${\psi }^{\prime }(u)=\sum _{j=1}^k{\gamma }_j{B}_j(u)={\gamma }^{T}B(u),$$

where B_j(u),j = 1, …, k, are the B-spline basis functions, k denotes the degrees of freedom, B(u) = {B₁(u), …, B_k(u)}^T, and γ = {γ₁, …, γ_k}^T. We choose B-splines because of their numerical stability,^18,20 but other basis functions, such as truncated power basis and P-splines, can also be adopted. The choice of approximating ψ′(·) rather than ψ(·) itself is due to two considerations: first, ψ′(·) is more frequently referred to in subsequent computation and inference steps; second, one usually can achieve better numerical stability with computing integration than differentiation. Consequently, we have $\psi (u)={\sum }_{j=1}^k{\gamma }_j{\tilde{B}}_j(u)={\gamma }^T\tilde{B}(u)$, where ${\tilde{B}}_j(u)={\int }_{\text{min}(0,u)}^{\text{max}(0,u)}{B}_j(s)ds,j=1,\dots ,k$, are the integrals of the B-spline basis functions and $\tilde{B}(u)={\left\{{\tilde{B}}_1(u),\dots ,{\tilde{B}}_k(u)\right\}}^T$. Hence, Model (2) can be rewritten as

$$m(t\mid X,Z)=g\left\{m_0(t)+{\alpha }^{T}X+{\gamma }^T\tilde{B}\left({\beta }^{T}Z\right)\right\}.$$ (3)

Throughout the article, we use quadratic B-splines in the basis expansion of ψ′(·), and ψ(·) is a cubic spline.

2.2 |. Estimation equations

For the simplicity of notation, we define V = (X, Z^T)^T, θ = (α^T, β^T, γ^T)^T, and $\varphi (V;\theta )={\alpha }^{T}X+{\gamma }^T\tilde{B}\left({\beta }^{T}Z\right)$. We employ the technique of the inverse probability of censoring weighting (IPCW) to handle censoring in our proposed estimation and inference procedures. We first assume that C is independent of covariates V. Let G(t) be the survival function of C, and construct a stochastic process as

$$M_i\left(t;\theta ,m_0(\cdot )\right)=\frac{{\delta }_{i}I\left(T_i>t\right)}{G\left(T_i\right)}\left[T_i-t-g\left\{m_0(t)+{\alpha }^T{X}_i+{\gamma }^T\tilde{B}\left({\beta }^T{Z}_i\right)\right\}\right],i=1,\dots ,n,$$

which is a mean-zero process at the true values of θ and m₀(·). Given a pre-specified g(·) and fixed coefficients θ, m₀(t) and can be estimated at each fixed t ∈ {t : 0 ≤ t ≤ τ} by solving the following estimating equation,

$$\sum _{i=1}^n\frac{{\delta }_{i}I\left(T_i>t\right)}{\widehat{G}\left(T_i\right)}\left[T_i-t-g\left\{m_0(t)+{\alpha }^T{X}_i+{\gamma }^T\tilde{B}\left({\beta }^T{Z}_i\right)\right\}\right]=0,$$ (4)

where $\widehat{G}(t)$ is the Kaplan-Meier estimator of G(t). Here we assume 0 < τ = inf{t : Pr(T ≥ t) = 0} < ∞ on τ to circumvent the technical difficulty on the tail behavior of limiting distribution. For a theoretical investigation, we can adopt Ying’s approach²² on asymptotic properties beyond τ to our method. Given ${\widehat{m}}_0(t;\theta )$, we then propose estimating equations for θ as follows:

$$\begin{gathered} U(\theta )={\left[U_{\alpha }^T(\theta ),U_{\gamma }^T(\theta ),U_{\beta }^T(\theta )\right]}^T \\ =\sum _{i=1}^n{\int }_0^{\tau }\frac{{\delta }_{i}I\left(T_i>t\right){\varphi }^{\prime }\left(V_i;\theta \right)}{\widehat{G}\left(T_i\right)}\left[T_i-t-g\left\{{\widehat{m}}_0(t;\theta )+{\alpha }^T{X}_i+{\gamma }^T\tilde{B}\left({\beta }^T{Z}_i\right)\right\}\right]dH(t)=0, \end{gathered}$$ (5)

where ${\varphi }^{\prime }(V;\theta )={\left(\frac{\partial \varphi (V;\theta )}{\partial \alpha },\frac{\partial \varphi (V;\theta )}{\partial y},\frac{\partial \varphi (V;\theta )}{\partial \beta }\right)}^T={\left(X^T,\tilde{B}{\left({\beta }^{T}Z\right)}^T,{\gamma }^{T}B\left({\beta }^{T}Z\right)Z^T\right)}^T$ and $H(t)={\sum }_{i=1}^n{\delta }_i\left(T_i\le t\right)$ is an increasing weight function on [0, τ]. Note that other forms of H(t) can be easily adopted as long as the function is increasing and converges almost surely to a deterministic bounded function. We denote the final estimators of θ as $\widehat{\theta }={\left({\widehat{\alpha }}^T,{\widehat{\gamma }}^T,{\widehat{\beta }}^T\right)}^T$ and ${\widehat{m}}_0(t)≔{\widehat{m}}_0(t;\widehat{\theta })$.

2.3 |. Implementation

In practice, instead of directly calculating the complex Jacobian matrix J(θ) = ∂U(θ)/∂θ, we consider an iterative procedure to estimate (α^T, γ^T)^T and β based on their corresponding estimating equations U_α(θ),U_γ(θ), and U_β(θ), each of which is numerically more stable and simpler. The Jacobian matrix of each equation can be easily derived by taking the derivative with respect to the parameters of interest. The Newton-Raphson method is used to solve for these parameters iteratively, and the algorithm is depicted as follows.

• Step 1: Assign initial value of β_ini. The initial value can be obtained from standard MRL models using R package “GMRL” with a pre-specified g(·) link function (e.g. multiplicative MRL model or additive MRL model) by assuming linear coefficients for all covariates.

• Step 2: Given β_ini and a fixed degrees of freedom k, the covariates consist of X_i and $\tilde{B}\left({\beta }_{ini}^T{Z}_i\right)$. We then estimate α and γ simultaneously using “GMRL” package and denote the estimators by α_ini and γ_ini.

• Step 3: Given α_ini, γ_ini and β_ini, update ${\widehat{m}}_0\left(t;{\alpha }_{ini},{\gamma }_{ini},{\beta }_{ini}\right)$ using Equation (4). Then, we fix α_ini and γ_ini and update β_ini based on U_β in Equation (5). Ensure ∥β_ini∥ = 1 with the first component to be positive.

• Step 4: Repeat step 2–3 until the convergence criterion is met.

Given a fixed degrees of freedom k, we recommend that knots be placed at equally spaced sample quantiles of the single index β^TZ, and obtain the corresponding estimator $\widehat{\theta }(k)$ from equation U θ(k) = 0. Similar to the idea of Ma and Wei,²³ we select the optimal k through minimizing the quadratic score function with a penalty term on the degrees of freedom as U (θ(k))^TU(θ(k)) + log(n)(k + d + p + q − 2), where q and p denote, respectively, the number of covariates in linear form and inside of the single index, and d is the degree of the spline functions.

2.4 |. Inference

To satisfy the constraints ∥β∥ = 1 and β₁ > 0, we reparameterize β = β(σ) = {(1 − ∥σ∥²)^1/2, σ₁, …, σ_p−1}^T with σ = (σ₁, …, σ_p−1)^T. The solution to Equation (5) can be denoted as ${\widehat{\theta }}_{\sigma }={\left({\widehat{\alpha }}^T,{\widehat{\gamma }}^T,{\widehat{\sigma }}^T\right)}^T$ and ${\widehat{m}}_{0\widehat{\sigma }}(t)≔{\widehat{m}}_0\left(t;{\widehat{\theta }}_{\sigma }\right)$. Note that the parametrizaiton of ${\widehat{\theta }}_{\sigma }$ is purely used to develop asymptotic theory of $\widehat{\theta }$ below. Next, we define additional notations: $N_i^c(t)=I\left(T_i\le t,{\delta }_i=0\right),\widehat{\pi }(t)=n^{-1}{\sum }_{i=1}^{n}I\left(T_i\ge t\right),{\widehat{\Lambda }}^c(t)=n^{-1}{\sum }_{i=1}^n{\int }_0^{t}d{N}_i^c(u)/\widehat{\pi }(u)$, ${\widehat{M}}_i^c(t)=N_i^c(t)-{\int }_0^{t}I\left(T_i\ge u\right)d{\widehat{\Lambda }}^c(u)$,

$${\widehat{M}}_i(t)=\frac{{\delta }_{i}I\left(T_i>t\right)}{\widehat{G}\left(T_i\right)}\left[T_i-t-g\left\{{\widehat{m}}_0(t)+\varphi \left(V_i;{\widehat{\theta }}_{\sigma }\right)\right\}\right],$$

$$\widehat{Q}(t)=n^{-1}\sum _{i=1}^{n}I\left(T_i\ge t\right){\int }_0^{\tau }{\widehat{M}}_i(u)\left\{{\varphi }^{\prime }\left(V_i;{\widehat{\theta }}_{\sigma }\right)-\overline{V}\left(u;{\widehat{\theta }}_{\sigma }\right)\right\}dH(u),$$

$\overline{V}\left(t;{\theta }_{\sigma }\right)=\frac{{\sum }_{i=1}^n{\delta }_i\widehat{G}{\left(T_i\right)}^{-1}I\left(T_i>t\right)g^{\prime }\left\{{\widehat{m}}_0\left(t;{\theta }_{\sigma }\right)+\varphi \left(V_i;{\theta }_{\sigma }\right)\right\}{\varphi }^{\prime }\left(V_i;{\theta }_{\sigma }\right)}{{\sum }_{i=1}^n{\delta }_i\widehat{G}{\left(T_i\right)}^{-1}I\left(T_i>t\right)g^{\prime }\left\{{\widehat{m}}_0\left(t;{\theta }_{\sigma }\right)+\varphi \left(V_i;{\theta }_{\sigma }\right)\right\}}$, where g′(x) = dg(x)/dx.

Theorem 1. Under the regularity conditions (C1) to (C4) stated in Web Appendix C, we have

1. The estimators $\widehat{\theta }$ and ${\widehat{m}}_0(t)$ exist and are consistent.

2. $\sqrt{n}\left(\widehat{\theta }-{\theta }_{*}\right)\to N\left\{0,A^{-1}{\Sigma }_{{\theta }_{*}}{\left(A^{-1}\right)}^T\right\}$ in distribution. The variance matrix components A and ${\Sigma }_{{\theta }_{*}}$ can be consistently estimated by $\widehat{A}$ and ${\widehat{\Sigma }}_{\widehat{\theta }}$. Specifically,

   $$\widehat{A}=n^{-1}\sum _{i=1}^n{\int }_0^{\tau }\frac{{\delta }_{i}I\left(T_i>t\right)}{\widehat{G}\left(T_i\right)}\left[g^{\prime }\left\{{\widehat{m}}_0(t)+\varphi \left(V_i;\widehat{\theta }\right)\right\}\left\{{\varphi }^{\prime }\left(V_i;\widehat{\theta }\right)-\overline{V}(t;\widehat{\theta })\right\}{\left\{{\varphi }^{\prime }\left(V_i;\widehat{\theta }\right)\right\}}^T-\frac{\partial {\varphi }^{\prime }\left(V_i;\widehat{\theta }\right)}{\partial {\widehat{\theta }}^T}\left[T_i-t-g\left\{{\widehat{m}}_0(t)+\varphi \left(V_i;\widehat{\theta }\right)\right\}\right]\right]dH(t),$$

   $${\widehat{\Sigma }}_{\widehat{\theta }}=\left(\begin{array}{ccc}\hfill \frac{{\widehat{\beta }}_2}{{\widehat{\beta }}_1},\dots ,\hfill & \hfill \frac{{\widehat{\beta }}_p}{{\widehat{\beta }}_1},\hfill & \hfill 0_{1\times k},0_{1\times q}\hfill \\ \hfill \hfill & \hfill I_{p-1+k+q}\hfill & \hfill \hfill \end{array}\right){\widehat{\Sigma }}_{{\widehat{\theta }}_{\sigma }}{\left(\begin{array}{ccc}\hfill \frac{{\widehat{\beta }}_2}{{\widehat{\beta }}_1},\dots ,\hfill & \hfill \frac{{\widehat{\beta }}_p}{{\widehat{\beta }}_1},\hfill & \hfill 0_{1\times k},0_{1\times q}\hfill \\ \hfill \hfill & \hfill I_{p-1+k+q}\hfill & \hfill \hfill \end{array}\right)}^T,$$

   where ${\widehat{\Sigma }}_{{\widehat{\theta }}_{\sigma }}=n^{-1}{\int }_{i=1}^n{\widehat{\xi }}_i^{\otimes 2}$, ${\widehat{\xi }}_i={\int }_0^{\tau }{\widehat{M}}_i(t)\left\{{\varphi }^{\prime }\left(V_i;{\widehat{\theta }}_{\sigma }\right)-\overline{V}\left(t;{\widehat{\theta }}_{\sigma }\right)\right\}dH(t)+{\int }_0^{\tau }\frac{\widehat{Q}(t)}{\widehat{\pi }(t)}d{\widehat{M}}_i^c(t)$, υ^⊗2 denotes υ^T for a column vector υ, I_p−1+k+q is an identity matrix of (p − 1 + k + q) dimension, 0_1×k and 0_1×q are zero vectors.

Because ${\widehat{\Sigma }}_{\widehat{\theta }}$ is analytically intractable to compute directly, we adopt a bootstrap resampling approach²⁴ to compute the empirical standard errors (SE) of the estimators. For a fixed single index u, the 95% confidence interval for ψ(u) is given by $\widehat{\psi }(u)\pm 1.96{\left\{\text{var}(\widehat{\psi }(u))\right\}}^{1/2}$, where $\widehat{\psi }(u)={\widehat{\gamma }}^T\tilde{B}(u)$ and $\text{var}(\widehat{\psi }(u))=\tilde{B}{(u)}^T\text{var}(\widehat{\gamma })\tilde{B}(u)$, or can be obtained as 2.5% and 97.5% sample quantiles of the estimated single-index function based on bootstrap samples.

2.5 |. Double-robust estimators

Our proposed Equation (5) uses the IPCW method and requires the modeling of censoring distribution. When censoring time is independent with covariates, the nonparametric Kaplan-Meier (KM) estimator performs well. We can easily extend to handle the covariate-dependent censoring by incorporating covariates into estimating censoring distribution, for example, using a Cox PH model. It is well known that a mis-specified censoring model may lead to biased estimators, and thus we further propose a double-robust extension, which would remain consistent when either the model for censoring distribution G(t|V) or a working model for the complete data distribution F(t|V) is correctly specified.

Define $Q_F(\theta ;t,V)≔\frac{1}{F(t\mid V)}{\int }_t^{\tau }D(\theta ;u,V)dF(u\mid V)$ and $Y_{F,G}(\theta ;T,\delta ,V)≔\frac{\delta D(\theta ;T,V)}{G(X)}-{\int }_0^{\tau }{Q}_F(\theta ;t,V)\frac{d{M}^c(t)}{G(t)}$, where $D(\theta ;T,V)={\int }_0^{\tau }I(T>t){\varphi }^{\prime }(V;\theta )\left[T-t-g\left\{{\widehat{m}}_0(t;\theta )+{\alpha }^{T}X+{\gamma }^T\tilde{B}\left({\beta }^{T}Z\right)\right\}\right]dH(t)$ and F(t|V) is the survival function of T given V. As shown in Rubin and van der Laan,²⁵ Y_F,G(θ; T, δ, V) has double robustness property that E[Y_F,G(θ; T, δ, V)|V] = 0 when either F or G is correctly specified. Thus, we have the estimating equations for double-robust estimators as

$$U_{DR}(\theta )=\sum _{i=1}^n\left[\frac{{\delta }_i{D}_i\left(\theta ;T_i,V_i\right)}{\widehat{G}\left(T_i\right)}-{\int }_0^{\tau }{\widehat{Q}}_F\left(\theta ;t,V_i\right)\frac{d{\widehat{M}}_i^c(t)}{\widehat{G}(t)}\right],$$

where $\widehat{F}(t\mid V)$ is an estimator for F(t|V) and can be estimated using the proposed PLSI GMRL Model (3), e.g.,

$$F(t\mid V)=\frac{m(0\mid V)}{m(t\mid V)}\text{ exp }\left\{-{\int }_0^t\frac{du}{m(u\mid V)}\right\}.$$

Note that $\widehat{\theta }$ and ${\widehat{m}}_0(t)$ for $\widehat{F}(t\mid V)$ should not depend on the censoring distribution assumption, and thus we consider obtaining the estimates from the quasi-partial score (QPS) approach proposed by Chen and Cheng.^10,26 The double-robust (DR) estimators denoted as ${\widehat{\theta }}_{DR}$ would be consistent if either the PLSI GMRL Model (3) or the censoring mechanism assumption is correct. We follow the similar iterative estimation procedures introduced in Section 2.3.

Remark: The estimating equations for the QPS approach for GMRL models are constructed based on zero-mean martingales.^10,26 An advantage of the QPS approach is that it does not require any specification of the censoring distribution. In fact, the QPS approach can also be considered for the estimation and inference of the PLSI GMRL models. After approximating the single-index component using finite-dimensional B-splines, the implementation are straightforward following procedures from Chen and Cheng.²⁶ However, when the censoring distribution is well modeled or random, the QPS method is often less efficient than the IPCW method.^7,27 In our simulation studies shown below, we also compared with the QPS estimators and demonstrated that the proposed DR estimators were more efficient compared to the QPS estimators.

2.6 |. Testing linearity of single-index function

If the single-index function can be reasonably assumed to be linear for a practical application, the generalized MRL models⁷ would suffice to fit the data. We propose a nonparametric resampling approach²⁸ to test the linearity of the single-index function ψ(u) by examining whether its derivative is a constant, e.g., H₀ : ψ′(u) = c for a non-zero constant c. Based on the estimation steps described above, ψ′(u) is estimated by ${\widehat{\gamma }}^{T}B(u)$. If there is a pre-specified c of interest, e.g., c = 1 for an identity function, we can directly test the hypothesis ψ′(u) = c. For an unknown c, we estimate its value by $\frac{1}{\left|b-a\right|}{\int }_a^b{\widehat{\gamma }}^{T}B(u)du$, where a and b denote the range of interest. Thus, given a $\sqrt{n}\text{-consistent}$ estimator $\widehat{c}$, we have $\sqrt{n}\left({\widehat{\gamma }}^{T}B(u)-\widehat{c}\right)\to \mathcal{G}-{\mathcal{G}}_c$, where ${\mathcal{G}}_c$ is the weak limit of $\sqrt{n}(\widehat{c}-c)$. We consider the Kolmogorov and Cramer-von Mises-type test statistics as $T_{1n}=\sqrt{n}{\text{ sup}}_u\left|{\widehat{\gamma }}^{T}B(u)-\widehat{c}\right|$ and $T_{2n}=\sqrt{n}\int \left|{\widehat{\gamma }}^{T}B(u)-\widehat{c}\right|du$, respectively. Take T_1n as an example, we propose the nonparametric testing procedure as follows. For each resampling step b = 1, …, B:

1. Obtain the resampled data $\left\{\left(T_i^b,{\delta }_i^b,X_i^b,Z_i^b\right),i=1,\dots ,n\right\}$

2. Estimate ψ′(u) as ${\tilde{\gamma }}^{T}B(u)$ based on the b-th set of resampled data

3. Compute the statistic of test of interest ${\tilde{T}}_{1n}^b={\text{max}}_u\sqrt{n}\left|{\tilde{\gamma }}^{T}B(u)-{\widehat{\gamma }}^{T}B(u)\right|$

We reject the null hypothesis if T_1n is larger than ${\tilde{T}}_{1-\alpha }^B$, which is the empirical (1 − α)-quantile of the simulated sample $\left\{{\tilde{T}}_{1n}^1,\dots ,{\tilde{T}}_{1n}^B\right\}$, and α ∈ (0, 1) is the pre-specified nominal size.

2.7 |. Restricted MRL

Sometimes, the scientific interest in the remaining life expectancy is restricted within a finite interval. For example, in the COVID-19 application, the recovery time varied due to patients’ characteristics and disease severity, but patients who stayed in hospital longer than 30 days or even 60 days could have a very different disease course from the acute patients. Therefore, we consider a 30-day restricted MRL in the data application. The restricted MRL function for a pre-specified time τ > 0 is m_τ(t) = E(T_τ − t|T_τ > 0), where 0 < t < τ, T_τ = min(T, τ), and m_τ(τ) = 0. Regression models for restricted MRL have been studied under the right-censored as well as the left-truncated data.^29,30,31 To incorporate the restricted MRL into our proposed PLSI GMRL model framework, we consider Equation (5) by replacing T_i with min(T_i, τ) and can follow similar estimating procedures.

3 |. SIMULATION STUDIES

3.1 |. Independent censoring

We conducted extensive simulations to evaluate the finite-sample performance of our proposed models and estimation procedures. We considered both multiplicative and additive MRL model settings, corresponding to g(t) = exp(t) and g(t) = t, respectively. The true single-index function ψ(·) was set to be linear, sine curve, and quadratic functions as follows:

• S1. Linear: g{m₀(t) + α^TX + β^TZ};

• S2. Sine curve: g{m₀(t) + α^TX + sin(5β^TZ)/2};

• S3. Quadratic: g{m₀(t) + α^TX + 2(β^TZ)²}.

The baseline MRL function was set to be m₀(t) = g⁻¹{(D₁t + D₂)I(D₁t + D₂ ≥ 0)}, where D₁ > −1 and D₂ > 0, and from the Hall-Wellner family. We set D₁ = −0.5 and D₂ = 0.5. True parameters were set as α_* = (0.1, −0.1)^T and β_* = (0.5, 0.5, −0.5, −0.5)^T. When g(t) = exp(t), covariates X = (X₁, X₂)^T ~ U[0, 0.5] and Z = (Z₁, Z₂, Z₃, Z₄)^T ~ U[0, 0.6] independently for all settings. When g(t) = t, the single-index covariates Z ~ U[0, 1] for all settings. To ensure a properly defined MRL function, we set linear covariates X ~ U[0.55, 0.9] in linear case, X ~ U[1, 1.4] in sine curve case, and X ~ U[0, 1] in quadratic case. Also, an independent censoring time C ~ exp(λ), which controlled a fixed censoring rate 10% or 20%. Throughout the simulations, we set the sample size to be 2000 or 4000. Under each simulation setting, 500 datasets were generated, and 500 bootstraps were conducted to obtain the empirical SEs of the estimators.

We used two equally spaced knots in our simulations and found that the model performance was not sensitive to the number of knots in a reasonable range (e.g., one to five knots) under our settings. The angle between the true parameter β_* and its estimator $\widehat{\beta }$, which was defined as $\omega \left({\beta }_{*},\widehat{\beta }\right)=\text{arccos }\left(\frac{〈{\beta }_{*},\widehat{\beta }〉}{‖{\beta }_{*}‖\cdot \Vert \widehat{\beta }\Vert }\right)$ with ⟨a, b⟩ denoting the inner product of two vectors a and b, was reported to evaluate the estimated single-index coefficients. A large value of ω indicated a large bias in the estimator $\widehat{\beta }$.

Table 1 presents the simulation results under independent censoring with a 10% censoring rate. To better compare the single-index coefficients from the PLSI GMRL model with the GMRL model,⁷ we normalized estimators $\widehat{\beta }$ under the GMRL model with $\Vert \widehat{\beta }\Vert =1$ and β₁ > 0. In the case of a linear single-index function (S1), both models performed reasonably well. The biases of $\widehat{\alpha }$ were small, SDs of the estimates were close to the empirical SEs, and the coverage probabilities (CPs) of the 95% confidence intervals (CIs) were close to the nominal level. For a fixed censoring rate, both $\omega \left({\beta }_{*},\widehat{\beta }\right)$ and SDs of the estimates decreased with increasing sample sizes. Compared with estimators from the multiplicative MRL model, the efficient loss of $\widehat{\beta }$ from the PLSI GMRL model was small (Table A.1).

TABLE 1.

Simulation results with independent censoring.

		α1				α2				$\omega ({\beta }_{*},\widehat{\beta })$
	N	Bias	SD	SE	CP	Bias	SD	SE	CP	Mean	SD
g(t) = exp(t)
S1. Linear case
GMRL	2000	0.001	0.082	0.088	95.8	0.006	0.086	0.088	95.0	6.90	3.07
PLSI GMRL	2000	0.001	0.082	0.088	96.0	0.006	0.086	0.089	95.2	7.41	3.38
GMRL	4000	0.001	0.063	0.062	94.2	0.001	0.062	0.062	95.6	4.74	1.93
PLSI GMRL	4000	0.001	0.063	0.062	94.4	0.001	0.062	0.062	96.0	4.87	1.96
S2. Sine curve case
GMRL	2000	−0.001	0.084	0.080	93.4	0.003	0.078	0.081	96.4	3.63	1.53
PLSI GMRL	2000	0.003	0.083	0.079	93.2	0.003	0.076	0.079	93.2	3.21	1.30
GMRL	4000	0.003	0.056	0.056	94.8	−0.005	0.058	0.057	94.4	2.60	1.12
PLSI GMRL	4000	0.003	0.055	0.055	95.4	−0.005	0.057	0.056	93.8	2.31	0.98
S3. Quadratic case
GMRL	2000	−0.005	0.088	0.087	95.8	−0.005	0.087	0.087	95.0	75.67	31.17
PLSI GMRL	2000	−0.004	0.088	0.086	95.2	−0.008	0.087	0.086	94.8	11.43	5.20
GMRL	4000	−0.001	0.062	0.061	93.2	−0.004	0.063	0.061	94.6	72.02	30.85
PLSI GMRL	4000	0.001	0.061	0.060	94.2	−0.005	0.062	0.061	93.6	8.01	3.58
g(t) = t
S1. Linear case
GMRL	2000	0.002	0.107	0.103	93.3	−0.010	0.108	0.103	94.1	9.77	4.15
PLSI GMRL	2000	0.002	0.107	0.103	92.7	−0.011	0.108	0.103	93.7	10.76	4.99
GMRL	4000	−0.002	0.076	0.074	94.2	0.003	0.074	0.074	94.8	6.82	2.94
PLSI GMRL	4000	−0.002	0.076	0.074	94.2	0.002	0.074	0.074	94.6	7.14	3.21
S2. Sine curve case
GMRL	2000	0.001	0.259	0.242	93.4	0.016	0.257	0.241	92.8	6.64	2.76
PLSI GMRL	2000	0.001	0.258	0.241	93.8	0.016	0.255	0.239	93.4	6.45	3.05
GMRL	4000	0.001	0.174	0.176	95.2	0.001	0.174	0.176	94.8	4.57	1.90
PLSI GMRL	4000	−0.001	0.174	0.175	95.4	0.002	0.173	0.175	94.6	4.15	1.80
S3. Quadratic case
GMRL	2000	−0.006	0.053	0.052	93.8	0.001	0.054	0.052	94.2	66.37	35.71
PLSI GMRL	2000	−0.002	0.050	0.050	94.0	0.002	0.052	0.050	94.4	9.35	4.83
GMRL	4000	−0.003	0.039	0.037	93.0	−0.002	0.038	0.037	94.0	65.54	34.92
PLSI GMRL	4000	0.001	0.037	0.035	92.8	0.001	0.037	0.035	93.8	6.19	3.00

GMRL: generalized mean residual life model; PLSI GMRL: partially linear single-index generalized mean residual life model; SD: sample standard deviation; SE: mean of estimated standard error; CP: empirical coverage probability of 95% confidence interval; $\omega \left({\beta }_{*},\widehat{\beta }\right)$ was calculated by arccos $\left(〈{\beta }_{*},\widehat{\beta }〉/\Vert \widehat{\beta }\Vert \cdot ‖{\beta }_{*}‖\right)$; Censoring rate was 10%.

When g(t) = exp(t) and under the nonlinear single-index scenarios (S2-S3), the proposed PLSI GMRL model outperformed the multiplicative MRL model in terms of efficiency and bias. When the true ψ(·) was a sine curve (S2), we observed low biases from both models because the single index function still satisfied a monotone linear trend over the majority of the data. However, the estimators under the PLSI GMRL model were more efficient compared to those under the multiplicative MRL model (Table A.1). When the true ψ(·) was quadratic (S3), we observed large biases from the multiplicative MRL model as expected, and the performance of the PLSI GMRL model remained well. When g(t) = t, the proposed PLSI GMRL model clearly outperformed the additive MRL model when the true ψ(·) was nonlinear (S2 and S3) in terms of biases, coverage probabilities, and efficiency. The estimated single-index coefficients were summarized in Table A.2.

Figure 1 visualizes the mean of the estimated single-index function $\widehat{\psi }(\cdot )$ and 95% CIs using the 2.5% and 97.5% sample quantiles of the estimated single-index function from 500 simulations. The estimated single-index functions approximated the true functions very well for both g(t) = exp(t) and g(t) = t. Simulation results with 20% censored data were also provided in Table A.3. Additional simulations were conducted under other baseline MRL functions, for instance, D₁ = −1/3 and D₂ = 1, mimicking an exponential distribution resulting from the right skewness for survival time when all covariates equal 0. The results were summarized in Table A.4.

FIGURE 1.

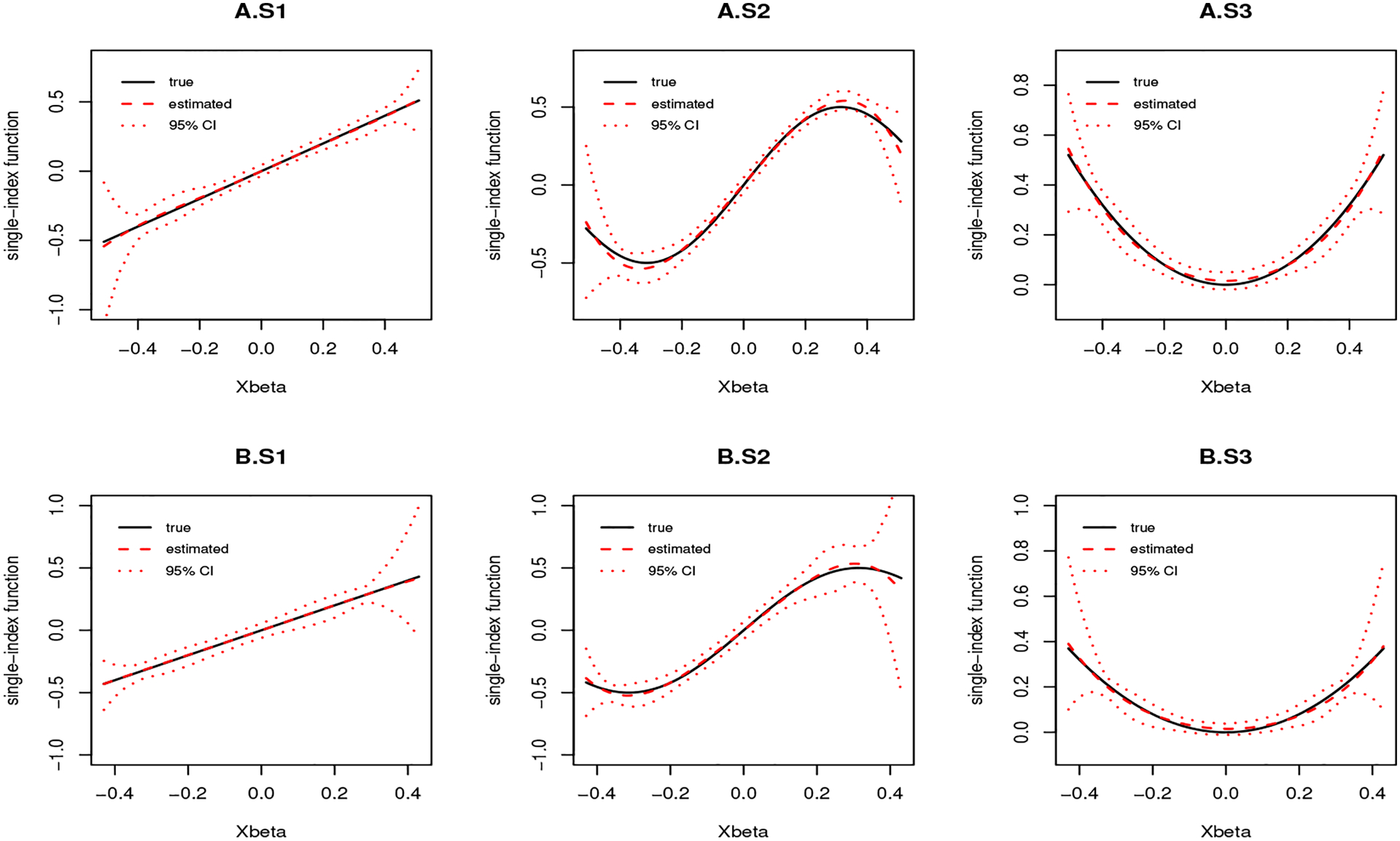
The mean of estimated single-index function with 95% confidence intervals when (A) g(t) = exp(t) and (B) g(t) = t with sample size 4000 and censoring rate 10%: (S1) linear single-index function; (S2) sine curve single-index function; (S3) quadratic single-index function.

3.2 |. Covariate-dependent censoring

In the case of covariate-dependent censoring, we evaluated the robustness of DR estimator ${\widehat{\theta }}_{DR}$ and compared its performance to regular IPCW estimator ${\widehat{\theta }}_{\mathit{\text{IPCW}}}$ and QPS estimator ${\widehat{\theta }}_{QPS}$ when g(t) = exp(t). Censoring time was generated from a Cox model λ(t|V) = λ₀(t)exp(a^TX + b^TZ), where a and b were vectors with each element equal to 2 and λ₀(t) = 1. All other settings remained the same as in previous simulations. Specifically, two IPCW estimators were considered here: ${\widehat{\theta }}_{IPC{W}_1}$ with a mis-specified censoring model using Kaplan-Meier (KM) estimate and ${\widehat{\theta }}_{IPC{W}_2}$ with a correctly specified censoring distribution using a Cox PH model. For DR estimator ${\widehat{\theta }}_{DR}$, we used KM estimator $\widehat{G}(t)$ to approximate censoring distribution and assumed a PLSI GMRL model as the working model for $\widehat{F}(t\mid V)$. As shown in Table 2, due to the mis-specified censoring distribution, ${\widehat{\theta }}_{IPC{W}_1}$ showed large biases in $\widehat{\alpha }$ and $\widehat{\beta }$, while IPCW₂ estimator ${\widehat{\theta }}_{IPC{W}_2}$ performed well since the censoring distribution was correctly specified. The DR estimator ${\widehat{\theta }}_{DR}$ successfully remained robust to the misspecification, having lower biased $\widehat{\alpha }$ with nominal CPs, smaller angle between $\widehat{\beta }$ and β_*, and smaller SDs comparing to IPCW₁. Although DR estimator required a slightly longer computation time due to modeling both censoring distribution and complete data distribution, it maintained relatively high efficiency compared with IPCW₂ when censoring distribution was correctly specified. Moreover, DR estimators were more efficient in all scenarios comparing to QPS estimators.

TABLE 2.

Simulation results under g(t) = exp(t) with covariate-dependent censoring.

		α1				α2				$\omega ({\beta }_{*},\widehat{\beta })$
	N	Bias	SD	SE	CP	Bias	SD	SE	CP	Mean	SD
S1. Linear case
IPCW1	2000	−0.096	0.099	0.097	85.8	−0.090	0.092	0.098	84.6	13.53	4.90
IPCW2	2000	0.003	0.090	0.089	93.8	−0.004	0.093	0.089	94.0	7.19	3.22
DR	2000	0.004	0.091	0.091	93.7	0.006	0.090	0.091	94.6	7.36	3.26
QPS	2000	0.004	0.102	0.091	93.8	0.004	0.093	0.091	94.7	7.94	3.56
IPCW1	4000	−0.096	0.073	0.072	72.8	−0.095	0.072	0.073	69.2	12.44	3.45
IPCW2	4000	0.002	0.064	0.063	95.6	0.001	0.065	0.062	93.6	4.78	2.08
DR	4000	0.003	0.066	0.066	95.4	0.004	0.067	0.066	94.1	4.96	2.14
QPS	4000	0.002	0.073	0.074	94.4	0.001	0.070	0.072	96.3	5.38	2.30
S2. Sine curve case
IPCW1	2000	−0.085	0.085	0.087	83.8	−0.081	0.090	0.087	83.4	5.88	2.01
IPCW2	2000	−0.006	0.076	0.079	95.6	−0.002	0.078	0.079	95.4	3.42	1.37
DR	2000	−0.002	0.082	0.083	93.5	0.004	0.083	0.083	94.3	3.37	1.44
QPS	2000	−0.009	0.096	0.099	95.2	−0.001	0.096	0.099	96.2	3.82	1.67
IPCW1	4000	−0.081	0.065	0.067	74.2	−0.081	0.066	0.068	75.3	5.50	1.56
IPCW2	4000	0.001	0.056	0.056	95.8	0.001	0.057	0.056	94.2	2.29	0.97
DR	4000	0.002	0.062	0.062	94.7	0.002	0.062	0.063	93.8	2.31	0.98
QPS	4000	0.003	0.072	0.072	95.6	−0.001	0.069	0.070	94.8	2.54	1.12
S3. Quadratic case
IPCW1	2000	−0.087	0.100	0.097	87.2	−0.082	0.093	0.095	88.3	12.02	5.89
IPCW2	2000	−0.005	0.083	0.087	95.8	0.001	0.087	0.087	94.2	11.62	5.23
DR	2000	0.002	0.090	0.091	96.4	0.004	0.089	0.089	94.7	11.54	5.63
QPS	2000	−0.002	0.096	0.095	93.7	0.002	0.091	0.092	95.6	13.07	7.07
IPCW1	4000	−0.082	0.069	0.069	75.3	−0.081	0.070	0.071	76.2	8.92	3.85
IPCW2	4000	0.004	0.062	0.061	93.4	−0.002	0.062	0.061	94.0	8.13	3.62
DR	4000	0.004	0.064	0.064	94.3	0.005	0.064	0.065	95.5	8.40	3.72
QPS	4000	0.001	0.070	0.070	95.7	0.001	0.067	0.070	94.6	9.21	4.30

SD: sample standard deviation; SE: mean of estimated standard error; CP: empirical coverage probability of 95% confidence interval; IPCW₁: inverse-probability-of-censoring weighting estimator with a mis-specified censoring distribution; IPCW₂: inverse-probability-of-censoring weighting estimator with a correctly specified censoring distribution; DR: double-robust estimator; QPS: quasi-partial score estimator; $\omega \left({\beta }_{*},\widehat{\beta }\right)$ was calculated by arccos $\left(〈{\beta }_{*},\widehat{\beta }〉/\Vert \widehat{\beta }\Vert \cdot ‖{\beta }_{*}‖\right)$; Censoring rate was 10%.

3.3 |. Type-I error and power of the proposed test

In addition, we conducted simulations to investigate the empirical performance of our proposed nonparametric test. Assuming g(t) = exp(t) and under the null hypothesis that ψ(·) is linear (S1), we examined the type-I error rate when censoring rate was 10% and 20% with a sample size N = 500,1000, and 2000. To evaluate the power of the proposed test, we chose the nonlinear single-index function as a sine curve (S2). We used the Kolmogorov test statistic T_1n throughout the simulations, and the critical values were determined by 1000 resamplings. As shown in Table 3, we observed that the empirical type-I error rate was slightly conservative, but it approached the nominal level with increasing sample size. The power showed that the test performed well to reject the null hypothesis when the true single-index function was nonlinear, and its power increased with the sample size. Overall, the proposed nonparametric test can be a useful tool in the single-index modeling framework to assess the linearity of the single-index function.

TABLE 3.

Simulation results of the nonparametric test for single-index function.

		Linear case	Since curve case
N	Censoring rate	Type-I error	Power
500	10%	0.026	0.194
	20%	0.032	0.182
1000	10%	0.029	0.530
	20%	0.036	0.422
2000	10%	0.043	0.892
	20%	0.040	0.800

Type-I error rate at 0.05 level.

4 |. APPLICATION

4.1 |. Time-to-recovery in Hospitalized COVID-19 Patients using NYULH EHR Data

We demonstrate the proposed models and estimation procedures through the NYULH COVID-19 EHR data. The database contained de-identified patient information regarding basic demographics, social history, medical history, medication use, lab results, and hospital encounter records since January 1st, 2020. Our analysis used data up to July 14th, 2020. Lab-confirmed COVID-19 patients who have been hospitalized within three days since diagnosis were included. Our primary interest focused on the time to recovery within 30 days since hospitalization. For patients discharged to home, acute rehabilitation facilities, and other skilled nursing facilities, the time to recovery was defined as the days from hospital admission to discharge. Similar to the Remdesivir trial for COVID-19,³² time to recovery for patients who died in hospital or discharged to hospice was set as infinity. Time to recovery for the patients who died or were hospitalized longer than 30 days were censored at 30-day. Patients who were transferred to other intermediate care facilities, discharged to long-term care hospitals, or left against medical advice were treated as censored. We considered similar covariates as in Petrilli et al⁵ and set age, sex, race, BMI, temperature, blood oxygen (SpO₂), and medical history be linear covariates. The biomarkers of procalcitonin, CRP, troponin, D-dimer, and ferritin at hospital admission were included in the single-index component, and each biomarker has been log-transformed due to skewness and standardized with a mean of 0 and a standard deviation of 1. Correlations of these biomarkers are shown in Figure B.1. A total of 2599 patients were included in the analysis and the censoring rate was 28.4%, where over 96% of the censoring was the administrative censoring at 30-day due to patient expiration.

In this application, since majority of the censoring was due to the administrative censoring at 30-day, we directly used the KM estimator for censoring distribution estimation. In general practice, we recommend modeling the censoring mechanism first using a Cox PH model and then reduced to the nonparametric KM estimator assuming the independent censoring distribution if appropriate. The pre-specified link function g(·) provides flexibility in assessing covariate effects on the different scales of the MRL function. For illustration, we considered the candidates as either g(t) = exp(t) or g(t) = t. To assess which model fits the data better, we introduce a procedure based on the standardized score process for model diagnosis (see the remark section below). Given estimated parameters $\widehat{\theta }$, the standardized score process over time domain t can be obtained by $U_s(\widehat{\theta };t)=J^{-1/2}(\widehat{\theta })U(\widehat{\theta };t)$, where $J(\widehat{\theta })$ is the Jacobian matrix of $U(\widehat{\theta })$. In the application, we graphically assessed the model fitting by visualizing $‖U_s(\widehat{\theta };t)‖$ in Figure B.2, and observed that the estimated value of the model with g(t) = exp(t) was much smaller than that of g(t) = t, indicating that g(t) = exp(t) fitted the data better. Moreover, we considered $S={\text{sup}}_t‖U_s(\widehat{\theta };t)‖$ as a numerical measure for overall fit of the model, which yielded values 445.7 and 692.8 for PLSI GMRL under g(t) = exp(t) and g(t) = t, respectively, and we thus considered g(t) = exp(t) in subsequent analysis and discussion.

The empirical SEs of the estimators were obtained by 1000 bootstrapping. In addition, we assessed the linearity of the single-index function using the proposed nonparametric test and observed a p-value less than 0.001, indicating the necessity of the PLSI GMRL model to account for possible nonlinear effects. The number of knots was determined by the criteria introduced in Section 2.3, and the estimators were stable with respect to the number of knots between 2 to 7. To compare with the GMRL model,⁷ we standardized the estimated coefficients of biomarkers with a Euclidean norm equal to one and the first component to be positive.

Table 4 summarizes the estimated coefficients and Figure 2 visualizes the estimated single-index function. Due to the data sparsity at the tails, lower and upper 1% data were excluded from the plot. The monotone increasing trend of $\widehat{\psi }(\cdot )$ indicated that the expected remaining recovery time increases with the single-index value. We observed that the increasing trend flattened at the right tail, which indicated that once patients at a severe status indicated by a high level of the combination of biomarkers, one-unit change in single-index value will not change much of the MRL anymore. While for patients with less severe status, one-unit change in single-index value could significantly impact the expected remaining recovery time within the next 30 days. These observations agreed with the testing result on the linearity of the single-index function. The PLSI GMRL model indicated that biomarker levels of procalcitonin, troponin, and D-dimer had significant prolonging effects on the remaining time to recovery but not with ferritin or CRP. In addition, the estimated effect for each biomarker separately was also provided while keeping all other biomarkers at median values (Figure 2 (B) to (F)).

TABLE 4.

Model results for NYULH COVID-19 data application.

	PLSI GMRL†			GMRL†
	Estimate	95% CI**		Estimate	95% CI**
Baseline information (exponential of coefficient)
Age	1.12*	1.09	1.15	1.12*	1.09	1.15
Sex: Male	1.06*	1.01	1.12	1.05*	1.01	1.12
Race: White	1.02	0.97	1.07	1.02	0.97	1.07
logBMI	1.06	0.94	1.20	1.06	0.94	1.20
SpO2	0.91*	0.89	0.94	0.91*	0.89	0.94
Temperature	0.98	0.96	1.01	0.99	0.96	1.01
Smoking: current/former	1.00	0.94	1.06	1.00	0.95	1.06
History of cardiac disease	1.06*	1.02	1.12	1.06*	1.01	1.11
History of pulmonary disease	1.02	0.94	1.09	1.02	0.94	1.09
History of diabetes	1.03	0.98	1.08	1.04	0.98	1.08
History of malignancy	1.11*	1.02	1.21	1.11*	1.01	1.21
Single-index component (coefficient)
Procalcitonin‡	0.91*	0.43	0.98	0.75*	0.51	0.89
Troponin‡	0.27*	0.05	0.86	0.34*	0.11	0.56
D-dimer‡	0.32*	0.01	0.57	0.40*	0.16	0.60
Ferritin‡	−0.01	−0.37	0.13	−0.02	−0.29	0.16
CRP‡	0.06	−0.16	0.39	0.40*	0.02	0.67

^*Estimated coefficient with p-value less than 0.05.

^**95% confidence intervals were estimated by 1000 simulations.

^†Pre-specified link function g(t) = exp(t) for both generalizedmean residual life model (GMRL) and partially linear single-index generalized mean residual life model (PLSI GMRL).

^‡Biomarkers in single-index component were log-transformed and standardized.

FIGURE 2.

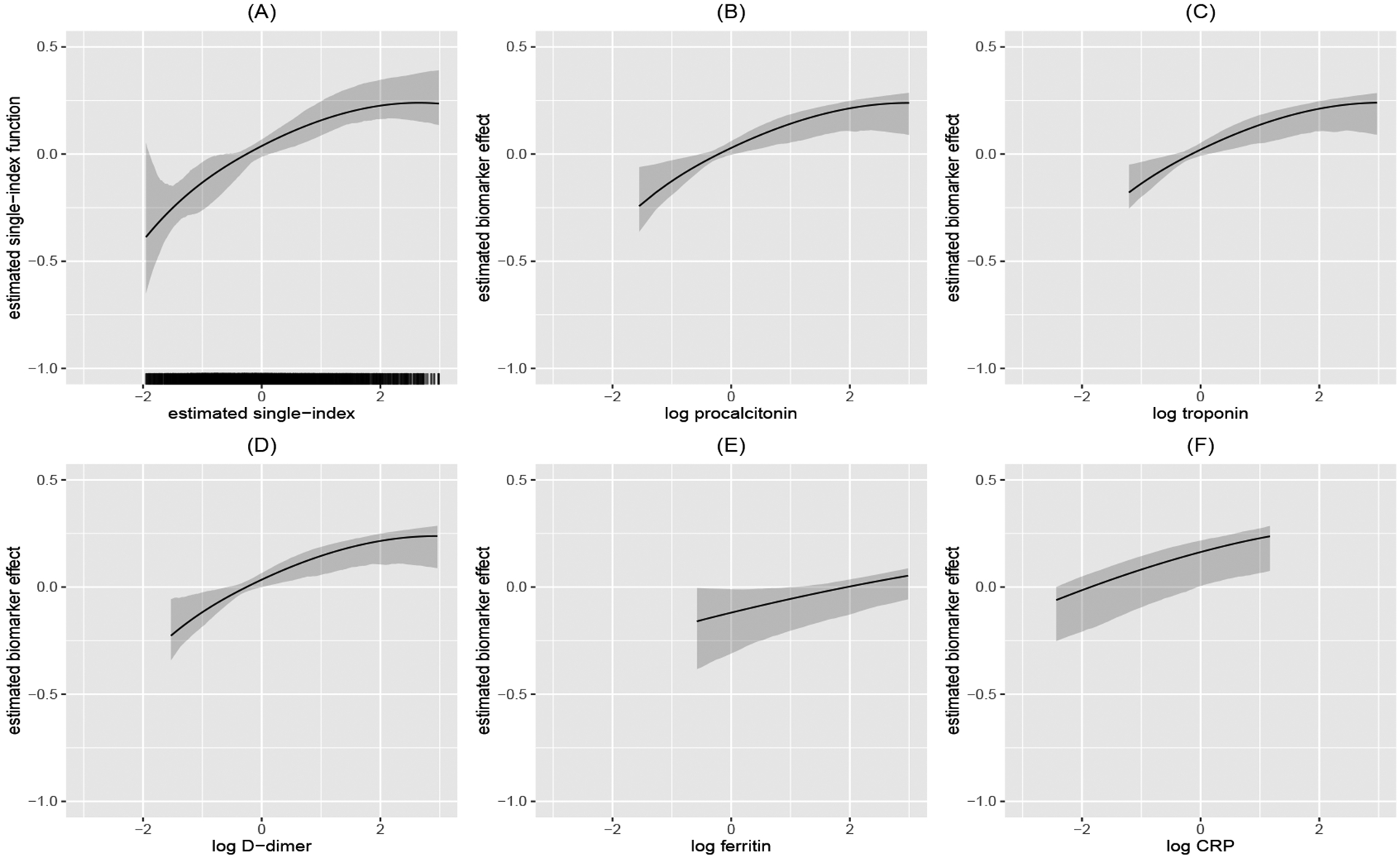
Estimated single-index function with 95% confidence intervals when g(t) = exp(t). All biomarkers were log-transformed and standardized. (A) Estimated single-index function; (B) Procalcitonin with other biomarkers fixed at median values; (C) Troponin with other biomarkers fixed at median values; (D) D-dimer with other biomarkers fixed at median values; (E) Ferritin with other biomarkers fixed at median values; (F) CRP with other biomarkers fixed at median values.

The interpretation of covariates in linear form under the PLSI GMRL model is straightforward. We observed that higher age, male, history of cardiac disease or malignancy had significant lengthening effects on the expected remaining recovery time, while a higher level of SpO₂ had a significant shortening effect on the expected remaining recovery time. Keeping all other covariates fixed, the expected remaining recovery time within the next 30 days was increased by 11% for COVID-19 patients with a history of malignancy. Moreover, the estimated MRL model can enable us to predict the expected recovery time of a COVID-19 patient within 30 days since hospitalization based on baseline information at admission. As illustrated in Figure B.3, two patients were considered with different profiles and all log-transformed biomarkers in the single-index component were kept at median values except for procalcitonin. Patient A represented a 35-year-old COVID-19 confirmed Caucasian female without any smoking history or disease history, having 25 kg/m² BMI, 90% SpO₂, and 38.5 Celsius temperature at admission. Patient B had a similar profile but with a history of cardiac disease, diabetes, and malignancy. The two curves show that expected recovery time increased with a higher procalcitonin level for both patients, and patient B had a longer expected recovery time than patient A due to underlying disease history.

Remark: We further conducted simulations to evaluate the empirical performance of the numerical measures for model diagnosis. Let the sample size be N = 5000, censoring rate be 10%, true parameters maintain the same values in Section 3. The number of knots was set to be the same for comparison purpose. Specifically, when the true model was PLSI GMRL with g(t) = exp(t), the proportion of numerical measure $S={\text{sup}}_t‖U_s(\widehat{\theta };t)‖$ indicating the correct model was 99.8%, 99.8%, and 81.2% for linear, sine curve, and quadratic single-index function, respectively. When the true model is PLSI GMRL with g(t) = t, the proportion of numerical measure $S={\text{sup}}_t‖U_s(\widehat{\theta };t)‖$ indicating the correct model was 97.8%, 100.0%, and 89.1% for linear, sine curve, and quadratic single-index function, respectively. The empirical performance was dependent on sample size, censoring rate, and effect size.

5 |. DISCUSSION

This paper studied inference procedures for the PLSI GMRL models that allow both linear and nonlinear covariate effects. This approach reduces dimensionality and provides an estimated single-index function for summarizing the joint effects of multiple covariates. We studied the asymptotic properties of the estimators under the assumption of fixed knots due to their practicality. Furthermore, the proposed nonparametric test can be used to determine whether a nonlinear single-index function is required and is a new contribution to the single-index modeling literature. When the null hypothesis of a linear single-index function is not rejected, we can gain efficiency and straightforward interpretation by assuming a parametric form for all covariates. The proposed models incorporating single-index techniques expand the analytical toolbox to analyze the MRL for time-to-event variables, especially when multiple correlated covariates exist. Indeed, not only in survival models, the single-index technique as a powerful tool is widely considered when modeling other types of outcomes as well.^16,33,34,35 With the advantage of straightforward interpretation, MRL models that directly represent an event’s residual time can be useful in many areas. Particularly during an outbreak of infectious diseases, a validated MRL model on length of hospitalization can help arrange clinical resources and facilitates planning.

Practically, MRL modeling is worthy of consideration in survival analysis under low censoring scenarios, of which the impact of a misspecified censoring model is often limited using the IPCW technique. As an alternative, the quasi-partial score (QPS) approach^26,9 can also be considered for PLSI GMRL estimation and avoid modeling of censoring mechanism. In the research of GMRL modeling under subcohort sampling designs, Jin et al²⁷ compared the performance of IPCW and QPS estimators under various censoring rates using full-cohort data. Both approaches were consistent under low censoring settings (10% or 30% censoring rate), and IPCW estimators were more efficient than QPS estimators. While for high censoring settings (80% censoring rate), GMRL models can be estimable with long-term follow-ups, and QPS estimators outperformed IPCW estimators in terms of bias and efficiency. To ensure consistency, we further studied the IPCW double-robust estimator, which requires either the model for censoring distribution or the model for complete data distribution being correctly specified. Through numerical investigations, we observed that the double-robust estimators alleviate the impact of a violation of independent censoring or a mis-specified model for covariate-dependent censoring mechanism. In addition to sample size and censoring rate, the performance of the proposed models and inference procedures would also depend on effect sizes of the covariates and signal strength of the single-index function. For a smaller sample with a moderate censoring rate (30% to 50%), the proposed method works well when the signal strength of the single-index function is relatively large.

The proposed PLSI GMRL models could also be extended to handle time-dependent covariates or time-varying coefficients, which would allow modeling repeated biomarkers and offer additional flexibility and accuracy. Moreover, the current selection of variables into the single-index function is based on the research of interest and set a prior. A formal procedure that could guide the selection of covariates into the single-index component could be a future research topic and helpful for researchers to better understand the covariate effects. For example, the approach to identifying linear versus nonlinear components by Zhang et al³⁶ could be used first to delineate the covariate structure and separate out the nonlinear components to be included into the single-index function. In addition, when the included number of single-index variables is large, combining the PLSL GMRL models with penalties on the single-index coefficients can be further explored. It is often of interest to identify those variables contributing most to the joint effects. In this case, the PLSI GMRL model with penalization can help identify these variables and simplify the modeling and interpretation.

Supplementary Material

supinfo

Table A.1 Simulation results of estimated single-index coefficients under g(t) = exp(t) with independent censoring.

Table A.2 Simulation results of estimated single-index coefficients under g(t) = t with independent censoring.

Table A.3 Simulation results under independent censoring with a 20% censoring rate.

Table A.4 Simulation results under independent censoring with a baseline MRL function $m_0(t)=g^{-1}\left\{\left(-\frac{1}{3}t+1\right)I\left(-\frac{1}{3}t+1\ge 0\right)\right\}$

Figure B.1 Correlation matrix of Pearson correlation coefficients of five log-transformed biomarkers.

Figure B.2 Standardized score process for model diagnosis.

Figure B.3 Predicted recovery time within 30 days since hospitalization based on different procalcitonin levels for patients with different baseline disease history.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from New York University Langone Health. Restrictions apply to the availability of these data.