Quantile Regression for Exposure Data with Repeated Measures in the Presence of Non-Detects

Abstract

Background:

Exposure data with repeated measures from occupational studies are frequently right-skewed and left-censored. To address right-skewed data, data are generally log-transformed and analyses modelling the geometric mean operate under the assumption the data is log-normally distributed. However, modeling the mean of exposure may lead to bias and loss of efficiency if the transformed data do not follow a known distribution. Additionally, left censoring occurs when measurements are below the limit of detection (LOD).

Objective:

To present a complete illustration of the entire conditional distribution of an exposure outcome by examining different quantiles, rather than modeling the mean.

Methods:

We propose an approach combining the quantile regression model, which does not require any specified error distributions, with the substitution method for skewed data with repeated measurements and non-detects.

Results:

In a simulation study and application example, we demonstrate that this method performs well, particularly for highly right-skewed data, as parameter estimates are consistent and have smaller mean squared error relative to existing approaches.

Significance:

The proposed approach provides an alternative insight into the conditional distribution of an exposure outcome for repeated measures models.

INTRODUCTION

The issue of correctly dealing with non-detect or left-censored exposure data is common in occupational health. Left censoring occurs when laboratory instruments have a limit of detection (LOD) below which, no measurement is given. Statistical methods have been proposed to analyze censored data. The substitution method, that is replacing a value (e.g. LOD/2 or LOD/$\sqrt{2}$) for values less than the LOD [1, 2], is regularly used by industrial hygienists. Unfortunately, the resulting regression parameter estimation can be biased in the presence of large proportion of censoring, and there is no unique substitution value for varying skewness [2]. Lubin et al. also indicated that this substitution method is not advisable unless less than 10% of measurements are below the LOD [3]. More recently, the use of a maximum likelihood estimation (MLE) approach has been advocated due to its validity and efficiency [4, 5, 6]. Additionally, the MLE method has been shown to perform best in terms of producing less biased estimates for the mean and standard deviation [2, 7], yet this method under log-normal and Weibull assumptions works poorly for highly skewed data [8, 9, 10], even though the data distribution is correctly specified [10].

In addition, occupational health data (e.g. the concentration of an analyte in a biological urine or blood sample, or an environmental hand wipe or air sample) are also generally right-skewed. Most traditional statistical analyses are performed under the assumption the data follow a normal distribution. As a result, the data are transformed using the natural logarithm, which then assumes the data follow a log-normal distribution [11]. However, if the transformed data do not follow a known distribution, modeling the conditional mean of exposure may not be ideal because the estimated mean and standard deviation might be sensitive to large values. Even when distributional assumptions are met, the existing estimation methods can lead to bias and less precision when the sample size is small. Moreover, the geometric mean (GM) (i.e. the exponentiated mean of the log-transformed data) might be unstable when the distribution of logged data is asymmetric [5].

Quantile regression is an alternative analytical method that makes no assumptions about the underlying distribution. Compared to the parametric mean regression methods, quantile regression, first introduced by Koenker and Bassett [12], allows heteroscedasticity in the error term, has advantages for skewed data, and is robust to outliers. Additionally, quantile regression can provide a complete illustration of the entire conditional distribution of a dependent variable [13]. That is, regardless of data skewness, no transformation is needed.

Previous work has shown that quantile regression is a robust method for analyzing non-normal data that can also be extended to scenarios with repeated measures [14, 15, 16]. Recently, Fu et al. extended their approach [17], combining between- and within-weighted estimating equations [16], to allow any working correlation structures. In this manuscript, we demonstrate that these methods can be extended to handle values below the LOD. First, we take different censoring scenarios into consideration for the estimating equations method of Fu et al. [17] and use it for exposure data with repeated measures. Second, we propose an approach combining this estimating equations method with the substitution method of Hornung and Reed [2] by placing the emphasis on fitting marginal quantile regression models to skewed and left-censored data with repeated measurements. We carry out a simulation study to compare our quantile regression model featuring one imputation method (substitution) with the mixed effects model featuring two imputation methods (substitution and MLE) under a range of LOD proportions. Finally, we demonstrate the existing and proposed approaches in application to pesticide data with repeated exposure measures.

METHODS

Notation and censored repeated measures model

Suppose we have a clustered study in which n independent subjects have M distinct repeated measurements. For example, M pre- and post-shift biological sampling outcomes (dependent variable) of study participants collected from n independent industries are used to investigate their association with hand wipe samples or breathing zone air samples. Sampling outcomes (repeated measures) from the same industry (subject) are typically positively correlated, which have to be taken into account when performing data analysis. Because no ordering occurs with the participants with the industry, the outcomes should be equally correlated. Repeated measures data can also be longitudinal, in which the outcomes are always measured for each subject over time. E.g., M biological sampling outcomes measured at multiple time points are collected from n independent workers. The correlations between two time points are supposed to decrease over time. Ignoring the correlation would result in biased standard error estimates of regression parameters, wide confidence intervals (CIs), and large p-values (conservative inference) [18]. The higher the correlation incorrectly acknowledged, the greater the bias occurred.

Assume that the correlated outcomes with repeated measurements follow a log-normal distribution, a censored repeated measurement model is given by

$$\log y_{ij}={\mathit{X}}_{ij}^T\beta +{\gamma }_{\mathit{i}}+{\delta }_{ij}\text{and}{y}_{ij}=\{\begin{array}{cc}\text{missing}\hfill & \text{if}{y}_{ij}<{\text{LOD}}_{ij},\hfill \\ {\tilde{y}}_{ij}\hfill & \text{if}{y}_{ij}\ge {\text{LOD}}_{ij},\hfill \end{array}\phantom{\}}$$ (1)

where y_ij, i = 1, … , n, j = 1, … , M, is a response or dependent variable that represents the exposure level measured for the ith subject at the jth measurement if no censoring at the LOD; the other response, ${\tilde{y}}_{ij}$, can be detected at or above the LOD and censored below the LOD; X_ij = [1, X_1ij, … , X_pij]^T is a known vector observed at measurement j for subject i; β = [β₀, β₁, … , β_p]^T is an unknown vector corresponding to the regression parameters. γ_i denotes the random effect for subject i, while δ_ij is the random effect for subject i at measurement j. These random effects are mutually independent and normally distributed with mean 0 and variances, ${\sigma }_{\gamma }^2$ and ${\sigma }_{\delta }^2$, accounting for between-subject and within-subject variabilities, respectively. The covariance structure is assumed to be compound symmetric or exchangeable, in which a common correlation parameter is required to be estimated.

After integrating out the given random individual effect, γ_i, in the likelihood function, L(.), the marginal likelihood function [19] for all responses, y_ij, can be expressed as

$$M(\beta ,{\sigma }_{\gamma },{\sigma }_{\delta }\mid y_{ij})=\int L(\beta ,{\sigma }_{\gamma },{\sigma }_{\delta }\mid y_{ij},{\gamma }_i)\mathrm{d}{\gamma }_i={\prod }_i\int {\prod }_{j}U(y_{ij}\mid \beta ,{\gamma }_i,{\sigma }_{\delta })V({\gamma }_i\mid {\sigma }_{\gamma })\mathrm{d}{\gamma }_i,$$ (2)

where $U(y_{ij}\mid \beta ,{\gamma }_i,{\sigma }_{\delta })=\{\begin{array}{cc}\Phi \left(\frac{\log {\text{LOD}}_{ij}-{\mathit{X}}_{ij}^T\beta -{\gamma }_i}{{\sigma }_{\delta }}\right)\hfill & \text{if}{y}_{ij}<{\text{LOD}}_{ij},\hfill \\ \frac{e^{-{\left(\log y_{ij}-{\mathit{X}}_{ij}^T\beta -{\gamma }_i\right)}^2∕2{\sigma }_{\delta }^2}}{\sqrt{2\pi }{y}_{ij}{\sigma }_{\delta }}\hfill & \text{if}{y}_{ij}\ge {\text{LOD}}_{ij}.\hfill \end{array}\phantom{\}}$

The maximum likelihood (ML) estimators, $\widehat{\beta }$, ${\widehat{\sigma }}_{\gamma }$, and ${\widehat{\sigma }}_{\delta }$, then can be obtained by minimizing the negative of the log-likelihood function in Equation (2). Note that the likelihood function for n independent subjects with no repeated measurements has been proved to be valid, and that its ML estimator holds strong consistency and asymptotic normality [4].

Quantile regression model

Assume we conduct a study in which n independent subjects (industries) are measured at each of M repeated measurements (sampling data from participants) for ease of illustration. Generally, the number of repeated measurements is permitted to vary across subjects. Let y_i = [y_i1, … , y_iM]^T denote the observed exposure outcome vector for the ith subject, and assume that the τth quantile of y_ij, j = 1, … , M ; i = 1, … , n, for τ ∈ (0,1) is presented as $Q(y_{ij}\mid {\mathit{X}}_{ij},\tau )={\mathit{X}}_{ij}^T{\beta }^{\tau }$, where X_ij = [1, X_1ij, … , X_pij]^T is a vector observed at measurement j for subject i, and ${\beta }^{\tau }=[{\beta }_0^{\tau },{\beta }_1^{\tau },\dots ,{\beta }_p^{\tau }]$ is an unknown vector in terms of the regression coefficients at the τth quantile. Let $S_{ij}^{\tau }=\tau -I[y_{ij}\le {\mathit{X}}_{ij}^T{\beta }^{\tau }]$ and ${\mathit{S}}_i^{\tau }=[S_{i1}^{\tau },\dots ,S_{iM}^{\tau }{]}^T$, where I(.) is an indicator function. y_ij is assumed to be a LOD_ij/2 if y_ij < LOD_ij [2]. The corresponding covariance matrix for ${\mathit{S}}_i^{\tau }$ is given by ${\mathit{V}}_i^{\tau }={\mathit{A}}_i^{1∕2}{\mathit{R}}_i^{\tau }(\alpha ){\mathit{A}}_i^{1∕2}$, where A_i = diag[τ(1 − τ), … , τ(1 − τ)] is a diagonal matrix denoting the marginal variances, and ${\mathit{R}}_i^{\tau }(\alpha )$ represents a symmetric positive definite correlation matrix with 1 along the diagonal and at least one unknown correlation parameter given by α. Additionally, ${\mathit{R}}_i^{\tau }$ is an identity matrix if an independence working model is assumed and utilized for the data without repeated measurements.

To find the estimate of the regression parameters, ${\widehat{\beta }}^{\tau }$, we consider the following optimal estimating equations [14, 16, 20, 21]

$${\sum }_{i=1}^N{\mathit{X}}_i^T{\Lambda }_i{\mathit{A}}_i^{-1∕2}{\mathit{R}}_i^{\tau -1}(\alpha ){\mathit{A}}_i^{-1∕2}{\mathit{S}}_i^{\tau }=0,$$ (3)

in which Λ_i = diag[f_i1(0), … , f_iM(0)] with f_ij(0) assumed to be a constant can be removed [16].

We note that the parameter estimates of the asymptotic covariance matrix are not easily obtained due to the inclusion of unknown error distribution the covariances of parameter estimates typically rely on. Therefore, an induced smoothing technique [22, 23] with efficiency and robustness preserved will be commonly adopted to reduce computational burdens resulting from the existing resampling method for unsmoothed estimating equations in the marginal quantile regression models [16, 20, 21].

When less than 25% of the data fall below the LOD, any sample quantiles above the 25th quantile (first quartile), including 50th quantile (sample median), 75th quantile (third quartile), and sample interquartile range, can be reported. 50th and 75th quantiles can still be obtained even if less than 50% of the data are censored. Higher quantiles, such as 90th or 95th, should be presented when potential outliers or influential points are detected.

Simulation study

We compared the regression parameter estimation performances of our proposed approach featuring one imputation method (substitution) for right-skewed and left-censored exposure data with correlated outcomes to the mixed effects model featuring two imputation methods (substitution and MLE) under different levels of proportions below the LOD. Two modeling cases are combinations of two right-skewed distributions in the presence of correlation among repeated measures from the same subject. All simulations with results presented in Tables 1-2 for the proposed methods were conducted using R version 3.6.3 [24].

Table 1.

Results for case 1 in which a log-normal distribution was created for the outcome data with three repeated measures.

			α = 0.3			α = 0.7
n	% Censor		LOD/2	MLE	Quantile	LOD/2	MLE	Quantile
100	10	Bias	−0.0013	−0.0004	0.0003	−0.0030	0.0007	0.0007
		MSE	0.0001	0.0001	0.0002	0.0001	0.0001	0.0003
		RE	1.000	1.016	0.659	1.000	1.100	0.513
	20	Bias	−0.0034	−0.0004	−0.0008	−0.0165	0.0008	−0.0004
		MSE	0.0001	0.0001	0.0002	0.0004	0.0001	0.0003
		RE	1.000	1.130	0.747	1.000	3.132	1.624
	30	Bias	−0.0035	−0.0005	−0.0034	−0.0302	0.0009	−0.0028
		MSE	0.0002	0.0001	0.0002	0.0011	0.0001	0.0003
		RE	1.000	1.362	0.833	1.000	7.931	3.995
	40	Bias	−0.0051	−0.0005	−0.0067	−0.0578	0.0010	−0.0064
		MSE	0.0004	0.0001	0.0003	0.0050	0.0002	0.0003
		RE	1.000	3.044	1.526	1.000	33.55	14.85
500	10	Bias	−0.0007	0.0002	−0.0012	−0.035	.00003	−0.0009
		MSE	.00002	.00002	.00004	.00004	.00002	0.0001
		RE	1.000	1.019	0.622	1.000	1.594	0.595
	20	Bias	−0.0028	0.0002	−0.0019	−0.0175	−.00003	−0.0019
		MSE	.00003	.00002	.00004	0.0003	.00002	0.0001
		RE	1.000	1.371	0.842	1.000	13.59	5.578
	30	Bias	−0.0028	0.0001	−0.0042	−0.0316	.00000	−0.0039
		MSE	.00004	.00002	0.0001	0.0010	.00003	0.0001
		RE	1.000	1.581	0.655	1.000	39.87	14.82
	40	Bias	−0.0030	0.0001	−0.0071	−0.0543	−.00004	−0.0073
		MSE	0.0001	.00002	0.0001	0.0032	.00002	0.0001
		RE	1.000	2.958	0.821	1.000	114.3	29.04

^aBias - empirical bias.

^bMSE - empirical mean squared error.

^cRE - relative efficiency. These are the italicized ratios that, for each setting (n), compare the empirical MSE from the LOD/2 substitution method to the MSE from the use of MLE method or quantile regression model.

Table 2.

Results for case 2 in which a chi-squared distribution with two degrees of freedom was created for the outcome data with three repeated measures.

			α = 0.3			α = 0.7
n	% Censor		LOD/2	MLE	Quantile	LOD/2	MLE	Quantile
100	10	Bias	0.0197	0.0210	−0.0008	0.0073	0.0138	0.0006
		MSE	0.0006	0.0006	0.0005	0.0003	0.0004	0.0007
		RE	1.000	0.921	1.279	1.000	0.741	0.413
	20	Bias	0.0186	0.0221	−0.0001	−0.0032	0.0166	0.0003
		MSE	0.0006	0.0007	0.0005	0.0003	0.0005	0.0007
		RE	1.000	0.823	1.194	1.000	0.588	0.424
	30	Bias	0.0192	0.0231	−0.0020	−0.0155	0.0195	−0.0022
		MSE	0.0006	0.0007	0.0005	0.0007	0.0006	0.0008
		RE	1.000	0.884	1.324	1.000	1.087	0.873
	40	Bias	0.0169	0.0236	−0.0057	−0.0477	0.0216	−0.0036
		MSE	0.0010	0.0008	0.0006	0.0044	0.0007	0.0008
		RE	1.000	1.261	1.679	1.000	6.211	5.668
500	10	Bias	0.0194	0.0207	−0.0010	0.0062	0.0127	−0.0007
		MSE	0.0004	0.0005	0.0001	0.0001	0.0002	0.0001
		RE	1.000	0.891	4.172	1.000	0.425	0.670
	20	Bias	0.0185	0.0219	−0.0017	−0.0045	0.0156	−0.0014
		MSE	0.0004	0.0005	0.0001	0.0001	0.0003	0.0001
		RE	1.000	0.742	3.859	1.000	0.274	0.609
	30	Bias	0.0192	0.0229	−0.0033	−0.0164	0.0185	−0.0031
		MSE	0.0004	0.0006	0.0001	0.0004	0.0004	0.0002
		RE	1.000	0.748	3.843	1.000	0.913	2.380
	40	Bias	0.0188	0.0234	−0.0068	−0.0415	0.0205	−0.0064
		MSE	0.0004	0.0006	0.0002	0.0021	0.0005	0.0002
		RE	1.000	0.762	2.801	1.000	4.373	10.85

^aBias - empirical bias.

^bMSE - empirical mean squared error.

^cRE - relative efficiency. These are the italicized ratios that, for each setting (n), compare the empirical MSE from the LOD/2 substitution method to the MSE from the use of MLE method or quantile regression model.

The settings with two different sample sizes (n = 100 and 500 subjects) represent moderate and large sample sizes. Each subject has three repeated measurements per subject (M = 3). Each setting is evaluated through 1,000 simulations. Moreover, we carry out two cases motivated by the literature of parametric and quantile regression models [7, 17, 21, 25]. In order to correspond with the censoring proportions detected in the application example, the data generated from these scenarios are subjected to four different levels of censoring (10%, 20%, 30%, and 40% censoring).

To examine the performances of the proposed methods, we utilize the linear model generated from log y_ij = β₀ + β₁x_i + ϵ_ij, i = 1, … , n; j = 1, … , M, where y_ij is the jth measurement for the ith subject, x_i is an independent variable following a uniform distribution of U (1, 10), and ϵ_ij is a random error [17]. Let ϵ_ij = q + e_ij and the use of q is to guarantee p(ϵ_ij ≤ 0) = τ ∈ {0.25,0.5,0.75}, the quantile level. The true values of β₀ = 0 and β₁ = 1 are corresponded to the marginal intercept and slope, respectively. If y_ij < LOD_ij, then y_ij are equal to LOD_ij/2 for substitution and quantile methods, and are treated as missing for MLE method. $y_{ij}=\widetilde{y_{ıj}}$ if y_ij ≥ LOD_ij.

Two cases are considered for e_i = [e_i1, … , e_i3]^T. Cases 1 and 2 incorporate correlated errors for models with repeated measures and assume that the random error follows a multivariate normal distribution, MVN (0, R(α)) (case 1) (Table 1) or a multivariate log-chi-squared distribution with two d.f., $\log {\chi }_2^2(R(\alpha ))$ (case 2) (Table 2). Two underlying distributions are considered in the simulation settings in order to better understand the pros and cons corresponding to the quantile model incorporating substitution approach and the random effects model using MLE approach. Inclusion of the chi-squared distributional cases being skewed to the right is motivated by an application example that will be later discussed. To account for different skewed patterns, we also carry out simulations for models with repeated measures assuming that e_i follows a more skewed chi-squared distribution with one d.f. The results are shown in the Supplementary Material. The three outcome distributions constructed here are similarly corresponded to the three pesticide exposures analyzed in the example. Note that, after taking log-transformation, these highly right-skewed data might lead to left-skewed distributions, in which means are less than medians.

An exchangeable correlation structure with a correlation parameter of α = 0.3 or 0.7 is incorporated into the cases 1 and 2 with repeated measurements. When the substitution and MLE methods are carried out for these cases, the random error, ϵ_ij, is replaced with the random effects, γ_i and δ_ij, for subject i and subject i at measurement j, respectively. Here the ratio of between-subject variance to between-subject and within-subject variances is given by 0.3 or 0.7. This correlation coefficient indicates that the proportion of the total variance in the outcome data that is accounted for by the clustering. We note that the given small and moderate correlations are close to the estimated correlation parameters in the application example.

In order to determine the differences in estimation performances of the three methods, we present empirical mean bias and mean squared error (MSE) for each of the non-intercept parameters corresponding to either the substitution approach, the MLE approach, or our proposed approach. We also provide ratio of MSE from estimate for β₁, which we refer to as relative efficiency (RE) in Tables 1 and 2. For any given RE, the numerator is the MSE resulting from the use of referent substitution approach, and the denominator is the MSE for the MLE method or the use of our approach. In comparing with the true mean value and calculating the empirical mean bias, MSE, and RE for the proposed method, we present estimation results at the 50th quantile (τ = 0.5) for any correlation and censoring.

RESULTS

In case 1 (Table 1), when the exposure data were log-normally distributed, the MLE approach gained greater efficiencies than the substitution and quantile approaches for any censoring proportions and sample sizes. The quantile method worked well for censoring proportions ≥ 20% and high correlation (α = 0.7). MLE indicates an efficiency advantage resulting from the asymptotic properties as sample size (n) and censoring proportion increases, as can be observed from corresponding biases and MSEs (Table 1).

When the data followed a skewed chi-squared distribution (case 2), our quantile method performed best when the correlation is low (α = 0.3), as parameter estimates are consistent and have smaller mean squared error relative to the existing approaches. In terms of high correlation, the quantile method outperformed the other methods for censoring proportion = 40% and n = 100, and censoring ≥ 30% and n = 500, while the substitution method had the highest REs when censoring proportions are ≤ 20% (Table 2). In addition, when a more skewed chi-squared distribution occurred with the exposure outcome data, the results demonstrated that the quantile method worked best overall (Table S1 in the Supplementary Material). We note that the proposed quantile approach can further provide regression parameter estimation at any quantiles greater than 10th, 20th, 30th, and 40th when censoring proportion are 10%, 20%, 30%, and 40%, correspondingly.

Overall, REs corresponding to the log-normal outcome data with repeated measures showed that our approach outperformed the existing methods when the skewed data consisted of low correlated repeated measurements and when the exposure outcome followed a more skewed distribution, whereas the MLE method was favorable in the settings of log-normally distributed outcome data.

EXAMPLE

The National Institute for Occupational Safety and Health carried out a study of children and spouses of farmers who were potentially exposed to pesticides through indirect take-home contamination in Iowa in the spring and summer of 2001 [26]. A total of 25 farm households with 66 children and 25 non-farm households with 51 children participated in the study (number of independent subject or n is 50). 235 and 182 urine samples were measured from children of farm and non-farm households for determination of exposure levels of three pesticides, which were chlorpyrifos [3,5,6-trichloro-2-pyridinol (TCP)], metolachlor (metolachlor mercapturate), and glyphosate (parent glyphosate). Numbers of samples collected from the farm and non-farm households ranged from 3 to 16 and from 3 to 15, respectively (number of repeated measures or M). The analytic limits of detection (LOD) were 3.32, 0.3, and 0.9 μg/l for chlorpyrifos, metolachlor, and glyphosate, respectively. The percentages of urine levels reported below the LOD were 0.24%, 39.1%, and 15.8% for the three analytes, and were 0.43% and 0%, 37.45% and 41.21%, and 18.72% and 12.09% for farm and non-farm households, correspondingly, in each analyte.

The corresponding distributions of these analytes were skewed to the right, as can be observed in Table 3 that all means are greater than medians, and had potential outliers that could impact the mean (Figure 1), both of which were motivations for the use of quantile model. Based on an examination of Quantile-Quantile plot, only the exposure data of chlorpyrifos were considered being log-normally distributed. Alternative examination is that, if the data are truly log-normal, the median has to be the same as the GM (Table 3). In contrast, the distributions of metolachlor and glyphosate exposure data were highly and less right-skewed, as the two chi-squared distributions with one and two degrees of freedom used in the simulation study (Tables S1 and 2). Both distributions of log-transformed outcomes were left-skewed with greater medians relative to means.

Table 3.

Mean, standard deviation (SD), median, interquartile range (IQR), geometric mean (GM), and geometric standard deviation (GSD) for each pesticide by data type.

Pesticide	Type	% Censoring	Mean (SD)	Median (IQR)	GM (GSD)
Chlorpyrifos	Original	0.43a 0b	18.22 (10.81)	15.80 (11.22–22.72)	15.79 (1.706)
	Log-transformed		2.76	2.76
Metolachlor	Original	37.45a 41.21b	1.274 (6.179)	0.460 (≤ LODc – 0.99)	0.453 (2.973)
	Log-transformed		−0.791	−0.777
Glyphosate	Original	18.72a 12.09b	2.916 (2.477)	2.550 (1.41–3.99)	2.157 (2.322)
	Log-transformed		0.769	0.936

^aCensoring proportions for farm household.

^bCensoring proportions for non-farm household.

^cThe analytic limits of detection (LOD) were 3.32, 0.3, and 0.9 μg/l for chlorpyrifos, metolachlor, and glyphosate, respectively.

Figure 1.

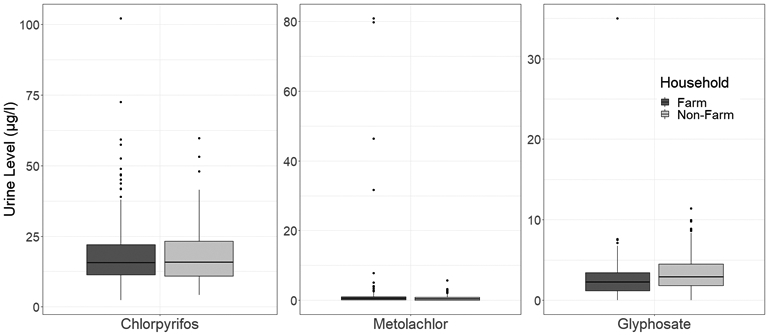
Boxplots of urine concentration levels (μg/l) under different pesticides stratified by household. The box indicates the interquartile range (IQR), the horizontal line within each box indicates the median, the upper whisker indicates the upper fence 1.5 IQR above the 75th quantile, the lower whisker indicates the lower fence 1.5 IQR below the 25th quantile, and the dots indicate potential outliers.

We utilize the model suggested in Curwin et al. [26], but employ quantile regression at three quantile levels, τ = 0.25, 0.50, and 0.75, given by

$$\log y_{ij}={\beta }_0+{\beta }_{1}Far{m}_{ij}+{\beta }_{2}Ag{e}_{ij}+{\beta }_{3}Femal{e}_i+{\beta }_{4}Creatinin{e}_{ij}+{ϵ}_{ij},$$

where y_ij is the pesticide concentration collected from the jth urine sample of the ith household. The variable of interest is an indicator for farm versus non-farm household. Three covariates are age in years, an indicator for gender, and creatinine level (mg/dl), which is included as an adjustment in the model [27]. Note that only 25th, 50th, and 75th quantiles are provided for ease of comparisons.

As in the simulation study, we analyze the data using substitution and MLE methods, and quantile regression with an exchangeable correlation structure under three given quantiles. Table 4 provides the estimates of regression parameters and corresponding standard errors (SEs), and the 95% confidence intervals (CIs). The factors in Table 4 are equivalent to exponent of the estimates. For example, the quantile regression at the 50th quantile produces a ratio of the medians of the outcome between farm and non-farm households, whereas substitution and MLE methods generate ratios of the mean values.

Table 4.

Parameter estimates, standard error (SE) estimates, 95% confidence intervals (CIs), and factors for covariate of interest resulting from analyses of the urine dataset.

Pesticide	Method	Quantile	Estimate	SE	95% CI	Factora
Chlorpyrifos	Substitution		0.16	0.10	−0.03 – 0.35	1.18
(0.43b)	MLE		0.16	0.09	−0.03 – 0.35	1.17
(0c)	Quantile	25th	0.10	0.09	−0.09 – 0.29	1.10
		50th	0.09	0.08	−0.07 – 0.25	1.10
		75th	0.14	0.10	−0.06 – 0.33	1.14
Metolachlor	Substitution		0.39	0.23	−0.06 – 0.85	1.48
(37.45b)	MLE		0.43	0.29	−0.14 – 1.01	1.54
(41.21c)	Quantiled	50th	0.49	0.36	−0.24 – 1.22	1.63
		75th	0.39	0.25	−0.11 – 0.88	1.47
Glyphosate	Substitution		−0.24	0.16	−0.55 – 0.07	0.79
(18.72b)	MLE		−0.24	0.14	−0.52 – 0.04	0.79
(12.09c)	Quantile	25th	−0.09	0.21	−0.52 – 0.34	0.92
		50th	−0.05	0.16	−0.37 – 0.28	0.95
		75th	−0.14	0.13	−0.39 – 0.12	0.87

^aExponent of the estimate.

^bCensoring proportions for farm household.

^cCensoring proportions for non-farm household.

^dResult of 25th quantile level for metolachlor not presented because the censoring proportions (37.45% and 41.21%) are greater than 25%. Any quantile levels larger than or equal to 42th can be calculated (see the Figure 2).

Figure 2 shows the detailed estimates of regression parameters (solid line) and 95% CIs (shaded area) for different quantiles by pesticide type using the quantile approach, compared to the estimates (dashed line) and 95% CIs (dotted line) using the MLE approach. The estimated correlation parameters used to construct the exchangeable correlation structure are 0.58, 0.19, and 0.40 for exposure data of chlorpyrifos, metolachlor, and glyphosate, respectively, expressing small to moderate correlation among samples collected from the farm and non-farm households.

Figure 2.

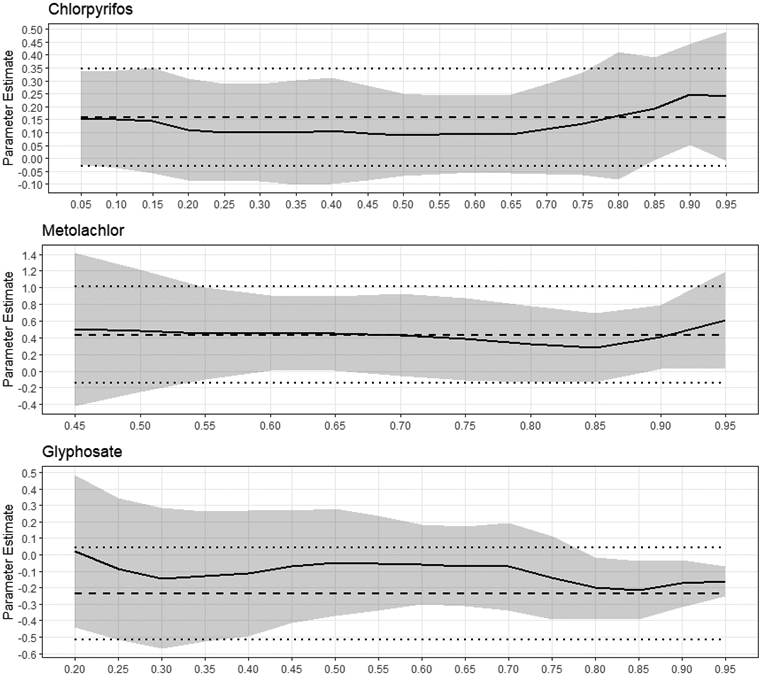
The panel depicts the proposed quantile regression method (solid lines) with 95% confidence intervals (shaded area) by different pesticide type. The dashed horizontal lines indicate the estimated coefficients for the mean model with 95% confidence intervals (dotted horizontal lines).

All approaches yield same directions and similar magnitudes for regression parameter estimates. Specifically, children in a farm household has higher exposures to chlorpyrifos and metolachlor relative to those in a non-farm household, whereas children from a non-farm household are more likely to expose to glyphosate (Table 4). In Figure 2, the magnitudes or impacts vary over different quantile levels for chlorpyrifos and glyphosate outcomes, but are constant for metolachlor. Note that our proposed approach produces smaller SE estimates than the referent approach at most quantiles, thus revealing the proposed method’s potential for efficiency improvement. The use of a quantile analysis presents a more complete description with respect to interest of variable by examining different quantiles for the left-censored and right-skewed pesticide distribution, rather than the mean analysis which gives focus on the unique regression parameter estimate.

DISCUSSION

Mean regression analyses for right-skewed exposure outcomes with non-detects or left censoring have been widely introduced in occupational and environmental health. However, for some real-world data the use of mean regression models may be sensitive to skewness and potential outliers could influence the mean more than the median. In such cases, the use of quantile analysis for modeling the conditional quantiles of the response variable is recommended. Therefore, we first proposed a modified approach for quantile regression to utilize detects above the LOD. This regression model assumed that no specified distribution for the error is needed. Furthermore, in the presence of within-subject variability, multiple exposure measurements per subject are demanded to accurately measure a subject’s exposure. As a result, we proposed an approach to model these right-skewed and left-censored data with repeated measurements, and through a simulation study we presented that our method is preferable to the existing approaches under scenarios of outcome data without repeated measures and highly right-skewed data.

Although for simplicity we only considered independence and exchangeable working correlation structures for marginal quantile regression models in the manuscript, first-order autoregressive (AR-1) working structure with less parsimonious form is available as well. Quantile regression has been regularly studied in longitudinal data [15, 16, 20,21]. Therefore, incorporating a AR-1 structure to the use of quantile regression is an additional advantage in terms of flexibility because it is preferred over the other structures in a longitudinal study and may not be accommodated in the existing left-censored repeated measures models [25]. Future study can be extended to use a general stationary autocorrelation structure [21] or a Gaussian pseudolikelihood selection technique [17], rather a parametric likelihood, to decide the most adequate working correlation structure for preventing the specification of any specified working structures.

The simulation study was analyzed via marginal quantile regression models with balanced repeated measurements, and univariable results were presented. Nonetheless, the proposed approach in this manuscript is applicable to subjects with varying repeated measurements and permits multiple categorical or continuous covariates, as can be seen in the application example. Future work can be developed to include time-dependent covariates for quantile regression model when observations among the same subject are repeatedly measured over time or in a longitudinal type [28]. In our simulations and application example, a unique censoring proportion and a single LOD/2 were given to apply to all measurements. The quantile approach also allows multiple LODs occurred with data in the absence and presence of repeated measures because the censoring proportion can always be calculated.

We mentioned that any sample quantiles above the censoring proportion are available. In order to obtain the regression parameter estimation at all quantile levels, multiple imputation, such as truncated multivariate normal distribution, can be used to impute log-transformed exposure data below the LOD [3]. When the exposure data are highly skewed, truncated multivariate gamma distribution may be an option for the use of imputation technique. However, the imputation methods are still restricted by the distributional assumption. In our simulation study, the results using LOD/2 produced better performance than the use of LOD/$\sqrt{2}$. However, when data are not highly skewed, LOD/$\sqrt{2}$ would be a better replacement for non-detectable values [2].

Our study has some limitations. The simulations were carried out assuming parametric distributions, and therefore other departures from log-normality and log-chi-squared distributions, i.e., inverse gamma distribution or data skewed to the left, might need to be evaluated. Readers are suggested to employ graphical and testing examinations to confirm if distributional assumptions are met. We recommend that the use of random effects model incorporating MLE method for dependent or outcome variable following a log-normal distribution; otherwise, the quantile model, a powerful complement to the mean regression model, should be carried out once the assumption of normality is violated. However, if sampled data deviates dramatically from its underlying distribution, and therefore no method would produce unbiased estimate. In such cases with unknown true underlying distribution, quantile regression will be always considered as a safe, i.e., not biased, approach, although this conservative method might result in some loss of efficiency, i.e., wide CIs and large p-values. Moreover, because of the increasingly complex multilevel or hierarchical data generation with respect to multiple levels of outcomes, future work accounting for other marginal quantile models is needed. The corresponding R code and functions for implementing the proposed approaches in this manuscript can be acquired by contacting the author at okv0@cdc.gov.

CONCLUSIONS

Quantile regression not only is advantageous to skewed exposure outcomes, but requires no assumption of parametric distribution for the residuals and no transformation for the outcome variable. The method provides an alternative insight into the conditional distribution of an exposure outcome above the LOD for independent and repeated measures models. Overall, quantile method is recommended for the analysis of left-censored exposure outcome when the data are heavily right-skewed or not log-normally distributed, especially in the presence of low correlated repeated measurements, based on simulation findings. This approach is also advocated when large censorings and high correlation with the log-normal outcome data. When the underlying distribution is correctly specified, MLE method generally performs best. However, in practice, specifying the true underlying distribution may not be the case. As a result, quantile regression model can always be considered as an appropriate method.