Revisiting the out of Africa event with a deep-learning approach

Summary

Anatomically modern humans evolved around 300 thousand years ago in Africa. They started to appear in the fossil record outside of Africa as early as 100 thousand years ago, although other hominins existed throughout Eurasia much earlier. Recently, several studies argued in favor of a single out of Africa event for modern humans on the basis of whole-genome sequence analyses. However, the single out of Africa model is in contrast with some of the findings from fossil records, which support two out of Africa events, and uniparental data, which propose a back to Africa movement. Here, we used a deep-learning approach coupled with approximate Bayesian computation and sequential Monte Carlo to revisit these hypotheses from the whole-genome sequence perspective. Our results support the back to Africa model over other alternatives. We estimated that there are two sequential separations between Africa and out of African populations happening around 60-90 thousand years ago and separated by 13-15 thousand years. One of the populations resulting from the more recent split has replaced the older West African population to a large extent, while the other one has founded the out of Africa populations.

Introduction

Recent fossil record analysis suggests that Homo sapiens appeared around 300 thousand years ago (kya) in Africa.¹ This hypothesis is corroborated by genetic data,² which estimated the deepest split between modern human populations at a similar time point. Although fossil records advocate the occurrence of multiple out of Africa (OOA) events for modern humans,³ recent genetic studies revealed that all modern non-African populations tested so far fit a model with a single OOA event that happened less than 100 kya.4, 5, 6 This conclusion indicates that earlier OOA migrations, documented by archaeological records, might have not left a substantial contribution to modern human populations, with a possible exception of this model suggested in Papuan populations (two out of Africa model).⁷ While the single OOA model is generally supported by both autosomal and uniparental data,8, 9, 10 some observations may reflect a more complex scenario. For example, uniparental data show that most of the haplogroups found in OOA populations have a younger time to the most recent common ancestor (tMRCA) than those found in Africa, with the notable exception of the sister Y haplogroups D and E. Haplogroup D can be found in isolated populations in Asia (i.e., Andamanese, Tibetan, Japanese, etc.), while haplogroup E is ubiquitous in sub-Saharan African populations. These two haplogroups coalesce together before coalescing with any other haplogroup found in OOA populations.^10,11 This observation might be explained by a back to Africa migration involving a population harboring the haplogroup E¹⁰ or a simple out of Africa with haplogroup E remaining in Africa but haplogroup D and other OOA haplogroups coming out of Africa together.¹² Furthermore, some genetic analyses suggest that the separation between Africa and OOA populations might not be a single split event but rather that it was constituted by structure and admixture between populations.13, 14, 15, 16

Testing these hypotheses (single out of Africa, back to Africa, and two out of Africa) is challenging because of the strong bottleneck of non-African populations,17, 18, 19 differential amount and source of archaic introgression,^4,20,21 and several migrations within Africa.^2,16 The lack of ancient genomic data older than 15 kya²² from Africa makes it difficult to address this issue from an ancient DNA perspective. However, neural networks (NNs) have been shown to be extremely powerful to disentangle such complex scenarios.²⁰

In the last few decades, the development of efficient and powerful computing infrastructure allowed us to gain substantial progress in the machine learning field, especially for computationally demanding algorithms such as NN^23,24 and Bayesian methods.^25,26 NN has been demonstrated to be a useful tool for specific types of tasks, such as classification or natural language processing.23, 24, 25^,27 However, NN requires a large amount of data as a training set. In some cases, this limitation can be overcome via the use of simulated data. Given that the modern tools allow for efficient simulation of large sets of synthetic genetic data,^28,29 NN is already adopted in population genomics for interpretation of the genomic data in terms of underlying demography^20,30,31 and positive selection.^32,33 However, unlike classical approaches, it is still challenging to measure the significance of a prediction performed by NN given that it is a black-box approach. Approximate Bayesian computation (ABC) can be used to weigh the accuracy of a NN-based prediction from the data itself without knowing the maximum likelihood function.^20,30,34 However, ABC may face the “curse of dimensionality” problem when high dimensional input data or summary statistics are used.³⁵ It performs less efficiently when the harnessed summary statistics do not capture enough information. Here, we used NN to reduce the dimensionality of the original summary statistics and to produce highly informative secondary summary statistics, which is used as input by ABC to perform statistical analysis. Sequential Monte Carlo (SMC, also known as the particle filter method)³⁶ is used to recursively predict posterior distribution from a prior. In every step, likelihood weight is calculated for each prior sample. Low likelihood samples are discarded, and new samples are resampled from a continuous distribution. In classical SMC, higher probability was given to newer samples, which have higher weights in resampling steps. The likelihood weights are calculated for all these samples and the cycle repeats until convergence is reached. SMC has a strong resemblance to genetic algorithms.³⁷ It has been shown that ABC estimation can be further improved by the use of SMC,38, 39, 40 but to date they have not been used together with NN.

Here, we present an improved version of ABC-DL (approximate Bayesian computation with deep learning)²⁰ along with ABC-DLS (approximate Bayesian computation with deep learning and sequential Monte Carlo method), which allows us to infer the most likely scenario among different competing demographic models as well as to estimate their parameter values with high precision. Our approach relies on an NN trained on simulated genetic data under the models being tested. However, it has three key improvements compared to other similar approaches. First, the use of the hdf5⁴¹ data format and tensor flow⁴² allows for extremely large training datasets. Second, the conventional NN approach is improved with ABC, which helps to provide statistical support for the NN prediction and to obtain posterior distribution for the model parameter values. Third, inspired by previous works,³⁸ we applied a modification of the SMC³⁶ approach to iterate the whole procedure. This algorithm improved the prediction accuracy substantially compared to previously implemented methods.^20,43 We apply this method to test the three OOA models mentioned above.

Material and methods

Real data

We have downloaded the high-coverage 1000 Genomes⁴⁴ vcf files produced by the Coriell Institute for Medical Research. We randomly selected five individuals to represent Africa, Europe, and East Asia originating at Yoruba from Ibadan, Nigeria (YRI), Utah residents with European origin (CEU), and Chinese Han from Beijing (CHB) populations (15 individuals in total). As an alternative dataset, we have also downloaded the high-coverage Human Genome Diversity Project (HGDP) vcf files⁴⁵ and randomly selected five Yoruba (YRI), five French (FRN), and five Han Chinese (HAN) individuals representing Africa, Europe, and East Asia (Table S1). Unless mentioned otherwise, the results presented here were obtained on the first dataset. In order to avoid introducing any bias by the including only a subset of mixing archaic humans due to availability of such genomes and mixing ancient genome with the modern humans, we decided not to use any ancient genome. Moreover, it is suggested that both Neanderthal and Denisova sequences, which are available, are distantly related with the introgressed populations,^46,47 suggesting an even more complicated model. As our primary objective is with the OOA event and to give all archaic populations the same treatment (because African archaic populations are not yet sequenced), they are treated as ghost populations in our simulations. We treated each dataset independently and kept only bi-allelic single-nucleotide polymorphisms (SNPs) with genotype calls present in every individual and lifted the genomic positions to GRCh37 coordinates by using Picard tools. Next, we used two alternative filtering approaches: (1) filtering out genes and CpG islands (for more details, please see Mondal et al., 2019²⁰) and (2) applying a mappability mask coming from SNPable¹³ for the 1000 Genomes dataset in Table S2. Filtering strategy 1 will be preferable to 2 in the case that the information of CpG islands and genes are available. In the absence of those information (for example non-human genetic data), our method can still reproduce similar result with filtering strategy 2. All the filtering was performed with vcftools and bcftools.^48,49 The vcf file was converted to joint unfolded site frequency spectrum (SFS) via an in-house code with scikit allel.⁵⁰ For unfolded SFS, we need to know ancestral allele and derived allele for the real data (for simulation, it is already known). We used 1000 Genome ancestral allele alignments of fasta files to polarize the alleles to ancestral and derived. When ancestral allele information is not present for a given SNP, we have removed that SNP from our analysis.

Genotype to site frequency spectrum

The SFS from the three populations (Africa, Europe, and East Asia) was computed as a tridimensional tensor from the sequenced or simulated data and further transformed into an array to be used as input by the NN. SFS is the total number of segregating sites for a given derived allele count present in each population.

$$\text{SFS}\left(\text{i},\text{j},\text{k}\right)=\sum _{m=1}^n\{\begin{array}{l}1,if{s}_1=iand{s}_2=jand{s}_3=k.\hfill \\ 0,otherwise.\hfill \end{array}$$

Where i, j, and k are the numbers of derived alleles count per SNP in pop1, pop2, and pop3, respectively, and n is the total number of segregating SNPs.

The whole SFS was represented as a row. We multiplied all the elements of the real SFS by a constant (frac) to make it comparable with the length of simulated regions if those do not match. For example, we multiplied the real SFS by 100/647 (or 0.1546) if we simulate a 100 megabase pair (Mb) region per simulation and the real data is coming from 647 Mb region (after filtering). In general, it is possible to use any summary statistics for our approach. We used SFS for our choice of summary statistics because it is straightforward to obtain and informative enough.^17,51

Simulations

All the simulations were done in msprime.²⁹ We simulated 100, 500, 1,500 or 3,000 1 Mb genomic regions per run (depending on the analysis step) for five individuals per population (African, European, and East Asian). For each run, we used a uniform recombination rate of 10⁻⁸ per base pair (bp) per generation (because SFS is not affected by the local recombination rate⁵²) and a mutation rate of 1.45 × 10⁻⁸ per bp per generation⁵³ while sampling demographic parameters from a uniform distribution within prior ranges shown in Table 1. We also alternatively used a mutation rate of 1.25 × 10⁻⁸ per bp per generation (only for Table S3).^54,55 We assumed generation time of 29 years.⁵⁶ Most of our simulations for SFS were done on multiple of 1 Mb regions, except Table S4 (which was produced by multiple of 25 Kb regions) and when we created mock SFS to test our DLS approach (simulation parameters coming from Tables 2, S5, and S6). To make the mock SFS similar to real data (which has a length of 647 Mb region after filtering), we simulated three 200 Mb regions and one 47 Mb region together to create a single SFS under a given model. We also simulated on multiple of 25 Kb regions (Table S4) to check whether the length of simulated regions can bias our result. 1 Mb regions were chosen for most of the simulated regions’ length because it is faster to produce.

Table 1.

Prior parameters range used for producing the site frequency spectrum (SFS)

Parameters	OOA_S	OOA_B	OOA_M
N_A	5,000–25,000	5,000–25,000	5,000–25,000
N_AF	10,000–150,000	10,000–150,000	10,000–150,000
N_EU	10,000–150,000	10,000–150,000	10,000–15,0000
N_AS	10,000–150,000	10,000–150,000	10,000–150,000
N_EU0	500–5,000	500–5,000	500–5,000
N_AS0	500–5,000	500–5,000	500–5,000
N_B	500–5,000	500–5,000	500–5,000
N_BC	N/A	500–40,000	N/A
N_AF0	N/A	500–40,000	N/A
N_MX	N/A	N/A	500–40,000
N_B0	N/A	N/A	500–40,000
T_FM (ky)	2–5	2–5	2–5
T_FS (ky)	0.1–10	0.1–10	0.1–10
T_DM (ky)	10–50	10–50	10–50
T_EU_AS (ky)	5–30	5–30	5–30
T_NM (ky)	5–50	5–50	5–50
T_XM (ky)	5–120	5–120	5–120
T_Mix (ky)	N/A	5–50	5–50
T_Sep (ky)	N/A	5–50	5–50
T_B (ky)	5–270	5–220	5–220
T_AF (ky)	5–700	5–700	5–700
T_N_D (ky)	330–450	330–450	330–450
T_H_A (ky)	120–250	120−250	120–250
T_H_X (ky)	450–700	450–700	450–700
Mix (%)	N/A	5–95	5–95
NMix (%)	1–3	1–3	1–3
DMix (%)	0–2	0–2	0–2
XMix (%)	0–10	0–10	0–10
FMix (%)	0–10	0–10	0–10

N/A means not applicable and ky means kilo or thousand years.

Table 2.

Posterior range for parameters of model B

Parameters	Mean	CI	Events (kya)
N_A	14,526	14,404–14,595	N/A
N_AF	26,436	25,535–28,595	N/A
N_EU	94,437	88,320–104,955	N/A
N_AS	127,071	112,953–138,256	N/A
N_EU0	1,838	1,794–1,922	N/A
N_AS0	760	739–776	N/A
N_BC	16,744	11,108–26,850	N/A
N_B	2,026	1,984–2,096	N/A
N_AF0	35,773	33,296–38,019	N/A
T_DM (ky)	18	17.7–18.4	18 (17.7–18.4)
T_EU_AS (ky)	15.1	14.7–15.6	33.1 (32.5–33.6)
T_NM (ky)	5.2	5–5.8	38.3 (37.6–39)
T_XM (ky)	15.7	14.5–16.3	48.7 (47.6–49.8)
T_Mix (ky)	15.1	14.1–16.5	48.2 (46.8–49.5)
T_Sep (ky)	9.8	8.6–11.3	57.9 (56.1–59.8)
T_B (ky)	13.4	12.7–13.7	71.3 (69.4–73.3)
T_AF (ky)	200.4	197.2–202.1	271.7 (268.6–274.8)
T_N_D (ky)	448.1	442–450.9	448.1 (442–450.9)
T_H_A (ky)	248.1	240.6–252.1	696.2 (688.9–703.4)
T_H_X (ky)	675.9	648.5–700.9	675.9 (648.5–700.9)
Mix (%)	91.14	90.28–91.57	N/A
NMix (%)	2.99	2.95–3	N/A
DMix (%)	0.67	0.61–0.72	N/A
XMix (%)	5.29	4.02–6.22	N/A

CI is the confidence interval of 2.5%–97.5% of respective parameters. ky means kilo years and kya means kilo or thousand years ago from now. ky here represents the time interval of the event and kya represents the estimated time that event happened from now. The relation between events and time intervals can be found in Table S10. N/A, not applicable.

In msprime, admixtures were represented as MassMigration (the fraction of a population replaced by another population in a single generation). In contrast, constant migrations under island models (where applicable) were represented as Migrationrate (the fraction of recipient population replaced by migrants from another population per generation).

The ABC-DLS analysis is efficient enough to be done on a single computer. The main bottleneck of the whole approach is the production of the simulated data. Msprime is fast, but the total amount of data, which needs to be simulated for the NN, is sometimes difficult to produce on a single computer (especially for parameter estimation). Thus, we have used a snakemake pipeline to produce the SFS on the cluster.⁵⁷ All the simulations with corresponding parameters were saved in a comma-separated value (CSV) file, which was then used by different approaches (approximate Bayesian computation via random forest [ABC-RF], ABC-DL, and ABC-DLS).

ABC-DL

We have implemented an improved version of ABC-DL²⁰ (here onward, we call this implementation DL, and the implementation that additionally uses SMC [called DLS] is described below) by using state-of-the-art machine learning packages in python. We used TensorFlow with Keras backend⁴² for building the NN and abc package for implementing ABC.⁵⁸ The use of hdf5 format⁴¹ enabled us to analyze the whole dataset without loading into the memory. This allows us to train the NN on extremely large simulated datasets.

Parameter estimation with DL

Here, we describe parameter estimation by using NN and ABC. We ran a total of 60,000 different simulations, each producing 3,000 of 1 Mb regions (3 Gb [gigabase pair] in total, roughly equal to the length of the human genome). Every line of the NN input is one such simulation performed under a given demographic model with the columns representing SFS elements and the parameters used for that simulation are used as known output. We ran parameter estimation by using this information and retrieve the parameters predicted on observed data for a given model. We used the known parameters as output for training the NN (y), and we used the SFS as input (x). Thus, we can think of the NN as a non-linear model for predicting the parameters from the SFS. We kept out 10,000 random lines for the testing dataset and ABC analysis, and the rest were used for training the NN. Both SFS and parameter values were normalized per column with MinMax scaler (from scikit-learn)⁵⁹ so that each data entry is within 0 and 1.

We used four hidden layers of a dense NN (Figure S1) with activation relu (from Keras package). These are basic building blocks for NNs. We used the linear layer (from Keras package) for the output layer with the same number of units as the number of parameters. We used the masking layer (from Keras package) at the beginning to remove cells with zero values from the learning algorithm. This was done so that NNs do not learn the absence of data. Then we used Gaussian noise injection (from Keras package) of 0.05 to introduce some noise (Figure S1) to reduce overfitting because this will force the NN learn the true parameters even though the SFS is slightly distorted (or noisy). We used logcosh as a loss function and Nadam for the optimizer (both from Keras package). Although we have used other more classical approaches (i.e., mean square error, stochastic gradient descent, etc.), we found this combination to be better suited for our approach. The NN ran through the training dataset several times (epochs) to increase accuracy. We used EarlyStopping (from Keras package) on loss coming from validation dataset with the patient of 100. This stopped the epoch cycle in case there was no improvement for the last 100 epochs (meaning the NN reached a convergence for the current data). We used the ModelCheckpoint (from Keras package) of the lowest loss result on validation data, as the last epoch is not guaranteed to have the lowest loss on validation data. We also used ReduceLROnPlateau (from Keras package) of factor 0.2 to reduce the learning rate if we reached minima for several epochs (ten by default). Learning rate too low at the start makes the NN learn slow, but in the later stage, high learning rate performs worse than lower learning rate.

After training is done, we used the testing dataset to predict the parameter from the SFS, which was then used for cross-validation tests and parameter prediction via loclinear from ABC⁵⁸ with the tolerance of 0.01. The whole approach is presented in a flowchart (Figure S2).

Model selection with DL

Here, we describe model selection by using NN and ABC. Unless stated otherwise, we simulated 2,000 simulations for each of the three demographic models tested (see full description of demographic models below). We simulated all the models for 3 Gb regions to make it equal for different approaches and finally scale the real data accordingly. This approach is preferable because we can train the NN only once for different length of real data. To test whether our scaling approach and the length of simulated region are not creating any biases, we also simulated an only 647 Mb region (equal to our filtering strategy 1) with the multiple of 25 Kb regions without using scaling in Table S4. The resulting CSV files (one per model) are used together as input for model selection. Model selection was repeated ten times both for DL and DLS. We found that if the results have high accuracy (posterior probability on observed data is >95% for the correct model), all the ten runs are essentially equal (which is expected).

We used SFS as input (x) for the NN and the model category as output (y) and removed the parameters values because they are not needed for this step. We used MinMax scaler from sklearn⁵⁹ only on the SFS data as above, and the names of the models are converted to one-hot encoding by pandas.Categorical (from pandas package) and Keras.utils.to_categorical (from Keras package). After concatenating files coming from all the competing models, we shuffled the rows by a custom code.⁶⁰ We left out around 1,000 random rows per model to test the power of NN (as a testing dataset) and for ABC analysis and used the rest to train the NN (as a training dataset). The rest of the approach is as described above (see parameter estimation with DL). We also tested these models with a much higher number of simulations (50,000 for training and 10,000 for testing and ABC analysis), but because we did not find any substantial differences in the results, we used 2,000 simulations (1,000 for training and 1,000 for testing and ABC analysis) per model throughout this study.

We used two hidden layers of the dense NN with the activation relu (Figure S1). We used the softmax layer (from Keras package) for the output layer with the same number of units as the number of trained models. We added the masking layer and a noise injection layer as above. We used a 1% dropout layer (from Keras package) within every dense layer to make it more robust. We used categorical_crossentropy for the loss function and adam for the optimizer (both from Keras package).

After the training was done, we used the testing dataset to predict models from the simulated SFS, which we then used to perform the cross-validation test by using ABC with the tolerance of 0.033 (which converts to 100 samples) in case of three models and 0.0066 (which converts to 100 samples) in case of 15 models via rejection (from abc package). We applied the model selection by abc.postpr (from abc package) to the real data. See a schematic representation in Figure S2.

ABC-DLS

Our implementation of the ABC-DL method was further improved by using the SMC approach,³⁶ which opens up a new way to make inferences for similar cases (here onward, we call this implementation DLS). Although SMC has lots of different implementation and can be quite complex, we used a simpler version of SMC here. In our implementation, we only selected the top 5% of best samples coming from every cycle of ABC and discarded the rest. The ranges of the parameter values were estimated from these top samples and new samples were drawn from the uniform distributions for these new posterior ranges. To introduce mutations in the algorithm, we increased the posterior range by 1% in every cycle. As a result, the simulated SFS, which is used as input for the NN, becomes more and more similar to real or observed SFS with every iteration of the algorithm.

Parameter estimation with DLS

This method uses the standard parameter estimation strategy of DL (described above) together with the modified SMC algorithm used for recursion.

For parameter estimation, we used the rejection method in ABC with a tolerance of 0.05 as the rejection method always generates posterior within the prior range. We obtained the posterior range by taking the minimum and the maximum values from the ABC output. This range was then used as a prior range for the next iteration. This cycle is repeated until decrease for all parameters is more than 0.95, suggesting it has reached convergence.

$$decrease=\frac{Posterio{r}_{max}-Posterio{r}_{min}}{Prio{r}_{max}-Prio{r}_{min}}$$

If the decrease is more than 95% for a parameter, the new posterior estimation is rejected for that parameter. Instead, we take the prior range of this step, expand it by 1% of its width and use it as a prior again. We used this strategy to prevent the posterior from shrinking or collapsing unless NN has found some accurate prediction for the parameter (decrease < 95%) and reduces the probability of missing the correct parameter value due to stochastic effect in a single cycle.

$$Posterio{r}_{min}=Prio{r}_{min}-\frac{\left(Prio{r}_{max}-Prio{r}_{\text{min}}\right)\times 1\text{\%}}{2}$$

$$Posterio{r}_{max}=Prio{r}_{max}+\frac{\left(Prio{r}_{max}-Prio{r}_{\text{min}}\right)\times 1\text{\%}}{2}$$

Simulations from every step were stored and re-used in subsequent cycles if their parameter values fell inside the new prior range. A flow chart of this strategy can be found in Figure S2C.

We used 10,000 simulations as a training dataset and 10,000 simulations for testing. The NN model is exactly as before (as used in DL, Figure S1). To make it more efficient, we started with simulating a total length of 100 Mb (each simulated region being 1 Mb long), and then we increased the total length stepwise (i.e., 0.5, 1.5, and 3 Gb). The priors for 100 Mb regions are the same as presented in Table 1. The final posterior (after convergence reached) of the run with 100 Mb is used as a prior for 0.5 Gb simulation and so on. We multiplied the observed SFS by frac accordingly to scale it to the simulated region length.

After the convergence was reached with 3 Gb in total, we finalized by running 50,000 training and 10,000 testing simulations with the DL method by using loclinear (from abc package) with the tolerance of 0.01. The flowchart of the method is represented in Figure S3.

Model selection with DLS

Here, we describe model selection by using NN, ABC, and SMC together. In principle, we can directly use the final output of the parameter estimation procedure by DLS for every model and then use it for the ABC classification approach. However, this approach would be inefficient given that only one model is true for our real dataset, and thus spending considerable resources to optimize parameters for unlikely scenarios does not make sense. Instead, we used the output of 100 Mb parameter optimizations from the DLS approach as a prior to every model, and then we used the model selection strategy of DL, as mentioned before. In other words, we first optimized the parameters for each model class by using 100 Mb of simulated sequence and then compare the different models between each other. We found out that we already have enough power to distinguish between models by using 100 Mb of total simulated sequence for most of the cases, except Table S7, where we used 500 Mb regions for optimization.

ABC-RF

We tested the real SFS against the three simulated models by using a similar ABC approach but with random forest⁶¹ (here onward, we call this implementation RF) as an inferential tool implemented in the abcrf R package.^43,62 First, we trained our model by using the bagging method applying the function abcrf, with no linear discriminant analysis, and 2,000 decision trees by using 1,000 simulations for each tested model. We then evaluated the performance of ABC-RF through a cross-validation dataset composed of 1,000 simulations for each tested model by using the function predict.abcrf. The same function and settings were used for inferring the best-supported model with the SFS obtained from real data described above. We performed parameter estimation for the most supported scenario applying regression as implemented in the regAbcrf model by using 1,000 decision trees. Each parameter was inferred separately. Similar to DL and DLS approaches, the whole procedure has been repeated ten times for model selection.

Demographic models

Simple out of Africa (model S)

In this simulation model, we have modeled a simple OOA event (Figure 1A) closely following Gravel et al.,¹⁹ except the migration rates are set to zero. All the main results were used without any migration rates, but we also tested models with migrations sometimes. When we simulated a model with constant migrations, we tried both a symmetrical migration matrix as in Gravel et al.¹⁹ (Table S8) and a nonsymmetrical one (Tables S9 and S10).

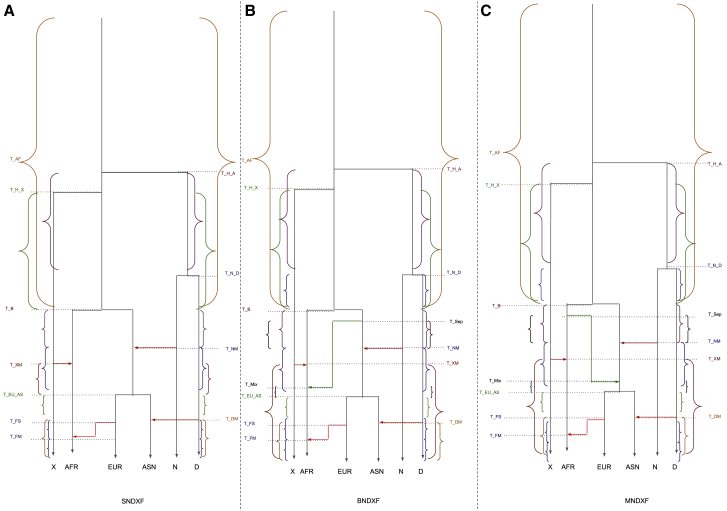
Figure 1.

The simplistic schema of the models

(A–C) Simple out of Africa (model S) (A), back to Africa (model B) (B), and out of Africa mixed (model M) (C). Please consult Table 1 for more details of time parameters (in y axis)and Table S10 for the interdependencies of those parameters. AFR is African, EUR is European, and ASN is East Asian. X is African archaic, N is Neanderthal, and D is Denisova.

Back to Africa (model B)

In this model, the basic OOA model still holds and additional changes required for the back to Africa migration (Figure 1B) are added. The basic idea was drawn from Poznik et al.¹⁰ In this scenario, the basal out of Africa population splits into back to Africa and OOA at T_Sep generations ago before the split between European and Asian populations (so that T_Sep is between T_B [the time of separation between Africa and OOA] and T_EU_AS [the time of separation between Europe and Asia]). Next, the back to Africa population migrated to Africa having an effective population size of N_BC and mixed with the ancestral African population at T_Mix generations ago with a mixing proportion of mix (the portion of ancestral African ancestry replaced). After the admixture, the effective population size of the African population is changed from N_AF0 to N_AF.

Mixed out of Africa (model M)

This model (Figure 1C) is similar to model S and has an additional population M separating from the African population T_Sep generations ago (again between T_B and T_EU_AS) and having an effective population size of N_MX. M mixed with OOA at T_Mix generations ago, and mix is the proportion of OOA ancestry being replaced by M. After the admixture, the effective population size of OOA is changed from N_B0 to N_B. The basic idea came from two OOA hypothesis.⁷

Recent admixture in Africa (model R)

As an alternative hypothesis, we also simulated a recent admixture model for the African population. After the OOA population had separated from the African population, the latter splits into two sub-populations in AF1 and AF2 with effective population size of N_AF1 and N_AF2 at T_Sep generations ago. At T_Mix generations ago, these two populations admixed with each other so that a fraction of AF1 equal to mix is replaced by AF2. After the admixture, the effective population size of the African population becomes the modern effective population size of Africa. We have not simulated Neolithic farmer migration from Europe for this scenario.

Other migrations as prior

We also added some pulse migrations or admixtures proposed by different studies on top of these basic models. We simulated OOA to have introgression from Neanderthal⁶³ at T_NM generations ago with the proportion of NMix. After the separation between Europeans and East Asians, the East Asian population has an introgression from Denisova^47,64 or an unknown archaic population²⁰ at T_DM and the amount is DMix. Neanderthal separated from Denisova or the unknown population around T_N_D generations ago, and Neanderthal-Denisovan lineage separated from the modern human lineage T_H_A generations ago.^65,66 The African population also has introgression from another unknown archaic population,^16,67,68 which introgressed at T_XM generations ago with the proportion of XMix. This unknown population separated from modern human lineage around T_H_X generations ago. We observed that our method is incapable of finding the effective population size for any archaic population (most likely because we did not use any ancient genome in our real data). Thus, we assumed them to be equal to N_A (ancestral effective population size). We also simulated Neolithic farmers, which separated from Europeans around T_FS generations ago with effective population size of N_A and admixed with the African population around T_FM generations ago with the proportion of Fmix.⁶⁹

For some events, their order is fixed (for example, the separation of European and Asian populations can only happen after the Neanderthal introgression on the basis of our prior assumption) and is described in Table S11.

Relate

We used Relate v.1.1.4,¹⁴ a method for inferring local trees, to validate our parameter estimates. Relate uses branch length of the local trees to estimate coalescent rate through time.¹⁴ Thus, we used it to compare effective population size trajectories and inter-population coalescent rates for the African, European, and East Asian populations between the real and simulated data. We applied Relate to YRI, CEU, and CHB samples (108, 99, and 103 individuals, accordingly) from the high-coverage version of the 1000 Genomes project as well as to genetic data simulated under each of the three models with optimized parameters (Tables 2, S5, and S6). For real data, chromosome 1 was used and a region of the same length was simulated.

We started with 2,054 high-coverage genomes from the 1000 Genomes Project. We kept positions that (1) are bi-allelic SNPs, (2) pass the 1000 Genomes filters and have the value of the QD (quality by depth) parameter above two and (3) have a missing rate below 10%. We phased and imputed the entire dataset by using Eagle version 2.4.1.⁷⁰ Next, we ran Relate on chromosome 1 for samples coming from the three focal populations. We used the GRCh38 recombination map, 1000 Genomes strict genomic mask, and a mutation rate of 1.45 × 10⁻⁸ per bp per generation. Next, we ran the effective population size estimation module of Relate for each population individually to obtain the effective population size trajectories and for population pairs to obtain the cross-coalescence rates.

For each model, we simulated a region of the same length as chromosome 1 with uniform recombination together for 100 African, 100 European, and 100 East Asian individuals by using msprime.²⁹ We used the 1000 Genomes strict mask for consistency between real and simulated data in terms of the length of the available sequence. After that, the simulated data were treated as described above.

We estimated effective population size for both real and simulated data as 1/2C, where C is the inferred intra-population coalescence rate. To estimate the relative inter-population coalescence rate, we used the following formula:¹³

$$C{\text{′}}_{12}=\frac{2\times C_{12}}{C_{11}+C_{22}},$$

where C₁₁ and C₂₂ are intra-population coalescence rates and C₁₂ is the inter-population coalescence rate.

Comparing mutation age distribution between the simulations and real data

Relate estimates branch length in generations for the inferred trees and thus allows us to obtain tMRCA for any given mutation mapped to a specific tree branch. This value for a given mutation may differ between populations, reflecting the history of the spread of the mutation. A joined distribution of mutations’ tMRCA in two populations may reflect the complex history and interactions between the two populations through time. Thus, we compared such two-dimensional tMRCA distributions obtained from the real genomes and from the genomes simulated under the demographic models tested (Neanderthal, Denisova, and Africa archaic introgression with the above three models [BNDX, MNDX, and SNDX] parameters coming from Tables 2, S5, and S6, respectively) for each of the three population pairs (CEU-YRI, CHB-YRI, and CEU-CHB). We first did a log10 transformation of the tMRCA values (Figure S4) and then did a kernel density estimation for each dataset (real, BNDX, MNDX, and SNDX) and each pair of populations to obtain a matrix of a two-dimensional distribution of allele ages. For the density estimation, we used the kde2d function from the MASS R package setting n (number of grid points) to 100. Next, we subtracted such a matrix obtained for the real data from each of the simulation matrices. Together with the distribution of this difference, we report the root-mean-square deviation between the two matrices.

$$RMSD=\sqrt{\frac{1}{N}\sum _{i=1}^N{d}_i^2},$$

where d_i is the difference between the value in the i^th cells of the matrix for the simulated and real distribution and N is the number of cells (100 × 100). Lower root-mean-square deviation (RMSD) value indicates less deviations between the tMRCA distribution of real and simulated data (Figure S5).

We also report the standard error of this value obtained by applying a jack-knife method by iteratively masking out a 50 Mb long region of the sequence (between 1 and 246 Mb of the GRCh38 reference sequence for chromosome 1 to avoid telomere regions with a high fraction of N bases) in a non-overlapping sliding window manner and calculating RMSD on the remaining non-masked sequence, resulting in five values.

Results

ABC-DLS

The general workflow for ABC-DLS (both for model selection and parameters estimation) includes the following steps. First, we simulated²⁹ multiple genetic datasets for each tested model by using demographic parameters sampled from a uniform distribution within prior ranges (Table 1). Next, we computed the SFS from these data and split the data into a training and a testing subset. We then trained the NN (implemented via TensorFlow with Keras backended⁴²) on the former dataset to either select between demographic models or to estimate the demographic parameters. The resulting NN is applied to the testing dataset as well as to the observed summary statistics data (see below as well as material and methods for more details). Next, we applied ABC to estimate support for the NN prediction on the observed data by comparing the NN prediction outcome between the observed data and the testing dataset (see material and methods, Figure S2, and also our previous paper²⁰). Finally, in cases when SMC is used, we essentially iterated the parameter estimation step by SMC. We kept the top five percent (equal to the tolerance level) of simulations from the testing dataset that best match the observed data. We then used the parameters of those simulations to update our prior range and sent it for next iteration until convergence was reached (Figures S3 and S4).

Before testing our primary hypothesis on real sequence data, we tested whether our approach (DLS) can reproduce the known results. The predicted parameters for real sequence data (see below for more details) are consistent with previous works from the literature^17,19,71(Table S7). We also tested our method on simulated data with known parameters under various models (model S, B, and M, see below for more information; simulation parameters coming from Tables 2, S5, and S6) and found that our approach with SMC correctly predicted the model in all the cases tested, suggesting it can find the correct model. Also, our method can infer the parameter values with high accuracy when the correct parameter values are known and coming from a mock observed SFS (Table S12).

Model selection

To test our hypothesis, we simulated three OOA models, simple model (model S), back to Africa model (model B), and mix model (model M), and all the models had introgression from Neanderthal to all OOA populations,⁶³ Denisova or unknown to Asia,^20,47,64 African archaic to Africa,^16,67,68,72 and European Neolithic farmers to Africa⁶⁹ (NDXF) (see material and methods for more details, Figure 1 and Table 1). We used the 1000 Genomes Project high-coverage genomes⁴⁴ (see material and methods for more details) of five Yoruba (African), five Utah residents with Northern and Western European ancestry (European), and five Han Chinese (East Asian) individuals as our real dataset. Next, we used three different methods to choose between the competing models: (1) RF that combines random forests with ABC;⁴³ (2) NN and ABC together (DL), which is an analogous but improved version of our previously published method, ABC-DL;²⁰ and (3) the method introduced here, DLS, which expands the DL method with SMC. Although all three methods identified the back to Africa model as the most probable one, the prediction certainty varied between methods (Tables 3 and 4). Both DL and DLS returned >95% probability for model B although RF gave lower support.

Table 3.

Cross-validation via different approaches on simulated data

	OOA_B	OOA_M	OOA_S
RF
OOA_B	92.85%	1.84%	5.31%
OOA_M	2.69%	84.71%	12.60%
OOA_S	6.17%	15.38%	78.44%
DL
OOA_B	88.03%	2.54%	9.43%
OOA_M	3.43%	77.78%	18.79%
OOA_S	5.78%	15.69%	78.52%
DLS
OOA_B	99.09%	0.00%	0.91%
OOA_M	0.00%	99.98%	0.02%
OOA_S	1.25%	0.30%	98.45%

Confusion matrix for misclassification is reported here via RF (random forest), DL (only neural network), and DLS (neural network and sequential Monte Carlo together) for random samples from the models with ABC.

Table 4.

Model selection via different approaches on real data

	OOA_B	OOA_M	OOA_S
RF	66.00%	16.40%	17.60%
DL	100.00%	0.00%	0.00%
DLS	100.00%	0.00%	0.00%

Posterior of votes for RF (random forest) and posterior model probabilities for DL (only neural network) and DLS (neural network and sequential Monte Carlo together) are reported here via the real data.

The DLS results were reproduced under different data filtering strategies, different datasets (Table S2), and different total length with different per block length of simulated regions (Table S4). We also tested whether our assumption of pulse migration events (three archaic introgression scenarios and recent migration of Neolithic farmers) could affect our inference. We tested different models with (1) no introgression and no farming migration (NI), (2) Neanderthal and Denisova introgression (ND), (3) Neanderthal, Denisova, and Africa Archaic introgression (NDX), and (4) Neanderthals and Denisova introgression with farming migration (NDF) using only DLS. Except for the no introgression model (Table S13), we always found the back to Africa model to be supported over simple and mix out of Africa models. When we compared all these 15 models together ([B, M, S] × [NI, ND, NDX, NDF, NDXF]) by using DLS, the back to Africa model with Neanderthal, Denisova, and African archaic introgression (BNDX) is supported over all other possibilities (P(BNDX|data) = 0.86) (Table S14). The model with Neolithic farming migration has a lower support (P(BNDXF|data) = 0.14). Both RF and DL were incapable of differentiating between these models as precisely as DLS (Tables S15 and S16). We further tested these two models (BNDX and BNDXF) with more precise priors by using more simulated data (see material and methods for more details) via DLS and rejected European Neolithic migration to Africa (Table S10). This result not only demonstrated the robustness of our inference for back to Africa but also independently supported other assumptions (except Neolithic migration) that were reported before, but not all of them were confirmed together.^{16,20,47,63,64,68,69} In addition to the 15 models described above, we also tested the recent admixture model (model R), which adds a split and follows admixture within Africa, both happening after the separation of the OOA population on top of the simple out of Africa model. Thus, both our best back to Africa (BNDX) and recent admixture models represent the modern African population as a result of admixture of two components and the main difference is those separations happened before or after OOA population separation. Based on our results model, back to Africa better fits the data compared to recent admixture (Table S17).

Parameter estimation

After demonstrating that back to Africa (BNDX) best explains the real data, we used the three methods described above (RF, DL, and DLS) to estimate the model’s parameters. The confidence intervals (CIs) returned by DLS are much narrower than those of the alternative approaches (Tables 2, S18, and S19). Hence, all the results discussed below are the ones obtained with DLS (Figure 2).

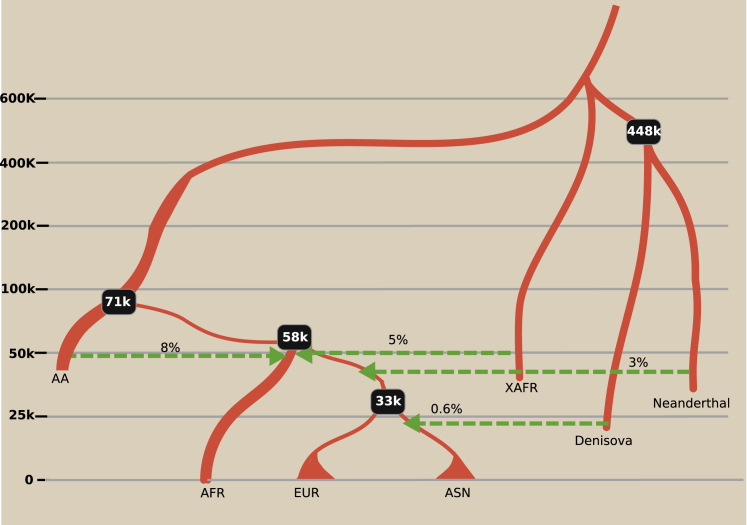
Figure 2.

Schematic of inferred demography

Model B with only mean posterior. K is kilo years ago, AFR is African, AA is Ancestral African, EUR is Europeans, ASN is East Asian, and XAFR is African Archaic. Black boxes represent mean posterior of separation time between populations. Thickness of the lines represent effective population size of their respective population although they are not according to scale.

Our inference suggests that first there was a separation between the ancient African population and a population ancestral to both back to Africa and the actual out of Africa populations (basal out of Africa) around 71.3 (CI 69.4–73.3) kya. This event was followed by a split between back to Africa and OOA 57.9 (CI 56.1–59.8) kya and an admixture between ancient African and back to Africa 48.2 (CI 46.8–49.5) kya. The Neanderthal introgression to OOA happened much later, 38.3 (CI 37.6–39) kya, suggesting that this back to Africa migration cannot explain the Neanderthal ancestry found in modern African populations.⁶⁹ Our method predicted the admixture proportion from back to Africa to be as high as 91% (CI 90.28–91.57), suggesting a massive replacement of the ancient African population.

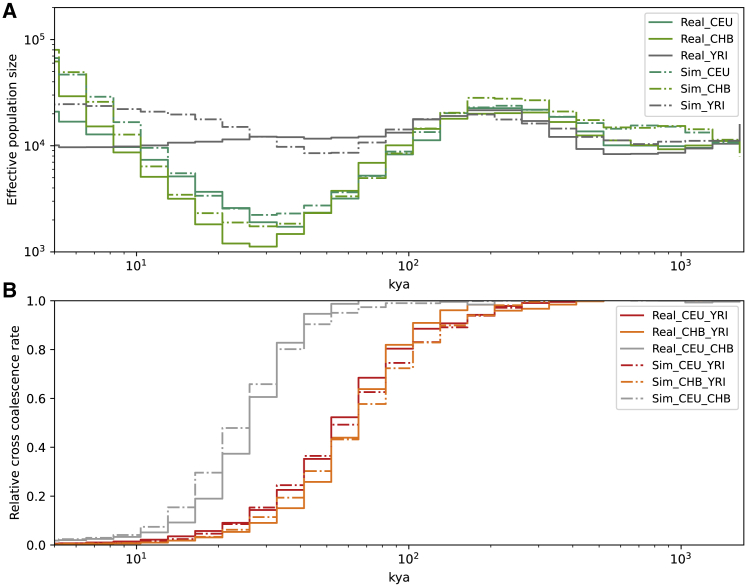
To independently validate our results, we compared effective population size trajectories and cross-coalescent rates obtained by applying Relate³² to real data as well as to data simulated under each of the three models with the mean posterior parameters (Tables 2, S5, and S6) predicted by DLS.¹⁴ We observe a close match between the estimates for the real data and our best model (Figure 3), which suggests our parameter estimation to be accurate. This similarity is particularly interesting given that we have not used any linkage disequilibrium (LD)-based summary statistics to optimize those parameters. On the other hand, neither the effective population size trajectory nor the cross-coalescent rate over time is informative enough to differentiate between these three models (data not shown). Specifically, the gradual separation between African and OOA populations, which was shown before with Relate and similar methods,^13,14 cannot be directly explained by the back to Africa or two out of Africa migration, as such gradual separation is also observed in our model S (Figure S6). However, the two-dimensional tMRCA distributions of mutations in population pairs (CEU-YRI and CHB-YRI) coming from Relate analysis best matches the distribution of the back to Africa model with lower RMSD value than other alternatives when comparing with real data (Figures S4 and S5).

Figure 3.

Effective population size trajectories and coalescence rates over time

(A and B) Here, we compare effective population size (A) and relative cross-coalescence rates (B) estimated by using Relate between the real and data simulated under the model B. (A) x axis in kya (kilo years ago) and y axis is the effective population size for corresponding populations presented in the inset. Both axes are in log scale. (B) x axis is in kya and y axis shows the relative cross coalescent rate for corresponding populations pairs presented in the insert. x axis is log scale.

Discussion

We here demonstrated that the ABC analysis can be substantially enhanced by using NN coupled with the SMC approach. Our methodology is suitable to test many hypotheses that can be simulated but cannot be extensively tested by other methods, especially for scenarios of admixture from ghost populations where the ancient genomes are unavailable and can accommodate any kind of summary statistics. Our model selection shows it can easily reach close to 100% accuracy in cross-validation steps with few simulations (2,000 samples), suggesting it can be used for testing much more complicated scenarios. We also found that our parameter estimation has high precision (most of the events have confidence interval width below 5,000 years), which can directly complement with the radiocarbon dating. In this study, we used SFS as summary statistics because it is effortless to calculate and has sufficient information.^17,51 Our results might be further improved by use of some LD-based summary statistics,^67,73 but we opted out because they are computationally demanding to produce and the improvement in the result is minimal (at least for the tested scenario). As we use SFS as our choice of summary statistics, our method is not affected by local recombination rate.⁵² Applying two different filtering strategies (see material and methodsfor more details) gave similar results, suggesting that our strategy is quite robust to the choice of the genomic regions to be analyzed.

In our models, we have not adopted any constant migrations between populations, although our approach can incorporate it. This is because we found out that our approach (parameter estimation via DLS) predicted non-zero migration rates when we used mock observed summary statistics data coming from a pulse migration model with no constant migrations and demographic parameters coming from mean values of Table 2 (Tables S9 and S10). This suggests that models including constant migrations may lead to equifinality as proposed by others⁷⁴ and/or that our approach is imprecise for estimating them.

Our results also comply with Y chromosome phylogeny and support back to Africa as proposed before.¹⁰ However, our estimated time of separation between populations is much younger than what is reported for the Y chromosomes. One explanation might be that we used a slightly higher mutation rate (1.45 × 10⁻⁸ per bp per generation)⁵³ instead of a slightly slower alternative (1.25 × 10⁻⁸ per bp per generation).^54,55 When we used the slower mutation rate, our estimation for most of the events time increased (Table S3). Indeed, the separation time between back to Africa and OOA populations corresponds to 72.8 (CI 72.4–73.3) kya, which is close to the estimate of tMRCA between haplogroups D and E (72 kya¹⁰).

Although back to Africa is preferred over other alternatives in most of the cases, considering no introgression as an option (NI) supported mixed out of Africa over other models (Table S13). This result might be a side effect of the Neanderthal introgression in OOA. Under certain conditions (i.e., older separation time between Africa and OOA [T_B]), mixed out of Africa model with no introgression and simple out of Africa with Neanderthal introgression are comparable (Neanderthal population behaves like the first OOA population in this scenario). However, this model was rejected when compared with other more complex models (Table S14). This false result suggests a possible drawback of our method as different demographic histories can give similar SFS patterns, which can bias our interpretation if demographic histories were not incorporated in the model correctly⁵² and also advocates for the importance of parameter estimation because it can give insight for the choice of selected model (especially if it does not match with the prior knowledge), which then can suggest more complicated scenarios to test.

The separation times between Homo sapiens and archaic populations are slightly older (877 [CI 773.1–982.3] kya for human and Neanderthal lineage divergence and 1,073.7 [CI 1,032.7–1,117.5] kya for human and African archaic) than those previously inferred^63,66, 67, 68 if we used a loose prior of 400–1,600 kya (Table S20). These deviations were not reproduced when we used simulated summary statistics generated under known parameters from Table 2. This may be specific to real sequence data and might be a side effect of some of our assumptions (for example, some unknown interactions between these populations that was not modeled here⁶⁵) or systematic biases due to the use of European reference genome⁷⁵ or recent changes of generation time or mutation rate per generation.^76,77 These results were obtained without using the ancient genome at all in our real SFS data to reduce any chances of bias. It would be interesting to revisit these results after incorporating ancient genome directly in our analysis.

We did not find support for a model of European Neolithic migration to West Africa, which was proposed recently.⁶⁹ We have to caution that our result is only true for the Yoruba population. As sub-Saharan African populations have quite diverged ancestry, this is not representative of the whole sub-Saharan African population. Nonetheless, our back to Africa model also fails to explain Neanderthal sequence identified in Yoruba. Even if we assume this migration has happened (model BNDXF), our predicted amount of migration is as low as 2.4% (Table S21), which results in the average total length of Neanderthal sequence in Yoruba to be less than 5 Mb as opposed to 17 Mb reported by Chen et al.⁶⁹ This suggests that most of the Neanderthal regions found in Yoruba should be explained by some other migration(s) (for example from human to Neaderthal⁶⁵). Alternatively, Neolithic farmers’ contribution might be so low on West African populations that our approach with the current format (with SFS as summary statistics) fails to detect it.

We chose Yoruba, European, and East Asian population as a representative population set to test the OOA model because they are quite well studied and show relatively less recent admixture than other populations (for example, South Asian, East African, or Central Asian, etc.), which makes our model relatively simpler than other alternatives. Although back to Africa is better in explaining the real data, there might be more complicated models characterized by additional migrations and admixture that better explain the observed data. We have tested the two out of Africa model under the mixed out of Africa model, but it is not thorough enough because we have not used the populations that are assumed to have a contribution from the first OOA population.⁷ It will be interesting to revisit this hypothesis with Papuan populations in the future.

Our back to Africa model can explain the reduction in effective population size of all African populations coinciding with the OOA event.⁷⁸ We would like to caution that although we are naming the model “back to Africa,” the OOA population did not need to be geographically out of Africa.^21,79 Our estimates, particularly the effective population size of back to Africa (N_BC) (which is more than 10,000), and the time of Neanderthal introgression (T_NM) compared to separation back to Africa population from OOA population (T_Sep) suggest that the split might have happened within Africa itself before the actual out of Africa event. In such a case, our results can be explained by the separation of West and East African population 87.8 kya (T_B) and then later the primary separation of OOA and East African population 72.8 kya (T_Sep) (assuming mutation rate of 1.25 × 10⁻⁸ per bp per generation^54,55 and generation time of 29 years⁵⁶). In this regard, our model is more akin to the Lipson et al., 2020¹⁶ model rather than what is suggested by Cole et al., 2020.¹⁵ If we assume the model from Lipson et al. to be true, the most parsimonious explanation would be that our back to Africa population represents the basal West African population that separated from OOA populations 72.8 kya (T_Sep). Our ancient African represents ghost modern,¹⁶ which contributed to modern West African population around 10% through admixture around 61.9 kya from our prediction. On the other hand, if we assume true the back to Africa event happened, then most likely the OOA event took place less than 90 kya (T_B). This suggests that most of the older fossils (>100 kya) found outside of Africa80, 81, 82 are unlikely to have contributed to OOA populations (assuming the main lineage of modern humans has not left Africa before that). Geographical location where back to Africa separated from OOA is immensely important for this hypothesis but cannot be estimated from our approach. It will be especially fascinating to test this hypothesis with ancient genomes originating at those areas from that time point when they will be available.

Published: October 8, 2021

Data and code availability

The code generated during this study are available at https://github.com/mayukhmondal/ABC-DLS. Please contact the corresponding author for further information.

Web resources

• 1000 Genome High Coverage, https://www.internationalgenome.org/data-portal/data-collection/30x-grch38

• Ancestral allele alignments, http://ftp.1000genomes.ebi.ac.uk/vol1/ftp/phase1/analysis_results/supporting/ancestral_alignments/

• HGDP, http://ftp.1000genomes.ebi.ac.uk/vol1/ftp/data_collections/HGDP/

• Keras Documentation, https://keras.io/