Abstract
Phase separation and transitions among different molecular states are ubiquitous in living cells. Such transitions can be governed by local equilibrium thermodynamics or by active processes controlled by biological fuel. It remains largely unexplored how the behavior of phase-separating systems with molecular transitions differs between thermodynamic equilibrium and cases in which the detailed balance of the molecular transition rates is broken because of the presence of fuel. Here, we present a model of a phase-separating ternary mixture in which two components can convert into each other. At thermodynamic equilibrium, we find that molecular transitions can give rise to a lower dissolution temperature and thus reentrant phase behavior. Moreover, we find a discontinuous thermodynamic phase transition in the composition of the droplet phase if both converting molecules attract themselves with similar interaction strength. Breaking the detailed balance of the molecular transition leads to quasi-discontinuous changes in droplet composition by varying the fuel amount for a larger range of intermolecular interactions. Our findings showcase that phase separation with molecular transitions provides a versatile mechanism to control properties of intracellular and synthetic condensates via discontinuous switches in droplet composition.
Significance
Most physicochemical properties and likely all biological functionality of intracellular droplets are downstream consequences of their local composition. Motivated by the ubiquity of many biomacromolecules to phase separate and change their molecular state, we theoretically investigate systems that can phase separate and in which two components interconvert with each other. Strikingly, our theory shows that such systems can switch droplet composition at thermodynamic equilibrium and in the presence of chemical reactions maintained away from equilibrium. Our reported switch paves the way for tightly regulating the composition of condensates in a broad class of mixtures composed of proteins or synthetic polymers. The mechanism underlying the compositional switch may also be relevant for the control of condensate-related functions in living cells.
Introduction
The ability to phase separate in aqueous solutions and to interconvert between distinct molecular states are two properties common among a large number of biomacromolecules. For example, DNA sequences composed of self-complementary strands phase separate into DNA-rich condensates that coexist with a DNA-poor phase (1, 2, 3). These sequences can also switch between an expanded (“open”) DNA configuration and a collapsed (“closed”) configuration in which the self-complementary strands of the same DNA are basepaired. Another example is proteins that form phase-separated condensates in vitro (4, 5, 6) and in living cells (7,8). Proteins attract each other, as well as other macromolecules such as RNA and DNA, for example, by sticky amino-acid patterns such as RGG repeats (9, 10, 11) or charged domains (12,13). These interaction sites are considered to drive protein phase separation but also mediate conformational transitions in which certain domains of the protein rearrange (14).
In living cells, phase separation of macromolecules such as proteins and RNA can also be actively controlled by biological fuel. Hydrolysis of ATP by kinase and phosphatase, for example, enables the regulation of the phosphorylation states of proteins. The number of phosphoryl groups attached to a protein, in turn, affects its net charge (15) and may modify localized interaction sites along the sequence (16). Thus, the phosphorylation state of proteins strongly determines their interactions and thereby their propensity to form aggregates and phase-separated compartments (17, 18, 19).
To effectively account for the impact of fuel on chemical reactions and phase separation, various theoretical models were proposed with chemical reactions that are devoid of thermodynamic constraints and thus break the detailed balance of the rates (20, 21, 22, 23). These systems give rise to novel nonequilibrium phenomena such as bubbly-phase separation (22) and shape instabilities leading to droplet division (24). Until now, there has been a strong focus on establishing new universality classes and observing new nonequilibrium phenomena. However, the physical mechanisms of how transitions between different molecular states affect phase separation remain largely unexplored, despite their ubiquity in biological systems. In particular, it remains unclear how these systems respond to thermodynamic perturbations such as temperature and concentration changes and how fuel-driven molecular transitions affect the phase separation behavior. This is mainly due to the lack of physical models for phase separation and chemical reactions with coarse-grained parameters that are linked to molecular properties of biological macromolecules.
To gain insight into how molecular transitions driven by fuel control phase separation, we propose a thermodynamic model for polymers such as DNA and proteins, which can phase separate and undergo transitions between two molecular states. At thermodynamic equilibrium, we show that the interplay between phase separation and molecular transitions gives rise to reentrant phase behavior as a function of temperature. Moreover, we find a discontinuous thermodynamic phase transition in droplet composition when changing the temperature. Similar behavior also exists away from thermodynamic equilibrium at which the consumption of fuel breaks the detailed balance of the rates associated with the molecular transition. In this case, droplet composition can abruptly switch upon small changes in fuel level. In contrast to the corresponding thermodynamic system, the fuel-driven molecular transition releases the Gibbs phase rule constraint. This release allows abrupt switches in droplet composition within a range of molecular interaction parameters that is significantly broader compared with the system at thermodynamic equilibrium. Owing to the very general nature of our model, our findings suggest that many different phase-separating macromolecules that are capable of undergoing molecular transitions can switch the composition of dense phases via fuel-driven molecular transitions.
Materials and methods
Model for phase separation and molecular transitions
Here, we consider mixtures composed of unstructured macromolecules, such as DNA or proteins, and a solvent W. In our model, these macromolecules can undergo molecular transitions (e.g., changes in conformation or charge) between two states, referred to as A and B. The transition between the two states is described similarly to a chemical reaction with the scheme illustrated in Fig. 1. The corresponding transition rates depend on thermodynamic control parameters such as temperature T and macromolecule concentration, as well as fuel volume fraction φF that drives the transition away from thermodynamic equilibrium. In our model, both components A and B can phase separate because of the attractive interactions among them (Fig. 1).
Figure 1.
Illustration of the model to study molecular transitions and phase separation. In our model, we consider three components: A, B, and solvent W. We consider reversible molecular transitions between A and B that are controlled by temperature T or fuel volume fraction φF. Molecular transitions occur in the dense and dilute phase, respectively. Depending on the molecular interactions of A and B molecules, the total volume fraction of both components and their composition (i.e., the relative amount of B molecules) changes in each of the phases. Please note that the conformations A and B represent two arbitrary states of the same molecule. Illustration by Mara Müller. To see this figure in color, go online.
Free energy density
We describe the mixture in the T-V-Ni ensemble making use of a free energy density f(T, φi) = F(T, V, Ni)/V, where F denotes the Helmholtz free energy depending on temperature T, volume V, and particle number Ni of component i. Particle numbers are related to volume fractions φi = Niνi/V, with νi denoting the corresponding molecular volumes. To describe the thermodynamic behavior of unstructured polymers, we use a Flory-Huggins free energy density of the form
| (1a) |
where kB is the Boltzmann constant, ri = νi/νW are the ratios of the molecular volumes relative to the solvent W, and i = A, B, W. For simplicity, we consider A and B having equal molecular volumes νA = νB ν and thus rA = rB r, implying that the molecular transition conserves the volume of the system, V = ∑νiNi. Moreover, in our model, all molecular volumes are constant, making the system incompressible at all times and leading to the incompressibility condition
| (1b) |
For simplicity, we consider the fuel (and potential waste products) to be dilute or having a small molecular volume, thus not affecting the incompressibility condition. The first term in Eq. 1a is the mixing entropy governing the tendency of the mixture to remain mixed (25,26). The second term describes the interactions among the molecules, where Ωij denotes the interaction parameter between the components i and j. These interaction parameters depend on temperature. To the lowest order, we can write (27)
| (1c) |
where eij and sij are temperature-independent interaction energies and entropies per molecule. The third term in Eq. 1a accounts for the free energy needed to create the molecular components (e.g., via molecular transitions), and ωi(T) denotes the internal free energy of component i (in units of kBT). In particular, ωB − ωA corresponds to the internal free energy difference between the two molecular states A and B, which we express as
| (2) |
Here, eint and sint are the energetic and entropic differences between state A and B. As a prototypical example, we consider conformational transitions leading to an energy and entropy increase converting A to B, i.e., eint > 0 and sint > 0. Such a scenario corresponds to, for example, polymers switching from a tightly bound configuration to an unfolded one. For a dilute system, the temperature at which the internal free energy difference vanishes, ωB(T) = ωA(T), defines the melting temperature
| (3) |
above or below which B or A is the favored molecular state.
Thermodynamic equilibrium
Chemical equilibrium is reached between molecular states if (28, 29, 30)
| (4) |
where the exchange chemical potentials are given by (29)
| (5) |
Here, f is the free energy density after using the incompressibility condition Eq. 1b. Exchange chemical potentials are related to the chemical potential difference between molecules and solvent, as explained in detail in Appendix A. Using the free energy density f (Eq. 1a), the condition of chemical equilibrium can be written as
| (6) |
This relationship represents the non-dilute mass action law at chemcial equilibrium for the molecular transition depicted in Fig. 1; for a general discussion of non-dilute chemical reactions in multicomponent mixtures, see (31). The condition of chemical equilibrium (6), together with incompressibility Eq. 1b, reduces the number of independent variables from three to one (see Appendices A.1 and A.2 for details). Here, we consider the total volume fraction of A and B
| (7) |
which is conserved in the molecular transition, as an independent variable. By means of Eqs. 6 and 7, we can recast Eq. 1a in the form f = f(T, φtot), which can be used to determine the phase diagram via the common tangent construction (i.e., Maxwell construction). In fact, imposing the equivalence between exchange chemical potential and osmotic pressure in both phases, the conditions for phase coexistence of the phase I and II read (32)
| (8a) |
and
| (8b) |
An example of Maxwell construction for the free energy density at chemical equilibrium is shown in Fig. 9, in Appendix A.3 and in Fig. 1 of (30).
Figure 9.
Stable and unstable free energy branches due to molecular transitions. Free energy of the mixture is shown as a function of the conserved quantity φtot, with the tilde indicating that all linear terms were subtracted for illustrative purposes. Molecular transitions can lead to the emergence of multiple solutions for a single φtot-value in the demixing region (white). We distinguish three branches: 1 and 3 are metastable, and 2 is a locally unstable branch. The common tangent (Maxwell construction) is shown in black and separates the demixing region from the mixed region (blue, red shapes). In the mixing region, the system is homogeneous, the free energy is convex, and all branches collapse. To see this figure in color, go online.
Nonequilibrium thermodynamics
Using irreversible thermodynamics, the kinetic equations for an incompressible, ternary mixture read (see Appendix C for the derivation)
| (9a) |
and
| (9b) |
where the inhomogeneous chemical potentials are given as (33)
| (10) |
These chemical potentials are related to the free energy
| (11) |
via = νiδF/δφi, where the free energy density f is given by Eq. 1a. Moreover, Λi is the diffusive mobility, which depends on volume fraction. To ensure that the diffusion coefficient of A and B is constant in the dilute limit, we use the following scaling form, Λi = Λi,0φi(1 − φA − φB) (34), and consider Λi,0 to be constant for simplicity. This choice indeed cancels the divergence stemming from the logarithmic terms in the free energy density. Thus, the diffusion constant in the dilute limit is given by Di = kBTΛi,0. For simplicity, we restrict ourselves to the special case of a zero Onsager cross-coupling coefficient.
The kinetics of the chemical transition is captured by the reaction flux s(φA, φB), which depends on the volume fraction of both molecular components. Here, we consider two different cases corresponding to different reaction fluxes. The first case is a system that relaxes toward thermodynamic equilibrium, suggesting the following form (for the derivation using linear response, see Appendix C):
| (12) |
where Λs denotes the mobility for the molecular transition, which we consider to be constant for simplicity. If chemical potentials are homogeneous ( = constant) and the chemical potentials of A and B are equal , the system is at thermodynamic equilibrium, self-consistently leading to ∂tφA = ∂tφB = 0 in Eqs. 9a and 9b.
The second case refers to a system in which the molecular transitions cannot relax toward thermodynamic equilibrium, i.e., the detailed balance of the rates is broken (23,35). In living or active systems, this is often facilitated by a “fuel” component F that affects the balance between the two molecular states and is, to a good approximation, maintained by chemical reaction cycles (36,37). Here, we consider a combination of the flux (12) and a second-order chemical reaction that depends on the fuel volume fraction φF (see Appendix D for details):
| (13) |
Here, k← and k→ are the volume-fraction-independent rate constants of the backward and forward transition, respectively. This independence of rate constants implies that detailed balance of the rates corresponding to the molecular transition is broken; for a conceptual discussion, see (23). In contrast to Eq. 12, a system with a reaction flux s given by Eq. 13 cannot fulfill the two equilibrium conditions of equal and spatially constant chemical potentials. Thus, stationary solutions to Eqs. 9a and 9b using Eq. 13 are nonequilibrium steady states. Consistently with this, in the absence of fuel (φF = 0), the reaction flux above reduces to Eq. 12, and the system can relax to thermodynamic equilibrium. In our model, the fuel level controls how far the system is maintained away from thermodynamic equilibrium.
Finally, we look for an equation for the fuel volume fraction φF. To this end, we focus on the case in which the diffusion of fuel is fast compared to the diffusion of the macromolecules A and B, respectively. This limit is indeed reasonable for many biological systems because diffusivities for example between phase-separating macromolecules (proteins, RNA, etc.) and ATP differ by about two orders in magnitude (38,39). For simplicity, we consider the case of fuel being conserved, i.e., it is maintained constant in time. This scenario applies to living cells under physiological conditions and in in vitro systems, in which these conditions could be realized by encapsulated ATP or regeneration of ATP. Moreover, we assume that the fuel molecules interact in the same way with A and B. In this case, we can quasi-statically enslave the fuel volume fraction φF to the total concentration of A and B,
| (14) |
where denotes the average volume fraction of fuel that is constant in time. The choice above allows to capture the partitioning of fuel by accounting for the spatial correlations between fuel and the total volume fraction φtot. The fuel-partitioning coefficient PF, which is experimentally accessible, determines the values of the parameters α and β in Eq. 14 (see Appendix E for a definition of PF and the link to α and β).
In the following, we choose three parameter sets for α and β corresponding to three qualitatively different scenarios. First, the fuel partitions inside the φtot-rich phase for α = 0 and β = 1/. Second, fuel is enriched outside corresponding to α = −β = 1/(1 − ). Finally, we also consider the case of a homogeneous fuel for α = 1, β = 0. The latter case has been studied, for example, in (20,40).
Results and discussion
Equilibrium phase diagrams
In this section, we study the equilibrium phase diagrams as a function of the total volume fraction φtot and a scaled temperature T/T0, with T0 = −eBB/kB. In such phase diagrams, the binodal lines separate demixed and mixed thermodynamic states. Along the binodals, we also depict the composition in terms of the relative abundance of B molecules, φB/φtot (see the color code in Fig. 2, a–c). We then study how such phase diagrams are affected by molecular transitions, described by the melting temperature Tm, defined in Eq. 3. As a reference system, we consider a binary mixture composed of only B and W molecules (black lines in Fig. 2, a–c). In all our studies, we choose r = 2 to account for differences in molecular volumes between macromolecules and water.
Figure 2.
Molecular transitions can lead to a lower dissolution temperature. The phase diagrams depict the mixed and demixed region in the plane spanned by total volume fraction φtot and rescaled temperature T/T0. The composition of each phase is indicated by the color code displayed on each branch of the binodal. The black line corresponds to the binary B-W reference mixture. For increasing Tm, the presence of molecular transitions reshapes the phase diagram. (a) For low Tm, the demixed region is bound from above by an upper critical solution temperature (UCST) similar to the binary case. (b) For Tm > −eBB/sint, the phase diagram becomes reentrant, i.e., bounded also from below by a lower dissolution temperature (LDT). (c) Increasing Tm further, the binodal is upshifted until the demixing region shrinks into a point for Tm = (r/2 + kB/sint) T0. Parameters for (a)–(c): Tm/T0 = 0.3, 0.6, and 1, and sint = 2.5kB for all. (d) Influence of eint and sint on the phase behavior, with the color code representing the critical density. Increasing the interaction entropy sint, the interval of relative energies −eint/eBB corresponding to the reentrant regime widens. All the results presented correspond to r = 2. To see this figure in color, go online.
Reentrant phase behavior
We first study the case of only attractive homotypic B-B interactions and neglect entropic contributions for simplicity (sij = 0 in Eq. 1c). Specifically, ΩBB = eBB/(kBT) and Ωij = 0 otherwise. With this choice of parameters, A can be thought of as an inert conformation in which the interacting sites are self-saturated because of the formation of internal bonds. Attractive homotypic interactions lead to phase coexistence between a φtot-rich and a φtot-poor phase, in the following referred to as the dense and dilute phase, respectively. Below the melting temperature Tm (Eq. 3), we find that coexisting phases are not only different in φtot but can also differ in the amount of B relative to A (see color code in Fig. 2, a–c). In particular, the dense branch of the binodal corresponding to large values of φtot is rich in B components, whereas the composition of the dilute branch (low φtot) changes with temperature. The composition, defined as the relative number of molecules in the B conformation, φB/φtot, remains rather uniform in the dense branch. In fact, in this example, attraction among B molecules is the only interaction considered; thus, the dense phase must be composed predominantly of B molecules. However, in the dilute and B-poor phase, the fraction of B is affected by temperature because molecular transitions, which favor A over B at low temperatures, dominate over the homotypic B-B interaction.
Increasing the melting temperature Tm enhances the dominance of the molecular transition at low temperatures leading to a qualitative change of the thermodynamic phase diagram (Fig. 2 b). In fact, we find a lower dissolution temperature (LDT), which implies a reentrant phase behavior. Such behavior is manifested as the possibility that both increasing and decreasing the temperature lead to a phase transition from a demixed to a mixed state, respectively. The lower dissolution temperature is given by (for a derivation, see Appendix B)
| (15) |
and is set by the competition between the homotypic interactions eBB and the molecular transition, which is characterized by the melting temperature Tm (Eq. 3). For attractive interactions, Eq. 15 fulfills Td < Tm, which is consistent with the fact that the majority of molecules have to be in the A state to undergo a phase transition to a mixed state for decreasing temperatures.
For even higher melting temperatures Tm, the upper critical solution temperature (UCST) Tc and critical volume fraction φc exceed the corresponding values in the binary case (black line in Fig. 2, a–c). This is because below Tm, the dilute and dense phases differ in composition, being enriched in A and B, respectively. If Tm is larger than the critical temperature of the reference binary system, this composition difference will emerge as soon as the homogeneous system demixes into two phases. Even though, with our choice of interaction parameters, B effectively repels both A and the solvent, differences in molecular volumes of A and B with respect to the solvent (i.e., r > 1) favor phase separating B from A. In other words, two coexisting phases of different solvent content are entropically disfavored. This entropic disadvantage implies that both phases will be upshifted in φtot, leading to two coexisting phases rich in B and A, respectively, instead of B and solvent rich, as in the binary reference. This entropic disadvantage of phase separating A with respect to B also explains the increase in critical temperature. The dependency of the critical temperature Tc on the melting temperature Tm is shown in Appendix A.4.
The qualitative difference among the phase diagrams can be summarized in terms of the internal entropy and energy differences between the two states A and B (Eq. 2); see Fig. 2 d. For eint < −eBB, the lower dissolution temperature (Eq. 15) vanishes, leading to phase diagrams with only a upper critical solution temperature. This upper critical solution temperature arises from a competition between B-B interactions and the mixing entropy (Fig. 2 a). If the internal energy gain of the molecular transition exceeds the strength of attractive B-B interaction, i.e., eint −eBB (corresponding to Tm −eBB/sint), there is a finite lower dissolution temperature Td leading to reentrant phase behavior. Reentrance arises from a competition between the attractive interactions eBB and the energetic difference between the two molecular states eint (see by inserting Eq. 3 into Eq. 15). Reentrance is absent at low Tm because B-B interactions dominate the molecular transition (eint < −eBB). Increasing Tm corresponding to eint > −eBB causes reentrant behavior because the energetic difference between the two molecular states eint exceeds the strength of the attractive B-B interaction. A further increase of Tm leads to a transition to a mixed region in the phase diagram. We found that the disappearance of demixed states in the phase diagram coincides with the upper critical point (φc, Tc) reaching φtot = 1, which corresponds to a system without solvent (see color-coded φc in Fig. 2 d). This observation can be used to analytically calculate the transition line between reentrant phase behavior (UCST and LDT) and mixed states by Tc(φtot = 1) = Td, where Tc(φtot = 1) = −r eBB/(2 kB) (for details, see Appendix B). We find a relationship for the transition line, −eint/eBB = 1 + sint r/(2 kB), which agrees with results from the Maxwell construction depicted in Fig. 2 d. This relationship implies that the reentrant region widens with the internal entropy difference sint. Larger sint leads to more phase-separating B molecules and thus favors phase coexistence over mixing. We can recast this relationship to get an upper bound for the melting temperature Tm = (r/2 + kB/sint) T0, corresponding to the phase diagram shrinking into a point.
First-order phase transition in droplet composition
Here, we chose the parameters in Eq. 1c such that Ωij = 0 for i or j = W and sij = 0 for simplicity. We consider attractive homotypic interactions for both molecular states, i.e., eAA < 0 and eBB < 0, and quantify the impact on the phase diagram of the relative A-A interaction strength eAA/eBB. For simplicity, we now fix Tm to a value for which reentrant behavior was observed in the case of only B-B interactions, as discussed in the last section. Because of the attractive homotypic A-A interaction, we find an additional demixing region in the phase diagram at low temperatures. This region is disconnected from the reentrant region of the phase diagram, which is located at higher temperatures (Fig. 3 a). This new region at low temperatures has an upper critical solution temperature and describes phase coexistence between φtot-rich and φtot-poor phases that are both mainly composed of A. Thus, these phase diagrams have two UCSTs and one LDT.
Figure 3.
Interplay between homo- and heterotypic interactions determine the phase diagrams of phase-separating systems with molecular transitions. (a and b) φtot − T/T0 phase diagrams with the composition along the binodal color coded, depicted for two prototypical cases discussed in the work. (a) A weak self-interaction among the A components creates a demixed region at low temperature, which leads to a second upper critical solution temperature. Here, eAA= 0.5 eBB and eAB = 0. (b) Increasing the strength of A-A homotypic interaction let the lower demixed region merge with the upper reentrant region, which generates a triple point. Here, eAA = 0.9 eBB and eAB = 0.1 eBB. (c) Classification of phase diagrams for different heterotypic A-B and homotypic A-A interactions, keeping eBB and Tm fixed. The classes are phase diagrams with one UCST and phase diagrams with reentrant behavior that either have one UCST and one LDT or two UCSTs and one LDT. The open circle symbol marks phase diagrams with a triple point (as shown in b), and circles with an x highlight cases in which the triple point collapses giving rise to a jump in the composition of the dense phase (see Fig. 4). Please note that for this classification, we considered temperatures down to T/T0 = 0.1. Here and for the rest of the work, we fix Tm = 0.615 T0. To see this figure in color, go online.
The phase diagram qualitatively changes when the strength of A-A attraction is increased toward the value of B-B interaction strength. In this case, the two separated domains in the phase diagram in Fig. 3 a merge. The resulting phase diagrams exhibit either only one UCST (data not shown) or one UCST and a triple point; see Fig. 3 b. At this triple point, three phases coexist that differ in φtot and A-B composition. The precise value of eAA at which both domains merge is influenced by the strength of the A-B heterotypic interaction; see Fig. 3 c.
For eAA being equal to the value eBB, the triple point temperature coincides with both the melting temperature Tm and the temperature of the first-order transition point at which the two branches of different A-B composition meet (indicated by a cross in Fig. 4 a). The result is a triple line; see the black horizontal line in Fig. 4 a. At the corresponding triple line temperature, three phases coexist for any value of φtot between the binodals. Crossing the triple line temperature leads to a discontinuous phase transition of the composition of the dense phase. In other words, in a finite system with a single droplet, the composition of the droplet discontinuously switches upon temperature changes between A rich and B rich. As mentioned, the triple line temperature is exactly the melting temperature Tm (defined in Eq. 3). The reason is that for eAA = eBB, both molecular states have the same phase separation propensity, leaving it to the internal free energy balance to determine the composition of the dense phase. Note that a discontinuous switch in A-B composition occurs also for total volume fractions approaching unity (see the black line in Fig. 4 a). However, for temperatures slightly below and above Tm, the system is homogeneous in this case. When A-A and B-B attraction strengths approach each other, the total volume fraction of the dilute branch decreases, and the two denser branches, each corresponding to different A-B composition, merge (Fig. 4 b). Thus, for the A-A attraction slightly weaker than the B-B attraction, crossing the temperature corresponding to the triple point leads to a jump in both composition and total volume fraction of the dense phase. For eAA = eBB, the jump only occurs in composition, whereas the total volume fraction exhibits a removable discontinuity.
Figure 4.
Systems with strong homotypic interactions exhibit a first-order phase transition in the composition of the dense phase. (a) In the limiting case of identical homotypic interaction strength combined with weak heterotypic interactions, eAA = eBB, eAB/eBB ≪ 1, the triple point temperature becomes equal to the melting temperature Tm. This leads to the formation of a triple line (black dashed line) at which a dilute phase coexists with two dense phases of different compositions. Such two dense phases have collapsed into the degenerate point at φtot = 1 (circle with x symbol). Note that both the order parameter φtot and the relative composition φB/φtot are discontinuous at Tm. (b) Volume fraction of the three phases coexisting at the triple point as a function of relative A-A interaction strength, eAA/eBB. For equal homotypic interactions, i.e., eAA = eBB, the two upper branches merge giving rise to the discontinuous transition in droplet composition. Here, eAB/eBB = 0.2 and the color code depicts composition of the phases. (c) Increasing the heterotypic interaction strength, the droplet composition shows three distinct behaviors with temperature: it can change discontinuously (eAB/eBB = 0.2); or the droplet first dissolves and then reforms with different composition (eAB/eBB = 0.4), where the shaded region corresponds to no drops; or its composition changes gradually (eAB/eBB = 1). We used φtot = 0.5 for all three curves. To see this figure in color, go online.
The discontinuous change in the composition of the dense phase is tied to the existence of a triple point. This triple point, in turn, arises from the tendency of the ternary mixture to form three coexisting phases stemming from similar attractive interactions among A and B molecules, respectively. However, molecular transitions affect the dimensionality of the three-phase-coexistence domain in the phase diagram. Three-phase coexistence is consistent with the Gibbs phase rule. In fact, because of the molecular transition, the system is reduced to an effective binary mixture solely characterized by the conserved variable φtot. This reduction does not suppress the three-phase-coexistence region because the Gibbs rule for a binary mixture at fixed temperature and pressure allows for a maximum of three coexisting phases. However, in our case, the molecular transition at thermodynamic equilibrium reduces the dimensionality of this region by at least one, giving rise to a triple point or even a triple line.
The coexistence of three phases, and thus also the triple point, is controlled by heterotypic interactions eAB (see Fig. 4 c). In particular, for strong attractive A-B interactions, three-phase coexistence is suppressed. Consistently, the triple point vanishes for increasing heterotypic interaction strength, implying that the composition of the dense phase cannot be varied discontinuously upon temperature changes. Instead, reentrance forces phase separation to vanish within a narrow intermediate temperature window (green shaded domain in Fig. 4 c). For even larger heterotypic interaction strength, the composition of the dense phase changes continuously (orange line in Fig. 4 c).
Kinetics of phase separation with detailed-balance-broken molecular transitions
In the last section, we focused on how temperature affects the composition of coexisting phases. Until now, there is no evidence that living systems control their temperature to regulate phase separation. Thus, we discuss how fuel-driven molecular transitions that are maintained away from thermodynamic equilibrium can control the composition inside droplets. For example, phosphorylation involving the hydrolysis of ATP is known to drive molecular transitions and thereby regulate protein phase separation (8,18,19).
To this end, we consider two prototypical parameter sets: 1) weak homotypic interactions of the A species and weak heterotypic A-B interactions (eAA/eBB ≪ 1, eAB/eBB ≪ 1) and 2) strong attractive A-A interactions and weak A-B heterotypic interactions (eAA = eBB, eAB/eBB ≪ 1). At thermodynamic equilibrium, we observed reentrant phase behavior for the first and the discontinuous phase transition in droplet composition for the second. To account for the effects of fuel on the molecular transition, we consider both a thermodynamic and a fuel-related contribution to the reaction flux; see Eq. 13. Most importantly, the fuel-related contribution breaks detailed balance of the rates. We numerically solve the kinetic Eqs. 9a, 9b, and 13 in two dimensions with periodic boundary conditions, combining the energy quadratization method (41, 42, 43) with the stabilization method (44) (see Appendices F and G for details).
Fuel controls nonequilibrium patterns
Breaking the detailed balance of the rates allows the system to settle into nonequilibrium stationary states, which differ from the thermodynamic equilibrium one in terms of droplet composition and droplet volume fraction. To classify these nonequilibrium states, we numerically solve Eqs. 9a and 9b using Eq. 13 and initialize the system with one droplet of total volume fractions and A-B composition taken from the corresponding thermodynamic phase diagrams. We find the emergence of various patterns ranging from equally sized droplets to rings and stripes (Fig. 5, a, b, f, and g; Videos S1, S2, S3, S4, S5, S6, and S7). The emergence of these patterns is determined by the partitioning of fuel into the droplets and the strength of homotypic and heterotypic interaction of A and B molecules, respectively. The influence of fuel partitioning arises from colocalization of fuel and total A and B material in the dense domains, thus affecting the balance between the two states. As a result, more fuel is more effective in maintaining the system away from thermodynamic equilibrium and a state with a single droplet.
Figure 5.
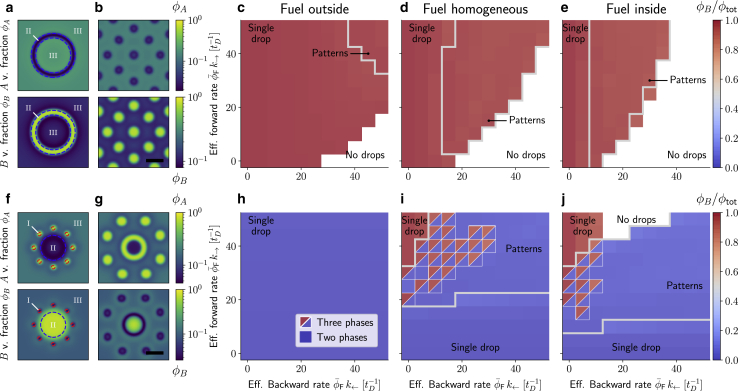
Molecular transition breaking detailed balance leads to nonequilibrium stationary states. We monitor the emergence of patterns by tracking the interface between A-rich (I), B-rich (II), and solvent-rich (III) domains (definition in Appendix G). As an example, such tracked interfaces are shown by dashed line in (a) and (f), in which the red and blue lines enclose A-rich and B-rich domains, respectively. These domains are the analog of demixed phases at thermodynamic equilibrium. For weak A-A self-interactions (eAA = 0.2 eBB, eAB = 0), we display two prototypical nonequilibrium stationary states due to the presence of the fuel (a and b), and we determine the values of the effective rates corresponding to such out of equilibrium patterns (c–e), with the color code indicating the composition of the dense domain in terms of the relative B amount, i.e., φB/φtot. Strikingly, fuel partitioning affects the boundaries of the region corresponding to patterns, along with the dissolution boundary. The more fuel partitions inside the dense domains, the more it is effective in making the system deviate from the equilibrium single droplet state. Here, φtot = 0.35, T/T0 = 0.55. For strong A-A self-interactions (eAA = eBB, eAB = 0.2 eBB), stationary patterns emerge that are composed of three domains distinct in composition (f and g). In the diagrams (h-j), such domains are indicated with two triangles of different colors in which each color corresponds to the composition of the two distinct dense phases. Here, φtot = 0.35, T/T0 = 0.525. The rates are measured in units of the inverse diffusion time tD = L2/DA, with L = 100 (see Appendix G for details). Scale bars, 20. To see this figure in color, go online.
The initial equilibrium drop evolves into a ring. For this movie the fuel is homogeneous in space and the effective rates are and .
The initial equilibrium drop evolves into a smaller drop surrounded by an outer ring. For this movie the fuel partitions inside the dense phase and the effective rates are and .
The initial equilibrium drop splits up into a ring and multiple drops. The ring gets unstable with time leading to a pattern composed of equally sized drops. For this movie the fuel partitions inside the dense phase and the effective rates are and .
The initial equilibrium drop breaks into smaller fragments, and subsequently, three of them elongate and align, forming a pattern reminiscent of stripes. For this movie the fuel partitions inside the dense phase and the effective rates are and .
For this movie the fuel is homogeneous in space and the effective rates are and .
When fuel is injected to the system, composed initially of an A-rich drop, a B-rich ring forms and then becomes a central drop. The remaining A material forms drops that initially fill the space but, at later times, A-richdroplets far from the central B-rich drop dissolve. For this movie the fuel partitions inside the droplet and the effective rates are and .
When fuel is injected to the system, a B-rich drop forms in the center of the initially A-rich drop. The remaining A material organizes into a ring wetting the B-rich central drop, and an outer layer of multiple drops. For this movie the fuel is homogeneous in space and the effective rates are and .
For case 1, characterized by weak A-A homotypic and heterotypic interactions, i.e., eAA/eBB ≪ 1 and eAB/eBB < 1, we find that the φtot-rich phase is mainly composed of B and that the inside composition hardly varies because of the presence of fuel (Fig. 5, c–e). However, the fuel can induce the formation of patterns that are significantly different from the initial single droplet at thermodynamic equilibrium (no fuel). For certain fuel partitioning, we find that there is an extended region in the k→-k← state diagrams where patterns emerge (gray line in Fig. 5, c–e). Strikingly, the location and the extent of these regions are significantly influenced by fuel partitioning. In particular, fuel partitioning inside φtot-dense domains favors the emergence of patterns for lower values of both effective forward and backward rates. Close to the onset of pattern formation, we observe stable ring-like patterns (Fig. 5 a; Video S1).
For increasing effective backward rate k←, we often observe rings coexisting with droplets (see Video S2). For even larger effective rates k←, rings break up, leading to the emergence of equally sized droplets (Fig. 5 b; Video S3). Equally sized droplets have been reported in a model using a Ginzburg-Landau type of free energy (40). For fuel partitioning inside, droplets tend to strongly deviate from their spherical shape (see Video S4) and deform into elongated domains reminiscent of stripes in pattern-forming reaction diffusion system (45). Fuel partitioning also affects the boundary in the state diagram beyond which droplets dissolve.
For case 2, characterized by strong A-A homotypic interactions, i.e., eBB = eAA, and weak heterotypic interactions, i.e., eAB/eBB ≪ 1, the behavior in the k→-k← state diagram changes significantly. In contrast to the previous case, for the temperature value chosen (T = 0.525T0), the initial equilibrium state is a droplet composed mainly of A. For fuel partitioning outside, the composition is approximately independent of the rate constants, and we exclusively find single A-rich droplets that coexist with a solvent-rich phase (Fig. 5 h). The rate independence implies that breaking the detailed balance of the rates for the molecular transition does not enable control of phase separation in this setting. This changes if fuel is homogeneously distributed between the inside and outside or if fuel dominantly partitions inside the droplet phase (Fig. 5, i and j). In these cases, increasing the effective forward rate for low effective backward rates leads to a transition from an A-rich droplet to a B-rich droplet. In other words, for a large effective forward rate, this leads to a droplet of switched composition.
Between the two regions in the k→-k← plane corresponding to single droplets of different composition (see Fig. 5, i and j), there is a region where we observe various kinds of patterns. In particular, for a low effective forward rate corresponding to the onset of pattern formation, we typically find that the shape of the A-rich domain deviates significantly from the initial single drop at thermodynamic equilibrium, whereas the composition of such domains remains close to the equilibrium value. Besides rings and equally sized drops, we also find patterns reminiscent of bubbly-phase separation (22) (see Video S5). For higher effective forward rates and low backward rates, we find patterns in which three domains of different compositions stably coexist (see two triangles of different colors in Fig. 5, i and j). Representative stationary patterns composed of three domains are shown in Fig. 5, f and g and Videos S6 and S7. These patterns are spherically symmetric, with a centered droplet enriched in B that is surrounded by a ring of smaller A-rich droplets of equal size. As mentioned above, for even higher effective forward rates, the system settles in a nonequilibrium stationary state composed of a single B-rich droplet.
For high values of k→ and k← in Fig. 5, h–j and in contrast to Fig. 5, c–e, we find that the local composition of each domain is no more governed by the equilibrium values of a ternary mixture undergoing molecular transitions at thermodynamic equilibrium (as discussed in Thermodynamic equilibrium). The reason is that the fuel-mediated molecular transitions (detailed balance broken) dominate the thermodynamic ones and that A-A interactions are sufficiently strong. Surprisingly, the local composition of each domain in the fueled system is almost equal to the equilibrium value of a ternary mixture without molecular transitions. Contrary to the equilibrium system with molecular transitions that is effectively described by only one independent variable (i.e., φtot), a ternary mixture without transitions has two degrees of freedom (i.e., φA and φB); the corresponding phase diagram for a fixed temperature is depicted in Fig. 6 a. For ternary mixtures at thermodynamic equilibrium and parameters corresponding to case 2, there is a triangle in the φA-φB phase diagram for which the vertices of the triangle correspond to the composition of each of the coexisting phases at thermodynamic equilibrium (shaded in orange in Fig. 6 a). In the presence of the detailed-balance-broken molecular transition, the composition in each domain is actually close to the vertices of the equilibrium triangle (see orange circles in Fig. 6 a). Changing the effective forward-backward transition rates amounts to moving the vector corresponding to the average volume fraction along the conserved trajectory φB = φtot − φA. We now set the effective backward rate k← = 0 and k→ = 2 × 103 and consider variations of the effective forward rate induced by the average fuel amount. Specifically, in the absence of fuel ( = 0), an A-rich phase coexists with a solvent-rich phase at thermodynamic equilibrium (blue domain in phase diagram). Intermediate amounts of fuel induce a transition to a nonequilibrium stationary state composed of three coexisting domains (see Fig. 6, b–d for representative stationary states at different fuel levels). For an even larger amount of fuel, the system transits to a nonequilibrium stationary state in which B-rich domains stably coexist with a solvent-rich domain. Although the three-phase-coexistence regime occupies the majority of the φA-φB plane, coexistence of three domains is actually only accessible over a narrow range of fuel values. To see this, compare the orange regions along the conserved trajectory in Fig. 6 a with the orange regions in Fig. 6 e. Thus, when the fuel is changed by an amount larger than this narrow window, the long-time, stationary state of the systems swaps from an A-rich to a B-rich domain. In general, this does not necessarily imply that the initial single droplet swaps its composition without dissolving. However, our results suggest the intriguing possibility that under some conditions, a droplet may be able to change its composition without losing its identity related to the profile of the total volume fraction.
Figure 6.
Breaking the detailed balance of the molecular transition enables controlling the number of distinct phases. (a) Changing fuel in the systems can be illustrated as a trajectory in the ternary phase diagram. Without fuel, the system demixes into two phases whose composition is set by thermodynamic equilibrium; the corresponding average volume fraction is indicated by the circled blue dot. The dashed lines connect the average volume fraction with the values in the respective demixed domains (blue dots). Increasing fuel pushes the average concentration from a region of two-phase coexistence (A and solvent rich, respectively) into a domain in which three phases coexist at equilibrium (orange shaded triangle). Increasing fuel further leads to two domains: A and solvent rich, respectively. Interestingly, the system demixes into domains whose volume fractions are well approximated by the corresponding equilibrium values. (b–d) φA and φB spatial profiles at the stationary state for increasing fuel average volume fraction . For moderate , the system exhibits three-phase coexistence (b), whereas for high values the composition of the dense phase switches (c). (e) The number of phases along with their density and composition as a function of the amount of fuel in the system. The parameters are the same as the lower panel of Fig. 5, with fuel partitioning inside. Scale bars, 20. To see this figure in color, go online.
Active switch of droplet composition
To test the possibility of a single droplet kinetically swapping its composition with time as the fuel is increased, we initially start with an A-rich droplet at thermodynamic equilibrium ( = 0) and gradually increase the average fuel volume fraction until it reaches a plateau value, and then we gradually decrease it (Fig. 7 a). As the average fuel volume fraction is increased, a B-rich domain appears in the center of the initial A-rich droplet. This domain grows and splits into concentric rings enriched in A and B, respectively (Fig. 7 d). The outermost B-rich domain radially propagates inwards and outwards, facilitating the formation of a final B-rich droplet. This inversion occurs approximately concomitant to the average fuel amount exceeding some specific value (Fig. 7 e). Thus, the composition has indeed swapped with time compared to the initial state. As the fuel is gradually decreased, B material is consumed, causing the droplet to shrink and a release of A material near its interface (see Video S8). This process forms an A-rich outer ring that relaxes with time to the spherical shape—the composition has swapped back to its initial value. These results highlight that the composition of a droplet can indeed be controlled and reversibly switched by fuel that breaks the detailed balance of the rates without dissolving and renucleating the droplet at another position.
Figure 7.
Fueling leads to droplet composition switch in time for a wide range of interaction parameters. The active switch in composition is achieved by changing fuel in time according to the protocol in (a). (b) Time traces of φA, φB, and φtot inside the dense phase show an abrupt compositional switch with time, reminiscent of the discontinuous switch observed at thermodynamic equilibrium when quasistatically varying the temperature. (c–e) Snapshots of φA-φB profile evolving in time within the first half of the fueling ramp shown in (a). The rescaled temperature is kept constant to T/T0 = 0.525. (f) We quantify the compositional switch by determining the difference in droplet composition between (1) the stationary state (corresponding to maximal fuel value in a) and (0) the initial equilibrium state: ΔB = with different homotypic and heterotypic interactions. The active conformational switch occurs within a broader range of parameters compared with the equilibrium system referred to as “Thermodynamic switch” (see values marked with white symbols). The parameters are the same as in the lower panel of Fig. 5, with fuel being homogeneous in space, T/T0 = 0.45, and φtot = 0.4, and the white circles were already shown in Fig. 3c. Scale bars, 20. To see this figure in color, go online.
When fuel is injected to the system, the initial A-rich drop becomes B rich. When subsequently fuel is taken out, the droplet switches back to its original composition. For this movie the fuel is homogeneous in space and the effective rates are and .
The control of phase composition by fuel that we report here is, in principle, applicable to a rather broad class of macromolecules. In our model, their interactions are characterized by the values of their homo- and heterotypic interaction parameters. Although the compositional switch controlled by temperature at thermodynamic equilibrium (“thermodynamic switch”) is only accessible within a narrow range of interaction parameters (see zoom in Fig. 3 c), the switching via fuel (“active switch”) is possible in a significantly broader range of interaction parameters, as shown in Fig. 7 f. To characterize this broader parameter range, we calculated the jump height of the compositional change, ΔB = , for various homo- and heterotypic interactions. These results show that for the temperature chosen, the region of the “active switch” is indeed much broader than the region corresponding to the “thermodynamic switch” (Fig. 7 f).
Conclusions
In this work, we derived and analyzed a theory of a three-component mixture composed of a solvent and a macromolecule that can exist in two different molecular states. Our model accounts for phase separation of such macromolecules from the solvent and reversible transitions between the two molecular states. We considered the macromolecules as polymeric molecules and thus described the interactions among all three components by a Flory-Huggins mean-field free energy. We discussed two scenarios that essentially differ with respect to their kinetics of the molecular transition: a thermodynamic system that is fully governed by the minimization of the free energy and a system in which the flux of the molecular transition is influenced by the amount of fuel. The presence of fuel makes the transition flux independent of the model free energy and thus breaks the detailed balance of the rates. In contrast to the thermodynamic system, the resulting stationary states exhibit a nonzero flux.
Our first key finding is that at thermodynamic equilibrium, molecular transitions can control the composition of molecular states in both, the dilute and the dense phase as a function of temperature. Strikingly, for similarly strong self-interactions between each molecular state, we found a discontinuous switch of the dense phase between states in which most macromolecules are either in one or the other state. Our second key finding is that a switch in composition can also be triggered in finite systems composed of macromolecule-rich droplets using fuel, a more likely control pathway in living cells in contrast to temperature. Most strikingly, we predict that such nonthermodynamic, fuel-related control of droplet composition is achievable within a much broader range of polymeric interaction parameters compared with the system at thermodynamic equilibrium. We summarize our findings of a thermodynamic and an active switch in droplet composition in Fig. 8. This broad parameter range renders our reported fuel-controlled, switch-like transition in droplet composition as a highly relevant mechanism to control the functionality of droplet-like condensates in living cells. Most physicochemical properties and likely all biological functionality of intracellular droplets result from the distinct local composition of the dense phase relative to its environment. Hallmark examples are the partitioning of specific molecules into protein-RNA condensates leading to, for example, increased organism fitness (46), controlled assembly hierarchies relevant for a functional tight junction (47), and initiation of transcription and splicing machinery (48). Moreover, the droplet composition also determines the rheological properties of condensates, e.g., its viscoelasticity (49), as well as its slow, glass-like aging kinetics (50). Our reported mechanism for switching droplet composition is easily accessible in parameter space and may represent a versatile and robust kinetic pathway of controlling the droplet-composition-related functionality in living cells.
Figure 8.
Illustration of thermodynamic and active compositional switch pathways. Starting from an A-rich droplet, its composition can be changed in two ways: raising the temperature (thermodynamic switch) or introducing fuel in the system, thus breaking the detailed balance of the rates (active switch). To see this figure in color, go online.
From a physics perspective, our results hint toward an unexplored question, namely what determines the number of coexisting distinct domains away from thermodynamic equilibrium. At thermodynamic equilibrium, the Gibbs phase rule sets an upper bound for the number of coexisting phases. In our specific case of an incompressible ternary mixture, the molecular transition has reduced the degrees of freedom to a single conserved variable. As a result, three-phase coexistence can only occur at a single point or line parameterized by the conserved variable. In contrast, in a ternary mixture without molecular transitions, there can be an extended two-dimensional domain in the phase diagram in which three phases coexist (Fig. 6). Thus, the molecular transition lowered the maximal dimensionality of the domain with three coexisting phases by one. Are there similar upper bounds in nonequilibrium systems, and if there are, can systems away from equilibrium increase or decrease this upper bound? Given our results, breaking the detailed balance of the transition rates, and thus maintaining the system away from thermodynamic equilibrium, releases the system from the Gibbs phase rule and allows the formation of at least three phases and potentially even more.
Author contributions
G.B., O.A.-A., and C.A.W. designed the project and worked out the theory. G.B. solved the equations numerically and illustrated the results. X.Z. developed the code to numerically solve the partial differential equations. G.B., O.A.-A., X.Z., and C.A.W. wrote the manuscript. All authors read and approved the manuscript.
Acknowledgments
We thank J. Bauermann, P. McCall, T. Harmon, L. Hubatsch, and F. Jülicher for fruitful discussions about the topic. Very special thanks go to P. McCall, K. Alameh, J. Bauermann, and D. Zwicker for very helpful feedback on the manuscript. We thank A. Serrão, P. Schwintek, A. Kühnlein, C. Mast, and D. Braun for inspiring discussions on DNA gel formation and application to the origin of life.
O.A.-A. acknowledges funding from the Armando and Maria Jinich postdoctoral fellowship for Mexican citizens. G. Bartolucci and C. Weber acknowledge the SPP 2191 “Molecular Mechanisms of Functional Phase Separation” of the German Science Foundation for financial support.
Editor: Samrat Mukhopadhyay.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.09.036.
Appendix a: Thermodynamic equilibrium
A.1: Conserved quantities and equilibrium condition of the molecular transition
To study the interplay between chemical reactions and phase separation, we consider the T-P-Ni ensemble and three different species, i = A, B, W. At equilibrium, the total number of species s, the number of independent components c, and the number of independent chemical reactions nr are related by (28)
| (16) |
In our case, we consider three species (s = 3), and by means of one chemical reaction (nr = 1; see Fig. 1), the number of independent components gets reduced by one; thus, the dimensionality of the corresponding phase diagram reduces. As the two independent composition variables (c = 2), we consider the quantities conserved in the reaction Fig. 1, namely NW (the number of solvent particles) and Ntot = NA + NB (the total amount of A and B molecules). To find the chemical potentials corresponding to such conserved quantities, we start from the Gibbs free energy G(T, P, Ni) and recall that its variation corresponding to a chemical reaction vanishes at chemical equilibrium:
| (17) |
where μi(T, P, Ni) = . In the specific case of the molecular transition depicted in Fig. 1, this gives
| (18) |
which simplifies the variation of G to
| (19) |
This result shows that at constant temperature and pressure, the Gibbs free energy only depends on the conserved variables, i.e., the total particle number Ntot and the solvent particle number NW. Moreover, we learn that the chemical potentials associated with these conserved quantities, Ntot and NW, are μA and μW, respectively.
To study the system at equilibrium utilizing the familiar common tangent construction (or Maxwell construction), we perform the Legendre transform to the T-V-Ni ensemble and switch to Helmholtz free energy F = G − PV, where the differential reads
| (20) |
In general, this transformation is difficult because the chemical equilibrium relation in Fig. 1 depends on pressure and thus expressing the free energy as a function of the conserved quantity introduces a nontrivial dependence on pressure.
A.2: Equilibrium condition of the molecular transitions in incompressible systems
For systems in which volumes vary only slightly with pressure, we can use incompressibility as a further approximation. Incompressibility is guaranteed if molecular volumes, νi = , are independent of temperature, pressure, and composition. Although incompressibility does not reduce the number of independent variables in the T-P-Ni ensemble, it provides a relation between Ntot, NW, and the volume in the T-V-Ni ensemble and thereby allows us to further reduce the number of independent variables by one.
However, this reduction via incompressibility requires a further condition, namely that molecular volumes are conserved in the molecular transition, Fig. 1. In our case, this corresponds to νA = νB. Thus, we obtain the following incompressibility relation connecting volume and particle numbers, V = NAνA + NBνB + NWνW = NtotνA + NWνW. This relationship states that variations of the total volume are caused by variations of the conserved quantities. Using νAdNtot + νWdNW = dV leads to the following differential of the Helmholtz free energy:
| (21) |
Here, we introduced the exchange chemical potential, defined as
| (22) |
which characterizes the free energy difference for exchanging A with solvent W. The pressure Π = is not the mechanical pressure. This pressure quantifies the response to variations of the total volume while Ntot is kept fixed. Thus, we can think of it as the pressure acting on a semipermeable membrane that separates the system from a solute. This pressure is commonly referred to as osmotic pressure.
Conservation of molecular volumes, νA = νB, allows one to rewrite the chemical equilibrium condition, Eq. 18, in terms of the exchange chemical potentials, leading to Eq. 4 in the main text.
A.3: Free energy density and Maxwell construction
Exploiting the chemical equilibrium condition (Eq. 6) and incompressibility (Eq. 7), we can recast the free energy in Eq. 1a in the form f = f(T, φtot). The existence of multiple solutions of the chemical equilibrium relation in Eq. 6 can lead to the formation of a free energy loop, as displayed in Fig. 9. We also show the common tangent construction (or Maxwell construction), that is used to determine the phase diagrams. For visualization purposes, we display = f − m φtot, where m = .
A.4: Relation between melting and critical temperature
In Fig. 10, we display the influence of the melting temperature Tm on the critical temperature Tc. We can identify two regimes: for melting temperatures lower than the reference B-W binary mixture critical temperature, Tc remains approximately constant and equal to the binary reference value. This is because at the onset of phase separation, most molecules are in the B conformation. For a representative phase diagram, see Fig. 2 b. For melting temperatures higher than the binary mixture critical temperature, the critical temperature Tc starts to deviate from the reference binary value and increases linearly with Tm. This scaling arises because at the onset of phase separation, both A and B conformations are present in the system, and this can lead to an entropic advantage. For a representative phase diagram, see Fig. 2 c. For Tm = (r/2 + kB/sint) T0, the demixing region vanishes.
Figure 10.
Critical temperature Tc as a function of the melting temperature Tm. We can identify two regimes: Tc = constant for low Tm and TcTm for high Tm. To see this figure in color, go online.
Appendix b: Lower transition temperature
Here, we describe the criterion for the existence of the first-order lower transition point. This point appears when the two solutions of the phase equilibrium coincide at φtot = 1, i.e., when the solution becomes a polymer blend composed of A and B only. If the interaction entropies in Eq. 1c are negligible, the critical temperature below which such a mixture demixes reads kBTc = r(eAA + eBB − 2 eAB)/2. Moreover, incompressibility at φtot = 1 reads
| (23) |
and
| (24) |
Because the chemical potential must be equal in the two coexisting phases for the system to phase separate at φtot = 1, the chemical equilibrium relation must have solutions that are symmetric with respect to the exchange φB → φA = 1 − φB, i.e.,
| (25) |
Using ωB − ωB = eint − Tsint, we find for the lower transition temperature
| (26) |
For the phase diagram to be reentrant, this temperature must be positive. Thus, we derive the condition eint > eBB − eAA. Setting eAA = 0 explains the vertical line at the boundary of the “UCST” and “UCST and LDT” regions in Fig. 2 d. We can also derive the condition for which the upper critical point merges with the lower first-order transition point, Tc = Td:
| (27) |
which, again in the case of eAA = eAB = 0, gives the line at the boundary of the “UCST and LDT” and “Mixed” regions in Fig. 2 d.
Appendix c: linear response theory for phase separation with molecular transitions
For isothermal systems, the change of the system entropy, , can be expressed in terms of the integrated rate of change of the total free energy density ftot = f + within the volume V and the free energy flux through the volume boundaries ∂V (51):
| (28) |
Using ∂tftot = /νi and the conservation law ∂tφi = −∂α(ji,ανi) + si, where ji,α is the particle flux and the molecular transition between A and B implies (si = −sj = s), we find for the entropy production
| (29) |
Partial integration leads to
| (30) |
where we have identified the free energy flux . In our special case of molecular transitions conserving the molecular volume, we have νA = νB = ν. Thus, if we write to linear order
| (31a) |
and
| (31b) |
the entropy will increase until the system approaches thermodynamic equilibrium. Here, Λs denotes the mobility for the molecular transition and Λi is the diffusive mobility, and we neglect cross couplings for simplicity. Moreover, we have used νA = νB = ν and absorbed it into the definition of the mobility Λs. The equilibrium conditions are = constant and . Note that for an infinitely large thermodynamic system, we can neglect the spatial derivative in the chemical potentials and express the equilibrium conditions in terms of the exchange chemical potentials = constant and (Eq. 4).
Appendix d: Chemical flux for molecular transitions with broken detailed balance
When the detailed balance of the molecular transition rates is broken and considering a nonlinear dependence of the chemical flux on the chemical potentials, the chemical flux in Eq. 13 can be written as (23,24)
| (32) |
Here, we imposed a chemical potential Δμ 0 that makes sure that the system cannot reach thermodynamic equilibrium with (Eq. 4). For homogeneous systems that obey + Δμ < kBT, the leading order of the chemical flux can be written as
| (33) |
In the following, we impose the chemical potential by a fuel component of volume fraction φF and expand Δμ(φA, φB, φF) to the lowest order (φi ≪ φW):
| (34) |
Defining k→ = Λs and k← = Λs, we get the chemical flux shown in Eq. 13.
Appendix e: Derivation of equilibrium fuel profile
We impose fuel conservation by keeping the spatial average of Eq. 14 fixed and equal to . This implies α + = 1, with being the total average volume fraction of macromolecules (see Eq. 7). In Eq. 14, we notice the coefficient β encodes correlations between fuel φF and total macromolecular material φtot. Maximal spatial correlation between φF and φtot is reached by maximizing β with the constraints α + = 1 and 0 < φF(x) < 1 everywhere in space. This leads to α = 0 and β = 1/. Maximal anticorrelation between φF and φtot is reached by minimizing β with the same constraints, leading to α = −β = 1/(1 − ). Finally, no correlation between φF and φtot, i.e., fuel homogeneously distributed in the system, is achieved for β = 0 and, because of fuel conservation, α = 1. This explains the choices of α and β introduced at the end of Nonequilibrium thermodynamics.
At equilibrium and for the case in which the fuel has only weak effects on the chemical flux (i.e., ), we can make the connection between the coefficients α and β in Eq. 14 and the fuel partitioning even more explicit. We recall the definition of partitioning coefficient of the fuel component, PF = , and of the total concentration, Ptot = . Here, I and II denote the dense and the dilute phase, respectively. We can express the fuel and total volume fractions in I and II, respectively, with the average fuel volume fraction that is considered to be maintained at some constant value, and the conserved total volume fraction :
| (35) |
and
| (36) |
where i = (F, tot}. The partition degree (52) reads
| (37) |
where the phase-separated volume in the limit of dilute fuel is given as
| (38) |
Evaluating Eq. 14 inside and outside the dense phase, we find
| (39) |
and
| (40) |
If the fuel partitions equally strong into both phases (PF = 1, and thus ξF = 1), we get α = 1 and β = 0. Consistently, this corresponds to a homogeneous fuel profile, φF(x) = . For a fixed Ptot > 1, the fuel partition coefficient PF determines the localization of the fuel. In particular, PF > 1 corresponds to fuel colocalizing with the total volume fraction φtot with β > 0. On the contrary, when PF < 1, the fuel and the total volume fraction φtot anti-colocalize with β < 0.
Appendix f: The energy quadratization method
We solve the kinetic Eqs. 9a, 9b, and 13 in two dimensions with periodic boundary conditions. First, we use the energy quadratization method (41, 42, 43) to map the free energy density function in Eq. 1a into a quadratic form
| (41) |
where q = and C is a constant to make sure + ∑i,jΩij(T)φiφj + C > 0. In this work, we use C = 10.
With this new free energy density function and new variable q, we rewrite the chemical potentials in Eq. 10 as
| (42) |
We then use the Crank-Nicolson method in time (second order) to discretize the partial differential equations as follows:
| (43a) |
| (43b) |
and
| (43c) |
where chemical potentials are given as
| (43d) |
We denote the operators
| (44) |
The stabilizing terms λi Δ, i = A, B are added, allowing larger time steps (44). We choose λi = Λi,0, i = A, B for all results shown in this work.
Then, we use the central finite difference method in space to discretize ((43a), (43b), (43c), (43d). The resulting system is linear and can be solved by the generalized minimal residual method (53).
Appendix g: interface tracking and parameter choices
The interfaces between A-rich, B-rich, and solvent-rich domains, shown by dashed red and blue lines in Fig. 5, a and f, are defined as the contour lines of the functions φA(x) and φB(x), respectively, corresponding to the value /2. Here, and correspond to the maximal and the minimal value of φtot(x) for a given time. When, instead, we are interested in identifying φtot-rich and φtot-poor phases, as in Fig. 7 b, without distinguishing between A and B conformations, we simply compare φtot(x) with .
We measure the effective rates in units of tD = L2/DA, which represents the time an A particle takes to diffuse across a length L = 100, where L corresponds to the system size. Moreover, the length scale approximates the droplet interface width (23). In all simulations, we set Λs = 5 .
For the first prototypical parameter set 1, (eAA = 0.2 eBB, eAB = 0), we have chosen κA = κB and κ = 0. For the second prototypical parameter set 2, (eAA = eBB, eAB = 0.2), we have chosen κB = 5 kκA and κ = 2 κA. This choice is motivated by the possibility of having active droplet inversion without dissolving the droplet and subsequently renucleating it. In particular, the hierarchy κB > κ > κA favors wetting of an A-rich layer onto a B-rich droplet. This is important in the second half of the fuel ramp (see Fig. 7 a) to produce A material not too far from the shrinking B-rich droplet (see Video S8).
We obtained solutions to (9a), (9b) for a total time period up to 40 tD. Within this time, the majority of patterns shown in Fig. 5 appeared to be stable and stationary.
Supporting material
References
- 1.Morasch M., Braun D., Mast C.B. Heat-flow-driven oligonucleotide gelation separates single-base differences. Angew. Chem. Int. Ed. Engl. 2016;55:6676–6679. doi: 10.1002/anie.201601886. [DOI] [PubMed] [Google Scholar]
- 2.Nguyen D.T., Saleh O.A. Tuning phase and aging of DNA hydrogels through molecular design. Soft Matter. 2017;13:5421–5427. doi: 10.1039/c7sm00557a. [DOI] [PubMed] [Google Scholar]
- 3.Jeon B.J., Nguyen D.T., et al. Saleh O.A. Salt-dependent properties of a coacervate-like, self-assembled DNA liquid. Soft Matter. 2018;14:7009–7015. doi: 10.1039/c8sm01085d. [DOI] [PubMed] [Google Scholar]
- 4.Broide M.L., Berland C.R., et al. Benedek G.B. Binary-liquid phase separation of lens protein solutions. Proc. Natl. Acad. Sci. USA. 1991;88:5660–5664. doi: 10.1073/pnas.88.13.5660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dumetz A.C., Chockla A.M., et al. Lenhoff A.M. Protein phase behavior in aqueous solutions: crystallization, liquid-liquid phase separation, gels, and aggregates. Biophys. J. 2008;94:570–583. doi: 10.1529/biophysj.107.116152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Patel A., Lee H.O., et al. Alberti S. A liquid-to-solid phase transition of the ALS protein FUS accelerated by disease mutation. Cell. 2015;162:1066–1077. doi: 10.1016/j.cell.2015.07.047. [DOI] [PubMed] [Google Scholar]
- 7.Brangwynne C.P., Eckmann C.R., et al. Hyman A.A. Germline P granules are liquid droplets that localize by controlled dissolution/condensation. Science. 2009;324:1729–1732. doi: 10.1126/science.1172046. [DOI] [PubMed] [Google Scholar]
- 8.Banani S.F., Rice A.M., et al. Rosen M.K. Compositional control of phase-separated cellular bodies. Cell. 2016;166:651–663. doi: 10.1016/j.cell.2016.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wang J., Choi J.M., et al. Hyman A.A. A molecular grammar governing the driving forces for phase separation of prion-like RNA binding proteins. Cell. 2018;174:688–699.e16. doi: 10.1016/j.cell.2018.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Franzmann T.M., Alberti S. Prion-like low-complexity sequences: key regulators of protein solubility and phase behavior. J. Biol. Chem. 2019;294:7128–7136. doi: 10.1074/jbc.TM118.001190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Martin E.W., Holehouse A.S., et al. Mittag T. Valence and patterning of aromatic residues determine the phase behavior of prion-like domains. Science. 2020;367:694–699. doi: 10.1126/science.aaw8653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nott T.J., Petsalaki E., et al. Baldwin A.J. Phase transition of a disordered nuage protein generates environmentally responsive membraneless organelles. Mol. Cell. 2015;57:936–947. doi: 10.1016/j.molcel.2015.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Brady J.P., Farber P.J., et al. Kay L.E. Structural and hydrodynamic properties of an intrinsically disordered region of a germ cell-specific protein on phase separation. Proc. Natl. Acad. Sci. USA. 2017;114:E8194–E8203. doi: 10.1073/pnas.1706197114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Guillén-Boixet J., Kopach A., et al. Franzmann T.M. RNA-induced conformational switching and clustering of G3BP drive stress granule assembly by condensation. Cell. 2020;181:346–361.e17. doi: 10.1016/j.cell.2020.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Monahan Z., Ryan V.H., et al. Fawzi N.L. Phosphorylation of the FUS low-complexity domain disrupts phase separation, aggregation, and toxicity. EMBO J. 2017;36:2951–2967. doi: 10.15252/embj.201696394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Li P., Banjade S., et al. Rosen M.K. Phase transitions in the assembly of multivalent signalling proteins. Nature. 2012;483:336–340. doi: 10.1038/nature10879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Aumiller W.M., Jr., Keating C.D. Phosphorylation-mediated RNA/peptide complex coacervation as a model for intracellular liquid organelles. Nat. Chem. 2016;8:129–137. doi: 10.1038/nchem.2414. [DOI] [PubMed] [Google Scholar]
- 18.Carlson C.R., Asfaha J.B., et al. Morgan D.O. Phosphoregulation of phase separation by the SARS-CoV-2 N protein suggests a biophysical basis for its dual functions. Mol. Cell. 2020;80:1092–1103.e4. doi: 10.1016/j.molcel.2020.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liu Z., Zhang S., et al. Liu C. Hsp27 chaperones FUS phase separation under the modulation of stress-induced phosphorylation. Nat. Struct. Mol. Biol. 2020;27:363–372. doi: 10.1038/s41594-020-0399-3. [DOI] [PubMed] [Google Scholar]
- 20.Glotzer S.C., Stauffer D., Jan N. Monte Carlo simulations of phase separation in chemically reactive binary mixtures. Phys. Rev. Lett. 1994;72:4109–4112. doi: 10.1103/PhysRevLett.72.4109. [DOI] [PubMed] [Google Scholar]
- 21.Lee C.F., Wurtz J.D. Novel physics arising from phase transitions in biology. J. Phys. D Appl. Phys. 2018;52:023001. [Google Scholar]
- 22.Tjhung E., Nardini C., Cates M.E. Cluster phases and bubbly phase separation in active fluids: reversal of the Ostwald process. Phys. Rev. X. 2018;8:031080. [Google Scholar]
- 23.Weber C.A., Zwicker D., et al. Lee C.F. Physics of active emulsions. Rep. Prog. Phys. 2019;82:064601. doi: 10.1088/1361-6633/ab052b. [DOI] [PubMed] [Google Scholar]
- 24.Zwicker D., Seyboldt R., et al. Jülicher F. Growth and division of active droplets provides a model for protocells. Nat. Phys. 2017;13:408–413. [Google Scholar]
- 25.Flory P.J. Thermodynamics of high polymer solutions. J. Chem. Phys. 1942;10:51–61. [Google Scholar]
- 26.Huggins M.L. Thermodynamic properties of solutions of long-chain compounds. Ann. N. Y. Acad. Sci. 1942;43:1–32. [Google Scholar]
- 27.Rubinstein M., Colby R.H. Oxford University Press; Oxford, UK: 2003. Polymer Physics. [Google Scholar]
- 28.Alberty R.A. John Wiley and Sons; Hoboken, NJ: 2003. Thermodynamics of Biochemical Reactions. [Google Scholar]
- 29.Gong P., Szleifer I. Competitive adsorption of model charged proteins: the effect of total charge and charge distribution. J. Colloid Interface Sci. 2004;278:81–90. doi: 10.1016/j.jcis.2004.05.023. [DOI] [PubMed] [Google Scholar]
- 30.Adame-Arana O., Weber C.A., et al. Jülicher F. Liquid phase separation controlled by pH. Biophys. J. 2020;119:1590–1605. doi: 10.1016/j.bpj.2020.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gitterman M. World Scientific; Singapore: 2009. Chemistry Versus Physics: Chemical Reactions Near Critical Points. [Google Scholar]
- 32.Safran S.A. CRC Press; Boca Raton, FL: 2003. Statistical Thermodynamics of Surfaces, Interfaces, and Membrane. [Google Scholar]
- 33.Krüger S., Weber C.A., et al. Jülicher F. Discontinuous switching of position of two coexisting phases. New J. Phys. 2018;20:075009. [Google Scholar]
- 34.Langer J.S., Bar-on M., Miller H.D. New computational method in the theory of spinodal decomposition. Phys. Rev. A. 1975;11:1417–1429. [Google Scholar]
- 35.Jülicher F., Ajdari A., Prost J. Modeling molecular motors. Rev. Mod. Phys. 1997;69:1269–1282. [Google Scholar]
- 36.Tena-Solsona M., Janssen J., et al. Boekhoven J. Accelerated ripening in chemically fueled emulsions. ChemSystemsChem. 2020;3:e2000034. [Google Scholar]
- 37.Donau C., Späth F., et al. Boekhoven J. Active coacervate droplets as a model for membraneless organelles and protocells. Nat. Commun. 2020;11:5167. doi: 10.1038/s41467-020-18815-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nenninger A., Mastroianni G., Mullineaux C.W. Size dependence of protein diffusion in the cytoplasm of Escherichia coli. J. Bacteriol. 2010;192:4535–4540. doi: 10.1128/JB.00284-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hubley M.J., Rosanske R.C., Moerland T.S. Diffusion coefficients of ATP and creatine phosphate in isolated muscle: pulsed gradient 31P NMR of small biological samples. NMR Biomed. 1995;8:72–78. doi: 10.1002/nbm.1940080205. [DOI] [PubMed] [Google Scholar]
- 40.Zwicker D., Hyman A.A., Jülicher F. Suppression of Ostwald ripening in active emulsions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2015;92:012317. doi: 10.1103/PhysRevE.92.012317. [DOI] [PubMed] [Google Scholar]
- 41.Yang X., Zhao J., Wang Q. Numerical approximations for the molecular beam epitaxial growth model based on the invariant energy quadratization method. J. Comput. Phys. 2017;333:104–127. [Google Scholar]
- 42.Zhao J., Yang X., et al. Wang Q. A general strategy for numerical approximations of non-equilibrium models–Part I: Thermodynamical systems. Int. J. Numer. Anal. Model. 2018;15:884–918. [Google Scholar]
- 43.Zhao X., Wang Q. A second order fully-discrete linear energy stable scheme for a binary compressible viscous fluid model. J. Comput. Phys. 2019;395:382–409. [Google Scholar]
- 44.Shen J., Yang X. Numerical approximations of Allen-Cahn and Cahn-Hilliard equations. Discrete Conti. Dyn. Syst. 2010;28:1669–1691. [Google Scholar]
- 45.Frey E., Halatek J., et al. Schwille P. In: Bassereau P., Sens P., editors. Springer; 2018. Protein pattern formation; pp. 229–260. (Physics of Biological Membranes). [Google Scholar]
- 46.Franzmann T.M., Jahnel M., et al. Alberti S. Phase separation of a yeast prion protein promotes cellular fitness. Science. 2018;359:eaao5654. doi: 10.1126/science.aao5654. [DOI] [PubMed] [Google Scholar]
- 47.Beutel O., Maraspini R., et al. Honigmann A. Phase separation of zonula occludens proteins drives formation of tight junctions. Cell. 2019;179:923–936.e11. doi: 10.1016/j.cell.2019.10.011. [DOI] [PubMed] [Google Scholar]
- 48.Guo Y.E., Manteiga J.C., et al. Young R.A. Pol II phosphorylation regulates a switch between transcriptional and splicing condensates. Nature. 2019;572:543–548. doi: 10.1038/s41586-019-1464-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Jawerth L.M., Ijavi M., et al. Fischer-Friedrich E. Salt-dependent rheology and surface tension of protein condensates using optical traps. Phys. Rev. Lett. 2018;121:258101. doi: 10.1103/PhysRevLett.121.258101. [DOI] [PubMed] [Google Scholar]
- 50.Jawerth L., Fischer-Friedrich E., et al. Jülicher F. Protein condensates as aging Maxwell fluids. Science. 2020;370:1317–1323. doi: 10.1126/science.aaw4951. [DOI] [PubMed] [Google Scholar]
- 51.Jülicher F., Prost J. Generic theory of colloidal transport. Eur Phys J E Soft Matter. 2009;29:27–36. doi: 10.1140/epje/i2008-10446-8. [DOI] [PubMed] [Google Scholar]
- 52.Weber C., Michaels T., Mahadevan L. Spatial control of irreversible protein aggregation. eLife. 2019;8:e42315. doi: 10.7554/eLife.42315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Saad Y., Schultz M.H. GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Statist. Comput. 1986;7:856–869. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The initial equilibrium drop evolves into a ring. For this movie the fuel is homogeneous in space and the effective rates are and .
The initial equilibrium drop evolves into a smaller drop surrounded by an outer ring. For this movie the fuel partitions inside the dense phase and the effective rates are and .
The initial equilibrium drop splits up into a ring and multiple drops. The ring gets unstable with time leading to a pattern composed of equally sized drops. For this movie the fuel partitions inside the dense phase and the effective rates are and .
The initial equilibrium drop breaks into smaller fragments, and subsequently, three of them elongate and align, forming a pattern reminiscent of stripes. For this movie the fuel partitions inside the dense phase and the effective rates are and .
For this movie the fuel is homogeneous in space and the effective rates are and .
When fuel is injected to the system, composed initially of an A-rich drop, a B-rich ring forms and then becomes a central drop. The remaining A material forms drops that initially fill the space but, at later times, A-richdroplets far from the central B-rich drop dissolve. For this movie the fuel partitions inside the droplet and the effective rates are and .
When fuel is injected to the system, a B-rich drop forms in the center of the initially A-rich drop. The remaining A material organizes into a ring wetting the B-rich central drop, and an outer layer of multiple drops. For this movie the fuel is homogeneous in space and the effective rates are and .
When fuel is injected to the system, the initial A-rich drop becomes B rich. When subsequently fuel is taken out, the droplet switches back to its original composition. For this movie the fuel is homogeneous in space and the effective rates are and .