What do across-subject analyses really tell us about neural coding?

Abstract

A key challenge in human neuroscience is to gain information about patterns of neural activity using indirect measures. Multivariate pattern analysis methods testing for generalization of information across subjects have been used to support inferences regarding neural coding. One critical assumption of an important class of such methods is that anatomical normalization is suited to align spatially-structured neural patterns across individual brains. We asked whether anatomical normalization is suited for this purpose. If not, what sources of information are such across-subject cross-validated analyses likely to reveal? To investigate these questions, we implemented two-layered feedforward randomly-connected networks. A key feature of these simulations was a gain-field with a spatial structure shared across networks. To investigate whether total-signal imbalances across conditions—e.g. differences in overall activity— affect the observed pattern of results, we manipulated the energy-profile of images conforming to a pre-specified correlation structure. To investigate whether the level of granularity of the data also influences results, we manipulated the density of connections between network layers. Simulations showed that anatomical normalization is unsuited to align neural representations. Pattern similarity-relationships were explained by the observed total-signal imbalances across conditions. Further, we observed that deceptively complex representational structures emerge from arbitrary analysis choices, such as whether the data are mean-subtracted during preprocessing. These simulations also led to testable predictions regarding the distribution of low-level features in images used in recent fMRI studies that relied on leave-one-subject-out pattern analyses. Image analyses broadly confirmed these predictions. Finally, hyperalignment emerged as a principled alternative to test across-subject generalization of spatially-structured information. We illustrate cases in which hyperalignment proved successful, as well as cases in which it only partially recovered the latent correlation structure in the pattern of responses. Our results highlight the need for robust, high-resolution measurements from individual subjects. We also offer a way forward for across-subject analyses. We suggest ways to inform hyperalignment results with estimates of the strength of the signal associated with each condition. Such information can usefully constrain ensuing inferences regarding latent representational structures as well as population tuning dimensions.

Introduction

It is widely believed that canonical brain computations determine the tuning properties of single neurons in cortex (Barlow and Hill, 1963; Carandini and Heeger, 2011; Gross et al., 1972; Hebb, 1949; Hubel and Wiesel, 1962; Logothetis and Sheinberg, 1996; Reynolds and Heeger, 2009; Richmond et al., 1987). In primates, the tuning properties of nearby neurons have been found to correlate in multiple cortical areas, ranging from sensory to high-level association areas (Fujita et al., 1992; Sugase et al., 1999; Tanaka, 1996; Tsunoda et al., 2001). Thus, it can be said that neural correlates of canonical brain computations often manifest in the primate brain at a fine spatial scale. A central goal of human systems neuroscience is therefore to identify fine-scale structure that is similar across individuals. In human systems neuroscience, however, recordings from single neurons in awake, behaving subjects are rare. Hence, to measure brain activity in healthy human subjects, non-invasive methods such as functional magnetic resonance imaging (fMRI) and electro- or magneto-encephalography (EEG/MEG) are typically used. Leave-One-Subject-Out Cross-Validated Representational Similarity Analysis (cvLOSO-RSA)—a method also referred to as Leave-One-Person-Out (LOPO) (Coggan et al., 2019, 2016; Flack et al., 2019; Rice et al., 2014; Watson et al., 2017a, 2017b, 2016a, 2016b, 2014; Weibert et al., 2018)—is a Multivariate Pattern Analysis (MVPA) method that attempts to identify spatially structured representations that are shared across individuals. It is one instructive instance of an across-subject analysis method recently used to motivate inferences regarding neural coding in humans. If this method were effective at achieving this goal, it would be of fundamental importance to the study of human cognition and sensory processing. However, we show here that cvLOSO-RSA is not suited to this purpose. We develop a theoretical framework for evaluating shared spatially-structured representations and global signals across subjects. We find that approaches that rely on spatial normalization are inadequate for the purpose of harnessing spatially-structured information, and therefore likely misleading when it comes to drawing conclusions that depend on such organization. We describe the behavior of across-subject analyses, such as cvLOSO-RSA, as well as standard within-subject correlation-based analysis approaches to RSA, to various forms of signal imbalance across conditions—e.g., due to low-level visual features (O’Toole et al., 2005) or otherwise endogenous sources of signal imbalance among experimental conditions. A key tension addressed in this manuscript thus relates to fundamental differences that exist between within-subject and across-subject tests of generalization. We do not address differences between leave-one-subject-out and leave-two (or more)-subjects-out cross-validation. We also offer a path forward. We use our framework to demonstrate that it is theoretically possible to identify fine-scale structure in populations of subjects by aligning data in a high-dimensional space using hyperalignment (Haxby et al. 2011). Moreover, we go beyond standard approaches to hyperalignment by identifying constraints that can further the ability of this method to draw correct inferences about representational similarity structures as well as population tuning dimensions.

How to meaningfully align voxels across subjects—e.g., to identify shared spatially structured representations—is not a trivial question. Is it even possible to establish such form of feature correspondence across brains of different subjects? Simply averaging voxel responses across subjects without meaningfully aligning voxels might be expected to lead to uninterpretable results, resulting in blurry patterns at best, or cases where patterns cancel each other out at worst. For this reason, MVPA normally proceeds by constructing classification models based on data extracted from each brain separately. Along similar lines, RSA proceeds by computing a measure of similarity between empirical Similarity Matrices (eSMs) and model Similarity Matrices (mSMs) separately for each subject¹. In a subsequent stage, RSA aggregates single-subject representational similarity measures and finally draws inferences regarding neural coding on the basis of these aggregate summary statistics. In this sense, RSA aims to solve—or more precisely, circumvent—the feature-correspondence problem by matching similarity matrices instead of brain patterns themselves.

In contrast to standard MVPA methods, a less frequent but potentially powerful analysis approach aims to detect shared large-scale patterns of neural activity that generalize across subjects (Mourão-Miranda et al., 2005; Poldrack et al., 2009; Shinkareva et al., 2008). The latter approach can allow a researcher to conclude that specific tasks lead to characteristic patterns of activity across cortex that are consistent across the population. Unlike the more conventional methods that test within-subject generalization, however, methods that seek across-subject generalization do not normally claim to harness fine-scale patterns of information. Accordingly, investigators using these methods typically target brain structures discernible at a macroscopic level of organization.

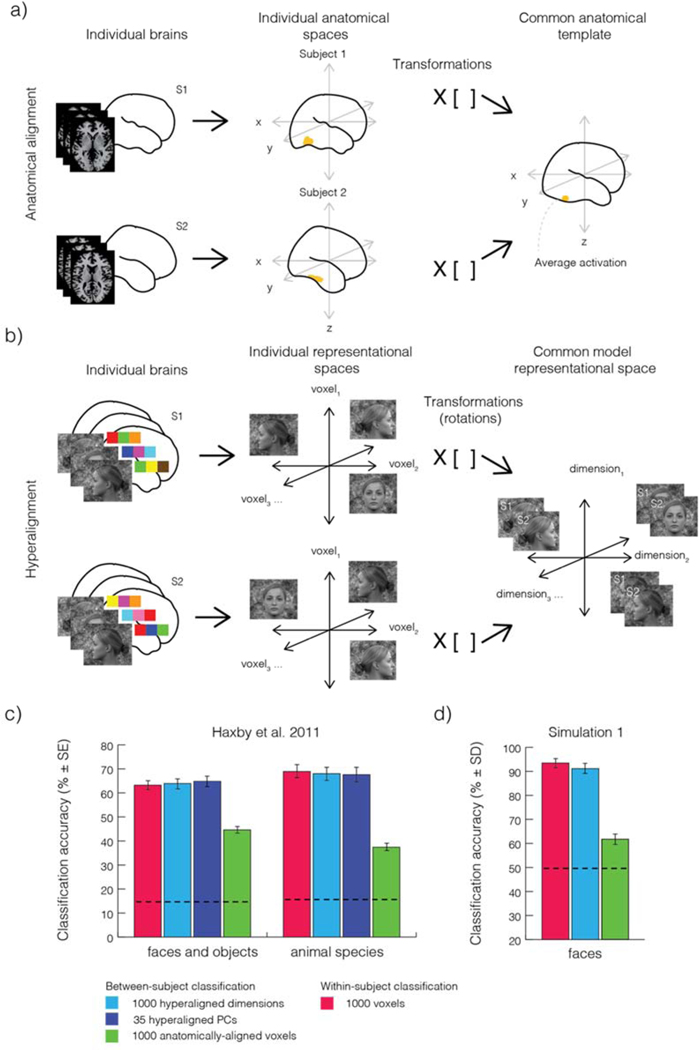
Making inferences about neural coding implicating fine-scale patterns of information by testing for generalization of brain patterns across individuals might seem impossible, given the well documented anatomical variability within healthy populations (e.g., Frost and Goebel, 2013; Zhen et al., 2017, 2015). In fact, several studies have provided empirical evidence that spatially-structured information generalizes poorly across subjects if spatial normalization is used to bring activation patterns from different subjects into correspondence (Clithero et al., 2011; Cox and Savoy, 2003; Haxby et al., 2011). Haxby et al., however, showed that a novel approach to “hyperalign” brain activation patterns across subjects, could, in principle, enable researchers to harness fine-scale structure while testing for generalization across subjects. The hyperalignment method depends on harnessing within-subject multivariate pattern structure that would be missed had the data been aligned anatomically across subjects. Instead, hyperalignment finds the linear transformation (orthogonal rotation, reflection, translation, and scaling) that optimally maps response patterns in one subject to those observed in a different subject. The goal of hyperalignment is thus to find a linear transformation that minimizes across subjects the sum of squared distances between the endpoints of the pattern-vectors associated with a set of experimental conditions. This procedure can enable the detection of fine-scale patterns of information across subjects. Intriguingly, Haxby et al. demonstrated that hyperalignment results in a dramatic increase in classification performance of brain activity patterns across subjects relative to anatomical alignment (see Figure 1c). Haxby et al. also found that generalization of information across subjects was as accurate as that observed within subjects. Given the demonstrated improvements in cross-subject decoding, we argue here that it may be feasible to study fine-scale activation patterns of activity across subjects after hyperalignment, but that such analyses are not possible after anatomical alignment alone.

Figure 1. Anatomical alignment, hyperalignment, and leave-one-subject-out generalization performance.

a) Anatomical alignment. Left, axial slices from two subjects, s1 and s2, demonstrating idiosyncratic anatomical features such as size, shape, and orientation. Middle, brains of these two subjects before anatomical normalization. Right, transformation matrix, T, bring points from s1 and s2 into optimal correspondence with an anatomical template. The matrix, T, implements a non-linear transformation to accommodate differences in brain anatomy across subjects. b) Hyperalignment matches individual subjects’ voxel spaces within a common high-dimensional space. An orthogonal matrix for a rigid rotation is found that minimizes the Euclidean distances between two sets of labeled vectors. Each labeled vector depicted in the center panel corresponds to the brain activation pattern associated with each condition. After applying the rotation matrix, T, voxels in the common space no longer correspond to single voxels in each subjects’ native space. c) Results of multivariate pattern analyses of two fMRI experiments from Haxby et al. (2011). Stimulus category information was decoded from anatomically-aligned data (green bars). Anatomical alignment, however, yields decoding accuracies substantially lower than within-subject decoding (red bars) and hyperaligned data (light and dark blue bars). d) Simulation 1. We hypothesized that systematic modulations in signal strength of different experimental conditions might explain above-chance decoding from anatomically aligned data. We tested this hypothesis with computer simulations. Classification of activation patterns across two-layered randomly connected networks was found to be significantly above chance (Simulation 1, green bars). Panel b was drawn after Figure 1a in Guntupalli et al. (2016). Results in panel c were plotted based on values in Haxby et al (2011).

We develop a theoretical framework for evaluating the impact of shared spatially-structured as well as global signals across subjects. We find that approaches that rely on spatial normalization are inadequate to harness spatially-structured information, and can therefore be fundamentally misleading. The problems with the method are expected to be maximal when it comes to detect finer-scale² neural patterns of activity. We exemplify our findings regarding the behavior of across-subject analyses with a concrete instance from the face recognition literature. We show how Leave-One-Subject-Out cross-validated RSA (cvLOSO-RSA) might lead to erroneous conclusions about neural coding. We also demonstrate the theoretical limits of what the method can show. Further, we demonstrate how global-signals can manifest in unexpected ways that might be easily mistaken as evidence of a fine-scale organization. Finally, offering a path forward, we show that fine-scale patterns may be studied across subjects when using hyperalignment, and we propose ways in which to refine the efficacy of such analyses.

This article is structured as follows. In the first part we rely on computer simulations to address two unresolved issues suggested by the original hyperalignment study (Haxby et al. (2011). First, although across-subject generalization of information was found by Haxby et al. to be strongly reduced after anatomical normalization compared with hyperalignment, it was still significantly larger than zero. We have identified a parsimonious and biologically plausible source of information that accounts for this observation. We used simulated data to test the hypothesis that global signals explain this observation. Second, we explored the impact of global-signals on cvLOSO pattern analyses. In particular, we studied the behavior of RSA analyses applied to simulated response patterns estimated by combining information from multiple subjects without hyperalignment (see Methods section for details). We suspected that global signals might lead after cvLOSO-RSA to conclusions regarding neural coding that would not hold for any one of the subjects when separately analyzed. If correct, such observation would indicate that such cvLOSO analyses are invalid.

In the second part of this paper, we demonstrate with a specific example drawn from the face recognition literature that across-subject RSA using anatomical normalization—as implemented by cvLOSO-RSA—can lead to erroneous conclusions regarding neural coding. We relied on a combination of computer simulations and the systematic resampling of images used in a recent publication. On this basis, we examine a recent study that used cvLOSO-RSA to test for mirror-symmetric coding of facial identity information in human face-responsive areas (Flack et al., 2019). We show that these results can be parsimoniously accounted for by biases at the level of experimental design, calling into question the conclusions of Flack et al. (2019).

Finally, in the third section we demonstrate that hyperalignment can, under some conditions, harness fine-scale information in analyses that test for generalization across subjects. We present two examples in which classic hyperalignment provides an improved, however systematically distorted, perspective of the latent correlation structure of the data. We suggest specific constraints to the hyperalignment method that can improve its ability to support inferences about representational format, population tuning dimensions, as well as the tuning properties of indirectly measured neural populations.

We conclude by broadly discussing the consequences of our findings for the interpretation of pattern analyses and suggest complementary analyses that can help to achieve a less biased characterization of neural representations.

Terminology

In this article, we consider the properties of (i) withholding data from one subject for model testing during cross-validation, and (ii) using data from all but the left-out subject during MVPA model training, as essential properties of what we refer throughout this manuscript as Leave-One-Subject-Out cross-validation (cvLOSO) (for a primer, see Varoquaux et al., 2017). Clearly, cvLOSO is a special case of leave-one-out cross-validation. During leave-one-out cross-validation, data from each relevant data partition (e.g., runs, blocks, and even possibly single events) are exhaustively left out for validation, one at the time, while data from the remaining data partitions are used to train, for instance, a classification model. In a similar fashion, during leave-one-out cross-validation the training and validation data partitions can be used to compute an empirical Similarity Matrix (eSM)—or, in other words, a Representational Dissimilarity Matrix (RDM) when using Kriegeskorte et al.’s (2008) terminology. Such eSMs can be used as basis either for ensuing classification analyses (e.g., Haxby et al., 2001) or RSA-like analyses (Aguirre, 2007; Edelman et al., 1998; Kiani et al., 2007; Kriegeskorte et al., 2008; Op de Beeck et al., 2001).

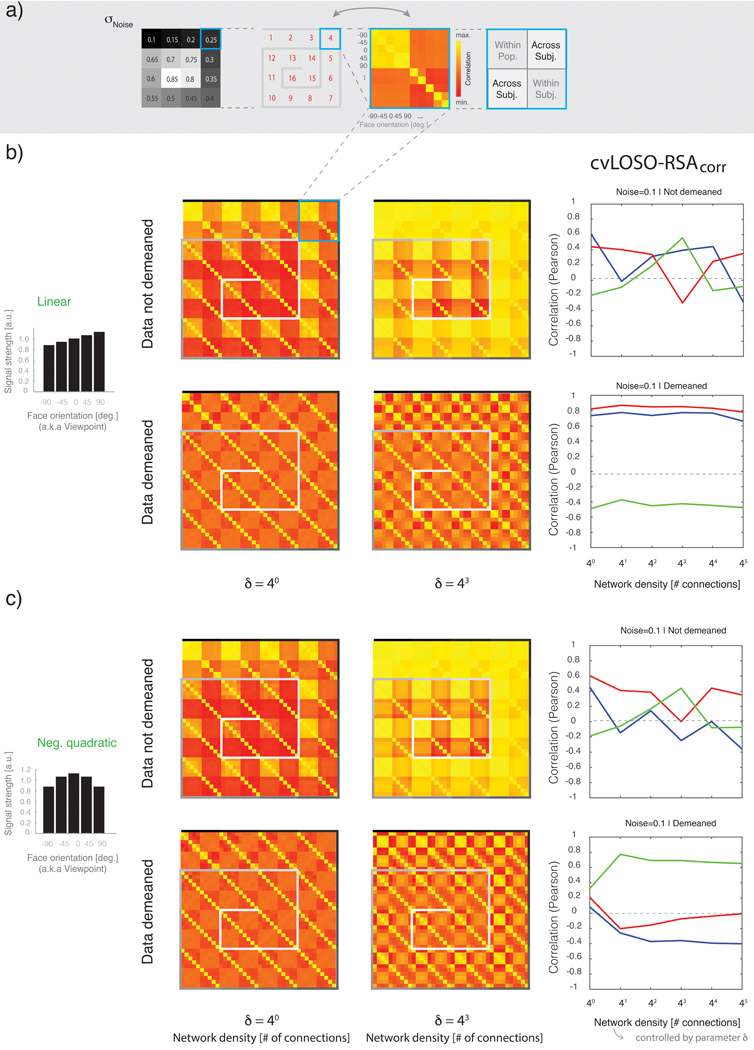
Specifically, the method termed Leave-One-Person-Out (LOPO) (Rice et al. 2014; Watson et al. 2014), and to which we refer here as cvLOSO-RSA_corr, is a sub-type of LOSO cross-validation (CV). In each CV fold, patterns associated with each of the relevant experimental conditions in the left-out subject are correlated with the average brain patterns for each condition estimated from the data from the remaining “left-in” subjects (see Figure 2). Crucially, this method assumes a meaningful common “population response” is estimated in each CV fold by computing across subjects, and for each condition, the average regression weight (or parameter estimate, or beta) in each voxel in a particular ROI. As illustrated in Figure 1, cvLOSO-RSA_corr relies on anatomical normalization to bring the brains of different subjects into correspondence before conducting pattern-correlation analyses³.

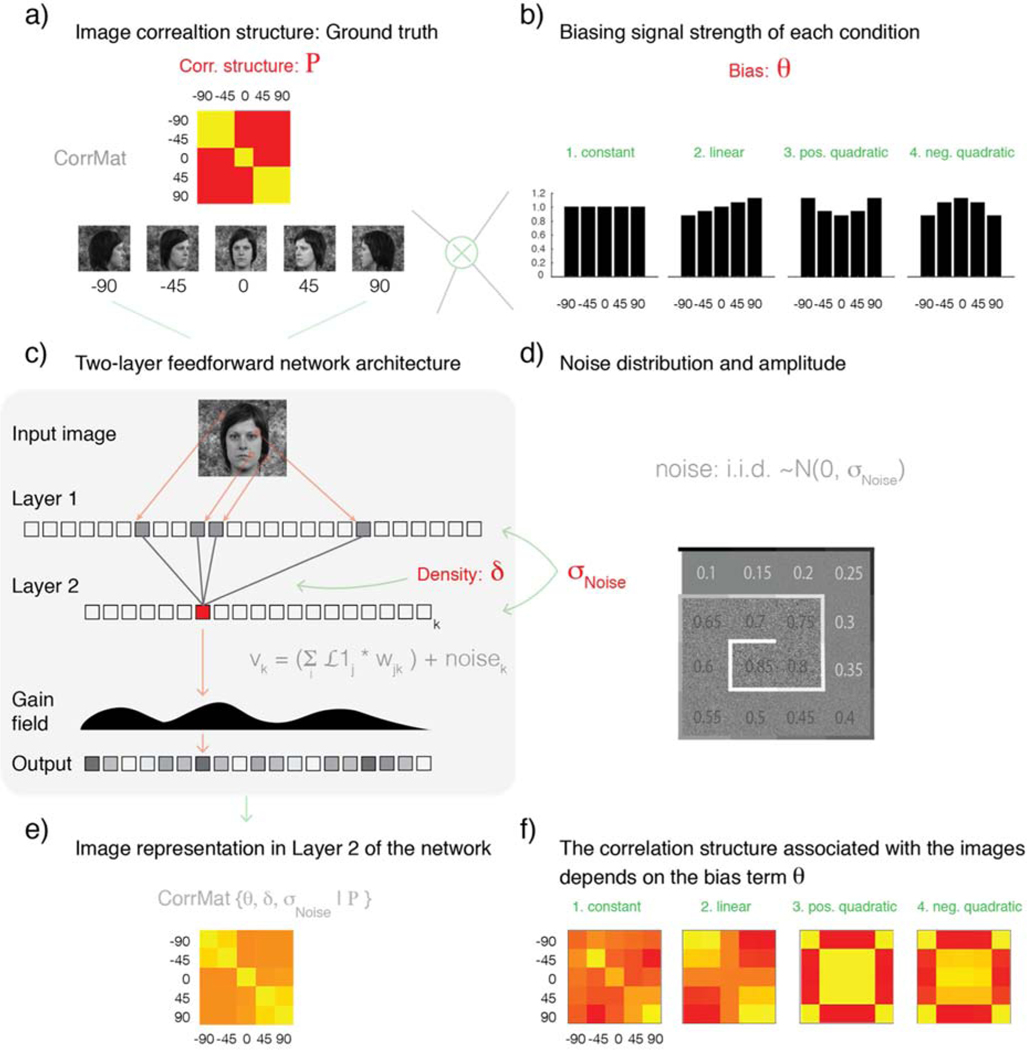
Figure 2. Simulation flowchart: activation patterns associated with five input images are obtained from parametrically specified, two-layered, randomly-connected networks.

a) Five images conforming to the correlation structure P (Rho) are fed into a two-layered network. The image-vectors associated with each of the five conditions are modulated by means of element-wise multiplication with one of four possible weighting vectors. b) The precise form of signal bias imposed by each weighting vector is controlled by parameter θ, which indexes one of four possible bias profiles: (1) flat (no bias), (2) linearly increasing, (3) positive quadratic, and (4) negative quadratic. The set of five basis image-vectors (shown in a) after modulation by one of the four described bias profiles are subsequently given as input to a two-layer network. c) Network architecture and parametrization. Each network is specified by two parameters: Density (δ) and noise standard deviation (σ_Noise). Parameter (δ) controls the number of randomly-specified feed-forward connections received by each Layer 2 unit. Layer 1 instantiates a retinotopic representation such that each unit’s activation corresponds to the luminance-level observed in one specific image location. Each Layer-2 unit in turn pools activity over its input units. The model further considers the addition of randomly generated noise before passing the observed Layer 2 activations through a gain field. The gain field aims to capture the fact that different measurement channels naturally exhibit different gains, and these gain changes are likely to correlate across subjects after anatomical alignment (see text for details). d) Parameter σ_Noise controls the amplitude of the i.i.d. Gaussian noise G(0, σ_Noise) added to each network unit. The 16 possible simulated noise-levels are represented by means of an inward-spiraling palette. e). Each parameter combination of noise and bias specified a network sub-variant. For each network sub-variant, patterns associated with each condition were simulated. These patterns were pairwise correlated to construct correlation matrices. As shown in panel f, the empirically observed correlation structure associated with the basis images conforming to correlation structure P varies substantially as a function of the signal bias profile.

In sum, and to be clear, throughout this manuscript we use the term cvLOSO-RSA_corr to denote the analysis method Andrews et. al. call “LOPO”. For clarity, the term RSA is accompanied by a sub-script indicating the similarity measure used to compute each eSM. The subscript “corr” indicates that RSA was conducted using the Pearson correlation as measure of pattern similarity. Alternative similarity measures include the Euclidean metric (RSA_Euc) and cosine similarity (RSA_cos).

Other MVPA analyses, such as Support-Vector Classification (SVC) (Cortes and Vapnik, 1995), also often rely on leave-one-out cross-validation to test for generalization of information across folds (but see Varoquaux, 2018). The terminology adopted here can be conveniently extended to refer to distinct SVC analysis flavors. For instance, to indicate that generalization is being tested across subjects (cvLOSO-SVC), or else within subjects; e.g., using Leave-One-Run-Out cross-validated SVC (cvLORO-SVC). A noteworthy variant of cvLORO classification is Haxby et al.’s split-halves correlation-based one nearest-neighbor classifier (Haxby et al., 2001; also see Haxby, 2012). In this case, the number of data partitions = 2 (even and odd runs), and consequently only one cross-validation fold per subject is possible.

A final clarification of perhaps unusual terminology used in this manuscript regards the term “total-signal”. We prefer the former term over arguably related and more common terms such as “regional average” or “overall activity” for one fundamental reason. While the average response of a region of interest may be zero, the length of the vector associated with the voxels that comprise that ROI may well exhibit a length larger than zero. In a multivariate sense, we propose here, it is the length of such fMRI pattern-vectors what matters, and not only the “regional average”. Moreover, while an ROI may exhibit the same regional average for each of a set of experimental conditions, it may simultaneously exhibit significantly different vector lengths. This would be an instance where balance is observed with regards to the regional average, albeit imbalance with regards to the total-signal observed across conditions. To clarify the matter, we suggest that fMRI pattern-vector length and direction can be conceptualized in analogy to the amplitude and phase of a sinusoidal function. Clearly, two sinusoids can exhibit distinct phases while exhibiting the same amplitude (or identical power in the case of more complex signals)—and vice versa. Evidently, similarity with regards to total-signal (“amplitude”) does not imply similarity with regards to spatial structure (“phase”).

Methods

A. Two-layer feedforward network architecture and implementation

We relied on computer simulations to investigate the relative impact of total-signal effects (of which global signals are a specific instance) and finer-scale patterns on cvLOSO-RSA analyses. The first goal of the simulations was to identify sources of residual information observed when cvLOSO-RSA analyses are implemented on fMRI data in which subjects are anatomically aligned using standard spatial normalization procedures, as opposed to aligning the data using hyperalignment (Haxby et al., 2011, 2014). We implemented a two-layer feedforward network in which the first layer instantiated a retinotopic representation of the stimulus and the second layer instantiated a high-order representation with large receptive fields that pooled activity over many nodes in the input layer (Figure 2). To explore the behavior of cvLOSO-RSA when a systematic mapping of network units does not exist across subjects, for each simulated subject (here instantiated by a network), we randomly generated a set of connections from each unit in Layer 2 to a subset of units in Layer 1. Connections between layers were unidirectional in that they propagated information from Layer 1 onto Layer 2.

The number of connections received by each Layer 2 unit was controlled by a density parameter, δ, which was parametrically varied across different instantiations of the model. The density parameter ranged between 4⁰ and 4⁵ (4ⁿ, where n = 0, 1, …, 5) (Figure 2) and served to parametrically control the level of granularity of the simulated data (Ramírez, 2018). When the density of connections is high, many connections exist between units in the 1^st and 2^nd layers, and pooling of responses from units in the 1^st layer by units of the 2^nd layer would result in decreased representational resolution of units in Layer 2 compared to units in Layer 1 (Kamitani and Sawahata, 2010; Kamitani and Tong, 2005; Op de Beeck, 2010a, 2010b). This is the case because averaging—like downsampling—is a non-invertible transformation and information is lost when data is subjected to such transformations. Therefore, the influence of fine-scale sources of information on pattern analyses is expected to become negligible as the granularity of the data degrades. The latter could occur, for example, due to a coarser sampling resolution of the underlying neural populations (i.e., large voxel sizes), or a lack of spatial clustering of neurons exhibiting similar tuning functions. Either of these possibilities could degrade the quality of the distinctions supported by Layer 2 units.

The simulation included two additional parameters. Parameter σ_Noise controlled the noise level, which was assumed to occur spontaneously and to be i.i.d. according to a zero-centered Gaussian distribution N(0, σ_Noise) across units (range: [σ_Noise = 0.1 to 0.85, step = 0.05]). Parameter θ controlled the form of the signal-level imbalances observed across the simulated experimental conditions. Signal-level imbalances across conditions simulated here included (i) linear, as well as (ii) negative- and (iii) positive-quadratic trends (see Figure 2b). We chose these three specific forms of signal imbalance across conditions because they have been previously shown to influence inferences regarding neural coding (Ramírez, 2018, 2017). We also included a case in which the signal was balanced across conditions (Figure 2b). The bias parameter was introduced to simulate the impact of global signals, which are different across conditions but shared across voxels. Imbalances in the signal can arise from either intrinsic or extrinsic factors. For example, an extrinsic source of imbalance would be differences in the mean luminance, or contrast, of the stimuli. An intrinsic imbalance could arise from an internally biased representation in which a specific stimulus class, or range of a dimension within a stimulus class, are overrepresented in the population (Ramírez et al., 2014). Such imbalances in the observed signal levels could also result from cognitive processes, such as attention (Boynton, 2011; Kastner and Ungerleider, 2000). The noise, density, and bias parameters enabled us to test the hypothesis that both the signal-to-noise ratio (SNR) and the level of granularity of the data affect the ability of cvLOSO-RSA analyses to recover ground truth in the simulation.

Gain field:

A key feature of the simulation was the inclusion of a gain field, which was assumed to have a spatial structure that was shared across subjects. The gain field was specified as a random vector in the interval [0 1]. The gain-field vector had the same number of entries as units in Layer 2 and was used to modulate responses in Layer 2 by means of element-wise multiplication. The structure of the gain field was defined to be identical across subjects. This feature of the simulation was intended to model a scenario in which fine-scale response patterns are uncorrelated across subjects, yet a gain field that is shared across subjects would introduce systematic co-variation among the measured activation patterns (see Figure 2c). Such covariation is indistinguishable from a fine-scale representation and could be easily mistaken as such by cvLOSO-RSA analyses.

Images:

To produce images (n = 5) according to the desired correlation structure P, we first generated three random vectors [1 × 10,000] using Matlab’s random number generator function (rand.m). This function pseudo-randomly samples real numbers uniformly distributed in the interval [0, 1]. We defined conditions 1 and 2, as well 4 and 5, to be identical. This led to a set of vectors M closely conforming to P where each column of M corresponds to a 2D image reshaped into the form of a vector (see Figure 2a).

$$P=\left[\begin{array}{ccccc}1& 1& 0& 0& 0\\ 1& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 1\\ 0& 0& 0& 1& 1\end{array}\right]$$

All vectors were specified to have the same mean and variance (μ = 0.5, σ² = 0.08). In this balanced signal-level case, the variance-covariance structure of the image-vectors required only scaling to effectively conform to their pre-specified correlation structure. To simulate the impact of total-signal imbalances across conditions, the basis set of vectors in M were multiplied by weighting vectors. The parameter θ specified an index (1, 2, 3, or 4), which in turn served to specify for each simulation one of four possible weighting vectors: v_Constant = [1, 1, 1, 1, 1], v_Linear = [0.8750, 0.9375, 1.0000, 1.0625, 1.1250], v_PosQuad = [1.1250, 0.9375, 0.8750, 0.9375, 1.1250], and v_NegQuad = [0.8750, 1.0625, 1.1250, 1.0625, 0.8750]. This modulation aims to capture, in a simplified way, the impact of image contrast on pattern analyses. The impact of total-signal imbalances across conditions was also explored by means of adding—instead of multiplying—to each column of M the corresponding value in the pertinent weighting vector. This second form of (additive) modulation captures the influence of global signal imbalances across conditions. The only difference between the negative and positive quadratic weighting vectors was the sign of the quadratic equation used to specify them. The linear weighting vector was specified with a linear equation. Weighting of the columns of M by the scalars in each weighting vector (one scalar per image), by definition preserved the correlation structure P of the images but changed their variance-covariance matrix. This occurs because scalar multiplication changes the sum of squares of each vector. Constant offsets of image-vectors also preserve their pre-specified correlation structure, P. The generated vectors when reshaped to form matrices can be naturally interpreted as grayscale images. In this way, a basis set of images was generated for each of the three broad categories of simulations considered here.

To summarize, we implemented two-layer, randomly-connected feedforward networks to investigate the impact of three key parameters on the outcome of cvLOSO-RSA_corr analyses: (1) density (δ) of connections from the first (input) layer to the second “high-level” layer, (2) form of the global-signal biases (θ) observed across experimental conditions, and (3) the strength of noise (σ_Noise) sources assumed to reside within each network unit. We expected, based on prior research, that these parameters would influence the correlation structure of simulated fMRI patterns. Each simulation instantiated one specific level of density, noise, and bias (Figure 2e). Simulated data from 20 random two-layer networks (emulating 20 experimental subjects) was thus passed through a multiplicative gain field that was shared across subjects. The signal component of the simulated data corresponds to the observed activation levels, concatenated across units of each layer, associated with each of the five simulated images fed as input to each network. The noise component corresponded to i.i.d. noise ~N(0,I), where 0 is the zero vector [5 × 1] and I the identity matrix [5 × 5]. Noise-level was modulated by scalar multiplication of the entries in the diagonal of I by σ_Noise. Simulations 2–5, which are reported in Figures 4–7, followed this general procedure. Simulations 1 and 6, further explained below, included an additional hyperalignment stage.

Please note that the networks implemented here have not been trained (e.g., by back-propagation) to perform a specific computation, as is the case in machine-learning applications (e.g. face recognition). The networks pass the pixel intensity value received as input on to the next layer according to a set of randomly specified connections. Our goal is to explore what happens when patterns of activity defined across a set of network-units are correlated across different randomly-connected networks. This is relevant from a neuroscientific perspective in that it enables us to explore the behavior of pattern analyses such as cvLOSO-RSA_corr that test for generalization of activity patterns across brains of different subjects.

B. Simulations 1 and 6: Hyperalignment

Simulations involving hyperalignment followed the approach described above in sub-section A with regards to network details and the data-generation process. Before MVPA of the simulated data, however, the response patterns associated with each of the 20 randomly connected networks (each simulating one experimental subject) were hyperaligned prior to performing pattern analyses. The hyperalignment algorithm, as introduced by Haxby et al. (2011), consists of the iterative application of procrustes transformations to the data (scaling, translation, rotation and reflection) with the purpose of minimizing the sum of squares of the differences observed between the response vectors associated with each of the stimulus classes across subjects.⁴ Hyperalignment thus corresponds to a set of linear transformations, iteratively applied to the data, with the goal of aligning multivariate response patterns across subjects. To ensure independence of the data used to estimate hyperalignment parameters and that used for pattern analyses, two independent sessions were generated for each simulated subject. For each session, independent noise was added to the generated brain patterns as described above—i.e., before passing activation patterns through the gain field. A second layer of i.i.d. noise distributed according to N(0, σ_Noise2) was added after passing responses through the gain field. Simulation 1, reported in Figure 1, as well as Simulation 6, reported in Figure 10, involved this hyperalignment stage.

C. Linear Support-Vector Classification analyses

Within-subject cross-validated SVC analyses:

(i). cvLORO-SVC.

Response patterns associated with each of the five simulated experimental conditions were generated as described in sub-section A (above) for 10 independent runs. The bias parameter θ was set to 3 (positive quadratic), the density parameter δ set to 1, and the noise amplitude set to 0.1. For this analysis, the network connectivity pattern was kept constant across runs and the noise independently generated for each run. This enabled us to implement non-circular analyses emulating within-subject decoding as implemented by Haxby et al. (2011). Specifically, the data for the 10 simulated runs were subjected to 10-fold Leave-One-Run-Out Cross-Validated Support-Vector Classification (cvLORO-SVC) using pairwise classifiers (linear kernel and default C parameter = 1) using the LIBSVM library (Chang and Lin, 2011) (https://www.csie.ntu.edu.tw/~cjlin/libsvm). All unique pairwise combinations were classified, and decoding accuracies associated with each pair of conditions obtained for each data fold.

Across-subject cross-validated SVC analyses:

(ii). cvLOSO-SVC.

Response patterns for 20 independent simulated subjects were generated as described above in subsection A. cvLOSO-SVC analyses (linear kernel, C = 1) were conducted, as in the within-subject analysis, but using as input to classifiers the response patterns for multiple simulated subjects instead of multiple runs for one subject.

(iii). Hyperaligned cvLOSO-SVC.

Analyses proceeded as the cvLOSO-SVC analysis described immediately above, except that data were hyperaligned before Support Vector Classification (SVC). For hyperalignment, we relied on the method proposed in Haxby et al. (2011). Data generated for each of the 20 randomly connected networks were hyperaligned to a common reference space. In short, one transformation matrix was obtained per subject by finding the Procrustes transformation (Schönemann, 1966) that minimized the sum of squared errors between response patterns of each subject in the derived common reference space. The MATLAB_2019b function procrustes.m was used to solve this minimization problem and obtain the transformation matrices. To assure independence of classification results from the hyperalignment procedure itself, two independent runs were generated for each randomly-connected two-layer feedforward network. Data from the first run were thus used for hyperalignment, while data from the second run were hyperaligned using the transformation matrices obtained in the previous analysis step. The last step in this analysis was to subject the hyperaligned data to cvLOSO-SVC analyses as described above in subsection (ii).

D. cvLOSO-RSA_corr analysis pipeline

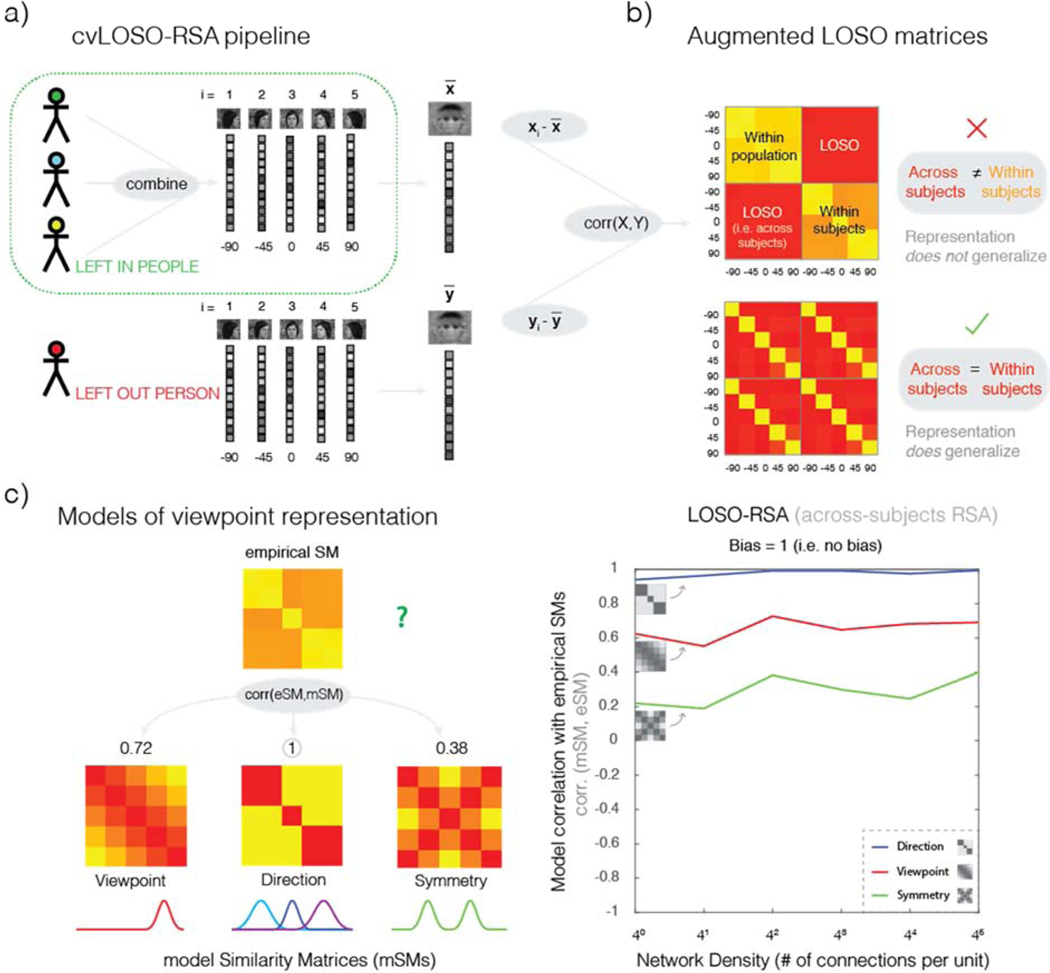
The cvLOSO-RSA_corr method (a.k.a. “LOPO”) has been previously described in detail (cf. Rice et al., 2014). We provide a summary of the steps used to implement this method (Figure 3a).

Figure 3. Leave-One-Subject-Out Cross-Validated Representational Similarity Analysis.

a) cvLOSO-RSA_corr analysis pipeline. In each iteration, one participant’s responses to each of five stimulus classes are left out and the remaining participants’ responses for each condition averaged. Population and single participant data are separately demeaned by subtracting the average response across conditions from that observed in each condition. The response patterns associated with each stimulus class in the population are then exhaustively pairwise correlated with the response patterns of each stimulus class in the left-out participant. This procedure leads to one LOSO matrix, as depicted in panel b. The number of leave-one-subject-out iterations equals the number of subjects. b) Augmented LOSO matrices. Each augmented LOSO matrix (here, 10 by 10) is comprised of 4 concatenated sub-matrices (here, 5 by 5). In both agLOSO matrices shown here, the LOSO quadrants (upper right and lower left quadrants) convey the results of across-subject analyses, as specified in a. The upper-left “within population” quadrant correlates the population pattern-estimates with themselves. The lower-right “within subject” quadrant correlates the left-out subject pattern-estimates with themselves. Top row, the displayed agLOSO matrix illustrates the case where single-subject patterns do not generalize across the population. In contrast, the agLOSO matrix shown below illustrates a case where the representation does generalize across the population. c) LOSO-RSA analysis. Correlation matrices associated with simulated data are correlated with three different models of viewpoint representation: Viewpoint, Direction, and Symmetry. Each model is encoded in the form of a model Similarity Matrix (mSM). The empirical similarity matrix (eSM) shown in c best correlates with the Direction mSM. Right, Representational Similarity Analysis. Each mSM (Direction, Viewpoint, and Symmetry) is correlated with eSMs computed on the basis of simulated data corresponding to different levels of network density (see Methods). Red line, Viewpoint model; blue line, Direction model; green line, Symmetry model. Model correlations with simulated data are shown on the y-axis. In this example, the Direction model best correlates with the data across all density levels.

Step 1: FMRI data for each subject is preprocessed using standard methods, normalized into MNI anatomical space, and resliced.

Step 2: The common response, for example, over 19 out of 20 subjects is estimated. cvLOSO-RSA_corr uses the FSL (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki) FLAME algorithm for this purpose, which implements a mixed-effects model to estimate in each voxel the mean response across subjects for each condition as well as fixed-effects and group-level random-effects variance components. Only the estimates of activation-levels associated with each condition, however, are used in ensuing RSA-like analyses. The unique response of the left-out subject is estimated using standard fixed-effects general linear modelling methods.

Step 3: Parameter estimates for each condition for the population and the left-out subject, for each independently localized ROI, are concatenated to form pattern vectors, one pattern associated with each relevant experimental condition.

Step 4: The mean response across conditions for the population is then subtracted from that observed for each condition (i.e., cocktail demeaning).⁵ The same is done for the left-out subject.

Step 5: RSA is conducted on the demeaned pattern vectors for the current cross-validation fold. cvLOSO-RSA_corr uses the Pearson correlation as measure of pairwise pattern similarity. The ensuing Pearson correlations are then Fisher-Z transformed.

Step 6: Steps 2–5 are iterated once for each of the 20 possible cross-validation folds, in the case where we have 20 subjects, and the Fisher Z-transformed correlation matrices for each cvLOSO-RSA_corr iteration saved. Finally, these similarity matrices are also averaged across folds for visualization.

Step 7: RSA analyses are implemented on the cvLOSO empirical similarity matrices (cvLOSO-eSMs) obtained for each region of interest. Statistical analyses proceed by evaluating the statistical significance of the correspondence observed between the similarity matrices from each ROI and the relevant model similarity matrices.

E. Representational Similarity Analyses (RSA)

RSA is explained in detail in Kriegeskorte et al. (2008) and Nili et al. (2014). This analysis method seeks to characterize the form of a neural representation based on the (dis)similarity structure of brain or behavioral measures. In the case of brain measures, the response patterns associated with a set of experimental conditions of interest are conceptualized as points in a high-dimensional space. Some measure of distance (or similarity)—e.g. linear (Pearson) correlations—are used to define the pairwise distances (or similarities) of each pair of experimental conditions. These distances are then summarized in the form of a Similarity Matrix (or Dissimilarity Matrix, depending on the researchers’ preferences) believed to characterize the information encoded in that brain area. Such empirically estimated similarity matrices are finally compared to candidate representational models. Each candidate model must therefore be translated into a matrix specifying the pairwise similarities expected given each of these models. In this paper we consider three candidate representational schemes of face-orientation information (see Figure 3c): (i) Direction, (ii) Viewpoint, and (iii) Mirror-symmetry. Throughout this paper the correlation structure of the images is known a priori—in all simulations ground-truth corresponds to the correlation structure associated with the Direction model. Consequently, if cvLOSO-RSA_corr were successful as means to conduct model selection, it would need to always favor the Direction model over the Viewpoint and Symmetry models.

F. Image resampling, descriptive analyses, and similarity analyses

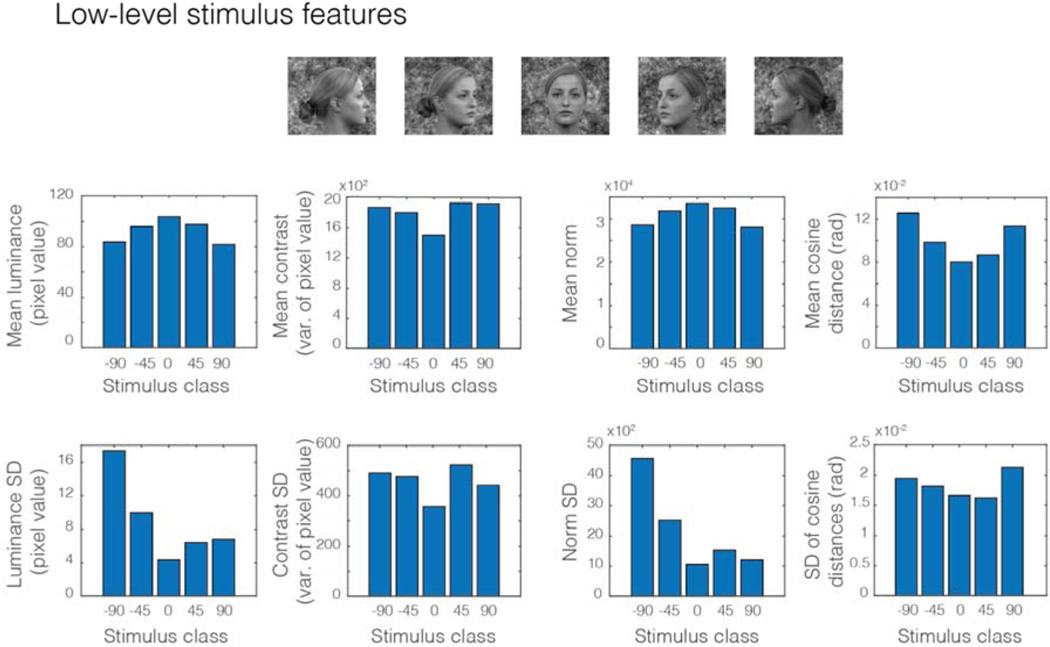
To test the predictions of the model presented above regarding possible low-level feature biases expected to lead to artefactual observations of “mirror symmetry” with the cvLOSO-RSA_corr method, we analyzed the images shown in Figure 1 of Flack et al. (2019). We used the images with the highest possible resolution made available by the publisher. These images were generated by Flack et al. by adding 1/f noise to the background of face images obtained from the Radboud Face Database (Langner et al., 2010).

Descriptive statistics

We computed the mean luminance, contrast (estimated by the variance), and norm of the grayscale images shown in Figure 8. Because five face identities were shown, each from five vantage points (−90°, −45°, 0°, 45°, 90°), we calculated averages of these low-level features across the five identities for each of the five face orientations. This is reasonable because the experimental design used by the authors was a block design where the same five identities, shown always in the same pose, were presented within a block of trials (see Flack et al. 2019 for details).

We also computed the standard deviation of the variances associated with the images pertaining to each stimulus class. Class was defined by the orientation in-depth (or viewpoint) of a face. The standard deviation of the variances within each condition is an indicator of the consistency of the images with regards to stimulus contrast. In turn, the average pairwise cosine distance (and its standard deviation) for the images associated with each stimulus class is a good index of the consistency of the structure of the images within each class, regardless of contrast.

Classes of stimuli that exhibit large variability in their cosine distances are expected to lead to less adaptation in a retinotopic representation if the eyes are always fixed at the center point of the screen. Paradoxically, they would also be expected to result in less consistent response patterns in a retinotopic representation, and therefore reduced signal strength from a multivariate perspective in the context of a blocked design. The influence of these factors (mean luminance, contrast, and image structure consistency) on GLM parameter estimates for a set of experimental conditions in a block design is not trivial. Conditions with larger contrast levels may lead to stronger responses in visual cortex (Avidan et al., 2002; Boynton et al., 1999; Gardner et al., 2005; Olman et al., 2003). In turn, while mean luminance levels are also expected to modulate the strength of responses in visual cortex (Kinoshita and Komatsu, 2001), the direction and nature of such modulations is not as straightforward (Boyaci et al., 2007; Yeh et al., 2009). Conditions that exhibit larger image variability may be also expected to result in a less distinctive—i.e. blurred—brain response patterns, and therefore exhibit less power when considering distributed response patterns as vectors.

Iterative local averaging of face images from an image database

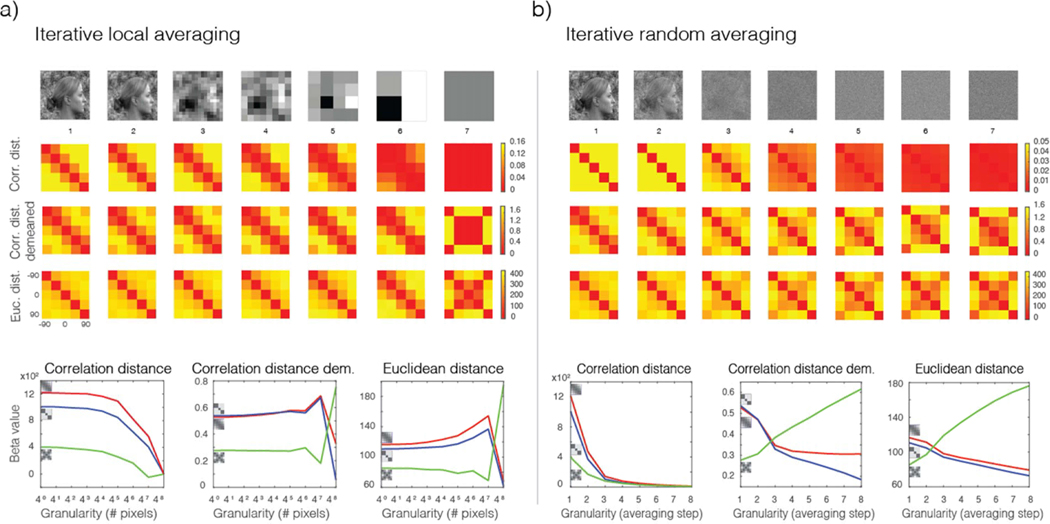
The similarity structure of stimuli included in visual experiments is often used as proxy for the way in which low-level features are represented in retinotopic visual cortex (e.g., Rice et al., 2014; Weibert et al., 2018). The reasoning is that if responses in a visual area other than V1 do not exhibit the similarity structure observed when analyzing the images directly, then this difference in “representational structure” cannot be attributed to low-level image features alone. Here, we show that unless the level of granularity of the analyzed neuro-images is known, the logic behind this analysis is questionable and the results are inconclusive. To show this, we analyzed the stimulus images we obtained from the Flack et al. (2019) paper. In order to instantiate different levels of granularity, the images were subjected to iterative local averaging before being fed into the network. This was accomplished by an algorithm in which in each local averaging step pixels falling within cells of increasing size were averaged. The size of these cells specified the size of the “grain” of the image, and therefore the level of granularity. We proceeded with the local-averaging analysis in powers of 4^p (p = 0, 1, 2, 3, 4, 5). In each consecutive local-averaging step, each new picture-element was obtained by first averaging the values of four contiguous pixels from the previous step. The rectangular source images were trimmed (± 1 pixel along the horizontal and vertical directions) and resized to fill a square matrix with dimensions fitting the maximal relevant power of 4. Dissimilarity matrices according to the normalized Euclidean and correlation distances were subsequently computed for each level of granularity. The latter was done both before and after cocktail demeaning of the images (see Figure 9a). Cocktail demeaning refers to the operation of subtracting the mean pattern (or image) across a set of conditions from that associated with each condition. Then, RSA (Kriegeskorte et al., 2008) was conducted on the distance matrices associated with the images and the relevant model templates. To perform RSA, model templates need to convey the dissimilarity structure expected for the data given each candidate representational scheme. Here, model templates correspond to those considered by Ramírez et al. (2014): Viewpoint (or face orientation) and Symmetry, supplemented by Flack et al.’s (2019) Direction model. The representational similarity between each model and empirical dissimilarity matrix was estimated by the regression coefficient (or beta) observed between these matrices, treated as vectors. Regression coefficients were estimated using the Matlab function glmfit with default parameters.

Iterative random averaging of face images from an image database

To complement the iterative local averaging analysis described above, we implemented a variant of this analysis where instead of averaging nearby pixels in each step, we averaged randomly selected pixels over the whole image. The purpose of randomly selecting pixels was to gradually destroy the statistical structure of the images, which by default included a strong anticorrelation between the left and right profile views of each face due to the inclusion of a bright face and darker hair (see Figure 9b). The aim of this analysis was to isolate the effects on the image distance matrices of signal strength, on the one hand, and the statistical structure of the images proper, on the other. Comparing RSA analyses where the spatial structure of the images is destroyed to analyses where this structure is preserved is a test for the impact of spatial structure and signal energy.

Results

We relied on computer simulations to investigate the relative influence of spatially-structured and total-signal effects on pattern analysis methods that use anatomical normalization to realign the data from multiple subjects. We suspected that total-signal effects (of which global signal effects are one specific instance) might account for the impoverished, albeit statistically significant, residual information detected by Haxby et al. (2011) after anatomical realignment (Figure 1c). Specifically, Haxby et al. found that decoding accuracies were substantially higher after hyperalignment than after anatomical alignment. We reasoned that finer-scale structure (i.e., sources of information other than total-signal effects) might account for the similar decoding accuracies observed when testing classifiers within- and across-subjects after hyperalignment (see Introduction for details). To disentangle the impact of total-signal and spatially-structured effects, we implemented two-layer randomly-connected feedforward networks (Figure 2). Because the connections observed across layers were idiosyncratic to each subject, such that the ordering was random across subjects, spatially-structured information cannot generalize across subjects. In contrast, information originating in total-signal effects will generalize across subjects, even if the underlying representations are not meaningfully aligned across subjects. Clearly, it would be inappropriate to characterize patterns of brain activity as having only two spatial scales, namely, fine and coarse. There is likely a broad spectrum of spatial scales when it comes to neural processing. In the context of our simulations, however, it is possible to distinguish total-signal effects and spatially-structured effects (regardless of their spatial scale). This is the case because we parametrically manipulate the strength of the signal associated with each condition, networks are randomly connected, and generalization tested across networks.

It is also fundamental to understand that aspects of the system being measured—total-signal imbalances across conditions, network density—and properties of the measurement process—gain fields, measurement scale—jointly determine the statistical properties of the data. The data are then analyzed using a specific set of data-analysis methods. Below, we investigate with simulations how properties of the measured system (randomly-connected networks) and properties of the measurement process (a shared gain field) interact with data transformations such as data-demeaning that may (or may not) be part of the specific analysis method under scrutiny—e.g., cvLOSO-RSA_corr (see Methods, section D for details).

1. cvLOSO-SVC is sensitive to total-signal energy

Decoding analyses with linear support-vector machines (SVMs) (Chang and Lin, 2011) (https://www.csie.ntu.edu.tw/~cjlin/libsvm) of data generated with Simulation 1 revealed that total-energy modulations were sufficient to achieve above-chance decoding even when fine-scale structure could not be exploited by the classification procedure (Figure 1d). As previously observed by Haxby et al., we also found that decoding performance within subjects significantly outperformed decoding analyses across subjects. Again, as originally observed by Haxby and colleagues, we also found that implementing hyperalignment before conducting SVM analyses led to substantially increased classification accuracies. Indeed, after hyperalignment, cvLOSO-SVC—which tests generalization of information across subjects—led to accuracies comparable to those observed when generalization was tested within subjects using cvLORO-SVC.

We reasoned that, if total-signal differences across conditions are sufficient to account for the residual effects described by Haxby et al. (2011) after anatomically aligning data from multiple subjects, then the similarity structure of the data revealed by cvLOSO-RSA_corr should predominantly reflect total-signal effects. Importantly, cvLOSO-RSA_corr should not reflect the fine-scale structure of the input images fed to a network. In this sense, the empirically observed similarity structure of the data would be expected to critically depend on the effectiveness of the method used to realign spatially-structured representations. If cvLOSO-RSA_corr is, as we suspect, unable to meaningfully align response patterns across subjects (as suggested by theoretical arguments and evidence by Cox and Savoy, 2003 and Haxby et al., 2011), then the results of cvLOSO-RSA_corr should be fully determined by total-signal effects—and not by spatially-structured information. We tested these predictions by implementing RSA analyses on data generated with Simulations 2–5. See Figure 2 for simulation structure, Methods sub-sections A and B for details, Figure 3 for a description of cvLOSO-RSA_corr, and Figures 4–7 for simulation results.

2. cvLOSO-RSA is insensitive to spatially-structured patterns

To explore the impact of total-signal effects and spatially-structured activation patterns on RSA analyses, we compared the outcome of RSA on simulated datasets (where ground-truth is known) as a function of the density (δ) of connections between network layers as well as the strength of the noise (σ_Noise) added in each simulation (see Methods). We expected that (i) when the density increases, and the impact of spatially-structured representations on pattern analyses therefore decreases, then, pattern analysis results would be increasingly determined by total-signal imbalances observed across experimental conditions. We further expected that (ii) the outcome of RSA analyses would reveal an interaction of network density (here controlled by parameter δ, which ranged between 4⁰ and 4⁵ connections between Layer 1 and Layer 2 units) by demeaning (yes, no), and that this interaction (iii) would not occur in the absence of a gain field with a structure that is shared across subjects. In other words, we expected that the use of data demeaning, an integral step of the cvLOSO-RSA_corr analysis pipeline, would influence the outcome and interpretation of such analyses. Furthermore, we expected that the extent of such impact would depend on the density- and noise-controlling parameters.

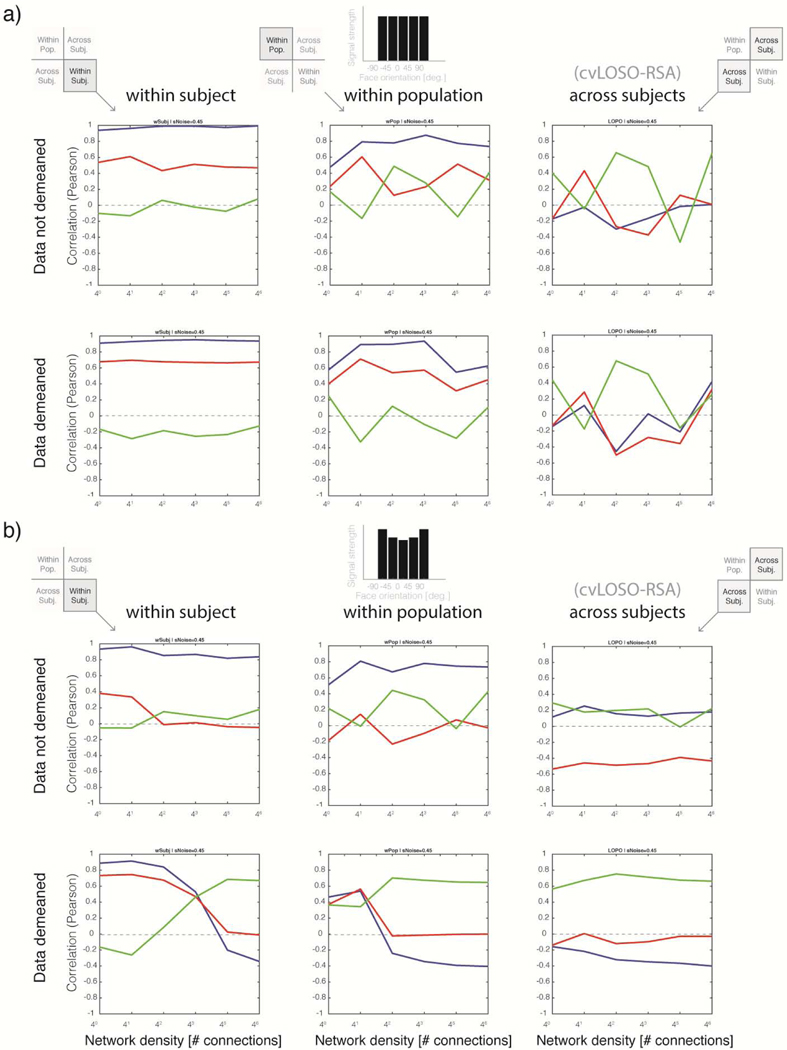
Simulation 2, which prescribed balanced signal-levels across conditions (see Figure 4b), demonstrates that when the density of network connections is low (and the granularity of the data in our simulations is therefore high) and the data are not demeaned, across-subject analyses provide no evidence of a structure that generalizes across subjects (Figure 4b). This is the case regardless of the simulated noise level. Because frequentist statistical analyses do not enable one to prove the null, however, we cannot conclude that a common structure does not actually exist. Fortunately, we know here that this corresponds to the ground truth; there is no spatially-structured pattern of activation here that is shared across subjects. A more informative analysis scrutinizing the within-subject quadrant of the augmented LOSO matrix (agLOSO-eSM_corr), nonetheless, would make it hard to miss the fact that the population does actually share a common representational structure—although it does not share common patterns of activation. This latent correlation structure is described by matrix P shown in Figure 2a. Because network units here by definition do not meaningfully align across subjects, this shared underlying correlation structure would be completely missed if a researcher were to only examine the LOSO sub-field of the augmented LOSO-eSM. Precisely this procedure is performed routinely by users of the cvLOSO-RSA_corr method.

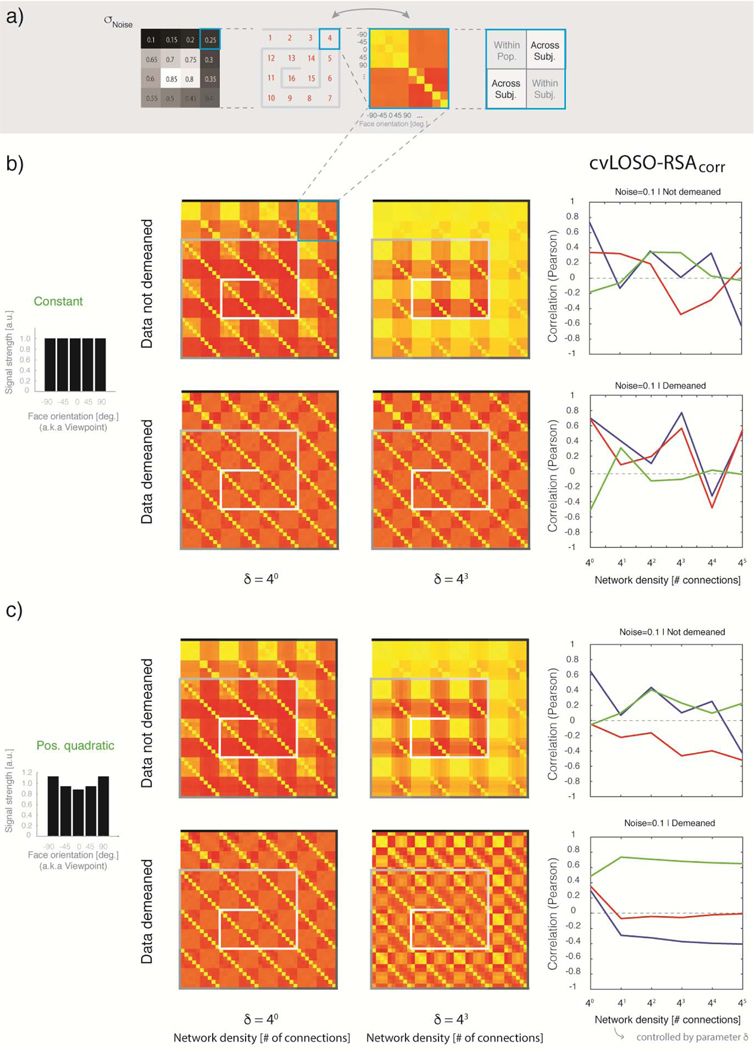
Figure 4. The impact of total-signal imbalances on cvLOSO-RSA_corr: balanced and positive quadratic bias profiles.

a) Graphic explanation of the organization of the shell-plots shown in panels b and c. Each shell-plot summarizes simulation results for one network-density level and consists of 16 inward-spirally concatenated augmented LOSO matrices; one per noise level (cf. Figure 2d). As an example, the 4^th agLOSO matrix, associated with σ_Noise = 0.25, is shown within a light-blue square. Each agLOSO matrix consists of four quadrants; within-population, within-subject, and across-subject (cf. Figure 3b for details). Each quadrant is in turn populated by a 5 by 5 empirical similarity matrix indexed by experimental condition—here, facial-viewpoint [−90° to +90°, step 45°]. b) Balanced signal case: The five bars shown at the top of panel a are of unit height, and indicate that the basis images given as input to each network were unmodulated (cf. Figure 2b). Total-signal levels are therefore balanced across conditions in this case. Twenty randomly connected two-layer networks were generated per simulation. Responses associated with each of the five basis images were then obtained for each instantiated network. The simulation results shown here correspond to 16 noise-levels (σ_Noise = 0.1 to 0.85, step = 0.05) and two density levels (δ = 4⁰ and 4³). Results are shown without demeaning (two shell-plots in the top row) and after demeaning of the simulated activation patterns (two shell-plots in the bottom row). Each shell-plot (40 by 40) is constructed by inward-spirally concatenating sixteen agLOSO matrices (10 × 10). The top-leftmost agLOSO matrix corresponds to the lowest simulated noise level (σ_Noise = 0.1). The remaining 15 levels of noise proceed clockwise, bending inwards, until reaching the cul-de-sac located towards the center of each shell-plot. The grayscale shade of the lines abutting each agLOSO matrix codes the level of noise associated with each simulation. A mini shell-plot including each greyscale shade and its associated noise magnitude is shown in panel a, leftmost column. The plots in the right-most column summarize cvLOSO-RSA_corr results as a function of network density for σ_Noise = 0.1. As explained in Figure 3c, the blue line shows RSA results for the Direction “model” (here, ground truth), red for the Viewpoint “model”, and green for the Symmetry “model”. cvLOSO-RSA_corr results proved unstable—regardless of noise level—and failed to recover ground-truth. In turn, the within-subject quadrant clearly resembles the true underlying correlation structure P (cf. Figure 2a) when noise-levels are low. b) Positive-quadratic bias: The layout of panel b is exactly as panel a. The only difference is that simulation results here correspond to the bias parameter θ = 3, prescribing a positive quadratic multiplicative modulation of the basis image-vectors. cvLOSO-RSA_corr leads to artefacts that might be easily mistaken for evidence of a spatially-structured representation that generalizes across the population. The form of this artefact—only observed when the data were demeaned—always agrees with the Symmetric model. However, we know here that ground-truth corresponds to the Direction model.

2.1. The augmented LOSO matrix: a useful tool for the interpretation of cvLOSO analyses

We use the term “augmented LOSO matrix” to denote the 10 by 10 correlation matrix that includes standard LOSO matrices on the 1^st and 3^rd quadrants, the average of all within-subject matrices in the 4^th quadrant, and the average of matrices associated with the population patterns in the 2^nd quadrant (Figure 3). Each quadrant corresponds here to a 5 by 5 matrix indexed by the same set of experimental conditions. cvLOSO-RSA_corr analyses usually ignore information in the 2^nd and 4^th quadrants of the augmented LOSO matrices, which we have reported here. Users of cvLOSO-RSA_corr only consider information in the 1^st and 3^rd quadrants, which are redundant because the augmented matrix is symmetrical about the main diagonal. For this reason, we recommend that LOSO-like analyses should routinely report the full augmented LOSO correlation matrix, instead of reporting a reduced portion of it (e.g., Rice et al., 2014; Flack et al. 2019). Above all, we encourage researchers to report and compare the within-subject and across-subject sub-fields of the augmented LOSO matrix, which more completely conveys the structure of the data. Failure to meaningfully realign patterns across subjects might manifest as a lack of structure, or even worse, an aberrant structure, on the LOSO sub-field of each agLOSO matrix. For examples of such aberrant structure see Figures 4–5. Crucially, inspection of the agLOSO matrix might help identify potential sources of concern. For example, in order to demonstrate that a representation generalizes across a population, it is critical to show consistency between correlation structures in the across-subject and within-subject quadrants, or to rule out that total-signal effects completely account for the results.

Figure 5. The impact of total-signal imbalances on cvLOSO-RSA_corr: linear and negative-quadratic bias profiles.

a) Graphic explanation of the organization of the shell-plots shown in panels b and c. Each shell-plot summarizes simulation results for one network-density level and consists of 16 inward-spirally concatenated augmented LOSO matrices; one per noise level (see Figure 4a for details). b) Simulation results for linear bias. Layout same as Figure 4b, except simulation results correspond to bias parameter θ = 2, prescribing linear modulation in the basis image-vectors. Top row, RSA without demeaning exhibits two prominent features. First, the within-subject and within population-quadrants behave similar to the no-bias case in Figure 4b. The most striking results are observed after data-demeaning; most prominently for high densities. Rightmost column summarizes cvLOSO-RSA_corr results across density levels. Note the negative bias always penalizing the mirror-symmetric model (in green), regardless of noise-level and density. Although ground truth coincides with the Direction model (blue line), the Viewpoint model (in red) always exhibits higher correlation to the data than the Direction model (in blue). c) Simulation results for negative quadratic bias. The observed pattern of results is very similar to that observed for the positive quadratic case. This demonstrates that both negative and positive quadratic imbalances in signal strength can lead to artefacts that might be erroneously attributed to a fine-scale mirror-symmetric code that generalizes across subjects.

3. RSA is sensitive to total-signal imbalances across experimental conditions

Next, we wondered to what degree and in what manner RSA analyses depend on the bias and density parameters considered in Simulations 2–5—viz. θ and δ. These simulations served to confirm that even when focusing on the within-subject sub-field of the augmented LOSO matrix, signal-to-noise imbalances across conditions have a non-negligible effect on RSA results. This applies both to standard within-subject as well as across-subject RSA_corr analyses. As shown in Figure 4c, when the network density and noise-levels are high, RSA results in our simulations proved to be practically determined by the SNR-profile observed across conditions, and not by the latent correlation structure P. Especially noteworthy, qualitatively similar effects were observed when simulating both additive and multiplicative biases. These results confirm the findings in Ramírez et al. (2014), demonstrating the nature and potential severity of SNR-effects even on standard within-subject RSA analyses. See Supplementary Figure 1 for an extended illustration of such SNR artifacts on RSA results.

4. Data demeaning misrepresents total-signal imbalances across conditions as putative fine-scale structure that generalizes across subjects

The influence of SNR-effects is a theme of general importance for the interpretation of pattern analyses and has consequently received considerable attention in recent years (Diedrichsen et al., 2011; Ramírez, 2018; Ramírez et al., 2014; Smith et al., 2011). However, similarly important is considering the potentially catastrophic impact of data demeaning (Garrido et al., 2013; Ramírez, 2017) on RSA analyses, including cvLOSO-RSA_corr. These effects are mathematically related to those described in the field of functional connectivity when evaluating the impact of global-signal regression (Fox et al., 2009; Gotts et al., 2020, 2013; Murphy et al., 2009; Saad et al., 2012). Here, we directly address the influence of data demeaning on LOPO analyses. How, precisely, do artefacts due to data demeaning manifest at the level of LOSO pattern analyses? To answer this question, we explored the impact of data demeaning on cvLOSO-RSA_corr. We compared agLOSO matrices before and after demeaning that were derived from two-layer randomly connected networks. In more detail, we compared the outcome of this method when (i) including and (ii) excluding from the analysis pipeline the data-demeaning step that is integral to cvLOSO-RSA (see Methods and Figure 3a). Any differences, ceteris paribus, observed between analyses with and without demeaning would demonstrate the impact of this transformation on cvLOSO-RSA results.

Figures 4c and 5b–c, which report the results of Simulations 3–5, all include some form of total-signal imbalance across conditions. These simulations consistently demonstrate that the correlation structure of the augmented LOSO matrices, and, of particular importance here, of the across-subject quadrants of these agLOSO matrices, dramatically changes after data demeaning. Compare the top and bottom rows, for example, in Figure 4c. These markedly inconsistent agLOSO matrices correspond to RSA results for exactly the same simulations albeit before (top row) and after (below) demeaning. As further shown in Figures 4–7, both positive-quadratic and negative-quadratic signal-level imbalances across conditions led to marked changes in the correlation structure of the data that could be easily mistaken as evidence of a fine-scale mirror-symmetrically tuned representation that generalizes across the population. Fortunately, we know that this deviates from ground truth. The simulated data reflects a representation that coincides in correlation structure with the Direction model.

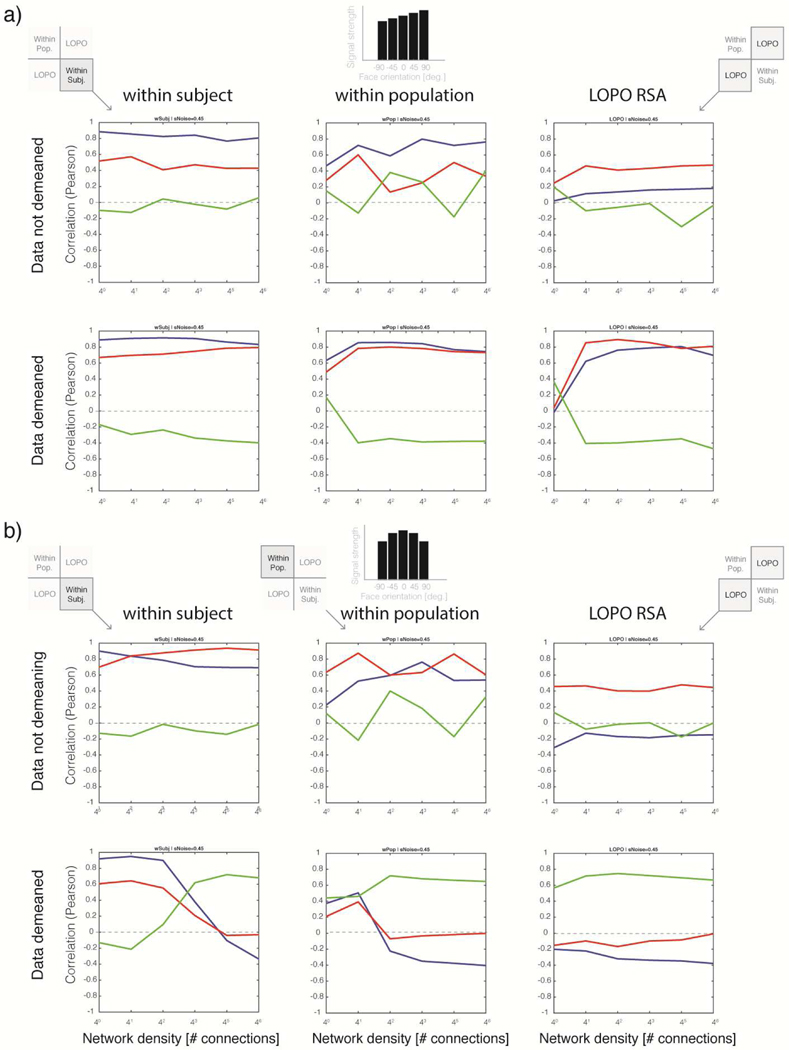
Figure 6. Within-subject, within-population, and across-subject RSA: Balanced and positive quadratic bias profiles.

a) Simulation results for the balanced case. Top row, RSA results without data demeaning. Left, within-subject RSA. Middle, within-population RSA. Right, across-subject RSA. In the absence of signal-level imbalances across conditions, within-subject and within-population results are consistent with ground-truth. As previously observed with lower noise levels (σ_Noise = 0.1, cf. Figs. 5–6), instead of the σ_Noise = 0.45 used here, across-subjects results proved unstable over densities and generally incompatible with ground truth. Bottom row, RSA results after demeaning the data. In the absence of signal-level imbalances, the pattern of results qualitatively matches the non-demeaned analysis. b) Simulation results for positive-quadratic biased case. Layout as in a. Without demeaning, RSA consistently favors the model compatible with ground truth. However, across-subject analyses on non-demeaned data (right column) incorrectly indicate a tie between the Direction and Symmetry models, while the Viewpoint model is penalized. Bottom row, RSA results after data demeaning. Left, strong interaction effects of density level and model correlation are evident for both within-subject and within-population analyses. Right, while across-subject analyses revealed a pattern of results stable across densities, the favored model—Symmetry, in green—was always incorrectly selected over its competitors after data exhibiting a positive-quadratic bias across conditions was demeaned.

Figure 7. Within-subject, within-population, and across-subject RSA: Linear and negative-quadratic bias profiles.

a) Simulation results for the linearly biased case. Top row, results for data without demeaning. Left, within-subject RSA. Middle, within-population RSA. Right, across-subject RSA. In the linearly biased case, within-subject and within-population results are roughly consistent with ground-truth. As found with lower noise levels (0.1 in Figures 5–6) instead of 0.45 as used here, across-subject results are volatile, inconsistent over densities, and incompatible with ground truth. Bottom row, RSA results for simulated data after demeaning. In the presence of a linear bias, the pattern of results partially replicates the non-demeaned analysis shown in the top row. However, an anti-symmetric bias is evident after demeaning. b) Simulation results for negative-quadratic biased case. Layout as in a. Top row, non-demeaned data. Without demeaning, RSA consistently favors the model compatible with ground truth for the within-subject analysis, albeit by a small margin. The within-population analysis behaves similarly, though it is more volatile. Across-subject analyses consistently albeit incorrectly select the Viewpoint model (in red) even without data demeaning. Bottom row, RSA results after data demeaning. Left, a strong interaction between density and all three models is evident, reminiscent of the positive-quadratic homologue analysis. Right, across-subject RSA after demeaning leads to results stable over densities and noise levels. However, the model favored here–Symmetry model, in green—is, again, systematically incorrect regardless of density and noise levels.

5. Interactions of network density, data demeaning, and RSA results

A feature that is noticeable when contemplating the agLOSO matrices shown in Figures 4 and 5 is that demeaning effects are usually more pronounced at higher network density levels. Interestingly, data-demeaning effects were also observed in quadrants other than the LOSO quadrant—i.e. in the within-subject and within-population quadrants of agLOSO matrices. To further describe the influence of density and noise levels, as well as their interactions with data demeaning, on RSA results other than cvLOSO-RSA_corr (across-subjects) we conducted further analyses on the activation patterns generated by Simulations 2–5. These results are presented in Figures 6–7. The main take-home message is that in the absence of total-signal imbalances across conditions (Figure 6a) RSA successfully selects the correct latent correlation structure of the data for the standard within-subject case. Surprisingly, this proved also possible for within-population RSA (see Discussion). In contrast, and as expected, cvLOSO-RSA_corr (which tests for generalization across-subjects) consistently failed at this attempt.

A further oddity evident in Figures 6–7 are complex interactions in the pattern of results produced by RSA analyses as a function of network density. The causes of each exemplar in the zoological garden of interaction patterns observed will be further considered in the discussion section. However, it seems essential to note here that (i) demeaning impacts the observed pattern of results in all four quadrants of the agLOSO matrix, (ii) interactions as a function of density are most prominent in the within-subject and within-population cases, and (iii) both with the noise-level considered in Figures 4–5 (σ_Noise = 0.1) as well as the increased noise-level contemplated in Figures 6–7 (σ_Noise = 0.45), cvLOSO-RSA_corr analyses led to erroneous conclusions determined by the observed form of signal bias. In particular, quadratic trends led to erroneous conclusions of mirror-symmetric coding. In turn, linear trends led to erroneous selection of the Viewpoint model. Interestingly, both the linear and negative-quadratic bias profiles led to erroneous selection of the Viewpoint model when the data were not demeaned during cvLOSO analyses. Clearly, this does not speak in favor of the idea of implementing data demeaning to overcome this potential form of bias. As already noted above, data demeaning would lead to erroneous selection of the Symmetry model. Taken together, these analyses serve to demonstrate that RSA cannot be relied upon for model selection unless no signal-level imbalances are observed across conditions, or else SNR-effects are accounted for as an integral part of RSA-like analyses, in the spirit of the model-guided approach to RSA proposed by Ramírez et al. (2014).

6. Simulations provide an explanation for results of Flack et. al. in the absence of a symmetric fine-scale representation

If positive-quadratic and/or negative-quadratic total-signal imbalances across conditions can result in artefactual observations of mirror-symmetry with cvLOSO-RSA_corr, as shown in Figures 4–7, we wondered if recent conclusions regarding mirror-symmetric coding in the human fusiform face area (FFA) (Flack et al., 2019) might be a consequence of undesired properties of cvLOSO-RSA_corr, combined with an experimental design that includes quadratic biases possibly leading to signal-level imbalances across experimental conditions. Two broad families of biases are relevant here. On the one hand, FFA may exhibit an endogenously driven stronger response to frontally viewed faces (Ramírez et al. 2014). If this were the case, even if low-level properties of stimuli were carefully balanced across conditions, cvLOSO-RSA_corr might still lead to artefactual observations of “mirror-symmetry”. Alternatively, or, more precisely, in addition to the possible endogenous source of signal bias just discussed, low-level imbalances across conditions—e.g., mean luminance and contrast—might also result in artefactual observations of mirror-symmetry. Indeed, Andrews and colleagues (e.g., Rice et al., 2014; Weibert et al. 2018; Coggan et al 2019) have argued that ventral visual responses in humans are influenced by low-level features. Similar claims were previously made by Yue et al. (2011). If this were the case, we reasoned, one might expect to observe quadratic biases in the stimuli utilized by Flack et al. (2019). If such imbalances across conditions were confirmed, and low-level features do in fact impact visual responses in ventral visual cortex as the abovementioned studies claim, then, artefactual observations of mirror-symmetry would be expected. These observations would not be informative regarding the form of tuning of the latent neural populations indirectly measured with fMRI methods. They are, instead, informative regarding the experimental design and images in the experiment.

Naturally, other forms of imbalance across conditions beyond mean luminance and contrast levels of images could also lead to artefactual observations of mirror-symmetry. For example, in the context of a block design, differing degrees of within-class image variability for different face-views could also plausibly lead to mirror-symmetric confounds likely to result in artefactual observations of mirror-symmetry when relying on RSA, and, in particular, on cvLOSO-RSA_corr. We directly tested these predictions by analyzing the images included in Figure 1 of the study by Flack et al. (2019) (see Methods).

7. Evaluation of model predictions

If we assume that the representation in human FFA is not mirror-symmetric, and accept the notion that cvLOSO-RSA_corr essentially reveals total-signal imbalances across experimental conditions, this would imply that either (i) the experimental design in Flack et al. (2019) includes mirror-symmetric low-level feature imbalances exhibiting quadratic trends, (ii) that an endogenous overrepresentation of the frontal face-views may be present, albeit undiscovered, in the data, or (iii) that both (i) and (ii) are the case. We decided to directly test the validity of the first of these options by analyzing the images included in the study by Flack et al. (2019).

7.1. Descriptive statistics of images: contrast, luminance, angular coherence, and norm.

As implied by alternative (i), above, we observed quadratic imbalances across experimental conditions as a function of the rotational angle of the analyzed facial stimuli. First, as also noted in Ramírez 2018 when reviewing the results reported by Guntupalli et al. (2017), we found an evident positive-quadratic trend associated with the mean contrast levels associated with each experimental condition. In other words, we noted that profile face views exhibited systematically higher contrast levels than half-profile views for this type of stimuli that includes dark and textured hair. The half-profile views, in turn, exhibited higher contrast than the frontal face views (Figure 8). This specific form of bias can, according to Simulations 1–3, lead to aberrant observations of mirror-symmetry when analyzed either with across-subject or standard within-subject RSA methods. Interestingly, however, we further observed a negative quadratic bias such that the frontal face-views exhibited higher mean luminance levels than the half-profile views, which in turn exhibited higher luminance levels than the profile views. This second source of bias also exhibiting a quadratic trend might also possibly, as shown by Simulations 1–3, lead to artefactual observations of mirror-symmetry. Finally, we also observed evidence of the third source of bias considered above. This is, we found that the variability of the structure of the images associated with the different face orientations—as reflected in their pairwise cosine distances—also exhibited a positive quadratic trend. More precisely, the consistency of the profile and half-profile views was considerably lower than the frontal face views (Figure 8). Taken together, these results support the hypothesis that low-level imbalances across conditions might explain the findings reported by Flack et al. (2019). In our view, this remains the most likely explanation in terms of parsimony.

Figure 8. Measurement of low-level features per stimulus class.

Average luminance, contrast, norm, and cosine distances are plotted for all five stimulus classes. Top row, one example of the five stimulus identities considered in these analyses. As predicted on the basis of the model proposed here (see main text), negative quadratic trends are observed for mean luminance as well as norm. Again, as predicted, positive quadratic trends are observed for mean contrast and cosine distance—the latter a measure of the consistency of the images associated with each class. Under each reported low-level feature, the standard deviation for that feature is plotted for each stimulus class. Positive quadratic trends are evident for the contrast and cosine distance standard deviations.

7.2. Evaluation of model predictions: iterative local averaging and iterative random averaging.

A straightforward consequence of Simulations 1–6 and the analyses reported immediately above is that the correlation structure of the very images, when themselves analyzed with RSA, might reveal a mirror-symmetric correlation structure—at least, this is, when re-sampled to reflect a regime where the granularity of the data is substantially reduced. In other words, we reasoned, if fine-scale sources of information were down-weighted, or even lost, due to averaging of local pixel neighborhoods, but existing global-signal biases persisted, then, the correlation structure of the data should morph from a non-symmetric to a mirror-symmetric correlation structure. A similar pattern of results would be expected for distance matrices relying on Euclidean distances as measure of pattern dissimilarity. To directly test these predictions, we implemented the iterative local-averaging and iterative random-averaging analyses described in the Methods section and illustrated in Figure 9. As a reminder, we note here that both of these analyses change the granularity of the data due to the iterative averaging operation that defines them. However, the consequences of these two analyses on the observed dissimilarity structure are expected to diverge. While iterative local averaging preserves genuine image structure encoded at spatial scales coarser than the current image grain (where image grain is determined by the number of pixels of the original image averaged to produce each pixel in the current image), iterative random averaging is expected to rapidly destroy the statistical structure of the image, regardless of spatial scale. Because evident quadratic trends are observed for the image luminance as a function of face-orientation, in the absence of spatial structure, pattern analyses will result in observations of mirror-symmetry. Precisely as expected, iterative local averaging led to the observation of symmetry when relying on the correlation-distance measure only for the coarsest granularity (Figure 9a). Consistent with our line of reasoning, this occurred only after data demeaning. A similar pattern of results was noted when conducting analogous image RSA analyses with the standardized Euclidean distance (as well as the Euclidean distance proper). Such effects are in our view totally expected considering that both the mean luminance and norms of the analyzed images revealed clear negative-quadratic trends (see Figure 8). As previously shown, in such cases RSA can lead to aberrant observations of mirror-symmetric matrices when relying on angular distances such as the correlation and the cosine distances (Ramírez 2017).

Figure 9. Influence of iterative local averaging and iterative random averaging on the similarity structure of images.

a) Iterative local averaging analysis. Sample images shown in top row. From left to right, images correspond to consecutive iterations where greyscale values are averaged in increasingly larger units. Dissimilarity matrices (DSM) shown below each image. The first DSM of the three shown beneath each level of granularity was computed according to the linear correlation and on non-demeaned vector representations of the images. The second dissimilarity matrix, shown immediately below, was identically computed, but on demeaned vector representations of the images. Finally, the third matrix was obtained using standardized Euclidean distance. From left to right matrices correspond to images with decreasing levels of granularity. Bottom, Representational Similarity Analysis results across all nine levels of granularity. Similarities between each model and empirical dissimilarity matrix were estimated by means of linear regression coefficients (or betas) between such matrices treated as vectors (see Methods for details). Red line, Viewpoint model. Blue line, Direction model. Green line, Symmetry model. b) Iterative random averaging analysis. Sample images are shown in the top row. From left to right, images correspond to consecutive random averaging steps. In each iteration, greyscale values are randomly permuted before averaging of the input image with the newly permuted image. Dissimilarity matrices here are organized as in a. RSA analyses were also conducted and organized as in a. Note the similarity of the pattern of results observed with Euclidean and correlation distances when the data are demeaned before similarity analyses. Also note the dominance of the Symmetry model for low levels of granularity. In contrast, the Viewpoint and Direction models are favored in analyses on images exhibiting higher levels of granularity.

8. Hyperalignment: Strengths and limitations

The simulations reported in this manuscript, as well as the complementary image analyses, show the severe limitations of across-subject analyses as a means to study fine-scale representations. Further, results show that cvLOSO-RSA_corr (one instructive instance of an across-subject analysis) is remarkably sensitive to total-signal imbalances across conditions, which in conjunction with the demeaning step that is integral to this pattern analysis method can lead to seemingly stable results that are nonetheless artefactual and misleading in nature. A key question, then, is what can a researcher do to overcome the limitations of cvLOSO-RSA_corr which, after all, is only but one variant of MVPA testing for across-subject generalization? We see at least two alternatives. While none is totally free of caveats, both can, if judiciously applied and carefully interpreted, lead to meaningful results. First, a researcher can conduct standard within-subject pattern analyses and carefully rule-out, or, alternatively, account for, potential imbalances across experimental conditions. A second potentially powerful alternative is to conduct hyperalignment, as suggested by Haxby et al. (2011). In this final section we report the outcome of Simulation 6, a small sub-set of cases that led always to failure with standard cvLOSO-RSA_corr (this is, as implemented by Andrews and colleagues, albeit excluding the data-demeaning step) but success with hyperaligned cvLOSO-RSA_corr when it came to recovering the underlying correlation structure from the data (Figure 10b, first two rows).

Figure 10. Hyperalignment: strengths and limitations.

a) Ground truth: correlation structure P. b) Non-hyperaligned and Hyperaligned cvLOSO-RSA_corr for positive-quadratic additive and multiplicative biases. Non-hyperaligned cvLOSO-RSA_corr (left column) and hyperaligned cvLOSO-RSA_corr (right column) correlation matrices associated with simulated response patterns to input images conforming to ground-truth. Icons next to each row indicate the form of total-signal bias of the pattern vectors fed to randomly connected two-layer feed-forward networks. Simulations in b (top row) reflect a positive-quadratic multiplicative bias. Simulations in the second row reflect a positive-quadratic additive bias. Non-hyperaligned cvLOSO-RSA_corr was conducted on non-demeaned data, while hyperalignment was performed as described in Haxby et al. (2011) (see Methods). cvLOSO-RSA_corr without Hyperalignment (left) was unable to recover the ground truth neither in the additive nor the multiplicatively biased case. In contrast, hyperaligned cvLOSO-RSA_corr (right) successfully recovered ground-truth in both cases. c) Non-hyperaligned and hyperaligned cvLOSO-RSA_corr results after attenuation of a single condition: high and low noise regimes. We modulated the basis image-vectors according to the new bias profile “one-tooth”. As expected, non-hyperaligned cvLOSO-RSA_corr was unable to recover ground truth regardless of the noise regime. Interestingly, however, in this strongly biased case hyperalignment inexactly recovered ground truth even in the lower-noise regime. We simulated a high-noise regime including a second source of noise added after passing response patterns from Layer 2 through the gain field. Hyperalignment results were detrimentally affected; note the highly correlated blocks (in shades of yellow) along the main and counter-diagonals. In sum, while hyperalignment provides a principled and possibly effective means to conduct across-subjects analyses, it is susceptible to potential SNR-effects that influence the correlation structure of the data and hence both RSA and other forms of MVPA.

Hyperalignment was conducted as described in Haxby et al. (2011) (see Methods). A first set of simulations (se Figure 10b, rows 1–2) included a positive-quadratic signal bias and low noise-levels (σ = 0.1). Multiplicative (top row) as well as additive signal modulations (middle row) were simulated. As shown in Figure 10b, across-subject analyses without hyperalignment failed to recover ground-truth in both cases, while analyses after hyperalignment succeeded at doing this in both cases.

Next, we investigated a more extreme form of bias in which only one condition was substantially attenuated. The logic being that while the magnitude of the biases introduced in Figure 10b were moderate (± 12.5%), a stronger modulation (50%) might lead to systematic differences due to poor alignment of the lower-SNR condition, which might in turn result in noticeable changes in the rank-ordering of the entries in the ensuing correlation matrices. Thus, we additively modulated the basis image-vectors according to the new bias profile “one-tooth”, depicted in Figure 10c (left). As expected, non-hyperaligned cvLOSO-RSA_corr was unable to recover ground truth regardless of the noise regime. In this strongly biased case, however, hyperalignment inexactly recovered ground truth (Figure 10c, top).

Finally, we simulated a high-noise regime considering the highest level of noise included in our previous simulations (σ_Noise = 0.85) as well as a second layer of noise (σ_Noise2 = 0.3) added after passing response patterns from Layer 2 through the gain field, and emulating sources of measurement noise such as thermal noise. Non-hyperaligned cvLOSO-RSA_corr was again, as expected, unable to recover ground truth. Hyperalignment results were, however, further detrimentally affected (Figure 10c, bottom).

The main take-home message here is that while hyperalignment is a principled and potentially powerful analysis approach, it is also to some degree sensitive to signal-level imbalances across experimental conditions. Such form of sensitivity can bias estimates of hyperalignment parameters. Such biases could, in turn, lead to unanticipated manifestations—e.g. systematic distortions—of empirical estimates of the underlying ground truth. Taking into consideration SNR-effects and their impact on hyperalignment parameters could prove beneficial and serve to constrain ensuing interpretations regarding representational structure and neural coding deriving from hyperaligned pattern analyses.

Discussion

In this article, we presented a framework for evaluating the impact of spatially structured activation patterns as well as total-signal effects across subjects. Simulations were implemented that parametrically manipulated the noise level and density of connections across layers of randomly-connected feedforward networks. These simulations were used to probe the behavior of cvLOSO-RSA_corr when different forms of bias were prescribed for the total-signal profile observed across experimental conditions. We compared cvLOSO-RSA_corr results both including and excluding the data-demeaning step that is normally implemented by users of this method, as well as different levels of network density and noise. Results revealed that cvLOSO-RSA_corr is unsuited to identify spatially structured representations, and, furthermore, that the method is highly sensitive to total-signal imbalances across conditions. Critically, we noted that the influence of data demeaning on cvLOSO-RSA_corr analysis results interacted with the form of total-signal bias across conditions as well as network density. We further investigated the behavior of cvLOSO-RSA_corr under various forms of signal bias. We found that such biases led to deceptive structures in LOSO similarity matrices that can be easily misinterpreted as evidence of a fine-scale representation that generalizes across the population. Simulations revealed that quadratic signal imbalances across conditions qualitatively reproduce the pattern of results recently reported by Flack et al. (2019) in human FFA—uncritically interpreted as evidence that neural populations bimodally tuned to mirror-symmetric face-views reside in this area. Analysis of the stimulus images reported in the former study confirmed quadratic trends in luminance, contrast, as well as within-class variability among the images associated with the different facial viewpoints considered in this study. Such biases, we show, can plausibly lead to artefactual observations of mirror-symmetry when using these methods.

cvLOSO-RSA_corr heavily depends on the assumption that anatomical normalization is able to align spatially-structured brain response patterns across subjects. This dependence is especially unjustified in the case of fine-scale representations. In contrast, theoretical arguments (Chaimow et al., 2011; Kamitani and Tong, 2005; Kriegeskorte et al., 2010; Ramírez et al., 2014) and empirical evidence (Cox and Savoy, 2003; Clithero et al., 2011; Haxby et al., 2011; Frost and Goebel, 2012; Zhen et al., 2015, 2017) suggest that this assumption is incorrect. We have advanced these arguments by demonstrating that residual information decoded with across-subject analyses relying on anatomical normalization can be fully explained in terms of total-signal imbalances across conditions. Our results suggest that anatomical alignment is not only clearly inferior to hyperalignment when it comes to recovering shared representations across the population, but also that the residual information detected by across-subject analyses does not necessarily imply that a shared spatial structure across the population has been identified. We also show that cvLOSO-RSA_corr after hyperalignment (Haxby et al., 2011), unlike non-hyperaligned cvLOSO-RSA_corr, proved in principle able to reveal spatially-structured representations that generalize across the population. We identify limitations of hyperalignment and propose constraints that can assist inferences regarding neural coding and representational structure based on this method.

Why is probing the validity and behavior of across-subject analyses important?

If cvLOSO-RSA_corr (one specific kind of across-subject analysis) were able to test for consistency of neural patterns across subjects, it would enable researchers to characterize shared spatially-structured representations across different sub-populations, as well as test for representational differences between healthy and clinical populations. If this were true, cvLOSO-RSA_corr might provide access to fine-scale representations, and even possibly reveal properties of indirectly sampled neural populations such as tuning functions within a particular brain area. In short, if these promises were true, it would constitute a powerful tool to many in the fields of human neuroscience, psychology, and psychiatry. The keystone on which the validity of cvLOSO-RSA_corr’s promise hinges, however, is its ability to address the correspondence problem—namely, is it possible, and if so, to what extent, to map response patterns across individuals onto a meaningful shared coordinate system? Four broad approaches have been advanced to address this challenge: (i) anatomical alignment, as used in cvLOSO-RSA_corr (Rice et al., 2014; Flack et al., 2019) as well as other somewhat similar analyses that do not claim to harness fine-scale patterns (Mouro-Miranda et al., 2005; Shinkareva et al. 2008; Poldrack et al., 2009), (ii) Representational Similarity Analysis (Kriegeskorte et al., 2008; Nili et al., 2014), (iii) hyperalignment (Haxby et al., 2011; 2014) and (iv) across-subject decoding in similarity space (Raizada and Connolly, 2012). We address each of these possibilities below. Note that methods of type (i) operate in voxel space, while (ii)-(iii) operate in similarity space.

The correspondence problem: four approaches, one challenge

Anatomical alignment is valid in the context of studies probing across-subject generalization, as long as it is used to support inferences regarding anatomically consistent macroscopic brain representations across the population—e.g., large-scale maps of activated and deactivated brain areas associated with specific tasks or task dimensions (Mourão-Miranda, et al., 2005; Shinkareva et al., 2008; Poldrack et al., 2009). The simulations presented here do not suggest that such uses of leave-one-subject-out cross-validation are invalid. However, our simulations do demonstrate that anatomical alignment is unsuited to solve the correspondence problem when it comes to spatially structured brain patterns in general, including fine-scale, coarse-scale, and even macroscopic maps that do not substantially align across subjects with respect to their anatomy. Standard cvLOSO-RSA_corr is in these cases likely to lead to misleading conclusions regarding neural coding.

Representational Similarity Analysis (Kriegeskorte et al., 2008) provides a second, and perhaps more principled, approach to address the correspondence problem. Under what conditions does RSA work (or fail)? RSA assumes that matching of empirical (dis)similarity matrices is a suitable means to relate similar representational schemes implemented in different brain areas, individuals, and even across species. To the extent that a chosen similarity measure captures the properties of interest (reviewed by Ramírez, 2018), this approach may prove successful at revealing information about spatially-structured brain representations. However, if the measurement process is ignored, as explicitly done by RSA, and signal imbalances across conditions are present in the data that do not match the form-of-tuning of the neural populations giving rise to these biased responses, then, RSA will lead to erroneous conclusions regarding neural coding (Ramírez et al., 2014; Ramírez, 2017). In a similar vein, RSA can also lead to the false conclusion that two representations match across subjects, when in fact they are incompatible. Incompatible representations (from a neural-tuning standpoint) can give rise to congruent distance matrices (in terms of the rank-ordering of their entries). Likewise, compatible representations (from a neural-tuning standpoint) can give rise to incongruent distance matrices due to peculiarities of the measurement method, experimental choices, and measurement scale. Thus, RSA is not generally assured—from a neural-tuning point of view—to provide meaningful results. We refer to this fundamental limitation of RSA as the representational fallacy.

Under what conditions is hyperalignment likely to work? A key assumption of hyperalignment (and RSA) is that inferences regarding neural coding are translation and rotation invariant. But this is not generally true (Ramírez 2017). More specifically, the hyperalignment procedure involves Procrustes transformations (Schönemann, 1966). This type of transformation admits translation, orthogonal rotations, and reflection, to align vectors onto a common coordinate system. But such shifts, as are caused by a translational component, can result in erroneous conclusions regarding neural coding. To the extent that hyperalignment aligns brain responses to a seed subject, and in this sense aims to preserve geometric relationships across subjects as well as anchor the hyperaligned space to the coordinate system of the seed-subject, it might be argued that pernicious shifts of the center of the coordinate system are unlikely if a largely shared representation truly exists in the population. Differently said, the approach seems viable to the extent that the assumption holds that representations across subjects are second-order isomorphic in R.A. Shepard and Chipman’s (1970) sense of the word. If representations are partially unique and partially shared, then, hyperalignment, to the extent that it includes a translation component as well as rotational components, and to the extent that hyperaligned responses are iteratively averaged as part of the hyperalignment algorithm, could possibly lead to representational confusion (Ramírez, 2017). The former is the case, precisely, due to unintended shifts of the origin of the coordinate system to a biologically (and/or psychologically) meaningless location. That said, it is also true that regardless of potential systematic distortions due to the hyperalignment procedure, spatially-patterned structure invisible to cvLOSO-RSA_corr can in principle be revealed by hyperaligned pattern analyses as shown above (see Figure 10). A second assumption of hyperalignment (and RSA) is that inferences regarding neural coding are generally rotation invariant. By this assumption we refer to the belief that after translation and rotation about an arbitrary axis, as done to achieve alignment of representations across subjects, inferences about neural properties such as tuning remain unchanged. Contrary to this belief, instances are conceivable in which rotation of brain patterns associated to a set of experimental conditions corresponding to incompatible underlying tuning functions—e.g., perfectly bimodal or completely unimodal—might perfectly match after orthogonal rotation and translation. This implies that while in some cases the assumption of rotation invariance, or at least some weaker form of rotation tolerance, might actually hold, cases are conceivable in which it might fail. Whether the assumptions of these methods usually hold, and, if so, to what extent, is fertile ground for future research.

Finally, across-subject decoding in similarity space (Raizada and Connolly, 2012) is an ingenious additional approach aiming to circumvent the correspondence problem. In this case, generalization across subjects proceeds by completely abstracting from the brain patterns themselves and focusing instead in the similarity relations observed across the experimental conditions under investigation. By moving away from actual brain patterns, and focusing instead on their distances, this method does indeed enable researchers to probe for information that generalizes across the population. In this sense, if two representational systems are second-order isomorphic In R.A. Shepard and Chipman’s (1970) sense of the word, then this method seems in principle suited to find information that generalizes across the population. One key decision, however, relates to the choice of similarity measure used to define relations in similarity space. Interestingly, while a Euclidian metric may provide one answer to a particular question, focusing on angular relationships among a set of experimental conditions could provide a different answer (Ramírez 2017; Ramírez 2018). For instance, while an angular distance measure may serve to demonstrate that the form of tuning of indirectly sampled neural populations is overwhelmingly unimodal—as found by Freiwald and Tsao (2010) in the middle face patches (ML/MF)—it is possible from an Euclidean point of view that a researcher may argue that the same representation, even when instantiated by unimodal tuning functions, may nonetheless in some sense also be mirror-symmetric. This brings us back to the issue regarding what the question is that a researcher is trying to answer, and what constitutes a valid data analysis scheme to address that question. Here, we show that cvLOSO-RSA_corr is unsuited to answer questions regarding neural activation patterns, regardless of spatial scale, as claimed by users of this method. For this very reason, cvLOSO-RSA_corr is unsuited—by definition—to inform the question whether neural populations in the human FFA are unimodally tuned as observed in ML/MF, or bimodally tuned to mirror-symmetric face views as observed in the macaque anterior-lateral face patch (AL). Please note that in macaques only AL was found to be populated by mirror-symmetrically tuned neural populations (Freiwald and Tsao, 2010; Meyers et al., 2015). Assuming a Euclidean perspective allows the somehow counterintuitive possibility that a population code is simultaneously strictly view-tuned (as observed in MFP), but also, in some sense, also simultaneously mirror-symmetric. Further consideration of how different read-out mechanisms might serve to multiplex different kinds of information in a neural population code requires further study.

Across-subject analyses: prominent features and current limitations

Pattern analyses that test for generalizability of information across subjects naturally lend themselves to random-effects statistical analyses—i.e. to test hypotheses about parameters that generalize to the population. This analysis approach thus circumvents the theoretical limitation of common hypothesis testing methods, such as the t-test, often mistakenly applied to information measures with the aim of enabling inference to the population (Allefeld et al., 2016). If hyper- or otherwise-aligned responses across subjects are assumed to meaningfully remap onto a common coordinate system, shared structure and decodable information as derived via cross-validation procedures would support inferences regarding parameters of theoretical interest to the population of subjects from which a sample was drawn. A second key property worth mentioning is that if a dataset includes a large number of subjects, then hyperalignment might prove remarkably beneficial from an informational perspective. This is, because a large number of datapoints can help regularize hyperalignment parameters estimated from noisy data and thus possibly achieve improved classification performance even when compared with the standard within-subject decoding scheme that is gold-standard in human neuroimaging studies today. However, we note that increased decoding performance does not necessarily imply capturing the relevant information a researcher is after. While decoding accuracy might at the limit approach perfection, this does not imply that such performance measures reflect the neural properties under investigation. For example, a linear decoder will sensitively exploit total-signal imbalances across conditions if they are present in the data. This, however, does not imply that the decoding accuracies or associated error-rate distributions reflect in the very least the form of tuning of indirectly sampled neural populations. In contrast, even if the decoding accuracies achieved by within-subject non-linear decoders were relatively low, they could, at least in principle, prove informative regarding the form of tuning of latent neural populations contributing to the observed signal—i.e., while alternative information-efficient across-subject analyses might not.

Finally, we point to potential limitations of similarity space approaches, including hyperalignment. Current analysis methods that focus on across-subject generalization are unsuited to study, for example, idiosyncrasies of unique individuals. This is, because if a generalization test is tailored to capture information that is common across a subject population, evidently, it cannot, without making further modelling and interpretational assumptions, be used to support inferences regarding subject-specific representational idiosyncrasies. In this sense, while commonalities are undisputedly of central interest to neuroscience, considering peculiarities of unique individuals, however, seems also essential from a psychological standpoint. A second, more technical, limitation worth noting is that the outcome of hyperalignment procedures is sensitive to signal-level imbalances across conditions, as well as measurement scale and noise properties. The form under which ensuing representational distortions may manifest on pattern analyses will depend on specifics of the system under study, the measurement process, as well as the observed profile of SNR imbalances across conditions. The approach we outline here to mitigate the inferential impact of such possible distortions is to estimate the signal-to-noise ratio (SNR) of brain patterns and then rely on computational simulations incorporating such information to generate a range of latent correlation structures that might have plausibly given rise to the empirical observations given the estimated SNRs. This approach derives from that used by Ramírez et al. (2014) to provide a biologically plausible account of the correlation structure associated with face-orientation (or viewpoint) information in the human right FFA. There, a model-guided approach to RSA is explained in detail considering SNR as well as further biologically interpretable parameters as constraints. Alternative theoretical frameworks worth exploring and/or adapting to a similar end include pattern component modelling (Diedrichsen et al. 2011), Bayesian RSA (Cai et al., 2019), as well as methods developed to find information common to different data tables adapted for their use with neuroimaging data (Abdi et al. 2009). A further alternative approach to test for generalization of representations across subjects is to rely directly on similarity relations between brain patterns, instead of brain patterns themselves (Edelman, 1999; Edelman et al., 1998; Raizada and Connolly, 2012). The MVPA method proposed by Raizada and Connolly (2012), like hyperalignment, can in principle circumvent the correspondence problem and meaningfully test for across-subject generalization of information. However, this method is not suited to draw inferences about neural properties such as the form-of-tuning of indirectly measured neural populations. In sum, pattern analyses aiming to support claims regarding neural properties cannot escape the need to consider the process by which brain measurements were acquired, the nature of the system under study, as well as the impact of noise descriptors (be it multivariate or univariate) on relevant parameter estimates and ensuing statistical analyses.

Further studies and approaches operating in voxel space (instead of similarity space)

Clithero et al. (2011) studied the effect of positive and negative reward on brain activity. They conducted within- and across-subject classification analyses of fMRI data. Areas exhibiting highest decoding accuracies using within-subject analyses also exhibited strongest univariate effects. These areas included primary visual, ventral-visual, and ventromedial prefrontal cortex. Across-subject decoding led to marked and widespread costs in terms of decoding accuracy. These results are fully consistent with our simulations (see Figure 1d). Interestingly, however, the magnitude of this cost was not homogeneously distributed over cortex; the relative location of peak accuracies among brain areas changed, and additional areas reached statistical significance. The authors were cautious to interpret their results as tapping into idiosyncratic and shared representations. An alternative interpretation is that differences between these two tests of generalization were driven by inter-regional variability when anatomically aligning brains, variability in gain field consistency across brain areas, and the impact of different number of training instances for within- and across-subject classification. This does not imply that these factors necessarily or fully account for the observations by Clithero et al., but it does emphasize that to draw definite conclusions it seems important to further understand and consider the influence of factors including those investigated here.

In a similar vein, informative and interesting observations relying on across-subject analyses have been made in the domain of language research. For example, Shinkareva et al. (2011) found information about object category (tools or dwellings) that generalized across both subjects and stimulus presentation modality (pictures or words). We do not challenge the merit and interest of such findings. However, we do argue that identifying the spatial scale of the signals giving rise to these observations will require a fuller understanding of the influence on machine-learning methods of the factors we examine here.

Inter-Subject Correlation (ISC) (Hasson et al., 2004; Nastase et al., 2019) is a further analysis method that relies on across-subject cross-validation and aims to enforce correspondence at the measurement level. ISC computes correlations between voxel time courses from different subjects and, as cvLOSO-RSA_corr, it usually relies on anatomical normalization to bring brains of different subjects into correspondence. As with cvLOSO-RSA_corr, one caveat is that if anatomical alignment fails to bring spatially structured representations into correspondence, the method will miss potentially important sources of co-variation. Finally, it is relevant to note that ISC assumes the validity of a specific model when computing correlations across subjects and interpreting them. Users of this method usually interpret ISCs as a combination of idiosyncratic and shared variance components plus noise. Invalidity of this mode of decomposition, as well as neglect of different sources of noise (as discussed immediately above) might lead to biased conclusions regarding brain function.

Gain fields

The consideration of a static measurement gain field (GF) is a prominent aspect of the framework implemented here to investigate the impact of spatially structured patterns and total-signal effects on cvLOSO-RSA_corr analyses. GFs were assumed to be identical across networks and modulate the amplitude of the response-levels associated with each stimulus image over units of layer 2 of the implemented randomly-connected networks. The inclusion of a measurement GF is noteworthy for the following reasons: First, because the outcome of pattern similarity analyses relying on the linear correlation as a measure of pattern similarity is sensitive to GFs, as previously observed with forward models (Ramírez et al. 2014). Second, and of particular importance here, GFs with a structure that is shared across subjects will generate a common direction in multivariate space along which total-signal effects will manifest. Such an underlying data component in voxel space, when subjected to data transformations (e.g. cocktail demeaning, or GLM mismodelling) that systematically change the angular relationships among multivariate response patterns, can play a determinant role on the observed outcome of LOSO analyses—as we have shown here. In the absence of a GF, randomly distributed responses over the population exhibiting a common non-zero mean value across units is expected to lead, on average, to similar activation levels across network units, as implied by the Law of Large Numbers. In the presence of a gain field, however, and especially for higher network densities, averaging across the population will lead to a distinct response profile where the average response level is proportional to the strength of the gain experienced by each unit within the GF. Indeed, as observed in Figures 6–7, in the within-population RSA analyses, systematic effects are observed for randomly-connected networks even in this case because: (i) averaging of responses over a moderate number of subjects is insufficient to completely cancel-out responses even if they are random, and, crucially, (ii) total-signal effects (be they multiplicative or additive in nature) of otherwise randomly distributed response patterns across the population will lead to a shared response profile due to the influence of the gain field. Investigating the impact of the degree of similarity of GFs from multi-channel measurements across the population, as well as the specific distribution GFs in each particular study, are topics that call for further empirical and computational investigation.

Gain fields (GFs), as used in the present study and in earlier work (Ramírez et al., 2014), influence the behavior of pattern classifiers. GFs are present in fMRI data for physical reasons. In the presence of a GF, for example, mean subtraction is assured to be ineffective when it comes to controlling for global effects across voxels as the source of a presumably “multivariate” pattern effect (Ramírez, 2016). Many researchers have noted and discussed the confounding effect of “univariate” effects, in contrast to genuinely “multivariate” effects, on MVPA analyses (Coutanche, 2013; Davis et al., 2014; Hebart and Baker, 2018; Smith et al., 2011). The key observation noted and clearly explained in Ramírez (2016) is that the influence of a gain field is assured to render mean subtraction ineffective as a way of controlling for global effects in pattern analyses. Differences in sensitivity across measurement channels, for example, due to voxels sampling different proportions of gray matter (Ramírez et al., 2014), as well as irregularities in the vasculature, will lead by necessity to non-homogeneous signal profiles across voxels even for spatially perfectly homogeneous (i.e., global) neural effects in cortex. This previously-overlooked observation explains why studies investigating the impact of pattern mean subtraction (Misaki et al., 2010), and using this method to “rule-out” global effects, find that this form of normalization has usually little, if any, impact on the observed pattern of results. In sum, subtraction of the mean across voxels is an ineffective way to rule-out global signal modulations on fMRI decoding analyses. This is because information about the intensity of the global effect will manifest as a non-additive modulation along the direction of the gain field. Such modulations are often also noticeable when inspecting the profile of standard deviations (or Euclidean norms) of the analyzed fMRI patterns. The relevance of considering the potential influence of GFs on pattern analyses can be thus seen to generalize well beyond cvLOSO-RSA_corr analyses.

Our simulations assumed that an identical GF is shared across networks. However, it seems unlikely that identical GFs actually underly multi-subject datasets after anatomical normalization. Our simulations implemented GFs in this way to highlight the relevance of this usually-ignored aspect of MVPA results, and to illustrate how it bears on the interpretation of cvLOSO-RSA_corr. We claim neither that the precise form nor degree of similarity across the population of our simulated GF are realistic in detail. However, anatomical alignment of fMRI data is indeed likely to induce positive correlations in GF structure across subjects. This is likely to be the case because of shared anatomical features across subjects, which are exploited by anatomical alignment algorithms. Such regularities will induce a degree of similarity in GF structure across individuals, for example, due to partial voluming at tissue boundaries. Further possible contributors to shared GFs are varying coil sensitivities in fMRI systems used to scan several subjects, as well as consistent anatomical locations of large veins across subjects that could lead to coarse-scale signal biases. The precise characterization of measurement GFs and their impact on pattern analyses is a topic that requires further investigation.

The augmented LOSO matrix: a useful tool for the interpretation of LOSO analyses

If insufficient constraints are imposed on overly flexible data analysis methods, one risk is that one discovers in the results whatever pattern was induced by the analysis method. A similar demon, in a different disguise, is that of inductive bias in the context of machine learning classifiers (Mitchell, 1997). Classification methods will tend to reveal whatever it is that they were tailored to reveal—e.g. due to the specified form of regularization or other properties of a classification algorithm. For such reasons, here we investigated the behavior of cvLOSO-RSA_corr (a.k.a. “LOPO”) to various forms of bias, noise levels, as well as network density. In order to best interpret cvLOSO-RSA_corr results, we propose here a simple heuristic: inspection of the augmented LOSO matrix, and not only of the usual LOSO quadrant of the agLOSO matrix (for details, see sub-section 2.1). We further suggest that information should be routinely provided explaining why an agLOSO matrix may look lower-triangular when, in theory, it should specify a square matrix populated by unique values in each of its cells. Without such additional information, it may prove impossible to make informed inferences regarding the underlying neural representations. Similarly, we suggest that univariate analyses should be routinely conducted alongside multivariate analyses, the data interrogated for possible SNR-imbalances across conditions, and if found, be reported and discussed.

Do our results imply that all published results based on cvLOSO-RSA_corr are necessarily wrong? The degree of confidence in the method—and its conclusions—depends on the nature of the inferences being made. If inferences require the detection of fine-grained information, as many believe is necessary when aiming to draw inferences about the form of tuning of indirectly measured neural populations (but see Freeman et al., 2013, 2011; Roth et al., 2018), then, the simulations reported here indicate that cvLOSO-RSA_corr is clearly unsuited to this purpose. If inferences are being made that implicate only coarse-scale representations, then cvLOSO-RSA_corr results may prove to be informative; but only if there are good reasons to believe that anatomical alignment successfully brings into correspondence such coarse-scale representations. Even if a coarse-scale representation underlies measured signals across a population of subjects, if anatomical alignment does not successfully bring them into correspondence, then, this method could easily lead to erroneous conclusions about neural coding. Finally, even if the spatial scale of the neural correlates of some brain process of interest were macroscopic and extremely “coarse scale” within each subject of a sampled population, but these macroscopic coarse-scale maps were inconsistently distributed with respect to prominent cortical anatomical features, then, cvLOSO-RSA_corr would remain unsuited to detect them. In contrast, cvLOSO-RSA_corr does seem well-suited to reveal total-signal imbalances across conditions that are anatomically consistent across the population, as well as spatially structured patterns—of any scale—that happen to align to anatomical landmarks in each subject so as to assure that they will remain detectable by cvLOSO-RSA_corr after anatomical normalization—i.e. after averaging of responses across subjects in each of the anatomically realigned voxels.

When specifically considering the observations of “mirror-symmetry” reported by Flack et al. (2019), it is key to note two things. First, the experimental design included quadratic low-level confounds (as predicted by our model). Such quadratic low-level feature confounds have been shown to plausibly lead to artefactual observations of mirror-symmetry (Ramírez et al., 2014; Ramírez, 2017; reviewed in Ramírez, 2018). This possibility was further substantiated by the simulations reported in this article tailored to address the behavior of cvLOSO-RSA_corr. Second, Weibert et al. (2018) (same group as Flack et al., 2019) previously reported evidence that low-level features are predictive of response patterns in FFA when using cvLOSO-RSA_corr. Strangely, in neither of the two experiments reported by Weibert et al. (2018) was any evidence of mirror-symmetric coding of viewpoint information observed in the FFA, even though they used stimuli very similar to those used by Flack et al. (2019). By the contrary, the reported cvLOSO-RSA_corr analysis results reported by Weibert et al. (2018) were clearly consistent with the “Viewpoint” model. A possible explanation of these inconsistent findings are interactions of cvLOSO-RSA_corr outcome with data normalization choices.

If stimulus low-level features are not controlled, as we have shown here, one might reach opposite conclusions regarding neural coding. Alternatively, if low-level features are controlled, however, a researcher might argue the results do not generalize beyond the specific stimuli used in the experiment, because they are not an ecologically representative sample (Brunswik, 1956). We see two ways forward. The first one involves conducting experiments manipulating contrast and orientation, and showing with a well-calibrated model that the form of the underlying viewpoint representation is consistent regardless of contrast—even if not itself contrast invariant. Such an approach would gain traction if analyzing the data with cvLOSO-RSA_corr led to contradictory conclusions that only depended on low-level features of the stimuli. A complementary approach is to acquire an ecologically valid sample of images and use those images to test an independently calibrated encoding model. This might provide evidence of a specifically view-tuned representation that generalizes to the ecologically representative sample of images.

Summary, conclusions and future directions

We presented a framework for evaluating the impact of spatially structured activation patterns as well as the influence of total-signal imbalances across conditions on the outcome of leave-one-subject-out cross-validated pattern analyses. Data were simulated using randomly-connected feedforward networks with a shared gain field. Results revealed that cvLOSO-RSA_corr is unsuited to identify spatially structured representations that generalize across subjects, regardless of spatial scale, and that the method is highly sensitive to total-signal imbalances across conditions. The influence of data demeaning on analysis results was shown to interact with the precise form of total-signal bias observed across conditions, as well as network density. Such biases and interactions led to deceiving structures in Leave-One-Subject-Out (LOSO) similarity matrices easily mistakeable as evidence of a fine-scale representations that generalize across the population.

Low-level imbalances across conditions—of the quadratic form predicted by our model—were confirmed when analyzing the images reported by Flack et al. (2019). Such biases led in the simulations reported here to artefactual observations of “mirror-symmetry”. These results provide a parsimonious explanation of the findings of mirror-symmetry reported by these authors. Our results also suggest not only that anatomical alignment is clearly inferior to hyperalignment when it comes to recovering shared spatially-structured representations across the population, but that the residual information detected after anatomical alignment can be parsimoniously accounted for as a byproduct of total-signal imbalances observed across conditions. Taken together, our findings call for a re-evaluation of the validity of LOSO analyses and their interpretation. We propose the augmented LOSO matrix as a valuable tool to this aim (see sub-section 2.1).

In line with the framework advanced here, we are currently working on the implementation of networks considering further key biologically interpretable parameters—i.e. beyond network density and noise level, as considered here. The overarching goal of such work is to account within a unitary framework for a plethora of seemingly inconsistent patterns of results reported over several studies probing the representations subserving viewpoint-invariant face recognition in primates. Focusing on comprehensive models that explain most (if not all) reported patterns of results, and using these models to guide the generation of maximally-informative future data, rather than taking putative inconsistencies at face value, will, we are convinced, in the end lead the field of human cognitive neuroscience forward.

Highlights.

• Randomly-connected networks used to probe across-subject pattern analyses

• Across-subject analyses proved insensitive to spatially structured patterns of activation

• Across-subject analyses proved sensitive to signal imbalances across conditions

• Data demeaning can induce deceptive similarity structures in across-subject RSA analyses

• Hyperalignment offers way forward, if influence of signal imbalances is considered