How Aromatic Are Molecular Nanorings? The Case of a Six‐Porphyrin Nanoring

Abstract

Large conjugated rings with persistent currents are novel promising structures in molecular‐scale electronics. A six‐porphyrin nanoring structure that allegedly sustained an aromatic ring current involving 78π electrons was recently synthesized. We provide here compelling evidence that this molecule is not aromatic, contrary to what was inferred from the analysis of ¹H‐NMR data and computational calculations that suffer from large delocalization errors. The main reason behind the absence of an aromatic ring current in these nanorings is the low delocalization in the transition from the porphyrins to the bridging butadiyne linkers, which disrupts the overall conjugated circuit. These results highlight the importance of choosing a suitable computational method to study large conjugated molecules and the appropriate aromaticity descriptors to identify the part of the molecule responsible for the loss of aromaticity.

The correct assessment of the aromaticity of a 78π‐electron six‐porphyrin nanoring hinges upon the choice of the computational method. Density functional approximations with a low percentage of long‐range Hartree–Fock exchange commit large delocalization errors and suggest the presence of an aromatic ring current. The transition from the porphyrins to the bridging butadiyne linkers is responsible for the absence of an aromatic ring current.

Introduction

Benzene is the paradigm of an organic aromatic molecule, exhibiting bond‐length equalization, cyclic electron delocalization, and exalted magnetic susceptibility. As such, benzene is just the smallest neutral annulene that presents π‐conjugated aromaticity; other annulenes possessing 4n+2 π electrons are also considered aromatic. It is well established that large annulenes suffer out‐of‐plane distortions and exhibit a poor overlap between π orbitals, thus favoring non‐symmetric conformations that are much less aromatic.[ ¹ , ² , ³ ] The larger the annulene, the less aromatic the molecule is expected to be. For this reason, it is difficult to find large aromatic macrocycles.[ ² , ⁴ , ⁵ ] Geometrical constraints are imposed in some large macrocyclic structures with the hope to preserve conjugation, aromaticity, and quantum coherence.

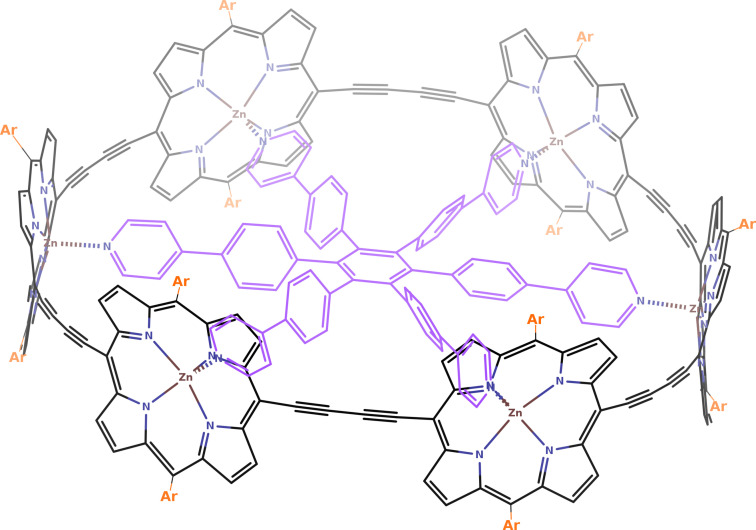
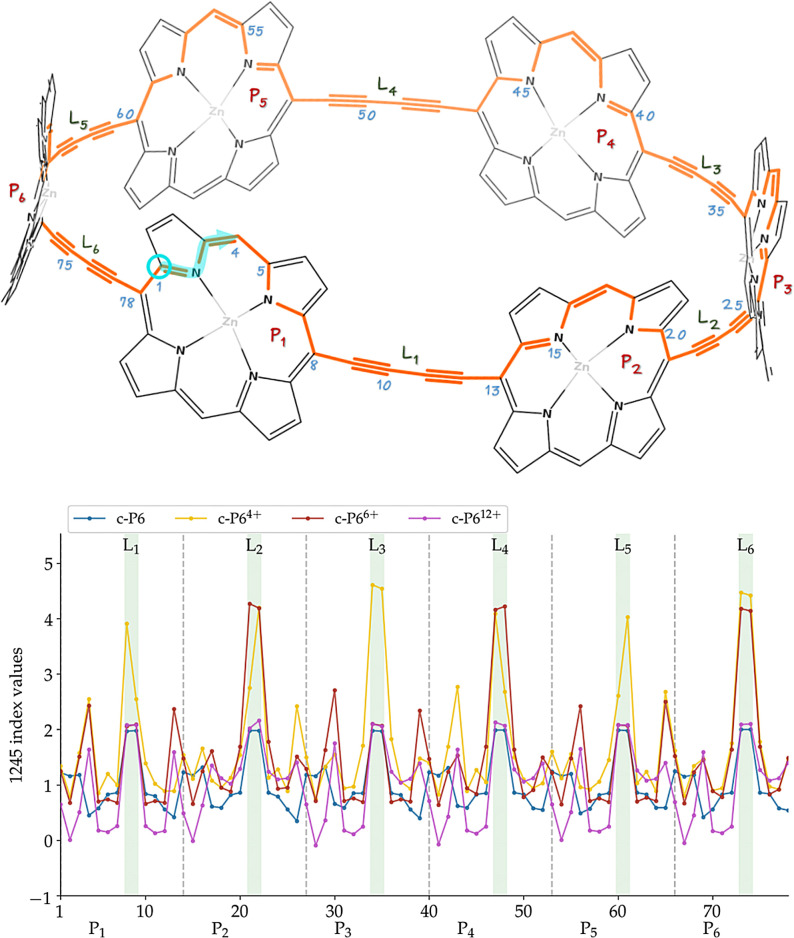
Among the molecules with the largest aromatic rings, it is worth highlighting the dodecaphyrin structures synthesized by Osuka and co‐workers,[ ⁶ , ⁷ ] which adopt twisted Möbius and Hückel conformations, the annulene‐with‐an‐annulene aromatic super‐ring structure of Wu et al., ^[8] and the π‐conjugated six‐porphyrin nanoring of Anderson and co‐workers (see Figure 1). ^[9] The latter work synthesized and analyzed the aromaticity of a six‐porphyrin nanoring (c‐P6⋅T6) in four different oxidation states (c‐P6⋅T6, c‐P6⋅T6⁴⁺, c‐P6⋅T6⁶⁺, and c‐P6⋅T6¹²⁺), concluding from ¹H‐NMR, NICS, and ACID analyses that the neutral and the c‐P6⋅T6¹²⁺ species are non‐aromatic, whereas c‐P6⋅T6⁴⁺ and c‐P6⋅T6⁶⁺ are, respectively, antiaromatic and aromatic.[ ⁹ , ¹⁰ ] These molecules were the first of a series of similar large macrocyclic structures exhibiting (anti)aromaticity.[ ⁹ , ¹¹ , ¹² , ¹³ , ¹⁴ ]

Figure 1.

Structure of c‐P6. For the nanoring structure with the aryl group substituents (orange) and the encapsulated template (purple) we will use the notation c‐P6⋅T6. In Ref. [9], they synthesized the compound with Ar=(3,5‐bis(trihexylsilyl))phenyl, whereas the computational studies used Ar=Ph for c‐P6⋅T6 and Ar=H for c‐P6.

Porphyrin nanorings are very attractive compounds because they offer an end‐free π‐conjugated system with remarkable properties such as photophysical and guest‐encapsulating, which might lead to a myriad of applications in the field of single‐molecule electronics,[ ¹⁵ , ¹⁶ ] serve as light‐harvesting antennas, ^[17] or investigate energy transfer in biomimetic systems, ^[18] among others.[ ⁹ , ¹³ , ¹⁹ , ²⁰ , ²¹ , ²² , ²³ , ²⁴ , ²⁵ ] In this sense, the interest and the utility of the compounds synthesized by the group of Anderson are beyond question. However, in this work, we demonstrate that the aromaticity of these large macrocycles is questionable. We perform a throughout analysis of these species using several density functional approximations (DFAs) and various tools to analyze the aromaticity, providing compelling evidence that the conclusions are highly sensitive to the level of calculation employed. In particular, B3LYP presents large delocalization errors that artificially enhance the aromaticity of c‐P6⁶⁺, whereas CAM‐B3LYP provides an excellent agreement with the experimental data available. Through careful computational analysis and the judicious examination of the ¹H‐NMR data, we conclude that c‐P6⁶⁺ is not aromatic.

Additionally, we perform a complete electronic structure study of the four oxidation states of the nanoring and analyze the aromaticity of these molecules. By studying the local aromaticity of the six porphyrins that compose the belt structure and the conjugated linkers (the butadiyne fragments linking the porphyrins), we identify the parts of the molecule that are responsible for the absence of the global aromatic ring current. Finally, we provide some hints that might aid in the synthesis of large aromatic nanorings.

Results and Discussion

The synthesized molecules consist of a belt nanoring structure of six porphyrins with aryl groups and an encapsulated template (c‐P6⋅T6, see Figure 1). There, Anderson et al. ^[9] computationally analyzed the aromaticity of the nanoring structure without the aryl groups and the template (i.e., c‐P6) because the nanoring belt structure is the one responsible for the aromaticity of these compounds. In this work, we have also analyzed the effect of adding the encapsulated template and the aryl groups to the c‐P6⁶⁺ structure.

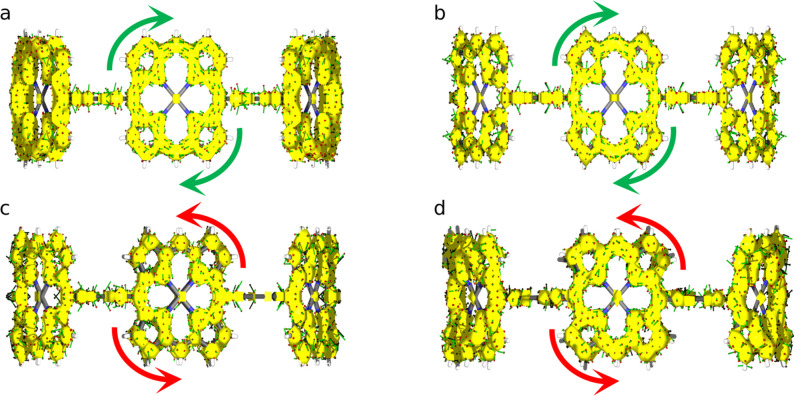
DFAs with a low percentage of Hartree–Fock (HF) exchange (typically, HF[%]≪50) at long interelectronic ranges are prone to present large delocalization errors, ^[27] leading to the unphysical overdelocalization of electrons, the underestimation of reaction barriers and charge‐transfer excitation energies, ^[27] the overestimation of the conductance of molecular junctions, optical responses,[ ²⁸ , ²⁹ ] the magnetizability of strong antiaromatic molecules, ^[30] electron conjugation, ^[31] and aromaticity,[ ³² , ³³ ] especially in large conjugated macrocycles.[ ² , ³ , ³⁴ , ³⁵ , ³⁶ , ³⁷ ] Anderson et al. ^[9] performed B3LYP (HF[%]=19), M06‐2X (HF[%]=54), and ωB97X (HF[%]=0–100) calculations with the 6‐31G* basis set but mostly employed the B3LYP results to analyze the aromaticity of these compounds. We have performed additional calculations with CAM‐B3LYP (HF[%]=19–65) and LC‐ωHPBE (HF[%]=0–100), ω being 0.1 and 0.2 (the larger ω, the larger HF[%] at long range). Although all methods give qualitatively the same structure for the neutral and the c‐P6¹²⁺ species, c‐P6⁴⁺ and c‐P6⁶⁺ present significantly different geometries depending on the amount of long‐range HF exchange present in the DFA. While CAM‐B3LYP, M06‐2X, and LC‐ωHPBE(ω=0.2) give a less symmetric structure for c‐P6⁶⁺, B3LYP and LC‐ωHPBE(ω=0.1) yield a symmetric aromatic species (see Tables 1 and S2). The first group of DFAs has a large percentage of HF exchange at long range, indicating that the latter DFAs may be suffering from delocalization errors. This is further reinforced by single‐point DLPNO‐CCSD(T)/def‐SVP‐C calculations that attribute much lower energy to the less symmetric c‐P6⁶⁺ structures of M06‐2X and CAM‐B3LYP geometries compared to the B3LYP one (see Table 2), and the fact that CAM‐B3LYP identifies the symmetric structure as a transition state (TS) connecting to equivalent minimal structures with non‐equivalent linkers (see Figure 2). Indeed, the B3LYP minimal geometry has a great resemblance with the geometry of this TS (see Table 1). The situation is reminiscent of the error committed by B3LYP in the potential energy surface of extended porphyrins, ^[34] and casts a shadow of doubt over the conclusions obtained using this B3LYP geometry. ^[9] In the case of c‐P6⁴⁺, single‐point DLPNO‐CCSD(T)/def‐SVP‐C calculations identify the B3LYP geometry as the lowest‐lying one. Although, in the latter case, the energy differences are so small with respect to other DFAs (2–8 kcal mol⁻¹), that one cannot unequivocally draw any conclusion about the geometries (see below for an assessment of the aromaticity of c‐P6⁴⁺ calculated with different geometries).

Table 1.

Comparison of CAM‐B3LYP and M06‐2X ground state geometries against the B3LYP one.^[a]

Species	RMSD(CAM‐B3LYP)	RMSD (M06‐2X)
c‐P6	0.05	0.04
c‐P64+	0.66	0.20
c‐P66+	0.22	0.21
c‐P612+	0.04	0.04
TS c‐P66+	0.06	0.07

[a] All root mean square deviations (RMSD) ^[26] are given with respect to the B3LYP minimum. TS c‐P6⁶⁺ corresponds to the transition state of c‐P6⁶⁺ connecting two energy minima (see Figure 2).

Table 2.

c‐P6⁴⁺ and c‐P6⁶⁺ DLPNO‐CC/Def‐SVP/C relative energy values with respect to the corresponding lowest value.^[a]

Species	Optimization	Geometry	ΔECCSD	ΔECCSD(T)
c‐P64+	B3LYP	min	0.0	0.0
	CAM‐B3LYP	min	−5.2	7.8
	M06‐2X	min	−1.8	5.5
c‐P66+	M06‐2X	min	0.0	0.0
	B3LYP	min	81.9	68.4
	CAM‐B3LYP	min	8.3	10.9
	CAM‐B3LYP	TS	32.4	25.0
	M06‐2X	TS	28.2	18.8

[a] All T₁ diagnostic ^[38] values are below 0.017. DFT calculations employed the 6‐31G* basis set. Energy in kcal mol⁻¹.

Figure 2.

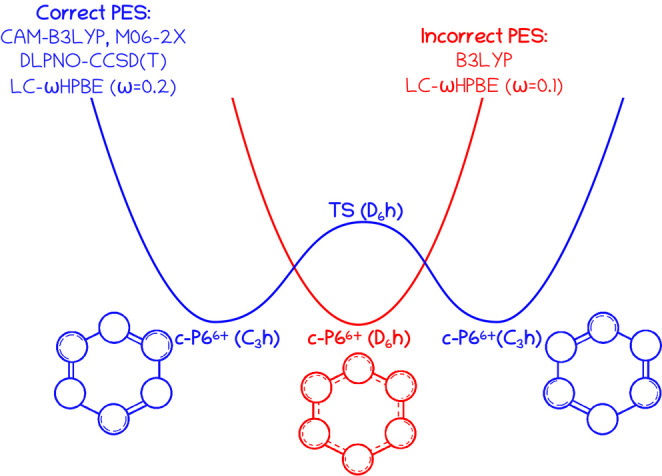
Sketch of the potential energy surface of c‐P6⁶⁺ around the energy minimum as described by different DFAs.

Thus far, we have analyzed the isolated nanoring model. At the B3LYP level of theory, the addition of the template and the aryl groups breaks the D _6h symmetry that was originally predicted by the naked nanoring, providing an overall geometry that is much closer to the CAM‐B3LYP C _3h geometry. For B3LYP, M06‐2X, and CAM‐B3LYP geometries, the root mean square deviations (RSMD) of the ¹H‐NMR chemical shifts of various relevant hydrogen atoms are collected in Table 3 (see Figure S1). Reproducing experimental ¹H‐NMR values is a very challenging computational task because they depend not only on the molecule's geometry but also on the solvent and the temperature. ^[39] However, CAM‐B3LYP geometry provides the closest agreement with the experiment for all compounds tested, whereas B3LYP′s provides the worst agreement (see Table 3), especially in the case c‐P6⁶⁺. Hence, we can safely conclude that CAM‐B3LYP geometries and the ¹H‐NMR of c‐P6, c‐P6⁶⁺, and c‐P6¹²⁺ conform to the experimental data, whereas, in the case of c‐P6⁴⁺, there are large discrepancies between the experimental data and all the examined DFAs. As we shall see in the following sections, obtaining the right geometry is crucial to correctly assess the aromaticity of c‐P6⁶⁺. Hereafter, unless otherwise explicitly indicated, we will refer to the results obtained from CAM‐B3LYP geometries.

Table 3.

Selected ¹H‐NMR chemical shift differences (in ppm).^[a]

Method	data	c‐P6⋅T6	c‐P6⋅T64+	c‐P6⋅T66+	c‐P6⋅T612+
CAM‐B3LYP	β‐α	2.40	0.09	−0.79	−2.15
	o′‐o	0.09	0.41	−0.19	−0.91
	α‐αtemp	−6.34	−1.92	−0.97	1.88
	β‐βtemp	−2.54	−0.44	−0.36	1.13
	RMSD	0.16	–	1.35	0.45
B3LYP	β‐α	1.95	−12.75	0.99	−4.37
	o′‐o	0.31	36.36	−7.23	−2.67
	α‐αtemp	−5.34	60.43	−12.26	5.63
	β‐βtemp	−1.97	49.10	−9.85	2.68
	RMSD	0.30	–	5.36	1.41
Experimental	β‐α	2.58	−2.80	−0.44	−2.48
	o′‐o	0.26	–	−1.87	−0.74
	α‐αtemp	−6.31	14.16	−2.83	2.77
	β‐βtemp	−2.34	12.57	−2.06	1.50

[a] RMSD are based on nine ¹H‐NMR differences with respect to the experimental data available in Ref. [9]. Data for c‐P6⋅T6⁴⁺ is taken from Ref. [13]. α^temp and β^temp are the corresponding data calculated on the isolated template (see Figure 1). See Figure S1 and Tables S3 and S4 for computational details, proton labels, and all ¹H‐NMR values.

We focus now on the local aromaticity of the porphyrins, which is assessed by studying the circular conjugation pathways that go through C−C or C−N bonds around each porphyrin. The pathway going through the C−N bonds of the imine group is labeled as “i”, whereas the one following the C−C bonds of the imine group is labeled as “o”. There are 16 pathways for each porphyrin but some of them are equivalent by symmetry. We employ ACID plots ^[40] as a magnetic criterion of aromaticity, as well as several electron‐delocalization measures of aromaticity. ^[41]

In Table 4, the results for all the possible pathways in the porphyrins of the neutral species are collected. The delocalization indices ^[47] do not show significant differences between neighboring C−N and C−C bonds in the imine group, indicating no clear preferential pathway in the porphyrins of c‐P6 (see Figure S3). AV_min, ^[46] which measures the least delocalized fragment along the pathway, does not find significant differences among the paths either, a fact which is further confirmed by the ACID plot of Figure 3 a. Other aromaticity measures like FLU[ ⁴² , ⁴³ ] or HOMA ^[44] find some differences between the pathways, but one should keep in mind that, unlike AV_min, these indices failed to identify the most aromatic pathway in simple porphyrins.[ ³ , ³⁵ ]

Table 4.

Aromaticity indices for the different pathways within the porphyrins of c‐P6 calculated at the CAM‐B3LYP/6‐31G* level of theory.^[a]

Pathway	FLU[ 42 , 43 ]	BOA	HOMA [44]	BLA	AV1245 [45]	|AVmin| [46]
oooo	0.023	0.235	0.658	0.050	1.64	0.57
iiii	0.007	0.071	0.927	0.017	0.92	0.52
ioio (2)	0.016	0.162	0.778	0.036	1.32	0.52
iiio (4)	0.012	0.119	0.848	0.027	1.13	0.52
iioo (2)	0.016	0.162	0.778	0.036	1.32	0.52
iooi (2)	0.016	0.162	0.778	0.036	1.32	0.52
oooi (4)	0.020	0.200	0.715	0.043	1.49	0.52

[a] The number in brackets indicates the number of equivalent pathways.

Figure 3.

ACID isosurface plots (isocontour value 0.06) for a) c‐P6, b) c‐P6⁴⁺, c) c‐P6⁶⁺, and d) c‐P6¹²⁺ at the CAM‐B3LYP/6‐31G* level of theory.

In Table 5, we collect the results of the most aromatic pathway of the porphyrins for all the oxidation states of the nanoring according to different aromaticity descriptors. All the indices find that the porphyrins of c‐P6 are less aromatic than those of porphin (see Table S6) but aromatic nonetheless. Although the indices do not agree on the most aromatic pathway of the porphyrins (see Tables S7 and S9), there is a consensus among the descriptors concerning the aromatic character of the porphyrins in c‐P6 and the fact that c‐P6⁴⁺′s, c‐P6⁶⁺′s, and c‐P6¹²⁺′s porphyrins are much less aromatic than those of c‐P6. ACID plots (see Figure 3) concur with these results, even though they identify the porphyrins in c‐P6⁴⁺ as aromatic.

Table 5.

Aromaticity indices for the most aromatic pathway of porphyrins calculated at the CAM‐B3LYP/6‐31G* level of theory.

Species	FLU	HOMA	AV1245	|AVmin|	ACID
c‐P6	0.007	0.927	1.64	0.57	A
c‐P64+	0.016	0.784	1.45	0.32	A
c‐P66+	0.017	0.760	1.33	0.24	NA
c‐P612+	0.027	0.426	0.63	0.04	NA/AA
porphin	0.006	0.968	2.16	1.28	A

¹H‐NMR results were also used by Anderson et al. ^[9] to assess the aromaticity of the porphyrins. According to the experiment (see Table 3), the differences between the shielding of α and β protons of the template (see Figure S1) are 2.58, −2.80, −0.44, and −2.48 ppm for c‐P6⋅T6, c‐P6⋅T6⁴⁺, c‐P6⋅T6⁶⁺, and c‐P6⋅T6¹²⁺, respectively. The latter values are associated with aromatic, antiaromatic, non‐aromatic, and antiaromatic porphyrins. CAM‐B3LYP values are 2.40, 0.09, −0.79, and −2.15 ppm, in good agreement with the experimental values, whereas the B3LYP values for c‐P6⋅T6⁴⁺, c‐P6⋅T6⁶⁺, and c‐P6⋅T6¹²⁺ show larger discrepancies.

Finally, we study how the constituent parts of the compound change upon oxidation of the nanoring. We have performed an effective oxidation state (EOS)[ ⁴⁸ , ⁴⁹ ] analysis of three different fragments of the nanoring: the zinc atoms (Zn), the porphyrins (P), and the linkers (L). The carbon shared by the porphyrin and the linkers is assigned to the porphyrin. The results of this analysis are collected in Table 6. In all species, the Zn atom has an EOS of +2, indicating that the oxidized electrons never come from the Zn atom. In c‐P6⁴⁺, the electrons are subtracted from the butadiyne linkers, distorting the overall symmetry that the linkers had in the neutral species. Interestingly, in compounds with higher oxidation states, c‐P6⁶⁺ and c‐P6¹²⁺, the electrons are subtracted from the porphyrins, restoring the symmetry of the neutral species. These results agree with the decrease of local aromaticity we have found with the aromaticity descriptors and help to explain the loss of symmetry in the case of c‐P6⁴⁺.

Table 6.

Effective oxidation States (EOS) of several fragments of the nanoring at the CAM‐B3LYP/6‐31G* level of theory.

Species	Zn	Porphyrins	Linkers
c‐P6	+2	0	−2
c‐P64+	+2	0	(−1)×4, (−2)×2
c‐P66+	+2	+1	−2
c‐P612+	+2	+2	−2

Now, we assess the global aromatic character of the nanoring structure, i.e., we focus on finding a closed conjugation pathway that goes around the nanoring belt. This pathway involves both the porphyrins and the linkers that bridge them. Since we have already studied the aromaticity of the porphyrins, we first focus on the butadiyne linkers and, afterward, we analyze the whole conjugated pathway involving both structures.

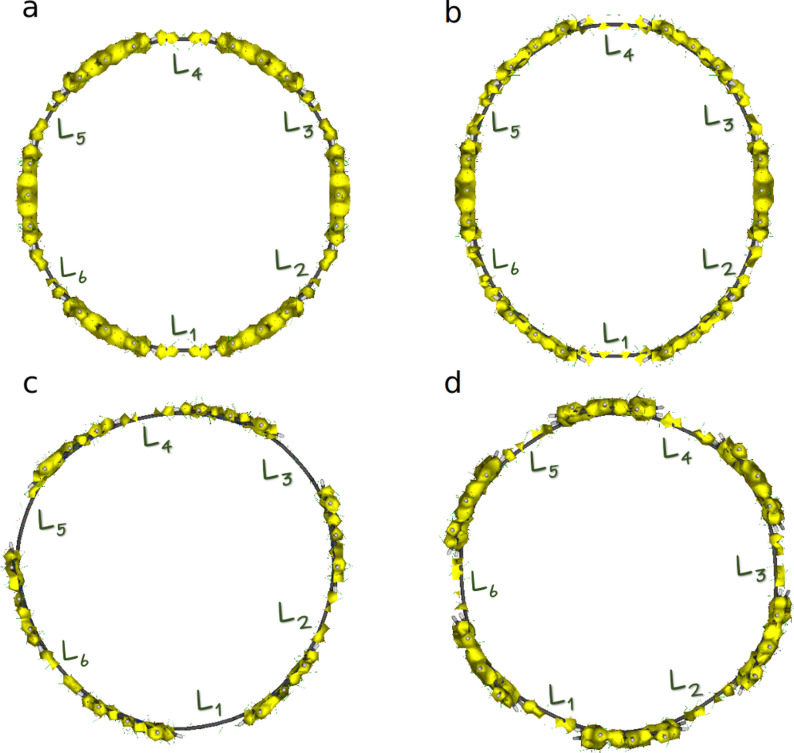
In Table 7, we collect the MCI ^[50] of the six carbons that compose each linker. MCI values measure the extent of electron delocalization along the carbon atoms in the linker, ^[51] which is rather small for c‐P6 and c‐P6¹²⁺, indicating that the linkers cannot contribute to forming a completely delocalized circuit along the nanoring belt (hence, c‐P6 and c‐P6¹²⁺ cannot be considered aromatic molecules). MCI values for c‐P6⁴⁺ and c‐P6⁶⁺ exhibit an alternated pattern, i.e., an uneven delocalization of the linkers, which also precludes the appearance of a global conjugated pathway that can be connected with aromaticity. This picture is corroborated by the ACID plots shown in Figure 4, where we can see disconnected sections around the position of the linkers for all oxidation states. From this analysis and the local aromaticity of the porphyrins, we can construct the schematic model of the four nanorings’ aromaticity that we collect in the first row of Figure 5.

Table 7.

MCI (×1000) values for the six carbon atoms that form the linker bridging two porphyrins.

Species/Linker	L1	L2	L3	L4	L5	L6
c‐P6	1	1	1	1	1	1
c‐P64+	20	4	4	20	4	4
c‐P66+	1	21	1	21	1	21
c‐P612+	1	1	1	1	1	1

Figure 4.

ACID isosurface plots (isocontour value 0.06) for a) c‐P6, b) c‐P6⁴⁺, c) c‐P6⁶⁺, and d) c‐P6¹²⁺.

Figure 5.

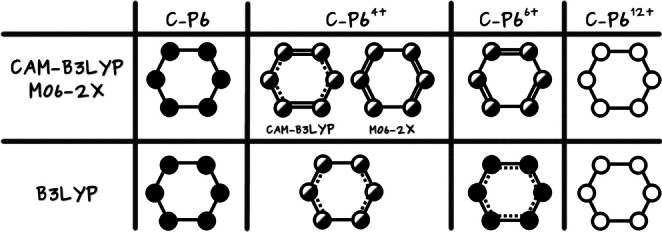
The global aromatic character of the nanoring from its constituent parts according to the optimized geometries obtained with different DFAs. Full, half‐full, and empty circles represent aromatic, weakly aromatic, and non‐aromatic porphyrins, respectively. The electron delocalization in the linkers increases from single solid lines (no delocalization) to solid‐dashed lines and, finally, double lines.

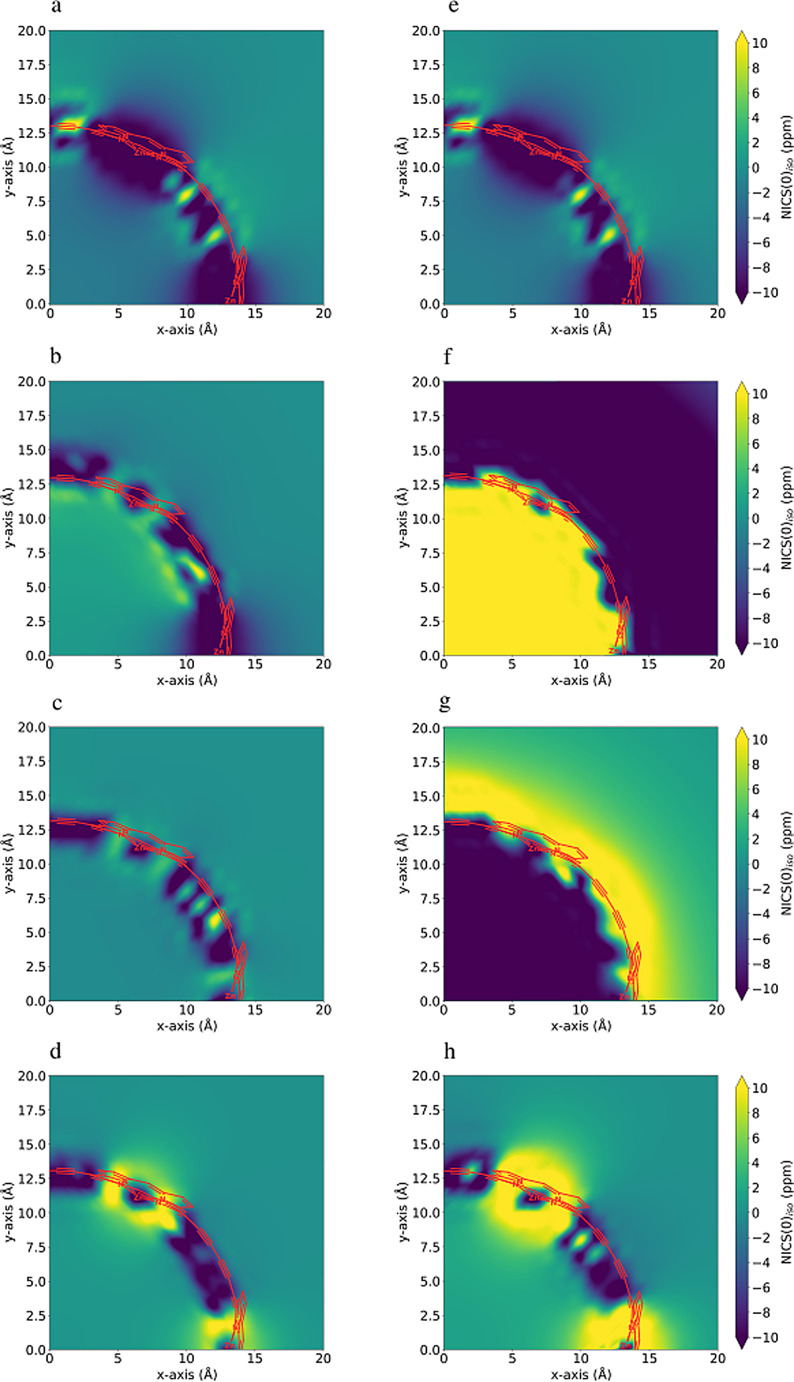
The global aromaticity of the nanoring can be further analyzed using several aromaticity criteria (for further details see the Supporting Information). We rely here on AV_min, ^[46] which measures the electron delocalization along the different aromatic pathways of the nanoring.[ ² , ³⁵ ] For c‐P6¹²⁺, AV_min is negligible for all the conjugation pathways, clearly establishing the non‐aromatic character of this molecule. For c‐P6, c‐P6⁴⁺, and c‐P6⁶⁺, the values of AV_min are negligible for most pathways except the one that passes through the nitrogen atoms of imine groups of each porphyrin. In this pathway, AV_min is also low but not negligible, which is reminiscent of some expanded porphyrin structures, which were considered very weakly aromatic or antiaromatic. ^[35] There is, however, an important difference concerning the latter case: in aromatic expanded porphyrins, the minimal value of electron delocalization was achieved twice or three times during the whole pathway (see Figure S4), whereas in the case of c‐P6⁴⁺ and c‐P6⁶⁺ there are multiple (over twenty) low‐delocalization fragments, as we can see in the delocalization profile of Figure 6. For this reason, all the nanorings in the present study are considered non‐aromatic, according to AV_min. Interestingly, for c‐P6⁴⁺, c‐P6⁶⁺, and c‐P6¹²⁺, the vast majority of these disconnection points occur in the transition from the porphyrin to the linker, whereas for c‐P6, the least delocalized fragment corresponds to an internal fragment inside the porphyrin. ACID confirms the most aromatic pathway indicated by AV_min, and its discontinuous isosurfaces (see Figure 4) also suggest that the molecules are non‐aromatic, especially c‐P6⁶⁺, for which large discontinuities also occur in the vicinity of the linkers. Finally, we have performed two‐dimensional NICS profiles[ ⁵² , ⁵³ ] and collected them in l.h.s. of Figure 7. In all cases, the values of the NICS inside and outside the nanoring belt are very close to zero, further confirming the global non‐aromatic character of these molecules.

Figure 6.

The 1245‐index distribution along the most aromatic path.

Figure 7.

NICS(0)_iso ^[54] grid plots for c‐P6, c‐P6⁴⁺, c‐P6⁶⁺, and c‐P6¹²⁺ species from top to bottom, respectively. a)–d) corresponding to the CAM‐B3LYP optimized geometries and e)–h) to the B3LYP ones. See Figure S15 and Table S14 for further details of this computation.

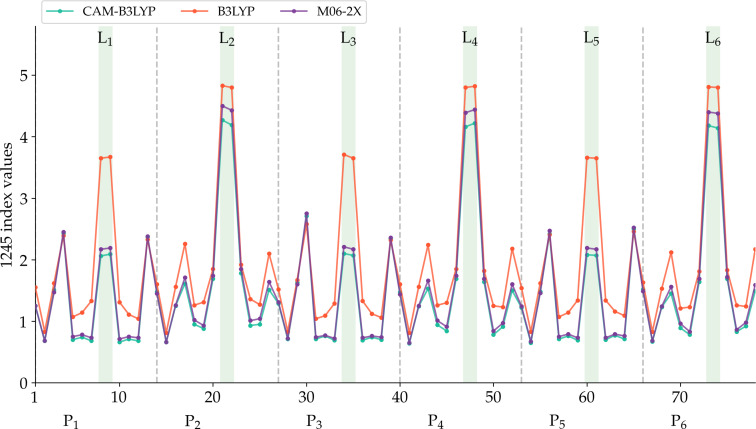
Figure 5, provides a qualitative comparison of the aromaticity analyses performed on CAM‐B3LYP (or M06‐2X) and B3LYP geometries. There are no significant differences for c‐P6 and c‐P6¹²⁺, as expected from the similarity of these geometries regardless of the DFA employed for the optimization. In fact, only for c‐P6⁶⁺, we obtain a completely different picture of the aromaticity from different methods. The large negative number of the two‐dimensional NICS profile in the vicinity of the nanoring center (see the r.h.s. of Figure 7) and the continuous ACID plots (Figure S14) indicate that the B3LYP geometry is globally aromatic. This is further corroborated by the larger AV_min value and, most importantly, by the 1245‐index distribution profiles (Figure 8), where we observe the drastic reduction in the number of fragments with a low delocalization. The comparison of the aromaticity measures between B3LYP and CAM‐B3LYP c‐P6⁴⁺ geometries also suggests that B3LYP overestimates the global antiaromaticity of this molecule, as the NICS (see Figure 7 and Table S14) shows a large positive value in the center of the ring and the ACID plots exhibit a continuous paratropic ring current (Figure S14). These results align with the recent results of Sundholm and co‐workers, which identify CAM‐B3LYP as a good method to calculate magnetizabilities ^[55] and the fact that B3LYP tends to overestimate the paramagnetic ring currents. ^[56] On the other hand, AV_min and the 1245‐index distribution profiles (Figure S8) are consistent with c‐P6⁴⁺ being a rather antiaromatic or a weakly aromatic molecule, regardless of the geometry. Since the results of no DFA satisfactorily conform to the experimental data, the results of c‐P6⁴⁺ should be taken with caution.

Figure 8.

The 1245‐index distribution along the most aromatic path of c‐P6⋅T6⁶⁺. See Figure 6 to locate the points of the molecule represented in the x‐axis.

Anderson and co‐workers’ strongest experimental evidence to assess the global aromaticity of c‐P6⁶⁺ comes from the NMR data. They study the (de)shielding of the trihexylsilyl groups (see Figure 1), the ortho protons (o and o′) in the aryl groups (see Figure S1), and the shielding difference between the α (or β) proton of the bound template and the free template, Δδ _α=δ _α−δ ${}_{\alpha {}^{\mathrm{temp}}}$ (Δδ _β=δ _β−δ ${}_{\beta {}^{\mathrm{temp}}}$ ). ^[13] The former data cannot be studied in the present paper due to the computational limitations that pose such large structure. However, we can analyze α, β, and ortho protons. The B3LYP geometry finds that δ _o′−δ _o is −7.23 ppm, whereas CAM‐B3LYP and M06‐2X results are −0.19 ppm and −0.36 ppm, respectively, which are in closer agreement with the experiment, ^[9] 1.87 ppm (see Tables 3 and S3). The CAM‐B3LYP values of Δδ _α and Δδ _β are in much better agreement with the experimental data than the B3LYP ones. Rikhaus et al. ^[13] argue that Δδ _α<0 and Δδ _β<0 are an indication of the presence of a global aromatic current (while the opposite is evidence of an antiaromatic current). However, this would indicate not only that c‐P6⋅T6⁶⁺ is globally aromatic, but also that c‐P6⋅T6 is even more aromatic than the former, which is not supported by any other experimental or computational data. We have also calculated Δδ _α and Δδ _β in a bound template in which we have eliminated the alleged current (by removing the bridging butadiyne linkers), and we have found negative and positive Δδ _α and Δδ _β, which would support the presence of a ring current even in the absence of connectivity among the porphyrins (see Supporting Information). These results bring about two important conclusions. First of all, it reinforces the idea that CAM‐B3LYP (or M06‐2X) are more adequate methods to obtain the geometry of potential aromatic molecules than B3LYP, which incurs large delocalization errors. Second, through various aromaticity probes, we have shown that the B3LYP geometry of c‐P6⁶⁺ corresponds to a quite aromatic molecule with δ _o′−δ _o=−7.23 ppm, and Δδ _α=−12.26 ppm. Hence, if the corresponding experimental values are only −1.87 ppm and −2.83 ppm, respectively, this is clearly suggesting that c‐P6⋅T6⁶⁺ is either very weakly aromatic or non‐aromatic, as the CAM‐B3LYP results indicate. This result is further reinforced by a recent finding ^[57] that the experimental aromatic stabilization energy of c‐P6⋅T6⁶⁺ is ca. 1.2 kcal mol⁻¹, which is relatively small for an aromatic molecule.

Conclusion

We have provided compelling evidence that the B3LYP description of c‐P6⁶⁺ suffers from severe delocalization errors that result in the overestimation of the aromaticity of this species. This is yet another proof[ ² , ³ , ³¹ , ³² , ³³ , ³⁴ , ³⁵ ] that DFAs with a low percentage of long‐range HF exchange should not be used to analyze aromatic compounds, especially large conjugated circuits. Computational results at the CAM‐B3LYP level conform with the experimental data for c‐P6, c‐P6⁶⁺, and c‐P6¹²⁺, whereas, for c‐P6⁴⁺, none of the DFAs we have employed provides a satisfactory agreement with the experiment. Through careful computational analysis and the judicious examination of the ¹H‐NMR data, we conclude that c‐P6⁶⁺ is not aromatic and that ¹H‐NMR data cannot be used to unequivocally assess the aromaticity of this species. Hence, none of the large nanorings studied can be considered aromatic, and the quest for large aromatic nanorings should be continued. Although an enhanced conjugation of some pathways passing through the porphyrins would help to increase the global aromaticity of these nanorings, our results show that the main reason behind the absence of an aromatic ring current in these nanorings is the low delocalization in the transition from the porphyrins to the bridging butadiyne linkers, which disrupts the overall conjugated circuit.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

I. Casademont-Reig, R. Guerrero-Avilés, E. Ramos-Cordoba, M. Torrent-Sucarrat, E. Matito, Angew. Chem. Int. Ed. 2021, 60, 24080.