Validation of a perioperative population factor VIII pharmacokinetic model with a large cohort of pediatric hemophilia a patients

Abstract

Aims

Population pharmacokinetic (PK) models are increasingly applied to perform individualized dosing of factor VIII (FVIII) concentrates in haemophilia A patients. To guarantee accurate performance of a population PK model in dose individualization, validation studies are of importance. However, external validation of population PK models requires independent data sets and is, therefore, seldomly performed. Therefore, this study aimed to validate a previously published population PK model for FVIII concentrates administrated perioperatively.

Methods

A previously published population PK model for FVIII concentrate during surgery was validated using independent data from 87 children with severe haemophilia A with a median (range) age of 2.6 years (0.03–15.2) and body weight of 14 kg (4–57). First, the predictive performance of the previous model was evaluated with MAP Bayesian analysis using NONMEM v7.4. Subsequently, the model parameters were (re)estimated using a combined dataset consisting of the previous modelling data and the data available for the external validation.

Results

The previous model underpredicted the measured FVIII levels with a median of 0.17 IU mL⁻¹. Combining the new, independent and original data, a dataset comprising 206 patients with a mean age of 7.8 years (0.03–77.6) and body weight of 30 kg (4–111) was obtained. Population PK modelling provided estimates for CL, V1, V2, and Q: 171 mL h⁻¹ 68 kg⁻¹, 2930 mL 68 kg⁻¹, 1810 mL 68 kg⁻¹, and 172 mL h⁻¹ 68 kg⁻¹, respectively. This model adequately described all collected FVIII levels, with a slight median overprediction of 0.02 IU mL⁻¹.

Conclusions

This study emphasizes the importance of external validation of population PK models using real‐life data.

What is already known about this subject

• Population PK models for FVIII are increasingly applied for dose individualization in haemophilia A patients.

• To guarantee an adequate performance of a population PK model in dose individualization, external validation is of importance.

• For the published perioperative population PK model for factor VIII concentrates, only internal validations have been conducted.

What this study adds

• The constructed population PK model in this study was able to adequately predict FVIII levels in children as well as adults.

• Before population PK models are clinically applied, they should be validated using data from an independent cohort of patients.

• Efforts should be put into collecting data from independent cohorts of patients to externally validate existing population PK models.

1. INTRODUCTION

Haemophilia A is caused by mutations in the coagulation factor VIII (FVIII) gene, resulting in a deficiency of functional FVIII. ¹ Haemophilia severity is categorized according to residual baseline FVIII levels, as patients with a FVIII level between 0.40 and 0.05 IU mL⁻¹ are considered mildly affected, a FVIII level between 0.01 and <0.05 IU mL⁻¹ is moderate and patients with a FVIII level <0.01 IU mL⁻¹ are considered severely affected. ² , ³ Due to FVIII deficiency, patients experience recurrent bleeding primarily in joints and muscles either spontaneously or after minimal trauma, which often leads to pain, swelling and joint damage, and, when treated inadequately, to invalidity. ⁴ To prevent bleeding, severe and some moderate patients are administered FVIII concentrates prophylactically multiple times per week.

In the perioperative setting, higher FVIII levels are targeted during longer periods of time to maintain haemostasis when compared to the non‐surgical prophylactic setting. ⁵ In general, a bolus dose is administered before surgery with subsequent intermittent dosing or continuous infusion with FVIII concentrates to maintain targeted trough levels. It has been demonstrated that perioperative dosing of FVIII concentrates can be individualized using individual PK parameters, as obtained from a perioperative population PK model using maximum a posteriori (MAP) Bayesian analysis. ⁶ This process can be applied iteratively to adjust FVIII doses, according to obtained FVIII blood samples during perioperative monitoring.

When constructing population PK models, the final model is, in general, validated internally using statistical or in silico simulation methods, evaluating the predictability of the model with the same data as used to construct the model. ⁷ However, to test an established population PK model, an external validation with data from patients not contributing to the construction of the final model provides the most stringent approach for model testing. ⁸ As an external validation requires the availability of an independent patient dataset, this type of validation is not performed frequently.

In this study, an external validation of a previously published perioperative population PK model was conducted using an external and independent dataset comprising 87 children undergoing 145 surgical procedures to replace, insert or remove a central venous access device (CVAD). ⁹ First, the predictive performance of a previously published perioperative population PK model ¹⁰ was evaluated, after which the paediatric surgical FVIII data were added to the original data to enrich the currently published perioperative FVIII population PK model.

2. METHODS

2.1. Patients and clinical data

In this study, data from severe and moderate paediatric (age < 18 years) haemophilia A patients undergoing a minor or major elective surgery were gathered retrospectively at the Great Ormond Street Hospital in London, UK. Surgeries were conducted to remove, replace and or insert a CVAD to facilitate FVIII concentrate administration. ⁹

In the perioperative period, patients received replacement therapy with one of the following products: recombinant FVIII concentrates (Advate and Recombinate: Baxter Bioscience, Thousand Oaks, CA, USA; Kogenate FS: Bayer, Berkeley, CA, USA; Refacto AF: Pfizer, New York, NY, USA; Helixate FS: CSL Behring, Marburg, Germany; Octanate and Nuwiq: Octapharma AB, Stockholm, Sweden; Innovate: Biomed Lublin, Lublin, Poland) or plasma‐derived FVIII concentrates (Monoclate‐P: CSL Behring, Kankakee, IL, USA). Other patient characteristics are described in Table 1.

TABLE 1.

General characteristics of the study population

	New cohort	Original cohort	Total cohort
	No. (%) or median [range]
Patient characteristics
No. of patients	87	119	206
Age (years)	2.57 [0.03–15.2]	39.6 [0.24–77.6]	7.79 [0.03–77.6]
Body weight (kg)	14.0 [4.00–57.0]	75.0 [5.00–111]	30.0 [4.00–111]
Severe haemophilia A (<0.01 IU mL−1)	87 (100)	83 (70)	170 (83)
Blood group Oa	30 (34)	50 (42)	80 (39)
Historical VWF levels (mmol L−1)
Antigen	–	1.13 [0.25–2.46]	1.13 [0–2.46]
Activity	–	1.15 [0.24–2.66]	1.15 [0.24–2.66]
Surgical characteristics
No. of surgical procedures	145	197	342
Total no. of patients undergoing:
1	50 (57)	75 (63)	125 (61)
2	26 (30)	25 (21)	51 (25)
3	4 (5)	10 (8)	14 (7)
>3	7 (8)	9 (8)	16 (8)
Minor surgical procedures	145 (100)	100 (51)	245 (72)
Major surgical procedures	0 (0)	97 (49)	97 (28)
Replacement therapy with FVIII concentrate
Mode of infusion
Occasions with continuous	0 (0)	117 (59)	117 (34)
Occasions with bolus	145 (100)	80 (41)	225 (66)
Product type
Recombinant	144 (99)	157 (80)	301 (88)
Plasma‐derived	1 (1)	40 (20)	41 (12)
PK data
Total number of observations	508	1584	2092
No. of observations per occasion	3 [1–18]	7 [1–25]	4 [1–25]
No. of doses per occasion	9 [2–50]	11 [3–44]	10 [2–50]
No. of observations prior to surgery	168 (20)	223 (18)	391 (19)
No. of observations Day 1 (0 h–24 h)	177 (26)	353 (25)	530 (25)
No. of observations Day 2 to Day 5 (24 h–120 h)	144 (33)	524 (32)	668 (32)
No. of observations Day >5 (>120 h)	19 (25)	484 (24)	503 (24)

kg, kilogram; and IU mL⁻¹, international units per millilitre; VWF: von Willebrand factor. ^a Blood group available in 175 of 206 patients. Adapted from Hazendonk et al. with permission. ¹⁰

The study was not subject to the Medical Research Involving Human Subjects Act and was approved by all Medical Ethics Committees in the Netherlands. In the United Kingdom, the study was approved by the Research Ethics Committee (NRES committee South Central‐Berkshire, REC reference 15/SC/0367); an opt‐out consent procedure was used to collect anonymized clinical data.

2.2. External validation

A previously published perioperative population PK model ¹⁰ was applied to the paediatric data, as described above, in order to evaluate its predictive performance. To obtain the predictive performance of the model, the predicted FVIII levels were compared with the measured FVIII levels using goodness‐of‐fit (GOF) plots. ¹¹ Moreover, the deviation between the measured and predicted FVIII levels was quantified with the median of the residuals, by subtracting the measured from the predicted FVIII levels. Furthermore, (prediction‐corrected) visual predictive checks (pdVPCs) were performed using Monte Carlo simulation of 2000 patients.

As covariate relationships allow explanation of the inter‐individual variability (IIV) or inter‐occasion variability (IOV), the distribution of etas can be plotted against covariate values to investigate possible relationships between the covariate and a population PK parameter. Moreover, to verify if the mean was different from zero, a one‐sample t‐test was conducted to verify if the mean was different from zero as the distribution of etas is regarded to be normally distributed.

2.3. Population pharmacokinetic modelling

The analysis of the perioperative FVIII dosing and FVIII level measurement data was performed simultaneously for all patients using NONMEM version 7.4 (ICON Development Solutions, Ellicott City, MD, USA). ¹² First‐order conditional estimation with interaction (FOCE+I) was applied to obtain estimates for all model parameters. If a pre‐operative FVIII level without prior dosing information was available for a patient, this measurement was considered by allowing all model compartments to be initialized to the value of FVIII level multiplied by the corresponding volume of distribution with the A_0 option in NONMEM. To aid model development, Perl‐speaks‐NONMEM (PsN) version 4.7.0 and Pirana version 2.9.1 were used. ¹³ , ¹⁴ , ¹⁵ After adding a parameter to the model, the objective function value (OFV) was used to determine if this allowed a significantly better description of the data. As the difference in the OFV (dOFV) between evaluated models is associated to the chi‐squared distribution, a difference greater than 3.84 was associated with a P‐value of <.05 with one degree of freedom.

Before constructing the population PK model, the original data that was used to construct the published perioperative population PK model was added to the current paediatric data (see Table 1). The modelling was initiated with a one‐compartment PK model. The previous analysis indicated that the lower measured FVIII levels for muroctocog alfa (Refacto AF) affects the estimation of the model parameters, ¹⁰ so this effect was considered as well in the structural model using the following equation:

$$C_{\mathit{\text{FVIII}},\mathit{ij}}=\left({\widehat{C}}_{\mathit{\text{PRED}},\mathit{ij}}+C_{\mathit{\text{base}},i}\right)-{\theta }_{\mathit{\text{prod}},i}{\left({\widehat{C}}_{\mathit{\text{PRED}},\mathit{ij}}+C_{\mathit{\text{base}},i}\right)}^{{\theta }_{\mathit{\text{Refacto}}\mathit{AF}}}+{\varepsilon }_{\mathit{ij}}$$ (1)

where C _FVIII,ij is the measured FVIII level for the ith individual and jth observation, C _PRED,ij is the predicted FVIII level by the population PK model, C _base,i is the measured endogenous FVIII level, θ _prod,i is the estimated effect fraction of a FVIII product on the measured FVIII level, θ _{Refacto AF} is a dichotomous covariate which has a value of 1 for the patients using muroctocog alfa and otherwise 0, and ε _ij is the residual error describing the residual unexplained variability (RUV). For modelling the RUV, additive, proportional and combined residual error models were considered. ¹⁶

Since FVIII PK data were available for both children and adults, PK parameters were normalized a priori to a body weight of 68 kg using the following equation:

$${\theta }_{\mathit{ik}}={\theta }_{\mathit{TV}}\times {\left(\frac{{\mathit{BW}}_{\mathit{ik}}}{68}\right)}^{{\theta }_{\mathit{BW}}}\times {\mathrm{e}}^{\left({\eta }_i+{\pi }_{\mathit{ik}}\right)}$$ (2)

where the subscripts i and k describe the number of the individual and the occasion, respectively, θ _TV is the estimated typical value for a population PK parameter, θ _ik is the estimated individual PK parameter, BW the value for body weight of the patient, θ _BW the allometric exponent and η and π describe the random effects accounting for IIV and IOV, respectively. Allometric exponents were fixed to 1 in case of a volume parameter (V1, V2) and to 0.75 for all clearance parameters (CL, Q2). ¹⁷ , ¹⁸

After construction of the structural model, patient characteristics, surgical and pathophysiological features were allowed to describe the unexplained IIV or RUV. The following continuous covariates were evaluated: age, body weight. Furthermore, the following categorical covariates were evaluated: having a minor or major surgical procedure, having blood group O, having moderate or severe haemophilia A, presence of inhibitors, receiving plasma‐derived or recombinant FVIII concentrate, brand of FVIII concentrate and if continuous infusion was applied. First, a univariate analysis was conducted for each covariate relationship. After adding a covariate relationship, the OFV determined if the relation was significant. Subsequently, all significant covariate relationships (P < .05) were re‐evaluated in a multivariate analysis, to test if simultaneous inclusion of the eligible covariates would still significantly decrease the OFV.

In the covariate analysis, a dichotomous covariate relationship was allowed using the following equation:

$${\theta }_i={\theta }_{\mathit{TV}}*{\theta }_{\mathit{cov}}$$ (3)

where θ _cov is the fraction of the typical PK parameter θ _TV and was only estimated if the covariate of interest was present, otherwise a value of 1 was used for θ _cov . This relationship was used to evaluate the following covariates: major surgical procedure, blood group O, brand of FVIII concentrate, if a patient received a recombinant FVIII product, presence of inhibitors, having severe haemophilia A and if continuous infusion was applied. For the age of the patient, a linear, a power and an exponential relationship were evaluated accordingly:

$${\theta }_i={\theta }_{\mathit{TV}}*\left(1+{\theta }_{\mathit{Age}}*\left(\mathit{AGE}-{\mathit{AGE}}_{\mathit{med}}\right)\right)$$ (4)

$${\theta }_i={\theta }_{\mathit{TV}}*{\left(\frac{\mathit{AGE}}{{\mathit{AGE}}_{\mathit{med}}}\right)}^{{\theta }_{\mathit{Age}}}$$ (5)

$${\theta }_i={\theta }_{\mathit{TV}}*e^{\left({\theta }_{\mathit{Age}}*\left(\frac{\mathit{AGE}-\mathit{AGE}\mathit{med}}{{\mathit{AGE}}_{\mathit{med}}}\right)\right)}$$ (6)

2.4. Model evaluation

The methods that allow performance of an external validation of a population PK model can also be applied to evaluate the constructed model and, hence, conduct an internal validation. The construction of a population PK model is a hierarchical process that is initiated with estimation of the simplest possible model. In each subsequent step, parameters are added to the model. With each step, the ability of the model to describe the data was evaluated using the OFV and GOF plots. Moreover, Monte Carlo simulations were used to evaluate whether the estimated typical values, IIV and IOV are appropriately estimated using pdVPCs. Prediction‐correction was applied for each VPC, since dosing was adapted to the measured FVIII levels during the perioperative period. ¹⁹

Furthermore, a non‐parametric bootstrap analysis was applied with resampling and replacement to test whether the model is robust to deviations in the data used to construct the model. ²⁰ This process was performed 1000 times to obtain medians and confidence intervals for the model parameters.

3. RESULTS

3.1. Patients and clinical data

The paediatric data consisted of 508 FVIII level measurements from 87 severe haemophilia A patients undergoing 145 minor surgical procedures. The age of the patients ranged from 0.03 to 15.2 years, with body weight ranging from 4 to 57 kg. As body weight was not available for ten of the patients, an imputation model using body weight and age of all other patients was constructed (Supplemental Table S1 and Figure S1). Other characteristics of the studied population are presented in Table 1.

3.2. External validation

FVIII levels for the patients from the new cohort were predicted with the published perioperative FVIII population PK model (Figure 1). For the population predicted FVIII levels (Figure 1A), an underprediction is shown for the clinically relevant FVIII levels between 0 and 1.5 IU mL⁻¹, as depicted by the red line which deviates from the line of identity (black line). The population FVIII levels in Figure 1A are predicted without taking IIV of clearance and central volume of distribution into consideration. MAP Bayesian analysis produced individual estimates for these parameters, from which the individual predicted FVIII levels can be calculated. In Figure 1B, the individual predicted vs measured FVIII levels are shown. The predictions were not symmetrically distributed around the line of identity as well, with a structural underprediction of the clinically relevant FVIII levels. The median of the residuals for the population and individual predicted FVIII levels for the clinically relevant FVIII level range (0–1.5 IU mL⁻¹) were −0.17 IU mL⁻¹ and −0.07 IU mL⁻¹, respectively.

FIGURE 1.

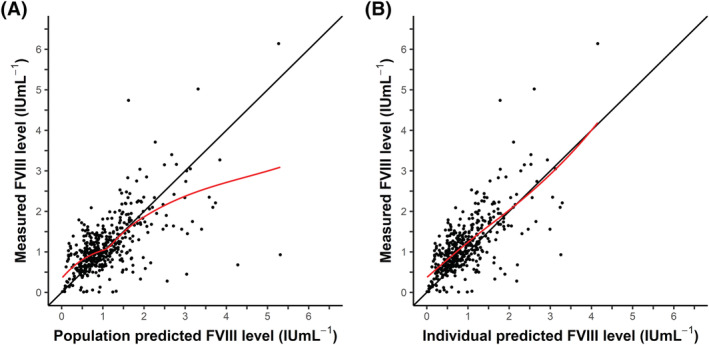
Predicted FVIII level vs measured FVIII level from the post hoc analysis of the new cohort. (A) Population predicted FVIII level vs measured FVIII level. For calculating the population predicted FVIII levels, no IIV was taken into account. (B) Individual predicted FVIII level vs measured FVIII level. To obtain the individual predicted FVIII level, IIV was taken into account. The black line (y = x) represents the line of identity. The red line depicts the local regression (LOESS) line, following the densest part of the data

In Figure 2, the post hoc values of the differences between the typical values from the population PK parameters of the original model and the individual PK parameter (etas) of clearance (CL) and the volume of distribution of the central compartment (V1) vs the age and body weight from each patient of the new cohort are shown. In each figure, the local regressor line (red line) is above the line y = 0 (black line), demonstrating a structural underprediction of the typical value for CL and V1. For a one‐year‐old paediatric patient with a body weight of 10 kg having a blood group other than O and having a minor surgical procedure, the model predicted values for CL and V1 obtained from the published population PK model were 68 mL h⁻¹ and 930 mL, respectively. However, as the mean of the distributions for eta of CL and V1 were 0.15 and 0.1, the calculated typical values become 79 mL h⁻¹ and 1027 mL. The mean of the eta distributions should be zero, as these distributions are regarded as normally distributed. The mean (eta = 0) then depicts the typical value of the population PK parameter. As a structural deviation from zero for the mean of the etas of CL (P < .001) and V1 (P < .001) was demonstrated, the typical values of CL and V1 from the published model were not adequate to predict the individual values for CL and V1 in the paediatric data.

FIGURE 2.

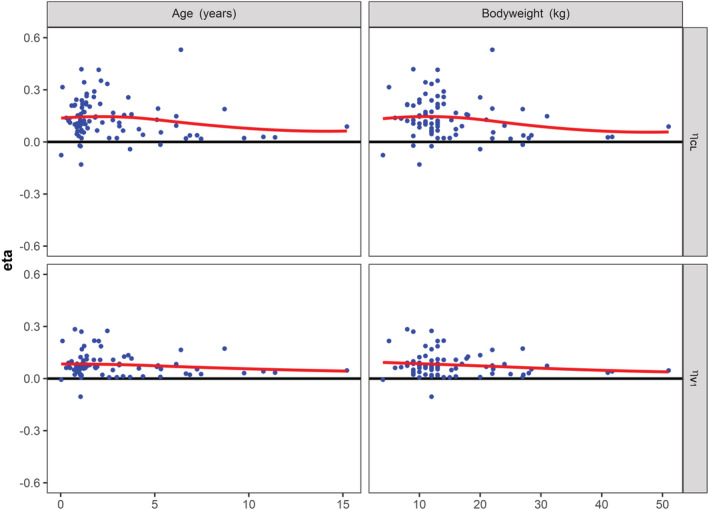
Eta of clearance and volume of distribution vs age and body weight for the new cohort. Post hoc values for eta of clearance (CL) and volume of distribution of the central compartment (V1) were obtained using the original population PK model and were plotted against age and body weight of the patients from the new cohort. Clearly, all the figures demonstrate a systematic bias from zero, as depicted by the locally estimated scatterplot smoothing (LOESS) line in red

Interestingly, the prediction‐corrected visual predictive check (pcVPC) demonstrated that the model was able to adequately predict the median observed FVIII levels (50th percentile; grey solid‐line), as these remained within the prediction interval (red boxes) of the 50th percentiles of the simulated FVIII levels (Figure 3). However, the variability shown by this prediction interval was large. Moreover, the IIV of CL and V1 and the RUV from the model were not adequate to predict the measured FVIII levels, as the 2.5th and 97.5th percentiles of the simulated FVIII levels (blue boxes) are above and below, respectively, the corresponding percentiles of the measured FVIII levels.

FIGURE 3.

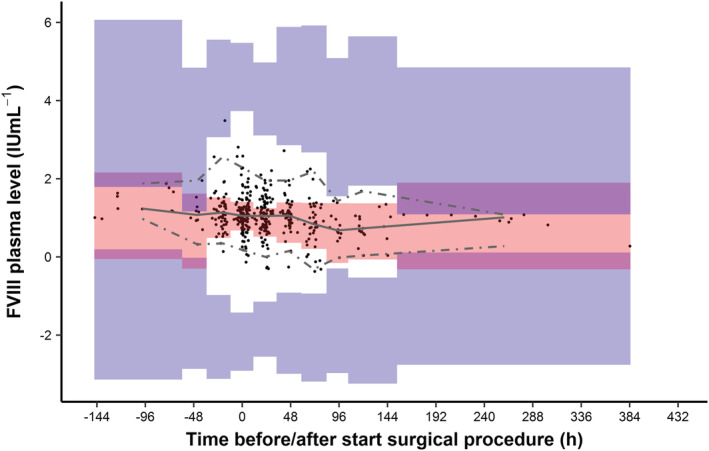
Prediction‐corrected visual predictive check of the original model for the new cohort. Time is defined as the time of start of the surgical procedure. Data with negative times represent samples taken before the start of the surgical procedure. Black dots represent the measured FVIII levels for all patients. Solid grey line represents the median and the dashed grey lines represent the 2.5th and 97.5th quantiles of the measured FVIII levels. Red and blue‐shaded areas show the 95% confidence intervals for the predicted individual FVIII levels, as obtained by 2000 Monte Carlo simulations using the original model. The binning of the areas for the prediction intervals were created using the auto‐bin option in Perl‐Speaks‐NONMEM. In total, approximately 5.7% of the measured FVIII levels were outside the 2.5th and 97.5th quantiles of the measured FVIII levels

3.3. Population pharmacokinetic modelling

As the published population PK model demonstrated an underprediction of the clinically relevant FVIII levels and underestimated the typical values of CL and V1, the population PK analysis was repeated. Therefore, the currently gathered data was added to the original data, comprising 75 adult and 131 paediatric haemophilia A patients undergoing 141 and 201 surgical procedures, respectively (Table 1).

The modelling steps taken to construct the population PK model are listed in Supplementary Table S2. A two‐compartment structural model with all parameters normalized to a body weight of 68 kg was statistically superior to a comparable one‐compartment model (dOFV = −199.2, P < .001). The precision of all model parameters was acceptable (relative standard error <25%). IIV and covariance could be estimated for CL and V1. The RUV was evaluated separately for each centre, which significantly improved the fit of the model to the data (dOFV = −25.6, P < .001). Moreover, none of the FVIII measurements were below the level of quantification (BLQ = 0.01 IU mL⁻¹). Table 2 lists the population PK parameter estimates from the structural model.

TABLE 2.

Estimated population PK parameters for the previously published original model, current structural model, current final model and bootstrap analysis of the current final model

	Original model a		Structural model			Final model			Bootstrap analysis
	Estimate	RSE (%)	Estimate	RSE (%)	Shr. [%]	Estimate	RSE (%)	Shr. [%]	Median	95% CI
Structural model
Clearance (CL; mL h−168 kg−1)	150	(8)	221	(4)		171	(7)		169.2	[149.6–204.4]
Volume of central compartment (V1; mL 68 kg−1)	2810	(4)	3350	(3)		2930	(4)		2913.8	[2722.4–3182.2]
Distribution CL to compartment 2 (Q2; mL h−1 68 kg−1)	160	(20)	170	(20)		172	(19)		167.9	[116.0–258.9]
Volume of compartment 2 (V2; mL 68 kg−1)	1900	(11)	1780	(11)		1810	(10)		1837.7	[1443.1–2210.9]
B‐domain deleted recombinant factor VIII	0.34	(13)	0.32	(12)		0.30	(14)		0.30	[0.21–0.37]
Inter‐individual variability (%CV)
IIV on CL	37	(14)	47.3	(8)	[9]	39.6	(10)	[11]	39.5	[32.0–52.1]
IIV on V1	27	(14)	31.6	(8)	[17]	27.5	(10)	[22]	27.3	[21.1–32.8]
Correlation between CL and V1	–		67.9	(9)		56.6	(12)		56.3	[47.6–56.9]
Residual variability
Additive residual variability (SD; IU mL−1)
Centres 1,2,3	0.15	(12)	0.12	(13)		0.12	(13)		0.12	[0.08–0.15]
Centres 4,5	0.05	(28)	0.06	(24)		0.06	(24)		0.06	[0.01–0.09]
Centre 6	–		0.19	(21)		0.17	(24)		0.16	[0.05–0.23]
Proportional residual variability (%CV)
Centres 1,2,3	18	(15)	19.8	(11)		19.7	(11)		0.20	[0.15–0.24]
Centres 4,5	23	(9)	21.2	(8)		0.21	(8)		0.21	[0.17–0.26]
Centre 6	–		19.2	(11)		0.22	(12)		0.21	[0.16–0.26]
Covariate relations
CL – Age (change with increasing age)	−0.17	(22)	–			−0.12	(26)		−0.12	[−0.18–−0.04]
CL – Blood group O (% difference)	26	(7)	–			14	(6)		14.2	[0.10–0.24]
CL – Major surgical procedure (% difference)	−7	(6)	–			–			–
V1 – Age (change with increasing age)	−0.09	(28)	–			−0.09	(24)		−0.09	[−0.13–−0.04]
Model characteristics
Objective function value	–		−3302.8			−3361.0			−3391.2	[−4126.2–−2714.1]
Condition number	–		23.3			63.0			–

RSE, relative standard error; CI, confidence interval as obtained using the 2.5th and 97.5th percentiles from the non‐parametric distributions; CV, coefficient of variation; Shr., shrinkage. Centres 1 to 5 depict data from haemophilia treatment centres in The Netherlands and Centre 6 depicts data from Great Ormond Street Hospital, London, UK. The typical values for CL and V1 are obtained for a haemophilia A patient weighing 68 kg, having an age of 40 years and not having blood group O:

^a

$\mathrm{CL}\left(\mathrm{mL}{\mathrm{h}}^{-1}\right)=171\times {\left(\frac{\mathrm{BW}}{68}\right)}^{0.75}\mathrm{x}{\left(\frac{\mathrm{AGE}}{40}\right)}^{-0.12}\times {1.14}^{\mathrm{BG}}$

$\mathrm{V}1\left(\mathrm{mL}\right)=2930\times {\left(\frac{\mathrm{BW}}{68}\right)}^{1.0}\times {\left(\frac{\mathrm{AGE}}{40}\right)}^{-0.09}$

In these equations, BW indicates actual body weight, AGE is the age of the patient, BG is group and 1 in the case of blood group O, and has a value of 0 otherwise.

IOV for CL and V1 was also evaluated with an occasion defined as one surgical procedure. Although a significant dOFV (−325.8, P < .001) was obtained for both parameters, the model became unstable in terms of parameter uncertainty and IOV was, therefore, omitted.

The structural model, as described above, was subsequently used to evaluate the covariate relationships. The covariate relationships for age were tested using Equation 4, 5 and 6. Based on the precision of the estimated model parameters, the extent of the reduction of the IIV on CL, and the improvement of the fit in terms of dOFV, the power relationship for age (Equation 5) performed best. Moreover, a power relationship also showed best performance in similar terms for age on V1. In the univariate analysis, the following relationships statistically improved the fit of the model: having a major surgical procedure, having severe haemophilia and having blood group O. However, in the multivariate analysis, having severe haemophilia did not show an improvement of the fit and was, therefore, omitted from the model.

3.4. Model evaluation

The robustness of the final model was evaluated using a bootstrap analysis. As the value 1 was contained in the confidence interval for the relationship of having a major surgical procedure on CL, this relationship was omitted. Subsequently, the final model was re‐evaluated using a bootstrap analysis (Table 2). In total, 1000 bootstrapped datasets were obtained and evaluated, from which 995 estimations were successful. All obtained medians were comparable to the estimated typical values from the final model and the confidence intervals agreed with the uncertainty found for parameters of the final model.

As compared to the published perioperative population PK model (Table 2), the estimated typical values of CL and V1 from the present final model were slightly increased from 150 to 171 mL h⁻¹ 68 kg⁻¹ and from 2810 to 2930 mL 68 kg⁻¹. For a one‐year‐old child weighing 10 kg, having a blood group other than O and having a minor surgical procedure, the typical value for CL slightly increased from 63.2 to 66.7 mL h⁻¹ 68 kg⁻¹, whereas the typical value for V1 was slightly reduced from 601 to 576 mL 68 kg⁻¹. Other typical values from the final model were comparable.

In Figure 4, the GOF plots of the final model are shown. The population predicted vs measured FVIII levels still demonstrated a slight underprediction of the FVIII levels from 0 to 1.5 IU mL⁻¹ (Figure 4A). In general, the individual predicted FVIII levels were symmetrically distributed showing the adequacy of the predictions from the final model (Figure 4B). In Figure 4C and D, the conditional weighted residuals (CWRES) are plotted vs predicted FVIII levels and time after start of the infusion. In both plots, the CWRES were randomly distributed around the line y = 0, illustrating the adequacy of the model. The median of the residuals for the population and individual predicted FVIII levels from the final model were −0.006 IU mL⁻¹ and 0.02 IU mL⁻¹, respectively.

FIGURE 4.

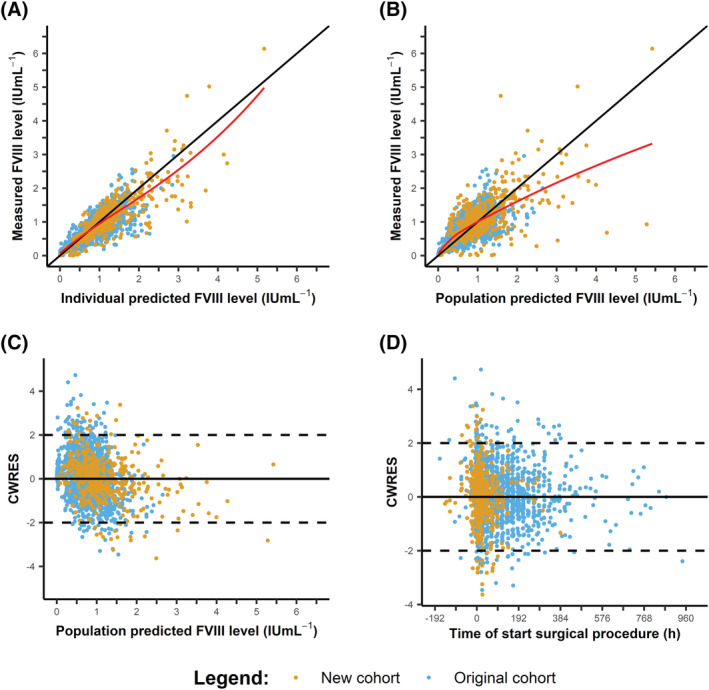
Goodness‐of‐fit of the plot of the final model for the total cohort. (A) Population predicted vs measured FVIII levels. (B). Individual predicted vs measured FVIII levels. (C) Conditional weighted residuals (CWRES) vs population predicted FVIII levels. (D) CWRES vs time, defined as the time of start of the surgical procedure. Negative times represent samples taken before the start of the surgical procedure. The measured FVIII levels from the original cohort are depicted in blue and for the new cohort in orange. In Figures (A) and (B), the LOESS line is depicted in red

In Figure 5, the distribution of the etas for CL and V1 are shown vs age and body weight of the total cohort. No deviation from zero (line y = 0) was obtained for the mean of the etas for CL (P = .88) and V1 (P = .55). For the paediatric data, similar results were obtained (Supplemental Figure S2).

FIGURE 5.

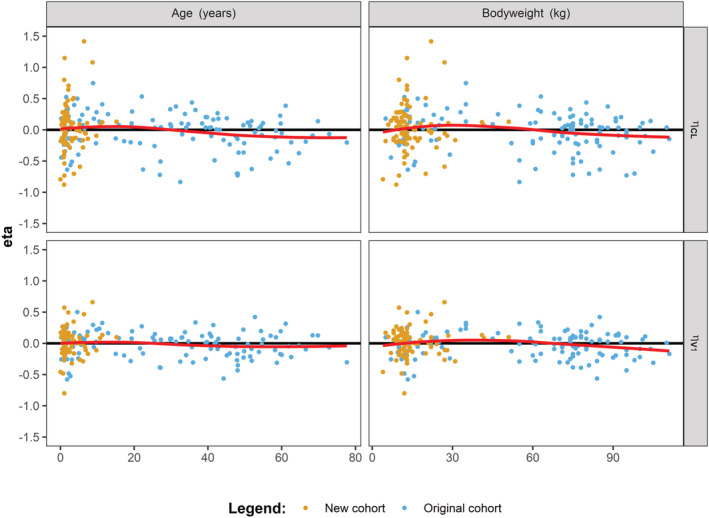
Etas of clearance and volume of distribution from the final model vs age and body weight for the total cohort. Post hoc values for eta of clearance (CL) and volume of distribution of the central compartment (V1) plotted against age and body weight of the patients from the total cohort. The locally estimated scatterplot smoothing (LOESS) line is depicted in red. The measured FVIII levels from the original cohort are depicted in blue and for the new cohort in orange

The pcVPC of the final model is shown in Figure 6. As the 2.5th, 50th and 97.5th quantile of the measured FVIII levels (shown by the red lines) are surrounded by the predicting intervals for the FVIII level predictions (coloured boxes) for each time interval (bin), the final model was shown to be adequately predicting the FVIII levels from the data without overt bias. To evaluate if the final model adequately predicted the FVIII levels for both paediatric patients and adults, a pcVPC was conducted with stratification using a dichotomous relation for age. As a result, a pcVPC was obtained for patients <12 years and patients ≥ 12 years (Supplemental Figure S3). Both pcVPCs adequately predicted the measured FVIII levels.

FIGURE 6.

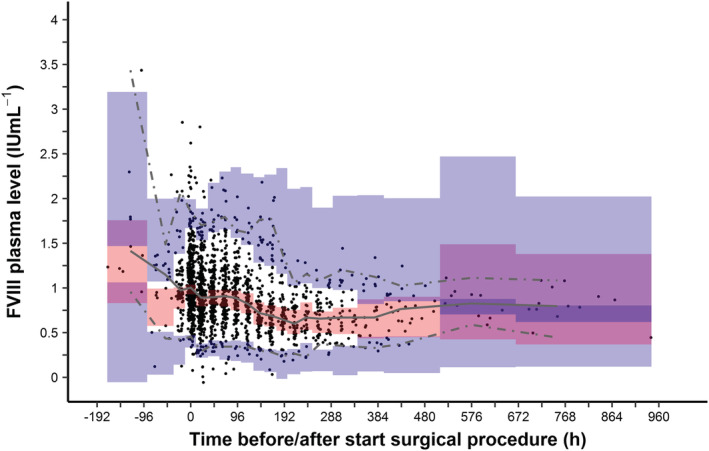
Prediction‐corrected visual predictive check of the final model for the total cohort. Time is defined as the time of start of the surgical procedure. Data with negative times represent samples taken before the start of the surgical procedure. Black dots represent the measured FVIII levels for all patients. Solid grey line represents the median and the dashed grey lines represent the 2.5th and 97.5th quantiles of the measured FVIII levels. Red and blue‐shaded areas show the 95% confidence intervals for the predicted individual FVIII levels, as obtained by 2000 Monte Carlo simulations using the final model. The binning of the areas for the prediction intervals were created using the auto‐bin option in Perl‐Speaks‐NONMEM. In total, approximately 6% of the measured FVIII levels were outside the 2.5th and 97.5th quantiles of the measured FVIII levels

4. DISCUSSION

In this study, a previously published perioperative population PK model for FVIII concentrate was validated using an independent dataset, containing data from children with haemophilia A undergoing minor surgical procedures. The previously published model underestimated the FVIII levels in the clinically relevant range from 0 to 1.5 IU mL⁻¹. Moreover, a structural underestimation was obtained for the etas for CL and V1 versus age and body weight. Therefore, a novel model was constructed using the original data and the collected paediatric data. As a result, a model was obtained comparable to the published population PK model. ¹⁰ The revised population PK model, as assessed by internal validation, adequately predicted the measured FVIII levels from both children and adults. In addition, the underestimation of CL and V1 was accounted for.

In the literature, external validations of a population PK model are not frequently described as this method requires an independent dataset. Such data are often laborious to collect, or require initiation of clinical trials. In most cases, population PK models are validated using the same dataset used to construct the model itself. Another technique is to utilize a substantial part of the data to construct the population PK model, whereas the remaining part of the data is used for validation. Previously, we reported our results of a comparison between three PK‐guided dosing tools performing MAP Bayesian analysis. ²¹ It was shown that, despite using the same input data, different individual PK parameter estimates were obtained and, hence, different recommended doses. These differences may arise due to differences between the applied population PK models implemented in the tools. Therefore, it is important to verify the predictive performance of population PK models using external validations, as these models may be applied in clinical practice to obtain dose recommendations.

In this study, only paediatric data was used to investigate the validity of the published population PK model, as the number of paediatric haemophilia A patients included in the model was clearly (too) small. Although we demonstrate in this study that the final model adequately describes the measured FVIII levels of paediatric haemophilia A patients, the validity of the original model for adult haemophilia A patients was not investigated. However, the predictive performance of the published population PK model is currently investigated in the OPTI‐CLOT trial, in which the population PK model is applied to obtain individualized dose recommendations for adult haemophilia A patients undergoing surgery. Nevertheless, a population PK model can be considered validated when the results of the validation study have demonstrated that the model adequately describes the observations from the total population on which the model was built. Of course, the dataset used for that external validation should be of sufficient size as well as comprise patients with characteristics similar to the characteristics of the patients used to construct the model. Therefore, this process of validation can be considered iterative and validation should be repeated until the total population contributing to the model construction has been covered.

In Figure 2, it was shown that the means from the distributions of eta from CL and V1 obtained using the published population PK model were significantly different from zero. As exponential models were used to describe the IIV, a value of zero for eta depicts the typical value of the corresponding PK parameter. In both cases, the means of the distributions were higher than zero, showing that the typical values for the paediatric population are higher than the typical values for CL and V1 from the published model. As mentioned above, different typical values between models will result in different individual PK parameter estimates. Therefore, it is important to account for these differences. When comparing the published model to the current final model, the estimates for CL and V1 were augmented from 150 mL h⁻¹ 68 kg⁻¹ to 171 mL h⁻¹ 68 kg⁻¹ and from 2810 mL 68 kg⁻¹ to 2930 mL 68 kg⁻¹, respectively. Figure 5 showed that the deviations from zero for both CL and V1 were accounted for in the final model. Moreover, it is known that weight‐normalized CL of paediatric patients is higher than that of adults. ²² As only paediatric data was added to the original data, this probably caused the increase in the typical values for CL and V1. Nevertheless, as patients were included with a slightly lower age as compared to patients from the original cohort, this may have contributed to the differences shown for the eta distributions from CL and V1.

In the modelling process, body weight of the patients was considered using allometric scaling of the population PK parameters. As the allometric exponents for CL and V1 were fixed a priori, the covariate relationship of both parameters with age could be estimated simultaneously with the relation of body weight. Supplemental Figure S4 shows the relationship between the post hoc values for CL and volume of distribution in steady‐state (Vss), which is the sum of V1 and V2 for a two‐compartment model, vs age. It is demonstrated that the values for CL and Vss are correlated to age for paediatric patients, as the values within the age range from 0 to 12 seem to increase linearly (Supplemental Figure S4A‐B). These values are calculated using the corresponding typical value of the parameter, the MAP Bayesian estimate and the associated covariate relationships. Looking at the body weight‐normalized values for CL, higher values for the individual PK parameters are obtained for paediatric patients. For Vss, however, only a very slight downward trend was observed vs age (Supplemental Figure S4D). Nevertheless, the latter is in agreement with the low value for the exponent (−0.09) from the final model.

5. CONCLUSIONS

The validation of a previously published perioperative population PK model using an independent external dataset comprising paediatric patients demonstrated significant deviations from zero for the means from the distribution of the etas for CL and V1. Moreover, population and individual predicted FVIII levels of the paediatric patients were underestimated. In the final model, the typical values of CL and V1 were increased, which accounted for the observed deviations. As assessed by internal validation, the final model accurately described the FVIII levels for both moderate and severe adult and paediatric haemophilia A patients. As different models may produce different individual PK parameters when applying Bayesian adaptive dosing using the same input data, it is important to have a validated model before it can be applied to obtain patient‐tailored doses.

COMPETING INTERESTS

M.C. has received grants from governmental research institutes, such as the Dutch Research Institute (NWO), ZonMW, Innovation fund, NWO‐NWA and unrestricted investigator‐initiated research grants as well as educational and travel funding from various companies over the years (Pfizer, Baxter/Baxalta/Shire, Bayer Schering Pharma, CSL Behring, Sobi Biogen, Novo Nordisk, Novartis and Nordic Pharma), and has served as a member on steering boards of Roche and Bayer. All grants, awards and fees received go to the institution. F.L. received research support from CSL Behring and Shire/Takeda for performing the WiN study; is a consultant for uniQure, Novo Nordisk and Shire/Takeda, the fees of which go to the institution; and has received a travel grant from Sobi. He is also a DSMB member for a study by Roche. R.M. reports grants from Bayer, grants from Shire, grants from Merck Sharpe Dome, grants from CSL Behring, other from Bayer, other from Shire, outside the submitted work. The other authors declare no competing financial interests. K.F. reports grants from CSL Behring, grants from Novo Nordisk, other from Takeda, other from Roche, other from Pfizer, outside the submitted work. F.M. reports grants from CSL Behring, grants from Pfizer, grants from Bayer, grants from Novo Nordisk, grants from Sobi, grants from Roche, grants from Takeda, outside the submitted work. D.H. reports grants from Octapharma, grants from Grifols, grants from Takeda, personal fees and other from Biomarin, personal fees and other from Uniqure, personal fees and other from Sobi, personal fees and other from Sanofi, personal fees from NovoNordisk, personal fees and other from Pfizer, personal fees from BIotest, personal fees and other from Takeda, personal fees from Spark, personal fees from Roche, personal fees from Bayer, outside the submitted work. B.G. reports grants from Baxter, grants from CSL Behring, outside the submitted work. R.L. reports other from Octapharma, other from Octapharma, during the conduct of the study; other from SOBI, other from SOBI, outside the submitted work. All other authors declare that they have no conflict of interests.

CONTRIBUTORS

T.P. and R.M. performed the analyses and wrote the manuscript. H.H. performed data collection, which was supervised by R.L. M.C. supervised the study and helped write the manuscript. All authors critically revised the manuscript and approved the final version.

Supporting information

Table S1 Model for body weight imputation using age

Table S2 Model building steps

Figure S1 Imputed body weight vs age

Figure S2 Eta of clearance and volume of distribution vs age and body weight for the original cohort

Figure S3 Prediction‐corrected visual predictive check of the final model for the total cohort

Figure S4 Prediction‐corrected visual predictive check of the final model stratified for an age of 12 years of the total cohort

Preijers T, Liesner R, Hazendonk HCAM, et al. Validation of a perioperative population factor VIII pharmacokinetic model with a large cohort of pediatric hemophilia a patients. Br J Clin Pharmacol. 2021;87(11):4408-4420. 10.1111/bcp.14864

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author on reasonable request.