Mapping gradient nonlinearity and miscalibration using diffusion‐weighted MR images of a uniform isotropic phantom

Abstract

Purpose

To use diffusion measurements to map the spatial dependence of the magnetic field produced by the gradient coils of an MRI scanner with sufficient accuracy to correct errors in quantitative diffusion MRI (DMRI) caused by gradient nonlinearity and gradient amplifier miscalibration.

Theory and Methods

The field produced by the gradient coils is expanded in regular solid harmonics. The expansion coefficients are found by fitting a model to a minimum set of diffusion‐weighted images of an isotropic diffusion phantom. The accuracy of the resulting gradient coil field maps is evaluated by using them to compute corrected b‐matrices that are then used to process a multi‐shell diffusion tensor imaging (DTI) dataset with 32 diffusion directions per shell.

Results

The method substantially reduces both the spatial inhomogeneity of the computed mean diffusivities (MD) and the computed values of the fractional anisotropy (FA), as well as virtually eliminating any artifactual directional bias in the tensor field secondary to gradient nonlinearity. When a small scaling miscalibration was purposely introduced in the x, y, and z, the method accurately detected the amount of miscalibration on each gradient axis.

Conclusion

The method presented detects and corrects the effects of gradient nonlinearity and gradient gain miscalibration using a simple isotropic diffusion phantom. The correction would improve the accuracy of DMRI measurements in the brain and other organs for both DTI and higher order diffusion analysis. In particular, it would allow calibration of MRI systems, improving data harmony in multicenter studies.

1. INTRODUCTION

Quantitative diffusion MRI (DMRI) comprises several related types of studies, such as computations of the apparent diffusion coefficients (ADCs), ¹⁶ , ¹⁸ , ²² , ³⁰ computations of diffusion tensor imaging (DTI) metrics, ¹ , ⁵ precise determination of the directions in which diffusion is the fastest from high angular resolution diffusion imaging (HARDI) datasets ³ , ⁷ , ³⁵ (primarily used for fiber tracking), and studying microscopic structure. ⁸ , ¹⁴ , ²¹ , ²⁹ All these applications are susceptible to systematic errors due to gradient nonlinearity and miscalibration that typically are not accounted for.

Gradient nonlinearity is described by gradient coil field maps (GCFMs). ¹⁰ The GCFM for the x‐gradient coil specifies the magnetic field as a function of position produced by the x‐gradient coil divided by the gradient of the field in the x‐direction present at magnet isocenter. Analogous GCFMs are defined for the y‐ and z‐ gradient coils. The GCFMs depend on the physical structure of the gradient coils and are not expected to change unless the coils are damaged in some way.

Gradient miscalibration is described by gradient gain correction factors (GGCFs). The x‐gradient GGCF is defined as the gradient actually produced by the x‐gradient coil at the origin when a unit gradient is requested. Analogous GGCFs are defined for the y‐ and z‐gradients. Gradient calibration is performed on‐site. Error in the calibration procedure and drift in gradient amplifiers can result in the GGCFs having values different from 1.

The product of each GCFM and the corresponding GGCF results in one set of field maps, the gain corrected gradient coil field maps (gcGCFMs), that describes both effects.

The diffusion weighting of an acquisition is typically described by a b‐matrix, ¹⁹ or alternatively, by a b‐value and a b‐vector. In an “ideal” acquisition, the diffusion weighting is uniform over the volume imaged and equal to the values prescribed by the user. Bammer et al ² have shown that the effects of gradient nonlinearity and miscalibration can be described by a spatially varying b‐matrix. They also showed how the gcGCFMs, if known, can be used to compute the “actual” b‐matrices, which can then be used in subsequent data analysis to eliminate the systematic errors. Unfortunately, the GCFMs and GGCFs are not in general known to the users. Many manufacturers treat GCFMs as proprietary, and GGCFs describe errors that remain after on‐site gradient calibration.

Different methods have been proposed to permit users to compute accurate b‐matrices, although none is routinely used in either research or clinical diffusion MRI studies. Rogers et al ²⁶ suggests measuring the GCFMs using phase contrast $B_0$ mapping. ²⁸ Their method involves multiple scans of a large oil phantom with different values of the linear shim settings. Since linear shim correction is usually performed by adding a DC offset to the current supplied to the gradient coils, the GCFMs can be computed from the differences in the field maps. As currently presented, this method focuses on the correction of gradient nonlinearities but not on the effects of gradient miscalibration. Tan et al ³² suggest computing the GCFMs using image distortions caused by the gradient nonlinearity, although they do not describe a protocol for measuring the distortions, which makes their method difficult to use in practice. In contrast, Tao et al ³³ describe in great detail a fiducial phantom specially designed for measuring image distortion and an algorithm for constructing the GCFMs from the imaging data; potential disadvantages of their method is the requirement of a special phantom required and the complexity of the data processing. It is also possible to use diffusion measurements to extract information about the gradient nonlinearity, which has the advantage of higher sensitivity; b‐values scale with the square of the gradient amplitude, while geometric distortions and phase shifts scale linearly. Published studies using diffusion measurements bypass the computation of the GCFMs and directly compute the corrected b‐matrices. Teh et al ³⁴ proposed modeling the effects of gradient nonlinearity as spatially dependent GGCFs, which can be computed from 3 sets of diffusion‐weighted images, each of which has diffusion sensitization by only one of the gradient coils. Lee et al ¹⁷ proposed scanning a uniform isotropic phantom with the same protocol used to scan the subject. The results of phantom measurements are then used to compute spatially dependent b‐values. In the Discussion section, we discuss the theoretical underpinnings of these methods with respect to those of the proposed method.

In this paper, we present a general method for measuring the gcGCFMs from a set of diffusion‐weighted images of a phantom having isotropic diffusion characteristics. Our method combines the advantages of the increased sensitivity (quadratic vs linear) of the diffusion‐based approaches with the theoretical rigor of the field mapping that is currently obtained only with the non‐diffusion‐based approaches. The method is designed to provide a general solution to the problem and the measured gcGCFMs can then be used to reduce systematic errors in all types of diffusion MRI studies, including ADC measurements, DTI, HARDI, and microstructural studies. In the subsequent sections, we present our method and demonstrate its efficacy by comparing uncorrected and corrected direction encoded color (DEC) maps, ²³ mean diffusivity (MD) maps and histograms, and fractional anisotropy (FA) maps and histograms of a DTI study of the phantom. We use the previously proposed NIH PVP diffusion MRI phantom. ¹¹ , ²⁵

2. METHODS

Note on units: The units we use in this paper are $\mathrm{\mu }{\mathrm{m}}^2/\mathrm{ms}(={10}^{‐3}{\mathrm{mm}}^2/\mathrm{s})$ for the diffusivity D and $\text{ms}/\mathrm{\mu }{\mathrm{m}}^2(={10}^3\mathrm{s}/{\mathrm{mm}}^2)$ for the b‐value b.

2.1. The cost function

Our goal is to measure the gcGCFMs by scanning an isotropic phantom with a Stejskal‐Tanner diffusion‐weighted pulse sequence. We begin by noting that the attenuation $E(\mathbf{r})$ due to diffusion in such images is

$$\begin{array}{c}E(\mathbf{r})\equiv \frac{S^{\alpha }(\mathbf{r})}{S_0(\mathbf{r})}=\exp (‐Dtr({\mathbf{b}}^{\alpha }(\mathbf{r})))\hfill \end{array}$$ (1)

where $\mathbf{r}$ is a position vector,

$S^{\alpha }(\mathbf{r})$ is the measured voxel value at $\mathbf{r}$ for series $\alpha$ (=1, 2, …, N), where N is the number of diffusion weighted images in the dataset,

$S_0(\mathbf{r})$ is the voxel value at $\mathbf{r}$ in the absence of diffusion weighting,

D is the diffusivity of the phantom, and

$tr({\mathbf{b}}^{\alpha }(\mathbf{r}))$ is the trace of the b‐matrix, ⁶ a symmetric tensor with components $b_{\mathit{ij}}^{\alpha }$ that describes the diffusion weighting of series $\alpha$.

Since the diffusivity D in the phantom is uniform, the spatial dependence of E is caused entirely by the spatial dependence of $\mathbf{b}$, which in turn depends on all sources of magnetic field gradients: $B_0$ inhomogeniety, eddy‐currents, magnetic susceptibility, and the fields described by the gcGCFMs. The method presented in this paper only corrects errors caused by fields described by the gcGCFMs. We also neglect the effects of the concomitant fields, which have been shown to be negligible for Stejskal‐Tanner pulse sequences. ⁴

We use a coordinate system in which ${\mathbf{B}}_0$, the main field of the scanner, points in the z‐direction. The gcGCFMs are the functions $B^k(\mathbf{r})$ that specify the normalized z‐component of the magnetic field at location $\mathbf{r}$ produced by gradient coil k (= x, y, or z). The gcGCFMs are normalized such that for an "ideal" gradient coil

$$\begin{array}{c}{\left(\frac{\partial B^k}{\partial r_j}\right)}^{\mathit{ideal}}={\delta }_{\mathit{jk}}\hfill \end{array}$$ (2)

Bammer et al ² have shown that the effect of gradient nonlinearity on the diffusion weighting can be described by the equations

$$\begin{array}{c}{\mathbf{G}}^{\alpha ,actual}(\mathbf{r})=\mathbf{L}\bullet {\mathbf{G}}^{\alpha ,pre},\hfill \end{array}$$ (3)

where ${\mathbf{G}}^{\alpha ,pre}$ is the prescribed diffusion weighting (b‐value $\times$ b‐vector) for series $\alpha$, ${\mathbf{G}}^{\alpha ,actual}(\mathbf{r})$ is the actual diffusion weighting (b‐value $\times$ b‐vector) for series $\alpha$ at point $\mathbf{r}$, and $\mathbf{L}$ is the transformation matrix whose elements $L_{\mathit{jk}}(\mathbf{r})$ are components of the gradient of the gcGCFMs.

$$\begin{array}{c}{L}_{\mathit{jk}}=\frac{\partial B^k}{\partial r_j}\hfill \end{array}$$ (4)

If imaging gradients are neglected the components of the b‐matrix are

$$\begin{array}{c}{b}_{\mathit{kl}}=G_k{G}_l\hfill \end{array}$$ (5)

Using Equations (5), (3) and (4), $tr(\mathbf{b})$ becomes

$$\begin{array}{c}\begin{array}{cc}tr(\mathbf{b})=\hfill & \left({\left(\frac{\partial B^x}{\partial x}\right)}^2+{\left(\frac{\partial B^x}{\partial y}\right)}^2+{\left(\frac{\partial B^x}{\partial z}\right)}^2\right)b_{\mathit{xx}}^{\mathit{pre}}+\left(\frac{\partial B^x}{\partial x}\frac{\partial B^y}{\partial x}+\frac{\partial B^x}{\partial y}\frac{\partial B^y}{\partial y}+\frac{\partial B^x}{\partial z}\frac{\partial B^y}{\partial z}\right)b_{\mathit{xy}}^{\mathit{pre}}+\hfill \\ \hfill & \left({\left(\frac{\partial B^y}{\partial x}\right)}^2+{\left(\frac{\partial B^y}{\partial y}\right)}^2+{\left(\frac{\partial B^y}{\partial z}\right)}^2\right)b_{\mathit{yy}}^{\mathit{pre}}+\left(\frac{\partial B^x}{\partial x}\frac{\partial B^z}{\partial x}+\frac{\partial B^x}{\partial y}\frac{\partial B^z}{\partial y}+\frac{\partial B^x}{\partial z}\frac{\partial B^z}{\partial z}\right)b_{\mathit{xz}}^{\mathit{pre}}+\hfill \\ \hfill & \left({\left(\frac{\partial B^z}{\partial x}\right)}^2+{\left(\frac{\partial B^z}{\partial y}\right)}^2+{\left(\frac{\partial B^z}{\partial z}\right)}^2\right)b_{\mathit{zz}}^{\mathit{pre}}+\left(\frac{\partial B^y}{\partial x}\frac{\partial B^z}{\partial x}+\frac{\partial B^y}{\partial y}\frac{\partial B^z}{\partial y}+\frac{\partial B^y}{\partial z}\frac{\partial B^z}{\partial z}\right)b_{\mathit{xy}}^{\mathit{pre}}.\hfill \end{array}\hfill \end{array}$$ (6)

where $tr(\mathbf{b})$, which depends on $\mathbf{r}$, is the trace of the “true” b‐matrix and $b_{\mathit{kl}}^{\mathit{pre}}$ are the elements of the prescribed b‐matrix.

Since the gcGCFMs obey Laplace’s equation, we can express them as a sum of solid harmonics ¹³ (see Appendix A). We then use Equations (1), (6), (A1)–(A5), and either Equation (A6) or (A7) to express the attenuation $E(\mathbf{r})$ as a function of either the expansion coefficients $c_{\mathrm{lm}}$ and $s_{\mathrm{lm}}$ (if Equation A6 is used) or the expansion coefficients ${\tilde{c}}_{\mathrm{lm}}$ and ${\tilde{s}}_{\mathrm{lm}}$ and the gain factors $g_k$ (if Equation A7 is used). The GCFMs are then described by Equation (A6) or (A7) with the expansion coefficients taking the values that minimize the cost function

$$\begin{array}{c}\mathrm{\Phi }={\sum }_{q\in mask}{\sum }_{\alpha }{\left(\frac{S_q^{\alpha }}{S_{0,q}}‐\exp (‐Dtr({\mathbf{b}}_q^{\alpha }))\right)}^2\hfill \end{array}$$ (7)

where q runs over the pixels in the mask and $tr({\mathbf{b}}_q^{\alpha })$ is the trace of the “true” b‐matrix in series $\alpha$ at the location of voxel q defined by Equation (6) (which implicitly depends on the expansion coefficients). In the Supporting Information, we show that for symmetric gradient coils and subject to signal‐to‐noise (S/N) limitations, 1 non‐diffusion‐weighted “$b=0$” image and 3 diffusion‐weighted images with b‐vectors (1,0,0), (0,1,0), and (0,0,1), contain sufficient information to determine all the expansion coefficients except $c_{00}^x$, $c_{00}^y$, and $c_{00}^z$, which are not important for our purposes since the basis functions corresponding to those terms are constants which don’t contribute to $\mathbf{L}$, and $c_{10}^x$, $s_{11}^x$, $c_{10}^y$, $c_{11}^y$, $c_{11}^z$, and $s_{11}^z$, which are zero for properly constructed gradient coils.

In the case where one wants to measure all the expansion coefficients, Equation (A6) should be used. In this case, $tr(\mathbf{b})$ and therefore $\mathrm{\Phi }$ depend on the the gcGCFM expansion coefficients $c_{\mathrm{lm}}$ and $s_{\mathrm{lm}}$. On the other hand, if the GCFM expansion coefficients are known and one only wishes to check the gradient calibration, Equation (A7) should be used, in which case $tr(\mathbf{b})$ and therefore $\mathrm{\Phi }$ depend on the gain factors $g_i$ and the (known) GCFM expansion coefficients ${\tilde{c}}_{\mathrm{lm}}$ and ${\tilde{s}}_{\mathrm{lm}}$.

2.2. Diffusivity of the phantom and its effect on results

To obtain best fit values for the expansion coefficients $s_{\mathrm{lm}}$ and $c_{\mathrm{lm}}$, the value of the diffusivity D of the phantom used for the calibration must be known. The diffusivity D of a PVP solution ¹¹ , ²⁵ depends on temperature T and the PVP concentration $C_{\mathit{PVP}}$. Previous calibration experiments ²⁷ provide an empirical expression of diffusivity D as a function of T and $C_{\mathit{PVP}}$:

$$\begin{array}{c}D=0.93445+(‐2.4033C_{\mathit{pvp}}+1.171C_{\mathit{pvp}}^2)+(.056603‐0.12862C_{\mathit{pvp}}+0.086C_{\mathit{pvp}}^2)T\hfill \end{array}$$ (8)

where D is in ${\mathrm{\mu }m}^2/\mathrm{ms}$, $C_{\mathit{pvp}}$ is a mass fraction and T is in Celsius. While the PVP concentration is generally well known, it is difficult to control and measure the temperature of the phantom, so the true value of D during a calibration measurement is generally not known with high accuracy. However, D can be estimated directly from the calibration dataset. To do this, we define an ROI near magnet isocenter, assume that the effects of gradient inhomogeneity are negligible (which should be true near isocenter) and fit the data to Equation (1) to determine D. The accuracy of this procedure is limited by 2 sources of systematic error: (1) incorrect gain settings and (2) time‐varying temperature of the phantom due to RF heating during the scan.

If the assumed value of D is incorrect, each of the 3 gain coefficients will be in error by the same factor

($\sqrt{(D_{\text{true}}/D_{\text{assumed}})}$). (This is true because Equation (6) depends only on the product $Dtr(\mathbf{b})$, and if expansion of Equation (A7) is used, $tr(\mathbf{b})$ is a homogeneous function of degree 2 of the $g_i$s.) Since the gain coefficients are all scaled by the same factor, the ratio of any 2 gain coefficients is unaffected by the error in D.

2.3. Data acquisition

2.3.1. Calibration datasets

Specification of diffusion weighting using b‐values and b‐vectors, as is done by most manufacturers, is not general enough to describe the contribution to the diffusion weighting of the imaging gradients, ¹⁹ which is therefore neglected. If the contribution to the diffusion weighting of the imaging gradients is not negligible, their effects can be greatly reduced by acquiring, for each diffusion direction, an additional image with the antipodal gradients, ie, the polarity of the diffusion pulses is reversed. ²⁰ To an excellent approximation, the error in the log of the attenuation due to the imaging gradients in the pair of images will be equal and opposite and therefore cancel each other out. Since no duplicate image is required of the non‐diffusion‐weighted image, this increases the minimum number of images to 7. Since the user in general doesn’t know whether or not the effect of the imaging gradients is negligible in the pulse sequence used, we recommend acquiring at least 7 images. For this paper we acquired multiple shells and multiple copies of the “$b=0$” images. Results of analysis using only a single shell (not shown) were essentially the same as results using the complete dataset, confirming our expectation that only one shell is needed.

The calibration dataset was acquired with a spin echo echo‐planar pulse sequence with a classical Stejskal‐Tanner pair of diffusion gradients and the following parameters: 77 axial slices, slice thickness = 2.5 mm, FOV = 256 mm, matrix size $104\times 101$ zero‐filled to $112\times 112$, TE = 127.5 ms, TR = 13.338 s. It comprises of 35 images: 5 “b = 0” images with almost no diffusion weighting ($b=5\times {10}^{‐3}\text{ms}/{\mathrm{\mu }\mathrm{m}}^2$), and 30 diffusion‐weighted images. The diffusion‐weighted images comprise of 5 “shells” with b‐values (0.5 ms/${\mathrm{\mu }m}^2$, 1.0 ms/${\mathrm{\mu }m}^2$, 1.5 ms/${\mathrm{\mu }m}^2$, 2.0 ms/${\mathrm{\mu }m}^2$, and 2.5 ms/${\mathrm{\mu }m}^2$) and, for each b‐value, 3 pairs of single axis antipodal gradients, ie, the b‐vectors were (1,0,0), (−1,0,0), (0,1,0), (0,−1,0), (0,0,1), and (0,0,−1).

2.3.2. Gain factor datasets

To test our ability to detect errors in the gain settings of the gradients, we acquired 7 additional calibration datasets for which we changed the gain settings in the calibration file, which determines the scaling between the amplitude of the gradient waveform generated by the pulse sequence and the amplitude of the current supplied by the gradient amplifiers. One of these datasets was a repeat of the standard calibration dataset; in each of the others, the gradient along one axis was either increased or decreased by 1%.

When analyzing the “gain” calibration datasets, we noticed that diffusivity changed from series to series. To investigate this further, we acquired an additional series of 23 calibration datasets without changing any parameters.

2.3.3. Oil phantom datasets

For comparison purposes, we also measured the GCFM using phase contrast $B_0$ mapping ²⁸ on images of a large oil phantom acquired with different linear shim settings. ²⁶

2.3.4. Test datasets

To test the effectiveness of our correction method, we acquired a DTI dataset of the phantom with the same scan parameters as the calibration data but different diffusion weightings. The test data comprise102 images; 6 “b = 0” images with almost no diffusion weighting ($b=5\times {10}^{‐3}\text{ms}/{\mathrm{\mu }\mathrm{m}}^2$), 32 images with $b=0.5\text{ms}/{\mathrm{\mu }\mathrm{m}}^2$, 32 images with $b=1.0\text{ms}/{\mu \mathrm{m}}^2$, and 32 images with $b=2.5\text{ms}/{\mathrm{\mu }\mathrm{m}}^2$. The same sets of directions, which have the b‐vectors uniformly distributed on the unit sphere, are used in each shell.

2.4. Image registration and ROI selection

All of the datasets used were preprocessed for eddy current correction using TORTOISE ¹² , ²⁴ (https://www.tortoisedti.org) with its default settings. To exclude background voxels from our ROI we used a mask computed in 3 steps:

1. Compute the average of the “$b=0$” images,

2. Exclude all voxels in the average “$b=0$” image with values less than 0.1 times the largest voxel value, and

3. Eroding the mask slice‐by‐slice with a square $3\times 3$ template to remove voxels on the edges.

Step 3, which can be repeated if necessary, is needed because in‐plane epi distortions in the image, which we don’t correct for in this paper, can cause artifacts at the boundary of the phantom. In particular, the phantom may have an air bubble at the top which causes large local image artifacts.

2.5. Data analysis

To evaluate the efficacy of the our proposed correction, we computed 4 sets of b‐matrices and used each set to compute DEC maps, MD images, and FA images of the test dataset. The b‐matrices used were:

1. the prescribed (uncorrected) b‐matrices (Unc),

2. the prescribed b‐matrices corrected as described in the theory section using coefficients supplied by the manufacturer (MFG),

3. the prescribed b‐matrices corrected as described in the theory section using coefficients computed by fitting the oil phantom data (OP), and

4. the prescribed b‐matrices corrected as described in the theory section using coefficients computed by fitting the diffusion calibration data (DIFF).

For the gain factor dataset, the gradient gain settings were computed only using the proposed DIFF method using first a constant diffusivity and later correcting for temperature induced changes in diffusivity of the phantom during the acquisition. The details of the temperature correction are reported in the Results section.

The MFG and OP gradient field models contain terms of higher order than are included in the DIFF GCFMs, but the contributions of the extra terms are negligible in the volume imaged in this study.

3. RESULTS

Figure 1 shows axial, sagittal, and coronal slices of DEC maps through the center of the phantom. In the first row, which shows the results with no gradient inhomogeneity correction, the effect of gradient nonlinearity appears as large areas of uniform color. The artifacts are greatly reduced in the corrected images. Interestingly, the dominant green hue still observable in the MFG and OP images is attenuated with the DIFF corrected images. This could be related to slight gradient miscalibration that is not accounted by MFG and OP.

FIGURE 1.

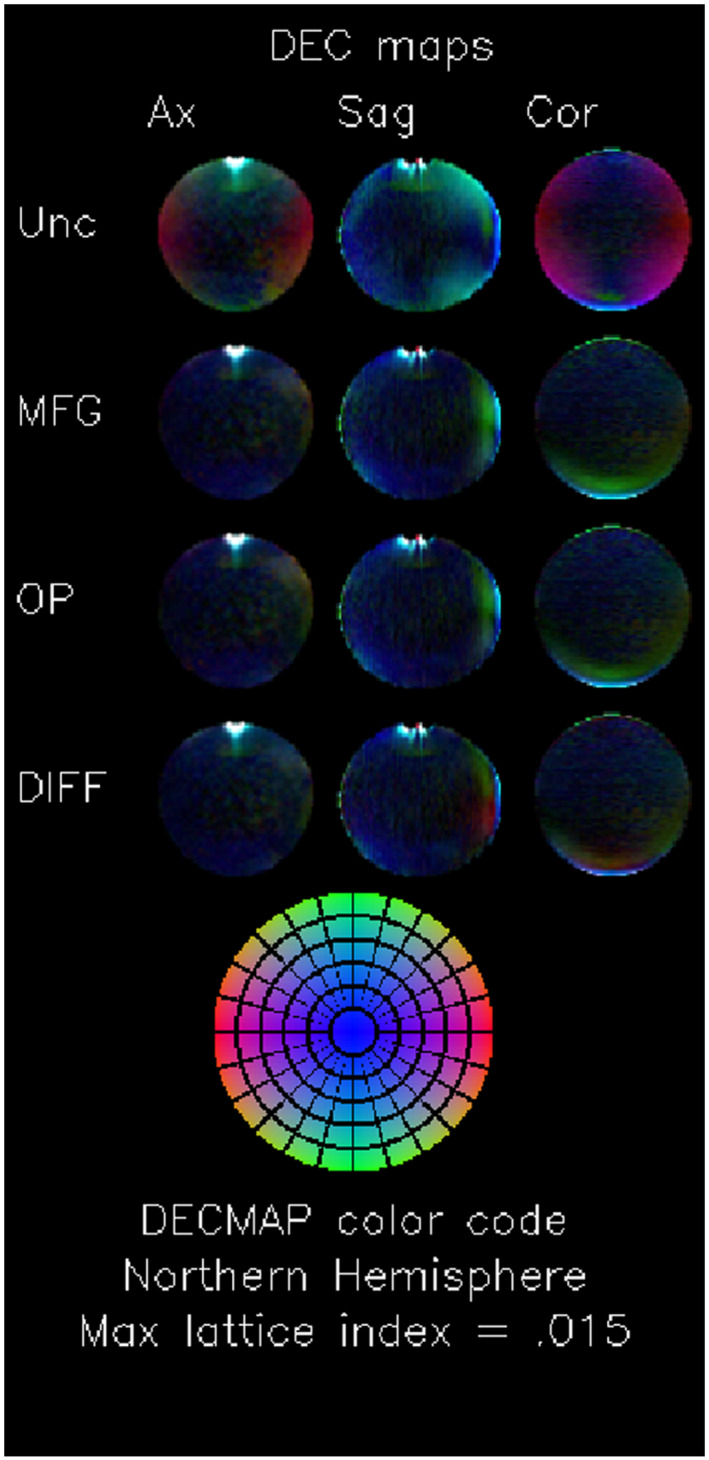
Direction encoded color (DEC) maps. Matrix of mean DEC maps. Each column contains a different plane: midline axial (Ax), midline sagittal (Sag), and midline coronal (Cor). Each row contains images computed using different GCFMs for the gradient nonuniformity correction: uncorrected (Unc), corrected using the manufacturer supplied GCFM (MFG), corrected using a GCFM computed from phase contrast images of an oil phantom (OP), and corrected using the method presented in this paper (DIFF). DEC maps depict the anisotropy of the computed diffusivity tensor; the color codes the direction of the eigenvector corresponding to the largest eigenvalue (L/R is red, A/P is green, and S/I is blue), and the brightness codes the fractional anisotropy. The images are scaled so that colors reach full brightness for an FA of .015. The bottom image shows the color corresponding to an FA of 0.15 for each point in the “Northern Hemisphere.” Since the true FA of an isotropic phantom is 0, the DEC map for an isotropic phantom should be black. The effect of thermal noise in the measurement results in a mottled map with no preferred direction. Gradient inhomogeneity introduces a spatial pattern of preferred directions, which appear as spatial patterns of color. The effects of gradient inhomogeneity is clearly seen as the red areas in the uncorrected coronal slices which do not exist in the corrected maps. The bright white regions with large errors at the top of the axial and sagittal images are caused by large local susceptibility‐induced field gradients due to the meniscus of the air bubble

Figure 2 shows axial, sagittal, and coronal slices of the MD map through the center of the phantom. In the first row, which shows the results with no gradient inhomogeneity correction, the systematic error is clearly visible. In the remaining rows, which show results with inhomogeneity correction applied, the effect is greatly reduced. The 3 sets of corrected images are similar.

FIGURE 2.

Mean diffusivity orthogonal slices. Matrix of mean difffusivity maps. Each column contains a different plane: midline axial (Ax), midline sagittal (Sag), and midline coronal (Cor). Each row contains images computed using different GCFMs for the gradient nonuniformity correction: uncorrected (Unc), corrected using the manufacturer supplied GCFM (MFG), corrected using a GCFM computed from phase contrast images of an oil phantom (OP), and corrected using the method presented in this paper (DIFF). The uncorrected maps have a much wider range of values and a clearly organized spatial pattern. The range of values in the corrected images is much smaller. The 3 GCFMs used for the corrections yield similar results. The regions with large errors at the top of the axial and sagittal images are caused by large local susceptibility‐induced field gradients due to the meniscus of the air bubble

Figure 3 shows a histogram of the values of MD in an ROI that includes most of the phantom. The ROI was chosen using the same criteria described in Section 2.4. The inhomogeneity correction reduces the standard deviation of the measured MD values in the ROI by a factor of more than 2 (see Table 1). On the right side of the histogram, one can observe that the tail of the distribution from DIFF data is slightly less pronounced than in the other correction methods. This is also consistent with the lowest SD reported in Table 1 and this small improvement may represent a contribution by the gradient miscalibration correction offered by DIFF.

FIGURE 3.

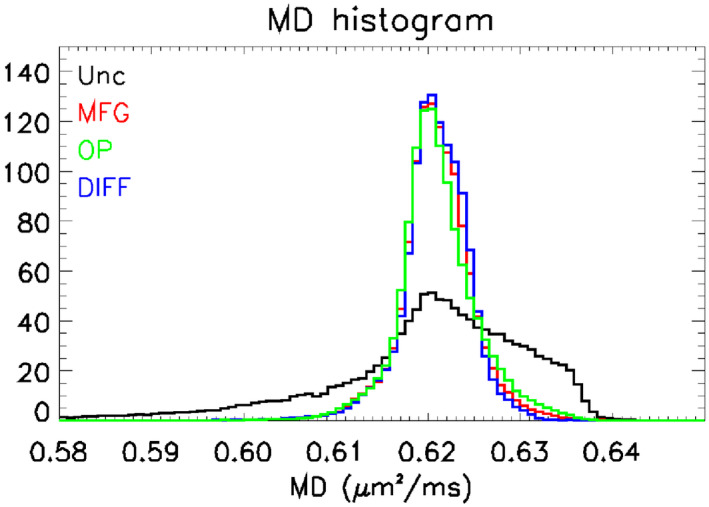
Mean diffusivity (MD) histograms. The figure shows histograms of values of MD. The traces are color coded to show the GCFMs used in the analysis: uncorrected (Unc, black), GCFM supplied by the manufacturer (MFG, red), GCFM measured from phase contrast images of an oil phantom (OP, green), and GCFM measured using the method presented in this paper (DIFF, blue). The effect of gradient nonlinearity is to widen and distort the shape of the MD histogram. The corrected histogram is much narrower and more symmetric; values for the standard deviations are given in Table 1

TABLE 1.

Width of peaks in MD histograms

Correction method	Standard deviation of MD $({10}^{‐2}\mathrm{\mu }{\mathrm{m}}^2/\text{ms})$
Unc	1.19
MFG	0.48
OP	0.51
DIFF	0.46

Figure 4 shows axial, sagittal, and coronal slices of the FA map through the center of the phantom. In the first row, which shows the results with no gradient inhomogeneity correction, the systematic error due to gradient inhomogeneity is clearly visible. In the remaining rows, which show results with inhomogeneity correction applied, the effect is greatly reduced.

FIGURE 4.

Fractional anisotropy (FA) orthogonal slices. Matrix of FA maps. Each column contains a different plane: midline axial (Ax), midline sagittal (Sag), and midline coronal (Cor). Each row contains images computed using different GCFMs for the gradient nonuniformity correction: uncorrected (Unc), corrected using the manufacturer supplied GCFM (MFG), corrected using a GCFM computed from phase contrast images of an oil phantom (OP), and corrected using the method presented in this paper (DIFF). The uncorrected maps contain larger values and a clearly organized spatial pattern. The 3 GCFMs used for the corrections yield similar results. The regions with large errors at the top of the axial and sagittal images are caused by large local susceptibility‐induced field gradients due to the meniscus of the air bubble

Figure 5 shows a histogram of the values of FA in the same ROI used for the MD histogram. As expected, the effect of the correction is to reduce the number of voxels with large values of FA; compared to the uncorrected histogram, the peaks in the corrected histograms are much narrower and shifted to the left (see Table 2). As noticed for MD, the DIFF method has the least pronounced tail among all the correction methods.

FIGURE 5.

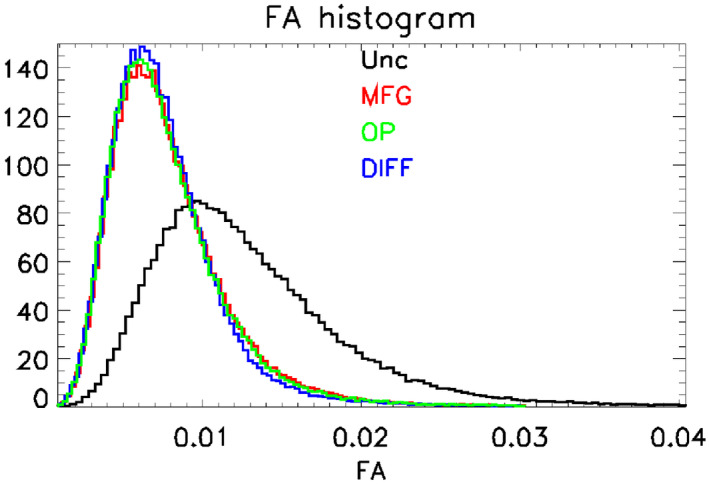
Fractional anisotropy (FA) histograms. The figure shows histograms of values of FA. The traces are color coded to show the GCFMs used in the analysis: uncorrected (Unc, black), GCFM supplied by the manufacturer (MFG, red), GCFM measured from phase contrast images of an oil phantom (OP, green), and GCFM measured using the method presented in this paper (DIFF, blue). The effect of gradient nonlinearity is to widen the peak in the histogram and to move it to the right. The correction narrows the peak and moves it to the left. The mean values of the peaks are given in Table 2

TABLE 2.

Mean values of FA

Correction Method	Mean of FA
Unc	$1.31\times {10}^{‐2}$
MFG	$0.83\times {10}^{‐2}$
OP	$0.81\times {10}^{‐2}$
DIFF	$0.79\times {10}^{‐2}$

To more extensively test the ability of our method to detect and correct errors in the gradient gain settings, we analyzed the “gain factor” dataset. In the first (reference) series, the default gradient coil gain settings were used. For each of the other sets, one of the gain settings was either increased or decreased by 1%. In the fitting procedure, we defined the cost function using Equation (A7), setting the expansion coefficients to the manufacturer supplied values and varying only $g_x$, $g_y$, and $g_z$.

Figure 6A shows the computed gain coefficients for all 7 series. The series labels describe the direction and polarity of the gain miscalibration. The series labeled (1,1,1) is the reference series that used the default gain settings set by the site engineer. The results in this series show a small but detectable miscalibration (up to 0.5% in the x axis).

FIGURE 6.

Measured gain factors for 7 calibration scans with different machine gain settings. Each column is labeled with the prescribed gain vector $(g_x,g_y,g_z)$, normalized such that the default calibration is (1,1,1). Subplot A shows the raw measured gain vectors. The different values of the gains in the first column indicate an error in the default gain calibration values. To isolate the effect of changing the calibration values, subplot B shows the ratio of measured gains in each scan to the measured gain in the corresponding direction in the first series. In this plot, in each column the ratios of the gains are correct, but there is an error in the absolute scaling, presumably due to an error in estimating D. In subplot C this error is removed by multiplying each column by an appropriate factor. The RMS error in the relative gain measurements is about $6\times {10}^{‐4}$

Figure 6B shows the ratios of the measured gain in each gradient in each deliberately miscalibrated series to the measured gain in the corresponding gradient in the reference series. The renormalization removes the effect of the initial miscalibration. This plot is hard to interpret because of errors in the determination of D, which changes during the course of the study due to RF heating of the phantom.

Figure 6C shows the same data renormalized to remove the effect of error in the determination of D. This plot shows how sensitive our method is to relative gradient miscalibration; the RMS error in the relative gain measurements is about $6\times {10}^{‐4}$.

The difference between the Figures 6 B and C are due to errors in the estimation of the diffusivity D. To examine this more closely, we acquired a series of 23 calibration datasets.

Figure 7 shows the diffusivity as a function of time computed for an ROI near isocenter, as described above. The linear increase of D with time is consistent with a linear increase in the temperature of the phantom, presumably caused by RF heating. Using Equation (8), we find that the temperature of the phantom increased from about ${22}^{\circ }\mathrm{C}$ for series 1 to ${26}^{\circ }\mathrm{C}$ for series 23.

FIGURE 7.

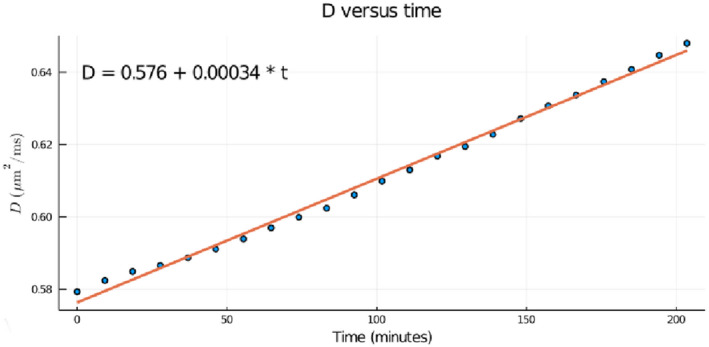
Changes in diffusivity and its effect on measurements of gradient gain measurements in a series of calibration scans. The figure shows the diffusivity D plotted against time for a series of calibration scans. Each calibration scan took about 551s to acquire, and they were acquired consecutively. The diffusivities were computed by defining an ROI in the center of the phantom and assuming that the actual diffusion weighting was the prescribed diffusion weighting. The measured diffusivity increases linearly with time, consistent with the expected effect of RF heating of the phantom during the scan. Using Equation (8), we find that during the scan, which took about 2 hr and 20 minutes, the temperature of the phantom increased from about $22.1^{\circ }\mathrm{C}$ to $25.8^{\circ }\mathrm{C}$

4. DISCUSSION

We have described and tested a method for measuring the gain corrected gradient coil field maps (gcGCFMs) of an MR scanner from diffusion measurements of an isotropic phantom. The approach was demonstrated by analyzing data acquired on a Philips scanner with symmetrical gradient coils using a classical Stejskal‐Tanner spin echo pulse sequence (2 identical diffusion sensitization pulses on opposite sides of the RF‐refocusing pulse).

The method presented in this paper computes the maps from a set of at least 4 (7 if diffusion weighting from imaging gradients is unknown and non‐negligible) diffusion‐weighted images of a spherical PVP phantom. (A theoretical analysis of the number of images required is presented in the Supporting Information.) The method can be used to correct errors in gradient amplifier calibration, and it is simple enough to be used for routine QA. We have shown that the residual systematic errors in FA and MD after correction using GCFMs computed using the proposed method are smaller than those remaining after correction using GCFMs determined using the oil phantom method (the OP field maps used in this paper did not include GGCFs) or by those provided by the manufacturer. This superior performance is probably due to the inclusion of correction for gradient calibration errors.

Although we have collected multi‐shell data to estimate the GCFMs, since the diffusion attenuation of PVP is known to be monoexponential, ²⁵ a set of images with a single shell data should suffice. The problem of finding the best b‐value to use for diffusion imaging has been investigated by Jones et al ¹⁵ and Xing et al ³⁶ . If the effects of $T_2$ decay are neglected, the optimum b‐value to use to measure D from a single‐shell acquisition with 1 $b=0$ image and 6 diffusion‐weighted images is $b=1.4/D$. ³⁶ We expect that the optimal b‐value for our purposes will be similar. Since the diffusivity of the 40% PVP phantom at room temperature is about 0.62 $\mathrm{\mu }{\mathrm{m}}^2/\text{ms}$, this acquisition would be specified by b‐values (0, 2.2, 2.2, 2.2) $\text{ms}/\mathrm{\mu }{\mathrm{m}}^2$ and b‐vectors (1,0,0), (0,1,0), and (0,0,1) for the diffusion‐weighted images.

The methods of Teh et al ³⁴ and Lee et al ¹⁷ also use diffusion measurements of an isotropic phantom to compute corrected b‐matrices.

Teh et al use the same set of 4 images that comprise our minimum set of calibration data. They compute, for each voxel, 3 “gain factors,” one for each gradient coil, which are then used to rescale the corresponding components of the b‐vectors (which are no longer unit vectors). This is equivalent to setting each diagonal element of $\mathbf{L}(\mathbf{r})$ equal to the corresponding “gain factor” and setting the off‐diagonal elements to zero.

Lee et al scan an isotropic diffusion phantom with the same set of b‐values and b‐vectors used to scan the subject, and use the results to compute, for each voxel and each image, a unique scaling factor for the b‐values. This is equivalent to working in a reference frame in which one axis (call it axis 1) points in the direction of the b‐vector, setting $L_{11}(\mathbf{r})$ to the measured scaling factor and all the other elements of $\mathbf{L}(\mathbf{r})$ to zero, and then rotating $\mathbf{L}(\mathbf{r})$ back to the lab frame. Note that the reference frame used is different for each image, but is the same for all voxels in a given image.

In both of these methods, we expect systematic errors to be introduced by the fact that these methods set to zero many elements of $\mathbf{L}$ that Equation (4) requires to be non‐zero. An additional source of systematic error in Lee et al is the use of a different $\mathbf{L}$ in each image; since all the data are acquired using the same hardware, every image should be described by the same matrix $\mathbf{L}$. Although the effects of these errors will be very small in scans of isotropic media, which are only sensitive to the symmetric part of $\mathbf{L}$, they would be relevant for anisotropic media. Therefore, for a general correction of gradient nonlinearity and gradient miscalibration that would work for both isotropic and anisotropic media, one needs to employ an approach in which the off‐diagonal elements of $\mathbf{L}$ are properly computed. In the Supporting Information, we show that the proposed method accomplishes this goal.

Three other non‐diffusion based methods potentially available for measuring the GCFMs are: (1) phase contrast SPGR imaging of a suitable oil phantom, ²⁶ , ²⁸ (2) image distortion of images of a fiducial phantom, ³³ and (3) field camera. ⁹ Of these 3 methods, we provided a direct comparison only with the oil‐phantom method. The histogram analysis of DTI‐derived quantities (Figure 3) and the analysis of the variance across the phantom after correction (Tables 1 and 2), show that the proposed method is slightly superior to the oil‐phantom based method. However, the main improvement for both methods is with respect to the uncorrected data.

The primary potential limitation of our method is the quality of EPI images of the phantom. In EPI images, magnetic field gradients caused by the magnetic susceptibility of the sample can cause significant distortions. To minimize such distortions, parallel imaging is commonly used. SENSE, one common method of parallel imaging, can generate ghosting artifacts. These ghosting artifacts are much more noticeable in images of phantoms than in images of brains. The images we present in this paper were acquired without parallel imaging.

Because the magnetic fields inside a uniform paramagnetic or diamagnetic sphere embedded in a uniform magnetic field are uniform and parallel to the applied field, there will be no susceptibility induced image distortions in an EPI image of such a sphere. The phantom we used is spherical, but due to imperfections in manufacturing, it has a small air bubble that causes image distortions. Use of a diffusion phantom without a meniscus would improve the performance of our method.

All the data used in this paper to validate our method were acquired with pulse sequences that contain pairs of identical diffusion sensitization gradients separated by an inversion RF pulse. Evaluation and optimization for diffusion pulse sequences with diffusion gradients that lack that symmetry will require further study. Although such sequences are frequently used because they are more efficient and generate smaller eddy currents, they generate images that contain artifacts caused by concomitant fields that cause additional systematic errors in quantitative diffusion imaging. ³¹ , ³²

The primary intended use of our GCFMs is the calculation of accurate b‐matrices for quantitative diffusion imaging. To simplify use of our method, software for using our method to analyze DTI data will be included in future versions the software package TORTOISE (www.tortoisedti.org). The output of TORTOISE will include corrected voxelwise b‐matrices that in turn could be used to compute corrected voxelwise b‐values and b‐vectors that most software packages use. As mentioned previously, the correction provided is valid for both isotropic and anisotropic media and would be useful for all applications of diffusion MRI from the simplest ADC computation to HARDI‐based tractography and microstructural imaging.

We are hopeful that the method presented in this paper will evolve into practical quality assurance protocols to help reduce errors and improve intersite harmony of DMRI results.

Supporting information

TEXT S1 The purpose of this supplement is to put our method on a sound theoretical footing by studying the mathematical problem of constructing the gcGCFMs (and a fortiori the transformation matrix L) from diffusion measurements of an isotropic phantom. We will show that, in general, a set of seven images (one b = 0 image and six images with diffusion sensitization directions) are sufficient to uniquely determine all the elements of L to within an additive constant, which is known to be zero for a properly constructed coil, and that only four images (one b = 0 image and three diffusion weighted images) are required if it is known a priori that the fields possess certain symmetries under reflection.

APPENDIX A.

A.1. EXPANSION OF gcGCFMs USING SOLID HARMONICS BASIS FUNCTIONS

The real solid harmonics are:

$$\begin{array}{cc}{u}_{\mathrm{lm}}^{\cos }\hfill & =N(l,m){\rho }^{\mathrm{l}}{P}_l^m(\cos (\theta ))\cos (m\varphi )\hfill \end{array}$$ (A1)

$$\begin{array}{cc}{u}_{\mathrm{lm}}^{\mathit{sin}}\hfill & =N(l,m){\rho }^{\mathrm{l}}{P}_l^m(\cos (\theta ))\sin (m\varphi )\hfill \end{array}$$ (A2)

where

$$\begin{array}{c}N(l,m)={(‐1)}^{\mathrm{m}}\sqrt{\frac{(2‐{\delta }_{m0})(l‐m)!}{(l+m)!}},\hfill \end{array}$$ (A3)

where the spherical polar coordinates of the position vector are $(R_0\rho ,\theta ,\varphi )$, $R_0$ is a scale factor with dimensions of distance, and $P_l^m(q)$ is the associated Legendre polynomial of degree l and order m. These basis functions are related to the usual Spherical Harmonics $Y_{\mathrm{lm}}$ ¹³ by the formulas

$$\begin{array}{cc}{u}_{\mathrm{lm}}^{\mathit{cos}}\hfill & ={\rho }^{\mathrm{l}}\sqrt{\frac{2\pi }{(1+{\delta }_{m0})(2l+1)}}(Y_l^{‐|m|}+{(‐1)}^{\mathrm{m}}{Y}_l^{|m|})\hfill \end{array}$$ (A4)

$$\begin{array}{cc}{u}_{\mathrm{lm}}^{\mathit{sin}}\hfill & =i{\rho }^{\mathrm{l}}\sqrt{\frac{2\pi }{(2l+1)}}(Y_l^{‐|m|}‐{(‐1)}^{\mathrm{m}}{Y}_l^{|m|})\hfill \end{array}$$ (A5)

(To within a normalization constant, this is the same set of basis functions that most manufacturers use to describe their gradients.)

The gcGCFMs can be expanded in solid harmonics:

$$\begin{array}{c}{B}^k=c_{00}^k+\sum _{l=1}^{\infty }\left(\sum _{m=0}^l\left(c_{\mathit{lm}}^k{u}_{\mathit{lm}}^{\mathit{cos}}(\rho ,\theta ,\varphi )+{\sum }_{m=1}^l{s}_{\mathit{lm}}^k{u}_{\mathit{lm}}^{\mathit{sin}}(\rho ,\theta ,\varphi )\right)\right),\hfill \end{array}$$ (A6)

where k labels the gradient direction (x, y, or z), and $c_{\mathrm{lm}}^k$ and $s_{\mathrm{lm}}^k$ are the expansion coefficients for the gcGCFMs.

It is sometimes useful to write the gcGCFMs in terms of gain factors $g_k$ and the GCFM expansion coefficients $c_{\mathrm{lm}}$ and $s_{\mathrm{lm}}$:

$$\begin{array}{c}{B}^k=g_k\left({\tilde{c}}_{00}^k+\sum _{l=1}^{\infty }\left(\sum _{m=0}^l\left({\tilde{c}}_{\mathrm{lm}}^k{u}_{\mathrm{lm}}^{\cos }(\rho ,\theta ,\varphi )+\sum _{m=1}^l{\tilde{s}}_{\mathrm{lm}}^k{u}_{\mathrm{lm}}^{\sin }(\rho ,\theta ,\varphi )\right)\right)\right).\hfill \end{array}$$ (A7)

Note that

$$\begin{array}{c}{\tilde{c}}_{11}^x={\tilde{s}}_{11}^y={\tilde{c}}_{10}^z=1.\hfill \end{array}$$ (A8)

and the expansion coefficients for the GCFMs and the gcGCFMs are related by

$$\begin{array}{cc}{c}_{\mathrm{lm}}^k\hfill & =g_i{\tilde{c}}_{\mathrm{lm}}^k\hfill \end{array}$$ (A9)

$$\begin{array}{cc}{s}_{\mathrm{lm}}^k\hfill & =g_i{\tilde{s}}_{\mathrm{lm}}^k.\hfill \end{array}$$ (A10)

The basis functions included in our fits and their spatial derivatives are: For the x‐gradient coils.

$$\begin{array}{cc}{u}_{11}^{\mathit{cos}}\hfill & =x\hfill \end{array}$$ (A11)

$$\begin{array}{cc}{u}_{31}^{\mathit{cos}}\hfill & =‐\sqrt{\frac{3}{8}}x(x^2+y^2‐4z^2)\hfill \end{array}$$ (A12)

$$\begin{array}{cc}{u}_{51}^{\mathit{cos}}\hfill & =\frac{\sqrt{15}}{8}x(x^4+y^4‐12y^2{z}^2+8z^4+2x^2(y^2‐6z^2))\hfill \\ u_{71}^{\mathit{cos}}\hfill & =‐\frac{\sqrt{7}}{32}x(5x^6+5y^6‐120y^4{z}^2+240y^2{z}^4‐64z^6+\hfill \end{array}$$ (A13)

$$\begin{array}{cc}& 15x^4(y^2‐8z^2)+15x^2(y^4‐16y^2{z}^2+16z^4))\hfill \end{array}$$ (A14)

$$\begin{array}{cc}\frac{\partial u_{11}^{\mathit{cos}}}{\partial x}\hfill & =1\hfill \end{array}$$ (A15)

$$\begin{array}{cc}\frac{\partial u_{31}^{\mathit{cos}}}{\partial x}\hfill & =‐\sqrt{\frac{3}{8}}(3x^2+y^2‐4z^2)\hfill \end{array}$$ (A16)

$$\begin{array}{cc}\frac{\partial u_{51}^{\mathit{cos}}}{\partial x}\hfill & =\frac{\sqrt{15}}{8}(5x^4+y^4‐12y^2{z}^2+8z^4+6x^2(y^2‐6z^2))\hfill \\ \frac{\partial u_{71}^{\mathit{cos}}}{\partial x}\hfill & =‐\frac{\sqrt{7}}{32}(35x^6+5y^6‐120y^4{z}^2+240y^2{z}^4‐64z^6+\hfill \end{array}$$ (A17)

$$\begin{array}{cc}& 75x^4(y^2‐8z^2)+45x^2(y^4‐16y^2{z}^2+16z^4))\hfill \end{array}$$ (A18)

$$\begin{array}{cc}\frac{\partial u_{11}^{\mathit{cos}}}{\partial y}\hfill & =0\hfill \end{array}$$ (A19)

$$\begin{array}{cc}\frac{\partial u_{31}^{\mathit{cos}}}{\partial y}\hfill & =‐\sqrt{\frac{3}{2}}xy\hfill \end{array}$$ (A20)

$$\begin{array}{cc}\frac{\partial u_{51}^{\mathit{cos}}}{\partial y}\hfill & =\frac{\sqrt{15}}{2}xy(x^2+y^2‐6z^2)\hfill \end{array}$$ (A21)

$$\begin{array}{cc}\frac{\partial u_{71}^{\mathit{cos}}}{\partial y}\hfill & =‐\frac{15\sqrt{7}}{16}xy(x^4+y^4‐16y^2{z}^2+16z^4+2x^2(y^2‐8z^2))\hfill \end{array}$$ (A22)

$$\begin{array}{cc}\frac{\partial u_{11}^{\mathit{cos}}}{\partial z}\hfill & =0\hfill \end{array}$$ (A23)

$$\begin{array}{cc}\frac{\partial u_{31}^{\mathit{cos}}}{\partial z}\hfill & =2\sqrt{6}xz\hfill \end{array}$$ (A24)

$$\begin{array}{cc}\frac{\partial u_{51}^{\mathit{cos}}}{\partial z}\hfill & =‐\sqrt{15}xz(3x^2+3y^2‐4z^2)\hfill \end{array}$$ (A25)

$$\begin{array}{cc}\frac{\partial u_{71}^{\mathit{cos}}}{\partial z}\hfill & =\frac{3\sqrt{7}}{2}xz(5x^4+5y^4‐20y^2{z}^2+8z^4+10x^2(y^2‐2z^2))\hfill \end{array}$$ (A26)

For the y‐gradient coils.

$$\begin{array}{cc}{u}_{11}^{\mathit{sin}}\hfill & =y\hfill \end{array}$$ (A27)

$$\begin{array}{cc}{u}_{31}^{\mathit{sin}}\hfill & =‐\frac{\sqrt{3}}{8}y(x^2+y^2‐4z^2)\hfill \end{array}$$ (A28)

$$\begin{array}{cc}{u}_{51}^{\mathit{sin}}\hfill & =\frac{\sqrt{15}}{8}y(x^4+y^4‐12y^2{z}^2+8z^4+2x^2(y^2‐6z^2))\hfill \end{array}$$ (A29)

$$\begin{array}{cc}{u}_{71}^{\mathit{sin}}\hfill & =‐\frac{\sqrt{7}}{32}y(5x^6+5y^6‐120y^4{z}^2+240y^2{z}^4‐64z^6+\hfill \\ \hfill & 15x^4(y^2‐8z^2)+15x^2(y^4‐16y^2{z}^2+16z^4))\hfill \end{array}$$ (A30)

$$\begin{array}{cc}\frac{\partial u_{11}^{\mathit{sin}}}{\partial x}\hfill & =0\hfill \end{array}$$ (A31)

$$\begin{array}{cc}\frac{\partial u_{31}^{\mathit{sin}}}{\partial x}\hfill & =‐\sqrt{\frac{3}{2}}xy\hfill \end{array}$$ (A32)

$$\begin{array}{cc}\frac{\partial u_{51}^{\mathit{sin}}}{\partial x}\hfill & =\frac{\sqrt{15}}{2}xy(x^2+y^2‐6z^2)\hfill \end{array}$$ (A33)

$$\begin{array}{cc}\frac{\partial u_{71}^{\mathit{sin}}}{\partial x}\hfill & =‐\frac{15\sqrt{7}}{16}xy(x^4+y^4‐16y^2{z}^2+16z^4+2x^2(y^2‐8z^2))\hfill \end{array}$$ (A34)

$$\begin{array}{cc}\frac{\partial u_{11}^{\mathit{sin}}}{\partial y}\hfill & =1\hfill \end{array}$$ (A35)

$$\begin{array}{cc}\frac{\partial u_{31}^{\mathit{sin}}}{\partial y}\hfill & =‐\sqrt{\frac{3}{8}}(x^2+3y^2‐4z^2)\hfill \end{array}$$ (A36)

$$\begin{array}{cc}\frac{\partial u_{51}^{\mathit{sin}}}{\partial y}\hfill & =\frac{\sqrt{15}}{8}(x^4+5y^4‐36y^2{z}^2+8z^4+6x^2(y^2‐2z^2))\hfill \\ \frac{\partial u_{71}^{\mathit{sin}}}{\partial y}\hfill & =‐\frac{\sqrt{7}}{32}(5x^6+35y^6‐600y^4{z}^2+720y^2{z}^4‐64z^6+\hfill \end{array}$$ (A37)

$$\begin{array}{cc}& 15x^4(3y^2‐8z^2)+15x^2(5y^4‐48y^2{z}^2+16z^4))\hfill \end{array}$$ (A38)

$$\begin{array}{cc}\frac{\partial u_{11}^{\mathit{sin}}}{\partial z}\hfill & =0\hfill \end{array}$$ (A39)

$$\begin{array}{cc}\frac{\partial u_{31}^{\mathit{sin}}}{\partial z}\hfill & =2\sqrt{6}yz\hfill \end{array}$$ (A40)

$$\begin{array}{cc}\frac{\partial u_{51}^{\mathit{sin}}}{\partial z}\hfill & =‐\sqrt{15}yz(3x^2+3y^2‐4z^2)\hfill \end{array}$$ (A41)

$$\begin{array}{cc}\frac{\partial u_{71}^{\mathit{sin}}}{\partial z}\hfill & =\frac{3\sqrt{7}}{2}yz(5x^4+5y^4‐20y^2{z}^2+8z^4+10x^2(y^2‐2z^2))\hfill \end{array}$$ (A42)

For the z‐gradient coils.

$$\begin{array}{cc}{u}_{10}^{\mathit{cos}}\hfill & =z\hfill \end{array}$$ (A43)

$$\begin{array}{cc}{u}_{30}^{\mathit{cos}}\hfill & =\frac{1}{2}z(‐3x^2‐3y^2+2z^2)\hfill \end{array}$$ (A44)

$$\begin{array}{cc}{u}_{50}^{\mathit{cos}}\hfill & =\frac{1}{8}z(15x^4+15y^4‐40y^2{z}^2+8z^4+10x^2(3y^2‐4z^2))\hfill \end{array}$$ (A45)

$$\begin{array}{cc}{u}_{70}^{\mathit{cos}}\hfill & =\frac{1}{16}z(‐35x^6‐35y^6+210y^4{z}^2‐168y^2{z}^4+16z^6‐\hfill \\ \hfill & 105x^4(y^2‐2z^2)‐21x^2(5y^4‐20y^2{z}^2+8z^4))\hfill \end{array}$$ (A46)

$$\begin{array}{cc}\frac{\partial u_{10}^{\mathit{cos}}}{\partial x}\hfill & =0\hfill \end{array}$$ (A47)

$$\begin{array}{cc}\frac{\partial u_{30}^{\mathit{cos}}}{\partial x}\hfill & =‐3xz\hfill \end{array}$$ (A48)

$$\begin{array}{cc}\frac{\partial u_{50}^{\mathit{cos}}}{\partial x}\hfill & =‐\frac{5}{2}xz(‐3x^2‐3y^2+4z^2)\hfill \end{array}$$ (A49)

$$\begin{array}{cc}\frac{\partial u_{70}^{\mathit{cos}}}{\partial x}\hfill & =‐\frac{21}{8}xz(5x^4+5y^4‐20y^2{z}^2+8z^4+10x^2(y^2‐2z^2))\hfill \end{array}$$ (A50)

$$\begin{array}{cc}\frac{\partial u_{10}^{\mathit{cos}}}{\partial y}\hfill & =0\hfill \end{array}$$ (A51)

$$\begin{array}{cc}\frac{\partial u_{30}^{\mathit{cos}}}{\partial y}\hfill & =‐3yz\hfill \end{array}$$ (A52)

$$\begin{array}{cc}\frac{\partial u_{50}^{\mathit{cos}}}{\partial y}\hfill & =‐\frac{5}{2}yz(‐3x^2‐3y^2+4z^2)\hfill \end{array}$$ (A53)

$$\begin{array}{cc}\frac{\partial u_{70}^{\mathit{cos}}}{\partial y}\hfill & =‐\frac{21}{8}yz(5x^4+5y^4‐20y^2{z}^2+8z^4+10x^2(y^2‐2z^2))\hfill \end{array}$$ (A54)

$$\begin{array}{cc}\frac{\partial u_{10}^{\mathit{cos}}}{\partial z}\hfill & =1\hfill \end{array}$$ (A55)

$$\begin{array}{cc}\frac{\partial u_{30}^{\mathit{cos}}}{\partial z}\hfill & =‐\frac{3}{2}(x^2+y^2‐2z^2)\hfill \end{array}$$ (A56)

$$\begin{array}{cc}\frac{\partial u_{50}^{\mathit{cos}}}{\partial z}\hfill & =\frac{5}{8}(3x^4+3y^4‐24y^2{z}^2+8z^4+6x^2(y^2‐4z^2))\hfill \end{array}$$ (A57)

$$\begin{array}{cc}\frac{\partial u_{70}^{\mathit{cos}}}{\partial z}\hfill & =‐\frac{7}{16}(5x^6+5y^6‐90y^4{z}^2+120y^2{z}^4‐16z^6+15x^4(y^2‐6z^2)+\hfill \\ \hfill & 15x^2(y^4‐12y^2{z}^2+8z^4))\hfill \end{array}$$ (A58)

Barnett Alan Seth, Irfanoglu M. Okan, Landman Bennett, Rogers Baxter, Pierpaoli Carlo. Mapping gradient nonlinearity and miscalibration using diffusion‐weighted MR images of a uniform isotropic phantom. Magn Reson Med. 2021;86:3259–3273. 10.1002/mrm.28890

DATA AVAILABILITY STATEMENT

Software for implementing the described method will be available at https://www.tortoisedti.org.