Disclosure of Ground‐State Zimmerman‐Möbius Aromaticity in the Radical Anion of [6]Helicene and Evidence for 4π Periodic Aromatic Ring Currents in a Molecular “Metallic” Möbius Strip

Abstract

In 1966, Zimmerman proposed a type of Möbius aromaticity that involves through‐space electron delocalization; it has since been widely applied to explain reactivity in pericyclic reactions, but is considered to be limited to transition‐state structures. Although the easily accessible hexahelicene radical anion has been known for more than half a century, it was overlooked that it exhibits a ground‐state minimum and robust Zimmerman‐Möbius aromaticity in its central noose‐like opening, becoming, hence, the oldest existing Möbius aromatic system and with smallest Möbius cycle known. Despite its overall aromatic stabilization energy of 13.6 kcal mol⁻¹ (at B3LYP/6‐311+G**), the radical also features a strong, globally induced paramagnetic ring current along its outer edge. Exclusive global paramagnetic currents can also be found in other fully delocalized radical anions of 4N+2 π‐electron aromatic polycyclic benzenoid hydrocarbons (PAH), thus questioning the established magnetic criterion of antiaromaticity. As an example of a PAH with nontrivial topology, we studied a novel Möbius[16]cyclacene that has a non‐orientable surface manifold and a stable closed‐shell singlet ground state at several density functional theory levels. Its metallic monoanion radical (0.0095 eV band gap at HSE06/6‐31G* level) is also wave‐function stable and displays an unusual 4π‐periodic, magnetically induced ring current (reminiscent of the transformation behaviour of spinors under spatial rotation), thus indicating the existence of a new, Hückel‐rule‐evading type of aromaticity.

Topology in chemistry: The consequences of Möbius topology are explored in anionic radicals of polycyclic aromatic hydrocarbons by DFT methods. A stable Zimmerman‐Möbius minimum in the noose region of the [6]helicene radical anion, constituting smallest and historically oldest Möbius aromatic cycle, is disclosed as well as a metallic Möbius cyclacenide nanohoop exhibiting an unprecedented 4π‐periodic strong aromatic ring current and unusual stability, defying Hückel's rule.

Introduction

Aromaticity is based on cyclic electron delocalization, and is a powerful concept in chemistry due to stabilization it imparts on molecules and transition states, resulting in unique reactivity and physical properties. ^[1] While nonplanar and/or chiral aromatics or those with curved surfaces are getting more attention lately because of their unique electronic and (chir)optical properties, ^[2] effects of surface manifold topology on polycyclic aromatic hydrocarbon (PAH) electronic structure remained almost unexplored.

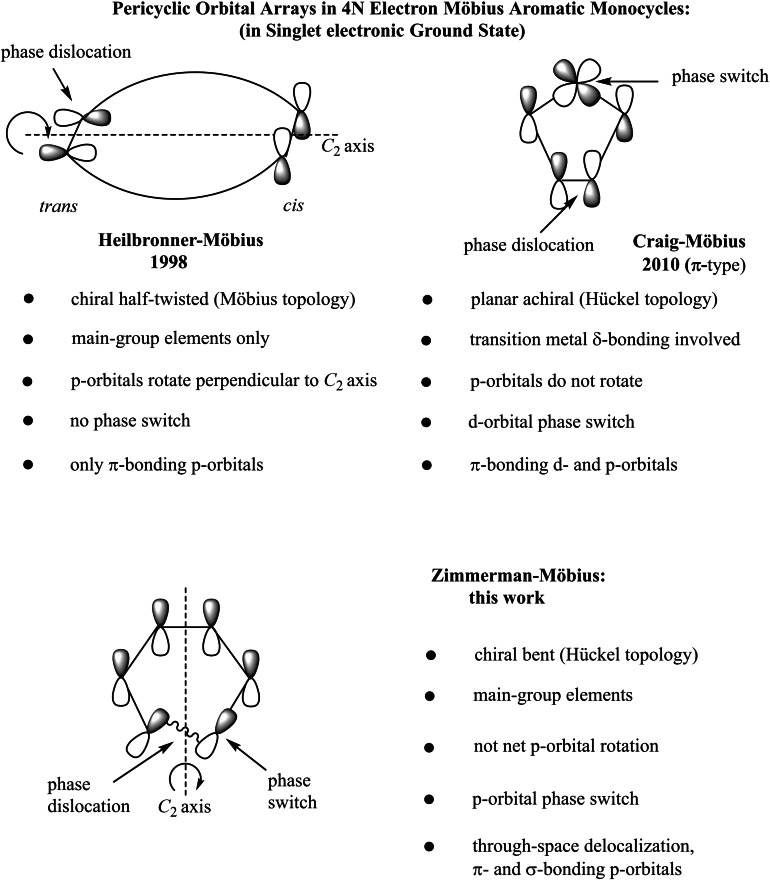
In contrast, the effects of orbital topology in one‐dimensional orbital arrays have been the focus of research since the 1960s. Nevertheless, the computational discovery of Heilbronner‐Möbius twisted annulenes at the end of the 20th century, and for which Hückel's 4N+2 electron rule is reversed because of a twist‐related orbital boundary condition (Scheme 1), ^[3] was unexpected,[ ⁴ , ⁵ , ⁶ , ⁷ , ⁸ ] and came decades after the theoretical prediction of such molecules with continuous p‐orbital overlap and an odd number of orbital phase inversions by Heilbronner in 1964 (Scheme 1). ^[9] Whereas Heilbronner anticipated Möbius annulenes to have 20 carbon atoms or more, Möbius aromaticity was first reported instead in 1998 for an unstable helical conformation of much smaller cyclononatetraenyl cation, discovered in the early 1970s. ^[3b] Only two years after Heilbronner's seminal paper, Zimmerman proposed a different type of Möbius orbital topology based aromaticity, exhibited by certain 4N electron transition states, and which has found widespread application since, to explain reactivity and bonding in thermal and photochemical antarafacial pericyclic reactions. ^[10]

Scheme 1.

Different ways of introducing orbital phase shifts (or phase dislocations) into molecules with cyclic electron delocalization. Longicyclic (purely σ‐bonding) orbital arrays are not included here and might allow further varieties of Craig or Zimmerman system through phase switching (by d‐ or p‐orbitals), or, in odd‐membered rings, through phase incommensurability. Corresponding transition states (i. e., potential energy surface saddle points) were meanwhile reported for all three types of Möbius aromatics.

Both Heilbronner‐ and Zimmerman‐Möbius systems are intrinsically chiral and topologically achiral (because they can racemize, and thereby be deformed into their enantiomer), while their orbital arrays and orbital interactions are markedly different. In Zimmerman‐Möbius systems, delocalization path needs to pass node of a p‐orbital (as a “phase switch”) once, to get to the other side of the π‐system (Scheme 1) and bonding between adjacent orbitals is not solely of π‐type (as in Heilbronner systems), but also of sigma type.

In Zimmerman‐Möbius transition states, through‐space delocalization across the gap where a sigma bond gets formed or broken, is necessarily involved. A further important difference between Heilbronner‐ and Zimmerman‐Möbius orbital arrays is a 180° net p‐orbital rotation in half‐twisted Heilbronner systems, which is 0° in merely bent Zimmerman systems (Scheme 1). As a result, still unknown stable Zimmerman‐Möbius molecules are expected to be less affected by strain and should therefore be more easily accessible and more robust than Heilbronner aromatics, which are prone to unwriggle to competing more stable antiaromatics with Hückel topology – unless they constitute the ground state conformation, which is extremely rare. Heilbronner‐Möbius transition states, either without bond breaking (i. e., with valence shifting)[ ^3a , ¹¹ ] or, alternatively, with conversion of π‐ into σ‐bonds (as in Zimmerman‐type T.S. for pericyclic reactions),[ ¹⁰ , ¹² ] have also been reported. In the latter case, Woodward‐Hoffmann rules are reversed due to Möbius geometry, as we showed in 2009. ^[12]

Another, more recent type of orbital topology based 4N electron aromaticity, is Craig‐Möbius aromaticity (Scheme 1). ^[13] It occurs in de novo designed cyclic organometallic compounds with transition metals, named after D. P. Craig, ^[14] who suggested even six years before Heilbronner that main group elements like phosphorus might use their unoccupied d‐orbitals in dπ–pπ bonds to connect in a phase consistent manner opposite faces of a planar (and achiral) 4N π Möbius heteroaromatic system.

We reported the first formal examples of such ground state Craig‐Möbius aromatic systems and their building principles with transition metals in 2010, ^[13] triggering a flurry of papers on this topic in the literature, even though the existence of such compounds had been hypothesized earlier by Rzepa. ^[15] Because of their planarity, Möbius and Hückel orbitals must coexist in these molecules, in contrast to situation in Zimmerman and Heilbronner systems. Hence, it has been proposed that several Möbius aromatic metallacycles possess hybrid Möbius and Hückel type cyclic electron delocalization. ^[13c]

Also in this case, Woodward‐Hoffmann rules are reversed for corresponding Craig‐Möbius aromatic transition state structures for pericyclic reactions, ^[16] for example, as was demonstrated recently by us for an allowed(!) all‐suprafacial [2π s+2π s] cycloaddition step in a model iron catalysed olefin metathesis reaction, nurturing the hope that Craig‐Möbius aromaticity could have already been observed unknowingly many times in organometallic reactions that seem to violate the Woodward‐Hoffmann rules. ^[16b]

In contrast to experimental realizations of Heilbronner‐Möbius ^[17] and Craig‐Möbius aromatic molecules, ^[18] Zimmerman‐Möbius ground‐state molecules have not yet been reported by experimentalists, probably because of the ease with which such a molecule is expected to undergo electrocyclization to a nonaromatic product, and because their implied helically bent all‐cis conformation is usually not thermodynamically stable and therefore only of transient existence. ^[19]

Results and Discussion

During a 1997 lab conversation, when he learned that the first author intended to find computationally the first Möbius aromatic molecules, Paul Schleyer suggested to his student to somehow “freeze in” antarafacial Zimmerman‐Möbius type transition state structures, for which Möbius aromaticity had been confirmed by Schleyer only a couple of years earlier through magnetic criteria. ^[20] However, the student discarded his supervisors′ idea, because it seemed impossible for him to stop the process of sigma bond formation right in the middle of the act, and realize thereby, so to speak, a “frustrated electrocyclization”. Hence, the first author headed back then straight on for the – now well‐known – half‐twisted Möbius annulenes, Heilbronner originally proposed.[ ^3a , ²¹ ]

An important property of aromatics and a hallmark of aromaticity itself, is a diamagnetic or diatropic (clockwise in field direction) induced ring current in a static magnetic field. ^[23] Vice versa, antiaromatics are characterized by paratropic (anticlockwise) ring currents, which only seemingly defy Lenz′ rule, because these currents are result of virtual excitations, rather than of classical magnetic induction, and therefore follow specific selection rules for transition between quantum levels. ^[23b] These induced aromatic ring currents indicate cyclic electron delocalization and are a premiere instrument to study electronic structure of polycyclic fully conjugated hydrocarbons, irrespective of their topology. ^[24]

Nucleus independent chemical shift (NICS) is a probe based on computation of the electronic shielding tensor, a mixed second derivative of orbital energy by magnetic field strength and orbital magnetic moment. ^[25] Its value can be used to assess and quantify strength and direction of induced ring currents in arbitrary cyclic (not necessarily planar or bond‐connected) arrays of atoms, when shielding probe is placed in their centre, because of reinforcing (deshielding) or weakening (shielding) effect of induced currents’ magnetic fields on applied external magnetic field. ^[26] NICS isotropic value (i. e., the trace) is employed in this paper to deduce the qualitative nature and, together with the NICS_zz component in some cases, also as an approximative quantitative measure for induced ring current strengths, as it was found very recently in an investigation of planar conjugated monocycles that value of this NICS component is reasonably well correlated with the value of total induced ring current density. ^[26d] As a convention, a diatropic current results in deshielding of external nuclei, while nuclei inside the cycle are more strongly shielded (and vice versa for paratropic currents).

As an immediate topological consequence, and in a fully conjugated polycyclic hydrocarbon, a local current running clockwise in one cycle, is equivalent to a (weaker) anti‐clockwise current in adjacent cycle (and vice versa): ring currents are coupled in a counter‐rotating manner, ^[27] in accord with Clar structures of isolated diatropic benzene rings in benzenoid polycyclic hydrocarbons. ^[28]

Please note that these paratropic currents in rings fused to a diatropic cycle are solely result of topology, and not going back to an electrodynamic “counter‐inductive” interaction of induced current in one cycle on current in the other. However, if local induced current in adjacent cycle is already paratropic (e. g., because it is a 4N electron antiaromatic Hückel system), this “topological” coupling is reinforcing on both adjacent opposite‐sense local currents. If conversely, current induced by external magnetic field is already diatropic in adjacent cycle (e. g., for a Hückel aromatic sextet), coupling results in a current strength reducing negative superposition.

Very recently, reports surfaced about observation of “peculiar” paramagnetic currents close to helix axis around noose‐like inner perimeter of helicenes. ^[29] Indeed, in hexa‐ (or [6]‐)helicene, 1 (Figure 1), in addition to expected local diatropicity of peripheral six‐rings, a paratropic “ring” current is observed in central opening or noose, apparently without presence of a closed loop path! At first glance, these observations may appear straightforward, based on an apparent topological analogy with acenes: global current in helicenes, running along inner part of perimeter, should have – for an outside observer – a direction opposite to same current, running along outer rim.[ ²⁹ , ³⁰ ]

Figure 1.

Computed helicene and circulene polycyclic aromatic hydrocarbons, [6]helicene radical anion, heptatrienyl anion and its electrocyclization TS with NICS(0) values (in italics), which imply diatropic (red) and paratropic (green) induced ring currents. The racemization TS for hexahelicene and its anion are also shown. Distances are given in pm. Only the lowest‐energy conformations are shown.

This picture thrives on a “Kirchhoff law” classical analogy to an induced perimeter current in a macroscopic (here deformed) conducting wire loop, that is, by the continuity rule for electric current. In quantum mechanics, however, this does not hold, because it would imply that a perimeter current can change its nature from diatropic to paratropic (or vice versa), when proceeding along its closed loop path comprising solely of bonded sp² carbons. In other words: a topological coupling is only possible for convex circuits. In addition, it implies that there could be a paratropic current, despite absence of a magnetic flux: because of Amperé’s law, induced current strength is given by a closed line integral of magnetic flux along the boundary of a surface area with corresponding magnetic flux density B. ^[31] So, how is there a paratropic current without a closed loop path ? ^[32]

The solution is surprisingly simple. When terminal helicene rings become fused, it's PAH manifold topology becomes obvious: central noose‐like opening is transformed into hub of a circulene, and helicenes′ inner perimeter is tied off to become a separate closed inner loop around this hub, for example, as in coronene 2 or corannulene 3. Induced disjoint concentric ring currents flowing around hub and outer rim of circulenes are coupled and therefore counter‐rotating. ^[33]

Unlike in circulenes, this paratropic current in hexahelicene involves through‐space as well as through‐bond delocalization and crosses the 3.21‐Å‐wide gap (only somewhat smaller than sum of van der Waals radii) between closest sp² carbons in terminal benzene rings. Gap distance equals experimentally determined pitch distance for the inner helix in hexahelicene. ^[34] It remains an open question whether there is also a global diatropic current in 1, because its perimeter does not follow Hückel's rule (i. e., it has 21 π‐electrons). As such a hypothetical current would run in direction opposite to that of paratropic noose current, both currents would cancel out when crossing the gap and became “invisible” there in current density plots, which could explain why such gap crossing currents had been overlooked so far.

Of course, paratropic NICS value in the centre of 1 can also partly be due to the probe being located in deshielding zone of the surrounding PAH framework (see the Supporting Information), whereas NICS_zz(0) value (with the z‐axis identical to the helix axis) is −3.0; this means that an implied gap‐crossing‐induced current would be dominantly diatropic. ^[26d] However, for such strongly warped PAH as 1, all three components (B _x , B _y and B _z ) of induced magnetic fields have to be carefully analysed and taken into account, rather than only the B^ind _z component. ^[35] It was found that doing so, reveals a deshielding cone along the helix axis, ^[35] in accord with our topological considerations above.

Because global diatropic current along outer [18]annulene perimeter in coronene, 2 (which is so stable and insensitive to oxidation by air that it even occurs in pure form as a soft mineral), ^[36] must be counter‐“balanced” by a paratropic “topological” ring current around its central hub, ^[33a] NICS value in centre of 2 is result of superposition of this paratropic current (i. e., of the reversed image of diatropic rim current) with local diatropic current of core benzene unit, and hence, is numerically very small (Figure 1). Diatropic local currents in each of – symmetry equivalent – peripheral six‐rings merge into a dominating global diatropic current running along molecules’ – Hückel rule fulfilling – 4N+2 π‐electron annulene perimeter, preventing a symmetry lowering Clar electronic structure with dominating local induced ring currents. ^[37] Note that counter‐rotating “topological” paratropic component of hub current wouldn't exist without (locally diatropic) aromatic sextets in peripheral rings. However, locally paratropic and peripheral fused, for example, pentalene, units could result in an inverted and topologically coupled magnetic response pattern. ^[33c] Nevertheless, it is not clear which physical mechanism should explain hypothetical “topological” coupling of concentric and independently induced counter‐rotating current loops, for example, when “annulene‐within‐an‐annulene” (AWA) models apply.

Trying to rationalize this interpretation in terms of topological invariants, we notice that acenes pertain to a both path‐ and simply connected topological space, whereas presence of counter‐rotating paratropic currents in 1 and 2 implies that topology of their electronic structure resembles that of a non‐simply connected washer‐ or “flattened doughnut”‐like manifold, that is, one in which not every circular path on the surface can be contracted to a single point still lying on that same surface. Counter‐rotating currents in 1 and 2 could, hence, be considered encircling a “hole” in their respective PAH surface, illustrating current direction is opposite to that along their (outer) perimeter.

In nonplanar, bowl‐shaped corannulene 3 (with a reported ASE of 44.5 kcal mol⁻¹), ^[37] magnetic shielding pattern is, at first glance, similar to that in coronene: a “symmetry breaking” Clar structure is avoided, and central NICS(0) value indicates a counter‐rotating paratropic hub current around non‐aromatic five‐ring. ^[29] However, absolute value of NICS in five‐ring is stepwise reduced with an increment of about 3 ppm per six‐ring, when the latter are successively de‐aromatized by selective hydrogenation of perimeters’ CC double bonds (see the Supporting Information): once three aromatic rings are “switched off” (note that global ring current could still flow over C(sp²)−C(sp²) bonds connecting remaining benzene rings), central NICS value drops from 9.4 to 0.5, that is, paratropic counter‐rotating hub current almost disappears!

This implies that global current in 3 around its 15 (i. e., 4N+3) π‐electron perimeter is insignificant (unlike the situation in 2), whereas local ring currents in benzene rings are topologically coupled to the paratropic hub current individually. In addition, it proves that paratropicity in central ring of this “buckybowl” is not due to local antiaromaticity, a situation similar to a recently reported [9]circulene derivative (but where hub current has, in our interpretation, to flow through‐space to get a closed loop path – as in [6]helicene), ^[29b] and which should hold also for purportedly “antiaromatic” pentagonal rings in C₆₀ fullerenes and similar “buckyballs”. ^[38]

Would radical anions of 1–3 exhibit similar magnetic response properties, we wondered? In hexahelicene radical anion 4, which can be readily prepared as a stable potassium salt in tetrahydrofuran, ^[39] we observed an apparent induced ring current pattern reversal with respect to that in 1: a global paratropic current along outer rim, together with a corresponding diatropic current around the opening close to the helix axis. NICS_zz(0) value is −6.0, in accord with the isotropic value. Notably, distance between closest terminal C(sp²) atoms, 3.11 Å, is smaller in 4, than in 1 – thus indicating the presence of an attractive force between C(sp²) termini in radical anion, absent in 1. Central diatropicity is unlikely to be result of topology, because paratropic rim current is global, rather than result of superposition of locally antiaromatic cycles. ^[40]

To test this anticipation, we have partially hydrogenated 4 on its outer perimeter, combined with replacement of a carbon lying on C ₂ axis by boron (to conserve C ₂ symmetry), thereby “switching off” local as well as global π‐electron currents in all six benzene rings: still we observed a significant diatropic current with NICS(0)=−4.8 ppm, running along “noose” of this helicene derivative, proving that at least the most part of the diatropic current in 4 is not topological in origin (as paratropic one in 1), but rather due to a local effect. As a corollary, it means that paratropic rim current must also cross the gap, albeit in opposite direction: because otherwise, current would have to change its nature along its course and no physical mechanism is apparent, how two concentric (counter‐rotating) and independently induced ring currents could be topologically coupled.

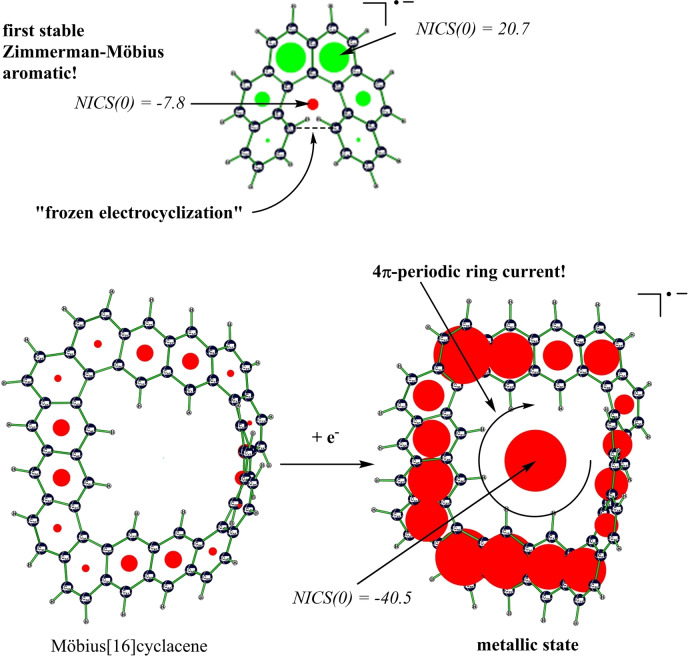
We noticed further that helical “noose” in 4 is an heptatrienyl anion motif (5, Figure 1), resembling a bent Zimmerman‐Möbius aromatic transition state structure for electrocyclic conrotatory ring closure, TS‐6: with eight delocalized π‐electrons and a single orbital phase inversion, heptatrienyl anion, 5, and corresponding moiety in 4 are Möbius aromatic, with ring current flowing through‐space over the gap!

NICS value in 5 is same as in hydrogenated derivative of 4, further corroborating this interpretation. Because of Coulomb repulsion, negative charge is delocalized almost exclusively over the outer rim of 4, rather than over the noose, but the magnetic response pattern is as if extra charge is added to the electron count of both “rim” and “hub” at the same time – an interesting molecular wave function effect that has, to the best of our knowledge, not been described before and contradicts an “annulene‐within‐an‐annulene” model. ^[41] Note that the (global) paratropicity revealed by positive NICS values in peripheral rings of 4 can therefore be rationalized as originating from Möbius 4N+2 π‐electron antiaromaticity of the 22 π‐electron (outer) perimeter, taking into account the (shared) negative charge and when the counter‐clockwise current crosses the gap. ^[42]

Moreover, whereas all‐cis 5 undergoes rapid electrocyclic ring closure via aromatic TS‐6, with a small 7.3 kcal mol⁻¹ barrier, Zimmerman‐Möbius heptatrienyl anion moiety in 4 is kinetically stable, and a transition state for ring closure could not be located! In addition, while all‐cis 5 is thermodynamically disfavoured with respect to its all‐trans conformer by 12.4 kcal mol⁻¹, all‐cis Möbius annulene motif in 4 is thermodynamically stable, being part of the rigid stereogenic [6]helicene scaffold. So it seems that Schleyer's 1997 idea of a “frozen” transition state structure for an electrocyclic conrotatory reaction has come true after all, and Möbius aromatic molecules could have been computationally discovered much earlier, as existence of Möbius aromaticity in hexahelicene anion was overlooked for decades! Our finding suggests that Möbius aromaticity could be present in smaller, more robust and more easily accessible 4N electron systems than previously assumed.

Because of its helical 3D shape, hexahelicene is intrinsically chiral with high optical rotation and interesting chiroptical properties, like circularly polarized luminescence[ ⁴³ , ⁴⁴ ] It is both optically and chemically stable, but known to racemize concertedly via a C _s symmetric saddle‐shaped transition state structure TS‐7 (Figure 1) ^[45] over a sizable barrier of 37.1 kcal mol⁻¹ at B3LYP/6‐31G* (35.4 kcal mol⁻¹ exptl.), ^[34] that is, it is topologically achiral, because it can be deformed into its enantiomer without bond‐breaking.

After we recognized that gap‐crossing Amperéan (current) loops in [6]helicene radical anion 4 must be dictated by Möbius topology, we expected that any induced gap crossing ring current in corresponding asymmetric transition state TS‐8 would have to observe Hückel topology. Curiously, there is no such current at all. The only significant induced ring current is paratropic, and located in central naphthalene moiety of anionic TS‐8.

Because counter‐rotating currents in neutral hexahelicene 1 are due to local diatropic currents in peripheral benzene rings, their nature isn't affected by topology change during racemization (Figure 1). However, as noose current in 4 is due to local Möbius aromaticity, it breaks down completely during racemization via TS‐8 (central NICS(0)=−1.4). Furthermore, and in contrast to TS‐7, TS‐8 is chiral, providing another example for a completely chiral racemization pathway of an “Euclidean rubber glove” molecule. ^[46]

Computationally, we determined lower bound of aromatic stabilization energy (ASE) of 4 as 13.6 kcal mol⁻¹, using a homodesmotic equation at B3LYP/6‐311+G (d,p) level (see the Supporting Information). Could this be due to 4’s central Möbius aromaticity, we wondered, or is paratropicity not limited to (energetically destabilized) antiaromatics? If answer to second question is yes, it would suggest that the concept of paratropicity as a reliable indicator of antiaromaticity must be rethought. Besides, hexahelicene radical anion 4 is 15.6 kcal mol⁻¹ lower in energy than neutral parent 1 (at B3LYP/6‐311+G(d,p)).

Hence, we considered radical anions of other 4N+2 π‐electron aromatics, whose dianions should be paratropic because of Hückel's rule. We expected therefore that these 4N+3 π‐electron systems are nonaromatic. Instead, we found that D _2h benzene radical anion is distinctly paratropic (NICS=136), while retaining about one third (11 kcal mol⁻¹) of benzene's aromatic stabilization energy.

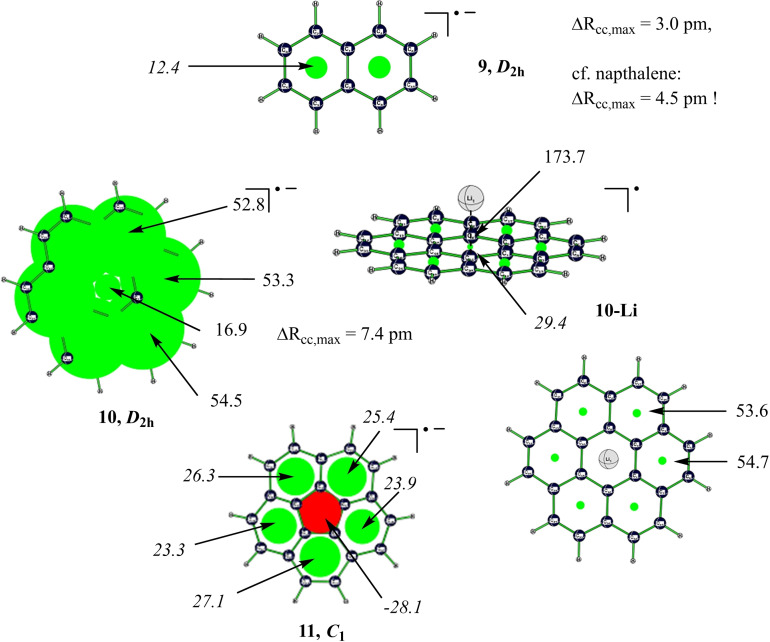
How about the higher congeners of benzene, for example acenes? Among PAHs with simply connected topology, acenes play a prominent role due to their unique electronic structure, which lead to applications as organic semiconductors, for example, in organic field effect transistors (OFET). ^[47] Smallest representative of acene radical anions, naphthalenide 9 (Figure 2), is readily obtained by reduction of naphthalene with alkali metals in liquid ammonia, that is, in Birch reduction involving solvated electrons or dielectrons as nucleophiles, ^[48] and also features a distinct global paramagnetic induced ring current in addition to its electronic paramagnetism, similar to situation in benzene (or to that in naphthalene‐like central moiety of TS‐8). Unlike in the conventional concept of antiaromaticity, which is considered to be accompanied by bond length alternation, π‐electrons are fully delocalized in 9, and perimeter CC bond length alternation is even smaller than in naphthalene itself (Figure 2)! Indeed, aromatic stabilization energy, computed with isomerization stabilization energy (ISE) method (see the Supporting Information), ^[49] is 27.3 kcal mol⁻¹, about one half of that of naphthalene itself (59.2 kcal mol⁻¹), which corroborates our anticipation that paratropicity and aromaticity are not always mutually exclusive.

Figure 2.

Computed naphthalenide and circulene radical anions with NICS(0) values (in italics) which imply diatropic (red) and paratropic (green) induced ring currents. For illustrative purposes, NICS values in ion pair 10‐Li are scaled down. Distances and maximum difference of perimeter CC bond lengths ΔR _cc are given in pm (for 9 at B3LYP/6‐311+G**).

Naphthalenide C₁₀H₈ ⁻ is a strong base and frequently used as powerful reductant in organic synthesis, for example, for reduction of graphene oxide to graphene, or to initiate anionic polymerisations. ^[50] In ethereal solutions, the anion forms a tight ion pair with an alkali metal cation, which often occupies one of the ring faces. Dark green solution colour of, for example, sodium naphthalenide is due to an absorption in visible light region, which we computed with TD‐DFT for the equilibrium geometry to be at 762 nm in THF (735 nm exptl.). ^[51] Naphthalenide does not disproportionate in naphthalene and its dianion, as we found that this is thermodynamically unfeasible. Instead, dianion obviously forms by further reduction with alkali metal.

Paratropicity of 9 is also inherited by N‐doped naphthalene, with a nitrogen atom replacing a bridgehead carbon and an aromatic stabilization energy for this neutral radical of 24.7 kcal mol⁻¹. Fusing two such N‐doped naphthalenes, doubly N‐doped C _2h tetracenes (i. e., di‐aza‐tetracenes) result – compounds with an even number of electrons, a stable closed shell wave function and ASE value of 39.2 kcal mol⁻¹ (see the Supporting Information). In addition, range of perimeter bond lengths is 136.8–143.5 pm (CC bonds) and 136.8–141.1 pm (CN bonds), indicating a structure with pronounced π‐electron delocalization – despite its magnetic “antiaromaticity”! Such “aromatic chimeras” could be interesting as organic semiconductors used in molecular electronics (e. g., in applications such as printable electronics, photovoltaics, sensors or light‐emitting displays) or for optical materials, due to their rather small HOMO‐LUMO gaps, and hence, near‐IR absorption edge. ^[52]

After this excursion into cata‐condensed aromatic hydrocarbons with their exclusive 4N+3 π‐electron paratropicity, we are not surprised that coronene radical anion, 10, is distinctly paratropic as well and forms (similar to naphthalenide) a close ion pair, 10‐Li, with a lithium cation (which sits above the face of the central ring, at 1.74 Å distance from its centre, a little more than half the van‐der Waals distance between graphite layers). This neutral species could be a suitable model for graphite anodes used in lithium‐ion secondary cell batteries, in which intercalated lithium atoms could be formally considered to reduce “graphene” sheets made of graphitic sp² carbons, to give compounds with maximum theoretical capacity and stoichiometry C₆Li. ^[53]

This finding stresses the ease of coronene reduction, matching its resistance to oxidation. A strong global paratropic current runs along formal 4N+3 electron perimeter of 10, implying a high mobility of all π‐electrons. Indeed, Breslow and co‐workers discovered that 4N electron antiaromatics are more conductive than 4N+2 electron aromatics. ^[54] As 4N electron systems are usually paratropic, our result suggests that it is this latter property, and not antiaromaticity as such, ^[27a] which indicates enhanced electric conductivity, and could therefore be also shown by other than 4N electron compounds. Due to superposition of paratropic perimeter current with local diatropicity of the core benzene unit, NICS in centre of 10 is much smaller than in peripheral rings. Note that in this case, negative charge does not add to electron counting of the hub, probably because the latter already achieved an aromatic sextet. Interestingly, 10 is 2.6 kcal mol⁻¹ lower in energy than 2, despite its paratropicity.

In corannulene radical anion, 11, magnetic response pattern appears reversed with respect to that of 3 at first glance: a sizable paratropic current, running along circulene anion rim, appears counterbalanced by a similarly strong diatropic current in the hub. However, six‐rings are not locally paratropic, precluding such a “counter‐balancing” current. Instead, magnetic shielding due to hub current (NICS=−28.1) is obviously caused by local aromatic sextet of central effective cyclopentadienyl anion, while paratropic rim current is in accord with Hückel antiaromaticity of the 4N electron [15]annulene anion perimeter. Again, magnetic response pattern reflects that extra charge adds to electron counting of both rim and hub at the same time (defying Coulomb repulsion), like it did for rim and noose region of [6]helicene anion 4 (again, to realize an aromatic hub!).

While topology of 1–3 would be that of non‐simply connected manifolds (when the hub is considered to encircle a hole in the middle), their surfaces are still orientable, that is, a clockwise loop path cannot be shifted on them to become anticlockwise. Hence, we wondered: what would happen to those perimeter currents in circulenes, helicenes and their anion radicals, when distinction of inner and outer perimeter disappears in a PAH with a non‐orientable surface and a single edge which runs twice around the molecules’ centre as it does in a Möbius nanohoop?

To reveal such physical consequences of Möbius strip topology, it is necessary to look at truly two‐dimensional, rather than merely one‐dimensional systems. Zimmerman‐Möbius transition states for electrocyclic reactions, half‐twisted Möbius annulenes, and even very recently designed poly‐para‐phenylene nanohoops with rings tilted to map the surface of a Möbius strip, ^[55] all possess trivial topology of a circle, because they are effectively one‐dimensional systems, and could, therefore, not reflect the unusual mathematical properties of a Möbius strip.

Most straightforward material to design Möbius strips from, are polycyclic benzenoid hydrocarbons made from cata‐condensed (i. e., fused) benzene rings. Indeed, Türker first studied, using a semiempirical MNDO (modified neglect of diatomic overlap) method, Möbius[n]cyclacenes, conceptually resulting from twisting and joining the ends of n‐acenes. ^[56]

In principle, a unique global induced edge current in a Möbius cyclacene could be either paratropic or diatropic, irrespective of charge and number of edge carbons. ^[57] Hückel's rule (as well as the anti‐Hückel rule for one‐dimensional Möbius systems) is therefore expected to be unable to predict direction of global currents in a Möbius cyclacene, due to their implied 4π periodicity, unlike, for example, 4N annulenes, which are paratropic in Hückel topology (no phase inversion) and diatropic in Möbius topology (with single phase inversion). This 4π periodicity implies a dependence on half‐integer values of magnetic flux (i. e., Φ/2). ^[57] Note, that the wave function itself must still be single valued everywhere. Such 4π periodicity is very rare in physics and has been observed until now only for so‐called Majorana zero mode (MZM) Josephson currents in p‐wave topological superconductors. ^[58] Already earlier, aromatic ring currents have been discussed in analogy to superconducting currents, and to persistent currents in mesoscopic metallic rings. ^[59]

When current circulates clockwise locally inside a benzene ring, it must also circulate equally clockwise in the space outside of it (i. e., in its complement) – in conflict with the concept of topologically “coupled currents”. However, if the current was globally diatropic, protons pointing outside must be deshielded, and more strongly shielded at the inner rim.

At first glance, a Möbius cyclacene with its non‐orientable PAH surface seems to break equivalence of differential and integral forms of Amperé’s circuit law in Maxwell's equations, based on Stokes’ theorem of vector calculus. ^[32] According to this theorem, line integral of a vector field over a closed loop is equal to flux of its curl through the surface bounded by that loop. To be well‐defined, that surface needs a unique direction of its normal vector, in other words: it must be orientable. Stokes’ theorem is, hence, not defined for non‐orientable surfaces like that of the Möbius strip.

However, because aromatic edge ring current encircles the molecules’ centre twice, magnetic induction simply involves Amperéan loops with winding number two, which is another topological invariant. As a result of interchain interaction, induced global ring currents may also additionally show common 2π‐periodicity as a sort of “shortcut”. Intriguingly, Türker already anticipated in 1998 a “4N peripheral circuit” in Möbius[4n]cyclacenes (which he considered closed shell systems!) and a violation of the Hückel rule, that is, he expected such a molecule to exhibit global aromaticity. ^[56]

Instead of resorting to very large systems (to avoid high strain energy), we studied a neutral nearly C ₂ symmetric (topologically) chiral, experimentally unknown, C₆₄H₃₂ Möbius[16]cyclacene, 12, which has moderate size because of two different benzene ring connectivities: in addition to acene‐type [a,d] fusion pattern, there are four “kinks” with two subsequent “phenanthrene‐type” [a,e] patterns. This benzenoid PAH has 4N π‐electrons along its perimeter, whereas benzenoid PAH with orientable surfaces all have 4N+2 π‐electron perimeters. Among PAH with orientable surfaces, only non‐benzenoid 4N electron PAH also can have 4N π‐electron perimeters. ^[27a] In contrast to several previous works on Möbius cyclacenes, ^[60] we found that 12 does not have a triplet ground state, but is rather a closed shell singlet with a stable wave function (at B3LYP/6‐31G*, singlet‐triplet gap is 36.4 kcal mol⁻¹). No global induced edge ring current is observed, as indicated by a near zero NICS(0) value.

Very recently, it was observed that local aromaticities in a hydrocarbon nanobelt of benzene rings are suppressed in favour of a global induced ring current around the whole macrocycle, when oxidation state is altered. ^[61]

Could, hence, at least radical anion of 4N electron Möbius cyclacene 12 have a 4N+1 π‐electron perimeter current similar to those in radicals of 4N+2 π‐electron systems (like 4 and 10)? With M06 functional, radical anion 13 has indeed a strong paratropic induced current along its edge (NICS=+54.3). At B3LYP‐D3/6‐31G* level (including Grimme's D3 semiempirical dispersion energy correction, see the Supporting Information), however, 13 is strongly diatropic (NICS=−52.0)! NICS absolute values in centre of 13 are larger than and of same sign than in any of peripheral benzene rings, irrespective of DFT functional employed. NICS_zz(0) value (with shielding tensor so oriented that z‐axis is perpendicular to the centre circle in xy‐plane and running through the origin) is −113.8 ppm(!), thus indicating an extremely strong total induced ring current. ^[26d] It seems, there are global induced ring currents running exclusively along the whole edge, completing their itinerary only after a 720° rotation, as if the radical's excess electron was running on a “Möbius” roller‐coaster. ^[62] After circulating around centre of the radical twice, that electron would therefore possess its initial spin orientation again, without an overall phase dislocation. Such a 4π periodicity under spatial rotations is unprecedented in chemistry and typical for behaviour of Dirac spinors under Lorentz transformations in Lie group SO(3), resulting in a pseudo‐spin orbital interaction due to the non‐Abelian gauge structure of a Möbius strip. ^[63]

To illustrate, one may conceivably replace the 3D curve of the edge of 12 by a conducting wire. Moving this device in a magnetic field, induces a cyclic current. Möbius cyclacene 12 is therefore a nanoscale analogon of a Möbius resistor or capacitor, made from a cyclic and half‐twisted strip of dielectric material, sandwiched between two conducting metal foils. Due to its unique topology, such a resistor would have near zero self‐inductance.

TD‐DFT computations revealed further peculiarities: 13 is characterized by an extremely low energy (23481 nm at B3LYP; 22619 nm at M06) “forbidden” HOMO→LUMO excitation in medium IR region, superimposed to an uncommon (low‐weight) LUMO→HOMO transition (please note that effectively, optical band gap is zero, as in a metal or semi‐metal), and with very small oscillator strength. A second excited state with sizable oscillator strength (f=0.11–0.12) belongs to a HOMO→LUMO+1 transition at an almost method‐independent wavelength (1594 nm at B3LYP; 1549 nm at M06), which has (at B3LYP) an additional lower weight contribution from a HOMO→LUMO transition.

Both B3LYP and M06 contain a certain amount of exact nonlocal Hartree‐Fock (HF) exchange, 20 % (B3LYP) and 27 % (M06), ^[64] to cope with the self‐interaction error, all DFT methods are suffering from. ^[65] Actual amount of HF exchange employed is usually derived by comparison with perturbation theoretical results. Even with M06‐2X (with a rather large and constant 54 % HF exchange in both long‐ and short‐range regimes), 4π‐periodic edge current is apparently dominating in 13, as indicated by a central NICS(0) value of +6.6 and an optical absorption edge at 2418 nm (f=0.15): a superposition of HOMO→LUMO and HOMO→LUMO+1 transitions, similar to “second” excited state at B3LYP, albeit with majority of weight for a HOMO→LUMO excitation.

Note that two‐dimensional Möbius cyclacene 12 can be considered as being built from two stacked (or one‐dimensional) Möbius annulenes: a Möbius[41]‐ and a Möbius[25]annulene that share two adjacent carbon atoms. Central NICS value in 13 could therefore be due alternatively to superposition of shielding of two 4N+2 electron Möbius antiaromatic anionic Möbius[25]annulene and Möbius[41]annulene motifs. However, when we blocked hypothesized 4π periodic induced edge current in 13 through partial hydrogenation of symmetry equivalent CC double bonds on delocalization pathways along outer rim and along inner perimeter, respectively (see the Supporting Information), we obtained NICS values (at M06‐2X) of merely +2.8 and of −0.7. This shows that even with such a high content of exact Hartree‐Fock exchange in the long‐range regime, as in M06‐2X, 4π periodic induced current mode is dominating, albeit with a paratropic sense.

On the other hand, and especially in long‐range regime (and for cyclic molecules), such unscreened Pauli repulsion as in M06‐2X must lead to unphysical results, because assumed permittivity is that of the vacuum (ϵ _r=1), so that the theory cannot recover the limit of the free electron gas and is therefore unsuitable for systems with itinerant electrons, that is, metallic systems, like zigzag edged chiral single‐walled carbon nanotubes (SWNT). ^[66] Hence, we recomputed Möbius[16]cyclacene 12 and its radical anion 13 with the HSE06 functional, which is known to give good results for metallic systems, because the Fermi hole is screened and content of exact HF exchange is “damped”, going from an initial value of 25 % in short range asymptotically to zero in the long range regime. ^[67]

However, 12 itself exhibits no global induced ring current (NICS is +0.5 in centre), whereas the NICS value in the centre of 13 is −40.5 ppm (with largest value among peripheral rings: −38.4), similar to the unscreened results at B3LYP with its small HF exchange content! We therefore see some justification to call this unforeseen effect in 13 “super aromaticity”, which is also a novel type of aromaticity not subject to Hückel or any other electron counting rule in which the total number of π‐electrons figure!

Protons pointing inwards resonate upfield by up to 40 ppm (a value usually observed, e. g., for metal hydrides!), while outer protons are up to 20 ppm(!) deshielded, which would probably be the highest value for a hydrocarbon ever observed. When we blocked the 4π edge ring current in 13 at the outer and inner rim in the same way as we did at M06‐2X/6‐31G* level, central NICS(0) value dropped to −2.0 and −0.5 for the HSE06 functional, respectively. This proves unequivocally the essential role of the complete delocalization pathway along the 64 carbon edge of the Möbius cyclacene for the existence of an unprecedented 4π‐periodic induced aromatic ring current. It is remarkable that “short‐circuiting” 2π‐periodic currents are practically absent, even though they are not blocked, that is, that replacement of physically unusual 4π‐periodic edge current by “ordinary” 2π‐periodic global aromatic ring currents is avoided. Möbius topology is apparently a prerequisite for existence of a global aromatic ring current in 13. A homodesmotic equation for blocking of edge delocalization at outer rim of 13 gives a lower bound for the aromatic stabilization energy of 46.0 kcal mol⁻¹.

It is remarkable that full 720° perimeter ΔR _cc,max value for 13 is 12.0 pm(!), which is huge for an aromatic compound, and typical of antiaromatic species. ^[3a] Obviously, strongly bond alternating systems can nevertheless be diatropic like 13, whereas distinctly bond equalized systems like 9, can still be paratropic. Unfortunately, TD‐DFT calculations with HSE06 failed, so that we could not compute the optical band gap. This failure might be due to the ridiculously small HOMO‐LUMO gap (of both α‐spin orbitals) of 0.0095 eV in 13, which is merely 0.22 kcal mol⁻¹, and equivalent to an “optical” transition at 2.8 THz(!), that is, in the far infrared, underlining again the metallic character of this radical anion.

In contrast, closed‐shell 12 has a sizable HOMO‐LUMO gap of 1.67 eV (equivalent to an absorption edge at 742 nm). This value is in accord with an earlier report for a different Möbius[16]annulene at B3LYP/6‐31G*. ^[60g] Due to the exciton binding energy, the actual optical absorption is expected to be at a larger wavelength. Indeed, a TD‐DFT computation gave 779 nm for the first electronic excitation, which would translate into a (for an insulator) rather small 0.08 eV exciton binding energy. The non‐vertical singlet‐triplet gap at HSE06/6‐31G* level amounts to 27.6 kcal mol⁻¹, which is still so large that it is very unlikely that a higher level (e. g., coupled cluster) computation would yield a triplet ground state. Magnetic response pattern of aromatic 12 does not match a Clar structure interpretation: it shows instead a domain‐like structure with four naphthalene‐like moieties, separated each by a pair of benzene rings with much smaller NICS(0) values (Figure 3). The asymmetric structure has almost C ₂ symmetry.

Figure 3.

Proposed computed novel closed‐shell Möbius[16]cyclacene 12 as an example of a hydrocarbon with a non‐orientable surface in different views and computed with different density functionals (bold‐face and in italics). NICS(0) values (in italics) imply diatropic (red) and paratropic (green) induced ring currents. Distances are given in pm. Note the fourfold symmetry in the magnetic response pattern of 12.

DFT functionals with a too high content of exact HF exchange in the long range regime and/or in which the HF exchange is not damped, are obviously not suitable to describe this type of unprecedented aromatic system. Please note that Möbius cyclacene radical anion 13 is not “Möbius aromatic” because there is an even number (two) of (annihilating) orbital phase inversions, which have to be passed on the 4π delocalization pathway along the edge of the radical, because the molecular wave function itself is, of course, 2π‐periodic.

Perhaps the most striking results are the energetics. Naphthalene has a negative electron affinity, ^[68] that is, its (paratropic) radical anion 9 has a 17.7 kcal mol⁻¹ higher total electronic energy than the neutral hydrocarbon (and an aromatic stabilization energy reduced by 31.9 kcal mol⁻¹, as compared to parent naphthalene). In contrast, Möbius cyclacene radical 13 has an absolute energy, even 37.5 kcal mol⁻¹ lower than that of 12! This shows that global aromaticity in 13 brought along a considerable extra stabilization. It also means that hydrocarbon 12 could be a formidable oxidant (which is more than unusual for a neutral hydrocarbon), whereas naphthalenide 9, for example, is a known powerful reductant. Alkali metal salts of Möbius cyclacenide 13 could even be air stable solids, in contrast to, say, sodium naphthalenide. In addition, protonation of 13 would result in a neutral hydrocarbon, which is expected to be an unusually strong CH acidic compound!

While paratropicity of naphthalenide, being half‐way between naphthalene and its dianion, is plausible, it is interesting that naphthalenide still retains also some of naphthalenes’ aromatic stabilization, despite its magnetic “antiaromaticity”. In contrast, diatropicity of Möbius cyclacenide 13 cannot be derived from its neutral parent 12. The (very pronounced) novel variety of global aromaticity in this topologically nontrivial molecule is apparently not due to a “cooperative effect” of π‐electrons, as aromaticity is usually regarded in chemistry, hence the violation of the time‐honoured Hückel rule. ^[69]

Conclusion

As a late realization of Schleyer's 1997 idea, we have reported, a first stable Zimmerman‐Möbius aromatic in the eight π‐electron heptatrienyl anion motif in the well‐known hexahelicene radical anion, which allows Möbius aromaticity to be studied and exploited in more robust, smaller and more easily accessible 4N electron systems than hitherto proposed. Perhaps most striking is the fact that the ring current in the [6]helicene noose region crosses the gap between terminal benzene rings “through space”; this suggests that this system could serve as a component of novel molecular electronic devices. As the hexahelicenide has been known for a much longer time than the Möbius annulenes, which have been designed later, it could be also considered the historically first actual Möbius aromatic system in its ground state.

We also found that several 4N+3 π‐electron radical anions of some well‐known PAH molecules with trivial simply connected topology are fully π‐electron delocalized and still aromatic to some extent, despite featuring exclusive global paratropic (“antiaromatic”) ring currents. This suggests that “antiaromaticity” is actually more complex than aromaticity. In addition to genuinely destabilized 4N electron antiaromatics, like cyclobutadiene or the D _4h ring‐flip transition structure of cyclooctatetraene, other systems with a 4N or 4N+3 π‐electron perimeter could exhibit an exclusive global paratropic, induced ring current (indicating π‐electron delocalization and high conductivity), while still being aromatically stabilized to a certain extent, as was first proposed by Aihara for dianions/dications of a 4N+2 π‐electron perimeter PAH like pyrene.[ ⁷⁰ , ⁷¹ ]

Proceeding to the more sophisticated, non‐orientable PAH manifold topology of the proposed closed‐shell Möbius cyclacene 12, we discovered a new type of non‐Möbius aromaticity in the unknown hydrocarbon radical anion 13, in which a single itinerant excess electron causes a very strong global aromatic ring current along the 4π‐edge of the whole molecule, reminiscent of the transformation behaviour of spinors under spatial rotation. Curiously, despite its Möbius topology, 13 is not Möbius aromatic, while Möbius aromatic 4 lacks Möbius topology. Möbius aromaticity, for example, in annulenes, is always the result of a phase dislocation.

We predict that this special variety of open‐shell aromaticity exists in topologically nontrivial 13, is novel and evades electron‐counting rules like the Hückel rule. Hence, there are no “magic” total numbers of π‐electrons responsible for the observed dramatic magnetic response, but solely the single itinerant excess electron with an energy close to the Fermi boundary, and which moves around freely as electrons in the “electron gas” of a metal do. To prepare 13, it could be sufficient to react 12 (once synthesized) with an alkali metal. Alkali‐metal‐doped PAH are often known to exhibit superconductivity at low temperatures. ^[73] So‐called “topological superconductors” have found much attention lately, especially in the context of quantum computing, in which qubits are realized by non‐Abelian anyons, that is, quasiparticles, which are their own antiparticle. ^[74] Experimental chemists are challenged to synthesize this herein proposed exotic material.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

M. Mauksch, S. B. Tsogoeva, Chem. Eur. J. 2021, 27, 14660.