Futures market and the contagion effect of COVID-19 syndrome

Abstract

The paper aims to investigate the existence of financial contagion between China and its major trading partners during the ongoing COVID-19 pandemic using the multivariate ADCC-EGARCH model. The analysis results reveal significant financial contagion in most developed and emerging markets having significant trade relationships with China during COVID-19 syndrome. The evidence about financial contagion is vital for regulators and different classes of market participants for varying purposes, and hence the results should find practical implications similar to policymakers, investors, and risk managers.

1. Introduction

In 2002 the world saw the Severe Acute Respiratory Syndrome Coronavirus (SARS-CoV), which impacted more than twenty-nine countries worldwide (Shaw, 2006), and in 2012, the emergence of the Middle East Respiratory Syndrome Coronavirus (MERS-CoV) was reported (Al-Tawfiq and Auwaerter, 2019). Since then, the world has always feared such a novel pathogen's recurrence that may cause a global contagion. The fear turned into reality when the novel Coronavirus (COVID-19) surfaced in Wuhan province in China. Little was anticipated that the COVID-19, in such a short span, would turn into a global menace, a "Black Swan" with severe economic and financial repercussions (Goodell, 2020). The vulnerability of the situation can be assessed by how the financial markets responded to this new development by recording a steep fall in all the benchmark indices, indicating the financial markets' fragility (Akhtaruzzaman et al., 2020).

Past research documented stock markets' responses to such outbreaks (Bhuyan et al., 2010), reporting that the infected country's asset returns exhibited increased cross-market linkages. Moreover, given the size of the pandemic's impact, it is imperative to study its aftermath on financial markets as it may provide new clues about how contagion can flow in through alternate channels contributing to financial upheavals.

Forbes and Rigobon (2002)1 define financial contagion as a significant increase in market co-movement after a shock to one country and differentiates it from interdependence. Research into financial contagion has spoken about contagion either in equity markets (Kenourgios et al., 2011) or the commodity market (Wang et al., 2019). Further attempts were made to study contagion through the trade links channel ( Akhtaruzzaman and Shamsuddin, 2016; Akhtaruzzaman et al., 2021 ) but practically remained silent about the derivative markets. Against Akhtaruzzaman et al. (2021)'s previous work exploring the contagion's flow during economic downturns caused by the financial crisis, especially the global financial crisis, the current paper analyzed contagion result of the sudden development of the COVID-19 syndrome, a major health hazard that emanated from China and spillovers to its major trading partners. Thus, it would be interesting to document such contagion effects in derivative markets, more so through the lens of financial market imperfections (Kaminsky and Reinhart, 2002) and thru periods of a worldwide pandemic. For the stated reason, the paper develops a framework to answer these questions; whether there is a significant increase in cross-market linkages during crises.

This paper enriches the literature by unveiling new evidence of financial contagion in the futures market by studying the seventeen different countries (Developed and Emerging), which are China's main trading partners. Furthermore, the study documents the contagion effect of COVID-19 on most countries. The empirical results are based on examining the three-block set-up. First, analyzing the entire period covering from 1st August 2015 to 31st July 2020. Second, the tranquil period from 1st August to 30th November 2019, and lastly, the crises period of 1st December 2019 to 31st July 2020.2 The period was mainly considered to isolate the transmission of China's contagion on its trading partners resulting from the COVID-19 pandemic and avoid any other events that may have impacted the study's results and robustness. Against the popularly used spot markets, this paper uses the futures markets. As it is well-documented in the literature that the futures market disseminates information faster into the prices than the spot market and hence aid in effective price discovery and thus serve as a better representative for asset markets (Banerjee et al., 2020; Bohl et al., 2011; Wu et al., 2005; Xu and Wan, 2015).

The study uses a bivariate asymmetric dynamic conditional correlation (ADCC) GARCH framework against the VAR framework used by Arezki and Liu (2020) as it falls short of capturing volatility dependence during a crisis (Hu, 2006). The DCC GARCH, unlike constant conditional correlation (CCC) GARCH and BEKK GARCH specification (Engle 2002; Tse and Tsui, 2002), as previous literature has unveiled that dynamic conditional correlation (DCC) GARCH yielded a more accurate estimation of conditional variances, whereas the study by Cappiello et al. (2006) showed that asymmetric dynamic conditional correlation (ADCC) GARCH model outclasses the DCC GARCH model with lower Bayesian Information Criterion (BIC) and higher log-likelihood value, and better adaptive to model the time-varying market integration. Besides, DCC GARCH does not account for asymmetries in conditional variances, covariances, and correlations, leading to an incorrect specification of the conditional variance-covariance matrix (Cappiello et al., 2006 ; de Goeij and Marquering, 2009). Following Cappiello et al. (2006) and Hou and Li (2016), this paper used the Asymmetric DCC GARCH model (ADCC), which incorporates the leverage effect into the conditional correlations. The rest of the paper's organization is as follows: Section 2 presents the data and descriptive statistics. Section 3 describes the methodology. Section 4 of the empirical results are presented, and Section 5 concludes the paper.

2. Data and descriptive statistics

The paper investigates financial contagion with the onset of COVID-19 between China and its main trading partners in index futures markets, using the major benchmark index futures contracts' daily prices. The sample period is from 1st August 2015 to 31st July 2020, which contains the daily end closing prices obtained from the Bloomberg database. The dataset contains the closing prices, volume, and open interest positions of each contract, and the daily returns are computed as the natural log of closing prices multiplied by 100 $\left(\text{ln}\left(\frac{P_t}{P_{t-1}}\right)*100\right)$ were the closing prices are P_t and P _t − 1. Following Akhtaruzzaman and Shamsuddin (2016) and Forbes and Rigobon (2002), the future prices are recorded in local currencies. Mink (2015) highlighted that returns converted into common currency against local currency were shown to bias the contagion test outcomes. Further, incorporating foreign exchange (FX) rates may spike additional volatility from the foreign exchange markets that might not be related to volatility in the index futures market (Sim and Zurbreugg, 1999). Studies by Hou and Li (2016) and Mink (2015) suggested that currency hedging in the forward markets may moderate the currency risk. Given this, the incorporation of the FX rate is evaded. China's main trading partners are presented in Fig. 1 . Table 1 reports the descriptive statistics of each index's future returns. The JB statistics suffices all the return series exhibit skewness and excess kurtosis and the non-normality condition.

Fig. 1.

China and its major trading partners.

Table 1.

Descriptive statistics of returns of China and other countries index futures contracts.

	Mean	Median	Std.	Skewness	Kurtosis	JB statistics
CSI 300	0.0208	0.0414	1.5151	−1.1746	17.5524	10,719.76⁎⁎⁎
S&P 500	0.0393	0.0501	1.2397	−0.8800	20.8515	15,874.23⁎⁎⁎
Nikkei 225	−0.3147	−0.5059	4.1495	0.4934	12.7291	4614.20⁎⁎⁎
KOSPI 200	0.018	0.067	1.173	0.022	15.001	7122.87⁎⁎⁎
DAX 30	0.0134	0.0518	1.3166	−0.6389	15.2691	7259.50⁎⁎⁎
Nifty 50	0.022	0.041	1.229	−1.711	27.553	29,473.69⁎⁎⁎
AEX In. Fut.	0.0103	0.0647	1.1930	−0.9817	15.9356	8537.90⁎⁎⁎
FTSE In. Fut.	−0.0092	0.0071	1.1621	−0.8879	14.7273	7151.40⁎⁎⁎
SGX In. Fut.	0.0221	0.0660	1.2458	−1.9278	30.7669	40,276⁎⁎⁎
TAIEX	0.0325	0.0545	1.1088	−0.2788	8.7079	1681.60⁎⁎⁎
MOEX In. Fut.	0.0494	0.0615	1.1359	−0.9576	12.6946	4850.1⁎⁎⁎
SPI ASX 200	0.0046	0.0651	1.1829	−1.1324	17.1787	10,411⁎⁎⁎
TSX 60	0.0136	0.0713	1.1895	−1.3842	44.8860	87,004⁎⁎⁎
IBrX 50	0.0202	0.0412	2.5975	−1.0133	19.5678	14,139⁎⁎⁎
CAC 40	0.0063	0.0430	1.3000	−1.3255	18.2284	11,917⁎⁎⁎
SET 50	−0.0039	0.0312	1.2836	−1.7912	26.8045	27,719⁎⁎⁎
FTSE MIB	−0.0056	0.0500	1.6159	−4.2504	85.7363	34,184⁎⁎⁎
IBEX 35	−0.0310	0.0230	1.3762	−1.6861	22.1543	18,866⁎⁎⁎

Note: The descriptive statistics values provided are reported only for the full sample period.

^⁎⁎⁎Indicate the significance level at 1%.

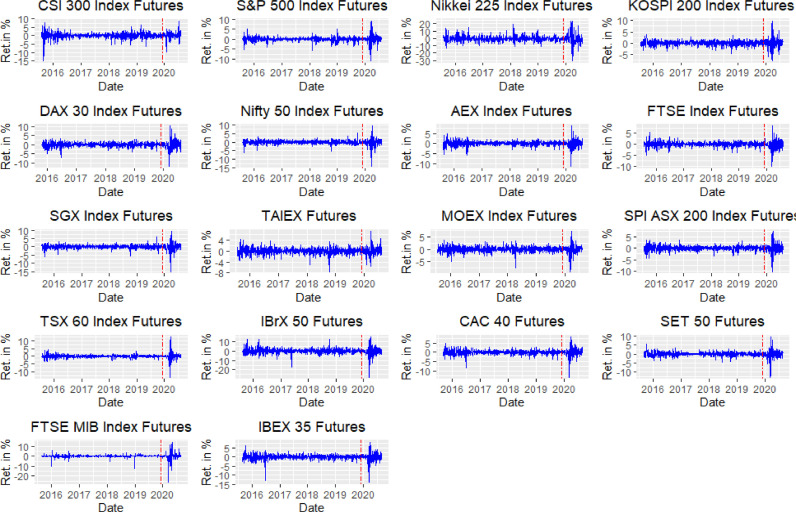
Fig. 2 presents the daily index futures returns of the CSI 300 against the trading partners' index futures market. China's index futures returns are more volatile in the pre-crisis period against the trading partners' ones. As seen in Fig. 2, the trading partners' returns exhibit an abrupt surge and all the more volatile against the CSI 300 daily in the crisis period, which may be attributed to the sudden development of uncertainty arising out of the COVID-19 crisis.

Fig. 2.

Index futures return series.

3. Methodology

In this study, first, the returns are modeled using a vector autoregressive (VAR) framework. The model is then extended to a bivariate asymmetric dynamic conditional (ADCC) GARCH framework to investigate the time-varying volatility spillovers in the index futures market.

The conditional mean of a bivariate VAR model is specified as follows:

$$r_t^d=a_o+\sum _{i=1}^I{a}_i{r}_{t-i}^d+\sum _{j=1}^J{a}_j{r}_{t-j}^f+{\epsilon }_t^d$$

$$r_t^f=a_o^{\sim }+\sum _{i=1}^I{a}_i^{\sim }{r}_{t-i}^d+\sum _{j=1}^J{a}_j^{\sim }{r}_{t-j}^f+{\epsilon }_t^f$$

Here $r_t^d$ represents the CSI 300 index futures returns and $r_t^f$ are the future returns of trading partner countries. a_o and $a_o^{\sim }$ are the intercept of each equation. $r_{t-i}^d$ and $r_{t-j}^f$ are the lagged returns and a_i, $a_i^{\sim }$, a_j, $a_j^{\sim }$ are the corresponding coefficients of the lag returns. ${\epsilon }_t^d$ and ${\epsilon }_t^f$ are the error terms of each equation assumed to be distributed with zero mean and constant variance $({\epsilon }_t/{\Omega }_{t-1}\sim \mathrm{N}(0,H_t))$ with (i, j) lag order. And the optimal lag length of the model is determined using the Akaike Information Criterion (AIC) and Likelihood ratio (LR).

Second, to investigate the cross-market linkages in the second moment, the VAR framework is extended to conditional heteroscedastic error structure to extrapolate the conditional variance-covariance matrix. Thus, as Cappiello et al. (2006) proposed, the ADCC GARCH model is employed to account for the time-varying correlation between the assets and capture the asymmetric impact of negative and positive news. The error structure is respecified as follows: $({\epsilon }_t/{\Omega }_{t-1}\sim \mathit{Stud}\mathit{enti}\mathit{zed}t(0,H_t,\kappa ))$ where H_t = D_tR_tD_t with $D_t=dia\left(\sqrt{h_{11,t}},\dots ..\sqrt{h_{nn,t}}\right)$ are the time-varying standard deviations obtained from the GARCH model and $R_t=diag{\left(Q_t\right)}^{-1/2}{Q}_{t}diag{\left(Q_t\right)}^{-1/2}$ and $Q_t=\left(1-a-b\right)\overline{Q}+a{u}_t{u}_{t-1}^{\prime }+b{Q}_{t-1}$ where Q_t defines the covariance of the standardized residuals u_t, $\overline{Q}$ is the unconditional covariance matrix of u_t $\left(\overline{Q}=Cov\left(u_t{u}_{t-1}^{\prime }\right)\right)$. And a and b are the non-negative scalars such that a + b < 1 to ensure stationarity and positive definiteness of $\overline{Q}$.

The error term ε_t follows a Student's t distribution with mean zero and conditional variance-covariance matrix H_t .The advantage of assuming error terms to follow Student's t distribution is that it accommodates the innovation's excess kurtosis (Baillie and Bollerslev, 1989) and thus serves robust estimation in deviations from normality (Tse, 1999). Ω_t − 1 is the information set till time instant (t − 1). κ is the degree of freedom for Student's t distribution controlling for the tail behavior.

The conditional heteroscedastic process is specified as follows:

$$log\left(h_{i,t}\right)={\omega }_i+{\alpha }_i\left[\frac{\left|{\epsilon }_{t-1}\right|}{\sqrt{h_{t-1}}}-\sqrt{\frac{2}{\pi }}\right]+{\beta }_{i}log\left(h_{i,t-1}\right)+\gamma \left(\frac{{\epsilon }_{t-1}}{\sqrt{h_{t-1}}}\right)$$

Basically, h _i,t follows the EGARCH process developed by Nelson (1991), and the specification ensures that the conditional variance is always positive with no restrictions imposed on the coefficients. α_i′s and β_i′s captures the ARCH and the GARCH effects, and γ is the representative of the asymmetry that is to incorporate the leverage effect of positive and negative shocks in the conditional volatility as failing to capture asymmetry leads to misspecification of the volatility process.

To calibrate the asymmetric volatility and the time-varying conditional correlation, DCC extends to the ADCC EGARCH framework following Cappiello et al. (2006) with the dynamics of Q_t expressed as follows:

$$Q_t=\left(\overline{R}-A^{\prime }\overline{R}A-B^{\prime }\overline{R}B-G^{\prime }\overline{S}G\right)+A^{\prime }{u}_{t-1}{u}_{t-1}^{\prime }A+B^{\prime }{Q}_{t-1}B+G^{\prime }{k}_{t-1}{k}_{t-1}^{\prime }G$$

where A, B, and G (A = a ², B = b ², G = c ²) are the N × N parameters matrices, u_t denotes the standardized residuals, $\overline{R}$ and $\overline{S}$ the unconditional matrices of u_t, k_t = I[u_t < 0] is equal to 1 or 0 otherwise. To have Q_t positive-definite the intercept term $\left(\overline{R}-A^{\prime }\overline{R}A-B^{\prime }\overline{R}B-G^{\prime }\overline{S}G\right)$ must be positive semidefinite along with the initial covariance matrix Q ₀ should be positive definite.

3.1. Test for the contagion effect

Following Celik (2012), the contagion effect is tested using the t-statistics to investigate the consistency of dynamic correlation between the index futures markets in the pre-crises and crises period, with the t –statistics3 specified as follows:

$$t=\frac{\left({\overline{\rho }}_{ij}^{crises}-{\overline{\rho }}_{ij}^{pre-crises}\right)-\left({\mu }_{\rho }^{crises}-{\mu }_{\rho }^{pre-crises}\right)}{\sqrt{\frac{s_{crises}^2}{n_{crises}}+\frac{s_{pre-crises}^2}{n_{pre-crises}}}}$$

where${\overline{\rho }}_{ij}^{crises}$ and ${\overline{\rho }}_{ij}^{pre-crises}$ the mean values of the dynamic conditional coefficients, ${\mu }_{\rho }^{crises}$ and ${\mu }_{\rho }^{pre-crises}$ the correlation coefficients in the pre and during crises period, and $s_{crises}^2$ and $s_{pre-crises}^2$ are the sample variances for both the DCC series (crises and pre-crises period) and n_crises and n _{pre − crises} are the sample size for the crises and pre-crises period.

4. Empirical results

At first, the paper begins with the estimation of the VAR model. Before estimating the VAR model, the stationarity condition for all the index futures return series is tested. Table 2 presents the stationarity test results using the Augmented Dickey-Fuller (ADF) and Philip-Perron (PP) tests. The results reject the null hypothesis of the ADF test and PP tests of the presence of unit root in all the index futures return series, and then they are used in the estimation of the VAR model. The best lag order is selected using the Final Prediction Error (FPE) criterion, Akaike Information Criterion (AIC), and Likelihood Ratio Criterion (LR) criterion for the VAR model. After VAR modeling,4 diagnostic tests have been performed on residuals to check for serial correlation and ARCH effect. The results of the test indicate that the residuals are free from serial and ARCH effects. After the VAR model's calibration, the next step is to run the ADCC EGARCH on the VAR equations' residuals.

Table 2.

Unit root test for the index futures return series.

	ADF test	PP test
CSI 200	−17.780⁎⁎⁎	−30.882⁎⁎⁎
S&P 500	−10.403⁎⁎⁎	−39.336⁎⁎⁎
Nikkei 225	−9.205⁎⁎⁎	−29.206⁎⁎⁎
KOSPI 200	−9.658⁎⁎⁎	−38.064⁎⁎⁎
DAX 30	−9.629⁎⁎⁎	−33.547⁎⁎⁎
Nifty 50	−8.777⁎⁎⁎	−37.621⁎⁎⁎
AEX In. Fut.	−10.449⁎⁎⁎	−33.669⁎⁎⁎
FTSE In. Fut	−9.7318⁎⁎⁎	−36.612⁎⁎⁎
SGX In. Fut.	−9.502⁎⁎⁎	−40.548⁎⁎⁎
TAIEX	−10.320⁎⁎⁎	−36.468⁎⁎⁎
MOEX In. Futures	−10.235⁎⁎⁎	−34.364⁎⁎⁎
SPI ASX 200	−8.732⁎⁎⁎	−40.242⁎⁎⁎
TSX 60	−9.001⁎⁎⁎	−41.450⁎⁎⁎
IBrX 50	−8.756⁎⁎⁎	−38.256⁎⁎⁎
CAC 40	−10.069⁎⁎⁎	−34.374⁎⁎⁎
SET 50	−9.076⁎⁎⁎	−38.905⁎⁎⁎
FTSE MIB	−7.204⁎⁎⁎	−37.714⁎⁎⁎
IBEX 35	−9.837⁎⁎⁎	−34.478⁎⁎⁎

Note: The ADF and PP test results are reported only for the entire sample.

^⁎⁎⁎Indicate the significance level at 1%.

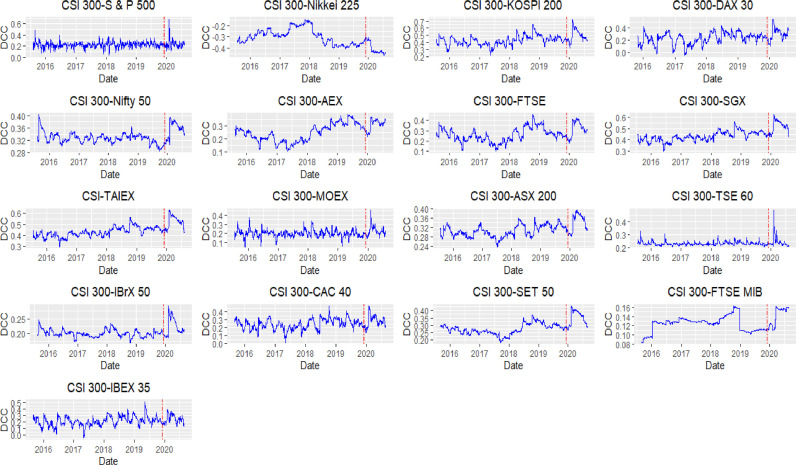
Table 3 presents the results of presents the results ADCC EGARCH (1,1) model for the full period following (Arouri et al., 2011). The results show that the ARCH and GARCH effects parameters, α and β are significant at an appropriate significance level, and their sum is less than one, thus sufficing the necessary condition of the finiteness of the conditional variances. Further, β is higher than α in all the series, indicating that the past variances tend to dominate the current variances. The leverage effect coefficient γ is positive and statistically significant at appropriate levels indicating that the negative shocks have a higher impact than the positive shocks. Both the ADCC parameters a and b are positive, and the sum is less than one to ensure positive definiteness. Parameters a and b, which are associated with short and long-term persistence of shocks on the dynamic conditional correlations, are significant. The exception being South Korea, Netherlands, and Canada was the short-term volatility persistence coefficient is found insignificant. The high values of b indicate the long-run persistence of volatility spillover among China's major trading partners. The joint distribution coefficient of shape (m) supports the best fit of the ADCC EGARCH based on Student-t distribution for both marginal and joint distribution represented by low values of the information criterion of AIC, BIC, and HQ. And that ADCC EGARCH is a better fit to model the time-varying conditional variances. The paper graphs the DCC in Fig. 3 .

Table 3.

Results of the ADCC EGARCH model.

	US	Japan	South Korea	Germany	India	Netherlands	UK	Singapore	Taiwan
Conditional variance
Const	−0.0137***	0.1918	−0.0003	0.0010	0.0305***	−0.0097**	−0.0046*	−0.0042	−0.0007
Arch (α)	−0.1794***	0.1427***	−0.0965***	−0.1536***	0.0011***	−0.1893***	−0.1513***	−0.1284**	−0.0777***
Garch (β)	0.9722***	0.9109***	0.9715***	0.9817***	0.8831***	0.9732***	0.9824***	0.9786***	0.9744***
Leverage (γ)	0.2174***	0.2394*	0.1369***	0.0854***	0.1709***	0.1198***	0.0719***	0.0873***	0.0990***
Joint
a	0.0436**	0.0061**	0.0121	0.0290**	0.0084**	0.0077	0.0127*	0.0094**	0.0102*
b	0.6476***	0.9885***	0.9462***	0.9349***	0.9582***	0.9860***	0.9741***	0.9186***	0.9737***
Shape
m	4.6590***	4.8427***	4.2386***	4.5358***	5.0969***	4.7551***	4.8731***	5.3304***	4.9432***
Information Criterion
AIC	5.5780	8.0185	5.7731	5.9508	5.7735	5.7618	5.7782	5.8353	5.8029
BIC	5.8224	8.2978	6.0170	6.2018	5.9358	6.0040	6.0167	6.0723	6.0404
HQ	5.6701	8.1247	5.8650	6.0456	5.8348	5.8530	5.8680	5.9425	5.8922
Log-likelihood
LL	−3245.185	−3960.274	−3369.342	−3349.812	−3285.67	−3391.411	−3467.674	−3531.722	−3503.069
	Russia	Australia	Canada	Brazil	France	Thailand	Italy	Spain
Conditional variance
Const	−0.0054	−0.0048	−0.0140***	0.0257***	−0.0013	−0.0001	0.0460	0.0053
Arch (α)	−0.0433**	−0.1145***	−0.1397***	−0.0671***	−0.1591**	−0.0566**	0.1059*	−0.1131***
Garch (β)	0.9695***	0.9827***	0.9794***	0.9824***	0.9707***	0.9902***	0.9577***	0.9673***
Leverage (γ)	0.1081***	0.1114***	0.1474***	0.1170***	0.1391***	0.1627***	0.1960***	0.1446***
Joint
a	0.0088*	0.0055**	0.0000	0.0090**	0.0224***	0.0051***	0.0010**	0.0228*
b	0.8141***	0.9784***	0.8492***	0.9655***	0.9340***	0.9840***	0.9952***	0.9149***
Shape
m	5.6673***	5.4730***	5.3405***	4.7176***	4.9015***	4.5301***	4.0000***	5.4170***
Information criterion
AIC	5.9152	5.7409	5.4475	7.4825	5.9009	5.8285	6.0361	6.1319
BIC	6.1876	5.9807	5.6918	7.7214	6.1432	6.0791	6.2801	6.3742
HQ	6.0186	5.8312	5.5396	7.5724	5.9922	5.9231	6.1281	6.2232
Log-likelihood
LL	−3001.550	−3421.964	−3170.657	−4419.824	−3474.708	−3288.573	−3522.385	−3612.957

Note: The results of the ADCC EGARCH model are for the full period of study.

***, ** and * indicate the significance level at 1%, 5%, 10% respectively.

Fig. 3.

DCC estimates of ADCC EGARCH model.

Table 4 shows the mean and variance of DCC values pre and during the crisis period, along with the contagion t-statistics. The mean and variance of the DCC for the crisis period are higher than that of the pre-crisis period. And the study finds empirical evidence of the contagion effect as a result of the COVID-19 crises emanating from China. Most developed and emerging markets, including the US, South Korea, Germany, India, Singapore, Taiwan, Russia, Australia, Canada, Brazil, Thailand, Italy, and Spain, have suffered contagion. The exception is Japan, Netherlands, the UK, France, where it was more interdependent than contagion. Therefore, the paper documents the contagion effect of COVID-19 on most of the developed and emerging futures markets that have trading relations with China.

Table 4.

Asymmetric dynamic correlation coefficient and contagion test.

	Mean	Variance	|t statistics|
Pre-crises China-US	0.1924	0.0009	1.77**
Crises China-US	0.3172	0.0010
Pre-crises China-Japan	−0.2753	0.0037	0.07
Crises China-Japan	−0.5024	0.1136
Pre-crises China-South Korea	0.3991	0.0063	3.69***
Crises China-South Korea	0.5693	0.0019
Pre-crises China-Germany	0.2026	0.0086	13.60***
Crises China-Germany	0.5454	0.0045
Pre-crises China-India	0.3128	0.0020	6.13***
Crises China-India	0.4243	0.0012
Pre-crises China-Netherlands	0.2235	0.0078	0.49
Crises China-Netherlands	0.4363	0.0343
Pre-crises China-UK	0.2460	0.0030	0.77
Crises China-UK	0.4680	0.0113
Pre-crises China-Singapore	0.3938	0.0029	22.20***
Crises China-Singapore	0.4440	0.0000
Pre-crises China-Taiwan	0.3938	0.0029	3.55***
Crises China-Taiwan	0.5761	0.0030
Pre-crises China-Russia	0.1733	0.0005	3.77***
Crises China-Russia	0.3109	0.0259
Pre-crises China-Australia	0.2800	0.0000	257.00***
Crises China-Australia	0.3955	0.0000
Pre-crises China-Canada	0.1881	0.0000	14.40***
Crises China-Canada	0.5417	0.0193
Pre-crises China-Brazil	0.1614	0.0000	140.00***
Crises China-Brazil	0.3967	0.0000
Pre-crises China-France	0.2226	0.0062	1.17
Crises China-France	0.3742	0.0190
Pre-crises China-Thailand	0.3938	0.0029	4.86***
Crises China-Thailand	0.3912	0.0059
Pre-crises China-Italy	0.0738	0.0000	4.79***
Crises China-Italy	0.2952	0.1300
Pre-crises China-Spain	0.1845	0.0047	1.81**
Crises China-Spain	0.2911	0.0316

Note: pre-crisis period is from 02.07.2015 to 29.11.2019. The crisis period is from 02.12.2019 to 31.07.2020.

***, ** and * indicate the significance level at 1%, 5%, 10% respectively.

5. Conclusions

This paper aims to test the existence of financial contagion between China and its trading partners during the COVID-19 crisis. The paper's main findings are that there is significant evidence of a sudden surge in correlation during the crisis period presenting evidence of contagion during the spread of the COVID-19 from China to these countries. Another finding is that both developed and emerging markets seem to suffer equally from the contagion effect. However, the analysis of the ADCC provides no evidence in favor of Japan, the Netherlands, the UK, and France.

This paper has important policy implications that channels of contagion may not only arise out of financial crises, but a pandemic situation like COVID-19 can also have severe repercussions for the economy and financial markets, which policymakers need to take note of. Further, the paper's findings may be of interest to policymakers, investors, risk, and portfolio managers.

The current study has examined contagion through cross-market linkages. Moreover, the COVID-19 crisis presented a unique opportunity to look at the alternative channels for contagion's flow. It would be interesting to test how contagion transmission can happen through trade intensity which is not a part of the current study. Future research, therefore, warrants exploring the transmission of contagion through the trading channels from China to its trading partner.

Author statement

Conception and design, Data acquisition, Analysis and interpretation of data, Drafting of the manuscript, Revision of the manuscript critically for important intellectual content.