Revisiting the Structure of Calcined and Hydrated AlPO‐11 with DFT‐Based Molecular Dynamics Simulations

Abstract

Published crystal structures of the AEL‐type aluminophosphate AlPO‐11 in its calcined form (space group $Ima2$ ) show some peculiar features, such as unusually short Al−O and P−O bonds and near‐linear Al−O−P angles. Although experimental evidence for the presence of dynamic disorder was presented, the nature of the associated distortions remained unresolved. In this study, ab initio molecular dynamics (AIMD) calculations in the framework of density functional theory (DFT) were employed to study the dynamic behaviour of this zeotype. At 100 K, static local distortions that break the $Ima2$ symmetry are present in the time‐averaged structures computed from the AIMD trajectories. At 300 and 500 K, the time‐averaged structures approach $Ima2$ symmetry. Although shortened Al−O and P−O bonds and near‐linear Al−O−P angles were found in the average structures, an analysis of radial and angular distribution functions confirmed their absence in the instantaneous structures. This deviation is due to a precession‐like motion of some oxygen atoms around the Al−P connection line, which moves their time‐averaged positions closer to this line. In hydrated AlPO‐11, some of the water molecules are coordinated to framework Al atoms, leading to an octahedral coordination of 1/5 of the Al sites. DFT optimisations and AIMD simulations on partially hydrated models delivered evidence for a preferential adsorption at the Al1 site. No dynamic disorder was observed for the hydrated form.

DFT‐based molecular dynamics simulations on the aluminophosphate zeotype AlPO‐11 reveal distinct differences between the local, instantaneous structure and the time‐averaged structure that is probed with diffraction experiments.

Introduction

The aluminophosphate zeotype AlPO‐11 was among the first AlPO₄‐based molecular sieves, reported in a seminal paper by Wilson, Flanigen and co‐workers in 1982. ^[1] AlPO‐11 is the type material of the AEL (AlPO₄‐ELeven) framework type code assigned by the International Zeolite Association. ^[2] In addition to the pure AlPO₄ form, several heteroatom‐substituted derivatives have been reported, including the silicoaluminophosphate SAPO‐11, ^[3] the germanoaluminophosphate GeAPO‐11, ^[4] and various metal (silico)aluminophosphates.[ ⁵ , ⁶ ] These heteroatom‐substituted systems, especially SAPO‐11, have received considerable attention as catalysts and catalyst supports.[ ⁷ , ⁸ ] The most prominent application of AEL‐type frameworks is the use of bifunctional Pt/SAPO‐11 catalysts for hydroisomerisation and hydrocracking reactions.[ ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ , ¹⁴ ] Application examples using monofunctional (non‐doped) catalysts include the skeletal isomerisation of 1‐pentene and m‐xylene using SAPO‐11 and CoAPO‐11,[ ¹⁵ , ¹⁶ , ¹⁷ ] the hydroxylation of phenol with Fe‐, Mn‐, Co‐, or CuAPO‐11,[ ¹⁸ , ¹⁹ ] and the potential use of SAPO‐11 and CrAPSO‐11 in methanol‐to‐olefin transformations. ^[20] AlPO‐11 has also been proposed as a suitable adsorbent to recover methane from biogas using pressure swing adsorption, ^[21] whereas CoAPO‐11 has been recently tested for the adsorption of phenol from cigarette smoke. ^[22] On a more fundamental level, AlPO‐11 can serve as a model system to study the structure and dynamics of molecules under confinement, as demonstrated for the case of adsorbed iodine molecules.[ ²³ , ²⁴ , ²⁵ ]

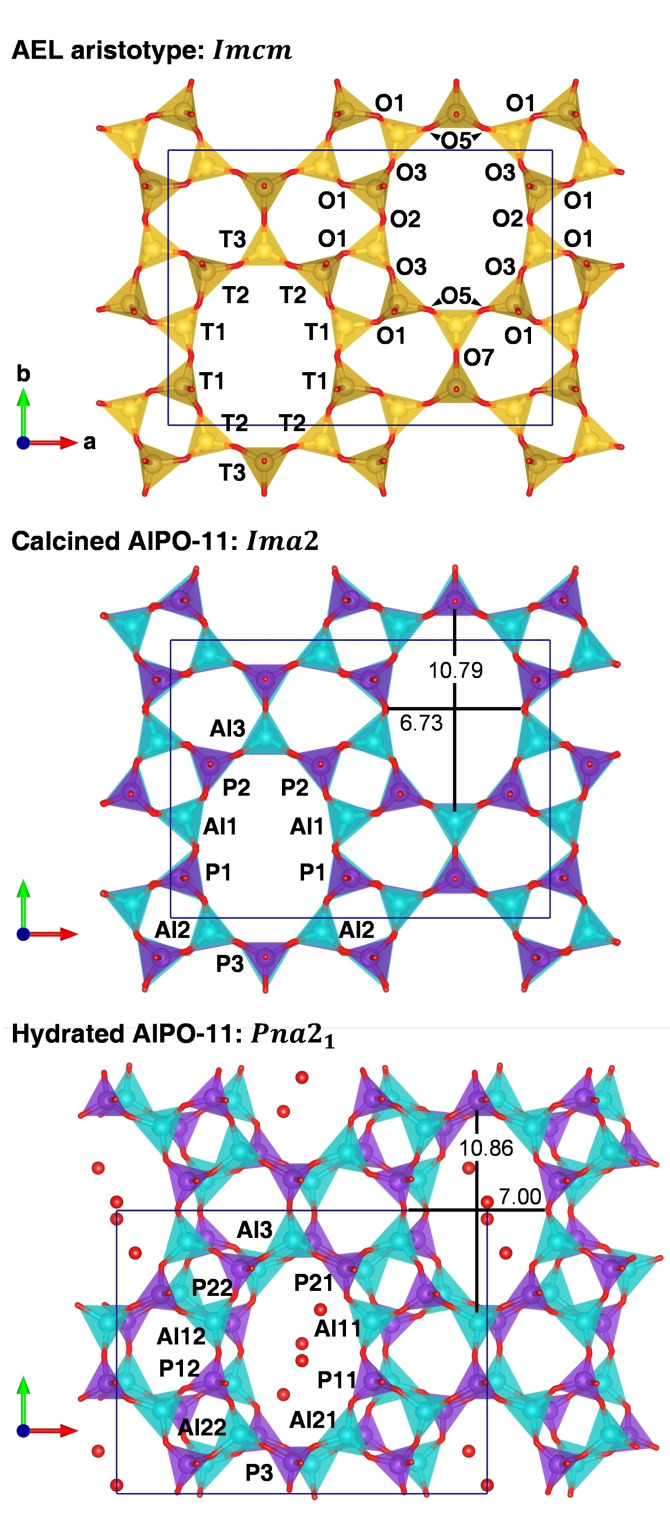
The structure of the calcined form of AlPO‐11 was refined from powder neutron diffraction data by Richardson et al., ^[26] based on a model proposed earlier by Bennett and Smith.[ ²⁷ , ²⁸ ] The aristotype of the AEL framework, shown in Figure 1, has $Imcm$ symmetry (a non‐conventional setting of space group $Imma$ , employed here in order to use the same axis system as for the lower‐symmetry structures presented subsequently). The AEL framework can be described as being composed of sheets containing 4‐, 6‐, and 10‐membered rings (4MR/6MR/10MR) that are stacked along the c axis. Each unit cell contains two such sheets, which are related by symmetry through the mirror plane perpendicular to c. The oxygen atoms O4, O6, and O8, which connect adjacent layers, lie on this mirror plane. Moreover, the “left” and “right” part of each 10MR are related through the mirror plane ⊥ a, with the T3, O7, and O8 atoms lying on this plane. Finally, the two 10MRs in the unit cell are related via an a glide plane ⊥ b. Altogether, this leads to a structure with straight, non‐intersecting 10MR channels whose walls are constituted by 6MRs. All of the three non‐equivalent TO₄ tetrahedra form the channel walls, with the positions of the individual T atoms shown in Figure 1.

Figure 1.

Visualisation of the AEL aristotype (top) ^[2] and the crystal structures of calcined and hydrated AlPO‐11 (middle and bottom).[ ²⁶ , ²⁹ ] T atom labels are included for one 10MR for all structures. O atom labels are shown only for the aristotype (labels of O4, O6, and O8, which connect the T1, T2, and T3 sites along c, are omitted). Compared to the original literature, the T atoms in hydrated AlPO‐11 were relabelled to match the labelling scheme of the other structures. For the crystal structures, Al3−P3 and O2−O2 distances across the 10MR channels are given (in Å). Cyan=aluminium, purple=phosphorus, red=oxygen, yellow=general T site.

Because Al−O−Al and P−O−P linkage are energetically unfavourable, the Al and P atoms in tetrahedral AlPO₄ frameworks are fully ordered, forming a strictly alternating arrangement containing only Al−O−P links. ^[30] The localisation of the two species at distinct sites entails a reduction in symmetry with respect to the aristotype, resulting in a structure with $Ima2$ symmetry. The three T sites split into six sites (Al1/Al2/Al3 and P1/P2/P3) and some of the oxygen sites also split (Table S1 in the Supporting Information compiles the atom labels used for the different forms of AlPO‐11). In this structure, the “left” and “right” parts of the 10MR channels are still related by a mirror plane, but mirror symmetry is lost between adjacent sheets stacked along c. To the author's knowledge, all experimental structure determinations of calcined and as‐synthesised AlPO‐11 and its silico‐ and metal‐aluminophosphate derivatives have used this space group symmetry.[ ²⁹ , ³¹ , ³² , ³³ , ³⁴ , ³⁵ ] However, $Pna{2}_1$ symmetry has been postulated for the rehydrated form of AlPO‐11.[ ²⁹ , ³² ] The reduction in symmetry leads to a further splitting of the T sites (5 Al and 5 P sites instead of three) and of several oxygen positions. In this phase, the stacked sheets are slightly shifted with respect to each other, resulting in an undulating shape of the 10MR channels (Figure 1).

In the $Ima2$ structure, the location of the Al3/P3, O7, and O8 atoms on the mirror plane restricts the possibility to relax the corresponding Al−O−P angles. For this reason, the Al3−O7−P3 and Al3−O8−P3 angles are fairly close to 180° (∼175° in the structure reported by Richardson et al. ^[26] ). As discussed for several zeolites and zeotypes, the observation of linear or near‐linear T−O−T linkages is usually considered as an artefact arising from static or dynamic disorder of oxygen atoms around a higher‐symmetry site.[ ³⁶ , ³⁷ , ³⁸ , ³⁹ , ⁴⁰ , ⁴¹ ] Near‐linear linkages typically coincide with a shortening of the apparent (measured) T−O bond lengths, often to chemically implausible values. Unusually short T−O bonds are indeed observed in the structures of AlPO‐11 and MnAPO‐11 in their as‐synthesised and calcined forms, especially around the Al3/P3 sites, with individual Al−O distances below 1.7 Å and P−O distances below 1.4 Å.[ ²⁶ , ³³ , ³⁴ , ³⁵ ] Pointing out this and several other crystal‐chemical issues (large scatter in Al−O−P angles, deviations from expected values in bond valence sums, etc.), Liu and Withers hypothesised that the instantaneous local crystal structure (which one can envisage as a “snapshot” at the local level) must differ from the time‐averaged long‐range structure obtained through conventional diffraction experiments. ^[42] Electron diffraction patterns obtained at room temperature showed prominent diffuse streaks, but no satellite reflections. These indications of static or dynamic local deviations from the $Ima2$ average structure were attributed to the excitation of several rigid unit modes of distortion. Although a precise determination of the nature of the distortions was not possible in the context of that study, these observations could imply that a distorted phase with lower symmetry might appear under cryogenic conditions. While no comprehensive attempts have been made to predict such a lower‐symmetry structure of AlPO‐11 computationally, two force‐field based studies proposed a structure in space group $P112$ . This $P112$ phase is energetically favoured by 1.4 kJ mol⁻¹ per AlPO₄ formula unit over the $Ima2$ phase according to the calculations performed by Henson et al., ^[43] whereas no energy difference was quantified in an earlier study by de Vos Burchart et al. ^[44] Apart from tabulating the lattice parameters, which show only a modest deviation from an orthogonal metric, the distorted structures were not discussed in either of these papers.

The local structural changes of AlPO‐11 upon hydration have been investigated by several authors. ²⁷Al NMR experiments were employed to show that a fraction of the aluminium sites are octahedrally coordinated in the hydrated phase because some adsorbed water molecules bond to framework Al atoms. Specifically, Barrie et al. observed octahedral coordination for 1/5 of the framework Al atoms, but found no indications that the hydration occurred preferentially at any of the non‐equivalent sites. ^[45] In contrast, subsequent NMR investigations by Peeters et al. and Bodart et al. provided evidence for a selective hydration of one of the 5 Al sites of the $Pna{2}_1$ structure,[ ⁴⁶ , ⁴⁷ , ⁴⁸ ] with Peeters et al. concluding that the Al21 site was selectively hydrated. The structure refined by Khouzami et al. in this space group contains a total of 8 H₂O molecules per unit cell. ^[29] Neither of the two positions of H₂O oxygen atoms (Ow) lie in close proximity to any framework Al atom, and the short distance from one of them to a framework oxygen atom of 2.08 Å appears unlikely. It is worth noting that 8 H₂O molecules per unit cell (u.c.) correspond to an adsorbed amount of only 0.06 g(H₂O) per g(AlPO‐11), whereas adsorption isotherm measurements delivered a saturation uptake in the range of 0.15 g(H₂O) per g(AlPO‐11), which corresponds to ∼20 H₂O/u.c. ^[49]

In a very early application of computational chemistry techniques to AlPO molecular sieves, Prasad et al. employed semiempirical calculations to study the adsorption of water in AlPO‐11. ^[50] The most favourable adsorption configuration was found for H₂O adsorbed at the Al3 site, consistent with a hydration of 1/5 of the Al sites observed in NMR experiments. A periodic density functional theory (DFT) study of this system was published in 2007 by Herréra‐Perez et al. ^[51] These authors compared the adsorption of water molecules at the three non‐equivalent Al sites of the $Ima2$ structure, assuming a complete hydration of each site by one H₂O per Al atom. The lowest (=most favourable) adsorption energy was found for the adsorption of water at the Al1 site. Moreover, the prominent shortening of the longest unit cell dimension upon hydration agreed very well with the diffraction results of Khouzami et al. ^[29] Herréra‐Perez et al. recognised that “the optimised minimum energy geometries are symmetry‐constrained and that other less symmetric structures might actually exist that belong to a subgroup of” $Ima2$ , but it seems that the more detailed analysis of the vibrational properties that they hinted at in their paper was never published. A later study by Pillai and Jasra also employed DFT calculations to study the adsorption of water in the pores of AlPO‐11. ^[52] Focussing on the role of framework‐H₂O and H₂O−H₂O hydrogen bonds, they did not discuss the formation of five‐ or six‐coordinated Al atoms.

Motivated by the open questions arising from previous experimental and computational investigations of AEL‐type materials, the present work uses a DFT‐based approach to address the following points:

1. Experimental investigations indicate that the local, instantaneous structure of calcined AlPO‐11 deviates from $Ima2$ symmetry. However, both the nature of the distortions and their temperature‐dependent behaviour remain unresolved. As all experiments so far have been carried out at room temperature, it is unknown whether the reduction of thermal motion would trigger a transition to an ordered lower‐symmetry phase.

2. Conflicting findings have been reported with regard to the location of the Al atoms that assume octahedral coordination in hydrated AlPO‐11. Neither the symmetry lowering upon hydration, observed in diffraction experiments, nor the NMR results reporting a hydration of 1/5 of the Al sites were taken into account in the only previous DFT study addressing the preferred water adsorption sites. ^[51]

On the one hand, insights into the instantaneous local structure of calcined AlPO‐11 should contribute to a better understanding of structure‐property relationships in AEL‐type materials, which could aid the development of new or improved applications. On the other hand, recent work has shown that five‐ or six‐coordinated Al atoms play an important role during topotactic transformations of aluminophosphates, which provide a potential synthesis route towards new AlPO frameworks. ^[53] In this regard, AlPO‐11, with its moderately complex crystal structure with three inequivalent T sites, appears as an attractive model system to study the preferential location of adsorbed water molecules, and identify underlying energetic factors.

In an preliminary DFT study of AlPO‐11 using the CASTEP code, ^[54] which employed the PBE‐TS functional,[ ⁵⁵ , ⁵⁶ ] a density functional perturbation theory calculation ^[57] performed for the $Ima2$ phase revealed the presence of several phonons with imaginary frequencies throughout the first Brillouin zone (Table S2b). ^[58] A search for potential lower‐symmetry phases could proceed by generating derived structures that are distorted according to the eigenvectors of these unstable modes. However, the large number of modes with imaginary frequencies would render a comprehensive sampling rather difficult. In addition, this approach would only give access to the lowest‐energy structure at 0 K. As the behaviour at finite temperature is of particular interest, the present study employs an approach based on DFT‐based molecular dynamics simulations (ab‐initio molecular dynamics – AIMD), which permit direct insights into the time‐averaged structure at different temperatures. The approach is partially inspired by recent work of Trudu et al., who used AIMD simulations to show that the average structure of purely siliceous ferrierite at elevated temperatures (450 K) contains straight Si−O−Si linkages, despite their apparent instability found in phonon calculations on the same system, ^[41] and by studies of Abatal et al. and Hoffman et al., who showed the benefits of using a combination of AIMD simulations and DFT‐based structure optimisations to explore multiple local minima in complex zeolite structures.[ ⁵⁹ , ⁶⁰ ] In addition to investigating the structure of guest‐free AlPO‐11, optimisations and AIMD simulations of partially hydrated system are used to study the relative stability of different locations of the Al‐coordinated water molecules, following earlier AIMD studies of hydrated AlPOs and SAPOs.[ ⁶¹ , ⁶² , ⁶³ ]

Computational methods

Structure optimisations and AIMD simulations made use of the CP2K code, which is based on the Gaussian and plane wave approach.[ ⁶⁴ , ⁶⁵ ] These calculations employed the PBE functional with the D3 dispersion correction proposed by Grimme and co‐workers (PBE‐D3), ^[66] using Goedecker‐Teter‐Hutter pseudopotentials developed by Krack for the core electrons. ^[67] The first Brillouin zone was sampled at the Γ point, only. The structure optimisations used a plane‐wave energy cutoff of 600 Ry and triple‐zeta Gaussian basis sets included in the CP2K distribution (TZVP‐MOLOPT‐GTH for H, O, P, TZVP‐MOLOPT‐SR‐GTH for Al). ^[68] Atomic coordinates and unit cell parameters were optimised. The following convergence criteria were applied: Maximal atomic displacement=2 ⋅ 10⁻⁵ bohr, force tolerance=10⁻⁶ Ha bohr⁻¹, and pressure tolerance=5 bar.

AIMD simulations of calcined AlPO‐11 were performed using the regular unit cell (no supercell), employing a plane‐wave energy cutoff of 600 Ry and double‐zeta Gaussian basis sets (DZVP‐MOLOPT‐SR‐GTH). These calculations were run in the NPT ensemble for a pressure of 0 bar and temperatures of 100 K, 300 K, and 500 K. The timestep in the integration of the equations of motion was set to 1 fs. A Nosé‐Hoover thermostat[ ⁶⁹ , ⁷⁰ ] and a Martyna‐Tobias‐Klein barostat ^[71] were used to control temperature and pressure, both with time constants of 500 fs. An equilibration phase of 5 ps (5,000 steps) was followed by a production phase of 15 ps (15,000 steps). The evolution of atomic coordinates and lattice parameters with time was stored in trajectory files (in PDB format), where three independent trajectories were computed for each temperature.

For partially hydrated AlPO‐11 models, a 1×1×2 supercell was used in the AIMD simulations to avoid interactions between images of octahedrally coordinated Al atoms that are direct neighbours along the channel axis (along c). These calculations used an energy cutoff of 500 Ry and DZVP‐MOLOPT‐SR‐GTH basis sets. They were also performed in the NPT ensemble (p=0 bar, T=300 K). Due to the presence of water molecules, a timestep of 0.5 fs was employed, in keeping with previous studies of hydrated zeolites and zeotypes.[ ⁶² , ⁶³ , ⁷² , ⁷³ ] Thermostat and barostat time constants were set to 250 fs. An equilibration phase of 5 ps (10,000 steps) was followed by a production phase of 15 ps (30,000 steps). For each of the three models with different octahedrally coordinated Al atoms, three independent trajectories were computed.

The analysis of the results made use of different tools: For each individual trajectory, the AIMD average structure was calculated with the VMD code. ^[74] In this procedure, the average Cartesian coordinates of every individual atom in the simulation cell were computed by averaging over the instantaneous positions stored in the trajectory. If the duration of the simulation is sufficiently long, the AIMD average structure should correspond to the time‐averaged structure that is accessible with diffraction experiments. A symmetry search on these average structures was then carried out with the DS Biovia Materials Studio package, which evaluates whether a given structure conforms to any higher space group symmetry within a given tolerance. ^[75] The Al−O and P−O bond distances and Al−O−P angles in DFT‐optimised and AIMD average structures were measured using Mercury. ^[76] Al−O and P−O radial distribution functions (RDFs) and Al−O−P angle distribution functions (ADFs) were computed with TRAVIS.[ ⁷⁷ , ⁷⁸ ] The reported RDFs and ADFs correspond to averages over three trajectories. All structure visualisations were prepared with VESTA. ^[79] Representative CP2K input files, DFT‐optimised structures (in CIF format), AIMD average structures (in CIF format), and production parts of the AIMD trajectories (in PDB format) have been deposited in the Figshare repository: https://doi.org/10.6084/m9.figshare.14791452.v1.

Results and discussion

DFT optimisation of calcined AlPO‐11

The optimisation of the structure of calcined AlPO‐11 used the crystal structure published by Richardson et al. (space group $Ima2$ ) as starting point. ^[26] The optimised unit cell parameters, average Al−O/P−O bond lengths and Al−O−P angles as well as their standard deviations are compiled in Table 1. In addition, the distribution of the individual distances and angles is shown in Figure 2. A comparison of the DFT‐optimised unit cell parameters to experimental values reveals a drastic overestimation of all three parameters, which amounts to +0.617 Å (+3.3 %) for a, +0.314 Å (+2.3 %) for b, and +0.322 Å (+3.8 %) for c. As a consequence, the unit cell volume is overestimated by almost 10 %. Such a large error is not typical for the PBE‐D3 functional, which delivered good agreement with experimental crystal structure data in other studies of zeolites and zeotypes.[ ⁶⁰ , ⁸⁰ , ⁸¹ , ⁸² ] Complementary calculations using the CASTEP code, which employed different exchange‐correlation functionals and dispersion correction schemes (Table S2a), delivered a qualitatively similar tendency to overestimate the unit cell dimensions, especially the length of the a axis.

Table 1.

Space group, unit cell parameters, average Al−O/P−O bond lengths and Al−O−P angles in experimental[ ²⁶ , ²⁹ ] and DFT‐optimised structures of calcined and hydrated AlPO‐11. For hydrated AlPO‐11, distances from Al atoms to H₂O oxygen atoms are also given.

	Calcined, exp	Calcined, DFT	Hydrated, exp	H2O@Al11, DFT	H2O@Al21, DFT	H2O@Al3, DFT
Space group	$Ima2$	$Ima2$	$Pna{2}_1$	$Pna{2}_1$	$Pna{2}_1$	$P1a1$
a/Å	18.485	19.102	18.056	18.277	19.167	19.676
b/Å	13.533	13.847	13.789	14.074	13.761	13.410
c/Å	8.370	8.692	8.126	8.245	8.299	8.397
V/Å3	2094	2299	2023	2121	2189	2216
d aver(Al−Ofw)/Å	1.669±0.085	1.738±0.008	1.712±0.018	1.770±0.048	1.770±0.051	1.767±0.043
d aver(P−Ofw)/Å	1.519±0.090	1.535±0.005	1.486±0.020	1.542±0.015	1.542±0.014	1.543±0.020
ω aver(Al−Ofw−P)/°	156.4±14.4	160.9±12.6	155.6±11.6	143.9±8.2	145.5±8.0	148.3±10.0
d aver(Al−Ow1)/Å	./.	./.	>3.0	1.969	1.961	1.936/1.909
d aver(Al−Ow2)/Å	./.	./.	>3.0	2.092	2.103	2.158/2.170

Figure 2.

Calcined AlPO‐11: Distribution of Al−O distances (left), P−O distances (centre), and Al−O−P angles (right) in the experimental crystal structure (black), DFT‐optimised structure (orange), and average structures obtained from AIMD simulations. Data points for 100/300/500 K are shown in blue/green/red, and those of individual trajectories are distinguished using different shades.

When looking at the bond lengths, the very large scatter of the individual values in the experimental structure, which was already pointed out in the original publication, ^[26] is apparent. A recent statistical analysis of a large body of zeolite/zeotype structure data reported bond length ranges of 1.67 to 1.79 Å for Al−O bonds and 1.47 to 1.57 Å for P−O bonds. ^[83] Many of the individual values in the crystal structure of AlPO‐11 fall outside these respective ranges, with outliers at both higher and lower distances, which are chemically implausible. In addition, the average Al−O distance in the AlPO‐11 structure is almost 0.07 Å shorter than the mean value computed over 292 zeolite crystal structures from the mentioned statistical analysis, pointing to systematic problems. The DFT optimisation of the structure corrects these issues and results in a narrow distribution of Al−O and P−O distances with plausible average values. The effect of the optimisation on the Al−O−P angles is altogether less pronounced. Although some individual angles change by more than 10 degrees (see Table S5 of the Supporting Information), the average Al−O−P angle increases only modestly, and the scatter of the individual values is similar for experimental and DFT‐optimised structures. The fact that the DFT optimisation leads to an overall increase of the T−O distances without concurrently decreasing the Al−O−P angles (in fact, slightly increasing them on average) explains why the unit cell parameters are overestimated so severely. The reasons for this significant deviation, and for the occurrence of many chemically implausible bond lengths in the experimental structure, can be elucidated on the basis of the AIMD calculations, as will be shown below.

AIMD simulations of calcined AlPO‐11

Unit cell parameters

Figure 3 visualises the average unit cell parameters a, b, c obtained from the production part of the respective AIMD trajectories. Numerical values including standard deviations are reported in the Supporting Information (Table S3). Across the three trajectories computed for each temperature, the average values of a, b, and c are always within a few 1/100 Å, indicating good reproducibility. All parameters increase with temperature, albeit to a different extent, with a showing the most marked positive thermal expansion in both absolute and relative terms. The average angles α, β, and γ remain close to 90° (Table S3), the most significant deviation occurring for γ in one of the 100 K trajectories (90.4°). All unit cell dimensions computed from the AIMD trajectories are considerably shorter than those obtained in the DFT optimisation (Table 1). It is most appropriate to use the average over the three 300 K trajectories for a comparison to experimental values, as the diffraction experiments were carried out at 295 K. ^[26] These average values of a=18.525 Å, b=13.551 Å, and c=8.348 Å are in near‐perfect agreement with the experimental unit cell parameters, with the largest deviation amounting to 0.040 Å (for a). The good agreement is also clearly visible in Figure 3. This highlights that the large discrepancy between experimental and DFT‐optimised lattice parameters is not caused by systematic errors related to the computational setup, such as a poor choice of exchange‐correlation functional and/or dispersion correction, but that it stems primarily from the neglect of thermal motion in the optimisation.

Figure 3.

Average lattice parameters a, b, c obtained from individual AIMD trajectories. Dashed lines indicate the experimental values measured at 295 K.

Symmetry search

The results of the symmetry search on the AIMD average structures are shown in Figure 4. In cases where different space groups were found upon increasing the tolerance up to the maximal value of 1.0 Å, all of them are reported. For the 100 K trajectories, the symmetry search finds space group $Pn11$ for two of the average structures, and space group $P112$ for the third one (non‐conventional a‐ and c‐unique settings are used to avoid a change of the axis system). In each case, the deviation of the AIMD average structure from the corresponding monoclinic symmetry amounts to only a few 1/100 Å, indicating a near‐perfect ordering of the distortions. Both of the space groups found are subgroups of $Ima2$ that retain one of the symmetry elements, either the n glide plane perpendicular to a or the twofold rotation axis parallel to c. The monoclinic angles are close, but not equal to 90°, with α≈90.15° in the $Pn11$ structures and γ=90.40° in the $P112$ structure. Even when the maximal symmetry search tolerance of 1.0 Å is used, space group $Ima2$ is not found. For the 300 K trajectories, the symmetry search delivers different sequences of subgroups of $Ima2$ for each trajectory before finding $Ima2$ with maximal deviations on the order of 0.4 to 0.5 Å (the maximal deviation corresponds to the magnitude of the largest displacement of any individual atom that is required in order to conform to the higher symmetry). It is worth noting that the maximal deviation from any symmetry (apart from $P1$ ) is relatively large (at least ∼0.15 Å), indicating that the distortions are much less ordered than at 100 K. When looking at the 500 K trajectories, the picture is qualitatively similar to that obtained for 300 K, but the maximal deviations of the AIMD average structures from $Ima2$ symmetry are much smaller, amounting to approximately 0.2 Å.

Figure 4.

Results of the symmetry search on AIMD average structures. Space group(s) found upon increasing the symmetry tolerance are shown as a function of the maximal deviation as printed by the Materials Studio symmetry search algorithm.

Taken together, the results of the symmetry search can be interpreted as follows: At 100 K, i. e., under cryogenic conditions, the structure of AlPO‐11 is distorted from the $Ima2$ symmetry. While two likely low‐temperature phases with different monoclinic symmetries can be proposed, the calculations do not allow for definitive conclusions whether only one of them would occur in a real AlPO‐11 sample, whether they would coexist, e. g., in different crystallites or domains within one crystal, or whether there would be no long‐range order of the distortions at all. At room temperature, there are pronounced local, instantaneous deviations from $Ima2$ symmetry, but no indications for the stability of a lower‐symmetry structure over extended periods of time. This is in perfect agreement with the observation of prominent diffuse scattering, but no satellite reflections in the work of Liu and Withers. ^[42] Upon further increasing the temperature, the increased thermal motion reduces the lifetime of the instantaneous distortions, bringing the average structure closer to $Ima2$ symmetry on the timescale that is covered by the AIMD simulations.

Comparison of high‐symmetry and low‐symmetry phases

The structures of the $Ima2$ phase and the two monoclinic phases found in the symmetry search on AIMD average structures obtained for 100 K are compared in Figure 5. Although the unit cells of the monoclinic phases remain pseudo‐orthorhombic, a few differences are prominently visible: First, the 10MR channels, perfectly elliptical in the $Ima2$ phase, are distorted to a windscreen‐like shape in both monoclinic phases. Second, the projection along the b axis shows that the AlO₄ and PO₄ tetrahedra are well aligned in the $Ima2$ structure, with all Al−O−P linkages that point along c lying in the bc plane. In the lower‐symmetry structures, the tetrahedra are rotated with respect to each other, and the Al−O−P linkages are no longer confined to that plane. Third, the mirror planes ⊥ a that relate pairs of neighbouring 6MRs are lost, and prominent distortions of these 6MRs are visible.

Figure 5.

Visualisation of the $Ima2$ phase (DFT‐optimised) and the monoclinic phases found in the symmetry search on 100 K AIMD average structures.

In order to understand the differences between the orthorhombic structure and the monoclinic structures on the one hand, and between the two monoclinic structures on the other hand, it is useful to consider that the AEL framework can be built up from columns of pairs of afi cages (face symbol 6⁵, t‐afi cage in the nomenclature of natural tilings ^[84] ). These columns run parallel to the c axis, and are linked to each other via 4MRs. The top part of Figure 6 shows a column segment consisting of four afi cages in the $Ima2$ structure, emphasising the symmetry of the arrangement. A visualisation of an analogous segment in the monoclinic structures (middle part of Figure 6) clearly shows the rotation of the (Al3)O₄ and (P3)O₄ tetrahedra in the central plane, which causes a reduction of several Al−O−P angles and breaks the mirror symmetry. As a consequence, the four afi cages of the segment are no longer equivalent by symmetry (emphasised through use of different colours in the tiling‐like representation). It should be noted that these distortions of column segments are essentially identical in both monoclinic phases, which is why Figure 6 shows only one of these segments (taken from the $Pn11$ structure). The two monoclinic phases differ, however, in the relative arrangement of neighbouring columns with respect to each other, as visualised in the bottom part of Figure 6: In the $P112$ phase, equivalent afi cages in neighbouring columns are not shifted with respect to each other along c, and all columns are slightly tilted in the same direction with respect to the bc plane. In contrast, neighbouring columns are shifted by $1/2$ c in the $Pn11$ phase, and they are tilted in opposite directions. These intricate structural differences also clarify why different subgroups of $Ima2$ can be reached through very similar distortions. As the local environment of all atoms is essentially identical in both phases, the energy difference between them is small, with DFT optimisations of the AIMD average structures delivering total energies that differ by less than 1 kJ mol⁻¹ per AlPO₄ formula unit. On this basis, it has to be expected that the orientation of one column is largely independent of the neighbouring columns in a real crystal, rendering a disordered arrangement more probable than the realisation of either of the predicted ordered monoclinic phases in real AlPO‐11 crystals. However, definitive conclusions would require an experimental investigation at low temperatures, where such a disorder of the columns should give rise to rather characteristic patterns of diffuse scattering.

Figure 6.

Top: Atomistic (left) and tiling‐like (right) representation of a column segment consisting of four afi cages in the $Ima2$ phase. The mirror and glide planes that relate the four afi cages are shown in blue and orange. Middle: Atomistic (left) and tiling‐like (right) representation of a column segment in the monoclinic phases. Bottom: Visualisation of the relative arrangement of neighbouring columns in the three phases.

Bond distances and angles

Whereas the AIMD average structures can be seen as being representative of the time‐averaged structure at the respective temperature (if only on the timescale of picoseconds), an analysis covering the individual frames of each trajectory can provide insights into the instantaneous structure. To this end, the distribution of Al−O and P−O bond lengths and Al−O−P angles in the AIMD average structures, shown in Figure 2, can be compared to the corresponding Al−O/P−O radial distribution functions (RDFs) and Al−O−P angle distribution functions (ADFs), shown in Figure 7, which were obtained from the whole trajectories. In the average structures computed from 100 K trajectories, the Al−O and P−O bond lengths are fairly narrowly distributed around the average values of 1.75 Å and 1.54 Å. The maxima in the RDFs are centred at approximately the same values. The Al−O−P angles in the average structures show a broader distribution, but the observed angles mostly remain in an interval between 129.5 and 153 degree, leading to a symmetric maximum centred at about 141°. A calculation of the cumulative ADF reveals that angles below 130° account for only 3.4 % of all angles found in the trajectory analysis, and only 1.8 % of all angles are larger than 155°. Altogether, this analysis shows that there are no systematic differences between the time‐averaged and instantaneous structures at 100 K.

Figure 7.

Al−O (left) and P−O (middle) radial distribution functions and Al−O−P angle distribution function (right) obtained from AIMD trajectories computed for different temperatures. Vertical bars indicate average bond distances in the AIMD average structures.

At 300 and 500 K, the Al−O and P−O bond lengths in the average structures show both a shift towards shorter average distances and a broader distribution when compared to the 100 K results: The Al−O bond distances fall in a range between 1.66 and 1.75 Å, with average values of 1.71 Å at 300 K and 1.70 Å at 500 K, and P−O bond distances range from 1.44 to 1.54 Å, with averages of 1.49 Å (300 K) and 1.48 Å (500 K). The Al−O−P angles, on the other hand, are drastically increased, as well as showing a broader distribution, falling between 139° and 180°, with the average angles amounting to 156° at 300 K and 160° at 500 K. An analysis of the individual angles reveals that the most prominent increases are found for angles around those oxygen atoms that constitute the links between sheets perpendicular to c (O4, O6, O8) and around oxygen atoms that are part of the (Al3)O₄/(P3)O₄ tetrahedra (O51/O52, O7, O8). There is a remarkable correspondence between the broad distribution of bond lengths and angles in the AIMD average structures and the experimental structure (first row of Figure 2), with the exception of some outliers at both shorter and longer T−O distances in the experimental structure that can probably be attributed to limited data quality.

It seems implausible to expect such a drastic bond shortening and increase of T−O−T angles upon temperature increase, and the RDFs and ADFs calculated from the 300 K and 500 K trajectories indeed show only rather intricate differences to the 100 K results. The Al−O and P−O RDFs become broader with increasing temperature, but the maxima do not shift to any appreciable extent. Short Al−O distances below 1.7 Å account for only 7/10 % of all distances observed at 300/500 K, and P−O distances below 1.5 Å make up for only 4/8 %. With regard to the Al−O−P angles, a slight shift towards higher angles is apparent, and a shoulder appears at the higher‐angle side. Nevertheless, angles above 155° remain of minor importance, as they account for only 12/17 % of all angles at 300/500 K. Near‐linear linkages are very rare, with angles above 170° accounting for just 1.0/1.8 % at 300/500 K. In contrast, such angles account for about 10 %/25 % of all Al−O−P angles in the AIMD average structures.

Altogether, these findings highlight very clearly that the instantaneous structure of AlPO‐11 at room temperature and elevated temperatures differs distinctly from the time‐averaged structure, even when the averaging period covers only a few picoseconds. The origins of the deviations can be understood by overlaying the trajectories of selected oxygen atoms with the average structure. As the differences in Al−O−P angles are especially pronounced for linkages involving the Al3/P3 sites, the local environment of one Al3 atom appears as a convenient choice for illustrative purposes. Figure 8 visualises the oxygen positions visited during AIMD simulations performed for 100 K, 300 K, and 500 K, in each case showing the environment of the same Al atom. The environment in the DFT‐optimised $Ima2$ structure is included for comparison. At 100 K, the oxygen atoms only undergo small oscillations, and all instantaneous positions lie very close to the respective average positions. An altogether different picture emerges at 300 K and 500 K: Here, the instantaneous positions of the oxygen atoms reveal a precession‐like motion around the Al−P connection line. Because different areas around the connection line are visited within the 15 ps of the simulation, the average positions lie rather close to that line, even though the oxygen atoms are rarely, if ever, actually located at these positions. On the basis of this observation, the deviations between instantaneous and average structure in terms of Al−O/P−O distances and Al−O−P angles can be explained straightforwardly, in turn explaining the occurrence of shortened bonds and near‐linear linkages in the structures determined from diffraction experiments.

Figure 8.

Visualisation of the environment of one Al3 atom in the DFT‐optimised structure (top left) and in selected AIMD average structures. For the AIMD cases, the trajectories of the oxygen atoms are shown as small dark red spheres, showing which points in space were visited by the oxygen atoms during the 15 ps of the simulation. Angles computed for the AIMD average structures are given below each panel.

It is worth noting that the behaviour visualised in Figure 8 does not correspond to a “hopping” between discrete oxygen positions, but that different areas around the Al−P connection line are visited with approximately equal probability. In an experimental structure determination, it would probably be possible to model the Bragg diffraction intensities reasonably accurately by refining several partially occupied oxygen positions. However, as no such discrete minima could be identified in the AIMD results, a physically more appropriate picture would involve a “donut‐shaped” electron density that envelops the Al−P connection. A similar deviation between time‐averaged and instantaneous position was found for the O2 atom in AFI‐type AlPO‐5 in a combined quasi‐elastic neutron scattering and AIMD study: ^[85] While the Al−O2−P angle in the crystal structure is close to 180°, with shortened bond lengths, ^[39] the time‐resolved investigations showed that the O2 atom undergoes a circular motion around the Al−P connection line, hardly ever lying on the line. Even at 100 K, this precession‐like motion is prominent in AlPO‐5, indicating a flatter potential energy surface than in AlPO‐11. At 300 K, sporadic “jumps” leading to an intermittent increase of the Al−O2−P angle were observed in addition to this circular motion, agreeing with the somewhat more frequent occurrence of near‐linear angles in the angular distribution functions computed for AlPO‐11 at 300 and 500 K.

Preferred water adsorption sites in AlPO‐11

DFT optimisation of partially hydrated AlPO‐11 models

Previous NMR studies indicated that 1/5 of all Al sites are octahedrally coordinated due to the adsorption of water, leading to AlO₄(H₂O)₂ environments.[ ⁴⁵ , ⁴⁶ , ⁴⁷ , ⁴⁸ ] Most of these studies also agreed that the adsorption occurs selectively at one of the five sites of the $Pna{2}_1$ structure.[ ⁴⁶ , ⁴⁷ , ⁴⁸ ] To obtain partially hydrated models, the symmetry of the DFT‐optimised $Ima2$ structure was lowered to $Pna{2}_1$ , resulting in five non‐equivalent Al sites in the unit cell, each with multiplicity 4. Because the Al11/Al12 and Al21/22 pairs of sites have exactly the same environment and become inequivalent only upon introduction of the water molecules, only the Al11, Al21, and Al3 atoms were considered as potential adsorption sites. Two water molecules were then placed manually in the environment of these Al sites, leading to three distinct models with 8 H₂O molecules per unit cell labelled H₂O@Al11, H₂O@Al21, and H₂O@Al3. It has to be noted that such partially hydrated systems are likely to be thermodynamically unstable, as the hydration occurs as a single “pore‐filling” step during which the Al‐coordinated water molecules are further stabilised through interactions with non‐coordinated “pore” water molecules.[ ⁴⁹ , ⁶² , ⁸⁶ ] However, the restriction to models containing only Al‐coordinated water molecules is convenient in the present context, since the generation of fully hydrated models would require further assumptions regarding the number and positions of the non‐coordinated water molecules. Given the rather distinct observations made for the three models, presented below, it appears reasonable to assume that the interactions with these “pore” water molecules would not alter the key findings.

According to the DFT optimisations, the H₂O@Al11 model represents the energetically most favourable case. It is favoured by 8.4 kJ mol⁻¹ (per H₂O molecule) over the H₂O@Al21 model, and by 24.0 kJ mol⁻¹ over H₂O@Al3. A symmetry search of the optimised structures delivers space group $Pna{2}_1$ for the H₂O@Al11 and H₂O@Al21 models, agreeing with experimental findings, ^[29] whereas only $P1a1$ symmetry is found for the H₂O@Al3 case (unlike for the AIMD average structures, the results of the symmetry search remain the same when hydrogen atoms are excluded). For H₂O@Al11, a comparison of the lattice parameters to those of the DFT‐optimised $Ima2$ structure shows a contraction along the a and c directions and a concurrent, less pronounced expansion along the b axis (Table 1). The same relative changes are observed in the experimental lattice parameters. In contrast, both the H₂O@Al21 and the H₂O@Al3 model show expansion along a and contraction along b, which are more pronounced for the latter case. The dimensions of the elliptical 10MR channels of the H₂O@Al11 structure are also fairly close to those of the experimental structure (d(Al3−P3)=11.05 Å, d(O21−O22)=7.08 Å, compare to values shown in the bottom panel of Figure 1), whereas considerable deviations are found for the other two models (Figure S1). Taken together, both the DFT total energy and the optimised structural parameters point to Al11 as the most likely water adsorption site, in agreement with the earlier DFT (B3LYP) study by Herrera‐Pérez et al., who studied models with $Ima2$ symmetry containing 16 H₂O molecules per unit cell, disregarding the experimental observation of a symmetry lowering upon hydration. ^[51]

The complete structures of the partially hydrated models are shown in Figure S1. A closer inspection of the H₂O@Al3 structure shows that adjacent AlO₄(H₂O)₂ octahedra are somewhat tilted with respect to each other, leading to the symmetry reduction to space group $P1a1$ . Figure 9 visualises the environment of the distinct octahedra in the three different models. In each case, one of the H₂O molecules lies above one of the adjacent 6MRs, with the Al−Ow1 bond pointing approximately along the c axis. Both hydrogen atoms of this water molecule, labelled Hw11 and Hw12, form relatively short hydrogen bonds to framework oxygen atoms, with d(H⋅⋅⋅O_fw) ranging from 1.65 Å to 1.91 Å. In contrast, the second H₂O molecule points into the 10MR channel and forms either no or (in the H₂O@Al3 model) only one, relatively long hydrogen bond. In all cases, the Al−Ow1 bond distance is significantly shorter than the Al−Ow2 distance. When looking at the distances from the Al atoms to framework oxygen atoms, listed in Figure 9, the rather short bonds between the Al3 and O7/O8 atoms in the H2O@Al3 model are noteworthy. Some of the associated Al−O−P angles are also relatively large, the most prominent example being the Al3a−O7a−P3a angle of 171° (Table S8). Such high angles are not found in the other partially hydrated models, which indicates that the adsorption of water molecules at the Al3 site causes significant strain in the local environment that cannot be fully relaxed. This larger strain can be understood when considering that the AlO₄(H₂O)₂ octahedra in the H₂O@Al3 case are neighbours, with only one PO₄ tetrahedron between them, whereas the octahedra are separated by two PO₄ and one AlO₄ tetrahedron in the H₂O@Al11 and H₂O@Al21 models. This tendency to avoid a close proximity of the AlO₄(H₂O)₂ octahedra can also explain the highly ordered structure of the hydrated phase, for which evidence has been obtained using both XRD and NMR experiments:[ ⁴⁶ , ⁴⁷ , ⁴⁸ ] Once an adsorption of two water molecules at one Al atom has occurred, an adsorption at any of the surrounding sites (separated only by one PO₄ tetrahedron) will become energetically less favourable. The constraints arising from the connectivity of the AEL framework leave an adsorption of water at 50 % of either the Al1 or the Al2 sites in an ordered fashion as the arrangements in which a) 1/5 of the Al sites are octahedrally coordinated an b) there are no neighbouring AlO₄(H₂O)₂ octahedra. This ordering is the cause of the symmetry reduction to space group $Pna{2}_1$ . While this geometric reasoning serves to explain why an octahedral coordination of the Al3 site is unfavourable, it does not resolve why the H₂O@Al11 case is favoured over H₂O@Al21, especially as Figure 9 shows that the local environments of the AlO₄(H₂O)₂ octahedra are rather similar.

Figure 9.

Environment of AlO₄(H₂O)₂ octahedra in different models of hydrated AlPO‐11. Hydrogen bonds are shown as thin black lines, and relevant interatomic distances are given for each case.

AIMD simulations of partially hydrated AlPO‐11 models

In order to corroborate that the relative stability of different adsorption sites remains unchanged at finite temperature, AIMD simulations for a temperature of 300 K were performed for the partially hydrated AlPO‐11 models. The potential energy was then extracted by averaging over the production part of each trajectory. Because the individual potential energy values are close together for the H₂O@Al11 and H₂O@Al21 trajectories, an average over the three trajectories was calculated. According to this average potential energy, the H₂O@Al11 model is favoured by about 5 kJ mol⁻¹ per H₂O molecule over the H₂O@Al21 model, agreeing reasonably well with the results of the DFT optimisations. For the H₂O@Al3 model, the scatter in the potential energy values obtained from different trajectories is much larger, but it is clearly the least stable case, being between 11 and 18 kJ mol⁻¹ per H₂O molecule less favourable than H₂O@Al11.

The average lattice parameters obtained from individual trajectories are tabulated in Table S6. For the H₂O@Al11 and H₂O@Al21 cases, the scatter among individual trajectories is small, and deviations in the angles from 90° are negligible. A symmetry search on the average structures delivers $Pna{2}_1$ symmetry within moderate tolerances (maximal deviation below 0.4 Å), but only after removal of the hydrogen atoms, which may participate in different, short‐lived hydrogen bonds during the simulation. The average lattice parameters of a=18.147 Å, b=14.004 Å, and c/2=8.232 Å of the H₂O@Al11 model agree rather well with the experimental values of Khouzami et al., with deviations of +0.5 %, +1.6 %, and +1.3 %, respectively, even though the experimental refinement was done on a fully hydrated sample. ^[29] For the H₂O@Al21 case, the much longer a axis leads to poorer overall agreement. For the H₂O@Al3 model, there are considerable deviations in the average lattice parameters among the different trajectories (Table S6), and some angles also deviate appreciably from 90°. The symmetry search finds no symmetry for any of the average structures in this case. A closer inspection of the individual trajectories reveals a movement of several water molecules away from their initial positions, resulting in a coexistence of six‐, five‐, and four‐coordinated Al3 atoms. Most of these water molecules diffuse into the channel interior, forming no close contacts to any framework atoms, but a few are bonded to Al11 or Al12 atoms at the end of the AIMD simulation. Moreover, there are a few instances where intra‐framework Al−O_fw bonds are broken, leading to the formation of terminal Al−OH and P−OH groups. The breaking of intra‐framework bonds could constitute an initial step of framework destruction, which is not observed upon hydration of AlPO‐11.

Figure 10 visualises the distribution of Al−O and P−O distances and Al−O−P angles in hydrated AlPO‐11 for the experimental structure, the three DFT‐optimised structures with water adsorbed at different sites, and the AIMD average structures. For the H₂O@Al11 and H₂O@Al21 cases, the DFT and AIMD results clearly show four distinct distance ranges, corresponding to tetrahedral Al−O_fw bonds (between 1.7 and 1.8 Å), octahedral Al−O_fw bonds (between 1.8 and 1.9 Å), Al−Ow1 bonds (approx. 2 Å), and Al−Ow2 bonds (approx. 2.1 Å). As the experimental structure refinement did not localise the AlO₄(H₂O)₂ octahedra, only tetrahedral Al−O_fw bonds are found in the corresponding distribution. A second discrepancy between experiment and calculation is observed at the high‐angle side of the Al−O−P angle distribution. However, given the apparent inaccuracies in the experimental structure, which does not include any Al‐coordinated water molecules, the agreement between calculation and experiment appears satisfactory.

Figure 10.

Hydrated AlPO‐11: Distribution of Al−O distances (left), P−O distances (centre), and Al−O−P angles (right) in the experimental crystal structure (black), DFT‐optimised structures, and average structures obtained from AIMD simulations.

A noteworthy difference with respect to the results for calcined AlPO‐11 (Figure 2) becomes apparent when comparing the results for the DFT‐optimised and AIMD average structures of the H₂O@Al11 and H₂O@Al21 models: In the calcined form, the Al−O and P−O distances in the AIMD average structures computed for 300 K are significantly lower than those in the DFT‐optimised structures, because the precession‐like motion of some oxygen atoms causes a reduction of the time‐averaged (“apparent”) bond lengths. This phenomenon is not observed to the same extent in the hydrated form, where the distance ranges of Al−O_fw and P−O_fw bonds are only slightly broadened in the AIMD average structures. Furthermore, near‐linear linkages with Al−O−P angles above 170° are absent. This indicates that the pronounced differences between instantaneous and time‐averaged structure that were observed in the calcined form disappear (or become at least much less significant) upon hydration, presumably because the formation of AlO₄(H₂O)₂ octahedra and of H⋅⋅⋅O_fw hydrogen bonds suppresses the precession‐like motion of framework oxygen atoms. For the H₂O@Al3 model, the removal of water molecules and the breaking of intra‐framework links lead to very broad distance and angle distributions with few discernible features, which also vary among different trajectories.

Conclusions

A DFT optimisation of calcined AlPO‐11 with $Ima2$ symmetry results in a drastic overestimation of the unit cell parameters with respect to experiment. In contrast, the inclusion of thermal motion by means of AIMD simulations affords excellent agreement with the experimental lattice parameters. At the lowest temperature considered, 100 K, the symmetry is lowered because local distortions that break the $Ima2$ symmetry are frozen in. These distortions result in narrow distributions of T−O distances and Al−O−P angles that are distinctly different from those of the $Ima2$ phase. The AIMD simulations using the conventional AlPO‐11 unit cell deliver two different low‐temperature phases with $Pn11$ and $P112$ symmetries. These structures are very close in energy and differ only in the relative arrangement of adjacent columns of pairs of afi cages. On this basis, it seems questionable whether either of these structures could be realised by cooling an AlPO‐11 sample, or whether the actual structure at low temperature corresponds to a quasi‐random arrangement of different columns (or possibly another ordered phase with a larger unit cell). To elucidate the nature of the disorder, an experimental low‐temperature investigation of AlPO‐11 that accounts for both Bragg and diffuse scattering would be warranted.[ ⁸⁷ , ⁸⁸ ] It should be especially fruitful to combine AIMD simulations and diffuse scattering studies with an analysis of the AlPO‐11 structure in the conceptual framework of rigid unit modes.[ ⁸⁹ , ⁹⁰ , ⁹¹ ]

AIMD simulations performed for 300 K and 500 K show that the average structure approaches $Ima2$ symmetry. Like the experimental structure, the AIMD average structures exhibit shortened T−O distances and near‐linear Al−O−P angles. On the other hand, the radial and angular distribution functions computed over all frames of the AIMD trajectories do not show these features. This systematic difference between time‐averaged and instantaneous structure can be understood when considering the movement of the involved oxygen atoms. Although their instantaneous positions maintain near‐equilibrium values of T−O distances and Al−O−P angles, their precession‐like motion causes the time‐averaged position to lie closer to the Al−P connection line, resulting in a shortening of the “apparent” bond lengths and a straightening of the angles. This behaviour can explain the occurrence of unusually short T−O bonds in the experimental structures of AlPO‐11 and MnAPO‐11, which were determined at room temperature.[ ²⁶ , ³³ , ³⁴ , ³⁵ ] Similar features have been observed in all‐silica ferrierite and AlPO‐5, and deviations between instantaneous and time‐averaged structure are not an unusual phenomenon in zeolite‐type frameworks.[ ⁴¹ , ⁸⁵ ] The presence of unusually short bonds and near‐linear T−O−T linkages in the room temperature crystal structure can serve as a useful indicator for such deviations. Since a reduction of temperature can lead to a “freezing” of the precession‐like motion, materials exhibiting such features are likely to show displacive phase transitions upon cooling, providing a potentially rewarding field for further research. The discrepancy between time‐averaged and instantaneous structures should also be detectable experimentally by comparing the results from a conventional structure refinement to those of a pair distribution function analysis, as the latter gives access to instantaneous interatomic distances.[ ⁹² , ⁹³ ]

With regard to the preferred adsorption sites of water, both DFT optimisations and AIMD simulations strongly point to a preferential formation of AlO₄(H₂O)₂ octahedra at 50 % of the Al1 sites. This is not only the thermodynamically most stable scenario, but also leads to the same relative changes in lattice parameters as observed experimentally. Because a nearest‐neighbour arrangement of the octahedra, i. e., a separation by only one PO₄ tetrahedron, is energetically unfavourable, the formation of octahedral Al atoms occurs in an ordered fashion, explaining the reduction in symmetry to space group $Pna{2}_1$ . Unlike calcined AlPO‐11, the partially hydrated phase shows no signs of disorder in AIMD simulations performed for 300 K, in other words, hydration leads to a disappearance of room temperature disorder, at least if only the framework and Al‐coordinated water molecules are considered (H₂O molecules located in the channels, which were not included in the simulations, are unlikely to be fully ordered). Recent work on the aluminophosphate PST‐5 has shown that the presence of five‐ or six‐coordinated Al atoms plays a pivotal role during topotactic transformations of AlPO₄ frameworks. ^[53] For this reason, the prediction and understanding of the preferred water adsorption sites in AlPOs is not only of fundamental interest, but it may also play a key role in the further development of transformation‐based pathways to generate new zeotypes.

Conflict of interest

The author declares no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

M. Fischer, ChemPhysChem 2021, 22, 2063.