Abstract
Successful clinical use of patient-specific models for cardiovascular dynamics depends on the reliability of the model output in the presence of input uncertainties. For 1D fluid dynamics models of arterial networks, input uncertainties associated with the model output are related to the specification of vessel and network geometry, parameters within the fluid and wall equations, and parameters used to specify inlet and outlet boundary conditions. This study investigates how uncertainty in the flow profile applied at the inlet boundary of a 1D model affects area and pressure predictions at the center of a single vessel. More specifically, this study develops an iterative scheme based on the ensemble Kalman filter (EnKF) to estimate the temporal inflow profile from a prior distribution of curves. The EnKF-based inflow estimator provides a measure of uncertainty in the size and shape of the estimated inflow, which is propagated through the model to determine the corresponding uncertainty in model predictions of area and pressure. Model predictions are compared to ex vivo area and blood pressure measurements in the ascending aorta, the carotid artery, and the femoral artery of a healthy male Merino sheep. Results discuss dynamics obtained using a linear and a nonlinear viscoelastic wall model.
Keywords: fluid mechanics, cardiovascular dynamics, uncertainty quantification, Bayesian inference, inverse problems, ensemble Kalman filter (EnKF)
1. Introduction
Numerous studies have used one-dimensional (1D) fluid dynamics models coupled with constitutive arterial wall models to predict wave propagation in arterial networks [1–8]. One-dimensional models are useful for understanding pulse wave propagation in arterial networks [4,7,9–12] and for coupling with 0D and 3D models to generate multiscale representations of larger parts of the cardiovascular system [13–20]. The relatively simple nature of these models allows them to be used in a patient-specific context [21], improving diagnosis of observed hemodynamic disorders, such as pulmonary arterial hypertension [22,23].
Successful use of such patient-specific models in clinical settings depends on the reliability of the model output. Yet, the accuracy of the model output can be traced back to uncertainties in the input parameters [24–26]. Many sources of uncertainty naturally exist in cardiovascular models due to the complexity and variability in the cardiovascular system itself [24,27]. For 1D cardiovascular models, input uncertainties are associated with vessel geometry, specification of equations predicting the fluid dynamics and the arterial wall model, and parameters used to specify the inflow and outflow boundary conditions [1,9], as described below:
-
(1)
Geometry. For large vessels, geometric properties such as vessel length, diameter and bending, as well as network connectivity, can be obtained from magnetic resonance imaging (MRI) [2,6,22,28] or computed tomography (CT) images [29–31]. Accuracy in these measurements depends on how still and how long the subject lies in the scanner, the choice of image segmentation technique, and the geometric approximations used in reconstructing the vessel and network connectivity from the imaging data [32,33]. This study compares numerical simulations with experimental data where high precision measurements of vessel length (via caliper) and diameter (via ultrasonic crystals) were made directly on single vessels during experimentation, both in vivo before excision and ex vivo after [34,35]. Vessels in this study are assumed to be nontapered (i.e., effects of bends and changes in vessel diameter along vessels are ignored).
-
(2)
Fluid dynamics. In this study, blood is assumed to be Newtonian with constant viscosity and density, and the flow is assumed to be fully developed. As a result, the velocity profile is assumed parabolic [4]. While density and viscosity can be measured fairly accurately in large arteries, the velocity profile is more flat than parabolic [4,36], which gives rise to error in computations. In addition, in smaller vessels viscosity is no longer constant [37]. For the straight vessel studied here, uncertainties associated with these assumptions are minor, particularly since the data are from ex vivo experimental studies in which measurements are not taken until steady pulsating flow has been obtained.
-
(3)
One-dimensional model. This study uses the 1D Navier–Stokes equations for conservation of momentum and volume to relate flow, pressure, and area. To close the system, these are coupled with a constitutive equation relating vessel area and pressure. The latter equation encodes either elastic [6,9,38–40] or viscoelastic [1–3,10,13,41,42] deformation. This 1D approximation is a simplification that does not account for flow disturbances within the network, particularly in the presence of junctions. Moreover, model parameters defining viscosity, flow velocity, vessel stiffness, viscoelastic relaxation, and amplitude are difficult to measure, therefore providing a significant source of uncertainty, even within the single vessel model studied here.
-
(4)
Inflow boundary condition. A boundary condition is specified at the network inlet. This can be done by applying a time-varying flow profile (which may be obtained from MRI measurements) or by using a model that predicts the pumping of the left heart. The flow at the inlet is complex [43], and even if predicted with a 3D heart model [44], it is associated with a significant level of uncertainty [45]. This study focuses on quantifying uncertainty related to the inflow boundary condition.
-
(5)
Outflow boundary conditions. Outflow boundary conditions are typically assigned using either a fractal tree model [6,46–48] or a three-element Windkessel model [2,4,14,49,50] to represent the impact of flow from vessels not included in the network. The measurements of branching angles and ratios in the small vessels used to specify fractal tree models are typically extracted from studies over several species and therefore are not precise. Numerical methods for estimating Windkessel model parameters (two resistors and a capacitor) exist for elastic models but do not hold for viscoelastic models used in this study [8], giving rise to uncertainty in parameter values.
-
(6)
Numerical approximation. In addition to the physical quantities described above, errors associated with the numerical scheme chosen to solve the fluid equations are another source of uncertainty. This study employs a 1D finite element method with specified spatial and time discretization schemes. Previous work studying the convergence of this solver showed that the time discretization significantly affects the accuracy of the numerical solution, while the spatial discretization does not [8]. The numerical error in the time discretization of the solver is used in this study as a means of assessing trust in the model predictions, as described in Sec. 2.3.
Even if measurement techniques for estimating the quantities addressed above were perfect, complete data needed to estimate all of these quantities do not exist. In particular, the lack of concurrent area, pressure, and flow data makes it difficult to validate 1D models. 1D flow and geometry data for large vessels can be extracted from MRI measurements [51], while blood pressure can be measured noninvasively in superficial arteries using Finapres or tonometry methodologies [52,53] or invasively in deeper vessels using a pressure transducer [54,55]. To obtain sufficient resolution, MRI flow measurements must be averaged over several cycles during breath-hold, while blood pressure measurements are instantaneous. Thus, while “complete” validation of 1D models is difficult, acknowledgment of associated uncertainties could significantly improve the use of model-based predictions.
Typical validation of 1D arterial network models includes comparison of predicted and measured flow obtained in networks with geometry specified from MRI measurements. A majority of these studies have been done with models that predict wall deformation using simple linear elastic wall models [6,8,9,14,23,28]. However, it is known that arterial wall deformation (particularly within the aorta) exhibits both nonlinear and viscoelastic characteristics [42]. Some studies have accounted for linear viscoelastic [2,7,13] or nonlinear elastic [31,56] deformation, yet to our knowledge none have accounted for nonlinear viscoelasticity. Accurate model prediction necessitates the use of nonlinear viscoelastic wall models along with matching inflow and outflow boundary conditions and other previously mentioned inputs [2,57]. All of these factors influence wave propagation as well as the type and nature of the reflected waves, thus impacting the shape of the pressure waveform [58].
Most of the studies discussed above are deterministic, i.e., the proposed models fit given waveforms without addressing how changes in input parameters affect output predictions. However, several recent studies [24–26,59–66] have noted the importance of quantifying uncertainty in the model output given variation in the input, which becomes especially important in developing trustworthy models to aid in clinical decision-making. To our knowledge, only a few of these studies have addressed this topic for 1D arterial network models. Chen et al. [24] conducted stochastic simulations within a 1D network to explore the sensitivity of blood flow and pressure to uncertainty in geometric and hemodynamic parameters, including blood density and viscosity. These parameters were randomized using a log-normal distribution, then model predictions of flow and pressure were computed. Sankaran and Marsden [25] took a similar approach, using stochastic collocation to examine uncertainties relating to vessel geometry, boundary conditions, and flow-split in 3D models for abdominal aortic aneurysm, carotid artery bifurcation, and a patient-specific Fontan surgery. Sankaran et al. [59] studied the impact of uncertainties in vessel geometry on patient-specific simulations of the coronary arteries, coupling stochastic collocation with a machine learning-based surrogate to the 3D model. More recently, Sankaran et al. [60] presented a data-driven approach using adaptive stochastic collocation to quantify uncertainties relating to vessel geometry, boundary conditions, and blood viscosity in a patient-specific model of the coronary arteries. This study analyzed the relative impact of uncertainties in minimum lumen diameter, lesion length, boundary resistance, and blood viscosity on blood flow simulations, highlighting the importance of uncertainty in minimum lumen diameter. Eck et al. [26] employed a generalized polynomial chaos (gPC) method computed by stochastic collocation to study the sensitivity of pressure waves to arterial stiffness, while Xiu and Sherwin [61] used gPC to explore uncertainty in pulse wave propagation in a reduced human arterial network model by randomizing a material parameter related to wave propagation speed. Xiao [62] employed a reduced-order unscented Kalman filter to estimate wall stiffness in the carotid artery, as well as Windkessel model resistance and compliance parameters in an idealized aortic bifurcation in a 3D fluid–solid interaction model. Eck et al. [63] recently presented a six-step procedure outlining uncertainty quantification and sensitivity analysis in cardiovascular models, focusing on Monte Carlo and polynomial chaos techniques, while Schiavazzi et al. [64] presented a framework for propagating uncertainties in clinical data to uncertainties in model parameters and model output, using Bayesian parameter estimation techniques, on a patient-specific 3D model simulating virtual stage II single ventricle palliation surgery. The closest related study is that of Brault et al. [65,66], which used projection-based gPC to investigate the sensitivity of 1D model output to uncertainty in the inlet boundary condition. Brault et al. prescribed a periodic inflow model with known form and randomized parameters such as mean and peak flow rate, treating them as independent, uniformly distributed random variables.
The primary objective of this study is to use ex vivo area and pressure data from three single vessels (the ascending aorta, the carotid artery, and the femoral artery) extracted from a healthy male Merino sheep to predict the inflow waveform. In particular, we aim to quantify uncertainty in the shape and magnitude of the estimated inflow waveform, then use this input uncertainty to quantify the corresponding uncertainty in the model output predictions of area and pressure at the center of the vessel for each of these three single vessels of different sizes taken from different locations in the arterial network. This is shown using both a linear and a nonlinear viscoelastic wall model.
The inflow boundary condition is estimated in this study using a Bayesian inverse problems approach [67,68], which provides a natural measure of uncertainty in the inflow estimation. We show how uncertainty in the inflow profile (i.e., the temporal profile prescribed at the vessel inlet boundary) can be propagated through the model to predict uncertainty in the model output at the center of the vessel. More specifically, we develop an iterative scheme based on the ensemble Kalman filter (EnKF) that estimates the inflow from a prior distribution of curves. The EnKF [69,70] has proven to be a useful tool in estimating both unknown model states and parameters in various applications, including weather prediction [71,72] and reservoir modeling [73]. Numerous variations of the original EnKF for state estimation have been derived; in particular, in this study we adapt the augmented EnKF for combined state and parameter estimation derived in Arnold et al. [74].
To our knowledge, this is the first study to propose a methodology for systematically estimating the inflow boundary condition and one of the first studies to address propagation of uncertainty in arterial network models. In our view, prediction of output uncertainty is essential in successfully rendering physiological models patient-specific for use in clinical decision-making. While the current study focuses on inflow estimation, this is just one example that provides a foundation for how such methodologies can be applied in this setting.
In addition to estimating the inflow boundary condition, this study also compares area and pressure predictions obtained using linear and nonlinear viscoelastic models. A previous study showed that including nonlinear elastic deformation is essential within the aorta, while linear elastic deformation was adequate to estimate wall deformation in smaller vessels including the carotid and femoral arteries [42]. However, that study was done without accounting for the fluid dynamics considered here. Results of this study show that the proposed methodology is able to estimate inflow boundary conditions and predict the corresponding output uncertainties for vessels of different size and that accounting for nonlinear viscoelastic deformation improves the estimation.
2. Materials and Methods
2.1. Experimental Data.
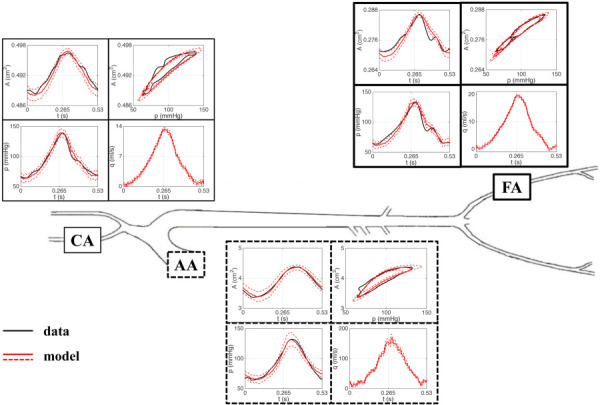
Data for this study include blood pressure and cross-sectional area measurements from the ascending aorta (AA), the femoral artery (FA), and the carotid artery (CA) of a healthy male Merino sheep, aged 18–24 months with an approximate weight of 32 kg. The excised vessel segments were mounted in the organ chamber of the mock circulation (shown in Fig. 1) and stretched to their in vivo length, which was measured using a high-precision caliper. The vessels were subjected to physiological hemodynamic conditions induced by a Jarvik heart pump. The external arterial diameter of each vessel was measured using sonomicrometry, and blood pressure was measured using a solid-state microtransducer. More details of the experimental protocol can be found in Armentano et al. [75] and Valdez-Jasso et al. [76]. In this work, we analyze the measured area and pressure data over one cardiac cycle in each of the AA, FA, and CA, treated as single vessels of different sizes taken from different locations in the network. The vessels, along with their corresponding area and pressure data, are shown in their network location in Fig. 2.
Fig. 1.
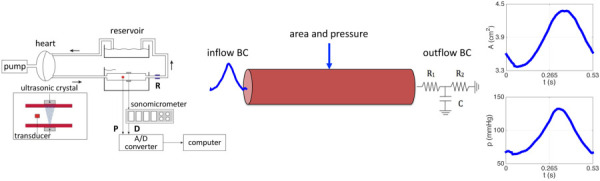
(Left) Mock circulation including a pneumatic pump, a perfusion line connected to the chamber with the mounted vessel segment, a resistance modulator (R), and a reservoir. Blood pressure (P) is measured with a microtransducer while the diameter (D) is measured with a pair of ultrasonic crystals using sonomicrometry. (Middle) The single, straight vessel segment shown with inflow and outflow boundary conditions. (Right) Time series data for area and pressure at the center of the vessel.
Fig. 2.
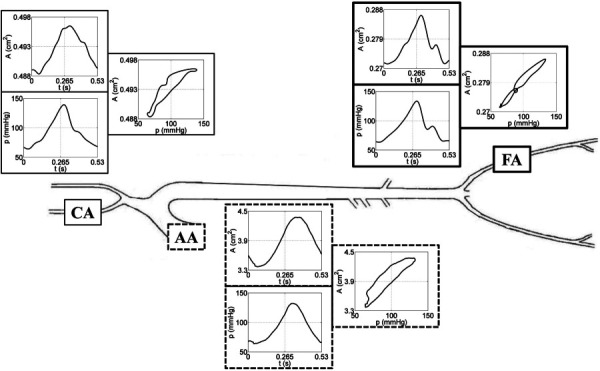
Arterial network representation showing (from left to right) the carotid artery (CA), the ascending aorta (AA), and the femoral artery (FA). Time series data for area and pressure, along with the corresponding area versus pressure loop, are shown at each vessel location.
2.2. Fluid Dynamics Model.
Blood flow, pressure, and area are predicted using a 1D fluid dynamics model derived from the Navier–Stokes equations under the assumptions that the vessels are cylindrical, that the vessel length is significantly greater than the vessel radius, that the blood is incompressible, that the fluid is Newtonian, and that the flow is axisymmetric with a parabolic velocity profile. Under these conditions, conservation of mass and momentum [3,8,77] is given by
| (1) |
where the blood density g ml−1 and viscosity 0.049 g s−1 cm−1 are assumed constant, with kinematic viscosity . The area of the vessel is denoted by (measured in cm2), the pressure by (mmHg), and the flow by (ml s−1).
Deformation of the arterial wall is predicted using a viscoelastic wall model of the form
| (2) |
where determines the viscoelastic relaxation with the parameter denoting the amplitude associated with the characteristic relaxation time . Area is related to pressure via the strain function , where is the zero-pressure area. The elastic response function in Eq. (2) can be linear or nonlinear. The linear Kelvin model has the form
| (3) |
with parameters the elastic modulus, the wall thickness, and the zero-pressure radius, while the nonlinear sigmoid model has
| (4) |
where denotes the maximal cross-sectional area, the characteristic pressure at which the vessel begins to saturate, and an exponent determining the steepness of the sigmoid curve [42].
The inflow at the proximal end of the vessel is estimated using the proposed EnKF scheme, while at the outlet, flow and pressure are related via a three-element Windkessel model
| (5) |
with two resistors and (dynes s cm−5) representing the characteristic impedance and total peripheral resistance, respectively, and a capacitor (cm5 dyne−1) denoting arterial compliance.
2.3. The EnKF-Based Inflow Estimator.
This study develops an EnKF-based iterative scheme based on the work by Arnold et al. [74] that, given discrete observations of area and pressure at the center of the vessel, estimates a time-varying flow profile from a prior distribution of curves; this scheme is hereby referred to as the EnKF-based inflow estimator. A brief review of the idea behind Bayesian filtering and the general augmented EnKF algorithm for state and parameter estimation is given in the Appendix. We adapt this methodology for the current application to perform inflow estimation in a 1D vessel.
To this end, we consider area and pressure evaluated at the center of the vessel at , where is the vessel length, as our model states, which we write in vector form as
| (6) |
and we treat the inflow curve as an unknown, time-varying parameter to be estimated at discrete time points , . Using the fluid dynamics model (1)–(2), we take a given inflow curve and compute the corresponding area and pressure curves at by employing a stabilized space-time finite element method based on the discontinuous Galerkin method, which we refer to in this paper as the “fluid solver” [3]. The spatial discretization of the fluid solver uses continuous linear polynomials, while the temporal discretization is defined by piecewise constant functions. Previous work studied convergence of the fluid solver using different wall models, varying the number of elements, the number of time steps per period, and the total number of periods [8]. Based on this work, we use 12 elements and a minimum of 400 time steps per period, ensuring convergence of the solver with both the linear and nonlinear wall models. We run the solver for 12 periods to guarantee that the effects of initial conditions wear off, requiring that the last and next-to-last periods differ by no more than a prescribed tolerance.
Further, we assume that we have noisy measurements of area and pressure at the center of the vessel at the same discrete time points , , which we model as
| (7) |
where and is some observation error. For simplicity, we can always discretize the inflow so that its discretized time points match the time points of the data.
2.3.1. Generating a Prior.
Let be a vector denoting the time-discretized inflow curve that we aim to estimate such that . Since the fluid solver requires a value of at each discretized time point , , we begin our EnKF-based scheme to estimate by assigning each entry an initial probability distribution with mean and variance , as illustrated in Fig. 3. In this study, we let be normally distributed, although the methodology developed here is not restricted by this choice. For each , the mean is chosen to be a point from a curve estimated a priori, and the standard deviation is selected based on our level of uncertainty in the shape and magnitude of the curve at that point, as described in the bullets below.
Fig. 3.
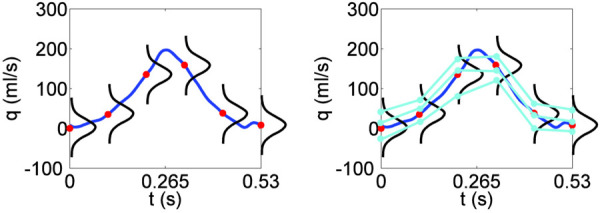
Illustration of how to form an initial ensemble of inflow profiles by assigning probability distributions at discretized points. Here, for example, a Gaussian distribution is assigned at each of six equispaced time points over the interval [0, 0.53] s. (Left) The assigned distributions have means given by the discretized points on the curve and fixed standard deviations. (Right) At each discretized time point, the corresponding distribution is sampled (here, the sample size is three) and the sample points are connected in an ascending manner to form physically plausible inflow profiles. These profiles are then smoothed with a cubic spline to enforce regularity (not pictured).
The choice of mean curve should encompass any a priori knowledge of the data that may help to get a sense of the possible shape of the inflow curve. The used in this work was obtained by the following procedure: Originally, measured blood pressure was prescribed at the inlet, and a corresponding flow was predicted using the fluid solver. However, as discussed by Anliker et al. [78], this flow had large negative components following systole. A small negative flow can be expected physiologically, reflecting a reversed flow into the heart upon valve closure. To obtain a positive flow, the Windkessel model parameters were adjusted, resulting in a cardiac output exceeding that known for sheep. Subsequently, the flow profile was scaled to ensure a mean cardiac output of 4.2 l per minute (common for sheep); for more details, see Battista et al. [8].
The standard deviation can be assigned differently at each based on some a priori information regarding the certainty in the shape of the curve or set to be the same for some . For simplicity, in our simulations we assigned the same at each , but we used a different for each of the three single vessels to reflect its respective scale.
Once a distribution is assigned to each entry in the time-discretized inflow curve, a random sample of size is drawn from the distribution at each , which results in samples
| (8) |
These samples are collected into vectors , where
| (9) |
which are then concatenated into a matrix . The rows of the matrix can be used to form our initial ensemble of discretized inflow profiles. Since connecting the sample points randomly may result in nonphysical flow profiles, we sort the columns of in ascending order to generate flow profiles that are physiologically plausible. The rows of the sorted matrix therefore comprise our initial ensemble of discretized inflow profiles , , with mean near . To enforce regularity and smoothness in the inflow profiles when solving the partial differential equations, each inflow curve is interpolated using a cubic spline so that the time discretization of the flow matches that needed to ensure convergence of the fluid solver.
2.3.2. Implementation.
After forming the initial ensemble of inflow curves, the EnKF-based inflow estimator is applied, comprising the following two-step procedure:
-
(1)Prediction Step: For each ensemble member , where :
-
(a)Use the fluid solver to compute the model states , where
that correspond to the inflow profile for two different time discretizations: one coarser (but converged) for prediction, denoted by ; the other finer and converged for error control, denoted by .(10) -
(b)Assuming that the model error is related to the time discretization error in the fluid solver, assign the standard deviation of the model innovation term for each ensemble member to be a factor of the difference between the two solutions computed in (a):
where and are the model state vectors at time computed with the coarse and fine time discretization, respectively, and is a multiplicative factor taken here to be . Hence is proportional to the error in the solver difference at each time for each ensemble member , allowing for individualized innovation [74,79].(11) -
(c)Compute the prediction state ensemble via the equation
where is a random vector with components for .(12) -
(d)Combine prediction states and inflow profiles to form an augmented prediction ensemble , where
and compute its mean using ensemble statistics(13) (14)
-
(a)
-
(2)Observation update: For each time point , , sequentially:
-
(a)Generate an observation ensemble of size about the observed value :
where for some observation noise covariance assumed here to be known and constant.(15) -
(b)Compute the prediction covariance matrix
(16) -
(c)Compute the Kalman gain matrix
where is the augmented observation matrix.(17) -
(d)Compute the posterior augmented ensemble using the formula
(18) -
(e)Compute posterior ensemble mean
and covariance(19) (20)
-
(a)
The two steps above comprise a single iteration of the algorithm, which may be run successively to ensure convergence of the filter. The algorithm results in a posterior ensemble of inflow profiles, yielding a mean inflow profile (referred to as the EnKF estimate) as well as an estimate of the variance of the ensemble at each discretized time point , . The variance of the resulting ensemble at each discretized time point provides a measure of uncertainty in the estimated inflow at that time point since the variance indicates how wide or narrow the posterior ensemble distribution is around the mean value of the estimated inflow at that point. Therefore, in this work, we use the standard deviation curves around the estimated mean inflow profile to represent our uncertainty in the inflow estimation.
The resulting mean inflow profile and standard deviation uncertainty curves are propagated through the model to generate model output predictions of area and pressure at the center of the vessel with corresponding predictions of uncertainty. The model output predictions of uncertainty obtained by propagating the standard deviation inflow uncertainty curves through the model are interpreted as representing a measure of uncertainty in the model output predictions of area and pressure obtained using the mean estimated inflow curve, thereby connecting the uncertainty in the estimated inflow with uncertainty in the resulting model output.
3. Results
The proposed EnKF-based inflow estimator was applied to estimate the unknown temporal flow profile prescribed at inlet boundary given area and pressure data measured at the center of a straight vessel for each of three single vessels (AA, CA, and FA, shown in Fig. 2). Area and pressure time series data for each vessel were provided at 107 discrete time points equispaced over the length of one cardiac cycle. The initial ensemble of inflow profiles for each simulation was formed as described in the methods section on generating prior curves (depicted in Fig. 3). For these simulations, geometry was assumed known and outflow boundary dynamics were determined using a three-element Windkessel model with known parameters.
The method was analyzed on the experimental and simulated AA data a priori to determine the effects of varying the number of ensemble members, the convergence of the inflow estimator after multiple iterations of the filtering algorithm, and the filter’s ability to estimate a flow that was able to predict measured area and pressure at the center of the vessel. Based on these results, for the following experiments an ensemble of size was used and the algorithm was run for one iteration. The EnKF computations were performed in matlab, while the fluid equations were solved in C++. Communication between the two platforms was done using text files. Results were obtained running the algorithm sequentially on a Mac OS X desktop computer with a 3.2 GHz Intel Core i3 processor and 8 GB RAM. Simulations took an average of 4.5 h each to complete.
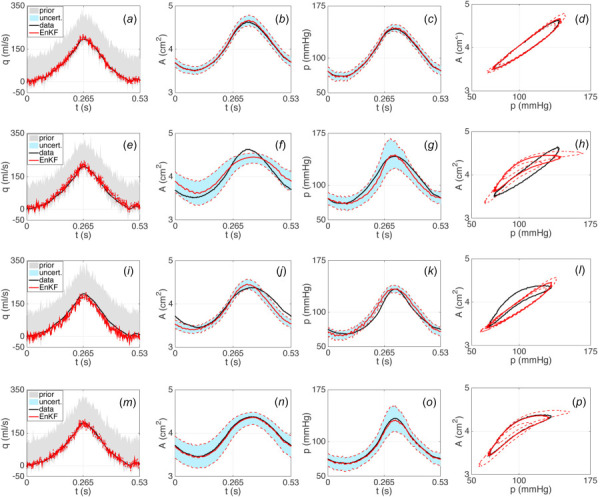
We first applied the EnKF-based inflow estimator to data from the ascending aorta using the linear Kelvin viscoelastic wall model (3) with known parameters to predict radial deformation. Parameters for the wall model were chosen to fit the data when inputting the a priori flow curve as the inlet boundary condition; these parameter values are listed in Table 1 along with the Windkessel model parameters for the outflow boundary condition. As described in the methods section, the two-step procedure of the inflow estimation algorithm was performed using the innovation model with standard deviation assigned in Eq. (11), with the coarse time discretization set to 428 time steps and the fine set to 856 time steps. The resulting estimated inflow waveform and 2 standard deviation uncertainty curves are shown in Fig. 4(a), while the corresponding model output predictions and output uncertainty curves are shown in Figs. 4(b)–4(d). While a majority of the area and pressure data is captured within the predicted uncertainty bounds, there is clear underestimation of the area time series shown in Fig. 4(b) toward the beginning of the cardiac cycle and of the pressure time series in Fig. 4(c) toward the end. The portions of the data not captured by the model predictions are more easily seen in the area versus pressure plot in Fig. 4(d).
Table 1.
Kelvin linear wall model parameters and Windkessel model outflow boundary condition parameters used for prediction of area and pressure in the ascending aorta. Parameter values are stated with three significant digits.
|
Kelvin wall model parameters |
Windkessel parameters |
||||||
|---|---|---|---|---|---|---|---|
| AA | 0.91 | 6.62 | 0.467 | 0.0546 | 776 | 1823 | 0.0386 |
Fig. 4.
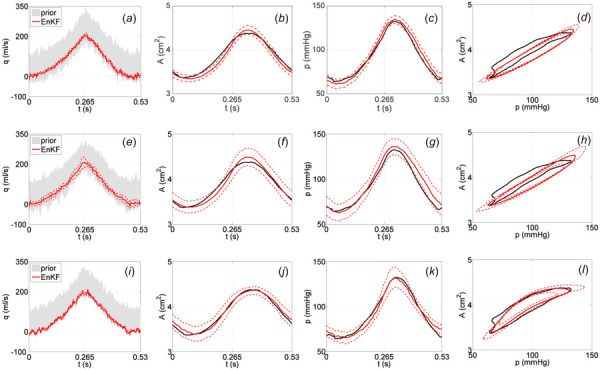
Results with AA data using the linear Kelvin wall model (top row), the linear Kelvin wall model with increased model innovation (middle row), and the nonlinear sigmoid wall model (bottom row). EnKF estimated inflow profiles (solid red) and 2 standard deviation curves (dashed red) obtained from an initial ensemble of inflow curves (gray cloud) are shown in ((a), (e), (i)). Predicted area and pressure curves using the EnKF estimated inflow profiles and 2 standard deviation curves are shown in ((b), (f), (j)) and ((c), (g), (k)), respectively. Corresponding area versus pressure curves obtained using the EnKF estimated inflow profiles are shown in ((d), (h), (l)). Area and pressure data are plotted in black.
Motivated by these results, we attempted to capture more of the data within the predicted uncertainty bounds by increasing the standard deviation of the model innovation term defined in Eq. (11) to include a multiple of the difference between the data and the baseline EnKF mean prediction in both area and pressure. This essentially directs the filter in a systematic manner to trust the data more than it trusts the model, which results in increased uncertainty in the estimated inflow and corresponding model predictions shown in Figs. 4(e)–4(h). The plots in Figs. 4(f) and 4(g) better capture the time series data for both area and pressure within the wider predicted uncertainty bounds.
In both of the aforementioned cases, the nonlinearity in the AA pressure-area data (showing decreased deformation with increased pressure) cannot be fully captured by the linear wall model. The area versus pressure plots in Figs. 4(d) and 4(h) make this especially clear. Inspired by results in Valdez-Jasso et al. [42], we extended the wall model to include nonlinear viscoelasticity. In particular, we used the nonlinear sigmoid viscoelastic wall model (4) with known parameters listed in Table 2, keeping the original implementation of the innovation standard deviation in Eq. (11). Table 2 also lists the Windkessel parameters used for the outflow. Results are shown in Figs. 4(i)–4(l), where the nonlinearity in the AA data is much better accounted for in the model predictions (especially visible in Fig. 4(l)). Tests using the sigmoid model (4) and increasing the innovation standard deviation in Eq. (11) did not show significant improvements. However, comparing the plots in Figs. 4(i)–4(l) to Figs 4(a)–4(d), it can be seen that using the sigmoid wall model results in an inflow estimate and corresponding model output predictions of area and pressure with wider uncertainty bounds about the mean curve than when using the Kelvin model. Simulations to confirm this result using synthetic data generated with a known inflow profile are included in the Appendix.
Table 2.
Sigmoid nonlinear wall model parameters and Windkessel model outflow boundary condition parameters used for prediction of area and pressure in the ascending aorta (AA), femoral artery (FA), and carotid artery (CA). Parameter values are stated with three significant digits
|
Sigmoid wall model parameters |
Windkessel parameters |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AA | 0.955 | 2.87 | 4.67 | 82 | 5.5 | 0.467 | 0.1 | 780 | 950 | 7.54 |
| FA | 0.275 | 0.237 | 0.326 | 105 | 1.03 | 0.787 | 0.02 | 4798 | 10,815 | 0.740 |
| CA | 0.392 | 0.482 | 0.503 | 91.5 | 2.98 | 0.477 | 0.071 | 7800 | 15,500 | 0.740 |
The aforementioned results for the ascending aorta suggest that, while resulting in wider uncertainty bounds, including nonlinear viscoelasticity in the wall model significantly improves predictions of area and pressure by better capturing nonlinearity present in the data. With this in mind, we applied the EnKF-based inflow estimator using the sigmoid wall model (4) with parameters in Table 2 to estimate the inflow profiles for the carotid and femoral arteries. We chose these single vessels as representatives to demonstrate the effectiveness of the proposed algorithm in estimating the inflow and corresponding uncertainty for vessels of different sizes from different locations within the arterial network. Resulting model predictions and uncertainty estimates for area and pressure in each vessel are shown in Fig. 5, which also includes the AA results from Figs. 4(i)–4(l) for completeness. As an additional measure of overall system performance, we used the estimated inflow profiles and standard deviation uncertainty bounds to predict the flow at the center of each vessel, also shown in Fig. 5 with corresponding uncertainty estimates.
Fig. 5.
Predicted area, pressure, and flow at the center of the vessel obtained using the EnKF estimated inflow profiles and 2 standard deviation curves for single vessels at different locations in the arterial network. Results are shown for (from left to right) the carotid artery (CA), the ascending aorta (AA), and the femoral artery (FA). Corresponding area versus pressure curves obtained using the EnKF estimated inflow profiles are also shown at each vessel location. Area and pressure data are plotted in black.
4. Discussion
The success of patient-specific models in clinical decision-making relies heavily on the accuracy of the model predictions. Uncertainty quantification plays a vital role in determining how the model output is affected by input uncertainties. For 1D fluid dynamics arterial models, as noted in the introduction, input uncertainties can be found in vessel geometry, fluid model assumptions, parameters specifying the arterial wall model, and parameters relating to the inflow and outflow boundary conditions.
The methodology developed in this study presents a promising technique for quantifying uncertainty in the inflow boundary condition along with the uncertainty in model predictions of area and pressure. More specifically, this study developed an EnKF-based iterative filtering scheme to systematically estimate the inflow boundary condition for a single, nontapered vessel given measurements of area and pressure at the center of the vessel, providing not only an estimate of the size and shape of the inflow profile but also a natural measure of uncertainty in the output.
4.1. Inflow Estimation.
To our knowledge, this is the first study to systematically estimate the inflow boundary condition. Brault et al. [65] acknowledged inflow uncertainty by assigning a periodic model with known form for the inflow and randomizing parameters including mean and peak flow rate, but that study relied on specification of the inflow by a parameterized equation. Brault et al. also relied on the assumption that randomized parameters could be adequately characterized using independent uniformly distributed random variables, and the study did not compare model output results to experimental data. Our methodology, on the other hand, does not require any explicit inflow model, offering more freedom in estimating the shape best suited to predict given area and pressure data, provided some a priori estimate of the inflow profile is available (see Fig. 3). Our use of the EnKF also allows for unique posterior distributions to be determined at each time-discretized point of the estimated inflow so that output predictions do not rely on the choice of an initial distribution.
Moreover, our proposed scheme provides a measure of uncertainty arising naturally in the inflow estimation that can be used to assess uncertainty in the model output predictions of area and pressure. The measure of uncertainty obtained in our inflow estimation is an inherent feature of the EnKF and stems from the use of Bayesian filtering to solve the inverse problem of estimating unknown model inputs. Other methods, such as gPC and stochastic collocation, prescribe uncertainty in the input by assigning distributions (with designated means and variances) to unknown input parameters, and then assess the sensitivity of model output with respect to these input uncertainties—input estimation is not explicitly performed. Chen et al. [24], Sankaran and Marsden [25], and Eck et al. [26] took this type of approach in quantifying uncertainties related to various input parameters, such as vessel geometry and physical parameters including blood density and viscosity. The Bayesian approach, on the other hand, assigns a prior distribution to each unknown input parameter, then estimates the input parameters themselves to find posterior input parameter distributions with mean and variance estimates which are then propagated through the model to assess corresponding output uncertainty.
When generating the prior ensemble of inflow profiles (see Sec. 2.3.1), the samples at each time-discretized point are connected in a structured fashion to produce an ensemble of physically plausible inflow profiles. The effects of correlation structure in the prior generation of inflow profiles on the resulting inflow estimates may be analyzed in future work. Further, Eq. (18) uses correlation between the area, pressure, and inflow at time to update the inflow at time but not at other time points along the inflow profile. An alternative approach would be to update all points in the inflow profile at each observation time, by modifying the algorithm to account for correlation between all of the points in the inflow profile and the model predictions of area and pressure at that time. However, this approach would require that the model be rerun after each observation update in order to recompute the area and pressure predictions, which would add significantly to the computing time and computational cost of running the algorithm. Future work may include implementing this type of approach and comparing the inflow estimation results with those obtained in this study.
Results using experimental area and pressure data [76] over one cardiac cycle taken from three excised vessels (AA, CA, and FA) in different locations along the arterial network in a healthy sheep show that the proposed EnKF-based inflow estimator is robust in finding an inflow profile that well matches the data starting from an ensemble of flow profiles with varying magnitudes and shapes. The experimental studies considered in this work were done in single, nontapered vessels, but previous work has used these data to show that measurements from individual vessel segments reflect dynamics observed within a network [8]. Future work may include adapting the EnKF-based inflow estimator developed in this study to accommodate use of tapered vessels as well as multiple vessels in network simulations.
Other future work includes optimizing the code to run more efficiently and at a lower computational cost, perhaps by ridding the matlab interface and implementing the filtering portion of the algorithm in C++. Moreover, the embarrassingly parallel nature of Bayesian filtering algorithms during state propagation (since each ensemble member is independently propagated) suggests a very natural way to parallelize the algorithm. Finally, while the EnKF is a very useful and efficient tool in these types of problems, the methodology developed in this work is not restricted by its use, and other Bayesian nonlinear filtering techniques, such as particle filtering, could be used instead if desired. Particle filtering may be particularly well suited for problems in which the resulting parameter distributions are thought to be non-Gaussian.
4.2. Additional Sources of Uncertainty.
While we focused only on inflow estimation in this study, assuming fixed values for the other typically uncertain model inputs listed in the introduction, our novel use of the EnKF in this setting can be extended to include estimation of additional model inputs, such as vessel geometry and outflow boundary condition parameters—the inflow estimation shown in this work is simply one example of how the proposed methodology can be used to quantify uncertainty in patient-specific cardiovascular models. Kalman-type Bayesian filtering was previously used by Xiao [62] to estimate input parameters including arterial wall stiffness in a 3D fluids model, yet its use in systematically estimating a time-dependent boundary condition for 1D arterial network models is new to this work. Since the model predictions of area and pressure are sensitive to the choice of wall model parameters and outflow boundary Windkessel model parameters listed in Tables 1 and 2, future work aims to optimize these parameters using Bayesian filtering methodology prior to or simultaneously while running the EnKF-based inflow estimator.
Further, the effectiveness of the EnKF-based inflow estimator was demonstrated in this study using patient-specific ex vivo area and pressure measurements over one cardiac cycle obtained from three single vessels (AA, CA, and FA) of different sizes and different arterial network locations in a healthy sheep. However, additional sources of uncertainty lie in the data themselves: there is variation, e.g., among different patients and across cardiac cycles, as well as measurement errors (both device and human). Differences in the ex vivo area and pressure data among the healthy sheep considered in this study can be seen in Battista et al. [8], where plots show the variation among different sheep for different single vessels at various locations in the arterial network. While data from one cardiac cycle from one sheep were analyzed in this study, the patient-specific capabilities of the methodology developed in this work could allow for a systematic comparison of inflow profiles estimated at different vessel locations using data over multiple cardiac cycles from different sheep.
4.3. Modeling Aspects.
Most 1D cardiovascular studies use flow data to discuss effects of viscoelasticity, although its expression relates area and pressure. This makes it difficult to validate predicted pressure-area dynamics. The experimental data [76] used in this study, however, contain measurements of both area and pressure, allowing us to directly assess the relation between the two quantities. Our simulations suggest that the nonlinearity in the pressure-area data is better captured using a nonlinear sigmoid wall model with assumed known parameters than a linear Kelvin model.
A previous study by Valdez-Jasso et al. [42] used the same data to compare the linear Kelvin model with the nonlinear sigmoid model as well as the nonlinear arctangent model proposed by Langewouters et al. [80]. Valdez-Jasso et al. concluded that the sigmoid model improved data prediction over the arctangent model for larger arteries like the aorta, while the Kelvin model was preferable for smaller, stiffer vessels like the carotid artery. In particular, the arctangent model was not able to predict unstressed vessel radius. However, that study neglected to consider the fluid dynamics, which may explain why our results show that use of the nonlinear sigmoid model improved prediction of pressure-area dynamics for all three vessels (AA, CA, and FA) regardless of size and network location. We did not consider the arctangent model here.
Although data from only one sheep were considered in this study to demonstrate the effectiveness of the EnKF-based inflow estimator, the patient-specific benefits of this methodology lie in its ability to analyze and quantify uncertainty for individual patients and then make comparisons. This ideology may be especially useful in analyzing patients with diseases such as hypertension and noting any differences that the estimation process may distinguish between patient types. This kind of analysis could have clinical implications if parameters relating to different patient groups (e.g., healthy control versus hypertensive) were distinguishable enough to potentially act has markers for disease.
5. Conclusions
This study developed a new iterative scheme based on the EnKF to systematically estimate the inflow boundary condition for a single, nontapered vessel given measurements of area and pressure at the center of the vessel. This estimation scheme provides not only an estimate of the size and shape of the inflow profile but also a natural measure of uncertainty in the model output, offering a promising technique for quantifying uncertainty in patient-specific 1D arterial network models. Results also suggest the use of nonlinear viscoelasticity in the arterial wall model in order to better capture nonlinearities in the data.
Acknowledgment
This work was supported by Grant No. NSF/DMS-1246991 (Research Training Group in Mathematical Biology at NC State), NSF/DMS-1122424, NSF/DMS-1022688, and Virtual Physiological Rat Project NIH/NIGMS 5P50GM094503 subaward to NC State.
Appendix A: Bayesian Filtering and the Augmented EnKF
Assume a differential equation model involving both model states and parameters , whose values may be uncertain or completely unknown. Further assume discrete, noisy observations , , of some model states. Given these observations, the inverse problem is to estimate the states and/or unknown model parameters. Inverse problems of this type are generally ill-posed [81–83].
In the Bayesian framework, states and parameters are treated as random variables with probability distributions, and their joint posterior density is connected to the likelihood function and prior distribution through Bayes’ theorem
| (A1) |
Assuming is a Markov process, an evolution-observation model can be written for the stochastic state and parameter estimation problem using discrete time Markov models: the state evolution equation is of the form
| (A2) |
where is a known propagation model, is an innovation process, independent of the state vector , and is a parameter, while the observation equation is of the form
| (A3) |
where is a known operator and is the observation noise, independent of . Denoting by the accumulated observations up to time , the aim is to sequentially update the posterior distribution using the following two-step scheme:
| (A4) |
This scheme can be viewed as a predictor–corrector method: the first step, known as the prediction step, uses the state evolution equation to make a prediction of the state propagation using only the current data, while the second step, the observation update, corrects that prediction by taking the new data into account.
When employing the augmented (or joint) EnKF [84], it is assumed that the current density is represented in terms of an ensemble comprising both states and parameters. Here, the notation denotes that our current model prediction (index on the left of the bar) and most recent data arrival (index on the right) are both at time . The prediction step of the filter uses the state evolution equation to update each ensemble member individually via the formula
| (A5) |
where is an independently drawn realization of the innovation process , which is often modeled as a normal random variable with zero mean and some known covariance. Prediction ensemble statistics are computed using the augmented state and parameter vectors which follows from defining an augmented evolution model where the propagation scheme for the static parameter is assumed to be perfect, i.e., constant. Hence, the prediction ensemble mean and prior covariance matrix are computed using the ensemble statistics formulas
| (A6) |
and
| (A7) |
respectively. When an observation arrives, an observation ensemble is generated via the formula
| (A8) |
where is an independently drawn realization of the observation noise process , also typically modeled as a zero mean, normally distributed random variable with known covariance matrix . In the case of a linear observation model where for some projection matrix , the observation model is extended for the augmented state by writing
| (A9) |
where is a zero matrix of size . The combined posterior ensemble is then obtained by the updating formula
| (A10) |
where the Kalman gain is given by
| (A11) |
The posterior mean vectors and covariance matrices for both the states and parameters are computed using the posterior ensemble statistics.
In this augmented state-parameter formulation of the EnKF, since the parameters are not updated in the prediction step in Eq. (A5) and are not observed quantities of the system, the parameters are updated in Eq. (A10) only through their cross-correlation with the model states, as encoded in the Kalman gain matrix (A11). This becomes evident by partitioning as
| (A12) |
and rewriting the Kalman gain in Eq. (A11) as
| (A13) |
in terms of the projection matrix from the extended observation model (A9).
Arnold et al. [74,79] developed methodology for modeling the innovation process in the state evolution equation (A2) by assuming that the covariance of the innovation term is related to the numerical discretization error in the solver used to propagate the states; that is, the authors let be a zero-mean, normally distributed random variable where the covariance matrix at each time step is assigned based on the difference between the solutions of higher and lower order numerical methods used to solve the model equations. More specifically, for each ensemble member , the innovation term in (A5) is a realization of the random variable , where the covariance matrix is defined as
| (A14) |
with standard deviation
| (A15) |
computed using the higher order method error control method [79]. Here, and are the model solutions using a lower order solver and a higher order solver, respectively, and is a safeguard factor to account for the omission of higher order terms. This method provides a systematic approach for estimating the innovation variance in the filter, offering a way to assign the model innovation in Eq. (A5) that is specific to each ensemble member at each time step, while avoiding unnecessary cost in manually choosing a fixed covariance matrix for the innovation term a priori.
In estimating the inflow boundary condition in this study, we set and treat each time-discretized point along the inflow profile as an unknown model parameter. Each time-discretized point in the inflow profile is then updated using its correlation with the corresponding model states (area and pressure) at that time via a modified version of the augmented EnKF, as described in Sec. 2.3. We apply the method of Arnold et al. [74,79] in estimating the variance of the model innovation term, using the numerical error in the time discretization of the fluid solver to set the standard deviation in Eq. (A15), as detailed in step 1(b) of the algorithm presented in Sec. 2.3.2.
Some works in the literature have cited issues using the augmented EnKF for parameter estimation in high-dimensional systems with strong nonlinearities, e.g., see Refs. [85] and [86], or multiplicative combinations of parameters [87]. A suggested alternative approach is to use a dual EnKF scheme involving two interacting filters: one to update the states, and one to update the parameters. Both heuristic [85] and Bayesian consistent [88] versions of the dual EnKF have been proposed. While the 1D model used in this study is nonlinear, particularly with the inclusion of the sigmoid wall model (4), we have not had such issues estimating the inflow profile parameters using the augmented EnKF-type scheme presented in this work. However, it would be possible to implement a dual state-parameter estimation scheme in this setting, which may prove useful if additional parameters (e.g., wall model parameters) were to be estimated along with the inflow profile.
Appendix B: Wall Model Comparison Using Synthetic Data
The results in Sec. 3, Fig. 4, show that using the nonlinear sigmoid wall model (4) in the fluid dynamics model (1)–(2) provides more accurate model predictions of the pressure-area data than using the linear Kelvin wall model (3), since the sigmoid model better captures the nonlinearity in the data. However, using the sigmoid wall model results in slightly wider uncertainty bounds about the estimated inflow than using the Kelvin wall model, which translates into wider uncertainty bounds about the corresponding model output predictions of area and pressure at the center of the vessel.
Motivated by this result, we performed simulations with synthetic data generated using a known inflow profile to explore the effects that the choice of wall model has on the EnKF-based inflow estimation and corresponding model output predictions, in terms of both accuracy and uncertainty. Taking the flow curve described in Sec. 2.3.1 as the known inflow profile, we generated two sets of synthetic area and pressure data: one using the linear Kelvin wall model (which we refer to as the “Kelvin data”) and parameters listed in Table 1, the other using the nonlinear sigmoid wall model (the “sigmoid data”) and parameters for the ascending aorta listed in Table 2. Each set consists of area and pressure time series data at 201 discrete time points, equispaced over the length of one cardiac cycle, with added Gaussian noise.
We then employed the EnKF-based inflow estimator using the different wall models to estimate the inflow profile relating to both the Kelvin and sigmoid data. Fig. 6 shows the results for each of the four combinations: Kelvin wall model on Kelvin data, sigmoid wall model on Kelvin data, Kelvin wall model on sigmoid data, and sigmoid wall model on sigmoid data. To numerically quantify the accuracy in the EnKF-based mean estimated inflow and corresponding model output predictions of area and pressure compared to the true inflow and corresponding synthetic area and pressure data, we compute the coefficient of determination ( ) values using the formula
Fig. 6.
Results using the linear Kelvin wall model (first and third rows) and the nonlinear sigmoid wall model (second and fourth rows) with synthetic AA data generated using the Kelvin model (first and second rows) and the sigmoid wall model (third and fourth rows). EnKF estimated inflow profiles (solid red) and 2 standard deviation curves (dashed red) obtained from an initial ensemble of inflow curves (gray cloud) are shown in ((a), (e), (i), (m)). Predicted area and pressure curves using the EnKF estimated inflow profiles and 2 standard deviation curves are shown in ((b), (f), (j), (n)) and ((c), (g), (k), (o)), respectively. Corresponding area versus pressure curves obtained using the EnKF estimated inflow profiles are shown in ((d), (h), (l), (p)). The area between 2 standard deviation uncertainty bounds is shaded in light blue. The true inflow profile and corresponding area and pressure data are plotted in black.
| (B1) |
where denotes the residual sum of squares between the estimated and true inflow (or model predictions and synthetic data) and denotes the total sum of squares proportional to the variance in the true inflow (or synthetic data). The ratio is known as the fraction of unexplained variance: the smaller this fraction is (i.e., the closer to one the value is), the smaller the unexplained variance due to error in the model estimate. To numerically quantify the uncertainty, we compute the area between the upper and lower uncertainty bounds ( standard deviation curves about the mean) on the EnKF-based estimated inflow and the corresponding upper and lower uncertainty bounds on the model output predictions. Table 3 lists the values and uncertainty estimates for each of the four cases.
Table 3.
Coefficient of determination ( ) values and uncertainty estimates for the estimated inflow profiles and corresponding area and pressure predictions computed using either a linear Kelvin or nonlinear sigmoid wall model on synthetic data generated using the different wall models (Kelvin or sigmoid). values are computed using formula (B1) between the mean estimated and true inflow profiles, as well as between the corresponding model output predictions and synthetic data for area and pressure. Uncertainty is represented as the area between the standard deviation uncertainty bounds on the mean estimated inflow and corresponding model predictions for area and pressure. values and uncertainty estimates are reported up to four decimal places.
|
|
Kelvin data |
Sigmoid data |
|||
|---|---|---|---|---|---|
| Wall model | Kelvin | Sigmoid | Kelvin | Sigmoid | |
| Value | Inflow | 0.9875 | 0.9724 | 0.9350 | 0.9886 |
| Area | 0.9970 | 0.8879 | 0.8842 | 0.9940 | |
| Pressure | 0.9976 | 0.9459 | 0.9412 | 0.9945 | |
| Uncertainty | Inflow | 8.7968 | 11.3713 | 9.1448 | 11.0369 |
| Area | 0.1111 | 0.2243 | 0.1083 | 0.2375 | |
| Pressure | 6.1033 | 13.3458 | 6.3483 | 11.9964 | |
In terms of the inflow estimation, the EnKF-based algorithm is able to estimate the true inflow profile fairly well in all four cases, especially when using the Kelvin wall model on the Kelvin data (shown in Fig. 6(a)) and the sigmoid wall model on the sigmoid data (Fig. 6(m)). This is also evident in the inflow values listed in Table 3. Although slightly larger when using the sigmoid wall model, the standard deviation uncertainty bounds are not significantly different in any of the four cases, as is also demonstrated with the inflow uncertainty estimates in Table 3.
Regarding the model output predictions, Figs. 6(b) and 6(c) show that applying the Kelvin wall model on the Kelvin data results in very accurate mean predictions of both area and pressure with tight uncertainty bounds. Use of the Kelvin wall model on the sigmoid data results in less accurate mean predictions but still has tight uncertainty bounds (Figs. 6(j) and 6(k)), while failing to capture the nonlinearities in the data (Fig. 6(l)). On the other hand, Figs. 6(n) and 6(o) show that applying the sigmoid wall model on the sigmoid data gives accurate mean predictions with wider uncertainty bounds than when using the Kelvin wall model. While use of the sigmoid wall model on the Kelvin data does not provide as accurate of mean predictions (Figs. 6(f) and 6(g)) as using the Kelvin wall model, the wider uncertainty bounds on the predictions are better able to capture the data than the tight bounds produced using the Kelvin model. The uncertainty estimates for area and pressure in Table 3 show that the Kelvin wall model has tighter bounds than the sigmoid model for both data sets.
These simulations demonstrate that while use of the Kelvin wall model results in tighter uncertainty bounds on the model predictions for both data sets, it fails to capture the nonlinearities in the sigmoid data. However, while use of the sigmoid wall model may result in better predictions of nonlinear data, the corresponding uncertainty bounds are wider.
Contributor Information
Andrea Arnold, Department of Mathematics, , North Carolina State University, , 2108 SAS Hall, 2311 Stinson Drive, Box 8205, , Raleigh, NC 27695-8205 , e-mail: anarnold@ncsu.edu.
Christina Battista, DILIsym Services, Inc., , Six Davis Drive, , Research Triangle Park, NC 27709 , e-mail: cbattista@dilisym.com.
Daniel Bia, Department of Physiology, , Universidad de la República, , Montevideo 11800, Uruguay , e-mail: dbia@fmed.edu.uy.
Yanina Zócalo German, Department of Physiology, , Universidad de la República, , Montevideo 11800, Uruguay , e-mail: yana@fmed.edu.uy.
Ricardo L. Armentano, Department of Biological Engineering, , CENUR Litoral Norte—Paysandú, , Universidad de la República, , Montevideo 11800, Uruguay , e-mail: armen@favaloro.edu.ar
Hien Tran, Department of Mathematics, , North Carolina State University, , 2108 SAS Hall, 2311 Stinson Drive, Box 8205, , Raleigh, NC 27695-8205 , e-mail: tran@ncsu.edu.
Mette S. Olufsen, Department of Mathematics, , North Carolina State University, , 2108 SAS Hall, 2311 Stinson Drive, Box 8205, , Raleigh, NC 27695-8205 , e-mail: msolufse@ncsu.edu
References
- [1]. Alastruey, J. , Passerini, T. , Formaggia, L. , and Peiro, J. , 2012, “ Physical Determining Factors of the Arterial Pulse Waveform: Theoretical Analysis and Calculation Using the 1-D Formulation,” J. Eng. Math., 77(1), pp. 19–37. 10.1007/s10665-012-9555-z [DOI] [Google Scholar]
- [2]. Reymond, P. , Merenda, F. Perren, F. , Rufenacht, D. , and Stergiopulos, N. , 2009, “ Validation of a One-Dimensional Model of the Systemic Arterial Tree,” Am. J. Physiol. Heart Circ. Physiol., 297(1), pp. H208–H222. 10.1152/ajpheart.00037.2009 [DOI] [PubMed] [Google Scholar]
- [3]. Steele, B. N. , Valdez-Jasso, D. , Haider, M. A. , and Olufsen, M. S. , 2011, “ Predicting Arterial Flow and Pressure Dynamics Using a 1D Fluid Dynamics Model With a Viscoelastic Wall,” SIAM J. Appl. Math., 71(4), pp. 1123–1143. 10.1137/100810186 [DOI] [Google Scholar]
- [4]. van de Vosse, F. , and Stergiopulos, N. , 2011, “ Pulse Wave Propagation in the Arterial Tree,” Annu. Rev. Fluid Mech., 43(1), pp. 467–499. 10.1146/annurev-fluid-122109-160730 [DOI] [Google Scholar]
- [5]. Wan, J. , Steele, B. N. , Spicer, S. A. , Strohband, S. , Feijoo, G. R. , Hughes, T. J. R. , and Taylor, C. , 2002, “ A One-Dimensional Finite Element Method for Simulation-Based Medical Planning for Cardiovascular Disease,” Comput. Methods Biomech. Biomed. Eng., 5(3), pp. 195–206. 10.1080/10255840290010670 [DOI] [PubMed] [Google Scholar]
- [6]. Olufsen, M. S. , Peskin, C. S. , Kim, W. Y. , Pedersen, E. M. , Nadim, A. , and Larsen, J. , 2000, “ Numerical Simulation and Experimental Validation of Blood Flow in Arteries With Structured-Tree Outflow Conditions,” Ann. Biomed. Eng., 28(11), pp. 1281–1299. 10.1114/1.1326031 [DOI] [PubMed] [Google Scholar]
- [7]. Mynard, J. P. , and Smolich, J. J. , 2015, “ One-Dimensional Haemodynamic Modeling and Wave Dynamics in the Entire Adult Circulation,” Ann. Biomed. Eng., 43(6), pp. 1443–1460. 10.1007/s10439-015-1313-8 [DOI] [PubMed] [Google Scholar]
- [8]. Battista, C. , Bia, D. , Zocalo German, Y. , Armentano, R. L. , Haider, M. A. , and Olufsen, M. S. , 2016, “ Wave Propagation in a 1D Fluid Dynamics Model Using Pressure-Area Measurements From Ovine Arteries,” J. Mech. Med. Biol., 16(2), p. 1650007. 10.1142/S021951941650007X [DOI] [Google Scholar]
- [9]. Alastruey, J. , Parker, K. H. , Peiro, J. , and Sherwin, S. J. , 2008, “ Lumped Parameter Outflow Models for 1-D Blood Flow Simulations: Effect on Pulse Waves and Parameter Estimation,” Commun. Comput. Phys., 4(2), pp. 317–336.https://www.researchgate.net/publication/228661502_Lumped_parameter_outflow_models_for_1-D_blood_flow_simulations_Effect_on_pulse_waves_and_parameter_estimation [Google Scholar]
- [10]. Alastruey, J. , Khir, A. W. , Matthys, K. S. , Segers, P. , Sherwin, S. J. , Verdonck, P. R. , Parker, K. H. , and Peiro, J. , 2011, “ Pulse Wave Propagation in a Model Human Arterial Network: Assessment of 1-D Visco-Elastic Simulations Against In Vitro Measurements,” J. Biomech., 44(12), pp. 2250–2258. 10.1016/j.jbiomech.2011.05.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11]. Huberts, W. , Bode, A. S. , Kroon, W. , Planken, R. N. , Huberts, J. H. M. , Bode, W. , Kroon, A. S. , Planken, W. , Tordoir, R. N. , J. H. M., van de Vosse, F. N. , and Bosboom, E. M. H. , 2012, “ A Pulse Wave Propagation Model to Support Decision-Making in Vascular Access Planning in the Clinic,” Med. Eng. Phys., 34(2), pp. 233–248. 10.1016/j.medengphy.2011.07.015 [DOI] [PubMed] [Google Scholar]
- [12]. Qureshi, M. U. , and Hill, N. A. , 2015, “ A Computational Study of Pressure Wave Reflections in the Pulmonary Arteries,” J. Math. Biol., 71(6), pp. 1525–1549. 10.1007/s00285-015-0867-2 [DOI] [PubMed] [Google Scholar]
- [13]. Raghu, R. , Vignon-Clementel, I., Figueroa, C., and Taylor, C., 2011, “ Comparative Study of Viscoelastic Arterial Wall Models in Nonlinear One-Dimensional Finite Element Simulations of Blood Flow,” ASME J. Biomech. Eng., 133, p. 081003. 10.1115/1.4004532 [DOI] [PubMed] [Google Scholar]
- [14]. Xiao, N. , Alastruey, J. , and Figueroa, C. , 2013, “ A Systematic Comparison Between 1-D and 3-D Hemodynamics in Compliant Arterial Models,” Int. J. Numer. Methods Biomed. Eng., 30(2), pp. 204–231. 10.1002/cnm.2598 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Vignon-Clementel, I. , Figueroa, C., Jansen, K., and Taylor, C., 2010, “ Outflow Boundary Conditions for 3D Simulations of Non-Periodic Blood Flow and Pressure Fields in Deformable Arteries,” Comput. Methods Biomech. Biomed. Eng., 13(5), pp. 625–640. 10.1080/10255840903413565 [DOI] [PubMed] [Google Scholar]
- [16]. Shi, Y. , Lawford, P. , and Hose, R. , 2011, “ Review of Zero-D and 1-D Models of Blood Flow in the Cardiovascular System,” Biomed. Eng. Online, 10, p. 33. 10.1186/1475-925X-10-33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Grinberg, L. , Cheever, E. , Anor, T. , Madsen, J. R. , and Karniadakis, G. E. , 2011, “ Modeling Blood Flow Circulation in Intracranial Arterial Networks: A Comparative 3D/1D Simulation Study,” Ann. Biomed. Eng., 39(1), pp. 297–309. 10.1007/s10439-010-0132-1 [DOI] [PubMed] [Google Scholar]
- [18]. Morris, P. D. , Narracott, A. , von Tengg-Kobligk, H. , Silva Soto, D. A. , Hsiao, S. , Lungu, A. , Evans, P. , Bressloff, N. W. , Lawford, P. V. , Hose, D. R. , and Gunn, J. P. , 2015, “ Computational Fluid Dynamics Modelling in Cardiovascular Medicine,” Heart, 102(1), pp. 1–11. 10.1136/heartjnl-2015-308044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Ismail, M. , Gravemeier, V. , Comerford, A. , and Wall, W. A. , 2014, “ A Stable Approach for Coupling Multidimensional Cardiovascular and Pulmonary Networks Based on a Novel Pressure-Flow Rate or Pressure-Only Neumann Boundary Condition Formulation,” Int. J. Numer. Methods Biomed. Eng., 30(4), pp. 447–469. 10.1002/cnm.2611 [DOI] [PubMed] [Google Scholar]
- [20]. Taelman, L. , Degroote, J. , Verdonck, P. , Vierendeels, J. , and Segers, P. , 2013, “ Modeling Hemodynamics in Vascular Networks Using a Geometrical Multiscale Approach: Numerical Aspects,” Ann. Biomed. Eng., 41(7), pp. 1445–1458. 10.1007/s10439-012-0717-y [DOI] [PubMed] [Google Scholar]
- [21]. Epstein, S. , Willemet, M. , Chowienczyk, P. J. , and Alastruey, J. , 2015, “ Reducing the Number of Parameters in 1D Arterial Blood Flow Modeling: Less is More for Patient-Specific Simulations,” Am. J. Physiol. Heart Circ. Physiol, 309(1), pp. H222–H234. 10.1152/ajpheart.00857.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22]. Lungu, A. , Wild, J. M. , Capener, D. , Kiely, D. G. , Swift, A. J. , and Hose, D. R. , 2014, “ MRI Model-Based Non-Invasive Differential Diagnosis in Pulmonary Hypertension,” J. Biomech., 47(12), pp. 2941–2947. 10.1016/j.jbiomech.2014.07.024 [DOI] [PubMed] [Google Scholar]
- [23]. Qureshi, M. U. , Vaughan, G. D. , Sainsbury, C. , Johnson, M. , Peskin, C. S. , Olufsen, M. S. , and Hill, N. A. , 2014, “ Numerical Simulation of Blood Flow and Pressure Drop in the Pulmonary Arterial and Venous Circulation,” Biomech. Model Mechanobiol., 13(5), pp. 1137–1154. 10.1007/s10237-014-0563-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24]. Chen, P. , Quarteroni, A. , and Rozza, G. , 2013, “ Simulation-Based Uncertainty Quantification of Human Arterial Network Hemodynamics,” Int. J. Numer. Methods Biomed. Eng., 29(6), pp. 698–721. 10.1002/cnm.2554 [DOI] [PubMed] [Google Scholar]
- [25]. Sankaran, S. , and Marsden, A. L. , 2011, “ A Stochastic Collocation Method for Uncertainty Quantification and Propagation in Cardiovascular Simulations,” ASME J. Biomech. Eng., 133(3), p. 031001. 10.1115/1.4003259 [DOI] [PubMed] [Google Scholar]
- [26]. Eck, V. G. , Feinberg, J. , Langtangen, H. P. , and Hellevik, L. R. , 2015, “ Stochastic Sensitivity Analysis for Timing and Amplitude of Pressure Waves in the Arterial System,” Int. J. Numer. Methods Biomed. Eng., 31(4), p. e02711. 10.1002/cnm.2711 [DOI] [PubMed] [Google Scholar]
- [27]. Formaggia, L. , Quarteroni, A. , and Veneziani, A. , 2009, Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System, Vol. 1, Springer, Milan, Italy. 10.1007/978-88-470-1152-6 [DOI] [Google Scholar]
- [28]. Steele, B. N. , Olufsen, M. S. , and Taylor, C. A. , 2007, “ Fractal Network Model for Simulating Abdominal and Lower Extremity Blood Flow During Rest and Exercise Conditions,” Comp. Methods Biomech. Biomed. Eng., 10(1), pp. 39–51. 10.1080/10255840601068638 [DOI] [PubMed] [Google Scholar]
- [29]. Ho, H. , Bartlett, A. , and Hunter, P. , 2011, “ Hemodynamic Simulation for an Anatomically Realistic Portal System,” Medical Image Computing and Computer-Assisted Intervention—MICCAI 2011, Fichtinger G., Martel A., and Peters T., eds., Springer, New York, pp. 347–354. 10.1007/978-3-642-23623-5_44 [DOI] [PubMed] [Google Scholar]
- [30]. Aslanidou, L. , Trachet, B. , Reymond, P. , Fraga-Silva, R. A. , Segers, P. , and Stergiopulos, N. , 2016, “ A 1D Model of the Arterial Circulation in Mice,” ALTEX, 33(1), pp. 13–28. 10.14573/altex.1507071 [DOI] [PubMed] [Google Scholar]
- [31]. Lee, P. , Carlson, B. E. , Chesler, N. , Olufsen, M. S. , Qureshi, M. U. , Smith, N. P. , Sochi, T. , and Beard, D. A. , 2016, “ Heterogeneous Mechanics of the Mouse Pulmonary Arterial Network,” Biomech. Model Mechanobiol., 15(5), pp. 1245–1261. 10.1007/s10237-015-0757-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32]. Moore, J. A. , Steinman, D. A. , and Ethier, C. R. , 1998, “ Computational Blood Flow Modelling: Errors Associated With Reconstructing Finite Element Models From Magnetic Resonance Images,” J. Biomech., 31(2), pp. 179–184. 10.1016/S0021-9290(97)00125-5 [DOI] [PubMed] [Google Scholar]
- [33]. Moore, J. A. , Steinman, D. A. , Holdsworth, D. W. , and Ethier, C. R. , 1999, “ Accuracy of Computational Hemodynamics in Complex Arterial Geometries Reconstructed From Magnetic Resonance Imaging,” Ann. Biomed. Eng., 27(1), pp. 32–41. 10.1114/1.163 [DOI] [PubMed] [Google Scholar]
- [34]. Bia, D. , Aguirre, I. , Zocalo, Y. , Devera, L. , Cabrera Fischer, E. , and Armentano, R. , 2005, “ Regional Differences in Viscosity, Elasticity, and Wall Buffering Function in Systemic Arteries: Pulse Wave Analysis of the Arterial Pressure-Diameter Relationship,” Rev. Esp. Cardiol., 58(2), pp. 167–174. 10.1157/13071891 [DOI] [PubMed] [Google Scholar]
- [35]. Bia, D. , Zocalo, Y. , Armentano, R. , de Forteza, E. , and Cabrera Fischer, E. , 2007, “ Acute Increase in Reversal Blood Flow During Counterpulsation is Associated With Vasoconstriction and Changes in the Aortic Mechanics,” 29th Annual International Conference of the IEEE EMBS, Lyon, France, Aug. 22–26, pp. 3986–3989. 10.1109/IEMBS.2007.4353207 [DOI] [PubMed] [Google Scholar]
- [36]. Schrauwen, J. T. C. , Koeze, D. J. , Wentzel, J. J. , van de Vosse, F. N. , van der Steen, A. F. W. , and Gijsen, F. J. H. , 2015, “ Fast and Accurate Pressure-Drop Prediction in Straightened Atherosclerotic Coronary Arteries,” Ann. Biomed. Eng., 43(1), pp. 59–67. 10.1007/s10439-014-1090-9 [DOI] [PubMed] [Google Scholar]
- [37]. Lighthill, J. , 1989, Mathematical Biofluiddynamics, 3rd ed., SIAM Regional Conference Series in Applied Mathematics, Philadelphia, PA. [Google Scholar]
- [38]. Stergiopulos, N. , Tardy, Y. , and Meister, J. J. , 1993, “ Nonlinear Separation of Forward and Backward Running Waves in Elastic Conduits,” J. Biomech., 26(2), pp. 201–209. 10.1016/0021-9290(93)90049-K [DOI] [PubMed] [Google Scholar]
- [39]. Pontrelli, G. , 2006, “ The Role of the Arterial Prestress in Blood Flow Dynamics,” Med. Eng. Phys., 28(1), pp. 6–12. 10.1016/j.medengphy.2005.04.013 [DOI] [PubMed] [Google Scholar]
- [40]. Reuderink, P. J. , Hoogstraten, H. W. , Sipkema, P. , Hillen, B. , and Westerhof, N. , 1989, “ Linear and Nonlinear One-Dimensional Models of Pulse Wave Transmission at High Womersley Numbers,” J. Biomech., 22(8–9), pp. 819–827. 10.1016/0021-9290(89)90065-1 [DOI] [PubMed] [Google Scholar]
- [41]. Perdikaris, P. , and Karniadakis, G. E. , 2014, “ Fractional-Order Viscoelasticity in One-Dimensional Blood Flow Models,” Ann. Biomed. Eng., 42(5), pp. 1012–1023. 10.1007/s10439-014-0970-3 [DOI] [PubMed] [Google Scholar]
- [42]. Valdez-Jasso, D. , D. Bia, Y. Zocalo, R.L. Armentano, M. A. Haider, and M. S. Olufsen, 2011, “ Linear and Nonlinear Viscoelastic Modeling of Aorta and Carotid Pressure-Area Dynamics Under In Vivo and Ex Vivo Conditions,” Ann. Biomed. Eng., 39(5), pp. 1438–1456. 10.1007/s10439-010-0236-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43]. Stankovic, Z. , Allen, B. D., Garcia, J., Jarvis, K. B., and Markl, M., 2014, “ 4D Flow Imaging With MRI,” Cardiovasc. Diagn. Ther., 4(2), pp. 173–192.http://cdt.amegroups.com/article/view/3630 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44]. McQueen, D. M. , and Peskin, C. S. , 2002, “ Heart Simulation by an Immersed Boundary Method With Formal Second-Order Accuracy and Reduced Numerical Viscosity,” 20th International Congress on Theoretical and Applied Mechanics, Mechanics for a New Millennium, Chicago, IL, Aug. 27–Sept. 2, Aref H., and Phillips J. W., eds., Springer, The Netherlands, pp. 429–444. 10.1007/0-306-46956-1_27 [DOI] [Google Scholar]
- [45]. Friman, O. , Hennemuth, A. , Harloff, A. , Bock, J. , Markl, M. , and Peitgen, H. O. , 2011, “ Probabilistic 4D Blood Flow Tracking and Uncertainty Estimation,” Med. Image Anal., 15(5), pp. 720–728. 10.1016/j.media.2011.06.002 [DOI] [PubMed] [Google Scholar]
- [46]. Cousins, W. , and Gremaud, P. A. , 2014, “ Impedance Boundary Conditions for General Transient Hemodynamics,” Int. J. Numer. Methods Biomed. Eng., 30(11), pp. 1294–1313. 10.1002/cnm.2658 [DOI] [PubMed] [Google Scholar]
- [47]. Perdikaris, P. , Grinberg, L. , and Karniadakis, G. E. , 2015, “ An Effective Fractal-Tree Closure Model for Simulating Blood Flow in Large Arterial Networks,” Ann. Biomed. Eng., 43(6), pp. 1432–1442. 10.1007/s10439-014-1221-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48]. Olufsen, M. , 1999, “ Structured Tree Outflow Condition for Blood Flow in Larger Systemic Arteries,” Am. J. Physiol., 276(1), pp. H257–H268.http://ajpheart.physiology.org/content/276/1/H257.short [DOI] [PubMed] [Google Scholar]
- [49]. Du, T. , Hu, D. , and Cai, D. , 2015, “ Outflow Boundary Conditions for Blood Flow in Arterial Trees,” PLoS One, 10(5), p. e0128597. 10.1371/journal.pone.0128597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50]. Reymond, P. , Vardoulis, O. , and Stergiopulos, N. , 2012, “ Generic and Patient-Specific Models of the Arterial Tree,” J. Clin. Monit. Comput., 26(5), pp. 375–382. 10.1007/s10877-012-9382-9 [DOI] [PubMed] [Google Scholar]
- [51]. Lee, V. S. , 2006, Cardiovascular MRI: Physical Principles to Practical Protocols, Lippincott Williams & Wilkins, Philadelphia, PA. [Google Scholar]
- [52]. Imholz, B. P. , Wieling, W. , van Montfrans, G. A. , and Wesseling, K. H. , 1998, “ Fifteen Years Experience With Finger Arterial Pressure Monitoring: Assessment of the Technology,” Cardiovasc. Res., 38(3), pp. 605–616. 10.1016/S0008-6363(98)00067-4 [DOI] [PubMed] [Google Scholar]
- [53]. Langwieser, N. , Prechtl, L. , Meidert, A. S. , Hapfelmeier, A. , Bradaric, C. , Ibrahim, T. , Laugwitz, K. L. , Schmid, R. M. , Wagner, J. Y. , and Saugel, B. , 1998, “ Radial Artery Applanation Tonometry for Continuous Noninvasive Arterial Blood Pressure Monitoring in the Cardiac Intensive Care Unit,” Clin. Res. Cardiol., 104(6), pp. 518–524. 10.1007/s00392-015-0816-5 [DOI] [PubMed] [Google Scholar]
- [54]. Jalonen, J. , 1997, “ Invasive Haemodynamic Monitoring: Concepts and Practical Approaches,” Ann. Med., 29(4), pp. 313–318. 10.3109/07853899708999354 [DOI] [PubMed] [Google Scholar]
- [55]. Lehman, L. W. , Saeed, M. , Talmor, D. , Mark, R. , and Malhotra, A. , 2013, “ Methods of Blood Pressure Measurement in the ICU,” Crit. Care Med., 41(4), pp. 34–40. 10.1097/CCM.0b013e318265ea46 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56]. Segers, P. , Stergiopulos, N. , Verdonck, P. , and Verhoeven, R. , “ Assessment of Distributed Arterial Network Models,” Med. Biol. Eng. Comput., 1997. 35(6), pp. 729–736. 10.1007/BF02510985 [DOI] [PubMed] [Google Scholar]
- [57]. Bessems, D. , Giannopapa, C. G. , Rutten, M. C. M. , and van de Vosse, F. N. , 2008, “ Experimental Validation of a Time-Domain-Based Wave Propagation Model of Blood Flow in Viscoelastic Vessels,” J. Biomech., 41(2), pp. 284–291. 10.1016/j.jbiomech.2007.09.014 [DOI] [PubMed] [Google Scholar]
- [58]. Nichols, W. W. , O'Rourke, M. F. , and Vlachopoulos, C. , 2011, Wave Reflections, in McDonald's Blood Flow in Arteries, CRC Press, Boca Raton, FL, pp. 195–224. [Google Scholar]
- [59]. Sankaran, S. , Grady, L. , and Taylor, C. A. , 2015, “ Impact of Geometric Uncertainty on Hemodynamic Simulations Using Machine Learning,” Comput. Methods Appl. Mech. Eng., 297, pp. 167–190. 10.1016/j.cma.2015.08.014 [DOI] [Google Scholar]
- [60]. Sankaran, S. , Kim, H. J. , Gilwoo, C. , and Taylor, C. A. , 2016, “ Uncertainty Quantification in Coronary Blood Flow Simulations: Impact of Geometry, Boundary Conditions and Blood Viscosity,” J. Biomech., 49(12), pp. 2540–2547. 10.1016/j.jbiomech.2016.01.002 [DOI] [PubMed] [Google Scholar]
- [61]. Xiu, D. , and Sherwin, S. J. , 2007, “ Parametric Uncertainty Analysis of Pulse Wave Propagation in a Model of a Human Arterial Network,” J. Comput. Phys., 226(2), pp. 1385–1407. 10.1016/j.jcp.2007.05.020 [DOI] [Google Scholar]
- [62]. Xiao, N. , 2014, “ Simulation of 3-D Blood Flow in the Full Systemic Arterial Tree and Computational Frameworks for Efficient Parameter Estimation,” Ph.D. dissertation, Stanford University, Stanford, CA. [Google Scholar]
- [63]. Eck, V. G. , Donders, W. P. , Sturdy, J. , Feinberg, J. , Delhaas, T. , Hellevik, L. R. , and Huberts, W. , 2016, “ A Guide to Uncertainty Quantification and Sensitivity Analysis for Cardiovascular Applications,” Int. J. Numer. Methods Biomed. Eng., 32(8), p. e02755. 10.1002/cnm.2755 [DOI] [PubMed] [Google Scholar]
- [64]. Schiavazzi, D. E. , Arbia, G. , Baker, C. , Hlavacek, A. M. , Hsia, T. Y. , Marsden, A. L. , Vignon-Clementel, I. E. , and Investigators, M. , 2016, “ Uncertainty Quantification in Virtual Surgery Hemodynamics Predictions for Single Ventricle Palliation,” Int. J. Numer. Methods Biomed. Eng., 32(3), p. e02737. 10.1002/cnm.2737 [DOI] [PubMed] [Google Scholar]
- [65]. Brault, A. , Dumas, L. , and Lucor, D. , 2015, “ Uncertainty Quantification of Inflow Boundary Conditions Effect on Pulse Wave Propagation in Human Arterial Network,” 4th International Conference on Computational and Mathematical Biomedical Engineering, Cachan, France, pp. 754–757. 10.1002/cnm.2859 [DOI] [PubMed]
- [66]. Brault, A. , Dumas, L. , and Lucor, D. , 2016, “ Uncertainty Quantification of Inflow Boundary Condition and Proximal Arterial Stiffness Coupled Effect on Pulse Wave Propagation in a Vascular Network,” Int. J. Numer. Methods Biomed. Eng., p. e02859. 10.1002/cnm.2859 [DOI] [PubMed]
- [67]. Calvetti, D. , and Somersalo, E. , 2007, Introduction to Bayesian Scientific Computing: Ten Lectures on Subjective Computing, Surveys and Tutorials in the Applied Mathematical Sciences, Springer, New York. [Google Scholar]
- [68]. Kaipio, J. P. , and Somersalo, E. , 2005, Statistical and Computational Inverse Problems, Springer, New York. [Google Scholar]
- [69]. Evensen, G. , 1994, “ Sequential Data Assimilation With a Nonlinear Quasi-Geostrophic Model Using Monte Carlo Methods to Forecast Error Statistics,” J. Geophys. Res., 99(C5), pp. 10143–10162. 10.1029/94JC00572 [DOI] [Google Scholar]
- [70]. Burgers, G. , van Leeuwen, P. J. , and Evensen, G. , 1998, “ Analysis Scheme in the Ensemble Kalman Filter,” Mon. Weather Rev, 126(6), pp. 1719–1724. [DOI] [Google Scholar]
- [71]. Majda, A. J. , Harlim, J. , and Gershgorin, B. , 2010, “ Mathematical Strategies for Filtering Turbulent Dynamical Systems,” Discrete Contin. Dyn. Syst., 27(2), pp. 441–486. 10.3934/dcds.2010.27.441 [DOI] [Google Scholar]
- [72]. Houtekamer, P. L. , Mitchell, H. L. , Pellerin, M. , Buehner, M. , Charron, M. , Spacek, L. , and Hansen, B. , 2005, “ Atmospheric Data Assimilation With an Ensemble Kalman Filter: Results With Real Observations,” Mon. Weather Rev., 133(3), pp. 604–620. 10.1175/MWR-2864.1 [DOI] [Google Scholar]
- [73]. Heidari, L. , Gervais, V. , Le Ravalec, M. , and Wackernagel, H. , 2013, “ History Matching of Petroleum Reservoir Models by the Ensemble Kalman Filter and Parameterization Methods,” Comput. Geosci., 55, pp. 84–95. 10.1016/j.cageo.2012.06.006 [DOI] [Google Scholar]
- [74]. Arnold, A. , Calvetti, D. , and Somersalo, E. , 2014, “ Parameter Estimation for Stiff Deterministic Dynamical Systems Via Ensemble Kalman Filter,” Inverse Probl., 30(10), p. 105008. 10.1088/0266-5611/30/10/105008 [DOI] [Google Scholar]
- [75]. Armentano, R. L. , Barra, J. G. , Pessana, F. M. , Craiem, D. O. , Graf, S. , Santana, D. B. , and Sanchez, R. A. , 2007, “ Smart Smooth Muscle Spring-Dampers. Smooth Muscle Smart Filtering Helps to More Efficiently Protect the Arterial Wall,” IEEE Eng. Med. Biol., 26(1), pp. 62–70. 10.1109/MEMB.2007.289123 [DOI] [PubMed] [Google Scholar]
- [76]. Valdez-Jasso, D. , Haider, M. A. , Banks, H. T. , Santana, D. B. , Zocalo German, Y. , Armentano, R. L. , and Olufsen, M. S. , 2009, “ Analysis of Viscoelastic Wall Properties in Ovine Arteries,” IEEE Trans. Biomed. Eng., 56(2), pp. 210–219. 10.1109/TBME.2008.2003093 [DOI] [PubMed] [Google Scholar]
- [77]. Battista, C. , 2015, “ Parameter Estimation of Viscoelastic Models in a 1-D Circulatory Network,” Ph.D. thesis, North Carolina State University, Raleigh, NC. [Google Scholar]
- [78]. Anliker, M. , Rockwell, R. L. , and Ogden, E. , 1971, “ Nonlinear Analysis of Flow Pulses and Shock Waves in Arteries,” Z. Agnew. Math. Phys., 22(3), pp. 563–581. 10.1007/BF01614000 [DOI] [Google Scholar]
- [79]. Arnold, A. , Calvetti, D. , and Somersalo, E. , 2013, “ Linear Multistep Methods, Particle Filtering and Sequential Monte Carlo,” Inverse Probl., 29(8), p. 085007. 10.1088/0266-5611/29/8/085007 [DOI] [Google Scholar]
- [80]. Langewouters, G. L. , Wesseling, K. H. , and Goedhard, W. J. A. , 1984, “ The Static Elastic Properties of 45 Human Thoracic and 20 Abdominal Aortas In Vitro and the Parameters of a New Model,” J. Biomech., 17(6), pp. 425–435. 10.1016/0021-9290(84)90034-4 [DOI] [PubMed] [Google Scholar]
- [81]. Hansen, P. C. , 1998, Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion (Mathematical Modeling and Computation), SIAM, Philadelphia, PA. 10.1137/1.9780898719697 [DOI] [Google Scholar]
- [82]. Aster, R. C. , Borchers, B. , and Thurber, C. H. , 2013, Parameter Estimation and Inverse Problems, 2nd ed., Academic Press, New York. [Google Scholar]
- [83]. Engl, H. W. , Hanke, M. , and Neubauer, A. , 2000, Regularization of Inverse Problems (Mathematics and Its Applications), Kluwer Academic Publishers, Boston, MA. [Google Scholar]
- [84]. Evensen, G. , 2009, “ The Ensemble Kalman Filter for Combined State and Parameter Estimation,” IEEE Control Syst. Mag., 29(3), pp. 83–104. 10.1109/MCS.2009.932223 [DOI] [Google Scholar]
- [85]. Moradkhani, H. , Sorooshian, S. , Gupta, H. V. , and Houser, P. R. , 2005, “ Dual State-Parameter Estimation of Hydrological Models Using Ensemble Kalman Filter,” Adv. Water Resour., 28(2), pp. 135–147. 10.1016/j.advwatres.2004.09.002 [DOI] [Google Scholar]
- [86]. Wen, X. H. , and Chen, W. H. , 2006, “ Real-Time Reservoir Updating Using Ensemble Kalman Filter: the Confirming Approach,” Soc. Pet. Eng. J, 11(4), pp. 431–442. 10.2118/92991-MS [DOI] [Google Scholar]
- [87]. Yang, X. , and Delsole, T. , 2009, “ Using the Ensemble Kalman Filter to Estimate Multiplicative Model Parameters,” Tellus, 61A(5), pp. 601–609. 10.1111/j.1600-0870.2009.00407.x [DOI] [Google Scholar]
- [88]. Ait-El-Fquih, B. , El Gharamti, M. , and Hoteit, I. , 2016, “ A Bayesian Consistent Dual Ensemble Kalman Filter for State-Parameter Estimation in Subsurface Hydrology,” Hydrol. Earth Syst. Sci., 20(8), pp. 3289–3307. 10.5194/hess-20-3289-2016 [DOI] [Google Scholar]


