Incorporating prior knowledge into regularized regression

Abstract

Motivation

Associated with genomic features like gene expression, methylation and genotypes, used in statistical modeling of health outcomes, there is a rich set of meta-features like functional annotations, pathway information and knowledge from previous studies, that can be used post hoc to facilitate the interpretation of a model. However, using this meta-feature information a priori rather than post hoc can yield improved prediction performance as well as enhanced model interpretation.

Results

We propose a new penalized regression approach that allows a priori integration of external meta-features. The method extends LASSO regression by incorporating individualized penalty parameters for each regression coefficient. The penalty parameters are, in turn, modeled as a log-linear function of the meta-features and are estimated from the data using an approximate empirical Bayes approach. Optimization of the marginal likelihood on which the empirical Bayes estimation is performed using a fast and stable majorization–minimization procedure. Through simulations, we show that the proposed regression with individualized penalties can outperform the standard LASSO in terms of both parameters estimation and prediction performance when the external data is informative. We further demonstrate our approach with applications to gene expression studies of bone density and breast cancer.

Availability and implementation

The methods have been implemented in the R package xtune freely available for download from https://cran.r-project.org/web/packages/xtune/index.html.

1 Introduction

Predicting outcomes based on genomic biomarkers, such as gene expression, methylation and genotypes, are becoming increasingly important for individualized risk assessment and treatment (Kamel and Al-Amodi, 2017). As an example, consider predicting mortality from breast cancer after surgical treatment based on gene expression profiles (Nuyten et al., 2006). Since genomic studies typically have more available features than subjects, a common approach to develop prediction models based on genomic features is to use regularized regression methods, which can handle high-dimensional data. In addition to regularization, sparsity inducing regression approaches, such as the LASSO can also perform feature selection. In the context of genomic studies, feature selection is critical for yielding interpretable models that provide insight into potential biological mechanisms and which can, in turn, facilitate adoption by practitioners. To enhance model interpretability, it is common to examine features selected in a model in relation to available information about gene function and previous studies. For example, analyses can be conducted to formally assess whether the selected features are enriched in particular metabolic pathways or gene ontology annotations. This kind of post hoc analysis relating genomic features to existing knowledge about them, hereafter referred to as genomic meta-features, can provide valuable biological insight and validation for a prediction model. In this article, we propose a new approach that exploits genomic meta-features a priori rather than post hoc, to improve prediction performance and feature selection, and to enhance the interpretability of models developed using penalized regression.

To incorporate meta-features into the model building process, our main idea is to use the penalty parameters in penalized regression as the instrument. Commonly, most regularized regression methods apply a single global penalty parameter to all regression coefficients, effectively treating all features or predictors equally in the model building process. This may result in over-shrinking of important coefficients and under-shrinking of unimportant ones, with a corresponding loss in prediction ability. We extend the standard LASSO regression to allow for penalty terms that depend on external meta-features. Specifically, rather than using a single penalty parameter to control the amount of shrinkage for all regression coefficients, our model allows each coefficient to have its own individual penalty parameter, which is, in turn, modeled as a log linear function of the meta-features. Some examples of prior knowledge include (i) gene function annotation from databases like the Gene Ontology Project (Ashburner et al., 2000); (ii) gene–disease co-occurrence scores from text-mining biomedical abstracts (Pletscher-Frankild et al., 2014; Rouillard et al., 2016); (iii) deleterious somatic mutations in the Catalogue of Somatic Mutations in Cancer (COSMIC) (Forbes et al., 2011). We focus on the LASSO penalty because of its widespread use but address potential extensions to other penalties in the discussion.

Previously, other variants of LASSO regression have been introduced to allow either coefficient-specific penalties or multiple tuning parameters. Yuan and Lin (2006) proposes group LASSO that extends LASSO to grouped predictors. The adaptive LASSO proposed by Zou (2006) also adjusts the penalty individually for each coefficient by using a vector of adaptive weights. The group LASSO applies only to grouping variables, and the adaptive LASSO uses pre-specified weights obtained from the initial estimate of the coefficients using the same data as the data used for regression. Neither of these approaches incorporates a general set of meta-features. Boulesteix et al. (2017) proposed the integrative LASSO with penalty factors method that assigns different penalty factors to different data modalities such as gene expression, methylation and copy number. They use cross-validation to choose the penalty parameters based on prediction performance. In practice, the number of different modalities they can allow is up to four, due to computational bottle-neck.

In addition to those above, several other methods have been proposed previously to make use of prior knowledge of the features. Tharmaratnam et al. (2016) suggests using biologic knowledge to derive a set of features that could replace the gene set by chosen by LASSO with minimal loss in predictive power. However, ‘experts’ are required to assess the importance of each gene. Tai and Pan (2007) partitions the features into groups and shrink the features of different groups by different magnitudes. Shrinkage for groups is considered fixed and arbitrary but is not data-dependent, and the use of an external dataset only provides information on the grouping of predictors. van de Wiel et al. (2016) proposes an adaptive group-regularized ridge regression that accounts for group structure as the group LASSO and allows group-specific penalties. However, the method requires partitioning of the features into different groups, and the external information is only used for guiding the partition. The approach proposed by Bergersen et al. (2011) is also in the form of the adaptive LASSO. Instead of constructing weights from the same data X and Y, they use the Spearman correlation coefficients or the ridge regression coefficients between the features X and external information as the penalty weights.

Our approach is distinguished from these methods in that (i) we adopt an empirical Bayes approach to estimate the hyperparameters instead of cross-validation, which allows us to estimate feature-specific tuning parameters; (ii) the magnitude of the penalty terms are modeled as a log-linear function of the external information and are estimated from a ‘second-level’ regression; (iii) our approach is not restricted to meta-features that define feature groupings but can handle meta-features of any type including quantitative ones.

2 Materials and methods

2.1 Model specification

We start by considering a standard linear regression model $Y=X\mathit{\beta }+$ϵ, where Y is the vector of observed responses for n subjects, X is an n × p matrix of genomic features, and ϵ represents independent errors with zero expectation and a common variance ${\sigma }^2$. The LASSO regression shrinks the regression coefficients by imposing a L₁ penalty on the sum of absolute value of regression coefficients (Tibshirani, 1996). The objective function of LASSO is:

$${\text{min}}_{\beta \in {\mathbb{R}}^p}\left\{\right||Y-X\beta |{|}_2^2+\lambda \sum _{j=1}^p\left|{\beta }_j\right|\}.$$ (1)

The tuning parameter λ controls the strength of regularization: with a larger value of λ, more regression coefficients β are shrunk toward zero. The choice of λ determines feature selection and is key to achieve good model performance.

Our method extends the objective function of LASSO to allow each coefficient β_j to have its own individual penalty parameter λ_j, which is in turn modeled as a log-linear function of the meta-features. The objective function of external information tuned (xtune) LASSO is:

$$\begin{array}{cc}{\text{min}}_{\beta \in {\mathrm{ℝ}}^p}\left\{\right||Y-X\beta & |{|}_2^2+\underset{j=1}{\overset{p}{\sum {\lambda }_j}}|{\beta }_j\left|\right\}\\ \mathit{\lambda }& =e^{Z\mathit{\alpha }}\end{array},$$ (2)

where $\mathit{\lambda }=({\lambda }_1,\dots ,{\lambda }_p)$ is a vector of tuning parameters, Z is the meta-feature data of dimension p × q, $\mathit{\alpha }$ is the second level coefficients of dimension $q\times 1$ that links external information Z to individual penalties $\mathit{\lambda }$. Note that the standard LASSO and the adaptive LASSO are two special cases of our model, corresponding to the case where Z is a single column of 1 s and Z the identity matrix of dimension p × p, respectively.

Fitting of xtune LASSO consists of two steps: (i) choose the penalty parameters vector $\mathit{\lambda }$ and (ii) estimate the regression coefficients $\mathit{\beta }$ given $\mathit{\lambda }$. The second step is easy to implement using standard softwares, such as the glmnet package in the R language (Friedman et al., 2010). For the first step, cross-validation is commonly used to select the single penalty parameter for standard lasso. However, with potentially a large number of penalty parameters to tune, cross-validation is not feasible for xtune LASSO. On the other hand, most penalized regression approaches have a Bayesian interpretation which provides a natural way to allow multiple tuning parameters and incorporate external information.

LASSO regression can be equivalently formulated as a Bayesian or random effects model where the coefficients are modeled with a double exponential (a.k.a. Laplace) prior distribution condition on ${\sigma }^2$ (Tibshirani, 1996). Assuming that the distribution of the response variable Y conditional on the regression coefficients $\mathit{\beta }$ and ${\sigma }^2$ follows a normal distribution, the LASSO coefficient estimates that solves Equation (1) can be equivalently characterized as the posterior mode, or maximum a posteriori (MAP) in a Bayesian model with the a double exponential prior distribution for $\mathit{\beta }$ conditional on ${\sigma }^2$. The regression coefficients $\mathit{\beta }$ that minimize the xtune LASSO objective function in Equation (2) is equivalent to the MAP estimator ${\mathit{\beta }}_{\mathit{MAP}}$ under the Bayesian formulation shown in Equation (3), which is conditional on ${\sigma }^2$. Therefore, we select the penalty parameter vector $\mathit{\lambda }$ for xtune LASSO in Equation (2) by estimating $\mathit{\lambda }$ as hyperparameters under the Bayesian formulation of xtune LASSO in Equation (3).

$$\begin{array}{cc}Y|X,\mathit{\beta }\hfill & \sim \mathcal{N}(X\mathit{\beta },{\sigma }^2{I}_n)\hfill \\ {\beta }_j|{\sigma }^2\hfill & \sim \text{Double} \text{Exponential}(0,\frac{{\lambda }_j}{2{\sigma }^2}),\hfill \\ \forall j=1,2,\mathrm{..},p\hfill \\ \mathit{\lambda }\hfill & =e^{Z\mathit{\alpha }}\hfill \end{array}.$$ (3)

The variance of the double exponential prior in the Bayesian formation of xtune LASSO in Equation (3) is $2/{\left(\frac{{\lambda }_j}{2{\sigma }^2}\right)}^2$. Thus, λ_j controls how far away from zero β_j can vary, i.e. the amount of shrinkage for coefficient β_j. A large λ_j implies a small β_j in magnitude. The hyperparameter α_k models in turn how the degree of shrinkage λ_j varies with the value of meta-feature k for feature k, z_kj. Specifically, because ${\lambda }_j=e^{{\alpha }_0}{e}^{{\sum }_{k=1}^q{\alpha }_k{z}_{jk}},\hspace{0.17em}{\lambda }_0=e^{{\alpha }_0}$ can be interpreted as the overall level of shrinkage across all regression coefficients. The hyperparameters ${\alpha }_{k,k>0}$ control the individual degree of shrinkage, above or below the overall level given by λ₀, that is applied to coefficient β_j. A positive α_k indicates that features with positive (negative) values of z_k should be shrunk more (less) relative to the overall level of shrinkage λ₀. Similarly, a negative α_k indicates that features with positive (negative) values of z_k should be shrunk less (more) relative to the overall level of shrinkage λ₀. A zero α_k indicates that meta-feature k does not affect the shrinkage of the regression coefficients. Thus, the hyperparameters α_k determine the importance of meta-feature k in determining the magnitude of the regression coefficients. The population variance parameter ${\sigma }^2$ can be estimated from the data or given a point-mass prior (Li and Lin, 2010). In this article, we estimate ${\sigma }^2$ using the method proposed by Reid et al. (2016) and assume it is ‘set in advance’. Park and Casella (2008) and Li and Lin (2010) used a specification that assigned a non-informative prior for ${\sigma }^2$ and used a Gibbs sampler based on full conditional distributions to obtain regression coefficients estimates. Our method is different in that, rather than extending the model to include Bayesian inference over the hyperparameters, we use an empirical Bayes approach that maximizes the log-likelihood of the hyperparameters. That is, the hyperparameters $\mathit{\alpha }$ are estimated from the data by first marginalizing over the coefficients β and then performing what is commonly referred to as empirical Bayes, evidence maximization or type-II maximum likelihood (Tipping, 2001).

2.2 Empirical Bayes parameter tuning

The empirical Bayes of hyperparameters $\mathit{\alpha }$ (hence $\mathit{\lambda }$) is obtained by maximizing the marginal likelihood calculated by integrating out the random effects $\mathit{\beta }$ from the joint distribution of Y and $\mathit{\beta }$. The marginal likelihood of $\mathit{\alpha }$ is given by:

$$\begin{array}{cc}L(\mathit{\alpha })\hfill & ={\int }_{{\mathbb{R}}^p}L(Y|X,\mathit{\beta })f(\mathit{\beta }|\mathit{\lambda }(\mathit{\alpha }))d\mathit{\beta }\hfill \\ \hfill & ={\int }_{{\mathbb{R}}^p}\mathcal{N}(Y|X\mathit{\beta },{\sigma }^2{I}_n)\text{Double} \text{Exponential}(\mathit{\beta }|0,\mathit{\alpha })d\mathit{\beta }\hfill \\ \hfill & ={\int }_{{\mathbb{R}}^p}\prod _{i=1}^n\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{{(Y_i-X_i\mathit{\beta })}^2}{2{\sigma }^2}}\prod _{j=1}^p\frac{\hspace{0.17em}\text{exp}(Z_j\alpha )}{4{\sigma }^2}{e}^{-\frac{\hspace{0.17em}\text{exp}(Z_j\alpha )}{2{\sigma }^2}\left|{\beta }_j\right|},\hfill \end{array}$$ (4)

When X is not orthogonal, the marginal likelihood resulting from the p-dimensional integral in Equation (4) does not have a usable closed-form solution. Foster et al. (2008) proposes using a Laplace approximation to the integral which has simple close-form solution. Motivated by their approach, we propose a simpler new approximation which uses a normal distribution with the same prior variance to approximate the double exponential distribution. That is, we use a normal distribution ${\beta }_j\sim \mathcal{N}(0,\frac{2}{{\tau }_j^2})$ to approximate the double exponential distribution ${\beta }_j\sim \text{Double} \text{Exponential}({\tau }_i)$, yields closed-form solution for the approximated marginal likelihood:

$$\begin{array}{cc}Y|X,\mathit{\beta }\hfill & \sim \mathcal{N}(X\mathit{\beta },I_n{\sigma }^2)\hfill \\ \mathit{\beta }\hfill & \sim \mathcal{N}(\mathit{0},{\mathit{V}}^{\mathit{-1}}),\hfill \end{array}$$ (5)

where $V=\text{diag}({\eta }_1,\dots {\eta }_p)=\text{diag}({\left(\frac{\mathit{\lambda }}{2{\sigma }^2}\right)}^2/2)$.

Therefore, the approximate log marginal negative likelihood of $\mathit{\alpha }$ integrating out $\mathit{\beta }$ is:

$$-\ell (\mathit{\alpha })=\text{log}\hspace{0.17em}\left|C_{\alpha }\right|+Y^T{C}_{\alpha }^{-1}Y$$ (6)

where $C_{\alpha }={\sigma }^{2}I+X{V}^{-1}{X}^T$. The approximated log likelihood (6) is then maximized to obtain $\mathit{\alpha }$ estimates. Once $\mathit{\alpha }$ known, hence the penalty parameters vector $\mathit{\lambda }$ known, the glmnet package in the R language is used to implement the LASSO with given penalty vector.

2.3 Marginal likelihood maximization

The objective function given by the negative marginal log-likelihood (Equation 6) is non-convex, making it intrinsically a challenging problem. We note that the approximated model (Equation 5) is closely related to the model specification of the Automatic Relevance Determination (ARD) (MacKay, 1992; Neal, 1995; Tipping, 2001) method widely used in the field of signal processing. Wipf and Nagarajan (2008, 2010) described a Majorization Minimization (MM) procedure that uses a reformulation of ARD to optimize the non-convex optimization function by solving a series of easier re-weighted L₁ problem. Motivated by their idea, we propose an iterative re-weighted L₂ optimization algorithm described in detail below. Note that this non-convex optimization problem is a special case of the difference of convex functions (DC) problem (Le Thi and Pham Dinh, 2018).

The log-determinate term $\text{log}\hspace{0.17em}\left|C_{\alpha }\right|$ is a concave function in $\mathit{\alpha }$ (Boyd and Vandenberghe, 2004). A majorization function of it is its slope at the current value α of $\text{log}\hspace{0.17em}\left|C_{\alpha }\right|$:

$$\mathit{\theta }={\nabla }_{\mathit{\alpha }}\hspace{0.17em}\text{log}\hspace{0.17em}\left|C_{\alpha }\right|=\text{diag}[X^T{C}_{\alpha }^{-1}X].$$ (7)

The $Y^T{C}_{\alpha }^{-1}Y$ term in Equation (6) is convex. Therefore, at current value of $\mathit{\alpha }$, the majorization function for $-\ell (\mathit{\alpha })$ is ${\ell }_{\mathit{\theta }}(\mathit{\alpha })\triangleq {\mathit{\theta }}^T\frac{1}{\eta }+Y^T{C}_{\alpha }^{-1}Y$. Given $\mathit{\theta },\hspace{0.17em}\mathit{\alpha }$ is updated by:

$$\mathit{\alpha }\leftarrow \underset{\alpha }{\text{argmin}}{\ell }_{\theta }(\alpha )\triangleq {\theta }^T\frac{1}{\eta }+Y^T{C}_{\alpha }^{-1}Y.$$ (8)

Although the objective function (Equation 8) is convex, it is slow to optimize in practice. We use one more MM procedure for optimizing (Equation 8). The data dependent term $Y^T{C}_{\alpha }^{-1}Y$ can be re-expressed as:

$$Y^T{C}_{\alpha }^{-1}Y=\underset{\delta }{\min }\frac{1}{{\sigma }^2}\left|\right|Y-X\delta |{|}^2+\sum _j{\delta }_j^2{\eta }_j.$$ (9)

We therefore introduce another auxiliary term δ, the upper-bounding auxiliary function for ${\ell }_{\mathit{\theta }}(\mathit{\alpha })$ is:

$${\ell }_{\theta }(\alpha ,\delta )\triangleq {\theta }^T\frac{1}{\eta }+\sum _j{\eta }_j{\delta }_j^2+\frac{1}{{\sigma }^2}\left|\right|Y-X\delta |{|}^2\ge {\ell }_{\theta }(\alpha ).$$ (10)

The $\mathit{\alpha }$ value that minimizes Equation (8) can be estimated by iteratively updating $\mathit{\delta }$ and $\mathit{\alpha }$ in Equation (10). For any $\mathit{\delta },\hspace{0.17em}\mathit{\alpha }$ is estimated by minimizing

$${\theta }^T\frac{1}{\eta }+\sum _j{\eta }_j{\delta }_j^2.$$ (11)

Given $\mathit{\alpha },\hspace{0.17em}\mathit{\delta }$ is updated by:

$$\delta \leftarrow \underset{\delta }{\text{argmin}}\left|\right|Y-X\delta |{|}^2+\sum _j{\eta }_j{\delta }_j^2.$$ (12)

Equation (12) has a weighted convex L₂ regularized cost function, and it can be optimized efficiently using glmnet. The iterative reweighed L₂ algorithm has the schema summarized in Algorithm 1. Simulations we conducted with continuous instead of binary meta-features yielded very similar results (data not shown).

Once the hyperparameters $\mathit{\alpha }$ are estimated, and therefore the penalties are known, the LASSO regression coefficients can be obtained using standard LASSO software (e.g. glmnet).

2.4 Extension to linear discriminant analysis for classification

So far, we have been focused on LASSO linear model where the response variable is continuous. Here, following the scheme proposed by Mai et al. (2012) that builds high dimensional linear discriminate analysis (LDA) upon sparse penalized linear regression, we extend the xtune LASSO model to the framework of LDA with a binary response variable $Y\in \{1,2\}$.

The LDA model assumes that X is normally distributed within each class, i.e.

$$\begin{array}{c}X|(Y=k)\sim \mathcal{N}({\mu }_k,\Sigma )\hfill \\ \text{Pr}(Y=k)={\pi }_k, k=1,2\hfill \end{array}$$

where μ_k is the mean of X within class k and Σ is the common within-class covariance matrix. We adopt the following procedure proposed by Mai et al. (2012) to predict the class of Y based on xtune LASSO linear penalized regression:

Step 1. Let $y_i=-\frac{n_1}{n}$ if Y _i = 1, and $y_i=\frac{n}{n_2}$ if $Y_2=2$.

Step 2. Compute the solution to a penalized least squares problem:

$$\begin{array}{c}({\widehat{\beta }}^{\text{LDA}},{\widehat{{\beta }_0}}^{\text{LDA}})=\underset{\beta ,{\beta }_0}{\text{argmin}}{n}^{-1}\sum _{i=1}^n{(y_i-{\beta }_0-x_i^T\beta )}^2+\sum _{j=1}^p{P}_{\lambda }({\beta }_j)\hfill \end{array}$$ (13)

Step 3. Estimate the LDA model on the reduced data ${\{Y_i,X_i^T{\widehat{\beta }}^{\text{LDA}}\}}_{i=1}^n$. Assign observation x to class 2 if

$$\begin{array}{cc}\{\hfill & x-({\widehat{\mu }}_1+{\widehat{\mu }}_2)/2{\}}^T{\widehat{\beta }}^{\text{LDA}}+{({\widehat{\beta }}^{\text{LDA}})}^T\widehat{\Sigma }{\widehat{\beta }}^{\text{LDA}}\hfill \\ \hfill & \{({\widehat{\mu }}_1-{\widehat{\mu }}_2{)}^T{\widehat{\beta }}^{\text{LDA}}{\}}^{-1}\hspace{0.17em}\text{log}(n_2/n_1)>0,\hfill \end{array}$$ (14)

where ${\widehat{\mu }}_1,n_1,{\widehat{\mu }}_2,n_2$ are the sample mean vector and sample size within class 1 and class 2, $\widehat{\Sigma }$ is the sample covariance matrix, $P_{\lambda }(.)$ is a generic sparsity-inducing regularization term, such as the single-penalty L₁ norm, Elastic-Net or adaptive L₁ norm in our case. We first solve Equation (13) using xtune LASSO, then predict response variable class by Equation (14).

3 Results

3.1 Simulation studies

3.1.1. Simulation setting

We performed a simulation study to evaluate the performance of the xtune LASSO under a range of scenarios obtained by varying the following key simulation parameters:

1. The true ability of the features to predict the outcome as measured by the signal to noise ratio (SNR) defined as $\text{Var}(X\mathit{\beta })/{\sigma }^2$.

2. The informativeness of the external metadata controlled by the number of non-zero hyperparameters α.

3. The number of predictor features p.

4. The sparsity level captured by the number of non-zero true regression coefficients $\mathit{\beta }$.

5. The overall magnitude of the non-zero entries of the true regression coefficient vector $\mathit{\beta }$ controlled by α₀.

6. The degree of correlation between features ρ.

The simulation data was generated according to the following steps: (i) set the parameter $\mathit{\alpha }$ controlling the informativeness of the external metadata; (ii) generate the external metadata matrix Z; (iii) generate the vector of regression coefficients $\mathit{\beta }$ based on $\mathit{\alpha }$ and Z; (iv) generate the feature data X; (v) generate outcome Y based on β, X and an independent drawn random error ϵ.

The external metadata matrix Z of dimension p × q was generated to have 0–1 entries indicating a grouping of features. Specifically, entry Z_jk indicates whether the jth feature belongs to group k (1) or not (0). The entries were independently generated to be zero or one with probability 0.2 and 0.8, respectively. A consequence of how Z was generated is that features can belong to more than one group, i.e. the groups can overlap. A column of 1 s was appended to Z corresponding to the second level intercept α₀, which controls the overall amount of shrinkage; the higher α₀; the smaller the regression coefficients.

The true regression coefficient β_j were generated by sampling from a double exponential distribution with local parameter μ = 0 and scale parameter $b=\text{exp}(Z_j\mathit{\alpha })$. Parameter δ controls the sparsity of the final $\mathit{\beta }$ vector. The $[p^{\delta }]$ largest βs in magnitude were retained, while all smaller entries were set to be zero. The feature matrix X was simulated by sampling from a multivariate normal distribution with mean vector zero and covariance matrix ${\Sigma }_{i,j}={\rho }^{|i-j|}$.

Finally, for each simulation replicate, an independent error term ϵ was sampled from a normal distribution with mean 0 and a variance corresponding to the pre-set SNR. The outcome was generated as $Y=X\mathit{\beta }+ϵ$. Each simulated data is split into a training set (n = 200) and a test set (n = 1000). The performance of the standard LASSO, adaptive LASSO and xtune LASSO were compared by the prediction R² computed on the test using the model fitted in the training set. The large test set guarantees that the generalization/test error was accurately estimated. Penalty parameter tuning for the standard LASSO was performed by 10-fold cross-validation. Implementation of adaptive LASSO utilizes the adalasso() function in the parcor R package. One hundred replicates were generated for each scenario.

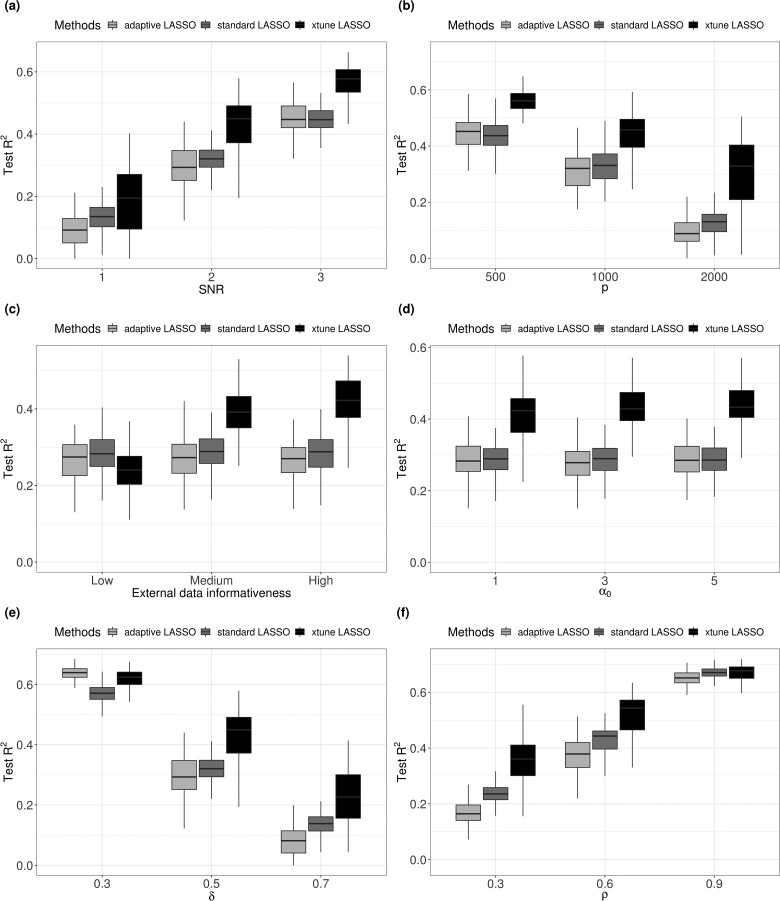
We considered the following six scenarios varying each of the main simulation parameters described above. The simulation results are summarized inFigure 1.

Fig. 1.

Simulation results. Subplot (a): SNR = 1, 2, 3, with n = 200, p = 1000, q = 10, ${\alpha }_0=3,\hspace{0.17em}\delta =0.5,\hspace{0.17em}\rho =0.2$. Subplot (b): p = 500, 1000, 3000, with n = 200, SNR = 2, q = 10, ${\alpha }_0=3,\hspace{0.17em}\delta =0.5,\hspace{0.17em}\rho =0.2$. Subplot (c): q = 10, 30, 50, with n = 200, p = 1000, SNR = 2, ${\alpha }_0=3,\hspace{0.17em}\delta =0.5,\hspace{0.17em}\rho =0.2$. Subplot (d): regression coefficients sparsity δ = $0.3,0.5,0.7$, with n = 200, p = 1000, SNR = 2, q = 10, ${\alpha }_0=3,\hspace{0.17em}\rho =0.2$. Subplot (e): overall penalty magnitude α₀ = 1, 3, 5, n = 200, p = 1000, SNR = 2, q = 10, $\delta =0.5,\hspace{0.17em}\rho =0.2$. Subplot (f): $\rho =0.3,0.6,0.9$, with n = 200, p = 1000, SNR = 2, q = 10, ${\alpha }_0=3,\hspace{0.17em}\delta =0.5$

1. $\mathit{SNR}=1,2,3$

2. $p=500,1000,3000$

3. External data informativeness: low, medium and high. We fixed the sub-set of the $\mathit{\alpha }=({\alpha }_0,-1,-0.78,-0.56,-0.33,-0.11,0.11,$  $0.33, 0.56,0.78,1).$The low external information is simulation from ${\alpha }_{\text{low}}=(\alpha ,\underset{60}{\underbrace{0,\dots ,0}})$. The medium external information is simulated from ${\alpha }_{\text{medium}}=(\alpha ,\underset{20}{\underbrace{0,\dots ,0}})$, and the high external information is simulated from ${\mathit{\alpha }}_{\text{high}}=\mathit{\alpha }$. The idea is that non-informative external information has many noise variables.

4. ${\alpha }_0=1,3,5$

5. $\delta =0.3,0.5,0.7$

6. Different correlation magnitude $\rho =0.3,0.6,0.9$

3.1.2. Simulation results

Figure 1a shows box plots (across simulation replicates) of the prediction R² for the standard, adaptive and xtune LASSO varying SNR. As SNR increases, the prediction performance increases for all methods, but the xtune LASSO has a better prediction accuracy across all levels of SNR considered.

When the p/n ratio gets higher, all three methods have decreased performance. However, xtune LASSO has a slower decreasing rate. When the p/n ratio is very high, we see that the performance of standard LASSO decreased dramatically, and xtune LASSO has significantly better prediction performance than standard LASSO (Fig. 1b). The R² for standard LASSO remain the same across different level of external data informativeness. The performance of xtune LASSO decreases with external information of lower informativeness (Fig. 1c).

Figure 1d shows the effect of decreased $\mathit{\beta }$ sparsity. The higher the value of δ, the less sparse the model and the more non-zero regression coefficients. The value of xtune LASSO becomes more apparent when the model is less sparse. With $\delta =0.5$, 31 out of 1000 features are non-zero. All three methods have decreased performance when the model has more non-zero features, but xtune LASSO has a slower decreasing rate. From Figure 1e, the overall amount of shrinkage seems to have little effect on the performance of all three methods. Notice that all three methods have a higher prediction ability when the signal features (non-zero) features are correlated with each other (Fig. 1f). The improved prediction of xtune LASSO over standard LASSO becomes smaller as the correlation between features increases. LASSO is known to have a decreased ability in variable selection when the features are highly correlated. It tends to select one variable from each highly correlated group and ignoring the remaining ones. Hebiri and Lederer (2013) studied the influence of correlation on LASSO prediction and suggested that correlation in features is not problematic for LASSO prediction; the prediction errors are mostly smaller for the correlated settings in experimental studies.

In summary, our simulation results showed that the LASSO with individual penalties informed by meta-features can outperform the standard LASSO in terms of prediction when (i) the meta-features are informative for the regression effect sizes, (ii) the true model is less sparse and (iii) the SNR is relatively high.

3.2 Applications

We exemplify the method’s performance on real data by considering two applications to clinical outcomes prediction using gene expression data.

3.2.1. Bone density data

In the first example, bone biopsies from 84 women were profiled using an expression microarray to study the relationship between bone mass density (BMD) and gene expression. The goal is to predict the total bone density based on the gene expression profiles. Bone density was measured by the hip T-score derived from biopsies, with a higher score indicating higher bone density. The data contains 22 815 gene expression features and were normalized using the RMA method as described in (Tharmaratnam et al., 2016). Gene expression levels were analyzed on a logarithmic-2 scale. The bone density dataset is publicly available from the European Bioinformatics Institute (EMBL-EBI) Array Expression repository ID E-MEXP-1618.

The external information consists of four covariates. The first covariate uses insights from a previous study that identified eight genes highly associated with bone density variation (Reppe et al., 2010). A binary external covariate indicates whether each gene is one of the eight genes identified or not. The second to fourth external covariates are evidence scores related to empirical P-values with continuous values that indicates the strength of functional annotations. They are extracted from the dbGAP Gene-Trait Associations dataset, GWASdb SNP-Phenotype Associations dataset and GWAS Catalog SNP-Phenotype Associations dataset (Li et al., 2012; Rouillard et al., 2016; Welter et al., 2013).

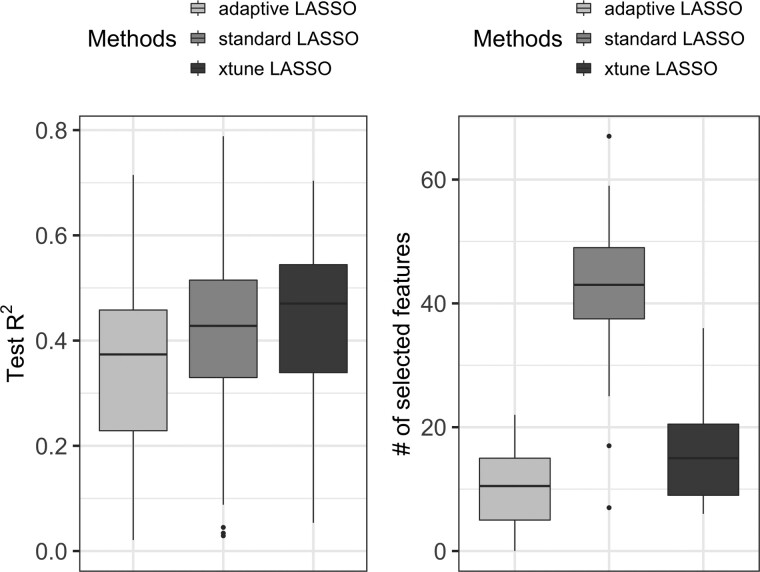
To illustrate the advantage of incorporating external information, we compare our proposed method to both standard LASSO and adaptive LASSO. The data were randomly split into a training data consisting of 80% of the observations and a test dataset consisting of 20% of the observations. We fitted the adaptive LASSO, standard LASSO, and our proposed method in the training data and evaluated their prediction performance in the testing data. We repeated 100 random splits of the full data into training and test sets. Figure 2 shows the MSE, R² and the number of selected (non-zero) expression features across the 100 splits.

Fig. 2.

Compare test R² and number of selected covariates of adaptive LASSO, standard LASSO and xtune LASSO using bone density data. The mean test R² is 0.27 for adaptive LASSO; 0.38 for the standard LASSO, and 0.43 for xtune LASSO. The mean number of selected covariates is 10 for adaptive LASSO, 43 for standard LASSO and 16 for the xtune LASSO

Overall, we see that the externally tuned LASSO has better prediction performance than the standard LASSO while selecting a more parsimonious model. The adaptive LASSO does not perform well in this data example. To gain further insight into the prediction performance results, we examined the penalties applied to the regression coefficients by each of the methods when fitted on the full data. The tuning parameter chosen by standard LASSO using cross-validation is 0.16, while for the xtune LASSO, the estimated tuning parameter is 0.26 for the gene expression features without external information and 0.016 for the expression features with external information, resulting in larger effects estimates for the latter group. The estimated α for the first external covariate is negative, which means the group of eight genes are penalized less than the genes not in this group. Among the identified genes, SOST and DKK1 are involved in the Wnt pathway which is central to bone turnover. ABCA8 and NIPSNAP3B are involved in transporting lipids across membranes and vesicular trafficking (Reppe et al., 2010).

3.2.2. Breast cancer data

In the second example, we apply the xtune LASSO to a breast cancer dataset. The data is from the Molecular Taxonomy of Breast Cancer International Consortium (METABRIC) cohort (Curtis et al., 2012) (https://ega-archive.org/dacs/EGAC00001000484). 29 476 gene expression profiles and three clinical variables (age at diagnosis, progesterone receptor status and lymph node status) were used for the prediction of five-year survival (survived or died). Patients followed-up for less than five years, with no record of mortality, were excluded from the analysis. We used a subset of the METABRIC data with patients that are Estrogen receptor (ER) positive and human epidermal growth factor receptor 2 (HER2) status negative. The data contains a discovery set of 594 observations and an additional validation set of 564 observations. The models were trained in the discovery set and tested on the validation set.

The external information used for the xtune LASSO model consists of six covariates. The first covariates is a binary variable indicating whether a predictor in X is a clinical feature (1) or a gene expression feature (0). The second covariate is a continuous variable with evidence scores for genes co-occurring with the breast cancer in abstracts of biomedical publications from the DISEASES Text-mining Gene–Disease Association Evidence Scores dataset (Pletscher-Frankild et al., 2014). The third covariate has count values for the number of times that each gene is used as one of major prognostic signatures for breast cancer. More specifically, breast cancer multigene prognostic signatures including OncotypeDX (21 genes), MammaPrint (70 genes), PAM50 (50 genes), EndoPredict (12 genes) and Breast Cancer Index (7 genes) have been validated through clinical trials and are recommended for classification, prognosis and prediction in breast cancer. We therefore believe genes that belong to one or more prognostic signatures are potentially more important than other genes. The frequency that each gene belongs to one of breast cancer prognostic signatures is used as the third external covariate. The fourth to sixth external covariates are based on the results of (Cheng et al., 2013), where groups of genes referred to as ‘metagenes’ that are prognostic in all cancers, including breast cancer were identified. In specific, (Cheng et al., 2013) analyzed six gene expression datasets from different cancer types and present three multi-cancer attractors with strong phenotype associations: a lymphocyte-specific attractor (LYM), a mesenchymal transition attractor strongly associated with tumor stage (MES), and a mitotic chromosomal instability attractor strongly associated with tumor grade (CIN). The LYM, MES and CIN metagenes consist of 169, 134 and 108 genes, respectively. The fourth to sixth external covariates are binary variables to indicate whether or not each gene belong to LYM, MES and CIN respectively.

We compared the xtune LASSO incorporating the meta-features described above, with the standard and the adaptive LASSO. As in the first example, standard LASSO was tuned by repeated 10 fold cross-validation and the adaptive LASSO is implemented using the adalasso() function in the parcor R package.

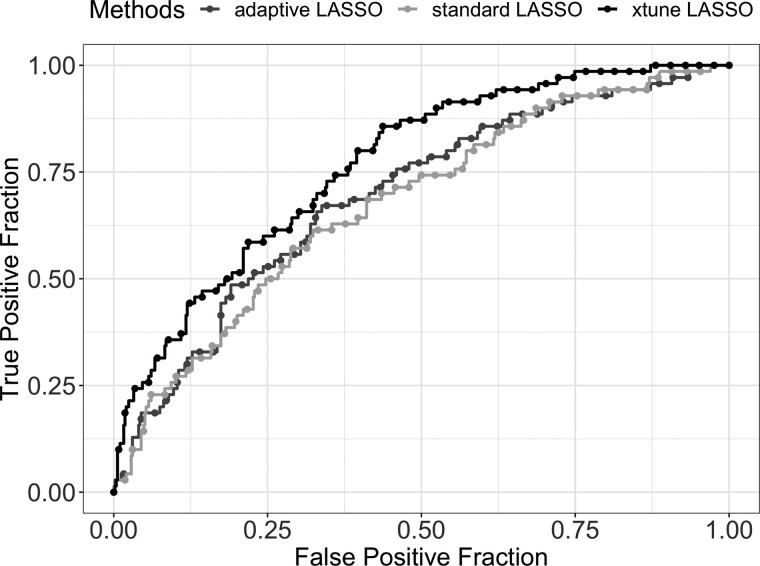
Table 1 compares the AUC, the number of selected features, and the computation time for the standard, the adaptive and the xtune LASSO. Figure 3 shows the receiver operating characteristic (ROC) curves for the three methods. The xtune LASSO has the best prediction performance among all three methods. The second level coefficients $\mathit{\alpha }$ estimated by xtune LASSO is $\mathit{\alpha }=(7.23,-4.55,-0.57,-0.13,-1.42,-0.47,-1.38)$. This illustrates how the xtune LASSO can induce differential shrinkage among the features according to their empirical importance. In this example, the three clinical variables are given a very small penalty in xtune LASSO and are all estimated to be non-zero. The xtune LASSO shrinks the coefficients corresponding to expression features that do not belong to any metagene (the vast majority) toward zero much more aggressively than the standard LASSO, while it shrinks the clinical variables and the expression features in metagenes LYM and MES much less than the standard LASSO. The standard LASSO shrink the coefficients for the two clinical variables to 0, effectively selecting them out of the model. Adaptive LASSO selected out one of the clinical variables (lymph node status). In agreement with our simulation results, the xtune LASSO also yielded a much more parsimonious model with only 13 selected features, while the standard LASSO selected 207 features. In terms of computation time, both adaptive LASSO (fitted using adalasso function) and xtune LASSO take more computation time than the standard LASSO fitted using glmnet.

Table 1.

Compare AUC, number of selected covariates and computation time (in minutes) for standard LASSO, adaptive LASSO and xtune LASSO

	Standard LASSO	Adaptive LASSO	xtune LASSO
AUC	0.677	0.718	0.767
No. of selected covariates	207	5	13
Computation time	2.26	39.28	11.00

Fig. 3.

ROC curves for adaptive LASSO, standard LASSO and xtune LASSO applied to the breast cancer dataset

4 Discussion

We introduced xtune LASSO, a new approach implemented in the namesake R package (Zeng and Lewinger, 2019) for integrating external meta-features to inform the tuning of penalty parameters in LASSO regression. We showed through simulation and real data examples that xtune could yield better prediction performance than standard LASSO by incorporating prior knowledge. These findings are consistent with the work of (van de Wiel et al., 2016), which proposed a method for estimating group-specific penalties for ridge regression and showed that the use of prior knowledge could improve prediction performance.

xtune LASSO differs from related methods (Boulesteix et al., 2017; Liu et al., 2018; Pan et al., 2010) in our use of an empirical Bayes approach to estimate the penalty parameters, rather than relying on cross-validation. In the particular case of no external meta-features (i.e. Z is a vector of 1 s), xtune performs empirical Bayes tuning of the single LASSO penalty parameter, providing an alternative to standard tuning by cross-validation. Cross-validation becomes impractical with more than a handful of penalty parameters, while empirical Bayes tuning allows xtune to handle a much larger number of individualized penalties.

The empirical Bayes approach in this article estimates the individual variances of the first-level regression coefficients by maximizing the marginal likelihood. This is also known as Type II maximum likelihood estimation, which has been employed for fitting the relevance vector machine model, a popular technique in the pattern recognition machine learning community. Instead of relying on cross-validation, the ‘Bayesian’ set-up has distinct advantages in terms of the penalty parameter choice by marginalizing them over the posterior distribution (Bhattacharya et al., 2014). Bayesian penalization methods (Li and Lin, 2010; Park and Casella, 2008) also have employed this connection and use hierarchical models to select the penalty parameter based on sampling strategies. A similar empirical Bayes approach has also been used by the penalized regression methods implemented in the EBglmnet R package (Huang and Liu, 2016). However, these methods do not incorporate information from external covariates, which is the main goal of this article.

An MM algorithm is used to minimize the non-convex objective function (6). While there may be multiple local minima to (6), we did not encounter multi-modality issues in the analyses described in the manuscript. The same estimates are obtained for different initial starting values of $\mathit{\alpha }$. In sensitivity analysis, we also tried directly optimizing the non-convex objective function (6) using standard methods (EM algorithm, gradient descent, L-BFGS algorithm), the same hyperparameter estimates are obtained but the MM algorithm is much faster than the other methods.

In both of our real data application examples, the meta-features are combination of continuous variables and categorical variables that group features into subsets. A categorical meta-feature also arises when the features originate from different data types (e.g. gene expression, methylation, somatic mutations). (Liu et al., 2018) showed that having separate penalty parameters for each data type can yield better prediction performance.

The gain in prediction performance in the proposed model depends to the relevance of the external information that is used to guide the penalization. The external information is relevant or ‘informative’ if it can help differentiate groups of predictors of different effect size or correlates with the importance of the predictors. Therefore, expert knowledge of the study domain is often crucial. A question that we have not addressed in the article is the how to decide whether the inclusion of an external covariate would be helpful before they are included in the model. In practice, the use of xtune LASSO is more demanding than the use of the standard LASSO as it requires more time and thought on the extraction, processing and interpretation of the external information. On the other hand, however, the process of finding and understanding external information about the predictors can help the investigators better understand the predictors, rather than fitting the model as a ‘black box’. We do not seek to claim that our approach always give a better performance as compared to standard LASSO or other related methods. Rather, we provides a way to integrate prior knowledge into the model building process and show that is quite competitive, especially on larger datasets and the meta-features are informative.

Although prediction performance has been our main focus of interest, our results also show that for the range of simulation scenarios we considered and in the two real data applications, xtune tends to yields sparser and, therefore, more interpretable models than standard LASSO regression. However, we did note that when the number of meta-features q relative to the sample size n is large, the $\mathit{\alpha }$ estimates may not be stable. A related limitation is that in its current implementation, xtune does not scale to ultra high dimensional datasets. Typical datasets that xtune LASSO can currently handle have sample size of up to $n\approx 5000$, with p ≈ 50 000 features and $q\approx 100$ meta-features. However, we believe that future algorithmic improvements, along with parallel computing, can extend the applicability of xtune to larger datasets and larger numbers of meta-features. To further widen the range of applicability of xtune, we are pursuing extensions to binary (logistic regression) and time to event (Cox regression) outcomes, as well as the incorporation of the Ridge and Elastic-Net penalties in addition to the LASSO.

Funding

This work was supported by the National Cancer Institute at the National Institutes of Health [P01 CA196569, R01 CA140561].

Conflict of Interest: none declared.