Characteristics of the Deconvolved Transient AEP from 80 Hz Steady-State Responses to Amplitude Modulation Stimulation

Abstract

This study aimed to validate the existence and investigate the characteristics of the transient responses from conventional auditory steady-state responses (ASSRs) using deconvolution methods capable of dealing with amplitude modulated (AM) stimulation. Conventional ASSRs to seven stimulus rates were recorded from 17 participants. A deconvolution method was selected and modified to accommodate the AM stimulation. The calculated responses were examined in terms of temporal features with respect to different combinations of stimulus rates. Stable transient responses consisting of early stage brainstem responses and middle latency responses were reconstructed consistently for all rate combinations, which indicates that the superposition hypothesis is applicable to the generation of approximately 80 Hz ASSRs evoked by AM tones (AM-ASSRs). The new transient responses are characterized by three pairs of peak-troughs named as n₀p₀, n₁p₁, and n₂p₂ within 40 ms. Compared with conventional ABR-MLRs, the n₀p₀ indicates the first neural activity where p₀ might represent the main ABR components; the n₁ is the counterpart of N10; the p₂ is corresponding to the robust Pa at about 30 ms; the p₁ and n₂ are absent of real counterparts. The peak–peak amplitudes show a slight decrease with increasing stimulation rate from 75 to 95 Hz whereas the peak latencies change differently, which is consistent with the known rate-effect on AEPs. This is direct evidence for a transient response derived from AM-ASSRs for the first time. The characteristic components offer insight into the constitution of AM-ASSRs and may be promising in clinical applications and fundamental studies.

INTRODUCTION

To extract transient auditory evoked potentials (tAEPs) using ensemble averaging techniques, the stimulus repetition rate must be restricted with adequate silencing that allows the rise and fall of the desired tAEP components. Therefore, the theoretical silent period defined by the interstimulus interval (ISI) should be larger than the full length of the tAEP to avoid overlaps among tAEP waves in response to adjacent stimuli. Such overlapping responses are typically referred to as the auditory steady-state response (ASSR), where the fundamental frequency of the ASSR is the same as the stimulus rate, or the reciprocal of the ISI. This is called the linear superimposition model, which relates ASSRs to the underlying tAEPs as indicated early in (Galambos, 1981 #17) Galambos et al. (1981) and supported by more recent reports (e.g., Burkard et al. 2017; Guérin-Dugué et al. 2018). In addition, the linear characteristics for single units of auditory cortex were also reported using frequency modulated stimuli with ripple spectral profiles (Kowalski et al. 1996a, b).

The linear superimposition can be represented by a linear convolution operation between the stimulus sequence and the unknown transient response (i.e., the tAEP associated with the stimulation unit). Various deconvolution methods were proposed to resolve the tAEP to obtain more temporal information by analyzing its morphological contents (e.g., Delgado and Özdamar 2004; Jewett et al. 2004). The first method employing the unique mathematical properties of the maximum length sequence (MLS) was applied to a number of experiments to restore the auditory brainstem response (ABR) with high rates (Burkard et al. 2017; Eysholdt and Schreiner 1982). To address some limitations with MLS, a new method called continuous loop averaging deconvolution (CLAD) was proposed and applied to restore ABRs and middle latency responses (MLRs) in various fundamental and clinical studies (Alhussaini et al. 2018; Bohórquez and Özdamar 2008; McNeer et al. 2009).

The rationale behind the deconvolution method is to design appropriate stimulus sequences capable of producing the responses containing adequate information to perform the deconvolution. Thus, most methods adopt varying ISIs within one stimulus sequence (e.g., Burkard et al. 2018; Valderrama et al. 2014). Rather than ASSRs produced by conventional periodic stimuli, this jittering sequence will produce responses with irregular overlaps to make the deconvolution computation possible. However, this may compromise the ASSR recordings because the calculated response representing the tAEP could be affected not only by the rate under investigation but also by the existence of ISI-jitter, as indicated in Tan et al. (2016; 2017). Furthermore, the use of a jittering sequence is convenient for transient stimulation elements — such as a click or tone burst — with a substantial silence period in between. However, it is difficult to make a jittering sequence fit with a routine protocol in ASSR acquisition using an oscillating stimulation such as an amplitude modulated (AM) tone.

This problem can now be addressed by a different method called multirate steady-state averaging deconvolution (MSAD) proposed in Wang et al. (2013). This method is capable of reconstructing a tAEP from several conventional ASSRs with slightly different stimulation rates. In other words, the MSAD adopts a rate-jittering sequencing strategy to accommodate more flexible stimulation configurations, thus allowing the study of deriving possible tAEP components from the ASSRs to the AM stimulation. Previous studies have shown that MSAD can reliably estimate tAEPs at high stimulation rates using transient sound stimulus elements, for example, tAEPs evoked by clicks at a 40 Hz stimulation rate (Tan et al. 2016; 2017). These click-tAEPs contained clear components that exist in ABRs and MLRs compared with the conventional low-rate AEPs and click-tAEPs at 40 Hz reconstructed by other methods (Özdamar et al. 2007).

ASSRs elicited by AM tones (AM-ASSRs for short) can specify the extent of frequency discrimination in hearing, a technique commonly used in the clinic. To date, there has been no attempt to retrieve the transient responses from AM-ASSRs (AM-tAEPs for short). This study thus has two goals: (1) to verify the existence of the tAEP underlying the AM-ASSR and identify the characteristic components according to the accumulated knowledge on tAEPs, (2) to investigate the consistency of the calculated AM-tAEPs by means of the combination of ASSRs to different stimulation rates. Because the 80 Hz-ASSR is a common clinical tool, we recorded AM-ASSRs to stimuli at rates between 70 and 100 Hz from healthy adults and attempted to reconstruct the underlying AM-tAEPs from different rate combinations of ASSRs using MSAD. The characteristic components of AM-tAEPs were identified and analyzed with respect to the rate combinations of ASSRs.

METHODS

Participants

Seventeen right-handed healthy young subjects (average age of 22.35 ± 1.46, seven females) participated in the experiment. Audiometric thresholds for all subjects were lower than 25 dB HL (obtained via air conduction pure tones at frequencies from 0.25 to 8 kHz). The experiment was approved by the human research ethics committee of Southern Medical University (No. 2015-KYLL-004), and corresponding informed consent forms were signed by every participant prior to the experiment.

The MSAD Method

According to the linear superposition generation theory of ASSRs, an ASSR is an overlapping response of the tAEPs associated with the acoustic stimulus element presented at a rapid rate. The profile of a conventional stimulus element — for instance, a click or tone-burst — consists of a burst of transient acoustic energy concentrated over a short duration with respect to the silent intervals in-between stimuli. Thus, the occurrence of stimulus elements is intuitively represented by a train of impulses called a stimulus sequence, which functions as an input to a system that outputs the ASSR. The digital version of this impulse train is represented by a binary sequence such as s(t) = {1, 0, 0, …, 1, 0, 0, …}, where 1 s represent the onset of a stimulus burst and 0 s represent the ISI (or the rate of stimulation) associated with no stimulation. A generic model for this dynamic can be characterized by a convolving process under an approximately linear assumption for the system:

$$y\left(t\right)=s\left(t\right)\ast x\left(t\right)$$ 1

where the output ASSR, denoted by y(t), is the convolution of the stimulus sequence s(t) and an unknown variable x(t) (* denotes the convolution operation). In this model, x(t) represents the transient response tAEP that characterizes the auditory system. The characteristics of such a living system in the early stage are heavily dependent on the stimulation, mainly including the profile of the sound element and the rate of the stimulus sequence. Therefore, in this model, we use a binary stimulus sequence to represent the occurrence of the stimulus elements irrespective of the profile of the sound elements.

Figure 1 illustrates an example of the MSAD process for AM stimulation. In this case, we define a modulation cycle of AM tone as an acoustic stimulation element with a symmetrical bell-shaped profile (1st row in 1st column). The AM tone can then be regarded as this acoustic stimulation element presented at the modulation rate. Similar to click or tone-burst stimulation sequences, we defined the 1 s as the onset of the acoustic stimulation element, and 0 s represent the bell-shaped period for the acoustic stimulation element. In this way, for an AM stimulation of any rate (or ISI_i, i = 1, 2, …, N), the binary sequence s_i, i = 1, 2, …, N, is illustrated by a train of circles, in which the solid circles represent the 1 s, and the open circles represent the 0 s (1st column).

Fig. 1.

Diagram of the MSAD process. The AM tones at specific modulation rates (represented by 1/ISI) are characterized by stimulus sequences s_i, i = 1, 2, …, N. The convolution matrix h₁ is constructed by using a number of successively time-delayed versions of s₁. Its number of columns and rows are equal to the length of the AM-tAEP x and the period of s₁, respectively. Then, several one-cycle ASSRs y_i in response to AM tones and the corresponding h_i can be spliced to form the multirate ASSR y and H, respectively. Various rate combination modes can be adopted. The corresponding AM-tAEP x can be estimated based on the available y and H through inverse transform

Therefore, the structure of the sequence is the same as the click-stimulation developed for MSAD (Wang et al. 2013), and in the same way, the matrix h_i (i = 1, 2, …, N) with reference to a stimulus sequence can be generated to equivalently describe the convolution process of (1). As an example, each row of matrix h₁ represents a successively time-delayed version of s₁. Note that each digit in h_i actually represents a time gap according to the sampling rate of the recording system. The size of h_i is determined by the length estimated for x, which must be truncated as the transient response decreases, and the height of h_i is determined by the ISI at a specific rate of stimulation (Fig. 1). Thus, using convolution matrix h_i, (1) can be rewritten in matrix form as

$$y_i={\mathbf{h}}_{i}x$$ 2

where y_i is a column vector representing a period of the observed ASSR at stimulation rate of 1/ISI_i (2nd column in Fig. 1); x denotes the underlying AM-tAEP to be solved which was assumed to almost invariable with respect to the stimulus rates within a limited extend (4th column in Fig. 1).

Since the solution to (2) does not exist for an ill-conditioned h_i, a practical extension of the convolution matrix was therefore proposed by defining H = [h₁^T, h₂^T, …, h_N^T]^T, which employs multiple ASSRs to stimuli of different rates, so that (2) becomes

$$y=\mathbf{H}x$$ 3

where y = [y₁^T, y₁^T, …, y_N^T]^T is a spliced multirate ASSR (3rd column in Fig. 1). This is a linear transform that offers a way to estimate x through inverse transform. However, the estimation of x from (3) is often ill-posed in the sense that recording noise/artifacts may give rise to a heavily unstable solution, which can be alleviated by regularization techniques as in Hansen (1987) and Wang et al. (2013). That is, in practice, (3) should be

$$y=\mathbf{H}x+n$$ 4

where n denotes the recording noise/artifacts. The estimation of x should then be

$$\widehat{x}={\mathbf{H}}^{-1}y=x+{\mathbf{H}}^{-1}n$$ 5

where the error H⁻¹n can be mitigated by a mathematical tool called singular value decomposition (SVD) combined with Tikhonov regularization (Wang et al. 2013). Thus, the estimation of x becomes

$$\widehat{x}={\left({\mathbf{H}}^{\mathbf{T}},\mathbf{H},+,\beta ,\mathbf{I}\right)}^{-1}{\mathbf{H}}^{\mathbf{T}}y$$ 6

where I is a unit matrix; β is the regularization parameter that determines the threshold level for truncated SVD filter and its valid value can be obtained according to a convenient graphical tool called L-curve (Wang et al. 2013).

Another problem that needs to be addressed is how to select the rate for each ASSR stimulation sequence, which is closely associated with the singularity of H and the known information used to solve x. To date, there is no theory guiding this selection. Therefore, we try different rate combinations to investigate the stability of x. We collected seven ASSRs to stimuli presented at rates between 70 and 100 Hz. We can then select at least 3 ASSRs, say {y₁, y₂, y₃}, and the corresponding {h₁, h₂, h₃} to estimate x. Other combinations of y_i and h_i can be tested as well to verify the solution (3rd column in Fig. 1). As the results show, ASSRs at three different modulation rates can be spliced to extract a reliable tAEP. In addition, the small jitter among these modulation rates may lead to more realistic tAEP at the mean modulation rates.

Stimulation

The stimulation consisted of seven trains of continuous AM pure tones with a 2500 Hz carrier separately modulated at 70–100 Hz in steps of 5 Hz, i.e., {70.42, 75.47, 80.32, 85.47, 90.30, 95.69, 100.50} Hz and 100 % modulation depth. An example of an AM tone is shown in the left-up corner of Fig. 1, in which the minimum value (zero) was defined as the onset of an AM element, which corresponds to modulation cycle in an AM tone sequence.

EEG Recording

The experiment was conducted in a sound-attenuated and electromagnetic-shielded booth. The participant was instructed to recline comfortably in a chair and ignore the sound stimulus that was monaurally presented to the right ear via an insert earphone (ER-3A Ethmotic Research, Elk Grove Village, IL, USA) at 79.1 dB peak SPL (calibrated in a 2-cc HA2 acoustic coupler using the sound level meter). The electroencephalograph (EEG) recordings were collected via SynAmps² amplifiers (Compumedics Ltd, Victoria, Australia) from three Ag/AgCl electrodes (Fz: input, M2: reference, Fpz: ground). The electrode sites were lightly abraded with scrubbing cream and cleaned with 75 % alcohol to decrease the contact impedance, which was kept at less than 5 kΩ during recording. The amplifier settings were 10⁵ for the amplification gain, 30–1000 Hz bandpass filter, and 20 kHz analog-to-digital rate. The EEGs were recorded in response to the AM tones, for which the modulation frequency was selected randomly to produce a recording run that contained more than 4500 AM elements. Each modulation frequency was presented in two repeated runs for each participant.

Data Processing and Analysis

The raw EEG data were exported to MATLAB (version R2017b; MathWorks Inc., Natick, MA, USA) for offline processing. The raw data were first segmented into epochs according to the onsets of the AM elements. A few epochs at the onset and offset of the AM stimulation were excluded from the data set, and epochs with amplitudes larger than 40 μV were also rejected. No less than 8100 epochs of EEGs for each modulation frequency in two recording runs remained in the subsequent analysis.

A mono-rate ASSR in the time domain was obtained by ensemble averaging over approximately 2700 EEG sweeps. Each sweep contains three epochs, which yields a three-cycle ASSR waveform to evaluate the recording. Three subjects were excluded from subsequent analysis due to poor quality responses. Fast Fourier transformation was performed on the three-cycle ASSRs for the subsequent frequency analysis. In the deconvolution calculation performed on the multirate ASSR, the selected three-cycle mono-rate ASSRs were averaged again to obtain a one-cycle ASSR to further enhance the signal-to-noise ratio (SNR).

As previously indicated, ASSRs to stimuli of different rates were combined to estimate the AM-tAEP. Table 1 lists the 15 combinations of available stimulation rates examined in this study. The criterion for selecting the combinations out of seven available rates is to minimize the rate-jitter (i.e., the maximum rate difference in a combination), which is equivalent to keeping the rate increment to 5 Hz in a combination. Five combinations had the minimum number of rates (three), and only one combination had the maximum number of rates (seven) (see Table 1).

Table 1.

Rate combination modes

Index	Rate combination (Hz)	Nominal rate (Hz)
1	70, 75, 80	75
2	75, 80, 85	80
3	80, 85, 90	85
4	85, 90, 95	90
5	90, 95, 100	95
6	70, 75, 80, 85	77.5 (80)
7	75, 80, 85, 90	82.5 (85)
8	80, 85, 90, 95	87.5 (85)
9	85, 90, 95, 100	92.5 (90)
10	70, 75, 80, 85, 90	80
11	75, 80, 85, 90, 95	85
12	80, 85, 90, 95, 100	90
13	70, 75, 80, 85, 90, 95	82.5 (85)
14	75, 80, 85, 90, 95, 100	87.5 (85)
15	70, 75, 80, 85, 90, 95, 100	85

The nominal rate was defined as the mean of the rates in the combination. The number in parentheses denotes the rate adopted to synthesize the ASSRs when the nominal rate was unavailable among the recorded ASSRs

As seen in Table 1, a spliced signal containing multirate ASSRs for each combination was used to reconstruct an AM-tAEP using the MSAD method. These tAEPs were used for visual inspection for the existence of valid components that were analogous to classical tAEPs obtained at low stimulus rates. They were then separately used as the template to synthesize an ASSR (syn-ASSR for short) by a forward convolution process. The mean rate of the combined ASSRs was referred to as a nominal rate. If this rate was used in the recorded ASSR (rec-ASSR for short) as well, it was then selected to synthesize the ASSR. Four nominal rates were not available in the rec-ASSRs, and so the closest one (parenthetical data in Table 1) was selected for the synthesis. Hotelling’s T² tests (Hotelling 1931; Picton et al. 1987) and correlation coefficients (MATLAB, version R2017b) between syn- and rec-ASSRs at the same rate were used to evaluate the reliability of the reconstructed AM-tAEPs and the rate-combination effects. The characteristic components were identified and compared in terms of peak amplitude and latency to investigate the rate effect by using repeated measures ANOVA (SPSS, version 22.0, IBM, Armonk, NY, USA).

The MATLAB code and data are freely available in figshare (https://doi.org/10.6084/m9.figshare.14775975).

RESULTS

Time and Frequency Profiles of the rec-ASSRs

In the time domain, three cycles of the grand averaged ASSR waveforms for seven stimulus rates are shown in Fig. 2A. These ASSRs present clear periodic troughs and peaks with a magnitude of less than 0.5 μV peak-to-peak. In the frequency domain, the dominant energy of the ASSRs is concentrated in the fundamental frequencies that can be used to characterize the ASSRs. Figure 2 B shows that the amplitudes of the fundamental frequencies of the ASSRs in Fig. 2A for all rates range from 0.1 to 0.15 μV, whereas the phase monotonously decreases from approximately 240 to 40° (Fig. 2C), indicating its dependence on the stimulation rate (the corresponding group delay is about 18 ms). Moreover, the ASSRs at 85 Hz and 90 Hz exhibit the maximal peak-to-peak amplitude. Frequency analysis also showed an evident frequency component at 2500 Hz that may represent the coupling effect from the carrier wave signal of the sound.

Fig. 2.

Time and frequency profiles of the grand averaged ASSRs across subjects. (A) Waveforms of the three-cycle ASSRs. (B) Amplitudes of the fundamental frequencies calculated from the ASSRs in (A). (C)Phases of the fundamental frequencies calculated from the ASSRs in (A)

Reliability of the Reconstructed AM-tAEPs

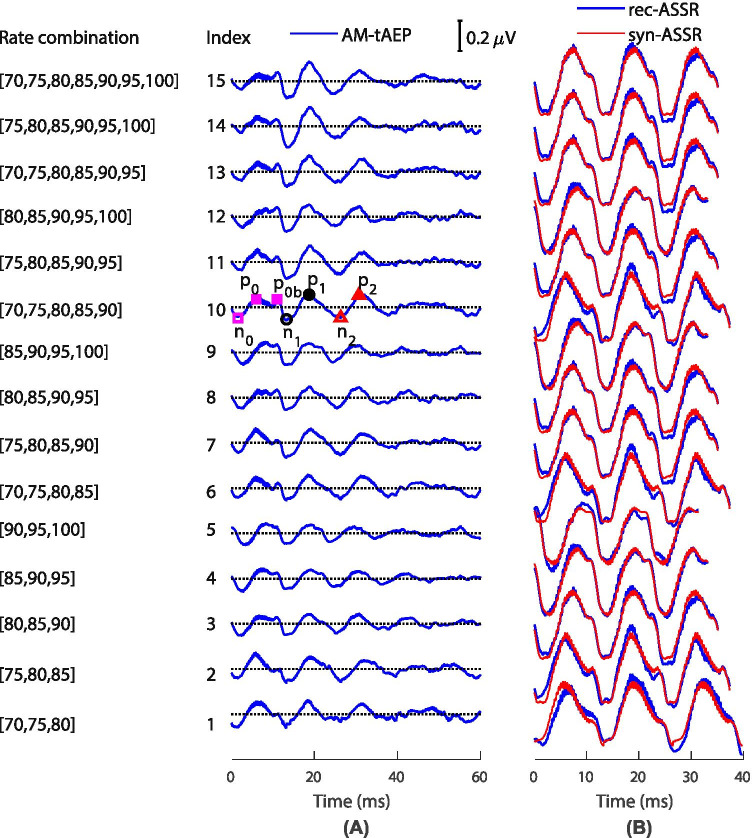
As indicated in Table 1, the AM-tAEPs were estimated with different rate combinations. Figure 3 A shows the reconstructed AM-tAEPs from the grand averaged ASSRs for all rate combinations. These AEPs show clear transient characteristics consisting of three main peak-valley pairs within 40 ms of the stimulus onset as well as some visible 2500 Hz carrier wave artifacts coupled from the stimulus device in the range of 0–10 ms. To justify the MSAD solution, the estimated AM-tAEPs were used to synthesize ASSRs (red curves in Fig. 3B), which served as predictions for the conventional rec-ASSRs, as shown in Fig. 2A and Fig. 3B (blue curves). Both ASSRs demonstrate a good morphological match and show an approximate doubling of the amplitude of the tAEPs due to the in-phase enhancement of the latter. The correlation coefficients (Pearson) between the syn- and rec-ASSRs are between 0.92 and 0.98 (i.e., r²(793) = 0.92, r²(745) = 0.94, r²(700) = 0.96, r²(661) = 0.98, r²(625) = 0.98, r²(745) = 0.92, r²(700) = 0.96, r²(700) = 0.98, r²(661) = 0.98, r²(745) = 0.92, r²(700) = 0.96, r²(661) = 0.98, r²(700) = 0.96, r²(700) = 0.96, r²(700) = 0.96; p < 0.0001 for index 1 to 15, respectively), indicating high similarity. Furthermore, frequency analysis with Hotelling’s T² test on the fundamental frequencies found no significant difference (p > 0.05, Table 2) between the syn- and rec-ASSRs.

Fig. 3.

AM-tAEPs and syn-ASSRs vs. rec-ASSRs. (A) AM-tAEPs reconstructed from different rate combinations based on the grand averaged rec-ASSRs. Characteristic components are labeled on Index 10: the open pink square for n_0, the filled pink square for p₀ and p_0b, the open black circle for n₁, the filled black circle for p₁, the open red triangle for n₂; and the filled red triangle for p₂. (B) Three-cycle syn-ASSRs in red overlapped with rec-ASSRs in blue at the same rate. The syn-ASSRs were constructed based on the corresponding AM-tAEPs to their left as templates

Table 2.

Relationships between syn- and rec-ASSRs (n: the number of subjects)

Index	syn-ASSRs at the fundamental frequencies		rec-ASSRs at the fundamental frequencies		Hotelling's T2
	Magnitude μV	Phase degree	Magnitude μV	Phase degree	F α = 0.05	p
1 (n = 10)	0.15 ± 0.16	168 ± 28	0.16 ± 0.16	165 ± 30	F(2,8) = 3.62		0.0760
2 (n = 10)	0.11 ± 0.05	126 ± 22	0.11 ± 0.05	131 ± 25	F(2,8) = 1.32		0.3197
3 (n = 12)	0.16 ± 0.13	96 ± 21	0.16 ± 0.13	94 ± 23	F(2,10) = 0.02		0.9849
4 (n = 10)	0.12 ± 0.05	53 ± 14	0.12 ± 0.05	50 ± 20	F(2,8) = 0.49		0.6301
5 (n = 10)	0.13 ± 0.08	26 ± 28	0.13 ± 0.08	25 ± 30	F(2,8) = 0.50		0.6218
6 (n = 10)	0.15 ± 0.13	129 ± 25	0.14 ± 0.12	135 ± 27	F(2,8) = 1.56		0.2678
7 (n = 13)	0.16 ± 0.13	102 ± 27	0.16 ± 0.13	98 ± 27	F(2,11) = 2.21		0.1556
8 (n = 12)	0.13 ± 0.07	96 ± 26	0.13 ± 0.08	95 ± 26	F(2,10) = 0.02		0.9801
9 (n = 11)	0.15 ± 0.13	57 ± 20	0.15 ± 0.13	55 ± 25	F(2,9) = 0.20		0.8184
10 (n = 10)	0.11 ± 0.05	124 ± 22	0.11 ± 0.05	131 ± 25	F(2,8) = 1.79		0.2285
11 (n = 13)	0.16 ± 0.13	101 ± 27	0.16 ± 0.13	98 ± 27	F(2,11) = 0.76		0.4902
12 (n = 10)	0.12 ± 0.04	53 ± 13	0.12 ± 0.05	50 ± 20	F(2,8) = 0.16		0.8549
13 (n = 13)	0.16 ± 0.12	100 ± 28	0.16 ± 0.13	98 ± 27	F(2,11) = 0.65		0.5425
14 (n = 10)	0.16 ± 0.14	97 ± 27	0.16 ± 0.14	94 ± 28	F(2,8) = 2.81		0.1187
15 (n = 13)	0.16 ± 0.12	99 ± 27	0.16 ± 0.13	98 ± 27	F(2,11) = 0.26		0.7741

The “n” in the column of “index” represents the number of subjects analyzed in the corresponding Hotelling’s T² test in order to satisfy the requirement of normal distribution. The differences of real and imaginary parts of the fundamental frequencies between the rec- and syn-ASSRs were analyzed in Hotelling’s T² test

Profile of the AM-tAEPs

All AM-tAEPs at nominal rates (the mean of rates in one combination) of 75–95 Hz are consistent with each other, containing a sequence of negative and positive peaks similar to classical AEPs but exhibiting inconsistent peak latencies (Fig. 3A). As indicated for the AM-tAEP obtained at 80 Hz (index 10 in Fig. 3A), we labeled the characteristic components of three pairs of peaks as n₀p₀, n₁p₁, and n₂p₂, sequentially, according to traditional AEP nomenclature (Picton 2011).

The conventional responses within 15 ms of stimulus onset are regarded as the ABR, and the responses between 15 and 100 ms are called the MLR (Picton 2011). Consequently, n₀, p₀, and n₁ can be considered counterparts of the ABR waves, while p₁, n₂, and p₂ are considered the MLR counterparts. Note that the duration for a stimulus element is, in this example, more than 10 ms for an 80 Hz modulating frequency; the waves within this range are actual responses to a sustained stimulation. Thus, the blunt peak p₀ is a sustained response to a relatively wide stimulation. Following p₀ is the protruding p_0b at approximately 11 ms, which is thought to be the first response to the offset of the stimulus element, while n₀ might be the response to the onset of the stimulus element.

The conventional MLR generally consists of more-stable Pa waves at approximately 30 ms and less-stable Pb waves at 50 ms (Picton 2011). Although p₁, at approximately 20 ms, and p₂, at approximately 30 ms, appear much earlier than Pa and Pb, more studies are needed to address their connections.

Effects of Nominal Rate on AM-tAEPs

Figure 4 replots the calculated AM-tAEPs at increasing nominal rates; for different rate combinations with the same nominal rate, we chose the combination with the fewest rate variations. Despite the high similarity in morphologies, some discrepancies can be found among the AM-tAEPs. For example, p_0b seems more evident at lower rates, and the n₀ latency is observed to regularly change with respect to the rate. Figure 4 B and C show the changes in the peak amplitude and latency as a function of the nominal rate. Figure 4 B shows the mean and standard deviation of the three peak-to-peak amplitudes, i.e., n₀p₀, n₁p₁, and n₂p₂. Basically, the amplitude appears to decrease with increasing rate, and only n₁p₁ exhibited a statistical rate effect (repeated measures ANOVA, p < 0.0001, Table 3). In contrast, the changes in latency show different patterns for the different components, as shown in Fig. 4 C and Table 3. Since waves p₀ and p_0b are too close to each other, they are considered as p₀ complex wave during latency analysis. Its peak-latency was defined as the latency of the middle point among points with two thirds of the peak-to-peak amplitude in p₀ complex. Early components n₀ and p₀ show an increase in latency with rate. But the statistical increase only exists in n₀ (p < 0.0001 for n₀; p = 0.097 for p₀); no significant trend is observed for middle component n₁ (p = 0.4898) while a slight increase is found for p₁ (p = 0.0158); and latency decreases can be clearly observed for latter components n₂ and p₂, (p < 0.05, see details in Table 3). These patterns suggest defined rate effects on the calculated AM-tAEPs, which calls for further study.

Table 3.

Effects of nominal rate on AM-tAEPs (n: the number of subjects)

Amplitude or latency	Amplitudes or latencies (mean ± sd.) at nominal rates									Repeated measures ANOVA
	75 Hz	77.5 Hz	80 Hz	82.5 Hz	85 Hz	87.5 Hz	90 Hz	92.5 Hz	95 Hz	F	p
n0p0/μV (n = 11)	0.18 ± 0.06	0.19 ± 0.06	0.17 ± 0.07	0.19 ± 0.07	0.18 ± 0.07	0.20 ± 0.08	0.19 ± 0.08	0.20 ± 0.07	0.18 ± 0.06	F(3.19,31.93) = 0.83*	0.4919
n1p1/μV (n = 10)	0.13 ± 0.04	0.16 ± 0.06	0.15 ± 0.05	0.16 ± 0.05	0.13 ± 0.04	0.15 ± 0.03	0.13 ± 0.03	0.14 ± 0.04	0.12 ± 0.04	F(8,72)  = 5.18	< 0.0001
n2p2/μV (n = 9)	0.11 ± 0.04	0.13 ± 0.06	0.12 ± 0.04	0.14 ± 0.05	0.11 ± 0.04	0.12 ± 0.02	0.11 ± 0.03	0.10 ± 0.02	0.09 ± 0.02	F(2.92,23.38) = 2.01*	0.1419
n0/ms (n = 10)	1.54 ± 0.80	1.70 ± 0.94	1.39 ± 0.66	1.71 ± 0.81	2.93 ± 0.99	3.71 ± 1.85	3.21 ± 1.14	3.69 ± 1.14	3.92 ± 1.00	F(2.77,24.89) = 12.15*	< 0.0001
p0/ms (n = 9)	6.99 ± 0.46	7.85 ± 0.77	7.46 ± 0.73	7.57 ± 0.67	8.07 ± 0.48	8.21 ± 0.74	8.41 ± 0.63	8.11 ± 0.57	8.82 ± 0.26	F(3.43,27.44) = 2.26*	0.097
n1/ms (n = 11)	13.35 ± 0.55	13.39 ± 1.35	13.45 ± 1.53	13.85 ± 0.78	13.81 ± 0.89	13.62 ± 1.63	13.82 ± 1.15	13.94 ± 0.76	13.64 ± 0.93	F(3.47,34.72) = 0.87*	0.4898
p1/ms (n = 9)	18.64 ± 0.49	18.37 ± 0.76	20.06 ± 2.04	20.70 ± 1.96	20.35 ± 2.55	19.48 ± 1.71	20.16 ± 1.67	20.31 ± 2.04	20.20 ± 1.74	F(8,64) = 2.60	0.0158
n2/ms (n = 11)	25.00 ± 2.56	25.79 ± 2.37	26.42 ± 1.15	25.94 ± 1.45	25.08 ± 1.60	25.10 ± 0.73	25.80 ± 1.32	24.75 ± 0.73	24.04 ± 0.86	F(3.28,32.80) = 2.94*	0.0434
p2/ms (n = 11)	31.56 ± 1.01	31.85 ± 1.47	33.46 ± 2.52	33.42 ± 2.57	31.10 ± 1.34	31.11 ± 1.14	31.25 ± 1.59	30.80 ± 2.97	31.45 ± 2.50	F(2.81,28.06) = 4.02*	0.0186

^* Greenhouse–Geisser adopted for violation of sphericity

DISCUSSION

In this study, we successfully reconstructed tAEPs for the first time from sinusoidal AM-stimulated ASSRs with seven modulation rates from 70 to 100 Hz. The resultant tAEPs occurred over approximately 40 ms, which could account for the generation of ASSRs with a superimposition model. The calculated tAEPs also justified the merit of MSAD since it is not dependent on the jittering of stimulus sequences, as used in other methods.

The tAEP is traditionally evoked at low stimulation rates to reveal the full length waveform. Higher rates may impact the behavior of some components with practical implications in revealing the integral characteristics of auditory pathways (Picton 2011). Further increasing the rate will eventually produce an ASSR presumed to be the superimposition of the implicit tAEP that can be reconstructed by deconvolution methods (Bardy et al. 2014; Eysholdt and Schreiner 1982; Jewett et al. 2004; Valderrama et al. 2014).

A number of studies show that deconvolved click-tAEPs at high rates of 40–100 Hz exhibit three main characteristic complexes, wave V of the ABR and waves NaPa and NbPb of the MLR as shown in conventional AEP components at low stimulation rates (Delgado and Özdamar 2004; Özdamar et al. 2007; Tan et al. 2016; Valderrama et al. 2014). In this study, AM-tAEPs from an approximately 80 Hz AM stimulation were found to show three main characteristic positive and negative peaks, as labeled in Figs. 3 and 4, where waves n₀, p₀, and n₁ are in the range of ABRs, while p₁, n₂, and p₂ occur in the range of MLRs. The ABR and MLR are mainly exogenous responses in first 100 ms in terms of latency. Thus, the waveform will be largely affected by the frequency and energy distributions of the sound element. The adopted AM-tone has a wide energy distribution in the time domain but very narrow frequency contents in contrast to the conventional burst-type stimulation characterized by the rise-time and duration of the stimulation element. As in 80 Hz AM tone, the rise-time and duration of the AM stimulation element are 6.25 ms and 12.5 ms whereas those of click/brief tone element are less than 0.8 ms/2 ms (for 2–1-2 brief tone with carrier frequency of 2500 Hz).

Fig. 4.

AM-tAEPs and their peak amplitudes and latencies with increasing stimulation rates. (A) AM-tAEPs of 75– 95 Hz replotted from Fig. 3A. Peaks are marked by different symbols: the open pink square for n₀, the filled pink square for p₀, the open black circle for n₁, the filled black circle for p₁, the open red triangle for n₂, and the filled red triangle for p₂. Characteristic components are labeled on the AM-tAEP of 80 Hz. (B) Peak–peak amplitudes of three characteristic components (mean and standard deviation). (C) Peak latencies of three pairs of characteristic components (mean and standard deviation)

The conventional ABR is considered a superposition of fast and slow components. The fast one contains small and rapid waves I–VII overlapped with a slow component that includes a broad positive peak at the early stage and a negative peak N10 (or slow negative wave, SN10, in some literature) at approximately 10–12 ms (Lins et al. 1995; Suzuki et al. 1986). The ABR components tend to be of longer latency, smaller amplitude, and more broadened morphology in response to rapid stimulation and/or slow rise-time sound element, as found in human (Beattie et al. 1984; Beattie and Boyd 1985; Picton 2011) and animals (Finneran et al. 2018; Jones et al. 2019). Specifically, the decreased amplitude mainly comes from the fact that the fast ABR components become weaker whereas the slow components are relatively stable and even stronger with increasing duration (Beattie et al. 1984; Beattie and Boyd 1985; Funasaka and Ito 1986; Suzuki et al. 1986). Early studies (Beattie et al. 1984; Beattie and Boyd 1985) reported three main components named as P10, N15, and P20 evoked by the tone-pip with 4 ms rise-time. These components exhibited similar structure to this reconstructed AM-tAEP (Fig. 3). Recently, Lachowska et al. (2012; 2016) extracted ABRs from 80 Hz quasi-ASSRs employed CLAD method. Their stimulation elements were windowed tone-bursts with different sustaining duration or width and carrying frequencies. Their wave V of ABR became flat and less identifiable with increasing stimulation width.

By MSAD method, we are able to study the extreme cases with the maximum width and minimum silence of the stimulation element. In this case, the fast components as occurred in click-ABRs were hardly identifiable. However, waves p₀ and p_0b can be ascribed largely to the main ABR components such as wave V, in response to the onset, sustaining and offset portion of the wide AM element being used. The transition n₀–p₀ may reflect the onset and sustained response to the broad AM energy, which represents the first neural activity identifiable in the auditory brainstem pathway. The wave p_0b occurred about 5 ms late from the falling edge of AM-tone, is supposed to be an offset response resembling wave V of click-ABR. The wave n₁ at approximately 13 ms is well matched to N10 in latency, and the n₀–n₁ interval is approximately 10 ms, which also corresponds to 100 Hz, as indicated in Lins et al. (1995). The latency of N10 was reported to be resistant to the stimulation rate but sensitive to the rise time of the stimulus (Dykstra et al. 2016; Tawfik and Musiek 1991), which agrees with the stable latency of n₁ with respect to the stimulus rates indicated in Fig. 4C. The slower rise time of AM elements may account for the delay in the n₁ latency.

The ABR (mainly wave V) is known as a good biomarker for auditory thresholds, while the N10 is reported to be more reliable in threshold detection than wave V with additional merit of frequency specificity (Tawfik and Musiek 1991). However, in the past decades, research has rarely focused on N10 because it is not clearly identifiable and easy to confuse with the postauricular muscle (PAM) response or a distorted version of the ABR due to inappropriate filter settings on EEG (Picton 2011). One recent MEG study (Dykstra et al. 2016) using tailored source analysis provided insights about N10 and suggested that this component may arise from the midbrain. Our results indicated that N10 (or n₁ in Fig. 4) could be reliably retrieved from high-rate ASSRs, which offers a promising application for N10.

Pa is the most stable characteristic component of the MLR. Its latency was found to remain at approximately 30 ms with increasing stimulus rates from 5 to 125 Hz for click stimulation (Özdamar et al. 2007; Valderrama et al. 2014). It seems that the latency and width of Pa match wave p₂ in this experiment. The latency discrepancy of p₂ is about 3 ms for rates ranging from 75 to 95 Hz, which is not surprising considering the relatively imprecise peak-timing due to the wide and irregular morphology of the MLR (Hall 1991). The relatively small amplitude of p₂ may be ascribed to the high rate and long rise-time of the AM element. The amplitude of Pa is known to decrease with increasing stimulation rates (Picton 2011; Özdamar et al. 2007). The rise-time was reported to have more effect on the amplitude than the latency for MLRs (Kodera et al. 1979; Xu et al. 1995; 1997).

The peak and trough between waves n₁ and p₂ are waves p₁ and n₂ that are found to be absent of exact counterparts in conventional ABR–MLRs. According to the latency and waveform, they were corresponding to P20 and its following trough in early studies (Beattie et al. 1984; Beattie and Boyd 1985; Suzuki et al. 1986). Although p₁ is in the range of wave Po of the MLR in terms of latency measurements, the strength and width are much more noticeable than those of Po. The n₂ is closer to p₂ than Na to Pa. In addition, the conventional No (i.e., N10) and Po are often found to be close to each other, and Po is usually quite weak or undetectable so that the NoPoNa complex may fuse into a single negative trough (Picton 2011). Despite these confusing characteristics, waves p₁ and n₂ are clear and well defined at the early MLR stage that more investigations should be undertaken to explore their implications and clinical applications in the future.

The stimulus rate is known to affect some AEP components in a consistent manner: an increasing rate will lead to latency increases and amplitude decreases. Such a rule is also applied to the estimated transient response by various deconvolution methods for high-rate stimulation (Holt and Özdamar 2016; Özdamar et al. 2007; Picton 2011; Valderrama et al. 2014). For example, Valderrama et al. (2014) reported that the amplitudes of waves V of the ABR and NaPa of the MLR monotonously decreased with increasing stimulus rate (45 to 250 Hz for the ABR; 8 to 125 Hz for the MLR). Özdamar et al. (2007) also reported a decreased amplitude of NaPa with rates increasing from 5 to 98 Hz. This can be ascribed to neural activity in terms of the adaptation and synchronization phenomena (Picton 2011). Nevertheless, some components may behave exceptionally; for example, the Pb component did not display a monotonic change with the rate. Pb amplitude resonance was reported at a nominal rate of approximately 40 Hz (Özdamar et al. 2007) or 67 Hz (Valderrama et al. 2014). In this study, we screened a narrow range of the nominal rate from 75 to 95 Hz. A mild amplitude decrease with increasing rate was observed in Fig. 4B. The early components (n₀ and p₀) show slightly longer latencies for higher rates, whereas the latencies for the later components show different patterns (see Fig. 4C). The solved tAEPs may suffer from a degree of bias ascribed to two factors. First, the underlying tAEPs from ASSRs of different rates in one combination might not be identical as assumed for the deconvolution algorithm. The solved tAEP is in essence a kind of averaged waveform of them. Second, the bias from the regularization technique tends to repress the solution. To alleviate these distortions, we have tried to use lower-jitter rates as shown in Table 1 and made careful adjustments to the regularization parameters with L-curve criterion (Johnston and Gulrajani 2000).

It has been conjectured that the composition of the AM-ASSR is analogous to that of the ASSR elicited by clicks at high rates. Specifically, Lins et al. (1995) suggests that the negative part of the 80 Hz AM-ASSR might partly be the superposition of wave N10 of the slow component of the ABR, while the positive part might be the superimposition of wave V of the fast component of the ABR. This hypothesis failed to take MLR components into account. At present, the scalp-recorded 80 Hz ASSR is assumed to reflect neural activities mainly in the brainstem but also partly in the cortex (Herdman et al. 2002; Holmes et al. 2018; Korczak et al. 2012; Luke et al. 2017). The results of this study thus provide consolidated evidence with well-defined characteristic waves in both ABRs and MLRs.

CONCLUSION

In the present study, the AM-tAEP was successfully reconstructed by the newly developed MSAD method from ASSRs for continuous AM stimulation at a few different stimulation rates from 70 to 100 Hz. This study thus offers direct evidence that the superimposition hypothesis can be extensively applied to the generation of AM-ASSRs with the decomposition method. Various rate combinations were screened to validate the existence and consistency of these AM-tAEPs, which can compensate for the absence of temporal information from ASSRs to AM stimulation. This finding may be promising as a new representation of auditory neural activity. The AM-tAEPs exhibit a series of characteristic components that represent neural activity that can be ascribed to the conventional ABR and MLR stages. Unlike tAEPs derived from high-rate click stimulation, which resembles components of typical ABRs and MLRs at low rates of stimulation, we observe novel components from the AM-tAEPs, which are temporally labeled as waves n₀, p₀, n₁, p₁, n₂, and p₂. Although we can associate these components with conventional ABR and MLR activity, further studies are needed to investigate their implications and characteristics.

Abbreviations

ABR

Auditory brainstem response

AEP

Auditory evoked potential

AM

Amplitude modulation

AM-ASSR

ASSR evoked by AM pure tone

AM-tAEP

Reconstructed tAEP from AM-ASSR and considered as the response elicited by one sound element in AM tone

ASSR

Auditory steady-state response

CLAD

Continuous loop averaging deconvolution

click-tAEP

Reconstructed tAEP from ASSR evoked by clicks at high rates and considered as the response evoked by one click stimulus in a click sequence at high repetition rates

EEG

Electroencephalograph

ISI

Interstimulus interval

MLR

Middle latency response

MLS

Maximum length sequence

MSAD

Multirate steady-state averaging deconvolution

SNR

Signal-to-noise ratio

SVD

Singular value decomposition, a mathematical tool

tAEP

Transient AEP

Author Contributions

All authors contributed to the study, conception and design. Material preparation, data collection and analysis were performed by Tao Wang, Yuner Chen, and Xiaodan Tan. The first draft of the manuscript was written by Xiaodan Tan and Qiuyang Fu. All authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Funding

This work was supported by the Science and Technology Program of Guangzhou, China under Grant 201,804,010,282.

Data Availability and Material

Data and material are available in figshare, https://doi.org/10.6084/m9.figshare.14775975.

Code Availability

Codes of software are available in figshare, https://doi.org/10.6084/m9.figshare.14775975.

Declarations

Ethics Approval

The experiment was approved by the Human Research Ethics Committee of Southern Medical University (No. 2015-KYLL-004).

Consent to Participate

Every participant signed the corresponding informed consent forms prior to the experiment.

Consent for Publication

All authors read and approved the final manuscript and publication.

Conflict of Interest

The authors declare no competing interests.