DXA-Based Bone Strain Index: A New Tool to Evaluate Bone Quality in Primary Hyperparathyroidism

Abstract

Context

Primary hyperparathyroidism (PHPT) is associated with impaired bone quality and increased fracture risk. Reliable tools for the evaluation of bone quality parameters are not yet clinically available. Bone Strain Index (BSI) is a new metric for bone strength based on Finite Element Analysis from lumbar spine and femoral neck dual-energy x-ray absorptiometry (DXA) images.

Objective

To assess the lumbar spine (LS), femoral neck (FN), and total hip (TH) BSI in PHPT patients compared with controls and to investigate the association of BSI with vertebral fractures (VFs) in PHPT.

Methods

This case-control study enrolled 50 PHPT patients and 100 age- and sex-matched control subjects from an outpatient clinic. The main outcome measures were LS-BSI, FN-BSI, and TH-BSI.

Results

FN bone mineral density (BMD) and one-third distal radius BMD were lower in the PHPT group than in controls (FN 0.633 ± 0.112 vs 0.666 ± 0.081, P = 0.042; radius 0.566 ± 0.07 vs 0.625 ± 0.06, P < 0.001). PHPT group has significant lower TBS score compared with controls (1.24 ± 0.09 vs 1.30 ± 0.10, P < 0.001). BSI was significantly higher at LS (2.28 ± 0.59 vs 2.02 ± 0.43, P = 0.009), FN (1.72 ± 0.41 vs 1.49 ± 0.35, P = 0.001), and TH (1.51 ± 0.33 vs 1.36 ± 0.25, P = 0.002) in PHPT. LS-BSI showed moderate accuracy for discriminating VFs (AUC 0.667; 95% CI, 0.513-0.820). LS-BSI ≥ 2.2 and was a statistically significant independent predictor of VFs, with an adjusted odds ratio ranging from 5.7 to 15.1.

Conclusion

BSI, a DXA-derived bone quality index, is impaired in PHPT and may help to identify PHPT subjects at high risk of fractures.

Primary hyperparathyroidism (PHPT) is a common endocrine disorder. It is characterized classically by hypercalcemia and high or inappropriately normal (unsuppressed) parathyroid hormone (PTH) levels. Major complications of PHPT include nephrolithiasis, osteoporosis, and fragility fracture (1), even if there is a high prevalence of asymptomatic disease in Western countries (2, 3). Although increased fracture risk at both vertebral and nonvertebral sites is well established clinically, bone mineral density (BMD) is typically reduced at the distal one-third forearm, a primarily cortical bone site, with relative preservation of the lumbar spine (LS), a predominantly trabecular site (4-6). High-resolution peripheral quantitative computed tomography (HRpQCT) has resolved these discrepant findings by demonstrating at the microarchitectural level that trabecular bone is also affected adversely in PHPT (7, 8). However, as primarily a research tool, HRpQCT is not widely available. Other, more readily available indices are needed to evaluate bone quality in the clinical setting. Recently, a pilot study applied 3D-DXA software to evaluate the hip. It confirmed the deterioration of cortical bone but not trabecular bone (9).

Trabecular bone score (TBS) is a useful noninvasive index of bone quality in PHPT. Studies on postmenopausal women with PHPT showed a reduction in TBS values (10, 11), in contrast to lumbar spine DXA, in which values are closer to normative controls. Questions remains whether vertebral fractures (VFs) can be readily detected in this clinical setting (12, 13).

Bone Strain Index (BSI) is a new DXA-derived skeletal parameter of deformation that is based on Finite Element Method (FEM) (14). It can be applied both to lumbar and femoral DXA scans (15). Recent clinical studies showed the usefulness of BSI as a complementary tool, together with other clinical risk factors, to identify patients at risk of fracture (16, 17) and to better characterize young patients affected by secondary osteoporosis (18, 19). Patients treated with teriparatide experienced an improvement of BSI over time (20).

The aim of this study was to compare the BSI measured at the LS and hip in subjects with PHPT versus controls. We also explored a possible association of BSI with morphometric vertebral fractures in PHPT.

Methods

Study Design and Population

We performed a case-control study including 150 subjects. Cases (n = 50) included subjects with PHPT who were consecutively enrolled from September 2017 to December 2019, at Campus Bio-Medico University of Rome. PHPT was defined as elevated or unsuppressed PTH concentrations and persistently elevated total, albumin-corrected, or ionized serum calcium levels (at least 2 different determinations, at least 3 months apart). Exclusion criteria were the following: any other condition that can affect bone and calcium metabolism; use of drugs affecting bone and calcium metabolism (ie, the use of glucocorticoids); early menopause; a history of possible high-energy VFs; metabolic bone diseases such as Paget disease and osteogenesis imperfecta.

For each case, 2 controls were identified from electronic medical records of the outpatient clinic of endocrinology at Campus Bio-Medico University of Rome, where they were referred for unrelated diseases (eg, thyroid nodules with euthyroidism). Controls were matched by age (±2 years), gender, and date of consultation at the outpatient clinic and were recruited using the aforementioned exclusion criteria. We included control subjects who had a BMD test, thoracolumbar radiograph, and blood testing to evaluate calcium metabolism for the first time. In all control subjects with osteoporosis and/or fragility fractures, secondary causes of osteoporosis were ruled out.

We defined asymptomatic subjects as those with primary hyperparathyroidism and no overt signs of the disease namely: osteitis fibrosa cystica, vertebral fractures, nephrocalcinosis, reduced renal function, muscle weakness, peptic ulcer disease, pancreatitis, neurocognitive symptoms (21).

Biochemical Analysis

Fasting blood samples were collected for the following: serum total calcium (normal, 8.4-10.2 mg/ dL) albumin (normal, 3.2-4.6 g/dL), serum phosphate (normal, 2.3-4.7 mg/dL) creatinine (normal, 0.55-1.2 mg/dL) and 25OH-vitamin D (normal, 30-100 ng/mL), that were measured by automated methods. Calcium values were corrected for albumin concentration. Ionized serum calcium (normal, 1.13-1.32 mmol/L) was measured by a potentiometric method on GEM PREMIER 4000 analyzers (Werfen, Le Pré-Saint-Gervais, France). Intact PTH (normal, 14-72 pg/mL) was measured by an immunochemiluminometric assay using a Modular E170 automatic analyzer (Roche Diagnostics, Indianapolis, IN, USA). Serum levels of beta CrossLaps (CTX) were assayed by the Cobas β-CrossLaps (ECLIA; β-CrossLaps/Serum, Roche Diagnostics, Basel, Switzerland), which uses 2 monoclonal antibodies against β-cross-linked CTX according to the manufacturer’s protocol. Serum levels of procollagen type 1 N-terminal propeptide (P1NP) were analyzed by Cobas Total P1NP (ECLIA; Roche Diagnostics) automated analyzer.

Dual-Energy X-ray Absorptiometry

We measured BMD by dual-energy x-ray absorptiometry (DXA) at the lumbar spine (L1-L4), total hip (TH), femoral neck (FN), and nondominant forearm (one-third distal radius) (Hologic Discovery QDR Instrument, MA, USA, version 13.3:3; coefficients of variation: LS, 0.97%; FN,1.49%; TH, 1.36%). Data were reported for absolute BMD, T-scores values (SD difference from mean values of sex-matched young, healthy individuals) and Z-score (SD difference from mean values of age and sex-matched healthy individuals). All scans were performed according to the International Society for Clinical Densitometry (ISCD) guidelines (22). Fractured vertebrae and vertebrae with structural changes were excluded from the analysis (T-score difference with the adjacent vertebra > 1.0). TBS was automatically derived from the same lumbar spine DXA region by dedicated software (Insight TBS, Medimaps Groupe, Geneve, Switzerland; version: 3.0.2.0).

Bone Strain Index

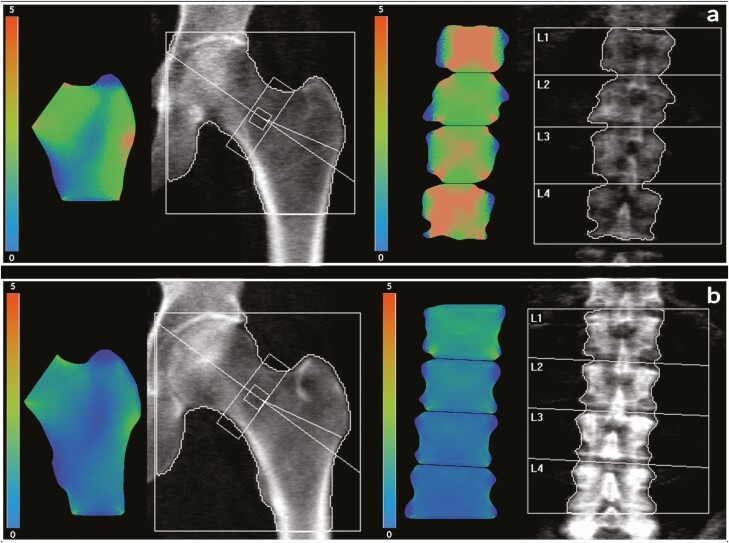
For BSI analysis, raw data from the DXA image were sent to a separate workstation in which the BSI software (Tecnologie Avanzate s.r.l., Torino, Italy) is installed. For the lumbar spine, BSI computation was determined by dividing each vertebra of the lumbar scan into several triangles following the contour provided by DXA software mapping (23). The DXA lumbar image was analyzed by a pattern drawn with the load applied to the upper plate and the constraints to each vertebra’s lower plate (24). At the femoral site, BSI was calculated on the premise of a lateral fall, with force applied to the greater trochanter and the constraints applied to the femoral head and shaft (25). In both spine and femur, stiffness of the elements was defined by the empirical relations described by Morgan et al (26), at each anatomic site. The resulting amount of strain presented graphically in different colors, led to the identification of areas with the higher strain concentration. The BSI value represents the average equivalent strain in the regions defined by DXA analysis, assuming a higher strain level (high BSI) indicates higher fracture risk (Figure 1). Finite Element Analysis computation was automatically performed on the computer by dedicated software both for lumbar spine and hip, using the same region of interest that is utilized for BMD calculations (15, 27). Each BSI examination takes about 5 seconds. The BSI analysis was conducted as a blinded analysis.

Figure 1.

Femoral and lumbar spine BSI images in a subject with hyperparathyroidism (a) and in a control subject (b). The corresponding values of BSI were: a, femoral neck BSI 2.33; total hip BSI 1.94; lumbar spine BSI 3.02. b, femoral neck BSI 1.13; total hip BSI 1.17; lumbar spine BSI 0.93.

Vertebral Fracture Assessment

Vertebral fracture (VF) assessment utilized dedicated vertebral fracture assessment software. Conventional spinal radiographs (T4-L4) in the lateral and the anteroposterior projections were also performed to confirm VFs among those with scoliosis and disk space osteoarthritis (28). A single experienced investigator read all images and scored VFs using the Genant semiquantitative method (grade 1, mild; grade 2, moderate; grade 3, severe) (29).

Ethics

The study was conducted in compliance with the Declaration of Helsinki and the International Conference on Harmonization Principles of Good Clinical Practice. Local ethics committees approved the research protocol and all participants gave informed consent allowing their anonymized information to be used for data analysis.

Statistical Analysis

According to our sample size, there will be an 80% probability to declare as statistically significant at α = 0.05 a standardized difference of 0.5 between groups (“medium-sized” difference according to Cohen) (30). Data distribution was evaluated using the Kolmogorov–Smirnov test. The difference between the means was analyzed using the unpaired Student t-test, after determining whether equal variance could be attributed to the subgroups according to Levene’s test. The nominal variables were described as a number and percentage and analyzed with contingency tables and the χ test. The associations between FN-BSI, TH-BSI, LS-BSI, LS-BMD, TH-BMD, FN-BMD, calcium, PTH, phosphate, 25OH-vitamin D, CTX, P1NP, and TBS were tested by either Pearson’s product-moment correlation or Spearman’s correlation as appropriate.

The performance of the FN-BSI, TH-BSI, and LS-BSI in detecting patients with prevalent VFs was tested by calculating the area under the receiver operating characteristics curve (AUC), whose results were interpreted as follows: 0.50 to 0.59: poor; 0.60 to 0.69: moderate; 0.70 to 0.79: good; 0.80 to 0.89: very good; and ≥0.90: excellent discrimination (31). For the only variable showing at least moderate accuracy in discriminating VFs (ie, LS-BSI) the optimal cutoff value was determined based on the maximum Youden index. Based on the identified optimal cutoff value, the sensitivity, specificity, and accuracy of LS-BSI were calculated.

Several logistic regression models were run to test the predictive power of the LS-BSI to predict VFs, adjusted for a different combination of relevant predictors, such as age, sex, body mass index (BMI), CTX, P1NP, and TBS. LS-BSI was converted into a dummy variable according to the identified threshold. The possible multicollinearity between continuous variable was tested by computing the variable inflation factor (VIF); no more than moderate correlation (VIF ranging from 1.2 to 2.2) was detected. Since age, BMI, CTX, P1NP, and TBS were nonnormally distributed, logarithmic or reciprocal transformations were performed, as appropriate, to achieve a more normal data distribution. For both age and TBS, the transformed data showed a worst distribution; consequently, untransformed data were used. Results were presented as odds ratio (OR) and 95% CI. The coefficient of the statistical models’ determination was calculated based on the Nagelkerke R², and the overall performance of the logistic models in predicting VFs was quantified with respect to discrimination as described by the AUC.

We also divided the population into subgroups of osteoporosis, osteopenia, and normal, based on the T-score according to WHO criteria (32) and we then evaluated the BSI in these subgroups.

A P value of <0.05 was considered significant. Statistical analysis was performed by SPSS version 26.0 statistical package (SPSS, Inc.).

Results

Clinical, Biochemical, and Radiologic Characteristics

Table 1 describes the population baseline characteristics, with corresponding differences between the 2 groups.

Table 1.

Baseline characteristics of the study population

Variable	n	PHPT (n = 50)	Control (n = 100)	P value
Demographic and clinical features
Age, years	150	65.2 ± 11.6	65.2 ± 8.2	0.996
Sex, female	150	47 (94%)	95 (95%)	0.535
BMI, kg/m2	150	27.9 ± 6.0	25.5 ± 4.4	0.011
Menopause age, years	142	50.2 ± 3.9	49.8 ± 3.1	0.517
Length of menopause, years	142	15.1 ± 9.6	15.7 ± 8.2	0.731
Biochemical analysis
Albumin-adjusted serum total calcium, mg/dL	150	10.8 ± 0.4	9.4 ± 0.4	<0.001
Serum phosphorus, mg/dL	150	2.8 ± 0.5	3.6 ± 0.5	<0.001
PTH, pg/dL	150	143.6 ± 72.4	52.6 ± 13.7	<0.001
25-OH vitamin D, ng/mL	150	32.0 ± 7.8	31.6 ± 12.0	0.849
Serum creatinine, mg/dL	150	0.7 ± 0.2	0.7 ± 0.1	0.886
GFR, mL/min/m2	150	88.0 ± 24.6	82.4 ± 15.5	0.146
CTX, ng/mL	50	0.5 ± 0.3	--	--
P1NP, ng/mL	50	71.9 ± 41.8	--	--
Bone measures
Vertebral fractures	150	18 (36.7%)	10 (10%)	<0.001
1/3 DR-BMD, g/cm2	89	0.566 ± 0.07	0.625 ± 0.06	<0.001
1/3 DR Z-score	89	-0.40 ± 1.02	0.42 ± 0.83	<0.001
FN-BMD, g/cm2	150	0.633 ± 0.112	0.666 ± 0.081	0.042
FN Z-score	150	-0.43 ± 0.99	-0.15 ± 0.81	0.070
FN-BSI	150	1.72 ± 0.41	1.49 ± 0.35	0.001
TH-BMD, g/cm2	150	0.793 ± 0.136	0.824 ± 0.102	0.130
TH Z-score	150	-0.01 ± 1.15	0.20 ± 0.90	0.207
TH-BSI	150	1.51 ± 0.33	1.36 ± 0.25	0.002
LS-BMD, g/cm2	150	0.869 ± 0.197	0.884 ± 0.129	0.632
LS Z-score	150	0.13 ± 1.97	0.19 ± 1.31	0.867
LS-BSI	150	2.28 ± 0.59	2.02 ± 0.43	0.009
TBS	150	1.24 ± 0.09	1.30 ± 0.10	0.001
LS T-score adjusted for TBS	150	-2.40 ± 1.05	-1.82 ± 1.02	0.002
LS Z-score adjusted for TBS	150	-0.41 ± 1.04	0.27 ± 0.99	<0.001
Osteoporosis	150	17 (34%)	17 (17%)	0.01
Osteopenia	150	29 (58%)	79 (79%)	0.003

Data reported as mean ± SD, except for sex, asymptomatic PHPT, vertebral fractures, osteoporosis and osteopenia (number and percentage).

The difference between the means was analyzed using the unpaired Student t-test. The nominal variables were analyzed with contingency tables and the χ test.

Abbreviations: BMD, bone mineral density; BMI, body mass index; BSI, Bone Strain Index; CTX, beta crosslaps (C-terminal cross-linking telopeptide); DR, distal radius; FN, femoral neck; LS, lumbar spine; P1NP, procollagen type 1 N-terminal propeptide; PHPT, primary hyperparathyroidism; TBS, trabecular bone score; TH, total hip.

There were no differences between groups in terms of age, sex, menopausal age, years after menopause, but PHPT patients had a significantly higher BMI. The albumin-adjusted total serum calcium and PTH levels were significantly higher in the PHPT group, as expected (P < 0.001); while phosphorus levels were significantly lower in PHPT compared to controls (P < 0.001) (Table 1).

A between-groups statistically significant difference was showed for FN-BMD (PHPT 0.633 ± 0.112 vs controls 0.666 ± 0.081; P = 0.042) and one-third distal radius BMD (PHPT 0.566 ± 0.07 vs controls 0.625 ± 0.06; P < 0.001). There were no differences for TH- and LS-BMD. A between-groups statistically significant difference was showed for FN T-score (PHPT −1.95 ± 1.0 vs controls −1.66 ± 0.72; P = 0.043) and one-third distal radius T-score (PHPT −2.19 ± 1.17 vs controls −1.24 ± 0.81; P < 0.001). Osteoporosis was evident in 17% of controls and in 34% of subjects with PHPT (P = 0.01). Osteopenic T-scores were evident in 79% of controls and in 58% of subjects with PHPT (P = 0.003). The majority of individuals with PHPT (62%) were asymptomatic.

The TBS was significant lower in PHPT compared with controls (1.24 ± 0.09 vs 1.30 ± 0.10; P = 0.001).

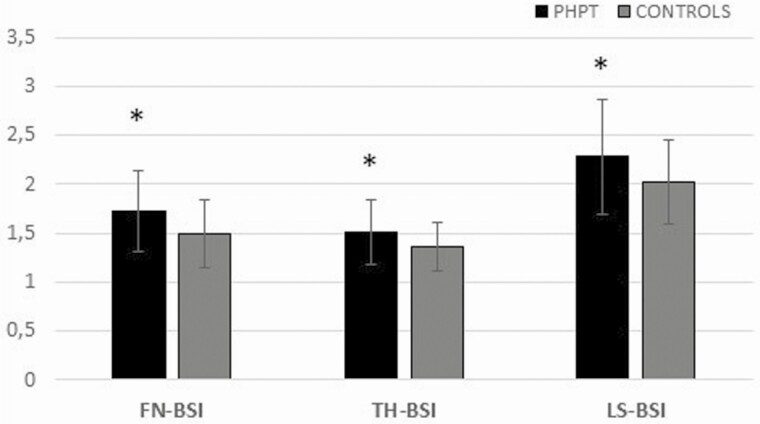
BSI was significantly worse (higher) between PHPT and control subjects at the FN (1.72 ± 0.41 vs 1.49 ± 0.35; P = 0.001), at the TH (1.51 ± 0.33 vs 1.36 ± 0.25; P = 0.002), and at the LS (2.28 ± 0.59 vs 2.02 ± 0.43; P = 0.009). Figure 2 describes the differences in BSI scores between PHPT and control patients.

Figure 2.

Evaluation of BSI in PHPT and control group. Data are presented as mean (bars) and SD (whiskers). *P < 0.01.

In subjects with osteoporosis, there was a significant difference between PHPT and controls in BSI at the FN (2.04 ± 0.29 vs 1.79 ± 0.28; P = 0.01) and the TH (1.76 ± 0.28 vs 1.59 ± 0.21; P = 0.04). In the group with osteopenic T-scores, PHPT subjects showed a higher BSI at the LS (2.26 ± 0.56 vs 2.00 ± 0.42; P = 0.01). A statistically significant higher prevalence of morphometric VFs was showed in the PHPT group (P < 0.001). The bivariate correlation analysis showed that TBS was significantly associated with LS-BSI (r = −0.59; P = 0.001).

In controls there is a significant difference in BSI between osteoporotic (n = 17) and nonosteoporotic subjects (ie, osteopenic T-scores n = 79 and normal T-scores n = 4) at the LS (2.25 ± 0.38 vs 1.98 ± 0.43; P = 0.017), TH (1.59 ± 0.21 vs 1.31 ± 0.24; P < 0.001), and FN (1.44 ± 0.34 vs 1.79 ± 0.28; P < 0.001).

Association Between BSI Parameters and VFs in PHPT Subjects

Using receiver operating characteristic analysis, we evaluated the accuracy of FN-BSI, TH-BSI, LS-BSI, LS-BMD, FN-BMD, TH-BMD, one-third distal radius-BMD, TBS, and TBS-adjusted LS T-score in detecting patients with prevalent VFs. LS-BSI was the only parameter showing a trend toward a statistically significant difference in subjects with morphometric VFs (no VFs: 2.14 ± 0.62; VFs: 2.48 ± 0.48; P = 0.051). No difference was detected either for FN-BSI (no VFs: 1.72 ± 0.47; VFs: 1.73 ± 0.33 P = 0.95) or for TH-BSI (No VFs: 1.52 ± 0.40; VFs: 1.51 ± 0.21; P = 0.94). Similarly, LS-BSI showed a moderate accuracy for discriminating VFs (AUC 0.667; 95% CI, 0.513-0.820; P = 0.054), while FN-BSI (AUC 0.532; 95% CI, 0.369-0.696; P = 0.709) and TH-BSI (AUC 0.529; 95% CI, 0.368-0.689; P = 0.740) showed poor accuracy. For LS-BSI, the optimal cutoff value was set at 2.2; based on this threshold, sensitivity, specificity, and accuracy were 77.8%, 61.3%, and 67.4%, respectively.

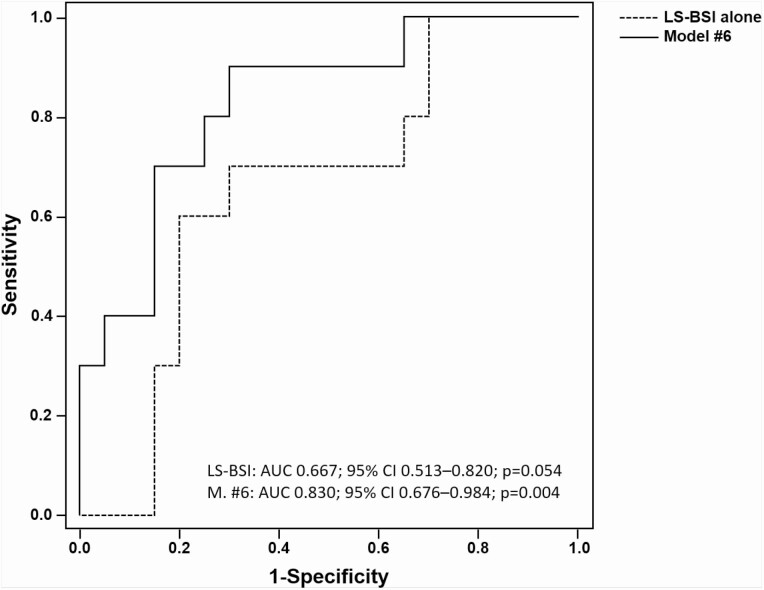
Table 2 shows the results of the multivariate analysis. In all explored regression models, adjusted LS-BSI ≥ 2.2 was a statistically significant independent predictor of morphometric VFs risk, with an adjusted OR ranging from 5.7 to 15.1. None of the considered adjustment covariates (ie, sex, age, BMI, CTX, P1NP, and TBS) showed a statistically significant association with VFs in any of the explored regression models. LS-BSI showed a progressively greater discrimination power in identifying patients with VFs risk when adjusted for other relevant covariates (AUC ranging from 0.74 to 0.83) (Table 2 and Figure 3).

Table 2.

Performance of LS-BSI to predict vertebral fractures in logistic regression models adjusted for different covariates

Model	R 2	LS-BSI ≥ 2.2 adjusted OR; 95% CI (P value)	Adjustments	AUC (95% CI); P value
# 1	0.243	6.887 (1.628-29.138); P = 0.009	Sex, Age	0.768 (0.597-0.938); P = 0.019
# 2	0.270	7.709 (1.752-33.924); P = 0.007	Sex, Age, BMI	0.795 (0.618-0.972); P = 0.009
# 3	0.376	9.602 (1.251-73.696); P = 0.030	Sex, Age, BMI, CTX, P1NP	0.825 (0.666-0.984); P = 0.004
# 4	0.189	5.739 (1.244-26.481); P = 0.025	TBS	0.735 (0.535-0.935); P = 0.039
# 5	0.251	7.152 (1.355-37.755); P = 0.020	TBS, Sex, Age, BMI	0.795 (0.616-0.974); P = 0.009
# 6	0.388	15.120 (1.059-215.786); P = 0.045	TBS, Sex, Age, BMI, CTX, P1NP	0.830 (0.676-0.984); P = 0.004

Abbreviations: AUC, area under the receiver operating characteristics curve; BMI, body mass index (kg/m²); CTX, collagen telepeptide (ng/mL); LS-BSI, lumbar spine bone strain index; P1NP, aminoterminal propeptide (ng/mL); TBS, trabecular bone score.

Figure 3.

ROC curve of LS-BSI alone or adjusted for confounders for detecting PHPT patients with prevalent vertebral fractures. Covariates in Model #6: LS-BSI, TBS, Sex, Age, BMI, CTX, P1NP.

Discussion

DXA is a key aspect of skeletal evaluation in bone loss syndromes such as PHPT (33-37), but it does not provide insight into skeletal microstructure. Thus, other imaging modalities are needed. The BSI is a recently developed option in this regard. BSI is based on Finite Element Method algorithms that evaluate the stress/strain conditions of the bone when a force is applied, simulating structural deformation. Higher BSI values indicate lower bone strength. This methodology has shown promise in predicting the risk of vertebral fracture in subjects with osteoporosis (17). This is the first study to evaluate BSI in subjects with PHPT. Compared with age-matched controls, patients with PHPT have higher BSI values at the lumbar spine, femoral neck, and total hip.

In agreement with previous studies (38), our cohort showed no differences between groups in total hip BMD and lumbar spine BMD. In contrast, BSI was significantly higher (worse) at all skeletal sites in the PHPT group. The increased BSI at the lumbar spine, a site enriched in trabecular bone, supports the hypothesis that trabecular bone, in addition to cortical bone, is adversely affected in PHPT. To date, HRpQCT has been the only technique able to quantitatively detect trabecular involvement in PHPT (7), at relevant sites, resolving the inconsistency between increased fracture risk at both vertebral and nonvertebral sites and relatively well-preserved trabecular bone as determined by BMD (38, 39). The advantage of BSI rests in its availability, through the DXA image of lumbar spine and hip regions, areas that HRpQCT cannot directly measure.

Another DXA-derived parameter that can assess bone quality in subjects with PHPT is TBS (10, 11, 13, 40, 41). However, the predictive ability of TBS to identify VFs in PHPT is still a matter of debate (10-13, 40-42). Our study confirmed a reduction of TBS in PHPT, but, in our cohort, TBS could not detect vertebral fractures. LS-BSI was the only parameter able to predict vertebral fractures. In PHPT, an LS-BSI over the threshold of 2.2, showed an approximately 6-fold increased risk of vertebral fractures. Of interest is a correlation between LS-BSI and TBS. This is not surprising because both methods address the bone quality of the trabecular compartment of bone. However, BSI can quantitate bone strength more precisely than TBS.

The evaluation of BSI in control subjects with osteoporosis showed a higher BSI at lumbar spine, femoral neck, and total hip than control subjects without osteoporosis. When we compared the controls with osteoporosis versus patients with PHPT and osteoporosis, there is a significant increase in femoral neck BSI in PHPT. This could suggest that in PHPT there are additional factors that impair bone quality than those found typically in postmenopausal women with osteoporosis. Of perhaps greater importance is the evaluation of BSI in subjects with T-scores in the osteopenic range. In these subjects, LS-BSI was higher as compared with controls. This particularly interesting observation indicates early involvement of the trabecular compartment of bone. It provides, thus, even more information vis a vis fracture risk than DXA in this disease. Detecting deterioration of bone quality in osteopenic subjects is particularly relevant since skeletal impairment, either by DXA or by the fracture itself, is currently a major criterion for decision-making in PHPT (43-45). Further research might offer more insights into how this new method might aid overall skeletal assessment in PHPT. A recent multicenter study performed BSI analysis of lumbar spine images showing its ability to predict re-fracture in patients with severe osteoporosis (17), and this finding was also confirmed by an Artificial Intelligence-based study (46). The BSI was a significant independent predictor of a subsequent re-fracture. Another study investigated the effect of teriparatide on different DXA-based parameters, including BSI (20). That study showed a positive effect of teriparatide on TBS and BSI, suggesting that the increase in BMD was accompanied by increased bone strength (20). Finally, a study on a cohort of patients with mastocytosis showed a good correlation between BSI and biochemical index of disease activity and also the BSI’s ability to discriminate whose patients with a higher risk of vertebral fracture (47). This methodology, thus, has the potential to lend insight into secondary causes of osteoporosis.

If further prospective studies confirm these findings, BSI may well become a useful tool to identify subjects at higher risk of vertebral and nonvertebral fractures.

The study has some limitations. First, the cross-sectional design of the study needs to be followed by prospective investigations. Second, as a single-site study, we await further single-site and multisite studies to add insights into our observations. We expect that larger prospective studies may well demonstrate the utility of BSI to evaluate bone quality in PHPT.

Glossary

Abbreviations

AUC

area under the curve

BMD

bone mineral density

BMI

body mass index

BSI

Bone Strain Index

CTX

crosslaps (C-terminal cross-linking telopeptide)

DXA

dual-energy x-ray absorptiometry

FN

femoral neck

HRpQCT

high resolution peripheral quantitative computed tomography

LS

lumbar spine

OR

odds ratio

P1NP

procollagen type 1 N-terminal propeptide

PHPT

primary hyperparathyroidism

PTH

parathyroid hormone

TBS

trabecular bone score

TH

total hip

VF

vertebral fracture

Additional Information

Disclosures: G. Tabacco, C. Messina, G. Sanson, S. Falcone, S. Manfrini, and F.M. Ulivieri disclosed no conflict of interest; A.M. Naciu disclosed lecture fees from Amgen; L. Rinaudo works for Technologic Srl; R. Cesareo disclosed lecture fees from Amgen and Bruno Farmaceutici; N. Napoli disclosed consultant for Lilly, Abiogen, and UCB; J.P. Bilezikian disclosed grant from the National Institutes of Health (DK32333); A. Palermo disclosed lecture fees from Amgen and Abiogen.

Data Availability

Some or all datasets generated during and/or analyzed during the current study are not publicly available but are available from the corresponding author on reasonable request.