Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2021 Nov 4;6(45):30442–30450. doi: 10.1021/acsomega.1c03740

Structural and Electronic Properties of Single-Atom Transition Metal-Doped Boron Clusters MB24 (M = Sc, V, and Mn)

Yue-Ju Yang †, Shi-Xiong Li †,*, De-Liang Chen †, Zheng-Wen Long ‡
PMCID: PMC8600523  PMID: 34805674

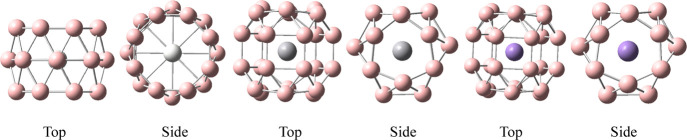
Abstract

graphic file with name ao1c03740_0010.jpg

A theoretical study of geometrical structures, electronic properties, and spectral properties of single-atom transition metal-doped boron clusters MB24 (M = Sc, V, and Mn) is performed using the CALYPSO approach for the global minimum search, followed by density functional theory calculations. The global minima obtained for the VB24 and MnB24 clusters correspond to cage structures. Interestingly, the global minima obtained for the ScB24 cluster tend to a three-ring tubular structure. Population analyses and valence electron density analyses reveal that partial electrons on transition-metal atoms transfer to boron atoms. The localized orbital locator of MB24 (M = Sc, V, and Mn) indicates that the electron delocalization of ScB24 is stronger than that of VB24 and MnB24, and there is no obvious covalent bond between doped metals and B atoms. The spin density and spin population analyses reveal that MB24 (M = Sc, V, and Mn) have different spin characteristics which are expected to lead to interesting magnetic properties and potential applications in molecular devices. The calculated spectra indicate that MB24 (M = Sc, V, and Mn) has meaningful characteristic peaks that can be compared with future experimental values and provide a theoretical basis for the identification and confirmation of these single-atom transition metal-doped boron clusters. Our work enriches the database of geometrical structures of doped boron clusters and can provide an insight into new doped boron clusters.

1. Introduction

With the development of science and technology, modern manufacturing technology is moving toward smaller scales. For example, the current semiconductor process has reached the nanometer level. If design and manufacturing can be conducted at the atomic scale, the bottleneck of semiconductor design and manufacturing is expected to be removed and potentially produce disruptive new materials and devices. Clusters are special structures situated between atoms, molecules, and bulk and have different properties compared with bulk materials. For example, the emergence of fullerene C60 is a new breakthrough in nanomaterial and nanotechnology,1 and the discovery of carbon nanotubes and graphene2,3 promoted carbon nanomaterials to become a vibrant scientific field. The physical properties of clusters are dependent on their size and shape, which can be changed to give them different physical properties owing to the quantum effect of electrons. Theoretical study of the structure and physical properties of clusters can provide guidance for the design and manufacture of new materials and new devices at the atomic level. Boron is a close neighbor of carbon, and scientists have also conducted extensive research on boron clusters. Boron atoms, with only three valence electrons (one less than carbon), can form polycentric chemical bonds and produce several interesting structures and properties.4−9 Experimental studies have found that anionic pure boron clusters, Bn–, with less than 38 atoms have a planar or quasi-planar structure.10,11 Theoretical studies have found that neutral pure boron clusters of different sizes of Bn have planar, tubular, cage-like, or other three-dimensional structures.4,8,12−14 In 2014, the breakthrough discovery of borospherene15 B40– produced a lot of research on boron clusters.16−24 Similar to fullerenes or carbon nanotubes, boron clusters may be used as molecular devices. Various chemical modifications are carried out to form boron-based nanomaterials with novel structures.

Similar to fullerenes, doping of metal atoms into boron clusters can produce new structures or properties.18,20−22,25−38 For example, in the case of an alkali metal, experimental research combined with theoretical calculation revealed that B20–, B22–, and B24 have a quasi-planar structure, quasi-planar structure, and double-ring tubular structure,10,39 respectively. However, both LiB20– and MB22– (M = Na and K) possess a double-ring tubular structure and Li2B24 possesses a three-ring tubular structure.26,40,41 In addition, Li-, Na-, or K-doped borospherene B40 is expected to become a nonlinear optical (NLO) nanomaterial.21 Because of their rich electronic structure characteristics, transition metals can combine with boron clusters to produce rich structures and properties. For example, the quasi-planar B12 cluster has a semisandwich structure after being doped with metal atoms such as Co and Rh.6,25 Neutral B24 has a double-ring tubular structure, while TiB24 and CrB24 have a cage structure after doping with one Ti or Cr atom.42 The single-atom Sc- or Ti-doped borospherene B40 is expected to become a hydrogen-storage material,18,20,22 transition metal-doped boron clusters MB12– (M = Co, Rh) can enhance chemical activity,28 and the single-atom Co-doped B40 is expected to be applied in molecular devices.27 Therefore, the study of transition metal-doped boron clusters provides important theoretical guidance for the study of new structures and new properties of boron clusters and the preparation of new boron nanomaterials. Herein, to obtain the structures and properties of transition metal-doped boron clusters MB24 (M = Sc, V, and Mn), extensive research has been conducted on the geometric structure, spectral properties, and electronic structure using the CALYPSO approach,43 in combination with the density functional theory method PBE0.44 The calculation results will be useful for future experimental data of MB24 (M = Sc, V, and Mn).

2. Computational Methods

Geometric structure searches of neutral MB24 (M = Sc, V, and Mn) clusters were implemented using particle swarm optimization (CALYPSO) software. CALYPSO is a powerful cluster structure search method, which has been successfully applied to boron and doped boron clusters.14,26 The PBE0/3-21G level was used for the preliminary structural search. In each generation, 70% of the structures were produced by particle swarm optimization (PSO) operations, while the others were randomly generated. There were nearly 2000 isomers initially obtained for each boron cluster.

Low-energy structures were then fully optimized at the PBE0/def2-TZVP and PBE0/6-311G* levels.44−46 Different spin multiplicities (doublet, quartet, and sextet) are tested for the system considered during the optimization process. After the geometry optimizations, frequency analyses were conducted and electronic structures were studied at the PBE0/6-311G* level. The PBE0/6-311+G* and PBE0/6-311G* are reliable levels for boron clusters;15,47−51 specifically, theoretical calculation results with the PBE0/6-311+G* level agree with the experimental results.15 To test the reliability of the PBE0/6-311G* level, we used the 6-311+G* basis set and 6-311G* basis set to calculate the infrared and Raman spectra, and the results show that the infrared and Raman spectra obtained are found to be almost the same using two basis sets. In addition, the bond length of V–V was simulated with the PBE0/6-311G* level. From the calculated results, the simulated bond length (2.64) of V–V is very close to the experimental bond length (2.77) of V–V obtained by Langridge-Smith et al.52 Therefore, the discussion below is on the basis of the PBE0/6-311G* level. All computations were performed using Gaussian 16 software.53 All analyses and various types of isosurface map drawings were realized using the Multiwfn 3.7(dev) code.54

3. Results and Discussion

3.1. Structures and Electronic Properties

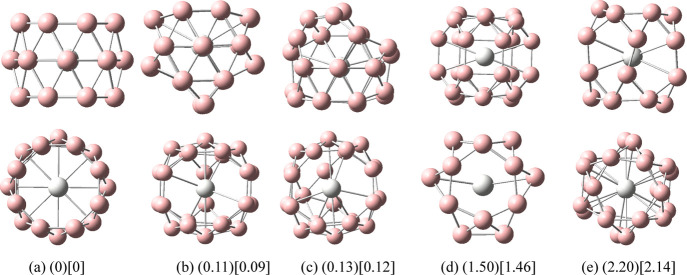
The five low-energy structures of transition metal-doped boron clusters MB24 (M = Sc, V, and Mn) are shown in Figures 1–3. The calculation results show that the low-energy structures of MB24 (M = Sc, V, and Mn) tend to form cage structures, and the lowest-energy structures of MB24 (M = Sc, V, and Mn) are characterized by the lowest spin multiplicity (doublet). Early research found that B24 has a double-ring tubular structure, and B24– has a planar structure. It can be seen from Figure 1 and the calculation results that after adding Sc atoms, the lowest energy structure I of ScB24 has a three-ring tubular structure, comprising three eight-membered rings. The lowest energy structure I has high symmetry (D8h), and the Sc atom is located at the center of the tube. The distance between the Sc atom and each B atom on the eight-membered rings at both ends is 2.59 Å, and the distance from the Sc atom to each B atom on the middle eight-membered ring is 2.30 Å. Similar to tubular B clusters, Sc-doped boron clusters are expected to become the basic unit of boron nanotube materials, which will be further synthesized into boron nanotubes.

Figure 1.

Figure 1

Open in a new tab

Structures of doped boron clusters ScB24. Values in parentheses are the relative energies (eV) of the five low-energy isomers for ScB24 at the PBE0/def2-TZVP level. Values in square brackets are the relative energies (eV) of the five low-energy isomers for ScB24 at the PBE0/6-311G* level. The top row is the side view and the bottom row is the top view. (a) I D8h; (b) II C2; (c) III C1; (d) IV Cs; and (e) V C2h.

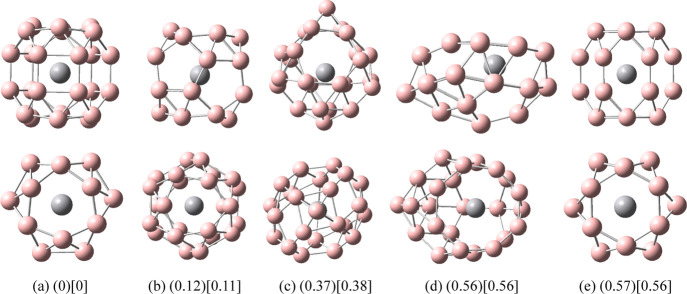
Figure 3.

Figure 3

Open in a new tab

Structures of doped boron clusters MnB24. Values in parentheses are the relative energies (eV) of the five low-energy isomers for MnB24 at the PBE0/def2-TZVP level. Values in square brackets are relative energies (eV) of the five low-energy isomers for MnB24 at the PBE0/6-311G* level. The top row is the side view and the bottom row is the top view. (a) I C2; (b) II C2h; (c) III C2h; (d) IV C1; and (e) V D2h.

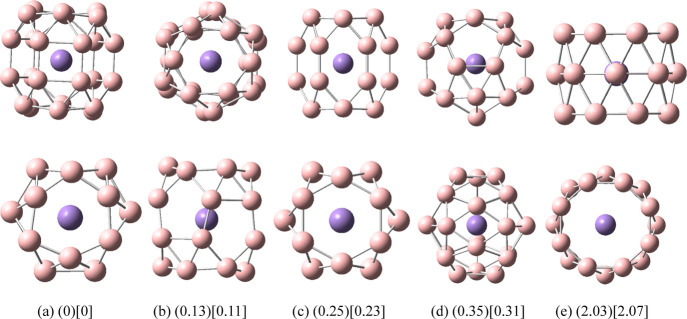
It can be seen from Figures 2 and 3 that the lowest energy structures of VB24 and MnB24 have similar cage structures comprising a six-membered ring at each end and two six-membered rings in the middle. Among them, VB24 has high symmetry (D3), and the V atom is located at the center of the cage. The distance between the V atom and each B atom on the six-membered rings at each end of the cage is 2.54 Å, and the distance between the V atom and each B atom on the two six-membered rings in the middle is 2.40 Å. The Mn atom of MnB24 slightly deviates from the center of the cage, which leads to a decrease in the symmetry of MnB24 (C2). In the following discussion, the main focus is on the study of the lowest energy structure I.

Figure 2.

Figure 2

Open in a new tab

Structures of doped boron clusters VB24. Values in parentheses are the relative energies (eV) of the five low-energy isomers for VB24 at the PBE0/def2-TZVP level. Values in square brackets are the relative energies (eV) of the five low-energy isomers for VB24 at the PBE0/6-311G* level. The top row is the side view and the bottom row is the top view. (a) I D3; (b) II C2h; (c) III C2; (d) IV Cs; and (e) V C2h.

Some of the ground-state parameters of transition metal-doped boron clusters MB24 (M = Sc, V, and Mn) are listed in Table 1, including the lowest harmonic frequency, dipole moment, atomic charge on doped transition-metal atoms, and Mayer bond level.55 The lowest harmonic frequency analysis (see Table 1 for the lowest harmonic frequencies of each cluster) confirmed that these lowest energy structures are indeed stable (no imaginary frequency). To further illustrate the stability of the clusters, the average binding energy of the clusters is calculated, as follows

3.1. 1

Table 1. Lowest Frequencies, Average Binding Energy, Charges on the Doped Atom, Dipole Moments (μ), and Mayer Bond Orders between Doped Metal Atoms and B Atoms of MB24 (M = Sc, V, and Mn).

  lowest frequencies/cm–1 average binding energy/eV charges on doped atom μ/debye Mayer bond order between doped atom M and B atom
ScB24 156 5.31 0.50 0 0.14–0.19
VB24 73 5.39 0.80 0 0.17–0.22
MnB24 135 5.31 0.97 0.1 0.08–0.24
Open in a new tab

The calculation results are listed in Table 1. The average binding energy of MB24 (M = Sc, V, and Mn) is approximately 5.3 eV, indicating that the stabilities of MB24 (M = Sc, V, and Mn) are not much different.

The charge population analysis shows that all the metal atoms show positive charges, indicating that electrons have been transferred to the boron atoms and the Mn atoms have transferred almost one electron. Because there is more than one outer valence electron of Sc, V, or Mn, only a small part of the electrons has been transferred. Analysis shows that the Mayer bond level of the metal atom M and B atom of these clusters is between 0.08 and 0.24 and it is less than 1, indicating that no obvious covalent bond is formed between the metal atom and the B atom. Because ScB24 and VB24 have high symmetry, D8h and D3, their dipole moments are 0. MnB24 exhibits a small dipole moment owing to its reduced symmetry, although its structure is similar to that of VB24.

Figures 4 and S1 and S2 (Supporting Information) show the localized orbital locator (LOL)56 of the valence electrons of ScB24, VB24, and MnB24. The LOL can well-describe the delocalization of electrons. Under the same isosurface value, a fatter (represents the bigger volume and wider connected area occupied by an isosurface map) isosurface means that electron delocalization is easier and a thinner isosurface means that electron delocalization is relatively difficult. When the isosurface value is 0.59 (data not shown), the isosurface maps of ScB24 are connected on the tube wall and the isosurface maps of VB24 and MnB24 are connected on the surface of the cage. Figure 4 shows the LOL when the isosurface value is 0.62. With this isosurface value, the isosurface diagram of ScB24 is still connected on the tube wall (both ends of the tube are also connected), while the isosurface diagrams of VB24 and MnB24 are broken on the surface of the cage. However, the upper and lower halves of the cage are still connected, indicating that the delocalization of the whole ScB24 molecule is stronger than that of the other two clusters. Figure 4 also shows that there is a wide blank area around the metal atom, showing that the metal atom does not form an obvious covalent bond with the surrounding B atoms, which is consistent with the Mayer bond level analysis. Figure S1 shows the LOL when the isosurface value is 0.72. Under this isosurface value, the isosurface diagram of ScB24 is still connected on the tube wall but the isosurface map is disconnected at both ends of the tube (see the isosurface diagram on the left in Figure S1a). Figure S2 shows the LOL when the isosurface value is 0.73. Under this isosurface value, all the isosurface maps of ScB24 are disconnected and there are no connected regions. The isosurface maps of VB24 and MnB24 show that there is still a connected area in the upper half or lower half of the cage, indicating that the local delocalization of ScB24 is weaker than the other two clusters. Tubular-structure ScB24 and cage-type VB24 and MnB24 are expected to become the basic units of boron nanomaterials and be further synthesized into boron nanotubes or other three-dimensional materials. Considering the electron delocalization characteristics of these clusters, they are expected to be applied to molecular devices or molecular switches.

Figure 4.

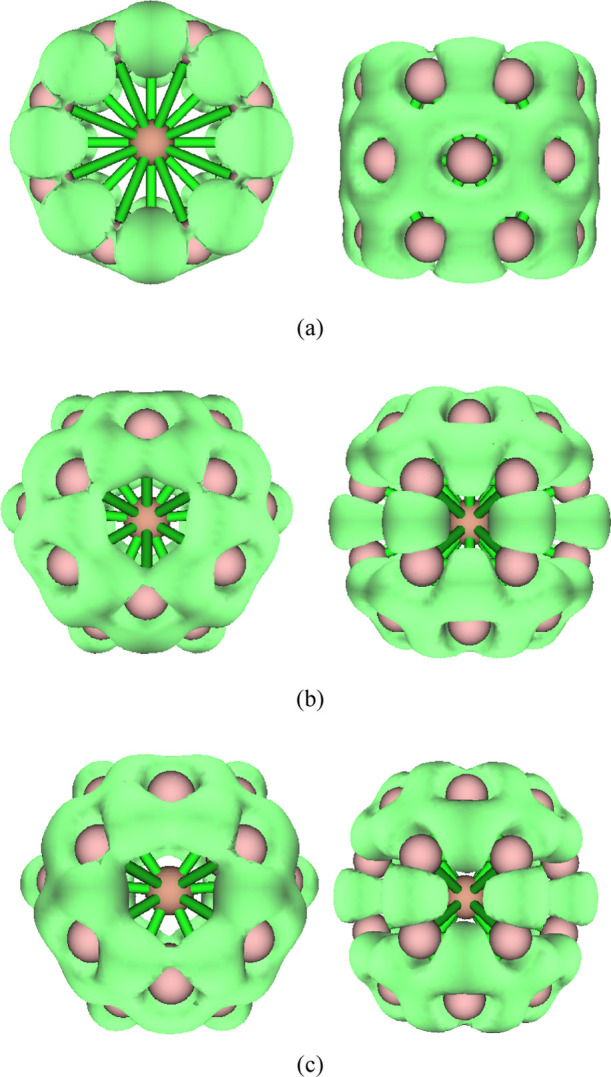
Figure 4

Open in a new tab

LOL with the isovalue set to 0.62. The left is the top view and the right is the side view. (a) ScB24; (b) VB24; (c) MnB24.

To further characterize the electron localization and chemical bonds, the electron localization function (ELF)57 of the valence electrons was analyzed, as shown in Figures S3–S5 (Supporting Information). Figures S3–S5 also show that there is a wide blank area around the metal atom, showing that the metal atom does not form an obvious covalent bond with the surrounding B atoms, which is consistent with the Mayer bond level and LOL analysis. In addition, with the increase in the isosurface value, the ELF isosurface shows similar characteristics to the LOL isosurface such as the delocalization of whole ScB24 molecule is stronger than that of the other two clusters.

Figures S6 and S7 (Supporting Information) show the isosurface diagrams of valence electron density for ScB24, VB24, and MnB24 with isosurface values of 0.16 and 0.20, respectively. Electron density describes the characteristics of electron distribution. Under the same isosurface value, a fatter (represents the bigger volume and wider connected area occupied by an isosurface map) isosurface means more electrons and a thinner isosurface means fewer electrons. The isosurface diagram of Sc is the thinnest and that of Mn is the thickest under the same isosurface value, indicating that the electron density of Mn is the highest. From the previous atomic charge population analysis, we found that the charges on Sc, V, and Mn were 0.5, 0.8, and 0.97, respectively. The valence electrons of Sc, V, and Mn are 3, 5, and 7, respectively, so when the transferred electrons are removed, the remaining valence electrons of Sc, V, and Mn should be 2.5, 4.2, and 6.03. From this, it can be inferred that under the same isosurface value, the isosurface map of the Mn atom is the thickest and that of Sc is the thinnest. In addition, because the B atom has three valence electrons in addition to part of the electrons transferred from the metal atom, it has between 3 and 4 valence electrons. Therefore, the electron density of the B atom should be greater than that of Sc but less than that of V and Mn. The calculation results (isosurface diagrams of valence electron density) show that as the value of the isosurface increases, the isosurface diagram of the Sc atom will disappear first and that of the B atoms in the ScB24 will disappear later (as shown in Figures S6a and S7a), indicating that the electron density of the B atoms is greater than that of Sc. With the increase in the isosurface value, the isosurface diagrams of the B atoms in VB24 and MnB24 will disappear first, and the electron density isosurfaces of V and Mn atoms will disappear later, indicating that the electron density of the B atoms is less than those of the V and Mn atoms. The electron density isosurface diagrams are qualitatively consistent with the atomic charge analysis results.

Figure 5 shows the isosurface diagram of the spin density of ScB24, VB24, and MnB24. Spin density reveals the distribution of unpaired electrons (single electrons) in three-dimensional space. A positive spin density means that there are more α electrons than β electrons, while a negative spin density means that there are more β electrons than α electrons. Figure 5 shows a spin density diagram for an isosurface value of 0.002. Green represents a positive value (α electrons), while blue represents a negative value (β electrons). It can be seen from Figure 5 that the unpaired single electrons of ScB24 are α electrons that are distributed on Sc and B atoms. The unpaired single electrons of VB24 are α electrons that are distributed on V atoms. The unpaired single electrons of MnB24 are both α and β electrons. Most of the unpaired α electrons are distributed on the Mn atom; only a small part of the unpaired α electrons is on two B atoms. The unpaired β electrons of MnB24 are distributed on the other B atoms. To further quantitatively analyze the distribution of unpaired single electrons on different atoms, the spin population is calculated. The spin population is defined as the α electron population minus the β electron population. For example, if the spin population of an atom is one, the α electron population of this atom is one more than its β electron population. A positive population corresponds to an α single electron, while a negative population corresponds to a β single electron. The spin population analysis shows that there is one unpaired α electron in the ScB24 system, of which 0.38 is on the Sc atom and the remaining 0.62 is on the B atom. This result is consistent with the spin density diagram. The VB24 system has one unpaired single α electron, of which 0.97 is on the V atom and the remaining 0.03 is on the B atom (this basically can be ignored). This result is also consistent with the spin density diagram. Although the total number of unpaired electrons in the MnB24 system is 1, 2.01 unpaired α electrons and 1.01 unpaired β electrons are distributed in the system, of which 1.83 α electrons are on the Mn atom and 0.18 α electrons are on the two B atoms; the 1.01 β electrons are distributed on the remaining B atoms. This result is also consistent with the spin density diagram. The spin density reflects chemical reactions or adsorption to a certain extent. The single electrons of ScB24 are all α electrons and are basically evenly distributed on the B atoms. The B atoms containing α single electrons can pair with free radicals or small molecules containing β single electrons to form new covalent bonds. For the MnB24 system, two B atoms with single α electrons can adsorb or react with free radicals or small molecules with single β electrons, while B atoms with single β electrons can adsorb or react with atoms, free radicals, or small molecules with α single electrons. In addition, these spin features are expected to produce interesting magnetic properties, which will further lead to potential applications in molecular devices.

Figure 5.

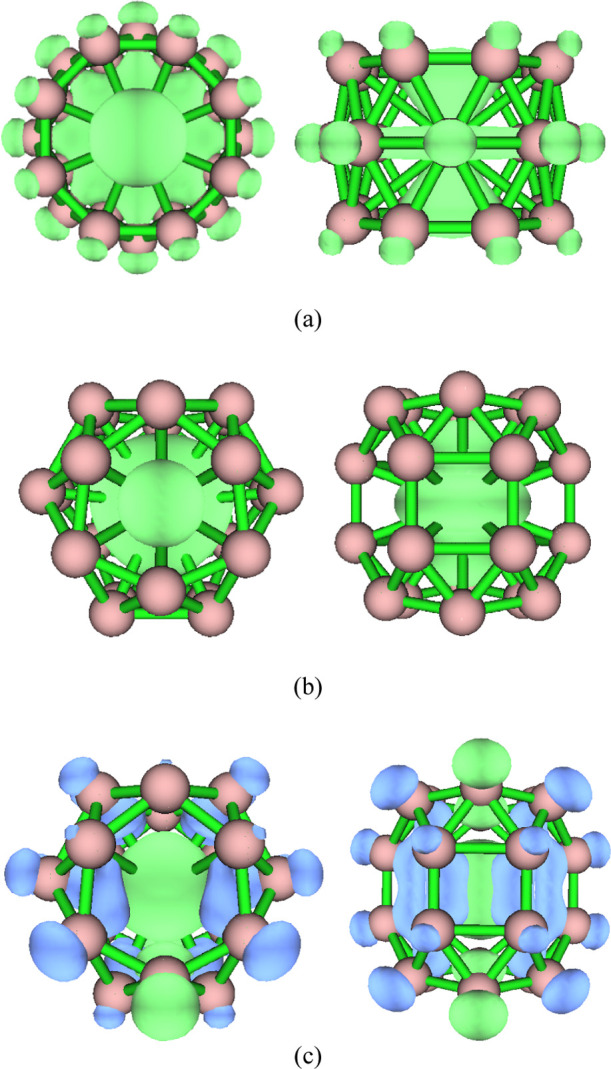
Figure 5

Open in a new tab

Spin density with the isovalue set to 0.002. Green represents a positive value (α electrons), and blue represents a negative value (β electrons). (a) ScB24; (b) VB24; and (c) MnB24.

3.2. Polarization Properties

To understand the polarization properties of the clusters, the polarizability of the system was calculated, including average isotropic polarizability α, average polarizability α̅ of a single atom, anisotropic polarizability Δα, and the first hyperpolarization β0. α is also called the linear optical coefficient. The anisotropic polarizability describes the response of the system to electric fields from different directions. The larger the value, the stronger is the anisotropic response to the external electric field. The first hyperpolarizability is also called the second-order NLO coefficient, which evaluates the NLO properties of molecules. It can be seen from Table 2 that the polarizability of ScB24 is slightly higher than that of VB24 and MnB24, indicating that the bonding interactions between the atoms within ScB24 are slightly stronger than those of VB24 and MnB24, and ScB24 is more likely to be polarized by an external electric field. The average polarizability of ScB24 is slightly greater than that of VB24 and MnB24, indicating that the electronic structures of VB24 and MnB24 are relatively stable. The anisotropic polarizability of VB24 is the smallest and that of ScB24 is the largest, indicating that VB24 has the weakest anisotropic response and ScB24 has the strongest response to an external electric field. It can be seen from Table 2 that the first hyperpolarizability of ScB24 is equal to 0, indicating that there is no NLO response; the first hyperpolarizability of VB24 is 0.436, indicating that the NLO response is extremely small, and MnB24 has a larger first hyperpolarizability, indicating that MnB24 has a strong NLO response.

Table 2. Polarizabilities of MB24 (M = Sc, V, and Mn).

  α/au α̅ /au Δα/au β0/au
ScB24 299.047 11.96 27.29 0
VB24 280.658 11.22 12.59 0.436
MnB24 284.329 11.37 19.91 53.83
Open in a new tab

3.3. Infrared and Raman Spectra

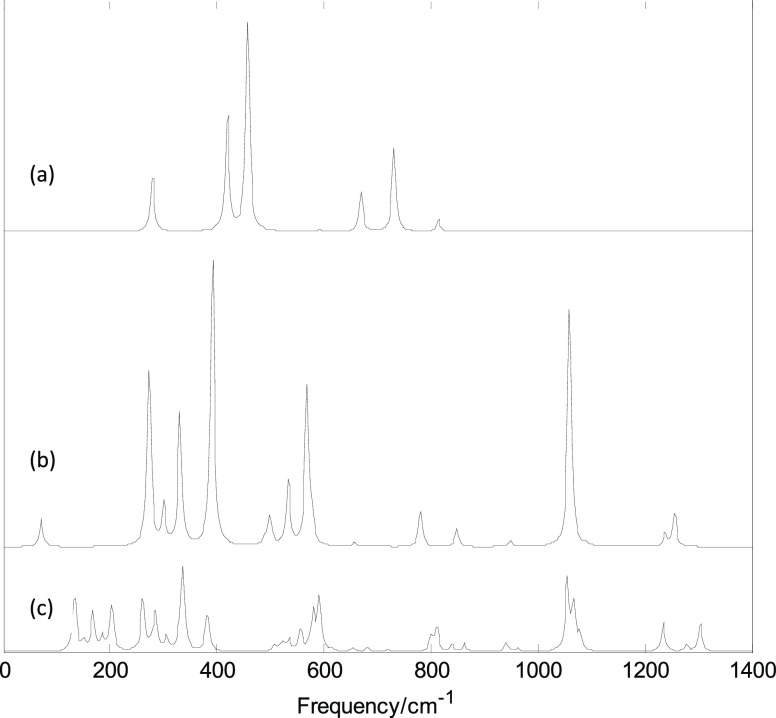
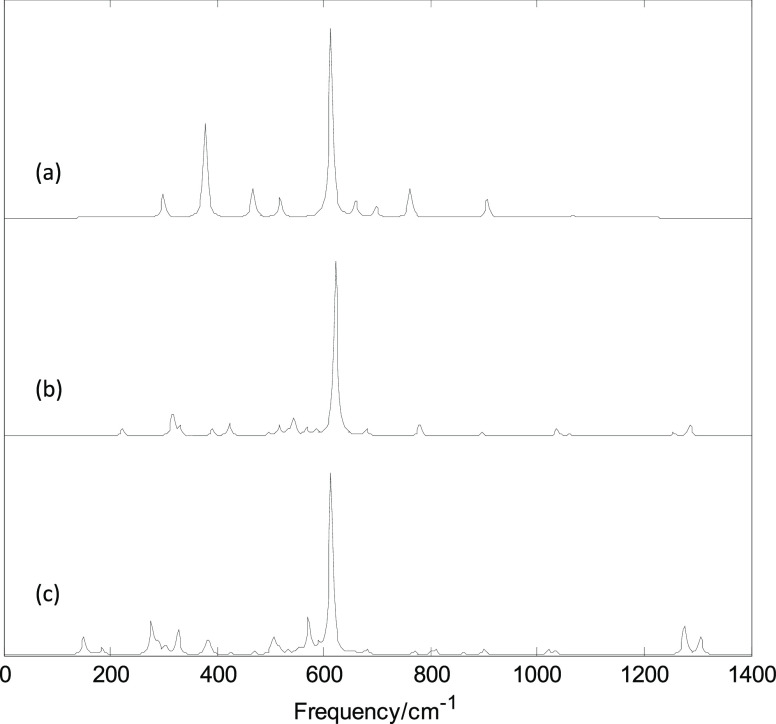
Figures 6 and 7 show plots of the calculated infrared and Raman spectra of MB24 (M = Sc, V, and Mn) with the PBE0/6-311G(d) method. Figure S8 (Supporting Information) shows the strongest infrared-active vibration mode and Raman-active vibration mode. The lowest harmonic frequencies of these clusters are listed in Table 1. From Table 1 and Figure 6, it can be seen that the cluster structure has a strong influence on the harmonic frequency because these vibration modes are derived from the stretching or bending vibrations of the atoms. Differences in the arrangement of atoms will lead to different modes of vibration. From the calculation results, it can be seen that among the 69 vibration modes of ScB24, only 13 modes are infrared-active and 56 are all inactive. Among the 13 infrared-active modes, five pairs are double-degenerate vibration modes, so there are eight infrared peaks. In the infrared spectrum of ScB24, the first and second peaks are located at 278 and 419 cm–1, respectively, and the second peak is produced by a pair of degenerate vibration modes. The third peak is the strongest, located at 457 cm–1, and is generated by a pair of degenerate vibration modes (in Figure S8a,b). The thick yellow arrow in Figure S8 is the direction vector of the dipole moment changed, caused by the vibration (under resonance approximations, only the infrared intensity of the mode whose dipole moment changes is not zero). The fourth to eighth peaks are located at 592, 669, 731, 813, and 857 cm–1, respectively. The eighth peak is not shown in the figure owing to its weak activity. The fifth, sixth, or eighth peak was generated by a pair of degenerate vibration modes. Among the 69 vibration modes of ScB24, 19 modes are Raman-active vibration modes and 50 are inactive modes. Among the 19 Raman-active modes, eight pairs are degenerate vibration modes. The strongest peak is located at 613 cm–1 and is generated by the radial breathing vibration of the boron atoms on the ring (the vibration mode is shown in Figure S8c). This radial breathing mode can reveal important characteristics of nanotubes. It can be seen from the calculation results that the 13 infrared-active modes are Raman-inactive and the 19 Raman-active modes are all infrared-inactive. Under the resonance approximation, the infrared intensity is not zero for only the mode where vibration changes the dipole moment and the Raman activity is not zero for only the mode where vibration changes the polarizability. Therefore, the 13 infrared-active modes did not cause changes in the polarizability and the 19 Raman-active modes did not cause changes in the dipole moment. These vibration characteristics are mainly due to the three-ring structure of ScB24 and the high D8h symmetry.

Figure 6.

Figure 6

Open in a new tab

Calculated infrared spectra with the PBE0/6-311G(d) method. (a) ScB24; (b) VB24; and (c) MnB24.

Figure 7.

Figure 7

Open in a new tab

Calculated Raman spectra with the PBE0/6-311G(d) method. (a) ScB24; (b) VB24; and (c) MnB24.

The calculation results show that among the 69 vibration modes of VB24, 41 modes are infrared-active vibration modes and 28 are inactive modes. The strongest infrared peak is also a pair of degenerate vibration modes (the vibration mode is shown in Figure S8d,e). Among the 69 vibration modes of VB24, there are 57 Raman-active modes and 12 inactive modes. The strongest Raman peak is located at 622 cm–1, which is also produced by the radial breathing vibration of boron atoms (the vibration mode is shown in Figure S8f). Among the 69 vibration modes of MnB24, 59 are infrared-active and 10 are inactive. The vibration mode of the strongest infrared peak is shown in Figure S8g. The 69 vibration modes of MnB24 are Raman-active modes, and the strongest Raman peak is located at 614 cm–1. This strongest peak is also generated by the radial breathing vibration of boron atoms (the vibration mode is shown in Figure S8h). It can be seen from Figure 6 that VB24 and MnB24 have some similar band characteristics, but owing to the low symmetry of MnB24, many new band characteristics are also generated, such as several stronger peaks around 200 cm–1. In addition, from Figure 7 and the calculation results, the strongest Raman peaks of the three structures are all located at approximately 610 cm–1, and they are all radial breathing modes. Although VB24 and MnB24 have cage structures, they can be considered variable-diameter tubes. The diameters of the rings are approximately 3.5 Å; therefore, the breathing mode of the three structures is located at approximately 610 cm–1. The characteristic peaks and band characteristics of the clusters can be used to identify these structures, which can be compared and analyzed in future experiments.

3.4. Electronic Absorption Spectra

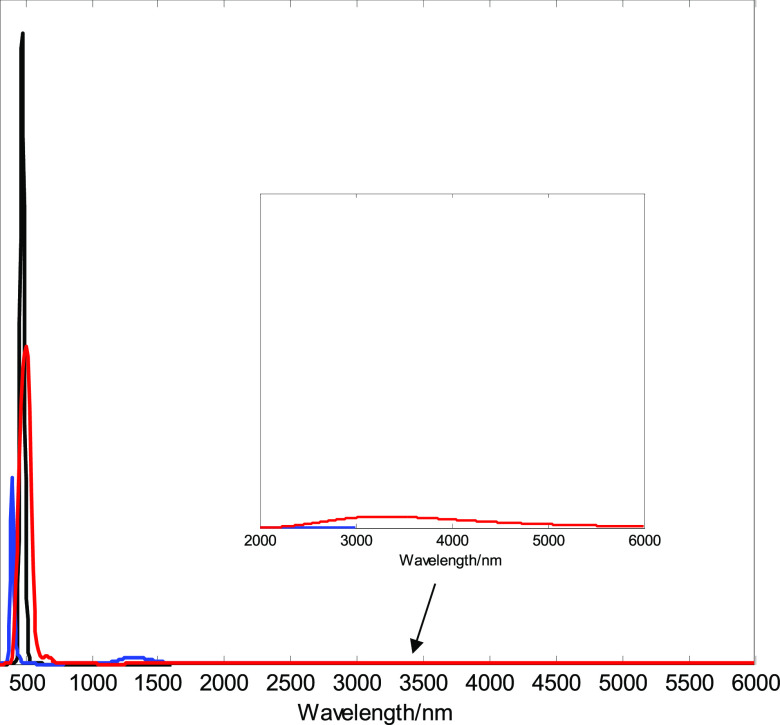
Based on the previous calculations, the TD-PBE0/6-311G* method was used to calculate the ultraviolet (UV)–visible spectrum of MB24 (M = Sc, V, and Mn) (excitation energy E, wavelength λ, and oscillator intensity f of the first 36 excited states). Figure 8 shows the electronic absorption spectra, and Table 3 shows some of the excited-state parameters. It can be seen from Table 3 that except for ScB24, the absorption peaks of these clusters extend to the infrared band. The wavelength of the first excited state of MB24 (M = Sc, V, and Mn) is in the infrared band, and the first excited state of ScB24 and VB24 is the forbidden excited state (oscillator intensity is 0) (see Table 3). The first excited states of ScB24, VB24, and MnB24 are mainly derived from the electronic transitions of β-HOMO → β-LUMO, β-HOMO → β-LUMO, and α-HOMO → α-LUMO, respectively. In addition, it can be concluded from Table 3 that the wavelength of the first excited state of MnB24 (3302 nm) is the largest, the wavelength of the first excited state of VB24 is 1984 nm, and the wavelength of the first excited state of ScB24 (1110 nm) is the shortest. Although the structures of VB24 and MnB24 are similar, their excitation characteristics are obviously different.

Figure 8.

Figure 8

Open in a new tab

Electronic absorption spectra. The black line represents ScB24, the blue line represents VB24, and the red line represents MnB24.

Table 3. Excitation Properties of MB24 (M = Sc, V, and Mn).

  wavelength of the first excited state (oscillator intensity) first absorption peak (corresponding excited states)
ScB24 1110 nm (0) 474 nm (30)
VB24 1984 nm (0) 1319 nm (3,4)
MnB24 3302 nm (0.0001) 3302 nm (1)
Open in a new tab

From Figure 8 and Table 3, it can be seen that only the first absorption peak of ScB24 is in the visible light band and the first absorption peaks of VB24 and MnB24 are both in the infrared light band. The first absorption peak of MnB24 in the main picture of Figure 8 is too weak to be displayed (see the inset for the enlarged absorption peak), which is located at 3302 nm. It can be seen from Table 3 that only the first absorption peak of MnB24 corresponds to the wavelength position of the first excited state, and the absorption is very weak. However, because the first and second excited states are forbidden excited states, the first absorption peak of VB24 corresponds to the wavelength (1319 nm) of the third and fourth excited states (degenerate). In particular, there is only one absorption peak in the UV–visible spectrum of ScB24, which is derived from the 30th excited state (wavelength is 474 nm), and the other excited states are forbidden excited states. The 30th excited state comes from the electronic transition of α-HOMO → α-LUMO + 7. The electron absorbs the photon to transition from the ground state to the excited state when the vibration intensity is not zero, then transitions from the highly excited state to the low excited state (nonradiative transition), and finally transitions from the lowest excited state back to the ground state and emits light. From the foregoing analysis, it can be inferred that the wavelengths corresponding to the first excited state of these clusters returning to the ground state are all in the infrared light region, so there are emission spectra in the infrared light band. The spectral characteristics of these clusters can be used to identify their structures.

4. Conclusions

In this work, density functional theory combined with the particle swarm optimization algorithm (CALYPSO) software is used to research the ground-state geometric structure of transition metal-doped boron clusters MB24 (M = Sc, V, and Mn). The electronic structures and spectral properties such as infrared and Raman spectra are further discussed. Research results include the following seven points: (1) ScB24 has a three-ring tubular structure, while VB24 and MnB24 have cage structures. (2) Charge population analysis and valence electron density analysis show that doped atoms transfer part of their electrons to boron atoms. (3) The LOL analysis shows that the electron delocalization effect of the entire ScB24 molecule is greater than that of VB24 and MnB24; however, the metal atoms and the surrounding B atoms do not form an obvious covalent bond. (4) The electron spin density analysis shows that ScB24 can adsorb free radicals or small molecules with β single electrons. For the MnB24 system, two B atoms with single electrons can adsorb free radicals or small molecules with β single electrons or react with free radicals or small molecules with β single electrons; B atoms with β single electrons can adsorb atoms, free radicals, or small molecules with α single electrons or react with atoms, free radicals, or small molecules with α single electrons. (5) The polarization analysis indicates that the average polarization of each atom of ScB24 is greater than that of VB24 and MnB24. The first hyperpolarization of ScB24 is 0, which indicates that there is no NLO response. (6) The infrared and Raman spectroscopies show that ScB24 has eight infrared-active characteristic peaks. The strongest Raman-active modes of ScB24, VB24, and MnB24 are located at approximately 610 cm–1. These characteristics can be compared with the experimental values. (7) Through the analysis of the electronic absorption spectra of the clusters, ScB24 is found to have the only strong absorption peak in the visible light region, and VB24 and MnB24 have weaker absorption peaks in the infrared light region. This research has enriched the structure of doped boron clusters and has certain theoretical guiding significance for the preparation of new boron nanomaterials, especially boron nanotubes.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (11804065) and the Central Guiding Local Science and Technology Development Foundation of China (grant no. QK ZYD[2019]4012).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c03740.

  • LOL of MB24 (M = Sc, V, and Mn); ELF of MB24 (M = Sc, V, and Mn); valence electron density of MB24 (M = Sc, V, and Mn); and vibrational modes of MB24 (M = Sc, V, and Mn) (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao1c03740_si_001.pdf (1MB, pdf)

References

  1. Kroto H. W.; Heath J. R.; O’Brien S. C.; Curl R. F.; Smalley R. E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. 10.1038/318162a0. [DOI] [Google Scholar]
  2. Iijima S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. 10.1038/354056a0. [DOI] [Google Scholar]
  3. Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Zhang Y.; Dubonos S. V.; Grigorieva I. V.; Firsov A. A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
  4. Boustani I. Systematic ab initio investigation of bare boron clusters:mDetermination of the geometryand electronic structures of Bn(n=2–14). Phys. Rev. B: Condens. Matter Mater. Phys. 1997, 55, 16426–16438. 10.1103/physrevb.55.16426. [DOI] [Google Scholar]
  5. Zhai H.-J.; Wang L.-S.; Alexandrova A. N.; Boldyrev A. I. Electronic structure and chemical bonding of B5– and B5 by photoelectron spectroscopy andab initiocalculations. J. Chem. Phys. 2002, 117, 7917–7924. 10.1063/1.1511184. [DOI] [Google Scholar]
  6. Zhai H.-J.; Kiran B.; Li J.; Wang L.-S. Hydrocarbon analogues of boron clusters--planarity, aromaticity and antiaromaticity. Nat. Mater. 2003, 2, 827–833. 10.1038/nmat1012. [DOI] [PubMed] [Google Scholar]
  7. Kiran B.; Bulusu S.; Zhai H.-J.; Yoo S.; Zeng X. C.; Wang L.-S. Planar-to-tubular structural transition in boron clusters: B20 as the embryo of single-walled boron nanotubes. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 961–964. 10.1073/pnas.0408132102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bean D. E.; Fowler P. W. Double Aromaticity in “Boron Toroids”. J. Phys. Chem. C 2009, 113, 15569–15575. 10.1021/jp905926j. [DOI] [Google Scholar]
  9. Chen Q.; Wei G.-F.; Tian W.-J.; Bai H.; Liu Z.-P.; Zhai H.-J.; Li S.-D. Quasi-planar aromatic B36 and B36- clusters: all-boron analogues of coronene. Phys. Chem. Chem. Phys. 2014, 16, 18282–18287. 10.1039/c4cp02032d. [DOI] [PubMed] [Google Scholar]
  10. Sergeeva A. P.; Popov I. A.; Piazza Z. A.; Li W.-L.; Romanescu C.; Wang L.-S.; Boldyrev A. I. Understanding boron through size-selected clusters: structure, chemical bonding, and fluxionality. Acc. Chem. Res. 2014, 47, 1349–1358. 10.1021/ar400310g. [DOI] [PubMed] [Google Scholar]
  11. Jian T.; Chen X.; Li S.-D.; Boldyrev A. I.; Li J.; Wang L.-S. Probing the structures and bonding of size-selected boron and doped-boron clusters. Chem. Soc. Rev. 2019, 48, 3550–3591. 10.1039/c9cs00233b. [DOI] [PubMed] [Google Scholar]
  12. Casillas R.; Baruah T.; Zope R. R. Geometry and electronic structure of neutral and charged B21 clusters. Chem. Phys. Lett. 2013, 557, 15–18. 10.1016/j.cplett.2012.10.076. [DOI] [Google Scholar]
  13. Pham H. T.; Duong L. V.; Pham B. Q.; Nguyen M. T. The 2D-to-3D geometry hopping in small boron clusters: The charge effect. Chem. Phys. Lett. 2013, 577, 32–37. 10.1016/j.cplett.2013.05.041. [DOI] [Google Scholar]
  14. Lv J.; Wang Y.; Zhu L.; Ma Y. B38: an all-boron fullerene analogue. Nanoscale 2014, 6, 11692–11696. 10.1039/c4nr01846j. [DOI] [PubMed] [Google Scholar]
  15. Zhai H.-J.; Zhao Y.-F.; Li W.-L.; Chen Q.; Bai H.; Hu H.-S.; Piazza Z. A.; Tian W.-J.; Lu H.-G.; Wu Y.-B.; Mu Y.-W.; Wei G.-F.; Liu Z.-P.; Li J.; Li S.-D.; Wang L.-S. Observation of an all-boron fullerene. Nat. Chem. 2014, 6, 727–731. 10.1038/nchem.1999. [DOI] [PubMed] [Google Scholar]
  16. Bai H.; Chen Q.; Zhai H.-J.; Li S.-D. Endohedral and exohedral metalloborospherenes: M@B40 (M=Ca, Sr) and M&B40 (M=Be, Mg). Angew. Chem., Int. Ed. 2015, 54, 941–945. 10.1002/anie.201408738. [DOI] [PubMed] [Google Scholar]
  17. Li S.-X.; Zhang Z.-P.; Long Z.-W.; Qin S.-J. Structures, stabilities and spectral properties of metalloborospherenes MB400/– (M = Cu, Ag, and Au). RSC Adv. 2017, 7, 38526–38537. 10.1039/c7ra05932a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Dong H.; Hou T.; Lee S.-T.; Li Y. New Ti-decorated B40 fullerene as a promising hydrogen storage material. Sci. Rep. 2015, 5, 9952. 10.1038/srep09952. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. An Y.; Zhang M.; Wu D.; Fu Z.; Wang T.; Xia C. Electronic transport properties of the first all-boron fullerene B40 and its metallofullerene Sr@B40. Phys. Chem. Chem. Phys. 2016, 18, 12024–12028. 10.1039/c6cp01096b. [DOI] [PubMed] [Google Scholar]
  20. Bai H.; Bai B.; Zhang L.; Huang W.; Mu Y.-W.; Zhai H.-J.; Li S.-D. Lithium-Decorated Borospherene B40: A Promising Hydrogen Storage Medium. Sci. Rep. 2016, 6, 35518. 10.1038/srep35518. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Shakerzadeh E.; Biglari Z.; Tahmasebi E. M@B40 (M = Li, Na, K) serving as a potential promising novel NLO nanomaterial. Chem. Phys. Lett. 2016, 654, 76–80. 10.1016/j.cplett.2016.05.014. [DOI] [Google Scholar]
  22. Tang C.; Zhang X. The hydrogen storage capacity of Sc atoms decorated porous boron fullerene B40: A DFT study. Int. J. Hydrogen Energy 2016, 41, 16992–16999. 10.1016/j.ijhydene.2016.07.118. [DOI] [Google Scholar]
  23. Li S.; Zhang Z.; Long Z.; Chen D. Structures, Stabilities, and Spectral Properties of Endohedral Borospherenes M@B400/- (M = H2, HF, and H2O). ACS Omega 2019, 4, 5705–5713. 10.1021/acsomega.9b00209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Li S.-X.; Zhang Z.-P.; Long Z.-W.; Chen D.-L. Structures, Electronic, and Spectral Properties of Doped Boron Clusters MB120/- (M = Li, Na, and K). ACS Omega 2020, 5, 20525–20534. 10.1021/acsomega.0c02693. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Popov I. A.; Li W.-L.; Piazza Z. A.; Boldyrev A. I.; Wang L.-S. Complexes between planar boron clusters and transition metals: a photoelectron spectroscopy and ab initio study of CoB12- and RhB12-. J. Phys. Chem. A 2014, 118, 8098–8105. 10.1021/jp411867q. [DOI] [PubMed] [Google Scholar]
  26. Liang W.-y.; Das A.; Dong X.; Cui Z.-h. Lithium doped tubular structure in LiB20 and LiB20-: a viable global minimum. Phys. Chem. Chem. Phys. 2018, 20, 16202–16208. 10.1039/c8cp01376d. [DOI] [PubMed] [Google Scholar]
  27. Wang W.; Guo Y.-D.; Yan X.-H. The spin-dependent transport of transition metal encapsulated B40 fullerene. RSC Adv. 2016, 6, 40155–40161. 10.1039/c6ra00179c. [DOI] [Google Scholar]
  28. Saha R.; Kar S.; Pan S.; Martínez-Guajardo G.; Merino G.; Chattaraj P. K. A Spinning Umbrella: Carbon Monoxide and Dinitrogen Bound MB12– Clusters (M = Co, Rh, Ir). J. Phys. Chem. A 2017, 121, 2971–2979. 10.1021/acs.jpca.6b12232. [DOI] [PubMed] [Google Scholar]
  29. Li S.-X.; Chen D.-L.; Zhang Z.-P.; Long Z.-W. Ground state structures and properties of Be atom doped boron clusters BeBn(n=10–15). Acta Phys. Sin. 2020, 69, 193101. 10.7498/aps.69.20200756. [DOI] [Google Scholar]
  30. Cheung L. F.; Kocheril G. S.; Czekner J.; Wang L.-S. Observation of Mobius Aromatic Planar Metallaborocycles. J. Am. Chem. Soc. 2020, 142, 3356–3360. 10.1021/jacs.9b13417. [DOI] [PubMed] [Google Scholar]
  31. Popov I. A.; Jian T.; Lopez G. V.; Boldyrev A. I.; Wang L.-S. Cobalt-centred boron molecular drums with the highest coordination number in the CoB16- cluster. Nat. Commun. 2015, 6, 8654. 10.1038/ncomms9654. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Jian T.; Li W.-L.; Popov I. A.; Lopez G. V.; Chen X.; Boldyrev A. I.; Li J.; Wang L.-S. Manganese-centered tubular boron cluster - MnB16-: A new class of transition-metal molecules. J. Chem. Phys. 2016, 144, 154310. 10.1063/1.4946796. [DOI] [PubMed] [Google Scholar]
  33. Chen T.-T.; Li W.-L.; Bai H.; Chen W.-J.; Dong X.-R.; Li J.; Wang L.-S. ReB8- and ReB9-: New Members of the Transition-Metal-Centered Borometallic Molecular Wheel Family. J. Phys. Chem. A 2019, 123, 5317–5324. 10.1021/acs.jpca.9b03942. [DOI] [PubMed] [Google Scholar]
  34. Cheung L. F.; Czekner J.; Kocheril G. S.; Wang L.-S. ReB6-: A Metallaboron Analog of Metallabenzenes. J. Am. Chem. Soc. 2019, 141, 17854–17860. 10.1021/jacs.9b09110. [DOI] [PubMed] [Google Scholar]
  35. Chen T.-T.; Li W.-L.; Chen W.-J.; Yu X.-H.; Dong X.-R.; Li J.; Wang L.-S. Spherical trihedral metallo-borospherenes. Nat. Commun. 2020, 11, 2766. 10.1038/s41467-020-16532-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Cheung L. F.; Kocheril G. S.; Czekner J.; Wang L.-S. MnB6-: An Open-Shell Metallaboron Analog of 3d Metallabenzenes. J. Phys. Chem. A 2020, 124, 2820–2825. 10.1021/acs.jpca.0c00949. [DOI] [PubMed] [Google Scholar]
  37. Chen W.-J.; Kulichenko M.; Choi H. W.; Cavanagh J.; Yuan D.-F.; Boldyrev A. I.; Wang L.-S. Photoelectron Spectroscopy of Size-Selected Bismuth-Boron Clusters: BiBn- (n = 6-8). J. Phys. Chem. A 2021, 125, 6751–6760. 10.1021/acs.jpca.1c05846. [DOI] [PubMed] [Google Scholar]
  38. Jiang Z.-Y.; Chen T.-T.; Chen W.-J.; Li W.-L.; Li J.; Wang L.-S. Expanded Inverse-Sandwich Complexes of Lanthanum Borides: La2B10- and La2B11-. J. Phys. Chem. A 2021, 125, 2622–2630. 10.1021/acs.jpca.1c01149. [DOI] [PubMed] [Google Scholar]
  39. Chacko S.; Kanhere D. G.; Boustani I. Ab initio density functional investigation of B24 clusters: Rings, tubes, planes, and cages. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 68, 035414. 10.1103/physrevb.68.035414. [DOI] [Google Scholar]
  40. Liang W.-y.; Das A.; Dong X.; Wang M.-h.; Cui Z.-h. Structural and electronic properties of MB22– (M = Na, K) clusters: tubular boron versus quasi-planar boron forms. New J. Chem. 2019, 43, 6507–6512. 10.1039/c9nj00661c. [DOI] [Google Scholar]
  41. Dong X.; Jalife S.; Vásquez-Espinal A.; Barroso J.; Orozco-Ic M.; Ravell E.; Cabellos J. L.; Liang W.-y.; Cui Z.-h.; Merino G. Li2B24: the simplest combination for a three-ring boron tube. Nanoscale 2019, 11, 2143–2147. 10.1039/c8nr09173k. [DOI] [PubMed] [Google Scholar]
  42. Lv J.; Wang Y.; Zhang L.; Lin H.; Zhao J.; Ma Y. Stabilization of fullerene-like boron cages by transition metal encapsulation. Nanoscale 2015, 7, 10482–10489. 10.1039/c5nr01659b. [DOI] [PubMed] [Google Scholar]
  43. Lv J.; Wang Y.; Zhu L.; Ma Y. Particle-swarm structure prediction on clusters. J. Chem. Phys. 2012, 137, 084104. 10.1063/1.4746757. [DOI] [PubMed] [Google Scholar]
  44. Adamo C.; Barone V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. 10.1063/1.478522. [DOI] [Google Scholar]
  45. Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  46. Krishnan R.; Binkley J. S.; Seeger R.; Pople J. A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. 10.1063/1.438955. [DOI] [Google Scholar]
  47. Chen B. L.; Sun W. G.; Kuang X. Y.; Lu C.; Xia X. X.; Shi H. X.; Maroulis G. Structural Stability and Evolution of Medium-Sized Tantalum-Doped Boron Clusters: A Half-Sandwich-Structured TaB12−Cluster. Inorg. Chem. 2018, 57, 343–350. 10.1021/acs.inorgchem.7b02585. [DOI] [PubMed] [Google Scholar]
  48. Li P.; Du X.; Wang J. J.; Lu C.; Chen H. Probing the Structural Evolution and Stabilities of Medium-Sized MoBn0/− Clusters. J. Phys. Chem. C 2018, 122, 20000–20005. 10.1021/acs.jpcc.8b05759. [DOI] [Google Scholar]
  49. Jin S.; Chen B.; Kuang X.; Lu C.; Sun W.; Xia X.; Gutsev G. L. Structural and Electronic Properties of Medium-Sized Aluminum-Doped Boron Clusters AlBn and Their Anions. J. Phys. Chem. C 2019, 123, 6276–6283. 10.1021/acs.jpcc.9b00291. [DOI] [Google Scholar]
  50. Ren M.; Jin S.; Wei D.; Jin Y.; Tian Y.; Lu C.; Gutsev G. L. NbB12–: a new member of half-sandwich type doped boron clusters with high stability. Phys. Chem. Chem. Phys. 2019, 21, 21746–21752. 10.1039/c9cp03496j. [DOI] [PubMed] [Google Scholar]
  51. Tian Y.; Wei D.; Jin Y.; Barroso J.; Lu C.; Merino G. Exhaustive exploration of MgBn (n = 10-20) clusters and their anions. Phys. Chem. Chem. Phys. 2019, 21, 6935–6941. 10.1039/c9cp00201d. [DOI] [PubMed] [Google Scholar]
  52. Langridge-Smith P. R. R.; Morse M. D.; Hansen G. P.; Smalley R. E.; Merer A. J. J. Chem. Phys. 1984, 80, 593–600. 10.1063/1.446769. [DOI] [Google Scholar]
  53. Frisch M. J.; Trucks G. W.; Schlegel H. B.; et al. Gaussian 16; Gaussian Inc.: Wallingford CT, 2016.
  54. Lu T.; Chen F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
  55. Mayer I. Charge, bond order and valence in the ab initio scf theory. Chem. Phys. Lett. 1983, 97, 270–274. 10.1016/0009-2614(83)80005-0. [DOI] [Google Scholar]
  56. Schmider H. L.; Becke A. D. Chemical content of the kinetic energy density. J. Mol. Struct.: THEOCHEM 2000, 527, 51–61. 10.1016/s0166-1280(00)00477-2. [DOI] [Google Scholar]
  57. Becke A. D.; Edgecombe K. E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. 10.1063/1.458517. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c03740_si_001.pdf (1MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES