Exploring Chemical Reaction Space with Reaction Difference Fingerprints and Parametric t-SNE

Abstract

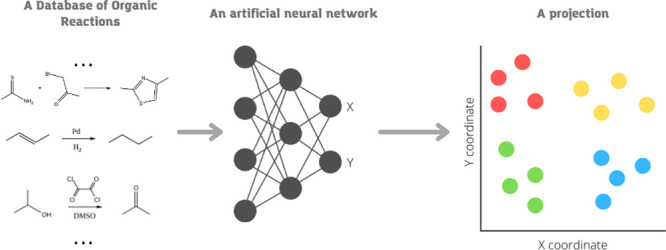
Humans prefer visual representations for the analysis of large databases. In this work, we suggest a method for the visualization of the chemical reaction space. Our technique uses the t-SNE approach that is parameterized using a deep neural network (parametric t-SNE). We demonstrated that the parametric t-SNE combined with reaction difference fingerprints could provide a tool for the projection of chemical reactions on a low-dimensional manifold for easy exploration of reaction space. We showed that the global reaction landscape projected on a 2D plane corresponds well with the already known reaction types. The application of a pretrained parametric t-SNE model to new reactions allows chemists to study these reactions in a global reaction space. We validated the feasibility of this approach for two commercial drugs, darunavir and montelukast. We believe that our method can help to explore reaction space and will inspire chemists to find new reactions and synthetic ways.

1. Introduction

Chemical space is the fundamental concept of organic chemistry. One can regard it as a set of all possible molecules that can exist and satisfy the predefined conditions. If someone regards only small molecules (below 500 Da), there are more than 10⁶⁰ compounds, and that is an enormous number.¹ Chemical reactions are tools that make it possible to traverse through the chemical space to reach new chemical compounds. There are more than 300 name reactions in organic chemistry that have a precise definition,² for example, Suzuki coupling,³ Grignard reaction, and so forth. At the same time, there are about 10⁸ described chemical reactions according to the largest chemical reaction database CASREACT.⁴ This known reaction set is too large to analyze it using humans’ expertise solely. Researchers need new computational approaches to support the exploration of the chemical reaction space.

However, the space of chemical reactions appears to have quite a complicated structure. It is hard to attribute many reactions to a certain type as they may be carried out with surprising agents or result in unexpected products.⁵⁻⁷ The current landscape of drugs is biased toward specific molecular scaffolds and overpopulated with certain shapes that are reachable with reactions chemists are used to (e.g., amide bond formation and S_NAr reactions).⁸ The detailed exploration can mitigate these shortcomings and boost drug discovery. New methods for the visualization of reaction space can provide useful insights to chemists and lead to a better understanding of nature. We believe that, in the “big-data” era, these methods should have the ability to extract information directly from data.

Among various machine learning techniques, the dimensionality reduction of multidimensional space for visualization purposes is particularly popular in cheminformatics. Medicinal chemists use this technique to better understand the chemical data.⁹ The dimensionality reduction methods can be either linear or non-linear. Linear methods assume that the multidimensional data points are located near a linear manifold of lower dimensionality, whereas non-linear methods allow non-linear manifolds. Linear methods include principal component analysis (PCA),¹⁰ canonical correlations analysis (CCA),¹¹ multidimensional scaling (MDS),¹² and many others.¹³ PCA is the most common linear approach; it aims to find the directions with the highest variation in the original multidimensional space. This method is fast and deterministic, but its performance is limited because of its linear nature. Non-linear methods include t-distributed stochastic neighbor embedding (t-SNE),¹⁴ self-organizing maps (SOMs),¹⁵ generative topographic mapping (GTM),¹⁶ and others.¹⁷ Chen and Gasteiger¹⁸ successfully used SOMs to obtain a map of chemical reaction space with distinct regions corresponding to reactions of aliphatic substitution, double C–C bond acylation, and arene acylation. The GTM method has been successfully applied in drug design.¹⁹ It was also recently used to visualize chemical reactions embedded into the latent space of a generative variational autoencoder.²⁰ The t-SNE method was used to explore the structure of bioactive organic molecules data sets.²¹ Probst and Reymond proposed a fresh view on chemical space mapping to non-Euclidean domains: tree map (TMAP).²² This method is based on the visualization of minimum spanning trees. In the following research,²³ Schwaller et al. proposed neural-based vector representations of chemical reactions and used these vectors for TMAP visualization of the reaction space in a fully data-driven way.

In this paper, we describe the application of the parametric t-SNE method to explore chemical reaction space. First, we describe several parametric t-SNE models trained on chemical reactions extracted from US patents. Then, we evaluate the performance of visualizations using a reference data set with predefined chemical reaction classes. Also, we explore the reaction space to reveal the regions comprising reactions united by the same chemical meaning, such as common reagents or the type of reaction. Finally, we use our approach to overview a set of reactions leading to the synthesis of some commercial drugs. We believe that our technique can provide a sensible overview of the chemical reaction space through similar types gathering in distinct clusters. This visualization technique can provide some chemical insights or aid in synthesis planning to speed up chemists’ work.

2. Results and Discussion

Our goal was to create a method for chemists to navigate in reaction space. A good visualization algorithm should group similar reactions in well-shaped clusters, and these clusters should at least be chemically reasonable.

First, we experimented with models trained on reaction difference fingerprints and BERT FP. The learning curves of these models are shown in Figure S1 in Supporting Information. As these curves indicate, overfitting does not occur and early stopping is not needed.

The accuracy scores of class separation with a LightGBM classifier are given in Table 1. First, we compare the performance of difference fingerprints from RDKit and BERT fingerprints. Our experiments revealed that the influence of the type of difference fingerprints on the qualities of projections is negligible. However, topological torsion descriptors demonstrated marginally better performance of the reaction class discrimination (Table 1).

Table 1. Accuracy Scores (%) for Classification of Reactions with an External LightGBM Classifier on Top of Projections Based on Difference Fingerprints From the RDKit and BERT FP^a.

	fingerprint and descriptors types
perplexity	MorganFP	AtomPairFP	Topological Torsion	BERT FP
10	84.0	83.1	86.4	78.1
30	83.5	82.8	85.8	77.2
100	82.9	81.3	85.1	76.0
500	79.2	75.5	81.4	71.8
multi-scale	84.3	83.1	87.0	77.5

^aA value in bold is the best score. The accuracy scores correspond to models trained for 80 epochs.

One can also see that the class separation accuracy decreases with higher perplexity values. However, multi-scale models outperform models with particular perplexities as they manage to “take the best” from all the projections with different values of this hyperparameter.

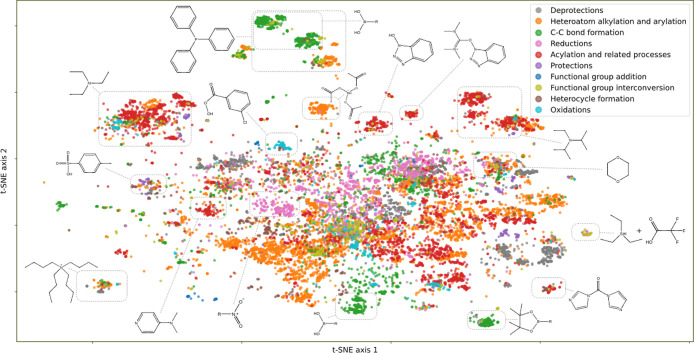
Figure 1 demonstrates the map of data set B produced with multi-scale t-SNE model trained on difference topological torsion reaction fingerprints. This model has subjectively the best visual quality and the highest accuracy score of class separation (Table 1).

Figure 1.

Projection of the data set B produced with a multi-scale parametric t-SNE model trained on topological torsion difference fingerprints. Colors reflect classes of reactions. Typical representative compounds are emphasized for some of the clusters. The clusters unite reactions that share typical molecules or fragments representative for that cluster. The points are quite densely located in the center of the map; therefore, for a closer study, a zoom-in is required, as in Figure 2.

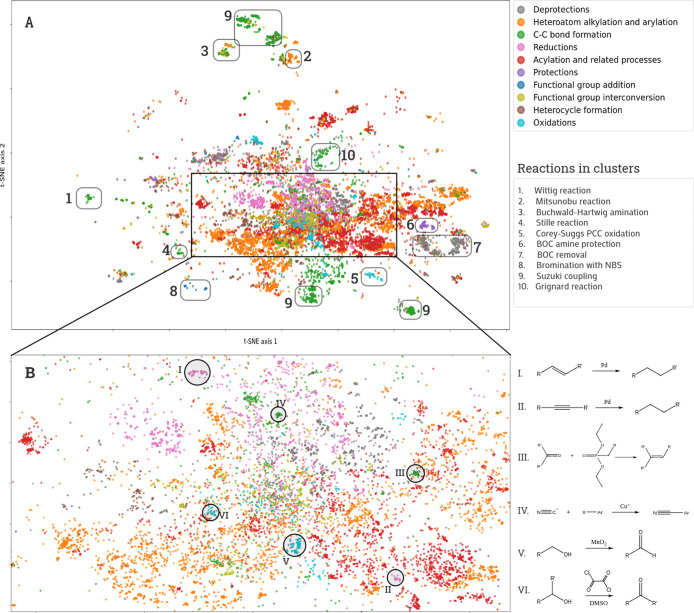
Each point in the projection represents a reaction. The map in Figure 1 shows a number of clusters, many of which are well-shaped, separate, and uniformly colored, albeit there are regions without a definite structure. One can see that there are some compounds or fragments which are present in every reaction within a cluster. These “core” structures in a reaction are agents or reactants’ substructures, and they have a heavy influence on the resulting coordinates. This can be explained regarding the formula for difference fingerprints. The subtraction of product fingerprints from reagent fingerprints leads to a vector representing the vectored form of fragments’ rearrangements. One can think of it as the quantified essence of the chemical reaction itself. Larger clusters unite reactions with common reagents, for example, acetic acid, and small dense clusters correspond to reactions involving infrequent reagents (Figure 1). Sometimes, the set of “core” agents in reactions in a cluster defines a specific recognizable reaction type (Figure 2); however, it is not always the case. The projection (Figure 2) contains clusters for Suzuki coupling, Stille reaction, Mitsunobu reaction, Wittig reaction, and so forth.

Figure 2.

(a) Projection of data set B produced with a multi-scale parametric t-SNE model trained on topological torsion difference fingerprints. Colors reflect classes of reactions. Some clusters corresponding to reactions of particular recognizable type are highlighted by rounded rectangles. (b) Zoom-in of a projection’s region is highlighted by a black rectangle. Some clusters corresponding to concrete reaction schemes are highlighted by black circles.

The noise in the reaction data sets affects the resulting projections. Commonly, it leads to the fission of large clusters into smaller ones. In this case, clusters share the same general reaction type but comprise reactions written with different amounts of detail. An illustrative example is shown in Figure 2 where one can see the cluster for Suzuki coupling that splits into two smaller clusters. One of them comprises less-detailed reactions, where only a reactant and an organoboron molecule are present. There are reactions with full details in another cluster: a base or a catalyst is denoted.

The scores from Table 1 suggest that BERT FP performs a bit worse compared to difference fingerprints. The map of chemical reaction space obtained with BERT FP is shown in Figure S2 in the Supporting Information. One can see well-shaped clusters on projections built on BERT FP. However, visually, these clusters are broader and have lower resolution. This fact limits the ability to see details. One should note that BERT FP demonstrated good performance in similar TMAP visualization,²³ and the reason why the performance of BERT FP declines in parametric t-SNE visualization requires further study.

One can use any reasonable distance function for the calculation of distances in high-dimensional space. The Jaccard (or Tanimoto) coefficient is broadly used in chemoinformatics to calculate the similarity between molecules. However, our experiments with Jaccard similarity revealed that this metric provides lower performance and results in less-structured clusters (see Figure S4 in Supporting Information). Moreover, the Jaccard index for non-binary vectors has greater computational complexity than Euclidean distance, limiting the batch size. In contrast, the usage of large batches commonly benefits the parametric t-SNE algorithm. This is the reason why we are using only Euclidean distance in all experiments described in this paper.

We found that the visualization quality heavily depends on the reaction’s representation. For the majority of reactions, the same reagents can be written either as agents or reactants. Because we did not use agents’ fingerprints for training (w^a = 0), we had to standardize the representation and define all agents as reactants. Our observations showed that standardization improves the visual quality: large unstructured clusters become clearer, and some small clusters merge on a reasonable basis.

All the results discussed so far were obtained with a neural network of four layers. We also experimented with different number of layers. Table 2 shows the accuracy scores of class separation for multi-scale models trained for 80 epochs on BERT FP and reaction difference fingerprints based on topological torsion descriptors. In the latter case, four layers show the best performance. In the former case, the model with five layers is the best by only a little margin.

Table 2. Accuracy Scores (%) for Classification of Reactions with an External LightGBM Classifier on Top of Projections Based on BERT FP and Reaction Difference Fingerprints Based on Topological Torsion Descriptors^a.

	reactions representation
number of layers	Topological Torsion difference	BERT FP
2	83.71	72.15
3	85.59	75.35
4	87.03	77.47
5	87.01	78.28

^aA value in bold is the best score. The accuracy scores correspond to multi-scale models trained for 80 epochs.

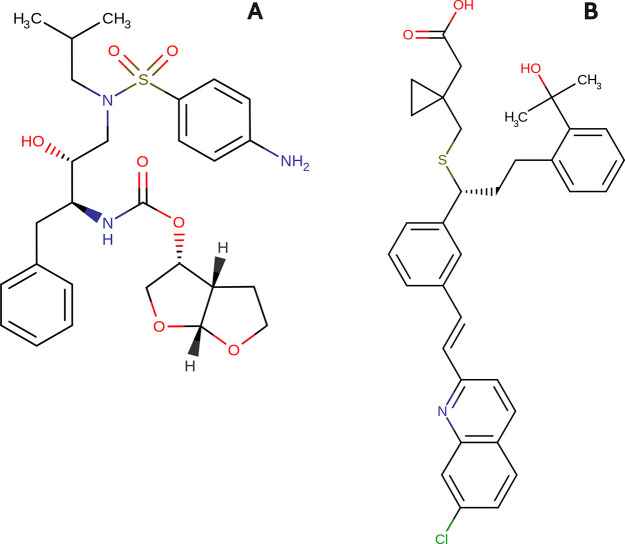
To demonstrate our method’s applicability to the medicinal chemistry challenges, we studied and visualized the final stages of the synthesis of two known drugs, darunavir and montelukast. Darunavir is a protease inhibitor that is used for the effective treatment of HIV-1 infection.²⁴ Montelukast is a leukotriene receptor antagonist used as part of an asthma therapy regimen and to treat seasonal allergic rhinitis.²⁵ The structures of darunavir and montelukast are shown in Figure 3. The information about last synthetic stages was taken from the Reaxys²⁶ database.

Figure 3.

Structures of darunavir (A) and montelukast (B).

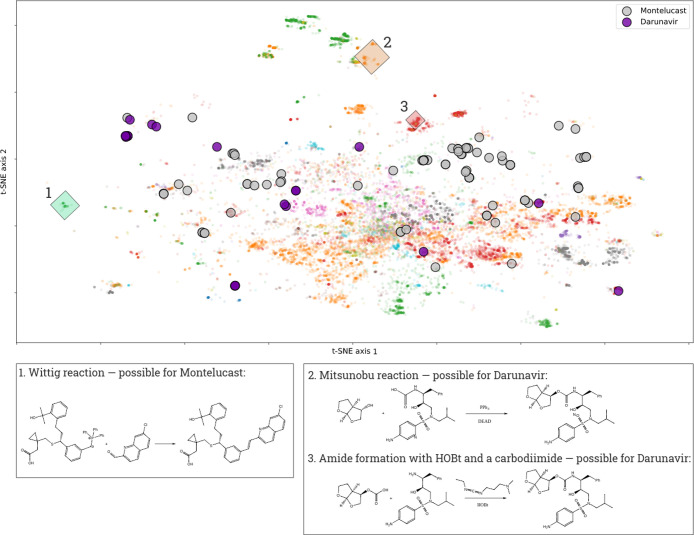
In Figure 4, purple and gray circles represent the reactions corresponding to the final stages of the synthesis of darunavir and montelukast. One can regard it as a “global landscape of chemical reactions,” on which the synthetic pathways can be represented in an illustrative way. The reaction points for both drugs are present in various parts of the reaction space. Exploring this map, one can analyze the typical kinds of chemical reactions used for the synthesis of a compound. However, more importantly, one can inspect the ways that have been unexplored yet. For example, after studying the map in Figure 4, one can discuss new possible synthetic ways to darunavir and montelukast, including Wittig reaction, Mitsunobu reaction, and amide formation with HOBt and a carbodiimide. We believe that our method could help a chemist to gain insights into some unexplored synthetic pathways of certain compounds.

Figure 4.

Map of single-step reactions leading to darunavir and montelukast drugs (purple and gray circles) is depicted on the global landscape of the reaction data set B. Clusters 1, 2, and 3 represent some reaction types that can be used for the synthesis of these drugs, but currently, there are no signs that these reactions have been used yet (no gray and purple circles in regions 1, 2, and 3). Therefore, there is an open possibility to extend the landscape of synthetic ways to these drugs.

The robustness of machine learning models is a concerning point in chemoinformatics.²⁷ We performed experiments with cross-validation to evaluate the stability of the method with respect to training data. We trained one of our models on six folds of the data set A. The model was based on difference topological torsion descriptors with perplexity set to 10. We trained the networks for 10 epochs because it was enough for the stable projection. Each fold for training comprised five-sixth of the data set A, and the holdout parts did not overlap between folds. The test subsets consisted of about 160,000 reactions. The scores for class separation for all six models are listed in Table 3.

Table 3. Accuracy Scores (%) for Classification of Reactions with an External LightGBM Classifier for Identical Models Trained on Six Folds of the Original Training Data set.

fold no.	1	2	3	4	5	6
accuracy score, %	83.86	84.17	83.84	84.40	83.90	84.15

All six models demonstrate quite similar performance with a score of 84%. A visual comparison of the projections showed that although the overall shape of the picture is subjected to fluctuations, the chemical sense of clusters is preserved between folds. We can conclude that a parametric t-SNE model based on difference topological torsion fingerprints for a reaction is robust with respect to the changes in the training data imposed by cross-validation. We think that this would be true for models based on other reaction fingerprints.

The parametric t-SNE method allows one to explore synthetic ways leading to the compounds of interest in an illustrative manner. However, as we mentioned before, the visual quality of the projections depends on the quality of the training data. We believe that the primary way for improving our models is the standardization and curation of raw reaction data. The alternative option is the usage of BERT fingerprints, which is described in²³ because they do not require a predefined split of reactants, reagents, and agents.

We also conducted experiments to understand the applicability of structural fingerprints for the visualization of the reaction space. The experiments revealed that structural fingerprints are not suitable for producing t-SNE maps with well-separated clusters. In Figure S3 (in Supporting Information), a parametric t-SNE projection is shown for a model trained on structural Morgan fingerprints with perplexity 30 for 80 epochs. One can see that the reactions are totally mixed up. The separability of reaction classes measured with the same LightGBM classifier as in Table 1 is 52.3%. All reactions are mixed without a definite structure. Structural fingerprints are essentially a cumulative fingerprint of all the molecular structures involved in a reaction. This does not reflect in any way the difference between reagents and products.

3. Conclusions

In this work, we demonstrated a method for the exploration of the reaction space. Our findings revealed that the parametric t-SNE method combined with difference fingerprints provides a basis for such a method. We studied two approaches of representing chemical reactions: structural and difference fingerprints. Our experiments showed that the structural fingerprints do not afford the discrimination ability, and the projections on the base of structural fingerprints are mixed. In contrast, the models build on top of the difference fingerprints can project to form well-shaped clusters with clear chemical meaning. These clusters correspond to known classes of chemical reactions. We believe that Morgan fingerprints are the optimal choice for reaction difference fingerprints, albeit quantitative evaluation of projection performance revealed that the models based on topological torsion descriptors provide marginally better projections than other types of difference fingerprints. The parametric t-SNE model can be easily applied to new reactions, and this fact opens the doors for chemists to investigate their own data sets of reactions on the global reaction landscape. We found that parametric multi-scale t-SNE outperforms vanilla t-SNE. Given the fact that multi-scale t-SNE does not require perplexity fine tuning, it seems to be preferable for visualization. We also studied the theoretical feasibility of this method for the investigation of the synthetic routes for two commercial drugs. We propose a set of potential reactions for the synthesis of these molecules. We suppose that our method can be a powerful tool for the study of the landscape of reaction space and will inspire new findings in studying chemical reactions and synthetic ways.

4. Materials and Methods

4.1. Data sets

In our work, we used the freely available chemical reaction data set created by Lowe.²⁸ It contains about 2 million organic reactions in the recent update.²⁹ To train the machine learning models, we utilized the slightly adjusted data set, which was used by Schwaller et al. to predict products of a reaction using a seq2seq model.³⁰ This data set, further referred to as data set A, contains SMILES-strings for single product reactions with atom mapping. Also, there are no duplicates in this data set.

To assess the visualization performance, we used a data set from the paper by Schneider et al.³¹ It comprises 50,000 reactions represented as standardized SMILES-strings. These reactions were labeled with one of the 10 classes (oxidations, reductions, C–C bond formations, heteroatom acylations, deprotections, etc.) The authors have labeled these reactions automatically using NameRxn software (version 2.1.84). The NameRxn algorithm is based on expert-defined SMIRKS patterns.³² We only took reactions from this data set that are not present in the training data and that comprise no more than 13 reactants. The final test data set consisted of 20,157 reactions, and we denote this data set as data set B.

4.2. Parametric t-SNE

The method of t-SNE,¹⁴ originally described in 2008, is a common approach in multidimensional data visualization. However, it has two major shortcomings. First, one cannot apply a prepared t-SNE model to new data. Second, the application of this method is limited only to relatively small data sets. In practice, it is only viable for data sets comprising 10⁵ or less multi-dimensional points, even with Barnes-Hut approximation³³ on modern computers. In our work, we used parametric t-SNE.³⁴ This approach allows to apply a prepared model to new reactions and requires modest computational resources. In the original t-SNE, the coordinates of the embedding points in the lower-dimensional space are optimized directly. In parametric t-SNE, a neural network with adjustable weights is used to project higher-dimensional space to the lower-dimensional one. The loss function of the neural network corresponds to the divergence between high- and low-dimensional data relations. At each training iteration, a batch of data points is picked to calculate a distance matrix d for all points in the batch with a predefined metric. The matrix d has size n × n, where n is the batch size. Then, the distance matrix is used to calculate the matrix of the conditional probability distribution p in a high-dimensional space (eq 1)

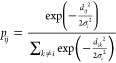1

One can interpret a row of the p_ij matrix as a Gaussian probability distribution over the batch such that the point j will be picked as a neighbor for the point i. Decrease in σ_i leads to the reduction in the number of nearest neighbors that have non-zero probabilities. All σ_i parameters are adjusted to achieve the desirable perplexity of distributions in all rows. One can regard the perplexity as an approximate number of neighbors taken into consideration in the original space. It is a hyperparameter of the algorithm. There is a connection between perplexity P and Shannon’s entropy H of a distribution (eq 2)

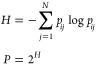2

Similar to eq 1, a probability distribution matrix q is built for low-dimensional embedding points (eq 3)

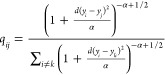3

where d(y_i – y_j) is the distance between the embedding points y_i and y_j and α is the number of degrees of freedom of the t-distribution. This distribution is heavy-tailed, and it helps to overcome the “crowding” problem.¹⁴ In our work, we defined α equal to one.

The choice of perplexity is arbitrary, and it strongly affects the lower-dimensional picture. At small perplexity values, a model focuses on preserving local neighborhoods while neglecting large-scale data interactions. At the same time, large values impair reproduction of small neighborhoods. These problems can be addressed by using multi-scale t-SNE.³⁵ In multi-scale t-SNE, conditional probabilities p_ij are calculated with eq 4

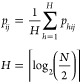4

where N is number of points in the batch. The conditional probability matrix is averaged over a range of perplexities, allowing a model to find a proper balance between reconstruction of both local neighborhoods in higher-dimensional space and its global structure.

The weights of the neural network are optimized by backpropagation, minimizing the Kullback–Leibler divergence L between distributions in a high-dimensional space and in a low-dimensional space (eq 5)

5

4.3. Model Training

We used a fully connected neural network as a projection function in parametric t-SNE. The information about the network architecture and the optimization procedure is given in the Supporting Information of this article. We trained several models on data set A with different hyperparameters and reaction representations. Data set A was split into subsets for training and validation to control overfitting and apply early stopping if necessary. The validation subset consisted of 150,000 reactions.

As reaction vector representations, we used several types of reaction fingerprints available in the RDKit package and reaction fingerprints based on the embeddings computed using BERT models recently proposed by Schwaller et al.²³ (further denoted as BERT FP). The BERT FP is obtained directly from a reaction SMILES string, while reaction fingerprints from the RDKit are constructed from molecular fingerprints of individual compounds involved in a reaction. We experimented with two common types of reaction fingerprints: structural fingerprints and difference fingerprints. The fingerprints available in the RDKit are Morgan Fingerprints (also known as extended-connectivity fingerprints, ECFP),³⁶ atom pair fingerprints (AtomPairFP),³⁷ and topological torsion descriptors.³⁸ One can regard a chemical reaction as a map between a set of reactants (reagents) and a set of products. Catalysts, solvents, and other molecules that are not involved in rearrangements of atoms directly on the way from reactants to products are regarded as agents. By calculating and combining compounds’ fingerprints, one can obtain fingerprint-based representations of chemical reactions. Structural fingerprints are obtained by concatenating fingerprint vectors for reactants, products, and, optionally, agents. Difference fingerprints are based on the linear combination of fingerprints for products, reactants, and agents (eq 6)

6

here w^na stands for a non-agent weight and w^a for an agent weight. In our experiments, agents were not included in the reaction fingerprints, so w^a = 0.

To calculate distances between points in higher-dimensional space prior to computing the conditional probability matrix, we used Euclidean distance and Jaccard dissimilarity. In the former case, models were trained with a batch size of 5000 and 500 in the latter case. Jaccard dissimilarity between vectors x and y is calculated with eq 7 for binary vectors and with eq 8 for vectors in general

7

8

In low-dimensional space, Euclidean distance was used.

We experimented with models trained with different perplexity values, 10, 30, 100, and 500. In addition to this, we also explored multi-scale models. We trained our models on GPU because it significantly boosts the training speed compared to the non-parametric t-SNE working on CPU.

4.4. Evaluation

We used B for the visual evaluation of the quality of reaction mapping. Because this data set contains predefined classes for reactions, one can use it as a reference point to evaluate the projection’s performance. From a bird’s view, our idea was to classify reactions only from their places in the resulting maps and compare them with the known classification. This approach follows the fundamental chemical tenet: similar compounds (in our case, reactions) should provide similar properties. We performed this experiment for several parametric t-SNE models to reveal their abilities to discriminate between reaction classes. These models vary in both hyper-parameters and types of fingerprints. We assessed the discrimination ability quantitatively with a gradient boosting model built on top of the 2D projections. We utilized the LightGBM³⁹ Python package. We trained a gradient boosting classifier with a set of fixed hyperparameters on every parametric t-SNE projection. The accuracy score for classification was used as the measure of class separability. Our observations reveal that the maps with better visual clusters separation have larger accuracy scores.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c04778.

• Architecture and training procedure of our neural network, learning curves, images of t-SNE projections built on BERT FP and reaction structural fingerprints, image of a t-SNE projection built on difference Morgan fingerprints (PDF)

The authors declare the following competing financial interest(s): Maxim V. Fedorov and Sergey Sosnin are cofounders of Syntelly LLC. Mikhail Andronov declares no competing interests.

Notes

The web demonstration is available in https://reactionspace.syntelly.com. The code is available at GitHub: https://github.com/Academich/reaction_space_ptsne.