Abstract
While cold chain management has been part of healthcare systems, enabling the efficient administration of vaccines in both urban and rural areas, the COVID-19 virus has created entirely new challenges for vaccine distributions. With virtually every individual worldwide being impacted, strategies are needed to devise best vaccine distribution scenarios, ensuring proper storage, transportation and cost considerations. Current models do not consider the magnitude of distribution efforts needed in our current pandemic, in particular the objective that entire populations need to be vaccinated. We expand on existing models and devise an approach that considers the needed extensive distribution capabilities and special storage requirements of vaccines, while at the same time being cognizant of costs. As such, we provide decision support on how to distribute the vaccine to an entire population based on priority. We do so by conducting predictive analysis for three different scenarios and dividing the distribution chain into three phases. As the available vaccine doses are limited in quantity at first, we apply decision tree analysis to find the best vaccination scenario, followed by a synthetic control analysis to predict the impact of the vaccination programme to forecast future vaccine production. We then formulate a mixed-integer linear programming (MILP) model for locating and allocating cold storage facilities for bulk vaccine production, followed by the proposition of a heuristic algorithm to solve the associated objective functions. The application of the proposed model is evaluated by implementing it in a real-world case study. The optimized numerical results provide valuable decision support for healthcare authorities.
Keywords: Supply chain management, COVID-19, Vaccine distribution, Cold chain, Decision tree analysis
1. Introduction
COVID-19 was declared a pandemic by the World Health Organization (WHO) on March 11, 2020, and as of October 2021, it had affected more than 238 million people globally with more than 4.8 million deaths, making it the deadliest medical emergency in modern history (World Health Organization 2021). The pandemic has been posing a significant threat to the healthcare sector, the economy and the stability of entire countries. It has disrupted the functioning of governments and societies at large (Sheraton et al. 2020). Surging COVID-19 cases are being addressed via extensive testing and tracing, social distancing requirements and lockdowns, all aimed at preventing the spread. At the same time, researchers and teams of pharmaceutical and medical experts are racing to develop, produce and distribute vaccines.
With the first ever vaccine being developed in 1798 for smallpox (Stewart and Devlin 2006), multiple diseases have been cured by such antidotes to trigger an immune response towards the virus. Vaccine development and manufacturing is a straining process, which is followed by trials in three phases (Ulmer et al. 2006). The results are evaluated by professionals, followed by a safety assessment of the vaccine by regulatory authorities. Currently, researchers worldwide are working continuously to develop and further refine vaccines against COVID-19 and its various mutations that have become prevalent. There are approximately 100 vaccine candidates under development at present, with a number of them already being administered since December 2020. After the successful trial of a vaccine and the declaration of its safety and efficacy, COVAX, which is led by the WHO, CEPI (the Coalition for Epidemic Preparedness Innovations) and GAVI (the Global Alliance for Vaccines and Immunizations), facilitates an equitable distribution and access to the vaccine for people around the globe.
This production and ensuing distribution of the vaccine is a multi-echelon process, which is complicated by the need to maintain the vital properties of the vaccine throughout and to prevent adulteration (Choi 2021). Each vaccine produced to date, including vaccines for COVID-19, has a temperature requirement for storage and transport ranging from −50 °C to +8 °C, i.e., lower than room temperature (Kumru et al., 2014, Centers for Disease Control and Prevention (CDC), 2019, United Nations (UN), 2020). To accommodate these requirements, cold chain management has come to the fore (Fleming et al. 2021), which was developed in the late 1800s. It was applied to the preservation of vaccines as early as 1950 (Lloyd and Cheyne 2017). Cold chain management is guided through several phases of loading, unloading, handling and storage, from the production of the vaccine to the administration to the beneficiary. To ensure the efficacy of the vaccine, the integrity of each step must be maintained throughout the supply chain (Salin and Nayga 2003). While cold chain management has been part of healthcare systems, enabling the efficient administration of vaccines in both urban and rural areas, the COVID-19 virus has created entirely new challenges for vaccine distributions. With virtually every individual worldwide being impacted, strategies are needed to devise best vaccine distribution scenarios, ensuring proper storage, transportation and cost considerations. However, current academic models do not consider the magnitude of distribution efforts needed in our current pandemic, in particular the objective that entire populations need to be vaccinated.
The vaccine distribution also needs to accommodate different groups of populations that are distinguished based on their priority to receive the vaccine, which is determined based on various attributes (Araz et al., 2012, Buccieri and Gaetz, 2013). Currently, available COVID-19 vaccines are prioritized by age group and profession. However, while the increasing availability of vaccines offers a glimmer of hope, the pressing challenge that many countries have been facing is the distribution of the vaccines to the needed locations. Strong planning and decision-making skills are needed, along with a proper supply chain designed to efficiently cater to the needs of people globally. As such, healthcare authorities need to make decisions on the right distribution strategy, especially in light of limited resources, availability of depots and distribution centres, and the stringent temperature requirements. The development of decision-support tools and models to facilitate such distribution decision are thus in dire need (Choi 2021).
Within this context, our contribution to the operations management literature is multi-fold. Specifically, we design a novel pandemic vaccine cold chain network and assist in the vaccine distribution process by providing guidance on how to make tactical and strategic decisions so that the vaccine can be effectively distributed to a population within the most expeditious timing possible. The specific research questions we aim to answer and that guide our research are as follows:
-
1.
What are best strategies for COVID-19 vaccine distributions to entire populations considering storage and transportation requirements as well as cost considerations?
-
2.
Since the availability of vaccines may be limited at first, what is the best vaccine distribution scenario to maximize the impact of the vaccine program and to best forecast future vaccine production?
-
3.
What are best location and allocation decisions for cold storage facilities, including both bulk vaccine production and distribution facilities?
We aim to address these questions by designing a cold supply chain considering a country’s entire population. To do so, a multi-echelon cold chain is designed by dividing the distribution process into three phases, offering a methodology for healthcare authorities to make appropriate decisions for executing the distribution process in a sophisticated manner. We expand on existing models and devise an approach that considers the needed extensive distribution and storage of vaccines, while at the same time being cognizant of costs. As such, we provide decision support on how to distribute the vaccine to an entire population based on priority. We do so by applying predictive analysis for three different scenarios and dividing the distribution chain into three phases. As the available vaccine doses are limited in quantity at first, we apply decision tree analysis to find the best vaccination scenario, followed by a synthetic control analysis to predict the impact of the vaccination programme to forecast future vaccine production. Our results suggest a decrease in mortality rate from 3% to 1.2%.
A key factor that enables an efficient, effective and fair response to the vaccine distribution during a pandemic is the presence of an adequate number of strategically located storage and vaccine production centres. For this, we formulate a mixed-integer linear programming (MILP) model for locating and allocating cold storage facilities for bulk vaccine production, followed by the proposition of a heuristic algorithm to solve the associated objective functions. The application of the proposed model is evaluated by implementing it in a real-world case study. The optimized numerical results provide valuable decision support for healthcare authorities to design an optimal vaccine distribution system that not only depends on individual factors, i.e., who should be vaccinated first, but also on the spatiotemporal factor indicating where vaccines should be provided first. Specifically, our results shown that prioritizing cities based on the number of active number of cases and death rate has a significant impact on reducing the overall number of cases in a country and on vaccinating vulnerable groups depending on the scenario-based criteria; this has a considerable effect on the reduction of the death rate. The model also helps predict the duration to vaccinate the population along with indicating the timely need and speed for vaccine production and delivery.
Overall, we believe that the proposed model can be a valuable decision-support aid as managers decide on optimizing the vaccine cold chain distribution process while minimizing overall costs and ensuring a fast and equitable distribution. For example, as part of the model, we also determine the optimal location of new storage facilities, helping healthcare authorities with these important choices. Considering the results of the proposed model in the planning stages of a vaccination drive will be invaluable, especially based on the insight generated through the predictive analysis, which assists in the determination of both the number of doses required and the target population with great accuracy. As such, we respond directly to the call by Choi (2021) who encouraged more research on best logistics and supply chain designs for vaccine distribution.
The remainder of this paper is organized as follows. After a review of the literature in Section 2, Section 3 describes the problem and formulates the mathematical model, including notations and assumptions. Section 4 presents the solution methodologies employed. Section 5 introduces the case study context, followed by the application of the solution methodologies and the discussion of the results. Section 6 concludes.
2. Literature review
The importance of networked vaccine supply chains has been demonstrated by the measles-mumps-rubella (MMR) and smallpox vaccination drives. Measles, having a reproductive number of 12 to 18, can affect a considerable portion of a population in a short time; it led to the death of over two million people before the introduction of the Expanded Program on Immunization (EPI) in 1980 (WHO 2019). Even after the establishment of a timely delivery system, rubella and measles continue to be a global health priority (WHO 2019), with measles to date accounting for more than 100,000 deaths globally. The high transmission rate of contagious and infectious diseases thus necessitates a highly trained public health staff and advanced immunization campaigns with adequate funds to reduce mortality. Supply chain management plays a critical part in addressing these challenges to public health by ensuring effective and efficient vaccine distribution, especially during epidemic outbreaks (Chowdhury et al. 2021).
Most vaccines are sensitive to heat and must thus be kept at a very low temperature, typically in the range between 2 °C and 8 °C. This necessitates a specific cold chain system that is effective in proper production, storage and distribution of the vaccines (Lin et al. 2020). Beginning with the temperature modulation at the manufacturing plant until the vaccination of the patient, maintaining the quality and efficacy of both the process and the product is of utmost importance (Kumru et al., 2014, Centers for Disease Control and Prevention (CDC), 2019, United Nations (UN), 2020). Research has thus been undertaken to offer guidance for the development of cold chain networks that can be applied to epidemics, considering for instance increasing vaccine coverage areas and the tracking of every dose as it moves through the vaccination process. As such, Hasanat et al. (2020) proposed an IOT-based real-time monitoring system for cold chains that enables continuous monitoring of the vaccine distribution and transportation process, and Antal et al. (2021) developed a blockchain-based vaccine supply chain system for transparent tracing of the COVID-19 vaccine from registration to delivery. Earlier research includes Bozorgi et al. (2014), who examined inventory models for cold items considering temperature-controlled units. While advanced technology can help in tracking the vaccine distribution process—for instance by the application of blockchain technology (Dutta et al. 2020)—and ensuring that the vaccines maintain their efficacy by temperature monitoring, the delivery of vaccines to remote regions can only be ensured if the entire vaccine cold chain system functions properly (Bierle 2020). Outside of the vaccine distribution problem, cold chain management has been studied within the context of determining the optimal shipping mode (Zhang and Lam 2018), designing hierarchical operational hub networks (Esmizadeh et al. 2021), or analysing outsourcing models in fresh agriproduct supply chains (Yu and Xiao 2021).
Operations management literature covering the vaccine cold chain is considerable (e.g., Bozorgi and Fahimnia, 2021, Enayati and Özaltın, 2020, Duijzer et al., 2018, Lemmens et al., 2016). As such, extant research dealt with the optimization of the vaccine production to address uncertainties in product supply and demand (Matrajt et al., 2020, Azadi et al., 2020), and government subsidies for vaccine production research and development were considered (Xie et al. 2021). Considering the context of developing countries, Tavana et al. (2021) proposed a mixed-integer linear programming model for equitable distribution of vaccines, classifying vaccines into three categories (cold, very cold and ultra-cold) to account for specific storage capacity needs. Due to these extensive cooling requirements, environmental impacts have also been considered (Saif and Elhedhli 2016). A further point of concern was the optimal allocation and management of resources (Gollust et al. 2020), which was for instance accomplished by the optimization of distribution networks (Rastegar et al. 2020). As within our current context the available doses of vaccines are insufficient to vaccinate an entire population immediately, the allocation problem of who should be vaccinated first needs to be considered, as well as where the storage facilities should be located. This is a novel problem, which we address in this paper, working towards the design of a fair and equitable distribution system.
We also frame our research within the operations and supply chain management literature on strategic decision making within the context of various epidemic and pandemic outbreaks (e.g., Ivanov 2020). Many of such studies focused on emergency response, resource allocation, procurement and distribution, and relief operation management (e.g., Govindan et al., 2020, Ivanov and Das, 2020, Anparasan and Lejeune, 2018, Preciado et al., 2013). However, the more specific contexts of disease propagation and virus spread have received very limited coverage within operations and supply chain management literature. Exceptions include Rachaniotis et al. (2012), who proposed a deterministic model for disaster management during an epidemic considering uncertain demand and distributed, limited resources, and Liu and Zhang (2016), who proposed a time series model to forecast errors for shipping and resource allocation. The vaccine distribution problem during a pandemic was covered by Savachkin and Uribe (2012), who considered a dynamic model to distribute medicine based on disease propagation, and Sun et al., 2014, Enayati and Özaltın, 2020, who offered advice for healthcare authorities regarding vaccine storage facility location selection, distribution plan efficiency, and resource allocation.
Models have also been proposed for the allocation phase of the vaccine. For example, Sun et al. (2009) formulated a game theory-based stockpile management framework, where each country faces a trade-off between storing the vaccine to vaccinate people in their own country and exporting it to other countries that are in greater need, with the objective to control the outbreak. Later, Preciado et al. (2013) developed an optimal model for the distribution of vaccines via a cold chain network to control the spread of influenza, and Mamani et al. (2013) examined the inefficiency in the allocation process of epidemic vaccines using game theory and suggested ways for improvement. Recently, Bertsimas et al. (2021) proposed a novel method for locating mass vaccination facilities within the context of COVID-19. In their work, they formulated a bilinear, non-convex optimization model and compared its effectiveness with benchmarks based on demographic and epidemiological information.
While these studies provide valuable insight, they are limited in that they focus on controlling an outbreak by optimizing the vaccination process for a small subset of the population. However, in the case of COVID-19, the entire population is in need to be vaccinated (although some may opt not to get the vaccine, for whichever reasons). No research was found that captures this magnitude of scope. We fill this void with the present research by developing a model that can efficiently address the vaccination needs of a country’s entire population by dividing the vaccination process into three phases, which will be discussed next.
3. Problem description
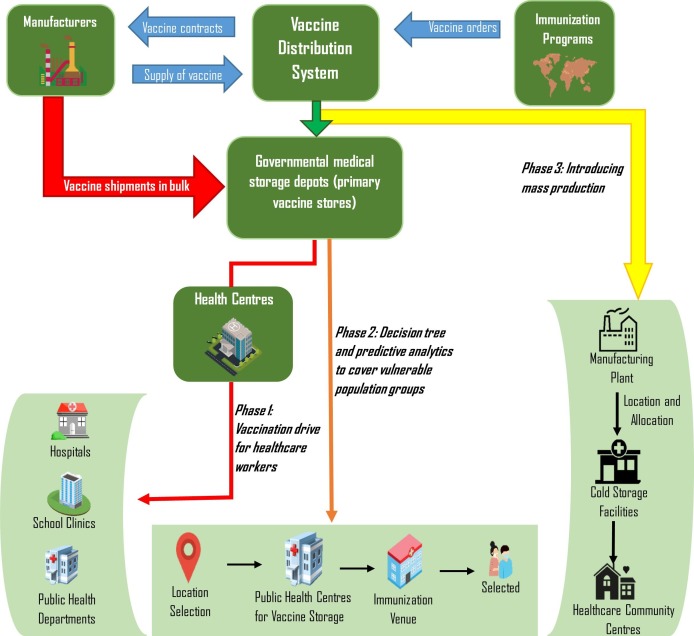
We formulate a multi-echelon dynamic cold chain distribution model for collection, storage and distribution of vaccine vials. Our model is both timely and important, since most countries are currently struggling with the vaccine distribution (Robbins et al. 2021). Especially extreme temperature requirements are posing significant challenges in distributing the vaccines to remote areas (Bukszpan 2020). Responding to these pressing demands, we develop a distribution network by applying predictive and risk analyses to provide a distribution strategy based on priority and availability. The process, which is divided into three phases, is depicted in Fig. 1 and described in the following.
Fig. 1.
Framework of the vaccine distribution system.
Phase 1 - In the beginning, priority will be assigned to first responders: doctors, nursing staff, medics and paramedics, including all healthcare workers (Naik et al., 2020, Persad et al., 2021). This will be followed by municipal corporation workers, and security and disaster management staffers. According to the principle of solidarity (Hechter, 1988), the risks they face in their service to society is reflected in their vaccine priority and substantiated based on their often greater exposure to situations where the virus can be transmitted. A further substantiation for this design choice lies in frontline workers playing a vital role in the COVID-19 vaccination drive. As such, many studies stress that physicians are the most influential individuals for vaccine decision-making (Edwards and Hackell 2016). Recommendations and behaviour (i.e., getting the vaccine) by physicians can bolster public and individual support for and confidence in the vaccination drive. Physicians who share their personal anecdotes about being immunized and immunizing their family members can be effective in encouraging vaccine uptake in vaccine hesitant populations (Bode and Vraga 2018). Even the Joint Committee of Vaccination and Immunization (JCVI), which advises the UK government on their vaccine distribution program, has advised that first priority be given to frontline workers. Vaccinating them will not only boost the foundation of a country’s healthcare and maintenance sector, but will also allow medical authority figures to share their experience with others.
Phase 2 - The model will address the vaccine distribution from manufacturers to patients based on critical parameters, such as transportation time to a particular location, cost, number of positive cases, percentage of positive cases relative to the entire population in a location, average age of the people in that location, and mortality rate due to COVID-19 in the particular location. In an initial step, a decision tree classifier based on artificial intelligence risk analysis will be applied to determine the cities to which the vaccine should be distributed first. This is then followed by the comparison of three different scenarios based on Deo et al. (2020) to determine an optimal scenario for vaccine distribution. The three scenarios are the following:
Scenario 1: Vaccinating the elderly population, with the objective to reduce mortality.
Scenario 2: Vaccinating members of the working-age population, with the objective to limit the spread of the infection.
Scenario 3: Vaccinating a fixed proportion of the population; the recommendation by the WHO will be applied, under which enough vaccines should be allotted to cover 3% of the population in every country.
We will assess the impact of these scenarios, which reflect the prioritization in most countries, on reducing the overall number of cases in the selected locations.
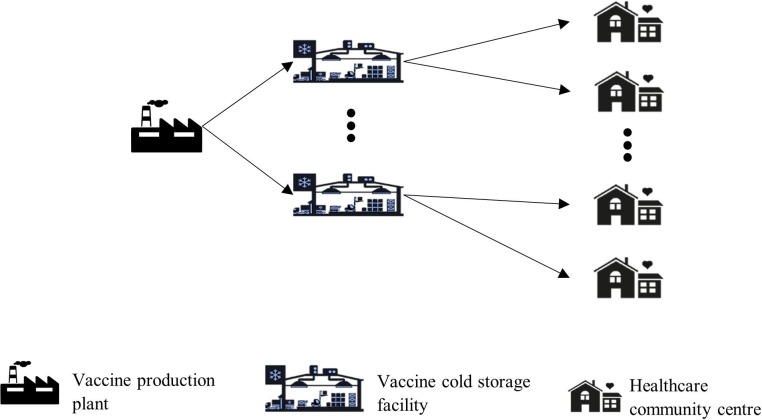
Phase 3 - Based on the impact created by the vaccine in phase 2, the production of the vaccine will be modelled to determine where additional storage facilities should be located. The idea here is to encourage local pharmaceutical industries to serve as bulk storage locations for the vaccines to address the immediate demand, while developing refrigerated inventory systems in every state of the country, and then gradually increasing the number of locations based on the decision tree for supplying the vaccine. For this, we formulate an optimal supply chain network for allocating storage facilities for ensuing vaccine distributing. The model consists of three echelons: vaccine production plants, storage facilities, and healthcare community centres (Fig. 2 ). Our optimal supply chain network will be primarily strategic in nature providing an overall dynamic network setup. In response to the day-to-day uncertainties, operational decisions are developed, while the tactical decisions, i.e., the delivery schedules, are constrained by WHO mandates—we consider these characteristics in our model. To formulate a real-time distribution chain, we make the following assumptions:
-
1.
The number of vaccine production plants and their locations are fixed.
-
2.
Vaccine cold storage facilities can be located at any current functioning regional or district vaccine distribution centre.
-
3.
Healthcare community centres at regional or local levels can be utilised as vaccination centres.
-
4.
Demand is considered to be stochastic in nature. The demand for vaccine at a healthcare community centre is determined based on the population area it covers in a particular region.
-
5.
There are no capacity constraints that limit the order quantity. An adequate amount of vaccine should be supplied to each healthcare community centre to meet the anticipated demand until the next replenishment.
-
6.
Each operational node has only one inbound flow, i.e., there is only a single source (the vaccine manufacturing plant) from which deliveries to a node (a vaccine cold storage facility) are made. Similarly, only one vaccine cold storage facility is assigned to one healthcare community centre.
-
7.
A log-normal distribution is fixed for the entire model.
-
8.
The length of each decision period is one day.
Fig. 2.
Diagram of the phase 3 distribution process.
Assumption (1) is based on the fact that countries manufacturing COVID-19 vaccines have a fixed number of production plants where the vaccine is currently produced (Pagliusi et al. 2020). Assumptions (2), (3) are considered to keep the vaccine storage facilities and the vaccination centres, respectively, at a manageable number. As such, our model does not consider the real-time construction of new facilities dedicated for COVID-19 vaccine distribution, since this would be quite a significant investment and require a considerable amount of time to be completed. Rather, we felt it to be more feasible and realistic to decide which of the storage facilities and community centres can be utilized for the administration of COVID-19 vaccines. Assumptions (4), (5) are based on the approach followed by the WHO to estimate the demand for the vaccines. Assumption (6) presents a realistic condition for the local distribution and vaccination centres. As such, while there may be qualified logistics personnel with deep expertise to handle complex delivery schedules from multiple sources at facilities in larger metropolitan areas, this may not be the case for facilities at the local level. Irrespective of this, keeping logistics operations as simple as possible is a reasonable objective, especially within the context of developing and emerging countries. Assumption (7) is implemented for analytical considerations, specifically so as to precisely predict the demand for the vaccine. As such, a truncated log-normal distribution is utilized to generate positive random numbers with upper and lower boundaries specified (Okakwula et al. 2018). Assumption (8) ensures continuous monitoring of the vaccine distribution process at each epoch. In addition, since vaccine requirements at the local level are dynamic in nature, daily monitoring might help in predicting the exact number of doses for the next day.
4. Methodology
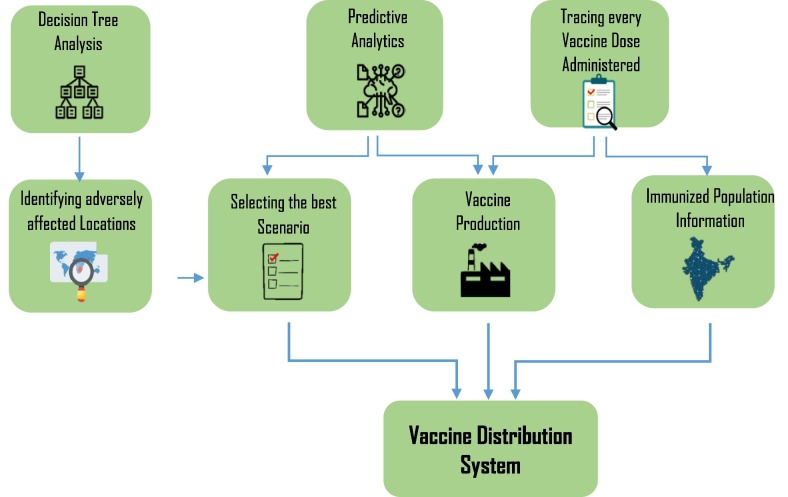
As noted earlier, the distribution process is divided into three phases. This section develops the methodology to manage this distribution process by various techniques and algorithms as depicted in Fig. 3 .
Fig. 3.
Mechanisms behind the vaccine distribution process.
4.1. Phase 1 distribution
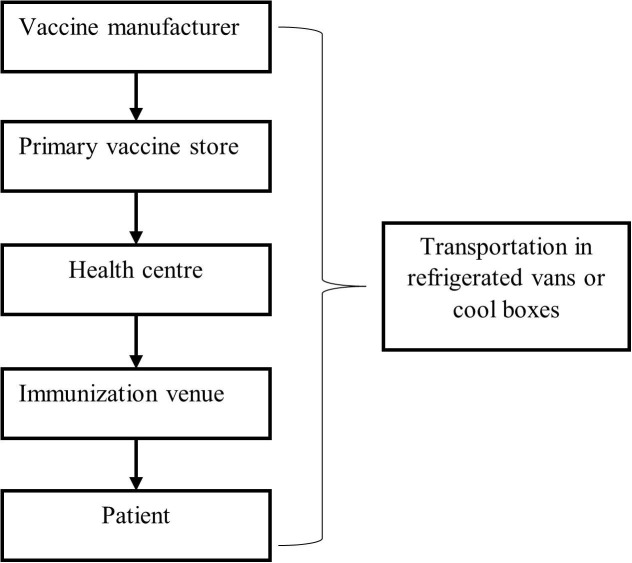
For the distribution in phase 1 we follow a standard cold chain model depicted in Fig. 4 , as the amount of available vaccine will be in limited quantity at first, allowing only a smaller portion of the population to be vaccinated. The benefit of using a standard cold chain model in this phase is that it enables every part of a country to be reached (Billah et al. 2017), ensuring that healthcare workers can receive the vaccine as soon as possible. Vaccines from the manufacturing plant will be transported to governmental cold storage facilities (primary vaccine stores) at various locations, from where they are then transported to the regional health centres. From here, it will be distributed to immunization venues.
Fig. 4.
Standard vaccine distribution cold chain.
4.2. Phase 2 distribution
Before the vaccination process can begin for the general population, healthcare authorities must identify how the available vaccines are to be allocated. In the beginning, since vaccines are scarce, vulnerable population groups must be prioritized. For this purpose, we augment the prediction analysis to prioritize population groups. At first, we utilize a decision tree classifier to identify cities most in need (storage facilities will be opened based on the number of cases in a city), followed by a prioritization of the population in these cities based on the three scenarios depicted in Section 3. We then perform a synthetic control analysis to assess the impact of the vaccination programme.
4.2.1. Decision tree analysis
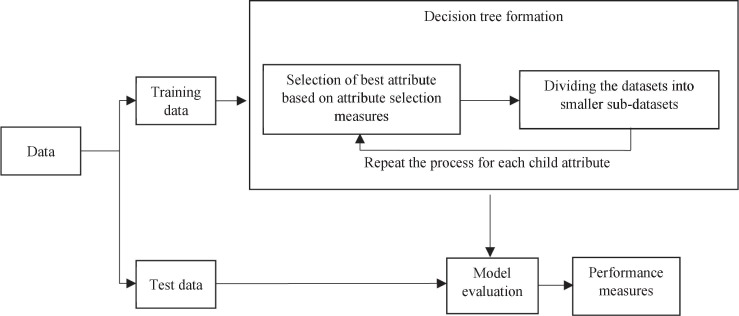
A decision tree is a classification system that supports decision-making with a consideration of the possible effects of the decisions. It is a flowchart-like tree structure that helps in modelling and extracting relevant information from large amounts of available data. An internal node represents an independent attribute (feature), a branch represents a decision rule, and leaf nodes represents the dependent attributes (outcomes). Fig. 5 illustrates the framework of the decision tree classifier.
Fig. 5.
Decision tree classifier.
Decision trees assist in identifying the features containing the most information and then spilt the dataset based on the values of these features, such that the target feature values at the resulting nodes are as accurate as possible. To do so, the informativeness of each feature needs to be measured, subsequently utilizing the feature with most information to split the data (Clairvoyant 2019). This process continues until pure leaf nodes are achieved. The informativeness is measured by a term called information gain, which can be computed based on the entropy of the dataset. The entropy is defined as the randomness of the data set and is given by
| (1) |
where is the probability that a target feature takes a specific value, . Information gain is then computed as follows:
| (2) |
Decision tree analysis also considers the Gini Index, which captures the probability of a specific feature being classified incorrectly when selected at random. The Gini Index is computed by subtracting the sum of squared probabilities of each class from one. It particularly favours larger partitions and is easy to implement, while the information gain measure favours smaller partitions with distinct values.
| (3) |
A feature with a lower Gini Index value is selected for the split.
4.2.2. Synthetic control method
We now analyse the impact of the vaccination programme predicted by the decision tree classifier. For this purpose, we utilize the Synthetic Control Method proposed by Abadie et al. (2010) and apply it to our context. The objective of applying the synthetic control method is to identify the reduction in the number of cases and the corresponding mortality rate due to the virus in a country. This is done by comparing the current situation (active number of cases and mortality rate) with the predicted results after the phase 2 vaccination programme.
Let us consider that we observe a country’s population over time periods, with the country only vaccinating a limited number of people at time , where ; the remaining population serves as potential controls (donor pools). The treatment effect for number of people at can then be defined as
| (4) |
where and represent the potential outcome with and without vaccination, respectively. With the observed outcome vector being , it can be denoted for each period as . However, for any period , the estimated vaccination impact is complicated by the missing counterfactual .
Abadie et al. (2010) provide guidance on how to identify the above treatment effects under the following general model for potential outcomes of all units:
| (5) |
| (6) |
where . For the treatment assignment mechanism given above, is not equal to 0 only when and . The treatment affects are captured by , with the potential outcomes of the treatment depending on a common factor and an error function , which can be defined as
| (7) |
where represents a vector of time-invariant measure predictors with time-specific parameters , denotes a vector of the time-invariant unobserved predictor variable with time-specific parameters , and represent unobserved zero-mean transitory shocks. In our scenario, the vector denotes the elements that do not get affected by the vaccination process, with denoting the elements that do get affected by the vaccination process. We consider a vector of weights such that and We further consider as the linear combination of the pre-treatment outcomes, which estimates the counterfactual. Abadie et al. (2010) states that as long as we select such that
| (8) |
then
| (9) |
is an unbiased estimator of . The vector is selected to minimize the inconsistency in the unobserved and observed data before the intervention, and between the treated and the synthetic control regions. This inconsistency is determined by the distance matrix represented as
| (10) |
where is a vector of including n covariates and pre-treatment characteristics for the vaccinated population, and is the vector of the matrix collecting the pre-treatment characteristics of the non-vaccinated population. In addition, is a diagonal matrix that assigns weights according to the relative importance of the covariates and the pre-intervention outcomes.
4.3. Phase 3 distribution
The model for phase 3 addresses the planning, production and distribution of the vaccine. The process begins with the vaccine production at the pharmaceutical plants situated at fixed locations. From there, the vaccine is transported to allocated cold storage facilities, from where it is subsequently distributed to nearby healthcare community centres based on demand. To reduce waiting time due to limited vaccine availability, demand is forecasted using predictive analysis via a mathematical model with cost considerations. As such, we formulate a mixed-integer linear programming (MILP) model considering various costs and constraints. The main aim of our model is to determine and specify the location and number of cold storage facilities, together with the required inventory levels and the allocation of storage facilities to healthcare community centres, so as to minimize transportation time for the entire supply chain network while at the same time minimizing cost. A key challenge here is to ensure that the proposed model is both cost- and time-efficient in addressing demand fluctuations.
We consider that the storage facilities can have multi-level capacities, which ensures that the demand of the community centres is fulfilled. We thus consider capacity planning as part of our model. To estimate the capacity along with total operational costs, we propose an algorithm that is performed until an optimal set of results is obtained.
4.3.1. Indices
| Set of healthcare community centres indexed by | |
| Set of potential storage facilities indexed by | |
| Set of plants indexed by | |
| Capacity level available at each storage facility indexed by | |
| Time period |
4.3.2. Parameters
| Unit cost of supplying the vaccine from storage facility to healthcare community centre | |
| Unit cost of supplying the vaccine from plant to storage facility | |
| The elapsed time between two consecutive vaccine orders for storage facility | |
| Fixed cost per unit time for opening and operating storage facility with capacity level | |
| Mean demand per unit of vaccine at healthcare community centre | |
| Variance of the demand per unit of vaccine at healthcare community centre | |
| Holding cost per unit of vaccine at storage facility | |
| Ordering cost of vaccine at storage facility from plant | |
| Capacity of storage facility with capacity level | |
| Space requirement of a vaccine unit at any storage facility | |
| Threshold level of stock at storage facility | |
| Lead time for ordering stock at storage facility | |
| Safety stock level at storage facility | |
| Reordering point for ordering stock at storage facility | |
| Stock quantity at storage facility | |
| Planning horizon |
4.3.3. Decision variables
| Is equal to 1, if a storage facility with capacity level is set up at potential site , otherwise 0 | |
| Is equal to 1, if the storage facility at site serves vaccine to healthcare community centre , otherwise 0 | |
| Is equal to 1, if the plant at site serves vaccine to storage facility at site otherwise 0 | |
| Mean demand of vaccine per unit time to be assigned to storage facility at site | |
| Variance of the vaccine demand per unit time to be assigned to storage facility at site |
4.3.4. Objective function
The objective is to design a cold supply chain distribution network that first determines the best possible sites for the allocation of storage facilities (the plant locations for the production of vaccines are considered fixed) and then provides decision-support for the distribution of the vaccines from the plants to the storage facilities, and from the storage facilities to nearby community health centres simultaneously, so that the vaccine can be distributed as quickly as possible to the population. The demand at the community centres is assumed to be stochastic in nature, where and are the mean and the variance, respectively. In addition to the total cost objectives considered in the model, i.e., opening cost, transportation cost and ordering cost, we capture a further critical parameter, i.e., safety holding stock, so that waiting time can be reduced. With the expediency of the vaccine’s distribution to the population being paramount to stop the spread, we considered this as a critical element in the model.
Within this framing, the opening cost considers the cost for opening a storage facility at a particular location, expressed in equation (11).
| (11) |
We consider a continuous inventory revision model (Manupati et al. 2019), which triggers an order of doses when the stock of vaccines falls below the threshold level . As such, when an order is placed by a community centre to a nearby storage facility, the stock level at the storage facility should meet the community centre’s demand during the lead time with a given probability 1-β. This probability captures the service level of the inventory stock system and is given by
| (12) |
where is the stochastic demand for storage facility during lead time , with being the maximum demand during the lead time, expressed in equation (13).
| (13) |
Here, represents the mean demand assigned to storage facility during the lead time, with representing the safety stock level that should be held at storage facility . Assuming a normal distribution, the reorder point can be calculated as
| (14) |
where depicts the variance at lead time . Since the lead time is assumed to be constant, the variance can be neglected, and equation (14) can be simplified as
| (15) |
where represents a standard normal distribution. From equation (15), the holding cost can be determined as
| (16) |
The first part of equation (16) represents the average holding cost of quantity Q, with the second part capturing the safety stock cost. The ordering and holding costs can thus be expressed as
| (17) |
Since we assumed that there is no capacity constraint to not curtail the order quantity, we can differentiate the objective function in terms of , and equalling it to zero we obtain
| (18) |
From equation (18) we obtain
| (19) |
Substituting equation (19) in equation (17) we derive the following:
| (20) |
| (21) |
| (22) |
Equation (22) captures the overall transportation cost incurred for the transportation of the vaccine from plant to storage facility , as well as the distribution of the vaccine from storage facility to community centre Thus, the overall objective function that seeks to minimize cost is presented in equation (23).
| (23) |
Subject to:
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
Constraint (24) ensures that the demand from storage facility is satisfied by only one plant . That the demand of the community centre is satisfied by storage facility is captured in constraint (25). Constraint (26) defines the capacity level of the storage facility. Constraint (27) computes the average demand served by storage facility , and constraint (28) ensures that only one storage facility is opened at one location. Finally, constraint (29) indicates the dual and decision variables with their respective values.
For the allocation phase, we assign the storage facilities to different parts of the country. For this, a distance matrix is formed that captures the distance between the storage facility locations to nearby healthcare community centres. In selecting a location for a storage facility, we develop criteria based on transportation facilities, freezer and cold storage refrigerators, and population density. However, the resultant problem then becomes NP-hard, which is why we propose the following algorithm to estimate the total cost of the model.
Step 1: The input parameters and variables for calculating the total costs are read.
Step 2: Distance matrices are created for the distance between each vaccine manufacturing plant and the proposed storage facilities locations, and from the storage facility locations to the healthcare community centres.
Step 3: With the collected data, operational costs are calculated, which is the sum of vaccine holding costs, transportation costs, ordering costs and storage costs.
Step 4: Random mean demand for each healthcare community centre is generated to calculate the variation in operational costs.
Step 5: Similar to the previous step, the random lead time for each healthcare community centre is generated to determine the variation in costs as calculated in the previous step.
Step 6: Iterations are performed until an optimal solution is obtained.
5. Experimentation and results
5.1. Case study context
We consider India as an illustrative case study to apply our model. India is an expansive country that accounts for 17.7% of the world’s total population. India has also been a country that has been most severely impact by COVID-19, especially recently due to the new Delta variant, accounting for close to 34 million confirmed cases and more than 450,400 deaths by October 2021 (WHO 2021).
In early 2021, 174 vaccines were in their pre-clinical development phase and 63 were in their clinical development phase (Soleimanpour and Yaghoubi 2021). On December 2, 2020, the United Kingdom released the first ever vaccine to stop the spread of COVID-19, with many more having been authorized for distribution since then. In India, Covishield by the Serum Institute of India and Covaxin by Bharat Biotech are manufactured and approved for distribution and application. India successfully started the vaccination drive on January 22, 2021, with the first phase including doctors, nursing staff, medics and paramedics, comprising all healthcare and frontline workers.
However, phase 1 of the vaccine distribution barely accounts for 2.3% of India’s population (Motkuri and Mishra 2020). To put an end to COVID-19, at least 70% of the population needs to be vaccinated. What is in the way of achieving this goal quickly is the vaccine distribution problem, i.e., the effective management of the cold chain starting from the manufacturer and ending with the receiver of the vaccine. Challenges include the appropriate prioritization of receivers, the production of enough vials, the delivery of the vaccine also to remote locations, the strategic location of storage facilities, administering the vaccine, and ensuring that individuals receive a second dose of the vaccine, if needed, to ensure the full efficacy of the vaccine.
We now proceed with a discussion of the results derived from the implementation of our proposed methodology within the context of India. We first invoke the decision tree classifier to determine the cities in most need of the vaccination, followed by predicting the best vaccination scenario. A synthetic control analysis is then carried out to predict the impact of the vaccination programme on the country by proceeding with the vaccination of the population in phase 2. Then, using the predicted results of the synthetic analysis, we forecast the needed vaccine production and the required number of storage facilities. We subsequently allocate these storage facilities to healthcare community centres located in both rural and urban parts of the country.
5.2. Prediction analysis (Phase 2)
In order to construct our prediction model, we conduct the following three steps.
Step 1: Data pre-processing
The first stage in data pre-processing is data collection, followed by a preparation and cleaning of the data. This involves removing rows with empty sets and converting data for evaluation and processing.
Data collection: We collected data for 4,000 cities and towns in India, out of which 300 cities have a population of more than 100,000. The data was collected with the following attributes from covidindia.org: number of active cases, number of deaths, population of the city, percentage of the population who is older than 50 years of age, percentage of the population who is under 18 years of age, percentage of the population having a chronic disease, and daily growth in the active number of cases. We commenced by selecting 135 cities across India whose active number of cases and deaths were more than 2% of the city’s population. We then classified the data based on metropolitan areas where the impact of COVID-19 was most severe.
Reliability: Reliability captures the overall uniformity of a measure, i.e., if a measure yields similar results under consistent conditions, it is said to have a high level of reliability. The coefficient alpha method is utilised to measure internal uniformity as a reliability indicator for the dependent variable. Table 1 articulates the coefficient alpha for the scaled variables.
Table 1.
Reliability.
| Alpha | No. of cities | No. of respondents (metropolitan areas) | Percentage of respondents |
|---|---|---|---|
| 0.87 | 4000 | 135 | 100 |
Step 2: Attribute selection
We used the filter “Correlation Attribute Eval” for evaluating the correlation between the class and other attributes. We then classified the data based on metropolitan areas where the impact of COVID-19 was most severe.
Step 3: Applying the algorithm
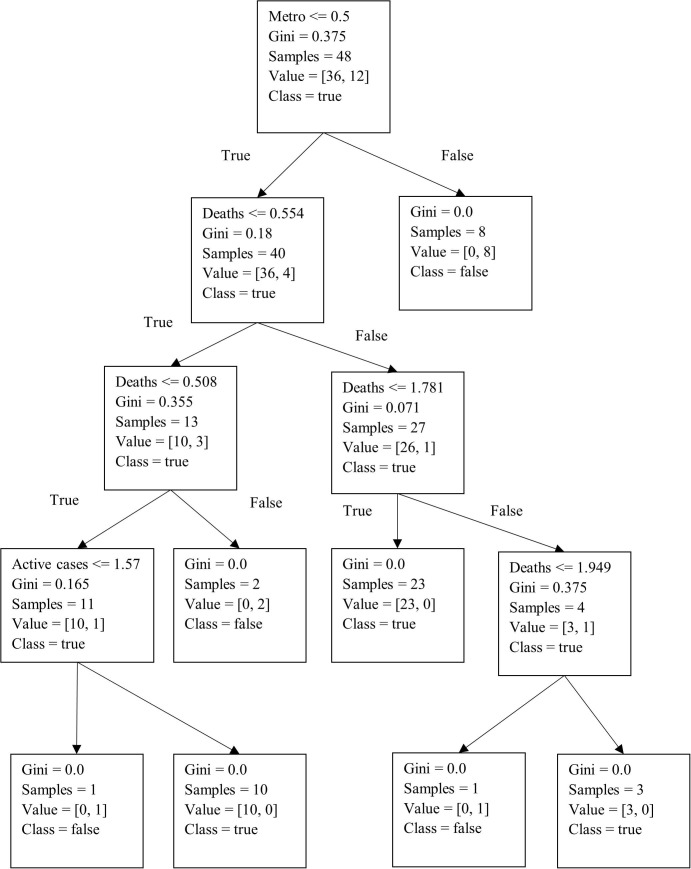
Subsequently, using Python, we developed a decision tree for the predictive analysis, with the results summarized in Fig. 6 . Furthermore, we utilized the K-fold cross-validation technique along with the decision tree algorithm to internally cross-verify and test the accuracy of our prediction results. The K-fold technique splits the data randomly into two parts, i.e., a training dataset and a test dataset. With this method, the dataset is divided into k sub-samples, in which sub-sample 1 is used for testing and the remaining k-1 sub-samples are used for training. The entire process is repeated k times by interchanging the test and the training data. The best model is then selected based on the minimum error (Gareth et al. 2013). This yielded a model with a predictive accuracy of 85.71% (n = 135). We can see from Fig. 6 that for a city to be selected, the active number of cases needs to be more than 1.57% of the city’s population, with deaths being more than 1.94% of the city’s population. Fig. 7 illustrates the results of the best predicted vaccination scenario. To derive this solution, we collected data for the 135 cities based on the three scenarios described in Section 3 under phase 2. Specifically, we divided a city’s population into two categories based on whether individuals were above or below 50 years of age, which is the cut-off point used in India to determine vaccine priority (Mishra 2021). The results indicate that if a city’s population that is below 50 years of age is less than 32%, the population that is above 50 years of age should be vaccinated first. The accuracy of this prediction model is 77.14% (n = 135).
Fig. 6.
Decision tree determining cities that should receive vaccine allotments.
Fig. 7.
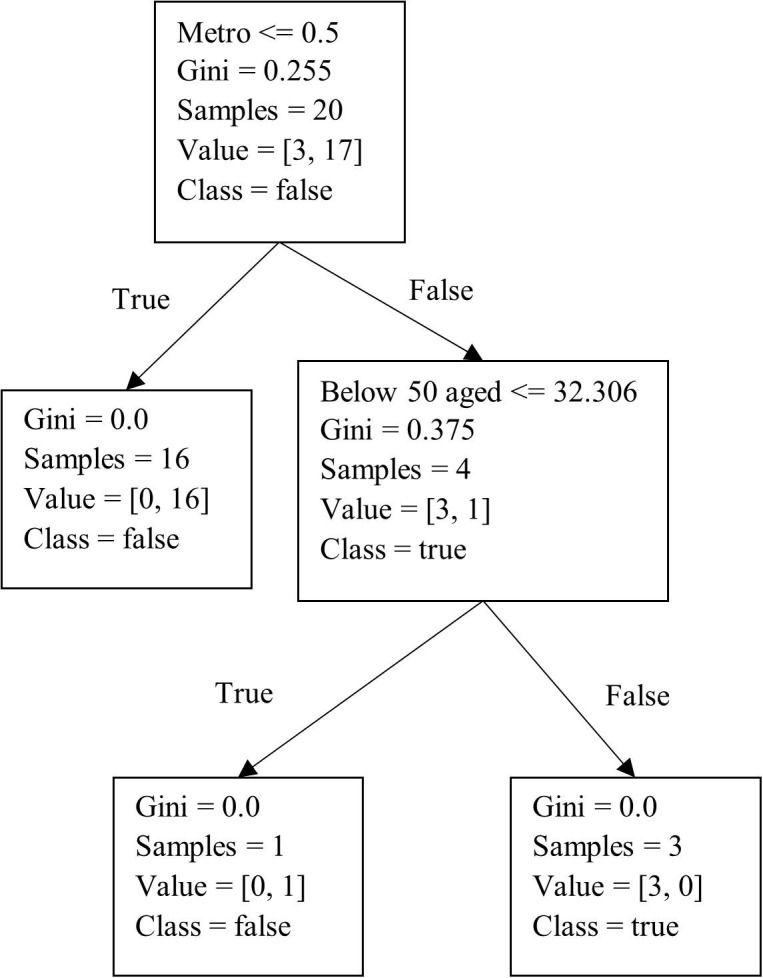
Decision tree to predict the best vaccination scenario.
5.3. Impact of the vaccination
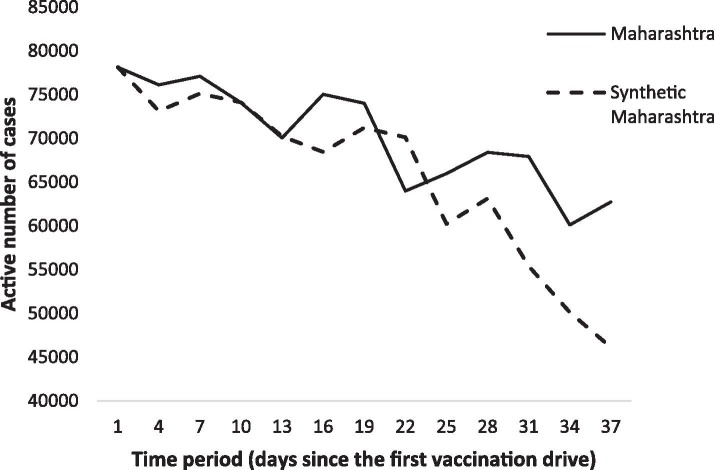
We now examine the post-vaccination impact on the active number of cases by vaccinating the portion of the population as predicted in the previous section. For this, we developed a synthetic control method algorithm to perform the analysis. The exercise was done with the most severely affected state of India, Maharashtra, whose population accounts for 9.28% of India’s population, or 112,374,333 people. The active number of cases prior to the start of phase 1 vaccinations was 78,145. Based on the prediction analysis from the prior section, if the vaccine is provided to 7,256,300 people, which is 6.45% of Maharashtra’s population, the impact on active COVID-19 cases would be as illustrated in Fig. 8 . In the graph, the line for Maharashtra denotes the results for the predicted number of active cases in the state without a vaccination drive, and the line for Synthetic Maharashtra represents the decrease in the number of cases with the vaccination drive.
Fig. 8.
Trends in the number of active cases: Maharashtra vs. Synthetic Maharashtra.
As noted above, we construct a donor pool based on the average number of active COVID-19 cases in other states that resemble Maharashtra. Table 2 compares the (real) results of Maharashtra’s pre-vaccination characteristics with the synthetic control analysis (based on the predicted results of Maharashtra), along with the average of active cases and mortality rates of other states resembling Maharashtra. We observe that the average of the mean values obtained from other states that did not vaccinate does not seem to provide a suitable control group (donor pool) for Maharashtra. Specifically, the average mortality rate and active number of cases were lower in the donor pool than in Maharashtra. Moreover, prior to the vaccination drive, the average active number of cases and the mortality rate were higher for the donor pool states than for Maharashtra. In contrast, the synthetic control results for Maharashtra accurately predict the value for the active number of cases and mortality rate prior to the vaccination drive.
Table 2.
Vaccination predictor mean values.
| Variables | Maharashtra |
Average of other control states | |
|---|---|---|---|
| Real | Synthetic | ||
| Active number of cases | 50,013 | 46,312 | 74,251 |
| Mortality rate (%) | 3% | 1.2% | 2.8% |
The above analysis assists in predicting the required doses to vaccinate the population in the distribution phase of the process. Ratio proportionality is utilized to predict vaccine production based on the results from the synthetic analysis. We specifically answer the following question: If 7,256,300 doses can reduce the active number of cases in Maharashtra to 40%, how much more vaccine is required to flatten the curve in the country? To answer this question, the results from the preceding analysis are now used as observed variables for carrying out the location- allocation problem in the next section.
5.4. Location-allocation (Phase 3)
The experimentations for the proposed phase 3 model were carried out on a PC with Intel Core i5-4302Y (1.70 GHz, 512 KB L2 cache) having a Windows 10 Home operating system with 8 GB RAM. The algorithm was developed on MATLAB and the results are depicted in Table 3 . For each iteration the model entries provide
-
a)
the total number of variables and the number of constraints after MATLAB pre-processing,
-
b)
the total number of community centres that can be utilised as vaccine cold storage facilities, and
-
c)
the optimal cost of the entire model and the optimal number of facilities that are to be allocated to the vaccine production plants.
Table 3.
Output of the proposed algorithm.
| Dimension | Number |
|---|---|
| Vaccine production units (plants) | 3 |
| Health care community centres | 24,855 |
| Available locations for vaccine storage facility | 188 |
| Number of variables | 14,321 |
| Number of constraints | 12,534,688 |
| Storage facility setups | 78 |
| Total costs | 4,682,460,810 |
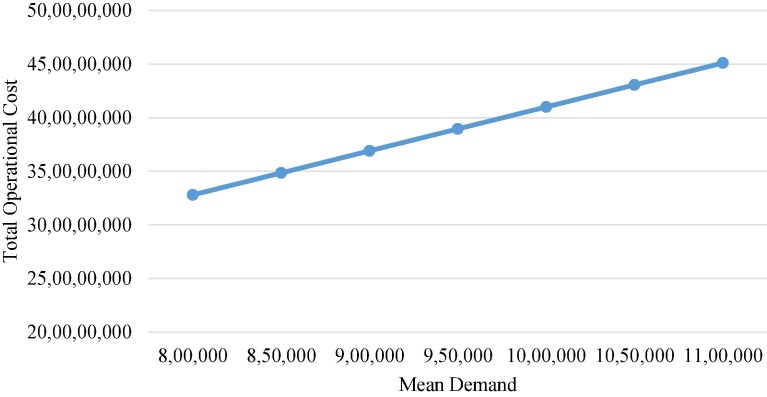
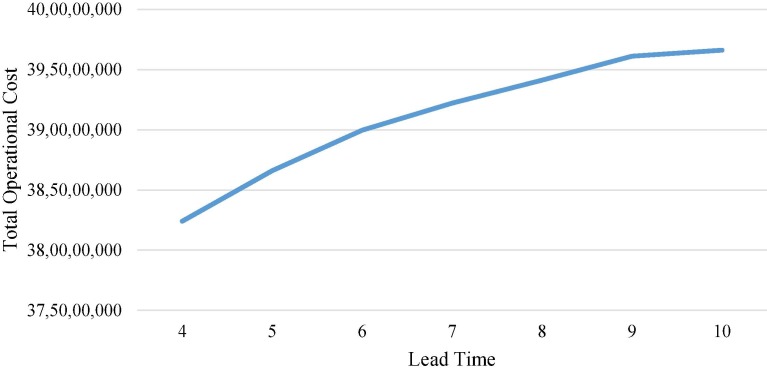
To evaluate the performance of the model, total operational costs are determined with respect to varying demand and lead times. Total operational costs are the sum of total storage and holding costs, transportation costs and ordering costs. As articulated in Fig. 9 , keeping the variance fixed at 32, the mean demand in the overall cold chain is varied from 800,000 to 1,100,000 units per order in 50,000 step increments at a constant lead time of 7 days. It can be seen from the figure that with the increase in demand, the costs incurred for each activity increase. As there is a linear proportional dependence of the model with respect to the demand, the graph is also linear. Fig. 10 describes the change in total operational costs with variations in lead times. It can be seen that as the lead time increases from 4 days to 10 days, with a fixed mean demand of 900,000 units per order and the variance at 32, lead time has a lesser impact compared to the mean demand, suggesting that while the lead time can vary, a very large lead time tends to be associated with high operational costs.
Fig. 9.
Effect of mean demand changes.
Fig. 10.
Effect of lead time changes.
5.4.1. Assessing solution quality
To evaluate the performance of our proposed heuristic algorithm, we conducted a comparison study by applying the Evolutionary Genetic algorithm NSGA-2 under similar constraints. Table 4 depicts the comparison results and concludes that the proposed heuristic algorithm is very effective when compared to the existing NSGA-2 for solving for the total operational costs with varying mean demand and lead times. The results are compared on the basis of variation in total cost with changes in mean demand and lead time data. The results obtained in this section provide insights into the magnitude of monetary resources required for setting up an entire distribution chain under uncertain situations. With that, the comparison study of the proposed algorithm with the NSGA-II illustrates the efficiency of this model and how it can be utilised for further continuous inventory system revisions.
Table 4.
Comparison of the proposed heuristic algorithm with NSGA-2
| Mean demand | Total operational costs |
Lead time | Total operational costs |
||
|---|---|---|---|---|---|
| Proposed heuristic | NSGA-2 | Proposed heuristic | NSGA-2 | ||
| 800,000 | 328,000,000 | 331,045,200 | 4 | 382,400,000 | 385,610,000 |
| 850,000 | 348,500,000 | 35,1238,000 | 5 | 386,600,000 | 389,450,000 |
| 900,000 | 369,000,000 | 369,510,000 | 6 | 389,962,330 | 401,250,000 |
| 950,000 | 389,500,000 | 394,500,000 | 7 | 392,210,650 | 441,285,000 |
| 1,000,000 | 410,000,000 | 418,426,000 | 8 | 394,125,355 | 448,512,000 |
| 1,050,000 | 430,500,000 | 442,520,000 | 9 | 396,114,500 | 449,125,000 |
| 1,100,000 | 451,000,000 | 464,851,000 | 10 | 396,615,620 | 451,000,000 |
The results obtained in this section provide insights into the magnitude of monetary resources.
5.5. Managerial implications
We now outline managerial implications that can be put into practice to improve the overall efficiency and accessibility of the proposed model. As such, our proposed model aids in developing best strategies for COVID-19 vaccine distributions to entire populations considering storage and transportation requirements as well as cost considerations (answering our first research question). Our vaccine distribution model is general enough so that it can serve as a basis for any human healthcare crisis affecting entire populations. With most current systems not being equipped to produce large quantities of vaccines and facing challenges in their distribution, we hope that our efforts in this paper, triggered by the COVID-19 crisis, serve as a starting point for healthcare authorities to plan and design their logistics, distribution and supply chain systems, making them more robust and resilient. We illustrated the applicability of our model within the context of India, which is a developing country with the second-highest population in the world. As such, we believe that the model can be easily adapted and applied in other contexts.
Since the availability of vaccines may be limited at first, we complemented our decision support with guidance on the best vaccine distribution scenario to maximize the impact of the vaccine program and to best forecast future vaccine production, ensuring an equitable distribution (answering our second research question). As such, our findings provide guidance for designing an optimal vaccine distribution system, which not only depends on individual factors, i.e., who should be vaccinated first, but also on the spatiotemporal factor indicating where vaccines should be provided first. Specifically, our results from the decision tree analysis and synthetic control method shown that prioritizing cities based on the number of active number of cases and death rate has a significant impact on reducing the overall number of cases in a country and on vaccinating vulnerable groups depending on the scenario-based criteria; this has a considerable effect on the reduction of the death rate. Associated with this objective was the determination of the best location and allocation of cold storage facilities, including both bulk vaccine production and distribution facilities (answering our third research question). The model also helps predict the duration to vaccinate the entire population along with indicating the timely need and speed for vaccine production and delivery. The insights obtained from this paper can further help in cost-cutting and budgeting, based on the corresponding objective included in the model. This can be particularly valuable for countries with constrained monetary resources allocated to the healthcare sector.
What is however critical in all of this are motivated and sufficient healthcare workers . In addition, people all over the world have expressed vaccine hesitancy, reluctance to wear masks, and been careless in terms of precautionary measures and restrictions imposed by governments. It is thus also critical to promote science-based information, curtail misinformation, and illustrate the great good vaccines can do to save lives. With such concerted efforts on all fronts, we are hopefully able to put an end to this pandemic soon.
6. Conclusion
The COVID-19 pandemic has taken a toll on life as we have known it worldwide. At the same time, the pandemic has triggered immense research efforts to develop vaccines, offering a glimmer of hope. What is now needed is insight into how to best distribute the vaccine through a vaccine cold chain network, which is what we aimed to do in this paper. Specifically, we proposed a dynamic vaccine cold chain model that can assist in vaccinating a population. Since vaccine availability is limited, at least at first, we developed a framework consisting of three phases. Phase 1 of the vaccine distribution process prioritized the vaccination of healthcare workers, for which we utilized a standard cold chain model, similar to what has been used for the polio vaccination. In phase 2 we formulated a decision tree classifier analysis to identify the cities whose population needs to be vaccinated most, and subsequently deduced the best way to carry out the vaccinations. This was followed by a synthetic control method, which we leveraged to predict the impact of the vaccination on future vaccine production demands. In phase 3, we developed a mixed integer linear programming model with the objective function estimating total network costs. The proposed model further determined the locations for vaccine storage facilities, taking into account uncertainties in demand and lead times. These facilities were then allocated to healthcare community centres for better and faster delivery of the vaccine. The model was optimized by a heuristic algorithm, with the results comparing favourably to the results obtained via a NSGA-2 algorithm, which was also used as a feasibility check.
We believe that the proposed model can be a valuable decision-support aid as managers decide on optimizing the vaccine cold chain distribution process while minimizing overall costs and ensuring a fast and equitable distribution. As part of the model, we also determined the optimal location of new storage facilities, helping healthcare authorities with these important choices. Considering the results of the proposed model in the planning stages of a vaccination drive will be invaluable, based on the insight generated through the predictive analysis, which assists in the determination of both the number of doses required and the target population with great accuracy. What may further aid in this process are technological advances like EVIN (Electronic Vaccine Intelligence Network), which can help in logistics tracking, or VVM (vaccine vial monitor), which can keep track of vaccine quality. In whichever direction the strategy is taken, what is paramount is that the public be informed about the process and distribution plans, which will engender trust and confidence that an end of the pandemic may be in sight.
We believe that our work offers a formidable foundation for future research. For instance, further research on developing an equitable vaccine distribution network by considering incomplete demand data under uncertain situations is needed. While we designed a location-allocation model for mass vaccine production and distribution, the consideration of vehicle routings can further improve the model and its applicability in remote areas, where transportation infrastructure may be less advanced. In addition, future research should consider disruption risks and yield problems that may be present, following the lead of scholars like Sinha et al., 2021, Arifoğlu and Tang, 2021. The cold chain management for vaccination distribution could further be strengthened by a real-time monitoring of the vaccine distribution process, for instance via blockchain technology along the lines of Antal et al. (2021). As such, a vaccine vial monitor like that used for the oral polio vaccine could be used to track possible vaccine adulteration, and a strict check to prevent vaccine wastage could be established at each vaccine depot. It is our hope that our research presented herein will serve as a foundation and inspiration for others to take this forward.
CRediT authorship contribution statement
Vijaya Kumar Manupati: Conceptualization, Data curation, Formal analysis, Writing – original draft. Tobias Schoenherr: Writing – review & editing. Nachiappan Subramanian: Investigation. M. Ramkumar: Investigation. Bhanushree Soni: Investigation. Suraj Panigrahi: Investigation.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Abadie A., Diamond A., Hainmueller J. Synthetic control methods for comparative case studies: Estimating the effect of California’s tobacco control program. J. Am. Stat. Assoc. 2010;105(490):493–505. [Google Scholar]
- Anparasan A.A., Lejeune M.A. Data laboratory for supply chain response models during epidemic outbreaks. Ann. Oper. Res. 2018;270(1-2):53–64. [Google Scholar]
- Antal, C.D., Cioara, T., Antal, M. and Anghel, I., 2021. Blockchain platform for COVID-19 vaccine supply management. arXiv preprint arXiv:2101.00983.
- Araz O.M., Galvani A., Meyers L.A. Geographic prioritization of distributing pandemic influenza vaccines. Health Care Manage. Sci. 2012;15(3):175–187. doi: 10.1007/s10729-012-9199-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arifoğlu K., Tang C.S. A two-sided incentive program for coordinating the influenza vaccine supply chain. Manuf. Serv. Oper. Manage. 2021 [Google Scholar]
- Azadi, Z., Eksioglu, S.D. and Geismar, H.N., 2020. Optimization of distribution network configuration for pediatric vaccines using chance constraint programming. arXiv preprint arXiv:2006.05488.
- Bertsimas D., Digalakis V., Jr., Jacquillat A., Li M.L., Previero A. Where to locate COVID-19 mass vaccination facilities? Nav. Res. Logist. 2021 doi: 10.1002/nav.22007. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bierle, A., 2020. Vaccine Delivery to Remote Regions of the World Using a Novel Delivery Platform. Master Thesis, University of New Mexico, https://digitalrepository.unm.edu/skc/2020/lobobites/1/.
- Billah, M.M., Zaman, K., Estivariz, C.F., Snider, C.J., Anand, A., Hampton, L.M., Bari, T.I., Russell, K.L. and Chai, S.J., 2017. Cold-chain adaptability during introduction of inactivated polio vaccine in Bangladesh, 2015. J. Infect. Dis., 216(suppl_1), S114-S121. [DOI] [PMC free article] [PubMed]
- Bode L., Vraga E.K. See something, say something: correction of global health misinformation on social media. Health Commun. 2018;33(9):1131–1140. doi: 10.1080/10410236.2017.1331312. [DOI] [PubMed] [Google Scholar]
- Bozorgi, A., Fahimnia, B., 2021. Transforming the vaccine supply chain in Australia: Opportunities and challenges. Vaccine, in press. [DOI] [PubMed]
- Bozorgi A., Pazour J., Nazzal D. A new inventory model for cold items that considers costs and emissions. Int. J. Prod. Econ. 2014;155:114–125. [Google Scholar]
- Buccieri K., Gaetz S. Ethical vaccine distribution planning for pandemic influenza: Prioritizing homeless and hard-to-reach populations. Public Health Ethics. 2013;6(2):185–196. [Google Scholar]
- Bukszpan, D., 2020. The challenges Pfizer faces distributing its COVID-19 vaccine to the masses. CNBC. November 25, 2020. https://www.cnbc.com/2020/11/25/challenges-pfizer-faces-distributing-covid-19-vaccine-to-the-masses-.html.
- Centers for Disease Control and Prevention (CDC), 2019. Vaccine Storage and Handling Toolkit. U.S. Department of Health and Human Services. https://www.cdc.gov/vaccines/hcp/admin/storage/toolkit/storage-handling-toolkit.pdf.
- Choi T.-M. Risk analysis in logistics systems: A research agenda during and after the COVID-19 pandemic. Transport. Res. Part E: Logist. Transport. Rev. 2021;145 [Google Scholar]
- Chowdhury, P., Paul, S.K., Kaisar, S. and Moktadir, M.A., 2021. COVID-19 pandemic related supply chain studies: A systematic review. Transport. Res. Part E: Logist. Transport. Rev., 102271. [DOI] [PMC free article] [PubMed]
- Clairvoyant, 2019. Entropy, information gain, and Gini index: the crux of a decision tree. The Clairvoyant Vision (blog), October 14 https://blog.clairvoyantsoft.com/entropy-information-gain-and-gini-index-the-crux-of-a-decision-tree-99d0cdc699f4.
- Deo, S., Manurkar, S., Krishnan, S. and Franz, C., 2020. Covid-19 Vaccine: Development, Access and Distribution in the Indian Context. ORF Issue Brief.
- Duijzer L.E., van Jaarsveld W., Dekker R. Literature review: The vaccine supply chain. Eur. J. Oper. Res. 2018;268(1):174–192. [Google Scholar]
- Dutta P., Choi T.M., Somani S., Butala R. Blockchain technology in supply chain operations: Applications, challenges and research opportunities. Transport. Res. Part E: Logist. Transport. Rev. 2020;142:102067. doi: 10.1016/j.tre.2020.102067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards K.M., Hackell J.M. Countering vaccine hesitancy. Pediatrics. 2016;138(3):e20162146. doi: 10.1542/peds.2016-2146. [DOI] [PubMed] [Google Scholar]
- Enayati S., Özaltın O.Y. Optimal influenza vaccine distribution with equity. Eur. J. Oper. Res. 2020;283(2):714–725. [Google Scholar]
- Esmizadeh Y., Bashiri M., Jahani H., Almada-Lobo B. Cold chain management in hierarchical operational hub networks. Transport. Res. Part E: Logist. Transport. Rev. 2021;147:102202. doi: 10.1016/j.tre.2020.102202. [DOI] [Google Scholar]
- Fleming M., Okebukola P., Skiba K. McKinsey & Company; White Paper, September: 2021. Port to Patient: Improving Country Cold Chains for COVID-19 Vaccines; p. 14. [Google Scholar]
- Gareth J., Daniela W., Trevor H., Robert T. An Introduction to Statistical Learning: With applications in R. Springer. 2013 [Google Scholar]
- Gollust S.E., Saloner B., Hest R., Blewett L.A. US adults’ preferences for public allocation of a vaccine for coronavirus disease 2019. JAMA Network Open. 2020;3(9):e2023020. doi: 10.1001/jamanetworkopen.2020.23020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Govindan K., Mina H., Alavi B. A decision support system for demand management in healthcare supply chains considering the epidemic outbreaks: A case study of coronavirus disease 2019 (COVID-19) Transport. Res. Part E: Logist. Transport. Rev. 2020;138:101967. doi: 10.1016/j.tre.2020.101967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasanat, R.T., Rahman, M.A., Mansoor, N., Mohammed, N., Rahman, M.S. and Rasheduzzaman, M., 2020, September. An IoT based real-time data-centric monitoring system for vaccine cold chain. In: 2020 IEEE East-West Design & Test Symposium (EWDTS) (pp. 1–5). IEEE.
- Hechter M. Principles of Group Solidarity. University of California Press; 1988. [Google Scholar]
- Ivanov D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transport. Res. Part E: Logist. Transport. Rev. 2020;136 doi: 10.1016/j.tre.2020.101922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanov D., Das A. Coronavirus (COVID-19/SARS-CoV-2) and supply chain resilience: A research note. Int. J. Integrated Supply Manage. 2020;13(1):90–102. [Google Scholar]
- Kumru O.S., Joshi S.B., Smith D.E., Middaugh C.R., Prusik T., Volkin D.B. Vaccine instability in the cold chain: mechanisms, analysis and formulation strategies. Biologicals. 2014;42(5):237–259. doi: 10.1016/j.biologicals.2014.05.007. [DOI] [PubMed] [Google Scholar]
- Lemmens S., Decouttere C., Vandaele N., Bernuzzi M. A review of integrated supply chain network design models: Key issues for vaccine supply chains. Chem. Eng. Res. Des. 2016;109:366–384. [Google Scholar]
- Lin Q.i., Zhao Q., Lev B. Cold chain transportation decision in the vaccine supply chain. Eur. J. Oper. Res. 2020;283(1):182–195. [Google Scholar]
- Liu M., Zhang D. A dynamic logistics model for medical resources allocation in an epidemic control with demand forecast updating. J. Operat. Res. Soc. 2016;67(6):841–852. [Google Scholar]
- Lloyd J., Cheyne J. The origins of the vaccine cold chain and a glimpse of the future. Vaccine. 2017;35(17):2115–2120. doi: 10.1016/j.vaccine.2016.11.097. [DOI] [PubMed] [Google Scholar]
- Mamani H., Chick S.E., Simchi-Levi D. A game-theoretic model of international influenza vaccination coordination. Manage. Sci. 2013;59(7):1650–1670. [Google Scholar]
- Manupati V.K., Jedidah S.J., Gupta S., Bhandari A., Ramkumar M. Optimization of a multi-echelon sustainable production-distribution supply chain system with lead time consideration under carbon emission policies. Comput. Ind. Eng. 2019;135:1312–1323. [Google Scholar]
- Matrajt, L., Eaton, J., Leung, T. and Brown, E.R., 2020. Vaccine optimization for COVID-19: Who to vaccinate first? medRxiv, https://doi.org/10.1101/2020.08.14.20175257. [DOI] [PMC free article] [PubMed]
- Mishra, H., 2021. Covid vaccination drive in India to begin from January 16, healthcare workers to get priority. India Today, January 9, https://www.indiatoday.in/coronavirus-outbreak/story/coronavirus-vaccination-drive-india-begin-from-january-16-healthcare-workers-priority-1757458-2021-01-09.
- Motkuri V., Mishra U.S. Human resources in healthcare and health outcomes in India. Millennial Asia. 2020;11(2):133–159. [Google Scholar]
- Naik, S., Paleja, A., Mahajan, M., Ramachandran, N., Dixit, S., Matthan, R., Pai, N. and Kotasthane, P., 2020. A COVID-19 vaccine deployment strategy for India. Indian Publ. Policy Rev., 1(2 (Nov-Dec)), 42-58.
- Okakwula I.K., Alayande A.S., Orukpe P.E. Accurate Probability Distribution Model Determination and Forecasting of Peak Load Demand in Nigeria. Jordan J. Electr. Eng. 2018;4(4):186–194. [Google Scholar]
- Pagliusi S., Jarrett S., Hayman B., Kreysa U., Prasad S.D., Reers M., Hong Thai P., Wu K.e., Zhang Y.T., Baek Y.O., Kumar A., Evtushenko A., Jadhav S., Meng W., Dat D.T., Huang W., Desai S. Emerging manufacturers engagements in the COVID-19 vaccine research, development and supply. Vaccine. 2020;38(34):5418–5423. doi: 10.1016/j.vaccine.2020.06.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Persad G., Emanuel E.J., Sangenito S., Glickman A., Phillips S., Largent E.A. Public perspectives on COVID-19 vaccine prioritization. JAMA Network Open. 2021;4(4):e217943. doi: 10.1001/jamanetworkopen.2021.7943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preciado, V.M., Zargham, M., Enyioha, C., Jadbabaie, A., Pappas, G., 2013, December. Optimal vaccine allocation to control epidemic outbreaks in arbitrary networks. In 52nd IEEE Conference on Decision and Control (pp. 7486–7491). IEEE.
- Rachaniotis N.P., Dasaklis T.K., Pappis C.P. A deterministic resource scheduling model in epidemic control: A case study. Eur. J. Oper. Res. 2012;216(1):225–231. [Google Scholar]
- Rastegar M., Tavana M., Meraj A., Mina H. An inventory-location optimization model for equitable influenza vaccine distribution in developing countries during the COVID-19 pandemic. Vaccine. 2021;39(3):495–504. doi: 10.1016/j.vaccine.2020.12.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robbins, R., Robles, R. and Arango, T., 2021. Here’s why distribution of the vaccine is taking longer than expected. The New York Times. January 11, 2021. https://www.nytimes.com/2020/12/31/health/vaccine-distribution-delays.html.
- Saif A., Elhedhli S. Cold supply chain design with environmental considerations: A simulation-optimization approach. Eur. J. Oper. Res. 2016;251(1):274–287. [Google Scholar]
- Savachkin A., Uribe A. Dynamic redistribution of mitigation resources during influenza pandemics. Socio-Econom. Plann. Sci. 2012;46(1):33–45. [Google Scholar]
- Sheraton M., Deo N., Dutt T., Surani S., Hall-Flavin D., Kashyap R. Psychological effects of the COVID 19 pandemic on healthcare workers globally: a systematic review. Psychiatry Res. 2020;292:113360. doi: 10.1016/j.psychres.2020.113360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinha P., Kumar S., Chandra C. Strategies for ensuring required service level for COVID-19 herd immunity in Indian vaccine supply chain. Eur. J. Oper. Res. 2021 doi: 10.1016/j.ejor.2021.03.030. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soleimanpour S., Yaghoubi A. COVID-19 vaccine: Where are we now and where should we go? Expert Rev. Vacc. 2021;20(1):23–44. doi: 10.1080/14760584.2021.1875824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart A.J., Devlin P.M. The history of the smallpox vaccine. J. Infect. 2006;52(5):329–334. doi: 10.1016/j.jinf.2005.07.021. [DOI] [PubMed] [Google Scholar]
- Sun L., DePuy G.W., Evans G.W. Multi-objective optimization models for patient allocation during a pandemic influenza outbreak. Comput. Oper. Res. 2014;51:350–359. [Google Scholar]
- Sun P., Yang L., De Véricourt F. Selfish drug allocation for containing an international influenza pandemic at the onset. Operations Research. 2009;57(6):1320–1332. [Google Scholar]
- Tavana M., Govindan K., Nasr A.K., Heidary M.S., Mina H. A mathematical programming approach for equitable COVID-19 vaccine distribution in developing countries. Ann. Oper. Res. 2021 doi: 10.1007/s10479-021-04130-z. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulmer J.B., Valley U., Rappuoli R. Vaccine manufacturing: Challenges and solutions. Nat. Biotechnol. 2006;24(11):1377–1383. doi: 10.1038/nbt1261. [DOI] [PubMed] [Google Scholar]
- United Nations (UN), 2020. Why optimized cold-chains could save a billion COVID vaccines. UN Environment Programme. https://www.unenvironment.org/news-andstories/ story/why-optimized-cold-chains-could-save-billion-covid-vaccines.
- Salin V., Nayga R.M. A cold chain network for food exports to developing countries. Int. J. Phys. Distrib. Logist. Manage.ent. 2003;33(10):918–933. [Google Scholar]
- World Health Organization (WHO), 2019. Feasibility Assessment of Measles and Rubella Eradication. https://www.who.int/immunization/sage/meetings/2019/october/3_Feasibility_Assessment_of_Measles_and_Rubella_Eradication_updatedSAGE.pdf.
- World Health Organization (WHO), 2021. WHO Coronavirus Disease (COVID-19) Dashboard 06 February 2021. World Health Organization. September 7. https://covid19.who.int/.
- Xie L., Hou P., Han H. Implications of government subsidy on the vaccine product R&D when the buyer is risk averse. Transport. Res. Part E: Logist. Transport. Rev. 2021;146 doi: 10.1016/j.tre.2020.102220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Y., Xiao T. Analysis of cold-chain service outsourcing modes in a fresh agri-product supply chain. Transport. Res. Part E: Logist. Transport. Rev. 2021;148:102264. doi: 10.1016/j.tre.2021.102264. [DOI] [Google Scholar]
- Zhang X., Lam J.S.L. Shipping mode choice in cold chain from a value-based management perspective. Transport. Res. Part E: Logist. Transport. Rev. 2018;110:147–167. [Google Scholar]