Abstract
The high voltage losses (), originating from inevitable electron-phonon coupling in organic materials, limit the power conversion efficiency of organic solar cells to lower values than that of inorganic or perovskite solar cells. In this work, we demonstrate that this can in fact be suppressed by controlling the spacing between the donor (D) and the acceptor (A) materials (DA spacing). We show that in typical organic solar cells, the DA spacing is generally too small, being the origin of the too-fast non-radiative decay of charge carriers (), and it can be increased by engineering the non-conjugated groups, i.e., alkyl chain spacers in single component DA systems and side chains in high-efficiency bulk-heterojunction systems. Increasing DA spacing allows us to realize significantly reduced and improved device voltage. This points out a new research direction for breaking the performance bottleneck of organic solar cells.
Subject terms: Devices for energy harvesting, Materials for devices
Complex morphology in donor/acceptor organic heterostructures hampers the understanding of device performance. Here, the origin of the high voltage loss in organic solar cells is ascribed to the too small spacing between the donor/acceptor molecules in the active layer, and the voltage loss can be reduced by increasing the donor/acceptor spacing.
Introduction
The performance of donor-acceptor (DA) organic solar cells based on the bulk-heterojunction (BHJ) concept1,2 has been improving rapidly3–10, as a result of the development of high-performance donor and acceptor materials with better optical, electrical, and morphological properties5,7,8,11–14. Peak external quantum efficiencies (s) and fill-factor () have now exceeded 80% for organic solar cells10,15–17. Nevertheless, the open-circuit voltage () is still much lower than that predicted by Shockley–Queisser theory18,19. The low , or in other words, the high voltage loss () limits the power conversion efficiency (PCE) of organic solar cells20–24.
consists of radiative () and non-radiative recombination voltage loss (), which for the DA organic solar cells are related to the properties of the charge transfer (CT) states formed at the DA interfaces25–28: While the radiative decay rate of the CT states () determines 22,29,30, the ratio of and the non-radiative decay rate of CT states () determines 22,27,31–35.
The main reason for the high in the organic solar cells is the high 21–24,27,32,36–40, and reducing it has been proven to be highly challenging. An effective strategy to reduce is to reduce the energetic difference between the local excited states () in the pristine donor or acceptor material and CT states, resulting in hybridization and an increase in the transition oscillator strengths of the -CT hybrid states35,41–45. However, the reduction in is in that case mostly the result of a higher , leading to increased 35,44. Thus, does not necessarily reduce, even though a reduced is achieved using this method.
The key to reduce , and realize a reduced , is to eliminate the non-radiative decay paths and reduce without increasing 22,23,32,34. This requires an understanding of the origin of the generally high in DA organic solar cells. Recently, it was suggested that the high in DA blends is related to the presence of the high-frequency carbon-carbon vibrational modes, leading to a strong vibrational coupling between CT and ground states22. Later, it was demonstrated that and were reduced in blends based on organic visible light-emitting materials, due to their higher energy of CT state ()38, compared to that of the solar cell materials, reducing the degree of vibrational wavefunction overlap, and thus the degree of coupling between the vibrational states. However, for solar light harvesting, it is highly undesired to realize a reduced by increasing , since the use of high gap organic semiconductors (required for high ) limits the spectral response range, and thus the photocurrent under solar illumination.
The classic theory for the non-adiabatic electronic transitions, as is used to describe non-radiative decay, starts with
| 1 |
where is the Planck constant, is the electronic coupling matrix element, and is the Frank–Condon factor describing the vibrational overlap. Including the high-frequency vibrational modes leads to increased , being the main reason for the high in organic photovoltaics. Although, also depends on FC and the transition dipole moment (M)24, it is possible to reduce without increasing . This requires reducing , a parameter exponentially dependent on the spacing between the donor and the acceptor molecules (DA spacing) forming the CT states46,47. A small DA spacing leads to a high value, and thus a high 48,49. On the other hand, a too large DA spacing will lead to inefficient dissociation of the states, causing geminate recombination of excitons and limiting the yield of free charge carriers41,50–54. Currently, most of the high-efficiency organic solar cells are with high peak s, which suggests that the value of DA spacing does not exceed that required for efficient electron transfer from D to A. However, it is unclear whether the DA spacing in organic blends is too small with respect to the maximum spacing tolerated, maintaining efficient charge transfer, and if it can be increased in favor of a reduced .
To answer the above question, the relationship between DA spacing and the rates for CT state formation and recombination needs to be established. In organic light-emitting diodes based on the thermally activated delayed fluorescence (TADF) exciplex emitters, tuning of the DA spacing has been achieved via engineering the chemical structure of the active material or the microstructure of the active layer55: Increasing the DA spacing was found to give rise to the reduced energy difference between the triplet and singlet CT states in the DA blend, and thus, increased device emission efficiency. However, for organic solar cells, the investigation regarding the DA spacing has been arduous, due to a lack of methods to reliably identify and tune the DA spacing in BHJ organic blends. In this work, we achieve a variation of the DA spacing by molecular structural engineering of the active materials, and we identify that the high in organic solar cells is indeed associated with a too small DA spacing. This is first demonstrated in solar cells based on double-cable donor-acceptor (DCDA) polymers, in which the donor and the acceptor molecules are chemically linked by alkyl chain linkers: A correlation between the length of the linkers and the DA spacing is observed, and both and of the solar cell reduce with increasing DA spacing. For solar cells based on the more conventional BHJ systems, increased DA spacing is realized by modifying the side chains of the donor and the acceptor materials: For DA spacings up to an estimated 5 Å, is also found to reduce with increasing DA spacing, leading to a reduction of by as much as 0.2 V. Since the dissociation efficiency of states in the blends with increased DA spacing remains high, we conclude that the DA spacing must be generally too small in the solar cells studied in this work. As the BHJ systems studied are used in the current state-of-the-art organic solar cells, this newly discovered origin for the high is likely also present in the currently highest efficiency devices, and overcoming it by increasing the DA spacing is expected to be a promising strategy to push s over the benchmark value of 20%.
Results
Structural analysis for the thin films of DCDA polymers
In order to reliably tune the DA spacing, we first utilize DCDA polymers for which the donor backbone is covalently linked to acceptor units using non-conjugated linker groups56–58. The DCDA polymers are a good model system for investigating the impact of DA spacing on CT state properties and in organic solar cells, since as compared to BHJ systems, they have relatively more stable and predictable morphological and crystalline properties, due to the spatial confinement of the donor and the acceptor molecules by chemical bonding58–61. The DCDA polymers studied in this work are based on a donor component similar to PBDB-T (poly[(2,6-(4,8-bis(5-(2-ethylhexyl)thiophen-2-yl)-benzo[1,2-b:4,5-b′]dithiophene))-alt-(5,5-(1′,3′-di-2-thienyl-5′,7′-bis(2-ethylhexyl)benzo [1′,2′-c:4′,5′-c′]dithiophene-4,8-dione))])3, linked to the acceptor component NDI (naphthalene diimide) by alkyl chain linkers based on different numbers of methylene groups (Fig. 1a). Both the donor and acceptor units in the DCDA polymers are commonly used as building blocks for efficient BHJ organic solar cells3,4,62,63, and their synthetic routes are provided in Supplementary Note 1.
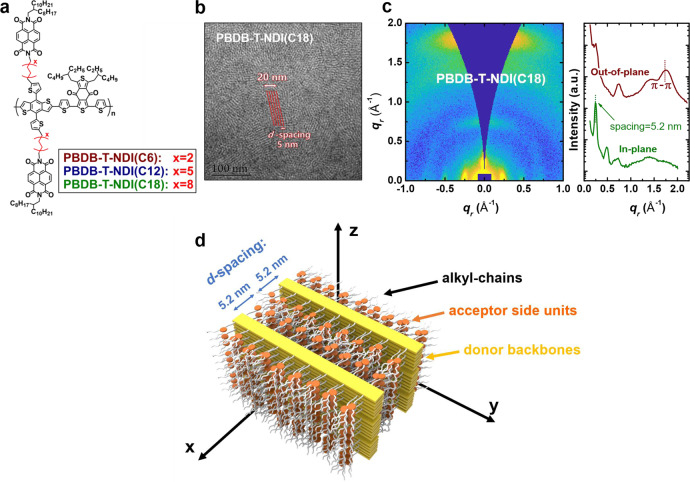
Fig. 1. Structural analysis for the thin films of DCDA polymers.
a Chemical structure of the DCDA polymers with different lengths of alkyl chain linkers. b TEM image and c GIWAXS pattern from the thin film based on PBDB-T-NDI(C18). d Schematic representation of the molecular arrangement in the ordered phases of the thin film based on PBDB-T-NDI(C18).
To evaluate the nano-scale packing structures in the thin films of the DCDA polymers, transmission electron microscope (TEM) measurements are performed. Prior to the measurements, the thin films were stained by the vapor of a 0.5 wt% RuO4 solution to enhance imaging contrast. Due to the selective staining of aromatic species by RuO4, the backbone of the polymer fully consisting of aromatic rings appears to be darker than the side units, as shown in Fig. 1b, as well as in Supplementary Fig. 10: Periodic patterns of black and white stripes can be observed in the TEM images, indicative of a high degree of structural order. The ordered stripes correspond to vertically oriented lamellar assemblies of the polymer with a d-spacing of ≈5 nm, where the backbones and the side units segregate alternately. The vertical orientation of the lamellar structures is also confirmed by grazing incident wide-angle diffraction (GIWAXS) patterns showing equatorial scattering at qx = 0.25 Å−1, being the second-order diffraction from the lamellae. Furthermore, in-plane stacking of the aromatic backbones is observed, as shown by the strong meridional scattering at qz = 1.75 Å−1 corresponding to a spacing of 3.6 Å (π-π). Moreover, the GIWAXS pattern shows a vertical streak located at qz = 0.25 Å−1. This scattering suggests structural order along the film normal, i.e., the direction of the π-π stacking, with a spacing of 2.6 nm approximating to the parallel stacking of seven backbones. The segmentation of the aromatic stacking originates from the incommensurability of the side units with alkyl chains and the rigid backbones with aromatic rings, a behavior commonly observed in supramolecular systems such as discotic liquid crystals64.
The assembled structure of the DCDA polymer (PBDB-T-NDI(C18)) in thin films is schematically shown in Fig. 1d. In these DCDA polymers, the CT state properties relevant for charge generation and recombination are determined by the intramolecular interfaces between the PBDB-T and NDI units. Therefore, the relevant DA spacing is related to the d-spacing, with the actual value of the DA spacing being considerably smaller than half of the d-spacing, due to the space taken by the side chains on the acceptor units (Fig. 1d). The d-spacing of the lamellae is expected to depend on the length of the alkyl linkers. Indeed, from the GIWAXS patterns (Supplementary Note 3) of the thin films of the DCDA polymers with shorter linkers, i.e., PBDB-T-NDI(C6) and PBDB-T-NDI(C12), we find that the structural properties are similar to that with longer linkers, and the lamellar packing remains. Also, we derive that the d-spacings are 3.6 and 4.6 nm, for PBDB-T-NDI(C6) and PBDB-T-NDI(C12), respectively, considerably shorter than that for PBDB-T-NDI(C18) (5.2 nm). This suggests a reliable tuning of the DA spacing by a decrease of the linker length in the ordered regions of the thin DCDA polymer films.
Molecular dynamic simulations (MD) are also employed mainly to investigate the spatial arrangement of the donor and the acceptor units in the DCDA polymers and determine the DA spacing in the amorphous parts of the films. As shown in Supplementary Fig. 14, the MD simulations predict that the NDI acceptor units of PBDB-T-NDI(C6) are restricted to the close vicinity of the donor backbones by the short alkyl chain linkers, facilitating the formation of intramolecular parallel π-stacking between the donor backbones and the acceptor units. This is the closest packing structure that one can expect for the packed aromatic rings with small spacing (or DA spacing as is for the stacked donor and acceptor molecules)65,66. On the contrary, the NDI acceptor units of the DCDA polymer with longer alkyl chain linkers, e.g., PBDB-T-NDI(C18), are pushed away from the donor backbone by the linker groups (Supplementary Fig. 14), due to the large size of the linker group occupying considerable space around the donor backbones. This significantly reduces the probability for the parallel π stacking between the donor and the acceptor units. Using the centroids to represent the locations of the conjugated structures in the donor and the acceptor units, we derive the radial distribution function (RDF) for the distances between the donor and the acceptor units (Supplementary Fig. 14): For PBDB-T-NDI(C6), the peak value of the shortest distances between the donor and the acceptor units, corresponding to the DA configuration with the closest spacing (most relevant for CT state formation), is 3.7 Å, and for PBDB-T-NDI(C18), the peak value is 4.2 Å. This shows that increasing the linker length indeed allows a tuning of the DA spacing also in the amorphous parts of the thin films of DCDA polymers.
CT state decay rates and in the DCDA solar cells
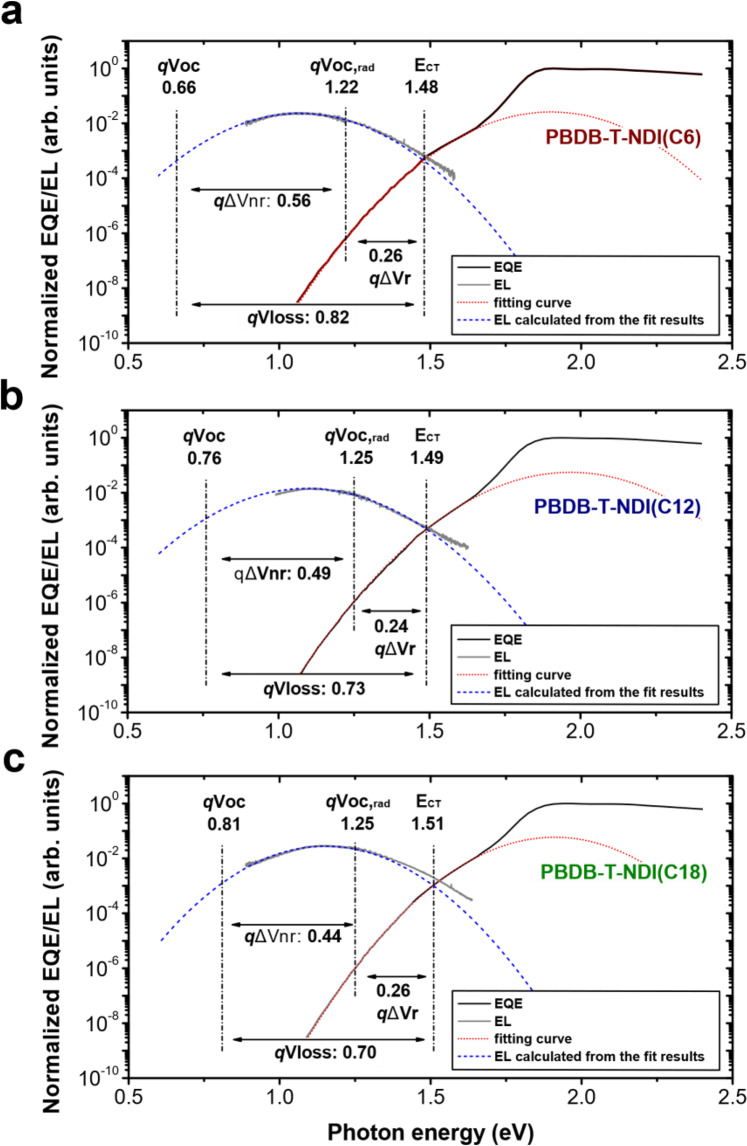
With tunable DA spacing in the thin films established, we can now evaluate its influence on key photovoltaic and recombination parameters in organic solar cells. The devices are based on an inverted architecture of ITO/ZnO/active layer/MoO3/Ag. We find that the of the solar cells strongly depends on linker length, as listed in Table 1: The of the solar cell based on PBDB-T-NDI(C6) with short linkers is 0.66 V, considerably lower than that based on PBDB-T-NDI(C18) with longer linkers (0.81 V). We also note that the of the solar cells, determined using the method described in the literature67–70, are very similar regardless of the length of the linkers (Fig. 2). Thus, , being the difference between and the measured , is significantly higher for the solar cell based on PBDB-T-NDI(C6) (0.82 V), compared to that based on PBDB-T-NDI(C18) (0.70 V), as indicated in Fig. 2 and summarized in Table 1. More importantly, using the photovoltaic , we determine the radiative limit for (). Then we calculate ()31,71 and find that is also higher in the solar cell based on PBDB-T-NDI(C6) (0.56 V), as compared to PBDB-T-NDI(C18) (0.44 V). On the other hand, the values of are similar in these devices, which suggests similar 29,41,44. Note that these results do not suggest that is completely independent of the DA spacing: There could be a small reduction in with the increased DA spacing, but this reduction could not be detected by the measurement of , due to the logarithmic dependence of on . Furthermore, the values for are verified by measuring the of the devices, details regarding the determination of the terms are provided in Supplementary Note 6.
Table 1.
Voltage loss values from the subgap measurements for the solar cells based on DCDA polymers.
| (V) | (eV) | a (V) | b (V) | c (V) | d (V) | |
|---|---|---|---|---|---|---|
| PBDB-T-NDI(C6) | 0.66 | 1.48 | 0.82 | 1.22 | 0.56 | 0.26 |
| PBDB-T-NDI(C12) | 0.76 | 1.49 | 0.73 | 1.25 | 0.49 | 0.24 |
| PBDB-T-NDI(C18) | 0.81 | 1.51 | 0.70 | 1.25 | 0.44 | 0.26 |
JV curves and the photovoltaic performance parameters of the solar cells are provided in Supplementary Note 9.
aCalculated using eq. , the method used to determine is provided in Supplementary Note 5.
bCalculated from the radiative limit for the dark saturation current, details in Supplementary Note 6.
cCalculated using eq. ; values are also verified by measuring , details in Supplementary Note 6.
dCalculated using eq.
Fig. 2. Voltage losses and CT state properties in the solar cells based on DCDA polymers.
and electroluminescence (EL) spectra of the solar cells based on a PBDB-T-NDI(C6), b PBDB-T-NDI(C12), and c PBDB-T-NDI(C18). The lower energy parts of the spectra are fitted by using the method described in the literature67–70 to determine the values for , and the fit results are used to calculate the emission spectra, which agree well with the measured EL spectra of the solar cells. Details regarding the determination of are provided in Supplementary Note 5.
From the above results, the increase in and decrease in with increasing chain length must therefore be mainly due to a decreased (). This is confirmed by the transient photovoltage decay (TPV) measurements: The voltage decay time, i.e., the lifetime of the photo-generated charge carriers, closely related to the inverse of CT state decay rate (), is approximately an order of magnitude higher for the solar cell based on PBDB-T-NDI(C18), compared to that based on PBDB-T-NDI(C6) (Details regarding the TPV measurements are given in Supplementary Note 7). These results provide strong evidence that an increased DA spacing, giving rise to a reduced vibrational coupling between the donor and the acceptor material, leads to reduced and suppressed .
Importantly, we expect that a larger DA spacing than in the PDBD-T-NDI(C18) case would be desirable. Because despite having the largest DA distance and the lowest , the photoluminescence (PL) of states of PDBD-T-NDI(C18) is still completely quenched (Supplementary Fig. 22), indicating that electron transfer is highly efficient72–75. Besides, we find that the peak values of the photovoltaic EQE of the solar cells based on the longer linkers are not lower, as compared to that based on the shorter linkers (Supplementary Fig. 22). Therefore, further increasing of the linker length in the DCDA polymer is expected to increase the DA spacing, and thus, to reduce and improve the performance of the solar cell, although the synthesis of such a material is highly challenging, due to the poor solubility of the raw material needed.
Impact of increased DA spacing on in BHJ solar cells
We now evaluate whether typical state-of-the-art BHJ solar cells based on non-chemically linked donor and acceptor materials would also benefit from a larger DA spacing. We vary the size of the donor material’s side chains and focus on their role in determining the DA spacing in the BHJ systems and the performance of solar cells. The reference BHJ systems are based on the classic donor polymer PBDB-T with 16 hydrocarbyl groups attached to the BDT (alkylthienyl-substituted benzo[1,2-b:4,5-b′]dithiophene) moiety3 mixed with a series of different high-performance non-fullerene acceptors, including IT4F7, ITIC5, and Y68. The reference systems are compared with the systems based on the PBDB-T(OD) donor having 40 hydrocarbyl groups on the BDT moiety. The chemical structures of the donor materials and the non-fullerene acceptors are shown in Fig. 3a.
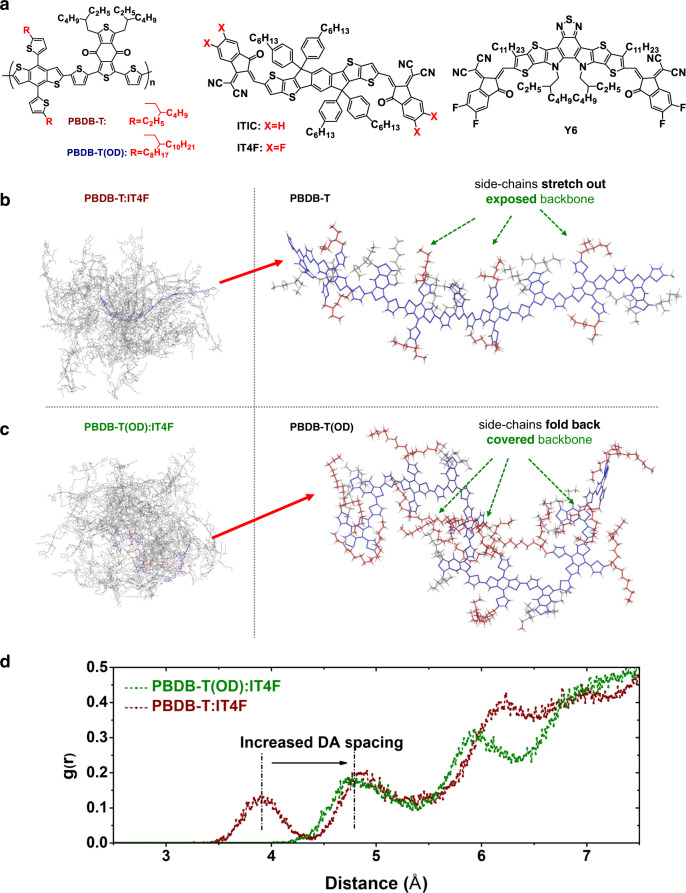
Fig. 3. Molecular dynamic simulations for the BHJ systems.
a Chemical structures of PBDB-T, PBDB-T(OD), and the acceptor materials used. MD simulation results for b PBDB-T and c PBDB-T(OD) blended with IT4F. The side chains of PBDB-T stretch out, leaving the conjugated backbones highly accessible to IT4F, allowing for close parallel π stacking between the backbones and IT4F, while the side chains of PBDB-T(OD) fold back, covering the backbones, reducing the probability for IT4F to stack on the donor backbones. d RDF of the distances between the donor backbones and IT4F for the blends based on PBDB-T and PBDB-T(OD).
The impact of the change of the side chain size on in the BHJ solar cells is very similar to the results observed from the solar cells based on DCDA polymers with varying size of linker groups, as listed in Table 2: Regardless of the acceptor used, the solar cells based on PBDB-T(OD) have significantly lower , as compared to those based on PBDB-T, due to lower , associated with lower (confirmed by TPV, shown in Fig. 4c and Supplementary Fig. 21). Thus, the lower in the solar cells based on PBDB-T(OD) is also associated with larger DA spacing.
Table 2.
Voltage loss values from the subgap measurements for the BHJ solar cells based on PBDB-T and PBDB-T(OD) mixed with different acceptors.
| (V) | a (eV) | b (V) | c (V) | d (V) | e (V) | |
|---|---|---|---|---|---|---|
| PBDB-T:IT4F | 0.71 | 1.40 | 0.69 | 1.15 | 0.44 | 0.25 |
| PBDB-T(OD):IT4F | 0.83 | 1.45 | 0.62 | 1.20 | 0.37 | 0.25 |
| PBDB-T:ITIC | 0.90 | 1.52 | 0.62 | 1.24 | 0.34 | 0.28 |
| PBDB-T(OD):ITIC | 0.99 | 1.56 | 0.57 | 1.27 | 0.28 | 0.29 |
| PBDB-T:Y6 | 0.67 | 1.42 | 0.75 | 1.04 | 0.37 | 0.38 |
| PBDB-T(OD):Y6 | 0.77 | 1.42 | 0.65 | 1.06 | 0.29 | 0.36 |
| PBDB-T(OD):Y6(OD) | 0.86 | 1.41 | 0.55 | 1.07 | 0.21 | 0.34 |
JV curves and the photovoltaic performance parameters of the solar cells are provided in Supplementary Note 9.
a instead of are listed for the solar cells based on Y6 and Y6(OD), details in Supplementary Note 5.
bCalculated using eq., the method used to determine is provided in Supplementary Note 5.
cCalculated from the radiative limit for the dark saturation current, details in Supplementary Note 6.
dCalculated using eq. ; values are also verified by measuring , details in Supplementary Note 6.
eCalculated using eq.
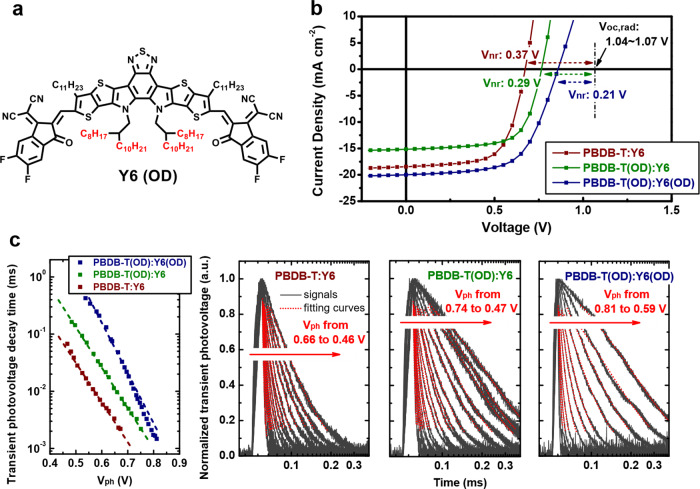
Fig. 4. Impact of side-chain modification on the performance of BHJ organic solar cells.
a Chemical structure of Y6(OD) with side chains considerably large than Y6. b JV curves of the solar cells based on PBDB-T, PBDB-T(OD), mixed with Y6 and Y6(OD). values, calculated from , are indicated. c TPV measurements performed on the solar cells based on the active materials with and without the side chain modification, the voltage decay lifetime values (left) are derived from the transient signals (right) of the solar cells measured under different steady-state illumination intensities (to generate different steady-state photovoltage, ()). The dash lines in the left plot are a guide to the eyes, and details regarding the measurements are provided in Supplementary Note 7.
Indeed, from MD simulations, we find that the DA spacing is considerably larger in the blends based on PBDB-T(OD). More specifically, for the blend based on PBDB-T, for instance, PBDB-T:IT4F (Fig. 3b), the side chains of PBDB-T stretch out, leaving the conjugated backbone fully exposed, and highly accessible to the acceptor molecules. This promotes an efficient formation of the parallel π-stacking between PBDB-T and the acceptors. On the contrary, in the blend based on PBDB-T(OD) (Fig. 3c), the large side chains of PBDB-T(OD) fold back to the conjugated backbone, taking up space around the backbone. This makes it highly difficult for the formation of close packing between PBDB-T(OD) and the acceptors. Thus, the distance between the conjugated donor backbones and the acceptor molecules is considerably larger in the blend based on PBDB-T(OD) than that based on PBDB-T. The RDF (Fig. 3d) shows a peak value for the DA configuration with the closest spacing at 3.9 Å for PBDB-T:IT4F, which increases to 4.8 Å for PBDB-T(OD):IT4F. Similar simulation results are found using ITIC or Y6 as the acceptor material (Supplementary Note 4), suggesting that the DA spacing is always larger in the blends based on PBDB-T(OD) with larger side chains.
The above results suggest that the DA spacing can also be increased in BHJ organic solar cells comprising state-of-the-art materials by using long side chains. Also in these devices, the increased DA distance leads to lower and higher , due to the reduced degree of vibrational coupling between CT and ground states. Since the PL quenching of both the donor and the acceptor states is highly efficient in the blends based on PBDB-T(OD), suggesting a highly efficient electron transfer process in these blends, despite having the DA spacing up to 5 Å (Supplementary Fig. 23). Accordingly, a further increased DA spacing is expected to lead to a higher degree of reduction in and a lower .
Inspired by the significant reduction in , achieved by modifying the side chains of the donor material, we now employ a new acceptor, Y6(OD) (Fig. 4a), with side chains being significantly larger than that of Y6, to construct solar cells. Remarkably, the of the solar cell based on PBDB-T(OD):Y6(OD) is lower by as much as 0.08 V, compared to that based on PBDB-T(OD):Y6 (Fig. 4b), and the lower is ascribed to a lower , confirmed by TPV measurements (Fig. 4c): The voltage decay lifetime in the solar cell based on PBDB-T(OD):Y6(OD) is almost two orders of magnitudes longer than that based on PBDB-T:Y6. This leads to a further increase of to up to 0.86 V, close to 0.2 V higher than that of the solar cell based on unmodified PBDB-T:Y6.
Discussion
The currently highest s in organic solar cells over 18%9,10,16,17,65,76 have been achieved with solution cast mixtures, without thorough consideration of the intermolecular DA spacing. Very few methods to quantify and control this spacing are available, and it has therefore been unclear if higher efficiencies can be reached by careful manipulation of the DA spacing, even though there are indications that an optimum distance, allowing for efficient photo-induced electron transfer but suppressed recombination of the CT state, exists: Indeed, in the analogous and highly efficient primary photo-induced long-range (tens of Å) electron transfer processes in photosynthesis, recombination of the charge-separated state is severely suppressed, the molecular orientation and distance of the special donor-acceptor pair in the reaction center is well defined and controlled by proteins holding the molecules in place47,66,77–79.
In this work, we achieved tuning of the DA spacing in both DCDA and BHJ organic solar cells, and observed a decreased non-radiative recombination and increased with increased DA spacing, while the increased spacing had little impact on the dissociation efficiency of the excitons at the donor-acceptor interface. Therefore, we concluded that all of the active materials systems studied in this work, and by extension, the current systems studied for organic solar cells in the literature could benefit from a larger DA spacing. We hope that the conclusion, i.e., the DA spacing in organic solar cells is generally too small, being the main reason for the too high in organic solar cells, will inspire researchers to focus on innovative methods to manipulate the DA spacing, and we envision that these methods, such as engineering the non-conjugated part of the active materials demonstrated here, will be of great importance for the future development of organic solar cells.
Methods
Statistics and reproducibility
All the characterizations and measurements performed in this work were repeated by different persons, and similar results were obtained.
Experimental
Details regarding the methods used in this work are provided in supporting information.
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Supplementary information
Acknowledgements
This work is financially supported by the National Natural Science Foundation of China (Grant No. 51973031, 51933001, 52073056, and 52073016), Shanghai Pujiang Program (Grant No. 19PJ1400500), the Natural Science Foundation of Shanghai (Grant No. 19ZR1401400), the Fundamental Research Funds for the Central Universities (Grant No. 2232021A09 and XK1802-2), the MOST (2017YFA0204702 and 2018YFA0208504), the Jiangxi Provincial Department of Science and Technology (No. 20192ACB20009), and the European Research Council (ERC, grant No. 864625). The authors thank Prof. Olle Inganäs for the discussion and his comments on the manuscript.
Author contributions
J.W. and X.J. contributed equally to this work; This project was designed by Z.T. and supervised by Z.T., W.L., and K.V.; J.W., X.J., and G.F. fabricated and optimized the devices; X.J. synthesized the DCDA polymers; J.W. performed JV, EQE, EQEEL, EL, and TPV measurements, supervised by Z.M.; HY.W. and X.F. measured TEM; HB.W. and Y.Y. did MD simulations; J.L. measured GIWAXS; Z.T. wrote the manuscript with K.V., and all authors contributed to the discussion and the finalizing of the manuscript.
Data availability
The data that support the findings of this study are available from the corresponding authors.
Competing interests
The authors declare no competing interests.
Footnotes
Peer review information Nature Communications thanks Fei Huang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Weiwei Li, Email: liweiwei@iccas.ac.cn.
Koen Vandewal, Email: koen.vandewal@uhasselt.be.
Zheng Tang, Email: ztang@dhu.edu.cn.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-021-26995-1.
References
- 1.Halls JJM, et al. Efficient photodiodes from interpenetrating polymer networks. Nature. 1995;376:498–500. [Google Scholar]
- 2.Yu G, Gao J, Hummelen JC, Wudl F, Heeger AJ. Polymer photovoltaic cells: enhanced efficiencies via a network of internal donor-acceptor heterojunctions. Science. 1995;270:1789–1791. [Google Scholar]
- 3.Qian D, et al. Design, application, and morphology study of a new photovoltaic polymer with strong aggregation in solution state. Macromolecules. 2012;45:9611–9617. [Google Scholar]
- 4.Zhang M, Guo X, Ma W, Ade H, Hou J. A large-bandgap conjugated polymer for versatile photovoltaic applications with high performance. Adv. Mater. 2015;27:4655–4660. doi: 10.1002/adma.201502110. [DOI] [PubMed] [Google Scholar]
- 5.Lin Y, et al. An electron acceptor challenging fullerenes for efficient polymer solar cells. Adv. Mater. 2015;27:1170–1174. doi: 10.1002/adma.201404317. [DOI] [PubMed] [Google Scholar]
- 6.Zhao W, et al. Fullerene-free polymer solar cells with over 11% efficiency and excellent thermal stability. Adv. Mater. 2016;28:4734–4739. doi: 10.1002/adma.201600281. [DOI] [PubMed] [Google Scholar]
- 7.Zhao W, et al. Molecular optimization enables over 13% efficiency in organic solar cells. J. Am. Chem. Soc. 2017;139:7148–7151. doi: 10.1021/jacs.7b02677. [DOI] [PubMed] [Google Scholar]
- 8.Yuan J, et al. Single-junction organic solar cell with over 15% efficiency using fused-ring acceptor with electron-deficient core. Joule. 2019;3:1140–1151. [Google Scholar]
- 9.Liu Q, et al. 18% efficiency organic solar cells. Sci. Bull. 2020;65:272–275. doi: 10.1016/j.scib.2020.01.001. [DOI] [PubMed] [Google Scholar]
- 10.Li, C. et al. Non-fullerene acceptors with branched side chains and improved molecular packing to exceed 18% efficiency in organic solar cells. Nat. Energy. 10.1038/s41560-021-00820-x (2021).
- 11.Li W, et al. A high-efficiency organic solar cell enabled by the strong intramolecular electron push–pull effect of the nonfullerene acceptor. Adv. Mater. 2018;30:1707170. doi: 10.1002/adma.201707170. [DOI] [PubMed] [Google Scholar]
- 12.Zhang H, et al. Over 14% efficiency in organic solar cells enabled by chlorinated nonfullerene small-molecule acceptors. Adv. Mater. 2018;30:1800613. doi: 10.1002/adma.201800613. [DOI] [PubMed] [Google Scholar]
- 13.Cui Y, et al. Over 16% efficiency organic photovoltaic cells enabled by a chlorinated acceptor with increased open-circuit voltages. Nat. Commun. 2019;10:2515. doi: 10.1038/s41467-019-10351-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cui Y, et al. Single‐junction organic photovoltaic cells with approaching 18% efficiency. Adv. Mater. 2020;32:1908205. doi: 10.1002/adma.201908205. [DOI] [PubMed] [Google Scholar]
- 15.Zheng Z, et al. A highly efficient non-fullerene organic solar cell with a fill factor over 0.80 enabled by a fine-tuned hole-transporting layer. Adv. Mater. 2018;30:1801801. doi: 10.1002/adma.201801801. [DOI] [PubMed] [Google Scholar]
- 16.Lin Y, et al. A simple n-dopant derived from diquat boosts the efficiency of organic solar cells to 18.3% ACS Energy Lett. 2020;5:3663–3671. [Google Scholar]
- 17.Zhang M, et al. Single-layered organic photovoltaics with double cascading charge transport pathways: 18% efficiencies. Nat. Commun. 2021;12:309. doi: 10.1038/s41467-020-20580-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shockley W, Queisser HJ. Detailed balance limit of efficiency of p‐n junction solar cells. J. Appl. Phys. 1961;32:510–519. [Google Scholar]
- 19.Kirchartz T, Taretto K, Rau U. Efficiency limits of organic bulk heterojunction solar cells. J. Phys. Chem. C. 2009;113:17958–17966. [Google Scholar]
- 20.Perez MD, Borek C, Forrest SR, Thompson ME. Molecular and morphological influences on the open circuit voltages of organic photovoltaic devices. J. Am. Chem. Soc. 2009;131:9281–9286. doi: 10.1021/ja9007722. [DOI] [PubMed] [Google Scholar]
- 21.Vandewal K, Tvingstedt K, Gadisa A, Inganäs O, Manca JV. On the origin of the open-circuit voltage of polymer–fullerene solar cells. Nat. Mater. 2009;8:904–909. doi: 10.1038/nmat2548. [DOI] [PubMed] [Google Scholar]
- 22.Benduhn J, et al. Intrinsic non-radiative voltage losses in fullerene-based organic solar cells. Nat. Energy. 2017;2:17053. [Google Scholar]
- 23.Chen X-K, Brédas J-L. Voltage losses in organic solar cells: understanding the contributions of intramolecular vibrations to nonradiative recombinations. Adv. Energy Mater. 2018;8:1702227. [Google Scholar]
- 24.Azzouzi M, et al. Nonradiative energy losses in bulk-heterojunction organic photovoltaics. Phys. Rev. X. 2018;8:031055. [Google Scholar]
- 25.Gould IR, et al. Radiative and nonradiative electron transfer in contact radical-ion pairs. Chem. Phys. 1993;176:439–456. [Google Scholar]
- 26.Marcus RA. Relation between charge transfer absorption and fluorescence spectra and the inverted region. J. Phys. Chem. 1989;93:3078–3086. [Google Scholar]
- 27.Vandewal K, Tvingstedt K, Gadisa A, Inganäs O, Manca JV. Relating the open-circuit voltage to interface molecular properties of donor:acceptor bulk heterojunction solar cells. Phys. Rev. B. 2010;81:125204. [Google Scholar]
- 28.Kirchartz T, Pieters BE, Kirkpatrick J, Rau U, Nelson J. Recombination via tail states in polythiophene:fullerene solar cells. Phys. Rev. B. 2011;83:115209. [Google Scholar]
- 29.Vandewal K. Interfacial charge transfer states in condensed phase systems. Annu. Rev. Phys. Chem. 2016;67:113–133. doi: 10.1146/annurev-physchem-040215-112144. [DOI] [PubMed] [Google Scholar]
- 30.Vandewal K, et al. Efficient charge generation by relaxed charge-transfer states at organic interfaces. Nat. Mater. 2014;13:63–68. doi: 10.1038/nmat3807. [DOI] [PubMed] [Google Scholar]
- 31.Rau U. Reciprocity relation between photovoltaic quantum efficiency and electroluminescent emission of solar cells. Phys. Rev. B. 2007;76:085303. [Google Scholar]
- 32.Chen X-K, Ravva MK, Li H, Ryno SM, Brédas J-L. Effect of molecular packing and charge selocalization on the nonradiative recombination of charge-transfer states in organic solar cells. Adv. Energy Mater. 2016;6:1601325. [Google Scholar]
- 33.Blank B, Kirchartz T, Lany S, Rau U. Selection metric for photovoltaic materials screening based on detailed-balance analysis. Phys. Rev. Appl. 2017;8:024032. [Google Scholar]
- 34.Liu X, Li Y, Ding K, Forrest S. Energy loss in organic photovoltaics: nonfullerene versus fullerene acceptors. Phys. Rev. Appl. 2019;11:024060. [Google Scholar]
- 35.Eisner FD, et al. Hybridization of local exciton and charge-transfer states reduces nonradiative voltage losses in organic solar cells. J. Am. Chem. Soc. 2019;141:6362–6374. doi: 10.1021/jacs.9b01465. [DOI] [PubMed] [Google Scholar]
- 36.Qian D, et al. Design rules for minimizing voltage losses in high-efficiency organic solar cells. Nat. Mater. 2018;17:703–709. doi: 10.1038/s41563-018-0128-z. [DOI] [PubMed] [Google Scholar]
- 37.Liu X, et al. Efficient organic solar cells with extremely high open-circuit voltages and low voltage losses by suppressing nonradiative recombination losses. Adv. Energy Mater. 2018;8:1801699. [Google Scholar]
- 38.Ullbrich S, et al. Emissive and charge-generating donor–acceptor interfaces for organic optoelectronics with low voltage losses. Nat. Mater. 2019;18:459–464. doi: 10.1038/s41563-019-0324-5. [DOI] [PubMed] [Google Scholar]
- 39.Rosenthal KD, et al. Quantifying and understanding voltage losses due to nonradiative recombination in bulk heterojunction organic solar cells with low energetic offsets. Adv. Energy Mater. 2019;9:1901077. [Google Scholar]
- 40.Perdigón-Toro L, et al. Excitons dominate the emission from PM6:Y6 solar cells, but this does not help the open-circuit voltage of the device. ACS Energy Lett. 2021;6:557–564. [Google Scholar]
- 41.Bixon M, Jortner J, Verhoeven JW. Lifetimes for radiative charge recombination in donor-acceptor molecules. J. Am. Chem. Soc. 1994;116:7349–7355. [Google Scholar]
- 42.Vandewal K, Tvingstedt K, Inganäs O. Polarization anisotropy of charge transfer absorption and emission of aligned polymer:fullerene blend films. Phys. Rev. B. 2012;86:035212. [Google Scholar]
- 43.Vezie MS, et al. Impact of marginal exciton-charge-transfer state offset on charge generation and recombination in polymer:fullerene solar cells. Acs Energy Lett. 2019;4:2096–2103. [Google Scholar]
- 44.Chen X-K, Coropceanu V, Brédas J-L. Assessing the nature of the charge-transfer electronic states in organic solar cells. Nat. Commun. 2018;9:5295. doi: 10.1038/s41467-018-07707-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bixon M, Jortner J, Cortes J, Heitele H, Michel-Beyerle ME. Energy gap law for nonradiative and radiative charge transfer in isolated and in solvated supermolecules. J. Phys. Chem. 1994;98:7289–7299. [Google Scholar]
- 46.Marcus RA, Sutin N. Electron transfers in chemistry and biology. Biochim. Biophys. Acta Bioenerg. 1985;811:265–322. [Google Scholar]
- 47.Closs GL, Miller JR. Intramolecular long-distance electron transfer in organic molecules. Science. 1988;240:440–447. doi: 10.1126/science.240.4851.440. [DOI] [PubMed] [Google Scholar]
- 48.Oevering H, Verhoeven JW, Paddon-Row MN, Warman JM. Charge-transfer absorption and emission resulting from long-range through-bond interaction; exploring the relation between electronic coupling andelectron-transfer in bridged donor-acceptor systems. Tetrahedron. 1989;45:4751–4766. [Google Scholar]
- 49.Oliver AM, Paddon-Row MN, Kroon J, Verhoeven JW. Orbital symmetry effects on intramolecular charge recombination. Chem. Phys. Lett. 1992;191:371–377. [Google Scholar]
- 50.Paddon-Row MN, et al. Factors affecting charge separation and recombination in photoexcited rigid donor-insulator-acceptor compounds. J. Phys. Chem. 1988;92:6958–6962. [Google Scholar]
- 51.Warman JM, et al. Long-distance charge recombination within rigid molecular assemblies in nondipolar solvents. J. Phys. Chem. 1991;95:1979–1987. [Google Scholar]
- 52.Warman JM, et al. Intramolecular charge separation and recombination in non-polar environments via long-distance electron transfer through saturated hydrocarbon barriers. Chem. Phys. 1993;170:359–380. [Google Scholar]
- 53.Roest MR, Oliver AM, Paddon-Row MN, Verhoeven JW. Distance dependence of singlet and triplet charge recombination pathways in a series of rigid bichromophoric systems. J. Phys. Chem. A. 1997;101:4867–4871. [Google Scholar]
- 54.Oevering H, et al. Long-range photoinduced through-bond electron transfer and radiative recombination via rigid nonconjugated bridges: distance and solvent dependence. J. Am. Chem. Soc. 1987;109:3258–3269. [Google Scholar]
- 55.Zhang M, Zheng C-J, Lin H, Tao S-L. Thermally activated delayed fluorescence exciplex emitters for high-performance organic light-emitting diodes. Mater. Horiz. 2021;8:401–425. doi: 10.1039/d0mh01245a. [DOI] [PubMed] [Google Scholar]
- 56.Cravino A, et al. A novel polythiophene with pendant fullerenes: toward donor/acceptor double-cable polymers. Chem. Commun. 2000;24:2487–2488. [Google Scholar]
- 57.Zerza G, et al. Photoinduced electron transfer in donor−acceptor double-cable polymers: polythiophene bearing tetracyanoanthraquinodimethane moieties. J. Phys. Chem. A. 2001;105:4172–4176. [Google Scholar]
- 58.Feng G, et al. ‘Double-cable’ conjugated polymers with linear backbone toward high quantum efficiencies in single-component polymer solar cells. J. Am. Chem. Soc. 2017;139:18647–18656. doi: 10.1021/jacs.7b10499. [DOI] [PubMed] [Google Scholar]
- 59.Feng G, et al. Thermal-driven phase separation of double-cable polymers enables efficient single-component organic solar cells. Joule. 2019;3:1765–1781. [Google Scholar]
- 60.Li C, et al. Crystalline cooperativity of donor and acceptor segments in double-cable conjugated polymers toward efficient single-component organic solar cells. Angew. Chem. Int. Ed. 2019;58:15532–15540. doi: 10.1002/anie.201910489. [DOI] [PubMed] [Google Scholar]
- 61.Jiang X, et al. Miscibility-controlled phase separation in double-cable conjugated polymers for single-component organic solar cells with efficiencies over 8 % Angew. Chem. Int. Ed. 2020;59:21683–21692. doi: 10.1002/anie.202009272. [DOI] [PubMed] [Google Scholar]
- 62.Würthner F, Stolte M. Naphthalene and perylene diimides for organic transistors. Chem. Commun. 2011;47:5109. doi: 10.1039/c1cc10321k. [DOI] [PubMed] [Google Scholar]
- 63.Zhang S, Qin Y, Zhu J, Hou J. Over 14% efficiency in polymer solar cells enabled by a chlorinated polymer donor. Adv. Mater. 2018;30:1800868. doi: 10.1002/adma.201800868. [DOI] [PubMed] [Google Scholar]
- 64.Hansen MR, et al. Fast and slow dynamics in a discotic liquid crystal with regions of columnar order and disorder. Phys. Rev. Lett. 2011;107:257801. doi: 10.1103/PhysRevLett.107.257801. [DOI] [PubMed] [Google Scholar]
- 65.Liu G, et al. Tandem organic solar cells with 18.7% efficiency enabled by suppressing the charge recombination in front sub‐cell. Adv. Funct. Mater. 2021 doi: 10.1002/adfm.202103283. [DOI] [Google Scholar]
- 66.Boxer SG. Mechanisms of long-distance electron transfer in proteins: lessons from photosynthetic reaction centers. Annu. Rev. Biophys. Biophys. Chem. 1990;19:267–299. doi: 10.1146/annurev.bb.19.060190.001411. [DOI] [PubMed] [Google Scholar]
- 67.Vandewal K, et al. The relation between open-circuit voltage and the onset of photocurrent generation by charge-transfer absorption in polymer: fullerene bulk heterojunction solar cells. Adv. Funct. Mater. 2008;18:2064–2070. [Google Scholar]
- 68.Vandewal K, et al. Increased open-circuit voltage of organic solar cells by reduced donor-acceptor interface area. Adv. Mater. 2014;26:3839–3843. doi: 10.1002/adma.201400114. [DOI] [PubMed] [Google Scholar]
- 69.Graham KR, et al. Importance of the donor:fullerene intermolecular arrangement for high-efficiency organic photovoltaics. J. Am. Chem. Soc. 2014;136:9608–9618. doi: 10.1021/ja502985g. [DOI] [PubMed] [Google Scholar]
- 70.Tang Z, et al. Relating open-circuit voltage losses to the active layer morphology and contact selectivity in organic solar cells. J. Mater. Chem. A. 2018;6:12574–12581. [Google Scholar]
- 71.Yao J, et al. Quantifying losses in open-circuit voltage in solution-processable solar cells. Phys. Rev. Appl. 2015;4:014020. [Google Scholar]
- 72.Schueppel R. Optimizing organic photovoltaics using tailored heterojunctions: a photoinduced absorption study of oligothiophenes with low band gaps. Phys. Rev. B. 2008;77:085311. [Google Scholar]
- 73.Tvingstedt K, Vandewal K, Zhang F, Inganäs O. On the dissociation efficiency of charge transfer excitons and Frenkel excitons in organic solar cells: a luminescence quenching study. J. Phys. Chem. C. 2010;114:21824–21832. [Google Scholar]
- 74.Greenham NC, Peng X, Alivisatos AP. Charge separation and transport in conjugated-polymer/semiconductor-nanocrystal composites studied by photoluminescence quenching and photoconductivity. Phys. Rev. B. 1996;54:17628–17637. doi: 10.1103/physrevb.54.17628. [DOI] [PubMed] [Google Scholar]
- 75.Shoaee S, et al. Acceptor energy level control of charge photogeneration in organic donor/acceptor blends. J. Am. Chem. Soc. 2010;132:12919–12926. doi: 10.1021/ja1042726. [DOI] [PubMed] [Google Scholar]
- 76.Jin K, Xiao Z, Ding L. 18.69% PCE from organic solar cells. J. Semicond. 2021;42:060502. [Google Scholar]
- 77.Closs GL, Calcaterra LT, Green NJ, Penfield KW, Miller JR. Distance, stereoelectronic effects, and the Marcus inverted region in intramolecular electron transfer in organic radical anions. J. Phys. Chem. 1986;90:3673–3683. [Google Scholar]
- 78.Wahadoszamen M, Margalit I, Ara AM, van Grondelle R, Noy D. The role of charge-transfer states in energy transfer and dissipation within natural and artificial bacteriochlorophyll proteins. Nat. Commun. 2014;5:5287. doi: 10.1038/ncomms6287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Park S, et al. Chlorophyll–carotenoid excitation energy transfer and charge transfer in Nannochloropsis oceanica for the regulation of photosynthesis. Comput. Biol. 2019;116:3385–3390. doi: 10.1073/pnas.1819011116. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding authors.