Orientation selectivity enhances context generalization and generative predictive coding in the hippocampus

Summary:

We learn and remember multiple new experiences throughout the day. The neural principles enabling continuous rapid learning and formation of distinct representations of numerous sequential experiences without major interference are not understood. To understand this process, here we interrogated ensembles of hippocampal place cells as rats explored 15 novel linear environments interleaved with sleep sessions over continuous 16-hour periods. Remarkably, we found that a population of place cells were selective to environment orientation and topology. This orientation selectivity property biased the network-level discrimination and re/mapping between multiple environments. Novel environmental representations emerged rapidly as more generic, but repeated experience within the environments subsequently enhanced their discriminability. Generalization of prior experience with different environments consequently improved network predictability of future novel environmental representations via strengthened generative predictive codes. These coding schemes reveal a high-capacity, high-efficiency neuronal framework for rapid representation of numerous sequential experiences with optimal discrimination-generalization balance and reduced interference.

Graphical Abstract

eTOC Blurb:

Liu et al. report that a population of hippocampal place cells display selectivity to spatial context orientation and topology, which biases the discrimination and remapping between multiple contexts. Repeated experience within a context enhances its representation discriminability while generalization across multiple contexts improves network predictability of future novel context representations.

Introduction:

Distinct representations of over a dozen sequential episodes encountered within a day are often maintained in memory until a decision or evaluation regarding their content (e.g., which one of the many visited rental homes to select) is performed at the end of the day (Brady et al., 2008; Voss, 2009). In the rodent hippocampus, place cells (O'Keefe and Dostrovsky, 1971) are sequentially activated at different locations along an animal’s trajectory and are partially controlled by the environment geometry (Leutgeb et al., 2005; Muller and Kubie, 1987; Wills et al., 2005) and distal cues (Lee et al., 2004; Monaco et al., 2014; Quirk et al., 1990). This sequential activation can be partly predicted from an internal repertoire of temporal sequences expressed during the pre-exploration sleep (Dragoi and Tonegawa, 2011, 2014; Liu et al., 2018). Therefore, spatial representations of the external world emerge continuously from the dynamic interplay between generative pre-existing activity patterns (Dragoi et al., 2003; Dragoi and Tonegawa, 2011; Liu et al., 2018) and those driven by the newly encountered external stimuli (Dragoi and Tonegawa, 2013a; Farooq and Dragoi, 2019; Farooq et al., 2019; Grosmark and Buzsaki, 2016; Lee and Wilson, 2002; Monaco et al., 2014).

Previous studies investigated how exposure to multiple environments instructs hippocampal place cell recruitment and spatial re/mapping in the rat (Alme et al., 2014; Rich et al., 2014). Consistently, these studies found that both CA3 place cell recruitment and spatial re/mapping across eleven 2-D boxes and rooms (Alme et al., 2014) and CA1 place cell recruitment across different linear segments along 48 m-long tracks within a room (Rich et al., 2014) appear to occur randomly, indicative of a large network capacity for spatial re/mapping. However, exactly how place cell recruitment and re/mapping are organized to encode geometric features (like orientation or landmark) and maintain large loads of distinct sequential information learned within a day without a major interference (Hasselmo and Wyble, 1997; McCloskey and Cohen, 1989; Peterson and Gentile, 1965; Underwood and Postman, 1960) between individual memories and limitation of network capacity has remained unknown. This is largely because until now the links between pre-existing sequential motifs and experience-related sequential activity patterns during run have only been measured in subjects exposed to single (Grosmark and Buzsaki, 2016; Lee and Wilson, 2002) or a small number (Dragoi and Tonegawa, 2013b; Liu et al., 2018) of experiences. Exposure to a few different sequential experiences on linear tracks has previously indicated that the pre-existing network dynamics employed for their distinct neuronal ensemble representation increase linearly with the number of experiences (Dragoi and Tonegawa, 2013b). However, it is highly likely that these dynamics would change significantly when challenged with one order of magnitude higher number of experiences. At the same time, formation of long-term representations of multiple experiences is achieved in several stages mapped onto corresponding distinct network operations during alternating sleep and wake brain states (Buzsaki, 1989; Farooq and Dragoi, 2019; Farooq et al., 2019; Lee and Wilson, 2002; Oudiette et al., 2013).

Here, we investigated waking and sleep hippocampal CA1 network dynamics employed to distinctly encode and represent a large number of sequential environments within a day, which revealed several novel schemes for representation of numerous experiences. Notably, we uncovered an orientation selectivity feature of place cells which biased neuronal re/mapping across multiple environments and led to an increase in generalization of context representations. Incorporation of generalized multisensory information including orientation and topology from other parallel environments greatly improved the predictive models of place cell sequence re/mapping derived from pre-exploratory sleep activity. The improved predictive codes could facilitate rapid encoding of multiple future novel experiences in the CA1.

Results:

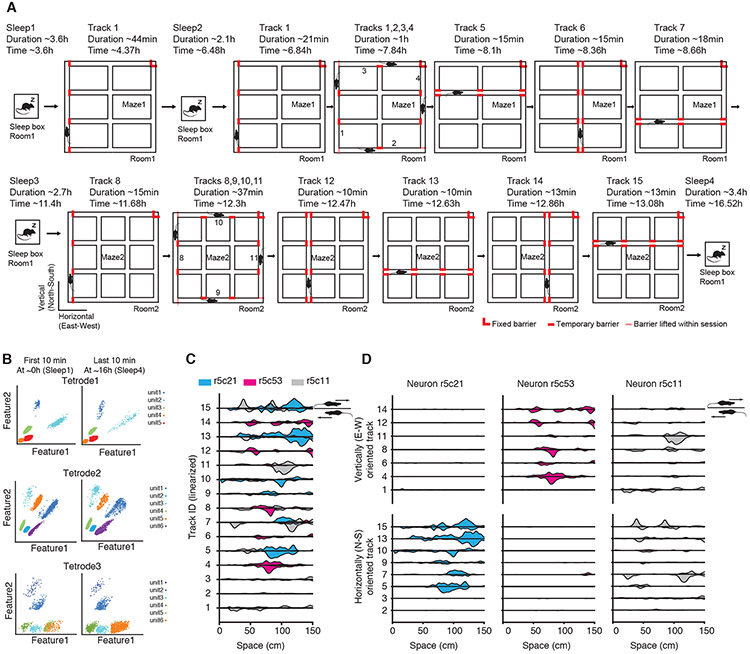
To reveal principles underlying distinct representations of numerous experiences we electrophysiologically recorded hippocampal CA1 neurons from 5 adult naïve rats while they explored 15 linear tracks interleaved with four sleep sessions over a 16 h period. Boundaries of the 15 horizontally oriented (i.e., East-West/E-W) or vertically oriented (i.e., North-South/N-S) 150 cm-long linear tracks were sequentially defined by opaque barriers dynamically placed into one of two elevated 2-D mazes located in two visually, acoustically, and spatially distinct rooms or compartments (Maze1: tracks 1-7, Maze 2: tracks 8-15; Figure 1A, Figure S1A-F). Interleaving sleep sessions occurred before all explorations (Sleep1, pre-experience), after exploring track1 (Sleep2), between exploring Maze1 and Maze2 (Sleep3), and after all explorations (Sleep4, post-experience).

Figure 1. Hippocampal CA1 pyramidal cell activity during sequential exploration of 15 linear tracks.

(A) Diagram of the experimental setup and timeline of the sleep and run sessions of an example rat. Red lines represent barriers used to define the boundaries of individual tracks.

(B) Spike sorting and configuration for three example tetrodes.

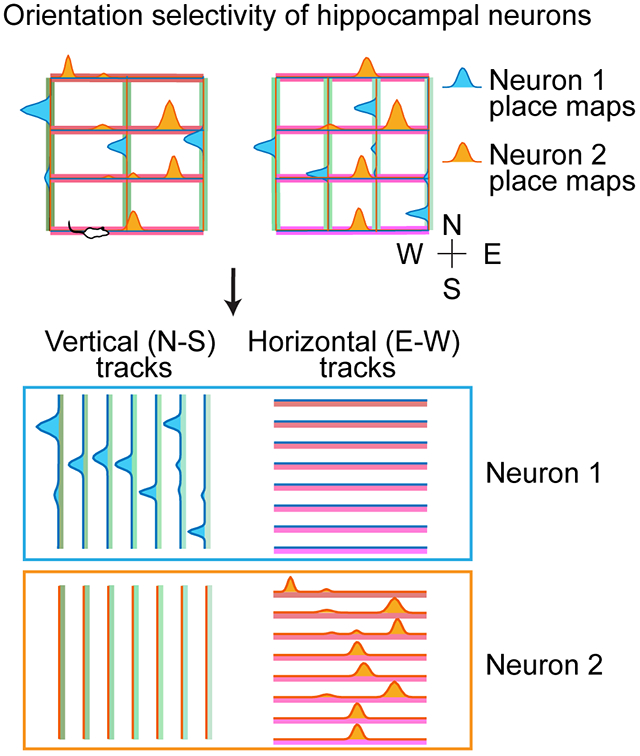
(C-D) Place maps of 3 example neurons across the 15 tracks depicting the orientation selectivity phenomenon. Place maps above and below the straight horizontal lines are from the two running directions on the same tracks. Tracks were arranged by run order (C) or grouped by their horizontal (East-West/E-W) or vertical (North-South/N-S) orientation (D). Note that neurons in blue and red color display orientation selectivity for horizontally (E-W) and vertically (N-S) oriented tracks respectively, and the neuron in gray displays no orientation selectivity.

See also Figure S1.

Orientation-selectivity and topology drive non-random re/mapping

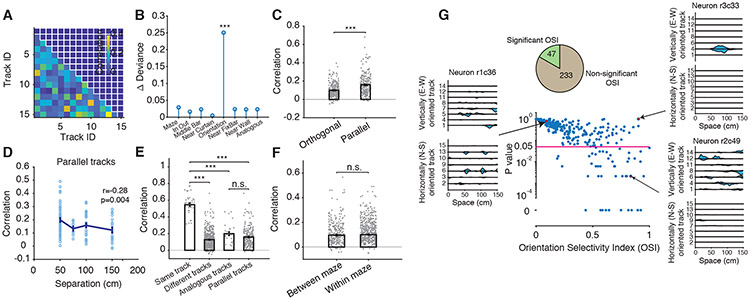
A total of 280 putative pyramidal neurons from 5 rats maintained stable spike amplitude throughout the long duration of the experiment (Figures 1B and S1G). Their spiking activity was used to calculate place maps (i.e., firing rate profile normalized by occupancy binned from the beginning to the end of each track) across the 15 tracks (Figure 1C). We observed a remarkable neuronal selectivity to track orientation in a group of neurons (Figure 1D). To quantify the impact of environment geometry on re/mapping (Dragoi and Tonegawa, 2013b; Leutgeb et al., 2005; Muller and Kubie, 1987; Wills et al., 2005), we assessed the similarity of spatial encoding between any two linear tracks by calculating the correlation between population-level place maps for each track pair (Figure 2A). We built a generalized linear model using these population-level place map correlation values as predictor and consistency of several geometric features as variables and found that track orientation had the single and largest impact on re/mapping (p< 10⁻⁷, Chi-square test, Figure 2B, Methods). Consistently, parallel track pairs had higher correlations than orthogonal pairs (Figure 2C, P=2×10⁻¹², n=280; 245, Wilcoxon rank-sum test; P<10⁻¹², for correlations at population place cell level), with spatially proximal parallel tracks exhibiting higher similarity (Figure 2D, Separation vs. Correlation: R=−0.28, P=0.004, n=105, Pearson’s correlation). Despite these non-random features of re/mapping across parallel tracks, the correlations between population place maps on different sessions on the same track (e.g., between the first and the second run sessions on track1, the same for track8; Figure 2E, R=0.55±0.02) were: 1. higher than those on different tracks (R=0.13±0.004, P<10⁻⁹, Wilcoxon rank-sum test) and 2. higher than those on analogous tracks between the Mazes (i.e., with overlapping position when superimposing the two Mazes, R=0.19±0.02, P<10⁻⁴, Wilcoxon rank-sum test). The high stability of place maps across two sessions on the same track and the increased re/mapping across different tracks together indicate that animals were not confused by their exposure to multiple experiences. Furthermore, we did not find a significant grouping of track re/mapping by Maze identity (Figure 2F, Maze: P=0.43, Wilcoxon rank-sum test), indicating that place cell ensembles primarily re/mapped as a function of track identity and orientation regardless of their Maze/room allocation. Importantly, the track pairs with analogous position across the two Mazes were not more strongly correlated than the group of all pairs of parallel tracks from across the two Mazes (P=0.64, Wilcoxon rank-sum test; Figure 2E). This further indicates that the animals were not confusing Maze2 for Maze1. Therefore, the 15 tracks, which were explored explicitly at separate times in randomized order regarding their orientation (Figure S1B-F) and with no task-related association between each other, have all premises to be represented as independent of each other as they can be (range of all parallel track pair correlations within and across the mazes was 0.12-0.19).

Figure 2. Orientation selectivity of hippocampal dorsal CA1 place cells.

(A) Example of population-level place map correlations between all track pairs in one animal during run.

(B) Contribution of track geometry features to place cell re/mapping estimated by a generalized linear model (GLM).

(C) Influence of track orientation on population-level place cell re/mapping measured by population-level place map correlations across track pairs.

(D) Population-level place map correlation between track pairs changes as a function of their physical separation.

(E) Correlations between population-level place maps during different sessions on: the same track, different tracks, track pairs with analogous spatial location across the Mazes, and all parallel tracks.

(F) Correlations between population-level place maps during sessions on tracks within the same Maze are similar to those during sessions on tracks across different Mazes.

(G) Distribution of orientation selectivity index (OSI) calculated by firing rate and its associated significance (P value) across the place cell population from all putative pyramidal neurons (center) and from three example neurons depicting one orientation non-selective neuron (left), one orientation selective neuron (bottom right) and one orientation non-selective neuron with high OSI (top right). Top-left pie chart, Proportion of neurons with significant and non-significant OSI.

Data are represented as mean±SEM. ***P < 0.001.

See also Figure S2.

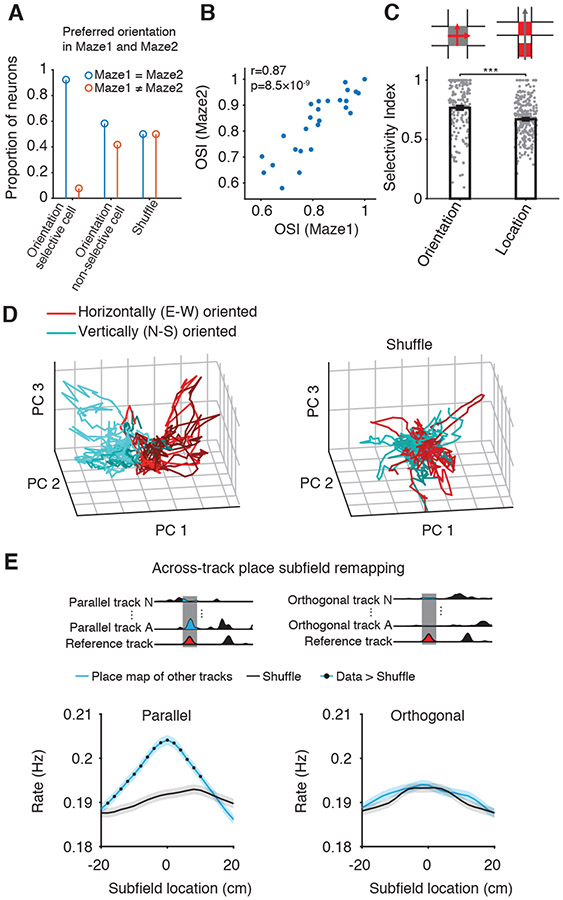
We quantified the selectivity of place cell firing rate as a function of track orientation by calculating an orientation selectivity index (OSI) and its statistical significance (P-value). We defined OSI as a neuron’s propensity to preferentially be activated on parallel versus orthogonal tracks and calculated its significance against 500 random shuffles of track orientations (Figure 2G; Methods). We found that 16.8% (47/280) of all neurons had significant, reliable orientation selectivity for horizontal (E-W) or vertical (N-S) orientations (8.57% and 8.21% of neurons; Figures 2G and S2A-C). An additional 19.6% of all neurons also had preferred orientation but were very selectively active only on few specific tracks and for this reason did not reach our stringent criteria for significance (Figure 2G). Interestingly, when OSIs were calculated using tracks from Maze1 alone, 92.3% of neurons with orientation selectivity on Maze1 preserved their preferred orientation in Maze2 (Figure 3A) and their OSIs were highly correlated across the two mazes (Figure 3B). This indicates that animals maintained their sense of orientation across the two Mazes and rooms despite clear re/mapping across different tracks. This finding suggests that there is a dissociation between the processes underlying re/mapping and those underlying (preserved) orientation.

Figure 3. Properties of orientation selective neurons.

(A-B), Preserved preferred orientation (A) and OSI strength (B) across the two Mazes for neurons with significant orientation selectivity on Maze1.

(C) Place cells OSI inside intersectional areas between orthogonal tracks (i.e., same location, different orientation) is stronger than their within-track location selectivity index (i.e., same orientation, different location).

(D) Clustering of trajectories of horizontally (E-W) and vertically (N-S) oriented population-level place maps of the 15 tracks projected in principal component space. Left, original population-level place maps. Right, space-shift shuffled population-level place maps.

(E) Across-tracks topology-dependent re/mapping of place subfields. Top cartoon, the method of extraction of the corresponding locations. Bottom, re/mapping of a place cell subfield on a linear track (Reference) preferentially occurs in locations topologically corresponding (i.e., same distance from track end) to non-zero activity of the cell on different parallel (left), but not orthogonal tracks (right). Black dots: space bins significantly higher than shuffle (P<0.05, Wilcoxon rank-sum test). ***P < 0.001.

See also Figures S2 and S3.

A classic feature of CA1 place cell activity during runs on linear tracks is their directional selectivity manifested at the level of maximal firing rate or absolute location of firing between the runs in the opposite directions (McNaughton et al., 1983; Muller et al., 1994). For each neuron, we calculated its direction selectivity index (DSI) similarly to its OSI, but using four moving directions (i.e., toward East, West, North, South) as variables instead of the two possible orientations (i.e., horizontal and vertical). The orientation selectivity property of place cells described here was more prevalent than their directional selectivity on linear tracks, which was expressed in only 10.3% of all neurons, 72.4% of which (21/29) were also orientation selective (Figure S2D-E). Animals’ moving direction did not show a significant contribution to re/mapping (P=0.89, Chi-square test; data not shown). Orientation selectivity could not be simply explained by an increased bidirectionality (Dragoi and Buzsaki, 2006; McNaughton et al., 1983; Navratilova et al., 2012) in place cell firing, the two properties being negatively correlated (R=−0.17, Figure S2F). Moreover, while the distinct distal cues across the two rooms contribute to place cell remapping across tracks of the two Mazes, they do not prevent the maintenance of orientation selectivity across the two rooms/Mazes. These properties differentiate orientation selectivity from the phenomenon of path equivalence (Derdikman et al., 2009; Singer et al., 2010). Anatomically, electrodes located in relatively more posterior CA1 areas recorded a higher proportion of orientation-selective neurons (Figure S2G-H). Place maps of orientation-selective neurons had relatively higher peak firing rates compared with non-orientation-selective neurons (Figure S2I).

Place cells are named for their selectivity to spatial locations (O'Keefe and Nadel, 1978). To compare neuronal orientation selectivity and location selectivity, we computed: 1. intersection-OSI using place cell activity during runs in orthogonal orientations within intersection areas (same location, different orientation; Figure 3C top, grey square/red arrows, Figure S3A) and 2. intersection location selectivity index (LSI) using their activity inside and outside intersection area in the same orientation (same orientation, different location; Figure 3C top, red squares). Surprisingly, we found that intersection-OSIs were higher than LSIs (Figure 3C, Figure S3B-C; P<10⁻¹⁶, n=280, Wilcoxon rank-sum test), indicating that track orientation can drive place cell activity stronger than its absolute location in the allocentric space. In addition, place cell population-level place maps in the inner intersectional areas were significantly correlated across runs in parallel orientations (Figure S3D-E, P<10⁻¹⁴, Wilcoxon rank-sum test). At the neuronal population level, the trajectories of population firing rate activity across orthogonal tracks separated well into two clusters in the principal component space (Figure 3D).

To further understand the nature of place cell re/mapping, we extracted the individual place cell subfields (mean=1.59 subfields/track/place cell, Figure S3F; see Methods). For each place cell, we studied the topology and re/mapping of its primary to tertiary place subfields which contain 65.5% of place map activity, across corresponding locations on other tracks (Figure S3F-G). We found that the location of primary-tertiary subfields on certain tracks topologically corresponded to portions with higher than chance firing levels on other tracks when the comparison was performed with other parallel, but not orthogonal tracks (parallel: P=10⁻³⁵, n=49,679; partial re/mapping, firing rate redistribution across multiple subfields; orthogonal: P=0.9, n=54,109, global re/mapping, one-way ANOVA tests; Figure 3E, Figure S3G). This indicates that place subfields did not re/map randomly across parallel tracks but were preferentially expressed (i.e., partly constrained) in topologically corresponding locations. This is consistent with our earlier finding that induction of intra-hippocampal long-term potentiation by stimulation of ventral hippocampal commissure fibers topologically constrains CA1 place subfield re/mapping to the locations of prior non-zero spiking activity of the same place cell on the same track (Dragoi et al., 2003). Overall, these results indicate that CA1 place cell re/mapping across multiple linear environments is not purely random but constrained by their geometric features, primarily orientation and topology. Therefore, CA1 spatial representations generalize across the more similar (i.e., parallel) environments and discriminate between the more different (i.e., orthogonal) ones. This is suggestive of a role for CA1 area in orientation categorization and topology generalization across environments.

Temporal dynamics of track discrimination and generalization

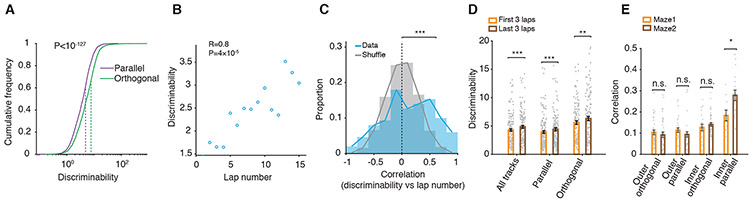
Discrimination and generalization of newly encountered environments relative to previous environments may express immediately or, alternatively, may develop following additional experience within the environment. We investigated the temporal dynamics of experience-driven discrimination and generalization between different environments at two behavioral timescales: 1. across multiple laps within-environment/session (i.e., laps-scale, mean duration of single-track sessions, T=18.3 minutes), and 2. across multiple environments/sessions within the day (i.e., sessions-scale, time between first and last track run sessions, T=9.4 hours). At the laps-scale, we defined ‘discriminability’ to quantify (Zhu et al., 2015) how well population-level place maps in single laps discriminated the current track from other tracks (Figure S4A, Methods). We found that overall discriminability by all putative pyramidal cells was higher between tracks with different orientation (i.e., orthogonal) than between those with the same orientation (i.e., parallel; Figure 4A, P=10⁻¹²⁸, n=2,615, Wilcoxon rank-sum test). Importantly, the single lap discriminability was initially low during the early laps, gradually increased in the later laps and was positively correlated (laps-scale) with the number of laps/revisits within the environment (Figure 4B-D, mean R=0.11, >shuffle P=52×10⁻⁴, Wilcoxon rank-sum test; first 3 laps vs. last 3 laps, P=10⁻⁴, n=150, Wilcoxon signed-rank test).

Figure 4. Temporal dynamics of context encoding and discrimination.

(A) Neuronal population-level place map discriminability between different parallel or different orthogonal tracks.

(B) Experience-dependent gradual increase in context discriminability as a function of lap number in an example run session at short, within-session timescale (i.e., laps-scale).

(C) Distribution of correlation values between discriminability and lap number across all run sessions and animals in the original data compared with lap number-shuffled data.

(D) Discriminability during the first 3 laps compared with the last 3 laps.

(E) Correlations between population-level place maps during sessions on the same Maze on: outer orthogonal tracks, outer parallel tracks, inner orthogonal tracks, and inner parallel tracks.

Data are represented as mean±SEM. *P < 0.05, **P < 0.01, ***P < 0.001, n.s., not significant.

See also Figure S4.

Discriminability between orthogonal tracks exceeded that between parallel ones both during early (57.9% higher) and late laps (61.1% higher) (Figure 4D), consistent with a hippocampal processing of orientation selectivity. In agreement, OSI of orientation selective neurons also increased from the early to the late laps (Figure S4B). These findings indicate a scenario in which: 1. rapid/early encoding/representation of a novel environment (i.e., during early laps) has a more generic character (i.e., it is less discriminated against other similar environments, like other parallel tracks), and 2. with repeated experience in the environment, the representation gradually increases its distinctiveness (i.e., accuracy) from other environments (Figure 4B, D). This suggests a within-session experience-driven gradual tradeoff between the speed and the accuracy of spatial encoding across individual laps within an environment, from rapid and less distinct in the early laps to delayed and more distinct in the later laps (Figure 4B-D).

Given the experience-driven gradual increase of discrimination within the session (laps-scale), we next investigated whether sessions-scale discrimination/generalization between different tracks across sessions can also be modulated by the extent of an animal’s experience with linear tracks. Sessions-scale similarity was quantified by the population-level place map correlation. The average sessions-scale similarity between pairs of different tracks was generally lower (Alme et al., 2014; Dragoi and Tonegawa, 2011, 2013b) than the same-track similarity (i.e., between different repeat sessions on the same track, Figure 2E). However, for the specific group of within-maze parallel inner tracks, which generally have the highest degree of similarity (Figure 2C-F), sessions-scale similarity increased from early sessions in Maze1 (i.e., Tracks 5 vs. 7) to the late sessions in Maze2 (i.e., Tracks 12 vs. 14 and 13 vs. 15; Maze1 vs. Maze2, P= 0.01, Wilcoxon rank-sum test; Figure 4E). Meanwhile, sessions-scale similarity between inner orthogonal track pairs did not change (P=0.57, Wilcoxon rank-sum test; Figure 4E). This suggests that the amount of prior experience on different tracks could contribute to the increased generalization observed across inner parallel track encoding. Animals’ velocity, within-session map stability, and sessions-scale similarity of within-maze parallel or orthogonal outer tracks did not change from the early (Maze1) to the late (Maze2) sessions (Figures S4C-D and 4E) further suggesting that increased sessions-scale generalization does not reflect an overall increased animal confusion. This sessions-scale generalization effect was unlikely to be an effect of global proactive interference (Peterson and Gentile, 1965) of later encodings by the earlier ones since it was expressed specifically for the inner (not the outer) parallel tracks and not for the orthogonal ones (Figure 4E). Altogether, our results indicate that repeated experience across laps within a linear track leads to an increased representational discrimination against other tracks (Figure 4D, laps-scale) while increased sampling of multiple tracks leads to an increased generalization of the representation of the most similar tracks (Figure 4E, sessions-scale).

Generative processes underlying recruitment of new place cell sequences

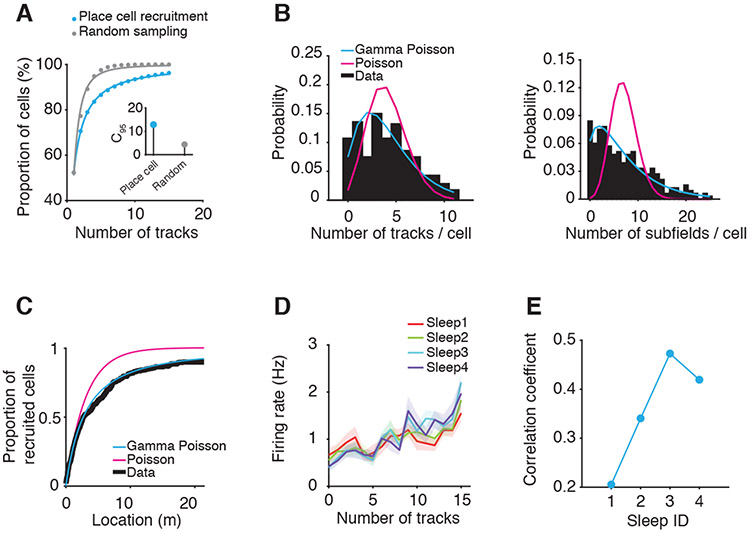
The investigate the processes governing the selection of active hippocampal neurons into place cells during encoding of single and multiple novel environments, we computed the cumulative probability of place cell recruitment during the encoding of the 15 different tracks (Figure 5A-C, Figure S5A). The 15 tracks recruited 269 out of the 280 putative pyramidal cells as place cells. A range of 40-72 place cells/animal were recorded simultaneously for the entire duration of the experiment (25± 0.7 simultaneous place cells per individual linear track across all tracks and animals). The neuronal doctrine models (i.e., single cell as the main unit for information processing) would predict a more linear function for neuronal recruitment with an early capacity saturation. However, here we found that the cumulative curve of neuronal recruitment into encoding numerous tracks was heavily non-linear and was best fitted by a hyperbolic ratio function (Naka and Rushton, 1966) (Figure S5B). Its parameters indicated that while exposure to the first of the 15 tracks (6.7% of the total number of tracks) recruited ~50% of the putative pyramidal neurons, the recruitment of 95% of all our putative pyramidal neurons (i.e., C₉₅ index, Figure 5A inset) required sequential exposure to 13 (87%) different tracks. The real network operation and capacity were much higher than those of a surrogate network that employed a random sampling of neurons as place cells across the 15 tracks (C₉₅ of random sampling is five tracks, P<0.008, Wilcoxon rank-sum test, Figure 5A inset). Exposure to all 15 tracks recruited 96% of all putative pyramidal neurons across all animals (N = 40, 51, 72, 48, 58 neurons in rats 1-5; Figure 5A and inset), indicating that most, if not all, putative CA1 pyramidal cells can become place cells. Moreover, we found that the number of different tracks encoded by an individual neuron was best described by a gamma Poisson distribution (Figure 5B left, gamma Poisson parameters r, p = 3.07, 0.43; the fit was better than the Poisson P=0, Likelihood-ratio chi-squared test). When we virtually connected all the 15 tracks into one 22.5-meter-long linear track, we found that the total number of place subfields expressed by each place cell along this long track similarly agreed with a gamma Poisson distribution (Figure 5B right, gamma Poisson parameters r, p = 1.48, 0.17). The predicted recruitment curve by gamma Poisson model matched the observed curve well (Figure 5C, Kolmogorov-Smirnov statistic = 0.03, P=0.9; see also Figure S5C-D). This distribution of the place cell selection process across multiple environments was consistent with a previous report on CA1 area place cell selection on an actual long linear track within one room (Rich et al., 2014). These neuronal selection features indicate that individual neurons are re-used across experiences and that network capacity to distinctly encode numerous environments is enhanced primarily via a combinatorial neuronal ensemble code rather than an individual neuron code (Dragoi and Tonegawa, 2013b; Liu et al., 2018).

Figure 5. Recruitment of place cells on the fifteen tracks.

(A) Cumulative place cell recruitment on the 15 tracks. Inset: C₉₅, number of tracks driving the cumulative recruitment of 95% of all neurons as place cells.

(B) Distribution of neuronal participation in the encoding/mapping of the 15 tracks (Left) and distribution of the number of place subfields/neuron (Right) compared with Gamma Poisson and Poisson distributions.

(C) Cumulative recruitment of place cells on a virtual 22.5 m-long track created by concatenation of all the 15 tracks.

(D) Relationship between the neuronal firing rate of putative pyramidal cells during the 4 sleep sessions and the number of tracks on which they express place subfields.

(E) Correlation between firing rate of neurons during sleep and the number of tracks in which they participated as place cells during run as a function of experience.

Data are represented as mean±SEM.

See also Figure S5.

Given the importance of neuronal ensemble coding, we investigated how coordinated was re/mapping across place cells. We searched (Cumin and Unsworth, 2007) for the ‘longest-common-sequence’ defined as the largest number of place cells whose primary subfields were active in the exact same order across track pairs. We found that sequences of 7.2±0.2 place cells could be selected and re-used in the same order during spatial encoding from one track to another (Figure S5E-F). This selection process was supported, in part, by the network organization into high-repeat neuronal tuplet motifs (Liu et al., 2018) (Figure S5G, P<10⁻³, n=12, Wilcoxon rank-sum test).

Neurons’ selection as place cells during track exploration is generally contributed by: 1. their spontaneous, internally-generated excitability and functional connectivity (Cai et al., 2016; Dragoi and Tonegawa, 2011, 2014; Liu et al., 2018) and 2. by multisensory drives from the external world (Farooq et al., 2019; Lee and Wilson, 2002; Monaco et al., 2014; Muller and Kubie, 1987) acting online during exploration or via replay (Lee and Wilson, 2002) of a recent activity. We found that the firing rate of neurons during sleep correlated with the number of tracks onto which they expressed a place subfield (Figures 5D and S5H). This correlation gradually increased as a function of experience, from Sleep1 (i.e., spontaneous, internally-generated excitability, R=0.21, P<10⁻³) to later sleep sessions (i.e., mixed internally- and externally-driven excitability, Sleep2-4: R=0.34-0.47, P<10⁻⁸, Pearson’s correlations; Figures 5E and S5I). The partial correlation between neuronal firing rates during Sleep4 while controlling for Sleep1 firing rates and the number of participating tracks was also significant (R=0.4, P<10⁻¹¹), consistent with a stronger contribution to neuronal firing rate expressed in sleep from the replay of prior multisensory drives. Overall, these findings indicate that both internally-generated and externally-driven neuronal activity contribute to neuronal selection during information encoding of novel linear tracks.

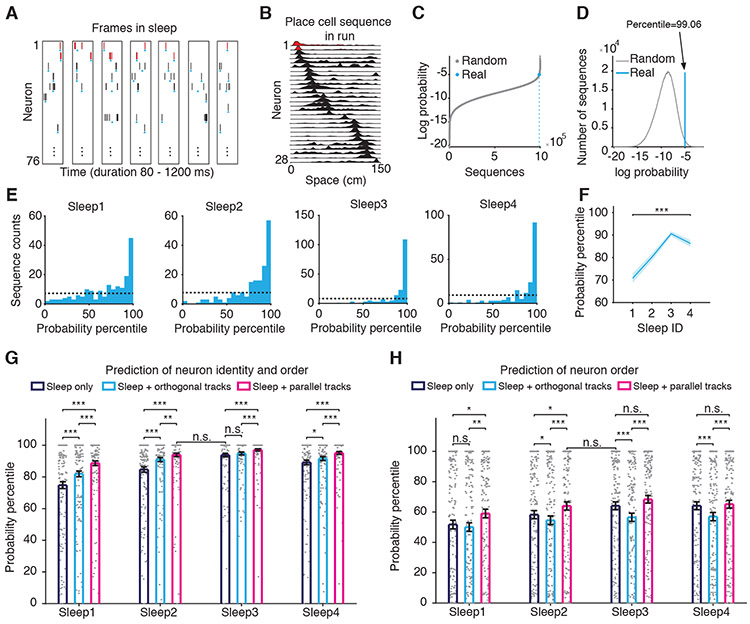
Given the externally driven orientation selectivity of neurons and the contribution of internally generated sleep mechanisms to neuronal selection during run, we wanted to investigate whether and how orientation selectivity might contribute to the experience-driven change in neuronal selection from sleep. To evaluate the internally-generated activity, for each sleep session we constructed a Markov chain model based on neuronal excitability and functional connectivity during the sleep frames alone (Figure 6A, Methods). We used this model to estimate (Liu et al., 2018) the probability of run sequences and of control-random sequences with equal length (Figure 6B-D, Methods). For each run and sleep session, we determined the percentile of the probability of each run sequence among the distribution of probabilities of 10⁶ random sequences. A higher percentile indicates a higher predictability/retrievability of a run sequence from the sleep sequences. Overall, we found that place cell sequences of the 15 tracks expressed high predictability/retrievability from every sleep session (Figure 6E, Figure S6A, P<10⁻¹⁵², n=150, highly left-skewed distributions, Kolmogorov-Smirnov tests). The percentiles of probabilities of run sequences inferred from sleep increased as a function of animal’s experience with linear tracks, from Sleep1 (generative preplay, no linear track experience) to Sleep2-4, likely due to prediction-error-based plasticity (Liu et al., 2018) reflected as generative replay (Figure 6F, Figure S5H, P<10⁻¹⁹, n=600, Kruskal-Wallis tests).

Figure 6. Generative processes underlying place cell sequences.

(A) Example spiking frames during slow-wave sleep used to extract neuronal order of firing. Spikes in red color exemplify temporal order between one pair of neurons across frames.

(B) Example place maps used for constructing run sequences. Place maps in red color correspond to the neurons emitting the spikes marked in red in (A).

(C) Probabilities of 10⁶ random sequences (gray) and of a real place cell run sequence (blue, dotted) estimated by an example sleep session.

(D) The determination of probability percentile of an example real run sequence (blue). The height of the blue line is arbitrary to match the height of the distribution in grey.

(E) Distribution of probability percentiles of the real place cell sequences during run (identity and order) during each sleep session. Horizontal dotted line represents chance distribution.

(F) The average probability percentile of all real run sequences (identity and order) inferred from sleep as a function of sleep ID. Note the overall increases of probability percentiles from pre- to post-experience sleep.

(G-H) Increase in the probability percentile for real run sequences, neuronal identity and neuronal order (G) and neuronal order alone (H) during run inferred using the Markov chain model built on neuronal sequences during the sleep alone (black), or a Markov chain model built on combined sleep and primary-tertiary subfield sequences expressed during the run sessions on different orthogonal (blue) or parallel (red) tracks.

Data are represented as mean±SEM. *P < 0.05, **P < 0.01, ***P < 0.001, n.s., not significant

See also Figure S6.

Next, run sequences expressed on certain tracks (i.e., called ‘in-run’ sequences) were also used in combination with sleep sequences (i.e., called ‘in-sleep’ sequences) to construct the Markov chain model (Methods). We found that the probability percentiles of run sequences (identity and order) estimated from the model combining sleep sequences with the run sequences on other parallel tracks were generally higher than those estimated from the model using only sleep sequences (Sleep+parallel tracks>Sleep only: P<4×10⁻³, n=150, Sleep1-4, Figure 6G; Sleep1-4: P=0.03, 0.02, 0.2, 0.4; n=150, Figure 6H, Wilcoxon signed-rank tests). At the same time, information from the other parallel tracks improved the predictive model stronger than the information from the orthogonal tracks (Sleep+parallel tracks>Sleep+orthogonal tracks, P<0.01, n=150, Sleep1-4, Figure 6G-H, Wilcoxon signed-rank tests). Therefore, integration of in-run (primary-tertiary place subfields) and in-sleep information improved the predictability of run sequences, and the contribution came primarily or exclusively from the other parallel tracks (Figure 6G-H). Notably, integration of in-run information about the other parallel tracks into the preceding sleep (Sleep2+parallel>Sleep only, P<0.05, Figure 6G-H) increased the predictive codes for the current ‘target’ tracks to a level commensurate to the one induced by the real exploration of the current ‘target’ tracks in the following sleep (Sleep3-4 only vs. Sleep2+parallel, P>0.05, Figure 6G-H). After a sufficient number of tracks were already explored (i.e., Maze1), integration of in-run information into later sleep sessions ceased to improve the inferred probability of neuronal order during run calculated from the later sleep sessions alone (Sleep3 only vs. Sleep3+parallel, Sleep4 only vs. Sleep4+parallel, P>0.05, Figure 6H). Given that orientation selectivity is contributed by a redistribution of place cell firing rate across different subfields (rate remapping) across parallel tracks, we hypothesized that secondary-tertiary subfields may be necessary for the improvement in predictive codes by prior experience. Indeed, we found that primary place subfields alone (42.1% of all place cells had multiple subfields on a given track, Figure S3F) were not sufficient to reveal the contribution of prior run-on-parallel-tracks experience to the prediction from sleep (Figure S6C-D). Altogether, these results demonstrate that: 1. generation of place cell sequences is contributed by both internally-generated and externally-driven network dynamics, 2. integration of generalized information about other similar (parallel) environments into the intrinsic sleep codes (i.e., preplay) can improve generative prediction of future place cell sequences in a new environment, and 3. this improvement is commensurate with the plasticity in generative replay (Liu et al., 2018) induced by the actual exploration of that new environment (i.e., replay).

Discussion:

Context representation is crucial for episodic memory function and for spatial navigation and mental travel (Eichenbaum and Cohen, 2014; Tulving, 2002). Here we have shown that hippocampal representation of specific linear environments is selective to their orientation and topology. The orientation selectivity property of CA1 place cells was preserved and transferred across different yet connected rooms despite global place subfield re/mapping between rooms. The differences in distal cues (visual, auditory) and Mazes (7 tracks in Maze1, 8 in Maze2) between rooms likely contributed to the global place cell re/mapping across Mazes. Meanwhile, rooms contiguity (ceiling, floor, walls) and Maze similarity in geometry and orientation may have helped the animals maintain their sense of orientation across the two Mazes and rooms.

Our finding of experience-dependent gradual generalization-discrimination tradeoff (Figure 4B-D) may indicate the existence of a continuum of representations flanked by two general operation modes (Kahneman, 2011; McClelland et al., 1995): one faster and more generic (e.g., ‘a horizontal (E-W) track’, Figure 4B-D, early laps) and one slower and more individualized (e.g., ‘track #9’, late laps). The more generic representation (early laps) is primarily driven by top-down mechanisms ignited by a strongly predictive network pre-configuration spontaneously expressed during pre-experience sleep (Dragoi and Tonegawa, 2011; Liu et al., 2018), which is partly innate and partly contributed by prior experience (Dragoi and Tonegawa, 2013a; Farooq and Dragoi, 2019; Tse et al., 2007). With repeated trials within the same environment, additional features from the external world could contribute to the slow-individualized discrimination (e.g., into individual tracks #1-15, Figure 4B-D, late laps).

CA3 and dentate gyrus areas are reported to be critical for pattern completion and pattern separation processes, respectively, while CA1 area undergoes a more linear, graded transformation across different contexts (Guzowski et al., 2004; Lee et al., 2004; Leutgeb et al., 2007). These and other previous studies primarily assessed binary representations between two 2-D contexts at fixed timepoints. Here, we compared the temporal dynamics of representations of 15 linear tracks and found that generalization across environments (akin to pattern completion) increased as a function of experience load while discrimination across environments (akin to pattern separation) increased as a function of repeated trials within an environment (Figure 4B-D, laps-scale). What remains to be understood is how neuronal ensembles from the upstream CA3 and the dentate gyrus would perform pattern completion and separation under this new, increased-load experimental paradigm.

Place cells in the dorsal hippocampus CA1 area were previously shown to lack head-directional tuning in 2-D environments (Muller et al., 1994; O'Keefe and Nadel, 1978) and to exhibit a strong directional selectivity in narrow linear environments (McNaughton et al., 1983; Muller et al., 1994), which would develop as a function of experience-dependent plasticity (Dragoi et al., 2003; Navratilova et al., 2012). The orientation selectivity phenomenon could not be simply attributed to an occupancy or behavioral bias (Burgess et al., 2005; Muller et al., 1994) since both animal occupancy and behavior across all the tracks were highly similar. We propose that orientation selectivity is predominantly contributed by an internal head direction signal from the upstream entorhinal cortex (Brandon et al., 2013; Giocomo et al., 2014; Sargolini et al., 2006) combined with a reduced subfield directionality due to increased track novelty (Navratilova et al., 2012), facilitated by a similarity in Maze configuration and continuity of distal room walls.

After extended experience across multiple days within an environment (Kinsky et al., 2020; Mankin et al., 2012; Ziv et al., 2013) or after rapid artificial induction of long-term potentiation of intra-hippocampal synaptic transmission (Dragoi et al., 2003), the place cell representation of the same environment can drift and appear re/mapped. In contrast to the extended timescale representational drift (i.e., over days), during our 16 h recording we only re-exposed our animals once to the same environment (tracks 1 and 8) over a relatively shorter time interval (~1-2 h) and were not able to track a long-term representational drift. Reported representational drift after ~24 h (Mankin et al., 2012) reduced place cell population vector correlations to levels (R~0.6) much higher than the correlations between different tracks reported in our study (R=0.13±0.004). This indicates that the place maps within the 16 h duration of our experiment were stable enough for the animals to rapidly distinguish between different tracks. The laps-scale place map changes from the early to the late laps (Figure 4B-C) might resemble an accelerated representational drift likely to enhance the discrimination from other environments.

Previously, we detected the existence of generative predictive codes for future novel place cell sequences during pre-experience sleep (Liu et al., 2018). These codes were updated in response to inferred undetermined external stimuli via prediction error and generative replay (Liu et al., 2018). Here we reveal that incorporation of generalized multisensory information about orientation and topology into the predictive codes of sleep strengthens the combined network predictive power for similar (parallel) future novel environments (Figure 6G-H). The degree by which the predictive codes were strengthened by parallel track generalization is commensurate with that of the plasticity in replay (Dragoi, 2020) induced by the actual exploration of the new (parallel) environments (Figure 6G-H). This suggests that mapping of an even larger repertoire of multisensory-driven hippocampal activity could further increase the network predictability for rapid encoding and representation of future novel experiences. Consistent with this idea, the inclusion of secondary and tertiary place subfields (likely representing additional multisensory contingencies) along with the primary subfields was critical in revealing the role of environment topology in increased predictive coding (Figures 6G-H, S6C-D). We propose that similar principles of combined representational features of internally-generated (top-down) and externally-driven (bottom-up) activity would be conducive to improved predictability in representation of future novel environments. Using a linear extrapolation of neuronal activity on 3 tracks and the preceding sleep, we estimated that hippocampal network capacity may be reached after exposure to 15 linear tracks (Dragoi and Tonegawa, 2013b). Here we show that, while initially linear, the functions governing the selection and allocation of place cells on numerous additional linear tracks become heavily non-linear. The multiple coding schemes demonstrated here support a hippocampal role in generative predictive coding, inference and discrimination-generalization of novel contextual information and are likely to generalize to the activity of additional areas of the brain.

STAR Methods:

RESOURCE AVAILABILITY

Lead contact:

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, George Dragoi (george.dragoi@yale.edu).

Materials availability:

This study did not generate new unique reagents.

Data and code availability:

• The reported data are archived on file servers at the Yale Medical School. Data reported in this paper will be shared by the lead contact upon request.

• Original code was deposited in Dataverse and is available at DOI https://doi.org/10.7910/DVN/KFCXTF.

• Additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Five Long-Evans adult male rats weighting ~350 g were used for data collection. Animal handling and experimental procedures were approved by the IACUC at Yale University and were performed in agreement with the NIH guidelines for ethical treatment of animals.

METHOD DETAILS

Surgery and experimental design

Animals were implanted bilaterally with 32 independently movable tetrodes (Rats 3-5) or two independently movable 64-channel 8-shank silicon octatrodes (Neuronexus probes, Rats 1-2) under isoflurane anesthesia. Craniotomy was performed above area CA1 of the hippocampus (centered at 4 mm post-bregma, 2 mm lateral to midline). The reference electrode was implanted posterior to lambda over the cerebellum. During the following several weeks post recovery, the tetrodes and silicon probes were advanced daily while animals rested and slept in a high-wall opaque sleeping box (30 x 45 x 40 (h) cm).

The experimental apparatus consisted of two 150 2× 150 cm rectangular elevated linear track mazes with additional parallel and orthogonal tracks inside the square arranged as described in Figures 1A and S1. All tracks were 150 cm long, 6.25 cm wide and 75 cm above the floor. Experimental sessions were conducted while the animals explored for chocolate sprinkle rewards placed at the ends of the linear tracks (one sprinkle at each end of the available track on each lap). Each track was explored for at least 10 laps for food rewards. Neuronal activity was recorded in naïve animals during the pre-experience sleep session (Sleep1) in the sleep box for ~2-4 h, after which the first linear maze (Maze1, tracks 1-7) was brought into the room and installed. Subsequently, the animals were transferred onto track1 of Maze1 for the first time and allowed to explore the 150 cm-long linear track while access to connected tracks was blocked by 20 cm-high, 10 cm-wide barriers. This was followed by a ~2 h sleep session in the sleep box (Sleep2) and a re-exposure to track1. While the animals were on track1, the end barriers were lifted in succession allowing the animals to explore for the first time 3 additional 150 cm-long linear tracks completing the outer tracks of Maze1 (tracks 1-4). Afterward, the animals were placed on and allowed to explore in succession tracks 5-7. Exploration of Maze1 was followed by a 2-4 h sleep session in the sleep box (Sleep3). Following Sleep3, the animals were directly transferred to the second maze (Maze2, tracks 8-15) located in another room or compartment through an opening in the curtain or a door separating the 2 rooms. The curtain and the door were opened during transfer and were closed at all the other times. The animals were held on experimenter’s arm during the transfer between Mazes during which time the global cues and topological relationship between two rooms/compartments were visible to the animal. Animals first explored track8 for one session, after which the end barriers were lifted in succession allowing the animals to explore all outer tracks of Maze2 (tracks 8-11) contiguously.

Subsequently, the animals were placed on and sequentially explored tracks 12-15 individually. After exploration of Maze2, the animals were placed in the sleep box for a 2-4 h sleep session (Sleep4). The sleep box was always placed in the same location of room1 for the whole duration of the experiment and was temporarily removed during the exploration of tracks 1-15. Additional details of all exploration and sleep sessions are provided in Figure 1A and Figure S1. For tracks 1 and 8, only the first exploratory session on these tracks was used for all the analyses with the exception of Figure 2E, which explicitly investigated the similarity between place maps on the two different sessions on the same track.

Electrophysiology data acquisition

Electrophysiological data acquisition was performed using a 128-channel digital Neuralynx data acquisition system (DigiLynx) with Cheetah software. Raw signals were recorded at 30 kHz and were digitally filtered between 1 and 6,000 Hz. Spikes were obtained by high pass filtering raw signal above 600 Hz and triggering signal acquisition by passing a 50 μV threshold. The animal’s position was monitored via a set of LEDs placed within the headstage and an overhead camera whose video capture was recorded by the Cheetah software.

Single cells were identified and isolated offline using the manual clustering method Xclust3 (Dragoi and Tonegawa, 2013b). Putative pyramidal cells were distinguished from interneurons based on spike width, average rate, and autocorrelations as published before (Dragoi and Tonegawa, 2013b). We collected 43, 51, 76, 48 and 62 pyramidal cells from the 5 animals.

After the completion of all experiments, all rats were perfused intracardially with 10% formalin and their brains were fixed, sectioned, and stained using Cresyl violet to reconstruct all electrode tracks.

Place maps and place subfields on linear tracks

Place maps were computed as the ratio between the number of spikes and the time spent in 2 cm bins along the track, smoothed with a Gaussian kernel with a standard deviation of 2 cm (Dragoi and Tonegawa, 2013b). Bins where the animal spent a total of less than 0.1 sec and periods during which the animal’s velocity was below 5 cm/s were excluded. Place subfields were defined as areas of a place map with >2 Hz activity contiguous for >10 cm. Place subfields were named primary to tertiary in the descending order of their peak firing rate. Place subfield length and peak rate were calculated after separating the direction of movement and linearizing the trajectory of the animal. The place subfield peak rate and location were given by the rate and location of the bin with the highest ratio between spike counts and time spent. Place subfield borders were defined as the points where the firing rate became less than 10% of the peak firing rate or 2 Hz (whichever was bigger) for at least 2 cm. Place cell Run sequences (two sequences/run) were calculated by ranking cells based on their primary place subfield location along the animals’ trajectory.

Place maps in tracks’ intersection areas

Intersection areas were defined as the crossing areas between two orthogonal inner tracks outside reward areas in each Maze. There were 6 intersection areas in total (Figure S3A). The place maps in the intersection areas of orthogonal tracks were separately calculated for each intersection area. Animals’ 2-D trajectory in the whole maze was separated into different directions (2 directions for each track) and different tracks, and binned in 3 cm × 3 cm. Bins with animal occupancy <0.05 s or animal velocity <5 cm/s were excluded. Effective intersection bins were defined as the space bins that have enough occupancy from both tracks and both directions. Place maps in intersection area were only calculated in the effective intersection bins. The ratio between the number of spikes and the time spent was calculated in each bin and smoothed with a Gaussian kernel with standard deviation of 3 cm to obtain 2-D place maps on each direction in each track.

Population-level place map correlation

Place maps of putative pyramidal neurons in each track were aligned together as a two-dimensional place map matrix with neurons as one dimension and spatial bin as another dimension. To compute the population-level place map correlation of a track pair, place map matrices of each track were first converted to 1-D vectors by concatenating the place maps of each neuron. The 1-D vectors of the two tracks in each track pair were aligned to corresponding neuron and space bin, and a Pearson’s correlation value between these two vectors was calculated as the population-level place map correlation between the two tracks:

$$r(A,B)=\frac{1}{N-1}\sum _{i=1}^N\left(\frac{A_i-{\mu }_A}{{\sigma }_A}\right)\left(\frac{B_i-{\mu }_B}{{\sigma }_B}\right)$$

where A and B are the population-level place map vectors of the two tracks being compared, μ and σ are the mean and the standard deviation, respectively.

Place maps per lap and track discriminability

The spikes of each lap when animal’s velocity was >5 cm/s were collected and normalized by the occupancy of the corresponding lap with 2 cm bin size resolution to generate place maps of each lap. This was performed for each lap of each run session on each track.

The neuronal population-level place maps on a certain lap in a certain track were compared with the whole-session place maps on each and all tracks using Pearson’s correlations. For the analysis of relationship between discriminability and orientation (Figure 4A), in each comparison between activity in a lap of the current track and another track, tracks parallel with the current track and tracks orthogonal with the current track were separately grouped and compared. For the other analyses, all tracks were used. The track which had the maximum correlation value with the lap place maps was defined as the online ‘predicted’ track during the run. The track in which the animal was actually running was defined as the ‘actual’ track (Zhu et al., 2015). For each lap, we compared the average similarity between population-level place map in single-lap and whole session on the same track with the corresponding neuronal population lap-session similarity across different tracks (Figure S4A); we computed ‘discriminability’ as the ratio between the two similarity values. The discriminability index (DI) of a lap was defined as:

$$DI=\frac{C_r}{E[C_w]}$$

where C_r is the correlation value between population-level place maps on the actual track and the lap place maps, C_w is the correlation value between population-level place maps on all the other tracks and the lap place maps. E[ ] represents expectation. To evaluate whether the correlation between discriminability and lap number (Figure 4B) was significantly positive, we broke the correspondence between lap number and discriminability by shuffling the lap number and then recalculated the correlation between the shuffled lap order with the discriminability. This was performed 100 times to construct a shuffle dataset of correlation values (Figure 4C). The differences between the shuffle dataset correlations and the original correlations were tested by a Wilcoxon rank-sum test.

Orientation selectivity, direction selectivity and location selectivity

The orientation selectivity of each neuron was quantified by comparing the place map on the horizontally (E-W) oriented and the vertically (N-S) oriented tracks (Figure 1A). The orientation selectivity index (OSI) was calculated as:

$$OSI=\mid \frac{R_h-R_v}{R_h+R_v}\mid$$

where R_h and R_v are the expectation of average firing rate when animals travel in horizontally (E-W) oriented and in vertically (N-S) oriented tracks, respectively.

For OSI in the intersectional areas, R_h and R_v are the average firing rates in the effective intersectional bins when the animals travel in horizontally (E-W) oriented and in vertically (N-S) oriented tracks, respectively.

The significance of orientation selectivity was evaluated by shuffling the orientation identity (i.e., horizontal (E-W) or vertical (N-S)) of all tracks 500 times and recalculating corresponding OSIs. The original OSI was compared with the OSIs of the shuffled tracks to determine whether the original OSI is higher than 95% of the shuffled data OSIs. The neurons that passed the significance test were considered orientation selective, while the neurons that did not pass significance were allocated to the orientation non-selective group. The neurons with high OSI and high P-values (i.e., non-significant) were not assigned as orientation selective at the single cell level, but they have the potential to contribute to the encoding of orientation at the neuronal population level. The value and significance of the direction selectivity index (DSI) was evaluated similarly to OSI by using the direction (0° / E, 90° / N, 180° / W or 270° / S) of each track. To compare orientation selectivity with location selectivity, we computed intersection-OSI for place cell activity using only the spatial bins in the intersection areas where the animals occupied the same physical location in the room coordinates while running along tracks of different orientation (same location, different orientation; Figure 3C, grey square/red arrows). We also computed location selectivity index (LSI) by comparing place maps inside and outside intersection areas while animals ran on the same track (same orientation, different location; Figure 3C, red squares).

The location selectivity was quantified by comparing the place maps on two locations on the same track:

$$LSI=\mid \frac{R_{in}-R_{out}}{R_{in}+R_{out}}\mid$$

where R_in is the average response inside intersectional area, R_out is the average response in another location outside intersectional area of the same track with an equal number of space bins outside intersectional area. Orientation selectivity lacks specificity to animal’s vectorial direction of movement on parallel tracks and manifests across tracks separated across two rooms having different external visual and auditory cues. Orientation selectivity may rely on animal’s rapid (re)orientation based on the continuity of the floor, ceiling, and distal walls between the rooms also available during the animal transfer between the rooms. These properties differentiate orientation selectivity from the phenomenon of path equivalence manifested on nearby parallel tracks where animals performed repeated exploration of analogous environments and developed direction-specific multi-track association by task similarity. It is possible that the similar Maze configurations across the two rooms (e.g., the fixed barrier, the overall shape and size of the Mazes) and the spatial continuity between the rooms played a role in maintaining a general sense of orientation for the animals across the 2 Mazes and rooms. However, given that orientation selectivity was expressed on linear tracks that were separated by as much as 1.5 m and 180° or located in different rooms containing different external cues and separated by opaque walls, its strong dependence on specific visual cues is less likely. Instead, different distal cues likely contributed to place cell remapping across the analogous tracks of the two Mazes and rooms despite preserved orientation selectivity.

Place cell recruitment

We calculated the cumulative number of neurons that became place cells (i.e., at least one subfield) in a certain number of linear tracks (Figure S5A). For one track, this is the average number of place cells in each one track normalized by the total number of putative pyramidal neurons. For multiple tracks (e.g., 5 tracks), this is how many place cells participated in at least one of the multiple tracks (e.g., one of the 5 tracks) normalized by the total number of pyramidal neurons.

Cumulative probability curve fitting

The cumulative recruitment of place cells across multiple tracks was fitted by linear, logarithmic (Weber-Fechner’s law), power (Stevens’ power law), exponential (Random sampling of uniform distribution), and hyperbolic ratio functions, using the least-square method as below:

Linear:

$$p=\alpha x+\beta$$

where α is the slope, β the intercept, p is the proportion of neurons that were recruited as place cells by at least one track, and x is the number of tracks.

Logarithmic:

$$p=\alpha \log x+\beta$$

where α is the sensitivity, β the baseline.

Power:

$$p=\alpha x^{\beta }$$

where α is the proportionality constant (i.e., scaling factor), β the exponent.

Exponential:

$$p=\alpha -\alpha {\beta }^x$$

where α is the saturation level (for example, in place cell recruitment, it represented the maximum proportion of neurons that would be recruited by an infinite number of tracks), β is the proportion of inactivation (for example, in place cell recruitment, it represented the proportion of silent neurons in one track).

Hyperbolic ratio function (Naka and Rushton, 1966)

$$p=\frac{x^n}{x^n+C_{50}^n}$$

where C₅₀ is the half-saturation constant (for example, in place cell recruitment, it represents the number of tracks required to recruit half of all neurons), n is an exponent describing cooperativity. C₉₅ was calculated as the x value when p=0.95.

Non-random re/mapping of place subfields

To estimate the non-randomness of re/mapping, the location of each place subfield was extracted and the firing rate profiles on the corresponding locations (distance from ends) on other tracks were collected and averaged. The firing rate profiles on random locations on other tracks were also collected and averaged to be compared with those in the corresponding locations. After evaluation of all place subfields of all tracks, the tracks were grouped according to their orientation. For each place subfield on a track, corresponding locations in other parallel and orthogonal tracks were separately collected and averaged to evaluate the impact of track orientation on remapping. Similarly, 1^st subfield and 2^nd-3^rd subfields comparisons were performed according to whether the starting place subfield was a primary subfield or a secondary-tertiary subfield.

Longest common sequence

If a multi-neuron sequence longer than chance occurred in the run sequences on multiple different tracks, we defined it as a longest-common-sequence. For every two run sequences on different tracks, we applied a length-growing method to search for the common sequences with the same neurons and in the same order, until the length of the common sequence could not be further extended (Cumin and Unsworth, 2007). Next, we shuffled the order of neurons in these two run sequences 500 times and re-extracted the common sequences. The length of common sequences from shuffled sequences were compared with the length of common sequence from the original run sequences. If the length of the common sequence from the original run sequences was higher than the length of 95% of the shuffles, the sequence was considered a significant longest-common-sequence.

Generalized linear model of geometric features

We applied generalized linear models (GLM) to investigate the contribution of geometric features to population-level place maps (correlation between track pair population vector). This method looked for geometric features that group place maps, i.e., when two tracks are similar in that geometric feature, their place maps are more similar. The geometric features of each track pair were extracted and their consistency between track pairs was used in the model. We extracted the following geometric features for each track: Maze (i.e., maze identity, Maze1 ∣Maze2), InOut (i.e., inner versus outer/on Maze-boundary tracks, inner∣outer), MiddleBar (i.e., number of non-rewarded track intersection areas, one∣two), NearCurtain (i.e., tracks 4&8, yes∣no), Orientation (i.e., horizontal (E-W)∣vertical (N-S)), NearFixBar (i.e., fixed barrier between tracks 3&4 and tracks 10&11, yes∣no), and NearWall (i.e., tracks closest to rooms walls, yes∣no). All track pairs were compared using these factors. For each track pair, we generated a vector of binary values (i.e., true/false) to indicate whether their geometric features were the same or different. This matrix of geometric similarity of all track pairs was used as predictor variables for the GLM. The linear model contains an intercept and a linear term for each predictor that was applied in the GLM. The link function of the GLM was the identity function f(μ) = μ. The distribution of response variables was a Normal distribution.

For the population-level place map model (Figure 2B), the population-level place map correlations of each track pairs were used as response variables. Deviance of the original GLM was calculated for each geometric feature. Deviance of a model M₁ is twice the difference between the loglikelihood of the model M₁ and the full model M_s. A full model is the model with the maximum number of parameters that can be estimated.

$$\text{Deviance}=-2(\log L(b_1,y)-\log L(b_S,y))$$

where L(b,y) is the maximum value of the likelihood function for a model with the parameters b for observation y; b₁ and b_s contain the estimated parameters for the model M₁ and the full model, respectively.

Next, each geometric feature was removed from the model to generate a reduced model for that geometric feature. The deviance of the reduced model was calculated again to be compared with the deviance of the full model. Only one feature was removed at a time. There is one reduced model for each geometric feature. The difference of deviance between the reduced model and the full model was considered as the contribution of that geometric feature.

Sequence detection during sleep

Spiking frames were detected during slow-wave sleep periods in the sleep box determined based on continuous long animal immobility (velocity below 1 cm/s for at least 5 minutes) and low theta/delta ratio (below 2, after Hilbert transform for respective frequencies, 6-12 Hz for theta and 1-4 Hz for delta, and smoothed with a 5s Gaussian) to exclude epochs of rapid-eye movement sleep. A spiking frame was defined as a transient increase in the multiunit firing activity of a population of at least six different putative pyramidal cells within a temporal window preceded and followed by at least 100 ms of silence that delimited the beginning and the end of the event. The duration of spiking frames was limited to 80-1,200 ms. The spikes of all cells that were emitted during the sleep frames were sorted by time, the spike time center of mass (COM) was calculated for each cell in each frame, and was used to determine the cells’ order in each spiking frame.

Markov model of sleep sequences

We constructed a first-order Markov chain model for neuronal sequence activity during sleep frames. All details of the model were published before (Liu et al., 2018). Briefly, each sleep frame was represented by the sequence of neurons identity. The alphabet of the model was neuron’s identity. The maximum likelihood was used to estimate the parameters. Conditional probability was derived from the transition matrix we computed from neuronal activity during sleep frames, and was given by:

$$p\mathrm{r}(x_i\mid x_{i-\mathrm{k}}\dots x_{i-2}{x}_{i-1})=\frac{n(x_{i-\mathrm{k}}\dots x_{i-2}{x}_{i-1}{x}_i)}{n(x_{i-\mathrm{k}}\dots x_{i-2}{x}_{i-1})}$$

where x_i is the i^th cell in the sleep sequence, n is the count of sequence, and k is the order of the model, which was set to 1 in the most cases in this study.

Conditional probability p2 was given by:

$$p2(x_i\mid x_{i-1})=\frac{n(x_{i-1}{x}_i)}{n(x_{i-1})}$$

where x_i is the i^th cell in a sleep sequence, n is the count of sequences.

The unconditional probability (p1) of each cell was given by:

$$p1(x_i)=\frac{n(x_i)}{N}$$

where N is the length of sequential activity during sleep frames.

To alleviate the noise induced by low firing cells, the zero values in the transition matrix were set to the minimum non-zero value in the transition matrix and the values of one were set to the maximum non-one value in the matrix.

The probability of any sequence whose alphabet was included in the alphabet of the model could be estimated. For a given sequence X, the probability was estimated by

$$pr(X)=pr(x_1)\prod _{i=2}^{n}pr(x_i\mid x_{i-1})$$

where X is the sequence of interest, x_i is the i^th cell, and n is the sequence length.

To evaluate the run sequences on the 15 tracks, for each run sequence, one million random sequences with the same length as the run sequence were generated by a uniform random sampling from all cells in the model. The probabilities of each of the random sequences and the real run sequence were estimated by the Markov model after which the percentile of run sequence probability among the distribution of probabilities of corresponding random sequences was calculated. The percentile was used to quantify the predictability/retrievability of the run sequence from sleep. To investigate run cell order prediction from sleep, the random sequences for a run sequence were generated by shuffling the order of place cells in the real run sequence. All random sequences consisted of the same (place) cell population as the run sequence, with different orders.

To test the effect of place subfields in prediction of run from sleep, for each run sequence we constructed a population of sequences of the same cell count using combinations of primary, secondary and tertiary place subfields (one subfield at a time/place cell). For the cells with multiple place subfields, each place subfield was used to construct different sequences and obtain all possible combinations of place subfields. We used the Markov model of the sleep to estimate the prediction percentile of these newly generated run sequences and computed a percentile distribution for each run sequence. The peak of the probability percentile distribution was defined as the probability percentile of the original run sequence, for each track.

As a test for the contribution of the primary subfields, we also performed this analysis by using only primary subfields to construct run sequences, whose percentile was estimated (Figure S6C-D).

We also investigated the effect of combining run information into the sleep Markov model. ‘In-run’ information was estimated from the run sequences on linear tracks while ‘in-sleep’ information was estimated from sleep sequences that built the previous Markov chain model. Given that hippocampal network expressed generalization and categorization of geometric features during run, we asked whether sequence predictability for a ‘target’ track can be improved by combining functional connectivity derived from sleep alone with the one from the external stimuli computed during runs on the other parallel or orthogonal ‘source’ tracks. For each target run sequence, we used the sequences in all parallel or, separately, all orthogonal tracks except for the target track to construct transition matrices. Then the Hadamard product of elements in the transition matrix of the sleep sequences and the transition matrices of the run sequences were calculated as a combined matrix, which was used to estimate the probability of the target run sequence. This probability was compared with the probability of random sequences generated by random sampling of neurons to obtain the percentile and predictability of the target sequence. For the orientation selective contribution of run information to sleep, each target sequence was estimated by using the combined transition matrix from the sleep sequences and the run sequences in tracks that were parallel with the target sequence. Neuron order estimation was performed by similar methods, but the random sequences were generated by shuffling the neuron order of the target sequence.

QUANTIFICATION AND STATISTICAL ANALYSIS

Analyses were performed using customized code written in MATLAB (R2017b, MathWorks) and Python (2.7). The comparison between multiple populations was tested by Kruskal-Wallis tests. The comparison between two populations of different sample size was tested by the Wilcoxon rank-sum test, while two populations with the same sample sizes were tested pairwise by the Wilcoxon signed-rank test. In figures, *P<0.05, **P<0.01, ***P<0.001. Data were represented as mean±standard error of the mean (SEM).

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
Isoflurane	Zoetis	ANADA # 200-070
Grip cement	Teets denture material	N/A
Carprofen	Norbrook	55529-131-11
Experimental models: organisms/strains
Rat/Long-Evans	Charles River	N/A
Software and algorithms
MATLAB R2015b, R2017b	MathWorks	https://www.mathworks.com/
Python	Python software foundation	https://www.python.org/
Xclust3	Wilson lab	https://github.com/wilsonlab/mwsoft64
Data acquisition software	Neuralynx	Cheetah
Custom code	Dataverse	https://doi.org/10.7910/DVN/KFCXTF
Other
128 Channel Digital Amplifier	Neuralynx	Digilynx
12.7 μm tungsten wires	Kanthal	PX000004
Silicon Probes	Neuronexus	Buz-64

Highlights:

• Hippocampal place cells display selectivity to context orientation and topology

• Orientation selectivity biases discrimination and remapping between contexts

• Repeated experience within a context enhances its representation discriminability

• Generalization of experience across multiple contexts improves predictive coding