Abstract
The traditional particle swarm optimization (PSO) path planning algorithm represents each particle as a path and evolves the particles to find an optimal path. However, there are problems in premature convergence, poor global search ability, and to the ease in which particles fall into the local optimum, which could lead to the failure of fast optimal path obtainment. In order to solve these problems, this paper proposes an improved PSO combined gray wolf optimization (IPSO-GWO) algorithm with chaos and a new adaptive inertial weight. The gray wolf optimizer can sort the particles during evolution to find the particles with optimal fitness value, and lead other particles to search for the position of the particle with the optimal fitness value, which gives the PSO algorithm higher global search capability. The chaos can be used to initialize the speed and position of the particles, which can reduce the prematurity and increase the diversity of the particles. The new adaptive inertial weight is designed to improve the global search capability and convergence speed. In addition, when the algorithm falls into a local optimum, the position of the particle with the historical best fitness can be found through the chaotic sequence, which can randomly replace a particle to make it jump out of the local optimum. The proposed IPSO-GWO algorithm is first tested by function optimization using ten benchmark functions and then applied for optimal robot path planning in a simulated environment. Simulation results show that the proposed IPSO-GWO is able to find an optimal path much faster than traditional PSO-GWO based methods.
Keywords: path planning, improved particle swarm optimization, robot, gray wolf algorithm, adaptive inertia weight, chaos
Introduction
Along with the development of automation technology and robotics, path planning is important in robot task execution when searching for an optimal path from the starting position to the target position with obstacle avoidance based on certain criteria.
There have been many achievements in robot path planning. The current path planning algorithms mainly include the colony algorithms (Liu et al., 2019; Ye et al., 2020; Zhang et al., 2020; Zhu et al., 2020), PSO (Krell et al., 2019; Wang Y. B. et al., 2019; Liu X. H. et al., 2021; Song et al., 2021), A* algorithms (Xiong et al., 2020; Liu Z. H. et al., 2021; Tang et al., 2021; Tullu et al., 2021), artificial potential field methods (Wang P. W. et al., 2019; Azmi and Ito, 2020; Song et al., 2020; Yao et al., 2020), genetic algorithms (Hao et al., 2020; Li K. R. et al., 2021; Wen et al., 2021), fuzzy control algorithms (Guo et al., 2020; Zhi and Jiang, 2020), fast marching algorithms (Sun et al., 2021; Wang et al., 2021; Xu et al., 2021), and deep reinforcement learning algorithms (Li L. Y. et al., 2021; Lin et al., 2021; Xie et al., 2021). PSO is an evolutionary computation algorithm that can be used to find the optimal solution through collaboration and information sharing between individuals in the group, as in path planning, the optimal solution is to find the shortest path. The PSO algorithm is easy to implement and has fewer adjustable parameters, however, it still has problems such as being easy to fall into the local optimum and slow convergence.
In response to these problems, researchers have extensively studied PSO improvement in recent years. Das and Jena (2020) used a genetic algorithm that inherits multiple crossover operators and bee colony operators as two evolutionary operators to improve the optimization ability of the PSO. Shao et al. (2020) designed the constant acceleration coefficient and the maximum speed as the adaptive linear variation to adapt to the optimization process. Further, a particle mutation strategy has been proposed to enhance the convergence speed of the algorithm. Li and Chou (2018) applied different strategies to realize the adaptive learning of the PSO; they turned the problem of path planning into a minimizing multi-objective optimization problem and proposed a new adaptive learning mechanism to improve the search ability of the PSO algorithm.
Although the performance of the PSO algorithm has been improved greatly, there are still some shortcomings when it is applied for complex problems (Phung and Ha, 2021), i.e., premature convergence, poor global search capability, and slow convergence speed. To this end, an improved particle swarm optimization combined gray wolf optimization (IPSO-GWO) is proposed in this paper. The GWO can sort the particles during iteration to find the particles with the optimal fitness value and lead other particles to search for the position of the particles with the optimal fitness value, which can greatly improve the search ability of the PSO algorithm in the global searching space. The chaos is further adopted to initialize the speed and position of the swarm particles and a new adaptive inertia weight is designed to improve the global search capability and convergence speed of the IPSO-GWO. When the algorithm falls into the local optimum, chaos can make the algorithm quickly jump out of the local optimum. Experiments on benchmark functions optimization test and the robot path planning simulation tests demonstrate that the IPSO-GWO algorithm has faster convergence speed.
The remainder of the paper is organized as follows. The Proposed Method section describes the proposed algorithm including environment settings, IPSO-GWO, chaos based and new inertial weight design. Experiments and result analysis are explained in third section. The conclusion is given in fourth section.
The Proposed Method
Environment Modeling
The working environment of the robot is established through a grid model, which can be divided into N × N squares, as seen in Figure 1. The black grid represents obstacles which are impassable, and the white grids represent feasible passing free areas, denoted as 0 and 1, respectively. The five-pointed star indicates the starting point and the green point is the target point. Then the grid model is placed in the coordinate system so as to establish the robot working environment.
Figure 1.
Environment modeling.
It can be seen from Figure 1 that the model is easy to construct, represent, and store data for processing and it is convenient for computer processing.
PSO Algorithm
The PSO algorithm is an intelligent optimization algorithm proposed by Kennedy and Eberhart (1995) based on the study of the living habits of animal flocks (Tang et al., 2020). Suppose the optimal solution of a certain problem exists in D dimensional space for a swarm with size m, and the population can be expressed as, Swarm = {x1, x2, …, xm} where xi(i = 1, ⋯, m) is the particle without mass, k represents the total number of the required iterations, and the position information of the ith particle in the kth iteration can be represented by a d-dimensional vector , the velocity of each particle can be represented as , i = 1, 2, ···, m. In each iteration, the position and velocity of the particles are dynamically adjusted according to the historical optimal fitness values of each particle and the population. The calculation for the (k + 1)th iterations of the ith particle in d-dimensional space can be written as,
| (1) |
| (2) |
where c1 and c2 represent the learning factors. c1 and c2 are the control variables to control the step lengths of the individual particle flying toward the local optimal value and the swarm optimal value, respectively. is the historical optimal fitness value of each particle in the optimization process, is the optimal fitness value reached by all particles, that is, the optimal fitness value of the population; the rand() function is to generate a random number between (0,1) to differentiate particles. The subscript d(1 ≤ d ≤ D) represents the dimension of the searching space. In the above Equation (1) and (2), the speed of the PSO is composed of the local and global three parts: represents the speed of the particle at the kth iteration, represents the information of the particle itself, and represents the part of the particle in the population for collaboration and information sharing.
PSO-GWO Algorithm
The PSO-GWO algorithm is an improved PSO version incentive inspired by gray wolf predation (Narinder and Singh, 2017; Teng et al., 2019; Gul et al., 2021). Different from bird flocks, the gray wolf pack is quite a strict socially hierarchical organization; its hierarchical arrangement is illustrated in Figure 2.
Figure 2.
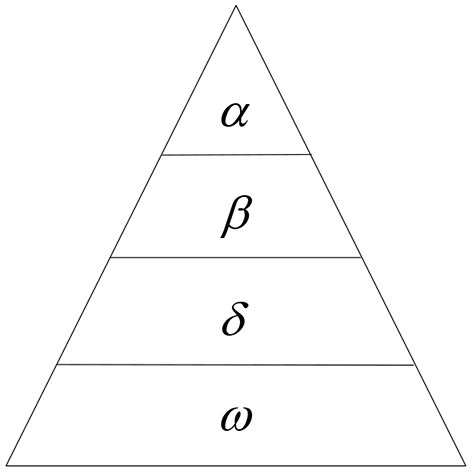
Grey wolf social hierarchy.
The first layer α in Figure 2 represents the leader in the population, where the leader α is the core of the wolf pack, being mainly responsible for leading and assigning tasks.
The second layer β in Figure 2 represents the think tank team, which is used to assist the leader in management, i.e., when leader α is vacant, β will quickly take over the position of α. In the entire wolf pack, the status of β is only lower than that of α. If α is occupied, β is an advisor to α and discipliner for the group.
The third layer δ follows the command and management of leader α and think tank, and are mainly responsible for care and supervision.
The function of the fourth layer, ω, is to balance the membership within the population.
The essence of the GWO is that the particle with the highest fitness is taken as the leader α to manage other particles. The specific steps of the GWO are summarized as follows:
Step 1: To initialize particles of one population in the searching space;
Step 2: To rank the particles according to the historical best fitness values;
Step 3: Taking three particles with the highest fitness values set as α, β and δ, the other particles are arranged in sequence. If an individual with a higher fitness value appears in the iterative process, it is set as the new leader α and pgd is updated with its individual fitness. xi = (xi1, xi2, ..., xiN) represents the position of the ith particle, and vi = (vi1, vi2, ..., viN) is the speed of the ith particle. In the k + 1 iteration, the positions of the three particles with the best fitness values in the population are updated via Equation (3), and the positions of the rest particles are updated via Equations (4) and (5):
| (3) |
| (4) |
| (5) |
As seen in Equations (3)–(5), the dimension of the spatial solution is d, and the current number of the iteration is k. c1, c2, and c3 represent the learning factors, rand() is a random number between (0, 1), and w represents the inertia weight coefficient. The larger w makes the algorithm better in global search, in contrast, the smaller w is more suitable for local search. The core idea of the PSO-GWO is to arrange the particles according to their fitness values during each iteration, and set the three particles with the best fitness values to α, β, and δ, while these three particles can predict the approximate range of the location where the optimal solution may exist, and the remaining particles can search the optimal solution within the predicted range. In such a way, the particles can find the optimal solution more quickly and effectively with the improved convergence performance, so the path planning ability of the PSO algorithm can be improved accordingly.
IPSO-GWO Algorithm
In the previous section, GWO was added to PSO to form the PSO-GWO algorithm, and the search ability of the PSO algorithm can be enhanced to improve its path planning ability, but the PSO algorithm still has the problem of premature convergence, and its convergence speed and global search ability can be further strengthened. Hence chaos and a new adaptive inertia weight are added to provide solutions for these problems.
PSO With Chaos
The PSO can randomly distribute particles while the optimal solution is highly related to the particle initialization. The more uniform the initial particle distribution, the richer the diversity of the group, and the faster the optimal solution can be obtained.
Chaos (Demir et al., 2020; Lian et al., 2020; Lu et al., 2020; Wu et al., 2020; Guo et al., 2021; Ouertani et al., 2021) refers to a nonlinear motion that can traverse all situations within a specified range. A chaotic sequence can represent all states in a prescribed space, which is commonly generated by mapping. Many researchers have found that chaotic mapping has unpredictable characteristics when studying chaotic mapping relations. Although it is somewhat unpredictable, certain laws can still be used in the mapping process. The most commonly used form of chaotic mapping is logistic mapping, as shown in Equation (6):
| (6) |
In Equation (6), 0 ≤ Z0 ≤ 1, Zi is the value obtained by i times Logistic mapping of Z0, and μ represents the control variable. When μ = 4, the system is within a completely chaotic state and the range of the chaotic space is [0, 1].
The steps of using chaos to initialize the PSO are summarized as follows. First, an n-dimensional vector Z1 = (z1, z2, …, zn) is randomly generated, and Equation (6) is used to map the other vectors so as to generate a chaotic sequence Z1, Z2, …, ZN. Then the chaotic sequence zi is inversely mapped from the chaotic space[0, 1] to the space [a, b] where the optimal solution is located, and the particle position is xij = a + (b − a)zij, j = 1, 2, …, n, i = 1, 2, …, N. Finally, the particles with higher fitness values are determined as the initial particles of the population.
When the PSO is trapped in the local optimum, the algorithm will select the historical optimal value of the particles in the iterative process and convert it into a chaotic sequence through inverse mapping to obtain the optimal position of the particle, then randomly replace a certain particle position in the current search space so that the local optimum can be jumped out by the algorithm. Whether particles fall into precocity is determined by the variance of the population fitness, calculated as,
| (7) |
where n is the size of the population, fi represents the adaptability of the first particle, and favg represents the average adaptability of the current swarm particles. The population variance σ2 reflects the precocious state of the particles. When σ2 is less than a certain threshold, it is calculated that the particle algorithm will fall into precocity. Then the chaos is applied to process the optimal particles to increase the diversity of the population. The detailed steps are described as follows.
Step 1: Select the optimal position in the iterative process and use the function Logistic to map it into the chaotic space [0, 1].
Step 2: Use logistics to generate a new sequence and inversely map the sequence to the population.
Step 3: Calculate the optimal adaptability of the particles and conclude whether the particle has jumped out of the local optimum; then record the optimal fitness value and set the corresponding particles to α, β, and δ.
Step 4: Use the current optimal chaotic particles to manage the particles in the particle swarm to make the particles leave the local optimum.
After the particle swarm performs the chaotic initialization operation, the particles are more evenly distributed in the search space, and the chaotic sequence can be used to reduce the prematurity, improve the diversity of particles, and enhance the convergence speed of the algorithm.
A New Adaptive Inertial Weight
It is known that the quality of PSO is closely related to inertia weight where the local search ability of the algorithm is higher with smaller inertial weight and global search capability is stronger with larger inertial weight. To enable the algorithm maintaining higher search ability during the entire operation process, many methods have been proposed to adjust the inertia weight (Li et al., 2019a,b; Gopal et al., 2020; Wang et al., 2020; Wang, 2021; Zhang et al., 2021). However, the current inertia weight improvement methods have a close relationship with the iteration number and cannot adapt to the nonlinear variations well. For this reason, this paper deals with the inertia weight via the particle adjacent fitness values. The inertia weight can be updated and calculated as,
| (8) |
In Equation (8), the global optimal fitness of the kth iteration is , and the global optimal fitness of the (k − 1)th iteration is ; the maximum ωmax and minimum ωmin of ω is set as 0.9 and 0.4, respectively. k is the current iteration number; MaxIter represents the maximum number of the iterations. It can be seen from Equation (8) that a is larger at the beginning of the iteration, so the algorithm has strong global searching ability, and a becomes smaller gradually at the later iteration stage, so the algorithm has strong local search ability. In summary, the inertia weight combined with the fitness ratio of the neighboring particles can adaptively adjust the size of w with the number of iterations so that the algorithm has a higher global search ability.
Path Planning
The steps of the IPSO-GWO algorithm for path planning are summarized as follows:
Step 1: The velocities and positions of the swarm particles are initialized by chaos using logistic function, while the position of each particle represents a path and the fitness of the particle represents the length of the path;
Step 2: Collision detection is performed on the path represented by the particles. If the path collides with an obstacle, the path is adjusted without obstacle collision;
Step 3: The fitness values of the particles are evaluated to select the three particles with the largest fitness values, set as α, β, and δ;
Step 4: To update the positions of particles α, β, and δ based on Equation (3), update the velocities and the positions of the rest particles via Equations (4) and (5);
Step 5: Determine whether the algorithm has fallen into prematurity via Equation (7); if so, chaos is applied to process the premature particles and jump to Step 2;
Step 6: Determine whether the algorithm meets the termination condition. If it is satisfied, the iteration stops and the optimal path is obtained; otherwise, continue to Step 2 for calculation.
Experiment and Result Analysis
Benchmark Experiments
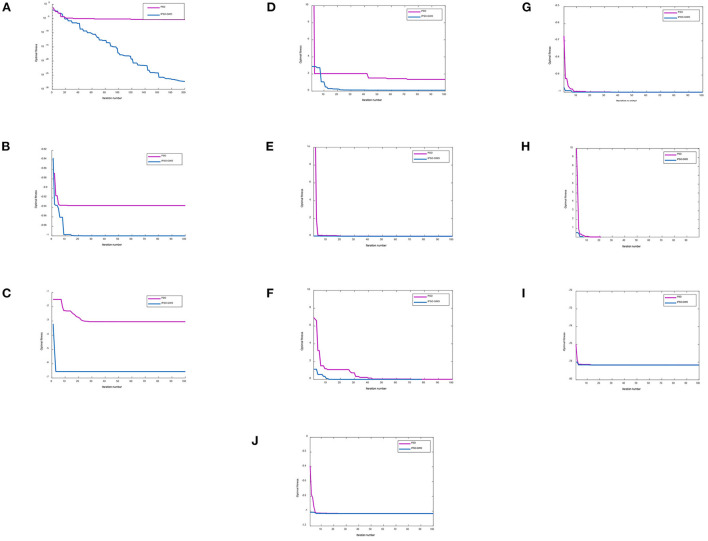
To verify the superiority of the IPSO-GWO algorithm, this paper uses MATLAB R2018b software to perform benchmark function tests on PSO and IPSO-GWO. The variables of the simulation experiments are set as follows: the population size is 50, the dimension of the optimization variable is 4, the learning factor c1 = c2 = 2.05, and the test functions of the simulation experiments are ten benchmark functions such as Drop Wave, Peaks, Rosenbrock, etc. For Rosenbrock function, the number of the iterations is 200, and the number of iterations of others is 100. Simulation experiments are performed on the above functions. The algorithm iteration curve is shown in Figure 3. The experimental results of the three test functions are analyzed and compared, as listed in Tables 1–10.
Figure 3.
Iteration comparison curves with different functions. (A) Iteration curve comparison diagram with Rosenbrock function. (B) Iteration curve comparison diagram with Drop Wave function. (C) Iteration curve comparison diagram with Peaks function. (D) Iteration curve comparison diagram with Bukin function. (E) Iteration curve comparison diagram with Booth function. (F) Iteration curve comparison diagram with Rastrigin function. (G) Iteration curve comparison diagram with Easom function. (H) Iteration curve comparison diagram with Levy function. (I) Iteration curve comparison diagram with Styblinski-Tang function. (J) Iteration curve comparison diagram with Six-Hump Camel function.
Table 1.
Rosenbrock function test results.
| Algorithm | Maximum | Minimum | Average value | Standard deviation | Global Minimum |
|---|---|---|---|---|---|
| PSO | 1.8143E−12 | 3.272E−16 | 1.70543E−13 | 4.4715E−13 | 0 |
| IPSO-GWO | 9.8215E−27 | 2.3419E−31 | 2.2383E−27 | 2.952E−27 | 0 |
Table 10.
Six-Hump Camel function test results.
| Algorithm | Maximum | Minimum | Average value | Standard deviation | Global minimum |
|---|---|---|---|---|---|
| PSO | −0.3852 | −1.0313 | −1.0185 | 0.0726 | −1.0316 |
| IPSO-GWO | −1.0141 | −1.0316 | −1.0307 | 0.0035 | −1.0316 |
Table 2.
Drop Wavefunction test results.
| Algorithm | Maximum | Minimum | Average value | Standard deviation | Global minimum |
|---|---|---|---|---|---|
| PSO | −0.93625 | −0.99997 | −0.99192 | 0.015633 | −1 |
| IPSO-GWO | −0.93625 | −1 | −0.99636 | 0.009047 | −1 |
Table 3.
Peaks function test results.
| Algorithm | Maximum | Minimum | Average value | Standard deviation | Global minimum |
|---|---|---|---|---|---|
| PSO | −3.0395 | −6.5511 | −4.62282 | 1.741408 | −6.5511 |
| IPSO-GWO | −3.0496 | −6.5511 | −5.50012 | 1.604133 | −6.5511 |
Table 4.
Bukin function test results.
| Algorithm | Maximum | Minimum | Average value | Standard deviation | Global minimum |
|---|---|---|---|---|---|
| PSO | 27.5233 | 1.3670 | 2.1584 | 3.3801 | 0 |
| IPSO-GWO | 2.8783 | 0.1078 | 0.3540 | 0.7018 | 0 |
Table 5.
Booth function test results.
| Algorithm | Maximum | Minimum | Average value | Standard deviation | Global minimum |
|---|---|---|---|---|---|
| PSO | 16.1673 | 0.0020 | 0.3429 | 2.1682 | 0 |
| IPSO-GWO | 0.0278 | 0.0001 | 0.0042 | 0.0076 | 0 |
Table 6.
Rastrigin function test results.
| Algorithm | Maximum | Minimum | Average value | Standard deviation | Global minimum |
|---|---|---|---|---|---|
| PSO | 6.9599 | 0.0073 | 0.5837 | 1.2599 | 0 |
| IPSO-GWO | 1.1406 | 0 | 0.0835 | 0.2501 | 0 |
Table 7.
Easom function test results.
| Algorithm | Maximum | Minimum | Average value | Standard deviation | Global minimum |
|---|---|---|---|---|---|
| PSO | −0.6713 | −0.9999 | −0.9934 | 0.0351 | −1 |
| IPSO-GWO | −0.9727 | −1 | −0.9992 | 0.0033 | −1 |
Table 8.
Levy function test results.
| Algorithm | Maximum | Minimum | Average value | Standard deviation | Global minimum |
|---|---|---|---|---|---|
| PSO | 10.9906 | 0.0016 | 0.2517 | 1.3966 | 0 |
| IPSO-GWO | 0.5333 | 0.0001 | 0.0191 | 0.0890 | 0 |
Table 9.
Styblinski-Tang function test results.
| Algorithm | Maximum | Minimum | Average value | Standard deviation | Global minimum |
|---|---|---|---|---|---|
| PSO | −76.0206 | −78.3296 | −78.2937 | 0.2377 | −78.3322 |
| IPSO-GWO | −77.9984 | −78.3322 | −78.3231 | 0.0468 | −78.3322 |
It can be seen from Figure 3 that, compared with the PSO and PSO-GWO algorithms, the IPSO-GWO algorithm converges the fastest. From Tables 1–10, it is seen that the results obtained from IPSO-GWO is closer to the global minimum, which verify that the performance of the IPSO-GWO algorithm is higher than those of the other algorithms.
Path Planning Experiments
To verify the superiority of the IPSO-GWO optimization in robot global path planning, we have carried out two kinds of path planning simulation tests: one is the test of IPSO with PSO, and the other is the test of IPSO with Genetic algorithm (GA) and Ant Colony Optimization (ACO). Both tests use 20 × 20 and 30 × 30 map environments. For IPSO-GWO and PSO, the population size is set to 50 and c1 = c2= 1.6. For GA, the crossover probability is set to 0.8, the mutation probability is set to 0.2, and the population size is set to 50. For ACO, the stimulating factor of the pheromone concentration α is set to 1, the stimulating factor of visibility β is set to 7, pheromone evaporation coefficient ρ is set to 0.3, pheromone intensity is set to 1, and the number of iterations of the four algorithms is set to 200. The experimental results are illustrated in Figures 4–7.
Figure 4.
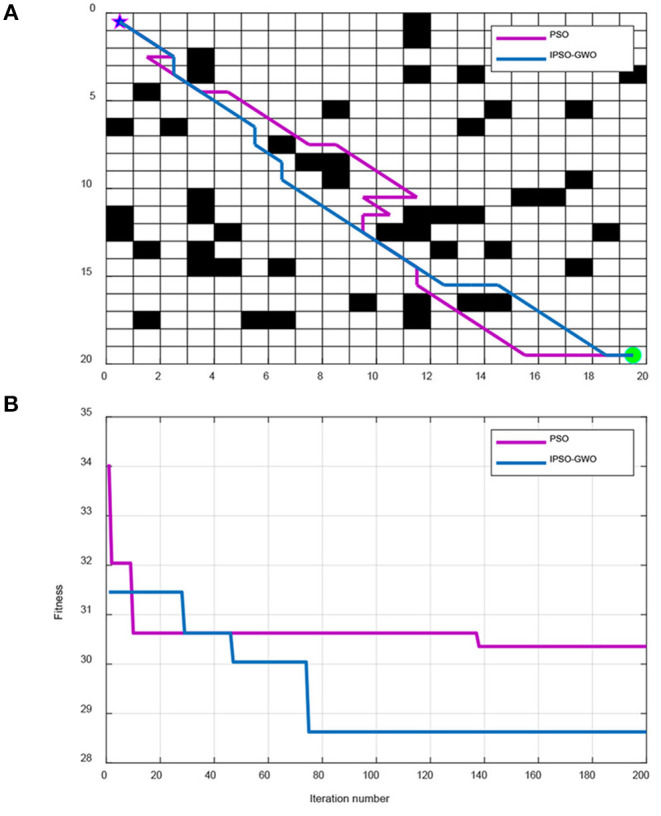
Simulation results of IPSO-GWO and PSO in 20 × 20 map environment. (A) Path comparison with PSO and IPSO-GWO algorithms. (B) Iterative curves with PSO and IPSO-GWO algorithms.
From Figure 4, IPSO-GWO and PSO simulate the path and iterative convergence curve of the path planning in a 20 × 20 map environment; it can be concluded that the PSO can obtain the optimal path at the 138th iteration with path length 30.36. Whereas the proposed IPSO-GWO can acquire the optimization at the 75th iteration with the obtained path length 28.63.
From Figure 5, IPSO and PSO simulate the path and iterative convergence curve of the path planning in a 30 × 30 map environment. The PSO algorithm searches for the optimal path at the 169th iteration, and the obtained path length is 45.36. The proposed IPSO-GWO can find the optimal path in the 86th iteration with acquired path length 42.77.
Figure 5.
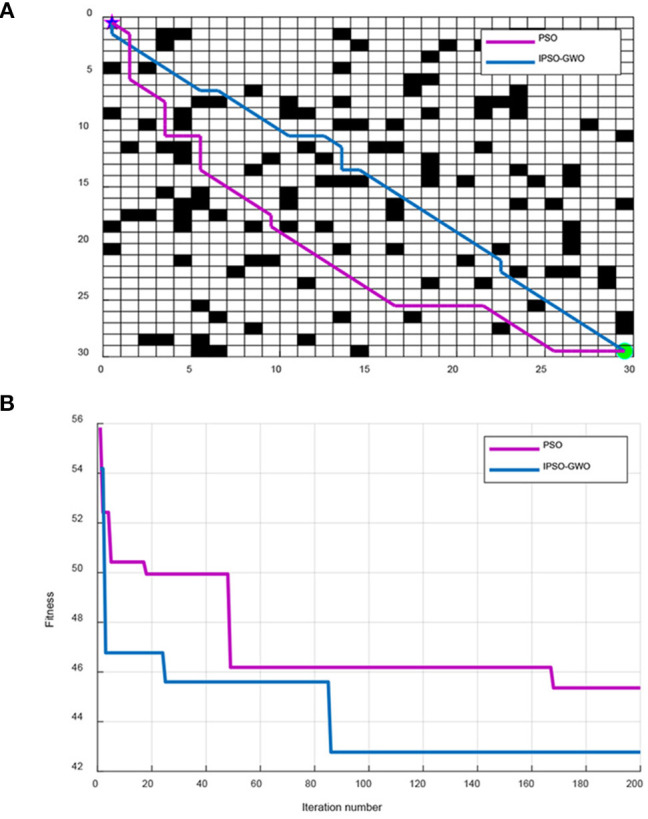
Simulation results of IPSO-GWO and PSO in 30 × 30 map environment. (A) Path comparison with PSO and IPSO-GWO algorithms. (B) Iterative curves with PSO and IPSO-GWO algorithms.
From Figure 6, IPSO, ACO, and GA are used to simulate the path and iterative convergence curve of the path planning in a 20 × 20 map environment. It can be seen that IPSO-GWO can acquire the optimal path length of 28.63 in the 11th iteration, the optimal path length found by ACO in the 62th iteration is 29.21, and the optimal path length found by GA in the 22nd iteration is 29.21. It can be concluded that the proposed IPSO-GWO algorithm converges faster in a 20 × 20 map environment with shortest path acquirement.
Figure 6.
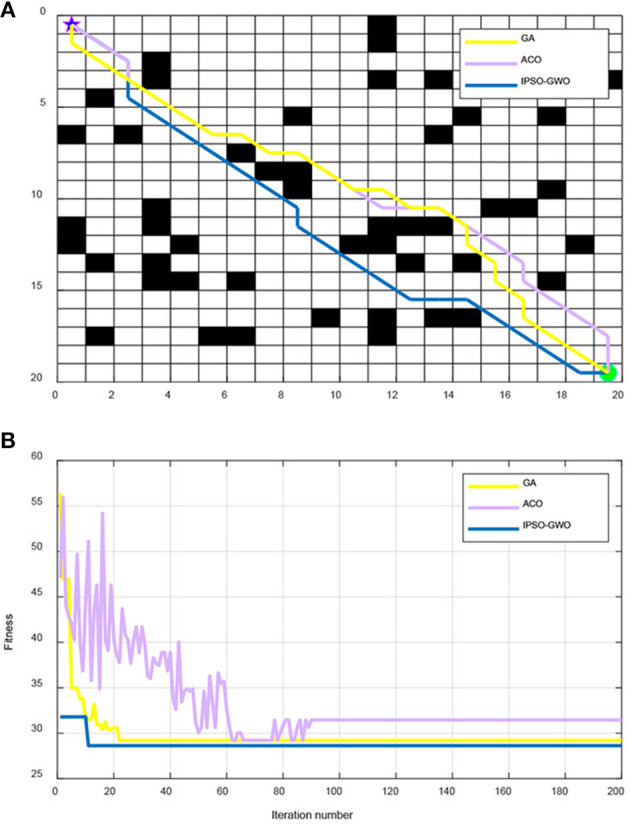
Simulation results of IPSO-GWO, GA, ACO in 20 × 20 map environment. (A) Path comparison with GA, ACO, and IPSO-GWO algorithms. (B) Iterative curve with GA, ACO, and IPSO-GWO algorithms.
From Figure 7, IPSO, ACO, and GA are used to simulate the path and iterative convergence curve of the path planning in a 30 × 30 map environment. It can be seen that IPSO-GWO can find the optimal path length of 42.77 in the 86th iteration, the optimal path length found by ACO in the 166th iteration is 42.77, and the optimal path length found by GA in the 33rd iteration is 45.11. It can also be concluded that although GA finds the optimal path faster, the path length is longer, whilst ACO finds the same optimal path as IPSO-GWO, but it is slower than IPSO-GWO. In summary, IPSO-GWO algorithm has the highest performance efficiency.
Figure 7.
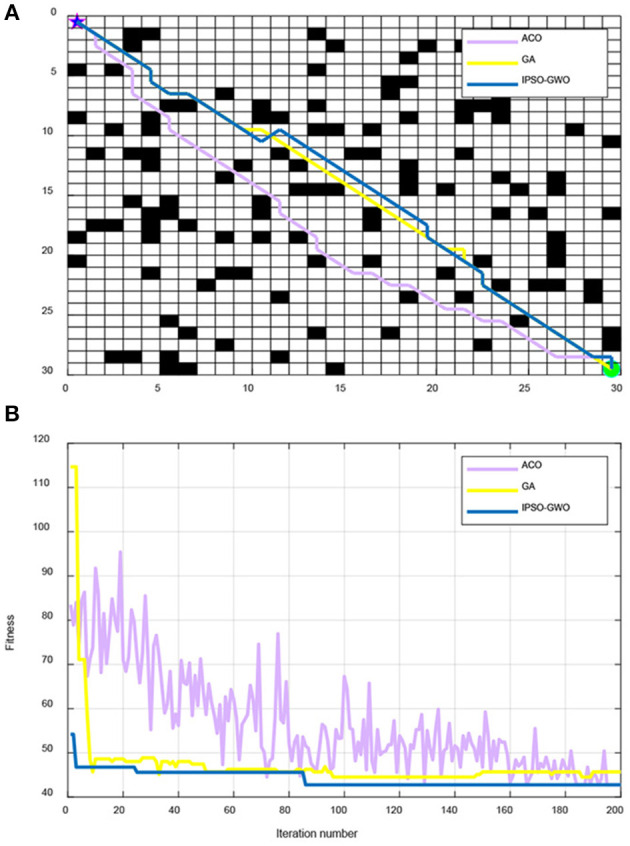
Simulation results of IPSO-GWO, GA, and ACO in 30 × 30 map environment. (A) Path comparison with ACO, GA, and IPSO-GWO algorithms. (B) Iterative curves with ACO, GA, and IPSO-GWO algorithms.
Conclusion
This paper makes a valuable contribution to the improvement of PSO algorithm in robot path planning in terms of convergence speed and shortest path acquirement. Combining the traditional PSO with the GWO, chaos, and a new adaptive inertia weight, it can address the problem of premature convergence and poor global search ability, and improve the convergence speed for faster path searching. The proposed IPSO-GWO algorithm has been tested against the traditional PSO for ten benchmark functions, and optimization results show that the IPSO-GWO converges faster without premature convergence. Comparing the IPSO-GWO with PSO and two other algorithms for path planning, the IPSO-GWO can find an optimal path with faster speed. In summary, the proposed IPSO-GWO algorithm exhibits higher performance in path planning with the combination of chaos for premature convergence avoidance. In the future, we will continue to apply the proposed IPSO-GWO algorithms in more practical applications.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
XC and JL: proposed the idea and designed the experiment in this study. CZ and JZ: performed the simulation experiments and analyzed the experiment results and wrote the manuscript. MZ: corrected the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the National Natural Science Foundation of China Program under Grant 62073198, by the Major Research Development Program of Shandong Province of China under Grant 2016GSF117009, and by the China Postdoctoral Science Foundation under Grant 2018M642680.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We acknowledge the support of the College of Electrical Engineering and Automation in Shandong University of Science and Technology and State Grid Dongying District of Dongying City Power Supply Company.
References
- Azmi M. Z., Ito T. (2020). Artificial potential field with discrete map transformation for feasible indoor path planning. Appl. Sci.-Basel. 10:8987. 10.3390/app10248987 [DOI] [Google Scholar]
- Das P. K., Jena P. K. (2020). Multi-robot path planning using improved particle swarm optimization algorithm through novel evolutionary operators. Appl. Soft Comput. 92:106312. 10.1016/j.asoc.2020.106312 [DOI] [Google Scholar]
- Demir F. B., Tuncer T., Kocamaz A. F. (2020). A chaotic optimization method based on logistic-sine map for numerical function optimization. Neural Comput. Appl. 32, 14227–14239. 10.1007/s00521-020-04815-9 [DOI] [Google Scholar]
- Gopal A., Sultani M. M., Bansal J. C. (2020). On stability analysis of particle swarm optimization algorithm. Arab. J. Sci. Eng. 45, 2385–2394. 10.1007/s13369-019-03991-8 [DOI] [Google Scholar]
- Gul F., Rahiman W., Alhady S. S. N., Ali A., Mir I., Jalil A. (2021). Meta-heuristic approach for solving multi-objective path planning for autonomous guided robot using PSO-GWO optimization algorithm with evolutionary programming. View Web Sci. Res. ORCID 12, 7873–7890. 10.1007/s12652-020-02514-w [DOI] [Google Scholar]
- Guo J., Li C. Y., Guo S. X. (2020). A novel step optimal path planning algorithm for the spherical mobile robot based on fuzzy control. IEEE Access 8, 1394–1405. 10.1109/ACCESS.2019.2962074 [DOI] [Google Scholar]
- Guo Z. L., Zhang W. S., Wang S. W. (2021). Improved gravitational search algorithm based on chaotic local search. Int. J. Bio-Inspired Comput. 17, 154–164. 10.1504/IJBIC.2021.114873 [DOI] [Google Scholar]
- Hao K., Zhao J. L., Yu K. C., Li C., Wang C. Q. (2020). Path planning of mobile robots based on a multi-population migration genetic algorithm. Sensors 20:5873. 10.3390/s20205873 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy J., Eberhart R. (1995). Particle swarm optimization, in Proceedings of ICNN'95 - International Conference on Neural Networks, Vol. 4, 1942–1948. 10.1109/ICNN.1995.488968 [DOI] [Google Scholar]
- Krell E., Sheta A., Balasubramanian A. P. R., King S. A. (2019). Collision-free autonomous robot navigation in unknown environments utilizing PSO for path planning. J. Artif. Intell. Soft Comput. Res. 9, 267–282. 10.2478/jaiscr-2019-0008 [DOI] [Google Scholar]
- Li G. S., Chou W. S. (2018). Path planning for mobile robot using self-adaptive learning particle swarm optimization. Sci. China-Inf. Sci. 61:052204. 10.1007/s11432-016-9115-2 [DOI] [Google Scholar]
- Li K. R., Hu Q. Q., Liu J. P. (2021). Path planning of mobile robot based on improved multiobjective genetic algorithm. Wireless Commun. Mobile Comput. 2021:8836615. 10.1155/2021/8836615 [DOI] [Google Scholar]
- Li L. Y., Wu D. F., Huang Y. Q., Yuan Z. M. (2021). A path planning strategy unified with a COLREGS collision avoidance function based on deep reinforcement learning and artificial potential field. Appl. Ocean Res. 113:102759. 10.1016/j.apor.2021.102759 [DOI] [Google Scholar]
- Li M., Chen H., Shi X., Liu S., Zhang M., Lu S. F. (2019a). A multi-information fusion “triple variables with iteration” inertia weight PSO algorithm and its application. Appl. Soft Comput. 84:105677. 10.1016/j.asoc.2019.105677 [DOI] [Google Scholar]
- Li M., Chen H., Wang X. D., Zhong N., Lu S. F. (2019b). An improved particle swarm optimization algorithm with adaptive inertia weights. Int. J. Inf. Technol. Decis. Mak. 3, 833–866. 10.1142/S0219622019500147 [DOI] [Google Scholar]
- Lian J. F., Yu W. T., Xiao K., Liu W. R. (2020). Cubic spline interpolation-based robot path planning using a chaotic adaptive particle swarm optimization algorithm. Math. Prob. Eng. 2020:1849240. 10.1155/2020/1849240 [DOI] [Google Scholar]
- Lin G. C., Zhu L. X., Li J. H. (2021). Collision-free path planning for a guava-harvesting robot based on recurrent deep reinforcement learning. Comput. Electron. Agric. 188:106350. 10.1016/j.compag.2021.106350 [DOI] [Google Scholar]
- Liu T. T., Song C. Y., Jiang J. Q. (2019). Robotic path planning based on improved ant colony algorithm. Lect. Notes Comput. Sci. 11554, 351–358. 10.1007/978-3-030-22796-8_3734198374 [DOI] [Google Scholar]
- Liu X. H., Zhang D. G., Zhang T., Jie Z., Zhang J. (2021). A new path plan method based on hybrid algorithm of reinforcement learning and particle swarm optimization. Eng. Comput. 10.1108/EC-09-2020-0500 [DOI] [Google Scholar]
- Liu Z. H., Liu H. B., Lu Z. G., Zeng Q. L. (2021). A dynamic fusion pathfinding algorithm using delaunay triangulation and improved a-star for mobile robots. IEEE Access 9, 20602–20621. 10.1109/ACCESS.2021.3055231 [DOI] [Google Scholar]
- Lu C., Gao L., Li X. Y., Hu C. Y., Yan X. S., Gong W. Y. (2020). Chaotic-based grey wolf optimizer for numerical and engineering optimization problems. Memetic Comput. 12, 371–398. 10.1007/s12293-020-00313-6 [DOI] [Google Scholar]
- Narinder S., Singh S. B. (2017). Hybrid algorithm of particle swarm optimization and grey wolf optimizer for improving convergence performance. J. Appl. Math. 2017, 1–15. 10.1155/2017/2030489 [DOI] [Google Scholar]
- Ouertani M. W., Manita G., Korbaa O. (2021). Chaotic lightning search algorithm. Soft Comput. 25, 2039–2055. 10.1007/s00500-020-05273-0 [DOI] [Google Scholar]
- Phung M. D., Ha Q. P. (2021). Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization. Appl. Soft Comput. 107:107376. 10.1016/j.asoc.2021.107376 [DOI] [Google Scholar]
- Shao S. K., Peng Y., He C. L., Du Y. (2020). Efficient path planning for UAV formation via comprehensively improved particle swarm optimization. ISA Trans. 97, 415–430. 10.1016/j.isatra.2019.08.018 [DOI] [PubMed] [Google Scholar]
- Song B. Y., Wang Z. D., Zou L. (2021). An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 100:106960. 10.1016/j.asoc.2020.106960 [DOI] [Google Scholar]
- Song J., Hao C., Su J. C. (2020). Path planning for unmanned surface vehicle based on predictive artificial potential field. Int. J. Adv. Robot. Syst. 17:1729881420918461. 10.1177/1729881420918461 [DOI] [Google Scholar]
- Sun X. J., Wang G. F., Fan Y. S., Mu D. D., Qiu B. B. (2021). A formation autonomous navigation system for unmanned surface vehicles with distributed control strategy. IEEE Trans. Intell. Transp. Syst. 22, 2834–2845. 10.1109/TITS.2020.2976567 [DOI] [Google Scholar]
- Tang B. W., Kui X., Pang M. Y., Zhu Z. X. (2020). Multi-robot path planning using an improved self-adaptive particle swarm optimization. Int. J. Adv. Robot. Syst. 17:1729881420936154. 10.1177/1729881420936154 [DOI] [Google Scholar]
- Tang G., Tang C. Q., Claramunt C., Hu X., Zhou P. P. (2021). Geometric A-star algorithm: an improved A-star algorithm for AGV path planning in a port environment. IEEE Access. 9, 59196–59210. 10.1109/ACCESS.2021.3070054 [DOI] [Google Scholar]
- Teng Z. J., Lv J. L., Guo L. W. (2019). An improved hybrid grey wolf optimization algorithm. Soft Comput. 23, 6617–6631. 10.1007/s00500-018-3310-y [DOI] [Google Scholar]
- Tullu A., Emdale B., Wondosen A., Hwang H. Y. (2021). Machine learning approach to real-time 3D path planning for autonomous navigation of unmanned aerial vehicle. Appl. Sci.-Basel. 11:4706. 10.3390/app11104706 [DOI] [Google Scholar]
- Wang D., Zhang J., Jin J. C., Liu D. Q., Mao X. P. (2021). Rapid global path planning algorithm for unmanned surface vehicles in large-scale and multi-island marine environments. PeerJ. Comput. Sci. 7:e612. 10.7717/peerj-cs.612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang P. W., Gao S., Li L., Sun B. B., Cheng S. (2019). Obstacle avoidance path planning design for autonomous driving vehicles based on an improved artificial potential field algorithm. Energies. 12:2342. 10.3390/en12122342 [DOI] [Google Scholar]
- Wang S. B. (2021). Asymptotic tracking control for nonaffine systems with disturbances. IEEE Trans. Circuits Syst. II: Exp. Briefs. 99, 1–1. 10.1109/TCSII.2021.3080524 [DOI] [Google Scholar]
- Wang S. B., Na J., Chen Q. (2020). Adaptive predefined performance sliding mode control of motor driving systems with disturbances. IEEE Trans. Energy Conv. 99, 1–1. 10.1109/TEC.2020.3038010 [DOI] [Google Scholar]
- Wang Y. B., Bai P., Liang X. L., Wang W. J., Zhang J. Q., Fu Q. X. (2019). Reconnaissance mission conducted by UAV swarms based on distributed PSO path planning algorithms. IEEE Access 7, 105086–105099. 10.1109/ACCESS.2019.2932008 [DOI] [Google Scholar]
- Wen T., Yang D. C., Liu W. F., Wen C. L., Cai B. G. (2021). A novel integrated path planning algorithm for warehouse AGVs. Chin. J. Electron. 30, 331–338. 10.1049/cje.2021.02.002 [DOI] [Google Scholar]
- Wu Y., Liu J. F., Li D. F. (2020). Chaotic dynamically dimensioned search algorithm. IEEE Access 8, 152474–152499. 10.1109/ACCESS.2020.3017210 [DOI] [Google Scholar]
- Xie R. L., Meng Z. J., Wang L. F., Li H. C., Wang K. P., Wu Z. (2021). Unmanned aerial vehicle path planning algorithm based on deep reinforcement learning in large-scale and dynamic environments. IEEE Access 9, 24884–24900. 10.1109/ACCESS.2021.3057485 [DOI] [Google Scholar]
- Xiong X. Y., Min H. T., Yu Y. B., Wang P. Y. (2020). Application improvement of A* algorithm in intelligent vehicle trajectory planning. Math. Biosci. Eng. 18, 1–21. 10.3934/mbe.2021001 [DOI] [PubMed] [Google Scholar]
- Xu J., Song K. C., Zhang D. F., Dong H. W., Yan Y. H., Meng Q. G. (2021). Informed anytime fast marching tree for asymptotically optimal motion planning. IEEE Trans. Indus. Electron. 68, 5068–5077. 10.1109/TIE.2020.2992978 [DOI] [Google Scholar]
- Yao Q. F., Zheng Z. Y., Qi L., Yuan H. T., Guo X. W., Zhao M., et al. (2020). Path planning method with improved artificial potential field-a reinforcement learning perspective. IEEE Access 8, 135513–135523. 10.1109/ACCESS.2020.3011211 [DOI] [Google Scholar]
- Ye X., Luo L., Hou L., Duan Y., Wu Y. (2020). Laser ablation manipulator coverage path planning method based on an improved ant colony algorithm. Appl. Sci.-Basel 10:8641. 10.3390/app10238641 [DOI] [Google Scholar]
- Zhang D. H., You X. M., Liu S., Pan H. (2020). Dynamic multi-role adaptive collaborative ant colony optimization for robot path planning. IEEE Access 8, 129958–129974. 10.1109/ACCESS.2020.3009399 [DOI] [Google Scholar]
- Zhang J., Sheng J. N., Lu J. W., Shen L. (2021). UCPSO: a uniform initialized particle swarm optimization algorithm with cosine inertia weight. Comput. Intell. Neurosci. 2021:8819333. 10.1155/2021/8819333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhi Y. H., Jiang Y. (2020). Design of basketball robot based on behavior-based fuzzy control. Int. J. Adv. Robot. Syst. 17:1729881420909965. 10.1177/1729881420909965 [DOI] [Google Scholar]
- Zhu S. N., Zhu W. Y., Zhang X. Q., Cao T. (2020). Path planning of lunar robot based on dynamic adaptive ant colony algorithm and obstacle avoidance. Int. J. Adv. Robot. Syst. 17:1729881419898979. 10.1177/1729881419898979 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.