Abstract
SARS-CoV-2 variants of concern exhibit varying degrees of transmissibility and, in some cases, escape from acquired immunity. Much effort has been devoted to measuring these phenotypes, but understanding their impact on the course of the pandemic—especially that of immune escape—has remained a challenge. Here, we use a mathematical model to simulate the dynamics of wild-type and variant strains of SARS-CoV-2 in the context of vaccine rollout and nonpharmaceutical interventions. We show that variants with enhanced transmissibility frequently increase epidemic severity, whereas those with partial immune escape either fail to spread widely or primarily cause reinfections and breakthrough infections. However, when these phenotypes are combined, a variant can continue spreading even as immunity builds up in the population, limiting the impact of vaccination and exacerbating the epidemic. These findings help explain the trajectories of past and present SARS-CoV-2 variants and may inform variant assessment and response in the future.
Keywords: SARS-CoV-2, COVID-19, variant of concern, VOC, transmissibility, immune escape, vaccination, nonpharmaceutical interventions, NPI, mathematical model
Graphical abstract
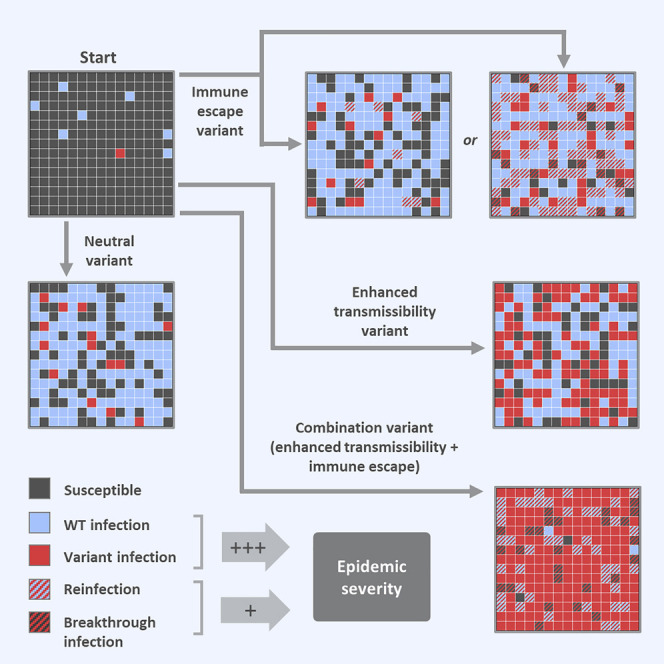
A modeling approach looking at the impact of SARS-CoV-2 variants with partial immune escape and/or increased transmissibility suggests that enhanced transmissibility is more strongly linked to epidemic severity and narrows the margin for control.
Introduction
The second year of the COVID-19 pandemic has been dominated by variants of concern (VOCs)—SARS-CoV-2 lineages that have driven resurgent waves of the disease, often more severe than earlier waves. As of November 11, 2021, the World Health Organization recognizes four VOCs: Alpha (lineage B.1.1.7), which was first identified in the United Kingdom; Beta (B.1.351), first reported in South Africa; Gamma (P.1), believed to have originated in Brazil; and Delta (B.1.617.2 and AY.x sub-lineages), first detected in India. Initially reported in late 2020 or early 2021, these four variants have now reached every continent except Antarctica (World Health Organization, 2021).
The spread of these variants has been attributed to some combination of enhanced transmissibility and partial immune escape. Alpha is estimated to be 43%–100% more transmissible than wild type (WT) (Davies et al., 2021; Volz et al., 2021) but is similarly neutralized by convalescent sera (Planas et al., 2021a; Supasa et al., 2021; Wang et al., 2021b) and is not associated with an increased risk of reinfection (Graham et al., 2021). There is some uncertainty regarding the transmissibility and immune escape of Beta because estimates of these quantities are inversely correlated. If immune escape is minimal, Beta may be up to 50% more transmissible than WT (Tegally et al., 2021). However, there is considerable evidence suggesting a moderate degree of immune escape, with significantly reduced neutralization by convalescent sera (Cele et al., 2021; Planas et al., 2021a; Wang et al., 2021b; Wibmer et al., 2021; Zhou et al., 2021); multiple studies have also reported that 40%–50% of convalescent serum samples exhibit no neutralizing activity against Beta virus or pseudovirus (Planas et al., 2021a; Wibmer et al., 2021; Zhou et al., 2021). However, T cell responses may remain largely intact even when antibody responses are compromised (Geers et al., 2021; Tarke et al., 2021). Gamma is believed to be 70%–140% more transmissible than WT (Faria et al., 2021) and perhaps has some degree of immune escape, with a modest reduction in neutralization by convalescent sera (Wang et al., 2021a). Gamma may reduce protection against reinfection by 21%–46%, although, as with Beta, estimates of transmissibility and immune escape are correlated (Faria et al., 2021). Finally, multiple analyses suggest that Delta is at least 60% more transmissible than Alpha (Allen et al., 2021; Dagpunar, 2021), and preliminary results suggest moderately reduced neutralization by convalescent serum (Hoffmann et al., 2021; Planas et al., 2021b).
The appearance of these variants has taken place against a backdrop of accelerated vaccine development and rollout. Numerous candidate COVID-19 vaccines entered phase III trials in the latter half of 2020, and many began distribution in late 2020 or early 2021. As of November 7, 2021, over 7 billion vaccine doses have been administered, but coverage remains highly variable: over 70% of people in high- and upper-middle-income countries have received at least one dose versus 40% of people in lower-middle-income countries and 4% of those in low-income countries (Mathieu et al., 2021). In the first several months after vaccination, most authorized vaccines demonstrate at least 70% efficacy against symptomatic COVID-19, and a few approach or exceed 90% efficacy (Abu-Raddad et al., 2021; Baden et al., 2021; Haas et al., 2021; Polack et al., 2020; Sadoff et al., 2021; Voysey et al., 2021). Instances of severe disease are relatively rare in vaccinated individuals, and deaths exceedingly rare, so estimates of efficacy against severe outcomes tend to be imprecise, but true efficacy against severe disease and death is likely very high for most vaccines.
Along with evidence for partial escape from naturally acquired immunity, there is mounting evidence that vaccines may offer reduced protection against some variants. There is little evidence to suggest that Alpha evades vaccine-induced immunity; neutralization by post-vaccination sera is similar to WT (Collier et al., 2021; Geers et al., 2021; Muik et al., 2021; Planas et al., 2021a; Supasa et al., 2021; Wang et al., 2021b), and minimal differences in vaccine effectiveness have been observed (Dagan et al., 2021; Emary et al., 2021; Haas et al., 2021; Kustin et al., 2021). However, studies report markedly reduced neutralization of Beta by post-vaccination sera (Becker et al., 2021; Garcia-Beltran et al., 2021; Geers et al., 2021; Lustig et al., 2021; Planas et al., 2021a; Zhou et al., 2021), and some observational studies suggest moderately lower vaccine effectiveness (Abu-Raddad et al., 2021; Kustin et al., 2021; Madhi et al., 2021), although others show no reduction (Mor et al., 2021). There is evidence suggesting slightly reduced neutralization of both Gamma and Delta by post-vaccination sera (Dejnirattisai et al., 2021; Hoffmann et al., 2021; Liu et al., 2021; Lustig et al., 2021; Planas et al., 2021b; Wang et al., 2021a); in the case of Delta, vaccine effectiveness may be reduced as well (Lopez Bernal et al., 2021).
For individuals, the implications of variants with partial vaccine escape are straightforward: protection decreases linearly with the product of the reduction in efficacy and the variant’s frequency in the population. Estimating the risk to an entire population is more complex. Due to the nonlinearity of epidemiological dynamics, population outcomes do not simply mirror those of individuals; for instance, a 30% reduction in vaccine efficacy does not translate to 30% fewer infections prevented or 30% more infections in vaccinated individuals. The same goes for transmissibility: a 50% increase in the average number of secondary infections from each case does not necessarily produce a proportional increase in the total number of infections.
The difficulty in predicting population-level outcomes from variant phenotypes has limited our ability to distinguish between variants of greater and lesser impact. “Variant of concern” is an umbrella designation that indicates the possibility of adverse consequences but not the probability or magnitude of those consequences. This may be a reflection of how challenging it is to quantify phenotypes like transmissibility, immune escape, and disease severity. Even with precise estimates, however, the leap from phenotype to population impact can be complex.
The situation would be more straightforward if variants existed in a vacuum, but they are part of a complex dynamical system. Variants may have selective advantages, but they are numerically disadvantaged by their late arrival, and the extent to which a variant overcomes this disadvantage depends on the timing of its emergence as well as its phenotype. Vaccination complicates the picture further: not only can it alter the balance between WT and variant, but it does so gradually, as vaccine rollout typically takes months. As a result, two variants with identical phenotypes could meet different fates simply by emerging under different circumstances.
The fact that population-level outcomes cannot be easily predicted from variant phenotypes does not mean that phenotypes are uninformative with respect to impact. Modeling can be used to examine outcomes across a range of scenarios, and examining the set of possible outcomes can inform our understanding of a variant’s potential impact. Here, we use a mathematical model to simulate the emergence and spread of different variants during the epidemic phase in populations that are controlling transmission through nonpharmaceutical interventions (NPIs) and vaccination. We focus on three hypothetical variants, which have enhanced transmissibility, partial immune escape, and both, respectively. We compare these variants in key outcomes, including the total number of infections and the number/percentage of infections averted by vaccination, to assess the population-level impact of different variant phenotypes. Since the relative impact of different variants may depend on the circumstances, we also consider how population outcomes are affected by the timing of vaccine rollout, vaccine efficacy, vaccination coverage, and discontinuation of NPIs. Finally, we present several secondary analyses that explore how our findings are affected by changing key model parameters and assumptions.
Results
A full description of the model can be found in the STAR Methods, but we include a short overview here to give context for the results. The following describes the default model conditions and assumptions, but analyses varying many of these assumptions are included in the results.
The model is an extended susceptible-infected-recovered (SIR) compartment model, which includes two strains—wild type (WT) and variant—as well as vaccination. The WT is assumed to have a basic reproduction number of 2.5, which is reduced to 1.5 by NPIs that remain in place throughout the simulation. Both the variant and the vaccine are introduced at specified times midway through the epidemic, and the vaccine is distributed at a constant rate until 100% coverage is reached. The vaccine is assumed to be 95% effective against WT, with efficacy against the variant proportional to cross-reactivity between the strains. Infection is assumed to confer sterilizing immunity against the infecting strain; protection against the other strain is proportional to the degree of cross-reactivity, which is assumed to be symmetrical. The model is run for a simulated duration of three years, except where noted otherwise, and we assume no waning of immunity over this period (a key reason why the results of this model should not be extrapolated beyond the epidemic phase). All simulations assume a population size of 100 million individuals.
The purpose of the model is to examine the impact of two key phenotypes—transmissibility and immune escape—on the population dynamics of emerging variants and the course of SARS-CoV-2 epidemics. In order to disentangle the effects of these traits and to explore their interactions, we consider three hypothetical variants: variant 1, with 60% increased transmissibility relative to WT; variant 2, with 40% immune escape (60% cross-protection); and variant 3, with both of these phenotypes. We also model a neutral variant, designated variant 0, which is effectively identical to WT and serves as a baseline for comparison with other variants. These variant phenotypes (or alternative phenotypes where applicable) are also listed for reference at the end of all figure legends.
Some existing variants probably have greater transmissibility and/or lower immune escape than reflected in these parameter values. Since our findings suggest transmissibility has a larger impact than immune escape, we deliberately use a low estimate of transmissibility and a high estimate of immune escape to avoid reinforcing this result. Although 40% immune escape lies at the upper end of the range of estimates for existing variants, higher degrees of escape are theoretically possible, if perhaps difficult to evolve (Kennedy and Read, 2017). Secondary analyses considering variants with higher and lower degrees of immune escape are included in the results.
Model behavior is analyzed in terms of the number of infections, which, when summed over the course of a simulation, we denote by epidemic size. We emphasize the number of infections, rather than the cases or individuals infected; the former denotes only those infections that are detected, while the latter ignores the fact that individuals may be infected more than once. We assume that epidemic size is roughly proportional to key outcomes such as total hospitalizations and total deaths and therefore use this outcome as a principal metric for comparison, although in some cases we distinguish between infections in susceptible and recovered/vaccinated individuals, as the latter are less likely to suffer severe disease and death. We also measure the population impact of vaccination by calculating the difference in epidemic size between simulations with and without vaccination.
Ability to increase to high frequency is driven primarily by transmissibility, not immune escape
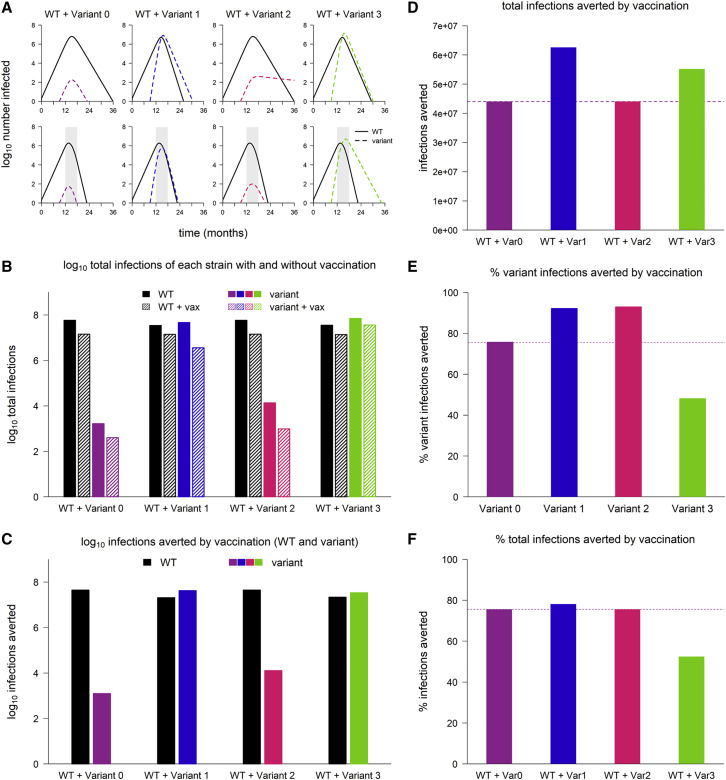
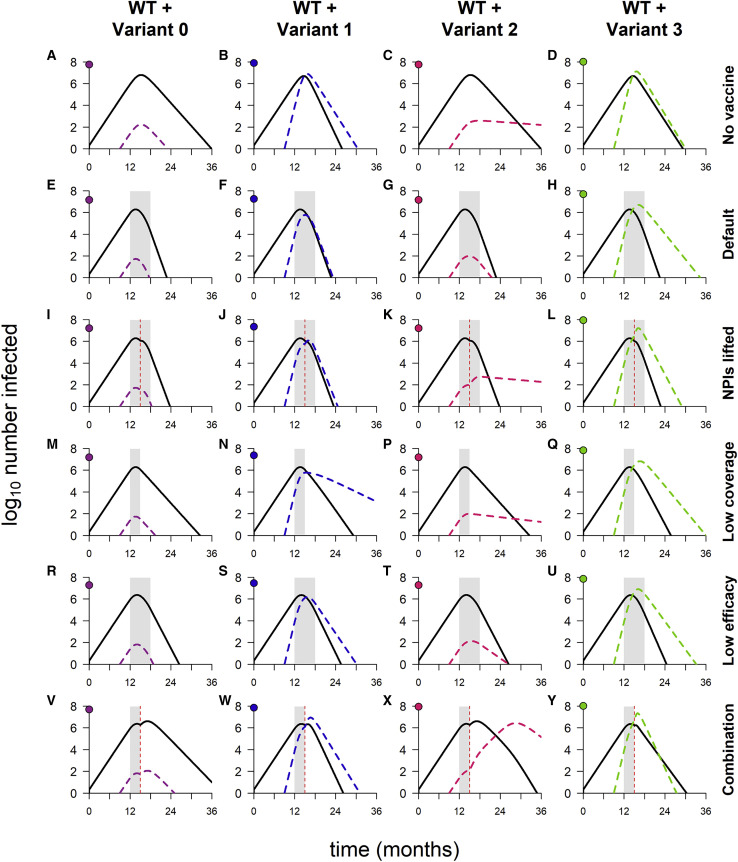
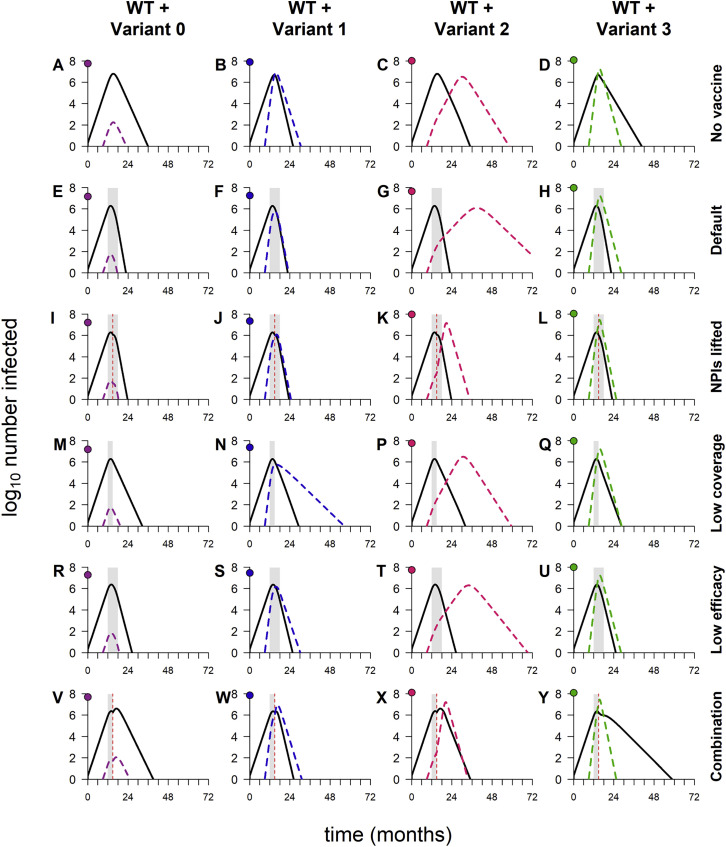
We start by examining the dynamics that result when variants are introduced into WT epidemics in the absence of vaccination. As expected, variant 0 (the neutral variant) behaves identically to WT: its growth and decline occur at the same times and at the same rates, only in smaller numbers (Figure 1 A). In contrast, variants 1 and 3, which both have enhanced transmissibility, spread faster than WT and quickly rise to high frequency. Variant 2, with partial immune escape, does not, and it infects far fewer people than WT over the course of the simulation (Figure 1B). When vaccination is added, variant 1 is rapidly controlled, as is variant 2, despite being partially refractory to the vaccine (Figure 1A). Although vaccination “flattens the curve” of variant 3 by reducing its transmission rate, it is unable to completely control this variant, which has a combination of enhanced transmissibility and immune escape.
Figure 1.
Sample dynamics of hypothetical variants
(A) Dynamics of WT and variant strains without vaccination (top row) and with vaccination (bottom row), shown on log scale. Solid/black lines, WT; dashed/colored lines, variants; gray shading, vaccine rollout. Subsequent panels reference the simulations in (A).
(B) Total infections with WT and variants with and without vaccination (log scale). Black bars, WT; colored bars, variants; solid bars, without vaccination; hatched bars, with vaccination.
(C) WT and variant infections averted by vaccination (log scale). Black bars, WT; colored bars, variants.
(D) Total infections (WT + variant) averted by vaccination (linear scale). Dashed line, total infections averted in simulation with variant 0.
(E) Percentage of variant infections averted by vaccination (linear scale). Dashed line, percentage averted in simulation with variant 0.
(F) Percentage of all infections averted by vaccination (linear scale). Dashed line, percentage averted in simulation with variant 0. In all simulations, the variant is introduced at 9 months; in simulations with vaccination, vaccine rollout starts at 12 months and is spread over 6 months. Variant phenotypes are as follows: variant 0, identical to WT; variant 1, 60% greater transmissibility; variant 2, 40% immune escape; variant 3, 60% greater transmissibility and 40% immune escape.
Variants do not necessarily undermine the population-level impact of vaccination
Calculating the number of infections averted by vaccination in the simulations from Figure 1A, we find that, surprisingly, variants do not necessarily reduce the population-level impact of vaccination. Compared to simulations with the neutral variant, vaccination averts as many or more variant infections, as well as more infections overall, in simulations with all three of the other variants (Figures 1C and 1D). For variants 1 and 2, vaccination also averts a higher percentage of variant infections (Figure 1E) and an equal or greater percentage of total infections (Figure 1F) compared to the neutral variant; however, this is not the case for variant 3. Thus, although immune escape reduces vaccine efficacy for an individual, it does not always follow that an emerging variant with partial immune escape will diminish the population impact of vaccination.
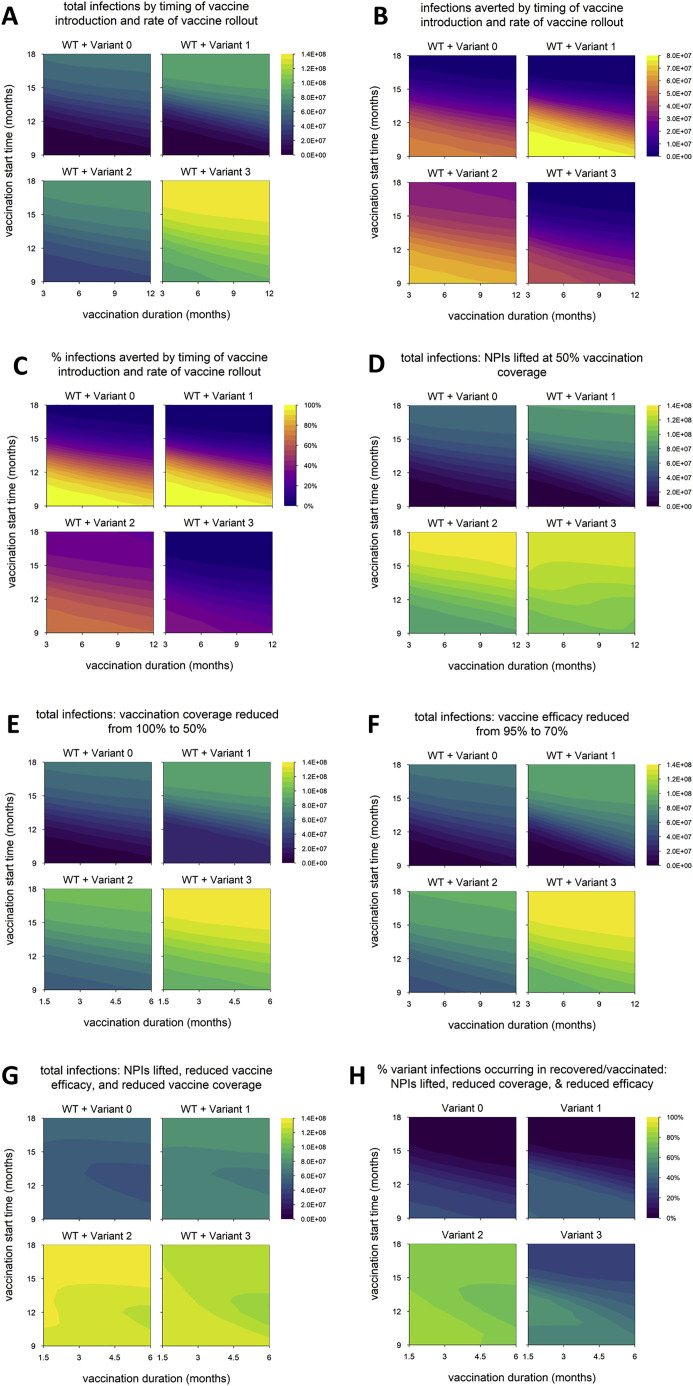
Epidemic size is affected more by transmissibility than by partial immune escape
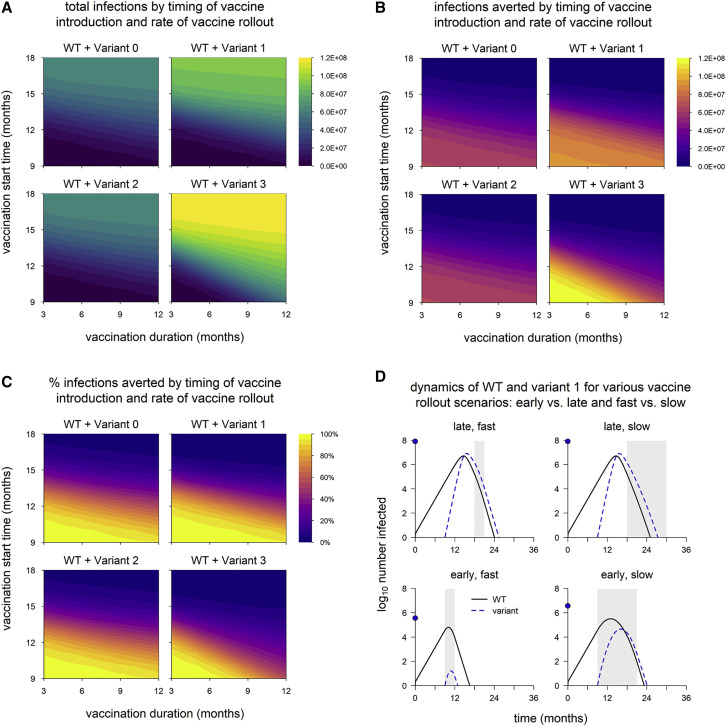
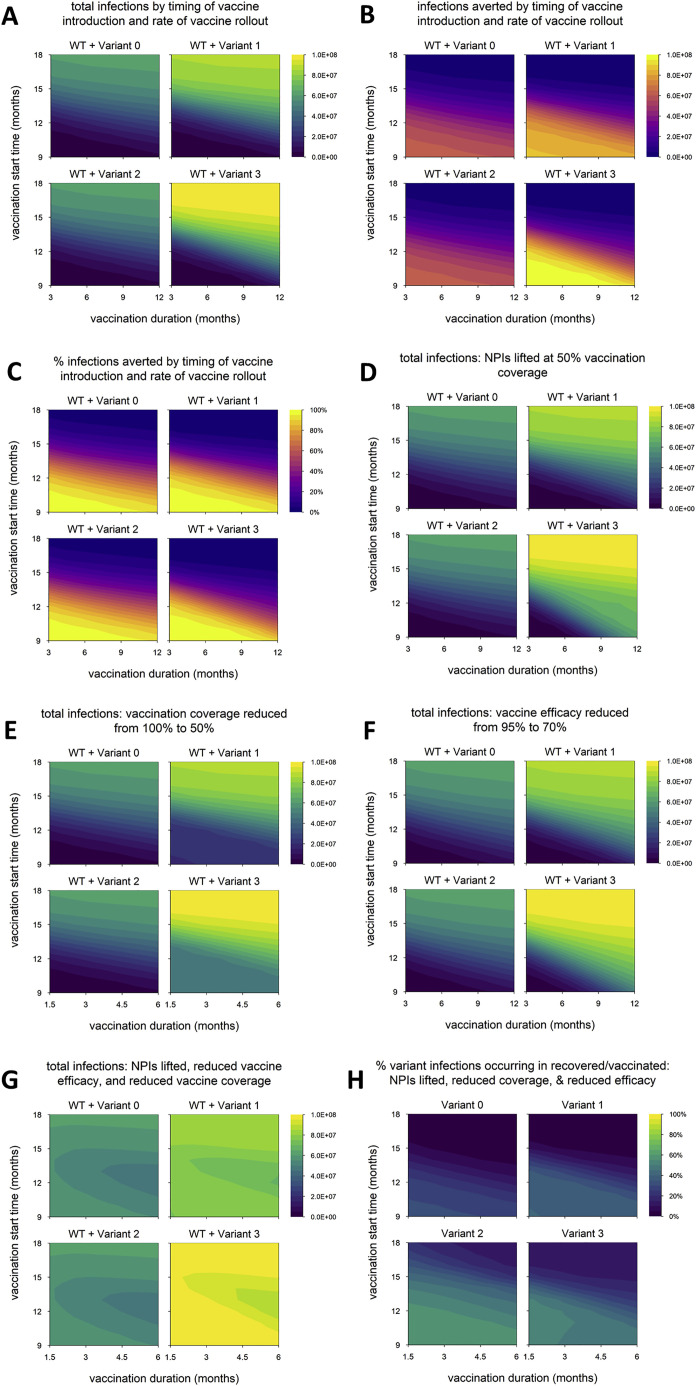
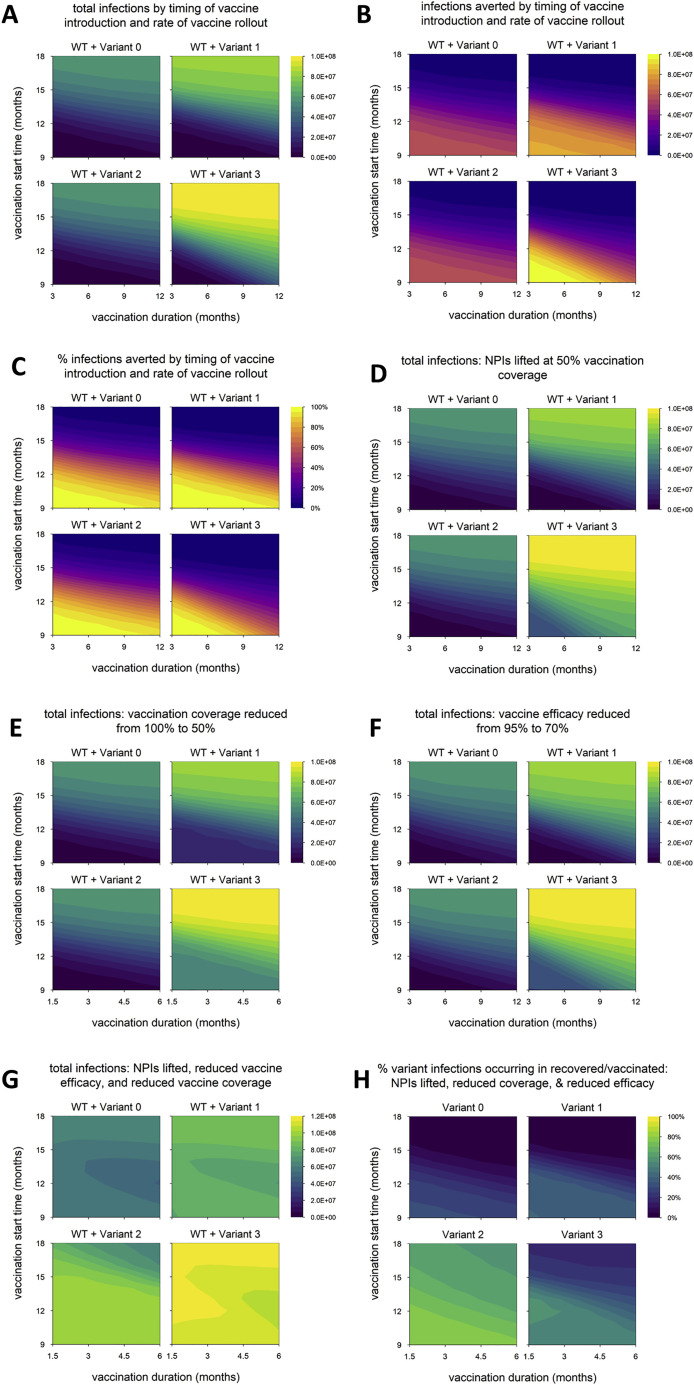
We next vary the timing of vaccine rollout—changing both the time at which vaccination begins and the rate at which the rollout proceeds—to examine how variants with different phenotypes behave across a range of vaccination scenarios. We find that the total number of infections is nearly identical between variant 0 (the neutral variant) and variant 2, which has partial immune escape (Figure 2 A); the number and percentage of infections averted by vaccination are likewise similar (Figures 2B and 2C). (Later, we show that these outcomes can change if control measures are significantly reduced, if both WT and variant are highly transmissible, or if the degree of immune escape is very high.) In contrast, variants 1 and 3, which both have enhanced transmissibility, can significantly increase epidemic size; the potential increase is particularly great for variant 3, which also has partial immune escape (Figure 2A). As noted above, the number of infections averted by vaccination is sometimes greater for variants 1 and 3 than for the neutral variant (Figure 2B). This occurs because these variants generate substantially more infections in the absence of vaccination; if a large enough fraction of these are prevented by vaccination, then more infections are averted in total. However, the percentage of total infections averted by vaccination is not much higher than with the neutral variant in any of the scenarios examined and is sometimes markedly lower, especially for variant 3 (Figure 2C).
Figure 2.
Epidemic size and vaccination impact vary with the time of vaccine introduction and pace of vaccine rollout
(A) Total infections (WT + variant) in simulations with each hypothetical variant, for varying rates of vaccination (duration, x axis) and time of vaccine introduction (start time, y axis); shaded contours represent total infections.
(B) Number of infections averted by vaccination.
(C) Percentage of infections averted by vaccination. Variant introduced at 9 months in all simulations.
(D) Dynamics of WT and variant 1 in simulations with the minimum and maximum values for vaccination duration (fast = 3 months; slow = 12 months) and start time (early = 9 months; late = 18 months). In each panel, the point on the y axis indicates the total number of infections over the entire simulation. Solid/black line, WT; blue/dashed line, variant; gray shading, vaccine rollout. Variant phenotypes are as follows: variant 0, identical to WT; variant 1, 60% greater transmissibility; variant 2, 40% immune escape; variant 3, 60% greater transmissibility and 40% immune escape.
Population-level outcomes are more sensitive to vaccination start time than the duration of vaccine rollout
Naturally, epidemic size increases when the start of vaccination is delayed or the pace of vaccine rollout slows (Figure 2A), and the reverse is true of vaccination impact: as vaccine rollout is delayed or slowed, the number and proportion of infections averted decrease (Figures 2B and 2C). These outcomes appear to be more sensitive to vaccination start time than the pace of vaccine distribution; a 1-month delay in starting vaccination impacts outcomes more than a 1-month increase in the duration of vaccine rollout. The sensitivity to vaccination start time is particularly pronounced for variants 1 and 3, which have increased transmissibility. Higher transmissibility increases the rate at which cases grow, which means the epidemic peaks earlier. A delay in starting vaccination can result in the peak of the epidemic being missed entirely, even if the pace of vaccine distribution is high (Figure 2D). However, if vaccination begins early, the effect on the final size of the epidemic can be considerable because it starts to take effect when the epidemic is still small, even if the rollout is slow.
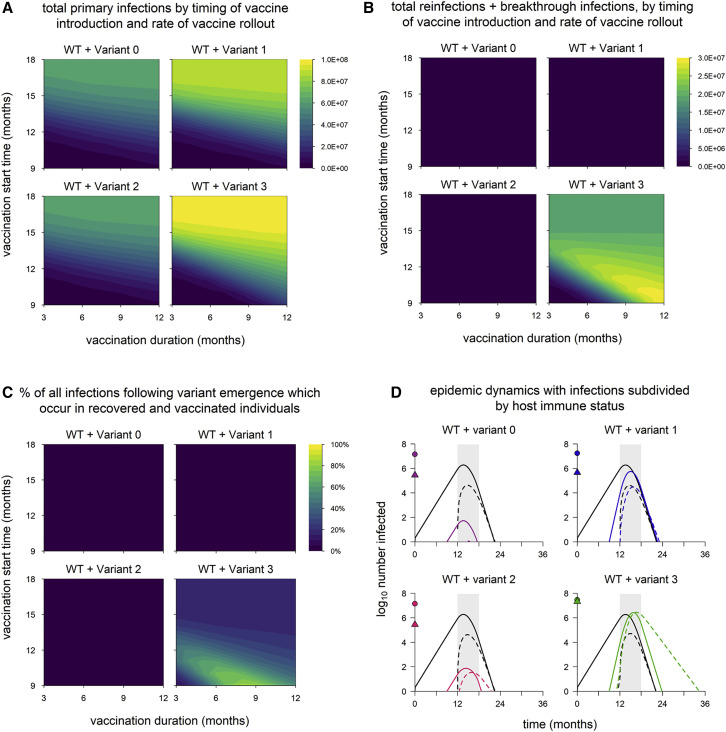
Reinfections and breakthrough infections remain rare with moderate immune escape unless aided by transmissibility
In any scenario involving variants, especially variants with immune escape, it is important to consider how many infections occur in people with immunity from prior infection or vaccination as a means of distinguishing between the potential to infect people with acquired immunity and the actual occurrence of such infections. In addition, infections in those with immunity are likely to be less severe than infections in susceptible (immunologically naive) individuals, so distinguishing between infections in susceptible and recovered/vaccinated hosts may better reflect epidemic severity. We therefore separated infections into those occurring in recovered/vaccinated individuals and those in individuals with no history of infection or vaccination (primary infections). Total numbers of primary infections exhibit the same patterns as overall epidemic size (Figures 2A and 3A), but infections in recovered and vaccinated individuals exhibit different behavior.
Figure 3.
Breakdown of infections by immune status (primary infections versus reinfections/breakthrough infections)
(A) Total primary infections.
(B) Total infections in recovered and vaccinated individuals (reinfections and breakthrough infections).
(C) Percentage of all infections occurring in recovered/vaccinated individuals (reinfections/breakthrough infections), starting from the time of variant emergence. Variant introduced at 9 months in all simulations.
(D) Dynamics of WT and variants, stratified by host immune status (susceptible versus recovered/vaccinated). The points on the y axis indicate the total number of primary infections (circles) and reinfections/breakthrough infections (triangles). Black lines, WT; colored lines, variants; solid lines, primary infections; dashed lines, infections in recovered/vaccinated individuals; gray shading, vaccine rollout (starting at 12 months and lasting 6 months). Variant phenotypes are as follows: variant 0, identical to WT; variant 1, 60% greater transmissibility; variant 2, 40% immune escape; variant 3, 60% greater transmissibility and 40% immune escape.
Reinfections and breakthrough infections (which we define as active, transmissible infections in previously infected and vaccinated individuals, respectively) are negligible in simulations with variants 1 and 2 (Figures 3B and 3C). Reinfections and breakthrough infections do occur with these variants (Figure 3D) but in small numbers, comprising less than 4% of all infections (WT + variant). This suggests that neither enhanced transmissibility nor a moderate degree of immune escape necessarily leads to significant numbers of reinfections/breakthrough infections. (Later, we show that immune escape variants do have the potential to produce widespread reinfections and breakthrough infections under some circumstances.) However, a combination of partial immune escape and increased transmissibility produces significant numbers of reinfections and breakthrough infections, accounting for up to 80% of all infections (WT + variant) following emergence (Figure 3C).
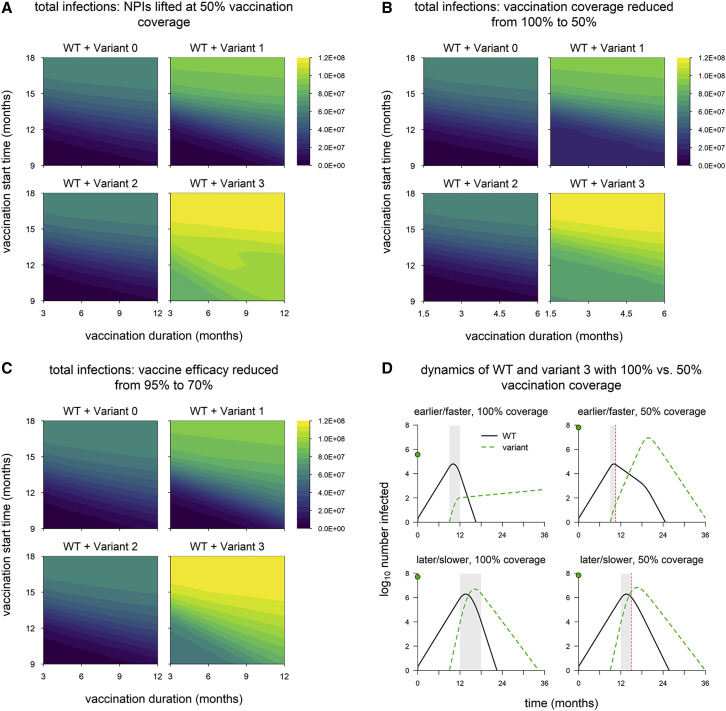
When control measures are weakened, the impact of variants with enhanced transmissibility plus partial immune escape is even greater
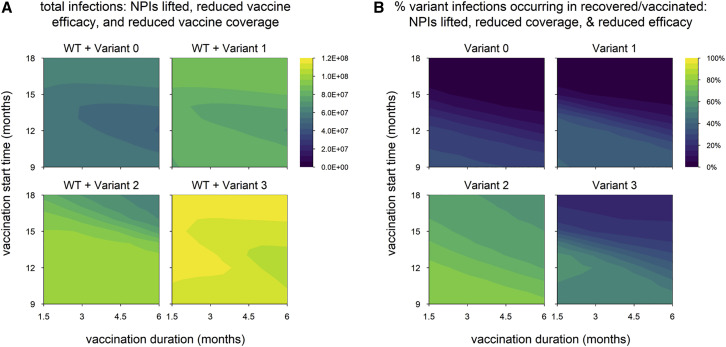
In the default model, aside from vaccine rollout, we assume optimal control measures: vaccination coverage reaches 100%, vaccine efficacy against WT is 95%, and NPIs are maintained indefinitely. We now explore how the impacts of different variants are affected by weakening control measures in various ways. We again run simulations in which we vary the timing of vaccine rollout and consider three changes to control measures: lifting NPIs once vaccination coverage reaches 50% (Figure 4 A), reducing the final vaccination coverage to 50% (Figure 4B), and reducing the vaccine efficacy versus WT to 70% (Figure 4C). (In the following section, we discuss a fourth scenario in which these three changes are implemented simultaneously.) In all three scenarios, we find that variant 2 still has a negligible impact on epidemic size, while epidemic size is markedly increased for variant 1 and especially variant 3. However, the difference between these two variants is larger than in the default model, suggesting that partial immune escape has a greater impact in these scenarios. Unlike in the default model (Figure 2A), epidemic size with variant 3 is considerable even when the vaccine rollout is early and fast. Variant 3 has the highest threshold for control: increased transmissibility means that transmission must be reduced by a larger amount to bring it under control, and partial immune escape means that a higher level of vaccination is required to achieve a given reduction in transmission. This is especially true early on, when there is less infection-induced immunity, which also helps to control transmission. Thus, the impact of weakening these control measures is particularly pronounced with earlier and faster vaccine rollout (dynamics shown in Figure 4D for the case where vaccination coverage is reduced from 100% to 50%).
Figure 4.
Epidemic size in scenarios with reduced control measures
(A) Total infections when nonpharmaceutical interventions (NPIs) are lifted once vaccination coverage reaches 50% (in default model, NPIs are maintained indefinitely).
(B) Total infections with vaccination coverage reduced from 100% to 50%.
(C) Total infections with vaccine efficacy against WT reduced from 95% to 70%.
(D) Dynamics of WT and variant 3 with earlier/faster versus later/slower vaccine rollout and 100% vaccination coverage versus 50% coverage. Simulation conditions as follows: earlier/faster vaccine rollout = starting at 9 months and lasting 3 months (100% coverage) or 1.5 months (50% coverage); later/slower rollout = starting at 12 months and lasting 6 months (100% coverage) or 3 months (50% coverage). Solid/black line, WT; green/dashed line, variant; gray shading, vaccine rollout; dashed red line, 50% vaccination coverage. In each panel, the point on the y axis indicates the total number of infections over the entire simulation. Variant introduced at 9 months in all simulations. Variant phenotypes are as follows: variant 0, identical to WT; variant 1, 60% greater transmissibility; variant 2, 40% immune escape; variant 3, 60% greater transmissibility and 40% immune escape.
Sufficiently weak control measures can lead to a second wave of infections with immune escape variants
We now consider the first of three scenarios in which the behavior of these hypothetical variants differs from the general findings above. For each scenario, we highlight the differences and consider the underlying dynamics.
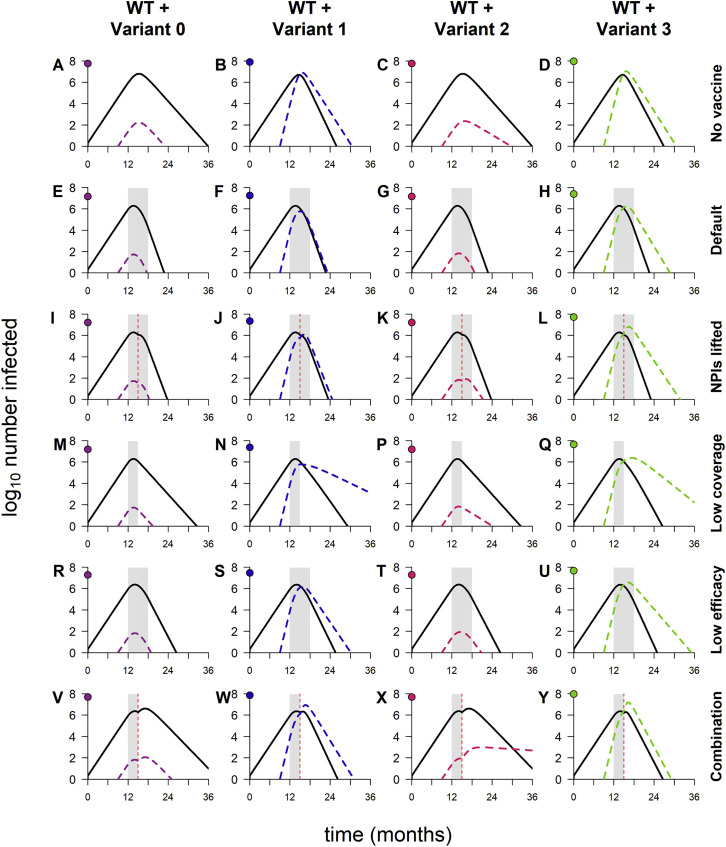
Above, we describe simulations in which control measures are weakened by lifting NPIs, reducing vaccination coverage, or decreasing vaccine efficacy. We now consider simulations in which these three changes are implemented simultaneously (Figure 5 ), and the results differ from previous findings in two ways. The first is that the timing of the vaccine rollout has no clear impact on epidemic size, suggesting that the weakened control measures are not able to bring any of the variants fully under control. Indeed, for variants 0, 1, and 3, the dynamics look similar to those observed in the absence of vaccination (Figures 6 A compared with 6V, 6B compared with 6W, and 6D compared with 6Y). Second, the epidemic size is dramatically increased in simulations with variant 2, in many cases exceeding the levels seen in the absence of vaccination (Figure 5A; also refer to Figure 2A). The increase is caused by a second wave of variant infections following the initial WT epidemic (Figure 6X); this second wave occurs in a “Goldilocks zone” in which the frequency of recovered/vaccinated hosts is sufficient to control the WT but not the variant. Higher levels of acquired immunity—induced either by vaccination or by widespread infection—are able to control the spread of both strains (Figures 6C, 6G, 6K, 6P, and 6T).
Figure 5.
Scenario with multiple changes to control measures (vaccination coverage reduced to 50%, vaccine efficacy reduced to 70%, and NPIs lifted when 50% of the population is vaccinated)
(A) Total infections.
(B) Percentage of variant infections composed of reinfections and breakthrough infections. Variant introduced at 9 months in all simulations. Variant phenotypes are as follows: variant 0, identical to WT; variant 1, 60% greater transmissibility; variant 2, 40% immune escape; variant 3, 60% greater transmissibility and 40% immune escape.
Figure 6.
Dynamics of WT and variants in simulations with varying combinations of control measures
(A–D) No vaccination, but NPIs are in place throughout.
(E–H) Default model conditions (NPIs in place throughout, 100% vaccination coverage, 95% vaccine efficacy against WT).
(I–L) NPIs lifted when vaccination coverage reaches 50%.
(M–Q) 50% vaccination coverage.
(R–U) 70% vaccine efficacy.
(V–Y) Combination of three conditions (50% vaccination coverage, 70% vaccine efficacy, and NPIs lifted when 50% of population vaccinated). In each panel, the point on the y axis indicates the log10 total number of infections. Variant introduced at 9 months in all simulations; in simulations with vaccination, the rollout begins at 12 months and lasts 6 months if final coverage is 100% and 3 months if final coverage is 50%. Solid/black lines, WT; colored/dashed lines, variants; gray shading, vaccine rollout; dashed vertical line, 50% population vaccinated. Variant phenotypes are as follows: variant 0, identical to WT; variant 1, 60% greater transmissibility; variant 2, 40% immune escape; variant 3, 60% greater transmissibility and 40% immune escape.
The second wave—and indeed any large second wave in a population with high levels of acquired immunity—is necessarily comprised predominantly of reinfections and breakthrough infections (Figure 5B), which tend to be milder than primary infections. When WT and variant waves occur simultaneously, as seen with variant 3 (Figure 6Y), the frequency of reinfections and breakthrough infections is lower (Figure 5B), as fewer recovered and vaccinated hosts are available to be (re)infected.
Degree of immune escape affects the propensity for a second wave of variant infections
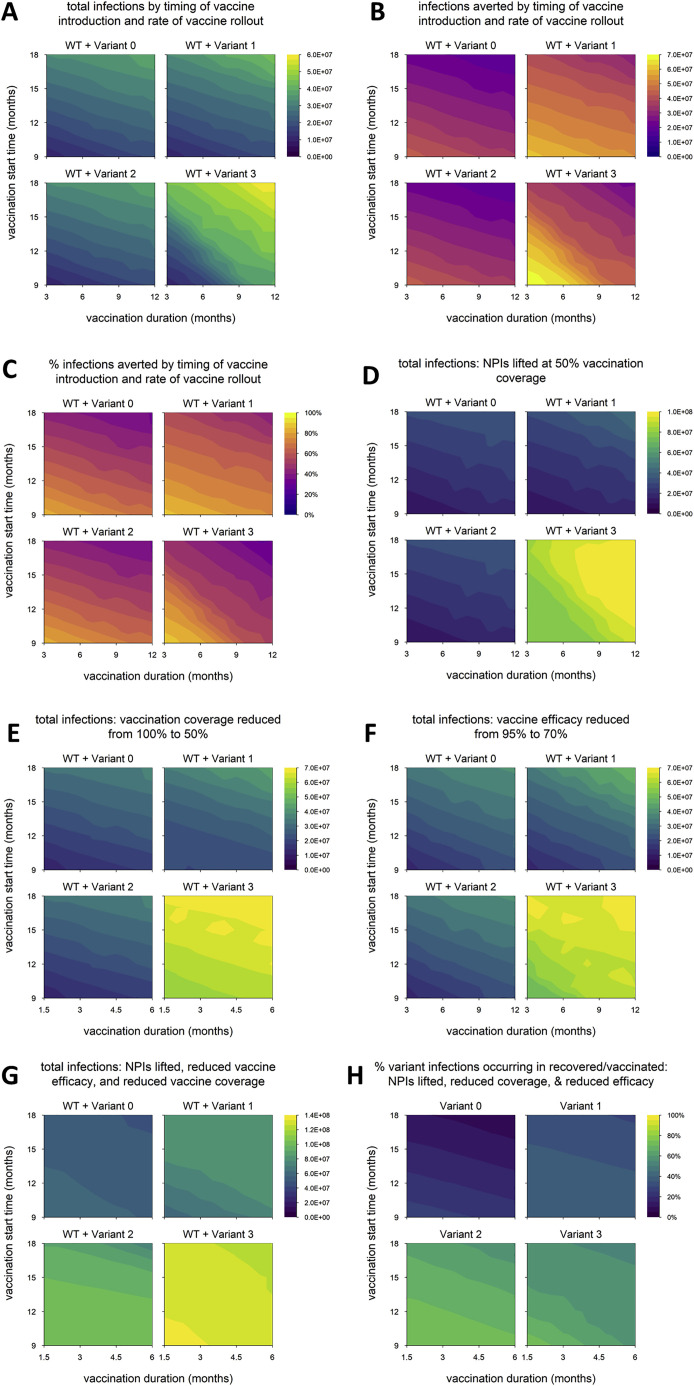
As mentioned in the introduction, variants with less than 40% immune escape have almost certainly arisen already, while variants with higher degrees of immune escape are at least a theoretical possibility. It stands to reason that these differences would affect the dynamics of immune escape variants, and so we now consider simulations in which we assign higher or lower values of immune escape to variants 2 and 3. In one set of scenarios, we assume 20% escape (or 80% cross-protection between WT and variant), while in the other we assume 80% escape (20% cross-protection). In both cases, we still assume a 60% increase in transmissibility for variants 1 and 3.
In general, a lower degree of immune escape does not qualitatively change our findings (Figures S1 and S2 ), except that variant 2 does not cause a second wave in the scenario with multiple changes to control measures (Figure S2X), resulting in fewer reinfections/breakthrough infections and fewer infections total (Figures S1G and S1H). In contrast, a very high level of immune escape significantly enhances the spread of variants 2 and 3 and limits the ability of vaccination to control these variants (Figures S3 and S4 ). Although the resulting epidemics are similar in size (Figure S3G), a higher proportion of variant 2 infections occur in recovered or vaccinated individuals, hinting at a lower disease burden (Figure S3H). The reason for the difference again lies in the timing of WT and variant waves; variant 2 peaks later than WT (Figures S4C, S4G, S4K, S4P, S4T, and S4X), which allows more recovered and vaccinated hosts to accumulate in the population, whereas variant 3 and WT peak simultaneously, providing fewer opportunities for reinfection and breakthrough infection (Figures S4D, S4H, S4L, S4Q, S4U, and S4Y).
Figure S1.
Epidemic outcomes for alternative model with lower degree of immune escape, related to Figures 2, 4, and 5
(A) Total infections (WT + variant) in simulations with each hypothetical variant, for varying rates of vaccination (vaccination duration, x axis) and time of vaccine introduction (vaccination start time, y axis); shaded contours represent total infections. (B) Number of infections averted by vaccination; shading represents number of infections averted. (C) Percentage of infections averted by vaccination; shading represents % infections averted. (D) Total infections with nonpharmaceutical interventions (NPIs) lifted when vaccination coverage reaches 50% (default condition is NPIs continued indefinitely). (E) Total infections with vaccination coverage reduced from 100% to 50%. (F) Total infections with baseline vaccine efficacy (against WT) reduced from 95% to 70%. (G) Total infections with the combination of conditions D through F (vaccination coverage reduced to 50%, vaccine efficacy reduced to 70%, and NPIs lifted when 50% of the population is vaccinated). Shading in panels D-G represents total infections. (H) Percentage of variant infections composed of reinfections and breakthrough infections under the combined conditions of panels D through F; shading represents percentage of variant infections occurring in recovered/vaccinated individuals. Variant introduced at 9 months in all simulations. Variant phenotypes are as follows: variant 0, identical to WT; variant 1, 60% greater transmissibility; variant 2, 20% immune escape; variant 3, 60% greater transmissibility and 20% immune escape.
Figure S2.
Dynamics of WT and variants, in simulations with varying combinations of control measures, for alternative model with lower degree of immune escape, related to Figure 6
Dynamics of WT and variants in simulations with varying combinations of control measures. (A-D) No vaccination but NPIs in place throughout. (E-H) Default model conditions (NPIs in place throughout, 100% vaccination coverage, 95% vaccine efficacy against WT). (I-L) NPIs lifted when vaccination coverage reaches 50%. (M-Q) 50% vaccination coverage. (R-U) 70% vaccine efficacy. (V-Y) Combination of three conditions (50% vaccination coverage, 70% vaccine efficacy, and NPIs lifted when 50% of population vaccinated). In each panel, point on y axis indicates log10 total number of infections. Variant introduced at 9 months in all simulations; in simulations with vaccination, rollout begins at 12 months and lasts 6 months if final coverage is 100%, 3 months if final coverage is 50%. Solid/black lines, WT; colored/dashed lines, variants; gray shading, vaccine rollout; dashed vertical line, 50% population vaccinated. Variant phenotypes are as follows: variant 0, identical to WT; variant 1, 60% greater transmissibility; variant 2, 20% immune escape; variant 3, 60% greater transmissibility and 20% immune escape.
Figure S3.
Epidemic outcomes for alternative model with higher degree of immune escape, related to Figures 2, 4, and 5
(A) Total infections (WT + variant) in simulations with each hypothetical variant, for varying rates of vaccination (vaccination duration, x axis) and time of vaccine introduction (vaccination start time, y axis); shaded contours represent total infections. (B) Number of infections averted by vaccination; shading represents number of infections averted. (C) Percentage of infections averted by vaccination; shading represents % infections averted. (D) Total infections with nonpharmaceutical interventions (NPIs) lifted when vaccination coverage reaches 50% (default condition is NPIs continued indefinitely). (E) Total infections with vaccination coverage reduced from 100% to 50%. (F) Total infections with baseline vaccine efficacy (against WT) reduced from 95% to 70%. (G) Total infections with the combination of conditions D through F (vaccination coverage reduced to 50%, vaccine efficacy reduced to 70%, and NPIs lifted when 50% of the population is vaccinated). Shading in panels D-G represents total infections. (H) Percentage of variant infections composed of reinfections and breakthrough infections under the combined conditions of panels D through F; shading represents percentage of variant infections occurring in recovered/vaccinated individuals. Variant introduced at 9 months in all simulations. Variant phenotypes are as follows: variant 0, identical to WT; variant 1, 60% greater transmissibility; variant 2, 80% immune escape; variant 3, 60% greater transmissibility and 80% immune escape.
Figure S4.
Dynamics of WT and variants, in simulations with varying combinations of control measures, for alternative model with higher degree of immune escape, related to Figure 6
Dynamics of WT and variants in simulations with varying combinations of control measures. (A-D) No vaccination but NPIs in place throughout. (E-H) Default model conditions (NPIs in place throughout, 100% vaccination coverage, 95% vaccine efficacy against WT). (I-L) NPIs lifted when vaccination coverage reaches 50%. (M-Q) 50% vaccination coverage. (R-U) 70% vaccine efficacy. (V-Y) Combination of three conditions (50% vaccination coverage, 70% vaccine efficacy, and NPIs lifted when 50% of population vaccinated). In each panel, point on y axis indicates log10 total number of infections. Variant introduced at 9 months in all simulations; in simulations with vaccination, rollout begins at 12 months and lasts 6 months if final coverage is 100%, 3 months if final coverage is 50%. Solid/black lines, WT; colored/dashed lines, variants; gray shading, vaccine rollout; dashed vertical line, 50% population vaccinated. All simulations run for an extended duration of six years (default condition is three years); variant introduced at 9 months; in simulations with vaccination, rollout begins at 12 months and lasts 6 months if final coverage is 100%, 3 months if final coverage is 50%. Solid/black lines, WT; colored/dashed lines, variants; gray shading, vaccine rollout; dashed vertical line, 50% vaccination coverage. Variant phenotypes are as follows: variant 0, identical to WT; variant 1, 60% greater transmissibility; variant 2, 80% immune escape; variant 3, 60% greater transmissibility and 80% immune escape.
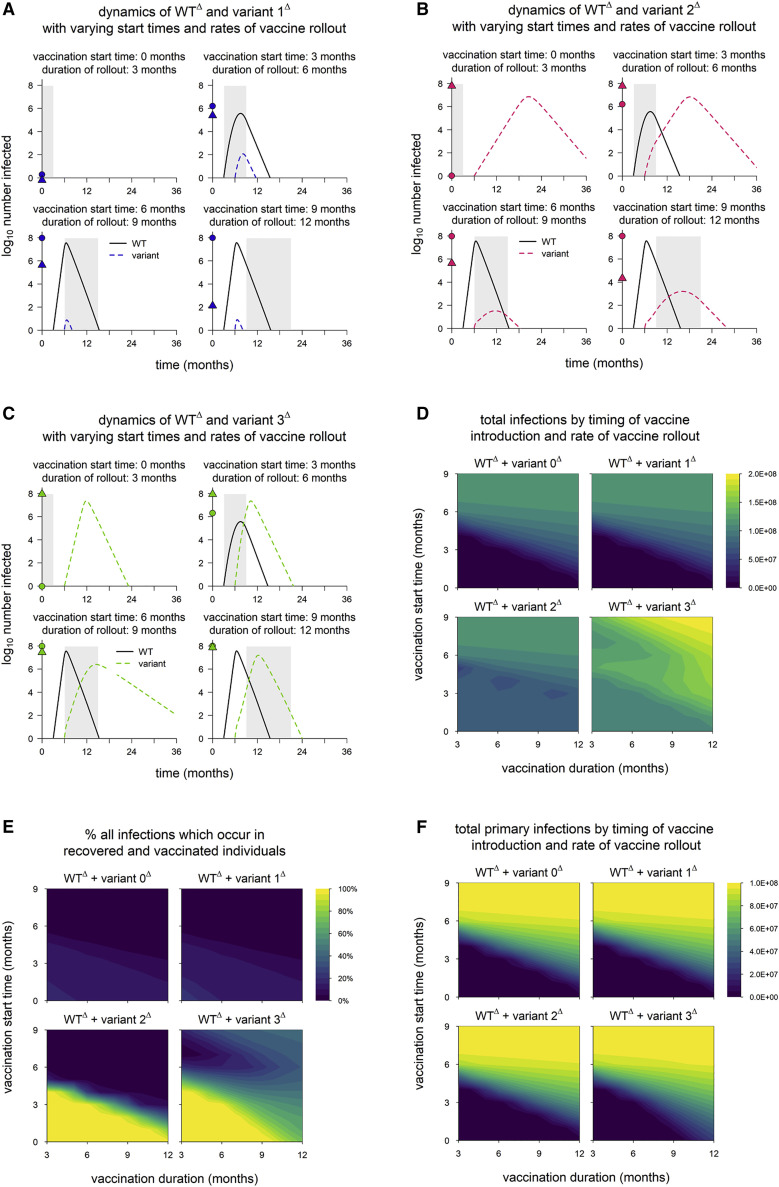
When all strains are highly transmissible, populations acquire high levels of immunity favoring immune escape variants
In the default model, we assume the WT strain has R0 = 2.5, similar to the SARS-CoV-2 virus that dominated through most of 2020. However, variants with significantly increased transmissibility—first Alpha, followed by Delta—subsequently replaced these less transmissible strains, effectively becoming—at least transiently—new wild types. We now consider a scenario in which the WT is highly transmissible, similar to Delta, with R0 = 6. (To avoid confusion with the default WT, we designate this alternative strain WTΔ and denote the associated variants by 1Δ, 2Δ, and so on.) To better approximate the circumstances in which these highly transmissible variants emerged, we assume that the vaccine rollout begins before or shortly after WTΔ appears, and because the spread of highly transmissible strains is accelerated (occurring over shorter time frames), we assume that variants emerge three months after WTΔ. Variant phenotypes are the same as in the default model but defined with respect to WTΔ; for instance, variant 1Δ has R0 = 9.6.
The key difference from earlier scenarios is that vaccination and/or a large WTΔ epidemic always generate high levels of immunity in the population prior to emergence of the variant. The resulting lack of susceptible hosts is sufficient to limit the spread of variant 1Δ (Figure 7 A) but not variant 2Δ or 3Δ. The latter variants are able to spread even when the entire population is vaccinated prior to their emergence (Figures 7B and 7C), although these infections are necessarily all breakthrough infections. For these variants, early and fast vaccine rollout has less impact on the total epidemic size (Figure 7D) but leads to an epidemic in which the majority of infections are breakthroughs and reinfections, which are generally mild (Figure 7E). As a result, earlier/faster vaccine rollout does reduce the total number of primary infections, a possible proxy for disease burden (Figure 7F). However, this is mainly attributable to the impact of vaccination on WTΔ, which means that vaccination must be timed to avert the WTΔ epidemic rather than subsequent waves of immune escape variants.
Figure 7.
WTΔ and variantΔ dynamics in simulations with full control measures
(A) Dynamics of WTΔ and variant 1Δ in simulations with different start times and rates of vaccine rollout.
(B) Dynamics of WTΔ and variant 2Δ.
(C) Dynamics of WTΔ and variant 3Δ. In (A)–(C), points on the y axis indicate the total numbers of primary infections (circles) and reinfections/breakthrough infections (triangles); gray shading indicates vaccine rollout.
(D) Total infections in simulations with each hypothetical variant.
(E) Percentage of all infections which occur in recovered/vaccinated individuals (reinfections and breakthrough infections).
(F) Total number of primary infections. In all simulations, WTΔ and variantΔ are introduced at 3 and 6 months, respectively. Vaccine coverage and efficacy are assumed to be 100% and 95%, respectively, and NPIs are maintained throughout all simulations. WTΔ is assumed to have R0 = 6, and variantΔ phenotypes are as follows: variant 0Δ, identical to WTΔ; variant 1Δ, 60% greater transmissibility; variant 2Δ, 40% immune escape; variant 3Δ, 60% greater transmissibility and 40% immune escape.
Qualitative findings are largely robust to changing structural model assumptions
Finally, we re-examine our findings after varying two aspects of the model structure. First, we change the way NPIs are implemented in the model. In the default model, NPIs simply reduce the transmission rate by 40%. The resulting dynamics are easy to interpret and analyze, but in reality, the dynamics of SARS-CoV-2 have been characterized by multiple waves that are at least partly driven by changes in the intensity of NPIs (e.g., mask use, social distancing, etc.). We developed an alternative implementation of the model in which the virus is kept in check by stronger NPIs that come into effect when prevalence exceeds a threshold (see STAR Methods). The findings (Figure S5 ) are largely similar to those of the default model, except that variant 1 does not perform as well, especially compared to variant 3. This occurs because sufficiently strong control measures can keep even highly transmissible variants in check, especially when complemented by vaccination and cross-immunity. The degree to which this occurs in practice will depend on the strength of NPIs, the responsiveness to case numbers (e.g., thresholds and lags for implementation), and the transmissibility of the variant.
Figure S5.
Epidemic outcomes for alternative model with rolling lockdowns, related to Figures 2, 4, and 5
(A) Total infections (WT + variant) in simulations with each hypothetical variant, for varying rates of vaccination (vaccination duration, x axis) and time of vaccine introduction (vaccination start time, y axis); shaded contours represent total infections. (B) Number of infections averted by vaccination; shading represents number of infections averted. (C) Percentage of infections averted by vaccination; shading represents % infections averted. (D) Total infections with nonpharmaceutical interventions (NPIs) lifted when vaccination coverage reaches 50% (default condition is NPIs continued indefinitely). (E) Total infections with vaccination coverage reduced from 100% to 50%. (F) Total infections with baseline vaccine efficacy (against WT) reduced from 95% to 70%. (G) Total infections with the combination of conditions D through F (vaccination coverage reduced to 50%, vaccine efficacy reduced to 70%, and NPIs lifted when 50% of the population is vaccinated). Shading in panels D-G represents total infections. (H) Percentage of variant infections composed of reinfections and breakthrough infections under the combined conditions of panels D through F; shading represents percentage of variant infections occurring in recovered/vaccinated individuals. NPIs switch between low intensity (reduce transmission by 30%) and high intensity (reduce by 70%) when the prevalence of infection (lagged by two weeks) crosses a threshold, which is set to 1% of the population. Variant introduced at 9 months in all simulations. Variant phenotypes are as follows: variant 0, identical to WT; variant 1, 60% greater transmissibility; variant 2, 40% immune escape; variant 3, 60% greater transmissibility and 40% immune escape.
Lastly, the default model assumes that immunity reduces the probability of infection by decreasing the rate of movement from uninfected to infected states (so-called “leaky” immunity). An alternative construction assumes that a given individual either does or does not develop immunity to a given strain following infection or vaccination (termed “all-or-nothing” immunity). Using an alternate model with all-or-nothing immunity (see STAR Methods), we obtain results that are qualitatively indistinguishable from leaky immunity, although the epidemic size is lower with all-or-nothing immunity (Figure S6 ) since some fraction of recovered and vaccinated individuals are completely refractory to infection.
Figure S6.
Epidemic outcomes for alternative model with all-or-nothing immunity, related to Figures 2, 4, and 5
(A) Total infections (WT + variant) in simulations with each hypothetical variant, for varying rates of vaccination (vaccination duration, x axis) and time of vaccine introduction (vaccination start time, y axis); shaded contours represent total infections. (B) Number of infections averted by vaccination; shading represents number of infections averted. (C) Percentage of infections averted by vaccination; shading represents % infections averted. (D) Total infections with nonpharmaceutical interventions (NPIs) lifted when vaccination coverage reaches 50% (default condition is NPIs continued indefinitely). (E) Total infections with vaccination coverage reduced from 100% to 50%. (F) Total infections with baseline vaccine efficacy (against WT) reduced from 95% to 70%. (G) Total infections with the combination of conditions D through F (vaccination coverage reduced to 50%, vaccine efficacy reduced to 70%, and NPIs lifted when 50% of the population is vaccinated). Shading in panels D-G represents total infections. (H) Percentage of variant infections composed of reinfections and breakthrough infections under the combined conditions of panels D through F; shading represents percentage of variant infections occurring in recovered/vaccinated individuals. Variant introduced at 9 months in all simulations. Variant phenotypes are as follows: variant 0, identical to WT; variant 1, 60% greater transmissibility; variant 2, 40% immune escape; variant 3, 60% greater transmissibility and 40% immune escape.
Discussion
In this work, we use a mathematical model to characterize the population-level impact of SARS-CoV-2 variants with different phenotypes across a wide range of scenarios. We find that variants with enhanced transmissibility invade easily in susceptible populations, while variants with partial immune escape do not; the latter can sometimes produce a second wave of infections, but these primarily occur in recovered and vaccinated individuals, who typically experience mild disease. Although the impact of partial immune escape on its own is relatively mild, variants with a combination of enhanced transmissibility and immune escape increase not just the total size of the epidemic but also the number of primary infections in susceptible hosts, who are more likely to suffer severe illness or death. Thus, partial immune escape can have severe consequences, but mainly when paired with enhanced transmissibility.
It is important to note that variant phenotypes are context-dependent, defined with regard to the strain with which they are competing. For instance, in our model, variant 3 has enhanced transmissibility as well as partial immune escape, and this variant considerably increases the severity of the epidemic when WT is the dominant strain. However, if variant 1 was to replace WT, then variant 3 would no longer have a transmissibility advantage and would essentially become variant 2. In this case, variant 3 would either fail to invade or cause a second wave consisting largely of reinfections and breakthrough infections.
These findings advance our understanding of the dangers posed by different variants. Currently, both the World Health Organization and the US Centers for Disease Control (CDC) and Prevention designate certain strains as “VOCs” using similar criteria, which include evidence of immune escape, vaccine escape, and/or enhanced transmissibility. In general, variants are not assigned threat levels or differentiated status, although the CDC would recognize variants with clear evidence of significant vaccine escape as “variants of high consequence.” Our findings suggest that variants with enhanced transmissibility have a strong tendency to invade and can significantly worsen an epidemic. Partial immune escape, in the absence of enhanced transmissibility, becomes a substantial proportion of the epidemic only when population immunity is in a “Goldilocks zone”—strong enough to impose effective selection but not so strong as to control transmission—and when invasion does occur, the variant primarily causes breakthrough infections and reinfections, which are usually mild.
These results provide a theoretical basis to understand the behavior of existing variants, anticipate the behavior of future variants, and develop appropriate strategies to mitigate the impact of VOCs in populations across the world. Our findings are consistent with the global sweeps by highly transmissible variants Alpha and Delta, as well as the failure of Beta (which shows evidence of partial immune escape) to reach high frequency in most areas. The ability to find patterns of risk by modeling different variants across a wide range of scenarios suggests that this is a useful approach to identify variant phenotypes of particular concern. Lastly, our work underscores the importance of vaccination on a global scale, as quickly as possible, to mitigate the impact of present and future variants.
Limitations of the study
An obvious limitation of our model is that it does not allow for the circulation of multiple variants. In reality, variants compete with one another as well as WT, and this may lead to complex behavior that is difficult to predict from pairwise interactions. It is particularly challenging to anticipate the dynamics of a system with multiple variants that each have some degree of enhanced transmissibility and immune escape, as the relative fitness of these strains may change as the level of immunity in the population increases. Additional modeling is therefore required to understand the risks associated with multiple variants circulating simultaneously.
We also use epidemic size as a rough proxy for the burdens of disease and mortality, stratifying only by immune status (susceptible versus recovered/vaccinated). More nuanced and useful estimates may be obtained by accounting for the gradual reduction of the infection fatality ratio, the age distribution of infections, and other details that affect morbidity and mortality. Our model is strictly focused on what happens to a variant following its emergence; the stochastic phenomenon of emergence itself is not considered here. The emergence of new variants is affected by control measures, such as NPIs and vaccination, that limit the size of the infected population and alter the strength of selection on different traits (Ashby and Thompson, 2021). This will be an important dimension to consider in future work, as the optimal strategies to minimize transmission of a particular variant may or may not be aligned with the best strategies to limit emergence (Ong et al., 2021; Sheikh et al., 2021).
Finally, the work presented here analyzes epidemic dynamics and does not consider phenomena that will be important determinants of endemic dynamics—most notably, the waning and boosting of immunity. Future work will need to consider the impacts of waning immunity, reinfection, boosters, and updated vaccines to understand how future variants could shape the burdens of infection and disease in the years to come.
STAR★Methods
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Software and algorithms | ||
| R version 4.1.0 | R Core Team | https://www.r-project.org/ |
| RStudio version 1.4.1717 | RStudio Team | https://www.rstudio.com/ |
| Two-strain model with vaccination | This paper; Open Science Framework | https://osf.io/z9x2p/ |
Resource availability
Lead contact
Requests for further information should be directed to and will be answered by the lead contact, Mary Bushman (mbushman@hsph.harvard.edu).
Materials availability
This study did not generate new unique reagents.
Method details
Model
Overview
We use an ordinary differential equation (ODE) compartment model to simulate the dynamics of WT and variant strains of SARS-CoV-2 in the context of nonpharmaceutical interventions (NPIs) and vaccine rollout. The model is an extended version of the standard SIR (susceptible-infected-recovered) model framework with two key changes. First, the model tracks two viral strains, which are denoted strain 1 (WT) and strain 2 (variant). Second, the model allows for strain-specific immunity to be acquired via infection and vaccination. In addition, the model is implemented with a wrapper that enables various events, such as variant emergence, vaccine rollout, or intensifying/relaxing control measures, to occur at pre-specified times and/or in response to the state of the system.
Infection states
In this compartment model, individuals are classified according to their current infection status as well as their infection and vaccination history. Four types of compartments exist: (susceptible), (infected), (recovered), and (vaccinated). Subscripts further distinguish between infection states and infection histories within the , , and classes (see below).
| State variable | Definition |
|---|---|
| Susceptible | |
| Infected with strain , previously susceptible | |
| Infected with strain , previously susceptible, vaccinated during current infection | |
| Recovered from strain | |
| Infected with strain , previously recovered (from strain ) | |
| Infected with strain , previously recovered (from strain ), vaccinated during current infection | |
| Recovered from both strain and strain | |
| Vaccinated (never infected) | |
| Infected with strain , previously vaccinated | |
| Vaccinated and recovered from strain | |
| Infected with strain , previously vaccinated, previously recovered from strain | |
| Vaccinated and recovered from both strain and strain |
Parameters
Movement between compartments is the result of three processes: infection, recovery, and vaccination. Infection is a mass-action process resulting from contact between infected individuals and individuals with partial or total susceptibility to infections. All individuals infected with a given strain are assumed to be equally infectious, with transmission rate for WT and for the variant (see Variant phenotypes). All infected individuals also have the same average duration of infectiousness, which is the inverse of the recovery rate, . Individuals may have varying susceptibility to each strain, depending on prior infection and/or vaccination. Upon recovery, individuals develop sterilizing immunity against the infecting strain and partial protection against the non-infecting strain; the degree of cross-protection is given by .
Once vaccine rollout is initiated (see Simulation Overview), a fixed number of individuals are vaccinated per day, but these individuals are drawn only from eligible compartments. By default, all unvaccinated individuals are eligible. The parameters and control the vaccine eligibility of infected and recovered individuals, respectively. Vaccination takes place in a single dose and is assumed to take effect immediately, unless the recipient is currently infected, in which case the vaccine takes effect upon recovery. The vaccine is assumed to have maximum efficacy against a perfect antigenic match. The degree of antigenic mismatch between the vaccine and strain is given by . Both infection-induced and vaccine-induced immunity are assumed to be durable, lasting longer than the duration of the simulations; waning of immunity is not included in the model.
| Parameter | Definition | Default value |
|---|---|---|
| Population size | 108 | |
| Reproduction number (WT) | 2.5 | |
| Recovery rate | 1/14 days-1 | |
| Transmission rate | ||
| Cross-reactivity between WT and variant | 1 or 0.6 | |
| Maximum vaccine efficacy | 0.95 | |
| Antigenic mismatch between vaccine and WT | 0 | |
| Antigenic mismatch between vaccine and variant | ||
| Eligibility of infected individuals for vaccination; 1 = eligible, 0 = ineligible | 1 | |
| Eligibility of recovered individuals for vaccination; 1 = eligible, 0 = ineligible | 1 | |
| Increase in transmissibility of variant relative to WT | 0 or 0.6 | |
| Time of variant introduction | 9 months | |
| Start of vaccine rollout | Varies | |
| Daily per-capita vaccination rate | Varies | |
| Final vaccination coverage | 100% | |
| Reduction in transmission due to nonpharmaceutical interventions | 0.4 |
Variant phenotypes
Variants are characterized in terms of two phenotypes: transmissibility and immune escape. The increase in transmissibility relative to WT is denoted by , giving a transmission rate of . Immune escape is the complement of cross-reactivity between WT and variant . The default phenotypes of the hypothetical variants modeled are as follows:
-
•
Variant 0 (neutral):
-
•
Variant 1 (more transmissible):
-
•
Variant 2 (partial immune escape):
-
•
Variant 3 (more transmissible + partial escape):
Equations
We use the shorthand for the per capita rate of vaccination among the eligible population. Once vaccination is initiated, a fraction of the population is vaccinated daily ( in absolute numbers), but because the eligible population fluctuates in size, it is necessary to calculate the rate at which individuals in eligible model compartments are vaccinated. We define as the eligible population at time , and calculate as follows:
| (1) |
We then define as follows:
| (2) |
In addition, because there are six infected compartments for each strain, we simplify the equations by defining new state variables representing the total number of infected individuals for each strain:
| (3) |
| (4) |
The rates of movement between compartments are shown alongside the model diagram in Figure S7 A. The differential equations for the model are given below ((5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15), (16), (17), (18), (19), (20), (21), (22), (23), (24)).
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
Figure S7.
Model diagrams and rates of movement between compartments, related to STAR Methods
(A) Default model with “leaky” immunity. (B) Alternative model with “all-or-nothing” immunity. Numbered terms at right give rates of movement associated with numbered arrows in each diagram.
Simulations
Setup
Three events occur in each simulation at designated times: introduction of a single WT infection at time , introduction of a single variant infection at time , and the beginning of vaccine rollout at time . We set months, and [9 months, 18 months] in all simulations except those with increased transmissibility of all strains, in which months, months, and [0, 9 months]. Vaccination proceeds at a constant rate, with a fixed proportion of the population vaccinated per day until the maximum coverage is reached (the duration of vaccine rollout is thus ). The total length of each simulation is three years, except for simulations with an increased level of immune escape, which have a simulated duration of six years.
Nonpharmaceutical interventions
NPIs are assumed to be maintained at a constant level throughout the simulation, with two exceptions: scenarios in which NPIs are lifted once vaccination coverage reaches 50% (see Control measures) and scenarios in which NPIs switch between high- and low-intensity states (see Rolling lockdowns). These control measures are assumed to reduce transmission of both strains by a factor .
Core set of simulations
Simulations were run with each variant in combination with WT; each pair was simulated with and without vaccination (Table S1). For each set of simulations, the start of vaccine rollout and the duration of vaccine rollout were varied in one-month increments over the ranges given in Table S1.
Model outcomes
Epidemic size
The main outcome compared across simulations is the cumulative number of infections, which is modeled as the sum of flows into all infected compartments. Similar quantities are defined for infections in naive individuals (previously belonging to compartment ) and in recovered/vaccinated individuals (coming from and compartments). The relative frequency of reinfections and breakthrough infections is obtained by dividing the number of infections in recovered/vaccinated individuals by the total number of infections.
Impact of vaccination
Vaccine impact is obtained by comparing numbers of infections between simulations with vaccination (sets 5-8 in Table S1) to otherwise identical simulations without vaccination (sets 1-4). If we denote the total number of infections with and without vaccination by and , respectively, vaccine impact can be measured in terms of the number of infections averted or the percentage of infections averted .
Strain dynamics
Strain dynamics are also shown in several figures; the number of infections with strain , or , is the sum of all the infected compartments for strain and . In one instance, infections are subdivided by the immune status of the host. Infections of naive individuals with strain are obtained as the sum of compartments and ; the latter is included because vaccination during infection does not take effect until the infection is cleared. Infections of recovered and vaccinated individuals with strain are obtained by summing the remaining infected compartments.
Varying model parameters
We run four sets of alternative scenarios in which control measures or variant properties are changed and two sets in which structural assumptions of the model are changed. The first set of scenarios (Control measures) is replicated across all but one of the other alternative scenarios, including those in the next section, Varying model structure.
Control measures
The default model configuration, with indefinite continuation of NPIs, complete vaccination coverage, and high vaccine efficacy, represents the best-case scenario in each of these areas; we therefore vary these assumptions to simulate realistic – not pessimistic – shortcomings. We consider three ways in which control measures might suffer (Table S2): lifting NPIs when vaccine coverage reaches 50%, decreasing the final vaccination coverage to 50%, and lowering the peak vaccine efficacy (against WT) to 70%. We repeat simulation sets 5-8 (Table S1) under each of these alternative parameterizations, as well as the combination of all three.
Lower and higher degrees of immune escape
The default model assumes that immune escape manifests as a 40% reduction in cross-reactivity with WT. This value is on the high end of escape estimates for existing variants, but lower degrees of escape almost certainly exist, and higher degrees of immune escape are theoretically possible. We therefore run simulations with a lower level of immune escape (20% escape or 80% cross-protection with WT) and a higher level (80% escape or 20% cross-protection). For variants with enhanced transmissibility, we still assume a 60% increase in R0. We repeat the simulations listed in Tables S1 and S2 for both scenarios; simulations with a higher level of immune escape are run for an extended duration (six years) because the occurrence of a second wave of variant infections in some scenarios increases the time frame over which epidemic dynamics are occurring.
Increased transmissibility of all strains
The default model assumes that the WT strain has an R0 of 2.5, which approximates the original SARS-CoV-2 virus. However, this strain has since been replaced by more transmissible variants. We therefore run simulations in which the WT has R0 = 6; the variant phenotypes are the same but are defined with respect to the new WT (i.e., all strains have R0 ≥ 6). We re-run the simulations listed in Table S1 (but not those in Table S2) under this alternative parameterization; however, the timing of events is shifted, with the WT and variant strains introduced at 3 and 6 months, respectively, and vaccine rollout beginning between 0 and 9 months.
Varying model structure
Finally, we run simulations under two alternative versions of the model which make different assumptions about nonpharmaceutical interventions and immunity, respectively. We repeat the simulations in Tables S1 and S2 under both alternative model versions.
Rolling lockdowns
In the default model, we assume that nonpharmaceutical interventions (NPIs) are fixed at an intensity that reduces transmission by 40%. This configuration generates dynamics that are easy to understand and analyze, but is not broadly representative of the dynamics of the COVID-19 pandemic. In many parts of the world, relatively weak NPIs are periodically supplanted by more stringent measures when case numbers grow too large; after a period of sustained decline, the more severe control measures are turned off again. We use an alternative model configuration to simulate this strategy, which we refer to as “rolling lockdowns.”
In the alternative configuration, NPIs switch between two different intensities, which reduce transmission by 30% and 70%, respectively. The high-intensity control measures are triggered when the number of current infections – lagged by 14 days to simulate various delays between infection and reporting – exceeds 1% of the total population. Control measures revert to the lower intensity when the number of infections (lagged by 14 days) drops below the threshold again. Shifts between low and high intensity of NPIs cannot occur less than 14 days apart (the length of the reporting lag), to ensure that shift is precipitated only by events following shift .
All-or-nothing immunity
The default model configuration assumes that partial cross-protection from infection or partial immunity from vaccination is imperfect at the individual level, meaning the probability of infection given exposure is reduced but not eliminated, and the degree of protection is the same for all individuals. This is sometimes called “leaky” immunity; an alternative formulation, termed “all-or-nothing” immunity, does not accommodate partial protection for individuals. Upon infection or vaccination, some individuals acquire complete, sterilizing protection, and others acquire no protection at all.
We use an alternative version of the ODE model described above to re-run the same scenarios with all-or-nothing immunity instead of leaky immunity. Although the names of the state variables are largely unchanged, many are defined differently (see below). In the default model, states are defined by history of infection and vaccination; in the alternative model, states are defined in terms of strain-specific immunity, regardless of how this immunity was acquired. For example, individuals in compartment are vaccinated and immune to strain , but the compartment is not specific to a single history, as it encompasses individuals with and without prior infection by strain .
| State variable | Definition |
|---|---|
| Susceptible | |
| Infected with strain , previously susceptible | |
| Infected with strain , previously susceptible, vaccinated during current infection | |
| Recovered and immune to strain | |
| Recovered and immune to both strain and strain | |
| Infected with strain , previously recovered (from strain ) | |
| Infected with strain , previously recovered (from strain ), vaccinated during current infection | |
| Vaccinated and immune to strain | |
| Vaccinated and immune to both strain and strain | |
| Vaccinated but not immune to either strain | |
| Previously vaccinated, immune to strain , currently infected with strain | |
| Previously vaccinated, not immune to either strain, currently infected with strain |
The model parameters are generally the same, except that parameters relating to partial immunity ( and ) are defined in terms of probabilities of protection, rather than degrees of protection (see below). Rates of movement between compartments are very different from the default model (Figure S7B), as are the differential equations ((25), (26), (27), (28), (29), (30), (31), (32), (33), (34), (35), (36), (37), (38), (39), (40), (41), (42), (43), (44)).
| Parameter | Definition | Default value |
|---|---|---|
| Probability of cross-protection given infection with either strain | 0 or 0.6 | |
| Maximum vaccine efficacy (probability of protection against perfect antigenic match) | 0.95 | |
| Probability vaccine fails to elicit immunity against strain 1 (due to antigenic mismatch) | 0 | |
| Probability vaccine fails to elicit immunity against strain 2 (due to antigenic mismatch) |
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
| (33) |
| (34) |
| (35) |
| (36) |
| (37) |
| (38) |
| (39) |
| (40) |
| (41) |
| (42) |
| (43) |
| (44) |
Acknowledgments
M.B. and B.P.T. were supported by the National Institute of Allergy and Infectious Diseases of the National Institutes of Health under award number R01AI128344. R.K., M.L., and W.P.H. were supported by the U.S. National Cancer Institute SeroNet cooperative agreement U01CA261277. W.P.H. was also funded in part by contract 200-2016-91779 with the Centers for Disease Control and Prevention (CDC). The findings, conclusions, and views expressed in this presentation are those of the author(s) and do not necessarily represent the official position of the CDC.
Author contributions
M.L., W.P.H., and M.B. conceived of the study. The model was developed by M.B., R.K., and B.P.T. M.B. programmed and analyzed the model, produced visualizations, and drafted the manuscript. All authors reviewed and edited the manuscript. Supervision was provided by W.P.H., and funding was acquired by M.L. and W.P.H.
Declaration of interests
R.K. discloses consulting fees from Partners In Health and the Pan American Health Organization. M.L. received funding through his institution from the CDC, NIH, UK National Institute for Health Research, and Pfizer and consulting fees or honoraria from Merck, Sanofi Pasteur, Janssen, and Bristol Myers Squibb. He is a member of the Scientific Advisory Board for CEPI, the Coalition for Epidemic Preparedness Innovations. W.P.H. serves on the Advisory Board of Biobot Analytics and has received compensation for expert witness testimony on the course of the SARS-CoV-2 pandemic. M.L. and R.K. are on secondments from Harvard to the CDC. The opinions in this paper are those of the authors in their academic capacities and do not reflect those of any government entity.
Published: November 19, 2021
Footnotes
Supplemental information can be found online at https://doi.org/10.1016/j.cell.2021.11.026.
Supplemental information
Data and code availability
-
•
This study did not use or generate data aside from the reproducible output of the mathematical model.
-
•
All original code, including that needed to generate the figures in the main text and supplemental information, has been deposited in Open Science Framework and is publicly available as of the date of publication. The digital object identifier (DOI) is listed in the key resources table.
-
•
Any additional information required to use or analyze the model described in this paper is available from the lead contact upon request.
References
- Abu-Raddad L.J., Chemaitelly H., Butt A.A., National Study Group for COVID-19 Vaccination Effectiveness of the BNT162b2 Covid-19 Vaccine against the B.1.1.7 and B.1.351 Variants. N. Engl. J. Med. 2021;385:187–189. doi: 10.1056/NEJMc2104974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen H., Vusirikala A., Flannagan J., Twohig K.A., Zaidi A., Chudasama D., Lamagni T., Groves N., Turner C., Rawlinson C., et al. Household transmission of COVID-19 cases associated with SARS-CoV-2 delta variant (B.1.617.2): national case-control study. Lancet Reg. Health Eur. 2021 doi: 10.1016/j.lanepe.2021.100252. Published online October 28, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashby B., Thompson R.N. Non-pharmaceutical interventions and the emergence of pathogen variants. medRxiv. 2021 doi: 10.1093/emph/eoac043. 2021.2005.2027.21257938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baden L.R., El Sahly H.M., Essink B., Kotloff K., Frey S., Novak R., Diemert D., Spector S.A., Rouphael N., Creech C.B., et al. COVE Study Group Efficacy and Safety of the mRNA-1273 SARS-CoV-2 Vaccine. N. Engl. J. Med. 2021;384:403–416. doi: 10.1056/NEJMoa2035389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker M., Dulovic A., Junker D., Ruetalo N., Kaiser P.D., Pinilla Y.T., Heinzel C., Haering J., Traenkle B., Wagner T.R., et al. Immune response to SARS-CoV-2 variants of concern in vaccinated individuals. Nat. Commun. 2021;12:3109. doi: 10.1038/s41467-021-23473-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cele S., Gazy I., Jackson L., Hwa S.H., Tegally H., Lustig G., Giandhari J., Pillay S., Wilkinson E., Naidoo Y., et al. Network for Genomic Surveillance in South Africa. COMMIT-KZN Team Escape of SARS-CoV-2 501Y.V2 from neutralization by convalescent plasma. Nature. 2021;593:142–146. doi: 10.1038/s41586-021-03471-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collier D.A., De Marco A., Ferreira I.A.T.M., Meng B., Datir R.P., Walls A.C., Kemp S.A., Bassi J., Pinto D., Silacci-Fregni C., et al. CITIID-NIHR BioResource COVID-19 Collaboration. COVID-19 Genomics UK (COG-UK) Consortium Sensitivity of SARS-CoV-2 B.1.1.7 to mRNA vaccine-elicited antibodies. Nature. 2021;593:136–141. doi: 10.1038/s41586-021-03412-7. [DOI] [PubMed] [Google Scholar]
- Dagan N., Barda N., Kepten E., Miron O., Perchik S., Katz M.A., Hernán M.A., Lipsitch M., Reis B., Balicer R.D. BNT162b2 mRNA Covid-19 Vaccine in a Nationwide Mass Vaccination Setting. N. Engl. J. Med. 2021;384:1412–1423. doi: 10.1056/NEJMoa2101765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dagpunar J. Interim estimates of increased transmissibility, growth rate, and reproduction number of the Covid-19 B.1.617.2 variant of concern in the United Kingdom. medRxiv. 2021 2021.2006.2003.21258293. [Google Scholar]
- Davies N.G., Abbott S., Barnard R.C., Jarvis C.I., Kucharski A.J., Munday J.D., Pearson C.A.B., Russell T.W., Tully D.C., Washburne A.D., et al. CMMID COVID-19 Working Group. COVID-19 Genomics UK (COG-UK) Consortium Estimated transmissibility and impact of SARS-CoV-2 lineage B.1.1.7 in England. Science. 2021;372:eabg3055. doi: 10.1126/science.abg3055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dejnirattisai W., Zhou D., Supasa P., Liu C., Mentzer A.J., Ginn H.M., Zhao Y., Duyvesteyn H.M.E., Tuekprakhon A., Nutalai R., et al. Antibody evasion by the P.1 strain of SARS-CoV-2. Cell. 2021;184:2939–2954.e9. doi: 10.1016/j.cell.2021.03.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emary K.R.W., Golubchik T., Aley P.K., Ariani C.V., Angus B., Bibi S., Blane B., Bonsall D., Cicconi P., Charlton S., et al. COVID-19 Genomics UK consortium. AMPHEUS Project. Oxford COVID-19 Vaccine Trial Group Efficacy of ChAdOx1 nCoV-19 (AZD1222) vaccine against SARS-CoV-2 variant of concern 202012/01 (B.1.1.7): an exploratory analysis of a randomised controlled trial. Lancet. 2021;397:1351–1362. doi: 10.1016/S0140-6736(21)00628-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faria N.R., Mellan T.A., Whittaker C., Claro I.M., Candido D.D.S., Mishra S., Crispim M.A.E., Sales F.C.S., Hawryluk I., McCrone J.T., et al. Genomics and epidemiology of the P.1 SARS-CoV-2 lineage in Manaus, Brazil. Science. 2021;372:815–821. doi: 10.1126/science.abh2644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia-Beltran W.F., Lam E.C., St Denis K., Nitido A.D., Garcia Z.H., Hauser B.M., Feldman J., Pavlovic M.N., Gregory D.J., Poznansky M.C., et al. Multiple SARS-CoV-2 variants escape neutralization by vaccine-induced humoral immunity. Cell. 2021;184:2372–2383.e9. doi: 10.1016/j.cell.2021.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geers D., Shamier M.C., Bogers S., den Hartog G., Gommers L., Nieuwkoop N.N., Schmitz K.S., Rijsbergen L.C., van Osch J.A.T., Dijkhuizen E., et al. SARS-CoV-2 variants of concern partially escape humoral but not T-cell responses in COVID-19 convalescent donors and vaccinees. Sci. Immunol. 2021;6:eabj1750. doi: 10.1126/sciimmunol.abj1750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graham M.S., Sudre C.H., May A., Antonelli M., Murray B., Varsavsky T., Kläser K., Canas L.S., Molteni E., Modat M., et al. COVID-19 Genomics UK (COG-UK) Consortium Changes in symptomatology, reinfection, and transmissibility associated with the SARS-CoV-2 variant B.1.1.7: an ecological study. Lancet Public Health. 2021;6:e335–e345. doi: 10.1016/S2468-2667(21)00055-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas E.J., Angulo F.J., McLaughlin J.M., Anis E., Singer S.R., Khan F., Brooks N., Smaja M., Mircus G., Pan K., et al. Impact and effectiveness of mRNA BNT162b2 vaccine against SARS-CoV-2 infections and COVID-19 cases, hospitalisations, and deaths following a nationwide vaccination campaign in Israel: an observational study using national surveillance data. Lancet. 2021;397:1819–1829. doi: 10.1016/S0140-6736(21)00947-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann M., Hofmann-Winkler H., Krüger N., Kempf A., Nehlmeier I., Graichen L., Arora P., Sidarovich A., Moldenhauer A.S., Winkler M.S., et al. SARS-CoV-2 variant B.1.617 is resistant to bamlanivimab and evades antibodies induced by infection and vaccination. Cell Rep. 2021;36:109415. doi: 10.1016/j.celrep.2021.109415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy D.A., Read A.F. Why does drug resistance readily evolve but vaccine resistance does not? Proc. Biol. Sci. 2017;284:20162562. doi: 10.1098/rspb.2016.2562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kustin T., Harel N., Finkel U., Perchik S., Harari S., Tahor M., Caspi I., Levy R., Leshchinsky M., Ken Dror S., et al. Evidence for increased breakthrough rates of SARS-CoV-2 variants of concern in BNT162b2-mRNA-vaccinated individuals. Nat. Med. 2021;27:1379–1384. doi: 10.1038/s41591-021-01413-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C., Ginn H.M., Dejnirattisai W., Supasa P., Wang B., Tuekprakhon A., Nutalai R., Zhou D., Mentzer A.J., Zhao Y., et al. Reduced neutralization of SARS-CoV-2 B.1.617 by vaccine and convalescent serum. Cell. 2021;184:4220–4236.e13. doi: 10.1016/j.cell.2021.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez Bernal J., Andrews N., Gower C., Gallagher E., Simmons R., Thelwall S., Stowe J., Tessier E., Groves N., Dabrera G., et al. Effectiveness of Covid-19 Vaccines against the B.1.617.2 (Delta) Variant. N. Engl. J. Med. 2021;385:585–594. doi: 10.1056/NEJMoa2108891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lustig Y., Zuckerman N., Nemet I., Atari N., Kliker L., Regev-Yochay G., Sapir E., Mor O., Alroy-Preis S., Mendelson E., Mandelboim M. Neutralising capacity against Delta (B.1.617.2) and other variants of concern following Comirnaty (BNT162b2, BioNTech/Pfizer) vaccination in health care workers, Israel. Euro Surveill. 2021;26:2100557. doi: 10.2807/1560-7917.ES.2021.26.26.2100557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madhi S.A., Baillie V., Cutland C.L., Voysey M., Koen A.L., Fairlie L., Padayachee S.D., Dheda K., Barnabas S.L., Bhorat Q.E., et al. NGS-SA Group. Wits-VIDA COVID Group Efficacy of the ChAdOx1 nCoV-19 Covid-19 Vaccine against the B.1.351 Variant. N. Engl. J. Med. 2021;384:1885–1898. doi: 10.1056/NEJMoa2102214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathieu E., Ritchie H., Ortiz-Ospina E., Roser M., Hasell J., Appel C., Giattino C., Rodés-Guirao L. A global database of COVID-19 vaccinations. Nat. Hum. Behav. 2021;5:947–953. doi: 10.1038/s41562-021-01122-8. [DOI] [PubMed] [Google Scholar]
- Mor O., Zuckerman N.S., Hazan I., Fluss R., Ash N., Ginish N., Mendelson E., Alroy-Preis S., Freedman L., Huppert A. BNT162b2 vaccine effectiveness was marginally affected by the SARS-CoV-2 beta variant in fully vaccinated individuals. J. Clin. Epidemiol. 2021;142:38–44. doi: 10.1016/j.jclinepi.2021.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muik A., Wallisch A.K., Sänger B., Swanson K.A., Mühl J., Chen W., Cai H., Maurus D., Sarkar R., Türeci Ö., et al. Neutralization of SARS-CoV-2 lineage B.1.1.7 pseudovirus by BNT162b2 vaccine-elicited human sera. Science. 2021;371:1152–1153. doi: 10.1126/science.abg6105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ong S.W.X., Chiew C.J., Ang L.W., Mak T.M., Cui L., Toh M.P.H.S., Lim Y.D., Lee P.H., Lee T.H., Chia P.Y., et al. Clinical and virological features of SARS-CoV-2 variants of concern: a retrospective cohort study comparing B.1.1.7 (Alpha), B.1.315 (Beta), and B.1.617.2 (Delta) Clin. Infect. Dis. 2021 doi: 10.1093/cid/ciab721. Published online August 23, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Planas D., Bruel T., Grzelak L., Guivel-Benhassine F., Staropoli I., Porrot F., Planchais C., Buchrieser J., Rajah M.M., Bishop E., et al. Sensitivity of infectious SARS-CoV-2 B.1.1.7 and B.1.351 variants to neutralizing antibodies. Nat. Med. 2021;27:917–924. doi: 10.1038/s41591-021-01318-5. [DOI] [PubMed] [Google Scholar]
- Planas D., Veyer D., Baidaliuk A., Staropoli I., Guivel-Benhassine F., Rajah M.M., Planchais C., Porrot F., Robillard N., Puech J., et al. Reduced sensitivity of SARS-CoV-2 variant Delta to antibody neutralization. Nature. 2021;596:276–280. doi: 10.1038/s41586-021-03777-9. [DOI] [PubMed] [Google Scholar]
- Polack F.P., Thomas S.J., Kitchin N., Absalon J., Gurtman A., Lockhart S., Perez J.L., Pérez Marc G., Moreira E.D., Zerbini C., et al. C4591001 Clinical Trial Group Safety and Efficacy of the BNT162b2 mRNA Covid-19 Vaccine. N. Engl. J. Med. 2020;383:2603–2615. doi: 10.1056/NEJMoa2034577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadoff J., Gray G., Vandebosch A., Cárdenas V., Shukarev G., Grinsztejn B., Goepfert P.A., Truyers C., Fennema H., Spiessens B., et al. ENSEMBLE Study Group Safety and Efficacy of Single-Dose Ad26.COV2.S Vaccine against Covid-19. N. Engl. J. Med. 2021;384:2187–2201. doi: 10.1056/NEJMoa2101544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheikh A., McMenamin J., Taylor B., Robertson C., Public Health Scotland and the EAVE II Collaborators SARS-CoV-2 Delta VOC in Scotland: demographics, risk of hospital admission, and vaccine effectiveness. Lancet. 2021;397:2461–2462. doi: 10.1016/S0140-6736(21)01358-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Supasa P., Zhou D., Dejnirattisai W., Liu C., Mentzer A.J., Ginn H.M., Zhao Y., Duyvesteyn H.M.E., Nutalai R., Tuekprakhon A., et al. Reduced neutralization of SARS-CoV-2 B.1.1.7 variant by convalescent and vaccine sera. Cell. 2021;184:2201–2211.e7. doi: 10.1016/j.cell.2021.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarke A., Sidney J., Methot N., Yu E.D., Zhang Y., Dan J.M., Goodwin B., Rubiro P., Sutherland A., Wang E., et al. Impact of SARS-CoV-2 variants on the total CD4+ and CD8+ T cell reactivity in infected or vaccinated individuals. Cell Rep Med. 2021;2:100355. doi: 10.1016/j.xcrm.2021.100355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tegally H., Wilkinson E., Giovanetti M., Iranzadeh A., Fonseca V., Giandhari J., Doolabh D., Pillay S., San E.J., Msomi N., et al. Detection of a SARS-CoV-2 variant of concern in South Africa. Nature. 2021;592:438–443. doi: 10.1038/s41586-021-03402-9. [DOI] [PubMed] [Google Scholar]
- Volz E., Mishra S., Chand M., Barrett J.C., Johnson R., Geidelberg L., Hinsley W.R., Laydon D.J., Dabrera G., O’Toole Á., et al. COVID-19 Genomics UK (COG-UK) consortium Assessing transmissibility of SARS-CoV-2 lineage B.1.1.7 in England. Nature. 2021;593:266–269. doi: 10.1038/s41586-021-03470-x. [DOI] [PubMed] [Google Scholar]
- Voysey M., Clemens S.A.C., Madhi S.A., Weckx L.Y., Folegatti P.M., Aley P.K., Angus B., Baillie V.L., Barnabas S.L., Bhorat Q.E., et al. Oxford COVID Vaccine Trial Group Safety and efficacy of the ChAdOx1 nCoV-19 vaccine (AZD1222) against SARS-CoV-2: an interim analysis of four randomised controlled trials in Brazil, South Africa, and the UK. Lancet. 2021;397:99–111. doi: 10.1016/S0140-6736(20)32661-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang P., Casner R.G., Nair M.S., Wang M., Yu J., Cerutti G., Liu L., Kwong P.D., Huang Y., Shapiro L., Ho D.D. Increased resistance of SARS-CoV-2 variant P.1 to antibody neutralization. Cell Host Microbe. 2021;29:747–751.e4. doi: 10.1016/j.chom.2021.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang P., Nair M.S., Liu L., Iketani S., Luo Y., Guo Y., Wang M., Yu J., Zhang B., Kwong P.D., et al. Antibody resistance of SARS-CoV-2 variants B.1.351 and B.1.1.7. Nature. 2021;593:130–135. doi: 10.1038/s41586-021-03398-2. [DOI] [PubMed] [Google Scholar]
- Wibmer C.K., Ayres F., Hermanus T., Madzivhandila M., Kgagudi P., Oosthuysen B., Lambson B.E., de Oliveira T., Vermeulen M., van der Berg K., et al. SARS-CoV-2 501Y.V2 escapes neutralization by South African COVID-19 donor plasma. Nat. Med. 2021;27:622–625. doi: 10.1038/s41591-021-01285-x. [DOI] [PubMed] [Google Scholar]
- World Health Organization . 2021. Weekly epidemiological update on COVID-19 - 10 August 2021.https://www.who.int/publications/m/item/weekly-epidemiological-update-on-covid-19---10-august-2021 [Google Scholar]
- Zhou D., Dejnirattisai W., Supasa P., Liu C., Mentzer A.J., Ginn H.M., Zhao Y., Duyvesteyn H.M.E., Tuekprakhon A., Nutalai R., et al. Evidence of escape of SARS-CoV-2 variant B.1.351 from natural and vaccine-induced sera. Cell. 2021;184:2348–2361.e6. doi: 10.1016/j.cell.2021.02.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
-
•
This study did not use or generate data aside from the reproducible output of the mathematical model.
-
•
All original code, including that needed to generate the figures in the main text and supplemental information, has been deposited in Open Science Framework and is publicly available as of the date of publication. The digital object identifier (DOI) is listed in the key resources table.
-
•
Any additional information required to use or analyze the model described in this paper is available from the lead contact upon request.