Abstract
The restrictions have been preferred by governments to reduce the spread of Covid-19 and to protect people's health according to regional risk levels. The risk levels of locations are determined due to threshold values based on the number of cases per 100,000 people without environmental variables. The purpose of our study is to apply unsupervised machine learning techniques to determine the cities with similar risk levels by using the number of cases and environmental parameters. Hierarchical, partitional, soft, and gray relational clustering algorithms were applied to different datasets created with weekly the number of cases, population densities, average ages, and air pollution levels. Comparisons of the clustering algorithms were performed by using internal validation indexes, and the most successful method was identified. In the study, it was revealed that the most successful method in clustering based on the number of cases is Gray Relational Clustering. The results show that using the environmental variables for restrictions requires more clusters than 4 for healthier decisions and Gray Relational Clustering gives stable results, unlike other algorithms.
Keywords: Covid-19, Risk levels, Restrictions, Unsupervised machine learning, Clustering, Gray relational clustering
1. Introduction
The Covid-19 epidemic has spread rapidly all over the world since 2019 and affects people's lives adversely. Countries make great efforts to solve the economic, health, and social problems caused by Covid-19. It is still tried to prevent the spread of the epidemic by some personal, regional, and national precautions related to the problems. In order to prevent the spreading of the virus, restrictions are applied regionally. In some cases, these limitations are expanded throughout the country and lead to curfews. The main factor for restrictions is the number of Covid-19 cases per 100,000 people. In the literature, it is stated that some environmental variables such as average age, population density, acreage, and air quality that affect the spreading of the virus should be used in the analysis. In the literature, it is stated that the average age (Ferguson et al., 2020, Wang et al., 2020) and crowded environments (Hutchins et al., 2020) increase the risk level of the pandemic. Although a few studies reveal that there is no significant relationship between air pollution and Covid-19 infection (Bontempi, 2020, Fattorini and Regoli, 2020, Conticini et al., 2020), some studies are emphasized that air pollution leads increasing of the risk levels and should be included in the analysis (Ciencewicki and Jaspers, 2007, Ye et al., 2016).
Due to Covid-19 cases, some restrictions are imposed such as curfews under age 18 and over age 65, closing restaurants and cafes, banning meetings and demonstrations, closing schools, transition to flexible working, banning intercity travels, curfew, etc. Decisions are partly taken by regional governments, while wider restrictions are by the central government in Turkey. The restrictions are applied based on the data announced by the Ministry of Health. In general, only the number of cases per 100,000 people is used as a parameter for restrictions. The criteria used to determine the risk groups by the fixed-threshold values (FV) in Turkey are given in Table 1 .
Table 1.
Case values in determining the risk groups in Turkey*.
| Risk levels | Number of cases | Color |
|---|---|---|
| Low risk provinces | Blue | |
| Middle risk provinces | Yellow | |
| High risk provinces | Orange | |
| Very high risk provinces | Red |
*Announced by the Ministry of Health of the Republic of Turkey on March 02, 2021
As seen in Table 1, provinces are evaluated in 4 different risk groups depending on the number of cases in 100,000 people. Restrictions are applied by the government according to risk levels. For example, the province with a number of cases between 0 and 20 that means no restrictions are defined as low risk and colored in blue. The other risk levels of the groups are determined with yellow, orange, and red, respectively. Using the FV can be thought of as a clustering technique, but it is not a suitable method for the clustering approach. New threshold values need to be determined when the number of cases increases, so the method will not use efficiently. Changes frequently in threshold values will create confusion for the determination of risk levels, lead to unhealthy groupings and decrease the efficiency of restrictions. In addition, it is not possible to apply this method in the analysis of datasets to which environmental variables are added. For these reasons, the FV method cannot offer a sustainable clustering opportunity. In this study, unsupervised machine learning techniques were applied to obtain regional risk groups instead of FV. Clustering that defined as the grouping of similar data is an important research area in machine learning (Han et al., 2012). Clustering techniques that can effectively identify regions with similar characteristics according to risk levels will make significant contributions to restriction decisions. It is observed in the literature that clustering analyses are preferred rarely in determining the risk levels related to Covid-19 cases.
Hierarchical (HC), K-Means (KM), and Fuzzy C-Means (FCM) are among the most preferred algorithms in the literature for clustering analysis applied according to dataset characteristics (Peters et al., 2013). In particular, the insufficient number of items in the dataset decreases the efficiency or may cause even failure. The limited sample and the inability to collect data in detail are the main problems for clustering Covid-19 cases. It is emphasized in some studies that Gray System Theory-based approaches offer much more performance in clustering datasets containing limited data (Wu et al., 2012, Fidan and Yuksel, 2020). In this context, our study has two purposes. The first aim is to specify the unsupervised machine learning algorithm having the least error in determining risk groups. So, clustering analysis was performed using HC, KM, FCM, and Gray Relational Clustering (GRC) algorithms. The second aim of the study is to compare the clustering performances of different datasets created by the number of cases, the population density, the average age, and the air pollution variables that are stated in the literature affecting the spread of Covid-19. In this context, clustering algorithms were applied to 4 datasets created with data belonging to 81 provinces in Turkey, and the clustering performances of algorithms were compared by Silhouette, Calinski-Harabasz, and Dunn indexes. The results revealed that the risk levels of the regions can be determined by using unsupervised machine learning techniques, and the most successful algorithms is GRC having the highest clustering performance.
2. Related works on clustering Covid-19 cases
The Covid-19 outbreak that spreads all over the world shortly after the first cases were seen in China in December 2019, has also become an attractive subject for academic researches. Researchers, who have limited data at the beginning of the epidemic, have more data about Covid-19 now. In researches, analyzes have been realized by using daily data, as well as data in a certain time period. In these studies, clustering, classification, and prediction have been realized based on the number of cases of countries and regions.
Claiming that traditional time series algorithms cannot give reliable results due to reasons such as the different lengths of the Covid-19 case numbers and the inconsistent ranges between the data, Zarikas et al. (2020) have developed a clustering method based on HC. The researchers performed the clustering analysis with the number of cases, active cases per population and active cases per area of 30 countries emphasized that population size and area size should also be used in the analyzes. Adam et al. (2020), who conducted a cluster analysis according to the transmission types of Covid-19 cases, divided the transmission sources of 1039 confirmed cases into 51 clusters. According to the results of the research, social environments such as cafes, restaurants, meetings, theaters are the first place accelerating the spread of infection. In this context, the first precaution should be the restriction of social environments. Maugeri et al. (2020), who carried out regional clustering of Covid-19 cases in Italy, used HC and KM algorithms. The researchers, grouped the regions under 4 clusters, stated that the KM algorithm is an alternative tool for measuring Covid-19 spread. In a study, HC and KM clustering algorithms were applied to multivariate time series. 32-day data was examined and it was found that there was a close similarity between the number of cases and deaths (James & Menzies, 2020). Virgantari & Faridhan (2020), who conducted cluster analysis with KM using the number of Covid-19 cases in Indonesia, grouped 34 provinces under 7 clusters with 680 confirmed case data occurring in one day. The study, which emphasized that the KM algorithm is a suitable option, has no comparisons with different algorithms. In another study, the Covid-19 case clustering of American states was carried out by using daily confirmed case data (Chen et al., 2020). The states were divided into 7 clusters by applying KM to the Nonnegative Matrix Factorization coefficients. Applying the same method to the number of cases on different days, the researchers determined the states be restricted and reopened. Stating that Hard Clustering methods will not work in determining the data in the intermediate regions, Mahmoudi et al. (2020) suggested that soft clustering will yield more successful results in Covid-19 case data. The researchers applied the FCM for clustering the virus spread and divided the countries into 3 risk groups. Crnogorac et al. (2021) carried out the Covid-19 case clustering of European countries with KM, HC, and Balanced Iterative Reducing and Clustering using Hierarchies (BIRCH) and compared the performances with the Silhouette metric. According to the comparison results, it was stated that there were no significant differences between performances and that three algorithms could be used in clustering Covid-19 cases. In a study investigating the effect of living areas on the spread of Covid-19, spatial clustering analysis was performed on the data obtained from the Indian Ministry of Health (Das et al., 2021). It was determined that the data on the living areas are an important factor in the spread of Covid-19. Kinnunen et al. (2021), which perform the clustering analysis of countries according to the economic policies applied to alleviate the restrictions in the Covid-19 process, used the Gaussian Mixture Model (GMM). They argued that GMM is a viable choice for large datasets, but fuzzy approaches would be more appropriate for comparative analysis of countries and regions (Kinnunen et al., 2021). In a recent study, it has been emphasized that using unsupervised machine learning methods for Covid-19 case analyzes will increase efficiency (Hozumi et al., 2021). In the study, KM was proposed for Covid-19 clustering analysis, Uniform Manifold Approximation and Projection (UMAP) is recommended for dimension reduction of the dataset.
In the literature, it is observed that the number of cases is the main variable for clustering analysis of Covid-19, environmental parameters are ignored, and HC and KM algorithms are generally applied to clustering. In addition to hard clustering approaches, there are also studies that suggest soft clustering methods. However, there are no studies using or suggesting the GRC method in the literature. GRC was emphasized as a method having very healthy results in clustering analyzes (Wu et al., 2012, Fidan, 2020). It is suggested especially in uncertainties arising from insufficient data (Fidan & Yuksel, 2020). In this context, it can be said that GRC is a viable option for the clustering of Covid-19 cases and the specifying regional risk levels.
3. Materials and methods
3.1. Dataset
The number of cases used in this study includes the number of Covid-19 cases seen in every 100,000 people approved on a provincial basis in Turkey announced by the Ministry of Health for February 20–26, 2021 (Turkish Ministry of Health, 2021). The population density and the average age of the provinces were collected from the Turkish Statistical Institute (TUIK) announced in 2020 (TUIK, 2021). The PM2.5 index was taken as a basis for the air pollution levels and the data were compiled from IQAir for 2020 (IQAIR, 2021). Data of the first 10 provinces in the dataset are presented in Table 2 . The full dataset can be seen in Appendix A.
Table 2.
Data of the first ten cities.
| Province | Covid-19 case (per 100.000) | Average age | Population density | Air pollution (PM2.5) | |
|---|---|---|---|---|---|
| P1 | Adana | 41,22 | 32,1 | 162 | 11,5 |
| P2 | Adıyaman | 116,2 | 27,7 | 90 | 36,1 |
| P3 | Afyon | 38,44 | 34,1 | 51 | 19,9 |
| P4 | Ağrı | 19 | 22,3 | 47 | 20 |
| P5 | Aksaray | 123,08 | 31,1 | 56 | 21,5 |
| P6 | Amasya | 110,5 | 38,1 | 59 | 31,7 |
| P7 | Ankara | 39,84 | 34,4 | 231 | 18,5 |
| P8 | Antalya | 78,11 | 35,0 | 123 | 18,4 |
| P9 | Ardahan | 58,37 | 33,6 | 20 | 21,9 |
| P10 | Artvin | 88,67 | 40,1 | 23 | 11,7 |
In order to compare the clustering performances, 4 different datasets were created with different variables. Thus, it is aimed to determine which variables increase the clustering performance. The datasets are given in Table 3 .
Table 3.
Building datasets.
| Dataset | Variables |
|---|---|
| Ds1 | Number of cases |
| Ds2 | Number of cases + Population density |
| Ds3 | Number of cases + Population density + Average age |
| Ds4 | Number of cases + Population density + Average age + Air pollution |
3.2. Unsupervised machine learning
It is a machine learning technique that is applied to determine the relationships, similarities, and patterns between values assuming that there will be data having more similarities than the others in a dataset (Alpaydın, 2010). Since there is no need for a supervisor, unsupervised machine learning does not include a training process. Thus, analysis of unlabeled data becomes possible. Due to the use of unlabeled data in the analysis, its performance is lower than other machine learning techniques. Unsupervised machine learning methods can be categorized under two general groups: association and clustering (Han et al., 2012). While the association method is used to identify patterns among unlabeled data, the clustering method is for grouping data. In this context, FV, which is used to group risk levels based on the number of Covid-19 cases, is not a valid clustering method for unsupervised machine learning. Because Covid-19 data is unlabeled, clustering will be the most appropriate method for determining regional risk groups.
Clustering defined as the grouping of data with similar characteristics is one of the most important unsupervised machine learning problems (Xu & Tian, 2015). In clustering analysis, it is desired to have similar data in the same groups and different data in separate groups as much as possible (Han et al., 2012). In other words, clustering is the process of grouping data having uncertainties in which group, according to their similarities and dissimilarities. The aim of clustering is to discover natural structures of data in a dataset according to their distances (Mirkin, 2005, Arbelaitz et al., 2013). Distance measures such as Cosine, Euclidean, Manhattan, Gini are applied to find the differences between the data (Fidan & Yuksel, 2020). There are many clustering methods having different approaches in the literature. Hierarchical, Partitional and Soft methods are among the most widely used approaches in the literature. The most preferred basic algorithms in these approaches are HC, KM, and FCM, respectively (Peters et al., 2013).
3.2.1. Hierarchical clustering
It is a clustering method has a binary tree structure that is performed by determining the closest pairs according to the distance between items. Two methods are used due to the tree structure namely agglomerative (bottom to top) and divisive (top to bottom) (Han et al., 2012). In the agglomerative method, each item in the dataset is considered as a single cluster initially. The closest two items determined by distance criteria are combined to form a cluster. Other items remain as a single cluster. In the second step, the closest item pairs are determined again and combined. This process continues until all items are in a single cluster. In the divisive method, all items are initially taken in a single cluster. The furthest item is thrown out of the cluster and considered as a separate cluster. This splitting process continues until each item creates a cluster on its own.
Finding the minimum distance between items is given in Eq. (1), determining the maximum distance is given in Eq. (2).
| (1) |
| (2) |
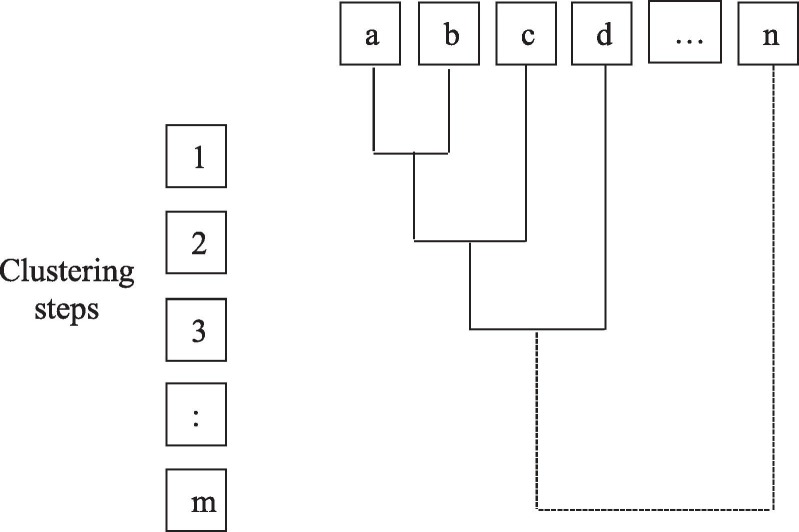
Eqs. (1) and (2) show the minimum and maximum values of the distance () between items. and indicate the item pairs, and indicates the distance between these items. According to the agglomerative approach, the scheme of HC is shown on the dendrogram in Fig. 1 , considering a data set with items.
Fig. 1.
Dendrogram of Agglomerative HC.
The dendrogram in Fig. 1 having an agglomerative tree structure shows the HC clustering of a dataset containing n items. So, clustering is performed by considering Eq. (1). Initially, each item represents a cluster and labelled as a, b, c, etc. The first item () is taken as a reference and the distance values for all items are calculated. The minimum value of these distances indicates the closest item to . In Fig. 1, item was found as the closest item to , and in the first step, and were combined into a cluster. The same process is repeated to find the second closest pair. This pairing process continues until all items are in one cluster.
HC is preferred especially when the number of clusters is uncertain since it does not require the number of clusters before analysis. In other words, it provides an advantage when the number of clusters cannot be determined as a parameter. It is also stated that it is more efficient than other clustering algorithms in the analysis of small datasets (Abbas, 2008). On the other hand, HC has disadvantages such as the long processing time, the inability to undo item pairing (Han et al., 2012), and fluctuation in the performance for small datasets (Fidan & Yuksel, 2020).
3.2.2. K-Means Clustering
The KM algorithm was described in MacQueen's work “Some Methods for Classification and Analysis of Multivariate Observations” in 1967. In the KM algorithm, it is aimed to determine the closest members to a randomly selected center for each cluster in order to create clusters (MacQueen, 1967). Distance measures such as Euclid, Manhattan, and Cosine are used to calculate the distance between members, and the average of the distance values of the items in the cluster is accepted as the cluster center (Han et al., 2012). Since each cluster is created with the distances of the members from the center, the item can be placed in only one cluster. Methods in which an item cannot belong to another cluster are called Hard Clustering (Peters et al., 2013).
The KM algorithm is used to split a dataset of elements into groups. The parameter is used to determine the number of clusters and . KM aims to minimize the sum of squares of distances () from cluster centers (See in Eq. (3)).
| (3) |
Eq. (3) shows that is an item in cluster . represents the arithmetic mean of cluster . After determining the cluster centers in the first step, they are determined again according to the cluster members formed in the second step, and the process is repeated. The process of re-appointment of the centers, called iteration, continues until the minimum value of is determined (Peters et al., 2013).
The KM algorithm is the most widely used algorithm in literature because it is simple to implement and has a high processing speed for small amounts of data. However, it has some shortcomings. The main problem of the KM algorithm is that effective results cannot be achieved when the initial centers cannot be selected appropriately (Jain et al., 1999). Another drawback is the requirement of the parameter before clustering analysis (Fidan & Yuksel, 2020). Determining the value before the analysis causes a problem in the uncertainty of the number of clusters. The algorithm that works very fast at small values slows down as the value increases (Peters et al., 2013). Besides, the differences in cluster densities and cluster sizes reduce the efficiency of the KM algorithm (Han et al., 2012).
3.2.3. Fuzzy C-Means clustering
Pioneering research on fuzzy theory in clustering was published in the study named “A New Approach to Clustering” to develop an alternative method for data reduction (Ruspini, 1969). However, the FCM algorithm, which provides the starting point for soft clustering algorithms, was developed by Bezdek. The basic idea in the FCM approach given in Fig. 2 is that each item has relational values in the range of [0,1] with all cluster centers (Bezdek, 1981).
Fig. 2.
Fuzzy clustering.
In FCM clustering, the distance between items is determined by Euclidean distance. The clustering criterion is to minimize the weighted sums of membership values determined by item distances. Eq. (4) shows the clustering criteria for clusters of items.
| (4) |
where is membership degree of item for cluster , and . is called fuzzifier parameter and As the value increases, the fuzziness increases. The approaches 1, FCM will be similar to the K-means algorithm in terms of its results (Wu, 2012). In the literature, it is recommended to set for better results (Bezdek, 1981, Peters et al., 2013). The membership function of item in cluster () is calculated by Euclidean distance is given in Eq. (5).
| (5) |
means that item is definitely in the cluster and cannot be included in another cluster. means that item is definitely not in the cluster . Membership values between and () indicates the degree of closeness of item to cluster . It must be noted that the sum of all membership values of an item must be equal to (Bezdek, 1981). So, if , item has at least two memberships functions greater than . In this case, item will belong to two clusters.
3.2.4. Gray relational clustering
Gray System Theory (GST), which was seen in literature firstly with the study named “Control Problems of Gray System” performed by Deng, is a method recommended for analysis of datasets containing small samples and incomplete information (Deng, 1982). In the GST, the certain unknown information is represented by black, the certain known information is represented by white, while the partial information is represented by gray (Liu et al., 2012). GST is seen as one of the most successful methods to be used in cases of uncertainty arising from insufficient data (Fidan & Yuksel, 2020).
Gray Relational Clustering (GRC), which is developed on the basis of GST, is a clustering method that determines similar observations according to gray relational coefficients (Jin, 1993). Since clusters consist of items grouped according to a certain rule, the clusters have homogeneity (Wu et al., 2012). It is an effective clustering method with its easy implementation and flexible structure (Fidan & Yuksel, 2020). In addition, since the number of clusters can be determined after the clustering analysis, it is more realistic than traditional clustering algorithms (Wu et al., 2012). It is stated that GRC, which has recently started to be seen in clustering literature, has a higher performance than partitional-based algorithms (Chang and Yeh, 2005, Wu et al., 2012, Fidan and Yuksel, 2020, Fidan, 2020).
The first process in the GRC method is to create the decision matrix with the dataset to be clustered. The decision matrix for a dataset that has items and features is shown in Eq. (6).
| (6) |
where represents the items and represents the features of an item . Secondly, normalization is applied to decision matrix against the negative effects of extreme values. If the high values in the dataset affect the analysis result positively, utility-based normalization, if low values affect the analysis positively; cost-based normalization is applied. Utility-based and cost-based normalizations are given in Eqs. (7) and (8), respectively. Thus, the normalization matrix is obtained seen in Eq. (9).
| (7) |
| (8) |
| (9) |
The absolute differences matrix shown in Eq. (11) is obtained by using Eq. (10) that calculates the differences between the normalization matrix and the reference item. For example, if the first item is a reference (), the differences between the second item () for criterion is calculated by . After the absolute differences are calculated for all features of , the process is repeated while as . Thus, the process of absolute differences is applied to all items for the first reference (while ).
| (10) |
| (11) |
Using the absolute differences matrix, Gray coefficients are calculated with the help of Eq. (12). is called distinguish parameter and value should be (Ertugrul et al., 2016).
| (12) |
where and . Since there will be as many gray coefficients as the number of features in an item, gray relational degrees are calculated by the arithmetic mean of the coefficients. In Eq. (13), the calculation of gray relational degrees for item is shown. The highest value in the series formed with gray relational degrees means the item with the highest relational level with the reference series. The item that is closest to the reference item and that will build a cluster is determined. The center of the cluster consisting of these two items is the arithmetic mean of the members. Thus, the first cluster has been built. After the first clustering, a new decision matrix is created and the next item is determined as a reference and the processes are repeated to build the next cluster.
| (13) |
3.3. Measuring clustering performance
Validation techniques are used to measure the performance of algorithms. The measurements, which are classified under two groups, are named as external validation and internal validation, respectively, according to whether the cluster items contain external data or not (Han et al., 2012). Since there is no external data capability in internal validation methods, the performance of clustering algorithms is decided due to the structure of the clusters. Silhouette index (SI), Calinski-Harabasz index (CH), and Dunn index (DI) are commonly applied methods in the literature for internal validation (Arbelaitz et al., 2013, Hassani and Seidl, 2017, Gupta and Panda, 2019).
3.3.1. Silhouette index
SI is widely preferred in the literature since it takes into account the compactness and separation together in determining clustering performances (Chaimontree et al., 2010, Liu et al., 2010, Arbelaitz et al., 2013, Mahi et al., 2018, Gupta and Panda, 2019). The calculation method of the SI is given in Eq. (14).
| (14) |
| (15) |
| (16) |
Eq. (14) is written considering that a dataset with items has clusters. Item in the equation is a member of cluster and . given in Eq. (15) is the arithmetic mean of the distances to the items in the cluster containing item . in Eq. (16) is the minimum value of the arithmetic mean of the distances of item from other cluster items. In other words, is the average distance of the closest cluster's items to item . Euclidean is used to determine the distance between items. The value in Eq. (15) and Eq. (16) is calculated by . For a multivariable dataset containing properties, distance is calculated as where and (Han, Kamber and Pei, 2012). The calculated SI value is . The closer value to the + 1 indicates that the performance of cluster analysis is high (Rousseeuw, 1987).
3.3.2. Calinski-Harabasz index
The CH index is an internal validation method calculated by the ratio of the separation value between the clusters to the dispersion value within the cluster (Calinski & Harabasz, 1974). The dispersion value is the distance of cluster items from the cluster center. The separation value between clusters is the distance of cluster centers from center of the entire dataset. The CH index for items and clusters is given in Eq. (17).
| (17) |
where and
In Eq. (17), is the inter-cluster divergence and is the intra-cluster divergence. and represent the number of items and the arithmetic mean of cluster , and represents the arithmetic mean of entire dataset. In other words, is the centroid of cluster and is the centroid of the dataset. is an item of the cluster.
The high CH value means the clustering algorithm has high performance (Liu et al., 2010). In addition, the maximum CH value shows the optimal number of clusters (Arbelaitz et al., 2013, Kettani et al., 2015). The CH index, also called Variance Ratio Criterion, is stated in some studies to be widely used because it gives more consistent results compared to other indexes, has an easy implementation, and has a low computational cost (Milligan and Cooper, 1985, Kettani et al., 2015, Harsh and Ball, 2016).
3.3.3. Dunn index
DI is another internal validation index measuring clustering performance by using the ratio of intra-cluster compactness and inter-cluster separation (Dunn, 1973). While the minimum distance between items in different clusters is taken as the basis for separation between clusters, the maximum diameter of the clusters represents the compactness (Arbelaitz et al., 2013). In other words, the DI given in Eq. (18) is the ratio of the minimum distance between items in all clusters to the maximum diameter among the clusters.
| (18) |
where and being different cluster items and . A high DI value means a high clustering performance, and the value with the maximum DI value indicates the optimal number of clusters (Arbelaitz et al., 2013).
4. Results and discussion
In the experimental study, hierarchical, partitional, soft clustering, and gray relational methods are used. For clustering analysis, Agglomerative HC for hierarchical, KM for partitional, FCM for soft clustering, and GRC were preferred. R was used for the HC, KM, and FCM algorithms. The GRC algorithm was improved by C#. The validation values of FV were found 0.67 for SI, 362.18 for CH and 0.046 for DI. Validation values according to the number of clusters of the algorithms are shown in Table 4 .
Table 4.
Clustering validation values of algorithms
| Data-set | Algo-rithm | k = 3 |
k = 4 |
k = 5 |
k = 6 |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SI | CH | DI | SI | CH | DI | SI | CH | DI | SI | CH | DI | ||
| Ds1 | HC | 0.65 | 299.64 | 0.038 | 0.63 | 309.16 | 0.044 | 0.53 | 354.47 | 0.032 | 0.51 | 407.23 | 0.032 |
| KM | 0.65 | 308.94 | 0.04 | 0.55 | 340.83 | 0.022 | 0.55 | 419.61 | 0.025 | 0.49 | 425.44 | 0.021 | |
| FCM | 0.64 | 276.17 | 0.028 | 0.56 | 301.93 | 0.006 | 0.56 | 396.94 | 0.018 | 0.42 | 380.12 | 0.009 | |
| GRC | 0.65 | 346.34 | 0.04 | 0.69 | 368.52 | 0.045 | 0.74 | 462.56 | 0.052 | 0.75 | 468.42 | 0.054 | |
| Ds2 | HC | 0.63 | 645.92 | 0.285 | 0.61 | 698.31 | 0.048 | 0.39 | 724.74 | 0.062 | 0.38 | 808.28 | 0.075 |
| KM | 0.58 | 655.85 | 0.127 | 0.57 | 759.78 | 0.084 | 0.44 | 746.81 | 0.062 | 0.36 | 881.42 | 0.034 | |
| FCM | 0.27 | 9.42 | 0.007 | 0.25 | 10.31 | 0.005 | 0.16 | 8.46 | 0.003 | 0.12 | 6.66 | 0.005 | |
| GRC | 0.52 | 781.46 | 0.082 | 0.53 | 751.84 | 0.084 | 0.55 | 892.14 | 0.092 | 0.54 | 894.38 | 0.098 | |
| Ds3 | HC | 0.63 | 642.91 | 0.069 | 0.6 | 693.33 | 0.101 | 0.42 | 728.61 | 0.105 | 0.41 | 791.65 | 0.134 |
| KM | 0.58 | 652.77 | 0.095 | 0.56 | 754.12 | 0.167 | 0.43 | 739.68 | 0.081 | 0.38 | 869.67 | 0.121 | |
| FCM | 0.25 | 8.87 | 0.022 | 0.21 | 10.24 | 0.012 | 0.15 | 8.46 | 0.012 | 0.1 | 6.65 | 0.015 | |
| GRC | 0.49 | 634.14 | 0.078 | 0.47 | 691.24 | 0.086 | 0.46 | 762.46 | 0.126 | 0.48 | 796.82 | 0.148 | |
| Ds4 | HC | 0.63 | 638.46 | 0.085 | 0.6 | 685.66 | 0.093 | 0.4 | 714.51 | 0.123 | 0.35 | 757.26 | 0.134 |
| KM | 0.58 | 648.15 | 0.097 | 0.56 | 745.09 | 0.150 | 0.42 | 728.35 | 0.116 | 0.38 | 849.94 | 0.108 | |
| FCM | 0.24 | 8.86 | 0.048 | 0.16 | 10.14 | 0.048 | 0.12 | 7.71 | 0.048 | 0.1 | 8.4 | 0.048 | |
| GRC | 0.42 | 748.42 | 0.092 | 0.52 | 756.62 | 0.098 | 0.48 | 812.32 | 0.138 | 0.5 | 856.14 | 0.146 | |
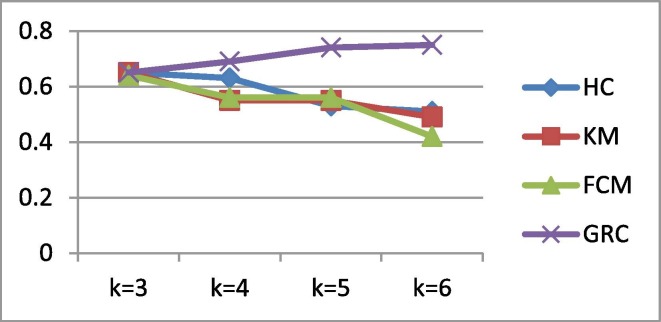
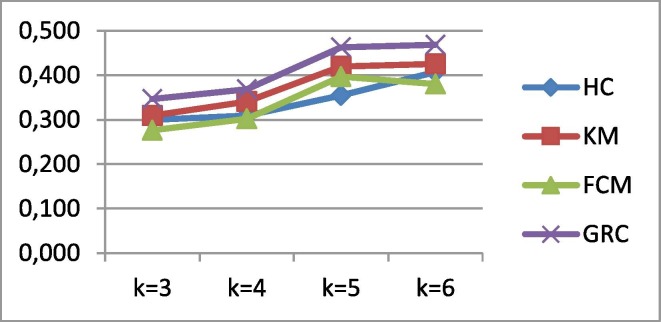
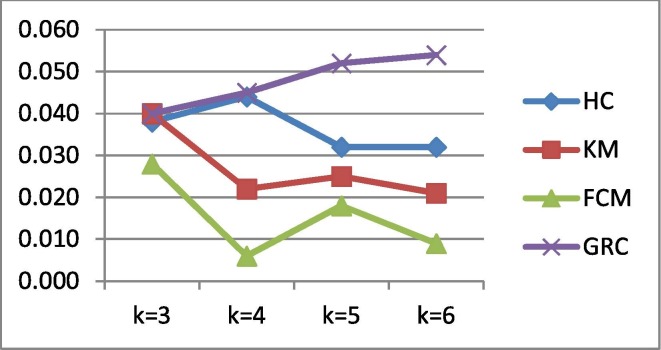
The Ds1 that contains only the number of cases was used for the analysis firstly. The number of cluster was set as 3, 4, 5, and 6, respectively and clustering validation values were calculated by SI, CH and DI. According to the SI and DI values in Ds1, It was observed that with the increase in the number of cluster in all algorithms except GRC, the performances of the algorithms decreased. A similar situation has been observed in other datasets built by adding parameters to Ds1. For clustering of Ds1, SI, CH and DI results revealed that the most successful clustering algorithm is the GRC. GRC has the highest performance in all analyses of Ds1. The highest GRC performance in Ds1 was observed as SI = 0.75, CH = 468.42 and DI = 0.054 at k = 6. In the case of k = 4 in Ds1 clustering, GRC performed more efficient compared to FV according to SI and CH values. The DI value of FV is almost the same as the DI value of GRC. This result proves that the GRC demonstrates more clustering performance for Ds1 than the FV and others algorithms. In the clustering analysis of Ds1, the algorithm performances due to the number of clusters are given in Fig. 3 for SI, Fig. 4 for CH and Fig. 5 for DI. In all metrics, it is seen that the most successful algorithm for all clusters in Ds1 is GRC. The risk groups of the provinces determined by FV and GRC for Ds1 are given in Table 5 .
Fig. 3.
SI values of the algorithms (for Ds1).
Fig. 4.
CH values of the algorithms (for Ds1).
Fig. 5.
DI values of the algorithms (for Ds1).
Table 5.
Provinces in risk groups according to FV and GRC (for Ds1, k = 4).
| Risk groups | Provinces by FV | Provinces by GRC |
|---|---|---|
| 1 | P4, P14, P17, P18, P26, P36, P38, P57, P60, P68, P71, P72, P77, P78 | P4, P18, P26, P36, P38, P45, P50, P57, P60, P68, P71, P72, P77, P78 |
| 2 | P1, P3, P7, P11, P13, P15, P21, P23, P24, P25, P29, P30, P31, P32, P33, P37, P39, P42, P43, P45, P46, P50, P55, P56, P61, P70, P76, P80 | P1, P3, P7, P14, P17, P15, P23, P24, P25, P29, P30, P33, P37, P39, P42, P43, P46, P56, P70, P76 |
| 3 | P8, P9, P10, P16, P19, P22, P27, P40, P41, P44, P47, P48, P49, P51, P52, P54, P58, P59, P62, P73, P79, P81 | P2, P5, P6, P8, P9, P10, P11, P13, P16, P19, P20, P21, P22, P27, P28, P31, P32, P35, P40, P41, P44, P47, P48, P49, P51, P52, P53, P54, P55, P58, P59, P61, P62, P66, P73, P79, P80, P81 |
| 4 | P2, P5, P6, P12, P20, P28, P34, P35, P53, P63, P64, P65, P66, P67, P69, P74, P75 | P12, P34, P63, P64, P65, P67, P69, P74, P75 |
In Table 5, the lowest risk level of the cities is shown as 1, and the highest risk level is shown as 4. According to FV announced by the Ministry of Health in Turkey, there are 14 cities in the lowest risk group. Similar to FV results, 14 provinces are clustered by GRC for risk group 1. Unlike FV, GRC has determined that P14 and P17 will be in the risk group 2 instead of the lowest risk group. In addition, P45 and P50, which are in the second risk group in FV, must be in the lowest risk group according to GRC.
In the datasets built by adding environmental variables, negligible small differences were observed in the performance values of the HC, KM, and GRC algorithms. However, according to all validation values, the adding variables revealed significant decreases in FCM performance. Failure of FCM was observed when the number of clusters increased in the same dataset too. In other words, our study obtained that FCM has the lowest performance in all datasets, all indexes, and all values. Unlike the studies that recommend Fuzzy approaches in determining risk levels (Mahmoudi et al., 2020, Crnogorac et al., 2021, Kinnunen et al., 2021), our results revealed that FCM cannot give healthy results. The main reason for FCM's fail is that there are limited items in the dataset. In FCM clustering, using a small number of items cause insufficient membership functions. Only in Ds1 clustering, FCM has a close performance to other algorithms. In this context, FCM may be preferred for only the dataset that includes the number of Covid-19 cases. However, the FCM algorithm should not be preferred in small datasets having multivariable.
The results in the cluster analysis of Ds2, Ds3, and Ds4 that created by adding environmental parameters such as population density, average age, and air pollution to Ds1 are surprising. In Ds2, Ds3, and Ds4, the highest performing algorithms vary according to datasets and validation indexes in k = 3 and k = 4, while GRC has the highest performances in k = 5 and k = 6 for all datasets and all metrics. In this context, the study reveals that HC, KM, or GRC may be choices in multivariable datasets for the small number of risk levels, but GRC should be preferred for more risk levels. On the other hand, as the number of clusters increases in these datasets, the performance of all algorithms decreases according to SI, increase according to CH and DI. However, all index values show that no significant decrease in GRC performance was observed with the increase in the number of clusters. For example, the lowest GRC performance by SI values of Ds1 is 0.65 when k = 3, and the highest is 0.75 when k = 6. In other words, the range of GRC performances in Ds1 according to the cluster numbers is 0.1. This value is 0.14 for HC, 0.16 for KM and 0.22 for FCM. A similar situation is observed in datasets Ds2, Ds3 and Ds4 for GRC. This result proves that GRC is a stable clustering algorithm similar to the findings of Fidan & Yuksel (2020). Our study emphasizes that GRC is the most stable algorithms for determining regional Covid-19 risk levels.
5. Conclusion and suggestion
One of the precautions to control the Covid-19 epidemic that has harmful effects on people globally is to impose restrictions. These restrictions that include limitations in social and economic life generally are decided according to the number of cases per 100,000 people regionally. Determining risk levels and grouping cities by fixed values can be seen as a kind of clustering method. However, this method is not a valid approach for clustering. This study aimed to demonstrate that it would be more realistic to use unsupervised machine learning techniques for determining the restricted locations.
The algorithms of the 4 clustering approaches, namely Hierarchical, Partitional, Soft, and Gray Relational, were applied to the 4 datasets created with the number of cases, the population density, the average age, and the air pollution of provinces. Clustering performances were determined by using SI, CH, and DI. It has been determined that the traditional algorithms have less performance because the datasets containing only the number of cases have insufficient data. If clustering will be realized with only the number of cases, it was proved that GRC is the most successful algorithm. In this context, this study reveals that GRC is a more suitable option instead of FV in determining the areas to be restricted according to the number of Covid-19 cases.
This study emphasizes that the number of clusters is an important issue if more variables are used in the datasets besides the number of cases in determining the restrictions. It has been observed that a high number of clusters increases cluster performances. In this context, it would be a suitable decision to identify as many risk groups as possible for restrictions. Thus, healthier and more effective restriction decisions can be made within the scope of reducing the spread of Covid-19. In clustering datasets with environmental variables for determining the restriction regions, it would be proper to use GRC, HC or KM for the number of clusters 4 and below (), but GRC should be chosen for the number of clusters 5 and above (). In this context, this study recommends for governments that restrictions should be determined by at least 5 risk levels and grouped the regions by using GRC.
CRediT authorship contribution statement
Huseyin Fidan: Conceptualization, Software, Methodology, Visualization, Formal analysis, Resources, Supervision, Project administration, Investigation, Writing – original draft, Writing – review & editing. Mehmet Erkan Yuksel: Data curation, Formal analysis, Investigation, Writing – review & editing.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A. Dataset
| Province | Risk levels (determined by FV) | Covid-19 case (per 100.000) | Average age | Population density | Air pollution (PM2.5) |
|---|---|---|---|---|---|
| P1 | 2 | 41,22 | 32,1 | 162 | 11,5 |
| P2 | 4 | 116,2 | 27,7 | 90 | 36,1 |
| P3 | 2 | 38,44 | 34,1 | 51 | 19,9 |
| P4 | 1 | 19 | 22,3 | 47 | 20 |
| P5 | 4 | 123,08 | 31,1 | 56 | 21,5 |
| P6 | 4 | 110,5 | 38,1 | 59 | 31,7 |
| P7 | 2 | 39,84 | 34,4 | 231 | 18,5 |
| P8 | 3 | 78,11 | 35,0 | 123 | 18,4 |
| P9 | 3 | 58,37 | 33,6 | 20 | 21,9 |
| P10 | 3 | 88,67 | 40,1 | 23 | 11,7 |
| P11 | 2 | 42,24 | 38,1 | 143 | 19,4 |
| P12 | 4 | 142,57 | 40,6 | 87 | 15,1 |
| P13 | 2 | 42,72 | 39,6 | 96 | 24,9 |
| P14 | 1 | 8,06 | 23,2 | 133 | 27,2 |
| P15 | 2 | 31,51 | 30,8 | 22 | 11,1 |
| P16 | 3 | 60,84 | 36,1 | 51 | 15,8 |
| P17 | 1 | 15,81 | 28,1 | 34 | 13,3 |
| P18 | 1 | 15,68 | 23,8 | 50 | 8,2 |
| P19 | 3 | 83,1 | 37,0 | 38 | 22,5 |
| P20 | 4 | 105,36 | 38,6 | 39 | 25,4 |
| P21 | 2 | 49,78 | 34,8 | 298 | 25 |
| P22 | 3 | 81,51 | 40,3 | 55 | 13,5 |
| P23 | 2 | 28,5 | 38,5 | 26 | 19,5 |
| P24 | 2 | 28,12 | 38,1 | 41 | 36 |
| P25 | 2 | 32,14 | 36,4 | 89 | 31,3 |
| P26 | 1 | 17,94 | 24,3 | 118 | 9,1 |
| P27 | 3 | 55,91 | 34,4 | 154 | 33,3 |
| P28 | 4 | 107,43 | 40,4 | 67 | 17,2 |
| P29 | 2 | 39,68 | 33,0 | 70 | 19,7 |
| P30 | 2 | 37,13 | 33,7 | 20 | 26,7 |
| P31 | 2 | 48,3 | 28,6 | 30 | 34,2 |
| P32 | 2 | 43,85 | 36,9 | 64 | 18,6 |
| P33 | 2 | 36,35 | 25,5 | 308 | 18,3 |
| P34 | 4 | 264,71 | 40,4 | 66 | 21,3 |
| P35 | 4 | 114,58 | 34,5 | 22 | 22,8 |
| P36 | 1 | 4,97 | 24,2 | 39 | 6,2 |
| P37 | 2 | 40,46 | 29,8 | 285 | 8,1 |
| P38 | 1 | 17,19 | 25,9 | 56 | 17,8 |
| P39 | 2 | 39,14 | 36,3 | 53 | 25,8 |
| P40 | 3 | 89,9 | 33,2 | 2 976 | 16,7 |
| P41 | 3 | 53,42 | 37,2 | 366 | 12,9 |
| P42 | 2 | 32,9 | 29,1 | 81 | 7,1 |
| P43 | 2 | 25,8 | 37,4 | 59 | 26 |
| P44 | 3 | 64,76 | 33,3 | 29 | 19,2 |
| P45 | 2 | 22,84 | 27,8 | 28 | 16,8 |
| P46 | 2 | 34,1 | 40,6 | 29 | 22,1 |
| P47 | 3 | 88,05 | 32,3 | 83 | 24,6 |
| P48 | 3 | 51,43 | 36,1 | 61 | 15,3 |
| P49 | 3 | 96,44 | 39,8 | 58 | 12,8 |
| P50 | 2 | 21,89 | 35,4 | 38 | 10,2 |
| P51 | 3 | 68 | 27,0 | 100 | 22,8 |
| P52 | 3 | 99,18 | 32,6 | 553 | 16,9 |
| P53 | 4 | 119,28 | 31,8 | 58 | 30,7 |
| P54 | 3 | 71,97 | 37,5 | 48 | 23,6 |
| P55 | 2 | 46,35 | 33,1 | 68 | 24 |
| P56 | 2 | 39,64 | 36,2 | 111 | 21,8 |
| P57 | 1 | 9,24 | 23,5 | 97 | 12,2 |
| P58 | 3 | 91,57 | 33,7 | 121 | 16,8 |
| P59 | 3 | 57,38 | 38,7 | 78 | 25,2 |
| P60 | 1 | 16,64 | 22,6 | 51 | 6,1 |
| P61 | 2 | 48,51 | 34,7 | 57 | 22,8 |
| P62 | 3 | 58,59 | 32,1 | 49 | 20 |
| P63 | 4 | 301,76 | 38,5 | 128 | 16,6 |
| P64 | 4 | 145,13 | 30,9 | 176 | 12,1 |
| P65 | 4 | 213,1 | 37,5 | 88 | 20 |
| P66 | 4 | 114,34 | 34,1 | 216 | 24,4 |
| P67 | 4 | 262,17 | 36,1 | 149 | 17,1 |
| P68 | 1 | 16,35 | 22,4 | 60 | 14,1 |
| P69 | 4 | 160,03 | 41,4 | 37 | 8,1 |
| P70 | 2 | 29,85 | 34,1 | 22 | 23,1 |
| P71 | 1 | 15,4 | 20,4 | 113 | 14,2 |
| P72 | 1 | 2,29 | 21,2 | 75 | 21 |
| P73 | 3 | 85,55 | 34,3 | 171 | 16,6 |
| P74 | 4 | 166,5 | 36,6 | 60 | 23,9 |
| P75 | 4 | 239,52 | 36,3 | 174 | 23,7 |
| P76 | 2 | 27,25 | 37,5 | 11 | 15,4 |
| P77 | 1 | 18,4 | 36,9 | 69 | 16,1 |
| P78 | 1 | 10,13 | 23,0 | 60 | 21,4 |
| P79 | 3 | 85,01 | 36,3 | 326 | 14,1 |
| P80 | 2 | 42,75 | 35,0 | 30 | 12,8 |
| P81 | 3 | 59,11 | 39,3 | 179 | 22,5 |
References
- Abbas O.A. Comparisons between data clustering algorithms. International Arab Journal of Information Technology. 2008;5(3):320–325. [Google Scholar]
- Adam D.C., Wu P., Wong J.Y., Lau E.H.Y., Tsang T.K., Cauchemez S., et al. Clustering and superspreading potential of SARS-CoV-2 infections in Hong Kong. Nature Medicine. 2020;26(11):1714–1719. doi: 10.1038/s41591-020-1092-0. [DOI] [PubMed] [Google Scholar]
- Alpaydın E. The MIT Press Cambridge; London, England: 2010. Introduction to Machine Learning. [Google Scholar]
- Arbelaitz O., Gurrutxaga I., Muguerza J., Perez J.M., Perona I. An extensive comparative study of cluster validity indices. Pattern Recognition. 2013;46(1):243–256. doi: 10.1016/j.patcog.2012.07.021. [DOI] [Google Scholar]
- Bezdek J.C. Plenum Press; New York, USA: 1981. Pattern Recognition with Fuzzy Objective Algorithms. [Google Scholar]
- Bontempi E. First data analysis about possible COVID-19 virus airborne diffusion due to air particulate matter (PM): The case of Lombardy (Italy) Environmental Research. 2020;186:109639. doi: 10.1016/j.envres.2020.109639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calinski T., Harabasz J. A dendrite method for cluster analysis. Communications in Statistics. 1974;3:1–27. [Google Scholar]
- Chaimontree S., Atkinson K., Coenen F. In: Advanced Data Mining and Applications Lecture Notes in Computer Science. Cao L., Feng Y., Zhong J., editors. Springer; Berlin, Heidelberg: 2010. Best Clustering Configuration Metrics: Towards Multiagent Based Clustering; p. 6440. [DOI] [Google Scholar]
- Chang K.C., Yeh F. Grey relational analysis based approach for data clustering. IEE Proceedings - Vision, Image and Signal Processing. 2005;152(2):165–172. [Google Scholar]
- Chen, J., Yan, J., & Zhang, P. (2020). Clustering US States by Time Series of COVID-19 New Case Counts with Non-negative Matrix Factorization. https://arxiv.org/abs/2011.14412. Accessed May 7, 2021.
- Ciencewicki J., Jaspers I. Air pollution and respiratory viral infection. Inhalation Toxicology. 2007;19(14):1135–1146. doi: 10.1080/08958370701665434. [DOI] [PubMed] [Google Scholar]
- Conticini E., Frediani B., Caro D. Can atmospheric pollution be considered a co-factor in extremely high level of SARS-CoV-2 lethality in Northern Italy? Environmental Pollution. 2020;261:114465. doi: 10.1016/j.envpol.2020.114465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crnogorac V., Grbic M., Dukanovic M., Matic D. In 2021 20th International Symposium INFOTEH-JAHORINA (INFOTEH) 2021. March). Clustering of European countries and territories based on cumulative relative number of COVID 19 patients in 2020; pp. 1–6. [DOI] [Google Scholar]
- Das A., Ghosh S., Das K., Basu T., Dutta I., Das M. Living environment matters: Unravelling the spatial clustering of COVID-19 hotspots in Kolkata megacity India. Sustainable Cities and Society. 2021;65:102577. doi: 10.1016/j.scs.2020.102577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng D. Control problems of grey systems. System and Control Letters. 1982;1(5):288–294. [Google Scholar]
- Dunn J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. Journal of Cybernetics. 1973;3(3):32–57. [Google Scholar]
- Ertugrul, I., Oztas, T., Ozcil, A., & Oztas, G. Z. (2016). Grey relational analysis approach in academic performance comparison of university: A case study of Turkish universities. European Scientific Journal, June 2016 SPECIAL edition, 128-139.
- Fattorini D., Regoli F. Role of the chronic air pollution levels in the Covid-19 outbreak risk in Italy. Environmental Pollution. 2020;264:114732. doi: 10.1016/j.envpol.2020.114732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson, N. M., Laydon, D., Nedjati-Gilani, G., et al. (2020). Report 9: impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. London: Imperial College. https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/report-9-impact-of-npis-on-covid-19/. Accessed April 18, 2021.
- Fidan H. Grey Relational Classification of Consumers' Textual Evaluations in E-Commerce. Journal of Theoretical and Applied Electronic Commerce Research. 2020;15(1):48–65. doi: 10.4067/S0718-18762020000100105. [DOI] [Google Scholar]
- Fidan H., Yuksel M.E. A Novel Short Text Clustering Model Based on Grey System Theory. Arabian Journal for Science and Engineering. 2020;45(4):2865–2882. doi: 10.1007/s13369-019-04191-0. [DOI] [Google Scholar]
- Gupta T., Panda S.P. In International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon) 2019. Clustering Validation of CLARA and K-Means Using Silhouette & DUNN Measures on Iris Dataset. [DOI] [Google Scholar]
- Han J., Kamber M., Pei J. Third Edition. Morgan Kaufmann Publications; USA: 2012. Data Mining Concepts and Techniques. [Google Scholar]
- Harsh A., Ball J.E. Automatic k-expectation maximization (a k-em) algorithm for data mining applications. Journal of Computations & Modelling. 2016;6(3):43–85. [Google Scholar]
- Hassani M., Seidl T. Using internal evaluation measures to validate the quality of diverse stream clustering algorithms. Vietnam Journal of Computer Science. 2017;4(3):171–183. [Google Scholar]
- Hozumi Y., Wang R., Yin C., Wei G.-W. UMAP-assisted K-means clustering of large-scale SARS-CoV-2 mutation datasets. Computers in Biology and Medicine. 2021;131:104264. doi: 10.1016/j.compbiomed.2021.104264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchins, H. J., Wolff, B., Leeb, R., et al. (2020). COVID-19 Mitigation Behaviors by Age Group-United States, April–June 2020. MMWR Morbity Mortality Weekly Report, 69, 1584–1590. DOI: http://dx.doi.org/10.15585/mmwr.mm6943e4external icon. [DOI] [PMC free article] [PubMed]
- IQAIR, 2021. https://www.iqair.com/world-most-polluted-cities. Accessed May 15, 2021.
- Jain A.K., Murty M.N., Flynn P.J. Data Clustering: A review. ACM Computing Surveys. 1999;31(3):264–323. [Google Scholar]
- James N., Menzies M. Cluster-based dual evolution for multivariate time series: Analyzing COVID-19. Chaos: An Interdisciplinary. Journal of Nonlinear Science. 2020;30(6):061108. doi: 10.1063/5.0013156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin X. Grey relational clustering method and its application. The Journal of Grey System. 1993;3:181–188. [Google Scholar]
- Kettani O., Ramdani F., Tadili B. Ak-means: An automatic clustering algorithm based on K-means. Journal of Advanced Computer Science & Technology. 2015;4(2):231. doi: 10.14419/jacst.v4i210.14419/jacst.v4i2.4749. [DOI] [Google Scholar]
- Kinnunen, J., Georgescu, I., Hosseini, Z., & Androniceanu, A. M. (2021). Dynamic indexing and clustering of government strategies to mitigate Covid-19. Entrepreneurial Business and Economics Review, 9(2), 7-20. 10.15678/EBER.2021.090201.
- Liu S., Forrest J., Yang Y. A brief introduction to grey systems theory. Grey Systems: Theory and Application. 2012;2(2):89–104. [Google Scholar]
- Liu Y., Li Z., Xiong H., Gao X., Wu J. Understanding of Internal Clustering Validation Measures. IEEE International Conference on Data Mining. 2010;911–916 doi: 10.1109/ICDM.2010.35. [DOI] [Google Scholar]
- MacQueen J. In Proc. of the 5th Berkeley Symp. on Mathematical Statistics and Probability. 1967. Some Methods for Classification and Analysis of Multivariate Observations; pp. 281–297. [Google Scholar]
- Mahi H., Farhi N., Labed K., Benhamed D. The Silhouette Index and the K-Harmonic Means algorithm for Multispectral Satellite Images Clustering. In International Conference on Applied Smart Systems (ICASS) 2018 doi: 10.1109/icass.2018.8652068. [DOI] [Google Scholar]
- Mahmoudi M.R., Baleanu D., Mansor Z., Tuan B.A., Pho K.-H. Fuzzy clustering method to compare the spread rate of Covid-19 in the high risks countries. Chaos, Solitons & Fractals. 2020;140:110230. doi: 10.1016/j.chaos.2020.110230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maugeri A., Barchitta M., Agodi A. Clustering approach to classify italian regions and provinces based on prevalence and trend of SARS-CoV-2 cases. International Journal of Environmental Research and Public Health. 2020;17(15):5286. doi: 10.3390/ijerph17155286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milligan G.W., Cooper M.C. An examination of procedures for determining the number of clusters in a dataset. Psychometrika. 1985;50(2):159–179. [Google Scholar]
- Mirkin B. Chapman & Hall/CRC; Boca Raton, Florida: 2005. Clustering for Data Mining: A Data Recovery Approach. [Google Scholar]
- Peters G., Crespo F., Lingras P., Weber R. Soft clustering – Fuzzy and rough approaches and their extensions and derivatives. International Journal of Approximate Reasoning. 2013;54(2):307–322. doi: 10.1016/j.ijar.2012.10.003. [DOI] [Google Scholar]
- Rousseeuw P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. Journal of Computational and Applied Mathematics. 1987;20:53–65. doi: 10.1016/0377-0427(87)90125-7. [DOI] [Google Scholar]
- Ruspini E.H. A new approach to clustering. Information and Control. 1969;15(1):22–32. [Google Scholar]
- TUIK. 2021. https://www.tuik.gov.tr/. Accessed May 12, 2021.
- Turkish Ministry of Health, https://covid19.saglik.gov.tr. Accessed April 20, 2021.
- Virgantari, F., & Faridhan, Y. E. (2020, November). K-Means Clustering of COVID-19 Cases in Indonesia’s Provinces. In Proceedings of the International Conference on Global Optimization and Its Applications Jakarta, Indonesia, 21-22.
- Wang D., Hu B.o., Hu C., Zhu F., Liu X., Zhang J., et al. Clinical characteristics of 138 hospitalized patients With 2019 novel coronavirus-infected pneumonia in wuhan, China. JAMA. 2020;323(11):1061. doi: 10.1001/jama.2020.1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu K.-L. Analysis of parameter selections for fuzzy c-means. Pattern Recognition. 2012;45(1):407–415. [Google Scholar]
- Wu W.-H., Lin C.-T., Peng K.-H., Huang C.-C. Applying hierarchical grey relation clustering analysis to geographical information systems – A case study of the hospitals in Taipei city. Expert Systems with Applications. 2012;39(8):7247–7254. [Google Scholar]
- Xu D., Tian Y. A Comprehensive survey of clustering algorithms. Annals of Data Science. 2015;2(2):165–193. doi: 10.1007/s40745-015-0040-1. [DOI] [Google Scholar]
- Ye Q., Fu J.-F., Mao J.-H., Shang S.-Q. Haze is a risk factor contributing to the rapid spread of respiratory syncytial virus in children. Environmental Science and Pollution Research. 2016;23(20):20178–20185. doi: 10.1007/s11356-016-7228-6. [DOI] [PubMed] [Google Scholar]
- Zarikas V., Poulopoulos S.G., Gareiou Z., Zervas E. Clustering analysis of countries using the COVID-19 cases dataset. Data in Brief. 2020;31:105787. doi: 10.1016/j.dib.2020.105787. [DOI] [PMC free article] [PubMed] [Google Scholar]