Mathematical modelling of COVID-19: A case study of Italy

Abstract

This manuscript describes a mathematical epidemiological model of COVID-19 to investigate the dynamics of this pandemic disease and we have fitted this model to the current COVID-19 cases in Italy. We have obtained the basic reproduction number which plays a crucial role on the stability of disease free equilibrium point. Backward bifurcation with respect to the cure rate of treatment occurs conditionally. It is clear from the sensitivity analysis that the developments of self immunities with proper maintaining of social distancing of the exposed and asymptomatic individuals play key role for controlling the disease. We have validated the model by considering the COVID-19 cases of Italy and the future situations of epidemicity in Italy have been predicted from the model. We have estimated the basic reproduction number for the COVID-19 outbreak in Italy and effective reproduction number has also been studied. Finally, an optimal control model has been formulated and solved to realize the positive impacts of adapting lock down by many countries for maintaining social distancing.

1. Introduction

In the history of worldwide disease spreading public faced threat at different times due to appearance of new diseases in the human society, among them some are infectious diseases and some others are vector born diseases. The most notable threatening disease spreading were the Black death in Europe, small pox in Mexico, SARS in China in 2002–2003, MERS in Saudi Arabia in 2012, AIDS, Cancer, Malaria, etc. [7], [12], [24]. In 2019–2020 the most threatening disease is the coronavirus disease (COVID-19), which is caused by novel coronavirus (SARS-CoV-2) [30]. As on $29\mathrm{th}$ March, 2020 the COVID-19 spreads throughout the world [26], [35], [36] and about 199 countries have been affected. As a result WHO declared this disease as the Pandemic. The COVID-19 first was identified in Wuhan, China. Throughout the country up to 29th March, 2020 about 81 439, 3300 people were infected, died, respectively and throughout the whole world the numbers are 679 079 and 31 772, respectively [37]. The coronavirus infections previously occurred in different countries with low degree of harmfulness: those were the SARS-Cov (Severe Acute Respiratory Syndrome) [10] and MERS-CoV (Middle East Respiratory Syndrome) [34]. Still the outbreak of coronavirus is ongoing with higher degree of harmfulness as a result huge number of people are infected throughout the world. It creates huge threat to the global public health as well as the financial system also [6], [23], [38]. Though the infection was first reported in Wuhan, China in December 2019 but due to human movements it spreads throughout the world [22]. The emergence of COVID-19 occurs in a crucial time because this time is the spring festival time in Asia, so a large number of people move from one place to another places [23] and the disease starts to spread to huge number of people who move from their working place to their home land as a consequence the disease spreads to the whole world.

The infection of this disease spreads among the people through interactions and the intensity of the spreading is very high. So a large number of people is infected in a short span of time. Due to shortfall of medical facility and not proper medicine a large number of people in different countries is not getting proper treatment as a result large number of infected people is dying. To save from this disease the only way is maintaining social distancing from the infected persons and sterilizing whole body specially hand when a person goes outside the home. Hence the minimization of people movements is only way to control to spread the disease. To control the spreading of disease Chinese government adopted lock down policy to minimize the people interactions on 23rd January, 2020 as a result all types of public traffic were suspended in the infected Wuhan and Hubei province [23]. Following the strategies of China the highly affected countries are adopting the same policy.

The phenomenon of backward bifurcation has serious consequences for controlling the disease. For backward bifurcation, the stable disease free equilibrium point co-exists with a stable endemic equilibrium when the basic reproduction number is less than unity. The epidemiological consequence of the phenomenon of backward bifurcation is that having the basic reproduction number less than unity is, although necessary, no longer sufficient for eliminating disease from the community. In recent years, the phenomenon of the backward bifurcation has arisen the interests in disease control (see [1], [2], [13], [15], [19], [25], [39]). In [39], the authors studied the backward bifurcation analysis of an epidemic model with saturated treatment. In [15], Garba et al. presented a deterministic model for the transmission dynamics of a single strain Dengue disease, which exhibits the phenomenon of backward bifurcation. In [1], [19], the authors described the phenomenon of backward bifurcation in the deterministic models for the transmission dynamics of Zika virus. Motivated by the above discussion, here we have studied the phenomenon of backward bifurcation in the epidemiological model of COVID-19, which signifies that the making the basic reproduction number less than unity is not enough to eradicate the COVID-19 disease from the community.

To study the COVID-19 disease dynamics and predict the presumed abundance of infected people in Italy, here we have formulated a five dimensional COVID-19 epidemic model. Here, we have divided total population into five classes, namely susceptible, exposed and asymptomatic, quarantine, infectious and recovered class. We have studied the condition of stability of the disease free equilibrium point (DFE) and the condition for backward bifurcation considering the cure rate of treatment as the bifurcation parameter. Also, we have fitted the model to the data on COVID-19 cases in Italy and we shall make some predictions on the epidemic in Italy. We have also reformulated the model as an optimal control problem by introducing the lock down controls adapted by the government of different countries to maintain the social distancing for controlling the epidemic. The effect of lock down will be studied in our present work and we shall investigate the effect of different model parameters, which can minimize the spreading of the disease.

Organization of the manuscript is as follows: In Section 2, we have formulated the model. The positivity and boundedness of solutions are discussed in Section 3. The evaluation of basic reproduction number and the DFE are given in Section 4. Section 5 is devoted for backward bifurcation and in Section 6, we validate the model with real data and estimate the model parameters. The estimation of the basic reproduction number for actual COVID-19 epidemics in Italy and the study of effective reproduction number have been given in Section 7. In Section 8, we have reformulated the model as an optimal control problem and finally in Section 9 some conclusions are summarized.

2. Model formulation

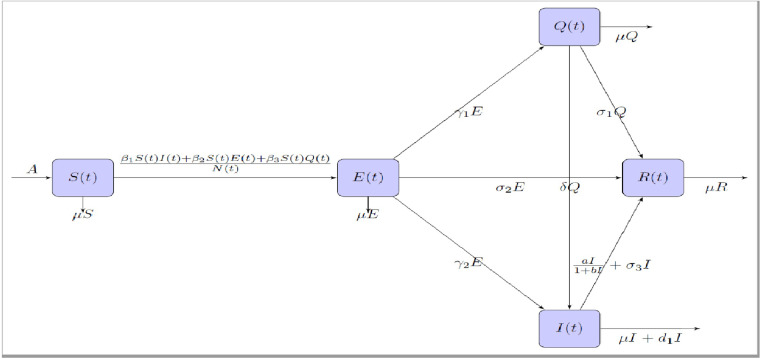
In formulating the model, we remember that the susceptible people ($S$) may be infected when they interact with the novel corona virus infected person. The COVID-19 infected person may not being infectious at the time of infection. The symptoms of COVID-19 may appear in as few as 2 days or as long as 14 days, during this incubation period the virus is contagious but the patient does not display any symptoms. So, the patient in that incubation period is able to transmit the virus to susceptible. Therefore, the asymptomatic transmission occurs in COVID-19 infections i.e. SARS-CoV-2 transmissions occur in the community from persons without symptoms [3], [11], [20], [32]. Transmission by persons who are infected but do not have any symptoms can arise from two different infection states: presymptomatic individuals (who are infectious before developing symptoms) and individuals who never experience symptoms (asymptomatic infections, which can be called as never symptomatic) [20]. The presymptomatic persons and the never symptomatic persons both go to infectious class $I$ after identification by the COVID test organized by the suitable authorities. A large number of cases in which the infected persons become infectious but asymptomatic and when susceptible individuals interact with them then infection spreads. The exposed individuals (infected but not infectious) and asymptomatic individuals are jointly included into the class $E$. The persons having symptoms like fever, cough, and shortness of breath are in quarantine and medical persons investigate them and after proper diagnosis COVID-19 positive patients are isolated. The individuals who stay in quarantine to maintain the social distancing from others have been included in the class $Q$ and those who are diagnosed as COVID-19 positive patients have been included into the class $I$. Two important points we have to take into consideration. One is the delay in diagnosis of the symptomatic patients for conformation of COVID-19 positive patient and due to this fact some non-diagnosed persons in the $Q$ class transmit the disease among the susceptible persons [17], [18], [23], [26]. Second is the limitation of medical facilities when a large number of people becomes infectious. Since till date there is no proper treatment to recovery from COVID-19, only way is the development of self immunity. For this reason it is essential to provide the support system to the infectious persons at the critical situations. But if a large number of people is being infectious in very short span of time then medical support system suppliers will not be able to provide proper support to all the infectious persons. To include this effect we have adopted the saturated treatment rate to the infectious populations in the form $\frac{aI\left(t\right)}{1+bI\left(t\right)}$, where $a$ is the cure rate of treatment and $b$ is the delay in treatment of the infectious persons. Thus, at time $t$ the total human population ($N\left(t\right)$)is divided into five class, namely, the susceptible $S\left(t\right)$, exposed and asymptomatic $E\left(t\right)$, quarantined ($Q\left(t\right)$), infectious $I\left(t\right)$ and the recovered $R\left(t\right)$ class i.e. $N\left(t\right)=S\left(t\right)+E\left(t\right)+Q\left(t\right)+I\left(t\right)+R\left(t\right)$. We assume that $S\left(t\right)$ becomes infected with the interaction of the $E\left(t\right),Q\left(t\right),I\left(t\right)$ classes with the rate of $\frac{{\beta }_{1}S\left(t\right)I\left(t\right)+{\beta }_{2}S\left(t\right)E\left(t\right)+{\beta }_{3}S\left(t\right)Q\left(t\right)}{N\left(t\right)}$, where the coefficients ${\beta }_1,{\beta }_2$ and ${\beta }_3$ denote the transmission rates of infections from the corresponding classes. Here we also assume that the new recruitment of the populations occurs from the susceptible class only. The flow diagram of the COVID-19 disease dynamics in the population has been displayed in Fig. 1 and the corresponding mathematical formulation of the transmission dynamics of COVID-19 is given below:

$$\left\{\begin{array}{cc}\frac{dS}{dt}\hfill & =A-\frac{{\beta }_{1}SI+{\beta }_{2}SE+{\beta }_{3}SQ}{N}-\mu S\hfill \\ \frac{dE}{dt}\hfill & =\frac{{\beta }_{1}SI+{\beta }_{2}SE+{\beta }_{3}SQ}{N}-({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )E\hfill \\ \frac{dQ}{dt}\hfill & ={\gamma }_{1}E-(\delta +{\sigma }_1+\mu )Q\hfill \\ \frac{dI}{dt}\hfill & ={\gamma }_{2}E+\delta Q-\frac{aI}{1+bI}-({\sigma }_3+d_1+\mu )I\hfill \\ \frac{dR}{dt}\hfill & ={\sigma }_{1}Q+{\sigma }_{2}E+{\sigma }_{3}I+\frac{aI}{1+bI}-\mu R\hfill \end{array}\right)$$ (1)

with initial conditions $S\left(0\right)>0$, $E\left(0\right)\ge 0$, $Q\left(0\right)\ge 0$, $I\left(0\right)>0$, $R\left(0\right)\ge 0$. All the model parameters have been interpreted in Table 1. In the Appendix, we have discussed the case for other expressions for treatment rate and analysed the model by introducing an extra compartment for deaths.

Fig. 1.

Flow diagram of disease transmission of COVID-19.

Table 1.

Model parameters and their descriptions.

Parameters	Interpretations
${\beta }_1$	Transmission rate of infection from $I$ class
${\beta }_2$	Transmission rate of infection from $E$ class
${\beta }_3$	Transmission rate of infection from $Q$ class
${\gamma }_1$	Rate at which $E$ class are quarantined
${\sigma }_1$	Auto recovery rate of $Q$ class
${\sigma }_2$	Auto recovery rate of $E$ class
$\delta$	Progression of $Q$ class to $I$ class after diagnosis
$A$	Recruitment rate
$\mu$	Normal death rate
$b$	Delay parameter in treatment
$a$	Cure rate of treatment
$d_1$	Disease induced death rate
${\sigma }_3$	Auto recovery rate of $I$ class
${\gamma }_2$	Rate at which $E$ becomes infectious (i.e. $\frac{1}{{\gamma }_2}$ is the incubation period)

3. Positivity and boundedness of solutions

Here, we shall show the positivity and boundedness of solutions of the model (1), which implies that the proposed model is biologically valid.

Theorem 1

All the solutions are feasible and the set

$\Omega =\left\{(S,E,Q,I,R)\in {\mathbb{R}}_{+}^5:S+E+Q+I+R\le \frac{A}{\mu }\right\}$ is a positively invariant set for the system (1) .

Proof

The $1^{st}$ component of the solution of the system (1) can be approximated by using the following inequality

$$\frac{dS}{dt}\ge -\left\{\frac{{\beta }_{1}I+{\beta }_{2}E+{\beta }_{3}Q}{N}+\mu \right\}S.$$

Integrating the above and using the initial condition, we have $S\left(t\right)\ge S\left(0\right)e^{-{\int }_0^t\{\frac{{\beta }_{1}I+{\beta }_{2}E+{\beta }_{3}Q}{N}+\mu \}dt}$.

Similarly, from the remaining four equations of (1) the following results can be obtained.

$$E\left(t\right)\ge E\left(0\right)e^{-({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )t},$$

$$Q\left(t\right)\ge Q\left(0\right)e^{-(\delta +{\sigma }_1+\mu )t},$$

$$I\left(t\right)\ge I\left(0\right)e^{-({\sigma }_3+d_1+\mu +a)t},$$

$$R\left(t\right)\ge R\left(0\right)e^{-\mu t}.$$

By using initial conditions we can conclude that all the solutions are feasible.

Next, adding all the equations of the system (1) we get

$$\frac{dN}{dt}=A-\mu N-d_{1}I\le A-\mu N.$$

Integrating, using the initial conditions and taking $lim\; sup$ as $t\to \infty$ we have ${lim\; sup}_{t\to \infty }N\left(t\right)\le \frac{A}{\mu }$.

Therefore, the set $\Omega$ is the positively invariant and attracting for the system (1).

Hence the theorem is proved. □

Thus, we have established that all components of the solutions of the system (1) are non-negative and ultimately bounded, which indicates that the model is biologically well behaved.

4. The basic reproduction number and the DFE

The basic reproduction number plays an important role in epidemiology. It indicates the transmissibility of the COVID-19 in the population. How rapidly the disease spreads is dependent on the value of the basic reproduction number $R_0$, which is the number of secondary infections one COVID-19 positive person will produce in the population. Clearly, the system (1) have the disease free equilibrium point (DFE) $E_0\left(\frac{A}{\mu },0,0,0,0\right)$ at which all the disease components are zeros. Now, we shall evaluate the basic reproduction number for the system (1) through next-generation approach [14].

Theorem 2

The basic reproduction number of the model (1) is

$R_0=\frac{{\beta }_1({\gamma }_1\delta +{\gamma }_2\delta +{\gamma }_2{\sigma }_1+{\gamma }_2\mu )}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )(\delta +{\sigma }_1+\mu )({\sigma }_3+d_1+\mu +a)}+\frac{{\beta }_2}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )}+\frac{{\beta }_3{\gamma }_1}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )(\delta +{\sigma }_1+\mu )}$ .

Proof

Here in the model (1) $E,Q,I$ are the infected compartments and we decompose the R.H.S. of the system (1) corresponding to the infected compartments as $ℱ-\mathcal{V}$, where

$ℱ=\left(\begin{array}{c}\hfill \frac{{\beta }_{1}SI+{\beta }_{2}SE+{\beta }_{3}SQ}{N}\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right)$and $\mathcal{V}=\left(\begin{array}{c}\hfill ({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )E\hfill \\ \hfill -{\gamma }_{1}E+(\delta +{\sigma }_1+\mu )Q\hfill \\ \hfill -{\gamma }_{2}E-\delta Q+\frac{aI}{1+bI}+({\sigma }_3+d_1+\mu )I\hfill \end{array}\right)$.

Now, we evaluate the derivative of $ℱ$ and $\mathcal{V}$ at DFE $E_0\left(\frac{A}{\mu },0,0,0,0\right)$ and we get two matrices $F$ and $V$, where

$F=\frac{\partial ℱ}{\partial x_j}=\left(\begin{array}{ccc}\hfill {\beta }_2\hfill & \hfill {\beta }_3\hfill & \hfill {\beta }_1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)$and $V=\frac{\partial \mathcal{V}}{\partial x_j}=\left(\begin{array}{ccc}\hfill ({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\gamma }_1\hfill & \hfill (\delta +{\sigma }_1+\mu )\hfill & \hfill 0\hfill \\ \hfill -{\gamma }_2\hfill & \hfill -\delta \hfill & \hfill ({\sigma }_3+d_1+\mu +a)\hfill \end{array}\right)$,

where $x_j=E,Q,I$.

The basic reproduction number $R_0$ is defined as the largest positive eigenvalue of the next-generation matrix $F{V}^{-1}$. Here, $\frac{{\beta }_1({\gamma }_1\delta +{\gamma }_2\delta +{\gamma }_2{\sigma }_1+{\gamma }_2\mu )}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )(\delta +{\sigma }_1+\mu )({\sigma }_3+d_1+\mu +a)}+\frac{{\beta }_2}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )}+\frac{{\beta }_3{\gamma }_1}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )(\delta +{\sigma }_1+\mu )},0,0$ are the eigenvalues of the next-generation matrix $F{V}^{-1}$. Therefore, from definition we have the basic reproduction number for the system (1) is

$$R_0=\frac{{\beta }_1({\gamma }_1\delta +{\gamma }_2\delta +{\gamma }_2{\sigma }_1+{\gamma }_2\mu )}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )(\delta +{\sigma }_1+\mu )({\sigma }_3+d_1+\mu +a)}+\frac{{\beta }_2}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )}+\frac{{\beta }_3{\gamma }_1}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )(\delta +{\sigma }_1+\mu )}.$$

Hence the theorem is proved. □

Theorem 3

When $R_0>1$ then the DFE $E_0$ is unstable and when $R_0<1$ then it is locally asymptotically stable.

Proof

The Jacobian matrix at DFE $E_0(A/\mu ,0,0,0,0)$ is

$$J\left(E_0\right)=\left(\begin{array}{ccccc}\hfill -\mu \hfill & \hfill -{\beta }_2\hfill & \hfill -{\beta }_3\hfill & \hfill -{\beta }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\beta }_2-{\gamma }_1-{\gamma }_2-{\sigma }_2-\mu \hfill & \hfill {\beta }_3\hfill & \hfill {\beta }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\gamma }_1\hfill & \hfill -\delta -\mu -{\sigma }_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\gamma }_2\hfill & \hfill \delta \hfill & \hfill -d_1-{\sigma }_3-a-\mu \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sigma }_2\hfill & \hfill {\sigma }_1\hfill & \hfill {\sigma }_3+a\hfill & \hfill -\mu \hfill \end{array}\right)..$$

So, the eigenvalues of the Jacobian matrix are $-\mu ,-\mu ,{\lambda }_1,{\lambda }_2,{\lambda }_3$, where ${\lambda }_i(i=1,2,3)$ are the roots of the following cubic:

$$\Phi \left(\lambda \right)\equiv {\lambda }^3+C_1{\lambda }^2+C_2\lambda +C_3=0,$$

where $C_1=\delta +3\mu +{\sigma }_1+{\sigma }_2+{\sigma }_3+{\gamma }_1+{\gamma }_2+d_1+a-{\beta }_2$, $C_2=(\delta +\mu +{\sigma }_1)({\sigma }_3+d_1+a+\mu )+({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu -{\beta }_2)(\delta +{\sigma }_1+{\sigma }_3+2\mu +d_1+a)-{\beta }_3{\gamma }_1-{\beta }_1{\gamma }_2$, $C_3=(\delta +\mu +{\sigma }_1)({\sigma }_3+d_1+a+\mu )({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )(1-R_0)$.

Two cases may arise.

Case (i): Let $R_0>1$. Then $C_3$ must be negative and so $\Phi \left(0\right)=C_3<0$. Again, $\Phi \left(\lambda \right)$ tends to $\infty$ as $\lambda$ tends to $\infty$. Since $\Phi \left(\lambda \right)$ is a continuous function of $\lambda$, hence by Bolzano theorem on continuous function we have $\Phi \left({\lambda }_i\right)=0$ for some ${\lambda }_i>0$. Thus, at least one eigenvalue of the Jacobian matrix is positive. Therefore, in this case $E_0$ is unstable equilibrium point.

Case (ii): Let $R_0<1$. Then $C_3$ must be positive. Again, $R_0<1$ implies that ${\gamma }_1+{\gamma }_2+{\sigma }_2+\mu -{\beta }_2>0$. This implies $C_1>0$. Again by calculating we have $C_1{C}_2-C_3>0$. Then Routh–Hurwitz criterion for polynomials implies that DFE $E_0$ is locally asymptotically stable.

Hence the theorem is proved. □

5. Backward bifurcation

In this section, we shall establish that the phenomenon of backward bifurcation takes place in the model (1) by considering the cure rate of treatment $a$ as the bifurcation parameter. The method developed by Castillo-Chavez and Song [5], [8] will be applied to determine the direction of the bifurcation at the critical value of the cure rate of treatment.

Theorem 4

Assume that $(\delta +\mu +{\sigma }_1)({\sigma }_3+d_1+a+\mu )+({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu -{\beta }_2)(\delta +{\sigma }_1+{\sigma }_3+2\mu +d_1+a)>{\beta }_3{\gamma }_1+{\beta }_1{\gamma }_2$ . Then the system (1) experiences the backward bifurcation at $R_0=1$ with respect to the cure rate of treatment if $\varphi >0$ , where $\varphi$ is defined in the text.

Proof

Let us rewrite the variables in the new form as $S=x_1,E=x_2,Q=x_3,I=x_4$ and $R=x_5$. Then, we rewrite the system (1) as

$$\left\{\begin{array}{cc}\frac{d{x}_1}{dt}\hfill & =A-\frac{{\beta }_1{x}_1{x}_4+{\beta }_2{x}_1{x}_2+{\beta }_3{x}_1{x}_3}{x_1+x_2+x_3+x_4+x_5}-\mu x_1≔f_1\hfill \\ \frac{d{x}_2}{dt}\hfill & =\frac{{\beta }_1{x}_1{x}_4+{\beta }_2{x}_1{x}_2+{\beta }_3{x}_1{x}_3}{x_1+x_2+x_3+x_4+x_5}-({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )x_2≔f_2\hfill \\ \frac{d{x}_3}{dt}\hfill & ={\gamma }_1{x}_2-(\delta +{\sigma }_1+\mu )x_3≔f_3\hfill \\ \frac{d{x}_4}{dt}\hfill & ={\gamma }_2{x}_2+\delta x_3-\frac{a{x}_4}{1+b{x}_4}-({\sigma }_3+d_1+\mu )x_4≔f_4\hfill \\ \frac{d{x}_5}{dt}\hfill & ={\sigma }_1{x}_3+{\sigma }_2{x}_2+{\sigma }_3{x}_4+\frac{a{x}_4}{1+b{x}_4}-\mu x_5≔f_5\hfill \end{array}\right)$$ (2)

We know that for $R_0=1$ the eigenvalues of the Jacobian matrix $J$ corresponding to the system (1) at DFE $E_0(A/\mu ,0,0,0,0)$ are $0,-\mu ,-\mu ,{\lambda }^{\prime },{\lambda }^{″}$, where ${\lambda }^{\prime },{\lambda }^{″}$ are the roots of the following quadratic equation:

$${\lambda }^2+C_1\lambda +C_2=0,$$

where $C_i(i=1,2)$ are defined in previous theorem.

Again, the condition $R_0=1$ is equivalent to $a=a^{\left[BB\right]}$, where

$$a^{\left[BB\right]}=\frac{{\beta }_1(({\gamma }_1+{\gamma }_2)\delta +{\gamma }_2({\sigma }_1+\mu ))}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )(\mu +\delta +{\sigma }_1)}{\left(1-\frac{{\beta }_2}{{\gamma }_1+{\gamma }_2+{\sigma }_2+\mu }-\frac{{\beta }_3{\gamma }_1}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )(\mu +\delta +{\sigma }_1)}\right)}^{-1}-({\sigma }_3+d_1+\mu ).$$

When $R_0=1$ i.e. when $a=a^{\left[BB\right]}$ then $\frac{{\beta }_2}{{\gamma }_1+{\gamma }_2+{\sigma }_2+\mu }<1$, which implies $C_1>0$. Again, by our assumption $C_2$ must be positive. Hence, $J\left(E_0\right)$ has a simple zero eigenvalue and all other eigenvalues have negative real parts. Therefore, we can apply Castillo-Chavez and Song bifurcation theorem. Let, for the critical value $a^{\left[BB\right]}$ of $a$, $W={(w_1,w_2,w_3,w_4,w_5)}^t$ and $V=(v_1,v_2,v_3,v_4,v_5)$, respectively, be the right eigenvector and the left eigenvector corresponding to the zero eigenvalue of the Jacobian matrix $J\left(E_0\right)$. Then $w_1=-1,w_2=\frac{\mu }{k_1},w_3=\frac{\mu {\gamma }_1}{k_1{k}_2},w_4=\frac{\mu ({\gamma }_2{k}_2+{\gamma }_1\delta )}{k_1{k}_2(k_3+a^{\left[BB\right]})}$, $w_5=\frac{1}{k_1{k}_2(k_3+a^{\left[BB\right]})}[{\sigma }_2{k}_2(k_3+a^{\left[BB\right]})+{\sigma }_1{\gamma }_1(k_3+a^{\left[BB\right]})+({\sigma }_3+a^{\left[BB\right]})({\gamma }_2{k}_2+{\gamma }_1\delta )]$, $v_1=0,v_2=\frac{k_3+a^{\left[BB\right]}}{{\beta }_1},v_3=\frac{{\beta }_3(k_3+a^{\left[BB\right]})+\delta {\beta }_1}{{\beta }_1},v_4=1,v_5=0$.

Now, the coefficient

$$\varphi =\sum _{k,i,j=1}^5{v}_k{w}_i{w}_j\frac{{\partial }^2{f}_k}{\partial x_i\partial x_j}=\frac{{\mu }^2}{k_1^2{k}_2^2{(k_3+a^{\left[BB\right]})}^{2}A{\beta }_1}\left(2abA{\beta }_1{({\gamma }_2+k_2)}^2-k_2{(k_3+a^{\left[BB\right]})}^2\left(2{\beta }_2\mu k_2(k_3+a^{\left[BB\right]})\right)\right)+\frac{{\mu }^2}{k_1^2{k}_2^2{(k_3+a^{\left[BB\right]})}^{2}A{\beta }_1}\left(\mu {\gamma }_1(k_3+a^{\left[BB\right]})({\beta }_2+{\beta }_3)+\mu ({\gamma }_2{k}_2+{\gamma }_1\delta )({\beta }_1+{\beta }_2)\right)\left(+{\beta }_2\left({\sigma }_2{k}_2+{\sigma }_1+({\gamma }_2{k}_2+{\gamma }_1\delta )\right)\right)$$

and the coefficient

$$\psi =\sum _{k,i=1}^5{v}_k{w}_i\frac{{\partial }^2{f}_k}{\partial x_i\partial a}=\frac{\mu ({\gamma }_2{k}_2+{\gamma }_1\delta )}{k_1{k}_2(k_3+a^{\left[BB\right]})},$$

with $k_1={\gamma }_1+{\gamma }_2+{\sigma }_2+\mu ,k_2=\delta +{\sigma }_1+\mu ,k_3={\sigma }_3+d_1+\mu$. Since the coefficient $\psi$ is obviously a positive number, hence the system (1) undergoes the backward bifurcation if $\varphi >0$.

Hence the theorem is proved. □

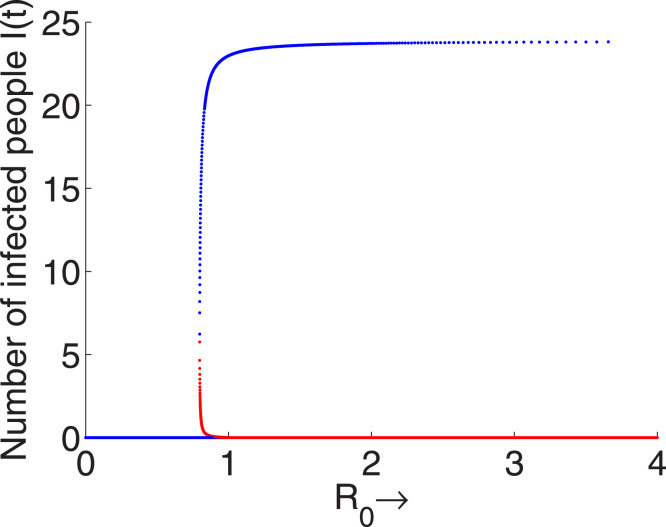
It is clear from Fig. 2 that there exists a critical value of the basic reproduction number, say $R_0^{\left[C\right]}$, such that for $R_0^{\left[C\right]}<R_0<1$, the system (1) contains two endemic equilibrium points where lower density is unstable and the upper density is stable. Thus, in this range two stable equilibrium points exist, among them one is disease free and the other is endemic. Hence, the condition $R_0<1$ is not sufficient to eradicate the disease, it depends on initial size of the populations. Again, it is clear from the expression of $R_0$ that it is a decreasing function of the cure rate of treatment ($a$), hence as the cure rate of treatment increases the value of $R_0$ will decrease and consequently the disease will be controlled. One can find three ranges of values of $a$ such as $0<a<a^{\left[C\right]}$, $a^{\left[C\right]}<a<a^{\left[BB\right]}$ and $a>a^{\left[BB\right]}$ for which, the DFE is unstable and one endemic is stable (i.e. disease will not be eradicated from the population) for $0<a<a^{\left[C\right]}$, two stable equilibrium points exist (i.e. elimination of disease depends on the initial size of the population) for $a^{\left[C\right]}<a<a^{\left[BB\right]}$ and for $a>a^{\left[BB\right]}$ disease will be eradicated from the population.

Fig. 2.

Backward bifurcation diagram of the system (1) for the parametric values ${\beta }_1=0.95,{\beta }_2=0.14,{\beta }_3=0.95,{\gamma }_1=0.1,{\gamma }_2=0.1,{\sigma }_1=0.01,{\sigma }_2=0.1,{\sigma }_3=0.1,b=20,\mu =0.06,d_1=0.004,A=10,\delta =0.6$. The red and blue lines, respectively, represent the lines of unstable and stable equilibrium points. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

For the considered values of the parameters if the cure rate of treatment ($a$) is greater than 32.01 then the disease will be eliminated from the population and for the range $2.501<a<32.01$ eradication of disease depends on the initial population size and if $a<2.501$ then disease will persist in the population. Thus eradication of the disease is highly dependent on the cure rate of treatment and hi-capacity of the cure rate of treatment is the indicative of disease elimination. Studying the bifurcation with respect to other parameters, it can be shown that the transmission rates of infections (${\beta }_1,{\beta }_2$ and ${\beta }_3$) and the auto recovery ${\sigma }_{1,2,3}$ (i.e. development of self immunity) play crucial role for controlling the disease. Due to the harmfulness of the extremely infectious disease COVID-19 the rate of infection depends on the interactions among the populations. So, lock down in the COVID-19 infected countries must play very important role to control the disease. As lock down is implemented in the population then interactions among the populations will be significantly reduced, which will be reflected in the expression of basic reproduction number ($R_0^L$) of the optimal control problem (3).

6. Model validation, parameter estimation and prediction

In this section, we shall validate the COVID-19 model (1) using real data, estimate the model parameters and finally varying the sensitive model parameters we shall give some predictions. For this purpose here we have considered the coronavirus cases in Italy and we shall estimate the best fitted model parameters.

To estimate the model parameters, we use non-linear least square method. The principle of this method is to minimize the objective function

$$f(\Sigma ,n)=\sum _{J=1}^n{\left(C_J^{\left[E\right]}\left(t\right)-C_J^{\left[P\right]}\left(t\right)\right)}^2,$$

where $\Sigma$ is the set of all parameters, $C_J^{\left[E\right]}\left(t\right)$ is the cumulative number of real infective cases, $C_J^{\left[P\right]}\left(t\right)$ is the cumulative number of model predicted infective cases at $J\mathrm{th}$ observation, and $n$ is the number of sample depending on the model parameters [4]. The cumulative number of infected can be found from the following formula:

$$\frac{d{C}^{\left[P\right]}\left(t\right)}{dt}={\gamma }_{2}E\left(t\right)+\delta Q\left(t\right).$$

Using Matlab minimization and the Matlab package fmincon we have estimated the model parameters.

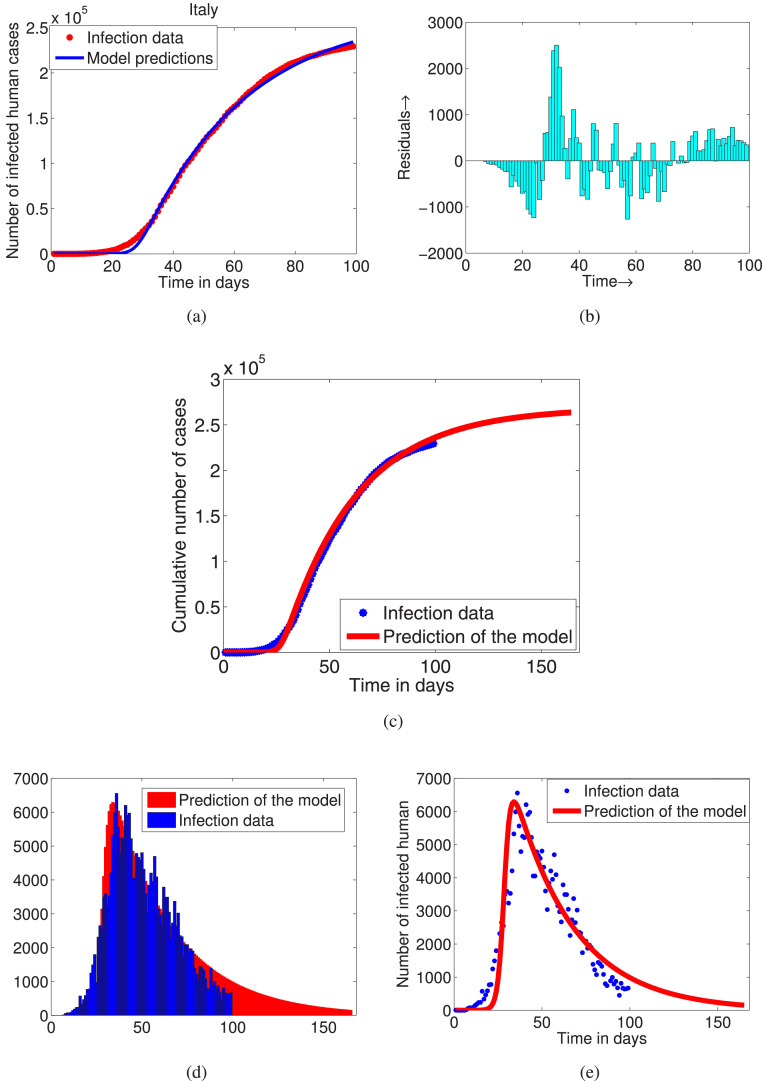
To estimate the model parameters we consider the cumulative number of infected cases of Italy from $14\mathrm{th}$ February to $23\mathrm{rd}$ May, 2020. To utilize fmincon software we consider the initial populations size as $S\left(0\right)=60461826,E\left(0\right)=5,Q\left(0\right)=5,I\left(0\right)=3,R\left(0\right)=0$ among them the $E\left(0\right)$ is estimated and $Q\left(0\right)$ is assumed and other three have been taken from [37]. The estimated model parameters and their sensitivity indices are given in Table 2. The model is fitted to the cumulative number of infected cases, which has been presented in Fig. 3(a) and the predictive number of cumulative and daily infected cases have been presented in Fig. 3 (c–e). The residuals of the fit is presented in Fig. 3(b), which shows that the residuals are small and random. Thus, we can conclude that the fit is reasonably good [24]. In Fig. 3, we have plotted the time series of infected population for 155 days after that a very few number of daily infected cases will come. It is clear from Fig. 3 that the state of being epidemic in Italy for COVID-19 will continue up to $3\mathrm{rd}$ week of July, 2020 and after that the disease will be controlled. Since for these values of the model parameters $R_0>1$, hence disease will persist in population for long time. Now the goal is to bring it below 1, because an epidemic with a basic reproductive number below 1 will gradually disappear.

Table 2.

Values of the model parameters with 95% confidence interval and their sensitivity indices for disease outbreak in Italy.

Parameters	Values	Confidence Intervals	Sources	Sensitivity Indices
${\beta }_1$	0.951449	(0.936794, 0.964688)	Estimated	0.009988
${\beta }_2$	0.581276	(0.575499, 0.587713)	Estimated	0.303441
${\beta }_3$	0.865583	(0.855259, 0.876974)	Estimated	0.686570
${\gamma }_1$	0.098267	(0.096968, 0.099438)	Estimated	0.005791
${\gamma }_2$	0.017199	(0.016947, 0.017386)	Estimated	−0.109335
${\sigma }_1$	0.053847	(0.052798, 0.054150)	Estimated	−0.571763
${\sigma }_2$	0.01819	(0.017823, 0.018318)	Estimated	−0.126044
${\sigma }_3$	0.123555	(0.122569, 0.125177)	Estimated	−0.001421
$d_1$	0.18	—–	[37]	−0.002071
$\delta$	0.000168	(0.000165, 0.000169)	Estimated	−0.001637
$a$	0.553732	(0.548153, 0.561560)	Estimated	−0.006372
$b$	10.164964	(10.075988, 10.333965)	Estimated	—–
$\mu$	0.010658	—–	[37]	−0.187145
$A$	1224	—–	[37]	—–

Fig. 3.

(a) Fitting model to cumulative cases in Italy, (b) residuals of the fit, (c) prediction of cumulative cases for $155$ days, (d) BAR diagram, (e) prediction of daily cases for $155$ days.

The considered model contains large number of parameters and almost all of them are involved in the basic reproduction number $R_0$. Now, the problem is to decide which parameters are most influential to control the epidemic. But for experimental design of the epidemic models the determination of the most effective parameters is essential [29]. For this purpose we shall use the normalized forward sensitivity index [9] for $R_0$ with respect to any characteristic model parameter $\alpha$, which is denoted by ${\Gamma }_{\alpha }$ and is defined by ${\Gamma }_{\alpha }=\frac{\alpha }{R_0}\frac{\partial R_0}{\partial \alpha }$. The sensitivity indices with respect to the model parameters are given in Table 2. It is clear from the table that the parameters ${\beta }_1,{\beta }_2,{\beta }_3,{\gamma }_1$ enhance the value of $R_0$ and so they enhance the epidemic whereas other parameters with negative sensitivity indices will reduce the epidemic. The most sensitive parameters are ${\beta }_2$ (the transmission rate of infection from $E$ class) and ${\sigma }_2$ (auto recovery rate of $E$ class).

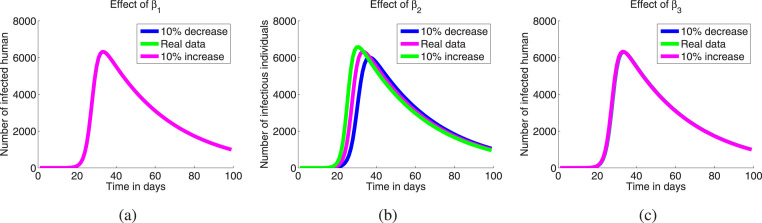
Now, we shall investigate the effect of the model parameters in changing disease dynamics. First keeping the values of other parameters fixed as given in Table 2, we vary only the transmission rate of infections. Numerically, we have verified that the transmission rate of infection from $E\left(t\right)$ (asymptomatic and exposed) class is most effective but other two transmission rates are not so (see Fig. 4 (a–c)). It is realistic feature because $I\left(t\right)$ and $Q\left(t\right)$ classes cannot spread much more infections as $E\left(t\right)$ can spread, because these two classes can infect only the medical persons and the persons who take care of them. So to minimize the disease spreading our target will be to minimize the contracts among the susceptible persons and the exposed & asymptomatic persons, which is possible if we increase the number of tests randomly in the areas where a single infected person is found, then the carrier of COVID-19 will be identified easily and they will be separated from the susceptible populations.

Fig. 4.

Effect of the transmission rate of infections: (a) ${\beta }_1$, (b) ${\beta }_2$, (c) ${\beta }_3$.

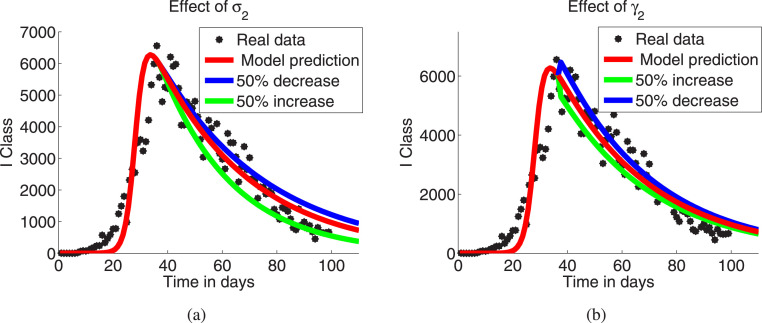
To control the spreading of disease Italy government adopted the lock down policy on $9\mathrm{th}$ March, 2020 and daily number of cases starts to decrease on $23\mathrm{rd}$ March i.e. after completion of the 14 days incubation period. Since the parameter ${\sigma }_2$ (auto recovery rate of $E$ class) has high negative sensitivity index, hence it can change the disease dynamics rapidly. To justify this we change its value on $23\mathrm{rd}$ March, then the prevalence significantly increases (decreases) as auto recovery rate of $E$ class ${\sigma }_2$ decreases (increases) (see Fig. 5(a)). But the parameter ${\gamma }_2$ is not so effective as its low sensitivity index (see Fig. 5(b)). Thus, the developments of self immunity with the proper maintenance of social distancing of the exposed and asymptomatic individuals play key role for controlling the epidemic disease COVID-19.

Fig. 5.

Effect of the model parameter: (a) ${\sigma }_2$, (b) ${\gamma }_2$.

7. Basic reproduction number of the COVID-19 outbreak in Italy

In this section, we shall estimate the basic reproduction number $R_0$ from the initial growth phase of actual epidemics in Italy. The effective reproduction number $R\left(t\right)$ which is time dependent, will also be estimated from daily new COVID-19 cases in Italy.

7.1. Estimation of $R_0$ for actual epidemics

Here by using the initial COVID-19 infected cases in Italy, we shall estimate $R_0$ by applying the method developed by [27], [31]. We suppose that the cumulative number of cases $C\left(t\right)\propto exp\left(\Lambda t\right)$, where $\Lambda$ is the force of infection. Then the infected compartments can be taken in the following form:

$$E\left(t\right)=E_{0}exp\left(\Lambda t\right)$$

$$Q\left(t\right)=Q_{0}exp\left(\Lambda t\right)$$

$$I\left(t\right)=I_{0}exp\left(\Lambda t\right),$$

where $E_0,Q_0,I_0$ are the constants and we assume that at the earlier phase of the epidemic the abundance of the infected class is very low compared to the total susceptible populations. So, we assume that the number of susceptible populations equals the number of total populations at the time of initial infection and so $S\left(t\right)=N\left(t\right)=\frac{A}{\mu }$. We also assume that at beginning of the epidemics the delay parameter $b$ in treatment is zero.

Putting the above values of $S\left(t\right),E\left(t\right),Q\left(t\right)$ and $I\left(t\right)$ in (1) and rearranging we get

$$\left(1+\frac{\Lambda }{D_1}\right)E_0=\frac{{\beta }_1{I}_0+{\beta }_2{E}_0+{\beta }_3{Q}_0}{D_1}$$

$$\left(1+\frac{\Lambda }{D_2}\right)Q_0=\frac{{\gamma }_1}{D_2}{E}_0$$

$$\left(1+\frac{\Lambda }{D_3}\right)I_0=\frac{{\gamma }_2{E}_0+\delta Q_0}{D_3},$$

where $D_1={\gamma }_1+{\gamma }_2+{\sigma }_2+\mu ,D_2=\delta +{\sigma }_1+\mu$ and $D_3={\sigma }_3+d_1+\mu +a$. Determining ${\beta }_2$ from the above three expressions and putting in the expression of $R_0$, we obtain

$$R_0=\frac{{\beta }_1({\gamma }_1\delta +{\gamma }_2\delta +{\gamma }_2{\sigma }_1+{\gamma }_2\mu )}{D_1{D}_2{D}_3}+\frac{A_1{B}_1{C}_1{D}_1{D}_2{D}_3-B_1{D}_2{\beta }_1{\gamma }_2-C_1{D}_3{\beta }_3{\gamma }_1-{\beta }_1\delta {\gamma }_1}{B_1{C}_1{D}_1{D}_2{D}_3}+\frac{{\beta }_3{\gamma }_1}{D_1{D}_2},$$

where $A_1=1+\frac{\Lambda }{D_1},B_1=1+\frac{\Lambda }{D_2},C_1=1+\frac{\Lambda }{D_3}$.

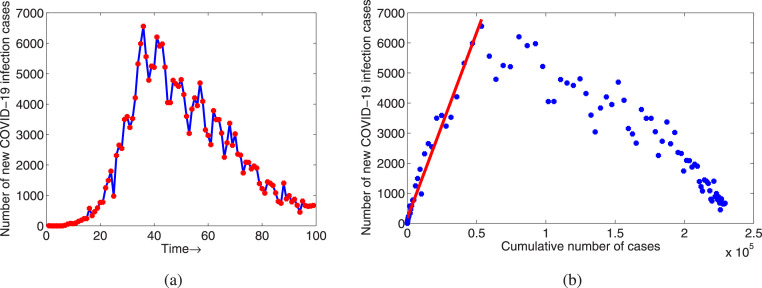
Following [27], we have the relation which is the number of new cases per day $\sim$ $\Lambda C\left(t\right)$. Now we plot new daily COVID-19 cases against the cumulative number of COVID-19 cases $C\left(t\right)$ in Italy from $14\mathrm{th}$ February to $23\mathrm{rd}$ May, 2020 (see Fig. 6). We fit a linear regression model by using the least square method to this exponential growth data. The force of infection $\Lambda$ is nothing but the slope of the fitted line (see Fig. 6(b)). Thus, we estimate the force of infection as $\Lambda =0.1232311997657\pm 0.0067125$ and from the above relation between the basic reproduction number and the force of infection, we can estimate the basic reproduction number as $R_0=2.766467198\pm 1.0985$.

Fig. 6.

(a) The time series of new cases of COVID-19 in Italy from $14\mathrm{th}$ February to $23\mathrm{rd}$ May, 2020, (b) the daily number of cases against the cumulative number of cases for the same time period.

7.2. The effective reproduction number

The basic reproduction number is the average number of secondary infection that is generated by a single infected person. But in reality the reproduction number varies with time for any epidemic system [31]. Depending on the reproduction number the planners update the epidemic control policy time to time. For this purpose here we have estimated the effective reproduction number ($R\left(t\right)$) using current COVID-19 infection data in Italy from $14\mathrm{th}$ February to $23\mathrm{rd}$ May, 2020. The estimation of $R\left(t\right)$ can be done from the following renewal equation [27], [33]

$$R\left(t\right)=\frac{B\left(t\right)}{{\int }_{\tau =0}^{\infty }B(t-\tau )g\left(\tau \right)d\tau },$$

where $B\left(t\right)$ is the number of new cases in the $t$th day and $g\left(\tau \right)$ is the generation interval distribution for the COVID-19 disease in Italy. The generation interval distribution $g\left(t\right)$ is the probability distribution function of time from infection of a person to the secondary infection case by that person. For simplicity here we assume that $b=0$. The generation interval distribution is the combination of the three exponential functions $D_1{e}^{-D_{1}t},D_2{e}^{-D_{2}t}$ and $D_3{e}^{-D_{3}t}$ in the following form :

$$g\left(t\right)=\sum _{i=1}^3\frac{D_1{D}_2{D}_3{e}^{-D_{i}t}}{\prod _{j=1j\ne i}^3(D_j-D_i)}$$

with mean of the distribution as $T=\frac{1}{D_1}+\frac{1}{D_2}+\frac{1}{D_3}$ and $\tau >0$. The above relation is valid when the force of infection $\Lambda >min\left\{-D_1,-D_2,-D_3\right\}$ [33].

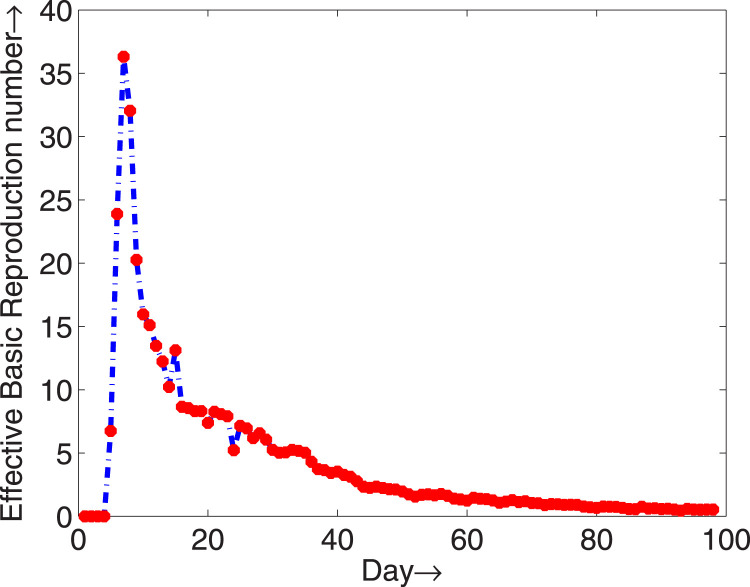
Using the estimated model parameters, we have calculated the effective reproduction numbers and presented them in Fig. 7. It is clear from the figure that the effective reproduction number diminishes below one after approximately 85 days from $14\mathrm{th}$ February, 2020 and the epidemic with $R_0<1$ will gradually disappear.

Fig. 7.

The effective reproduction number for COVID-19 in Italy from $14\mathrm{th}$ February to $23\mathrm{rd}$ May, 2020.

8. The optimal control problem

To minimize the COVID-19 infections every country is adopting the lock down policy. The lock down is a policy that is to minimize the spreading of COVID-19 infections by controlling the movements of populations to maintain social distancing. For applying lock down the interactions among $S\left(t\right)$ class with $E\left(t\right),I\left(t\right),Q\left(t\right)$ classes are reduced and consequently the transmission rates of infections must decrease. To include this lock down effect in the model, we have replaced ${\beta }_1,{\beta }_2$ and ${\beta }_3$ by ${\beta }_1(1-u_1),{\beta }_2(1-u_2)$ and ${\beta }_3(1-u_3)$, respectively where $0\le u_i\le 1(i=1,2,3)$. Again, for adapting lock down each country is facing huge financial losses. For adapting complete lock down the loss is very huge, so some countries are adapting partial lock down. The $u_i^{,}s$ are proportional to how many areas are implemented under lock down or how well lock down is maintaining. If there is no lock down then $u_i^{,}s$ are all zero and if total lock down is implemented then $u_i^{,}s$ are all 1. The main goal of this study is to minimize the COVID-19 infections as well as the cost or financial loss of implementing the controls. Thus, we reformulate the system (1) as an optimal control problem which is given below:

$$\left\{\begin{array}{cc}\frac{dS}{dt}\hfill & =A-\frac{{\beta }_1(1-u_1)SI+{\beta }_2(1-u_2)SE+{\beta }_3(1-u_3)SQ}{N}-\mu S\hfill \\ \frac{dE}{dt}\hfill & =\frac{{\beta }_1(1-u_1)SI+{\beta }_2(1-u_2)SE+{\beta }_3(1-u_3)SQ}{N}-({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )E\hfill \\ \frac{dQ}{dt}\hfill & ={\gamma }_{1}E-(\delta +{\sigma }_1+\mu )Q\hfill \\ \frac{dI}{dt}\hfill & ={\gamma }_{2}E+\delta Q-\frac{aI}{1+bI}-({\sigma }_3+d_1+\mu )I\hfill \\ \frac{dR}{dt}\hfill & ={\sigma }_{1}Q+{\sigma }_{2}E+{\sigma }_{3}I+\frac{aI}{1+bI}-\mu R\hfill \end{array}\right)$$ (3)

Here, we construct the objective functional $J$, which has to be minimized, where

$J(u_1,u_2,u_3)={\int }_0^T(A_{1}E+A_{2}Q+A_{3}I+\frac{A_4}{2}{u}_1^2+\frac{A_5}{2}{u}_2^2+\frac{A_6}{2}{u}_3^2)dt$.

The constants $A_1,A_2,A_3$ are, respectively, the loss due to the presence of $E,Q$, and $I$ class and the constants $A_4,A_5,A_6$, respectively, represent the loss due to implementing these controls. We assume that all the controls will be implemented for the time interval $[0,T]$ and they will be stopped after the time $T$. Now, the problem is to find optimal functions $u_i^{\ast }\left(t\right)$ $(i=1,2,3)$ satisfying $J(u_1^{\ast },u_2^{\ast },u_3^{\ast })=min\{J(u_1,u_2,u_3),(u_1,u_2,u_3)\in U\}$, where the control set $U=\{(u_1,u_2,u_3)/u_i\left(t\right)$ is Lebesgue measurable on $[0,1],0\le u_i\left(t\right)\le 1$ for all $t\in [0,T],i=1,2,3\}$.

Theorem 5

The control functions $u_i^{\ast }$ $(i=1,2,3)$ exist for which $J(u_1^{\ast },u_2^{\ast },u_3^{\ast })=min\{J(u_1,u_2,u_3):(u_1,u_2,u_3)\in U\}$ .

Proof

The integrand of the objective function $J(u_1,u_2,u_3)$ is clearly a convex function. Also, the system (3) satisfies the Lipschitz property with respect to the state variables, because the solutions of the system (3) are bounded. It implies the existence of the optimal control functions. Hence the theorem is proved. □

Theorem 6

The optimal control functions$u_i^{\ast }$$(i=1,2,3)$which minimize the objective functional$J$over the region$U$are$u_1^{\ast }=max\left\{0,min\left\{\frac{({\lambda }_2^{\ast }-{\lambda }_1^{\ast }){\beta }_1{S}^{\ast }{I}^{\ast }}{N^{\ast }{A}_4},1\right\}\right\}$,$u_2^{\ast }=max\left\{0,min\left\{\frac{({\lambda }_2^{\ast }-{\lambda }_1^{\ast }){\beta }_2{S}^{\ast }{E}^{\ast }}{N^{\ast }{A}_5},1\right\}\right\}$and$u_3^{\ast }=max\left\{0,min\left\{\frac{({\lambda }_2^{\ast }-{\lambda }_1^{\ast }){\beta }_3{S}^{\ast }{Q}^{\ast }}{N^{\ast }{A}_6},1\right\}\right\}$, where,$S^{\ast },E^{\ast },Q^{\ast },I^{\ast },R^{\ast }$are, respectively, the optimum values of$S,E,Q$,$I,R$and$({\lambda }_1^{\ast },{\lambda }_2^{\ast },{\lambda }_3^{\ast },{\lambda }_4^{\ast },{\lambda }_5^{\ast })$is the solution of the system(4)with the conditions (5) and $N^{\ast }=S^{\ast }+E^{\ast }+Q^{\ast }+I^{\ast }+R^{\ast }$ .

Proof

The Lagrangian of the optimal control problem is $L=A_{1}E+A_{2}Q+A_{3}I+\frac{A_4}{2}{u}_1^2+\frac{A_5}{2}{u}_2^2+\frac{A_6}{2}{u}_3^2$. Now, we define the Hamiltonian $H$ for the problem which is as follows:

$H=A_{1}E+A_{2}Q+A_{3}I+\frac{A_4}{2}{u}_1^2+\frac{A_5}{2}{u}_2^2+\frac{A_6}{2}{u}_3^2+{\lambda }_1\left(t\right)\frac{dS}{dt}+{\lambda }_2\left(t\right)\frac{dE}{dt}+{\lambda }_3\left(t\right)\frac{dQ}{dt}+{\lambda }_4\left(t\right)\frac{dI}{dt}+{\lambda }_5\left(t\right)\frac{dR}{dt}$.

In order to determine the adjoint equations with transversality conditions, we apply Pontryagin’s maximum principle [16], [21], [28] that gives $\frac{d{\lambda }_1\left(t\right)}{dt}=-\frac{\partial H}{\partial S},\frac{d{\lambda }_2\left(t\right)}{dt}=-\frac{\partial H}{\partial E},\frac{d{\lambda }_3\left(t\right)}{dt}=-\frac{\partial H}{\partial Q},\frac{d{\lambda }_4\left(t\right)}{dt}=-\frac{\partial H}{\partial I},\frac{d{\lambda }_5\left(t\right)}{dt}=-\frac{\partial H}{\partial R}$ with the transversality conditions ${\lambda }_i\left(T\right)=0,i=1,2,3,4,5$. Thus, the adjoint variables ${\lambda }_i$, $i=1,2,3,4,5$ can be obtained from the following:

$$\left\{\begin{array}{c}\frac{d{\lambda }_1}{dt}=\mu {\lambda }_1+\frac{\{{\beta }_1(1-u_1)I+{\beta }_2(1-u_2)E+{\beta }_3(1-u_3)Q\}(N-S)}{N^2}({\lambda }_1-{\lambda }_2)\hfill \\ \frac{d{\lambda }_2}{dt}=-A_1+\frac{N(1-u_2){\beta }_2-\{{\beta }_1(1-u_1)I+{\beta }_2(1-u_2)E+{\beta }_3(1-u_3)Q\}}{N^2}S({\lambda }_1-{\lambda }_2)\hfill \\ +({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu ){\lambda }_2-{\gamma }_1{\lambda }_3-{\gamma }_2{\lambda }_4-{\sigma }_2{\lambda }_5\hfill \\ \frac{d{\lambda }_3}{dt}=-A_2+\frac{N(1-u_3){\beta }_3-\{{\beta }_1(1-u_1)I+{\beta }_2(1-u_2)E+{\beta }_3(1-u_3)Q\}}{N^2}S({\lambda }_1-{\lambda }_2)\hfill \\ +(\delta +{\sigma }_1+\mu ){\lambda }_3-\delta {\lambda }_4-{\sigma }_1{\lambda }_5\hfill \\ \frac{d{\lambda }_4}{dt}=-A_3+\frac{N(1-u_1){\beta }_1-\{{\beta }_1(1-u_1)I+{\beta }_2(1-u_2)E+{\beta }_3(1-u_3)Q\}}{N^2}S({\lambda }_1-{\lambda }_2)\hfill \\ +\{{\sigma }_3+d_1+\mu +\frac{a}{{(1+bI)}^2}\}{\lambda }_4-\{{\sigma }_3+\frac{a}{{(1+bI)}^2}\}{\lambda }_5\hfill \\ \frac{d{\lambda }_5}{dt}=\frac{\{{\beta }_1(1-u_1)I+{\beta }_2(1-u_2)E+{\beta }_3(1-u_3)Q\}S}{N^2}({\lambda }_2-{\lambda }_1)+\mu {\lambda }_5\hfill \end{array}\right)$$ (4)

with the conditions

$${\lambda }_1\left(T\right)=0,{\lambda }_2\left(T\right)=0,{\lambda }_3\left(T\right)=0,{\lambda }_4\left(T\right)=0,{\lambda }_5\left(T\right)=0.$$ (5)

To determine optimal control functions, we use the optimality conditions $\frac{\partial H}{\partial u_i}=0$$(i=1,2,3)$ and we get $u_1^{\ast }=max\left\{0,min\left\{\frac{({\lambda }_2^{\ast }-{\lambda }_1^{\ast }){\beta }_1{S}^{\ast }{I}^{\ast }}{N^{\ast }{A}_4},1\right\}\right\}$, $u_2^{\ast }=max\left\{0,min\left\{\frac{({\lambda }_2^{\ast }-{\lambda }_1^{\ast }){\beta }_2{S}^{\ast }{E}^{\ast }}{N^{\ast }{A}_5},1\right\}\right\}$, $u_3^{\ast }=max\left\{0,min\left\{\frac{({\lambda }_2^{\ast }-{\lambda }_1^{\ast }){\beta }_3{S}^{\ast }{Q}^{\ast }}{N^{\ast }{A}_6},1\right\}\right\}$. Here, $S^{\ast },E^{\ast },Q^{\ast },I^{\ast },R^{\ast }$ are, respectively, the optimum values of $S,E,Q,I,R$ and $({\lambda }_1^{\ast },{\lambda }_2^{\ast },{\lambda }_3^{\ast },{\lambda }_4^{\ast },{\lambda }_5^{\ast })$ is the solution of the system (4) satisfying the conditions (5).

Clearly, $\frac{{\partial }^{2}H}{\partial u_1^2}=A_4>0$, $\left|\begin{array}{cc}\hfill \frac{{\partial }^{2}H}{\partial u_1^2}\hfill & \hfill \frac{{\partial }^{2}H}{\partial u_1\partial u_2}\hfill \\ \hfill \frac{{\partial }^{2}H}{\partial u_2\partial u_1}\hfill & \hfill \frac{{\partial }^{2}H}{\partial u_2^2}\hfill \end{array}\right|=A_4{A}_5>0$and $\left|\begin{array}{ccc}\hfill \frac{{\partial }^{2}H}{\partial u_1^2}\hfill & \hfill \frac{{\partial }^{2}H}{\partial u_1\partial u_2}\hfill & \hfill \frac{{\partial }^{2}H}{\partial u_1\partial u_3}\hfill \\ \hfill \frac{{\partial }^{2}H}{\partial u_2\partial u_1}\hfill & \hfill \frac{{\partial }^{2}H}{\partial u_2^2}\hfill & \hfill \frac{{\partial }^{2}H}{\partial u_2\partial u_3}\hfill \\ \hfill \frac{{\partial }^{2}H}{\partial u_3\partial u_1}\hfill & \hfill \frac{{\partial }^{2}H}{\partial u_3\partial u_2}\hfill & \hfill \frac{{\partial }^{2}H}{\partial u_3^2}\hfill \end{array}\right|=A_4{A}_5{A}_6>0$.

Thus, the control functions $u_i^{\ast }$ $(i=1,2,3)$ minimize the objective functional $J$. Hence the theorem is proved. □

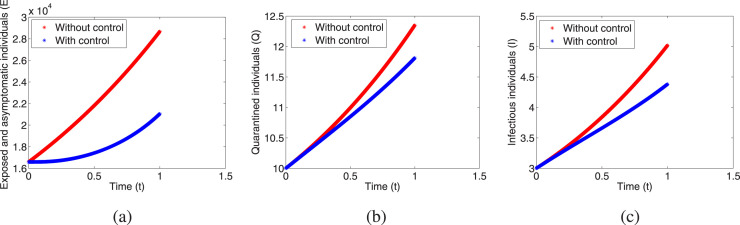
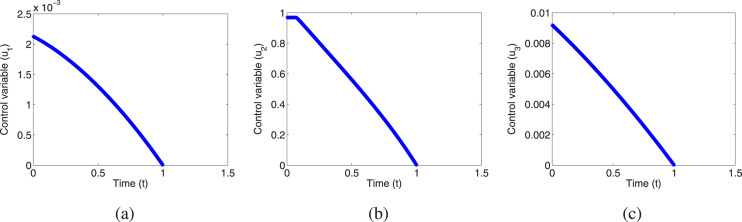
To justify the theoretical findings of the optimal control problem (3), we solve it numerically by using forward–backward sweep method. This method combines the forward application of a fourth order Runge–Kutta method for the state system (3) with the backward application of a fourth order Runge–Kutta method for the adjoint system (4). Here, we assume $T=1$ unit of time. For this simulation we have considered the parametric values which are given in Table 2 with $A_1=0.1,A_2=0.01,A_3=0.05,A_4=10,A_5=150,A_6=20$ and the initial conditions $S\left(0\right)=60461826,E\left(0\right)=16583,Q\left(0\right)=10,I\left(0\right)=3$ and $R\left(0\right)=0$. From Fig. 8(a)–(c) we can compare the exposed and asymptomatic, quarantined and infectious populations at any time $t\in [0,1]$ between the system with no control and the system with the controls. The optimal control functions $u_i^{\ast }\left(t\right)$ ($i=1,2,3$) have been represented by Fig. 9(a)–(c).

Fig. 8.

Time series of the populations with controls and without controls: (a) Exposed and asymptomatic individuals, (b) quarantined individuals, (c) infectious individuals.

Fig. 9.

The optimal control functions: (a) $u_1\left(t\right)$, (b) $u_2\left(t\right)$, (c) $u_3\left(t\right)$.

Again, it can be easily proved that the basic reproduction number $R_0^L$ of the model (3) is

$$R_0^L=\frac{(1-u_1){\beta }_1({\gamma }_1\delta +{\gamma }_2\delta +{\gamma }_2{\sigma }_1+{\gamma }_2\mu )}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )(\delta +{\sigma }_1+\mu )({\sigma }_3+d_1+\mu +a)}+\frac{(1-u_2){\beta }_2}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )}+\frac{(1-u_3){\beta }_3{\gamma }_1}{({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )(\delta +{\sigma }_1+\mu )}.$$

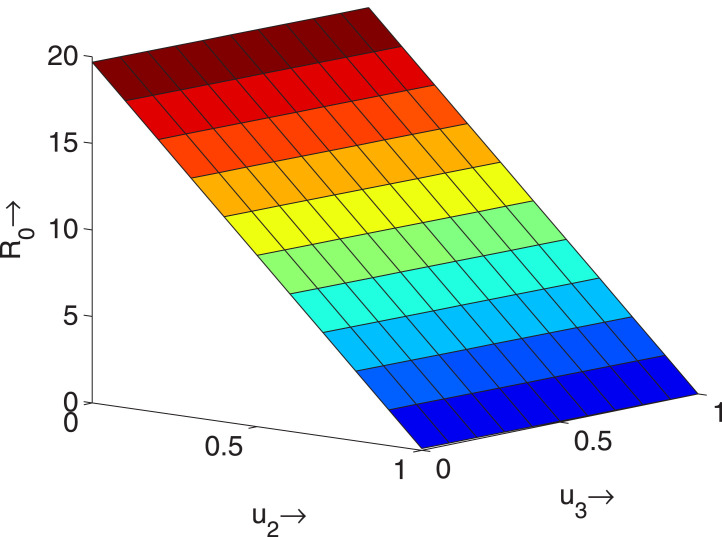
It is clear from the expression of the basic reproduction number $R_0^L$ that the quantities $u_i^{,}s$ can reduce the value of the basic reproduction number i.e. these quantities must be good controller for the disease spreading. If values of $u_i^{,}s$ increase then $R_0^L$ decreases i.e. the lock down must play an important role for controlling the disease. In Fig. 10, we see that the control $u_2$ is so effective to control the disease, because if $u_2$ increases, the basic reproduction number significantly decreases and if we make it less than unity for large value of $u_2$, then disease will be controlled.

Fig. 10.

Effect of the controls $u_2$ and $u_3$ on $R_0$, when $u_1=0.01$.

9. Conclusions

This paper deals with an epidemic compartmental model to investigate the dynamics of pandemic COVID-19 and to predict the future epidemic situations in Italy. Here, we have considered three disease compartments, namely exposed-asymptomatic, quarantine and infectious. To include the effect of limited medical facilities, here we have considered the rate of treatment as saturated type. The basic reproduction number has been obtained for the proposed model, which plays key role for analysing the stability of DFE. The system experiences backward bifurcation with respect to the cure rate of treatment conditionally. The epidemiological implication of this result is that making the basic reproduction number less than unity is not sufficient to eliminate the COVID-19 disease from the community. Thus the basic reproduction number less than unity is only a necessary but not a sufficient condition for eliminating COVID-19, because the stable disease free equilibrium point co-exists with a stable endemic equilibrium. To validate the model and for further predictions we consider the current COVID-19 cases in Italy from 14th February to $23\mathrm{rd}$ May, 2020 and we have estimated the best-fitted model parameters. From the simulations we see that the disease will be controlled in July, 2020 in Italy. The sensitivity analysis shows that the transmission rate of infection from exposed and asymptomatic class plays important role for disease spreading and the development of self immunity of that class is very influential in the model output. We have estimated the basic reproduction number $R_0$ from the initial growth phase of actual COVID-19 epidemics in Italy and the time dependent effective reproduction number $R\left(t\right)$ has also been estimated from daily new COVID-19 cases in Italy.

We have also formulated an optimal control problem by considering the effects in the transmission rates of infections due to implementing lock down policy by many countries. We have solved it both analytically and numerically. The main objective of analysing this optimal control problem is to minimize the COVID-19 positive cases as well as the total costs or financial losses for implementation of controls due to adapting lock down by countries. A comparative study between the system with lock down and the system without lock down has been presented that shows the positive impacts of taking lock down for controlling the epidemic. The effects of lock down on the basic reproduction number have also been shown and it has been shown that the basic reproduction number decreases as the lock down policy is implemented and if we can make it less than unity then the epidemic will disappear. The formulation of optimal control problem is a theoretical modelling and it can be applied by using real data in some countries. The proposed model of COVID-19 has some limitations. Here we consider saturated treatment function to describe the saturation phenomenon of the limited medical resources. If some countries or communities have the potential to adapt very strong medical resources in very short span of time then the saturated treatment function will not be used in the model. Again, we did not consider vaccination term in our model though the COVID-19 vaccines have reached billions of people worldwide.

Appendix.

(i) To recovery from infectious diseases, the treatment of infected population is one of the important methods. In classical epidemic models, the linear treatment function $T\left(I\right)=rI,I\ge 0$ (where $r$ is a positive constant) is used, but if the number of infected population is very large then it is not always possible to provide such type of treatment. To avoid this the constant treatment function $T\left(I\right)=\left\{\begin{array}{c}r,I>0\hfill \\ 0,I=0\hfill \end{array}\right)$(where $r$ is a positive constant) is used sometimes, but in reality the treatment is not a constant function. The saturated treatment function $T\left(I\right)=\frac{aI}{1+bI}$ (where $a,b$ are positive constants) is a better alternative for new outbreak diseases like COVID-19 in new region or area, because at the beginning of the outbreak there is small of effective treatment due to negligence or lack of knowledge about the disease. Then the treatment rate is increased with the improving of treatment conditions of hospitals including skillful treatment techniques and effective medicines. Finally, the treatment rate is reached to its maximum due to the boundedness of medical resources of any countries or communities.

Usually the consideration of the saturated treatment function in the model implies the existence of backward bifurcation in the system. The infected being delayed for treatment is one of the origins which lead to the backward bifurcation. The consideration of linear or constant treatment rate in the model does not ensure the phenomenon of backward bifurcation, it may change the number of endemic equilibria in the system.

(ii) If we introduce an extra compartment $D$ for the deaths, then the model equations will be as follows:

$$\left\{\begin{array}{cc}\frac{dS}{dt}\hfill & =A-\frac{{\beta }_{1}SI+{\beta }_{2}SE+{\beta }_{3}SQ}{N}-\mu S\hfill \\ \frac{dE}{dt}\hfill & =\frac{{\beta }_{1}SI+{\beta }_{2}SE+{\beta }_{3}SQ}{N}-({\gamma }_1+{\gamma }_2+{\sigma }_2+\mu )E\hfill \\ \frac{dQ}{dt}\hfill & ={\gamma }_{1}E-(\delta +{\sigma }_1+\mu )Q\hfill \\ \frac{dI}{dt}\hfill & ={\gamma }_{2}E+\delta Q-\frac{aI}{1+bI}-({\sigma }_3+d_1+\mu )I\hfill \\ \frac{dR}{dt}\hfill & ={\sigma }_{1}Q+{\sigma }_{2}E+{\sigma }_{3}I+\frac{aI}{1+bI}-\mu R\hfill \\ \frac{dD}{dt}\hfill & =d_{1}I\hfill \end{array}\right)$$

Thus, if we introduce the death compartment $D$, then the dynamics of the model will not be changed, because the last equation is a redundant equation as other equations do not contain $D$.

But at the time of parameter estimation, we will be able to predict the probable number of death cases in current time as well as the future time. This prediction is important biologically, because we can validate the model by comparing the result of model simulated death cases with the exact number of death cases.