Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2021 Dec 1.
Published in final edited form as: Neuroimage. 2021 Oct 2;244:118627. doi: 10.1016/j.neuroimage.2021.118627

Quantification of volumetric morphometry and optical property in the cortex of human cerebellum at micrometer resolution

Chao J Liu a, William Ammon a, Viviana Siless a, Morgan Fogarty b, Ruopeng Wang a, Alessia Atzeni c, Iman Aganj a, Juan Eugenio Iglesias a,c,d, Lilla Zöllei a, Bruce Fischl a,d, Jeremy D Schmahmann e, Hui Wang a,*
PMCID: PMC8603939  NIHMSID: NIHMS1753471  PMID: 34607020

Abstract

The surface of the human cerebellar cortex is much more tightly folded than the cerebral cortex. Volumetric analysis of cerebellar morphometry in magnetic resonance imaging studies suffers from insufficient resolution, and therefore has had limited impact on disease assessment. Automatic serial polarization-sensitive optical coherence tomography (as-PSOCT) is an emerging technique that offers the advantages of microscopic resolution and volumetric reconstruction of large-scale samples. In this study, we reconstructed multiple cubic centimeters of ex vivo human cerebellum tissue using as-PSOCT. The morphometric and optical properties of the cerebellar cortex across five subjects were quantified. While the molecular and granular layers exhibited similar mean thickness in the five subjects, the thickness varied greatly in the granular layer within subjects. Layer-specific optical property remained homogenous within individual subjects but showed higher cross-subject variability than layer thickness. High-resolution volumetric morphometry and optical property maps of human cerebellar cortex revealed by as-PSOCT have great potential to advance our understanding of cerebellar function and diseases.

Keywords: Cerebellum, Polarization-sensitive optical coherence, tomography, Layer thickness, Cell density, Myelin, Cross-subject variability

1. Introduction

The cerebellum contains between 70 and 80% of the neurons in the human nervous system, the vast majority of which are granule cells in the cerebellar cortex (Herculano-Houzel, 2010). The cerebellum is interconnected through afferent and efferent pathways with the cerebral cortex, pontine and olivary precerebellar nuclei, thalamus, and spinal cord. The cerebellum has long been known to be critical for the coordination of movement and it has become apparent from neuroanatomical, electrophysiological, neuroimaging, and clinical studies that its impact on the nervous system is equally important for cognitive and emotional functions (Koziol et al., 2014; Lawrenson et al., 2018; Schmahmann et al., 2019). For example, lesions in the cognitive and limbic regions of cerebellar posterior lobe lead to dysmetria of thought, with impairments of the cerebellar modulation of intellect and emotion manifesting as the cerebellar cognitive affective syndrome (Schmahmann et al., 2019; Schmahmann and Sherman, 1998; Stoodley et al., 2016). There have been fundamental advances in understanding cerebellar corticonuclear connections, circuitry and physiology in animal models (Apps et al., 2018; De Zeeuw and Ten Brinke, 2015; Voogd and Ruigrok, 2012), as well as functional and structural connectivity in human subjects (Castellazzi et al., 2018; D’Angelo and Casali, 2013; Palesi et al., 2017), but there are still considerable knowledge gaps in understanding cerebellar cortical organization and function in the healthy human brain and how these contribute to pathophysiology and clinical phenomenology in diseases of the cerebellum.

Current volumetric analysis of cerebellar morphometry comes mostly from magnetic resonance imaging (MRI) (Boillat et al., 2018; Sereno et al., 2020). The tightly convoluted pattern of the cerebellar cortex, the limited resolution of MRI, and partial volume effects have impeded comprehensive visualization of the cerebellar folia (Sereno et al., 2020). Optical imaging methods provide superior resolution compared to MRI techniques. Among them, polarization sensitive optical coherence tomography (PSOCT) provides label-free and depth-resolved contrasts that originate from light scattering and tissue birefringence (de Boer et al., 1997). When applied to brain imaging, the reflectivity contrast from PSOCT reveals the gross anatomy and provides quantification of the scattering coefficient of different anatomical structures (Wang et al., 2017; Yang et al., 2020). White matter tracts at microscopic scale can be quantified by polarization-based retardance contrast due to birefringence, an optical property resulting from structural anisotropy (Wang et al., 2011). In particular, the different cortical layers of the cerebellum have showed distinctive optical properties, such as light scattering (Brezinski et al., 1997) and birefringence (Liu et al., 2017). We previously reported automatic serial PSOCT (as-PSOCT) integrated with a tissue slicer and a PSOCT system, which proved to be an effective way to map cubic centimeter samples of human brain (Wang et al., 2018). The as-PSOCT technique makes it possible to examine large-scale cerebellum samples at microscopic resolution.

In this work, we used as-PSOCT to reconstruct cubic centimeters of ex vivo human cerebellum samples across five subjects at micrometer scale resolution. The layer thickness and scattering coefficient were quantified to evaluate the morphometric and optical properties of the cerebellar cortex. We further investigated the within-subject and cross-subject variability of cortical layer thickness and scattering coefficient. This quantification may facilitate development of novel biomarkers for neurodegenerative disorders in the cerebellum.

2. Material and methods

2.1. Human cerebellum samples

Five human cerebellum samples (age at death: 62 ± 10 years, mean ± standard deviation (s.t.d.), 4 males and 1 female) were used in this study. The brains were obtained from the Department of Neuropathology of the Massachusetts General Hospital (MGH), and all subjects were neurologically normal prior to death. The samples were fixed by immersion in 10% formalin for at least two months. The postmortem interval did not exceed 24 h. The samples were cut into parasagittal slabs and the parts corresponding to lobules Crus-I and Crus-II were further blocked and embedded in agarose for serial sectioning and imaging. The ex vivo imaging procedures are approved by the Institutional Review Board of the MGH.

2.2. System and data acquisition

The as-PSOCT system has previously been described in detail (Wang et al., 2018). The system was composed of an in-house built polarization-maintaining fiber based spectral-domain PSOCT centered at 1300 nm, motorized xyz translational stages, and a vibratome to section the tissue block (Fig. S1). The customized software, written in C++, coordinated data acquisition, xyz stage translation, and vibratome slicing for automatic imaging of tissue blocks. One volumetric acquisition composed of 420 A-lines by 420 B-lines covering a field of view (FOV) of 2.8 mm × 2.8 mm took 3.5 s at an A-line rate of 51 kHz. The axial resolution was estimated to be 3.5 μm in tissue. We obtained a lateral resolution of 5.9 μm with a 4 × telescope and a scan lens (LSM03, Thorlabs, Newton, NJ). The voxel size was 6.7 × 6.7 × 2.5 μm.

The software performed data reconstruction in real time. Inverse Fourier transform of interference-related spectral oscillations yielded complex depth profiles in the form of A1,2 (z) exp[iɸ1,2(z)], where A and ɸ denote the amplitude and phase as a function of depth z, and the subscripts represent the polarization channels. Reflectivity, R(z), and phase retardance, δ(z), of the depth profile (A-line), were obtained by R(z) ∝ A1(z)2 + A2(z)2, and δ(z) = arctan [A1(z)/A2(z)], respectively. As the effective imaging depth was limited to 200 μm in the highly scattered ex vivo human brain tissues, to increase data acquisition efficiency for large-scale samples, the software saved three-dimensional (3D) reflectivity within the 290 μm depth range for offline scattering coefficient calculations, as well as two-dimensional (2D) en-face images of average intensity projection of reflectivity and average retardance.

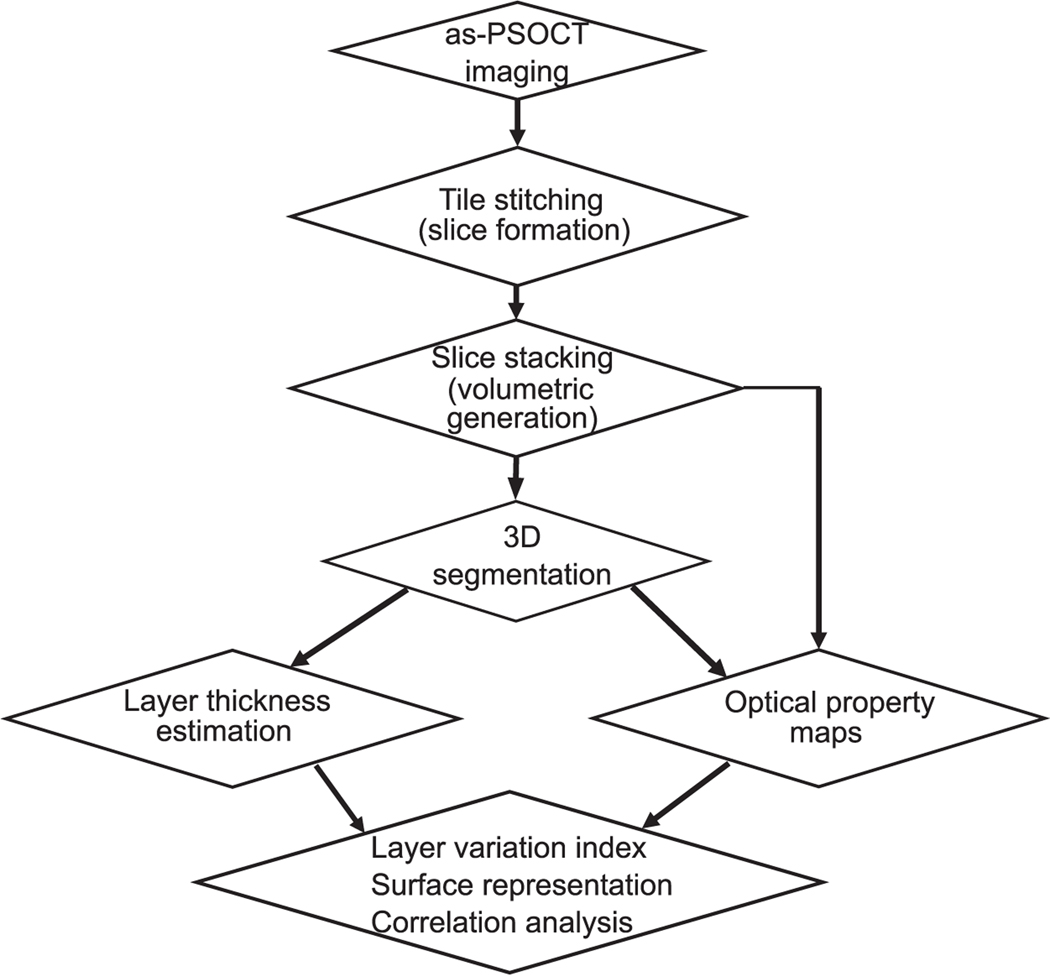
We imaged the block face surface via tile scans with 50% overlapping. To obtain the volumetric reflectivity data as well as the en-face images of each slice, we stitched the tiles in the sagittal plane using rigid registration to compute the overlap between tiles and linear blending for image fusion in the Fiji software (Preibisch et al., 2009). A 100 μm thick slice was removed from the tissue surface by the vibratome to expose the deeper region until the whole volume was imaged. The en-face images of individual slices were stacked together to render the cubic centimeters of cerebellum tissue. The pixel size of the en-face stack was 100 μm in z. We then down-sampled the volumetric images (en-face reflectivity and retardance) to a voxel size of 10 μm × 10 μm × 100 μm. Our data acquisition, image formation, and analysis pipeline is illustrated in Fig. 1.

Fig. 1.

Fig. 1.

Open in a new tab

as-PSOCT data acquisition and analysis pipeline.

2.3. Cortical layer and white matter segmentation

Segmentation of the cerebellar cortex was performed using a semi-automated method. Manual segmentation was first conducted on one out of five adjacent sagittal slices for each volume in the Freeview software (part of the FreeSurfer software package) (Fischl, 2012). The boundaries of the molecular layer, the granular layers, and the white matter were drawn based on the volumetric retardance images, and a label was created for each of the structure. An automated algorithm called SmartInterpol was then applied to complete the rest of the slices (Atzeni et al., 2018). SmartInterpol uses a combination of label fusion and deep learning methods to transfer the segmentations from the labeled to the unlabeled slices, and has two major advantages: (i) reducing the burden of manual delineation; and (ii) producing segmentations that are smooth in the orthogonal views, which is very difficult to achieve with completely manual tracing. The label fusion component of SmartInterpol relies on affine and nonrigid registration methods available in the publicly available NiftyReg package (Modat et al., 2010; Ourselin et al., 2001), whereas the deep learning component relies on a fully convolutional network (Shelhamer et al., 2016). The convolutional network was pretrained on ImageNet, fine-tuned on all manually labeled slices and further fine-tuned for each “sandwich ” using the two labeled slices at each end. The segmentation results were used to compute the layer thickness for the cerebellum as described in the following section.

2.4. Quantification of morphometric and optical properties

2.4.1. Layer thickness estimation

To calculate the layer thickness in 3D, we first interpolated the volumetric segmentation from a voxel size of 10 μm × 10 μm × 100 μm to an isotropic voxel size of 10 μm × 10 μm × 10 μm. A voxel-based algorithm was then applied on the up-sampled segmentation volume to estimate the thickness of the molecular and granular layers of the cerebellar cortex (Aganj et al., 2009). The algorithm considered lines passing through the voxel inside the segmented layer (in 193 3D orientations uniformly distributed on the sphere), computed the length of each line intersecting with the layer boundaries, and selected the shortest length as the estimated thickness. To facilitate further analysis of layer thickness, we used the thickness of the skeleton of the segmented structure. The skeleton of the cortex was identified in the 3D thickness volume as a one-voxel-wide mask positioned in the middle of the layer. The shortest line passing through each voxel was first identified, and skeleton voxels were chosen as those the segment lengths to the left and the right of which had a difference smaller than one (Aganj et al., 2009).

2.4.2. Optical properties

We quantified the voxel-wise attenuation coefficients following the method of Vermeer et al. In the near-infrared spectral range, light attenuation within the tissue is dominated by scattering, whereas absorption is negligible. Therefore, we used the scattering coefficient (μs), calculated as μs(i)=I(i)/[2Δ∑j=i+1dI(j)],, to represent the optical properties, where i is the pixel number in depth, I is the reflectivity signal, Δ is the pixel size in depth, and d is the total imaging depth (Vermeer et al., 2013). We then averaged μs along 100 μm in depth to get an en-face μs map for a slice (voxel size: 10 μm × 10 μm × 100 μm).

2.4.3. Layer variation index

Variation index was a term we defined in the study, which represented the heterogeneity of layer thickness or μs within a subject. It was calculated as VariationIndex=〈Qupper,25%(X)〉/〈Qlower,25%(X)〉, where X represents the measurement (layer thickness or μs), ⟨⟩ is the mean operation, Qupper, 25% is the top quartile of the measurements and Qlower, 25% is the bottom quartile of the measurements. A variation index ≈ 1 indicates a uniform distribution in the measurement, whereas a variation index ≫ 1 indicates high heterogeneity. The variation index was calculated for thickness and μs of the granular and molecular layer, respectively, in each subject.

2.4.4. High order moment analysis

We also calculated the third order moment skewness and the fourth order moment kurtosis from all layer thickness and μs measurements for each subject. Skewness signifies asymmetry of the distribution: negative/positive skewness indicate a longer tail on the left/right of the distribution, respectively. Kurtosis indicates the flatness of the image histogram. For a normal distribution, kurtosis is equal to 3. Distributions whose kurtosis values are larger than 3, have sharper peaks, whereas distributions with kurtosis less than 3 are flatter.

2.5. Surface mapping of morphometric and optical properties

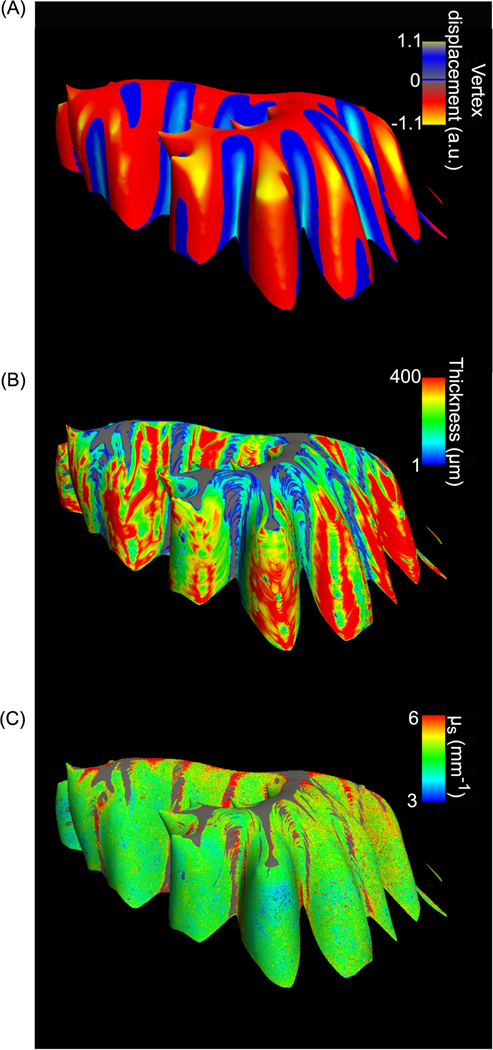
To better visualize the metric maps for the whole sample, we used FreeSurfer, an open source MRI analysis software (Fischl, 2012), to create surfaces and map the morphological analysis and the optical properties to the surface. First, we tessellated the segmented volume and created an outer surface for each layer. We smoothed the surface with adjacent 128 vertices and inflated the smoothed surface to better visualize the folding patterns in the cerebellar cortex. The inflation process moved the vertices in the crown of folium and the depth of fissure to a mid-surface in between, and generated a displacement map for each vertex showing the distance it traveled to reach the inflated surface. The vertex displacement indicated how high and deep the folding patterns were in the cerebellar cortex.

Using FreeSurfer, we also mapped the layer thickness and scattering coefficient volume to the smoothed surface, using the corresponding values along the surface normal, at a depth of 150 μm below the surface. This surface mapping allowed us to inspect the relationship of those metrics with respect to the crown of folium and depth of fissure regions identified by the displacement map during surface inflation.

2.6. Correlation between morphometric and optical properties

We calculated correlation coefficients between the layer thickness and μs volumes for the 5 subjects, to evaluate the correlation between morphometric and optical properties. The greater number of voxels in the folia compared to the fissures, specifically in the granular layer, potentially leaned towards a folial bias; and therefore, we used the layer thickness and μs on the skeleton for the correlation analysis. The en-face μs stack was upsampled to match the voxel size (10 μm × 10 μm × 10 μm) of the morphometric analysis before correlation analysis.

2.7. Statistical analysis

A paired-sample t-test was used to compare (i) averaged cortical layer thickness, and (ii) variation index of layer thickness, and (iii) variation index of μs, and (iv) skewness/kurtosis of layer thickness, as well as (v) skewness/kurtosis of μs between the molecular layer and the granular layer. A one-way ANOVA was used to compare μs measurements in molecular layer, granular layer, and white matter across the five subjects. A p-value smaller than 0.05 indicated the rejection of the null hypothesis that the quantification arose from the same distribution. To quantitatively evaluate the cross-subject variability, we calculated the coefficient of variation (CV, equal to the standard deviation divided by the mean) from the mean layer thickness and layer-specific mean μs across the five subjects.

3. Results

3.1. Reconstruction of human cerebellum samples at micrometer-scale resolution

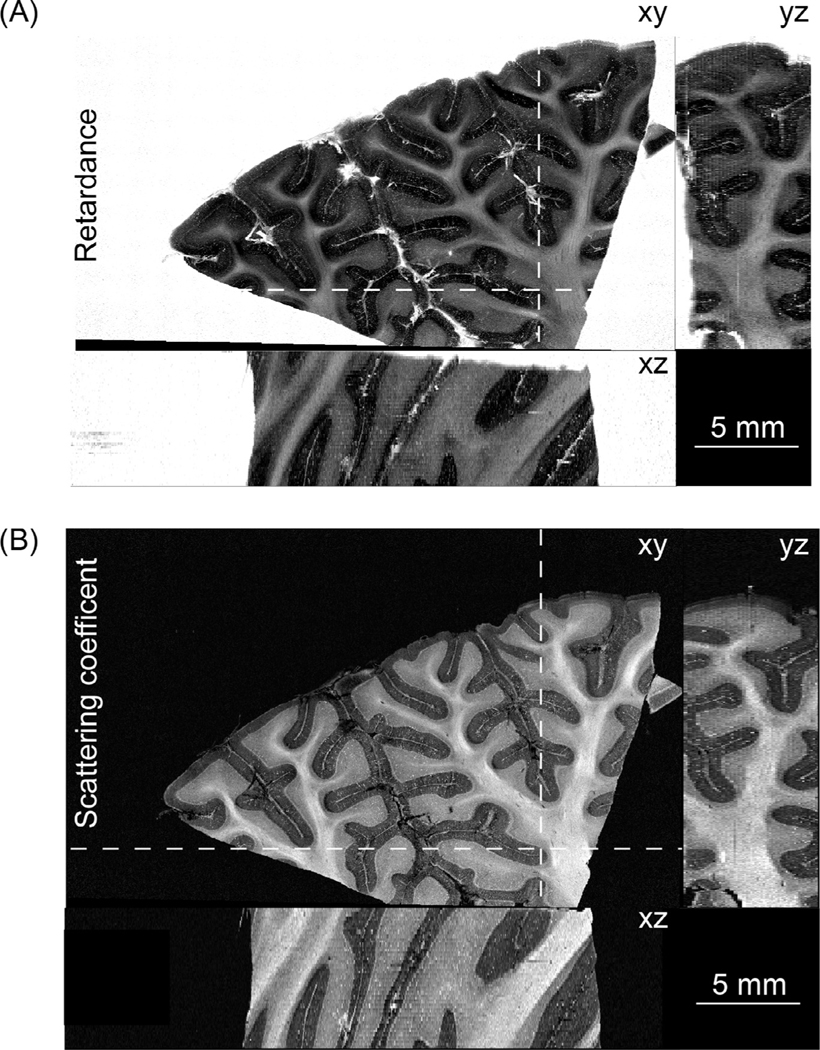
Each of the five human cerebellum samples imaged by as-PSOCT was about 4 cm3. The sample shown in Fig. 2 was 2.8 × 1.8 × 0.75 cm3. We first reconstructed the en-face retardance images of the 75 slices and stacked them together to recover the whole cerebellar volume (Fig. 2 A). The white matter showed higher retardance values compared with the cerebellar cortex. Furthermore, the granular layer showed higher retardance than the molecular layer, in agreement with the findings in previous studies (Liu et al., 2017; Wang et al., 2018). We then calculated the μs map of each slice by averaging depth-wise μs and stacked them together to represent the volumetric reconstruction. The coronal, axial, and sagittal planes of the μs images revealed similar anatomical structure to the retardance images (Fig. 2 B). The molecular layer, granular layer, and white matter showed distinctive μs characteristics.

Fig. 2.

Fig. 2.

Open in a new tab

Volumetric reconstruction of human cerebellar tissue (2.8 × 1.8 × 0.75 cm3) from as-PSOCT. The orthogonal views of (A) retardance images and (B) scattering coefficient maps are shown. The locations of the axial (xz) and coronal (yz) planes in A and B are indicated by the dashed lines on xy-plane. Scale bars: 5 mm.

The prominent retardance contrast allows segmentation of the cerebellar cortex and the white matter, with the former further divided by cortical laminar structures including the molecular and granular layers (Fig. 3). Due to the resolution limit of the down-sampled reconstruction, we did not segment the interleaved Purkinje cell monolayer. Remarkably, as mentioned in Section 2.3 above, the semi-automated segmentation reduced the labor time by a factor of five and also yielded less inter-slice variability at structural boundaries where subtle contrast challenged the consistency of human judgement in the full manual segmentation (Fig. 4). As a result, the volumetric segmentations were inherently smooth. The structural segmentation enables further analysis of morphometric and optical properties in a layer-specific manner.

Fig. 3.

Fig. 3.

Open in a new tab

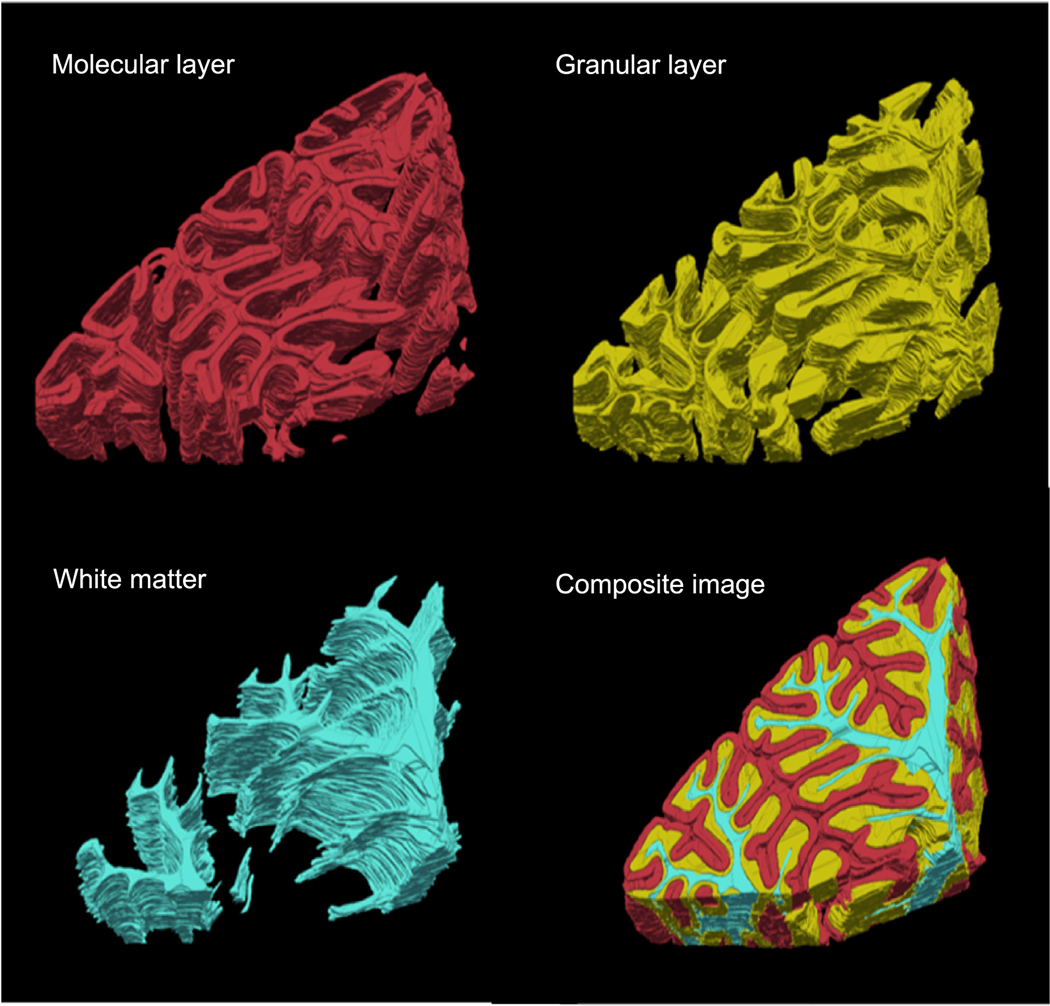
Volume rendering of segmented molecular layer (red), granular layer (yellow) and white matter (cyan) for the cerebellar lobules. The whole segmented volume is shown in the composite image of the three structures.

Fig. 4.

Fig. 4.

Open in a new tab

Comparison of full manual (top) and semiautomatic (bottom) cerebellum segmentation on a cross-slice viewing plane. Black arrows highlight the inconsistency from manual segmentation and the smoothness from semiautomatic segmentation.

3.2. Morphometric and optical properties of human cerebellar cortex

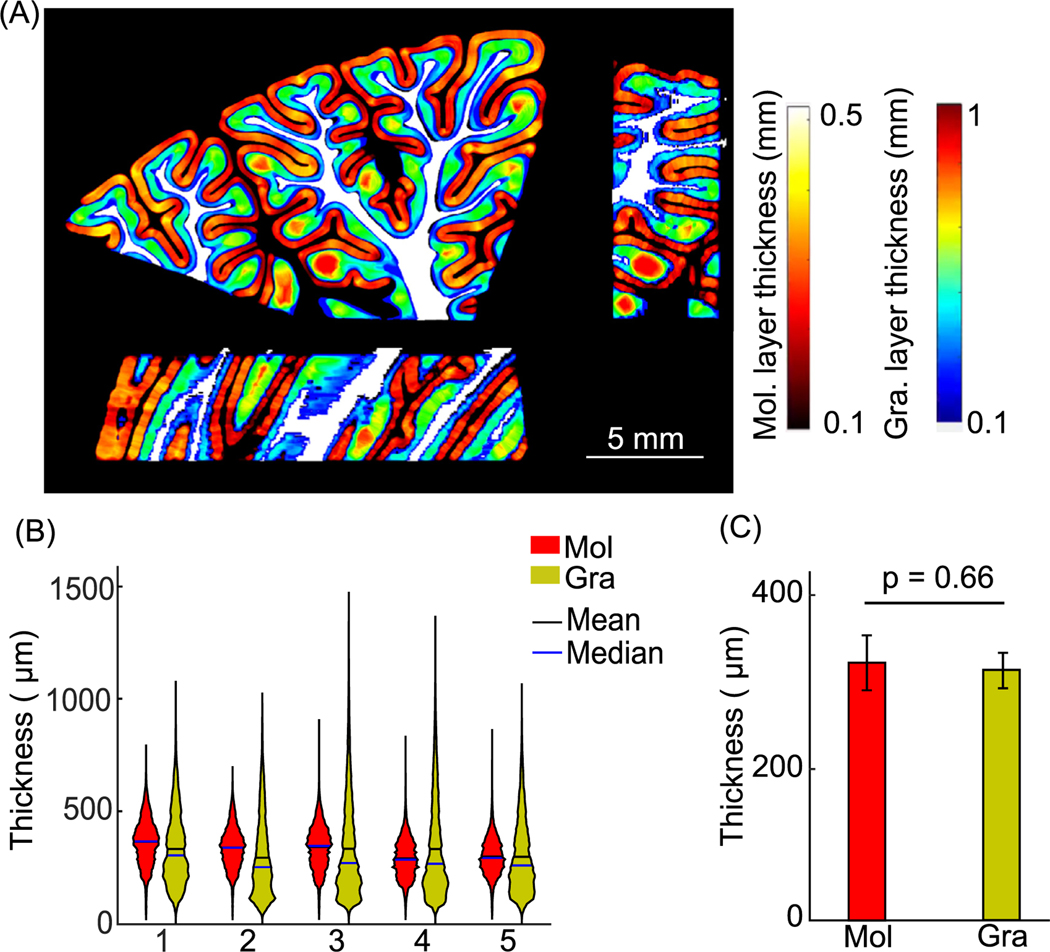
We quantified the thickness of the molecular and granular layers from the five cerebellar samples. The thickness maps of the molecular and granular layers were obtained using a voxel-based algorithm and visualized in one cerebellar volume as an example (Fig. 5 A). The value at every voxel represents the thickness of the corresponding layer calculated at that voxel. We then examined the thickness distribution of the molecular and granular layers in the five subjects (Fig. 5 B). The distribution within a layer was consistent across all subjects, while the distributions of the thickness in the molecular and granular layers revealed distinct patterns. The distribution of thickness of the granular layer was skewed to the lower end while having a long tail towards higher thickness, whereas the distribution of thickness of the molecular layer was narrower and more symmetric. The molecular and granular layers shared similar mean thickness, 322 ± 32 μm and 319 ± 20 μm respectively (Fig. 5 C, mean ± s.t.d., p = 0.66, paired-sample t-test, n = 5 subjects).

Fig. 5.

Fig. 5.

Open in a new tab

Cortical layer thickness in five cerebellar samples. (A) Molecular and granular layer thickness estimation in orthogonal views. The molecular and granular layer thicknesses are indicated by the hot and jet color bars, respectively. White matter is shown in white for anatomical reference. Scale bar: 5 mm. (B) Violin plots of molecular and granular layer thickness in individual subjects. The width and height of the violin plots correspond to the frequency and the value of thickness measurements. The mean and median of the measurements are also shown in the plots as black and blue solid lines. (C) Average cortical layer thickness of the five subjects (p = 0.66, paired-sample t-test). Error bars indicate standard deviations. Mol: molecular layer; Gra: granular layer.

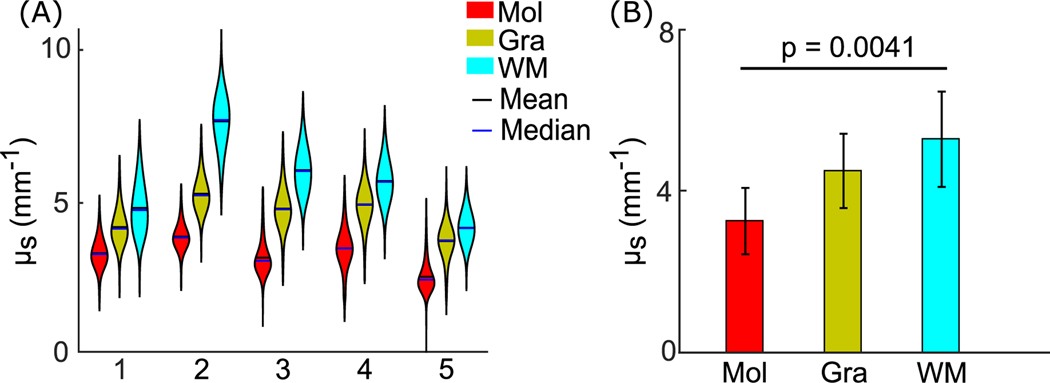
Tissue microstructure changes the light scattering events and thus manifests in the optical properties. After obtaining the scattering coefficient map (Fig. 2 B) and the volumetric segmentation (Fig. 3), we further analyzed μs in the molecular layer, the granular layer, and the interior of the white matter. Within individual subjects, white matter had the highest μs, followed by the granular layer and the molecular layer (Fig. 6 A). We then evaluated μs across five subjects and found consistent patterns, with μs of 3.3 ± 0.5 mm−1, 4.6 ± 0.6 mm−1, and 5.7 ± 1.3 mm−1 in molecular layer, granular layer, and white matter, respectively (Fig. 6 B, mean ± s.t.d., p = 0.0041, one-way ANOVA, n = 5 subjects). However, we did not find a significant difference between the molecular and granular layers (p = 0.11, one-way ANOVA with Dunn-Sidak correction, n = 5 subjects), possibly related to a limited sample size. Due to the effect of speckle noise in OCT imaging, we observed extremely high and low values in the μs data (Fig. S2A). We excluded the μs values outside the three-sigma confidence intervals for the further analysis; however, the exclusion did not change the μs pattern in these structures and the statistical analysis (Fig. S2B).

Fig. 6.

Fig. 6.

Open in a new tab

Optical scattering coefficient measurements in five cerebellar samples. (A) Violin plots of μs measurements in molecular layer, granular layer, and white matter in individual subjects. The width and height of the violin plots correspond with the frequency and the value of μs measurements. The mean and median of the measurements are represented as black and blue solid lines. (B) Average μs measurements in the molecular layer, granular layer, and white matter across the five subjects (p = 0.0041, one-way ANOVA). Error bars indicate standard deviations. Mol: molecular layer; Gra: granular layer; WM: white matter.

To better visualize the morphometric and optical properties of the convoluted cerebellar cortex, we created surfaces for the granular layer and mapped layer thickness and scattering coefficient volumes to those surfaces. The inflated surface map showed negative displacement in the crown of the folium while positive displacement in the depth of the fissure (Fig. 7 A), as is to be expected from a surface inflation displacement. Furthermore, we observed the higher values located at the crown of the folium and lower values located at the depth of the fissure in the mapped thickness (Fig. 7 B). The gray regions located at the deepest fissure were masked out given that the volume-to-surface mapping used the values 150 μm below the outer surface, which already passed the granular layer into the white matter. Therefore, this process indicated that the deepest fissure had a thickness less than 150 μm. On the other hand, the optical property map showed more homogenous values over the cortex (Fig. 7 C). We also performed surface mapping of morphometry and optical property in the other 4 subjects and found similar patterns. We further quantified the variations of layer thickness and optical properties in the cerebellar cortex in the following sections.

Fig. 7.

Fig. 7.

Open in a new tab

Surface mapping of the granular layer. The vertex displacement map on the inflated surface indicates the crown of folium (red) and depth of fissure (blue) (A), surface maps of layer thickness (B), and optical properties (C) of the subject shown in Fig. 2 and Fig. 3. Color bars in (A)-(C) indicate the vertex displacement from the original surface to the inflated one, layer thickness and μs values, respectively, along the surface normal at a depth of 150 μm below the outer surface. Gray regions in (B) and (C) are masked out from the surface map (A).

3.3. Within-subject variation of morphometric and optical properties in cerebellar cortex

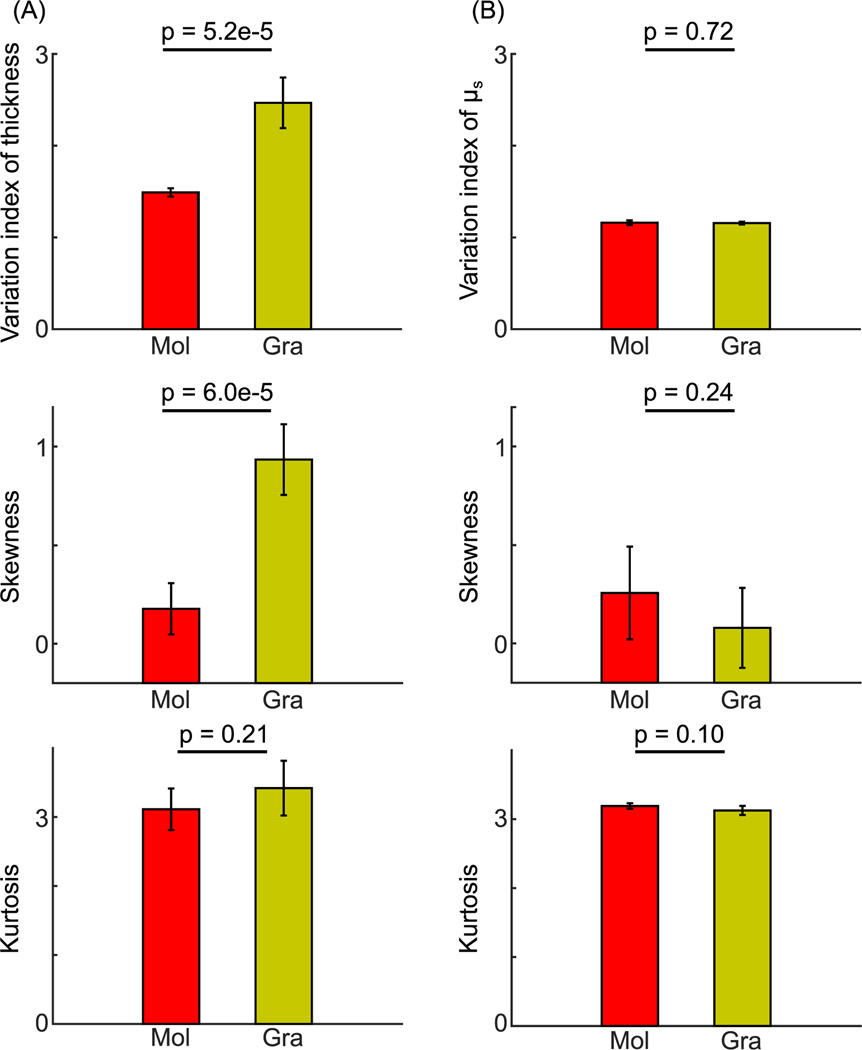
To further understand the heterogeneity of morphometric and optical properties within individual layers, we evaluated the variation index of layer thickness and μs in the cerebellar cortex. We found that granular layer thickness varied more than molecular layer thickness by a factor of 1.6. The variation index of thickness between the two layers were significantly different (Fig. 8 A, top panel, 2.5 ± 0.3 and 1.5 ± 0.05, respectively, mean ± s.t.d., p = 5.2e-5, paired-sample t-test, n = 5 subjects). The skewness showed that the layer thickness was more right-skewed in the granular layer than in the molecular layer (Fig. 8 A, middle panel, 0.9 ± 0.2 and 0.2 ± 0.1, respectively, mean ± s.t.d., p = 6e-5, paired-sample t-test, n = 5 subjects); while the kurtosis between the two layers were similar (Fig. 8 A, bottom panel, 3.4 ± 0.3 and 3.1 ± 0.3, respectively, mean ± s.t.d., p = 0.24, paired-sample t-test, n = 5 subjects). The morphometric analysis indicated a high variation and asymmetry in the distribution of thickness in the granular layer, implying more complex folding patterns compared to that in the molecular layer.

Fig. 8.

Fig. 8.

Open in a new tab

Within-subject variation of morphometric and optical properties in the cerebellar cortex. (A) The variation index (p = 5.2e-5), skewness (p = 6e-5) and kurtosis (p = 0.21) of the molecular and granular layer thickness. (B) The variation index (p = 0.72), skewness (p = 0.24) and kurtosis (p = 0.1) of μs in the molecular and granular layers. Error bars indicate standard deviations among the five subjects. Mol: molecular layer; Gra: granular layer. The p-values are obtained from paired-sample t-tests.

In contrast to the pronounced variations in morphology, the optical properties were more spatially uniform within a layer, with a variation index close to one. The variation indices of μs in the molecular layer and the granular layer were similar (Fig. 8 B, top panel, 1.2 ± 0.01 and 1.2 ± 0.03, respectively, mean ± s.t.d., p = 0.72, paired-sample t-test, n = 5 subjects). This was further confirmed by the skewness and kurtosis of μs. We found similar skewness (Fig. 8 B, middle panel, 0.1 ± 0.2 and 0.2 ± 0.2, respectively, mean ± s.t.d., p = 0.24, paired-sample t-test, n = 5 subjects) and kurtosis (Fig. 8 B, bottom panel, 3.1 ± 0.1 and 3.2 ± 0.03, respectively, mean ± s.t.d., p = 0.1, paired-sample t-test, n = 5 subjects) between the molecular and granular layers.

3.4. Cross-subject variation of morphometric and optical properties in the cerebellar cortex

The results in Section 3.2 show that the mean layer thickness was comparable across the five subjects (Fig. 5 C), while the mean optical properties exhibited greater variations (Fig. 6 B). To quantitatively evaluate the cross-subject variability, we calculated the coefficient of variation (CV, equal to the standard deviation divided by the mean) from the mean layer thickness and layer-specific mean μs across the five subjects. The CV of the mean layer thickness in the molecular and granular layers was 9.8% and 6.3%, respectively. In contrast, we found the CV of the mean μs to be higher than that of the mean layer thickness, resulting in 15.2% and 13.0% in the molecular and granular layers, respectively. It is noted that despite the highly convoluted patterns, the mean thickness of a layer differed by less than 10% across the subjects, indicating a low cross-subject variability in mean thickness of human cerebellar cortex within the age range of this study.

3.5. Correlation between morphometric and optical properties in the cerebellar cortex

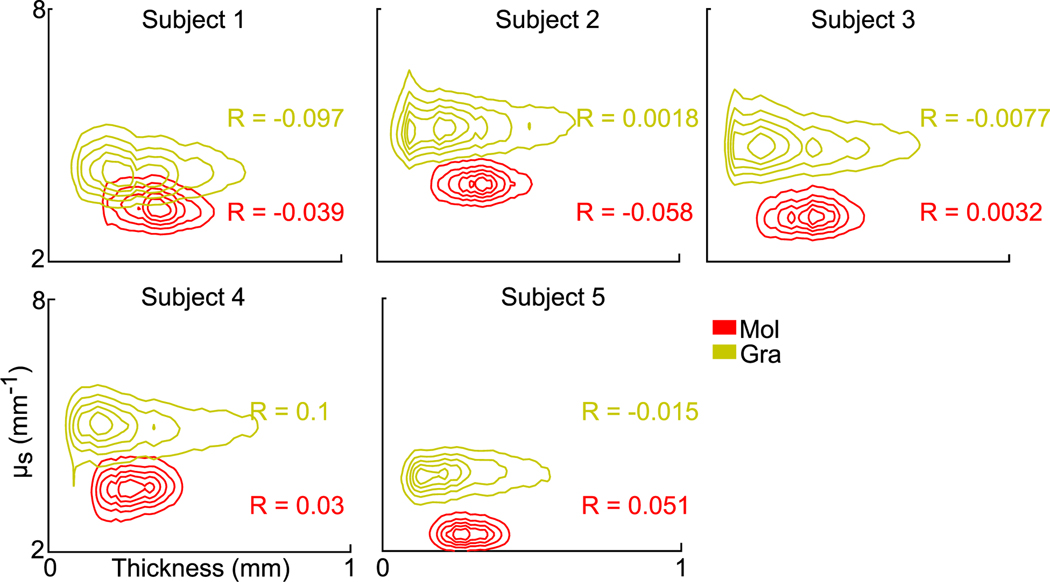
We analyzed the correlation between layer thickness and μs by quantifying the correlation coefficients (R) between these two measures. The layer thickness exhibited little correlation with μs in either the molecular or granular layers of the five cerebellar samples (Fig. 9). The correlation coefficient with the largest magnitude that we observed was 0.1. The contours in Fig. 9 illustrate the 2D distribution of thickness – μs with correlation coefficients shown for every subject. Overall, no significant correlation was found between layer thickness and optical properties.

Fig. 9.

Fig. 9.

Open in a new tab

Contour plots of 2D distribution between thickness and μs measurements in the molecular and granular layers of five cerebellar samples. The correlation coefficients (R) between layer thickness and μs are shown for each subject in molecular and granular layers. Mol: molecular layer; Gra: granular layer.

4. Discussion

Over 100 years after Santiago Ramón y Cajal’s pioneering work in identifying neurons and axonal tracts, human brain mapping at micrometer resolution still remains challenging. The next generation of optical imaging methods requires rapid acquisition rates and volumetric reconstruction in large-sized sample. The as-PSOCT technique supports 3D reconstruction of cubic centimeters of human brain samples at 3–10 μm resolution. In this study, we presented the quantification of morphometric and optical properties in large cerebellum volumes using as-PSOCT.

To characterize the morphometry of the human cerebellar cortex, we first measured cortical layer thickness from the volumetric reconstruction (Fig. 5). Compared to conventional 2D histological techniques, we provided reliable morphometrical measurements of layer thickness in 3D (Wang et al., 2018). MRI techniques have been used to estimate total cerebellar volume (Hara et al., 2016) and visualize the cerebellar cortical layers in-plane (Marques et al., 2010). However, the resolution of MRI limits its ability to measure the layer thickness in the cerebellum. By using as-PSOCT, we showed that the mean thickness of both the molecular layer and the granular layer is ∼320 μm, and the thickness in the depth of the fissure was smaller than one pixel even with state-of-the-art 100 μm resolution ex vivo MRI technique (Edlow et al., 2019). Quantification of the folding morphology is important in order to establish biomarkers from neuroimaging data, especially in neurological diseases (Mangin et al., 2010). Current gyrification measurements from MRI (Schaer et al., 2012) have been applied only to the cerebral cortex, while the small folia in the cerebellar cortex remain unexplored. With high resolution as-PSOCT, we qualitatively showed that high layer thickness values were seen at the crown of the folium and that low thickness was situated at the depth of the fissure in the granular layer (Fig. 7). Surface mapping of the granular layer suggested a convoluted folding pattern in the cerebellar cortex. We also found a high variation of thickness in the granular layer that had not been reported before from quantitative analysis (Fig. 8 A). Surface mapping of the molecular layer is more challenging due to tight space between adjacent folia and requires significant amount of work in the future. Future work will also include an automatic definition of crown and depth of the fissure as well as quantitative analysis of the folding pattern in the cerebellar cortex. The high-quality data generated by as-PSOCT can be used to fit MR models to construct a neuroarchitectural map of the human cerebellum, an approach not available using current imaging techniques.

The current as-PSOCT study only imaged a block of cerebellum. As a result, potential error might be introduced in layer thickness estimation from cutting and segmentation biases, in which cortical layers were partially blocked off. In four out of five samples, we only segmented lobular parts that have intact folia located in the middle of the tissue block. The average molecular layer thickness of these 4 subjects was 309 ± 21 μm. In one sample where partial inclusion of cortical layers was inevitable due to tissue integrity problems, we segmented the whole volume as shown in Figs. 2, 3, and 7. In this subject, the molecular layer thickness was 328 μm, which fell within the same range defined by the other 4 subjects. As the number of voxels on the sample boundary only represented a small fraction of the total number of voxels in the image, we found that the bias introduced by tissue blocking to be negligible and not to change the statistical results or conclusion of our layer thickness measurements.

Our as-PSOCT system allows quantification of a scattering coefficient map. We found different scattering characteristics in the laminar structures (Figs. 2 B and 6). Myelin content, neuron size and cell density all contribute to the scattering in brain tissues. A recent study found a strong linear relationship between myelin content and the scattering coefficient, while the neuron density revealed a secondary contribution that moderately modulated the tissue scattering (Chang et al., 2021). The folial white matter is composed of bundles of myelinated axons. Consequently, the high scattering in the white matter is associated with optical properties of myelin compared to cortex (Wang et al., 2011). Within the cerebellar cortex, the granular layer is densely packed with granule cells and contains myelinated axons in the adult brain (Liu et al., 2017). The optical properties generated by as-PSOCT enabled the quantitative assessment of microstructural features of cerebellar tissues, which may serve as a potentially useful tool for the evaluation of pathological process. Many cerebellar neurodegenerative diseases include loss of Purkinje neurons and atrophy of the cerebellar cortex, such as multiple system atrophy and the spinocerebellar ataxias (Koeppen, 2018). Optical scattering changes have been observed in neurodegenerative disease (Hanlon et al., 2008), especially in spinocerebellar ataxia type 1 (Liu et al., 2018). Therefore, the scattering coefficient may serve as a new biomarker of the neuropathology in cerebellar neurodegeneration, including alterations in myelin and cell density.

In the samples from the five subjects, we found the CV of the mean μs to be higher than the CV of mean layer thickness. Therefore, we observed higher cross-subject variability in the optical properties than in the morphology for our five samples. These results may suggest that optical properties can serve as a sensitive marker of neuropathology, identifiable before large-scale histopathological changes can be detected. It is also noticeable that some variation in the optical properties may be attributed to individual sample variabilities. The duration of formalin fixation (Hsiung et al., 2005) and the inevitable variation in postmortem interval among subjects may affect the scattering coefficient thus causing cross-subject variability. We will include more samples to further explore such a limitation in future studies.

The homogeneous optical properties within the molecular and granular layers and the lack of correlation with thickness of the layers is a novel observation (Figs. 8 B and 9), suggesting a uniformity of cellular and myelin density despite the pronounced folding patterns in the cerebellar cortex (Fig. 8 A). Morphological analysis reported by MRI has focused on the impact of neurological diseases on the cerebrum (Graham and Sharp, 2019; Im et al., 2008). In a topographical analysis of demyelination and neurodegeneration in multiple sclerosis subjects, for example, Haider et al. found heterogeneous neurodegeneration between the gyri and the sulci (Haider et al., 2016). Here we performed similar morphological analyses to investigate the layer thickness and optical property in the crown of folium and the depth of fissure of the cerebellum, using MRI software on the high resolution as-PSOCT volumes (Fig. 7). Although the current study focused on the normal control samples, those analyses can be extended to explore a variety of neurodegenerative diseases. For example, it is possible that the cortex at the crowns and depths of the cerebellar folia are affected differently in spinocerebellar ataxia type 1, in which the Purkinje cell layer and granular layer show heterogeneous characteristics of neuronal loss (Genis et al., 1995). The analysis of morphometric and optical properties of the human cerebellum opens new avenues to investigate spatial-structural patterns of neuropathology in cerebellar disorders. The current study is limited to postmortem characterization. The morphometry of cerebellar cortex from as-PSOCT can serve as a source of ground truth to build characterizations for in vivo technologies to improve their interpretability.

In the current study we used a low numerical aperture objective to image the cerebellar samples. Due to the limit of lateral resolution, we did not analyze the thin Purkinje cell layer. However, it is important to acknowledge that Purkinje cells are a critical information processing hub in the cerebellum. The as-PSOCT system has the potential to incorporate high numerical aperture objectives to visualize Purkinje cells and other cells (Magnain et al., 2015; Wang et al., 2016). Further developments of our technique are under way to provide this level of cellular information necessary for the study of neurological diseases. Another technical development would be to improve the accuracy of depth-resolved optical property estimation for better analysis of high-resolution volumetric data (Amaral et al., 2019; Wang et al., 2017).

5. Conclusions

We used as-PSOCT to reconstruct volumetric representations of the human cerebellum and quantify morphometric and optical properties in postmortem cerebellar tissue in five samples. We recovered the laminar structure of the folia, which cannot be achieved by MRI. The laminar structures in the cerebellar cortex were differentiated by both retardance and scattering coefficient contrasts. The layer thickness and folding index revealed a complex folding pattern in the cerebellar cortex, where the thickness varied greatly in the granular layer. The thickness in the molecular layer was less variant. We also found a uniform distribution of cell and myelin content reflected in the homogeneous optical properties within a cortical layer despite the complicated folding patterns. Conversely, the higher cross-subject variability for optical properties than for cortical thickness in the cerebellum suggested that the optical properties may serve as a more sensitive parameter to evaluate pathological conditions. High-resolution as-PSOCT data supports a detailed atlas to be built in the cerebellum that will enable in vivo prediction in MRI assessment that would not otherwise be possible. Quantification in morphometric and optical properties may serve as new biomarkers in cerebellar diseases such as multiple system atrophy and spinocerebellar ataxias, and therefore have the potential to influence pathological evaluations in scalable population size.

Supplementary Material

Supplementary

Acknowledgments

We greatly appreciated the insightful discussions with Dr. Douglas Greve for this work. This work was supported by the National Institutes of Health (NIH), specifically: in part by the BRAIN Initiative Cell Census Network grant (U01MH117023), the National Institute of Child Health and Human Development (R21HD106038), the National Institute for Biomedical Imaging and Bioengineering (R00EB023993, R21EB018907, U01EB026996, R01EB019956, R01EB006758, R01EB023281, P41EB030006, P41EB015896), the National Institute of Mental Health (R01MH123195, R01MH121885, RF1MH123195), the National Institute on Aging (R01AG064027, R01AG008122, R01AG016495, R01AG070988, R56AG068261, R56AG064027), the National Institute of Diabetes and Digestive and Kidney Diseases(K01DK101631), and the National Institute for Neurological Disorders and Stroke (R01NS0525851, R21NS072652, R01NS070963, R01NS083534, 5U01NS086625, 5U24NS10059103, R01NS105820), as well as Shared Instrumentation Grants (S10RR023401, S10RR019307, and S10RR023043). Additional support was provided by the NIH Blueprint for Neuroscience Research (5U01MH093765), part of the multi-institutional Human Connectome Project, as well as by the European Research Council (Starting Grant 677697, project “BUNGEETOOLS ”) and by Alzheimer’s Research UK (Interdisciplinary Grant ARUK-IRG2019A-003).

Footnotes

Data and code availability statement

Manual segmentation tool of Freeview is available as part of the open-source software FreeSurfer: https://surfer.nmr.mgh.harvard.edu/fswiki/DownloadAndInstall . The layer thickness code is available at https://www.nitrc.org/projects/thickness . Data used in this work are available upon request.

Disclosures

B.F. has a financial interest in CorticoMetrics, a company whose medical pursuits focus on brain imaging and measurement technologies. B.F.’s interests were reviewed and are managed by MGH and Partners HealthCare in accordance with their conflict of interest policies. J.D.S. is site principal investigator for Biohaven Pharmaceuticals NCT03952806, NCT02960893 and NCT03701399, and holds the copyright with The General Hospital Corporation to the Brief Ataxia Rating Scale, Cerebellar Cognitive Affective Syndrome Scale, and the Patient Reported Outcome Measure of Ataxia.

Credit authorship contribution statement

Chao J. Liu: Formal analysis, Investigation, Data curation, Writing - original draft. William Ammon: Formal analysis, Investigation, Data curation, Writing - original draft. Viviana Siless: Methodology, Formal analysis, Data curation. Morgan Fogarty: Methodology, Formal analysis, Data curation. Ruopeng Wang: Methodology, Data curation. Alessia Atzeni: Methodology, Data curation. Iman Aganj: Methodology, Formal analysis, Data curation, Writing - review & editing. Juan Eugenio Iglesias: Methodology, Formal analysis, Data curation, Writing - review & editing. Lilla Zöllei: Formal analysis, Data curation, Writing - review & editing. Bruce Fischl: Conceptualization, Writing - review & editing, Funding acquisition. Jeremy D. Schmahmann: Formal analysis, Data curation, Writing - review & editing. Hui Wang: Conceptualization, Methodology, Formal analysis, Investigation, Data curation, Writing - review & editing, Funding acquisition.

Supplementary materials

Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.neuroimage.2021.118627.

References

  1. Aganj I, Sapiro G, Parikshak N, Madsen SK, Thompson PM, 2009. Measurement of cortical thickness from MRI by minimum line integrals on soft-classified tissue. Hum. Brain Mapp. 30, 3188–3199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Amaral MM, Zezell DM, Monte AFG, de Cara ACB, Araújo JCR, Antunes A, Freitas AZ, 2019. General model for depth-resolved estimation of the optical attenuation coefficients in optical coherence tomography. J. Biophoton. 12, e201800402. [DOI] [PubMed] [Google Scholar]
  3. Apps R, Hawkes R, Aoki S, Bengtsson F, Brown AM, Chen G, Ebner TJ, Isope P, Jörntell H, Lackey EP, Lawrenson C, Lumb B, Schonewille M, Sillitoe RV, Spaeth L, Sugihara I, Valera A, Voogd J, Wylie DR, Ruigrok TJH, 2018. Cerebellar modules and their role as operational cerebellar processing units. Cerebellum 17, 654–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Atzeni A, Jansen M, Ourselin S, Iglesias JE, 2018. A probabilistic model combining deep learning and multi-atlas segmentation for semi-automated labelling of histology. In: Frangi AF, Schnabel JA, Davatzikos C, Alberola-López C, Fichtinger G. (Eds.), Medical Image Computing and Computer Assisted Intervention – MICCAI 2018. Springer International Publishing, Cham, pp. 219–227. [Google Scholar]
  5. Boillat Y, Bazin PL, O’Brien K, Fartaria MJ, Bonnier G, Krueger G, van der Zwaag W, Granziera C, 2018. Surface-based characteristics of the cerebellar cortex visualized with ultra-high field MRI. Neuroimage 172, 1–8. [DOI] [PubMed] [Google Scholar]
  6. Brezinski ME, Tearney GJ, Boppart SA, Swanson EA, Southern JF, Fujimoto JG, 1997. Optical biopsy with optical coherence tomography: feasibility for surgical diagnostics. J. Surg. Res. 71, 32–40. [DOI] [PubMed] [Google Scholar]
  7. Castellazzi G, Bruno SD, Toosy AT, Casiraghi L, Palesi F, Savini G, D’Angelo E, Wheeler-Kingshott CAMG, 2018. Prominent changes in cerebro-cerebellar functional connectivity during continuous cognitive processing. Front. Cell. Neurosci. 12, 331–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chang S, Varadarajan D, Yang J, Chen IA, Kura S, Magnain C, Augustinack JC, Fischl B, Greve DN, Boas DA, Wang H, 2021. Scalable mapping of myelin and neuron density in the human brain with micrometer resolution. bioRxiv, 2021.2005.2013.444005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. D’Angelo E, Casali S, 2013. Seeking a unified framework for cerebellar function and dysfunction: from circuit operations to cognition. Front. Neural Circ. 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. de Boer JF, Milner TE, van Gemert MJ, Nelson JS, 1997. Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography. Opt. Lett. 22, 934–936. [DOI] [PubMed] [Google Scholar]
  11. De Zeeuw CI, Ten Brinke MM, 2015. Motor learning and the cerebellum. Cold Spring Harb. Perspect. Biol. 7 a021683-a021683. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Edlow BL, Mareyam A, Horn A, Polimeni JR, Witzel T, Tisdall MD, Augustinack JC, Stockmann JP, Diamond BR, Stevens A, Tirrell LS, Folkerth RD, Wald LL, Fischl B, van der Kouwe A, 2019. 7 Tesla MRI of the ex vivo human brain at 100 μm resolution. Sci. Data 6, 244. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fischl B, 2012. FreeSurfer. Neuroimage 62, 774–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Genis D, Matilla T, Volpini V, Rosell J, Davalos A, Ferrer I, Molins A, Estivill X, 1995. Clinical, neuropathologic, and genetic studies of a large spinocerebellar ataxia type 1 (SCA1) kindred: (CAG)n expansion and early premonitory signs and symptoms. Neurology 45, 24–30. [DOI] [PubMed] [Google Scholar]
  15. Graham NS, Sharp DJ, 2019. Understanding neurodegeneration after traumatic brain injury: from mechanisms to clinical trials in dementia. J. Neurol. Neurosurg. Psychiatry 90, 1221–1233. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Haider L, Zrzavy T, Hametner S, Höftberger R, Bagnato F, Grabner G, Trattnig S, Pfeifenbring S, Brück W, Lassmann H, 2016. The topograpy of demyelination and neurodegeneration in the multiple sclerosis brain. Brain 139, 807–815. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hanlon EB, Perelman LT, Vitkin EI, Greco FA, McKee AC, Kowall NW, 2008. Scattering differentiates Alzheimer disease in vitro. Opt. Lett. 33, 624–626. [DOI] [PubMed] [Google Scholar]
  18. Hara D, Maki F, Tanaka S, Sasaki R, Hasegawa Y, 2016. MRI-based cerebellar volume measurements correlate with the International Cooperative Ataxia Rating Scale score in patients with spinocerebellar degeneration or multiple system atrophy. Cerebellum Ataxias 3 14–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Herculano-Houzel S, 2010. Coordinated scaling of cortical and cerebellar numbers of neurons. Front. Neuroanat. 4, 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hsiung P−L, Nambiar PR, Fujimoto JG, 2005. Effect of tissue preservation on imaging using ultrahigh resolution optical coherence tomography. J. Biomed. Opt. 10, 1–9. [DOI] [PubMed] [Google Scholar]
  21. Im K, Lee JM, Seo SW, Hyung Kim S, Kim SI, Na DL, 2008. Sulcal morphology changes and their relationship with cortical thickness and gyral white matter volume in mild cognitive impairment and Alzheimer’s disease. Neuroimage 43, 103–113. [DOI] [PubMed] [Google Scholar]
  22. Koeppen AH, 2018. The neuropathology of the adult cerebellum. Handb Clin Neurol 154, 129–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Koziol LF, Budding D, Andreasen N, D’Arrigo S, Bulgheroni S, Imamizu H, Ito M, Manto M, Marvel C, Parker K, Pezzulo G, Ramnani N, Riva D, Schmahmann J, Vandervert L, Yamazaki T, 2014. Consensus paper: the cerebellum’s role in movement and cognition. Cerebellum 13, 151–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lawrenson C, Bares M, Kamondi A, Kovács A, Lumb B, Apps R, Filip P, Manto M, 2018. The mystery of the cerebellum: clues from experimental and clinical observations. Cerebellum Ataxias 5, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Liu CJ, Rainwater O, Clark HB, Orr HT, Akkin T, 2018. Polarization-sensitive optical coherence tomography reveals gray matter and white matter atrophy in SCA1 mouse models. Neurobiol. Dis. 116, 69–77. [DOI] [PubMed] [Google Scholar]
  26. Liu CJ, Williams KE, Orr HT, Akkin T, 2017. Visualizing and mapping the cerebellum with serial optical coherence scanner. Neurophotonics 4, 011006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Magnain C, Augustinack JC, Konukoglu E, Frosch MP, Sakadzic S, Varjabedian A, Garcia N, Wedeen VJ, Boas DA, Fischl B, 2015. Optical coherence tomography visualizes neurons in human entorhinal cortex. Neurophotonics 2, 015004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Mangin JF, Jouvent E, Cachia A, 2010. In-vivo measurement of cortical morphology: means and meanings. Curr. Opin. Neurol. 23, 359–367. [DOI] [PubMed] [Google Scholar]
  29. Marques JP, van der Zwaag W, Granziera C, Krueger G, Gruetter R, 2010. Cerebellar cortical layers: in vivo visualization with structural high-field-strength MR imaging. Radiology 254, 942–948. [DOI] [PubMed] [Google Scholar]
  30. Modat M, Ridgway GR, Taylor ZA, Lehmann M, Barnes J, Hawkes DJ, Fox NC, Ourselin S, 2010. Fast free-form deformation using graphics processing units. Comput. Methods Programs Biomed. 98, 278–284. [DOI] [PubMed] [Google Scholar]
  31. Ourselin S, Roche A, Subsol G, Pennec X, Ayache N, 2001. Reconstructing a 3D structure from serial histological sections. Image Vision Comput. 19, 25–31. [Google Scholar]
  32. Palesi F, De Rinaldis A, Castellazzi G, Calamante F, Muhlert N, Chard D, Tournier JD, Magenes G, D’Angelo E, Gandini Wheeler-Kingshott CAM, 2017. Contralateral cortico-ponto-cerebellar pathways reconstruction in humans in vivo: implications for reciprocal cerebro-cerebellar structural connectivity in motor and non– motor areas. Sci. Rep. 7, 12841. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Preibisch S, Saalfeld S, Tomancak P, 2009. Globally optimal stitching of tiled 3D microscopic image acquisitions. Bioinformatics 25, 1463–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Schaer M, Cuadra MB, Schmansky N, Fischl B, Thiran J−P, Eliez S, 2012. How to measure cortical folding from MR images: a step-by-step tutorial to compute local gyrification index. J. Vis. Exp. e3417 -e3417. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Schmahmann JD, Guell X, Stoodley CJ, Halko MA, 2019. The theory and neuroscience of cerebellar cognition. Annu. Rev. Neurosci. 42, 337–364. [DOI] [PubMed] [Google Scholar]
  36. Schmahmann JD, Sherman JC, 1998. The cerebellar cognitive affective syndrome. Brain 121 (Pt 4), 561–579. [DOI] [PubMed] [Google Scholar]
  37. Sereno MI, Diedrichsen J, Tachrount M, Testa-Silva G, d’Arceuil H, De Zeeuw C, 2020. The human cerebellum has almost 80% of the surface area of the neocortex. Proc. Natl. Acad. Sci. 117, 19538. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Shelhamer E, Long JT,D, , 2016. Fully convolutional networks for semantic segmentation. arXiv:1605.06211. [DOI] [PubMed] [Google Scholar]
  39. Stoodley CJ, MacMore JP, Makris N, Sherman JC, Schmahmann JD, 2016. Location of lesion determines motor vs. cognitive consequences in patients with cerebellar stroke. Neuroimage Clin. 12, 765–775. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Vermeer KA, Mo J, Weda JJ, Lemij HG, de Boer JF, 2013. Depth-resolved model-based reconstruction of attenuation coefficients in optical coherence tomography. Biomed. Opt. Express 5, 322–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Voogd J, Ruigrok TJH, 2012. Chapter 15 cerebellum and precerebellar nuclei. In: Mai JK, Paxinos G. (Eds.), The Human Nervous System. Academic Press, San Diego, pp. 471–545. [Google Scholar]
  42. Wang H, Akkin T, Magnain C, Wang R, Dubb J, Kostis WJ, Yaseen MA, Cramer A, Sakad ž i ć S, Boas D, 2016. Polarization sensitive optical coherence microscopy for brain imaging. Opt. Lett. 41, 2213–2216. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Wang H, Black AJ, Zhu J, Stigen TW, Al-Qaisi MK, Netoff TI, Abosch A, Akkin T, 2011. Reconstructing micrometer-scale fiber pathways in the brain: multi– contrast optical coherence tomography based tractography. Neuroimage 58, 984–992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Wang H, Magnain C, Sakad ž i ć S, Fischl B, Boas DA, 2017. Characterizing the optical properties of human brain tissue with high numerical aperture optical coherence tomography. Biomed. Opt. Express 8, 5617–5636. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Wang H, Magnain C, Wang R, Dubb J, Varjabedian A, Tirrell LS, Stevens A, Augustinack JC, Konukoglu E, Aganj I, Frosch MP, Schmahmann JD, Fischl B, Boas DA, 2018. as-PSOCT: volumetric microscopic imaging of human brain architecture and connectivity. Neuroimage 165, 56–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Yang J, Chen IA, Chang S, Tang J, Lee B, Kılıç K, Sunil S, Wang H, Varadarajan D, Magnain CV, Chen S, Costantini I, Saverio FP, Fischl B, Boas DA, 2020. Improving the characterization of ex vivo human brain optical properties using high numerical aperture optical coherence tomography by spatially constraining the confocal parameters. Neurophotonics 7, 1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary
NIHMS1753471-supplement-Supplementary.docx (278.8KB, docx)

RESOURCES