Abstract
Optical-resolution photoacoustic microscopy (OR-PAM) enjoys superior spatial resolution and has received intense attention in recent years. The application, however, has been limited to shallow depths because of strong scattering of light in biological tissues. In this work, we propose to achieve deep-penetrating OR-PAM performance by using deep learning enabled image transformation on blurry living mouse vascular images that were acquired with an acoustic-resolution photoacoustic microscopy (AR-PAM) setup. A generative adversarial network (GAN) was trained in this study and improved the imaging lateral resolution of AR-PAM from 54.0 µm to 5.1 µm, comparable to that of a typical OR-PAM (4.7 µm). The feasibility of the network was evaluated with living mouse ear data, producing superior microvasculature images that outperforms blind deconvolution. The generalization of the network was validated with in vivo mouse brain data. Moreover, it was shown experimentally that the deep-learning method can retain high resolution at tissue depths beyond one optical transport mean free path. Whilst it can be further improved, the proposed method provides new horizons to expand the scope of OR-PAM towards deep-tissue imaging and wide applications in biomedicine.
Keywords: Photoacoustic microscopy, Deep penetration, Deep learning
1. Introduction
Photoacoustic microscopy (PAM) offers high-resolution imaging of rich optical-absorption contrasts in vivo and provide structural, functional, and molecular information of biological tissues [1], [2]. Optical-resolution photoacoustic microscopy, often termed as OR-PAM, uses tightly focused laser beam for excitation and thus has diffraction-limited resolution to resolve single capillaries and monitor microvascular level biological processes. OR-PAM has gained intense attention in the past decade [3], [4], [5], [6] and has seen many preclinical and clinical applications in neuroscience [7], tumor angiogenesis [8], histology [9], [10], dermatology [11], and many others [12], [13], [14].
Limited by strong scattering in biological tissue, the penetration depth of OR-PAM is within one optical transport mean free path (~ 1 mm for biological tissues). It would be impactful if OR-PAM can see deeper into tissue. One attempt is to explore whether OR-PAM performance can be inferred or constructed through computation based on deep-penetrating, albeit low-resolution, photoacoustic signals. Acoustic-resolution PAM (AR-PAM) does not focus light tightly and thus can extend to several millimeters to centimeters deep [2], [15]. AR-PAM also waives the necessity for single-mode fiber (SMF) or costly single-mode lasers to produce high-quality focused laser beam. Thus, lower cost multimode pulse laser like laser diode or light-emitting diode (LED) can be used as the light source [16], [17], [18]. On the other hand, SMF is replaced with fiber bundle or multimode fiber (MMF) for optical delivery in AR-PAM. This allows for higher optical damage threshold and coupling efficiency, resulting in higher power output or pulse repetition rate, that is, an increased imaging speed. Imagine that if a relationship can be built or learned between superficial AR-PAM and OR-PAM data sets, and the validity of the relationship remains for deeper tissue regions or different organs, then deep-penetrating optical-resolution photoacoustic microscopy could be achieved through learning the acoustic-resolution photoacoustic signals at that depth.
Here, we propose a deep learning method to transform low-resolution AR-PAM images into high-resolution ones that are comparable to OR-PAM results. This allows us to combine the advantages of deep penetration of AR-PAM and high resolution of OR-PAM. Apart from that, lower cost yet higher speed OR-PAM imaging could also be achieved based on the usage of AR-PAM apparatus, as less restrictions on the laser source and larger scanning step size can be adopted. In the past few years, there have been a number of deep learning applications aimed at enhancing the performance of photoacoustic imaging [19], [20], such as increasing the contrast [21] or penetration depth [22] under low fluence illumination, improving the lateral resolution for out-of-focus region in AR-PAM [23], and enhancing OR-PAM images acquired under low laser dosage or sampling rate[24], [25]. Besides, deep learning has seen applications in photoacoustic computed tomography (PACT) that mainly involve image enhancement from suboptimal reconstruction [26], [27] and artifact removal [28], [29]. Several related deep learning applications include single image super-resolution [30], [31], [32], [33], microscopic image enhancement [34], [35], [36] and microscopic imaging transformation [37], [38]. It has been shown that conventional convolutional neural network (CNN) trained with pixel-wise loss tends to output over-smoothed results [33]. In contrast, the generative adversarial network (GAN) model with residual blocks, trained with perceptual loss, performs particularly well for these problems.
In this study, we adopt Wasserstein GAN with gradient penalty (WGAN-GP) [39] as the training network to transform low-resolution AR-PAM images to match high-resolution OR-PAM images obtained at the same depth. In the following sections, we first describe the integrated OR- and AR-PAM system for data acquisition and the WGAN-GP model used for PAM imaging transformation. The trained network is first tested with in vivo mouse ear vascular images and the performance is compared with that of a typical blind deconvolution method. We further apply the network to in vivo mouse brain AR-PAM data to verify its validity for different tissue regions. After that, the performance of the network on deep-tissue imaging is evaluated with a hair phantom. We show that, with the proposed PAM imaging transformation, deep-penetrating OR-PAM imaging could be achieved at depths that are way beyond the depth limit of traditional OR-PAM. Whilst it can be further improved, the proposed method provides new insights to expand the scope of OR-PAM towards deep-tissue imaging and wide applications in biomedicine.
2. Methods
2.1. Integrated OR- and AR-PAM system
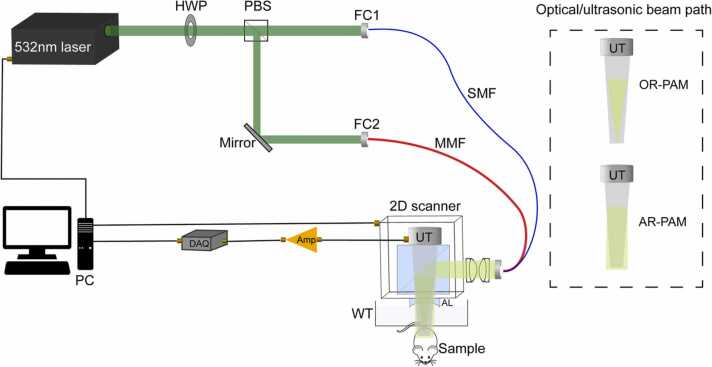
An integrated OR- and AR-PAM system was built in this study to acquire photoacoustic data, as shown in Fig. 1. The laser source is a 532 nm wavelength pulsed laser whose pulse width is 7 ns (VPFL-G-20, Spectra-Physics). The laser output is directly delivered into the PAM probe [6] by a 2-m single-mode fiber (SMF, P1–460B-FC-2, Thorlabs Inc) for OR-PAM imaging, or by a 1-m multi-mode fiber (MMF, M105L01–50–1, Thorlabs Inc) to support AR-PAM imaging. In experiment, the pulse energy for the OR- and AR-PAM was ~ 80 nJ and ~ 2000 nJ, respectively. The fiber coupling efficiencies of the SMF and the MMF were measured to be ~ 60% and ~ 90%, respectively. Noted that the optical/acoustic beam combiner in the probe reflects the optical beam to the sample and, in the meanwhile, transmits the produced ultrasound wave to the piezoelectric transducer (V214-BC-RM, Olympus-NDT). The central frequency and bandwidth of the ultrasound transducer used in the experiments are 50 MHz and 40 MHz, respectively. The optical-resolution and acoustic-resolution settings are switched by using different fibers only; usually after the entire scanning of OR-PAM for an image is finished, we switch the single mode fiber to a multimode fiber manually for AR-PAM imaging. This has endowed our integrated PAM system with the ability to yield automatically co-registered OR and AR imaging data sets [40]. The switch is controlled by the combination of a half-wave plate (HWP, GCL-060633, Daheng Optics) and a polarizing beam splitter (PBS, PBS051, Thorlabs Inc). When most light is reflected by the PBS to the MMF, light becomes diffusive in the sample so that the imaging resolution is determined acoustically by the acoustic lens (#45–697, Edmund optics), which collimates the photoacoustic waves. When most light transmits through the PBS to the SMF, light is tightly converged onto tissue sample, producing an optical focus coaxially and confocally aligned with the acoustic focus to optimize the detection sensitivity. The detected PA signals by the ultrasound transducer are amplified (ZFL-500LN+, Mini-circuits) and then transferred to the data acquisition card (DAQ, ATS9371, Alazar Tech), which is connected to the computer. Two-axis linear stage (L-509.10SD, Physik Instrument) is used to mount the scanning probe, which creates two-dimensional raster scanning to obtain volumetric A-line data. In our system, the lateral resolution of OR-, AR-PAM modules are about 4.5 µm and 50 µm, respectively.
Fig. 1.
Schematic of the integrated OR- and AR-PAM system, with the optical (green) and ultrasonic (gray) beam path in the probe for OR- and AR-PAM illustrated separately. Note that the SMF and MMF are not connected to the probe at the same time but separately instead. AL, Acoustic lens; Amp, amplifier; DAQ, data acquisition; FC, fiber coupler; HWP, half-wave plate; MMF, multi-mode fiber; PBS, polarization beam splitter; SMF, single-mode fiber; UT, ultrasound transducer; WT, water tank. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
2.2. Sample preparation
Several 6-week healthy ICR mice were anesthetized with isoflurane. Before imaging, the sample (e.g., mouse ear) was applied with ultrasound gel (Aquasonic 100) and fixed on a glass platform, beneath the water tank. The PAM probe was put above the target and immersed in the water tank to ensure acoustic coupling. All procedures involving animal experiments were approved by the Animal Ethical Committee of the City University of Hong Kong. An area of 5 × 5 of the mouse ear was imaged by OR-PAM at a step size of 2.5 µm, and then the same field of view (FOV) was scanned by AR-PAM at the same step size with OR-PAM. 14 pairs of AR- and OR-PAM vascular images of different mouse ears were acquired. Apart from ears, PAM imaging of mouse brain vasculature was also conducted. The skin hairs of mouse brain were removed by using hair removal cream (Veet, Hong Kong) before the experiment. Then the scalp was disinfected and cut with a surgical scissor. The exposed cerebral vessels were scanned at a step size of 2.5 µm within a FOV of 5 × 5 , using AR-PAM only.
To evaluate the imaging transformation performance at different depths, chicken breast tissues were sliced into different thicknesses to cover a few human hairs for AR-PAM imaging, which was used to mimic optical targets imaged at different tissue depths. We acquired AR-PAM images over a FOV of 5 × 5 mm2 of human hairs that were not covered or covered with tissues of thickness of 700, 1300, and 1700 µm, respectively. The pulse energy for AR-PAM in the phantom experiment was increased with increasingly thick chicken breast slice covered above the hair pattern.
2.3. Image pre-processing and data augmentation
The acquired PAM images in this study are maximum amplitude projections (MAP) of volumetric acquisitions, that is, 3D A-line data that are typically sized of (2000, 2000, 512) in which 2000 is the image size along each direction and 512 is the number of samples for one A-line. The A-line data need to be processed before conducting MAP, which is based on the actual condition of raster scanning. Usually, we need to flip the A-line data of even columns, and sometimes to translate upwards or downwards the A-lines at some positions to avoid image dither or ghosting caused by motor sweeping dislocations. It is almost inevitable for the acquired PAM images to contain noise, such as isolated bright spots that compress the image grayscale level or stain noises especially in OR-PAM images. Thus, all PAM images were first normalized to 0–1 before applying a 5 × 5 median filter to remove the extremely bright spots and mitigate the stain noises. After that, considering the training of deep neural network requires a large data set but the collected data was limited from experiment, data augmentation [41], [42], [43] was conducted using a Python library Albumentations [44]. There were mainly geometry and grayscale image transformation operations to teach the deep networks the desired invariance properties [43]. For geometry transformation, we conducted flipping along different directions (horizontal, vertical, and diagonal), random affine transformation (including translation, scaling and ± 15° rotation), random cropping and padding, as well as elastic deformation, to mimic different spatial distributions of blood vessels. Also, 10% synthetic AR-PAM images were further blurred using a random kernel or Gaussian filter. For grayscale transformations, we had random gamma (gamma value ranging from 0.6 and 1.4) adjustment to tune the image grayscale range. 10% synthetic AR-PAM images were further adjusted on random brightness and contrast, for modeling the illumination intensity discrepancies in the imaging system. These techniques aimed to artificially increase the data distribution of available PAM images for training, with the hope for the networks to learn the robustness against deformation and gray value variations [43] and to gain better generalization ability. In this study, 14 pairs of PAM vascular images of the mouse ear were acquired experimentally. Among them, 11 pairs were used to synthesize 528 image pairs that constitute the training set. The remaining three PAM image pairs were used for network tests, free of image augmentation.
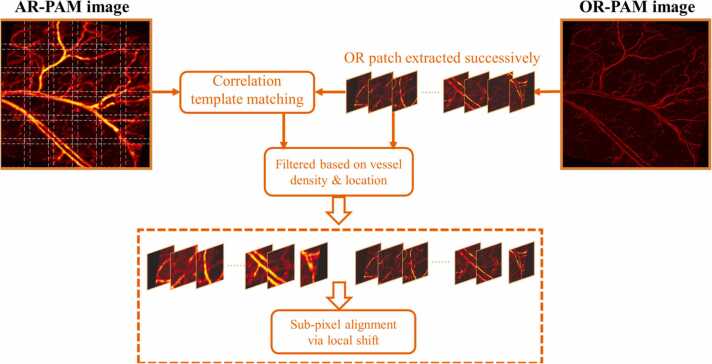
Since the acquired PAM images are of large size that our network cannot process directly, an entire PAM image is thus cut into small image patches, which also greatly increases the amount of training data. Noted that regular image patch extraction (and stitching) is enough for network evaluation on a test PAM image, while different strategy that combines accurate image patch alignment was adopted for generating the training set. This is mainly because the pixel-wise loss would be used to guide the neural network to learn a statistical PAM imaging transformation. As illustrated in Fig. 2, a template-matching algorithm based on image intensity correlation is employed, implemented in MATLAB. The image patches of size 390 × 390 are first extracted successively from an entire OR-PAM image with an overlap of 64 pixels in both horizontal and vertical directions, which work as the templates to find the highest-correlation matched patches in the corresponding AR-PAM image. This is done by calculating the 2D cross-correlation matrix between the OR patch and the entire AR image, in which the maximum value indicates the most likely matched AR patch. The cropped patches in AR-PAM image will be filtered based on two criteria before forming pairs with their OR templates: if the vessel density is not enough (less than half of the mean) or the location differs greatly (more than 10 pixels in any direction), the cropped AR-OR patch would be abandoned. Note that the matched image patches are still not accurately aligned at the sub-pixel level. Thus, additional local shift (shift amount is determined by the traversal search) between the extracted image patches is applied by bilinear interpolation. Eventually, the precisely registered images are cropped with three pixels on each side to avoid registration artifacts, forming the input-label pairs of size 384 × 384 for network training. Also noted that the image patch size 384 being the sum of two powers of 2 (i.e., 256 + 128), which may also suit the GPU allocation and speed up training.
Fig. 2.
The process of image patch extraction and alignment via correlation template matching. The OR patches were extracted successively, with each used as a template to find the highest correlated AR patch. The paired image patches were filtered with the criteria for vessel density and location before being applied with sub-pixel alignment.
2.4. GAN model and network training
To achieve PAM imaging transformation, we adopted a GAN-based framework for a deep neural network in this study. GAN was initially introduced by Goodfellow et al. in 2014 and has been proven a powerful generative model for super-resolution [31], [33] and many other imaging-related applications [37], [38]. There are two sub-networks in a GAN, namely the Generator and the Discriminator, being trained simultaneously. The Generator takes an AR image as the input and produces a resolution-enhanced image, which is then passed onto the Discriminator to determine its similarity to the ground truth OR image. There is an adversarial training between the Generator G and the Discriminator D: G tries to fool D by generating an image that closely resembles its OR label, while D tries to distinguish the generated fake data from the real one. Conventionally a GAN is trained to minimize the cross-entropy error (also referred to as the Jensen–Shannon divergence) between the generated and real data distribution. However, it has been observed a GAN inclines to be unstable and difficult to converge during such training, mainly owing to the vanishing gradient problem of the Generator and model collapse [39], [45], [46], [47]. To cure the problem, Wasserstein GAN was proposed [46], [47]; it uses Wasserstein distance to replace the Jensen–Shannon divergence as the objective to be optimized. The min-max game between the two sub-networks G and D within a GAN that adopts Wasserstein distance can be formulated by
| (1) |
where D is subject to 1-Lipschitz function , denotes the real OR image distribution, and the generated data distribution is implicitly defined by with following AR image distribution . Hereby, Wasserstein GAN was used for our PAM imaging transformation.
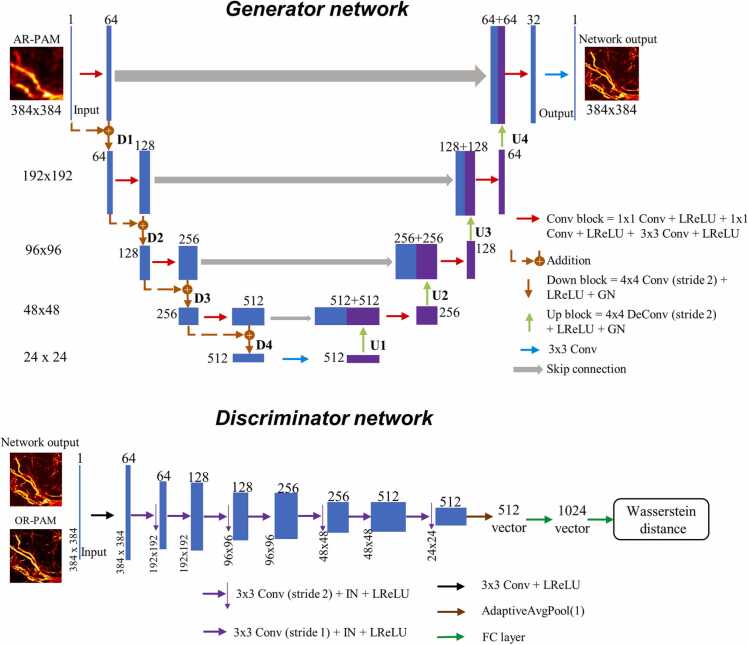
The WGAN model used for the imaging transformation from AR- to OR-PAM is illustrated in Fig. 3. The Generator network follows the U-Net architecture [43] that is composed of an encoder and a decoder path. The network can process an input AR image in a multiscale fashion, enabling the network to learn the imaging transformation at various scales. The encoder path comprises four residual convolutional blocks [32], [48] that are connected by a down-sampling block. Each convolutional block is composed of two convolutional and a convolution, with a Leaky Rectified Linear Unit LReLU layer (slope 0.2) following every convolutional layer. The down-sampling block consists of a convolutional layer with a kernel of size 4 and stride 2, an LReLU layer and a Group Normalization (GN) layer [49]. After four down-sampling blocks, a convolutional layer is bridged to the decoder path, in which the feature maps are up-sampled. The decoder, similar to the encoder, is also composed of four convolutional blocks (but no residual structure) that are connected by the up-sampling block. The up-sampling is performed with transposed convolution (also referred to deconvolution) layer, which forms the block together with an LReLU layer and a GN layer. Finally, a convolutional layer following the last convolutional block output a clearly resolved image of the same size and channel as the input. The Discriminator is a typical CNN used for image classification, except for the removal of sigmoid activation in the output layer. Started with a convolutional layer (with LReLU activation), seven convolutional blocks are followed, in which a feature map decreases its spatial size while increasing the number of channels. Each convolutional block consists of a convolutional layer with a kernel size of 3 and stride of either 2 or 1, a Instance Normalization (IN) layer[50] and a LReLU layer (slope 0.2). Note that the down-sampling of size and the increasing of channel is conducted alternately in the convolutional blocks through the control of kernel stride and number. The output of the last convolutional block is applied with adaptive average pooling and outputs a feature map f size . With two full-connected layers followed, the final output of the Discriminator is the scalar denoting the Wasserstein distances of input from OR image data distribution.
Fig. 3.
The architecture of the WGAN model used for PAM imaging transformation.
The behavior of optimization-based imaging transformation is principally driven by the choice of the objective/loss function. For the Generator, the primary objective is to minimize the pixel-wise loss, which is represented by the mean absolute error (MAE) between the network output image and the ground truth OR image , given by
| (2) |
whereis the image patch size. Besides, MAE in the frequency domain (FMAE) calculated from the magnitude of the 2D Fourier transform of and is also employed, which provides the optimizer information about the vessel orientation [24], given by
| (3) |
The perceptual loss of the Generator is defined as a weighted sum of the above two items, with the weighting factor of 1 for and a small weighting factor of for the FMAE loss since it may contribute to training instability [51]. In addition to perceptual loss, the adversarial loss returned by the critic network D is crucial to achieving PAM imaging transformation, which provides an adaptive loss term and may help the Generator jump out of local minima. We define the Generator loss as the weighted combination of perceptual loss and adversarial loss (with coefficient ), given by
| (4) |
In an attempt to enforce the Lipschitz constraint, in this study we adopt an improved Wasserstein GAN, that is, WGAN-GP [39], in which the gradient norm of the Discriminator’s output with respect to its input is constrained to 1. In this case, the Discriminator loss with gradient penalty is given by
| (5) |
where denotes the random sampling distribution and is the penalty coefficient.
The training of our WGAN-GP model was implemented in Pytorch (v1.8.0) on Microsoft Windows 10 operating system, using a graphics workstation based on an Intel Xeon CPU, an NVIDIA 3070 GPU, and 64 GB RAM. There were 16,849 aligned pairs of PAM image patches in the training set. A small weight initialization method was adopted for the GAN, in which the initialization parameters of all convolution and deconvolution layers of the GAN, calculated by MSRA initialization (also known as Kaiming initialization [52]), were multiplied by 0.1. Both two sub-networks were optimized using AdamW [53], i.e., Adam optimizer with decoupled weight decay regularization of and , and were trained with the same initial learning rate of 1 × 10−4. For the loss function of the GAN model, the weight of adversarial loss term in the Generator loss was set to and 10 for the gradient penalty coefficient in the Discriminator loss. It should be noted that to seek an adversarial equilibrium between the two sub-networks for GAN training, we can tune their learning rate or adjust the optimization times for the Generator or the Discriminator within each iteration. The total training epochs were 12 and the batch size was set as 2 for the GAN to be trained with mini-batch gradient descent, which took about 0.804 s for each iteration.
2.5. Blind deconvolution for AR-PAM image deblurring
Compared with high-resolution OR-PAM vascular images, images acquired with AR-PAM in situ have lower spatial resolution and are visually blurry. From the perspective of image deconvolution, it is reasonable to treat the OR-PAM image as the object itself while the corresponding AR-PAM image as the result of a convolution of the object and the system point spread function (PSF). As it is infeasible to model the PSF of such a conceptual PAM imaging system, we turn to use statistical blind deconvolution to iteratively recover the object and improve the estimation of PSF with an initial guess from a blurry AR-PAM image. This functions as the baseline, for a beneficial comparison with the deep learning enabled PAM imaging transformation regarding the performance of deblurring or resolution improvement.
Note that blind image deconvolution, as a highly ill-posed inverse problem, requires estimating both the blur kernel and object from a degraded image. Currently, most blind deconvolution methods fall into the variational Bayesian inference framework [54], with main differences coming from the form of the likelihood, the choice of priors on the object, and the blur kernel and the optimization methods to find the solutions [55]. Here, we used a general blind deconvolution method that adopts expectation-maximization optimization, to find the maximum posterior solution with flat priors. Besides that, a fractional-order total variation image prior was also tried [56], as the total variation is a popular regularization technique in image deconvolution. The blind deconvolution was implemented with 30 iterations for each input blurry image using MATLAB.
3. Results
3.1. Network feasibility: evaluation with in vivo mouse ear photoacoustic images
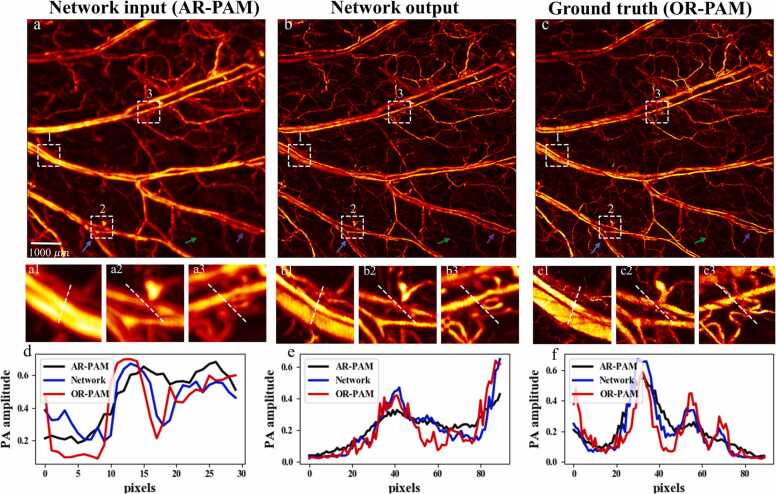
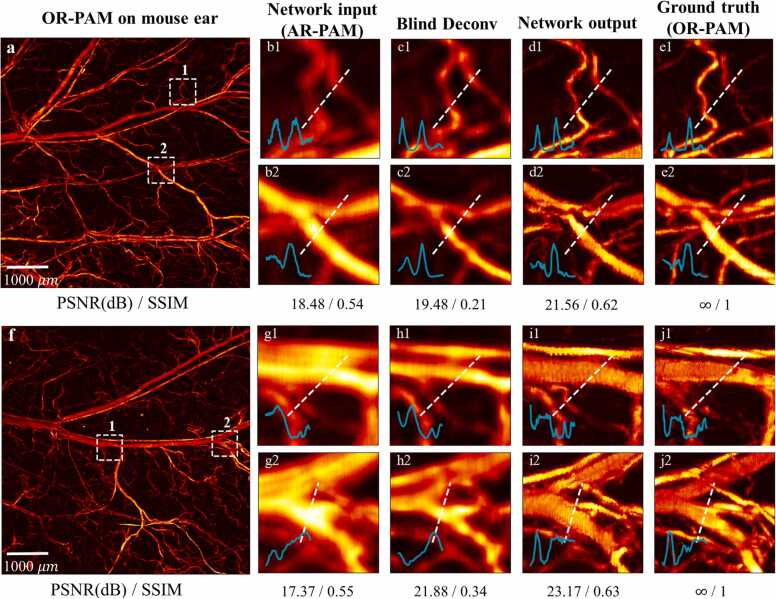
The feasibility of the WGAN-GP network was evaluated with the PAM image pairs of living mouse ear vasculature that were not included in network training. The results are shown in Fig. 4. Visually, the improvement of resolution is obvious with the network transformation, and quite many small vessels that have been hidden in the AR-PAM image are now resolved by the network. To better evaluate the improvement, three regions of interest (ROIs) indicated by a white dashed box in AR-PAM, network output, and OR-PAM images are chosen and compared. Taking a close look at them, clearly resolved blood vascular details are presented in the network output, which matches well with the ground truth (OR-PAM image) in the same region. Moreover, the signal intensity profiles along the cyan dashed lines within each ROI are compared. As seen, the AR-PAM imaging tends to generate overly smoothed signal intensity profiles due to its low resolution, while the network is capable of distinguishing vessels hierarchically. The sharp signal intensity profiles inside each ROI of the network output shares good consistency with those of the ground truth OR-PAM image, verifying the feasibility and reliability of our PAM imaging transformation. To explore the deblurring effect of the AR-to-OR network deeply, we here give specific analyses with three examples. The first example is that a blurred vascular plexus denoted by the blue arrow has been clearly resolved by the network, which matches well with the ground truth. Next, the green arrow shows a single capillary that is missed in the AR-PAM image and barely discernible in the network output, but is clearly shown in the OR-PAM image. Another example described by the purple arrow is the network find a limitation in resolving some closely spaced parallel blood vessels. It suggests that given extremely blurry pixels, the network may fail to reconstruct the full feature of the target. That said, this is also the point to indicate the feasibility and capability of the network of enhancing AR images while maintaining fidelity without generating fake features. Our findings reveal that the deblurring performance of the network is highly dependent on the quality, such as signal-to-noise ratio, of the given AR-PAM image. It is the case that most of the blurry blood vessels could be clearly resolved by the network, which possess good fidelities and meanwhile, some subtle distinctions from the ground truth OP-PAM images.
Fig. 4.
An experimentally obtained AR-PAM vascular image of mouse ear (a) is fed to the trained WGAN-GP model for imaging transformation. The resultant network output (b) is comparable to the ground truth OR-PAM image (c) of the same sample. Three ROIs marked with the white dashed boxes in (a1-a3) AR-PAM image, (b1–b3) transformed results, and (c1-c3) the ground truth OR-PAM image respectively, are enlarged and compared. Comparison of the cross-sectional profiles along the white dashed lines inside (a1, b1, c1), (a2, b2, c2), and (a3, b3, c3) are also provided in (d), (e) and (f) respectively. The blue arrow in (a-c) represents a vascular plexus that is originally blurred in AR-PAM but is now clearly resolved by the network; the green arrow shows a single capillary which is missed in the AR-PAM image and barely discernible in the network output, while clearly shown in the OR-PAM image; the purple arrow indicates a failure for the network to resolve some closely spaced parallel blood vessels that show up in the ground truth image. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.2. Network performance: comparison and characterization
The performance of the network transformation is characterized via two aspects. First, the deblurring performance on mouse ear AR-PAM images of the network is compared with that using a blind deconvolution method, as shown in Fig. 5. Apart from perceptual quality, two representative metrics including peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) [57] are also provided for comparison. PSNR is defined via the mean squared error (MSE) between an image to be evaluated and its ground truth OR image and the logarithmic form is given by:
| (6) |
in which denotes the maximum of OR image. SSIM evaluates an image quality perceptually, which also incorporate luminance and contrast information, defined as:
| (7) |
where and are the mean (variance) of an image to be evaluated and its OR label, respectively; denotes the covariance between the two images; are the constants to stabilize the division, respectively. In Fig. 5, two ROIs marked in a white dotted box are enlarged and compared. For ROI 1 in the first ear vasculature image (Fig. 5a), the single capillaries are resolved well for both blind deconvolution and network output, while the latter resembles better to the OR-PAM result. In ROI 2, the vessel bifurcation contains different types of vessels that the deconvolution method fails to produce rich vessel details, but the network output can distinguish vessels hierarchically. In the second case (Fig. 5b), we show that the WGAN-GP model can easily separate the large arteries and the small veins attached, as shown in both two ROIs, while the deconvolution method can merely distinguish them partially. Besides that, the comparison of signal intensity profiles inside each ROI also reveals that the network output results correlate better with the ground truth. It is worth noting that neither deconvolution nor the network could match the ground truth in every detail because some subtle capillaries were missed in the original AR-PAM image, as mentioned earlier. Also, note that compared with the AR-PAM image that appears overly smooth, the network output gets sharp with latent capillary artifacts generated sometimes (see d2 and e2 in Fig. 5), which might undermine the tricky metric like SSIM. In short, the network significantly outperforms blind deconvolution in deblurring blood vessels that the clearly resolved images are perceptually comparable to the experimentally acquired OR-PAM images.
Fig. 5.
Qualitative deblurring performance of deep learning in comparison with that using blind deconvolution. Two examples of mouse ear vascular images are presented, shown in the entire OR-PAM images (a) and (f). For each example, two ROIs marked with white dashed box are enlarged and compared. In the first example (a), (b1-e1) are for ROI 1 and (b2-e2) for ROI 2; in the second example (f), (g1-j1) are for ROI 1 and (g2-j2) for ROI 2; all correspond to AR-PAM, blind deconvolution, GAN output, and ground truth, respectively. Cross-sectional profiles along the white dashed lines inside (b1-e1), (b2-e3), (g1-j1) and (g2-j2) are provided for comparison. Metrics like PSNR and SSIM with respect to the entire OR-PAM image are also provided for reference. Blind Deconv, Blind Deconvolution.
Apart from qualitative analyses, enhancements on mouse ear data are compared and quantified by calculating metrics, including PSNR, SSIM, and PCC (Pearson correlation coefficient). PCC is expressed by:
| (8) |
where denotes the covariance between an image to be evaluated and its OR label, and are the standard deviation of the image and its OR label, respectively. The comparison is performed between test image patches, with the results given in Table 1. The network produces overall better results than the blind deconvolution method in improving all three metrics. The small variances in all the metrics for the network outputs also indicate the robust performance of our AR-to-OR network. To be specific, the mean PSNR improves from ~ 16.77 to ~ 20.02 dB, while SSIM (improved by 13% averagely) and PCC (averagely by 3%) only see modest improvement. Noted that the blood vessel image is overall sharpened by the network, some blurred capillary discrepancies also become sharper. As metrics like SSIM and PCC are very sensitive to these artifacts, only modest improvements are found in these metrics, although the image resolution improvement is significant, as can be seen from Fig. 5. Regarding the deconvolution method, it improves PSNR slightly for the test set, while failing to improve the other metrics, even degrading SSIM. It should be mentioned that the results were obtained using flat prior, a general image prior in the blind deconvolution method. Even worse results were found with the popular total variation regularization [56]. All these suggest that the enhancement of AR-PAM images towards high-resolution OR-PAM images is challenging with blind deconvolution. In contrast, deep learning enabled PAM imaging transformation may help solve this tricky inverse problem, with perceptual satisfactory deblurred results and improved metrics.
Table 1.
Quantitative comparison between deep learning and blind deconvolution in evaluating image enhancement, in which the metrics are represented in the form of mean ± standard deviation.
| PSNR | SSIM | PCC | |
|---|---|---|---|
| AR-PAM | 16.77 ± 2.61 dB | 0.54 ± 0.06 | 0.76 ± 0.08 |
| Blind Deconvolution | 18.05 ± 1.71 dB | 0.27 ± 0.07 | 0.76 ± 0.09 |
| Network output | 20.02 ± 1.51 dB | 0.61 ± 0.05 | 0.78 ± 0.08 |
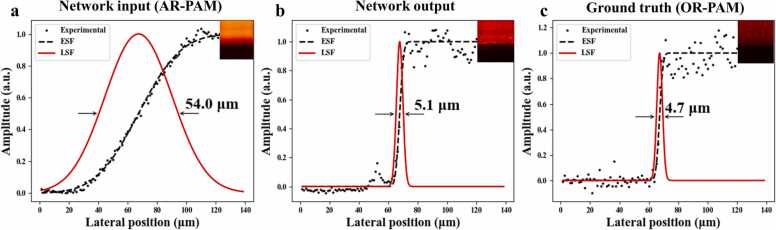
To further characterize the spatial resolution improvement after the network transformation, the edge response of a sharp blade was measured with the OR- and AR-PAM settings. As.illustrated in Fig. 6, the normalized experimental PA data were fitted by edge spread function (ESF, black dashed line); whose derivative gave the line spread function (LSF, in red line). The full width at half maximum (FWHM) of LSF was used to represent the system’s lateral resolution. We can see that in the network output, the edge response curve in situ has become much steeper, which means that the blurred edge in AR-PAM imaging is now clearly resolved. The lateral resolution has been accordingly improved from ~ 54.0 µm in AR-PAM to ~ 5.1 µm, which is quite comparable to that of the ground truth (OR-PAM), ~ 4.7 µm. Although the measurements might vary slightly at different locations of the blade edge, this exemplifies the significant resolution enhancement via our network transformation.
Fig. 6.
Demonstration of lateral resolution enhancement of AR-PAM by deep learning. Lateral resolution of (a) AR-PAM, (b) network output, and (c) OR-PAM was measured to be ~ 54.0 µm, ~ 5.1 µm, and ~ 4.7 µm, respectively, using the edge response of a sharp blade. ESF, edge spread function; LSF, line spread function. The color insets are the blade images of AR-PAM, network output, and OR-PAM, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.3. Network generalization: application for in vivo mouse brain photoacoustic imaging
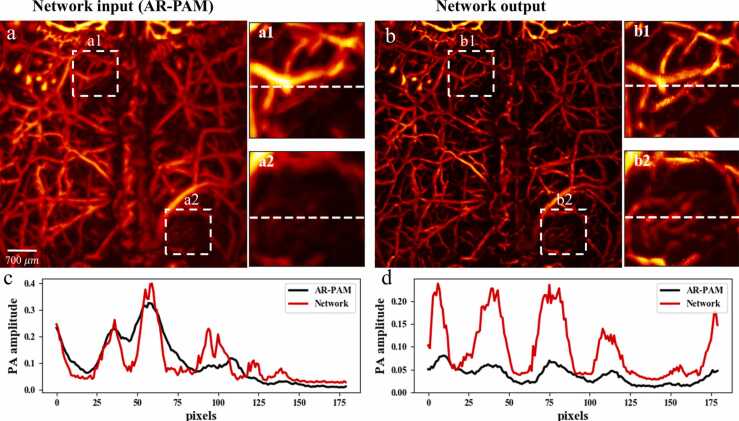
Thus far, the feasibility and effect of the proposed network to achieve OR-PAM resolution based on AR-PAM images have been demonstrated, where both training and test data sets were obtained from in vivo mouse ears. To validate the generalization of the network, in vivo mouse cerebrovascular images were acquired and fed into the network; only AR-PAM images were available in this group of experiments, following a realistic application scenario without labeling. Fig. 7 shows the original AR-PAM and network output images of mouse brain vasculature. It can be observed that the network output has sharper vascular patterns and enhanced vascular signals. Two ROIs indicated by white dashed boxes in both AR-PAM image and network output are enlarged and compared. Significantly improved image quality was achieved by our network, free from noticeable artifacts. The vascular signal intensity profiles for the same region along the horizontal direction are also used to assess the transformation performance. We can see that the network output follows basic trends of vascular signals in the AR-PAM image but yields many refiner details and can clearly distinguish different vascular signals. This is consistent with the fact that enhanced intensities and sharper cerebral vessels were produced. Even without a ground truth OR-PAM image, the above comparisons could, to some degree, verify the reliability of our approach and the significant improvement it achieves. More importantly, it is worth mentioning that even the given mouse brain data has quite different vascular structures from the ear and some cerebral vessels are within at deeper tissues, the trained network can still cope with them, which verifies the universal applicability of the proposed method to the brain vasculature.
Fig. 7.
Application of the network on in vivo mouse brain AR-PAM images. (a) is the network input (AR-PAM image) and (b) is the network output. Two ROIs in both network input (a1, a2) and output (b1, b2) are enlarged and shown. Comparison of signal intensity profiles along the horizontal dashed line in (c) the first ROI and (d) the second ROI are also given.
3.4. Network application: preliminary extension for deep-tissue OR-PAM
To further explore the application of the proposed network for deep-tissue photoacoustic imaging, we prepared a hair phantom by covering human hairs with chicken breast slices of different thicknesses. As the thickness of the tissue sample can be adjusted gradually, it is possible to find out the maximum imaging depth that our network transformation could handle in the experiment. Fig. 8 shows the evaluation results of our network based on AR-PAM images of hair pattern that were not covered or covered with tissue slice of a thickness of 700, 1300, and 1700 µm. Note that there was slight position shift of the hairs beneath when changing the tissue slices of various thicknesses, which, however, does not affect the evaluation of image enhancement at different depths. Since ground truth OR-PAM images were no longer available in these tissue depths, we thus used contrast-to-noise ratio (CNR) and hair edge 10–90% rise distance [58], to indicate the imaging SNR and resolution performance under different penetration depths. The logarithmic CNR using the decibel scale is given by:
| (9) |
Fig. 8.
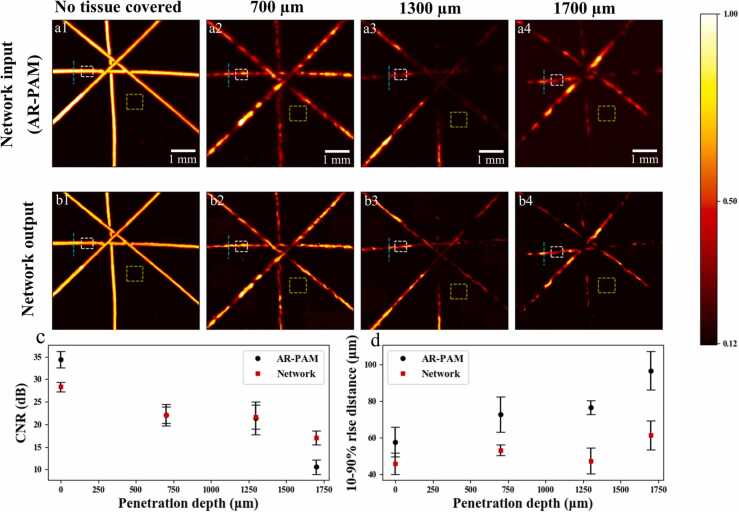
Preliminary demo for deep-penetrating OR-PAM imaging using a hair phantom covered with chicken tissues of different thicknesses. (a1–a4) Experimentally acquired AR-PAM images. (b1–b4) Network output results corresponding to tissue thicknesses of 0 (no tissue covered), 700, 1300, and 1700 µm. The white and green dashed boxes in (a1–a4) and (b1–b4) denote the ROIs for object and background, respectively, and the cyan lines indicate the positions for measuring the hair edge 10–90% rise distance. (c) CNR and (d) measured hair width versus different penetration depths (tissue thicknesses) for both AR-PAM images and the network output results. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
where and denote the mean intensity of hair object and background noise respectively, and the standard deviation of background noise. Practically, the white dashed boxes in both the AR-PAM images (Fig. 8a1–a4) and network outputs (Fig. 8b1–b4) were selected as the ROIs to measure the object signal, while the bigger yellow dashed boxes were denoted as the backgrounds. Note that altogether 10 different areas of object and background were used for average CNR calculation at each penetration depth, but only one ROI is marked in Fig. 8 for conciseness. Regarding the measured hair edge sharpness under different imaging depths, the 10–90% rise distance of hair edge at the positions marked by the cyan dashed lines were used. Again, multiple such positions were selected to obtain an averaged metric at each depth.
From Fig. 8a and b, we can see that for AR-PAM images, overall both hair signal and the contrast decrease with increasing penetration depth, due to the weak and diffusive optical excitation in situ under increasingly strong scattering. Note that the signals in some target areas at the thickness of 1700 µm case might be a bit stronger, mainly due to the increased laser pulse energy and the possible existence of microporous structure in the chicken tissue slices. Nevertheless, the overall image signal at 1700 µm is weaker than that at 1300 µm, in which the hair signal incompleteness caused by strong optical scattering was more serious. The network outputs follow a similar trend, but enjoys enhanced contrast, especially for penetration depths of 1300 and 1700 µm that have been sufficiently beyond the diffusion limit. Quantitatively, as shown in Fig. 8c and d, the CNR drops from ~ 34.9 dB to ~ 10.6 dB and the measured 10–90% rise distance increases from ~ 57 µm to ~ 95 µm for AR-PAM images in the range of 1700 µm tissue depth. With deep learning, the CNR declines only to ~ 17.1 dB. More strikingly, the measured 10–90% rise distances merely see a slight increase from ~ 46 µm to ~ 60 µm, suggesting a greatly improved lateral resolution for tissue depth up to 1700 µm. To sum up, this hair phantom experiment reveals potentials for deep-tissue OR-PAM with our approach, which can remarkably enhance imaging resolution and SNR.
4. Discussions
To achieve high-resolution OR-PAM imaging in deep tissue, we propose a deep neural network to transform blurry images acquired with an AR-PAM setting to match the OR-PAM results. The network was first trained with AR- and OR-PAM data sets experimentally obtained from in vivo mouse ear. Then, the performance of the network was validated with AR-PAM mouse ear images that were not used in network training, yielding superior lateral resolution comparable to the ground truth OR-PAM images. It should be emphasized that although the network training was implemented with data obtained from the mouse ear, the successful application for in vivo mouse brain photoacoustic imaging verifies the universal applicability of the developed network. Our method could thus be extended to other imaging scenarios or deep tissue where experimental OR-PAM is not possible. Apart from the benefit for deep penetration, the transformation capability also initiates other potentials: an inexpensive multimode pulsed laser source can be adopted to reduce the system cost, as the beam quality requirement in AR-PAM is way less demanding; a multimode fiber can be used for light delivery that is equipped with much higher beam coupling efficiency and optical damage threshold, allowing laser pulses at higher repetition rates delivered to the ROI and hence stronger signals and faster imaging speed; larger scanning step size can be adopted for AR-PAM set-up which can significantly reduce the time of raster scanning. All these, in combination, empower conceivable all-round boost of penetration depth, SNR, cost control, as well as scanning speed to OR-PAM.
That said, a few more aspects need to be discussed herein. There are mainly two limitations of our approach. The first is related to the artifacts, which might be generated by the network due to several reasons. In the network training phase, not all capillary patterns inside the paired AR- and OR-PAM images are always consistent due to the relatively large resolution discrepancy. Some physically existing local capillaries might be missed as they are represented by only blurry and dispersive pixels in AR-PAM. Such inconsistency could be an obstacle for the network to conduct pixel-to-pixel transformation in the training phase. In the network test phase, it is intuitive that the quality of the network output is highly dependent on that of the input AR-PAM data; the network may produce inaccurate pixel predictions when there are extremely blurry and dispersive pixels in the input. Hence, there may be some subtle distinctions between the network output and the ground truth OR-PAM image, mainly because of the latent capillary missing and artifacts. These subtle distinctions lead to limited improvements of metrics like SSIM (averagely by 13%) and PCC (averagely by 3%) that are sensitive to the perfect pixel-by-pixel match between the network output and ground truth. To minimize the latent artifacts and improve the metrics, we adopted data preprocessing and network training methods carefully. Accurate registration in the process of image patch extraction is of crucial importance, in which the sub-pixel alignment between the AR and OR image pairs allows the network to optimally learn a pixel-to-pixel transformation. Besides, the design and training of the network also play an important role. Different from conventional CNN where the optimization is solely driven by a pixel-wise loss that tends to produce overly smoothed results, the WGAN-GP model we used benefits from the adversarial training where the adaptive adversarial loss is crucial to guide the Generator network to generate images resembling OR labels. Further improvement could be made by acquiring more PAM image data used for training, to equip the network with stronger and more general imaging transformation ability. Lastly, it should also be emphasized that the aim of the network is not to perfectly transform AR-PAM images in all details, but to approximate the resolution of OR-PAM as possible as it can. The other limitation is our transformation method still finds a distance to ideal deep-tissue OR-PAM imaging. As mentioned earlier, the quality of the network output is highly dependent on that of the input AR-PAM data; the low SNR and spatial resolution of AR-PAM imaging at depths in tissue pose a physical limit for our image-based post-processing method. Nevertheless, with the recent developments towards faster and more efficient photoacoustically guided wavefront shaping [59], [60], [61], we believe ideal OR-PAM imaging at depths in the tissue will be possible soon.
More recently, a similar research was reported [62], where simulated rather than experimentally acquired AR-PAM data generated by blurring the corresponding OR-PAM images were used and did not experimentally demonstrate its ability of deep-penetration imaging. In addition, its conventional network model is also different from the WGAN-GP model in our study. Also note that the proposed PAM imaging transformation method in this work should be distinguished from single image super resolution and blind deconvolution, although they are closely related. For image super resolution, the aim is to reconstruct the baseline resolution when given an input solely down-sampled from the baseline image; but for our network, it is to approximate the resolution of OR-PAM from another poorer imaging modality. For the blind deconvolution method, it has been shown earlier that it failed to recover high-quality images, whether in flat priors or fractional-order priors. The deblurring performance is inclined to be suboptimal, as it is often difficult to determine the PSF of the conceptual imaging system from ground truth OR to AR images. What’s more, the computation cost of deconvolution is demanding due to the multiple iterations it requires for parameter updates. In our example, it took about one and half minutes for producing a deblurred image with 30 iterations on average. In comparison, the trained network could rapidly output a high-resolution image from the blurry input within seconds.
5. Conclusion
In this study, a WGAN-GP neural network is designed and trained based on co-registered AR-to-OR PAM images experimentally acquired from in vivo mouse ears. The feasibility and reliability of the proposed network to improve imaging resolution are demonstrated in vivo. The network outputs have also been compared with those obtained with a blind deconvolution method, showing perceptually better image deblurring results and improved evaluation metrics. Moreover, the transformation capability can be extended to other types (e.g., the brain vessel) or deep tissues (e.g., chicken breast slice of 1700 µm thickness) that are not readily accessible by OR-PAM. Note that the proposed method has its limitations, such as the existence of artifacts in the network output and the performance dependence on the input data quality (AR-PAM images). As an extension to the imaging depth of OR-PAM via computation, the proposed method potentially provides new insights to expand the scope of OR-PAM towards deep-tissue imaging and wide applications in biomedicine.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (NSFC) (81930048, 81627805), Hong Kong Innovation and Technology Commission (GHP/043/19SZ, GHP/044/19GD), Hong Kong Research Grant Council (15217721, R5029-19, 25204416, 21205016, 11215817, 11101618, 11103320), and Guangdong Science and Technology Commission (2019BT02X105, 2019A1515011374). All authors declare no conflict of interests.
Biographies

Shengfu Cheng is a Ph.D. student at the Department of Biomedical Engineering in the Hong Kong Polytechnic University. He received his Bachelor degree from Sichuan University. His research interests include deep learning application for photoacoustic imaging and multimode fiber based endoscopy.

Yingying Zhou is a Ph.D. student at the Department of Biomedical Engineering, The Hong Kong Polytechnic University. She received bachelor’s degree from the SUN YAT-SEN UNIVERSITY. Her research focuses on photoacoustic microscopy and its applications.

Jiangbo Chen is a Ph.D. student at the Department of Biomedical Engineering, City University of Hong Kong. He received bachelor’s degree from the Northeast Forestry University, and received Master degrees from Harbin institute of technology. His research focuses on photoacoustic imaging.

Dr. Huanhao Li obtained his Ph.D. from the Hong Kong Polytechnic University in 2021. His research interest is to study the optical scattering and wavefront shaping. Specifically, how the optical speckle pattern encodes information and development of the advanced algorithms to overcome the scrambled wavefront are of focus.

Lidai Wang received the Bachelor and Master degrees from the Tsinghua University, Beijing, and received the Ph.D. degree from the University of Toronto, Canada. After working as a postdoctoral research fellow in the Prof Lihong Wang's group, he joined the City University of Hong Kong in 2015. His research focuses on biophotonics, biomedical imaging, wavefront engineering, instrumentation and their biomedical applications. He has invented single-cell flowoxigraphy (FOG), ultrasonically encoded photoacoustic flowgraphy (UE-PAF) and nonlinear photoacoustic guided wavefront shaping (PAWS). He has published more 30 articles in peer-reviewed journals and has received four best paper awards from international conferences.

Dr. Puxiang Lai received his Bachelor from Tsinghua University in 2002, Master from Chinese Academy of Sciences in 2005, and Ph.D. from Boston University in 2011. After that, he joined Dr. Lihong Wang’s lab in Washington University in St. Louis as a Postdoctoral Research Associate. In September 2015, he joined The Hong Kong Polytechnic University, and currently, he is an Associate Professor in Department of Biomedical Engineering. Puxiang’s research focuses on the synergy of light and sound as well as its applications in biomedicine, such as wavefront shaping, photoacoustic imaging, acousto-optic imaging, and computational optical imaging. His research has fueled more than 50 premium journal publications, such as Nature Photonics and Nature Communications, and his research has been continuously supported by national and regional funding agents with allocated budget of more than 25 million Hong Kong dollars.
Contributor Information
Lidai Wang, Email: lidawang@cityu.edu.hk.
Puxiang Lai, Email: puxiang.lai@polyu.edu.hk.
References
- 1.Wang L.V. Multiscale photoacoustic microscopy and computed tomography. Nat. Photonics. 2009;3(9):503–509. doi: 10.1038/nphoton.2009.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wang L.V., Yao J. A practical guide to photoacoustic tomography in the life sciences. Nat. Methods. 2016;13(8):627–638. doi: 10.1038/nmeth.3925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Maslov K., Zhang H.F., Hu S., Wang L.V. Optical-resolution photoacoustic microscopy for in vivo imaging of single capillaries. Opt. Lett. 2008;33(9):929–931. doi: 10.1364/ol.33.000929. [DOI] [PubMed] [Google Scholar]
- 4.Wang L., Maslov K., Yao J., Rao B., Wang L.V. Fast voice-coil scanning optical-resolution photoacoustic microscopy. Opt. Lett. 2011;36(2):139–141. doi: 10.1364/OL.36.000139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhou Y., Chen J., Liu C., Liu C., Lai P., Wang L. Single-shot linear dichroism optical-resolution photoacoustic microscopy. Photoacoustics. 2019;16 doi: 10.1016/j.pacs.2019.100148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhou Y., Liang S., Li M., Liu C., Lai P., Wang L. Optical-resolution photoacoustic microscopy with ultrafast dual-wavelength excitation. J. Biophotonics. 2020;13(6) doi: 10.1002/jbio.201960229. [DOI] [PubMed] [Google Scholar]
- 7.Cao R., Li J., Ning B., Sun N.D., Wang T.X., Zuo Z.Y., Hu S. Functional and oxygen-metabolic photoacoustic microscopy of the awake mouse brain. Neuroimage. 2017;150:77–87. doi: 10.1016/j.neuroimage.2017.01.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jin T., Guo H., Jiang H.B., Ke B.W., Xi L. Portable optical resolution photoacoustic microscopy (pORPAM) for human oral imaging. Opt. Lett. 2017;42(21):4434–4437. doi: 10.1364/OL.42.004434. [DOI] [PubMed] [Google Scholar]
- 9.Zabihian B., Weingast J., Liu M.Y., Zhang E., Beard P., Pehamberger H., Drexler W., Hermann B. In vivo dual-modality photoacoustic and optical coherence tomography imaging of human dermatological pathologies. Biomed. Opt. Express. 2015;6(9):3163–3178. doi: 10.1364/BOE.6.003163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wong T.T., Zhang R., Hai P., Zhang C., Pleitez M.A., Aft R.L., Novack D.V., Wang L.V. Fast label-free multilayered histology-like imaging of human breast cancer by photoacoustic microscopy. Sci. Adv. 2017;3(5) doi: 10.1126/sciadv.1602168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Berezhnoi A., Schwarz M., Buehler A., Ovsepian S.V., Aguirre J., Ntziachristos V. Assessing hyperthermia-induced vasodilation in human skin in vivo using optoacoustic mesoscopy. J. Biophotonics. 2018;11(11) doi: 10.1002/jbio.201700359. [DOI] [PubMed] [Google Scholar]
- 12.Zhou Y., Cao F., Li H., Huang X., Wei D., Wang L., Lai P. Photoacoustic imaging of microenvironmental changes in facial cupping therapy. Biomed. Opt. Express. 2020;11(5):2394–2401. doi: 10.1364/BOE.387985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhou Y., Liu C., Huang X., Qian X., Wang L., Lai P. Low-consumption photoacoustic method to measure liquid viscosity. Biomed. Opt. Express. 2021;12(11):7139–7148. doi: 10.1364/BOE.444144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dai H., Shen Q., Shao J., Wang W., Gao F., Dong X. Small molecular NIR-II fluorophores for cancer phototheranostics. Innovation. 2021;2(1) doi: 10.1016/j.xinn.2021.100082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Park S., Lee C., Kim J., Kim C. Acoustic resolution photoacoustic microscopy. Biomed. Eng. Lett. 2014;4(3):213–222. [Google Scholar]
- 16.Zhong H., Duan T., Lan H., Zhou M., Gao F. Review of low-cost photoacoustic sensing and imaging based on laser diode and light-emitting diode. Sensors. 2018;18(7):2264. doi: 10.3390/s18072264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Erfanzadeh M., Zhu Q. Photoacoustic imaging with low-cost sources; a review. Photoacoustics. 2019;14:1–11. doi: 10.1016/j.pacs.2019.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li X., Tsang V.T., Kang L., Zhang Y., Wong T.T. High-speed high-resolution laser diode-based photoacoustic microscopy for in vivo microvasculature imaging. Vis. Comput. Ind. Biomed. Art. 2021;4(1):1–6. doi: 10.1186/s42492-020-00067-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Grohl J., Schellenberg M., Dreher K., Maier-Hein L. Deep learning for biomedical photoacoustic imaging: a review. Photoacoustics. 2021;22 doi: 10.1016/j.pacs.2021.100241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yang C.C., Lan H.R., Gao F., Gao F. Review of deep learning for photoacoustic imaging. Photoacoustics. 2021;21 doi: 10.1016/j.pacs.2020.100215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hariri A., Alipour K., Mantri Y., Schulze J.P., Jokerst J.V. Deep learning improves contrast in low-fluence photoacoustic imaging. Biomed. Opt. Express. 2020;11(6):3360–3373. doi: 10.1364/BOE.395683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Manwar R., Li X., Mahmoodkalayeh S., Asano E., Zhu D.X., Avanaki K. Deep learning protocol for improved photoacoustic brain imaging. J. Biophotonics. 2020;13(10) doi: 10.1002/jbio.202000212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Harma A.S., Ramanik M.P. Convolutional neural network for resolution enhancement and noise reduction in acoustic resolution photoacoustic microscopy. Biomed. Opt. Express. 2020;11(12):6826–6839. doi: 10.1364/BOE.411257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.DiSpirito A., Li D., Vu T., Chen M., Zhang D., Luo J., Horstmeyer R., Yao J. Reconstructing undersampled photoacoustic microscopy images using deep learning. IEEE Trans. Med. Imaging. 2020;40(2):562–570. doi: 10.1109/TMI.2020.3031541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhao H.X., Ke Z.W., Yang F., Li K., Chen N.B., Song L., Zheng C.S., Liang D., Liu C.B. Deep learning enables superior photoacoustic imaging at ultralow laser dosages. Adv. Sci. 2021;8(3) doi: 10.1002/advs.202003097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hauptmann A., Lucka F., Betcke M., Huynh N., Adler J., Cox B., Beard P., Ourselin S., Arridge S. Model-based learning for accelerated, limited-view 3-D photoacoustic tomography. IEEE Trans. Med. Imaging. 2018;37(6):1382–1393. doi: 10.1109/TMI.2018.2820382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Davoudi N., Dean-Ben X.L., Razansky D. Deep learning optoacoustic tomography with sparse data. Nat. Mach. Intell. 2019;1(10):453–460. [Google Scholar]
- 28.Guan S., Khan A.A., Sikdar S., Chitnis P.V. Fully dense UNet for 2-D sparse photoacoustic tomography artifact removal. IEEE J. Biomed. Health. 2020;24(2):568–576. doi: 10.1109/JBHI.2019.2912935. [DOI] [PubMed] [Google Scholar]
- 29.Vu T., Li M.C., Humayun H., Zhou Y., Yao J.J. A generative adversarial network for artifact removal in photoacoustic computed tomography with a linear-array transducer. Exp. Biol. Med. 2020;245(7):597–605. doi: 10.1177/1535370220914285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dong C., Loy C.C., He K., Tang X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015;38(2):295–307. doi: 10.1109/TPAMI.2015.2439281. [DOI] [PubMed] [Google Scholar]
- 31.C. Ledig, L. Theis, F. Huszár, J. Caballero, A. Cunningham, A. Acosta, A. Aitken, A. Tejani, J. Totz, Z. Wang, Photo-realistic single image super-resolution using a generative adversarial network, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 4681–4690.
- 32.B. Lim, S. Son, H. Kim, S. Nah, K. Mu Lee, Enhanced deep residual networks for single image super-resolution, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2017, pp. 136–144.
- 33.X. Wang, K. Yu, S. Wu, J. Gu, Y. Liu, C. Dong, Y. Qiao, C. Change Loy, Esrgan: enhanced super-resolution generative adversarial networks, in: Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 0–0.
- 34.Rivenson Y., Gorocs Z., Gunaydin H., Zhang Y.B., Wang H.D., Ozcan A. Deep learning microscopy. Optica. 2017;4(11):1437–1443. [Google Scholar]
- 35.Zhao H.X., Ke Z.W., Chen N.B., Wang S.J., Li K., Wang L.D., Gong X.J., Zheng W., Song L., Liu Z.C., Liang D., Liu C.B. A new deep learning method for image deblurring in optical microscopic systems. J. Biophotonics. 2020;13(3) doi: 10.1002/jbio.201960147. [DOI] [PubMed] [Google Scholar]
- 36.Cheng S.F., Li H.H., Luo Y.Q., Zheng Y.J., Lai P.X. Artificial intelligence-assisted light control and computational imaging through scattering media. J. Innov. Opt. Health Sci. 2019;12(4) [Google Scholar]
- 37.Rivenson Y., Wang H.D., Wei Z.S., de Haan K., Zhang Y.B., Wu Y.C., Gunaydin H., Zuckerman J.E., Chong T., Sisk A.E., Westbrook L.M., Wallace W.D., Ozcan A. Virtual histological staining of unlabelled tissue-autofluorescence images via deep learning. Nat. Biomed. Eng. 2019;3(6):466–477. doi: 10.1038/s41551-019-0362-y. [DOI] [PubMed] [Google Scholar]
- 38.Wang H.D., Rivenson Y., Jin Y.Y., Wei Z.S., Gao R., Gunaydin H., Bentolila L.A., Kural C., Ozcan A. Deep learning enables cross-modality super-resolution in fluorescence microscopy. Nat. Methods. 2019;16(1):103–110. doi: 10.1038/s41592-018-0239-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin, A.C. Courville, Improved training of wasserstein gans, in: Proceedings of the Advances in Neural Information Processing Systems, 2017, pp. 5767–5777.
- 40.Xing W., Wang L., Maslov K., Wang L.V. Integrated optical-and acoustic-resolution photoacoustic microscopy based on an optical fiber bundle. Opt. Lett. 2013;38(1):52–54. doi: 10.1364/ol.38.000052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dosovitskiy A., Fischer P., Springenberg J.T., Riedmiller M., Brox T. Discriminative unsupervised feature learning with exemplar convolutional neural networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016;38(9):1734–1747. doi: 10.1109/TPAMI.2015.2496141. [DOI] [PubMed] [Google Scholar]
- 42.E. Castro, J.S. Cardoso, J.C. Pereira, Elastic deformations for data augmentation in breast cancer mass detection, in: Proceedings of the 2018 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), 2018, pp. 230–234.
- 43.O. Ronneberger, P. Fischer, T. Brox, U-net: convolutional networks for biomedical image segmentation, in: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, 2015, pp. 234–241.
- 44.Buslaev A., Iglovikov V.I., Khvedchenya E., Parinov A., Druzhinin M., Kalinin A.A. Albumentations: fast and flexible image augmentations. Information. 2020;11(2):125. [Google Scholar]
- 45.I. Goodfellow, Nips 2016 Tutorial: Generative Adversarial Networks, arXiv preprint arXiv:1701.00160, 2016.
- 46.M. Arjovsky, L. Bottou, Towards Principled Methods for Training Generative Adversarial Networks, arXiv preprint arXiv:1701.04862, 2017.
- 47.M. Arjovsky, S. Chintala, L. Bottou, Wasserstein generative adversarial networks, in: Proceedings of the International Conference on Machine Learning, 2017, pp. 214–223.
- 48.K. He, X. Zhang, S. Ren, J. Sun, Deep residual learning for image recognition, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770–778.
- 49.Y. Wu, K. He, Group normalization, in: Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 3–19.
- 50.D. Ulyanov, A. Vedaldi, V. Lempitsky, Instance Normalization: The Missing Ingredient for Fast Stylization, arXiv preprint arXiv:1607.08022, 2016.
- 51.Nguyen T., Xue Y., Li Y., Tian L., Nehmetallah G. Deep learning approach for Fourier ptychography microscopy. Opt. Express. 2018;26(20):26470–26484. doi: 10.1364/OE.26.026470. [DOI] [PubMed] [Google Scholar]
- 52.He K., Zhang X., Ren S., Sun J. Delving deep into rectifiers: surpassing human-level performance on imagenet classification. Proc. IEEE Int. Conf. Comput. Vis. 2015:1026–1034. [Google Scholar]
- 53.I. Loshchilov, F. Hutter, Decoupled Weight Decay Regularization, arXiv preprint arXiv: 1711.05101, 2017.
- 54.Ruiz P., Zhou X., Mateos J., Molina R., Katsaggelos A.K. Variational Bayesian blind image deconvolution: a review. Digit. Signal Process. 2015;47:116–127. [Google Scholar]
- 55.Bishop T.E., Babacan S.D., Amizic B., Katsaggelos A.K., Chan T., Molina R. Blind Image Deconvolution. CRC Press; 2017. Blind image deconvolution: problem formulation and existing approaches; pp. 21–62. [Google Scholar]
- 56.Chowdhury M.R., Qin J., Lou Y. Non-blind and blind deconvolution under poisson noise using fractional-order total variation. J. Math. Imaging Vis. 2020;62(9):1238–1255. [Google Scholar]
- 57.Wang Z., Bovik A.C., Sheikh H.R., Simoncelli E.P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004;13(4):600–612. doi: 10.1109/tip.2003.819861. [DOI] [PubMed] [Google Scholar]
- 58.Fauver M., Seibel E.J., Rahn J.R., Meyer M.G., Patten F.W., Neumann T., Nelson A.C. Three-dimensional imaging of single isolated cell nuclei using optical projection tomography. Opt. Express. 2005;13(11):4210–4223. doi: 10.1364/opex.13.004210. [DOI] [PubMed] [Google Scholar]
- 59.Lai P., Wang L., Tay J.W., Wang L.V. Photoacoustically guided wavefront shaping for enhanced optical focusing in scattering media. Nat. Photonics. 2015;9(2):126–132. doi: 10.1038/nphoton.2014.322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Chaigne T., Gateau J., Katz O., Bossy E., Gigan S. Light focusing and two-dimensional imaging through scattering media using the photoacoustic transmission matrix with an ultrasound array. Opt. Lett. 2014;39(9):2664–2667. doi: 10.1364/OL.39.002664. [DOI] [PubMed] [Google Scholar]
- 61.Zhao T., Ourselin S., Vercauteren T., Xia W. High-speed photoacoustic-guided wavefront shaping for focusing light in scattering media. Opt. Lett. 2021;46(5):1165–1168. doi: 10.1364/OL.412572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Z. Zhang, H. Jin, Z. Zheng, Y. Luo, Y. Zheng, Photoacoustic microscopy imaging from acoustic resolution to optical resolution enhancement with deep learning, in: Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), 2021, pp. 1–5.