Highlights
-
•
Predictions of frequency domain simulations agreed with experimental measurements.
-
•
The semi-empirical bubbly-liquid model led to more consistent simulation results.
-
•
Performance for antinode prediction showed potential for design applications.
-
•
Knowledge gaps were identified for multi-frequency sonoreactor simulation methods.
Keywords: Sonochemiluminescence, Pressure acoustics, FEM, Computational modelling, Sonoreactor
Abstract
Recently, multi-frequency systems were reported to improve performance in power ultrasound applications. In line with this, digital prototyping of multi-frequency sonoreactors also started gaining interest. However, the conventional method of simulating multi-frequency acoustic pressure fields in the time-domain led to many challenges and limitations. In this study, a multi-frequency sonoreactor was characterised using frequency domain simulations in 2-D. The studied system consists of a hexagonal sonoreactor capable of operating at 28, 40 and 70 kHz. Four frequency combinations were studied: 28–40, 28–70, 40–70 and 28–40–70 kHz. A semi-empirical, modified Commander and Prosperetti model was used to describe the bubbly-liquid effects in the sonoreactor. The root-mean-squared acoustic pressure was compared against experimental validation results using sonochemiluminescence (SCL) images and was noted to show good qualitative agreement with SCL results in terms of antinode predictions. The empirical phase speed calculated from SCL measurements was found to be important to circumvent uncertainties in bubble parameter specifications which reduces error in the simulations. Additionally, simulation results also highlighted the importance of geometry in the context of optimising the standing wave magnitudes for each working frequency due to the effects of constructive and destructive interference.
Nomenclature
Common Mathematical Operators
Laplacian operator
Imaginary part of complex number
Real part of complex number
Complex conjugates shorthand
Imaginary unit i
Euler’s number
Function representation
Period averaged properties
Symbols
Attenuation coefficient / imaginary part of complex wavenumber (Np. m−1)
Bubble volume fraction (dim.)
Ratio of specific heats (dim.)
Propagation wavenumber / real part of complex wavenumber (m−1)
Measured wavelength in SCL images (m)
Liquid viscosity (Pa.s)
Liquid density (kg.m−3)
Surface tension of liquid (N.m−1)
Commander and Prosperetti linearised parameter (dim.)
Dimensionless thermal diffusivity
Angular frequency (rad.s−1)
Bubble resonance frequency (rad.s−1)
Transducer effective surface area (m2)
Commander and Prosperetti damping factor (dim.)
Sound speed in pure liquid (m.s−1)
Phase speed of bubbly-liquid mixture (m.s−1)
Empirically determined phase speed (m.s−1)
Thermal diffusivity of gas in bubbles (m2.s−1)
Frequency (Hz)
Maximum frequency to be simulated (Hz)
Wavenumber (m−1)
Complex-valued wavenumber (m−1)
Commander and Prosperetti complex-valued wavenumber (m−1)
Maximum element size (m)
Denotes the total number of harmonic fields in the system
Denotes the mth harmonic field
Minimum number of nodes per wavelength
Bubble density/ number of bubbles per unit volume (m−3)
Measured calorimetry power (W)
- ,
Space-dependant pressure field (Pa)
Absolute pressure (Pa)
Bubble initial pressure (Pa)
Sum of absolute pressures of all harmonics / maximum pressure potential (Pa)
Root-mean-squared pressure (Pa)
Transducer boundary condition pressure (Pa)
- ,
Time-dependant acoustic pressure field (Pa)
Total time-dependant acoustic pressure field (Pa)
Time-averaged mean-squared pressure (Pa)
Ambient pressure around bubble (Pa)
Bubble radius (m)
Bubble equilibrium radius (m)
Time (s)
Linear coefficient for bubble fraction relation (Pa−1)
1. Introduction
The use of power ultrasound in chemical engineering have become a widely researched topic owing to its wide range of applications spanning many fields. For example, the use and development of power ultrasound technology had been reported in chemical syntheses [1], separation processes [2], biotechnology [3], and food processing [4]. The technology of power ultrasound and by extension sonoreactors rely on the phenomena of cavitation to achieve desired physiochemical effects. Cavitation occurs when a liquid medium is subjected to ultrasonic waves which leads to large oscillations in local acoustic pressure. This pressure variation causes bubbles to form and collapse with high energy intensities. The energy released can drive different mechanisms, such as radical generation, agitation, and catalysis [5]. With the promising future of power ultrasound in mind, research on the design of sonoreactors have been increasing in recent years.
In this day and age, computational simulations have become an indispensable tool for the design and optimisation of industrial equipment. A well-posed numerical model can provide useful data comparable to empirical measurements [6]. Additionally, computational methods also allow digital prototyping, which is a more efficient way to evaluate and optimise reactor designs. Pressure field simulations of sonoreactors were often carried out with the focus to determine two key design parameters: the location of antinodes (cavitating regions); and the acoustic pressure magnitude [6]. The former is important for the identification of dead zones and to evaluate effective reactor volumes, while the latter is often used in the calculation of other physical parameters such as the temperature field, flow field and reaction rates.
Sonoreactor simulations can be done in the time domain or the frequency domain. Early studies revolved around time-dependant finite difference or finite volume methods [7], [8], [9]. However, in the past two decades the focus shifted towards the use of time-harmonic, frequency domain studies instead [6]. Using the Helmholtz equation, frequency domain studies approximate the steady state performance of a sonoreactor by assuming a harmonic response of a single frequency in the sonoreactor. Frequency domain modelling is commonly used due its ease of implementation, lower resource requirements and being much easier to solve then their time-dependant counterparts. This is evident in the large number of recent studies where frequency domain simulations were used to design and optimise ultrasonic equipment [10], [11], [12], [13]. The specification of wave attenuation is also simpler in frequency domain models. Additionally, since sonoreactor design often deals with the steady state behaviour of the equipment, there is little incentive in carrying out computationally expensive transient simulations.
Current simulations can be categorised into those that consider the propagation medium as a pure liquid [12], [14], [15], [16], [17], and those that consider the effects of bubbles in the medium [13], [18], [19], [20], [21], [22]. Bubbly-liquid models gained popularity in recent times as it is believed to provide a better representation of the fluid property in ultrasonic systems. Two popular bubbly-liquid models are the Commander and Prosperetti [23] and the nonlinear Helmholtz models [24], [25], [26], both derived from the Caflisch equation [27]. The incorporation of bubbly-liquid attenuation in ultrasonic systems became a major focus in the past decade when it was noted that the presence of bubbles in an ultrasonic system not only induce significant energy loss, but also alters the wave propagation speed [23]. The consideration of these effects is crucial to accurately simulate the magnitude and antinode locations in a sonoreactor. Compared to pure liquid models, studies using bubbly-liquid models reported more realistic results in terms of pressure magnitude predictions, especially for systems with high cavitation intensities [18], [24].
A notable rising trend in the field of sonoreactor and power ultrasound research is the application of multi-frequency ultrasound. There have been an increasing number of studies that reported better results by combining multiple frequencies as opposed to using a single operating frequency [28], [29]. These findings were further supported by higher cavitation signal measurements found in dual-frequency systems [30], [31] as well as theoretical studies using simulations of bubbles dynamics [32], [33]. As research began to focus on the potential of multi-frequency ultrasound in many applications [34], [35], [36], the design of multi-frequency sonoreactors gained interests in recent times.
In light of this, it was noted that research on multi-frequency sonoreactor design were scarce. Much of the knowledge regarding the design of industrial scale sonoreactors can be said to be still in the early-to-mid stages. This is due to the large number of design factors that have to be accounted for, which cause reactor design to depend on the application of interest [37], [38]. The large number of parameters and considerations in designing sonoreactors further incentivise the development of computational methods, which can provide a reliable environment for digital prototyping. On the topic of multi-frequency sonoreactor simulations, there are a few knowledge gaps that needs to be addressed. First and foremost, despite the recent developments of frequency domain models for sonoreactors, the simulations are inherently limited to simulating a single frequency at a time. Additionally, sonoreactor simulation studies that considered multi-frequency systems are very limited, and thus little can be said about the effectiveness and efficiencies of the methodologies involved. A traditional approach would be to use time-domain simulations to account for multiple frequencies acting simultaneously. To the extent of the authors’ knowledge, there were only two published works that considered multi-frequency simulations in sonoreactors to date. The first is an early study published by Servant et al. [39] who briefly investigated multi-frequency pressure field simulations. The pressure fields were solved using a modified Caflisch equation coupled with linearised bubble interactions for two frequencies in a 1-L reactor. While their study managed to solve for the 3-D time-dependant pressure fields of multi-frequency systems, there was a lack of comprehensive discussion and validation for the results. Another study was recently published by Tangsopa [40] who applied transient simulations to optimise an ultrasonic cleaning tank by assuming a pure liquid medium. They considered single frequency cases using time-harmonic simulations and multi-frequency cases using transient simulations (up to = 750 and noted some key points of interests. Notably, the transient simulations took 16 times longer to solve for the required data and used significantly more computational resources.
Despite being a straightforward solution to the problem, time-domain simulations present a glaring number of drawbacks and challenges. At ultrasonic frequencies, the solver time-steps would have to be very small (down to a few microseconds) in order to satisfy stability restrictions [40]. Coupled with long simulation times to approach steady state if the geometry is complex, this can lead to large memory requirements. There is also the issue of error accumulation with time and the difficulty in solving highly nonlinear attenuation models that is prone to numerical blow-up. It should also be considered that many advancements in bubbly-liquid models are easier to solve in the frequency domain. For one to consider bubbly-liquid contributions in the time-domain, one could solve the nonlinear Caflisch equation [27]. However, it was reported that the strong nonlinearities within the model makes it a very difficult undertaking [41]. Thus, the use of time-dependant simulations for digital prototyping of multi-frequency sonoreactors is resource consuming and possibly prone to error.
The multitude of challenges that come with the use of transient simulations have led to the search for other alternatives to approach the problem. Studies on wave and signal propagation had shown that frequency domain methods can be used to characterise time-domain problems, even in non-harmonic cases [42]. For example, one could obtain the frequency–response of a system by transforming the transient input into the frequency domain and obtaining the time-domain response through the inverse Fourier transform. Similarly, frequency domain solutions of important harmonics in a sonoreactor can be used to predict its multi-frequency response. It is believed that this approach can be used to tackle the issues highlighted for the multi-frequency sonoreactor simulations as a means to circumvent the many difficulties of dealing with the time-domain.
The main aim of this research is to investigate a method in which the multi-frequency pressure field in a sonoreactor is predicted using frequency domain simulations, based on a number of simplifying assumptions. The frequency domain acoustic pressure fields were simulated using a modified, semi-empirical Commander and Prosperetti model [23]. The steady state acoustic pressure field within a multi-frequency sonoreactor was characterised as a root-mean-squared pressure field. In this study, a hexagonal tank sonoreactor with the capability to operate at a combination of three frequencies was used to provide comprehensive validation for the method. The reactor was specifically fabricated to investigate the use of multi-frequency ultrasound [43], [44] and thus would be able to provide a much more extensive and reliable empirical results for the validation of the simulation method. The studied frequencies are 28, 40 and 70 kHz which are commonly used for bath-type ultrasonic tanks. The simulated pressure fields were validated against standing wave patterns obtained using sonochemiluminescence (SCL) to gain insight on the performance of the proposed method, with a focus on the prediction of multi-frequency antinodes.
2. Theory
2.1. Frequency domain analysis of acoustic pressure fields
The governing equation for acoustic pressure fields in the frequency domain can be written as a Helmholtz equation:
| (1) |
where is the space-dependant pressure field which is harmonic in time with respect to an angular frequency . The solution for depends on the boundary conditions and wavenumber . The complex wavenumber can be expressed in the form:
| (2) |
The real part of the wavenumber, is also known as the propagation wavenumber [45], which relates to the phase speed. The phase speed in the bubbly-liquid mixture can be obtained from the relation:
| (3) |
The imaginary part of the wavenumber, is also known as the attenuation coefficient and it describes energy dissipation for propagating waves in the medium.
2.2. The bubbly-liquid model for acoustic pressure fields
The bubbles that emerge from dissolved gasses or through the cavitation effect was reported to greatly alter the behaviour of wave propagation in ultrasonic systems. Firstly, the presence of bubbles can reduce the phase speed in the mixture [27]. Additionally, the bubbles also act as scatterers and cause energy dissipation. Based on the work of Wjingaarden [46], Caflisch et al. derived a wave equation to describe wave propagation in bubbly liquids [27]. The Caflisch equation describes the behaviour of a time-dependant pressure field when considering bubbly liquids:
| (4) |
The equation was derived on the assumption that the bubbly liquid is treated as a continuum. The solution of the time-dependant pressure field is governed by the phase speed of the pure liquid , the liquid density , the bubble fraction and the boundary conditions. The bubble fraction is a state variable and can be related to the bubble radius and volumetric bubble density . For a simple case of monodispersed bubbles, the relationship can be written as:
| (5) |
The Caflisch equation is often closed with differential equations describing bubble dynamics which governs the expansion and collapse of bubble equilibrium radius . However, this method of solving the Caflisch equation proved to be challenging and resource intensive, especially for systems with strong cavitation activity, high frequencies and large geometries [47].
2.3. Frequency domain bubbly-liquid model – Commander and Prosperetti model
By linearising the system of differential equations involved for the Caflisch model, Commander and Prosperetti [23] derived an analytical expression for a complex wavenumber to describe the behaviour of bubbly liquids in the frequency domain. This model had regained popularity in the past decade to describe the attenuation in ultrasonic systems [13], [48]. The complex wavenumber squared for the monodisperse Commander and Prosperetti model can be expressed as:
| (6) |
Where , , and are the angular frequency, bubble density and equilibrium bubble radius respectively. In order to calculate the bubble resonance frequency and damping factor , two dimensionless parameters are required. The first parameter is the dimensionless thermal diffusivity:
| (7) |
where is the thermal diffusivity of the gas in the bubbles. Next, a dimensionless complex-valued parameter describing linearised bubble behaviour can then be calculated as:
| (8) |
where is the ratio of specific heats of the gas. The real part is used to calculate the bubble resonance frequency :
| (9) |
while the imaginary part is used to obtain the damping factor :
| (10) |
2.4. Approximation of multi-frequency pressure fields using frequency domain simulations
In this section, the theoretical basis of the proposed method is shown. The development of the following methods referenced the information presented in Chapter 1.2 in the work of Ginsberg [45]. Consider a space domain which experiences two sinusoidal time-harmonic pressure fields and at frequencies of and respectively. The time-harmonic pressure fields can be represented as:
| (11) |
| (12) |
The space-dependant pressure amplitudes and can be obtained from Helmholtz equations for each harmonic:
| (13) |
| (14) |
Assuming that the system is linear, the superposition principle allows the total pressure experienced by the domain, to be written as the sum of two pressure fields:
| (15) |
where denotes the complex conjugates. A time-averaged mean-squared value of can be obtained using Parseval’s theorem [45], where represents the Helmholtz equation solution for the harmonic:
| (16) |
In this study it was assumed that the steady state, time-averaged acoustic pressure in the sonoreactor can be interpreted as the root-mean-squared pressure, which can be written for two harmonics as:
| (17) |
A more general form that can be used for more than two harmonics can be written as:
| (18) |
The root-mean-squared pressure is a function of space and can be calculated directly from the frequency domain magnitudes in a multi-frequency system (e.g. Eqns. (13), (14)). The above approach is valid if the total pressure does not depend on the phase of the components, in which the mean value of their product is zero. The above reasoning forms the foundation of the method proposed in this study. As opposed to solving for multi-frequency pressure fields in the time-domain, it is instead proposed that the results from individual frequency domain simulations to be used to characterise a multi-frequency sonoreactor using the root-mean-squared pressure, with the key assumption that all fields are harmonic and sinusoidal.
2.4.1. Effect of bubbly liquid on the acoustic pressure field
Cavitation bubbles were known to have a profound effect on the resulting acoustic pressure field. These effects are incorporated into the Helmholtz equations through the specification of the propagation wavenumber and attenuation coefficient . In the following sections, a semi-empirical method used for this study is described. The real part which governs the phase speed was empirically determined from available SCL measurements, while the bubbly-liquid attenuation was calculated from a nonlinear pressure-dependant Commander and Prosperetti model. The reasoning behind this decision shall be comprehensively discussed.
2.4.2. Specification of the propagation wavenumber
In this study, the propagation wavenumber was determined from empirical wavelength measurements instead of calculating it from the bubbly-liquid model. The reason for this is two-fold. The first reason relates to the issue where there is a significant degree of uncertainty in specifying an accurate representation of the bubble fraction in terms of equilibrium radius and bubble density (See: Section 2.4.4). As noted in a previous study [49], such uncertainties can lead to large deviations in antinode predictions, which can lead to incorrect conclusions in the main investigation of this study. The second reason relates to the nonlinear bubble density used in the simulation (See: Section 2.4.4), where it was found that the use of the full nonlinear Commander and Prosperetti model to cause the solver to occasionally fail to achieve convergence at certain geometries or transducer pressures, even after tuning the solvers to recommended settings. This was believed to be caused by the highly nonlinear relation between the phase speed and the multi-frequency pressure field, which led to oscillatory behaviour in the solvers.
As the main focus of this study is to evaluate the viability of using frequency domain simulations to characterise multi-frequency pressure fields, the bubbly-liquid model used in this study was simplified to improve consistency and reduce unnecessary ambiguities that would complicate the investigation. The propagation wavenumber was thus tuned from single frequency sonochemiluminescence (SCL) measurements and assumed to be constant in space for all simulated frequencies. This approach however requires a few concerns to be addressed. Firstly, the suitability of the constant phase speed tuned from SCL measurements has to be considered. Realistically, the phase speed in the reactor would vary in space due to the changes in the bubble fraction. Since the ultrasonic irradiation is evenly distributed in the sonoreactor, it is assumed that this variance in phase speed to be small. Secondly, the bubbly liquid is a dispersive medium, where the phase speed is a function of frequency, , such as that described by the dispersion relation (Eqn. (6)). Thus, it should be acknowledged that this study also assumes that the effect of dispersion to be negligible. It would later be seen that in the results the above assumptions were mainly justified for the studied system.
2.4.3. Specification of the attenuation coefficient
The main incentive of using a bubbly-liquid model is to incorporate the attenuation of bubbly-liquid systems to prevent the overprediction of pressure magnitudes. Additionally, it was noted in a previous study that the lack of an attenuation mechanism can lead to the calculation of unrealistic cavitation regions [49]. In this study, the attenuation of the system was extracted from the Commander and Prosperetti model (Eqn. (6)). Considering that the pressure fields of multiple harmonics propagate simultaneously through the same domain, it was assumed that the attenuation of a single bubble field is applied for all involved frequencies. However, since the attenuation is a function of a single frequency, it was also assumed that the attenuation was calculated for a frequency loading of the dominant frequency (brightest standing wave) identified from the SCL images. The 40 kHz bubbly-liquid attenuation was used for three simulations (28–40, 40–70, and 28–40–70 kHz) while the 28–70 kHz simulation was performed using 28 kHz bubbly-liquid attenuation. This simplified approach was used as an approximation as there is currently limited knowledge available on predicting bubbly-liquid attenuation in multi-frequency systems.
2.4.4. Nonlinear bubble density parameter for bubbly-liquid attenuation
A major challenge in acoustic pressure simulations concerning bubbly liquids involves providing a convincing description of bubble parameters in the liquid. An important variable is the bubble fraction which depends on the equilibrium radius and bubble density (Eqn. (5)). As it was with many past studies, a monodisperse assumption was applied with an equilibrium bubble radius of [[18], [47]]. The magnitude of the bubble density parameter then influences the bubble fraction for the pressure field. The main difficulty in specifying stems from the fact that available cavitation bubble data were only available for small-scale studies and measured in close proximity to the transducers [50], [51], [52]. Bubble data for large sonoreactors were difficult to obtain while evidence is lacking for the use of lab-scale measurements to describe bubble behaviour in large geometries. To deal with this limitation, past studies tend to approach it using simplified methods. The simpler approach assumes a constant value of for the entire domain [49], [53] while the other involves specifying as a spatial function of pressure [18]. In this study, the latter was adapted with reference to past works [13], [18], [48] as it was believed to be more comprehensive. The method assumes a linear relationship between the bubble fraction and the local absolute pressure as:
| (19) |
where is a linear coefficient tuned against a bubble fraction at a reference pressure magnitude. For a monodisperse assumption, the substitution of Eqn. (5) into Eqn. (19) allows to be written as:
| (20) |
Jamshidi et al. [18] assigned the bubble fraction of 0.1 to 500 bar of acoustic pressure, which led to . This was in part inspired by Dähnke [54] who assumed the relation based on available bubble measurements. The same relation was later used in other studies and was reported to work relatively well in terms of predicting the acoustic pressure magnitude [13], [48].
In this study, the approach was modified for a multi-frequency case. First it was assumed that the spatial bubble fraction parameter is a function of effective pressure of the multi-frequency system, . While single frequency studies specified as a function of absolute pressure , it was believed that the root-mean-squared pressure would provide a better representation when this formulation is extended to the composite pressure field of multi-frequency systems as supported by findings in Section 5.4. The modified relationship used in this study can then be written as:
| (21) |
Since the value of the equilibrium bubble radius was fixed as a consequence of the monodisperse assumption, the bubble density parameter in the simulation would vary as a function of spatial root-mean-squared pressure as:
| (22) |
Past studies also involved specifying a conditional statement in which the medium was assumed to be a pure liquid () if the pressure is below the cavitation threshold [18]. This was not applied in this study. This is because empirical measurements had shown that bubble fraction values can still be significant even below the cavitation threshold [52]. There are also considerations on the effects of bubble migration and the inherent presence of dissolved gasses in the sonoreactor, which makes assuming a bubble fraction of zero to be less representative.
3. Materials and methodology
3.1. Physical properties of the sonoreactor
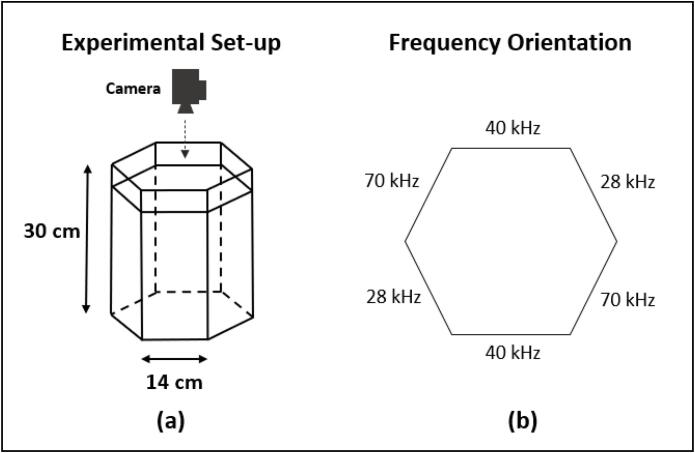
The sonoreactor used in this investigation is identical to that of previously published studies [43], [44], [49]. The hexagonal vessel (Sonictron, Malaysia) possesses 6 pressure emitting vertical walls and is capable of operating at 28, 40 and 70 kHz. Vibrations of each frequency is emitted from a pair of opposing surfaces and can be operated independently at a design power rating of 300 W. Fig. 1 shows a simplified representation of the sonoreactor, as well as the orientation of the frequencies associated to the pressure emitting walls.
Fig. 1.
Representation of the geometry and orientation of the studied sonoreactor. (a) Visual representation of the hexagonal sonoreactor dimensions from which SCL images were obtained and (b) The orientation of the frequencies involved with respect to simulation geometry and SCL results.
3.2. Experimental data
Multiple SCL images were taken from the top of the sonoreactor as shown in Fig. 1(a) using long exposure photography (30 s), and the images that showed clear representation of the standing waves were used in the validation studies. Image analysis software ImageJ was used to post-process the SCL data by first subtracting background luminance values using a dark frame image taken without any SCL activity [44]. This was followed by applying a Gaussian blur filter to smooth out pixel noise. The contrast was then adjusted by setting the saturated pixel value to 6% to better visualise the standing wave patterns.
Calorimetry data for the specification of pressure boundaries are shown in Table 1 [55]. The pressure boundaries for each frequency were calculated from calorimetry measurements using the equation:
| (23) |
Table 1.
Calorimetry data for power measurements from Tiong et al. [55] used to calculate the pressure boundary condition used in the simulations.
| Operation | Frequency (kHz) | Power, OM (W) | Total Surface Area, As (m2) | PTr,28 (bar) | PTr,40 (bar) | PTr,70 (bar) |
|---|---|---|---|---|---|---|
| Double frequency | 28 + 40 | 403.7 | 0.165 | 0.86 | 0.86 | – |
| 28 + 70 | 528.5 | 0.165 | 0.98 | – | 0.98 | |
| 40 + 70 | 446.8 | 0.165 | – | 0.90 | 0.90 | |
| Triple frequency | 28 + 40 + 70 | 657.3 | 0.248 | 0.89 | 0.89 | 0.89 |
where represents the measured power output from calorimetry measurements and is the total surface area of the pressure-emitting surface. Pressure magnitude values in Table 1 were obtained on the assumption that the pressure intensity is equally distributed across the entire emitting surface.
3.3. Estimation of phase speed using single frequency SCL measurements
As discussed in Section 2.4.2, the phase speed used in the frequency domain simulations were obtained empirically from SCL image data. It should be informed that in order to reduce error, only SCL images of single frequency operations (28 kHz, 40 kHz, and 70 kHz only) that forms distinct standing wave patterns were used to determine the averaged phase speed. The process involved are similar to the wavelength tuning method discussed in a past study [49]. After smoothing and establishing the scale of the images, the ‘Plot Profile’ function in ImageJ was used to plot and measure the distances between the peaks of the standing waves. The wavelength is the twice the average distance between peaks :
| (24) |
The empirical phase speed was calculated from the measured wavelengths for each frequency as:
| (25) |
Finally, a single averaged phase speed, was obtained and used in the multi-frequency simulations.
4. Numerical simulation
4.1. Simulation parameters
The physical parameters used for the simulations were shown in Table 2. The parameters were assumed to be constant in the domain. It was assumed that the gas within the bubbles resembles that of air and exhibits ideal gas behaviour. Physical properties for water and air were taken at 20 °C.
Table 2.
Simulation parameters used in the study, properties were obtained at 20 °C and were assumed to be constant unless stated otherwise.
| Parameter | Value | Unit | Description |
|---|---|---|---|
| 2.19 × 10-5 | m2/s | Diffusivity of air within bubble | |
| 1481 | m/s | Speed of sound in pure water | |
| 1.41 | – | Adiabatic index for air | |
| 0.001 | Pa.s | Dynamic viscosity of water | |
| 997 | kg/m3 | Density of water | |
| 0.0725 | N/m | Surface tension of water |
4.2. Simulation set-up
The commercial FEM software COMSOL Multiphysics 5.2 was used to carry out the pressure field simulations in 2-D space with a full-scale geometry using the Pressure Acoustics module. Frequency domain studies were used to obtain time-harmonic pressure fields in the simulations. A few key assumptions were considered, notably the assumption that the pressure fields and vibrating walls are sinusoidal and time-harmonic. Next, only harmonics that correspond to the frequencies of active transducers in the multi-frequency system were considered in the simulation (e.g. only 28 and 40 kHz harmonics are simulated for the 28–40 kHz operation). The frequency response of other possible harmonics in the system (e.g. broadbands formed from bubble oscillations) were neglected in this study. Lastly, acoustic streaming effects on the formation of standing waves were also assumed to be negligible based on the minimal streaming activity observed in the SCL data.
The mesh was generated based on restrictions recommended by the software manual for acoustic problems, and the maximum element size was calculated from:
| (26) |
where is the maximum element size, is the minimum number of nodes per wavelength, and is the highest simulated frequency. Mesh independence of the simulations was confirmed through mesh refinement until a consistent solution was obtained at . The nonlinear solver in the software was used to accommodate the nonlinearities in the model. The simulations were performed using an AMD Ryzen 7 3700X CPU (3593 MHz, 8 cores) with 64 GB of available physical memory (RAM).
4.3. Boundary conditions
The pressure-emitting boundary conditions for the simulated harmonics were specified in terms of pressure and it was assumed that the acoustic power measured from calorimetry data (Table 1) was distributed equally between the two emitting boundaries for each simulated harmonic. This was represented using a Dirichlet boundary condition:
| (27) |
Additionally, Dirichlet sound soft boundaries were used to represent inactive walls. This specification assumes that the inactive boundaries are infinitely soft.
| (28) |
The choice of using a Dirichlet boundary to represent non-emitting boundaries was done mainly to be consistent with the pressure-emitting boundaries. A study by Rashwan et al. [10] revealed that the use of sound soft or sound hard boundaries can lead to slight differences in pressure fields. However, preliminary simulations revealed that due to the significant degree of attenuation used in the current investigation, the slight differences caused in the specification of inactive wall boundaries were found to not affect key observations in this study.
4.4. Frequency domain simulations for multi-frequency systems
For each dual- or tri-frequency case, a summary of the steps involved in obtaining the steady state pressure field approximation is as follows:
-
1.
Bubble density magnitudes were obtained for a range of root-mean-squared pressures using Eqn. (22), and an attenuation interpolation curve was plotted using the Commander and Prosperetti model (Eqns. 6 - 10 and Eqn. (2)).
-
2.
Frequency domain simulations were carried out for each involved frequency to obtain their corresponding harmonic pressure field solutions.
-
3.
The root-mean-squared pressure field, was calculated from time-harmonic solutions using Eqn. (18).
-
4.
The bubble density field and by extension the attenuation field in the simulation domain was calculated from based on the interpolation plot specified in Step 1.
-
5.
Steps 2 to 4 were iterated until the nonlinear pressure and attenuation fields were converged.
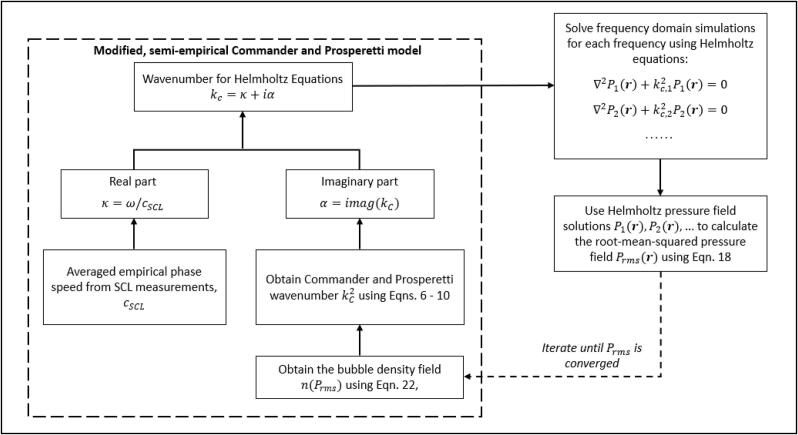
A graphical representation of the simulation methodology is given below in Fig. 2.
Fig. 2.
Graphical representation of the mathematical model and the iteration loop. The real part of the wavenumber was determined from the empirical phase speed while the attenuation was iterated from the nonlinear Commander and Prosperetti model.
5. Results and discussion
5.1. Processing and analysis of sonochemiluminescence (SCL) images
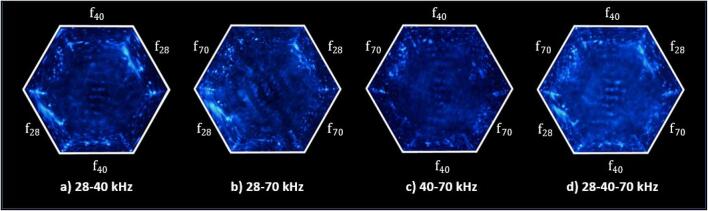
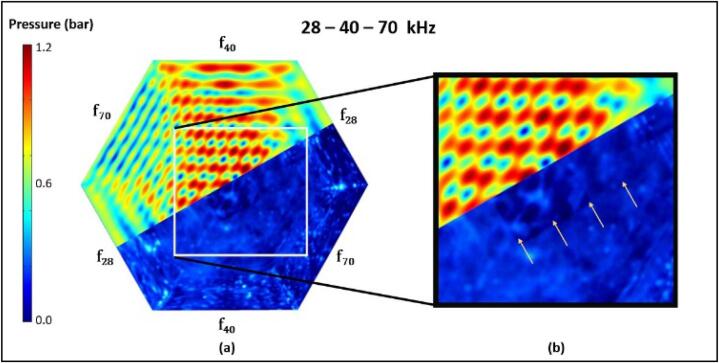
Fig. 3 depicts top-down SCL images captured for four multi-frequency configurations of the studied sonoreactor. The frequency combinations considered in this study were 28–40, 28–70, 40–70 and 28–40–70 kHz. Readers are referred to previously published works [44], [55] for a comprehensive discussion on the SCL characterisation of the reactor used in this study, notably on the comparison between single and multi-frequency operation.
Fig. 3.
SCL images taken for four different operating configurations of the hexagonal sonoreactor. The contrast of the images has been adjusted to facilitate better identification of the formation of standing wave patterns.
The presence of standing wave patterns was found for all cases, notably near the centre of the reactor. They are shown as brighter (antinodes) and dimmer (nodes) bands forming between the pressure-emitting walls. Fig. 3 also shows the presence of bright regions near the edges of the reactor, noticeably for the 28 kHz walls. While these can be possibly interpreted as high pressure regions, the validity of SCL visual data near the edges were less reliable due to possible uncertainties caused by the reflecting metal walls. Considering that the camera was positioned above the middle of the sonoreactor, visual data could also be increasingly warped (through refraction) as the region of interest lies further away from the centre. Thus, the simulation results in this study were mainly validated and discussed based on a region of interest near the centre of the reactor.
Fig. 3 also shows standing waves of different frequencies to have notable differences in terms of SCL brightness. With reference to Fig. 3(a), (c) and (d), 40 kHz standing waves were observed to be the brightest and most dominant, followed by 28 kHz standing waves. The 70 kHz standing waves were very dim for all images and could not be distinctively characterised with the only exception being the 28–70 kHz case shown in Fig. 3(b). The general obscurity of the 70 kHz standing wave can be attributed to its shorter wavelength and thus thinner antinode bands which resulted in them being susceptible to visual noise. Additionally, as attenuation was known to increase with frequency [23], it is possible that the 70 kHz pressure field may have exhibited relatively lower SCL activity due to a higher rate of energy dissipation.
5.2. The modified Commander and Prosperetti model
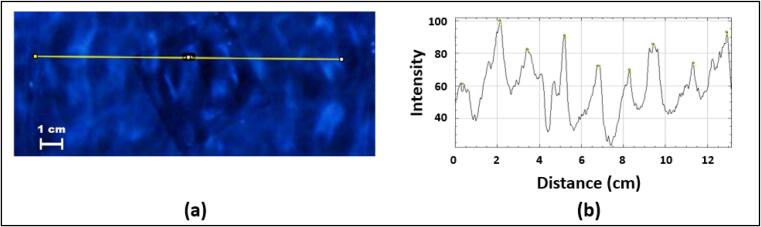
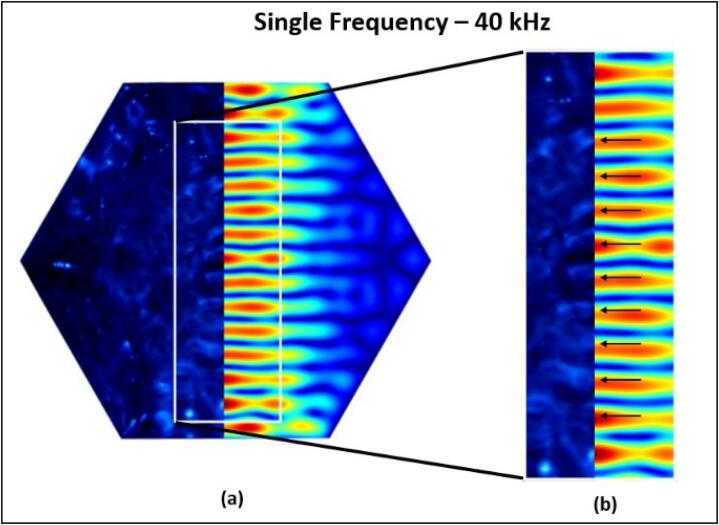
The phase speed used in the simulations was calculated from SCL image measurements of single frequency (28, 40 and 70 kHz) standing waves using the methods discussed in Section 2.4.2. Fig. 4 briefly depicts the process for determining the empirically measured phase speed. In the example, a well-developed standing wave pattern (40 kHz) was measured using the “Plot Profile” function in ImageJ. The resulting normalised luminosity plot for the yellow line drawn in Fig. 4(a) is shown in Fig. 4(b), from which the distances between the peaks were measured to obtain the averaged empirical phase speed.
Fig. 4.
Representation of an example of how the empirical phase speed was extracted from single frequency SCL image. (a) A cropped region from a 40 kHz SCL standing wave obtained from the sonoreactor. (b) A normalised luminosity plot in which the distance between peaks (bright bands) was measured using the image processing software ImageJ.
The value of the averaged empirical phase speed was calculated to be . This value is lower than that for pure water (20 °C) at . The best explanation for this is the presence of cavitation bubbles, which was proven to drastically reduce sound speed in water [56]. The important implication of this result is that if the simulations were to be conducted by neglecting bubble effects and assuming for a pure liquid, the predicted location of the antinodes could possibly show unrealistic deviations especially at higher frequencies. This finding highlighted the importance of bubbly liquid property specification in the bubbly liquid model in order to accurately capture the reduction in phase speed by bubbles. A previous study have found that uncertainties in the specification of bubble parameters led to inaccurate predictions of the phase speed in the Commander and Prosperetti model [49].
Fig. 5(a) shows the SCL image obtained from the sonoreactor operating at a single frequency of 40 kHz. The image was compared against the simulation results of the semi-empirical Commander and Prosperetti model using . Fig. 5(b) showed good agreement between the simulation and the SCL image, which can be largely expected as the wavelength was tuned. However, it is interesting to note that there a slight deviation in the comparison which could be caused by the fact that the phase speed is actually not a true constant in the liquid medium but instead varies slightly in space. On the other hand, it is also likely that disturbances in the liquid medium led to visual distortions of the SCL data. Nonetheless, it was noted that the constant empirical phase speed should provide a good representation of the phase speed in the bubbly liquid and thus was used to further investigate the multi-frequency cases.
Fig. 5.
Validation of the semi-empirical Commander and Prosperetti model on single frequency (40 kHz) SCL image of the sonoreactor. (a) Left side: SCL image, right side: simulation results. (b) Zoomed-in view on the agreement between simulated antinodes and SCL antinodes.
A limitation of the Commander and Prosperetti model is that the attenuation is a function of frequency. Considering that waves of different frequencies simultaneously travel through the same bubble field, it would make sense for the same energy dissipation to affect all frequencies instead of each frequency to have their own attenuation curve. The simplified approach in this investigation assumed that the 40 kHz attenuation is dominant in 28–40, 40–70, and 28–40–70 kHz cases, while the 28 kHz is dominant in the 28–70 kHz case. Fig. 6 shows the bubble density parameter (Eqn. (22)) and the corresponding attenuation coefficient plotted against .
Fig. 6.
Bubble density (left axis) and its associated attenuation magnitude (right axis) plotted as a function of root-mean-squared pressure for the harmonic fields of 28 and 40 kHz.
Compared to the well-studied effects of bubbly-liquid attenuation in single frequency systems, the current understanding of frequency domain bubbly-liquid models for multi-frequency systems is still very limited. While it is likely that the simplified attenuation model could underestimate the attenuation, the results from the model indicated a significantly better estimation compared to a pure liquid model [49]. However, the consequence of this limitation is that the pressure magnitude predictions from the simulations are to a great extent a qualitative approximation of the studied multi-frequency system. Future studies should further examine and improve the methods of describing bubbly-liquid attenuation in multi-frequency systems. One possibility is to develop the energy dissipation mechanism directly from multi-frequency bubble dynamics, similar to the development of the nonlinear Helmholtz model [24], [26].
5.3. Experimental validation using SCL images
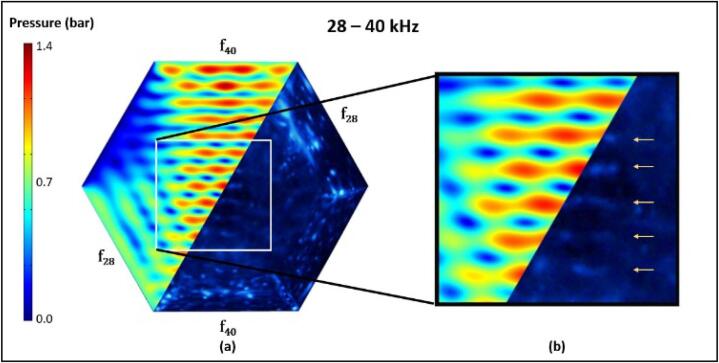
Fig. 7(a) shows the superimposition of the simulated effective pressure field onto one of the SCL images for the 28–40 kHz case. A magnified view on the region of interest is shown in Fig. 7(b), where it can be observed that the high regions aligned well with bright SCL bands captured for the 40 kHz standing wave. Fig. 8 shows the same simulation superimposed onto another image that better captured the 28 kHz standing wave, where it can be seen that the 28 kHz standing waves exhibit similar agreement albeit with dimmer and less obvious bands.
Fig. 7.
(a) Comparison between predicted from simulation and SCL data for the 20 – 40 kHz case, (b) region of interest showing the agreement of the 40 kHz standing wave.
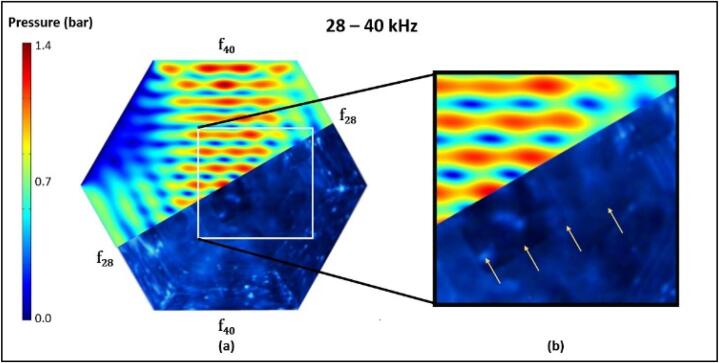
Fig. 8.
(a) Comparison between predicted from simulation and SCL data for the 20 – 40 kHz case superimposed along the 28 kHz standing wave, (b) region of interest showing the agreement of the 28 kHz standing wave.
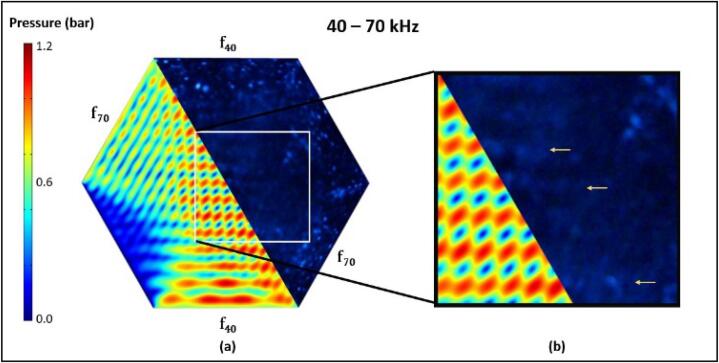
For the case of the 40–70 kHz dual-frequency operation, less conclusive results were obtained. SCL bands identified for the 40–70 kHz images were significantly dimmer compared to other frequency combinations. This resulted in standing waves that were less distinct. The low intensity of the 70 kHz standing wave led to it being indistinguishable from surrounding visual noise and thus validation was limited. However, further inspection did reveal that the 40 kHz standing wave bands agreed well with the simulated antinode locations as shown in Fig. 9(b).
Fig. 9.
(a) Comparison between predicted from simulation and SCL data for the 40 – 70 kHz case, (b) region of interest showing the weak agreement of the 40 kHz standing wave.
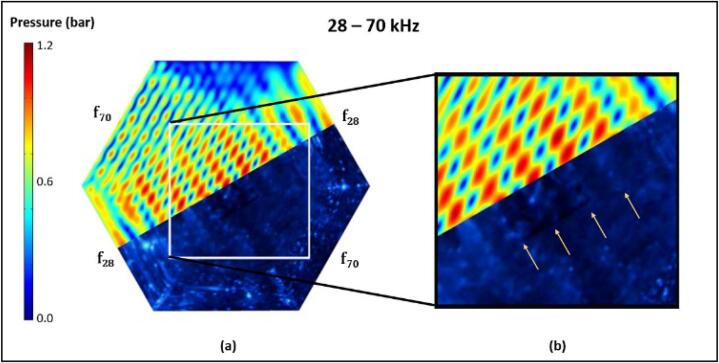
Compared to the previous two cases where a single standing wave dominates, the 28–70 kHz SCL images managed to yield clear dual-frequency standing waves. It is worth noting that this was largely unexpected as the 70 kHz SCL standing wave formations were difficult to be characterised at this scale due to their short wavelength and susceptibility to visual noise. This may be caused by the larger frequency difference in the 28–70 kHz case, which led to more distinguishable composite patterns and lower visual interference compared to other cases. The findings shown later in Section 5.4, Fig. 17 also indicates a possibility that the clarity of the 28–70 kHz standing wave may be caused by similar antinode magnitudes whereby both standing waves exhibit similar magnitudes.
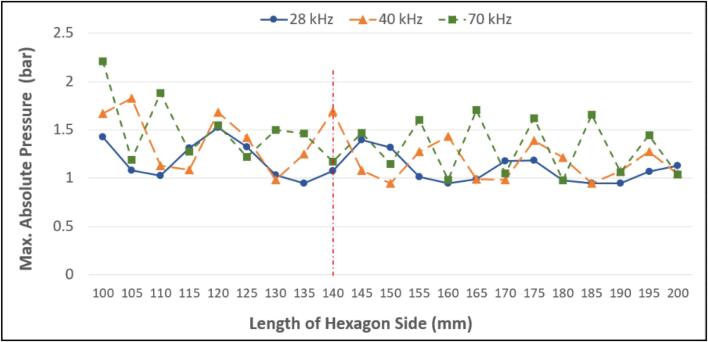
Fig. 17.
Plot of the peak absolute pressure simulated for frequencies of 28, 40 and 70 kHz against a series of hexagonal sonoreactor sizes. The simulations were carried out in hexagonal 2D geometry with increasing dimensions. The physical sonoreactor used in this study has a side length of 140 mm (shown as the vertical line).
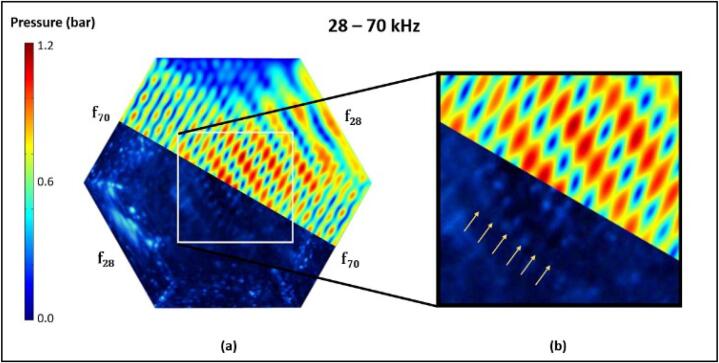
The observations in Fig. 10 provided an important insight on the behaviour of higher frequency pressure fields in sonoreactors and further supported the validity of the empirical phase speed in the multi-frequency cases. As seen in Fig. 10(b), the 28 and 70 kHz standing waves showed clear superimposition in the SCL image. The 28 kHz bands in Fig. 11 are also much more distinct. Comparison results in Fig. 10(b) and 11(b) showed the best agreement between simulation and SCL out of all studied cases.
Fig. 10.
(a) Comparison between predicted from simulation and SCL data for the 28 – 70 kHz case superimposed along the 28 kHz standing wave, (b) region of interest showing very good agreement.
Fig. 11.
(a) Comparison between predicted from simulation and SCL data for the 28 – 70 kHz case superimposed along the 70 kHz standing wave, (b) region of interest showing very good agreement for the fine 70 kHz wave patterns.
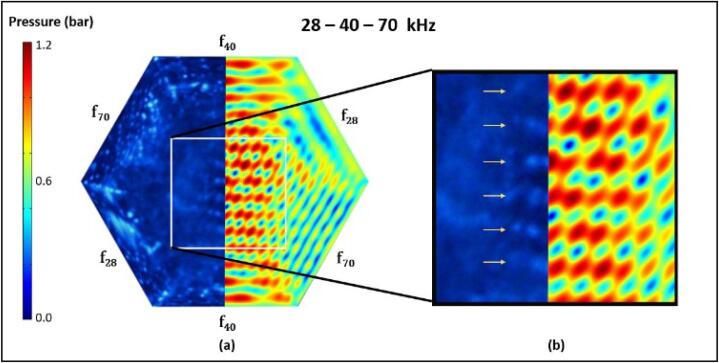
Tri-frequency SCL images showed 40 kHz standing waves to be the most dominant, followed by 28 kHz and 70 kHz. The results in Fig. 12 and Fig. 13 reconfirmed the findings in dual-frequency cases where the standing wave patterns coincided well with the SCL data, notably with a clear dominance by the 40 kHz standing waves.
Fig. 12.
(a) Comparison between predicted from simulation and SCL data for the tri-frequency case superimposed along the 40 kHz standing wave, (b) region of interest comparing the 40 kHz standing wave.
Fig. 13.
(a) Comparison between predicted from simulation and SCL data for the tri-frequency case superimposed along the 28 kHz standing wave, (b) region of interest comparing the 28 kHz standing wave.
With respect to the above dual- and tri- frequency cases, it can be said that for the considered regions of interest, the antinode locations predicted by the simulations compared well with the SCL images. Another notable finding is that the simulations surprisingly managed to predict stronger standing waves for the 40 kHz pressure field, which was also reflected in the SCL images.
5.4. Analysis of pressure magnitude data from simulation results
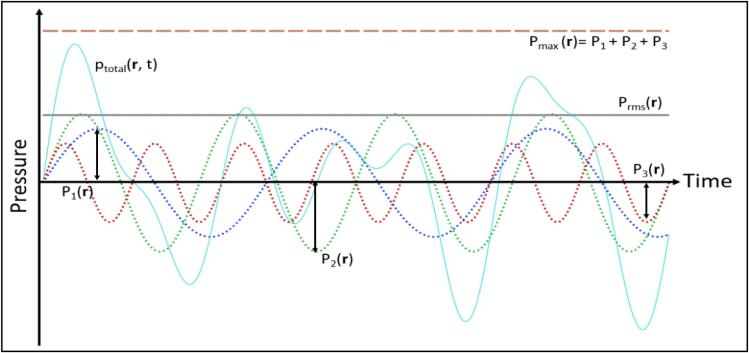
In this section, the use of the root-mean-squared pressure (Eqn. (17), (18)) to characterise the cavitation intensity in a multi-frequency system is discussed. Traditionally, past monoharmonic sonoreactor simulations assessed the potential for cavitation activity based on the absolute acoustic pressure, [6]. However, the same rationale is not suitable for multi-frequency systems since the domain now experiences multiple pressure fields. For this study, it was assumed that the potential for cavitation activity was related to the root-mean-squared pressure , which can be interpreted as the time-averaged effective pressure at each space coordinate. However, another considered alternative is the sum of absolute pressures, which is henceforth referred to as the maximum achievable pressure magnitude:
| (29) |
To illustrate the comparison, Fig. 14 shows the pressure variation at a single point in space experiencing three time-harmonic sinusoidal pressure fields oscillating at their respective amplitudes , and . The total pressure at the space coordinate is summed from the contributions of three harmonics. The difference between the root-mean-squared pressure and the maximum achievable magnitude is also shown.
Fig. 14.
Illustration of the idea between using (horizontal solid line) or (horizontal dotted line) to characterise the pressures experienced by a single point in space. The figure shows three pressure components (fine-dotted curves) of different frequencies oscillating at magnitudes , and . represents the total pressure at each point in time (solid curve).
It is important to investigate in between the two, with the aim to find out which is more suitable to be used to characterise the cavitation activity in the multi-frequency simulation. Firstly, the peak pressure values in the simulations calculated using each method is tabulated in Table 3.
Table 3.
Comparison between peak values of and calculated from the frequency domain simulations for each investigated frequency combination.
| Simulation | Peak root-mean-squared pressure, , bar | Peak maximum pressure, , bar |
|---|---|---|
| 28 – 40 kHz | 1.365 | 2.478 |
| 28 – 70 kHz | 1.358 | 2.715 |
| 40 – 70 kHz | 1.121 | 2.203 |
| 28 – 40 – 70 kHz | 1.185 | 3.168 |
It is clear that the problem with using is that the magnitude becomes larger as the number of considered frequencies increases. One could easily see how using Eqn. (29) to characterise cavitation potential can lead to overprediction when considering many harmonics.
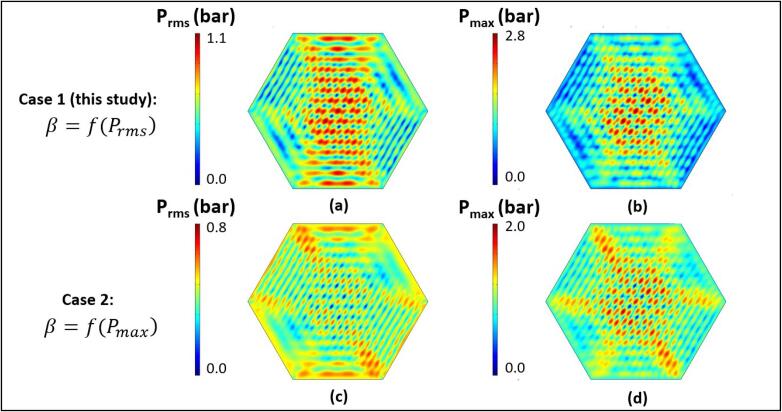
Another situation which was investigated is the specification of the pressure-dependant bubble fraction in Eqn. (21). To visualise how the use of instead of in Eqn. (21) would differ from the current methods, a simple case study was also conducted for the triple-frequency set-up by setting:
| (30) |
The results of the case study are summarized in Fig. 15. For each case, the simulated pressure fields were plotted in terms of both and . It is clear that the pressure fields predicted for Case 2 was significantly lower than Case 1. The approach in Case 2 also predicted that in the triple-frequency sonoreactor to have antinode pressures c.a. 0.8 bar, much lower than Case 1 which was around 1.1 bar. This was the consequence of determining attenuation magnitude based on , which led to higher attenuation values. Additionally, for the pressure fields shown in Fig. 15(b) and (d), the result from Case 2 also provided a much lower pressure magnitudes compared to that of Case 1. Another notable finding was that if one were to qualitatively compare the relative wave patterns formed by the pressure fields in Fig. 15 to the SCL images in Fig. 3, it can be seen that Fig. 15(a) best represents the patterns observed in the SCL images. The pressure field predicted in Fig. 15(a) correctly showed the dominance and shape of the 40 kHz standing wave, which compared well with tri-frequency SCL images in Fig. 12, Fig. 13.
Fig. 15.
Case study on two different interpretations of the acoustic pressure magnitude for the tri-frequency case; (a) & (c): Pressure field characterised using ; (b) & (d): Pressure field characterised using .
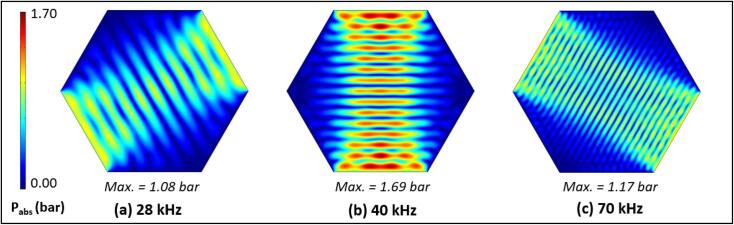
An interesting observation that is evident in the SCL images is the dominance of the 40 kHz standing waves over the 28 and 70 kHz standing waves. Fig. 16 shows the individual frequency domain pressure fields simulated for the triple-frequency. The images are plotted on the same scale and it is evident that the 40 kHz harmonic showed higher absolute pressure magnitudes.
Fig. 16.
Single frequency components simulated for the triple frequency case. Image (a), (b) and (c) represents the 28, 40 and 70 kHz frequency domain pressure fields used to calculate the 28–40-70 kHz r.m.s. pressure. The simulated fields are plotted using a shared colour legend to facilitate comparison for the pressure magnitudes.
The main explanation to this observation can be related to the effect of geometry on the studied sonoreactor. Since the three frequencies possess different wavelengths and the distances between opposing walls are the same, the interaction between two opposing propagating waves is different due to the differences in phase. It turned out for the current geometry the 40 kHz standing wave experienced a larger degree of constructive interference over the 28 and 70 kHz harmonics. This is evident when one simulates the same system in different reactor sizes. Fig. 17 shows the maximum absolute pressure calculated for geometries with different sizes. The length of the hexagonal geometry was investigated from 10 to 20 cm and the effect of geometry on the simulated pressure field is clearly shown.
First, it was noted that the absolute pressure slightly trends downwards as the size of the reactor increases due to the effects of attenuation. The effect of geometry on the pressure magnitude of each frequency leads to an oscillating pattern as constructive and destructive interference alternate with the changing geometry. The physical sonoreactor used for the SCL characterisation corresponds to a side length of 140 mm in which the 40 kHz frequency experiences a peak due to strong constructive interference. On the other hand, pressure magnitudes of the 28 and 70 kHz standing waves were found to be close to each other. This could potentially explain the SCL results observed in Fig. 10, Fig. 11, in which both 28 and 70 kHz was found to be equally visible, forming a very distinct composite standing wave pattern, as opposed to the dominant 40 kHz pattern found in other cases. This finding highlights the important interaction between the geometry and the wavelength (phase speed) in sonoreactor design. This is especially important when the possibility of constructive and destructive inference is high, such as in vessels with opposite propagating waves or geometries that exhibit strong reflections.
5.5. Discussion on the proposed method for simulating multi-frequency sonoreactors
In this study, the idea of predicting multi-frequency pressure fields using frequency domain simulations was investigated as an alternative to transient simulations used by past studies [39], [40]. By far the most important results were shown in Section 5.3, where the pressure field simulations were able to provide good results in the regions of interest when validated against their SCL counterparts. This showed that for the studied system, the results of the frequency domain simulations could be used to reliably predict the location of multi-frequency antinodes which is crucial for sonoreactor designs. These observations could lead to the method being a potential alternative to transient simulations to computationally characterise multi-frequency pressure fields. The key advantage of the proposed method over traditional transient simulations includes much faster solution time, memory consumption as well as being able to incorporate frequency domain attenuation methods and boundary conditions. It is believed that this method is efficient in preliminary digital prototyping where designs of multi-frequency sono-equipment can be quickly evaluated and optimised.
There are however a few considerations that should be kept in mind, such as the studied bath type system operates at relatively low acoustic pressures (c.a. 1 bar). As it was well-known that nonlinear acoustic bubble interactions are more intense in higher pressures, the reliability of the method is still unclear for systems operating at pressures much higher than the Blake threshold, such as ultrasonic horns. While the antinode predictions are promising, evidence is lacking for the case of pressure magnitude predictions due to experimental limitations. However, the pressure magnitudes predicted by the simulations were within realistic expectations as opposed to using a pure liquid model that predicted unrealistic magnitudes [49]. As for the characterisation of cavitation potential, the results from the case study in Section 5.4 suggests that the root-mean-squared pressure may be a good indicator to predict the cavitating regions, as it managed to capture the standing wave behaviour similar to those observed in the SCL images as shown in Fig. 15(a).
It is also important to discuss certain aspects of the semi-empirical model used in this study. Notably, the use of the empirical phase speed as opposed to a fully theoretical model. The empirical phase speed for the simulations have played an important part in the good agreement in terms of multi-frequency antinode patterns. This highlighted an issue which was often overlooked in past studies, which is the importance of the phase speed parameter on the antinode predictions. While less obvious in ultrasonic systems in geometries that only span a few wavelengths, the deviations of the antinode predictions caused by errors in phase speed can be significant when considering larger systems. For this study, the geometries that spanned multiple wavelengths such as the 70 kHz case meant that errors in wavelength prediction could accumulate and eventually lead to clear deviations if the phase speed data is not specified properly. A disadvantage of the fully theoretical model is that the uncertainties in specifying bubble parameters could lead to significant deviation as found in a past study [49].
This study also presented the use of a phase speed measured from single frequency standing waves which has led to successful agreements in antinode predictions in multi-frequency cases. This leads to few interesting points of discussion. Firstly, it is possible that the bubble content for the multi-frequency sonoreactor may not differ much from single frequency cases. At the time of writing, past evidence suggests a rather complex relationship between energy input and cavitation activity, where a higher energy input may not yield higher cavitation activity [38]. One should certainly not exclude the possibility of there being a more complex mechanism governing the bubble fraction property in multi-frequency ultrasonic systems. Additionally, the finding in which a single constant phase speed managed to properly capture the behaviour of three different frequencies suggests that the dispersive effects of the medium in the studied system may be negligible. Nonetheless, the results did not show any unrealistic deviations and thus the applicability of the simplified method is believed to be justified for the scope of this study. It should however be noted that the method is only applicable to systems from which empirical wavelength data can be reliably obtained.
On the topic of limitations of the current study, it should be highlighted that the performance of the frequency domain method used in this investigation was only carried out in 2D. This was due to limitations in obtaining reliable 3D data for such a large geometry, especially when considering high frequency standing waves up to 70 kHz. Thus, it is suggested that for future work the model should be further validated for systems with varying geometries and acoustic powers to strengthen the findings of this study. Another point of interest that should be addressed in the future is the modelling of attenuation in the multi-frequency pressure field. In this study, the problem was simplified by approximating the attenuation from the Commander and Prosperetti model as function of the root-mean-squared pressure. Future works are suggested to consider developing a more comprehensive approach to capture the macro-effects of bubble attenuation under pressure loadings of multiple frequencies.
Overall, the purpose of this paper is to bring attention to the development of a more resource efficient simulation methodology for the purpose of multi-frequency sonoreactor design, with the goal of achieving a method which is suitable for fast digital prototyping. As the knowledge gap remains to be very large, it is hoped that the ideas brought up in this study would inspire further development and research on the topic.
6. Conclusion
In this study, a method using frequency domain simulations was investigated as a means to predict the pressure fields formed in a multi-frequency sonoreactor. The simulations were carried out using a semi-empirical, modified Commander and Prosperetti model. A few important simplifying assumptions were made to adapt the model to describe the behaviour of a bubbly-liquid medium experiencing the pressure fields of multiple frequencies. The steady-state cavitation potential was interpreted as the root-mean-squared pressure field and the simulation results were validated against sonochemiluminescence (SCL) images. The main points concluded from this study are:
-
1.
The root-mean-squared acoustic pressure fields calculated from the frequency domain simulations using a nonlinear bubbly-liquid attenuation model yielded good qualitative agreement with SCL results in terms of antinode predictions. These results indicate that this method can potentially be used as an alternative to transient simulations during digital prototyping of multi-frequency sonoreactors by having a faster solution time and lower memory consumption. It is believed that the method is suitable in preliminary digital prototyping of multi-frequency systems. To further strengthen the validity and applicability of the method, additional validations should be carried out in the future for a larger range of conditions.
-
2.
The approach of using an empirical phase speed measured from single frequency SCL data managed to circumvent uncertainties in bubble parameter specifications. Additionally, it was also able to represent the multi-frequency systems based on the validation results using SCL. This finding can potentially be useful in terms of characterising more complex systems using simple empirical methods.
-
3.
Additional simulations to investigate the suitability of the root-mean-squared pressure to represent multi-frequency cavitation activity showed promising results and the method was able to agree well with SCL measurements.
-
4.
Due to various limitations, the bubbly-liquid attenuation model used for this study was simplified based on a few assumptions to adapt for multi-frequency simulations. While the pressure magnitude predictions were found to be within realistic values, further investigation on this matter is required to improve the current methodology.
-
5.
Analysis of the single frequency pressure fields of the tri-frequency combination revealed that the dominance of the 40 kHz standing wave in the SCL measurements can be attributed to geometrical effects. For the geometry of the studied hexagonal reactor, the 40 kHz standing wave was found to experience constructive interference which led to higher antinode pressures. This finding highlights the importance of the interaction between the geometry and wavelength of an ultrasonic system.
CRediT authorship contribution statement
Jin Kiat Chu: Conceptualization, Methodology, Software, Investigation, Validation, Formal analysis, Writing – original draft, Visualization. T. Joyce Tiong: Supervision, Conceptualization, Methodology, Project administration, Writing – review & editing. Siewhui Chong: Supervision, Project administration. Umi Aisah Asli: Software, Resources. Yeow Hong Yap: Supervision, Project administration.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors would like to thank the University of Nottingham Malaysia for studentship funding to JKC, Prof. Sivakumar Manickam for the ultrasonic equipment, and Derick Liew for the collection of SCL data. We duly acknowledge the funding from Universiti Tunku Abdul Rahman for the article processing charge.
References
- 1.Banerjee B. Recent developments on ultrasound assisted catalyst-free organic synthesis. Ultrason. Sonochem. 2017;35:1–14. doi: 10.1016/j.ultsonch.2016.09.023. [DOI] [PubMed] [Google Scholar]
- 2.Wen C., Zhang J., Zhang H., Dzah C.S., Zandile M., Duan Y., Ma H., Luo X. Advances in ultrasound assisted extraction of bioactive compounds from cash crops – A review. Ultrason. Sonochem. 2018;48:538–549. doi: 10.1016/j.ultsonch.2018.07.018. [DOI] [PubMed] [Google Scholar]
- 3.Wang X., Majzoobi M., Farahnaky A. Ultrasound-assisted modification of functional properties and biological activity of biopolymers: A review. Ultrason. Sonochem. 2020;65 doi: 10.1016/j.ultsonch.2020.105057. [DOI] [PubMed] [Google Scholar]
- 4.Bhargava N., Mor R.S., Kumar K., Sharanagat V.S. Advances in application of ultrasound in food processing: A review. Ultrason. Sonochem. 2021;70 doi: 10.1016/j.ultsonch.2020.105293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.K. Yasui Acoustic Cavitation and Bubble Dynamics 1st ed., 2018 Springer International Publishing 10.1007/978-3-319-68237-2.
- 6.Tudela I., Sáez V., Esclapez M.D., Díez-García M.I., Bonete P., González-García J. Simulation of the spatial distribution of the acoustic pressure in sonochemical reactors with numerical methods: A review. Ultrason. Sonochem. 2014;21(3):909–919. doi: 10.1016/j.ultsonch.2013.11.012. [DOI] [PubMed] [Google Scholar]
- 7.Dähnke S., Swamy K.M., Keil F.J. Modeling of three-dimensional pressure fields in sonochemical reactors with an inhomogeneous density distribution of cavitation bubbles. Ultrason. Sonochem. 1999;6(1-2):31–41. doi: 10.1016/S1350-4177(98)00026-1. [DOI] [PubMed] [Google Scholar]
- 8.G. Servant, J.L. Laborde, A. Hita, J.P. Caltagirone, A. Gérard, On the use of ultrasound in chemistry:Modelling of sonoreactors. Determination of cavitation bubble emergence, bubble migration through time, fluid flow induced by the propagation of an ultrasound wave. Comparison of theoretical and experimental results, in: K. C.R., K. V. (Eds.), Am. Soc. Mech. Eng. Press. Vessel. Pip. Div. PVP, EDF Div. R and D, ADEI, Route de Sens-Ecuelles, 77818 Moret-sur-Loing Cedex, France, 2001: pp. 13–26. https://www.scopus.com/inward/record.uri?eid=2-s2.0-0347412143&partnerID=40&md5=1012ca130383b6d10fe817bdb6376c70.
- 9.Vanhille C., Conde C., Campos-Pozuelo C. Finite-difference and finite-volume methods for nonlinear standing ultrasonic waves in fluid media. Ultrasonics. 2004;42(1-9):315–318. doi: 10.1016/j.ultras.2004.01.024. [DOI] [PubMed] [Google Scholar]
- 10.Rashwan S.S., Mohany A., Dincer I. Development of efficient sonoreactor geometries for hydrogen production. Int. J. Hydrogen Energy. 2021;46:15219–15240. doi: 10.1016/j.ijhydene.2021.02.113. [DOI] [Google Scholar]
- 11.Abramov V.O., Abramova A.V., Bayazitov V.M., Nikonov R.V., Voitov Y.I., Fedulov I.S. The pecularities of ultrasonic equipment design for stabilization of dispersed structures of alumosilicic reagents for wastewater treatment. Ultrason. Sonochem. 2020;64:105041. doi: 10.1016/j.ultsonch.2020.105041. [DOI] [PubMed] [Google Scholar]
- 12.Tangsopa W., Thongsri J. Development of an industrial ultrasonic cleaning tank based on harmonic response analysis. Ultrasonics. 2019;91:68–76. doi: 10.1016/j.ultras.2018.07.013. [DOI] [PubMed] [Google Scholar]
- 13.Hussain M.N., Janajreh I. Acousto-chemical analysis in multi-transducer sonochemical reactors for biodiesel production. Ultrason. Sonochem. 2018;40:184–193. doi: 10.1016/j.ultsonch.2017.07.009. [DOI] [PubMed] [Google Scholar]
- 14.Lewis J.P., Gardner S., Corp I. A 2D finite element analysis of an ultrasonic cleaning vessel: Results and comparisons. Int. J. Model. Simul. 2007;27(2):181–185. doi: 10.1080/02286203.2007.11442415. [DOI] [Google Scholar]
- 15.Sutkar V.S., Gogate P.R., Csoka L. Theoretical prediction of cavitational activity distribution in sonochemical reactors. Chem. Eng. J. 2010;158(2):290–295. doi: 10.1016/j.cej.2010.01.049. [DOI] [Google Scholar]
- 16.Wei Z., Weavers L.K. Combining COMSOL modeling with acoustic pressure maps to design sono-reactors. Ultrason. Sonochem. 2016;31:490–498. doi: 10.1016/j.ultsonch.2016.01.036. [DOI] [PubMed] [Google Scholar]
- 17.Rashwan S.S., Dincer I., Mohany A. Investigation of acoustic and geometric effects on the sonoreactor performance. Ultrason. Sonochem. 2020;68 doi: 10.1016/j.ultsonch.2020.105174. [DOI] [PubMed] [Google Scholar]
- 18.Jamshidi R., Pohl B., Peuker U.A., Brenner G. Numerical investigation of sonochemical reactors considering the effect of inhomogeneous bubble clouds on ultrasonic wave propagation. Chem. Eng. J. 2012;189–190:364–375. doi: 10.1016/j.cej.2012.02.029. [DOI] [Google Scholar]
- 19.Jordens J., Honings A., Degrève J., Braeken L., Gerven T.V. Investigation of design parameters in ultrasound reactors with confined channels. Ultrason. Sonochem. 2013;20(6):1345–1352. doi: 10.1016/j.ultsonch.2013.03.012. [DOI] [PubMed] [Google Scholar]
- 20.B. Lebon I. Tzanakis K. Pericleous D. Eskin Numerical Modelling of the Ultrasonic Treatment of Aluminium Melts: An Overview of Recent Advances, Mater 12 2019 (Basel, Switzerland) 10.3390/ma12193262 3262. [DOI] [PMC free article] [PubMed]
- 21.Delacour C., Stephens D.S., Lutz C., Mettin R., Kuhn S. Design and Characterization of a Scaled-up Ultrasonic Flow Reactor. Org. Process Res. Dev. 2020;24(10):2085–2093. doi: 10.1021/acs.oprd.0c00148. [DOI] [Google Scholar]
- 22.Sarac B.E., Stephens D.S., Eisener J., Rosselló J.M., Mettin R. Cavitation bubble dynamics and sonochemiluminescence activity inside sonicated submerged flow tubes. Chem. Eng. Process. - Process Intensif. 2020;150:107872. doi: 10.1016/j.cep.2020.107872. [DOI] [Google Scholar]
- 23.Commander K.W., Prosperetti A. Linear pressure waves in bubbly liquids: Comparison between theory and experiments. J. Acoust. Soc. Am. 1989;85(2):732–746. doi: 10.1121/1.397599. [DOI] [Google Scholar]
- 24.Louisnard O. A simple model of ultrasound propagation in a cavitating liquid. Part I: Theory, nonlinear attenuation and traveling wave generation. Ultrason. Sonochem. 2012;19(1):56–65. doi: 10.1016/j.ultsonch.2011.06.007. [DOI] [PubMed] [Google Scholar]
- 25.Jamshidi R., Brenner G. Dissipation of ultrasonic wave propagation in bubbly liquids considering the effect of compressibility to the first order of acoustical Mach number. Ultrasonics. 2013;53(4):842–848. doi: 10.1016/j.ultras.2012.12.004. [DOI] [PubMed] [Google Scholar]
- 26.Trujillo F.J. A strict formulation of a nonlinear Helmholtz equation for the propagation of sound in bubbly liquids. Part I: Theory and validation at low acoustic pressure amplitudes. Ultrason. Sonochem. 2018;47:75–98. doi: 10.1016/j.ultsonch.2018.04.014. [DOI] [PubMed] [Google Scholar]
- 27.Caflisch R.E., Miksis M.J., Papanicolaou G.C., Ting L. Effective equations for wave propagation in bubbly liquids. J. Fluid Mech. 1985;153:259–273. doi: 10.1017/S0022112085001252. [DOI] [Google Scholar]
- 28.Brotchie A., Grieser F., Ashokkumar M. Sonochemistry and Sonoluminescence under Dual-Frequency Ultrasound Irradiation in the Presence of Water-Soluble Solutes. J. Phys. Chem. C. 2008;112(27):10247–10250. doi: 10.1021/jp801763v. [DOI] [Google Scholar]
- 29.Son Y., Lim M., Cui M., Khim J. Estimation of Sonochemical Reactions under Single and Dual Frequencies Based on Energy Analysis. Jpn. J. Appl. Phys. 2010;49(7):07HE02. doi: 10.1143/JJAP.49.07HE02. [DOI] [Google Scholar]
- 30.Avvaru B., Pandit A.B. Experimental investigation of cavitational bubble dynamics under multi-frequency system. Ultrason. Sonochem. 2008;15:578–589. doi: 10.1016/j.ultsonch.2007.06.012. [DOI] [PubMed] [Google Scholar]
- 31.Guédra M., Inserra C., Gilles B., Béra J.-C. Numerical investigations of single bubble oscillations generated by a dual frequency excitation. J. Phys. Conf. Ser. 2015;656:12019. doi: 10.1088/1742-6596/656/1/012019. [DOI] [Google Scholar]
- 32.Suo D., Govind B., Zhang S., Jing Y. Numerical investigation of the inertial cavitation threshold under multi-frequency ultrasound. Ultrason. Sonochem. 2018;41:419–426. doi: 10.1016/j.ultsonch.2017.10.004. [DOI] [PubMed] [Google Scholar]
- 33.Ye L., Zhu X., Liu Y. Numerical study on dual-frequency ultrasonic enhancing cavitation effect based on bubble dynamic evolution. Ultrason. Sonochem. 2019;59 doi: 10.1016/j.ultsonch.2019.104744. [DOI] [PubMed] [Google Scholar]
- 34.Wongwuttanasatian T., Jookjantra K. Effect of dual-frequency pulsed ultrasonic excitation and catalyst size for biodiesel production. Renew. Energy. 2020;152:1220–1226. doi: 10.1016/j.renene.2020.01.149. [DOI] [Google Scholar]
- 35.Matafonova G., Batoev V. Dual-frequency ultrasound: Strengths and shortcomings to water treatment and disinfection. Water Res. 2020;182 doi: 10.1016/j.watres.2020.116016. [DOI] [PubMed] [Google Scholar]
- 36.Wang Y.-Y., Yan J.-K., Rashid M.T., Ding Y., Chikari F., Huang S., Ma H. Dual-frequency sequential ultrasound thawing for improving the quality of quick-frozen small yellow croaker and its possible mechanisms. Innov. Food Sci. Emerg. Technol. 2021;68 doi: 10.1016/j.ifset.2021.102614. [DOI] [Google Scholar]
- 37.Gogate P.R., Wilhelm A.M., Pandit A.B. Some aspects of the design of sonochemical reactors. Ultrason. Sonochem. 2003;10:325–330. doi: 10.1016/S1350-4177(03)00103-2. [DOI] [PubMed] [Google Scholar]
- 38.Gogate P.R., Sutkar V.S., Pandit A.B. Sonochemical reactors: Important design and scale up considerations with a special emphasis on heterogeneous systems. Chem. Eng. J. 2011;166(3):1066–1082. doi: 10.1016/j.cej.2010.11.069. [DOI] [Google Scholar]
- 39.Servant G., Laborde J.L., Hita A., Caltagirone J.P., Gérard A. On the interaction between ultrasound waves and bubble clouds in mono- and dual-frequency sonoreactors. Ultrason. Sonochem. 2003;10:347–355. doi: 10.1016/S1350-4177(03)00105-6. [DOI] [PubMed] [Google Scholar]
- 40.Tangsopa W., Thongsri J. A dual frequency ultrasonic cleaning tank developed by transient dynamic analysis. Appl. Sci. 2021;11:1–20. doi: 10.3390/app11020699. [DOI] [Google Scholar]
- 41.Lebon G.S.B., Tzanakis I., Pericleous K., Eskin D. Experimental and numerical investigation of acoustic pressures in different liquids. Ultrason. Sonochem. 2018;42:411–421. doi: 10.1016/j.ultsonch.2017.12.002. [DOI] [PubMed] [Google Scholar]
- 42.Prinn A.G. On Computing Impulse Responses from Frequency-Domain Finite Element Solutions. J. Theor. Comput. Acoust. 2021;29(01):2050024. doi: 10.1142/S2591728520500243. [DOI] [Google Scholar]
- 43.Manickam S., Zainal Abidin N.B., Parthasarathy S., Alzorqi I., Ng E.H., Tiong T.J., Gomes R.L., Ali A. Role of H2O2 in the fluctuating patterns of COD (chemical oxygen demand) during the treatment of palm oil mill effluent (POME) using pilot scale triple frequency ultrasound cavitation reactor. Ultrason. Sonochem. 2014;21(4):1519–1526. doi: 10.1016/j.ultsonch.2014.01.002. [DOI] [PubMed] [Google Scholar]
- 44.Tiong T.J., Liew D.K.L., Gondipon R.C., Wong R.W., Loo Y.L., Lok M.S.T., Manickam S. Identification of active sonochemical zones in a triple frequency ultrasonic reactor via physical and chemical characterization techniques. Ultrason. Sonochem. 2017;35:569–576. doi: 10.1016/j.ultsonch.2016.04.029. [DOI] [PubMed] [Google Scholar]
- 45.J.H. Ginsberg Acoustics-A Textbook for Engineers and Physicists 1st ed., 2018 Springer International Publishing 10.1007/978-3-319-56847-8.
- 46.Wijngaarden L.V. One-Dimensional Flow of Liquids Containing Small Gas Bubbles. Annu. Rev. Fluid Mech. 1972;4(1):369–396. doi: 10.1146/fluid.1972.4.issue-110.1146/annurev.fl.04.010172.002101. [DOI] [Google Scholar]
- 47.Lebon G.S.B., Tzanakis I., Djambazov G., Pericleous K., Eskin D.G. Numerical modelling of ultrasonic waves in a bubbly Newtonian liquid using a high-order acoustic cavitation model. Ultrason. Sonochem. 2017;37:660–668. doi: 10.1016/j.ultsonch.2017.02.031. [DOI] [PubMed] [Google Scholar]
- 48.Fang Y., Yamamoto T., Komarov S. Cavitation and acoustic streaming generated by different sonotrode tips. Ultrason. Sonochem. 2018;48:79–87. doi: 10.1016/j.ultsonch.2018.05.011. [DOI] [PubMed] [Google Scholar]
- 49.Chu J.K., Tiong T.J., Chong S., Asli U.A. Investigation on different time-harmonic models using FEM for the prediction of acoustic pressure fields in a pilot-scale sonoreactor. Chem. Eng. Sci. 2022;247 doi: 10.1016/j.ces.2021.116912. [DOI] [Google Scholar]
- 50.Burdin F., Tsochatzidis N.A., Guiraud P., Wilhelm A.M., Delmas H. Characterisation of the acoustic cavitation cloud by two laser techniques. Ultrason. Sonochem. 1999;6(1-2):43–51. doi: 10.1016/S1350-4177(98)00035-2. [DOI] [PubMed] [Google Scholar]
- 51.Labouret S., Frohly J. Bubble size distribution estimation via void rate dissipation in gas saturated liquid. Application to ultrasonic cavitation bubble fields. Eur. Phys. J. Appl. Phys. 2002;19(1):39–54. doi: 10.1051/epjap:2002047. [DOI] [Google Scholar]
- 52.Pflieger R., Bertolo J., Gravier L., Nikitenko S.I., Ashokkumar M. Impact of bubble coalescence in the determination of bubble sizes using a pulsed US technique: Part 1 – Argon bubbles in water. Ultrason. Sonochem. 2021;73 doi: 10.1016/j.ultsonch.2021.105532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Dogan H., Popov V. Numerical simulation of the nonlinear ultrasonic pressure wave propagation in a cavitating bubbly liquid inside a sonochemical reactor. Ultrason. Sonochem. 2016;30:87–97. doi: 10.1016/j.ultsonch.2015.11.011. [DOI] [PubMed] [Google Scholar]
- 54.Dähnke S.W., Keil F.J. Modeling of linear pressure fields in sonochemical reactors considering an inhomogeneous density distribution of cavitation bubbles. Chem. Eng. Sci. 1999;54(13-14):2865–2872. doi: 10.1016/S0009-2509(98)00340-6. [DOI] [PubMed] [Google Scholar]
- 55.Tiong T.J., Chandesa T., Yap Y.H. Comparison of sonochemiluminescence images using image analysis techniques and identification of acoustic pressure fields via simulation. Ultrason. Sonochem. 2017;36:78–87. doi: 10.1016/j.ultsonch.2016.11.003. [DOI] [PubMed] [Google Scholar]
- 56.Silberman E. Sound Velocity and Attenuation in Bubbly Mixtures Measured in Standing Wave Tubes. J. Acoust. Soc. Am. 1957;29(8):925–933. doi: 10.1121/1.1909101. [DOI] [Google Scholar]