Abstract
Conformational sampling of biomolecules using molecular dynamics simulations often produces a large amount of high dimensional data that makes it difficult to interpret using conventional analysis techniques. Dimensionality reduction methods are thus required to extract useful and relevant information. Here, we devise a machine learning method, Gaussian mixture variational autoencoder (GMVAE), that can simultaneously perform dimensionality reduction and clustering of biomolecular conformations in an unsupervised way. We show that GMVAE can learn a reduced representation of the free energy landscape of protein folding with highly separated clusters that correspond to the metastable states during folding. Since GMVAE uses a mixture of Gaussians as its prior, it can directly acknowledge the multi-basin nature of the protein folding free energy landscape. To make the model end-to-end differentiable, we use a Gumbel-softmax distribution. We test the model on three long-timescale protein folding trajectories and show that GMVAE embedding resembles the folding funnel with folded states down the funnel and unfolded states outside the funnel path. Additionally, we show that the latent space of GMVAE can be used for kinetic analysis and Markov state models built on this embedding produce folding and unfolding timescales that are in close agreement with other rigorous dynamical embeddings such as time independent component analysis.
I. INTRODUCTION
In recent years, computer simulations of biomolecular systems have gained huge attention due to advances in theoretical methods, algorithms, and computer hardware. This enabled efficient exploration of processes in atomic scale using molecular dynamics (MD) simulations.1 In a MD simulation, one integrates Newton’s equations of motion where the forces between atoms in the system are described by a parameterized force field. Exploration of the high-dimensional space typically requires long-timescale simulations or the use of some enhanced sampling techniques.2,3 These simulations usually generate a large amount of high dimensional data, making analyzing the important features of protein folding such as free energy landscape (FEL) and identifying metastable states a challenging task.4 Therefore, dimensionality reduction techniques are often used to describe the processes such as folding and conformational transitions of proteins.5
The ideal FEL should consist of heavily clustered data points, where each cluster is positioned in a local free energy minimum and corresponds to long-lived metastable states separated by kinetic bottlenecks (i.e., free energy barriers).6 This ideal FEL is the cornerstone of many kinetic models that describe the dynamics of the system using, for example, Markov state models (MSMs).7–9 Traditional methods to capture FEL rely on identifying relevant collective variables (CVs) that are well-suited to describe the physical processes or to distinguish different states. However, finding the right collective variables for the system of interest requires a physical/chemical intuition about the process of interest.10,11 This makes it necessary to define a low-dimensional representation of the system that can capture the essential degrees of freedom or the important CVs of the system of interest. There are various methods for dimensionality reduction and finding optimal representation of complex FEL, such as principal component analysis (PCA),12 time independent component analysis (TICA),13,14 Isomap,15 sketch map,16 and diffusion map.17 PCA-based methods assume an underlying linear manifold, which is generally not correct. Some of the nonlinear manifold methods such as Isomap assume data to be isomorphic to a hyperplane, which leads to topological instabilities. Moreover, these methods involve computation of distances (geodesic or other kernel based) between all pairs of points, which makes it unscalable to larger MD simulation trajectories. In diffusion maps, one needs to calculate the Gaussian kernels, which can be computationally expensive and not scalable to large-scale MD simulation data.
Machine learning (ML) has recently emerged as a powerful alternative tool for learning informative representations, and in particular, variational autoencoder (VAE) have shown great potential for unsupervised representation learning.18 An autoencoder has two parts: encoder and decoder. The encoder network reduces the input data to a low-dimensional latent space, and the decoder maps the latent representation back to the original data. In the VAE framework, regularization is added to the model by forcing the latent space to be similar to a pre-defined probability distribution (e.g., Gaussian), which is called a prior. VAEs have recently been used for CV discovery in MD simulations,19–21 enhanced sampling,22,23 and dimensionality reduction methods.24,25
In a simple VAE, the prior is a simple standard distribution, which can lead to over-regularization of the posterior distribution and results in posterior collapse.26 This makes the output of the decoder almost independent of the latent embedding and can result in poor reconstruction and highly overlapping clusters in the latent space.24 On the other hand, a Gaussian prior is limited since the learnt representation can only be unimodal and cannot capture multimodal nature of data such as protein folding simulation where there exist multiple metastable states during the folding process.27
In this work, we employ a Gaussian mixture variational autoencoder (GMVAE) that directly acknowledges the multimodal nature of protein folding simulations and can construct the ideal multi-basin FEL. This is achieved by modeling the latent space as a mixture of Gaussians by using a categorical variable that identifies which mode each data point comes from. Therefore, GMVAE model simultaneously performs dimensionality reduction and clustering.28 The features in our model are the normalized distance map between Cα atoms of the protein. We test our model on three long-timescale protein folding simulations taken from the work of Lindorff-Larsen et al.29 These include Trp-cage (208 µs), BBA (325 µs), and villin (125 µs). We show that the model can learn the funnel-shaped landscape of protein folding and cluster the conformational space with high accuracy that corresponds to different structural features of protein. Furthermore, we show that despite the fact that the GMVAE embedding does not make use of any dynamical information, it is able to describe the kinetics of protein folding and the folding and unfolding timescales obtained by making a Markov model on this embedding are in close agreement with other works using a rigorous dynamical model to describe the kinetics.
II. METHODS
Variational inference methods convert an intractable inference problem into an optimization one. While the classical variational methods are limited to conjugate priors and likelihood, VAEs allow for the use of arbitrary function approximators (i.e., neural networks) as the conditional posterior.18
VAEs can be approached from two different perspectives: variational inference and neural networks. In the variational inference, the main idea is to learn a distribution in the latent space that truly captures the distribution of the dataset. In particular, given a dataset x, the goal of variational inference is to infer the latent space representation z, i.e., to accurately model p(z|x). The Bayes theorem gives the relation between the posterior p(z|x), the prior p(z), and the likelihood p(x|z) as
| (1) |
The denominator in this equation p(x) is called the evidence, which requires marginalization over all latent variables and thus is intractable. Therefore, in variational inference, one seeks an approximate posterior qϕ(z|x) with learnable parameters ϕ and minimizes the Kullback–Leibler divergence (KL) between the approximate and the true posterior. The KL divergence shows the difference between two probability distributions and is defined as
| (2) |
By re-writing this equation and using the Bayes rule, we get the following:
| (3) |
Due to Jensen’s inequality, the KL divergence is a non-negative term, which makes the last term in the equation called evidence lower bound (ELBO) to act as a lower bound for the log-likelihood of the evidence,
| (4) |
Therefore, we can now write Eq. (3) as
| (5) |
This has the implication that minimizing the KL divergence or maximizing the log-likelihood of evidence can done by maximizing the ELBO.
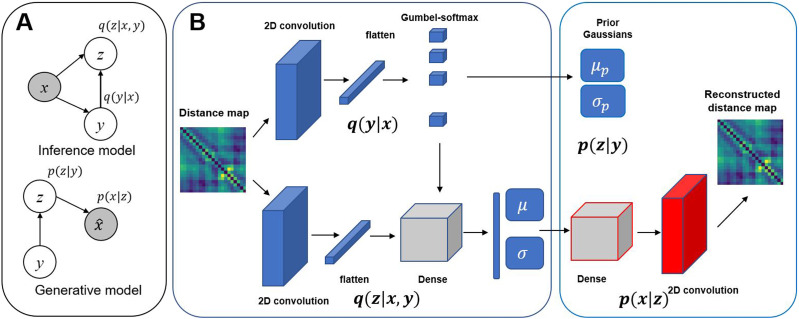
The graphical model of GMVAE is shown in Fig. 1(a). In the generative part (decoder) of the network, a sample z is drawn from the latent space distribution pβ(z|y) of cluster y, which is parameterized by parameters β using the decoder part of the neural network. This can be used to generate the conditional distribution pθ(x|z) parameterized by another neural network θ. The generative process for GMVAE can be written as
| (6) |
| (7) |
| (8) |
| (9) |
FIG. 1.
(a) Graphical model for inference and generative parts of GMVAE. The gray circles represent the observed data (b) Schematic of the GMVAE architecture. In this architecture, q(y|x) refers to cluster assignment probabilities, q(z|x, y) is the approximate posterior, and μ and σ are the mean and variance of each Gaussian in the approximate posterior of the encoder network. p(z|y) is the prior Gaussian, and μp and σp are the mean and Gaussians of the prior Gaussians in the decoder network.
In these equations, π = 1/K is the uniform categorical distribution, where K is the number of clusters, and Cat(π) refers to the categorical distribution for discrete variable y. N() refers to the normal distribution, where μθ, μβ, , and are the means and variances learned by the neural nets parameterized by θ and β. Variational inference of GMVAE can be done by maximizing the ELBO, which can be written as
| (10) |
The approximate posterior of the inference model qϕ,ψ(z, y|x) can be factorized into two distributions as follows:
| (11) |
where qϕ(y|x) gives the cluster assignment probabilities, and thus, . qψ(z|x, y) is a Gaussian mixture where the parameters of each Gaussian are learned by the encoder part of neural network. In this model, categorical variable y represents a discrete node for each categorical distribution, which cannot be backpropagated and thus is substituted with a Gumbel-softmax distribution, which approximates this categorical distribution with a continuous one. This can be written as
| (12) |
where τ is called the temperature parameter that controls the smoothness of distribution where at small temperatures samples are close to one-hot encoded and at large temperatures the distribution is more smooth. gi are the samples drawn from a Gumbel (0,1) distribution.
Using the generative and inference model, the ELBO can be written as
| (13) |
| (14) |
The second term in the loss is called the cross-entropy and the last term is the mean squared error between the true and the reconstructed data.
A. Model parameters
The model architecture is shown in Fig. 1(b). The GMVAE model was implemented in Tensorflow. Convolutional layers were applied along with pooling for their ability to recognize features in images. The exponential linear unit (Elu) activation function was used in each layer, and a softmax activation was used for the cluster assignment probability. The means and variances of distributions were obtained using no activation and softplus activation, respectively. Adam was used as an optimizer in all models.30 We have optimized the hyperparameters of the model based on the reconstruction loss. The chosen hyperparameters for each protein are shown in Table I. During training, we split the data into a train/validation set with a fraction of 0.8 for the training set and 0.2 for the validation set. The latent space dimension was chosen using a grid search for minimizing the reconstruction loss of the validation set for each protein.
TABLE I.
Chosen hyperparameters for each protein.
| Systems | Number of layers | Number of neurons | Latent dimension | Number of clusters | Batch-size | Temperature | Kernel size | Learning rate | Number of filters | Pooling sizes |
|---|---|---|---|---|---|---|---|---|---|---|
| Trp-cage | 2 | 64 | 5 | 8 | 5000 | 0.1 | [3,3] | 0.001 | [64,64] | [1,1] |
| BBA | 2 | 64 | 6 | 9 | 5000 | 0.1 | [3,3] | 0.001 | [64,64] | [2,2] |
| villin | 3 | 64 | 5 | 6 | 2500 | 0.05 | [3,3,3] | 0.001 | [64,64,32] | [2,2,1] |
The number of clusters is another hyperparameter that must be specified for training the model. Varolgüneş et al.25 used a thresholding scheme to pick the clusters that have class probabilities more than a pre-defined cutoff. In this paper, we adapted a similar procedure. To select this hyperparameter, we first started with a random number of clusters (e.g., 10) and computed the membership probability of each point in the input. Then, we used a cutoff value (0.95) to count the number of clusters with membership probabilities higher than the cutoff. We then trained the model with the recovered number of clusters from the previous training. We found that this number is highly robust to the other hyperparameters of the model. We also found that after the first round of training, the number of recovered clusters do not change using the same probability assignment cutoff. Each model was trained for 100 epochs of training. The temperature parameter in Gumbel-softmax controls the smoothness of distribution. We also tried annealing the temperature parameter starting with a high value (5) and lowering it to 0.1 during the first 40 epochs of training and then keeping it the same for the rest of training. However, we found that the model would diverge after a few epochs of training and having a fixed and small value of temperature parameter gives the best results. Since the GMVAE model gives a probabilistic cluster assignment that is the probability of each data point belonging to each cluster (fuzzy-clustering), we used a k-nearest neighbor method to compute a hard-cluster assignment using the neighborhood of each point in the embedding. For the kinetic analysis, we used the PyEMMA package31 to build the transition matrix. In each case, the embedding was discretized using 500 K-means cluster points and the transition probability matrix was built by counting the number of transitions between different states at lag-time τ. The implied timescales are computed from the eigenvalues of the transition probability matrix,
| (15) |
To test the Markovianity of the transition matrix, the implied timescales are plotted against the lag-time and then the smallest τ is chosen such that the implied timescales have converged. A coarse-grained transition matrix is later built by assigning the K-means points to the closest GMVAE clusters, yielding a coarse-grained view of dynamics. The folding and unfolding timescales are obtained from this coarse-grained matrix.
III. RESULTS
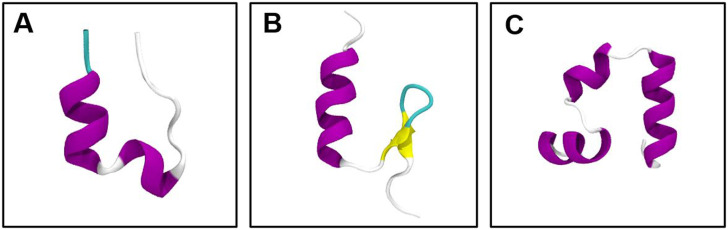
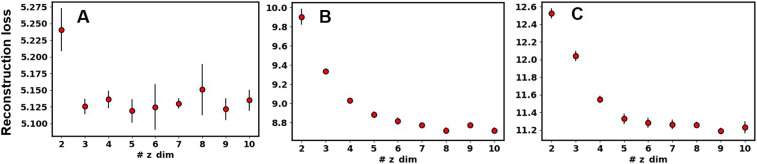
Here, we tested the performance of the GMVAE model for dimensionality reduction and clustering of three protein folding systems, including Trp-Cage (pdb: 2JOF),32 BBA (pdb: 1FME),33 and villin (pdb: 2F4K).34 The native folded structure of these proteins is shown in Fig. 2. We show that the GMVAE embedding captures the free energy landscape of these proteins with well-separated clusters. We analyze the structural properties of each cluster and show that each cluster corresponds to a different structural feature in the protein. The total loss, cross-entropy loss, and reconstruction loss show a decreasing behavior for both the train and validation sets in all three proteins and are shown in the supplementary material, Figs. S1–S3. For visualizing the latent space of GMVAE, we used a low-dimensional latent space (2 or 3) and show that this embedding mimics the funnel-shaped landscape of protein folding where the folded state resides down the funnel and the unfolded states are outside the funnel. For the rest of our analysis on each protein, we used an optimized number for latent-space dimension based on a cross-validated reconstruction loss. Figure 3 shows a cross-validated reconstruction loss as a function of latent space dimension for each protein. Higher dimensional embeddings result in better reconstruction loss for all proteins. This means, to capture the complex protein folding landscape, we need a high dimensional latent space in our GMVAE model. To test whether the GMVAE clusters give meaningful structural information, we sampled 5000 data points from the center of each cluster and compared the distribution of root mean squared deviations (RMSDs) of the whole protein and specific domains of each cluster to the folded state. Moreover, we show that building a Markov model on the embedding of GMVAE produces folding and unfolding timescales that are in close agreement with the timescales obtained from constructing a Markov model on a dynamical embedding such as TICA.
FIG. 2.
Native folded structure of studied proteins. (a) Trp-cage, (b) BBA, and (c) villin headpiece.
FIG. 3.
Reconstruction loss vs latent space dimension for (a) Trp-cage, (b) BBA, and (c) villin headpiece.
A. Trp-cage
As the first example, we test our GMVAE model on an ultra-long 208 µs explicit solvent simulation of the K8A mutation of the 20-residue Trp-cage TC10b at 290 K by Lindorff-Larsen et al.29 Numerous experimental and computational studies have been performed on Trp-cage.35–37 The folded state of Trp-cage shown in Fig. 2(a) contains an α-helix (residues 2–8), a 310-helix, and a polyproline II helix, and the tryptophan residue is caged at the center of the protein. Two different folding mechanisms have been identified for Trp-cage to date:38 one where Trp-cage goes through a hydrophobic collapse into a molten globule followed by the formation of N-terminal helix and the native core (nucleation-condensation) and second the pre-formation of the helix from the extended conformation and the joint formation of the 310-helix and hydrophobic core (diffusion–collision). The second mechanism is identified as the dominant folding pathway for Trp-cage.
Here, we investigated Trp-cage folding trajectories using the GMVAE model for embedding and clustering. The features are the normalized distances between the Cα atoms of Trp-cage in the trajectories. Hyperparameter K that identifies the number of clusters is unknown a priori. To choose a reasonable number for each cluster, we started from a higher estimate for the number of clusters (e.g., 10) and trained the model. Then, we used a cutoff (0.95) to find the number of clusters with membership probability more than the cutoff value. We found that only 8 out of 10 clusters had higher than 0.95 membership probability. Next, we trained the model again with eight clusters. At this stage, we found that all clusters had membership probabilities higher than our original cutoff. Moreover, we found the same number of clusters regardless of the other hyperparameters for the model such as the number of layers. Although the 2D or 3D latent spaces are used for visualization purposes, higher latent space embeddings are needed to describe the folding energy landscape more accurately. To choose an optimum latent-space dimension, we computed a cross-validated reconstruction loss for different values of latent space dimension from 2 to 10. The results for Trp-cage are shown in Fig. 3(a). We chose a five-dimensional latent space for clustering this protein. Other hyperparameters such as the batch-size, learning rate, number of layers, temperature of Gumbel-softmax, kernel size, number of filters, and pooling sizes were optimized using a grid search method based on reconstruction loss. The chosen hyperparameters for each protein are listed in Table I. The total, reconstruction, and cross-entropy losses using the determined hyperparameters in Table I are shown in Fig. S1. Reconstruction and cross-entropy losses for both training and validation data show a decreasing behavior, demonstrating the convergence of the model after 100 epochs of training.
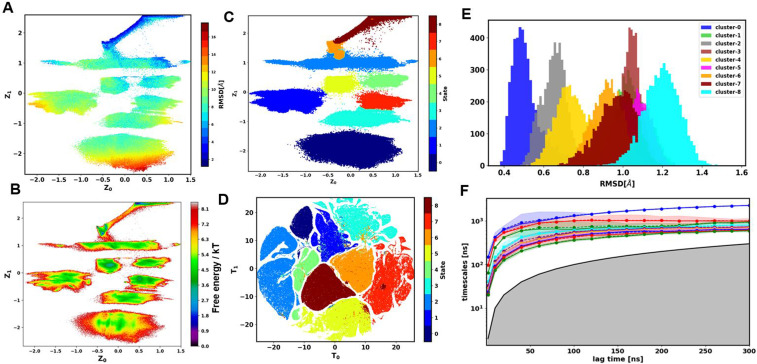
Figure 4(a) shows the three-dimensional embedding (z-dim = 3) of Trp-cage trajectories colored based on the RMSD with respect to the crystal structure. The gradual change in color from high RMSD (red) to low RMSD (blue) in the landscape demonstrates that the low-dimensional embedding can capture the protein folding process. Figure 4(b) shows the first two dimensions of the latent embedding colored based on RMSD. The high RMSD and low RMSD regions are well separated on this landscape. The folded state has a narrow distribution and is the narrow wedge of the folding funnel. We computed the free energy landscape on the first two dimensions of the latent space [Fig. 4(c)]. The free energy landscape shows multiple wells that are separated by diffuse regions in between them. The wells correspond to the centers of GMVAE clusters, and the diffuse region is the transition region between different conformational states. Hard-cluster assignment in the 3D latent space is shown in Fig. S4(A). Next, based on Fig. 3(a), we used a five-dimensional latent space for clustering Trp-cage. To visualize the 5D latent space, we only take data points with membership assignment probabilities higher than 0.75 and used t-distributed stochastic neighborhood embedding (T-SNE)39 for transforming the five-dimensional embedding into two dimensions. The T-SNE results for Trp-cage are shown in Fig. 4(d). The clusters are highly separated on this landscape. To ensure that GMVAE clusters corresponds to different structures during folding, we sampled 5000 points from the center of each cluster and computed the RMSD distribution of the protein with respect to the folded state [Fig. 4(e)]. The folded state (cluster 5) has a narrow distribution, while other unfolded and misfolded states have wider distributions with higher RMSD values. Representative structures of each cluster are shown in Fig. 5. We have also computed the RMSD distribution of residues 11–15 comprising the 310-helix for different states. The results are shown in Fig. S4(B).
FIG. 4.
Results of GMVAE for Trp-cage. (a) 3D embedding (zdim = 3) colored with RMSD with respect to the folded state. (b) First two dimensions of latent space (zdim = 3) colored with RMSD. (c) Free energy landscape of the first two dimensions of embedding (zdim = 3). (d) TSNE visualization of 5D latent space colored based on the argmax of their cluster assignment probabilities (only points with more than 0.75 membership probability are shown). (e) RMSD distribution of Trp-cage in different clusters. (f) Implied timescale (ITS) plot for MSM construction.
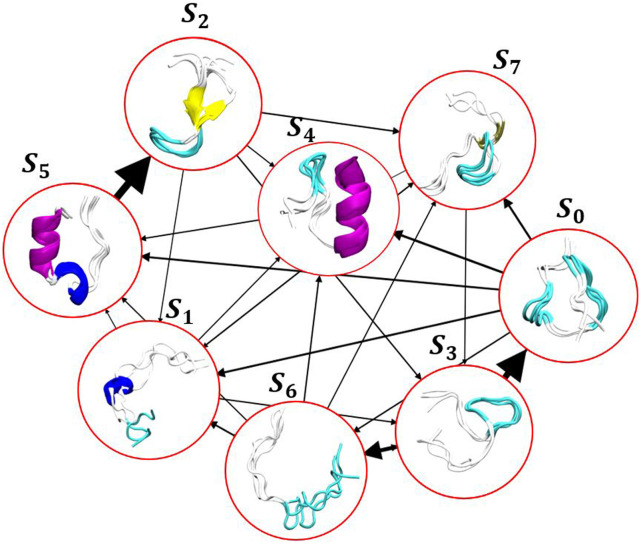
FIG. 5.
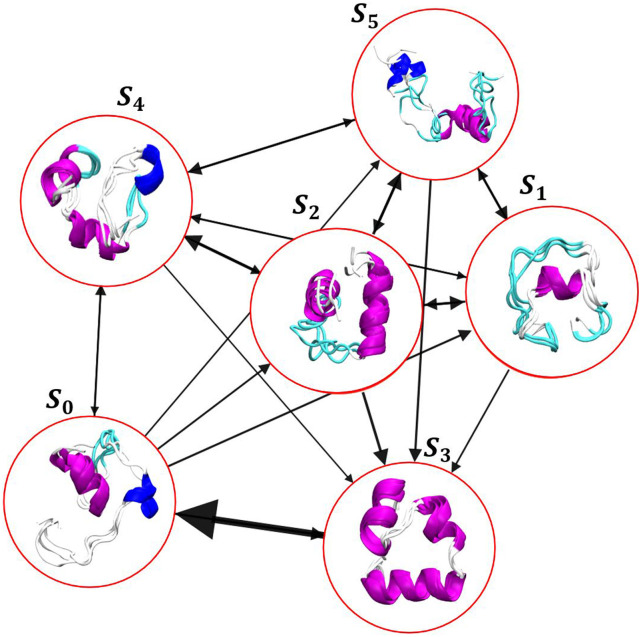
Trp-cage folding transitions: the thickness of lines corresponds to the transition probability between the two states. Transitions with probabilities less than 0.05 are not shown for clarity.
Next, we built a MSM on the 5D embedding by choosing 300 K-means points and discretizing the trajectories based on this clustering on the GMVAE embedding. The implied timescales for this transition matrix are shown in Fig. 4(f). Based on this, we chose a lag-time of 160 ns to build the MSM. To compute the mean-first passage time (MFPT) between different GMVAE clusters, we coarse-grained the 300-state transition matrix into eight states that corresponded to the GMVAE clusters. The folding and unfolding times based on the coarse-grained Markov model are 11.62 and 4.85 µs, respectively. The folding and unfolding times are in good agreement with the values reported by Lindorff-Larsen et al.29 who reported 14.4 and 3.1 µs as the folding and unfolding times of this protein using the average lifetime in the folded and unfolded states observed in trajectories using a contact based definition of folded and unfolded states. A visualization of the eight metastable states found by GMVAE model is shown in Fig. 5. The arrows between different states show the transition between different conformations, and the arrow thickness relates to the transition probability between different clusters obtained by coarse gaining the Markov model into eight GMVAE clusters. The native folded state S5 accounts for about 18% of the total distribution, and the unfolded ensemble represents the remaining 82%. Folding mostly proceeds via the molten globule state S0 or the near-folded state S4.
B. BBA
The second example is the ββα fold protein (BBA), which is a 28-residue fast folding protein. The nuclear magnetic resonance (NMR) structure of this protein is shown in Fig. 2(b). This protein contains an antiparallel β sheet at the N terminal and a helical conformation at its C terminus. For finding the optimum number of clusters, we first trained the model with 10 clusters and only nine clusters were recovered using a 0.95 cutoff. Next, we trained the model with nine clusters and found that all the clusters have probabilities higher than our cutoff. We also observed that training the model with different hyperparameters would yield the same number of clusters. To better visualize the latent space, we trained the model with two dimensions. The resulting latent space colored based on RMSD with respect to folded state is shown in Fig. 6(a). Unfolded and folded states are well separated on this 2D embedding. The free energy landscape on this embedding is shown in Fig. 6(b). It is observed that all clusters reside in the wells of the free energy landscape. There are also some diffuse and high energy states between the wells, which correspond to transitions between different metastable states. These regions are also where the model is least certain about cluster assignment. To transform the fuzzy clustered output of GMVAE into hard-cluster assignment, we used a k-nearest neighbor algorithm and assigned each point to the most likely cluster in its neighborhood using 500 neighbors. The result is shown in Fig. 6(c), which exhibits highly separated and non-overlapping clusters in the 2D embedding. In this embedding, state 8 corresponds to the folded state and state 6 is the near-folded (misfolded) state, and all the other states are the unstructured or unfolded conformations. The highly non-overlapping clusters in the GMVAE landscape show the ability of this model to separate a vastly diverse set of protein conformations from a protein folding trajectory.
FIG. 6.
(a) 2D embedding of BBA colored based on RMSD to the folded state. (b) 2D free energy landscape of BBA based on 2D embedding. (c) Clusters in 2D embedding of BBA using kNN for cluster assignment. (d) TSNE visualization of 6D latent space colored based on the argmax of their cluster assignment probabilities (only points with more than 0.75 membership probability are shown). (e) Histograms of RMSD for different clusters. (f) ITS plot based on 6D latent space.
The 2D embedding latent space cannot fully capture the complex folding landscape. Therefore, we optimized the latent space dimension based on a cross-validated reconstruction loss in Fig. 3(b). Next, based on this result, we used a six-dimensional latent space for the rest of our analysis. The T-SNE visualization of this six-dimensional landscape is shown in Fig. 6(d). We have studied the structural properties of each cluster by sampling 5000 data points from the center of each cluster. Figure 6(e) shows the distribution of RMSD of each cluster with respect to the folded state. Cluster 0 is the folded state with the sharpest and lowest RMSD distribution. Other clusters have wider and higher RMSD distributions and correspond to misfolded or unfolded states. Representative structures for each cluster are shown in Fig. 7. We also investigated the details of structural features for each cluster by calculating the RMSD distribution of specific domains in BBA. Figure S5 shows the distribution of RMSD of the antiparallel β-sheet (residues 7–14) (left panel) and the α-helical (right figure) parts of BBA (residues 16–26) with respect to the folded structure. The folded state (cluster 0) has the lowest RMSD in both domains, while cluster 4 has a low RMSD in the antiparallel β-sheet domain but a higher RMSD in the α-helical domain.
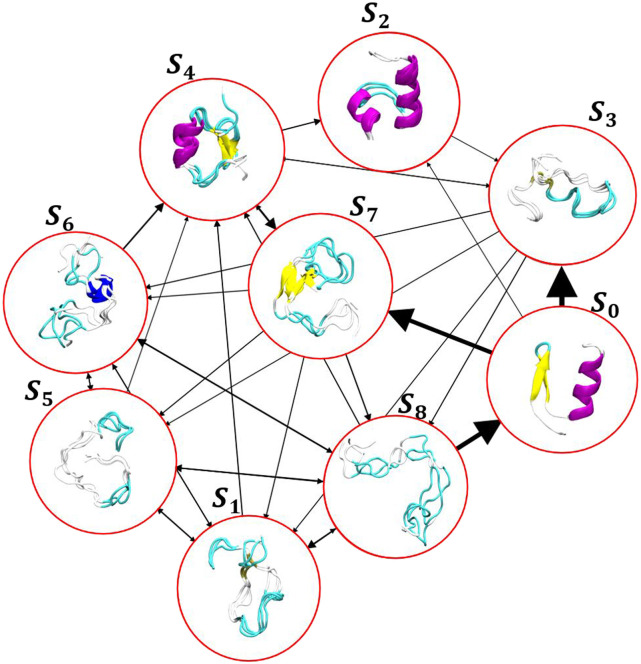
FIG. 7.
BBA transitions: the arrows show the transition between different clusters, and the arrow thickness represents the transition probability between the corresponding clusters. Transition with probabilities less than 0.1 is not shown for clarity.
To perform a Markov model on this embedding, we first clustered this embedding using 500 K-means and discretized the trajectories based on the points. To choose the proper lag-time for the MSM model, we plotted the implied timescales [Fig. 6(f)] and picked 220 ns and built the transition probability matrix. Next, to compute the transition timescale between different GMVAE clusters, we assigned each of the 500 K-means clusters to the closest cluster in GMVAE and then computed the mean-first passage times (MFPTs) between clusters. The folding and unfolding timescales calculated here are 15.2 and 7.42 µs, respectively, which are in close agreement with the values reported by Lindorff-Larsen et al.29 Figure 7 illustrates the representative structures of each cluster, which are sampled from the mean of each distribution in the latent space. The transition between different states is shown with the arrow where the width of each arrow represents the transition probability.
C. Villin
The last example is a 35-residue villin-headpiece subdomain, which is one of the smallest proteins that can fold autonomously. It is composed of three α-helices denoted as helix 1 (residues 4–8), helix 2 (residues 15–18), and helix 3 (residues 23–32) and a compact hydrophobic core. The observed experimental folding timescale for wild-type villin is about 4 µs, and the replacement of two lysine residues (Lys65 and Lys70) with uncharged Norleucine (Nle) yields a mutant with a folding time of less than one microsecond.40 The folding landscape of the villin double mutant has been studied by both experiments and computer simulations.41–44 Folding a double mutant of villin was studied using long-timescale molecular dynamics by Lindorff-Larsen et al. and is used here.29
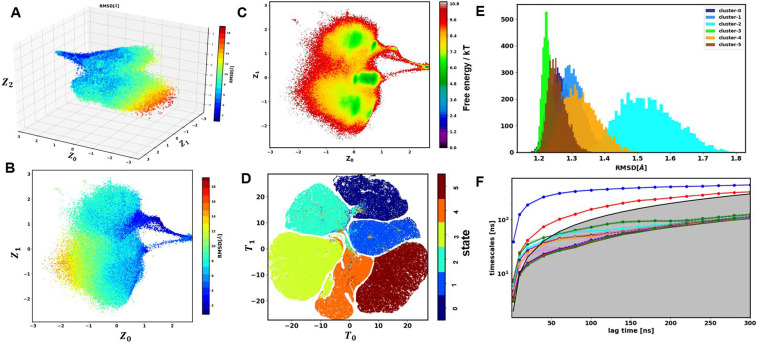
The number of clusters for villin was found as described for other proteins. We started with seven clusters and found that only six clusters were recovered using a 0.95 cutoff for cluster probability. The training and validation losses for this protein are shown in Fig. S3. The latent embedding using a 3D latent space is shown in Fig. 8(a) where each point is painted based on RMSD with respect to the folded structure. The first two dimensions of this 3D embedding colored based on RMSD are shown in Fig. 8(b). Figure 8(c) shows the free energy landscape on the first two dimensions of the embedding. Due to fast transitions between different states in villin, unlike BBA, the FEL has larger diffuse regions with smaller basins at the center of each cluster. The presence of large diffuse regions on this landscape means that the metastable states in the folding of villin are short lived and transition between each other quickly. The optimum latent space dimension for villin was found to be 5 [Fig. 3(c)]. Other hyperparameters for villin were optimized based on a cross-validated reconstruction loss, and the chosen hyperparameters are shown in Table I. The T-SNE visualization of this 5D latent space is shown in Fig. 8(d), which shows highly separated clusters. Figure 8(e) shows the RMSD distribution of each cluster in 5D latent space with respect to the folded structure. Cluster 3 corresponds to the folded state where the RMSD distribution is the narrowest and smallest. Figure 9 shows the representative structure of each cluster in 5D latent space. Structural properties of specific domains in different clusters were studied using the RMSD distribution of helices 1, 2, and 3 with respect to the folded structure. The results are shown in Fig. S6. Each cluster has a different distribution for the helical residues of the protein, which are Gaussian. Cluster S0 has a low RMSD for helices 1 and 2 but higher RMSD values for helix 3. Secondary structure calculations showed that S0 has folded helix 1 and helix 2 but unfolded helix 3. Most clusters have folded or near-folded helix 1, except for cluster S4. Cluster S3 is the folded state where are helices are folded with more than 80% probability. Helix 3 is only folded in S3 and S5, which shows the importance of this helix in proper folding of villin.
FIG. 8.
GMVAE embedding results for villin. (a) 3D latent space (zdim = 3) colored with RMSD. (b) First two dimensions of 3D latent space colored based on RMSD. (c) FEL based on first two dimensions of latent space. (d) TSNE plot for 5D latent space (only points with more than 0.75 membership probability are shown). (e) Distribution of RMSD for villin with respect to the folded state. (f) ITS plot for Markov model construction based on 5D embedding.
FIG. 9.
Transitions between different states in villin-headpiece simulation. The thickness of the arrows corresponds to the transition probability between the two states. Transitions with less than 0.1 probability are now shown for clarity.
Next, we built a Markov model on this embedding by choosing 500 K-means cluster points for discretizing the trajectories. The implied timescales for this discretization are shown in Fig. 8(d). A lag-time of 220 ns was chosen to build the transition matrix. The 500 K-means clusters were then assigned to their nearest GMVAE clusters to build a coarse-grained transition matrix. The folding and unfolding times obtained based on the constructed MSM on this embedding are 2.25 and 1.54 µs, respectively, which are in good agreement with the values reported by Lindorff-Larsen et al. (2.8 µs) and others building a Markov model using TICA.29,45,46 Figure 9 shows the structures of each cluster and the transition probability between different states. The highest transition probability S3 → S0 corresponds mostly to unfolding of helix 3. Therefore, proper folding of helix 3 leads to the formation of native contacts and native helices. Piana et al.47 studied the double mutant (Nle/Nle) of villin and found a sparsely populated intermediate that involved the formation of helix 3 and the turn between helices 2 and 3. This corresponds to cluster S2 in our analysis that has near-folded helix 3. Mori and Saito48 studied the molecular mechanics for folding of villin and the Nle/Nle double mutant. They found that the mutation Lys → Nle speeds up the folding transition by rigidifying helix 3.
D. Discussion and conclusion
Here, we demonstrated the use of a deep learning algorithm, Gaussian mixture variational autoencoder (GMVAE), to help analyze and interpret the highly complex landscape of protein folding trajectories. The variational autoencoder framework has been extensively used in the field of molecular dynamics simulations for dimensionality reduction,24,25 enhanced sampling,22,23 and collective variable discovery.19–21 Noe and co-workers proposed a time-lagged autoencoder (TAE) that can find the low-dimensional embedding for high dimensional data while capturing the slow dynamics of the underlying processes.49 Although Chen et al.50 showed that TAE is limited in finding the optimal embedding for the dynamical system, in general, it finds a mixture of slow and maximum variance modes. Ward et al. introduced DiffNets, which are deep autoencoders that identify structural features for predicting biochemical differences between protein variants from MD simulation trajectories.51
The GMVAE model acknowledges the multi-basin nature of protein folding by enforcing a mixture of multiple Gaussian as the prior model for the variational autoencoder. We applied our model to three long-timescale protein folding trajectories, namely, Trp-cage, BBA, and villin headpiece, all of which have been extensively characterized in previous studies.29 In all cases, we showed that the model is able to characterize different features of the structure that could correspond to folded, misfolded, or unfolded states. The low-dimensional embedding obtained by GMVAE for these proteins resembles the folding funnel where the folded states lay down the funnel and unfolded ensemble states are outside the funnel. This can be intuitively described from the conformational entropy point of view. The unfolded state has larger variations in the structure, which causes the variance of Gaussian learned by GMVAE to be larger than the folded cluster having a narrower distribution. This along with the continuity of the latent space makes the landscape funnel-shaped. To verify that the clusters obtained by GMVAE correspond to different structural features of proteins during folding, we computed the global and local RMSD of each cluster with respect to the folded structure. As expected, the distribution of RMSD for different clusters follows a Gaussian where the folded state has the lowest and narrowest RMSD and the unfolded (extended) structure has the highest and widest RMSDdistribution.
We used normalized distance maps as the features in our machine learning model, which are practical ways to represent the simulation dataset of proteins. Other features such as contact maps can also be used as the input to the model, which would give a lower resolution embedding due to the amount of information in the contact maps relative to distance maps. Specifically, in our model, we used convolutional operations, which are known for their great ability to recognize and process the image dataset. It is worth noting that our GMVAE model is different from a simple Gaussian mixture model (GMM). In a GMM, the parameters of the model are optimized iteratively through the expectation-maximization algorithm.52 GMM has been used to cluster the FEL of proteins. Westerlund and Delemotte used GMM to construct and cluster the FEL of binding Ca2+ to calmodulin and found a novel pathway involving salt bridge breakage and formation.53 However, GMM requires the use of a few handcrafted features and a high number of collective variables can lead to over-fitting the model. On the other hand, since the GMVAE model is trained by gradient descent and is a deep learning architecture, it does not suffer from the same shortcomings of GMM. Unlike the GMVAE model proposed by Varolgüneş et al.25 that learns the cluster assignment through a stochastic layer, we replace this with a deterministic layer using Gumbel-softmax distribution, which makes the model end-to-end differentiable and leads to better performance.54,55 The temperature parameter in Gumbel-softmax was tuned along with other model hyperparameters during training. The best hyperparameters for each protein were chosen based on a cross-validated reconstruction loss. The number of clusters is a hyperparameter in the GMVAE. However, we showed that to find an optimum number of clusters, we first start with a higher estimate of the number of clusters in each protein. Then, using a cutoff for cluster assignment probability, we find the number of clusters with membership probability higher than a defined cutoff. Next, we train the model with the recovered number of clusters from the previous step. We showed that at this stage, all clusters have membership probabilities higher than the chosen cutoff (0.95). This also means that the model has converged to the optimum number of clusters in the system. Notably, the number of recovered clusters was found to be the same regardless of other hyperparameters in the model. However, the number of clusters can be dependent on the chosen cutoff. On the other hand, this can be viewed as a hierarchical clustering where based on the clustering resolution, which correlates with the cutoff value in our process, different structures are embedded in the same cluster. The latent space dimension is another important hyperparameter that needs to be optimized. To find the optimum latent space dimension for each protein, we calculated a cross-validated reconstruction loss for different values of latent-space dimension for each protein. The reconstruction loss reduces as the latent space dimension increases and it reaches a plateau. For each protein, we pick the latent space dimension where the reconstructions loss reaches this plateau.
Beyond the static characterization of the protein folding trajectories, we tested whether the model is able to characterize the kinetics of protein folding. We built a high resolution Markov model on the embedding obtained by GMVAE and computed the MFPTs between different states. Interestingly, the folding timescales obtained by the model are in good agreement with the folding times reported by other groups constructing a MSM on a TICA landscape, which characterizes the dynamics of folding. We should note that our model does not utilize any lag-time for the construction of the low-dim embedding; however, it is able to describe the folding timescales with reasonable accuracy. However, for some of the most dynamic proteins such as villin with fast folding timescales, only the first two implied timescales converge after 220 ns and the other implied timescales are below the maximum likelihood threshold, which makes the model unable to give meaningful information about these faster processes. This might be remedied by adding dynamical information to the model by using a lag-time in the training process. Further improvements to the model could include graph embedding of protein structures instead of using a distance map. This will be studied in our future work.
SUPPLEMENTARY MATERIAL
See the supplementary material for the training and validation loss and the results of the GMVAE model with different number of clusters for Trp-cage, BBA, and villin.
ACKNOWLEDGMENTS
This work was partially supported by the National Heart, Lung, and Blood Institute at the National Institute of Health for B.R.B. and M.G. In addition, it was partially supported by the National Science Foundation (Grant No. CHE-2029900) to J.B.K. The authors acknowledge the Biowulf High-Performance Computation Center at the National Institutes of Health for providing the time and resources for this project. They would also like to thank D. E. Shaw research group for providing the simulation trajectories.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
DATA AVAILABILITY
The data that support the findings of this study are openly available in GitHub at http://www.github.com/ghorbanimahdi73.
REFERENCES
- 1.Hospital A., Goñi J. R., Orozco M., and Gelpí J. L., “Molecular dynamics simulations: Advances and applications,” Adv. Appl. Bioinf. Chem. 8, 37 (2015). 10.2147/AABC.S70333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yang Y. I., Shao Q., Zhang J., Yang L., and Gao Y. Q., “Enhanced sampling in molecular dynamics,” J. Chem. Phys. 151, 070902 (2019). 10.1063/1.5109531 [DOI] [PubMed] [Google Scholar]
- 3.Bernardi R. C., Melo M. C., and Schulten K., “Enhanced sampling techniques in molecular dynamics simulations of biological systems,” Biochim. Biophys. Acta, Gen. Subj. 1850, 872–877 (2015). 10.1016/j.bbagen.2014.10.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Glielmo A., Husic B. E., Rodriguez A., Clementi C., Noé F., and Laio A., “Unsupervised learning methods for molecular simulation data,” Chem. Rev. 121, 9722 (2021). 10.1021/acs.chemrev.0c01195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lemke T. and Peter C., “EncoderMap: Dimensionality reduction and generation of molecule conformations,” J. Chem. Theory Comput. 15, 1209–1215 (2019). 10.1021/acs.jctc.8b00975 [DOI] [PubMed] [Google Scholar]
- 6.Hegger R., Altis A., Nguyen P. H., and Stock G., “How complex is the dynamics of peptide folding?,” Phys. Rev. Lett. 98, 028102 (2007). 10.1103/PhysRevLett.98.028102 [DOI] [PubMed] [Google Scholar]
- 7.Chodera J. D., Swope W. C., Pitera J. W., and Dill K. A., “Long-time protein folding dynamics from short-time molecular dynamics simulations,” Multiscale Model. Simul. 5, 1214–1226 (2006). 10.1137/06065146x [DOI] [Google Scholar]
- 8.Chodera J. D., Singhal N., Pande V. S., Dill K. A., and Swope W. C., “Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics,” J. Chem. Phys. 126, 155101 (2007). 10.1063/1.2714538 [DOI] [PubMed] [Google Scholar]
- 9.Chodera J. D. and Noé F., “Markov state models of biomolecular conformational dynamics,” Curr. Opin. Struct. Biol. 25, 135–144 (2014). 10.1016/j.sbi.2014.04.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dobson C. M., “Protein folding and misfolding,” Nature 426, 884–890 (2003). 10.1038/nature02261 [DOI] [PubMed] [Google Scholar]
- 11.Onuchic J. N. and Wolynes P. G., “Theory of protein folding,” Curr. Opin. Struct. Biol. 14, 70–75 (2004). 10.1016/j.sbi.2004.01.009 [DOI] [PubMed] [Google Scholar]
- 12.Abdi H. and Williams L. J., “Principal component analysis,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2, 433–459 (2010). 10.1002/wics.101 [DOI] [Google Scholar]
- 13.Schwantes C. R. and Pande V. S., “Improvements in Markov state model construction reveal many non-native interactions in the folding of NTL9,” J. Chem. Theory Comput. 9, 2000–2009 (2013). 10.1021/ct300878a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pérez-Hernández G., Paul F., Giorgino T., De Fabritiis G., and Noé F., “Identification of slow molecular order parameters for Markov model construction,” J. Chem. Phys. 139, 015102 (2013). 10.1063/1.4811489 [DOI] [PubMed] [Google Scholar]
- 15.Balasubramanian M., Schwartz E. L., Tenenbaum J. B., de Silva V., and Langford J. C., “The isomap algorithm and topological stability,” Science 295, 7 (2002). 10.1126/science.295.5552.7a [DOI] [PubMed] [Google Scholar]
- 16.Ceriotti M., Tribello G. A., and Parrinello M., “Simplifying the representation of complex free-energy landscapes using sketch-map,” Proc. Natl. Acad. Sci. U. S. A. 108, 13023–13028 (2011). 10.1073/pnas.1108486108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nadler B., Lafon S., Coifman R. R., and Kevrekidis I. G., “Diffusion maps, spectral clustering and reaction coordinates of dynamical systems,” Appl. Comput. Harmonic Anal. 21, 113–127 (2006). 10.1016/j.acha.2005.07.004 [DOI] [Google Scholar]
- 18.Kingma D. P. and Welling M., “Auto-encoding variational Bayes,” arXiv:1312.6114 (2013).
- 19.Chen W. and Ferguson A. L., “Molecular enhanced sampling with autoencoders: On-the-fly collective variable discovery and accelerated free energy landscape exploration,” J. Comput. Chem. 39, 2079–2102 (2018). 10.1002/jcc.25520 [DOI] [PubMed] [Google Scholar]
- 20.Schöberl M., Zabaras N., and Koutsourelakis P.-S., “Predictive collective variable discovery with deep Bayesian models,” J. Chem. Phys. 150, 024109 (2019). 10.1063/1.5058063 [DOI] [PubMed] [Google Scholar]
- 21.Chen W., Tan A. R., and Ferguson A. L., “Collective variable discovery and enhanced sampling using autoencoders: Innovations in network architecture and error function design,” J. Chem. Phys. 149, 072312 (2018). 10.1063/1.5023804 [DOI] [PubMed] [Google Scholar]
- 22.Ribeiro J. M. L., Bravo P., Wang Y., and Tiwary P., “Reweighted autoencoded variational Bayes for enhanced sampling (RAVE),” J. Chem. Phys. 149, 072301 (2018). 10.1063/1.5025487 [DOI] [PubMed] [Google Scholar]
- 23.Bonati L., Zhang Y.-Y., and Parrinello M., “Neural networks-based variationally enhanced sampling,” Proc. Natl. Acad. Sci. U. S. A. 116, 17641–17647 (2019). 10.1073/pnas.1907975116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bhowmik D., Gao S., Young M. T., and Ramanathan A., “Deep clustering of protein folding simulations,” BMC Bioinf. 19, 484 (2018). 10.1186/s12859-018-2507-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Varolgüneş Y. B., Bereau T., and Rudzinski J. F., “Interpretable embeddings from molecular simulations using Gaussian mixture variational autoencoders,” Mach. Learn.: Sci. Technol. 1, 015012 (2020). 10.1088/2632-2153/ab80b7 [DOI] [Google Scholar]
- 26.Guo C., Zhou J., Chen H., Ying N., Zhang J., and Zhou D., “Variational autoencoder with optimizing Gaussian mixture model priors,” IEEE Access 8, 43992–44005 (2020). 10.1109/access.2020.2977671 [DOI] [Google Scholar]
- 27.Dill K. A., Ozkan S. B., Shell M. S., and Weikl T. R., “The protein folding problem,” Annu. Rev. Biophys. 37, 289–316 (2008). 10.1146/annurev.biophys.37.092707.153558 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dilokthanakul N., Mediano P. A., Garnelo M., Lee M. C., Salimbeni H., Arulkumaran K., and Shanahan M., “Deep unsupervised clustering with Gaussian mixture variational autoencoders,” arXiv:1611.02648 (2016).
- 29.Lindorff-Larsen K., Piana S., Dror R. O., and Shaw D. E., “How fast-folding proteins fold,” Science 334, 517–520 (2011). 10.1126/science.1208351 [DOI] [PubMed] [Google Scholar]
- 30.Kingma D. P. and Ba J., “Adam: A method for stochastic optimization,” arXiv:1412.6980 (2014).
- 31.Scherer M. K., Trendelkamp-Schroer B., Paul F., Pérez-Hernández G., Hoffmann M., Plattner N., Wehmeyer C., Prinz J.-H., and Noé F., “PyEMMA 2: A software package for estimation, validation, and analysis of Markov models,” J. Chem. Theory Comput. 11, 5525–5542 (2015). 10.1021/acs.jctc.5b00743 [DOI] [PubMed] [Google Scholar]
- 32.Barua B., Lin J. C., Williams V. D., Kummler P., Neidigh J. W., and Andersen N. H., “The Trp-cage: Optimizing the stability of a globular miniprotein,” Protein Eng., Des. Sel. 21, 171–185 (2008). 10.1093/protein/gzm082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sarisky C. A. and Mayo S. L., “The ββα fold: Explorations in sequence space,” J. Mol. Biol. 307, 1411–1418 (2001). 10.1006/jmbi.2000.4345 [DOI] [PubMed] [Google Scholar]
- 34.Kubelka J., Chiu T. K., Davies D. R., Eaton W. A., and Hofrichter J., “Sub-microsecond protein folding,” J. Mol. Biol. 359, 546–553 (2006). 10.1016/j.jmb.2006.03.034 [DOI] [PubMed] [Google Scholar]
- 35.Meuzelaar H., Marino K. A., Huerta-Viga A., Panman M. R., Smeenk L. E., Kettelarij A. J., van Maarseveen J. H., Timmerman P., Bolhuis P. G., and Woutersen S., “Folding dynamics of the Trp-cage miniprotein: Evidence for a native-like intermediate from combined time-resolved vibrational spectroscopy and molecular dynamics simulations,” J. Phys. Chem. B 117, 11490–11501 (2013). 10.1021/jp404714c [DOI] [PubMed] [Google Scholar]
- 36.English C. A. and García A. E., “Charged termini on the Trp-cage roughen the folding energy landscape,” J. Phys. Chem. B 119, 7874–7881 (2015). 10.1021/acs.jpcb.5b02040 [DOI] [PubMed] [Google Scholar]
- 37.Sidky H., Chen W., and Ferguson A. L., “High-resolution Markov state models for the dynamics of Trp-cage miniprotein constructed over slow folding modes identified by state-free reversible VAMPnets,” J. Phys. Chem. B 123, 7999–8009 (2019). 10.1021/acs.jpcb.9b05578 [DOI] [PubMed] [Google Scholar]
- 38.Deng N.-j., Dai W., and Levy R. M., “How kinetics within the unfolded state affects protein folding: An analysis based on Markov state models and an ultra-long md trajectory,” J. Phys. Chem. B 117, 12787–12799 (2013). 10.1021/jp401962k [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.van der Maaten L. and Hinton G., “Visualizing data using t-SNE,” J. Mach. Learn. Res. 9, 2579 (2008). [Google Scholar]
- 40.Kubelka J., Eaton W. A., and Hofrichter J., “Experimental tests of villin subdomain folding simulations,” J. Mol. Biol. 329, 625–630 (2003). 10.1016/s0022-2836(03)00519-9 [DOI] [PubMed] [Google Scholar]
- 41.Sormani G., Rodriguez A., and Laio A., “Explicit characterization of the free-energy landscape of a protein in the space of all its Cα carbons,” J. Chem. Theory Comput. 16, 80–87 (2019). 10.1021/acs.jctc.9b00800 [DOI] [PubMed] [Google Scholar]
- 42.Lei H., Su Y., Jin L., and Duan Y., “Folding network of villin headpiece subdomain,” Biophys. J. 99, 3374–3384 (2010). 10.1016/j.bpj.2010.08.081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chong S.-H. and Ham S., “Examining a thermodynamic order parameter of protein folding,” Sci. Rep. 8, 7148 (2018). 10.1038/s41598-018-25406-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Beauchamp K. A., Ensign D. L., Das R., and Pande V. S., “Quantitative comparison of villin headpiece subdomain simulations and triplet–triplet energy transfer experiments,” Proc. Natl. Acad. Sci. U. S. A. 108, 12734–12739 (2011). 10.1073/pnas.1010880108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Suárez E., Wiewiora R. P., Wehmeyer C., Noé F., Chodera J. D., and Zuckerman D. M., “What Markov state models can and cannot do: Correlation versus path-based observables in protein-folding models,” J. Chem. Theory Comput. 17, 3119–3133 (2021). 10.1021/acs.jctc.0c01154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pan A. C., Weinreich T. M., Piana S., and Shaw D. E., “Demonstrating an order-of-magnitude sampling enhancement in molecular dynamics simulations of complex protein systems,” J. Chem. Theory Comput. 12, 1360–1367 (2016). 10.1021/acs.jctc.5b00913 [DOI] [PubMed] [Google Scholar]
- 47.Piana S., Lindorff-Larsen K., and Shaw D. E., “Protein folding kinetics and thermodynamics from atomistic simulation,” Proc. Natl. Acad. Sci. U. S. A. 109, 17845–17850 (2012). 10.1073/pnas.1201811109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Mori T. and Saito S., “Molecular mechanism behind the fast folding/unfolding transitions of villin headpiece subdomain: Hierarchy and heterogeneity,” J. Phys. Chem. B 120, 11683–11691 (2016). 10.1021/acs.jpcb.6b08066 [DOI] [PubMed] [Google Scholar]
- 49.Wehmeyer C. and Noé F., “Time-lagged autoencoders: Deep learning of slow collective variables for molecular kinetics,” J. Chem. Phys. 148, 241703 (2018). 10.1063/1.5011399 [DOI] [PubMed] [Google Scholar]
- 50.Chen W., Sidky H., and Ferguson A. L., “Capabilities and limitations of time-lagged autoencoders for slow mode discovery in dynamical systems,” J. Chem. Phys. 151, 064123 (2019). 10.1063/1.5112048 [DOI] [Google Scholar]
- 51.Ward M. D., Zimmerman M. I., Meller A., Chung M., Swamidass S., and Bowman G. R., “Deep learning the structural determinants of protein biochemical properties by comparing structural ensembles with DiffNets,” Nat. Commun. 12, 3023 (2021). 10.1038/s41467-021-23246-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Dempster A. P., Laird N. M., and Rubin D. B., “Maximum likelihood from incomplete data via the EM algorithm,” J. R. Stat. Soc., Ser. B 39, 1–22 (1977). 10.1111/j.2517-6161.1977.tb01600.x [DOI] [Google Scholar]
- 53.Westerlund A. M. and Delemotte L., “InfleCS: Clustering free energy landscapes with Gaussian mixtures,” J. Chem. Theory Comput. 15, 6752–6759 (2019). 10.1021/acs.jctc.9b00454 [DOI] [PubMed] [Google Scholar]
- 54.Figueroa J. A. and Rivera A. R., “Is simple better?: Revisiting simple generative models for unsupervised clustering,” in Second Workshop on Bayesian Deep Learning (NIPS, 2017). [Google Scholar]
- 55.Jang E., Gu S., and Poole B., “Categorical reparametrization with Gumble-Softmax,” in International Conference on Learning Representations (ICLR 2017) (OpenReview.net, 2017). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See the supplementary material for the training and validation loss and the results of the GMVAE model with different number of clusters for Trp-cage, BBA, and villin.
Data Availability Statement
The data that support the findings of this study are openly available in GitHub at http://www.github.com/ghorbanimahdi73.