Reinforcement learning links spontaneous cortical dopamine impulses to reward

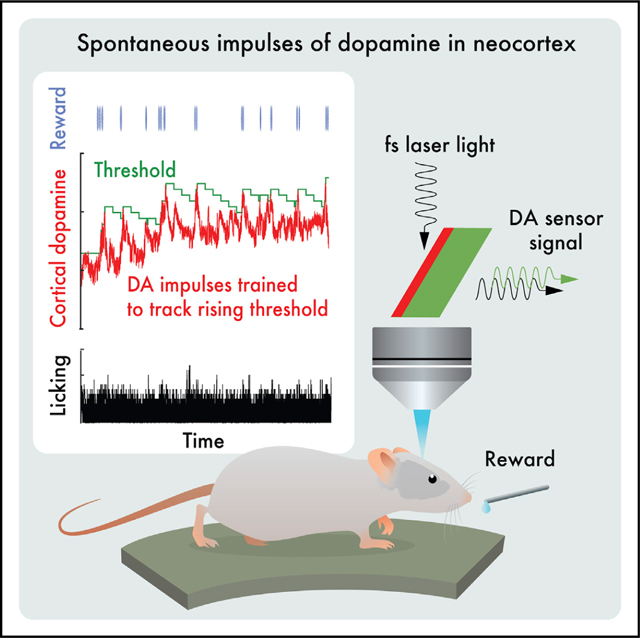
SUMMARY

In their pioneering study on dopamine release, Romo and Schultz speculated “…that the amount of dopamine released by unmodulated spontaneous impulse activity exerts a tonic, permissive influence on neuronal processes more actively engaged in preparation of self-initiated movements….”¹ Motivated by the suggestion of “spontaneous impulses,” as well as by the “ramp up” of dopaminergic neuronal activity that occurs when rodents navigate to a reward,^2–5 we asked two questions. First, are there spontaneous impulses of dopamine that are released in cortex? Using cell-based optical sensors of extrasynaptic dopamine, [DA]_ex,⁶ we found that spontaneous dopamine impulses in cortex of naive mice occur at a rate of ∼0.01 per second. Next, can mice be trained to change the amplitude and/or timing of dopamine events triggered by internal brain dynamics, much as they can change the amplitude and timing of dopamine impulses based on an external cue?^7–9 Using a reinforcement learning paradigm based solely on rewards that were gated by feedback from real-time measurements of [DA]_ex, we found that mice can volitionally modulate their spontaneous [DA]_ex. In particular, by only the second session of daily, hour-long training, mice increased the rate of impulses of [DA]_ex, increased the amplitude of the impulses, and increased their tonic level of [DA]_ex for a reward. Critically, mice learned to reliably elicit [DA]_ex impulses prior to receiving a reward. These effects reversed when the reward was removed. We posit that spontaneous dopamine impulses may serve as a salient cognitive event in behavioral planning.

In brief

Foo et al. found that spontaneous impulses of dopamine release occur in cortex of naive mice at a rate of ∼0.01 per second. Using a reinforcement learning paradigm based on rewards that were gated by real-time measurements of extrasynaptic dopamine, mice could learn to volitionally modulate their spontaneous impulses.

Graphical abstract

RESULTS

We measured extrasynaptic dopamine ([DA]_ex) in primary somatosensory (S1) cortex of mice, which is known to exhibit stimulus-dependent¹⁰ and experience-dependent synaptic plasticity.¹¹ Extrasynaptic dopamine is converted into an optical signal by cell-based neurotransmitter fluorescent-engineered reporters (CNiFERs).⁶ The CNiFERs are implanted into cortex and observed with in vivo two-photon microscopy¹² through a thin-skull craniotomy that minimizes neuroinflammation.¹³ We chose this approach for a multitude of reasons. First, we wish to make a direct measurement at the site of action rather than infer release from the spiking output of dopaminergic neurons that project to S1 cortex.^14–16 This is particularly important in light of differences in somatic spiking and dopaminergic release.^17,18 Second, D2-CNiFERs leverage the specificity of D2 dopamine G-protein-coupled-receptors (GPCRs) and thus have physiological nanoMolar sensitivity for [DA]_ex.⁶ This enables D2-CNiFERs to detect small changes in [DA]_ex with high sensitivity and with fast temporal resolution, i.e., <0.25 s. The same approach of using GPCRs was taken with recent single-wavelength, molecular sensors.^19,20 Third, CNiFERs report a change in [DA]_ex through dual-wavelength fluorescence resonant energy transfer (FRET), which is relatively insensitive to optical bleaching, drift, and motion of the head compared with single-wavelength detectors. In fact, we compared the use of a genetically encoded dopamine sensor, GRAB_DA, against that of the CNiFERs (Figure S1); while GRAB_DA was more sensitive to fast transients, it did not have the long-term stability needed for the current experiments.

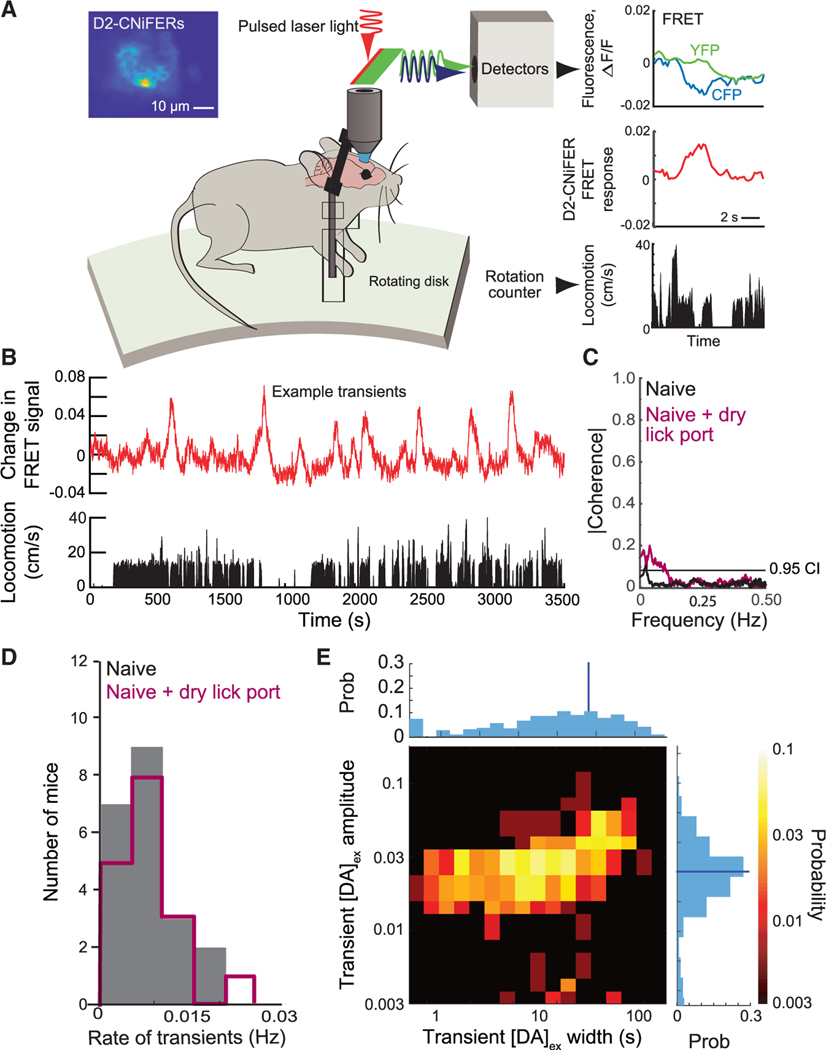
We began with open-loop measurements on naive mice that had no prior experience with the apparatus (7 mice). The animals were implanted with D2-CNiFERs below a thinned-skull optical window, allowed to recover, and studied under head-fixed conditions on a running disk (Figure 1A). For these naive animals, we observed spontaneous, transient increases, i.e., impulses, in [DA]_ex(Figure 1B). Interestingly, there is negligible statistical coherence between changes in [DA]_ex and the speed of locomotion (Figure 1C). As an average over all animals, spontaneous dopamine transients occur at a rate of 0.007 ± 0.001 Hz (mean ± SE; Figure 1D) or about once every 140 s. The peak amplitude of spontaneous impulses is distributed across roughly a 3-fold range of values(Figure 1E). These values are far from the saturation level for dopamine binding by the CNiFERs and correspond to almost an order of magnitude range in [DA]_ex.⁶ The lifetime of the impulses is near-uniformly distributed from 1 s in width up to 100 s with a mean value of 12 s (Figure 1E). We take 100 s as the operational break point between dopamine impulses and changes in basal [DA]_ex, which we refer to as tonic events. All told, these data support the presence of spontaneous [DA]_ex impulses in cortex.

Figure 1. Characterization of spontaneous dopamine impulses ([DA]_ex) in naive mice in the absence of reward in an apparatus without a lick port or overt stimulation.

(A) Open-loop measurement of cortical [DA]_ex using D2-CNiFERs with in vivo two-photon microscopy. Increases in [DA]_ex are observed as an increase in YFP fluorescence with a concomitant decrease in CFP fluorescence and vice versa. The CNiFER signal is reported as the fractional change in FRET.²¹ Inset: fluorescence image of D2 Cni-FER implant in cortex is shown.

(B) Time series shows changes in D2 CNiFER FRET, reflecting spontaneous transients in [DA]_ex, i.e., dopamine impulses, along with measurement of the rate of locomotion.

(C) The magnitude of the spectral coherencemagnitude, averaged over all animals (xx mice), between the locomotion rate and [DA]_ex. Data without lick port in black and with dry port in maroon are shown; dashed line is 0.95 confidence level.

(D) Distribution of spontaneous dopamine impulserate for all naive animals. Histograms without lick port (gray) and with port (maroon) are statistically indistinguishable (KS test; p = 0.99).

(E) Two-dimensional histogram of spontaneousimpulses in [DA]_ex across all animals without lick port. Top row is the cumulative of all widths; the average full width half maximum relative to baseline was 15.1 ± 1.3 s (blue line). Right column is the cumulative of amplitudes; 0.1 corresponds to [DA]_ex ~20 nM;⁶ the average was 0.056 ± 0.002 (blue line).

See also Figure S1.

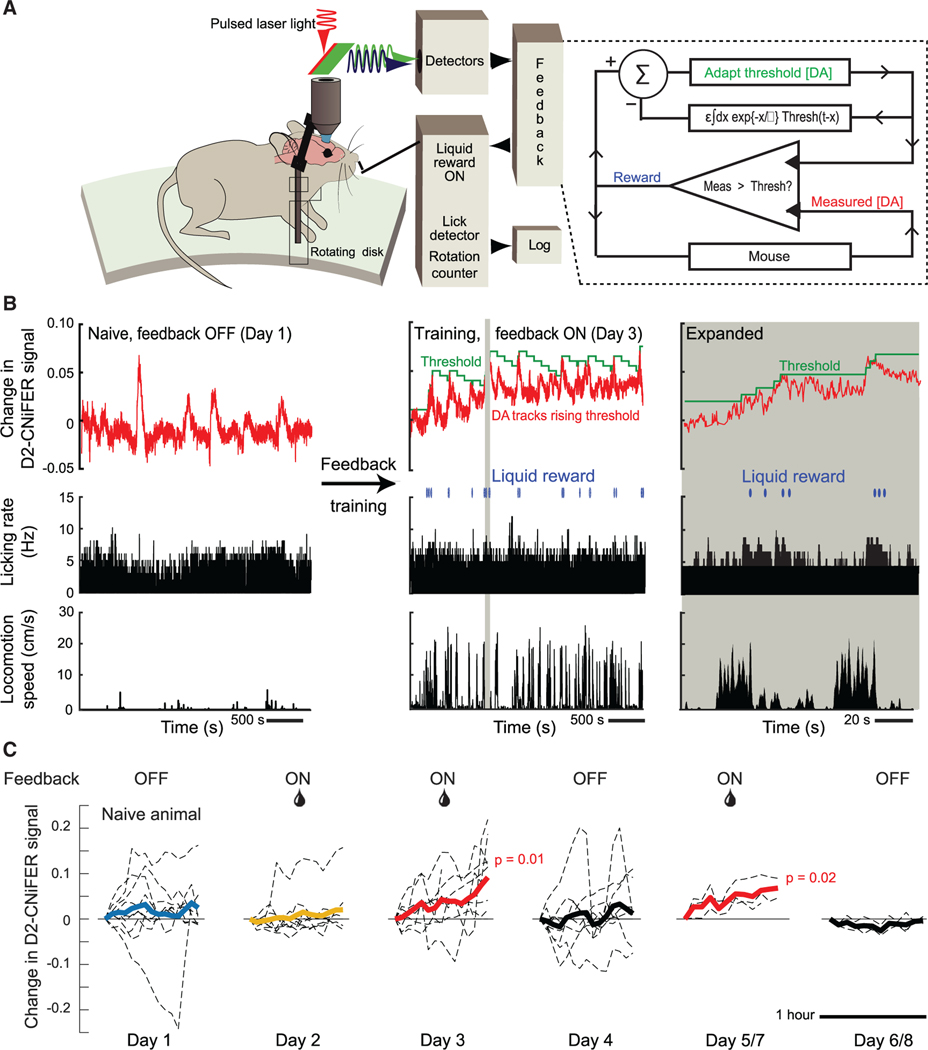
We next asked whether spontaneous [DA]_ex events could be subject to volitional control. To address this, we designed an experiment with three sequential epochs: baseline (day 1), feedback “ON” (days 2 and 3), and feedback “OFF” (day 4). To determine the baseline [DA]_ex, we performed open-loop measurements with naive mice. These measurements are identical to the assay of spontaneous events (Figure 1A) but with the addition of a dry lick port (Figure 2A). In the feedback ON epoch, we introduced a closed-loop system for reinforcement training.^22,23 The mouse now received a sucrose-water drop reward through the lick port if there was an increase in [DA]_ex above a threshold concentration; the determination was evaluated every 0.25 s (Figure 2A). Importantly, there was no external cue; mice were simply rewarded for elevations in cortical [DA]_ex. To motivate mice to actively increase the peak level of [DA]_ex, we incorporated an adaptive staircase algorithm,²⁴ analogous to a progressive ratio in classical conditioning, that was based on the [DA]_ex level in the feedback loop. Increases in [DA]_ex triggered a progressively higher threshold for reward, while the threshold was gradually lowered if [DA]_ex was unchanged or decreased. In the feedback OFF epoch on day 4, the reward was omitted. Additional epochs of feedback ON and OFF were performed in a subset of mice.

Figure 2. Closed-loop feedback reinforcement training to volitionally link spontaneous impulses in [DA]_ex to reward.

(A) The setup for the open loop experiment (Figure 1A) is augmented. We use the measured D2-CNiFER response as a proxy for [DA]_ex and drive the delivery of a liquid reward based on the [DA]_ex signal (red) relative to an adaptive staircase threshold (green) updated every 0.25 s. If [DA]_ex exceeds the threshold, a drop (0.1 mL) of sucrose water (10% w/v) is released via the lick port and the threshold is incremented by 0.005 signal units. The value of the threshold also exponentially decreases, in discrete steps of 0.005, with a time constant of 225 s, since the last increment.

(B) Example data show the open-loop naive response on day 1 and an increase of tonic [DA]_ex with closed-loop reinforcement on day 3; the adaptive staircase threshold follows the reward to within the decay time constant. A 130-s segment of data highlighted by the beige band is expanded.

(C) Rolling average of [DA]_ex impulses for all mice. The averaging window was 235 s. On day 2, tonic [DA]_ex did not significantly increase relative to that of naive mice (p = 0.69). By day 3, tonic [DA]_ex increased significantly (p = 0.01). The increase extinguished when reward was withheld on day 4 (p = 0.73) and reinstated when reward was restored on day 5 or 7 (p = 0.02) compared to feedback withheld on day 6 or 8.

We detect spontaneous impulses in [DA]_ex in the absence of any reward, as seen in the example baseline data of Figure 2B (left panel). Transient increases in [DA]_ex occurred with an average rate of 0.008 ± 0.001 Hz (18 mice), statistically indistinguishable from that of naive animals in the absence of a port (Figure 1D). Unlike the case without a lick port, however, running and changes in [DA]_ex weakly but significantly co-fluctuated over long timescales (Figure 1C), although the tonic level of [DA]_ex stayed relatively constant over the period of the trial (Figure 2C, day 1). Lastly, mice naturally lick the dry port such that [DA]_ex and licking very weakly co-fluctuated. In total, these data confirm the presence of spontaneous [DA]_ex impulses in the baseline epochs and add to the results for naive animals (Figures 1A–1E).

On the 1^st day of feedback training (9 mice), cortical [DA]_ex remains essentially constant over the 1 h of ON training (Figure 2C, day 2). By contrast, the closed-loop reinforcement during the 2^nd day of feedback ON training led to a large, statistically significant increase in [DA]_ex over the period of training (p = 0.01; Figure 2C, day 3). As shown in the example of Figure 2B (center and right panels), mice tracked the increasing values of the threshold initiated by the adaptive staircase algorithm. Thus, the mice learned to augment their [DA]_ex by approximately 10% on day 2 relative to the beginning of the session for this example. Remarkably, the increase in tonic [DA]_ex was abolished by disabling the reward, i.e., feedback OFF epoch, subsequent to the 2 days of training (Figure 2C, day 4). To confirm that learning to volitionally control [DA]_ex was not extinguished by a single session of no reward (3 mice), we restored feedback ON training and reward on the next day (day 5) and observed a significant increase in [DA]_ex (p = 0.02), similar to that on day 3. This increase in tonic [DA]_ex was again absent when feedback was omitted on day 6 (Figure 2C, days 5 and 6). Taken together, these results imply that learning is effective and that mice can volitionally control their cortical [DA]_ex when provided with feedback via an immediate reward.

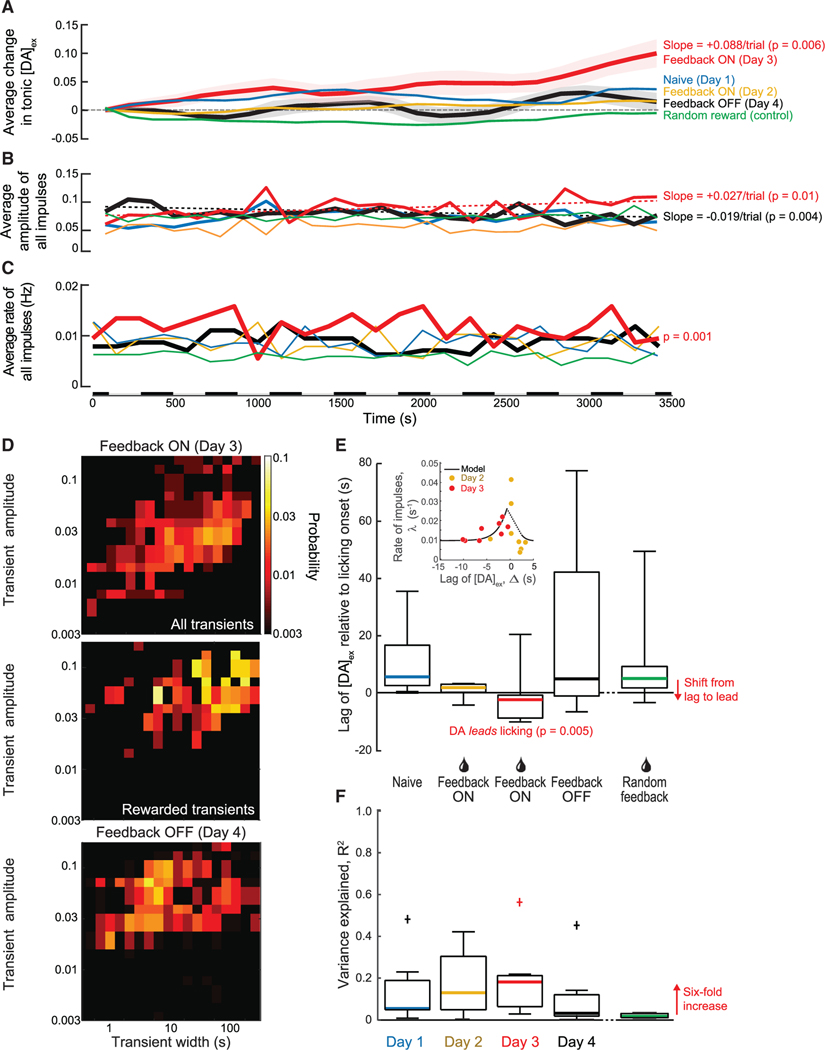
The feedback-driven increase in [DA]_ex consists of a slowly increasing tonic level peppered with transient dopamine impulses (Figure 2B, middle and right panels). We decomposed the response into tonic and transient components. On the 2^nd day with feedback training (day 3), we observed a statistically significant (p = 0.006) and approximately monotonic increase in the tonic level of [DA]_ex compared to the relatively flat level in naive mice (Figure 3A). There was no significant change in [DA]_ex for the feedback OFF epochs. We examined two aspects of the [DA]_ex impulses. First, we find that the amplitude of the impulses significantly increases (p = 0.01), by a factor of 0.27/1.00 or approximately 1/3 that of the tonic increase, over the time of the trial (Figure 3B). There was a significant decrease (p = 0.01) in the amplitude of the impulses for the feedback OFF epochs (Figure 3B). Second, we observed a small but significant increase (p = 7 × 10⁻⁵) in the frequency of dopamine impulses across subjects (Figure 3C). Here, there was no significant change for the feedback OFF epochs. These reversible changes in both the tonic level of [DA]_ex and the impulses signify the importance of the feedback reward training during the session.

Figure 3. Population-averaged changes in [DA]_ex over the course of our reinforcement paradigm.

(A) Tonic [DA]_ex shows a significant increase relative to naive, baseline animals after feedback training (day 3; p = 0.006); the increase is Δ[DA]_ex = 0.088. Day 2 and day 4 showed no significant change in tonic [DA]_ex, p = 0.37 and 0.66, respectively. Randomly rewarded mice also did not show a significant change in tonic [DA]_ex compared to naive animals (p = 0.61).

(B) The amplitude of [DA]_ex impulses significantly increased over the course of the trial with feedback training (day 3; p = 0.01). With feedback OFF, there was a significant decrease in amplitude over the course of the trial (day 4; p = 0.004). The data for day 1 and day 2 and the case of random reward showed no significant change in [DA]_ex impulse amplitude over time; p = 0.43, p = 0.77, and p = 0.67, respectively.

(C) The rate of [DA]_ex impulses was significantly higher relative to baseline animals with feedback training (day 3; p = 0.001). Day 2 and day 4 showed no significant change in [DA]_ex impulse frequency; p = 0.65 and 0.37, respectively. The rate for animals with random reward was significantly less than that for naive animals (p = 10⁸). Alternating bars along time axis indicate intervals for binned data in (A)–(C).

(D) Distribution of amplitudes and widths of [DA]_ex impulses for trained mice with feedback ON (day 3; top), a subset of rewarded impulses when feedback is ON (day 3; center), and when feedback reinforcement is OFF (day 4; bottom). The amplitudes with feedback training ON were significantly larger compared to baseline animals (day 3; p = 10⁻⁷) and compared to feedback OFF (day 4; p = 10⁻²⁹). The widths were significantly greater with feedback ON compared to those for baseline animals (p = 10⁻²²) and when feedback was OFF (p = 10⁻¹⁵). Rewarded impulses had an amplitude of 0.078 ± 0.002 and an average width of 44.2 ± 1.6 s and were significantly greater than the impulses when feedback was OFF (day 4; p = 10⁻⁸ and p = 10⁻²⁹, respectively).

(E) Standard boxplot shows the timing of the onset of [DA]_ex impulses relative to the onset of licking; the solid bars are the median times. The mean and standard error of the lag times of [DA]_ex impulses relative to licking are on +11.0 ± 3.5 s on day 1, +0.6 ± 0.9 s on day 2 allowing for a single outlier, −5.1 ± 1.4 s on day 3 allowing for a single outlier, with [DA]_ex now leading, and +22.8 ± 11.9 s on day 4. Impulses also lagged licking for randomly rewarded mice (+10.9 ± 7.9 s). A two-sample t test with respect to baseline animals yields p = 0.04 (day 2), p = 0.005 (day 3), p = 0.9 (day 4), and p = 0.3 (random); including the single outliers drops the evidence against a null hypothesis to p = 0.6 (day 2) and the still highly significant value p = 0.02 (day 3). The inset shows a scatterplot of the number of rewarded impulses versus lag time for individual mice on day 2 and day 3, together with a fit of the model (Equations 6 and 7 in STAR Methods) to the data.

(F) Standard boxplot shows the variance explained by an optimal linear filter that predicts licking from the measured [DA]_ex. “+” indicates an outlier that was not included in the mean. Solid bars indicate median. The values of R² for days 2 and 3 are significantly different than zero, with p = 0.030 and p = 0.037. The data for random reward, although very small at 0.019, are also significant (p = 0.027; n = 12) as a result of the large sample. Note 6-fold increase on 2^nd day of feedback ON (day 3).

See also Figures S2 and S3.

Feedback-driven impulses of [DA]_ex last 43 s on average, significantly longer than events in the naive mouse (12 s; p = 10⁻²⁸; cf. Figures 1E and 3D) or when feedback was removed (p = 10⁻¹⁵; Figure 3D), but well within the 100-s operational definition of dopamine impulses.

An increase in the tonic level of [DA]_ex could, in principle, result from the summation of multiple, slow, transient events. This possibility is unlikely for several reasons. First, in numerical tests of this possibility, we found that integration of dopamine impulses against a range of slow temporal filters, with decay times from 100 to 1,000 s, does not lead to a result with the observed increase in tonic level of [DA]_ex (Figures S2A and S2B). Second, a tonic increase in [DA]_ex is not observed with random rewards or on day 1 of reinforcement.

Could mice have associated an unknown systematic cue from our experimental setup? To address this, we examined in a separate cohort of mice (3 animals) the effect of rewarding at random intervals during the 1-h training on days 2 and 3 (Figure 2C). Random rewards were delivered following a Poisson distribution at a rate equal to the mean frequency of transients in [DA]_ex, i.e., 0.017 Hz, for mice trained on feedback. Mice that received rewards at random times did not show an increase in tonic [DA]_ex or in the frequency, amplitude, or width of [DA]_ex transients (Figures 3A–3C), in comparison with naive mice over the same time period (Figures S2C and S2D). Importantly, the onset of licking did not correlate with increases in [DA]_ex (Figure 3E). Lastly, the extent of locomotion (Figures 1B and 2B), which has no overt function in the learning paradigm, is poorly predicted by [DA]_ex (Figure S3), consistent with an incidental role.

Changes in timing of dopamine release are a hallmark of dopamine reinforcement learning. In classical reinforcement learning with liquid rewards, anticipatory licking is triggered by the conditioned stimulus, i.e., cue. However, in our experiments, there is no overt cue. Nonetheless, a critical test is to determine whether animals alter the timing of their dopamine dynamics with training. The expectation is that impulses of [DA]_ex will occur prior to a reward after training, as opposed to following a reward. Indeed, we found this timing of [DA]_ex impulses relative to the onset of licking shifts over the course of training. Naive mice naturally lick the dry port such that [DA]_ex and licking weakly co-fluctuated with the increase in [DA]_ex, lagging that of licking by 11.0 ± 3.5 s (Figure 3E). In contrast, with feedback ON, the timing of the onset of dopamine has significantly advanced; p = 0.04 and p = 0.005 for days 2 and 3, respectively. For day 3, the advance is by 16 s, with the onset of [DA]_ex impulses now occurring ahead of licking, i.e., lag of −5.1 ± 1.4 s (Figure 3E). Thus, feedback reinforcement reversed the temporal order of [DA]_ex impulses and licking in trained mice so that the enhanced dopamine signal now predicts the outcome of a movement, i.e., licking.

In addition to changes in timing, we calculated the predictability of licking by [DA]_ex under all conditions in terms of the variance-explained (R²), a metric for the strength of the predictability of licking from dopamine events. We found that there is a 6-fold increase in R² with feedback ON for day 3 compared to the case of random feedback (Figure 3F; cf. 3rd with 5th column). This increase in R² was absent when feedback was removed, i.e., feedback OFF on day 4 (Figure 3F; cf. 4th with 5th column).

Is there a theoretical means to understand how reinforcement can alter the rate and timing of stochastically occurring impulses of dopamine? We constructed a minimal theory that posits a generator of impulses and a hypothetical integrator of impulses above threshold (model in STAR Methods). The arrival of impulses is modeled as a shot effect with a Poisson rate and a stochastic distribution of amplitudes.^25,26 A set of coupled, leaky integrator equations ties the shift in lag time of impulses relative to a reward with the increase in rate of dopamine transients that may lead to impulses that cross a threshold. The model has two parameters that are numerically fit to data, i.e., a temporal scale for the impact of the lag time, which is fit with a full width at half maximum of 3 s, and a scale for the change in rate. We compared the predicted rate of rewarded impulses versus the lag time for the individually rewarded trains on day 2 and day 3 (inset in Figure 3E). The predicted relation, which is not monotonic, is in qualitative agreement with the data.

DISCUSSION

Dopamine is a ubiquitous neurotransmitter in the brain that signals many aspects of cognitive processing.⁹ Early studies showed that a fraction of dopaminergic neurons in the midbrain produce impulses of spiking activity in response to a novel stimulus, even one that is not associated with a reward.²⁷ Further, such impulses may occur as a precursor to self-generated motion.^28,29 Most famously, unexpected rewards produce a transient increase in the spike rate of dopaminergic neurons that project to cortex and lead to increases in the concentration of [DA]_ex in the midbrain and in cortex.⁸ With repeated pairing of a neutral cue with a delayed reward, dopaminergic neurons shift their firing from the time of the reward to the time of the cue.^6,8 The increase in [DA]_ex now represents the expectation of an upcoming reward, and the amplitude of this increase signals the probability of the reward.^9,20,30 A final twist is that the meaning of dopamine signals may change with experience.³¹

Here, we focused on the type of dopamine release in the cortex and report on a different behavior of dopamine impulses. In now classic literature, brief impulses of dopamine, in the context of Pavlovian conditioning, have been shown to represent reward prediction errors.⁷ Notably, phasic dopamine firing and release advance in time from the presentation of reward to that of the earliest reward-predicting cue as animals learn to associate the cue with reward.^6,8 We observed spontaneous dopamine impulses in the absence of both sensory stimuli and reward in naive, head-fixed, awake animals on a treadmill. These dopamine impulses do not appear to report a reward prediction error, as there are no cues in the apparatus that would indicate the presence of reward. Furthermore, we find that these transients are not causally linked to the initiation of motor activity, i.e., licking or running (Figures 1C and 3F), as would be suggested by previous studies.^32,33 While we only measure licking and running behavior, it should be noted that dopamine appears to invigorate rather than initiate motor behavior,^33,34 and spontaneous motor behavior is, in fact, associated with a reduction in the firing rate of midbrain substantia nigra pars compacta neurons in the absence of cues or reward.^32,35

The striatum receives extensive input from dopaminergic neurons from substantia nigra pars compacta and the ventral tegmentum area (VTA) of the basal ganglia. Past studies have almost exclusively focused on measuring dopamine dynamics of neurons in this region. However, anatomical studies have shown that a fraction of dopaminergic neurons in VTA project to all layers of somatosensory cortex, albeit with a bias to layer 5/6,¹⁴ and that these neurons do not extend processes to striatum.¹⁵ Furthermore, neurons in somatosensory cortex broadly express dopamine receptors; while the density of such receptors is highest in deep layers, a significant fraction of cells in the superficial layers express dopamine receptors.^36,37 Global activation of these receptors by the iontophoretic application of dopamine to somatosensory cortex leads to inhibition of activity in approximately half of the neurons measured.³⁸ Our work suggests the importance of further extending studies of dopamine dynamics to a cortical region with known plasticity.¹¹

Our feedback scheme for reinforcement learning is modeled after schemes used in brain-machine interface (BMI) experiments.^39–41 Yet we did not supply cues related to the feedback signal other than the reward. In typical BMI experiments, animals are provided a real-time sensory feedback signal, e.g., an auditory tone,⁴¹ that is modulated by the neuronal activity of interest. In particular, one BMI study found that animals were unable to modulate the neuronal activity toward the reward target in the absence of such cues.⁴¹ In another study that involved learning to move a cursor based on neuronal activity in motor cortex, monkeys first needed to learn the task using their hands to control a physical joystick that moved a cursor on the screen. They then transferred this capability to pure control by neuronal activity. Unlike these BMI studies, we did not supply cues related to the feedback signal other than the reward (Figure 2A). Yet animals were able to perform our task and receive reward. This suggests that animals have an internal sense of [DA]_ex, most likely derived from the normal functioning of DA-GCPRs on cortical cells.

Our results highlight the potential role of internal brain dynamics in modulating as well as creating the spontaneous dopamine events. We observed that reinforcement learning may be used to train animals to initiate extrasynaptic impulses of dopamine in return for a reward (Figures 2 and 3). Pairing of a self-initiated increase of [DA]_ex to a sucrose drop award is learned without a cue across two sessions (Figures 2B and 2C) and is readily unlearned and relearned across sessions (days 4 and 5 in Figure 2C). A minimal theory that posits a generator of impulses with stochastically assigned amplitudes and a hypothetical integrator of impulses above threshold can account for the data. These are judged to be physiologically plausible processes (inset in Figure 3E). We further conjecture that an animal’s sense of spontaneous dopamine impulses may motivate it to search and forage in the absence of known reward-predictive stimuli.^18,42 In this scenario, dopamine serves as a false, albeit stochastic, reward prediction error that motivates search through the role of dopamine as an anticipation signal for a future reward. Successful forages serve to amplify this motivational process. The broad temporal range of spontaneous events (Figures 1F and 3D) is consistent with search strategies.⁴³

In contrast to dopamine impulses, tonic dopamine appears to affect how animals interact with their environment and explore. In particular, manipulations of tonic levels of [DA]_ex modified how animals examined novel stimuli in various operant conditioning tasks^44–47 and the effort that animals were willing to exert to receive reward.^48,49 It is not clear whether tonic and phasic dopamine signals are independently controlled from one another.^50,51 A previous study⁵² found that explicitly modeling tonic dopamine as a separate signal in the reward prediction error signal could reproduce the results of dopamine depletion on the response rate of rats rewarded on a fixed ratio reward schedule. While the authors used the average reward rate as an estimate of tonic dopamine, they note “…we should expect the tonic average reward signal to be used predictively and not only reactively, which would require it to be somewhat decoupled from the actual obtained phasic reward signal.”⁵² Therefore, our results suggest that tonic dopamine can be volitionally modulated independently of sensory stimuli.

A final point is that our focus has been on dopamine because of its well-known role in reward and prediction and the malleability of dopaminergic transmission with training. Yet our experiments do not speak to the possibility that other modulatory systems may also have spontaneous release in cortex. Other modulatory systems may be similarly or even more malleable in terms of volitional control of extrasynaptic neuromodulator concentration via feedback reinforcement training. The current results should be seen as a springboard to motivate and advance studies on the stochastic nature of neuromodulatory systems in general. In as much as the stochastic nature of synaptic release and that of random neuronal firing play a role in all aspects of brain function, including decision making, foraging, and attention,⁵³ the stochastic nature of neuromodulation may add a new dimension to brain dynamics.

STAR*METHODS

Detailed methods are provided in the online version of this paper and include the following:

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by Dr. David Kleinfeld (dk@physics.ucsd.edu).

Materials availability

This study did not generate new unique reagents.

Data and code availability

The datasets supporting the current study, and an associated “read me” file, are available at https://datadryad.org/stash/share/He3oAHCTB6W0fUlaULv2i-WtySJu3LqkQJavqKsLBSo.

The code for the model is available at https://github.com/aljdf/DopamineTransients_Foo2021.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

The Institutional Animal Care and Use Committee at the University of California San Diego approved all protocols. Adult, male C57BL/6 mice, age P30 to P45, were maintained in standard cages on a natural light-dark cycle. For surgery, mice were anesthetized with isoflurane (Butler Schein). Body temperature was monitored and maintained at 37°C. Subcutaneous injections of 5% (w/v) glucose in saline were given every 2 h for rehydration. Buprenorphine (0.02 mg/kg, Butler Schein) was administered i.p. for post-operative analgesia.

METHOD DETAILS

Choice of dopamine indicator

CNiFERs are dual-wavelength sensors. This helps ensure that our measurements were relatively insensitive to motion and bleaching of fluorophores. D2-CNiFERs provide sensitivity from [DA]_ex »2 to 200 nM and have a 2 s temporal resolution.⁶ While single-wavelength genetically-encoded fluorescent probes whose optical properties depend on [DA]_ex, have been developed,^19,20 these are all single wavelength so that it is difficult to compensate for drift. Further, we found that the signal from a current single-wavelength sensor substantially diminished over the multi-day period of our experiments, while that from CNiFERs was stable (Figure S1).

Injection of mice for CNiFER measurements and/or GRAB_DA expression

CNiFER cells were implanted for imaging as described.⁶ GRAB_DA expression was induced by injection of 0.5 – 1.0 uL of 10¹³ μg/ml of an AAV2 virus containing the GRAB_DA sequence under the synapsin promoter.²⁰ The injections were made in frontal somatosensory cortex, 1.5 M/L, 1.5 R/C using a quartz glass pipette. At least three weeks were allowed for expression of the virus. A thin skull craniotomy¹³ was made for animals that did not express GRAB_DA, whereas an open craniotomy was made for animals that expressed GRAB_DA. The craniotomies were 3 – 4 mm in diameter. In GRAB_DA expressing animals, CNiFER cells were injected as close as possible to the GRAB_DA expression area without overlapping or rupturing pial vessels, typically 60 – 100 μm away.

TPLSM imaging

In vivo imaging¹² was performed with a custom-built two-photon laser-scanning microscope.⁵⁴ Two-photon imaging was need to image through the thin skull to minimize the potential for inflammation consistent with high signal to noise ratio.¹³ Control of scanning and data acquisition was achieved through the ScanImage software platform (Vidrio). Excitation light at 840 nm was used to excite the CFP portion of TN-XXL. Fluorescence was collected by a 25X dipping objective (HCX-IRAPO, Leica). The fluorescent signal was split into two channels using a 506 nm long-pass dichroic mirror. Each channel was further bandpass filtered: 465 ± 20 nm for measurement of emission by CFP (F_{465 nm}) and 520 ± 20 nm for emission by YFP (F_{520 nm}) and the change in FRET signal, denoted ΔR(t)/R, was calculated as

$$\frac{\text{ΔR}(t)}{R}=\frac{F_{520\text{nm}}(t)/F_{520\text{nm}}}{F_{465\text{nm}}(t)/F_{465\text{nm}}}-1$$ (Equation 1)

where á F_{520 nm}ñ and á F_{465 nm}ñ refer to the baseline values determined from a LOWESS fit (see Quantification and statistical analysis). Running activity was recorded using a rotary encoder (TRD-S360BD, Koyo Electronics) attached to the underside of a rotation platform (Figures 2A and 3A). Licking activity was recorded using an optical lickometer (Sanworks LLC). The analog signals were recorded using a PowerLab 8.35 device (ADInstruments) acquiring at 1 kHz and synchronized with the two-photon imaging data using the frame trigger output of ScanImage.

Naive only

After one day of recovery from surgery, mice were water deprived (24h/day). Imaging began the following day. The animals were placed in a stationary head-frame fixed on top of a wheel; no lick port pas present nor was a reward or cues were given. The animals were allowed to locomote freely. Each imaging session lasted for one hour, after which the animals were returned to their home cages. Animals were given unrestricted access to water for one hour after imaging. Animals were imaged under identical conditions for four successive days.

Adaptive threshold feedback training

After one day of recovery from surgery, mice were water deprived (24h/day). Imaging began the following day. During the first day of imaging, the animals were placed in a stationary head-frame fixed on top of a wheel with a lick port. No reward or cues were given, and the animals were allowed to lick and run freely. For imaging trials with feedback reinforcement, animals were placed in the same head-frame, but given a reward, 0.1 mL of 10% (v/v) sucrose water, for increasing their measured neuromodulator concentration. Real-time readout of neuromodulator concentration and reward administration were done using custom written ScanImage user functions. Each imaging session lasted for one hour, after which the animals were returned to their home cages. Animals were given unrestricted access to water for one hour after imaging. Animals were imaged once a day for 4 – 6 consecutive days, depending on the optical quality of the CNiFER implants.

Rewards were dispensed using a gravity fed solenoid (VAC-100 PSIG, Parker Instrumentation) system. A 50 mL reservoir of 10% (v/v) sucrose water was hung from a stand, and a solenoid was used to control the flow of liquid coming out of the reservoir. The output of this solenoid was routed to the input of the lick port. A second solenoid controlled the vacuum which was connected to the output of the lick port. The timing and control of both solenoids used a National Instruments board (USB-6211, National Instruments) interfaced with ScanImage. The initial threshold for reward was determined by taking 80% of the average amplitude of spontaneous neuromodulator transients from the first day of imaging data, and the threshold increment was 50% of this initial reward threshold. Reward administration occurred 0.25 s after the detection of the neuromodulator concentration rising above the threshold level, with a minimum delay of 3.5 s between rewards. At a time of 0.5 s after reward administration, a vacuum was activated for 1 s to remove any leftover sucrose water. The reward threshold was increased by the threshold increment whenever a reward was administered. If animals did not receive a reward within 225 s of the previous reward, the reward threshold was decreased by the threshold increment, down to a minimum of the initial threshold.

MODEL

To study the learning dynamics related to stochastic dopamine impulses, we built a phenomenological model of the dopamine transients and their relationship to reward seeking behavior, i.e., licking. In our model, the dopamine concentration, denoted D(t) in the equations rather than the observed [DA]_ex, are taken as a shot noise process. Here, pulses of dopamine follow a Poisson process with rate λ; they decay with timescale τ; and the average amplitude of discrete jumps in D(t) is A. For mathematical tractability we assume the amplitude of each pulse follows an exponential distribution. We write

$$\tau \frac{d}{dt}D(t)=-D(t)+\sum _k{a}_k\delta \left(t-t_k\right),$$ (Equation 2)

where t_k is the time of impulse k, a_k ∼Exp(A), and δ(·) is the Dirac delta function. At steady-state, the dopamine concentrations follow a gamma distribution for this process^25,26

$$\text{P}(D)=\frac{D^{\tau \lambda -1}}{\text{Γ}(\tau \lambda )A^{\tau \lambda }}{\text{e}}^{-\text{D}/A},$$ (Equation 3)

The probability that the dopamine concentration lies above a threshold, denoted θ, is then

$$\text{P}(D>\theta )={\int }_{\theta }^{\infty }dDP(D)=\frac{\gamma (\tau \lambda ,\theta /\text{A})}{\text{Γ}(\tau \lambda )},$$ (Equation 4)

where we have used Γ(·) for the gamma function and γ(·,·) for the incomplete gamma function.

Next we consider the effect of transiently crossing threshold on the rate of dopamine pulses. We assume that there is some stable steady state rate of pulses, denoted λ₀. When the transient dopamine exceeds a threshold, the rate is increased by an amount λ₁, if the pulse arrives in close proximity to a reward. We denote the lag between dopamine pulse and reward by Δ and the width of the learning window by Δ_w. The equation for the change in the dopamine pulse rate reads

$$\frac{d}{dt}\lambda (t)\propto \left({\lambda }_0-\lambda \right)+{\lambda }_1\text{Θ}(D-\theta )e^{-\left|\text{Δ}\right|/{\text{Δ}}_w},$$ (Equation 5)

where Θ(·) is the Heaviside function. We are interested in the steady state behavior of the system, so the timescale of changes in λ, i.e., the proportionality constant in Equation 5, will not enter our analysis.

We similarly assume that the delay Δ relaxes to a baseline value Δ₀ and that every time the dopamine exceeds threshold it changes by some amount Δ₁. This gives,

$$\frac{d}{dt}\text{Δ}(t)\propto \left({\text{Δ}}_0-\text{Δ}\right)+{\text{Δ}}_1\text{Θ}(D-\theta )$$ (Equation 6)

At steady state we set all time-derivatives to zero and use the probability of exceeding threshold to obtain,

$$\text{Δ}={\text{Δ}}_0+{\text{Δ}}_1\frac{\gamma (\tau \lambda ,\theta /A)}{\text{Γ}(\tau \lambda )}$$ (Equation 7)

and

$$\lambda ={\lambda }_0+{\lambda }_1\frac{\gamma (\tau \lambda ,\theta /A)}{\text{Γ}(\tau \lambda )}{e}^{-\left|{\text{Δ}}_0+{\text{Δ}}_1\frac{\gamma (\tau \lambda ,\theta /A)}{\text{Γ}(\tau \lambda )}\right|/{\text{Δ}}_W}$$ (Equation 8)

Equation 8 is a nonlinear equation for the rate of dopamine impulses at steady state as a function of itself, the model parameters, and the threshold θ. We stress that θ should be related to, but is not identical to, the threshold on dopamine set experimentally. The reason is that that threshold changes transiently during learning, and the experiments include baseline changes of the dopamine concentration that are beyond the scope of the model. We therefore solve the equation for λ numerically over a broad range of values for θ. Once λ = λ(θ) is obtained, we compute Δ = Δ (λ, θ) by substituting into Equation 7.

We are interested in the qualitative behavior of the model. Thus four of the six parameters were chosen based on averaging the experimental results over animals without studying the effects of varying the parameter systematically. Specifically, we set λ₀ = 0.01 Hz (Figure 1D), τ = 30 s (Figure 1E), Δ₀ = 5 s (Figure 3E), and Δ₁ = −21 s (Figure 3E); the final assignment is based on the argument that if threshold is exceeded “easily,” the dopamine pulse rate will decay to Δ₀ - Δ₁ (Equation 6). The earliest delay we measured for an animal averaged over one day of the experiment was −16 s, so we set Δ₁ = −21 s. This parameter choice is based on the animal with largest delay since we want the model to apply to all animals during the closed loop learning of Day 2 and Day 3. The remaining two parameters, λ₁ and Δ_w, were fit numerically to data. We focused on positive values of λ₁ because the dopamine rate increases when threshold is crossed, although nontrivial solutions of Equation 7 exist when λ₁ is negative.

We fit the parameters (Δ_ω, λ₁) across the dataset of each animal at Day 2 and Day 3 (insert, Figure 3E) by minimizing the sum of the squared error over all data. We used 1000 values of q between 10⁻⁷ and 10³ that were equally spaced on a logarithmic scale. The lowest sum of squared errors was found for Δ_w = 1.6 s and λ₁ = 0.087 Hz. We note that for some value of the parameters the solution of λ = λ(Δ) is discontinuous, i.e., for some values of Δ there is no corresponding rate λ that solves Equation 8. For the purposes of fitting we linearly interpolated λ = λ(Δ) between the points of discontinuity since the model equations are solved at steady-state while individual animals are measured during the transient process of learning (interpolation indicated by dashed line in inset to Figure 3E).

QUANTIFICATION AND STATISTICAL ANALYSIS

All data analysis was done using MATLAB. TN-XXL fluorescence traces were normalized to baseline intensities measured from an initial period of 600 s at the beginning of each imaging trial during which no reward was given. The neuromodulator concentration was calculated as the fractional change in the FRET ratio.⁶ The FRET response was separated into a baseline and phasic component by performing a LOWESS fit on the data using a window size of 470 s and a step size of 4.7 s. The fitted curve was defined as the baseline (low-frequency) component, and the residual (high-frequency) was defined as the transient component. GRAB_DA fluorescence traces were also normalized to baseline intensities measured from the initial 600 s period without reward. Baseline trends in the GRAB_DA fluorescence traces were corrected using the same method as the FRET response; a LOWESS fit using the same parameters was subtracted from the trace and the residual was used.

Licks were detected from the lickometer data by low pass filtering the lickometer signal, subtracting a 3-sample median filter of the signal and detecting the subsequent rising edges. The licking frequency was calculated by taking a 1 s window around the sample point and counting the number of licks in the window. Running speed was similarly calculated from the encoder signal by detecting both rising and falling edges and counting the number of edges in a 0.235 s window around the sample point.

Significant transient were detected from the transient component of the FRET response as those epochs whose amplitude exceeded 2-times the root-mean-square level of the noise. The amplitude was calculated as the maximum value in each detected transient epoch, and the width was the full width at half maximum amplitude (FWHM) of the transient.

The onset of neuromodulator transients was defined as the point at which the ratio ΔR/R increased by 2-times the root-mean-square level of the baseline noise. The onsets of licking and running bouts were calculated in a similar manner. Onset times were calculated separately for each imaging trial from the average transient-triggered response. The lags of the FRET signal behind the licking and running signals were defined as the difference in the onset time.

All statistics were calculated with a one-sided Student’s t test. Standard box plots were used; the box held the middle quartiles, the colored line indicates the median value, the whiskers denote the full range of the data except for outliers, which are determined by Chauvener’s criterion and shown as separate points.

A linear model was used to fit the FRET response to the licking and running traces.⁵⁵ The transfer function of the model was calculated directly from the power spectra of the respective traces as the cross power divided by the input power. New models were fit for each imaging trial, and the variance explained, i.e., R², was calculated directly from the predicted FRET. Spectral power density and spectral coherence were calculated using multi-taper methods⁵⁶ with a time-bandwidth product of 10 and the Chronux package.⁵⁷

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and virus strains
AAV-hSyn-DA4.4	Yulong Li Laboratory	N/A
Chemicals, peptides, and recombinant proteins
Isoflurane	Henry Schein	Cat. No. 1182097
Buprenorphine Hydrochloride, Injection	MWI Veterinary Supply	Cat. No. 60969
Cyclosporine	Teva Generics	Cat. No. 00093-5742-65
Sucrose	Sigma Aldrich	Cat. No. S0389
Experimental models: cell lines
Human: Cell line HEK293: M1-CNiFER	David Kleinfeld Laboratory	N/A
Human: Cell line HEK293: D2-CNiFER	David Kleinfeld Laboratory	N/A
Experimental models: organisms/strains
Mouse: C57BL/6J	The Jackson Laboratory	RRID: IMSR_JAX:000664
Software and algorithms
MATLAB	MathWorks	RRID: SCR_001622
ScanImage	Vidrio	RRID: SCR_014307
Chronux	Cold Spring Harbor Laboratory	RRID: SCR_005547
Other
Optical Lickometer	Sanworks	Cat. No. 1020
Rotary Encoder	Koyo Electronics	Cat. No. TRD-S360BD
National Instruments USB board	National Instruments	Cat. No. USB-6211
PowerLab/8SP	AD Instruments	RRID: SCR_018833
Solenoid Valve	Parker Instrumentation	Cat. No. 003-0137-900

Highlights.

• Extrasynaptic levels of dopamine in mouse cortex exhibit spontaneous impulses

• Impulses are broadly distributed in amplitude and time, with a rate of about 0.01/s

• Feedback was used to train mice to volitionally control their spontaneous impulses

• Mice learned to reliably modulate dopamine impulses in order to receive a reward