Accuracy of diffuse correlation spectroscopy measurements of cerebral blood flow when using a three-layer analytical model

Abstract

Diffuse correlation spectroscopy (DCS) is a non-invasive optical technology for the assessment of an index of cerebral blood flow (CBFi). Analytical methods that model the head as a three-layered medium (i.e., scalp, skull, brain) are becoming more commonly used to minimize the contribution of extracerebral layers to the measured DCS signal in adult cerebral blood flow studies. However, these models rely on a priori knowledge of layer optical properties and thicknesses. Errors in these values can lead to errors in the estimation of CBFi, although the magnitude of this influence has not been rigorously characterized. Herein, we investigate the accuracy of measuring cerebral blood flow with a three-layer model when errors in layer optical properties or thicknesses are present. Through a series of in silico experiments, we demonstrate that CBFi is highly sensitive to errors in brain optical properties and skull and scalp thicknesses. Relative changes in CBFi are less sensitive to optical properties but are influenced by errors in layer thickness. Thus, when using the three-layer model, accurate estimation of scalp and skull thickness are required for reliable results.

1. Introduction

Adequate cerebral blood flow (CBF) is critical for the delivery of oxygen and nutrients necessary to maintain neuronal health and function. Quantification of CBF can provide a biomarker that can aide in diagnosis, management, and prognosis, particularly in the context of brain injury and diseases associated with ischemia or inadequate cerebrovascular autoregulation [1,2].

Diffuse correlation spectroscopy (DCS) is an optical modality that can be used to quantify an index of cerebral blood flow (CBFi, cm²/s) non-invasively at the bedside. In DCS, a coherent near-infrared source is placed on the forehead, and a photon counting detector is placed some distance away to detect temporal fluctuations in the intensity of multiply scattered reflected light. These measured fluctuations are traditionally related to an index of blood flow in the underlying tissue by modeling the head as a semi-infinite, homogeneous medium [1,2]. Unfortunately, this gross oversimplification of the head geometry can lead to significant signal contamination from extracerebral (skull/scalp) layers, particularly when the depth to the brain is non-negligible [3–7]. To minimize extracerebral signal contributions, multiple studies have highlighted the importance and validated the accuracy of multi-layered models that approximate the head as a series of infinite slabs to separate cerebral signal contributions from extracerebral artifacts [3,4,8–11].

Multi-layered models rely on a priori knowledge of layer optical properties and thicknesses to estimate blood flow within each layer. In theory, layer optical properties (namely, the absorption and reduced scattering coefficients) can be measured with near-infrared spectroscopy (NIRS), and scalp and skull thickness can be assessed from anatomical images obtained via Magnetic Resonance or Computed Tomography [4,10]. In reality, these measures are often not readily available. Thus, optical properties and layer thickness are most commonly assumed from literature. Unfortunately, errors in these assumed values can lead to appreciable errors in the estimation of brain blood flow. Indeed, when using the two-layer model wherein the head is modeled as a cerebral (gray and white matter) and extracerebral (skull, scalp, cerebrospinal fluid) layer, Gagnon et al. demonstrated that errors in the assumed absorption coefficient of the cerebral layer as well as errors in the thickness of the extracerebral layer can significantly confound estimations of CBFi [3].

Although a handful of publications have utilized a two-layer model of the head, recent work suggests that a three-layer model that accounts for scalp, skull, and brain provides a superior fit to measured DCS data and is able to more accurately estimate brain blood flow [4,10]. While it is assumed that the three-layer model would be similarly susceptible to the confounding influences of errors in optical properties and layer thickness as seen by Gagnon et al. in the two-layer model [3], the magnitude of these confounds has yet to be determined. Herein, we investigate the sensitivity of both CBFi and relative changes in CBFi (rCBFi) to inaccuracies in layer optical properties and thicknesses when fitting DCS data to the three-layer solution of the correlation diffusion equation. We hypothesize that while errors in optical properties and layer thickness will significantly confound estimations of CBFi, relative changes in CBFi will be largely insensitive to these errors. To test this hypothesis, we employ a series of in silico experiments wherein data is simulated with either the three-layer slab model or Monte Carlo simulation of photon propagation in a realistic human head geometry.

2. Methods

2.1. Three-layer analytical model simulations

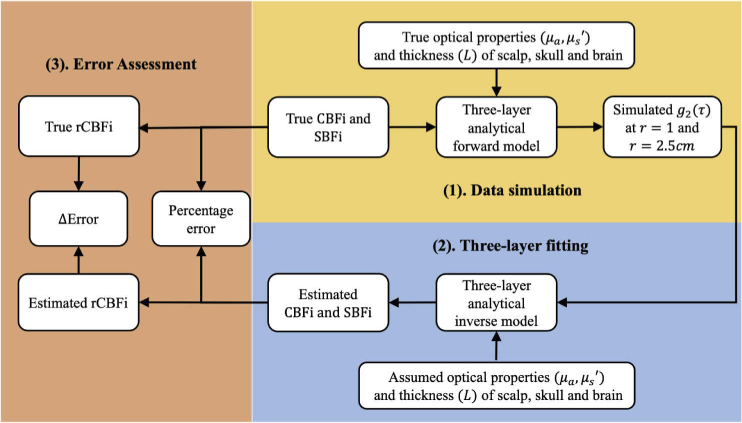
The flow chart of our overall experimental protocol is outlined in Fig. 1. To investigate the influence of inaccuracies in layer optical properties and thicknesses on the estimations of CBFi and rCBFi, we first simulated data across a wide range of physiologically-relevant layer optical properties, thicknesses, and flow indices using the three-layer solution to the correlation diffusion equation. We next fit these simulated data using assumed optical properties and layer thicknesses that differed from the "true", i.e., simulated, values to obtain an estimate for scalp and cerebral blood flow indices. Finally, we calculated the percentage error between the estimated and true values of CBFi, and we also investigated errors between estimated and true rCBFi. Below we detail these experimental steps.

Fig. 1.

Flow chart of experimental protocol. First, we simulated $g_1(\tau )$ at 1 and 2.5 cm for a wide range of physiologically relevant layer optical properties and thicknesses using the three-layer solution to the correlation diffusion equation. Next, simulated data were simultaneously fit for SBFi and CBFi using the three-layer model with assumed optical properties/thicknesses. Finally, we assessed the accuracy of both CBFi and relative changes of CBFi by comparing the estimated and true CBFi and rCBFi.

Data simulation In practice, accurate estimation of layer optical properties and thickness is challenging; thus, values for these parameters are typically assumed from literature. However, the true values for any given subject are likely off from these assumed values. To simulate this typical experimental reality, we first compiled a range of optical properties in the near-infrared range and skull/scalp thicknesses that have previously been reported for the adult human head (Table 1) [12–20]. We independently explored the influence of each parameter in Table 1 by manipulating one parameter at a time and holding all others constant at the middle of the reported ranges. For each parameter, we sampled 11 evenly spaced values within the reported range. For each of these 11 values, we simulated 12 evenly spaced values of CBFi $\in$ [2e-8, 9e-8] cm²/s [10,21] and 6 values of scalp blood flow index (SBFi) $\in$ [1/8, 1/3]×CBFi [22–26]. For each of these parameter combinations, normalized field autocorrelation functions $g_1(r,\tau )$ were simulated at 1 and 2.5 cm, which are commonly used source-detector separations in other DCS studies [21,27–30]. This data was then converted to an intensity autocorrelation function, $g_2(r,\tau )$ , using the Siegert relation with $\beta =0.5$ [31]. Thus, in total, we simulated 12,672 $g_2(\tau )$ curves (8 parameters × 11 values/parameter × 12 CBFi × 6 SBFi × 2 separations = 12,672).

Table 1. Optical properties ( ${\mu }_a$ and ${\mu }_s^{\prime }$ ) and thickness ( $L$ ) for scalp, skull, and brain. For each parameter, we report the range of values that we simulated, the value we assumed when fitting simulated data, and the range of error between simulated and assumed values.

	${\mu }_a$			${\mu }_s^{\prime }$			$L$
	Range (cm−1)	Assumed value (cm−1)	% Error	Range (cm−1)	Assumed value (cm−1)	% Error	Range (cm)	Assumed value (cm)	% Error
scalp	0.05, 0.15	0.10	−33, 100	8,12	10	−16, 25	0.15, 0.53	0.34	−36, 127
skull	0.05, 0.15	0.10	−33, 100	8,12	10	−16, 25	0.35, 1.10	0.73	−34, 107
brain	0.05, 0.25	0.15	−33, 200	2,6	4	−33, 100	$\mathrm{\infty }$

Data were simulated using the three-layer solution to the correlation diffusion equation for the normalized electric field autocorrelation function, $g_1(r,\tau )$ , at delay time $\tau$ and source-detector separation, $r$ [8]:

$$g_1(r,\tau )=\frac{{\int }_0^{\mathrm{\infty }}\widetilde{G_1^0}(s,\tau )s{J}_0(sr)ds}{{\int }_0^{\mathrm{\infty }}\widetilde{G_1^0}(s,0)s{J}_0(sr)ds},$$ (1)

where $J_0$ is zero order Bessel function, and

$$\widetilde{G_1^0}(s,\tau )=\frac{numerator}{denominator},$$

$$\begin{array}{ll}\hfill numerator& ={\beta }_1{D}_1\cosh ({\beta }_1(L_1-z_s))[{\beta }_2{D}_2\cosh ({\beta }_2{L}_2)+{\beta }_3{D}_3\sinh ({\beta }_2{L}_2)]\\ & +{\beta }_2{D}_2[{\beta }_3{D}_3\cosh ({\beta }_2{L}_2)+{\beta }_2{D}_2\sinh ({\beta }_2{L}_2)]\sinh ({\beta }_1(L_1-z_s)),\\ denominator& ={\beta }_2{D}_2\cosh ({\beta }_2{L}_2)[{\beta }_1(D_1+{\beta }_3{D}_3{z}_0)\cosh ({\beta }_1{L}_1)\\ & +({\beta }_3{D}_3+{\beta }_1^2{D}_1{z}_0)\sinh ({\beta }_1{L}_1)]\\ & +\sinh ({\beta }_2{L}_2)[{\beta }_1({\beta }_3{D}_1{D}_3+{\beta }_2^2{D}_2^2{z}_0)\cosh ({\beta }_1{L}_1)\\ & +({\beta }_2^2{D}_2^2+{\beta }_1^2{\beta }_3{D}_1{D}_3{z}_0)\sinh ({\beta }_1{L}_1)].\end{array}$$

Here, $L_i$ is the thickness of layer $i$ , $z_0=1/({\mu }_{a,1}+{\mu }_{s,1}^{\prime })$ , $z_s=1/{\mu }_{s,1}^{\prime }$ , and ${\beta }_i=s^2+3{\mu }_{a,i}{\mu }_{s,i}^{\prime }+6{\mu }_{s,i}^{\prime 2}{k}_{0,i}^2{P}_i⟨\mathrm{\Delta }{r}_i^2(\tau )⟩$ , ${\mu }_{a,i}$ and ${\mu }_{s,i}^{\prime }$ are the absorption and reduced scattering coefficients of layer $i$ , $k_{0,i}$ is the wave number of layer $i$ ( $k_{0,i}=2\pi n_i/\lambda$ , where $\lambda$ is wavelength of light, $n_i$ is the reflect index of layer i), $P_i$ is the probability of scattering off of a moving scattering in the layer $i$ (set to 1 for these simulations), and $⟨\mathrm{\Delta }{r}_i^2(\tau )⟩$ is the mean-square displacement of the moving scatters in layer $i$ , which we assume takes the form of $D_i\tau$ , where $D_i$ is the effective diffusion coefficient (cm²/s) of layer $i$ . Herein, we assumed layer 1 was scalp, layer 2 was skull, and layer 3 was brain. We assumed flow dynamics in the skull layer were negligible, i.e., $D_2=0$ . We define scalp blood flow index (SBFi) as $D_1$ and cerebral blood flow index (CBFi) as $D_3$ .

Estimating CBFi and rCBFi Each simulated data set (consisting of $g_2(\tau )$ at $r=$ 1 and 2.5cm) was fit to Eq. (1) for CBFi and SBFi simultaneously using a single cost function:

$${\chi }^2=\sum _{j=1}^{N_r}\sum _{k=1}^{N_{\tau }}{[g_2(r_j,{\tau }_k,CBF{i}_{true},SBF{i}_{true})-g_2(r_j,{\tau }_k,CBF{i}_{estimated},SBF{i}_{estimated})]}^2$$

Here $N_r$ is the number of detectors (2 for our simulations) and $N_{\tau }$ is the number of $\tau$ s. We minimized ${\chi }^2$ using fminsearchbnd [32] in MATLAB (Mathworks) with bounds for both CBFi and SBFi $\in$ [1e-11,1e-6] cm²/s. For these fits, we assumed fixed values for ${\mu }_{ai}$ , ${\mu }_{si}^{\prime }$ and $L_i$ reported in Table 1.

Because DCS is often used to measure relative changes in cerebral blood flow, we also used our simulated data set to estimate relative changes in CBFi (rCBFi). We define $rCBF{i}_{true}=(CBF{i}_{true}-CBF{i}_0)/CBF{i}_0\times 100\mathrm{\%}$ , where $CBF{i}_0$ =5.2e-8 cm²/s. This choice of baseline CBFi, which led to a simulated range of $rCBF{i}_{true}\in [-61,74]\mathrm{\%}$ , was chosen somewhat arbitrarily, as we found that the choice of baseline does not influence our findings (see Appendix 1). We also define $rCBF{i}_{estimated}=(CBF{i}_{estimated}-CBF{i}_{estimated,0})/CBF{i}_{estimated,0}\times 100\mathrm{\%}$ , where $CBF{i}_{estimated,0}$ is the value obtained by fitting the simulated data at $CBF{i}_0$ .

Finally, we evaluated the accuracy in CBFi and rCBFi. For each simulated dataset, the percentage error in CBFi was defined as $(CBF{i}_{estimated}-CBF{i}_{true})/CBF{i}_{true}\times 100\mathrm{\%}$ . The error in the rCBFi was calculated as $rCBF{i}_{estimated}-rCBF{i}_{true}$ .

2.2. Monte Carlo simulations with a realistic human head geometry

To confirm the results from our three-layer slab simulations, we next performed voxel-based Monte Carlo (MC) simulations [33] using a realistic MRI-based human head atlas from BrainWeb [34,35]. This atlas is segmented into five tissue types: scalp, skull, cerebrospinal fluid (CSF), gray matter, and white matter. For our purposes, we merged CSF, gray matter, and white matter into one tissue type that we refer to herein as brain. The overall experimental protocol for the MC simulated data followed that outlined in Fig. 1; however, instead of using the three-layer model to simulate data, simulations were performed with Monte Carlo eXtreme (MCX) [33] with the head atlas geometry. As in the three-layer simulations, we independently explored the influence of ${\mu }_a$ and ${\mu }_s^{\prime }$ of scalp, skull, and brain layers by manipulating one parameter at a time and holding all others constant at the middle of the literature-reported ranges (Table 1). Unlike the three-layer simulations, we did not simulate a range of scalp and skull thickness given the fixed anatomy of the head atlas. In total we performed 66 simulations with MCX (6 parameters × 11 values/parameter). For these simulations, the anisotropic factor (g) and index of refraction (n) were set to 0.89 [33] and 1.4 [36], respectively, for all layers. Five hundred million photons were launched from a 1 mm diameter source positioned over the right frontal cortex. Detectors (1 mm in diameter) were placed 1 and 2.5 cm from the source. Because MCX limits the total number of detected photons per simulation to 1 million, simulations were run separately for each source-detector separation to ensure a sufficient number of photons were detected by the 2.5 cm detector.

For each detected photon, MCX records the total pathlength traveled and total number of random walk steps. This information was used to calculate the unnormalized electric autocorrelation function $G_1(r,\tau )$ [37],

$$G_1(r,\tau )=\frac{1}{N_p}\sum _{n=1}^{N_p}exp(\sum _{i=1}^{N_{tis}}-\frac{1}{3}{Y}_{n,i}{k}_0^2⟨\mathrm{\Delta }{r}^2(\tau ){⟩}_i)exp(-\sum _{i=1}^{N_{tis}}{\mu }_{a,i}{L}_{n,i}).$$ (2)

Here N_p is the number of detected photons at separation $r$ , ${\text{N}}_{tis}$ is the number of tissue types (3 for our simulations), ${\text{Y}}_{n,i}$ is the dimensionless momentum transfer for the n^th photon in the i^th tissue type, L_n,i is the total path length of n^th photon in i^th tissue type, and ${\mu }_{a,i}$ is the absorption coefficient of the i^th tissue type. As in our three-layer simulations, we assumed the mean square displacement of the $i^{th}$ layer ( $⟨\mathrm{\Delta }{r}^2(\tau ){⟩}_i)$ took the form of $6D_i\tau$ , where $D_i$ is the effective diffusion coefficient of the $i^{th}$ layer. As in the three-layer simulations, we simulated 12 values for CBFi (i.e., D₃) $\in$ [2e-8, 9e-8] cm²/s and 6 values of SBFi (i.e., D₁) $\in$ [1/8, 1/3]×CBFi. We assumed blood flow in the skull is negligible, i.e., D₂ = 0 [25,38]. Thus, in total, we simulated 864 $G_1(\tau )$ curves (6 parameters × 12 CBFi × 6 SBFi × 2 separations = 864). Each simulated $G_1(r,\tau )$ was normalized to $G_1(r,0)$ , and then the Siegert relationship with $\beta$ =0.5 was used to estimate $g_2(r,\tau )$ [31].

Simulated data sets were fit to Eq. (1) for CBFi and SBFi using assumed layer optical properties (Table 1) and measured layer thickness (L_scalp=0.6 cm and L_skull=0.6 cm). Error in CBFi and rCBFi were calculated as in Section 2.1.

3. Results

3.1. CBFi is most sensitive to layer thicknesses and brain optical properties

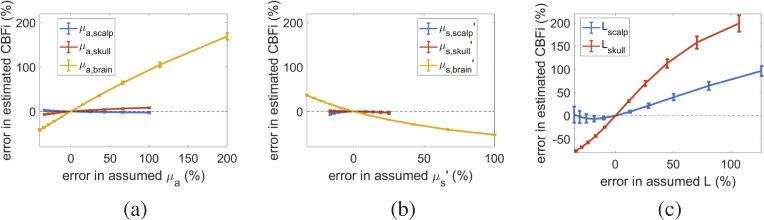
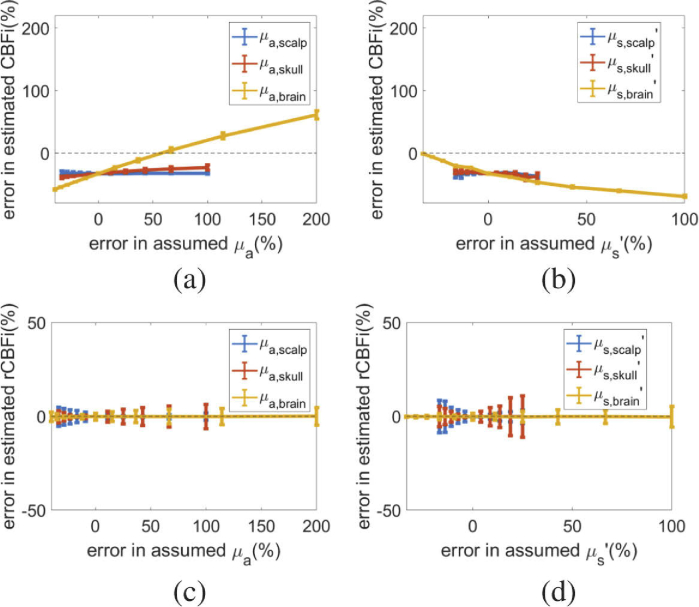
For all 72 CBFi and SBFi combinations tested, we found that inaccuracies of the absorption and reduced scattering coefficients in both the scalp and skull layers have a negligible influence on the estimation of CBFi (average error < 10 $\mathrm{\%}$ , Fig. 2(a,b)). However, inaccuracies of ${\mu }_a$ and ${\mu }_s^{\prime }$ of the brain layer can significantly affect the accuracy of CBFi. Specifically, we found the error in CBFi is approximately linearly proportional to errors in brain ${\mu }_a$ and inversely proportional to errors in brain ${\mu }_s^{\prime }$ . Further, we found that CBFi is highly sensitive to inaccuracies in both scalp and skull thickness (Fig. 2 c). On average, error in CBFi increases monotonically with error in skull thickness, while errors in scalp thickness always lead to an overestimation of CBFi.

Fig. 2.

Error in cerebral blood flow index (CBFi). Error in estimated CBFi as a function of (a) error in assumed absorption coefficient ( ${\mu }_a$ ), (b) error in assumed reduced scattering coefficient ( ${\mu }_s^{\prime }$ ), and (c) error in thickness (L) of scalp (blue), skull (red) and brain (yellow) layers. Data are reported as mean/standard deviation across all combinations of simulated CBFi and SBFi using the three-layer model. The horizontal dotted grey line denotes no error in CBFi.

3.2. Relative changes in CBFi are sensitive to layer thickness

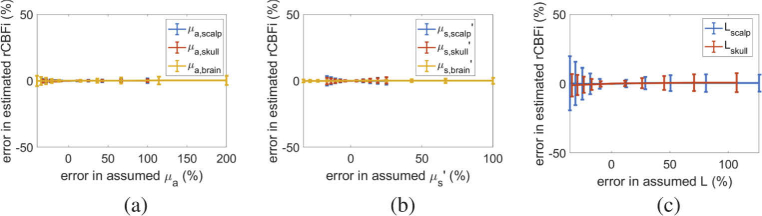
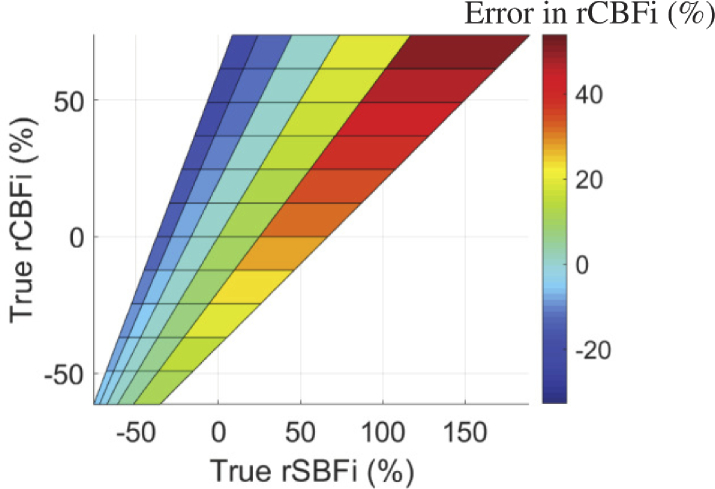
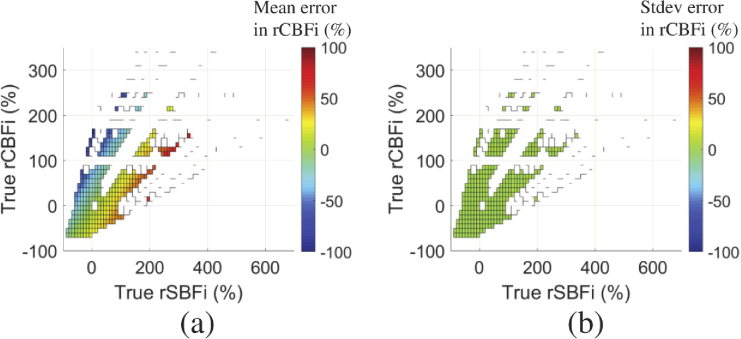
In contrast to CBFi, relative changes in CBFi are insensitive to errors in ${\mu }_a$ and ${\mu }_s^{\prime }$ of all layers (average error < 10 $\mathrm{\%}$ , Fig. 3(a,b)). However, rCBFi can be significantly influenced by errors in layer thickness. While on average, the error in rCBFi as a function of error in assumed skull/scalp thickness is small, there is a large standard deviation across samples of varying rCBFi/rSBFi (Fig. 3(c)). As shown in Fig. 4, the error in rCBFi is heavily influenced by the magnitude of rSBFi.

Fig. 3.

Error in relative change in cerebral blood flow index (rCBFi). Error in estimated rCBFi as a function of (a) error in assumed absorption coefficient ( ${\mu }_a$ ), (b) error in assumed reduced scattering coefficient ( ${\mu }_s^{\prime }$ ), and (c) error in thickness (L) of scalp (blue), skull (red) and brain (yellow) layers. Data are reported as mean/standard deviation across all combinations of simulated rCBFi and rSBFi.

Fig. 4.

Color map of the error in estimated rCBFi obtained when underestimating scalp thickness by ∼35% as a function of the true rCBFi and rSBFi.

3.3. Validation in Monte Carlo simulated data

As shown in Fig. 5, results from Monte Carlo simulations with a realistic head geometry largely confirm the conclusions from the three-layer simulations. Of note, however, we found that when fitting MC data to the three-layer model and using the known layer optical properties and thickness, the estimated CBFi was always underestimated from the true CBFi by ∼30%. The origin of this underestimation is not known, although we posit it may arise from the curvature of the head. This underestimation notwithstanding, we found that errors in ${\mu }_a$ and ${\mu }_s^{\prime }$ of the skull and scalp have a negligible influence on error in CBFi, while errors in brain ${\mu }_a$ and ${\mu }_s^{\prime }$ confound CBFi in the same manner (Fig. 5(a,b)), as observed in Fig. 2 with the three-layer simulations. Despite these errors in CBFi, relative changes of CBFi were minimally influenced by errors in ${\mu }_a$ and ${\mu }_s^{\prime }$ within all layers (Fig. 5(c,d)).

Fig. 5.

Error in CBFi and rCBFi with Monte Carlo simulated data on realistic head geometry. (a-b) Error in estimated CBFi as a function of (a) error in assumed absorption coefficient ( ${\mu }_a$ ) and (b) error in assumed reduced scattering coefficient ( ${\mu }_s^{\prime }$ ) of scalp (blue), skull (red) and brain (yellow) layers. Data are reported as mean/standard deviation across all combinations of simulated CBFi and SBFi. The horizontal dotted grey line denotes no error in CBFi. (c-d) Error in estimated relative changes of CBFi (rCBFi) as a function of (c) error in assumed ${\mu }_a$ and (d) error in assumed ${\mu }_s^{\prime }$ of scalp (blue), skull (red) and brain (yellow) layers. Data are reported as mean/standard deviation across all combinations of simulated rCBFi and rSBFi.

4. Discussion

When estimating brain blood flow in the adult with DCS, a handful of work has demonstrated the relative superiority of modeling the head as a 3-layer slab consisting of scalp, skull, and brain over the homogeneous model that lumps these layers together [4,8,10,25]. However, the added complexity of the 3-layer model requires additional a priori knowledge of numerous parameters, including layer optical properties and thicknesses. While Li et al. qualitatively discussed the influence of uncertainties in these parameters on the determination of blood flow in the bottom layer through intuitive deduction, the magnitude of these influences and how they translate to errors in relative change in CBFi are lacking [8]. In this work, we build upon Li’s preliminary findings to rigorously quantify the influence of inaccuracies in layer optical properties and thicknesses on estimation of cerebral blood flow index and relative changes in this index when using the three-layer analytical model to fit measured DCS data taken on the human head.

We find that CBFi is largely insensitive to errors in optical properties ( ${\mu }_a$ , ${\mu }_s^{\prime }$ ) of the skull and scalp layers; however, CBFi is greatly influenced by errors in ${\mu }_a$ and ${\mu }_s^{\prime }$ of the brain layer (Fig. 2(a,b)). Specifically, error in CBFi is positively correlated with errors in brain ${\mu }_a$ and inversely correlated with errors in brain ${\mu }_s^{\prime }$ . In contrast, relative changes in CBFi are insensitive to errors in optical properties of all layers (Fig. 3(a,b) and Fig. 5(c,d)). This result aligns well with Li et al. [8], which posited that the influence of scalp and skull optical properties on CBFi should be minimal since it mainly affects the decay of $g_2(\tau )$ at long delay times, and that underestimations of brain ${\mu }_a$ will lead to underestimation of CBFi.

Another significant source of error in the estimation of both CBFi and relative change in CBFi came from errors in scalp and skull thickness. Error in CBFi is positively correlated with errors in skull thickness, with an underestimation of skull thickness leading to an underestimation of CBFi, whereas both under- and over-estimations in scalp thickness can lead to overestimations of CBFi (Fig. 2(c)). For rCBFi, the average error across all combinations of rSBFi and rCBFi is negligible despite errors in skull and scalp thickness; however, there is a large standard deviation in this rCBFi error, meaning that for some combinations of rSBFi and rCBFi, the error in rCBFi due to errors in skull and/or scalp thickness can be quite large (>50%, Fig. 4). These results align with a former investigation of the two-layer model that found estimation of relative changes of blood flow index of the deep layer are most sensitive to the inaccuracies in thickness of the top layer [3].

Taken together, when employing the three-layer model to fit for CBFi, these results suggest it is best practice to measure the optical properties of the brain layer (e.g., via frequency-domain near-infrared spectroscopy [17] or time-domain near-infrared spectroscopy [26,39]) and the thickness of scalp and skull layers (e.g., via anatomical images obtained from computed tomography or magnetic resonance [4,10]). For recovery of relative changes in CBFi, accurate estimation of brain optical properties is not necessary; however accurate quantification of skull and scalp thicknesses is needed if quantification of rCBFi to within ∼25% is desired. If this information is not available, results should be interpreted with caution.

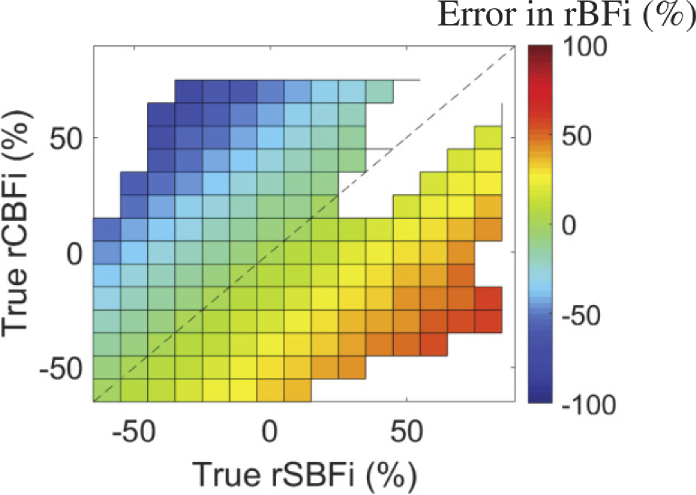
Several investigations have demonstrated that the homogeneous model leads to underestimation of relative changes of CBFi because of signal contamination from extracerebral layers, thus emphasizing the importance of the three-layer model [4,10]. Nevertheless, numerous DCS validation studies have employed the homogeneous model and have shown strong agreement between relative changes in blood flow measured with DCS and relative changes in brain blood flow measured by other perfusion modalities [40–42]. We observed a special case that help explain this apparent discrepancy, i.e., an underestimation of brain blood flow with the homogeneous model yet strong agreement with other perfusion modalities. In our simulations, we found that when scalp and brain blood flow change by the same fractional amount, the homogeneous model can accurately estimate relative changes in CBFi (Appendix 2). Given that several DCS validation studies were performed with interventions that alter both scalp and cerebral blood flow, e.g., manipulation of arterial blood pressure or carbon dioxide tension [40,41,43], this finding may help explain the good agreement observed in former validation experiments that used the homogeneous model.

Our study has several limitations. First, we note that our relative changes in estimated CBFi do not account for changes in optical properties between baseline and activation states. Certainly, brain ${\mu }_a$ may change due to various interventions (e.g, functional activation) that are also known to influence perfusion, and these changes may induce further uncertainty in rCBFi if they are not adequately accounted for. If the absorption coefficient in the brain increases from baseline, we would overestimate relative changes of CBFi by assuming a fixed ${\mu }_a$ . In contrast, changes in ${\mu }_a$ of the scalp will have significantly less influence on the estimation of relative changes of CBFi. Second, while the three-layer model is a vast improvement over the more commonly employed homogeneous model, it ignores the curvature of the head, heterogeneity in layer optical properties and perfusion, as well as heterogeneity in skull and scalp thickness. Moreover, it does not consider the influence of cerebral spinal fluid, a non-scattering layer of low-absorbing fluid with negligible blood flow that may significantly confound the estimation of CBFi [7]. Recently, Wu et al. employed a Monte Carlo-based fitting method using a realistic head geometry to estimate brain blood flow that overcomes several of these limitations [25]. However, given the complexity of this approach, which requires segmentation of anatomical MR images, and considering the relative ease of implementing the three-layer model, we find that the three-layer model is a good choice for estimating relative changes of CBFi. Another limitation of our study is that the simulations are limited to two source-detector separations (1 and 2.5cm). Of course, the error in CBFi and rCBFi will be dependent on the choice of source-detector separations; this influence of source-detector separation will be rigorously characterized in future work. Finally, we note that we did not consider measurement noise in our simulations. Because both noise in the measured signal and inaccuracies in the assumed parameters can cause errors in estimation of CBFi, an investigation without noise enables us to isolate the influences caused by errors in optical properties/thickness from that of noise. Future work can investigate the influence of noise on the accuracy of CBFi and rCBFi estimations with the three-layer model by using the noise model developed in [44] or through $\mathit{\text{in vitro}}$ experiments with layered optical phantoms with known dynamic properties.

5. Conclusion

In summary, this investigation demonstrates that accurate estimation of CBFi with the three-layer solution to the correlation diffusion equation relies on a priori knowledge of brain optical properties as well as skull and scalp thickness. Estimation of relative changes in cerebral blood flow index is insensitive to layer optical properties, although it can be influenced by errors in scalp and skull thickness. Thus, we recommend that without measurement of layer thickness and brain optical properties, results obtained form the three-layer model should be interpreted with caution.

Appendix 1: Choice of baseline CBFi does not influence estimation of errors in relative change in CBFi

For the results shown in Fig. 3, we arbitrarily chose one baseline to calculate rCBFi. To demonstrate that the choice of baseline does not the influence error in rCBFi, we focus on the case when scalp thickness is underestimated by ∼35%, i.e., when the largest variation in error of rCBFi is observed in Fig. 3. Using the 72 datasets simulated at this scalp thickness underestimation (consisting of 12 CBFi × 6 CBFi/SBFi ratios), we calculate the relative change in CBFi of the i^th sample using the j^th sample as baseline: $rCBF{i}_{true,ij}=(CBF{i}_{true,i}-CBF{i}_{true,j})/CBF{i}_{true,j}\times 100\mathrm{\%}$ . We then calculate the estimated relative change in rCBFi as $rCBF{i}_{estimated,ij}=(CBF{i}_{estimated,i}-CBF{i}_{estimated,j})/CBF{i}_{estimated,j}\times 100\mathrm{\%}$ , where here $CBF{i}_{estimated,i}$ is the value of CBFi obtained when fitting the sample with $CBF{i}_{true,i}$ . Finally, we calculate the error in rCBFi as $Erro{r}_{ij}=rCBF{i}_{estimated,ij}-rCB{F}_{true,ij}$ . We find that the standard deviation in this error across samples with the same rCBFi_true and rSBFi_true (but different baselines) is < $5\mathrm{\%}$ (Fig. 6(b)), suggesting that the choice of baseline does not affect the error in rCBFi.

Fig. 6.

Error in relative change in cerebral blood flow (rCBFi) when underestimating scalp thickness by ∼35%. (a) Mean error in estimated rCBFi across samples of differing baseline CBFi and SBFi as a function of true rCBFi and true rSBFi. (b) Standard deviation of the error in estimated rCBFi across samples of differing baseline CBFi and SBFi as a function of true rCBFi and rSBFi. Missing data points are due to the limited combinations of CBFi and SBFi that were simulated.

Appendix 2. Semi-infinite homogeneous model can be used to accurately estimate relative changes in CBFi under unique conditions

In this section, we demonstrate that the semi-infinite homogeneous model can accurately estimate relative changes in CBFi in the special case wherein SBFi and CBFi change by the same fractional amount. We used the three-layer model (Eq. (1)) to simulate 72 $g_2(r=2.5cm,\tau )$ curves (12 CBFi × 6 SBFi/CBFi ratios), assuming layer optical properties and thicknesses fixed at the assumed values in Table 1. Next, we fit each simulated curve for a blood flow index (BFi) using the semi-infinite, homogeneous solution to the correlation diffusion equation [31], assuming a homogeneous absorption coefficient ( ${\mu }_a$ = 0.2 $c{m}^{-1}$ ) and reduced scattering coefficient ( ${\mu }_s^{\prime }$ = 10 $c{m}^{-1}$ ). For each simulated curve, we calculated a true relative change in CBFi of the i^th sample using the j^th sample as baseline as $rCBF{i}_{true,ij}=(CBF{i}_{true,i}-CBF{i}_{true,j})/CBF{i}_{true,j}\times 100\mathrm{\%}$ . We then calculated the corresponding estimate of relative change in BFi as $rBF{i}_{estimated,ij}=(BF{i}_{estimated,i}-BF{i}_{estimated,j})/BF{i}_{estimated,j}\times 100\mathrm{\%}$ , where here $BF{i}_{estimated,i}$ is the value of BFi obtained when fitting the sample with $CBF{i}_{true,i}$ . Finally, we calculated the error in rBFi as $Erro{r}_{ij}=rBF{i}_{estimated,ij}-rCB{F}_{true,ij}$ . We found that the while the $Erro{r}_{ij}$ in rBFi can be quite appreciable, in the unique case where rCBFi_true = rSBFi_true, the error in rBFi is negligible (< 5%, Fig. 7), suggesting that the semi-infinite homogeneous model can accurately relative changes in CBFi when CBFi and SBFi change same fractional amount.

Fig. 7.

Homogeneous model accurately estimates relative change in BFi (rBFi) when scalp and brain flow change by the same fractional amount. Color map of the error in estimated rBFi obtained with the homogenous model as a function of true rCBFi and rSBFi. Missing data points are due to the limited combinations of CBFi and SBFi that were simulated. Dotted line denotes the line of unity where rCBFi = rSBFi

Funding

National Institutes of Health10.13039/100000002 (F31HL154703 (ES), RO1-HL152322(EMB)).

Disclosures

The authors declare no conflicts of interest.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.